Решение задач линейного программирования в MS Excel. С помощью какой команды можно решать простые задачи оптимизации в ms excel
Решение задач линейного программирования в MS Excel
Инструментом для решений задач оптимизации в MS Excel служит надстройка «Поиск решения». Процедура поиска решения позволяет найти оптимальное значение формулы, содержащейся в ячейке, которая называется целевой. Эта процедура работает с группой ячеек, прямо или косвенно связанных с формулой в целевой ячейке. Чтобы получить по формуле, содержащейся в целевой ячейке, заданный результат, процедура изменяет значения во влияющих ячейках.
Если данная надстройка установлена, то «Поиск решения»запускается из меню «Сервис». Если такого пункта нет, следует выполнить команду «Сервис — Надстройки...» и выставить флажок против надстройки «Поиск решения».
Решение задачи оптимизации состоит из трёх этапов.
A. Создание модели задачи оптимизации.
B. Поиск решения задачи оптимизации.
C. Анализ найденного решения задачи оптимизации.
Рассмотрим подробнее эти этапы.
Этап А.
На этапе создания модели вводятся обозначения неизвестных, на рабочем листе заполняются диапазоны исходными данными задачи, вводится формула целевой функции.
Этап В.
Команда «Сервис — Поиск решения» открывает диалоговое окно «Поиск решения», в котором, в свою очередь, имеются следующие поля:
«Установить целевую ячейку» — служит для указания целевой ячейки, значение которой необходимо максимизировать, минимизировать или установить равным заданному числу. Эта ячейка должна содержать формулу.
«Равной» — служит для выбора варианта оптимизации значения целевой ячейки (максимизация, минимизация или подбор заданного числа). Чтобы установить число, введите его в поле.
«Изменяя ячейки» — служит для указания ячеек, значения которых изменяются в процессе поиска решения до тех пор, пока не будут выполнены наложенные ограничения и условие оптимизации значения ячейки, указанной в поле «Установить целевую ячейку».
«Предположить» — используется для автоматического поиска ячеек, влияющих на формулу, ссылка на которую дана в поле «Установить целевую ячейку». Результат поиска отображается в поле «Изменяя ячейки».
«Ограничения» — служит для отображения списка граничных условий поставленной задачи.
«Добавить» — служит для отображения диалогового окна «Добавить ограничение».
«Изменить» — служит для отображения диалоговое окна «Изменить ограничение».
«Удалить» – служит для снятия указанного ограничения.
«Выполнить» – служит для запуска поиска решения поставленной задачи.
«Закрыть» — служит для выхода из окна диалога без запуска поиска решения поставленной задачи. При этом сохраняются установки сделанные в окнах диалога, появлявшихся после нажатий на кнопки «Параметры, Добавить, Изменить или Удалить».
«Параметры» — служит для отображения диалогового окна «Параметры поиска решения», в котором можно загрузить или сохранить оптимизируемую модель и указать предусмотренные варианты поиска решения.
«Восстановить» — служит для очистки полей окна диалога и восстановления значений параметров поиска решения, используемых по умолчанию.
Для решения задачи оптимизации выполните следующие действия.
1. В меню «Сервис» выберите команду «Поиск решения».
2. В поле «Установить целевую ячейку» введите адрес или имя ячейки, в которой находится формула оптимизируемой модели.
3. Чтобы максимизировать значение целевой ячейки путем изменения значений влияющих ячеек, установите переключатель в положение, соответствующее максимальному значению.
Чтобы минимизировать значение целевой ячейки путем изменения значений влияющих ячеек, установите переключатель в положение соответствующее минимальному значению.
Чтобы установить значение в целевой ячейке равным некоторому числу путем изменения значений влияющих ячеек, установите переключатель в положение значению и введите в соответствующее поле требуемое число.
4. В поле «Изменяя ячейки» введите имена или адреса изменяемых ячеек, разделяя их запятыми. Изменяемые ячейки должны быть прямо или косвенно связаны с целевой ячейкой. Допускается установка до 200 изменяемых ячеек.
Чтобы автоматически найти все ячейки, влияющие на формулу модели, нажмите кнопку «Предположить».
6. Нажмите кнопку «Выполнить».
7. Чтобы сохранить найденное решение, установите переключатель в диалоговом окне Результаты поиска решения в положение «Сохранить найденное решение».
Чтобы восстановить исходные данные, установите переключатель в положение «Восстановить исходные значения».
Этап С.
Для вывода итогового сообщения о результате решения используется диалоговое окно «Результаты поиска решения».
Диалоговое окно «Результаты поиска решения» содержит следующие поля:
«Сохранить найденное решение» - служит для сохранения найденного решения во влияющих ячейках модели.
«Восстановить исходные значения» — служит для восстановления исходных значений влияющих ячеек модели.
«Отчеты» — служит для указания типа отчета, размещаемого на отдельном листе книги.
«Результаты» - используется для создания отчета, состоящего из целевой ячейки и списка влияющих ячеек модели, их исходных и конечных значений, а также формул ограничений и дополнительных сведений о наложенных ограничениях.
«Устойчивость» - используется для создания отчета, содержащего сведения о чувствительности решения к малым изменениям в формуле (поле «Установить целевую ячейку», диалоговое окно «Поиск решения») или в формулах ограничений.
«Ограничения» - используется для создания отчета, состоящего из целевой ячейки и списка влияющих ячеек модели, их значений, а также нижних и верхних границ. Такой отчет не создается для моделей, значения в которых ограничены множеством целых чисел. Нижним пределом является наименьшее значение, которое может содержать влияющая ячейка, в то время как значения остальных влияющих ячеек фиксированы и удовлетворяют наложенным ограничениям. Соответственно, верхним пределом называется наибольшее значение.
«Сохранить сценарий» — служит для отображения диалогового окна Сохранение сценария, в котором можно сохранить сценарий решения задачи, чтобы использовать его в дальнейшем с помощью диспетчера сценариев MS Excel.
Одной из возможных задач и моделей линейной оптимизации является задача о планировании производства.
Предприятие должно производить изделия видов: , причем количество каждого выпускаемого изделия не должно превысить спрос и одновременно не должно быть меньше запланированных величин соответственно. На изготовление изделий идет m видов сырья , запасы которых ограничены соответственно величинами Известно, что на изготовление i-ro изделия идет единиц j-го сырья. Прибыль, получаемая от реализации изделий равна соответственно . Требуется так спланировать производство изделий, чтобы прибыль была максимальной и при этом выполнялся план на производство каждого изделия, но не превышался спрос на него.
Аналитическая математическая модель. Обозначим через количества единиц изделий , выпускаемых предприятием. Прибыль, приносимая планом (целевая функция), будет равна:
.
Ограничения на выполнение плана запишется в виде: для . Чтобы не превысить спрос, надо ограничить выпуск изделий: для . И, наконец, ограничения на сырье запишутся в виде системы неравенств:
при условии, что неотрицательны.
Похожие статьи:
poznayka.org
Решение прикладных задач в Excel
Разделы: Информатика
Цель урока:
- Познакомить с основными технологическими приемами при решении задач оптимизации;
- Приобрести навыки работы с надстройками Excel;
- Научить использовать инструменты Excel Поиск решения и Подбор параметра.
Задача учителя: Показать приемы использования функций Excel Поиск решения и Подбор параметра.
Методика проведения урока
Excel позволяет не только производить расчеты, но и решать сложные задачи из различных сфер деятельности, такие как решение уравнений, задачи прогнозирования и оптимизации и другие. Решение задач такого вида может быть осуществлено с помощью инструмента Поиск решения.
Формулировка таких задач может представлять собой систему уравнений с несколькими неизвестными и набор ограничений на решения. Поэтому решение задачи надо начинать с построения соответствующей модели.
Для того чтобы надстройка Поиск решения загружалась сразу при запуске Excel:
- Выберите команду Кнопка Office, Параметры Excel;
- В диалоговом окне слева выберите команду Надстройки, а справа выделите команду Поиск решения и нажмите ОК.
Для того чтобы команда Подбор параметра находилась на панели быстрого доступа необходимо:
- Выберите команду Кнопка Office, Параметры Excel;
- Слева в диалоговом окне выберите команду Настройки, справа – все команды и ОК;
- В окне команд выберите команду Подбор параметра и нажмите Добавить.
Познакомимся с этими командами на примере.
Задача. Предположим, что мы решили производить 2 вида полок А и В. На изготовление модели А требуется 3 м3 досок, на изготовление модели В - 4 м3 досок. За неделю можно получить не более 1800 м3 досок. На изготовление модели А требуется – 15 минут, модели В – 30 минут. Рабочая неделя для 4 сотрудников составляет 160 часов. Сколько полок А и В надо изготовить, чтобы получить максимальную прибыль, если полка А стоит 3500 рублей, полка В – 4800 рублей.
Технология работы:
- Запустите табличный процессор Excel.
- Заполните
таблицу в соответствии с образцом:
А
В
1
Наименование
2
А
3
В
4
5
Прибыль
6
7
Затраты на материалы
8
Затраты по времени
9
- Щелкните правой кнопкой мыши по ячейке В2 и переименуйте ее в x, так как сначала у нас количество полок вида А равно x. Аналогично переименуйте ячейку В3 в y.
- Целевая функция, определяющая нашу прибыль, выглядит следующим образом: ПРИБЫЛЬ=3500*x+4800*y.
- Затраты по материалам равны 3*x+4*y. Затраты по времени равны 0,25*x+0,5*y.
- Выделим
ячейку В5 и выберем меню Данные, после чего активизируем команду Поиск решения. Заполним
ячейки этого окна следующим образом:
и нажмем Выполнить. Если все сделано правильно, то решение будет таким, как указано ниже:
Введем эти данные в нашу таблицу и получим:
|
|
||
|
1 |
Наименование |
|
|
2 |
А |
|
|
3 |
В |
|
|
4 |
|
|
|
5 |
Прибыль |
=3500*x+4800*y |
|
6 |
|
|
|
7 |
Затраты на материалы |
=3*x+4*y |
|
8 |
Затраты по времени |
=0,25*x+0,5*y |
|
9 |
|
|
Из решения видно, что оптимальный план выпуска полок составляет 520 штук вида А и 60 штук вида В. Полученная максимальная прибыль составит 2108000 рублей.
Покажем применение еще одной команды для решения этой задачи. Пусть мы хотим получать максимальную прибыль в размере 2500000 рублей. Используем функцию Подбор параметра для определения новых значений. Выберем эту команду и заполним ячейки окна следующим образом:
и нажмем ОК. Получим следующее решение:
В данном случае изменяли количество полок вида В. Заметим, что необходимо увеличить затраты по времени и затраты по материалам, т.е. надо получать не менее 2127 м3 досок в неделю.
Можно выбрать в качестве Изменяя значения ячейки количество полок вида А.
Тогда при решении получим следующие значения:
В данном случае также необходимо будет увеличить затраты на материалы – потребуется 2136 м3 досок и затраты по времени.
Анализ данного примера показывает, что с помощью Excel можно решать различные экономические задачи. Можно найти все оптимальные решения и выбрать наиболее подходящее с точки зрения дополнительных критериев.
Т. о. рассматривается важная задача, как формирование умений и навыков при решении практических задач в экономике.
Литература:
1. Макарова, Н. В. Информатика. Задачник по моделированию. - 9 класс. – СПб.: Питер, 2001.
2. Чернов, А. А., Чернов, А. Ф. Информатика. Сборник элективных курсов. – 9 класс. – Волгоград: Учитель, 2007.
Поделиться страницей:xn--i1abbnckbmcl9fb.xn--p1ai
Решение задач на оптимизацию с помощью MS EXEL
Надстройка MS Excel "Поиск решений" позволяет решать широкий круг задач на оптимизацию. Думаю, многие посетители сайта изучали в институте линейное программирование или исследования операций. "Поиск решений" в Excel позволяет в считанные секунды находить оптимальные решения достаточно сложных моделей, кстати не только линейных, без знания алгоритмов и длительных рутинных итерраций.Оптимизационные модели широко используются в экономике и технике. Среди них задачи подбора сбалансированного рациона питания, оптимизации ассортимента продукции, транспортная задача и пр., и пр.
Модели всех задач на оптимизацию состоят из следующих элементов:
1. Переменные - неизвестные величины, которые нужно найти при решении задачи.
2. Целевая функция - величина, которая зависит от переменных и является целью, ключевым показателем эффективности или оптимальности модели.
3. Ограничения - условия, которым должны удовлетворять переменные.
Поиск решения такой модели рассмотрим на примере вопроса, поступившего на форум. Итак, сам вопрос:
Издательский дом «Геоцентр-Медиа» издает два журнала: «Автомеханик» и «Инструмент», которые печатаются в трех типографиях: «Алмаз-Пресс», «Карелия-Принт» и «Hansaprint» (Финляндия), где общее количество часов, отведенное для печати и производительность печати одной тысячи экземпляров ограничены и представлены в следующей таблице: Спрос на журнал «Автомеханик» составляет 12 тысяч экземпляров, а на журнал «Инструмент» -не более 7,5 тысячи в месяц. Определите оптимальное количество издаваемых журналов, которое обеспечит максимально выручку от продажи.
Давайте разберемся, что здесь является переменными, что целевой функцией, что ограничениями.
Найти нам необходимо оптимальное количество издаваемых журналов каждого вида. А издавать их можно в трех типографиях на разных условиях. Вот и получается, что нам необходимо определить размер тиража каждого журнала напечатанного в каждой типографии. Это и будут наши переменные.
По какому принципу их подбирать, что считать эффективным, что нет. Перед нами поставлена задача получить максимальную выручку. Таким образом, цель - максимальная выручка.
Теперь ограничения. В условиях сказано, что каждая типография может выделить на наш тираж только определенное время. Длительность печати тысячи единиц тиража каждого журнала каждой типографией известна.
Таким образом, произведение объема тиража на длительность печати тысячи единиц для каждой типографии не может быть больше заданного количества времени.
Еще одно важное ограничение, о котором обычно забывают - переменные должны быть неотрицательными.
Попытаемся представить модель в Excel.
Переменные, то есть объем тиража, находятся в ячейках B10:C12. Целевая функция - в ячейке D13. Обратите внимание, целевая функция построена формулой, ссылаясь на ячейки с переменными и исходные данные (стоимость единицы тиража).
Также формулами подсчитывается фактическое время печати тиража в каждой из типографий (ячейки E3:E5).
Все готово, приступаем решению задачи с помощью надстройки.
Включается она через меню Сервис - Поиск решений. Если такого пункта меню нет, войдите в меню Сервис - Надстройки и отметьте галочкой соответствующую надстройку. Может понадобиться установочный комплект Office.
Перед Вами появится следующий диалог:
Здесь указываем адрес целевой ячейки, отмечаем, что ее нужно привести к максимальному значению, изменяя ячейки $B$10:$C$12. Диапазоны можно указывать мышью - станьте в нужное поле диалога и выделите на листе нужные ячейки. Адрес автоматически попадет в диалог.
Добавляем ограничения. После нажатия кнопки Добавить появляется диалог:
Вспоминаем. У нас фактическое время печати тиража в каждой типографии не может превышать заданного лимита.
Для Алмаз-Пресс ограничение будет таким E3 <= D3. В ячейке E3 должна быть формула суммы продолжительности печати тиража первого и вторго журналов в этой типографии, полученной перемножением тиража на норму времени.
Думаю, понятно, как ввести в диалог описанное ограничение.
Если нажать Ок, ограничение будет добавлено, а диалог закроется. Чтобы несколько раз не открывать диалог, сделана кнопка Добавить. Ограничение сохраняется, а диалог очищается для добавления следующего ограничения. Аналогично добавляем ограничения для оставшихся типографий.
Ограничения неотрицательности можно также задать с помощью этого диалога - для каждой ячейки с объемом тиража установить ограничение >=0.
Но учитывая, что такие ограничения встречаются в задачах на оптимизацию слишком часто, разработчики надстройки предусмотрели возможность быстрой установки ограничения неотрицательности для всех переменных модели. Нажимаем Ok, возвращаемся в первый диалог и нажимаем кнопку Параметры.
Здесь достаточно отметить галочку Неотрицательные значения.
Все модель готова к расчету:
Нажимаем Выполнить.
Через пару секунд Вы будете иметь оптимальное решение.
Теперь выберите Сохранить решение и нажмите Ok.
Можете проверить решение, пробуя подставлять другие значения тиража, перераспределяя тираж между типографиями. Вряд ли Вам удастся улучшить результат.
Конечно, результат не стопроцентный. Бывают слишком сложные модели, модели совсем не имеющие решений (модели с несходимыми ограничениями). Кроме того, если Вы обратили внимание, в параметрах модели можно задать максимальное время решения, число итерраций, точность и другие установки. Но это для профессионалов.
Что радует, все настройки модели (целевая ячейка, область переменных, ограничения, параметры) сохраняются в книге и при изменении исходных данных их не нужно вводить заново. Достаточно открыть надстройку и запустить повторный поиск решения.
stud24.ru
Решение задач в Excel с помощью средств «Поиск решения» и «Подбор параметра»
Excel имеет большие возможности для работы с различными математическими средствами, позволяющими решать самые разнообразные инженерно-технические и научные задачи. Большинство из них не входят в базовый набор функций Excel, а подключаются дополнительно. Подключение осуществляется через кнопку Officeв меню кнопки Параметры Excel → Настройки. Выберите из меню строки Управление (нижний правый угол окна) Надстройки Excelи нажмите кнопку Перейти. В открывшемся окне выберите необходимые надстройки.
Основные надстройки, поставляемые вместе с пакетом Excel:
– Пакет анализа. Мощный инструмент обработки статистических данных, обеспечивающий дополнительные возможности для анализа.
– Мастер суммирования. Позволяет автоматизировать создание формул для суммирования данных в столбце таблицы и использовать частичные суммы.
– Мастер подстановок. Автоматизирует создание формулы для поиска данных в таблице по названию столбца и строки и позволяет использовать поиск с параметром.
– Поиск решения. Используется для решения уравнений и задач оптимизации.
Средство Поиск решения.Запускается командой Данные → Анализ → Поиск решения. Элементы диалогового окна:
установить целевую ячейку –адрес ячейки с целевой функцией;
равной – значение, к которому стремиться целевая функция;
изменяя ячейки –адреса влияющих ячеек;
параметры –открывает окно для задания ограничений на значения влияющих ячеек.
Средство Подбор параметра.Запускается командой Данные → Работа с данными → Анализ «что-если» → Подбор параметра.
Практическая часть
Задание 5.12. Решить систему нелинейных уравнений с помощью средства Поиск решения.
(1)
Выполнение.
В основу метода решения системы нелинейных уравнений положено то, что геометрически решения системы (1) описывают точки пересечения прямой ( ) с окружностью ( ) радиуса равному . Решения заданной системы удовлетворяют и следующему уравнению:
(2)
Вместо системы (1) будем решать уравнение (2). Решений будет два.
Чтобы применить метод Поиск решения необходимо, предварительно, найти начальное приближение решений. Для этого построим таблицу значений левой части уравнения (2) по переменным х и у на интервале (– 1.7; +1.7) с шагом 0.3. Границы интервала взяты на основании того, что корни уравнения лежат внутри круга, радиус которого приблизительно равен =1.73.
Для построения таблицы выполняем:
1. В ячейки А2:А14 вводим значения х (в интервале [–1.7, 1.7]), а в ячейки В1:N1 – значения y в таком же интервале.
2. В ячейку В2 вводится формула =($A2^2+B$1^2-3)^2+(2*$A2+3*B$1-1)^2 –уравнение (2).
3. Копируем формулу ячейки B2 вдиапозон B2:N14.
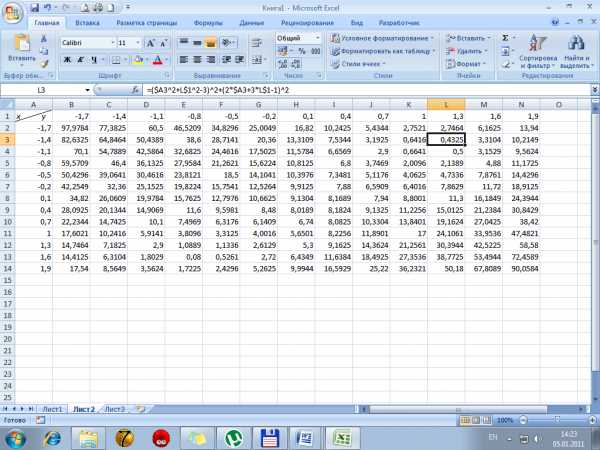
В соответствии с формулой (2) за начальные значения х и y берутся значения в тех ячейках заполненного диапазона, где функция принимает наименьшие значения. Под значения первого корня отводим ячейки А16:В16, а А17:В17 – под значения второго корня.
Для системы (1), в соответствии с полученной таблицей первое минимальное значение 0,4325. В ячейку А16мы вводим 1.3 – значение x, в В16 – 1.4 – значение y. В ячейку С16 вводим формулу =(А16^2+В16^2-3)^2+(2*A16+3*B16-1)^2.
Открываем окно Поиска решенийи устанавливаем: Целевая ячейка – $C16; Изменяя ячейки – $A16:$B16; установить параметр – Минимальному значению. Нажимаем кнопку Выполнить.
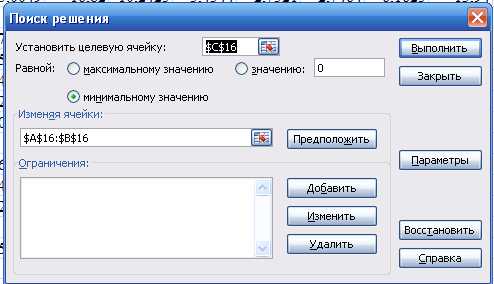
Значение корней уравнения появятся в ячейках А16 и В16. Второй корень находим аналогично, взяв следующее наименьшее значение 0,08.
Задание 5.13. Найти корни кубического уравнения (полинома) с одним неизвестным с помощью средства Подбор параметра.
Выполнение.
Сначала находим интервалы, на которых существуют корни полинома. Такими интервалами, являются промежутки, на концах которых функция меняет знак. С этой целью построим таблицу значений полинома на интервале (-1,1) с шагом 0.2 и построим график. Для этого:
1. Введем в ячейку A2 значение –1 , а в A3 – значение: – 0.8.
2. Используя маркер заполнения, заполним ячейки до А12.
3. В ячейку B2 вводим формулу: = A2^3 – 0,01*A2^2 – 0,7044*A2 + 0,139104.
4. Заполняем диапазон B3:B12.
5. По полученным значениям строим график заданного полинома.
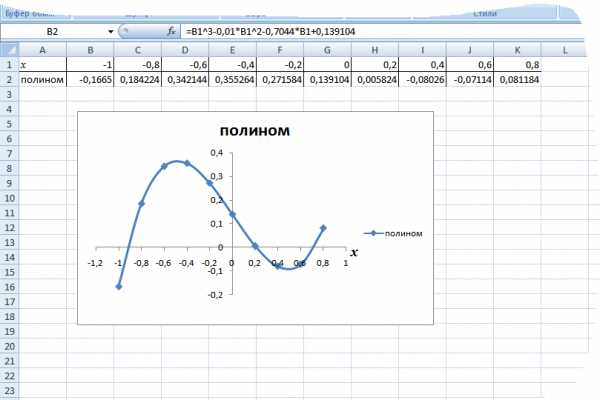
Мы увидим, что для нашего случая полином меняет знак на интервалах [-1,-0.8], [0.2, 0.4] и [0.6, 0.8], т.е. пересекается с осью x. Интервалов три – столько корней имеет уравнение третьей степени. Корни локализованы.
Теперь зададим точность нахождения значений корней. На вкладке Office → Параметры Excel → Формулы → Параметры вычислений задаем относительную погрешность 0,00001 и предельное число итераций 1000 (число последовательных приближений).
Отводим на новом рабочем листе ячейку С2 под первый корень, соответственно ячейки C3 и C4 под второй и третий корни полинома.
Корни будем находим методом последовательных приближений. Поэтому в ячейку С2 вводим сначала значение, являющееся первым приближением к искомому корню. В нашем случае возьмем первый отрезок и в нем среднее значение, т.е. – 0,9. Соответственно в ячейки С3 и С4 вводим приближенные значения для второго и третьего корней: +0,3 и +0,7.
Для нахождения корня с помощью Подбора параметра уравнение надо представить в таком виде, чтобы его правая часть не содержала переменную. В нашем примере этого не требуется. Отводим ячейку D2 под функцию, для которой ведется поиск первого корня. Причем вместо неизвестной x у этой функции должна указываться ссылка на ячейку, отведенную под искомый корень. Таким образом, в ячейку D2вводится формула:
= C2^3 – 0,01*C2^2 – 0,7044*C2 + 0.139104.
Копируем эту формулу в ячейки D3 и D4 для второго и третьего корней полинома. С помощью инструмента Подбор параметранаходим первый корень:
1. Выбираем команду Данные → Работа с данными → Анализ «что-если» → Подбор параметра. На экране появится диалоговое окно.
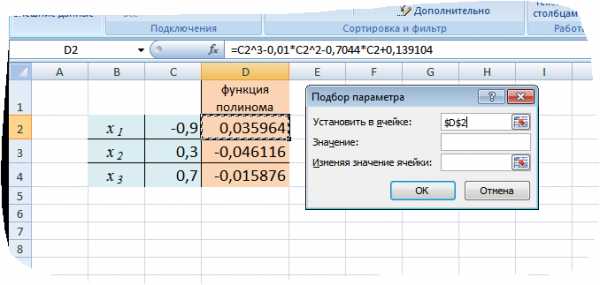
2. В поле Установить в ячейке введем ссылку на ячейку D2, в которой введена формула, вычисляющая значение левой части полинома.
3. В поле Значение вводим 0 – значение из правой части уравнения.
4. В поле Изменяя значение ячейки введем С2 –ссылка на ячейку, отведенную под первый корень.
5. Нажимаем ОК.
Получим окно с результатами:
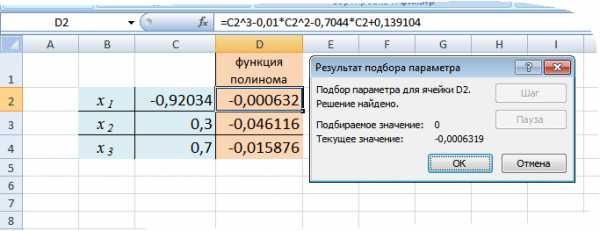
Закрыв окно, найденное приближенное значение корня помещается в ячейку D2. В данном случае оно равно –0,92034.
Аналогично, повторив действия 1–5 для каждого из оставшихся корней, в ячейках D3 и D4 находим их значения. Соответственно, они равны 0,21021 и 0,72071.
Похожие статьи:
poznayka.org