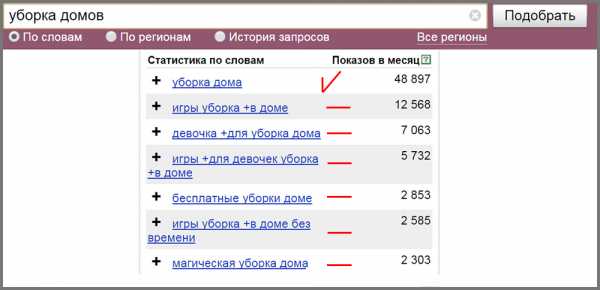
Формы записи задач линейного программирования. Математическая модель задачи линейной оптимизации может быть записана в следующей форме
MatProg_-_TESTY - Стр 2
первую
Задачи исследования операций в экономике это:
оптимизации цели системы при ограничениях на множество допустимых состояний системы
Задача линейной оптимизации называется вырожденной, если:
а) в столбце свободных членов симплексной таблицы имеется по крайней мере один нулевой элемент;
б) в столбце свободных членов симплексной таблицы все элементы положительные;
в) если в симплексной таблице имеются нулевые элементы.
3а разрешающий столбец при нахождении максимума целевой функции задачи линейной оптимизации выбирается тот:
а) в котором находится наименьший отрицательный элемент строки функции, за исключением элемента, находящегося в столбце свободных членов (ДА)
б) в котором находится отрицательный элемент строки функции;
в) в котором все элементы неотрицательные. НЕТ
Задача целочисленного линейного программирования переменные:
Принимают целые значения , ограниченные сверху
Задачи решаемые методом математического программирования являются:
а) любой класс задач
б) класс экстремальных задач
в) класс задач на экстремум (максимум или минимум) функции со многими неизвестными ДА
Задачей нелинейного программирования является задача, у которой:
а) нелинейной является целевая функция
б) некоторые или все ограничения являются нелинейными
в) функция и ограничения являются нелинейными
г) выполняется хотя бы одно из условий а, б или в
Задача линейного программирования на максимум решается графическим методом. Укажите точку, в которой целевая функция достигает своего максимального значения.
а) А (НЕТ)
б) Б ???
в) В
г) Г
Задача нелинейного программирования с ограничениями неравенствами может быть решена методом множителей Лагранжа если:
ограничения неравенства привести к равенствам и наложить условие неотрицательности на дополнительные переменные.
Задачу линейного программирования можно решить
а) Методом Лагранжа; б) графическим методом; в) методом наименьших квадратов; г) симплексным методом.
Задачу максимизации целевой функции Max Z=10Х1+2Х2-3Х3 можно заменить задачей минимизации целевой функции:
Z= -10Х1-2Х2+3Х3
Значение целевой функции в задаче Max Z=2x1+x2 при ограничениях х1-х2<=2 х1+3х2>=3 7х1-х2>=2 x1>=0, x2>=0 равно:
∞
Значения неизвестных системы линейных уравнений находятся:
а) по формуле Х= А-1 В, где А-1 – обратная матрица к матрице А из коэффициентов при неизвестных системы уравнений; В – вектор-столбец свободных членов
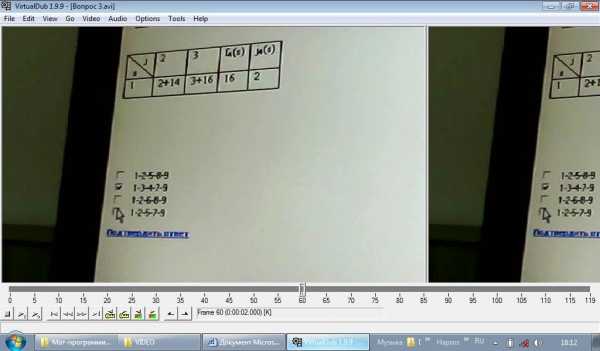
Запишите путь ………… длины между пунктами 1 и 9:
а) 1-2-5-8-9
б) 1-3-4-7-9 НЕТ
в) 1-2-6-8-9 НЕТ
г) 1-2-5-7-9
Какое программное средство можно использовать для нахождения ранга матриц, обратных матриц, решение систем линейных уравнений и оптимизационных задач?
Microsoft Exel
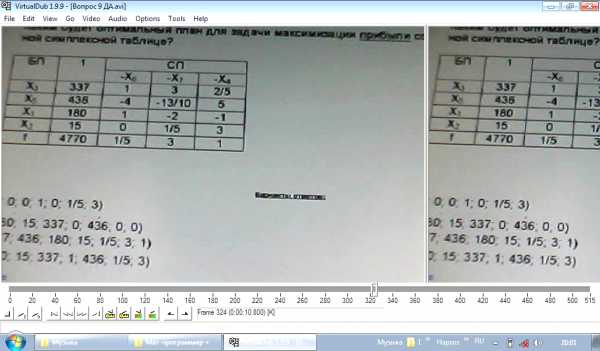
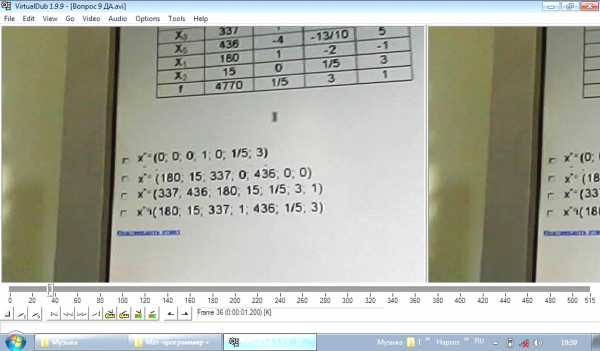
Каким (или какой) будет оптимальный план для задачи максимизации прибыли согласно даннной симплексной таблицы:
Ответ Б (ДА)
Какая функция Exel применяется для нахождения обратной матрицы?
Функция МОБР из диалогового окна Мастер функции
Какая функция Exel применяется для нахождения произведения матриц?
Математическая функция МУМНОЖ из диалогового окна Мастер функции
Каждой занятой клетке в таблице в транспортной задачи соответствует уравнение:
а) ui + vj < cp
б) ui + vj = cp ДА
в) ui + vj ≥ cp
г) ui ∙ vj = cp, где ui и vj - потенциалы
Когда при решении задачи ЦЛО методом ветвей и границ на максимум функции заканчивается вычислительный процесс?
а) когда получено целочисленное решение
Какая команда Microsoft Excel используется для нахождения экстремума функции линейных задач математического программирования?
а) Поиск решения из меню Сервис;
б) Параметры из меню Сервис;
в) Любая команда из меню Сервис.
Какое из реккурентных соотношений для решения задачи фрмирования производственной программы по критерию минимизации затрат с учетом ограниченности производственных мощностей и складских площадей для хранения продукции является верным?
ответ Б
Какие из перечисленных элементов включает математическая модель задачи:
а) целевую функцию
б) теорему
в) систему ограничений
г) целевую функцию, систему ограничений, совокупность неизвестных (план задачи) х = (х1;……хn) ДА
д) доказательство
е) график
Какие методы относятся к методам нахождения начального опорного плана в транспортной задаче:
а) метод аппроксимации; б) метод минимального элемента; в) метод Лагранжа; г) метод Фогеля; д) метод «северо-западного угла».
Какая команда Excel применяется для нахождения оптимального решения нелинейных задач?
Поиск решения из меню Сервис
Критерием оптимальности при нахождении минимума функции транспортной задачи служит:
а) неотрицательность значений потенциалов; б) неположительность оценок незаполненных клеток транспортной таблицы; в) неотрицательность оценок заполненных клеток транспортной таблицы; г) неотрицательность оценок незаполненных клеток транспортной таблицы.
Какое из утверждений верно:
а) каждой задаче линейной оптимизации можно поставить в соответствие задачу, называемую двойственной к исходной; (ДА)
б) для некоторых типов задач линейной оптимизации существует задача, называемая двойственной к исходной задаче;
в) каждой задаче линейной оптимизации можно поставить в соответствие несколько задач, двойственных к исходной.
Какое из утверждений верно:
а) если исходная задача является задачей максимизации целевой функции, то двойственная - задачей минимизации целевой функции;
б) если исходная задача является задачей максимизации целевой функции, то двойственная - также задача максимизации;
в) если исходная задача является задачей максимизации, то двойственная может быть как задачей минимизации, так и задачей максимизации.
Какое из утверждений верно?
а) потенциал i-го поставщика ui (i=1,m) является двойственной оценкой единицы запаса груза
этого поставщика.
б) потенциал j-го потребителя vj (j=1,n) является двойственной оценкой единицы запаса груза
этого поставщика.
Какое из утверждений верно?
а) двойственные оценки являются показателем дефицитности ресурсов и продукции;
б) двойственные оценки являются показателем влияния ограничений на значение функции;
в) двойственные оценки являются показателем эффективности производства отдельных видов продукции с позиций критерия оптимальности;
д) верными являются все утверждения пунктов а), б), в) и г).
Какое из утверждений верно?
а) задача математического программирования — это задача на экстремум одного неизвестного;
б) задача математического программирования — это задача на экстремум функции многих переменных с ограничениями на область их изменения; ДА
в) задача математического программирования — это многовариантная задача, позволяющая найти какое-либо решение.
Какое из утверждений верно:
а) двойственные оценки являются инструментом сопоставления суммарных затрат и результатов.
б) верными являются все отверждения
в) двойственные оценки являются показателем дефицитности ресурсов и продукции.
в) двойственные оценки являются показателем влияния ограничений на значение функции.
г) двойственные оценки являются показателем эффективности производства отдельных видов продукции с позиции критерия оптимальности. ДА
Какое из утверждений верно?
а) динамическое программирование — математический метод для нахождения оптимальных решений многошаговых (многоэтапных) задач;
б) динамическое программирование — математический метод для нахождения всевозможных решений задач экономики, физики, биологии;
в) динамическое программирование — метод нахождения множества решений задачи управления во временном аспекте;
д) динамическое программирование — математический метод для нахождения решений дифференциальных уравнений.
Какое из рекуррентных соотношений для решения п-этапной задачи нахождения оптимального маршрута перевозки груза из города А в город В является верным, если S — состояние системы, a j — номер города?
Ответ Б
Какое из записанных дополнительных ограничений построено верно по ограничении:
Ответ В
Какой командой вызывается диалоговое окно Параметры поиска решения?
а) Поиск решения;
б) Параметры диалогового окна Поиск решения;
в) Выполнить.
Ответ Б
Для клетки (1; 4) замкнутый цикл представлен в таблице
| 1)
| 2)
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3)
| 4)
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Ответ 2) (ДА)
Какие флажки необходимо установить в диалоговом окне Параметры поиска решения для решения линейной оптимизационной задачи?
а) Линейная модель;
б) Неотрицательные значения;
в) Флажки, указанные в пунктах а) и б).
Критерием оптимальности при нахождении минимума функции транспортной задачи служит:
а) неотрицательность характеристик Sij свободных клеток таблицы транспортной задачи;
б) неотрицательность оценок загруженных клеток таблицы транспортной задачи;
в) отрицательность оценок загруженных клеток;
г) равенство нулю потенциалов.
Критическим путем на сетевом графике проекта называется:
путь максимальной продолжительности
Какие дополнительные условия можно вводить при решении транспортной задачи?
а) запрет перевозки от i -го оставщика j-му потребителю;
б) фиксированную поставку груза;
в) нижнюю границу на поставку груза;
г) верхнюю границу на поставку груза;
д) все условия, перечисленные в пунктах а) — г) ДА
Коэффициенты целевой функции в двумерной задаче линейной оптимизации:
указывают направление движение к точке экстремума целевой функции
Математическая модель состояний экономической системы описывается:
ни каких ограничений на тип уравнений или неравенств не предусмотрено
Математическая модель транспортной задачи это:
задача линейного программирования
Математическая модель целевой функции экономической системы задается:
ни каких ограничений на вид целевой функции не предусмотрено
Математическая модель задачи линейной оптимизации может быть записана в следующей форме:
а) общей;
б) симметричной;
в) канонической;
г) Лагранжа;
д) числовой.
Математическая модель задачи линейной оптимизации записана в форме:
F = 8x1 +6x2 –3x3 (max)
x1≥0, x2≥0, х3≥0.
1) симметричной;
канонической;
общей;
матричной.
Матрица строки и столбцы которой соответствуют вершинам графа, а элементы число ребер связывающих вершины называется матрицей:
Смежности
Модель двойственной задачи построенной к данной
f = 8х1 - 4х2+ 7х3 max.
2х1+ 3х2 - 4х3106,
5х1+ 4 х2 + х3 205,
4х1+ 2х2+ 8х3 340.
хj 0, (j=.
принимает следующий вид:
Матрица строки и столбцы которой соответствуют вершинам и ребрам графа, а элементы 1 или 0 в зависимости от наличия связи между вершинами и ребрами:
Инцидентностей
Метод Парето:
сокращает область поиска компромиссных решений многокритериальной оптимизации
Метод при котором для нахождения начального опорного плана записывается число в первую клетку:
а) метод Фогеля
б) метод северо-западного угла (ДА)
в) метод потенциалов
г) метод наименьшего элемента
Между переменными прямой и двойственной задачи можно:
а) установить взаимно однозначное соответствие;
б) произвести замену переменных;
в) установить регрессионную зависимость между переменными;
г) привести подобные члены.
Множители Лагранжа λi (i=1,m) показывают:
на сколько изменится значение функции в оптимальном решении при изменении правой части i-го ограничения на единицу:
Модель транспортной задачи это:
а) модель задачи линейной оптимизации;
б) модель сетевого планирования
в) модель динамического программирования или это.
Модифицированные жордановы исключения применяются для нахождения:
а) обратной матрицы;
б) ранга матрицы;
в) решений систем линейных уравнений;
г) решения задач оптимизации;
д) всего перечисленного в пунктах а), б), в) и г).
Начальный опорный план транспортной задачи ищется методом:
Северо-западного угла
Фогеля
Начальный опорный план транспортной задачи можно составить:
а) методом Жордана;
б) методом минимальной стоимости;
в) методом аппроксимации;
г) методом Фогеля;
д) применяя методы пунктов б) и г).
Найдите верные утверждения применительно к задаче рационального использования ограниченных ресурсов:
а) двойственные оценки в оптимальном решении задачи характеризуют дефицитность ресурсов;
б) ресурс, полностью использованный в оптимальном решении, является дефицитным, его двойственная оценка — больше нуля;
в) если ресурс расходован не полностью, то он избыточен, его двойственная оценка равна нулю;
г) если ресурс расходуется не полностью, то он избыточен, его двойственная оценка больше нуля.
На рисунке изображен случай, когда своего максимального значения функция f(х) достигает
|
Найдите правильное преобразование неравенства 11Х1 + 3Х2 > -19
-11Х1 – 3Х2 < 19
Область допустимых решений задачи линейной оптимизации:
а) может быть объединением двух выпуклых многоугольников НЕТ
б) может быть окружностью
в) может образовывать невыпуклый многоугольник с отрицательными координатами вершин.
г) может быть пустым множеством (ДА)
Область допустимых решений задачи линейной оптимизации:
а) может быть пустым множеством;
б) не может быть пустым множеством;
в) может быть точкой;
г) может быть отрезком прямой;
д) может быть окружностью;
е) может образовывать выпуклый многоугольник (в пространстве — многогранник).
Область допустимых решений задачи нелинейного программирования может быть:
а) выпуклой
б) вогнутой
в) из нескольких частей
г) выпуклой, вогнутой и состоять из нескольких частей
Основным принципом, на котором базируется оптимизация в задачах динамического программирования, является:
а) принцип оптимальности Р. Беллмана;
б) принцип особенностей вычислительного метода;
в) принцип планового соответствия переменных;
г) принцип дуализма.
Оценка свободной клетки ( 2; 1) равна
|
| ||||||||||||||||||||||||||||||||||||
studfiles.net
Mat_progr_-_testy_-_Igor - Стр 2
первую
Задачи исследования операций в экономике это:
оптимизации цели системы при ограничениях на множество допустимых состояний системы
Задача линейной оптимизации называется вырожденной, если:
а) в столбце свободных членов симплексной таблицы имеется по крайней мере один нулевой элемент;
б) в столбце свободных членов симплексной таблицы все элементы положительные;
в) если в симплексной таблице имеются нулевые элементы.
3а разрешающий столбец при нахождении максимума целевой функции задачи линейной оптимизации выбирается тот:
а) в котором находится наименьший отрицательный элемент строки функции, за исключением элемента, находящегося в столбце свободных членов (ДА)
б) в котором находится отрицательный элемент строки функции;
в) в котором все элементы неотрицательные. НЕТ
Задача целочисленного линейного программирования переменные:
Принимают целые значения , ограниченные сверху
Задачи решаемые методом математического программирования являются:
а) любой класс задач
б) класс экстремальных задач
в) класс задач на экстремум (максимум или минимум) функции со многими неизвестными ДА
Задачей нелинейного программирования является задача, у которой:
а) нелинейной является целевая функция
б) некоторые или все ограничения являются нелинейными
в) функция и ограничения являются нелинейными
г) выполняется хотя бы одно из условий а, б или в
Задача линейного программирования на максимум решается графическим методом. Укажите точку, в которой целевая функция достигает своего максимального значения.
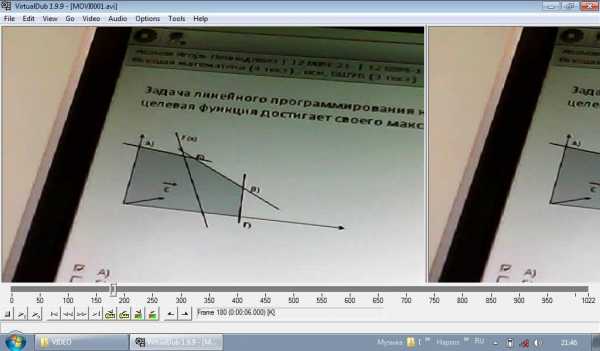
а) А (НЕТ)
б) Б ???
в) В
г) Г
Задача нелинейного программирования с ограничениями неравенствами может быть решена методом множителей Лагранжа если:
ограничения неравенства привести к равенствам и наложить условие неотрицательности на дополнительные переменные.
Задачу линейного программирования можно решить
а) Методом Лагранжа; б) графическим методом; в) методом наименьших квадратов; г) симплексным методом.
Задачу максимизации целевой функции Max Z=10Х1+2Х2-3Х3 можно заменить задачей минимизации целевой функции:
Z= -10Х1-2Х2+3Х3
Значение целевой функции в задаче Max Z=2x1+x2 при ограничениях х1-х2<=2 х1+3х2>=3 7х1-х2>=2 x1>=0, x2>=0 равно:
∞
Значения неизвестных системы линейных уравнений находятся:
а) по формуле Х= А-1 В, где А-1 – обратная матрица к матрице А из коэффициентов при неизвестных системы уравнений; В – вектор-столбец свободных членов
Запишите путь ………… длины между пунктами 1 и 9:
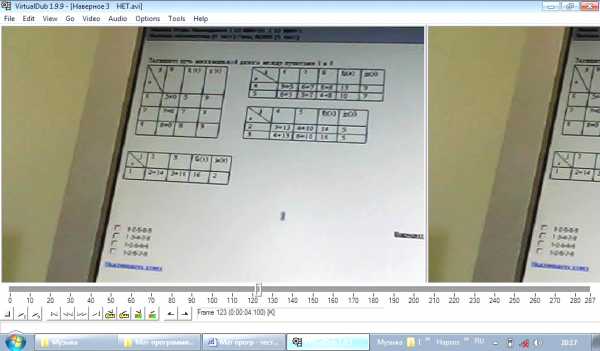
а) 1-2-5-8-9
б) 1-3-4-7-9 НЕТ
в) 1-2-6-8-9 НЕТ
г) 1-2-5-7-9
Какое программное средство можно использовать для нахождения ранга матриц, обратных матриц, решение систем линейных уравнений и оптимизационных задач?
Microsoft Exel
Каким (или какой) будет оптимальный план для задачи максимизации прибыли согласно даннной симплексной таблицы:
Ответ Б (ДА)
Какая функция Exel применяется для нахождения обратной матрицы?
Функция МОБР из диалогового окна Мастер функции
Какая функция Exel применяется для нахождения произведения матриц?
Математическая функция МУМНОЖ из диалогового окна Мастер функции
Каждой занятой клетке в таблице в транспортной задачи соответствует уравнение:
а) ui + vj < cp
б) ui + vj = cp ДА
в) ui + vj ≥ cp
г) ui ∙ vj = cp, где ui и vj - потенциалы
Когда при решении задачи ЦЛО методом ветвей и границ на максимум функции заканчивается вычислительный процесс?
а) когда получено целочисленное решение
Какая команда Microsoft Excel используется для нахождения экстремума функции линейных задач математического программирования?
а) Поиск решения из меню Сервис;
б) Параметры из меню Сервис;
в) Любая команда из меню Сервис.
Какое из реккурентных соотношений для решения задачи фрмирования производственной программы по критерию минимизации затрат с учетом ограниченности производственных мощностей и складских площадей для хранения продукции является верным?
ответ Б
Какие из перечисленных элементов включает математическая модель задачи:
а) целевую функцию
б) теорему
в) систему ограничений
г) целевую функцию, систему ограничений, совокупность неизвестных (план задачи) х = (х1;……хn) ДА
д) доказательство
е) график
Какие методы относятся к методам нахождения начального опорного плана в транспортной задаче:
а) метод аппроксимации; б) метод минимального элемента; в) метод Лагранжа; г) метод Фогеля; д) метод «северо-западного угла».
Какая команда Excel применяется для нахождения оптимального решения нелинейных задач?
Поиск решения из меню Сервис
Критерием оптимальности при нахождении минимума функции транспортной задачи служит:
а) неотрицательность значений потенциалов; б) неположительность оценок незаполненных клеток транспортной таблицы; в) неотрицательность оценок заполненных клеток транспортной таблицы; г) неотрицательность оценок незаполненных клеток транспортной таблицы.
Какое из утверждений верно:
а) каждой задаче линейной оптимизации можно поставить в соответствие задачу, называемую двойственной к исходной; (ДА)
б) для некоторых типов задач линейной оптимизации существует задача, называемая двойственной к исходной задаче;
в) каждой задаче линейной оптимизации можно поставить в соответствие несколько задач, двойственных к исходной.
Какое из утверждений верно:
а) если исходная задача является задачей максимизации целевой функции, то двойственная - задачей минимизации целевой функции;
б) если исходная задача является задачей максимизации целевой функции, то двойственная - также задача максимизации;
в) если исходная задача является задачей максимизации, то двойственная может быть как задачей минимизации, так и задачей максимизации.
Какое из утверждений верно?
а) потенциал i-го поставщика ui (i=1,m) является двойственной оценкой единицы запаса груза
этого поставщика.
б) потенциал j-го потребителя vj (j=1,n) является двойственной оценкой единицы запаса груза
этого поставщика.
Какое из утверждений верно?
а) двойственные оценки являются показателем дефицитности ресурсов и продукции;
б) двойственные оценки являются показателем влияния ограничений на значение функции;
в) двойственные оценки являются показателем эффективности производства отдельных видов продукции с позиций критерия оптимальности;
г) двойственные оценки являются инструментом сопоставления суммарных затрат и результатов;
д) верными являются все утверждения пунктов а), б), в) и г).
Какое из утверждений верно?
а) задача математического программирования — это задача на экстремум одного неизвестного;
б) задача математического программирования — это задача на экстремум функции многих переменных с ограничениями на область их изменения; ДА
в) задача математического программирования — это многовариантная задача, позволяющая найти какое-либо решение.
Какое из утверждений верно:
а) двойственные оценки являются инструментом сопоставления суммарных затрат и результатов.
б) верными являются все отверждения
в) двойственные оценки являются показателем дефицитности ресурсов и продукции.
в) двойственные оценки являются показателем влияния ограничений на значение функции.
г) двойственные оценки являются показателем эффективности производства отдельных видов продукции с позиции критерия оптимальности. ДА
Какое из утверждений верно?
а) динамическое программирование — математический метод для нахождения оптимальных решений многошаговых (многоэтапных) задач;
б) динамическое программирование — математический метод для нахождения всевозможных решений задач экономики, физики, биологии;
в) динамическое программирование — метод нахождения множества решений задачи управления во временном аспекте;
д) динамическое программирование — математический метод для нахождения решений дифференциальных уравнений.
Какое из рекуррентных соотношений для решения п-этапной задачи нахождения оптимального маршрута перевозки груза из города А в город В является верным, если S — состояние системы, a j — номер города?
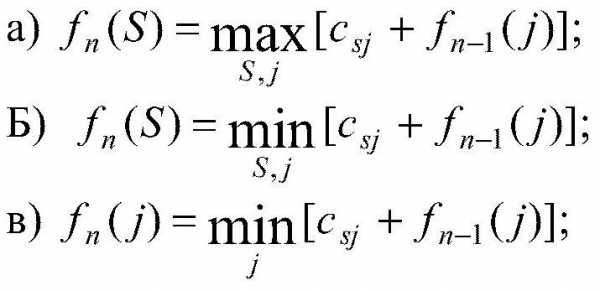
Ответ Б
Какое из записанных дополнительных ограничений построено верно по ограничении:
Ответ В
Какой командой вызывается диалоговое окно Параметры поиска решения?
а) Поиск решения;
б) Параметры диалогового окна Поиск решения;
в) Выполнить.
Ответ Б
Для клетки (1; 4) замкнутый цикл представлен в таблице
| 1)
| 2)
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3)
| 4)
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Ответ 2) (ДА)
Какие флажки необходимо установить в диалоговом окне Параметры поиска решения для решения линейной оптимизационной задачи?
а) Линейная модель;
б) Неотрицательные значения;
в) Флажки, указанные в пунктах а) и б).
Критерием оптимальности при нахождении минимума функции транспортной задачи служит:
а) неотрицательность характеристик Sij свободных клеток таблицы транспортной задачи;
б) неотрицательность оценок загруженных клеток таблицы транспортной задачи;
в) отрицательность оценок загруженных клеток;
г) равенство нулю потенциалов.
Критическим путем на сетевом графике проекта называется:
путь максимальной продолжительности
Какие дополнительные условия можно вводить при решении транспортной задачи?
а) запрет перевозки от i -го оставщика j-му потребителю;
б) фиксированную поставку груза;
в) нижнюю границу на поставку груза;
г) верхнюю границу на поставку груза;
д) все условия, перечисленные в пунктах а) — г) ДА
Коэффициенты целевой функции в двумерной задаче линейной оптимизации:
указывают направление движение к точке экстремума целевой функции
Математическая модель состояний экономической системы описывается:
ни каких ограничений на тип уравнений или неравенств не предусмотрено
Математическая модель транспортной задачи это:
задача линейного программирования
Математическая модель целевой функции экономической системы задается:
ни каких ограничений на вид целевой функции не предусмотрено
Математическая модель задачи линейной оптимизации может быть записана в следующей форме:
а) общей;
б) симметричной;
в) канонической;
г) Лагранжа;
д) числовой.
Математическая модель задачи линейной оптимизации записана в форме:
F = 8x1 +6x2 –3x3 (max)
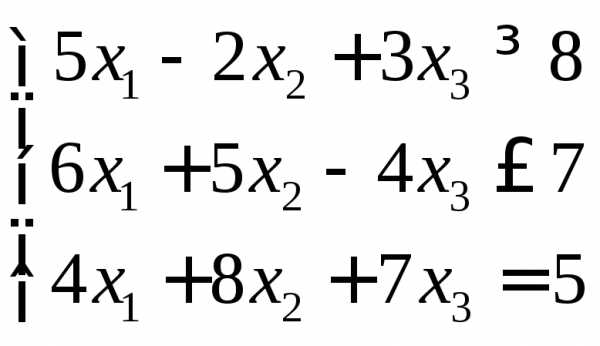
x1≥0, x2≥0, х3≥0.
1) симметричной;
канонической;
общей;
матричной.
Матрица строки и столбцы которой соответствуют вершинам графа, а элементы число ребер связывающих вершины называется матрицей:
Смежности
Модель двойственной задачи построенной к данной
f = 8х1 - 4х2+ 7х3 
max.
2х1+ 3х2 - 4х3
106,
5х1+ 4 х2 + х3 
205,
4х1+ 2х2+ 8х3 
340.
хj 0, (j=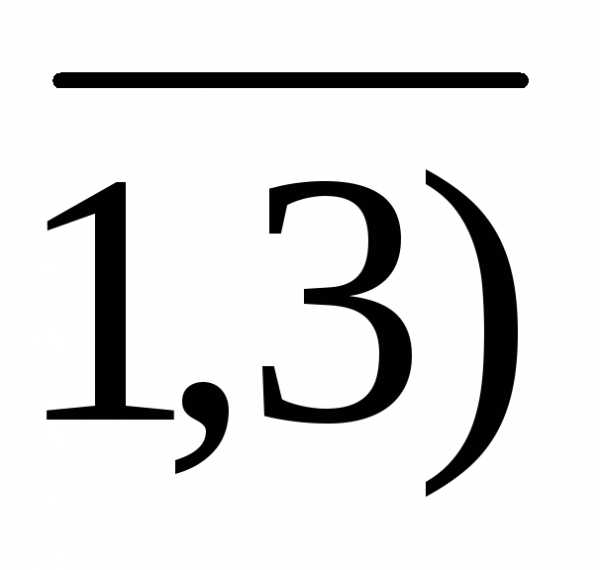
.
принимает следующий вид:
Матрица строки и столбцы которой соответствуют вершинам и ребрам графа, а элементы 1 или 0 в зависимости от наличия связи между вершинами и ребрами:
Инцидентностей
Метод Парето:
сокращает область поиска компромиссных решений многокритериальной оптимизации
Метод при котором для нахождения начального опорного плана записывается число в первую клетку:
а) метод Фогеля
б) метод северо-западного угла (ДА)
в) метод потенциалов
г) метод наименьшего элемента
Между переменными прямой и двойственной задачи можно:
а) установить взаимно однозначное соответствие;
б) произвести замену переменных;
в) установить регрессионную зависимость между переменными;
г) привести подобные члены.
Множители Лагранжа λi (i=1,m) показывают:
на сколько изменится значение функции в оптимальном решении при изменении правой части i-го ограничения на единицу:
Модель транспортной задачи это:
а) модель задачи линейной оптимизации;
б) модель сетевого планирования
в) модель динамического программирования или это.
Модифицированные жордановы исключения применяются для нахождения:
а) обратной матрицы;
б) ранга матрицы;
в) решений систем линейных уравнений;
г) решения задач оптимизации;
д) всего перечисленного в пунктах а), б), в) и г).
Начальный опорный план транспортной задачи ищется методом:
Северо-западного угла
Фогеля
Начальный опорный план транспортной задачи можно составить:
а) методом Жордана;
б) методом минимальной стоимости;
в) методом аппроксимации;
г) методом Фогеля;
д) применяя методы пунктов б) и г).
Найдите верные утверждения применительно к задаче рационального использования ограниченных ресурсов:
а) двойственные оценки в оптимальном решении задачи характеризуют дефицитность ресурсов;
б) ресурс, полностью использованный в оптимальном решении, является дефицитным, его двойственная оценка — больше нуля;
в) если ресурс расходован не полностью, то он избыточен, его двойственная оценка равна нулю;
г) если ресурс расходуется не полностью, то он избыточен, его двойственная оценка больше нуля.
На рисунке изображен случай, когда своего максимального значения функция f(х) достигает
|
Найдите правильное преобразование неравенства 11Х1 + 3Х2 > -19
-11Х1 – 3Х2 < 19
Область допустимых решений задачи линейной оптимизации:
а) может быть объединением двух выпуклых многоугольников НЕТ
б) может быть окружностью
в) может образовывать невыпуклый многоугольник с отрицательными координатами вершин.
г) может быть пустым множеством (ДА)
Область допустимых решений задачи линейной оптимизации:
а) может быть пустым множеством;
б) не может быть пустым множеством;
в) может быть точкой;
г) может быть отрезком прямой;
д) может быть окружностью;
е) может образовывать выпуклый многоугольник (в пространстве — многогранник).
Область допустимых решений задачи нелинейного программирования может быть:
а) выпуклой
б) вогнутой
в) из нескольких частей
г) выпуклой, вогнутой и состоять из нескольких частей
Основным принципом, на котором базируется оптимизация в задачах динамического программирования, является:
а) принцип оптимальности Р. Беллмана;
б) принцип особенностей вычислительного метода;
в) принцип планового соответствия переменных;
г) принцип дуализма.
Оценка свободной клетки ( 2; 1) равна
|
| ||||||||||||||||||||||||||||||||||||
studfiles.net
Какой командой вызывается диалоговое окно Параметры поиска решения?
а) Поиск решения;
б) Параметры диалогового окна Поиск решения;
в) Выполнить.
Ответ Б
Для клетки (1; 4) замкнутый цикл представлен в таблице
Ответ 2) (ДА)
Какие флажки необходимо установить в диалоговом окне Параметры поиска решения для решения линейной оптимизационной задачи?
а) Линейная модель;
б) Неотрицательные значения;
в) Флажки, указанные в пунктах а) и б).
Критерием оптимальности при нахождении минимума функции транспортной задачи служит:
а) неотрицательность характеристик Sij свободных клеток таблицы транспортной задачи;
б) неотрицательность оценок загруженных клеток таблицы транспортной задачи;
в) отрицательность оценок загруженных клеток;
г) равенство нулю потенциалов.
Критическим путем на сетевом графике проекта называется:
путь максимальной продолжительности
Какие дополнительные условия можно вводить при решении транспортной задачи?
а) запрет перевозки от i -го оставщика j-му потребителю;
б) фиксированную поставку груза;
в) нижнюю границу на поставку груза;
г) верхнюю границу на поставку груза;
д) все условия, перечисленные в пунктах а) — г) ДА
Коэффициенты целевой функции в двумерной задаче линейной оптимизации:
указывают направление движение к точке экстремума целевой функции
Математическая модель состояний экономической системы описывается:
ни каких ограничений на тип уравнений или неравенств не предусмотрено
Математическая модель транспортной задачи это:
задача линейного программирования
Математическая модель целевой функции экономической системы задается:
ни каких ограничений на вид целевой функции не предусмотрено
Математическая модель задачи линейной оптимизации может быть записана в следующей форме:
а) общей;
б) симметричной;
в) канонической;
г) Лагранжа;
д) числовой.
Математическая модель задачи линейной оптимизации записана в форме:
F = 8x1 +6x2 –3x3 (max)
x1≥0, x2≥0, х3≥0.
1) симметричной;
2) канонической;
3) общей;
4) матричной.
Матрица строки и столбцы которой соответствуют вершинам графа, а элементы число ребер связывающих вершины называется матрицей:
Смежности
megaobuchalka.ru
Формы записи задач линейного программирования
Симметричной (стандартной) формой записи ЗЛП называется задача максимизации целевой функции (2.1) при ограничениях вида (2.2) и (2.5) или задача минимизации целевой функции (2.1) при ограничениях вида (2.4) и (2.5), т.е.
;
,
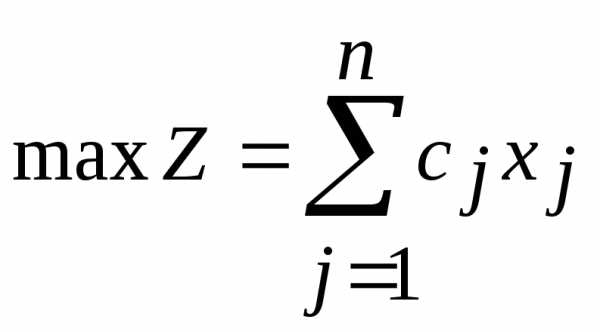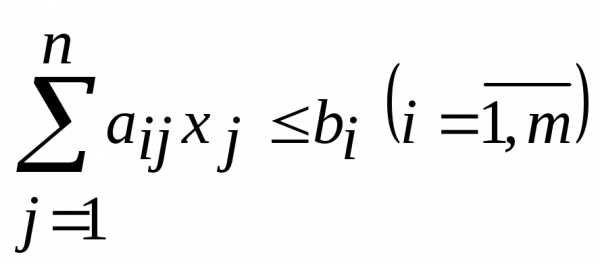или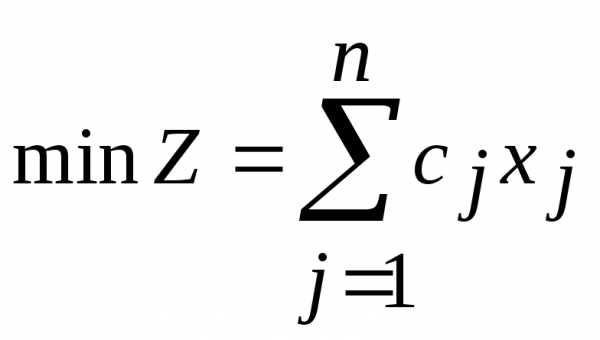 
;
,
,
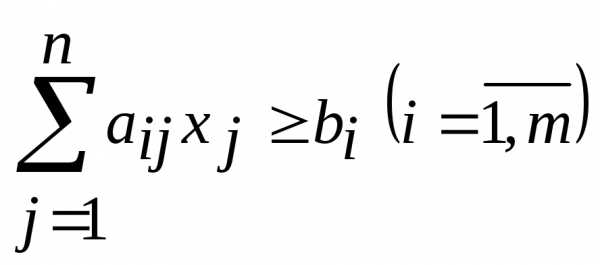где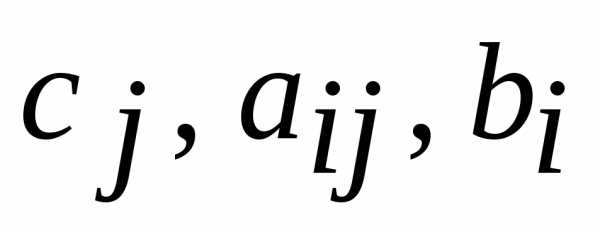 
– заданные действительные числа.
Канонической формой записи ЗЛП называется задача минимизации или максимизации целевой функции (2.1) при ограничениях вида (2.3) и (2.5), т.е.
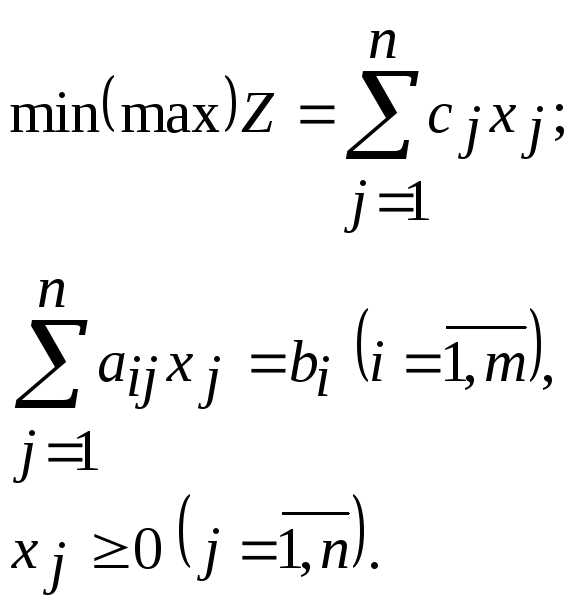
Приемы, позволяющие переходить от одной формы записи условий задач к другой
Переход от задачи на минимум к задаче на максимум осуществляется умножением целевой функции на «–1». Действительно, если функция
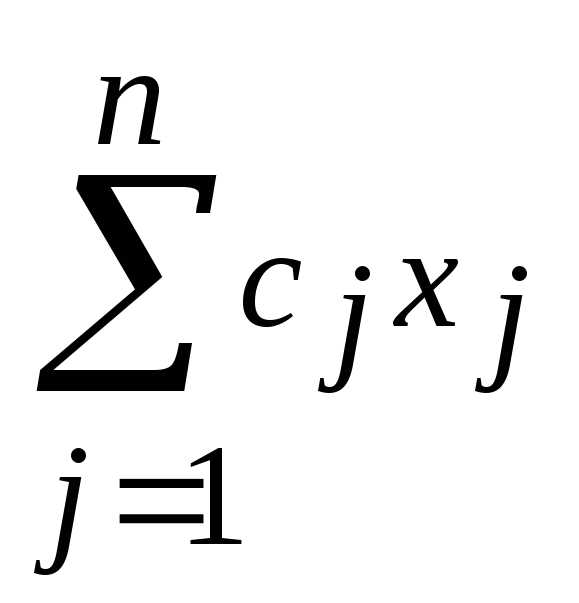достигает минимума при значениях 
, то функция 
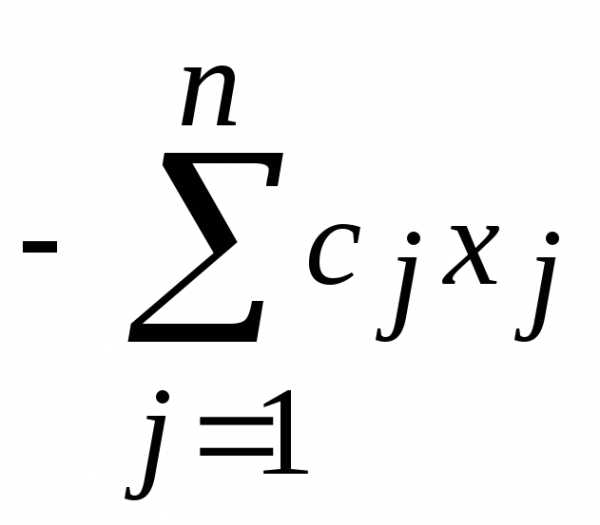достигает при тех же значениях переменных максимума.
Переход от неравенства вида к неравенствам вида (и наоборот) также осуществляется умножением исходного неравенства на –1.
Переход от неравенства к равенству осуществляется введением дополнительной неотрицательной переменной . К примеру, если первое ограничение имеет вид
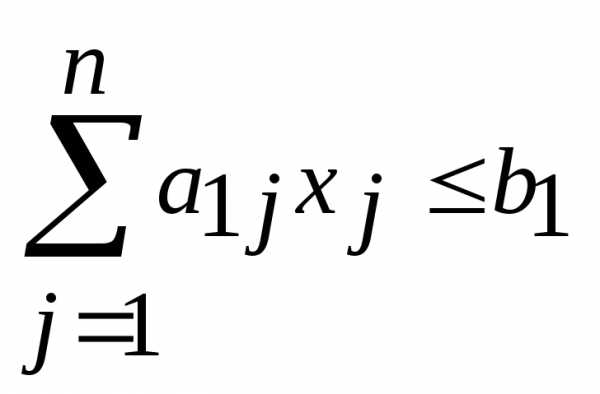, то, вводя неотрицательную переменную
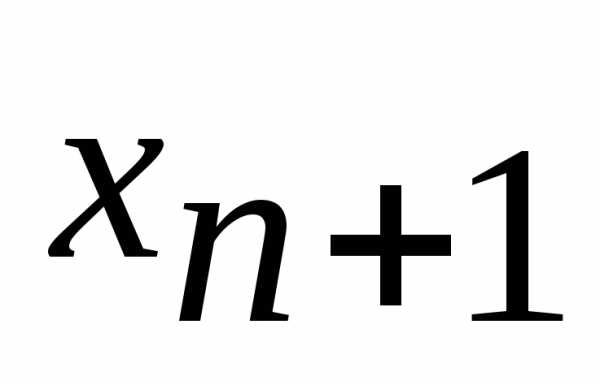, получим
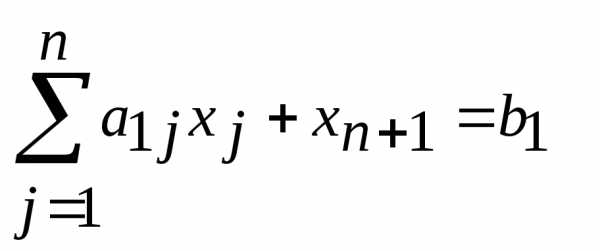, если второе ограничение имеет вид
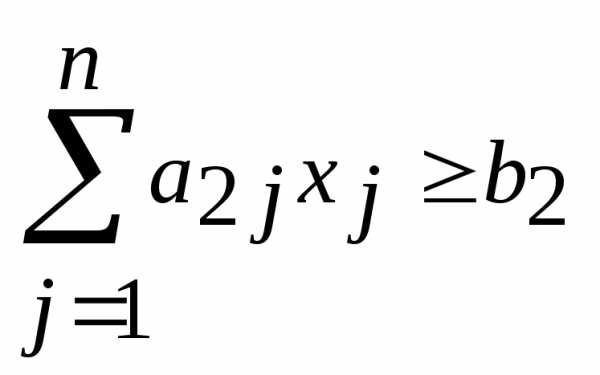, то, вводя неотрицательную переменную
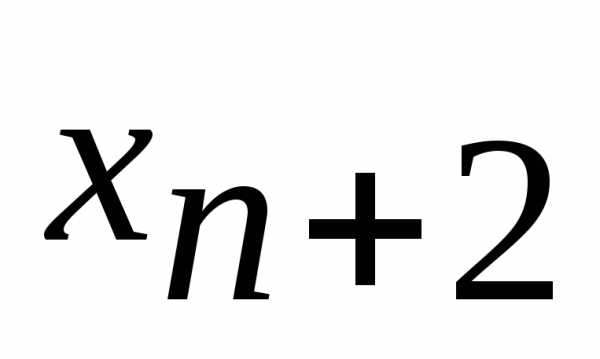, получим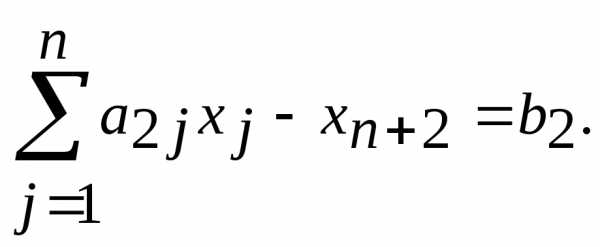
При переходе от равенств к неравенствам можно руководствоваться следующим: если дано А=B, то это можно формально записать в виде двух неравенств А В, А В;
Введение условий неотрицательности переменных. Пусть на переменную
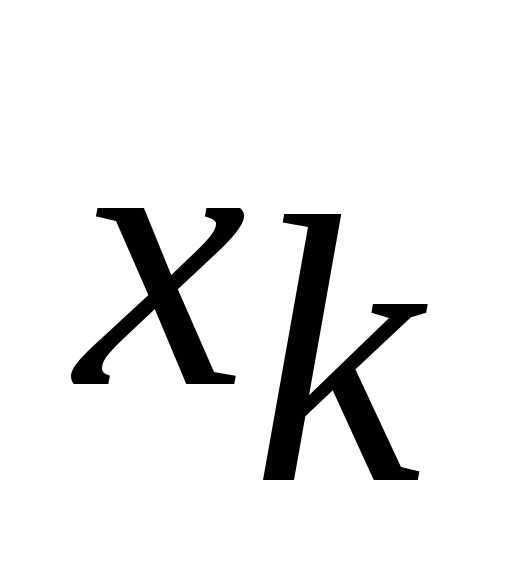это условие не было наложено, тогда вместо этой переменной можно ввести две неотрицательные переменные
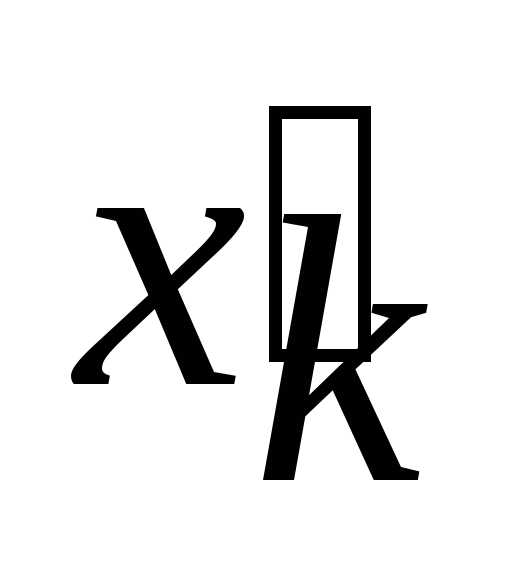и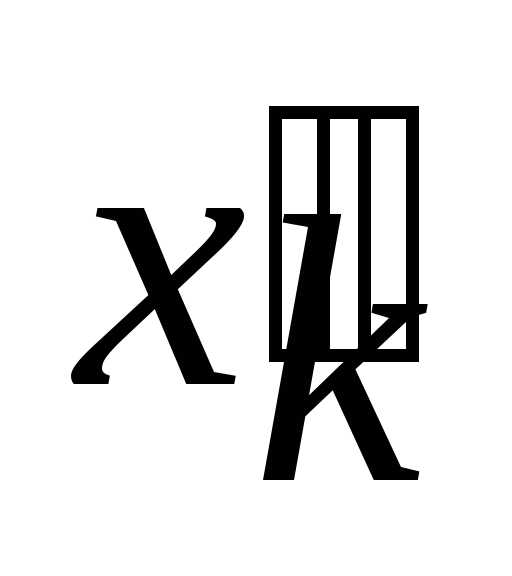
и представить, где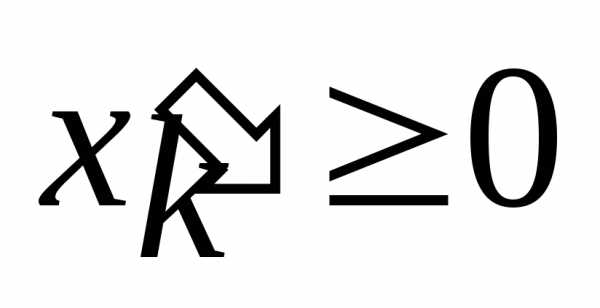
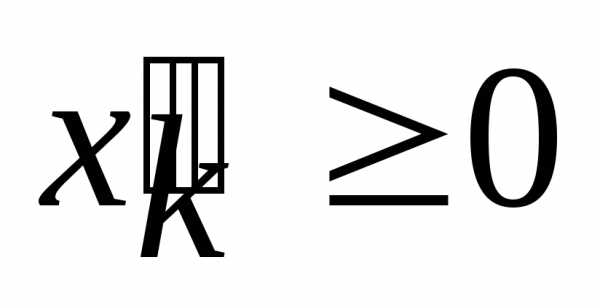. Это всегда возможно.
Изложенными приемами общая ЗЛП может быть сведена к симметричной и канонической формам записи ЗЛП и наоборот. Однако, поскольку в процессе таких преобразований мы вводили дополнительные переменные, то после того, как задача решена, нужно произвести обратный переход к исходным переменным, определяющим непосредственный экономический смысл задачи.
Пример 4
Пусть математическая модель задачи имеет следующий вид
;
Для получения общей задачи линейного программирования необходимо, чтобы на все переменные было наложено условие неотрицательности. Для наложения этого ограничения на переменную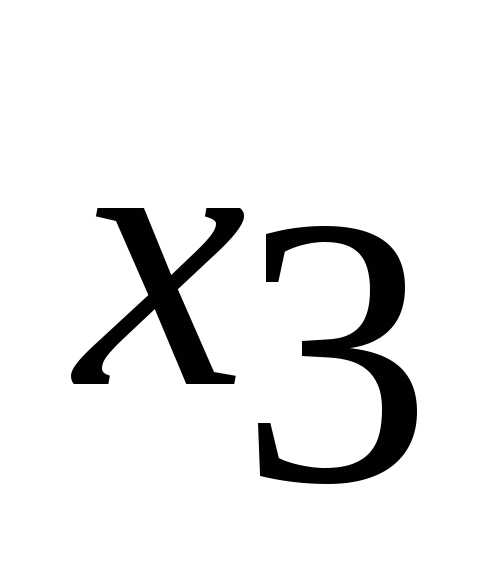 
воспользуемся правилом 5. Введем новые неотрицательные переменные
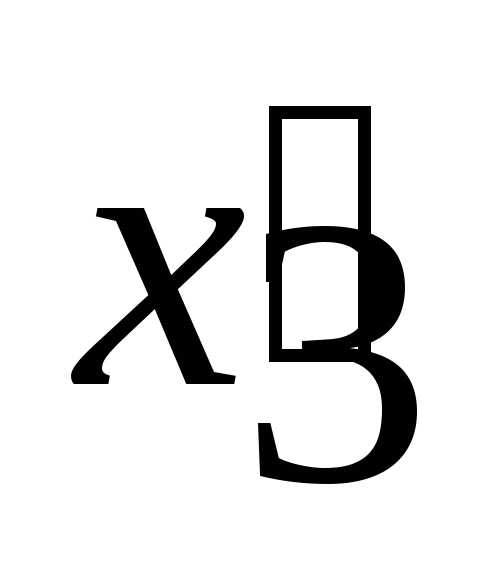и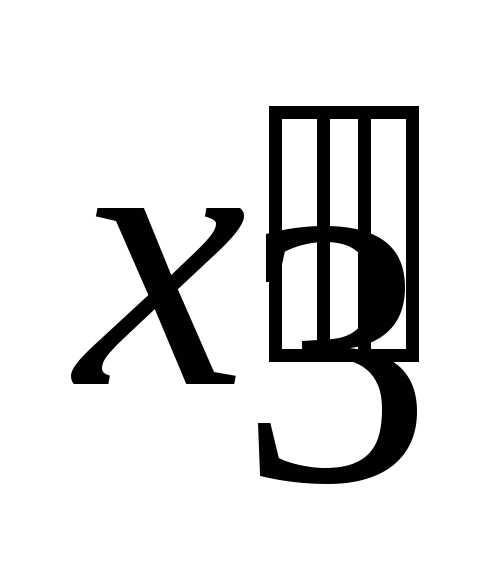
и представим, где
и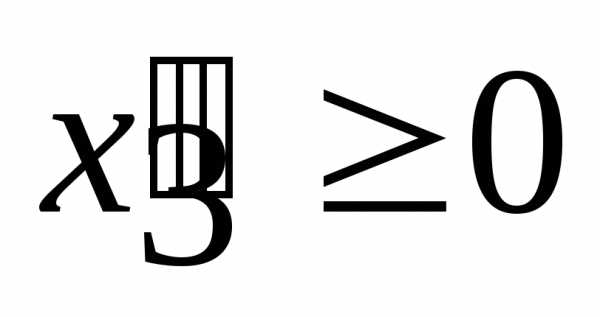
.
Тогда ОЗЛП будет иметь вид
;
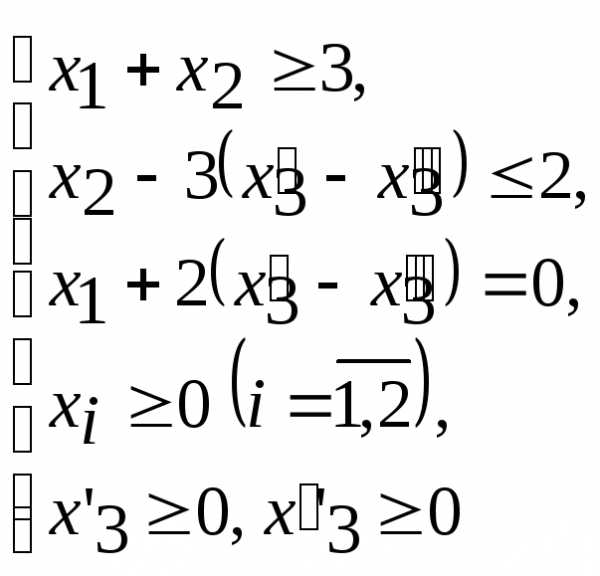
или (раскрыв скобки):
;
В симметричной (стандартной) форме записи задача будет иметь вид
;
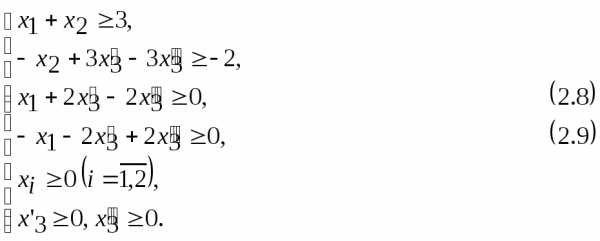
Здесь ограничение (2.6) умножено на –1, а ограничение (2.7) заменено двумя ограничениями:
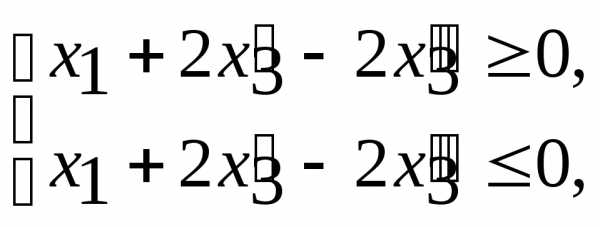
откуда, домножив второе ограничение на –1, получим ограничение (2.9) вида .
Таким образом, из ограничения (2.7) получены ограничения (2.8) и (2.9).
В канонической форме записи ЗЛП будет иметь вид
;
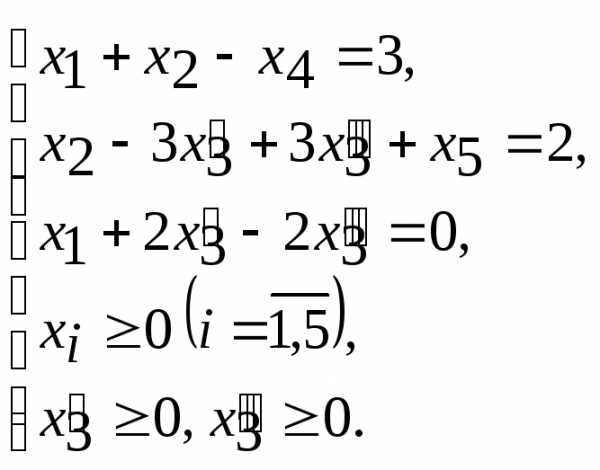
Пример 5
Экономико-математическую модель задачи, составленную в примере 2, представим в канонической форме записи:
;
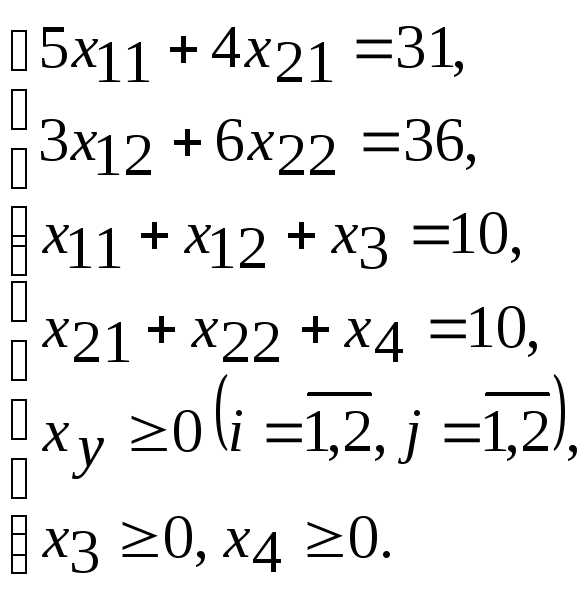
Введенные дополнительные переменные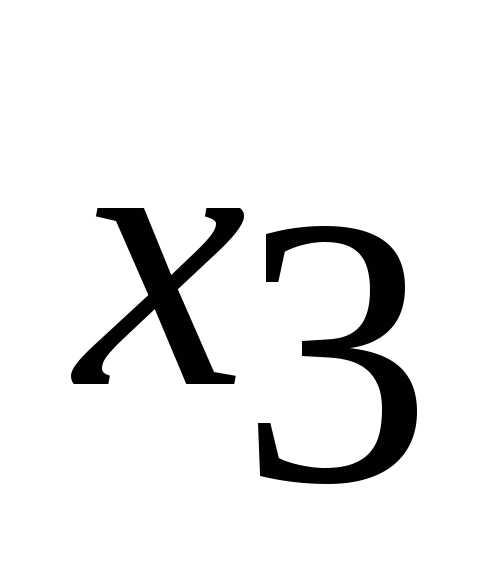 
и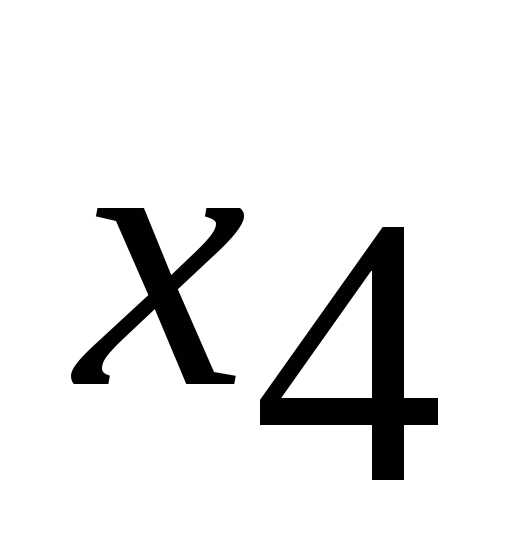
имеют экономический смысл, связанный с содержанием задачи. Здесь
,
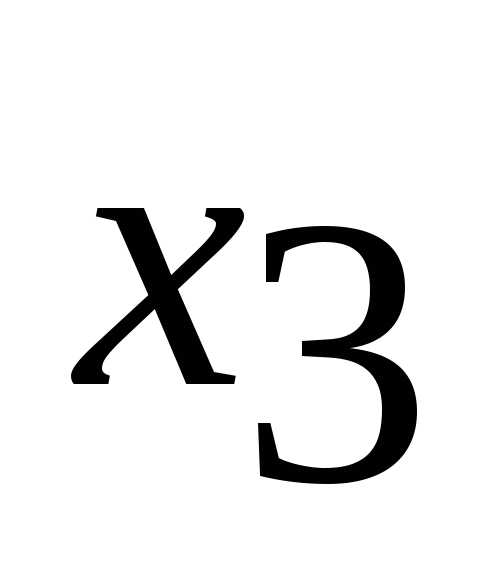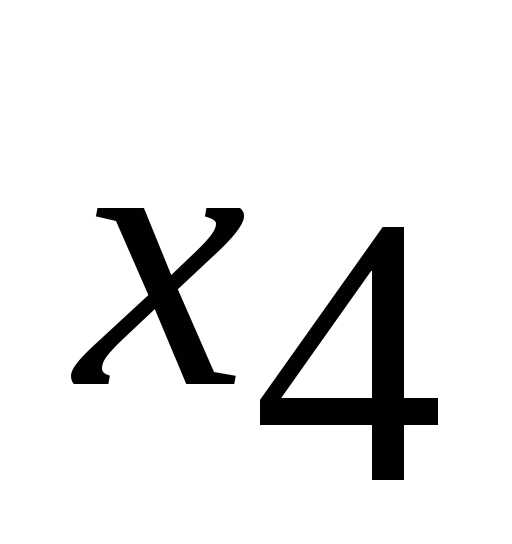– время простоя оборудования А1 и А2 соответственно.
Графический метод решения злп
Графическим методом можно решать любые задачи линейного программирования (ЗЛП) с двумя переменными (
=2), а также ЗЛП с
>2 переменными, если в ее канонической записи число неизвестных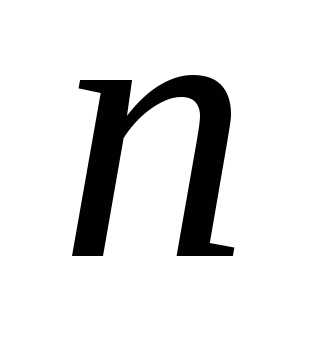
и число линейно независимых уравнений
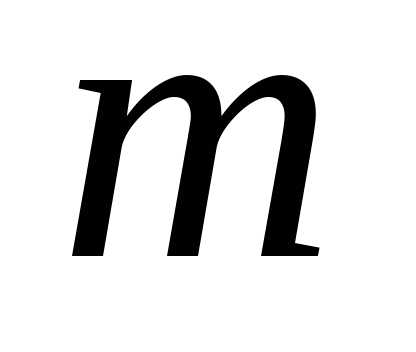связаны соотношением.
Пример 6
Решим графически задачу ЛП, экономико-математическая модель которой составлена в примере 3.
;
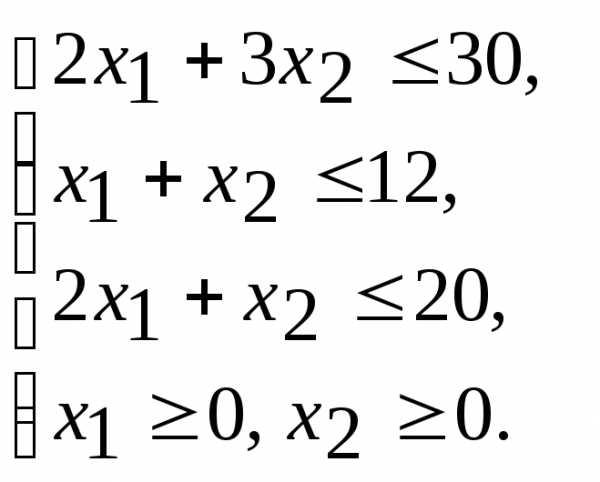(2.10)
Вначале построим многоугольник решений или ОДР задачи (рисунок 1). Для этого в системе координат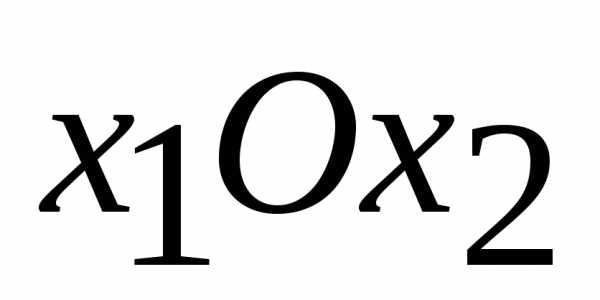 
на плоскости изобразим граничные прямые:
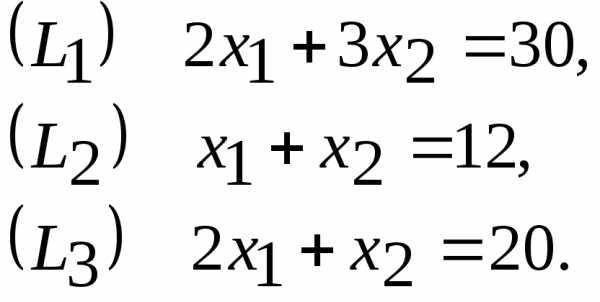
Затем определим, какую полуплоскость определяет соответствующее неравенство, подставив координаты какой-нибудь точки, например начала координат. Ограничения (2.10) означают, что ОДР лежит в I четверти системы координат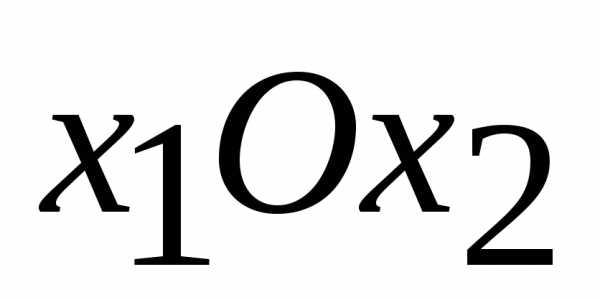 
. Соответствующие полуплоскости на рисунке показаны стрелками. Пересечение указанных полуплоскостей и определяет многоугольник решений данной задачи (ОДР).
Для того чтобы построить прямую , строим направляющий вектор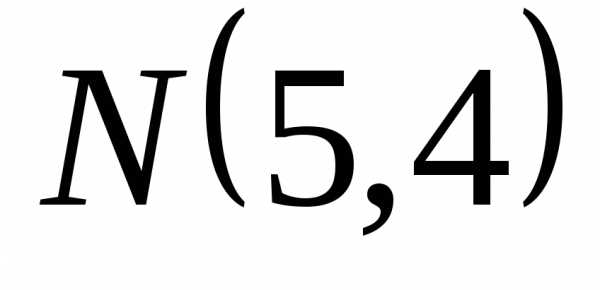
, который перпендикулярен прямойZ. Прямая, проходящая через начало координат и перпендикулярная вектору 
, и будет прямая
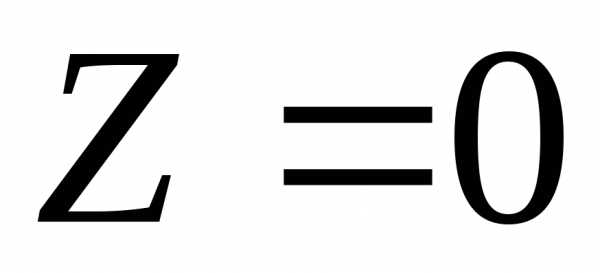. Затем прямую
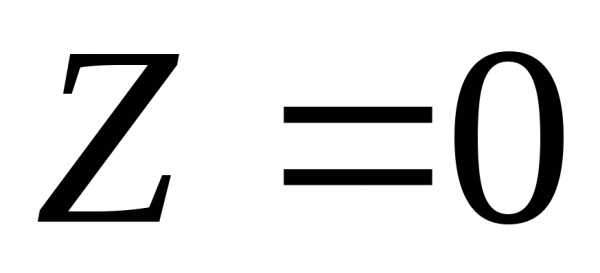перемещаем параллельно самой себе в направлении вектораN по многоугольнику решений (ОДР) (рисунок 1). Последняя точка соприкосновения прямой 
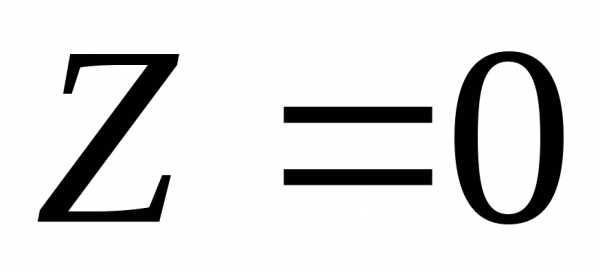с ОДР и есть оптимальное решение.
Рисунок 1
Вектор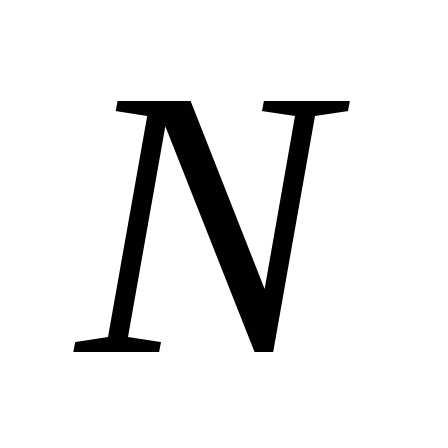 
указывает направление возрастания целевой функцииZ. Оптимальное решение ЗЛП может достигаться лишь в точках, принадлежащих границе многоугольника решений. В нашем примере, как видно из рисунка 1, функция Z принимает максимальное значение в точке 
. Точка
лежит на пересечении прямых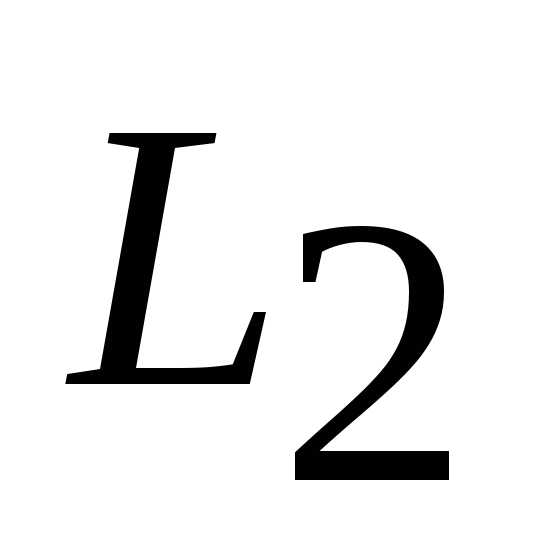
и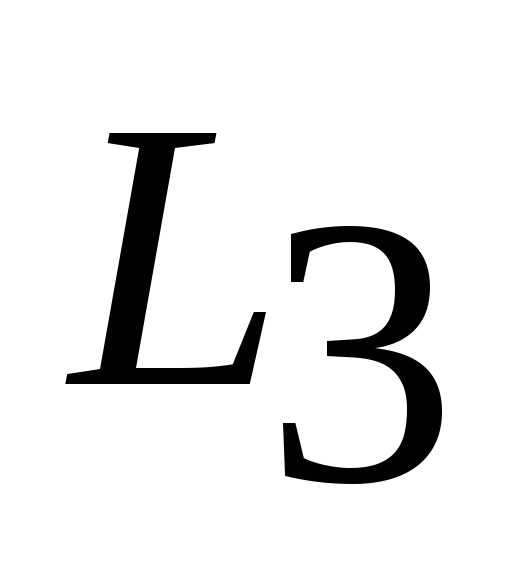
. Для определения ее координат необходимо решить систему уравнений:
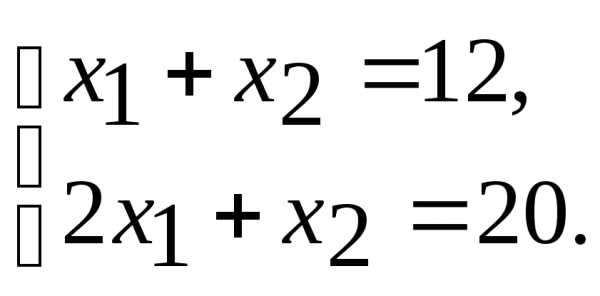
Откуда . Это и есть оптимальный план задачи. Подставив значение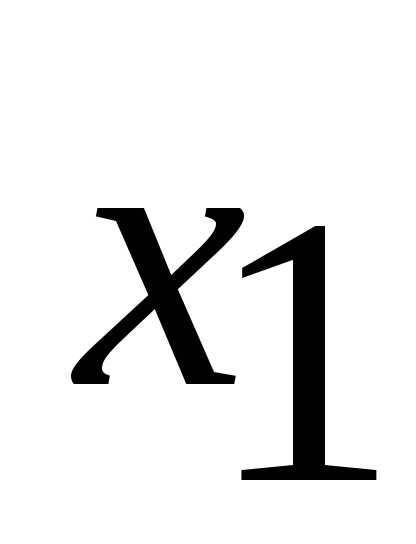
и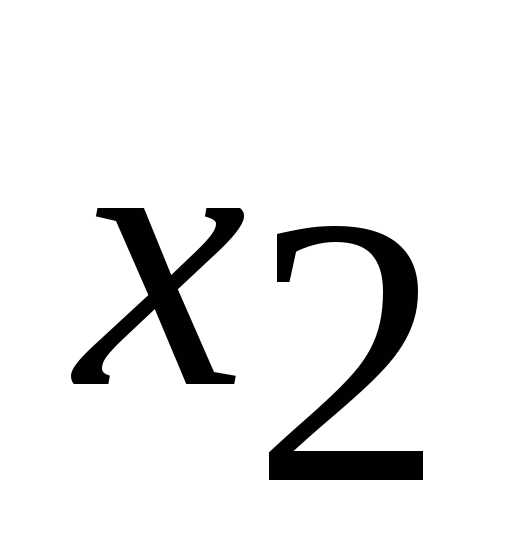
в целевую функциюZ, получаем
.
Таким образом, для того чтобы получить максимальную прибыль в размере 56 ден. ед., необходимо запланировать выпуск 8 ед. продукции вида П1 и 4 ед. продукции П2.
studfiles.net
Составить математическую модель задачи линейного программирования – приведение злп к каноническому виду
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ФГОУ ПО “ПСКОВСКИЙ КОЛЛЕДЖ СТРОИТЕЛЬСТВА И ЭКОНОМИКИ”
Предмет “Математические методы”
Задача линейного программирования
Курсовая работа
Студента группы 315-ПО
Андреева Дмитрия Александровича
Руководитель курсовой работы
Васильева Наталья Анатольевна
Псков 2009 г.
Содержание
Введение
Глава Ι Линейное программирование
§ 1 Общая постановка задачи линейного программирования
§ 2 Математическая модель задачи линейного программирования
§ 3 Каноническая форма задачи линейного программирования
Глава ΙΙ Решение задачи симплексным методом
§ 1 Постановка задачи
§ 2 Составление математической модели задачи
§ 3 Алгоритмы решения задачи симплексным методом
§ 4 Построение начального опорного решения методом Гаусса
§ 5 Решение задачи
§ 6 Вывод
Заключение
Литература
Введение
В настоящее время множество задач планирования и управления в отраслях народного хозяйства, а также большой объём частных прикладных задач решаются методами математического программирования. Наиболее развитыми в области решения оптимизационных задач являются методы линейного программирования. Эти методы позволяют описать с достаточной точностью широкого круга задач коммерческой деятельности, таких, как планирование товарооборота; размещение розничной торговой сети города; планирование товароснабжения города, района; прикрепление торговых предприятий к поставщикам; организация рациональных перевозок товаров; распределение работников торговли должностям; организация рациональных закупок продуктов питания; распределение ресурсов; планирование капиталовложений; оптимизация межотраслевых связей; замена торгового оборудования; определение оптимального ассортимента товаров в условиях ограниченной площади; установление рационального режима работы.
В задачах линейного программирования критерий эффективности и функции в системе ограничений линейны.
Если содержательный смысл требует получения решения в целых числах, то такая задача является задачей целочисленного программирования.
Если в задаче математического программирования имеется переменная времени, а критерий эффективности выражается через уравнения, описывающие течение операций во времени, то такая задача является задачей динамического программирования.
Во многих экономических моделях зависимости между постоянными и переменными факторами можно считать линейными.
Использование методов математического программирования в коммерческой деятельности связано со сбором необходимой информации коммерсантом, экономистом, финансистом, затем постановкой задачи вместе с математикой. Поскольку методы математического программирования уже реализованы на компьютере в виде пакета стандартных программ, то доступ к ним обычно прост, автоматизирован и не составляет особых трудностей.
Тогда эксплуатация модели включает в себя сбор и обработку информации, ввод обработанной информации в ЭВМ, расчеты на основе разработанных программ календарных планов и, наконец, выдачу результатов вычислений (в удобном для пользователей виде) для их использования в сфере производственной деятельности.
Глава Ι Линейное программирование
§ 1 Общая постановка задачи линейного программирования
Линейное программирование – это направление математического программирование изучающая методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейной целевой функцией. Для решения задач линейного программирования составляется математическая модель задачи и выбирается метод решения.
Постановка задачи коммерческой деятельности может быть представлена в виде математической модели линейного программирования, если целевая функция может быть представлена в виде линейной формы, а связь с ограниченными ресурсами описать посредством линейных уравнений или неравенств. Кроме того, вводится дополнительное ограничение – значения переменных должны быть неотрицательны, поскольку они представляют такие величины, как товарооборот, время работы, затраты и другие экономические показатели.
Геометрическая интерпретация экономических задач даёт возможность наглядно представить, их структуру, выявить особенности и открывает пути исследования более сложных свойств. Задача линейного программирования с двумя переменными всегда можно решить графически. Однако уже в трёхмерном пространстве такое решение усложняется, а в пространствах, размерность которых более трёх, графическое решение, вообще говоря, невозможно. Случай двух переменных не имеет особого практического значения, однако его рассмотрение проясняет свойства задач линейного программирования, приводит к идее её решения, делает геометрически наглядными способы решения и пути их практической реализации.
§ 2 Математическая модель задачи линейного программирования
Перед решением задачи составляем её математическую модель.
Математическая модель – это совокупность соотношений состоящие из линейной целевой функции и линейных ограничений на переменную.
Принцип составления математической модели.
1. Выбирают переменные задачи.
Переменными задачи называются величины
которые полностью характеризуют экономический процесс, описанный в задачи. Обычно записываются в виде вектора X = () Причём )
2. Составляют систему ограничения задачи.
Система ограничений – это совокупность уравнений и неравенств, которым удовлетворяют переменные задачи и которая следует из ограниченности экономических условий задачи.
В общем виде система записывается в виде
3. Задают целевую функцию.
Целевая функция – это функция Z(X) которая характеризует качество выполнения задачи, экстремум которой надо найти. В общем виде целевая функция записывается Z(X) =
(max, min)
т.о. математическая модель имеет вид найти переменные задачи
удовлетворяющие системе ограничений:
и условию неотрицательности
0 (j = ), которая обеспечивает экстремум целевой функции Z(Y) =
Допустимым решением задачи линейного программирования называется любой набор значений переменных удовлетворяющий системе ограничений и условной неотрицательности.
Множество допустимых решений образует область допустимых решений задачи (ОДР).
Оптимальным решением называется допустимое решение задачи, при котором целевая функция достигает экстремума.
§ 3 Каноническая форма задачи линейного программирования
Математическая модель задачи должна иметь каноническую форму.
Если система ограничения состоит только из уравнения и все переменные удовлетворяют условию неотрицательности, то задача имеет каноническую форму.
Если в системе есть хотя бы одно неравенства или какая–либо переменная неограниченна условию неотрицательности, то задача имеет стандартную форму. Чтобы привести задачу к каноническому виду надо:
перейти от неравенств к уравнению следующим образом: в левую часть неравенств вводим дополнительную переменную с коэффициентом (+1) для неравенства (
) и (-1) для неравенства () дополнительные переменные не наложены целевые неотрицательности, то её заменяют разностью двух неотрицательных переменных, то есть: = – (
Общий вид канонической формы:
Глава ΙΙ Решение задачи симплексным методом
Симплексный метод – это метод последовательного улучшения плана (решения), наиболее эффективный и применяется для решения любой задачи линейного программирования.
Название метода от латинского simplecx – простой т.к. из начального область допустимых решений задачи имела простейший вид. Идеи метода предложил российский математик Контарович Л.В. в 1939 году и затем эту идею развил и разработал Дж. Данциг в 1949 году.
Симплексный метод позволяет за конечное число шагов либо найти оптимальное решение либо доказать что его нет.
§ 1 Постановка задачи
На предприятии в процессе производства используется 3 вида станков Ι, ІΙ, ІΙІ. При этом расходуется сырьё, трудовые ресурсы, и учитываются накладные расходы.
laservirta.ru
Мат прогр - тесты - Игорь +
первую
Задачи исследования операций в экономике это:
оптимизации цели системы при ограничениях на множество допустимых состояний системы
Задача линейной оптимизации называется вырожденной, если:
а) в столбце свободных членов симплексной таблицы имеется по крайней мере один нулевой элемент;
б) в столбце свободных членов симплексной таблицы все элементы положительные;
в) если в симплексной таблице имеются нулевые элементы.
3а разрешающий столбец при нахождении максимума целевой функции задачи линейной оптимизации выбирается тот:
а) в котором находится наименьший отрицательный элемент строки функции, за исключением элемента, находящегося в столбце свободных членов (ДА)
б) в котором находится отрицательный элемент строки функции;
в) в котором все элементы неотрицательные. НЕТ
Задача целочисленного линейного программирования переменные:
Принимают целые значения , ограниченные сверху
Задачи решаемые методом математического программирования являются:
а) любой класс задач
б) класс экстремальных задач
в) класс задач на экстремум (максимум или минимум) функции со многими неизвестными ДА
Задачей нелинейного программирования является задача, у которой:
а) нелинейной является целевая функция
б) некоторые или все ограничения являются нелинейными
в) функция и ограничения являются нелинейными
г) выполняется хотя бы одно из условий а, б или в
Задача линейного программирования на максимум решается графическим методом. Укажите точку, в которой целевая функция достигает своего максимального значения.
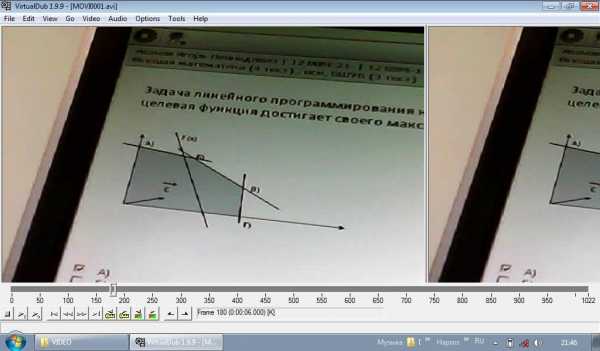
а) А (НЕТ)
б) Б ???
в) В
г) Г
Задача нелинейного программирования с ограничениями неравенствами может быть решена методом множителей Лагранжа если:
ограничения неравенства привести к равенствам и наложить условие неотрицательности на дополнительные переменные.
Задачу линейного программирования можно решить
а) Методом Лагранжа; б) графическим методом; в) методом наименьших квадратов; г) симплексным методом.
Задачу максимизации целевой функции Max Z=10Х1+2Х2-3Х3 можно заменить задачей минимизации целевой функции:
Z= -10Х1-2Х2+3Х3
Значение целевой функции в задаче Max Z=2x1+x2 при ограничениях х1-х2<=2 х1+3х2>=3 7х1-х2>=2 x1>=0, x2>=0 равно:
∞
Значения неизвестных системы линейных уравнений находятся:
а) по формуле Х= А-1 В, где А-1 – обратная матрица к матрице А из коэффициентов при неизвестных системы уравнений; В – вектор-столбец свободных членов
Запишите путь ………… длины между пунктами 1 и 9:
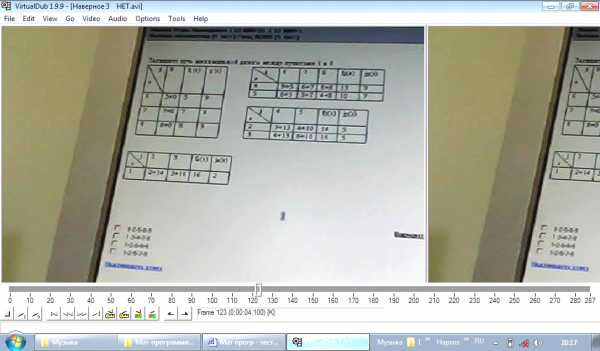
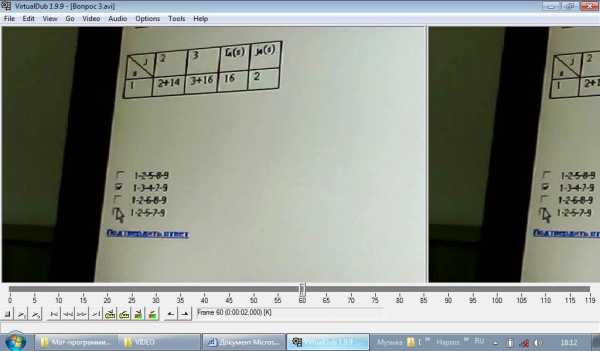
а) 1-2-5-8-9
б) 1-3-4-7-9 НЕТ
в) 1-2-6-8-9 НЕТ
г) 1-2-5-7-9
Какое программное средство можно использовать для нахождения ранга матриц, обратных матриц, решение систем линейных уравнений и оптимизационных задач?
Microsoft Exel
Каким (или какой) будет оптимальный план для задачи максимизации прибыли согласно даннной симплексной таблицы:
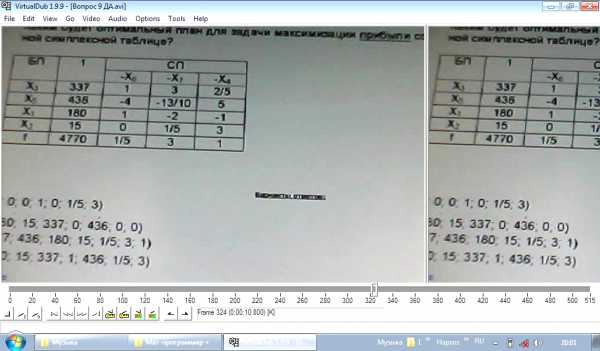
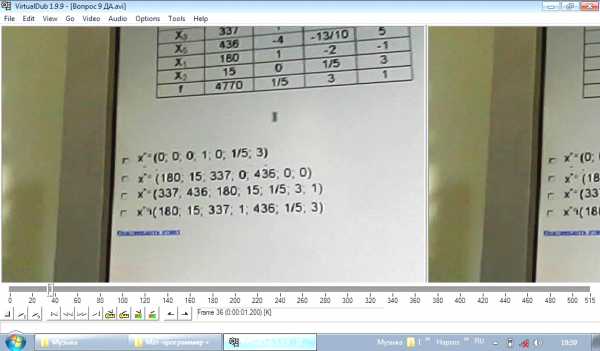
Ответ Б (ДА)
Какая функция Exel применяется для нахождения обратной матрицы?
Функция МОБР из диалогового окна Мастер функции
Какая функция Exel применяется для нахождения произведения матриц?
Математическая функция МУМНОЖ из диалогового окна Мастер функции
Каждой занятой клетке в таблице в транспортной задачи соответствует уравнение:
а) ui + vj < cp
б) ui + vj = cp ДА
в) ui + vj ≥ cp
г) ui ∙ vj = cp, где ui и vj - потенциалы
Когда при решении задачи ЦЛО методом ветвей и границ на максимум функции заканчивается вычислительный процесс?
а) когда получено целочисленное решение
Какая команда Microsoft Excel используется для нахождения экстремума функции линейных задач математического программирования?
а) Поиск решения из меню Сервис;
б) Параметры из меню Сервис;
в) Любая команда из меню Сервис.
Какое из реккурентных соотношений для решения задачи фрмирования производственной программы по критерию минимизации затрат с учетом ограниченности производственных мощностей и складских площадей для хранения продукции является верным?
ответ Б
Какие из перечисленных элементов включает математическая модель задачи:
а) целевую функцию
б) теорему
в) систему ограничений
г) целевую функцию, систему ограничений, совокупность неизвестных (план задачи) х = (х1;……хn) ДА
д) доказательство
е) график
Какие методы относятся к методам нахождения начального опорного плана в транспортной задаче:
а) метод аппроксимации; б) метод минимального элемента; в) метод Лагранжа; г) метод Фогеля; д) метод «северо-западного угла».
Какая команда Excel применяется для нахождения оптимального решения нелинейных задач?
Поиск решения из меню Сервис
Критерием оптимальности при нахождении минимума функции транспортной задачи служит:
а) неотрицательность значений потенциалов; б) неположительность оценок незаполненных клеток транспортной таблицы; в) неотрицательность оценок заполненных клеток транспортной таблицы; г) неотрицательность оценок незаполненных клеток транспортной таблицы.
Какое из утверждений верно:
а) каждой задаче линейной оптимизации можно поставить в соответствие задачу, называемую двойственной к исходной; (ДА)
б) для некоторых типов задач линейной оптимизации существует задача, называемая двойственной к исходной задаче;
в) каждой задаче линейной оптимизации можно поставить в соответствие несколько задач, двойственных к исходной.
Какое из утверждений верно:
а) если исходная задача является задачей максимизации целевой функции, то двойственная - задачей минимизации целевой функции;
б) если исходная задача является задачей максимизации целевой функции, то двойственная - также задача максимизации;
в) если исходная задача является задачей максимизации, то двойственная может быть как задачей минимизации, так и задачей максимизации.
Какое из утверждений верно?
а) потенциал i-го поставщика ui (i=1,m) является двойственной оценкой единицы запаса груза
этого поставщика.
б) потенциал j-го потребителя vj (j=1,n) является двойственной оценкой единицы запаса груза
этого поставщика.
Какое из утверждений верно?
а) двойственные оценки являются показателем дефицитности ресурсов и продукции;
б) двойственные оценки являются показателем влияния ограничений на значение функции;
в) двойственные оценки являются показателем эффективности производства отдельных видов продукции с позиций критерия оптимальности;
г) двойственные оценки являются инструментом сопоставления суммарных затрат и результатов;
д) верными являются все утверждения пунктов а), б), в) и г).
Какое из утверждений верно?
а) задача математического программирования — это задача на экстремум одного неизвестного;
б) задача математического программирования — это задача на экстремум функции многих переменных с ограничениями на область их изменения; ДА
в) задача математического программирования — это многовариантная задача, позволяющая найти какое-либо решение.
Какое из утверждений верно:
а) двойственные оценки являются инструментом сопоставления суммарных затрат и результатов.
б) верными являются все отверждения
в) двойственные оценки являются показателем дефицитности ресурсов и продукции.
в) двойственные оценки являются показателем влияния ограничений на значение функции.
г) двойственные оценки являются показателем эффективности производства отдельных видов продукции с позиции критерия оптимальности. ДА
Какое из утверждений верно?
а) динамическое программирование — математический метод для нахождения оптимальных решений многошаговых (многоэтапных) задач;
б) динамическое программирование — математический метод для нахождения всевозможных решений задач экономики, физики, биологии;
в) динамическое программирование — метод нахождения множества решений задачи управления во временном аспекте;
д) динамическое программирование — математический метод для нахождения решений дифференциальных уравнений.
Какое из рекуррентных соотношений для решения п-этапной задачи нахождения оптимального маршрута перевозки груза из города А в город В является верным, если S — состояние системы, a j — номер города?
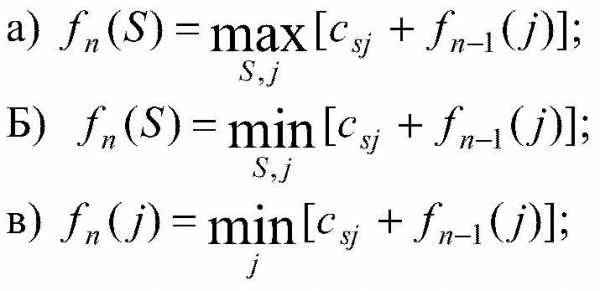
Ответ Б
Какое из записанных дополнительных ограничений построено верно по ограничении:
Ответ В
Какой командой вызывается диалоговое окно Параметры поиска решения?
а) Поиск решения;
б) Параметры диалогового окна Поиск решения;
в) Выполнить.
Ответ Б
Для клетки (1; 4) замкнутый цикл представлен в таблице
| 1)
| 2)
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3)
| 4)
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Ответ 2) (ДА)
Какие флажки необходимо установить в диалоговом окне Параметры поиска решения для решения линейной оптимизационной задачи?
а) Линейная модель;
б) Неотрицательные значения;
в) Флажки, указанные в пунктах а) и б).
Критерием оптимальности при нахождении минимума функции транспортной задачи служит:
а) неотрицательность характеристик Sij свободных клеток таблицы транспортной задачи;
б) неотрицательность оценок загруженных клеток таблицы транспортной задачи;
в) отрицательность оценок загруженных клеток;
г) равенство нулю потенциалов.
Критическим путем на сетевом графике проекта называется:
путь максимальной продолжительности
Какие дополнительные условия можно вводить при решении транспортной задачи?
а) запрет перевозки от i -го оставщика j-му потребителю;
б) фиксированную поставку груза;
в) нижнюю границу на поставку груза;
г) верхнюю границу на поставку груза;
д) все условия, перечисленные в пунктах а) — г) ДА
Коэффициенты целевой функции в двумерной задаче линейной оптимизации:
указывают направление движение к точке экстремума целевой функции
Математическая модель состояний экономической системы описывается:
ни каких ограничений на тип уравнений или неравенств не предусмотрено
Математическая модель транспортной задачи это:
задача линейного программирования
Математическая модель целевой функции экономической системы задается:
ни каких ограничений на вид целевой функции не предусмотрено
Математическая модель задачи линейной оптимизации может быть записана в следующей форме:
а) общей;
б) симметричной;
в) канонической;
г) Лагранжа;
д) числовой.
Математическая модель задачи линейной оптимизации записана в форме:
F = 8x1 +6x2 –3x3 (max)
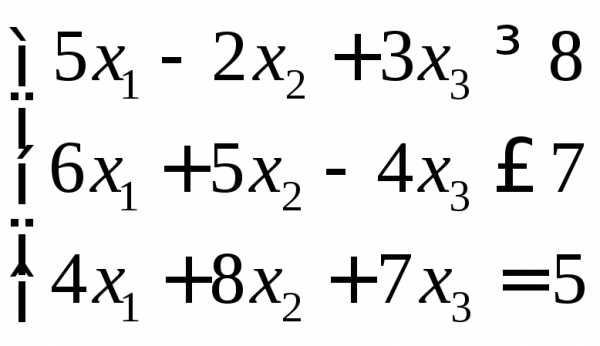
x1≥0, x2≥0, х3≥0.
1) симметричной;
канонической;
общей;
матричной.
Матрица строки и столбцы которой соответствуют вершинам графа, а элементы число ребер связывающих вершины называется матрицей:
Смежности
Модель двойственной задачи построенной к данной
f = 8х1 - 4х2+ 7х3 
max.
2х1+ 3х2 - 4х3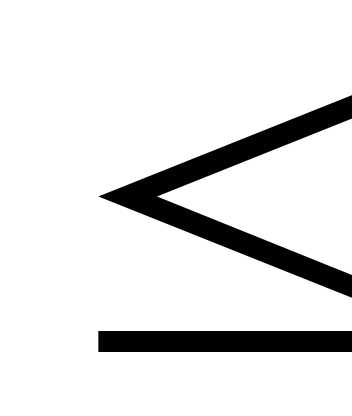
106,
5х1+ 4 х2 + х3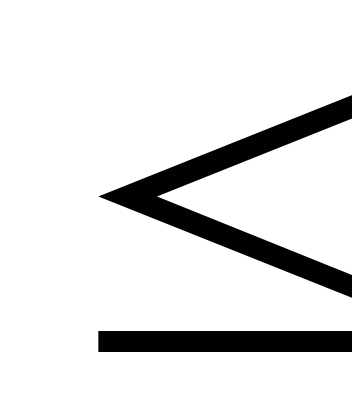 
205,
4х1+ 2х2+ 8х3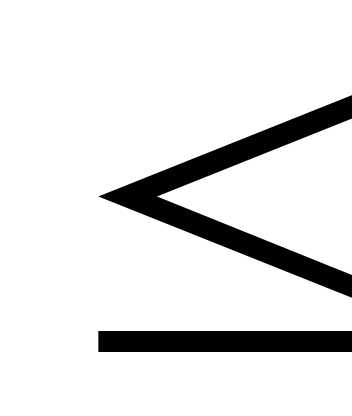 
340.
хj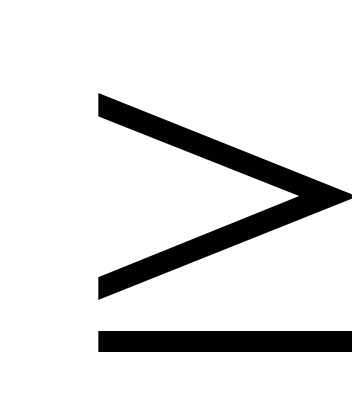 
0, (j=
.
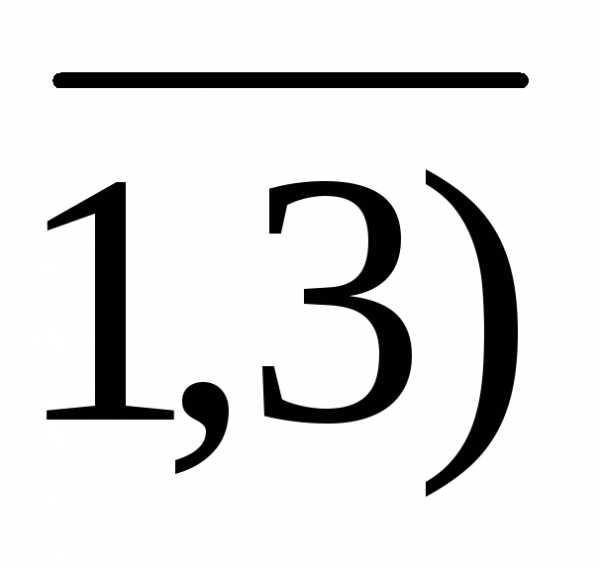принимает следующий вид:
Матрица строки и столбцы которой соответствуют вершинам и ребрам графа, а элементы 1 или 0 в зависимости от наличия связи между вершинами и ребрами:
Инцидентностей
Метод Парето:
сокращает область поиска компромиссных решений многокритериальной оптимизации
Метод при котором для нахождения начального опорного плана записывается число в первую клетку:
а) метод Фогеля
б) метод северо-западного угла (ДА)
в) метод потенциалов
г) метод наименьшего элемента
Между переменными прямой и двойственной задачи можно:
а) установить взаимно однозначное соответствие;
б) произвести замену переменных;
в) установить регрессионную зависимость между переменными;
г) привести подобные члены.
Множители Лагранжа λi (i=1,m) показывают:
на сколько изменится значение функции в оптимальном решении при изменении правой части i-го ограничения на единицу:
Модель транспортной задачи это:
а) модель задачи линейной оптимизации;
б) модель сетевого планирования
в) модель динамического программирования или это.
Модифицированные жордановы исключения применяются для нахождения:
а) обратной матрицы;
б) ранга матрицы;
в) решений систем линейных уравнений;
г) решения задач оптимизации;
д) всего перечисленного в пунктах а), б), в) и г).
Начальный опорный план транспортной задачи ищется методом:
Северо-западного угла
Фогеля
Начальный опорный план транспортной задачи можно составить:
а) методом Жордана;
б) методом минимальной стоимости;
в) методом аппроксимации;
г) методом Фогеля;
д) применяя методы пунктов б) и г).
Найдите верные утверждения применительно к задаче рационального использования ограниченных ресурсов:
а) двойственные оценки в оптимальном решении задачи характеризуют дефицитность ресурсов;
б) ресурс, полностью использованный в оптимальном решении, является дефицитным, его двойственная оценка — больше нуля;
в) если ресурс расходован не полностью, то он избыточен, его двойственная оценка равна нулю;
г) если ресурс расходуется не полностью, то он избыточен, его двойственная оценка больше нуля.
На рисунке изображен случай, когда своего максимального значения функция f(х) достигает
|
Найдите правильное преобразование неравенства 11Х1 + 3Х2 > -19
-11Х1 – 3Х2 < 19
Область допустимых решений задачи линейной оптимизации:
а) может быть объединением двух выпуклых многоугольников НЕТ
б) может быть окружностью
в) может образовывать невыпуклый многоугольник с отрицательными координатами вершин.
г) может быть пустым множеством (ДА)
Область допустимых решений задачи линейной оптимизации:
а) может быть пустым множеством;
б) не может быть пустым множеством;
в) может быть точкой;
г) может быть отрезком прямой;
д) может быть окружностью;
е) может образовывать выпуклый многоугольник (в пространстве — многогранник).
Область допустимых решений задачи нелинейного программирования может быть:
а) выпуклой
б) вогнутой
в) из нескольких частей
г) выпуклой, вогнутой и состоять из нескольких частей
Основным принципом, на котором базируется оптимизация в задачах динамического программирования, является:
а) принцип оптимальности Р. Беллмана;
б) принцип особенностей вычислительного метода;
в) принцип планового соответствия переменных;
г) принцип дуализма.
Оценка свободной клетки ( 2; 1) равна
|
| ||||||||||||||||||||||||||||||||||||
studfiles.net
5. Математические модели в задачах оптимизации.
Обычно решение задач оптимизации Химико-технологических процессов и производств предполагает наличие их математической моделей. Всякое аналитическое (математическое) соотношение или однозначный алгоритм, устанавливающий связь между параметрами (координатами) оптимизируемой системы носит название математической модели этой системы. Математическая модель в общем виде м.б. записана следующим образом:
(1), где 
- вектор параметров модели.
Если
- не определен с точностью до числовых значений, то функция (1) будет называться мат. описанием. В общем случае мат.модель включает соотношение (1), алгоритм определения
, программная реализация алгоритмов. Алгоритм решения, кроме соотношения (1), предполагает задание граничных или начальных условий.
может и не выражаться набором каких-либо элементарных функций, а задаваться системами алгебраических , дифференциальных, интегральных и др. видах уравнений или задаваться к.л. алгоритмом, например, алгоритмом распознавания образов, искусств, нейронные сети. Символ 
указывает на наличие однозначной связи между параметрами процесса и системы и задает вид этой связи.
Может определяться и в вероятностном смысле, т.е. устанавливать связь между векторами математических ожиданий (средних значений) координат системы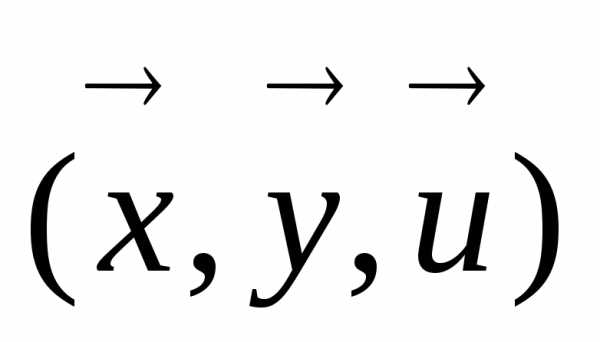
. В этом случае, когда присутствует операция усреднения, модель будет называться стохастической (вероятностной).
Решение системы (2). Иногда удается получить аналитическое решение системы (1) в виде (2). Чаще всего это алгоритм решения системы (1)
Если влияние неконтролируемых возмущений для условия данного процесса можно пренебречь или учесть их путем усреднения и текущей параметрической идентификации модели (1), например, с применением рекуррентных многошаговых процедур на основе алгоритма стохастической аппроксимации, являющейся решением стохастического уравнения, то решение (2) примет вид: (4) , где 
- вектор скорректированных параметров модели. Т.к. векторв модели в текущий момент времени является числом – константой, то его можно ввести в операторf : 
(5)
Критерий оптимальности зависит от выходных координат объекта у, являющихся результативными показателями для этого процесса, характеризующих состояние системы и м.б. представлен в виде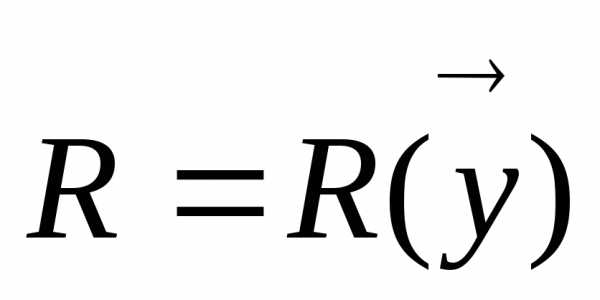 
(6)
С учетом (5) выражение для критерия можно записать в виде (7),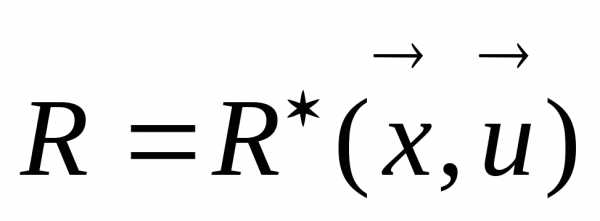 
(8) .
6. Постановка задачи оптимизации. Графическая интерпретация задачи оптимизации.
С учетом соотношения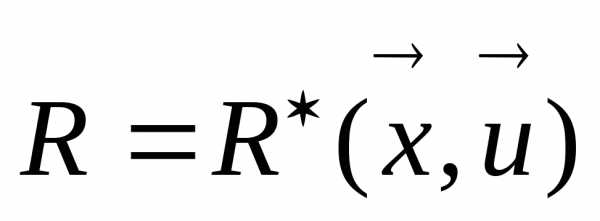 
(8) задачу оптимизации можно сформулировать: требуется найти вектор управления
такой, что при заданном векторе
критерий оптимальностиR принял бы наилучшее значение. При этом управление 
связаны между собой в общем случае соотношениями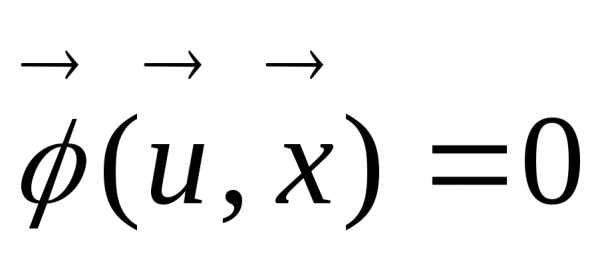
(9),
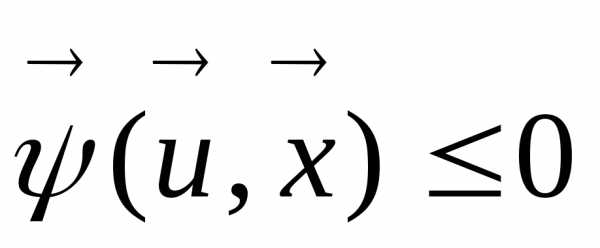(10), которые являются ограничениями в форме равенств (9) и неравенств (10) в задаче оптимизации. Часто эти ограничения являются критериями в многокритериальной задаче оптимизации, в которой
- главный критерий, а
и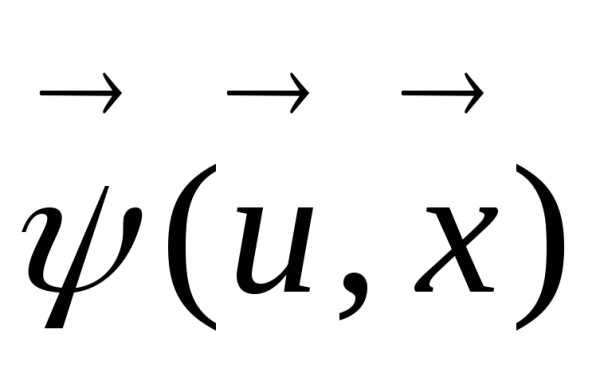
переводятся в разряд ограничений.
Решение задачи оптимизации без учета ограничения (9), (10) называется решением задачи безусловной оптимизации с одним критерием R. С учетом (9), (10) задачи оптимизации будут называться задачами условной оптимизации. Используя выражения (8), (9), (10) постановку задачи оптимизации формально можно записать 
(11)
Т.к. в задаче оптимизации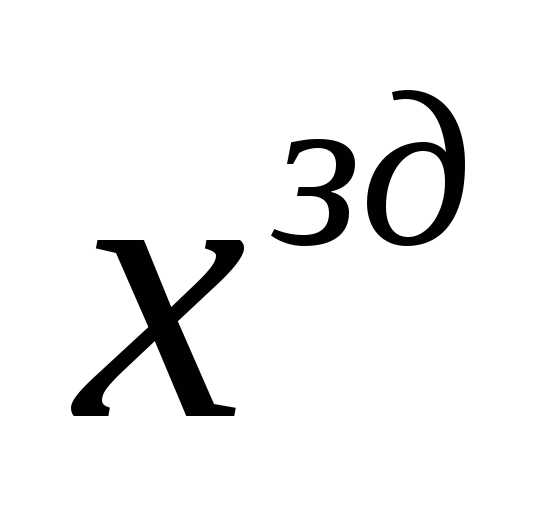 
(задание значение вектора) выступает как константа, то можно записать следующим образом:,
,
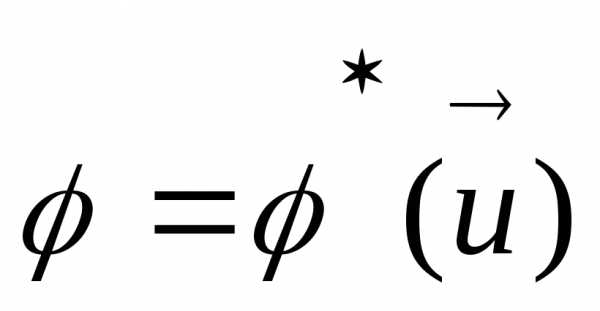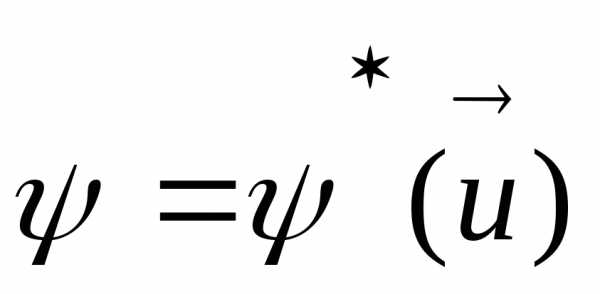(12).
Задачу (11) можно сформулировать и в след. виде (13)
В дальнейшем при изложении методов оптимизации с учетом соотношения (12) будем записывать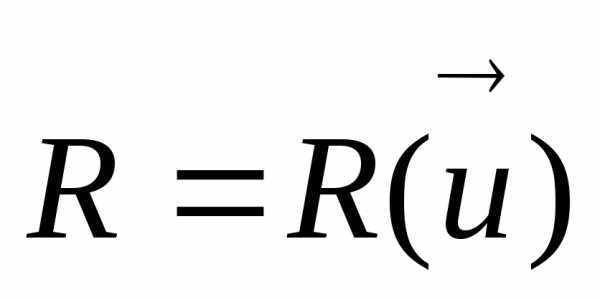 
,
,
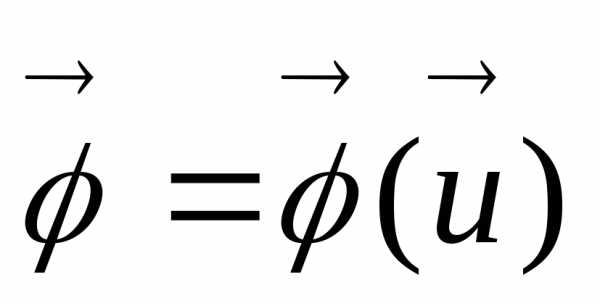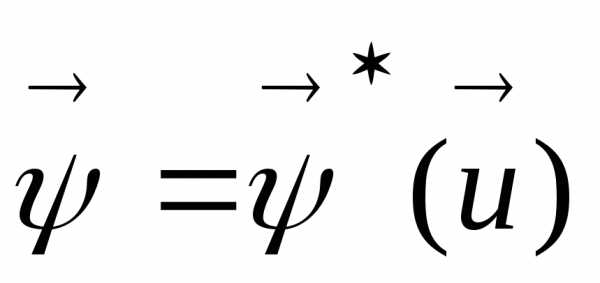
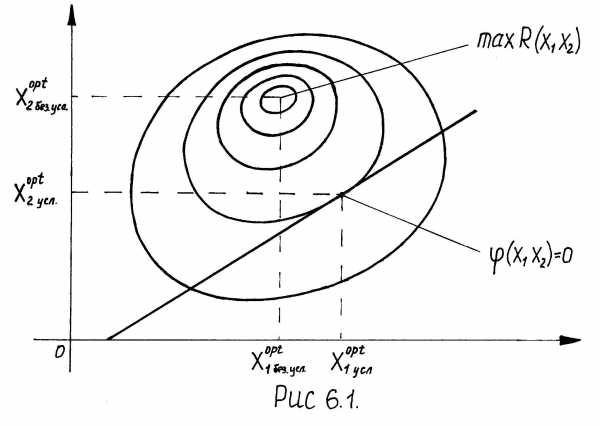
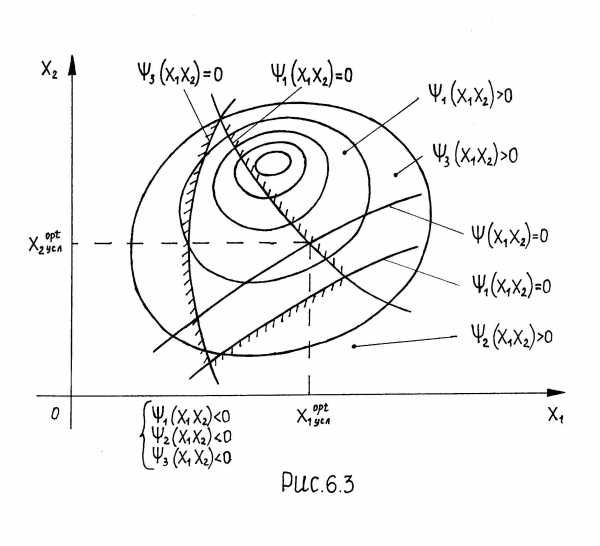
В соответствии с (13) графически задачу оптимизации можно интерпретировать следующим образом: рассмотрим задачу с 2-мя управлениями: рис 6. 1,2,3.
Пусть R(x1,x2) имеет max. , то
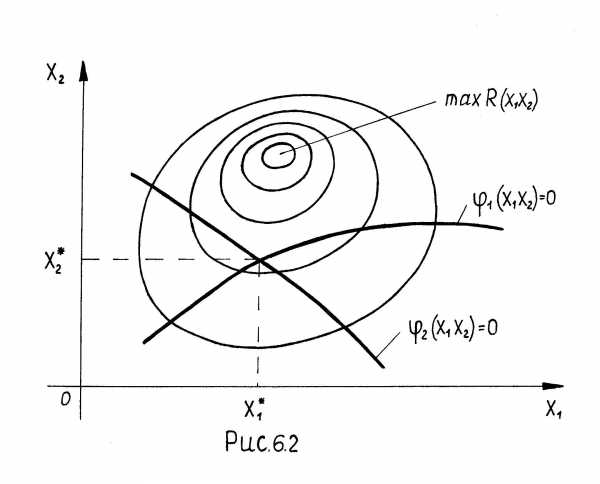
; при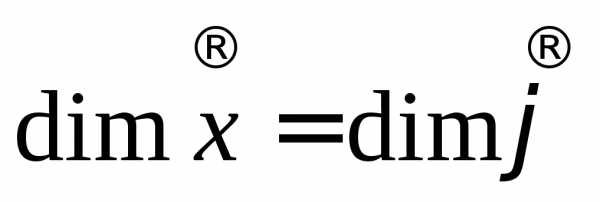
задачи оптимизации нет (рис. 6.2).
Если размерность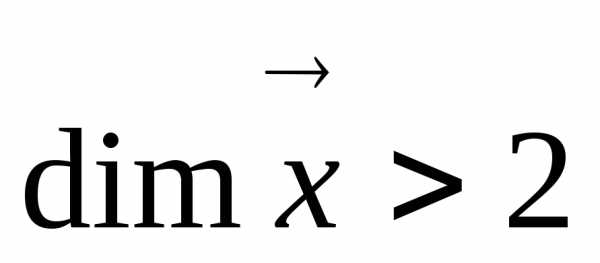 
, то для графической интерпретации отклика поверхности
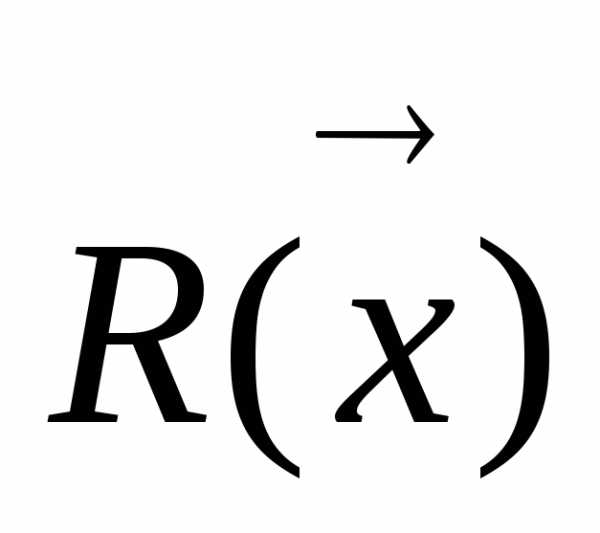берут 2 оси (координат) и через них проводят плоскость. Плоскостями, параллельными плоскости, проходящей через выбранные оси, рассекает плоскость
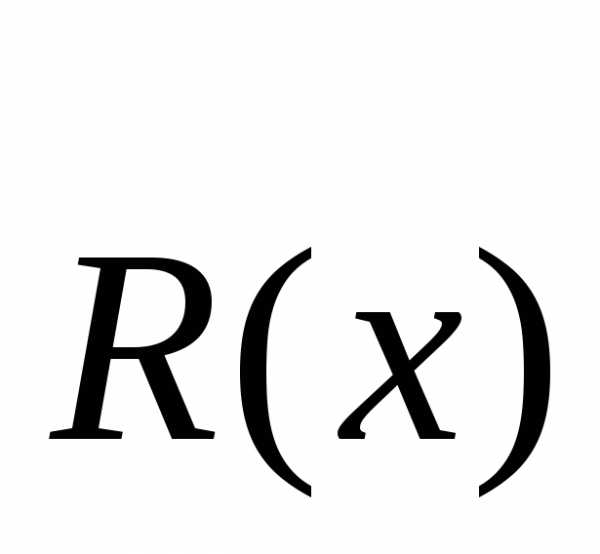(рис 6.3).
. 
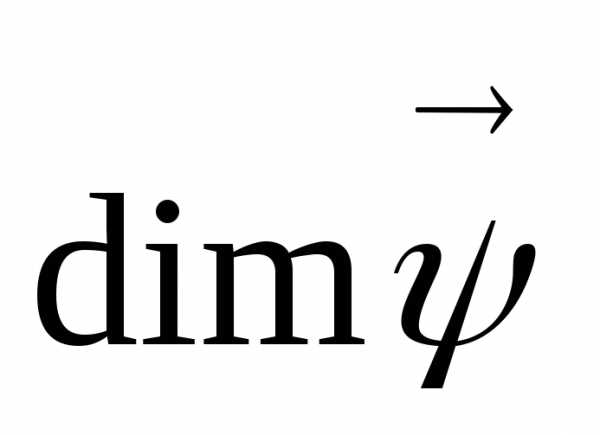- любая.
Задача оптимизации в действующей технологии является определение оптимальных значений заданий регулятора технологических процессов.
studfiles.net
