АЛГОРИТМ ТОПОЛОГИЧЕСКОЙ ОПТИМИЗАЦИИ НА ОСНОВЕ МЕТОДА ESO. Топологическая оптимизация

Топологическая оптимизация геометрии изделия как путь повышения прибыльности предприятия

Геометрия без ограничений | Создание ячеистых и сетчатых структур | Сокращение числа единиц в сборке

Если говорить сухим академическим языком, топологическая оптимизация – это процесс изменения конструкции, структуры детали и ее варьирующихся параметров при заданном критерии оптимальности с сохранением или улучшением ее функционала.

Объясним более доступно на конкретном примере. Возьмем две детали, выполняющие одну и ту же функцию с определенными нагрузками и имеющие определенный ресурс (см. рисунок ниже). По сути, это одна и та же деталь, но с разной геометрией. Геометрия первой детали оптимизирована для изготовления стандартными методами производства: на фрезерном, токарном станке и средствами других технологий металлообработки. Это простая и плоская геометрия, ее легко добиться при обработке на станке. У второй детали геометрия более сложная, и сделать ее на станке представляет серьезные трудности.

Оптимизация геометрии детали средствами аддитивных технологий

Геометрия без ограничений

Когда еще не существовало аддитивных технологий, а были только субтрактивные, то вопрос геометрии не стоял так остро и решался доступными способами. Топологическая оптимизация позволяет изменить стандартную геометрию на геометрию, специально адаптированную под определенную технологию. И это может быть и традиционная технология (например, литье), и аддитивный процесс.

Согласно данным, у второй детали меньше напряжение, меньше перемещение под нагрузкой и, самое главное, вес уменьшился на 1 кг. Для одной детали немного, но если их выпускают сто тысяч в год, то суммарно мы можем сэкономить сто тонн металла только на одной детали.

Так выглядит процесс топологической оптимизации

Программное обеспечение для топологической оптимизации не строит модель объекта с нуля. В него загружается геометрическая модель изделия, ранее изготовленного другим методом. На рисунке приведен пример изделия с простыми плоскими формами и заклепками, болтами, приваренными ребрами. Когда мы загрузили модель, мы отмечаем места, которые не полежат изменению. В данном случае это крепления. Все остальное, что не попало в эти зоны, но принадлежит детали, является так называемой design space, то есть той зоной, где программа может менять геометрию.

Затем мы в соответствии со служебным назначением изделия накладываем нагрузки, которые деталь должна выдерживать, то есть создаем силовую схему нагрузок. И далее, на основе заданных нами параметров, программа начинает создавать новую оптимизированную геометрию. Между двумя неизменными местами для крепления она выстраивает новую модель. Она анализирует напряжение в каждом сечении – выдерживает его сечение или нет. Если не выдерживает, то программа меняет сечение.

Процесс построения новой модели довольно затратный по времени и требует больших вычислительных ресурсов. Этот метод моделирования называется методом конечных элементов. Для каждой точки изделия программа составляет и решает интегральные уравнения, учитывая при этом взаимосвязи между всеми точками. В результате расчета получается новая геометрия. Затем конструктор может изменить что-то в модели, если это необходимо. В итоге получается CAD-модель.

Далее для верификации модель загружается в другое программное обеспечение, в котором она проходит финальную проверку на максимальные деформации, напряжения и пр. Затем геометрия утверждается и может быть передана в производство. При этом программное обеспечение умеет оптимизировать геометрию под разные виды производства: под литье, штамповку, ковку или под аддитивное производство.

Топологическая геометрия, как правило, имеет аморфные формы, в ней нет плоских, прямых линий, могут быть сплайны второго порядка. При соблюдении тех же самых свойств и нагрузочных характеристик такое моделирование позволяет уменьшить массу изделия, и, следовательно, сократить издержки на производство. Понижение массы изделия при сохранении функционала изделия – это задача номер один в самолетостроении, авиакосмической отрасли и автомобилестроении.

Создание ячеистых и сетчатых структур

Создание решетчатых структур

В природе такие структуры встречаются очень часто. Кости птиц могут быть почти пустотелыми, а кость млекопитающих представляет из себя жесткую оболочку с губчатой структурой внутри. Это позволяет выдерживать те же нагрузки при меньших затратах организма на выращивание такой кости и меньшем весе.

Топологическая оптимизация дает возможность делать решетчатые структуры разных форм и размеров (например, гексагоновые) или создавать ячеистую структуру, а снаружи – твердую оболочку. Стандартными методами такую структуру нельзя изготовить – только с использованием аддитивных технологий.

Сокращение числа единиц в сборке

Схема смесителя жидкости с газом

Это еще одно преимущество топологической оптимизации вместе с аддитивными технологиями. Пример: на рисунке изображен типичный сатуратор (смеситель жидкости с газом). Внутри трубы стоит маленький фильтр. Чтобы установить его туда, необходимо эту деталь сделать разъемной в двух частях, сделать фланцы для крепления, а также прокладки, болты и т.д.

С помощью аддитивных технологий можно в одном корпусе создать и саму трубу, и мелкий фильтр внутри, и канал вокруг для распределения газа.

Оптимизированный смеситель в едином корпусе

В итоге, применяя 3D-печать металлом, получаем в едином корпусе единую деталь, одну единица хранения. Отсутствует операция сборки, нет прокладок, которые могут течь, нет больших фланцев, на которых уходил металл.

При анализе показателей видим, что вес детали уменьшился, прокладок нет, время сборки стало нулевым.

Если мы уменьшаем вес детали в самолете всего на 200 г, а в нем таких деталей 100, то мы экономим 20 кг, а при ресурсе самолета в 25 лет это огромная экономия топлива или лишняя полезная нагрузка.

Таким образом, топологическая оптимизация – это программное обеспечение, которое создает геометрию без ограничений.

blog.iqb-tech.ru

Четыре основных ошибки при топологической оптимизации

Топологическая оптимизация – это подход к оптимизации конструкции, ищущий наилучшее распределение материала в заданной области для заданных нагрузок и граничных условий. Применение топологической оптимизации на этапе проектирования помогает найти вариант дизайна конструкции с наиболее рациональным распределением материала и пустот в объёме, таким образом заметно снизить его массу.

Но действительно ли так просто отыскать желаемую форму детали? Сложность, как и время поиска можно заметно снизить, если правильно использовать ANSYS Topology Optimization или другой продукт, позволяющий проводить сложную топологическую оптимизацию. В данной статье разобраны основные ошибки, которые возникают у пользователей, впервые столкнувшихся с топологической оптимизацией.

1. Указание некорректной области для оптимизации

Процесс топологической оптимизации начинается с выбора области, в рамках которой оптимизатор проводит поиск. В идеале, конечно, можно указать в качестве этой области весь свободный объём, однако делать так обычно возможности нет. Пожалуй, одним из наиболее значимых факторов при выборе области для оптимизации является учёт взаимодействия детали в сборке.

Использование геометрической модели уже существующей детали – плохой вариант, так как она уже имеет (скорее всего) неоптимальное распределение материала. Топологический оптимизатор же «не умеет» добавлять материал, он ищет оптимальный вариант конструкции путём удаления участков геометрии из заданной области.

Объясним прошлый абзац при помощи примера (см. рисунок 1). Сравнивая результаты оптимизации, можно отметить, что они очень чувствительны к тому насколько свободно алгоритм поиска распределения материала мог распоряжаться объёмом.

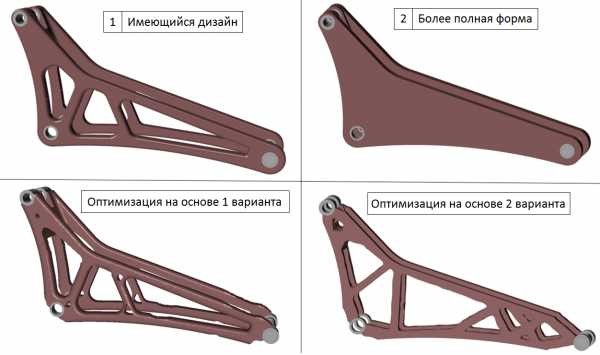
Рисунок 1 – Пример выбора области для топологической оптимизации

И в том и в другом случаях поиск оптимального распределения материала осуществлялся внутри соответствующей области, но в первом случае часть отверстий в этой области уже существовала. Таким образом в первом случае ANSYS Topology Optimization, имея возможность лишь удалять «излишки» материала, не может добавить его там, где в исходной геометрии есть отверстия. В результате при одинаковых массах, второй вариант дизайна получился на 25% более жёстким.

2. Определения областей для обязательного сохранения

После указания области для оптимизации (в рамках которой программа будет искать результат) важно также определить те области, которые точно нужно сохранить. Чаще всего это участки, через которые компоненты контактируют друг с другом или просто части, без которых нормальное функционирование детали невозможно.

3. Низкая плотность сетки

Результаты топологической оптимизации чувствительны к конечно-элементной сетке, то есть полученная форма конструкции может отличаться при расчётах на различных сетках. В связи с этим использование недостаточно мелкой сетки может приводить к неудовлетворительным результатам. С измельчением сетки некоторые участки оптимизированной области становятся всё сложнее и начинают состоять из всё более мелких элементов. Для учёта вышеперечисленного эффекта в ANSYS Topology Optimization рекомендуется подбирать размер конечных элементов таким, чтобы как минимум три элемента умещалось по толщине наименьшей грани предполагаемой формы детали.

4. Неверная оценка времени оптимизации и проектирования

Пожалуй, главное заблуждение при использовании топологической оптимизации заключается в том, что по нажатию кнопки «Solve» вы получаете готовый конечный дизайн или форму детали. На самом деле всё немного не так. Результаты оптимизации лишь показывают в каких областях материал необходим, а в каких – нет с точки зрения тех ограничений и целевой функции, которые были использованы.

Рисунок 2 – Топологическая оптимизация детали и последующая обработка результатов

В редких случаях результаты оптимизации можно сразу или после минимальной обработки использовать в качестве конечной формы детали. Чаще всего, однако, время обработки результатов едва ли не больше, чем время расчётов, на основании которых эти результаты получены. Для учёта конечной формы детали обычно необходимо принять во внимание все особенности изготовления. В качестве иллюстрации вышесказанного обратите внимание на пример детали, оптимизацию которой выполняли инженеры Volkswagen (рисунок 2).

Также немаловажно, что часть времени (иногда значительная) обязательно уйдёт на обработку дизайна в SpaceClaim. Таким образом, процесс нахождения формы детали заметно увеличивается.

Теперь, когда вы знакомы с основными ошибками при топологической оптимизации, надеюсь, вам будет легче решать свои задачи нахождения оптимальной формы конструкции.

Статья подготовлена с использованием материалов сайта innovationintelligence.com

cae-club.ru

Топологическая оптимизация

Специалист по Civil Engineering Игорь Останин о подходах к топологической оптимизации, природных арках и поисках оптимальных форм

Как оптимизировать структуру и форму окружающих нас предметов? Решением этой задачи занимается топологическая оптимизация. Как развитие 3D-печати и вычислительных мощностей повлияло на развитие области и чем объясняется природная оптимизация, рассказывает научный сотрудник Центра Сколтеха по научным и инженерным вычислительным технологиям для задач с большими массивами данных Игорь Останин.

ПостНаука и Сколковский институт науки и технологий представляют курс «Математическое моделирование», составленный на основе магистерской программы «Вычислительные системы в науке и технике».

Топологическая оптимизация — это в некотором смысле попытка автоматизировать труд инженеров. Разрабатывать конструкции, которые достаточно эффективны для решения определенных задач, инженеры научились довольно давно: несущие балки, детали самолетов, корпуса подводных лодок и так далее. Для каждого конкретного приложения инженер может сказать, как приблизительно должна выглядеть та или иная деталь. Но насколько оптимальной будет такая деталь? Можно ли придумать форму лучше? И если да, то насколько лучше?

Эти вопросы могут быть сформулированы на достаточно строгом математическом языке в виде задачи оптимизации, и при определенных допущениях на них может быть дан единственно верный ответ. Представим, что у нас есть кронштейн, который одним концом жестко заделан в стену, а другой конец тяжело нагружен. Можно ли придумать для него такую форму, которая минимизирует запасенную в нем упругую энергию (меру его жесткости), и при этом потратить минимум материала? Топологическая оптимизация дает ответ на этот и подобные вопросы.

Помимо задач оптимизации жесткости и прочности, топологическая оптимизация используется, в частности, при разработке микроструктур метаматериалов. Например, сконструировать такую микроструктуру, чтобы после ее периодического повторения и усреднения на макроуровне получить желаемые упругие свойства.

История топологической оптимизации

Сама идея структурной оптимизации, то есть возможности разумно экономить материал, появилась в начале XX века. Первую, пионерскую работу в 1904 году написал Митчелл (Anthony George Maldon Michell (1904) The limits of economy of material in frame-structures, Philosophical Magazine, Vol. 8(47), p. 589–597). В контексте численных методов о структурной оптимизации впервые стали говорить одновременно с появлением метода конечных элементов, то есть в 1960-е годы.

Наиболее интересные идеи топологической оптимизации появились в 1980-е годы, и на их основе были разработаны хорошие, законченные теории. Но настоящий всплеск интереса к этой теме начался вместе с широким распространением трехмерной печати. Оптимизировать структуру только полдела, ее ведь нужно еще и реализовать. А если оптимальная структура настолько сложна, что ее не позволяет сделать ни один станок с числовым программным управлением? Именно здесь на помощь приходит 3D-печать. На рубеже 2000–2010-х годов истекли некоторые ключевые патенты на технологии, связанные с 3D-печатью. После этого она стала развиваться экспоненциально, и, как следствие, все вспомнили про топологическую оптимизацию. Благодаря этому появился инструмент, позволяющий печатать смоделированные структуры.

Техники топологической оптимизации

Самой первой техникой топологической оптимизации была SIMP — Solid Isotropic Material with Penalization. Исследователи достаточно быстро поняли, что задача оптимизации как поиска распределения материала изначально была сформулирована плохо. Изменение топологии, то есть появление в заполненной области сквозных отверстий или полостей, приводит к появлению огромного количества равноценных структур. Более того, чем мельче вводимые полости или отверстия, тем лучше можно получить оптимизируемый функционал — число, которое сопоставляется структуре. На практике же такие микроперфорированные решения нам неинтересны, и их появление лишь артефакт постановки задачи.

Как же получить адекватное решение? В этом поможет регуляризация: нужно по возможности уменьшить пространство поиска, объяснив в задаче, что именно мы ищем. Например, нам нужна структура с каким-то конечным числом элементов или структура по возможности с небольшой площадью поверхности. Кроме того, нужно сформулировать задачу так, чтобы она была, что называется, выпуклой: чтобы в направлении улучшения свойств можно было двигаться потихоньку, маленькими итерациями, а в конце концов прийти к наилучшей структуре.

Классическая формулировка задачи топологической оптимизации SIMP позволяет сделать именно это: с одной стороны, сформулировать изначально невыпуклую задачу в удобном для градиентного спуска виде, не делая ее при этом глобально выпуклой, но создавая выпуклые подзадачи на каждом локальном шаге. С другой стороны, при помощи техники фильтрации мы можем определить необходимый размер детали.

Этот метод не сразу получил признание, потому что он довольно сложен и не существует его прямой и понятной инженерной интерпретации. В SIMP подразумевается, что в области, в которой мы моделируем, нужно сначала найти серое (иначе говоря, промежуточное) распределение, то есть размазать условную балку и сталь для нее в виде промежуточной плотности, а потом постепенно собрать эту плотность в отдельные элементы конструкции. Такой подход может показаться на первый взгляд несколько странным: совсем неочевидно, как его можно интерпретировать. Поэтому до определенного момента прикладники относились к этой технике скептически.

Потом появилась еще одна техника, которая стала конкурировать с SIMP. Она основана на так называемом жадном вырезании: мы берем сплошной кусок материала и начинаем вырезать материал в тех местах, где упругая энергия минимальна. Основная цель — по возможности оставлять полезные для данной конструкции области, несущие нагрузку, где есть напряжение, а ненапряженные области удалять. Таким образом, двигаясь итеративно, мы получаем конструкции, близкие к тому, что генерирует SIMP. Такая техника довольно просто реализуется и называется «эволюционная структурная оптимизация» (Evolutionary Structural Optimization, ESO). В более общей постановке двунаправленной ESO (Bidirectional ESO, BESO) позволяется не только удалять, но и добавлять эффективный материал, что позволяет найти более эффективные структуры.

Две техники — простая и вычислительно незатратная BESO, а также несколько более математически строгая SIMP — сегодня активно конкурируют. Они были реализованы во многих коммерческих пакетах и стали широко применяться в современной индустрии.

Естественная оптимизация

Когда я учился в Университете Миннесоты в США, я узнал о существовании природных арок. Их можно увидеть в национальных парках Юты и Аризоны. Это естественные формации, которые похожи на арки, созданные людьми, но на самом деле это природные образования. Я задался вопросом: как могла появиться такая красота? Возникла идея: что, если материал разрушается именно там, где нет напряжения? Это вполне следует из закона сухого трения: чем сильнее мы что-то прижимаем, тем труднее это сдвинуть. Это достаточно хорошо обоснованный и широко используемый закон геомеханики.

Спустя некоторое время, в 2014 году, была опубликована статья в Nature Geoscience со сходной идеей. Прочитав ее, я понял, что появление таких естественных арок — это не что иное, как реализация алгоритма эволюционной структурной оптимизации в природе. Я и мои коллеги написали об этом статью “Natural Erosion of Sandstone as Shape Optimisation” в Scientific Reports, которая привела к напряженным дискуссиям.

С одной стороны, это очень красивая идея, которая вызвала значительный всплеск интереса и энтузиазма у наших коллег. У нас есть свидетельства того, что именно так все и происходит: природа формирует оптимальные, стабильные катенарные арки. Если мы возьмем цепь за концы, то увидим, что она провисает по определенной линии, известной как катеноида, или цепная линия. Если перевернуть эту линию, получится наиболее стабильная арка. В случае с цепью все звенья могут сопротивляться только нагрузке на растяжение, а цепь моментально меняет форму, если появляется какой-то изгибающий момент. Поэтому в уравновешенной цепи нет никаких изгибов и сдвигов, только чистое растяжение. Если сменить направление гравитации и перевернуть цепь, то получится система, которая находится в состоянии чистого сжатия. А типичные материалы, используемые в гражданском строительстве, равно как и естественные геоматериалы, хорошо выдерживают состояние сжатия и относительно легко разрушаются изгибающими моментами и сдвигами. Именно благодаря этим свойствам природа воспроизводит катенарные арки, которые остаются стабильными в геологических масштабах.

С другой стороны, процессы эрозии все же слишком сложны, чтобы можно было безапелляционно говорить об однозначной связи эрозии и феноменологических алгоритмов оптимизации формы, не говоря уже о конкретных математических постановках задачи оптимизации. Из-за этого наша работа получила и немало обоснованной критики.

Современные направления в теории топологической оптимизации

Топологическая оптимизация сама по себе — подраздел теории оптимизации, но с некоторой спецификой, связанной с ее развитием в плотном контексте практических приложений. В этой области работают инженеры, которым важен практический результат. Если они получили конструкцию легче на 5%, обладающую той же жесткостью и прочностью, что и предыдущая, — это и есть их результат. Но также топологическую оптимизацию изучают чистые математики и вычислители, которых интересует именно теоретическая, а не инженерная сторона вопросов.

У математических методов оптимизации тоже есть характеристики, которые позволяют оценить их эффективность: насколько быстро они сходятся, насколько устойчивы, насколько сложные формы и топологии позволяют получить. Здесь развивается абстрактная теория о существовании и единственности подобных решений. На текущий момент с математической стороны, по крайней мере в плане чистого вариационного исчисления, теория более-менее завершена, достаточно понятны все основные формулировки оптимизации формы и оптимизации топологии, их свойства и способы решения.

Активно развиваются области, связанные с методами быстрой оптимизации. Одной математической постановки недостаточно: нужно реализовать эту постановку и научить компьютер быстро решать задачу. И в этой области сейчас сосредоточены очень большие усилия как теоретического, так и технического характера. Как создать параллельный алгоритм оптимизации для распределенных вычислений? Как уменьшить число степеней свободы? В численном решении рано или поздно все сводится к системе линейных уравнений, которую тоже надо как-то решать. По возможности она должна как-то удобно решаться — не школьным методом Гаусса, который требует число операций, пропорциональное кубу числа неизвестных, а быстрее. В этой области сейчас сосредоточены основные усилия математиков-прикладников.

Один из интересных трендов последних лет — использование топологически оптимальных конструкций в дизайне и архитектуре. Это делается не из желания сэкономить, а скорее из эстетических соображений. Топологическая оптимизация обычно приводит к конструкциям, похожим на естественные структуры — гладким, без концентрации напряжения, то, что называют bionic design. Еще одно модное направление — топологическая оптимизация в природе, в том числе неживой. Это естественные процессы, которые эквивалентны математической оптимизации. Эти результаты активно популяризируются среди инженеров. Ведь и сегодня далеко не все из них знают о существовании топологической оптимизации.

nangs.org

Топологическая оптимизация как форма искусства

Слева направо: оригинальная деталь, промежуточный результат и окончательный вариант модели.

Arup

Инженерная компания Arup провела обычную операцию — топологическую оптимизацию модели детали, которая должна удерживать вместе шесть кабелей. Операция простая, но деталь в результате приобрела совершенно фантастический вид, а заодно стала выгодной в производстве.

Изначально деталь выглядела как труба, к которой приварены шесть крепежных петель — конструкция простая, но тяжелая, да и материала на нее уходит много. Первая попытка оптимизации модели в Autodesk Within дала изящный результат, но в новой версии деталь получила большое количество ажурных поддержек, которые дополнительно приходится удалять на этапе постобработки. Кроме того, за основу была взята оригинальная модель, достаточно большая по размерам.

Arup

Инженеры проконсультировались с компанией CRDM/3D Systems, которая специализируется на аддитивном производстве, и снова оптимизировали модель детали, однако в этот раз добавили ограничения, задаваемые в том числе параметрами 3D-принтера, на котором планировалось изготовить деталь методом селективного лазерного спекания. В частности, учитывалась толщина слоя, высота рабочей камеры и количество деталей, изготавливаемых принтером за один раз. Получившуюся модель еще немного доработали вручную, изменив расположение крепежных отверстий, высоту детали и убрав материал там, где позволил структурный анализ детали.

Arup

Результат получился интересным и совсем не похожим на изначальный вариант. Во-первых, по подсчетам инженеров, через 2-5 лет аддитивное производство окончательной оптимизированной версии детали станет дешевле, чем традиционное. Во-вторых, расчеты указывают на возможное сокращение материала до 60 процентов по сравнению с оригинальной деталью при сохранении заявленных характеристик по максимальной нагрузке в 109 килоньютонов на каждый кабель.

Arup

В-третьих, это красиво.

nplus1.ru

Топологическая оптимизация конструкций в ANSYS Mechanical

Топологическая оптимизация позволяет с помощью МКЭ расчетов снижать массу и улучшать жесткостные характеристики конструкций. Начиная с 17 версии в ANSYS Workbench Mechanical включены широкие возможности по решению задач топологической оптимизации.

Под оптимизацией топологии понимают изменения в конструкции, включающие создание новых границ тела и удаление существующих. Целью топологической оптимизации является увеличение или уменьшение заданного свойства конструкции (например, уменьшение энергии деформации, увеличение главной собственной частоты) при удовлетворении определенных условий (например, снижение материалоемкости).

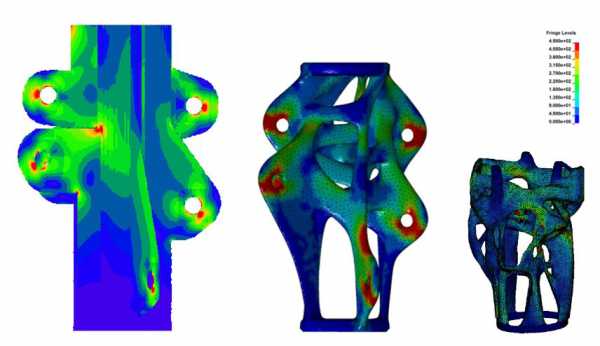
1. Декартова КЭ (конечно-элементная)сетка оптимизируемой конструкции

2. Граничные условия и нагрузки: синим –закрепления, красным – силы

3. Наборы элементов, исключенных изпространства проектирования конструкции

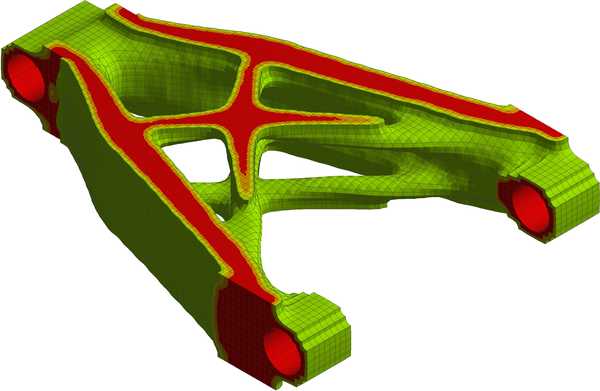
4. Результат оптимизации – распределениематериала в конструкции

5. Необработанные контуры новойтопологии конструкции в формате STL

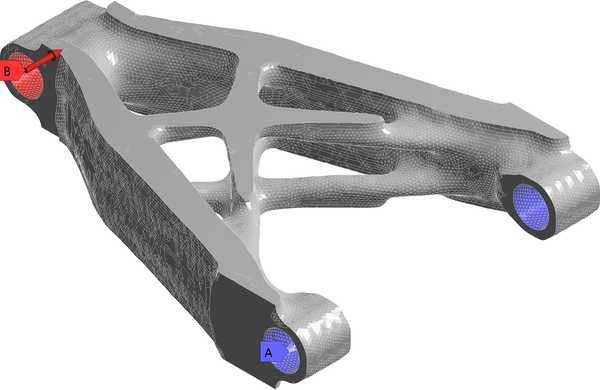
6. Граничные условия и нагрузки, приложенныек конструкции после обработки

7. Автоматизировано построенная КЭ сеткадля новой топологии

8. Результат поверочного расчета – поле

напряжений в конструкции с новой топологией

Начиная с 17 версии в ANSYS Workbench Mechanical включены возможности по решению задач топологической оптимизации. Топологическая оптимизация, выполняемая средствами программного обеспечения ANSYS, выполняется в нескольких этапов.

На первом этапе проводится постановка и решение прочностной задачи методом конечных элементов (МКЭ) в ANSYS Mechanical. Для этого задается контурная геометрическая область конструкции, ее механические свойства, условия закрепления и действующие нагрузки.

ANSYS обладает обширной встроенной библиотекой свойств материалов для расчетов. Геометрия модели может быть импортирована из основных CAD систем: SolidWorks, Autodesk Inventor, PTC Creo, Catia v5, Solid Edge, Rhinoceros, SketchUp, Siemens NX, AutoCAD. При использовании иной CAD системы, как например Компас-3D, геометрия передается через один из многочисленных открытых форматов: Parasolid, STEP, SAT, IGES.

Нагрузки на конструкцию не только задаются в ANSYS Mechanical, но получаются в рамках многодисциплинарных расчетов или импорта из внешних файлов (как результаты сторонних расчётов). Так, например, может быть учтено давление, создаваемое потоком на крыло или приложена распределенная нагрузка согласно ГОСТ или СНиП.

После решения прочностной задачи начинается непосредственная работа по топологической оптимизации конструкции. Формулируется целевая функция – снижение податливости конструкции, испытывающей один или несколько вариантов нагружения, увеличение собственных частот, ограничение по деформациям или иная.

Для корректной работы алгоритма описывается пространство проектирования: определяется область конструкции, топология которой может меняться, и область, для которой изменения запрещены. Дополнительное удобство обеспечивают инструменты, контролирующие возможность изготовления получаемой топологии. Эти инструменты позволяют требовать соблюдения линейной или циклической симметрии топологии, проверять возможность изготовления детали путем литья или фрезеровки, отсутствие внутренних полостей. Также возможен контроль минимального или максимального размера вновь получаемых элементов топологии конструкции.

После задания всех необходимых настроек алгоритма оптимизации остается указать желаемый процент снижения материалоемкости и запустить расчет.

По итогам расчета ANSYS Mechanical позволяет экспортировать полученную топологию в формате STL. На этом можно заканчивать оптимизацию, но программное обеспечение ANSYS позволят сделать намного больше – а именно выполнить поверочный расчет.

ANSYS SpaceClaim Direct Modeler, один из самых совершенных на рынке инструментов прямого моделирования геометрии, способен прочитать, проверить, исправить и существенно упростить STL геометрию. Обработанная в SpaceClaim STL модель конвертируется в формат, пригодный для повторного расчета.

ANSYS Meshing, основной сеточный генератор ANSYS, обладает специализированным алгоритмом построения качественной сетки на телах, обладающих сложной топологией и высокой сложностью поверхностей. Алгоритм позволяет получить сетку высокого качества без необходимости ручной подготовки геометрии.

После создания КЭ модели с новой топологией поверочный расчет в ANSYS Mechanical позволит быть уверенным в работоспособности облегченной конструкции.

multiphysics.ru

Топологическая оптимизация помогла облегчить крыло самолета

sebastien lebrigand / Flickr

Исследователи из Датского технического университета использовали метод топологической оптимизации для улучшения характеристик правой консоли крыла пассажирского лайнера Boeing 777. По итогам оптимизации исследователи пришли к выводу, что такой метод позволяет снизить массу конструкции крыла по меньшей мере на два-пять процентов по сравнению с традиционной конструкцией, используемой сегодня. Работа датских исследователей опубликована в Nature.

Топологическая оптимизация представляет собой способ улучшить ту или иную конструкцию с точки зрения распределения материала при сохранении общих прочностных характеристик неизменными. В общих чертах такой метод автоматизированного или частично автоматизированного улучшения позволяет оптимизировать конструкцию, рационально распределив материал и пустоты в объеме и снизив ее массу. Результат топологической оптимизации внешне обычно напоминает нечто, созданное природой.

Для своего эксперимента исследователи использовали программное обеспечение топологической оптимизации, запущенное на французском суперкомпьютере Curie. Для оптимизации ученые взяли внутреннюю конструкцию правой консоли крыла пассажирского лайнера Boeing 777 длиной 27 метров. Его трехмерную модель исследователи разбили на 1,1 миллиарда вокселей, небольших структурных единиц, трехмерных аналогов двумерного пикселя. При оптимизации программа рассчитывала нагрузки сначала для каждого воксела в отдельности, а затем для их совокупности.

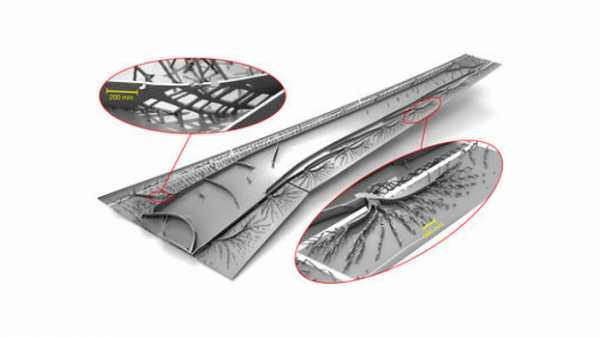
Конструкция крыла после оптимизации

Technical University of Denmark

Получавшаяся после каждой оптимизации трехмерная модель подавалась на вход программы несколько сотен раз. В результате новая внутренняя структура крыла получилась плавной, внешне напоминающей сосудистую сетку. Новая конструкция получилась легче, но ее общая гибкость и устойчивость к нагрузкам сохранилась. По оценке исследователей, такая оптимизация позволит добиться уменьшения потребления топлива самолетом на 40-200 тонн в год в зависимости от конструкции самого летательного аппарата.

Одна консоль крыла лайнера Boeing 777 имеет три лонжерона (продольные силовые элементы) и более 30 нервюр (перпендикулярные ребра). При оптимизации программное обеспечение уменьшило количество лонжеронов до двух, а число нервюр — до трех, причем последние расположились ближе к корню крыла. Вместо множества нервюр трехмерная модель внутренней конструкции крыла самолета получила структурные образования, наподобие ветвей. Следует отметить, что программа учла необходимость свободного пространства для топливных баков и механизации.

Топологическая оптимизация обычно используется для улучшения конструкции отдельных небольших элементов. По утверждению датских ученых, такой метод был применен к крупной конструкции впервые.

Сегодня авиаразработчики не рассматривают радикальное изменение конструкции крыла в качестве метода повышения экономичности самолетов. Внутреннюю структуру крыла в обозримой перспективе серьезно менять не планируется, однако исследователи работают над оптимизацией формы и внешних элементов этого аэродинамического элемента. В частности, в Евросоюзе разрабатывается проект ламинарного крыла, два прототипа которого впервые были испытаны в конце сентября текущего года.

Ламинарное крыло должно иметь очень гладкую поверхность и невысокий профиль, чтобы обеспечить ламинарный, невозмущенный, воздушный поток на как можно большей своей площади. Для создания гладкого крыла планируется использовать несколько технологий, включая более плотную подгонку стандартных элементов конструкции друг к другу. Предполагается, что ламинарное крыло будет иметь на 50 процентов меньшее лобовое сопротивление по сравнению со стандартным. Это позволит снизить потребление топлива самолетом в полете на пять процентов.

Василий Сычёв

nplus1.ru

АЛГОРИТМ ТОПОЛОГИЧЕСКОЙ ОПТИМИЗАЦИИ НА ОСНОВЕ МЕТОДА ESO | Опубликовать статью РИНЦ

Брюхова К.С.1, Максимов П.В.2

1Магистрант, 2Кандидат технических наук, доцент, Пермский национальный исследовательский политехнический университет

АЛГОРИТМ ТОПОЛОГИЧЕСКОЙ ОПТИМИЗАЦИИ НА ОСНОВЕ МЕТОДА ESO

Аннотация

В работе представлено решение задачи топологической оптимизации опорной конструкции. Разработан алгоритм топологической оптимизации, использующий критерий, учитывающий распределение напряжений в конструкции. Алгоритм написан на языке APDL ANSYS. В представленных результатах присутствует примеры оптимизации конструкции с различными значениями параметра оптимизации. При использовании представленного в работе алгоритма получена оптимизированная конструкция, в которой появляются участки, представляющее собой подобие балочно-стержневых конструкций.

Ключевые слова: топологическая оптимизация, метод конечных элементов, ANSYS, методы оптимизации.

Bryukhova K.S.1, Maksimov P.V.2

1Master student, 2PhD in Engineering, associate professor, Perm National Research Polytechnic University

THE ALGORITHM OF TOPOLOGY OPTIMIZATION BASED ON THE ESO-METHOD

Abstract

The paper presents a solution to the problem of the topological optimization of the support structure of the shop. The algorithm uses the topological optimization criterion taking into account the distribution of stresses in the structure. The algorithm is written in apdl ANSYS. The results of the present represented by examples of design optimization with different values of the optimization parameter. When using the algorithm presented in this work, the optimized design is obtained, in which there are areas representing the similarity of rod structures.

Keywords: topological optimization, finite elements method, ANSYS, optimization methods.

Топологическая оптимизация – математический подход, решающий проблему оптимального распределения материала в ограниченном пространстве с учетом действующих нагрузок и граничных условий таким образом, чтобы решение удовлетворяло требуемым условиям. При этом анализ конструкции выполняется методом конечных элементов, в то время как сама оптимизация может выполняться одним из известных методов оптимизации.

Постановка задачи топологической оптимизации

Один из подходов топологической оптимизации состоит в минимизации податливости и максимизации функции жесткости, при ограничениях в виде граничных условий и условий нагружения. Так же в приоритете стоит максимальное достижение в конструкции состояния равнопрочности.

Формула пересчета перегруженности модели, с учетом распределения напряжений в конструкции выглядит следующим образом:

σ= σmin/σmax, (1)

где σmin, σmax – минимальное и максимальное значение интенсивности напряжений по Мизесу, найденные среди всего набора значений интенсивностей, вычисленных в центральных точках конечных элементов.

Описание разработанного алгоритма топологической оптимизации

Решается задача о разработке алгоритма топологической оптимизации на основе метода ESO. Математическая основа метода ESO достаточно проста. В текущей работе принято решение усложнить описываемым образом известный метод, а в последующем заимствовать и интегрировать в модифицированный алгоритм некоторый функционал метода BESO.

Для решения данной задачи предлагается следующий алгоритм:

Заданная проектная область подробно разбивается на конечные элементы. Для построенной конечно-элементной модели задаются граничные условия и условия нагружения.
Производится расчет напряженно деформированного состояния конструкции.
Определяется максимальное и минимально эквивалентное напряжение по Мизесу в центральных точках каждого элемента, они потребуются для дальнейших расчетов.
Производится расчет критерия оптимизации

φ = (σmax – σmin)*e – σmin, (2)

где φ – критерий оптимизации; e – коэффициент оптимизации, который на текущем этапе подобран после ряда численных экспериментов, коэффициент дает лучшие результаты с точки зрения сходимости (сходится быстрее за меньшее количество итераций). Так же, благодаря подобранному параметру, конструкция быстрее становиться равнопрочной, то есть указанный далее коэффициент перегруженности модели достигает нужного значения близкого к единице.

Очень часто при топологической оптимизации конструкций возникает проблема, когда элементы располагаются как бы в шахматном порядке, то есть связь, между двумя существующими элементами, производится только за счет одного узла, что в последующем требует дополнительной инженерной доработки уже после выполнения топологической оптимизации конструкции. При подобранном критерии и при более мелкой сетке такая проблема практически исчезает. Понятно, что если же сетка будет недостаточно мелкой, то конструкция будет выглядеть более грубо и критерий оптимизации не сможет полностью решить сложившуюся проблему.

Так же благодаря данному критерию последующее распределение напряжений будет более гладким.

Определяется общая характеристика распределения напряжений в конструкции. Для этого рассчитывается отношение минимального эквивалентного напряжения к максимальному эквивалентному напряжению во всей оптимизированной конструкции, а после записывается получившееся значение. Тем самым становиться возможно определить равнопрочность конструкции, в идеале данное отношение должно стремиться к единице.
Производится вычисление массы. Вычисление массы может производиться на каждой итерации, чтобы далее было возможно качественно и количественно оценить падение массы в процессе топологической оптимизации конструкции.
Производится проверка значения критерия оптимизации во всех элементах, если он ниже полученного значения, то записывается номер соответствующего элемента в специальный массив, который будеv использоваться на следующем шаге.
Проверяется, является ли конструкция равнопрочной. То есть рассматривается значение, записанное на шаге 5. Если это значение равно или выше заданного значения (заданное значение должно быть меньше единицы или равно ему, смотря, какого результата необходимо добиться), то конструкция является равнопрочной, а цикл завершается, и пункт 9 не выполняется (в случает с циклом while это условие является условием выхода из цикла), а выполняются пункты, следующие за пунктом 10, которые уже не входят в цикл по элементам. В противном случае выполняются последующие шаги, и цикл начинается заново.
С использованием технологии умерщвления элементов, представленной в пакете ANSYS (EKILL) исключаются из расчета элементы, номера которых записывались на шаге 7.

При умерщвлении конечного элемента программа ANSYS фактически не удаляет “убитые” элементы. Вместо этого она деактивирует их, умножая их жесткость (или проводимость, или другой аналогичный параметр) на коэффициент уменьшения (ESTIF). Этот коэффициент по умолчанию равен 1.0E-6, но можно задать и другие значения.

Проводится расчет напряженно деформированного состояния для оптимизированной конструкции.
В программе установлен счетчик, по которому пользователь сможет определить номер итерации, на которой он остановился, либо остановилась сама программа.

В текущей реализации модифицированного алгоритма, как и в методе ESO, не предполагается «серых» областей.

Процесс топологической оптимизации конструкции носит итерационный характер, на каждом шаге которого при помощи метода конечных элементов определяется напряженно-деформированное состояние, реализуемое в конструкции с измененной конфигурацией при заданных силовых и кинематических граничных условиях.

Результаты работы алгоритма топологической оптимизации

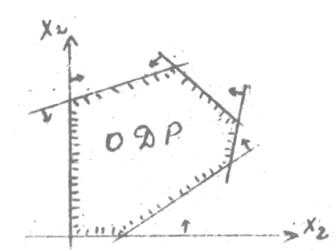
Продемонстрируем работу алгоритма топологической оптимизации, реализованного с помощью метода конечных элементов в пакете ANSYS, для плоской задачи теории упругости на примере кронштейна (рисунок 1), имеющего в начальном состоянии форму прямоугольника.

Рис.1 – Начальная расчетная схема

Кронштейн жестко закреплен по левой стороне. На кронштейн сверху действует распределенная нагрузка. Требуется найти такую форму кронштейна, при которой последний будет иметь наименьшую массу, но при этом конструкция должна быть равнопрочной (то есть отношение минимального напряжения конструкции к максимальному должно быть близко к единице).

На рисунке 2 показана последовательно изменяющаяся в результате оптимизации форма кронштейна:

Рис.2 – Формы кронштейна на различных шагах оптимизации

На рисунке 2 представлены шаги итерационного процесса оптимизации, критерием “умерщвления” элементов являлось достижение эквивалентными напряжениями по Мизесу значений, заданных по формуле (2). Наблюдается образование условно балочно-стержневой конструкции, представляющей собой взаимно перпендикулярные стержни. При этом, в ходе оптимизации количество этих стержней уменьшается. Так стержни, направленные из нижнего левого угла в верхний правый угол, сохраняют свое количество, при этом уменьшая толщину. Перпендикулярные же им стержни постепенно разгружаются и в итоге пропадают. В частности, основную нагрузку воспринимает один стержень, расположенный посередине.

Заключение

При использовании представленного в работе алгоритма получена оптимизированная конструкция, в которой появляются участки, представляющие собой подобие тонких балочно-стержневых элементов. В текущей постановке вопросы потери устойчивости таких элементов не рассматривались. В дальнейшем планируется учитывать критерий потери устойчивости прямо в ходе итерационного процесса.

После проведения ряда численных экспериментов подобран оптимальный критерий оптимизации для заданной конструкции.

В дальнейшем планируется учет в алгоритме более сложных критериев оптимизации разработанного критерия, а также модификация предложенного алгоритма оптимизации. Предлагается введение «замороженных» неизменяемых областей, к которым, в первую очередь, должны быть отнесены границы приложения нагрузок, области закреплений.

Работа выполнена при финансовой поддержке Министерства образования и науки РФ (договор №02.G25.31.0168 от 01.12.2015 г. в рамках реализации постановления Правительства РФ № 218)

Литература

Bendsoe, Martin P. Topology Optimization: Theory, methods and applications / Martin P. Bendsoe // Ole Sigmund. – Germany : Springer, 1995. –370 c.
Сысоева В.В., Чедрик В.В. Алгоритмы оптимизации топологии силовых конструкций // ученые записки ЦАГИ, том XLII. –с.91-102. –2011
Джилавян С.А., Хуршудян Ас.Ж. Оптимизация топологии упругого основания прямоугольной пластинки, подверженной воздействию подвижной нагрузки // XII всероссийское совещание по проблемам управления ВСПУ–2014. –с.1745-1756. –2014.
Яров В.А., Прасоленко Е.В. СТРОИТЕЛЬНЫЕ КОНСТРУКЦИИ ЗДАНИЯ И СООРУЖЕНИЯ // Вестник ТГАСУ № 3. –с.89-102. –2011.
Rozvany G.I.N., Zhou N., Sigmund O. Topology Optimization in Structural Design // In: Advances in Design Optimization. – Adeli, 1994, London. –p.240–299.

References

Bendsoe, Martin P. Topology Optimization: Theory, methods and applications / Martin P. Bendsoe // Ole Sigmund. – Germany : Springer, 1995. –370 c.
Sysoeva V.V., CHedrik V.V. Algoritmy optimizacii topologii silovyh konstrukcij // uchenye zapiski CAGI, tom XLII. –s.91-102. –2011.
Dzhilavyan S.A., Hurshudyan As.ZH. Optimizaciya topologii uprugogo osnovaniya pryamougol’noj plastinki, podverzhennoj vozdejstviyu podvizhnoj nagruzki // XII vserossijskoe soveshchanie po problemam upravleniya VSPU–2014. –s.1745-1756. –2014.
YArov V.A., Prasolenko E.V. STROITEL’NYE KONSTRUKCII ZDANIYA I SOORUZHENIYA // Vestnik TGASU № 3. –s.89-102. –2011
Rozvany G.I.N., Zhou N., Sigmund O. Topology Optimization in Structural Design // In: Advances in Design Optimization. – Adeli, 1994, London. –p.240–299.

research-journal.org