Методы поисковой оптимизации (стр. 1 из 2). Метод оптимизации

Классификация методов оптимизации

Различают методы однокритериальной оптимизации ( поиск оптимума единственной целевой функции) и многокритериальной оптимизации (принятия решения при многих критериях, в частности сводят векторную задачу к последовательности скалярных задач).

Методы локальной оптимизации обеспечивают отыскание одного локального минимума, а методы глобальной оптимизации направлены на установление всех локальных минимумов.

Различают также методы непрерывной и дискретной (в том числе комбинаторной) оптимизации, методы линейного и нелинейного программирования, методы условной и безусловной оптимизации, методы одномерной оптимизации и методы оптимизации функций многих переменных.

Рациональные методы ориентированы на некоторую математическую модель оптимизируемой функции; эвристические алгоритмы обычно не используют никакой модели целевой функции, а основывают процесс оптимизации на формализованной человеческой интуиции и других нестрогих предположениях.

Методы оптимизации подразделяют также на детерминированные и стохастические. Стохастические алгоритмы используют элементы случайности при выборе направления или длины шага в процессе оптимизации. Отметим, что стохастические методы оптимизации применяются к детерминированным задачам (случайность намеренно вводится в алгоритм для того, чтобы обеспечить достижение цели).

Стохастические алгоритмы в свою очередь подразделяются на алгоритмы (прямого) случайного поиска и алгоритмы стохастической аппроксимации градиента.

2. Постановка задачи линейного программирования

Линейное программирование - раздел математики, в котором изучаются методы решения задач на отыскание экстремумов (максимума, минимума) линейной функции при наличии ограничений в виде линейных уравнений или линейных неравенств.

2.1 Общая задача линейного программирования (злп)

Найти решение X(),

при котором функция

(2.1)

достигает экстремума – максимума (минимума)

при выполнении условий

(2.2)

(2.3)

Значения предполагаются известными (выявлены на стадии анализа реальной ситуации).

Линейная функция (2.1) называется целевой функцией (линейной формой), х1, х2,...,хn- аргументами целевой функции.

Условия (2.2) называются ограничениями задачи,

Условия (2.3) показывают, что аргументы могут быть любого знака.

Решение X(), системы (2.2) называется допустимым решением ЗЛП, если числа - неотрицательны.

Совокупность всех допустимых решений называется областью допустимых решений задачи (ОДР).

Допустимое решение, которое обращает в максимум (минимум) целевую функцию (2.1) называется оптимальным решением ЗЛП.

2.2 Математические модели задач линейного программирования

Рассмотрим некоторые экономические задачи, которые являются задачами линейного программирования.

Пример 1. Задача использования сырья

Для использования двух видов продукции P1 и P2 используется три вида сырья S1, S2 и S3,запасы сырья соответственно равны 40,60,50 единиц сырья. Затраты сырья на изготовление единицы продукции P1 соответственно равны 2,8,5. Затраты сырья на изготовление единицы продукции P2 соответственно равны 5,3,6. Прибыль от реализации единицы продукции каждого вида соответственно равна 100, 200 у.е.

Необходимо составить математическую модель плана выпуска продукции, при котором прибыль от реализации изделий будет максимальной.

Решение

Условие задачи запишем в следующую таблицу:

Вид сырья	Запасы	Затраты сырья на ед. изделий вида
Вид сырья	Запасы	P1	P2
S1	40	2	5
S2	60	8	3
S3	50	5	6
Прибыль от единицы продукции		100	200

Составим математическую модель задачи:

пусть — количество единиц продукцииP1,

— количество единиц продукции P2, планируемое к выпуску.

Тогда целевая функции – суммарная прибыль от реализации изделий имеет вид:

Ограничения по запасам сырья записываются следующими неравенствами:

Если продукция P1 не выпускается, то , а если выпускается, то х1 > 0, аналогично и для Р2, следовательно имеют место условия неотрицательности:

Таким образом, математическая модель данной задачи линейного программирования имеет вид:

Найти оптимальный план производства X(,), такой, что

Пример 2. Задача составления рациона (задача «о диете»)

На животноводческой ферме каждое животное ежедневно должно получать не менее 7 единиц питательного вещества S1, 9 единиц вещества S2 и 14 единиц вещества S2 Для составления рациона используют два вида корма. Содержание количества единиц питательных веществ в 1 кг корма приведены в таблице.

Необходимо составить рацион нужной питательности, причем затраты на него должны быть минимальными.

Вещества	Кол-во ед. питательных веществ в кг. корма
Вещества	Корм 1	Корм 2
S1	2	5
S2	8	5
S3	5	4
Стоимость 1 кг корма	14	26

Решение

Составим математическую модель задачи

пусть — количество килограммов корма 1,

— количество килограммов корма 2.

Ограничения на питательность рациона по трем видам питательных веществ

S1, S2 , S3 имеют вид

условия неотрицательности :

Затраты на питание выражаются целевой функцией:

studfiles.net

Метод оптимизации - Энциклопедия по экономике

Эта система позволяет за счет интеграции отдельных расчетов повысить комплексность разрабатываемых плановых рекомендаций. Объемы производства, направления распределения продукции, трудовых и финансовых ресурсов, показатели себестоимости, рентабельности, производительности труда др. должны определяться в одном цикле на основе отраслевых взаимосвязанных моделей. Благодаря использованию быстродействующих средств вычислительной техники резко увеличивается число вариантов плановых расчетов и обеспечивается возможность сократить сроки разработки народнохозяйственных планов и быстрее доводить их до предприятий. Применение экономико-математических методов оптимизации позволяет принимать наилучшие варианты плановых решений. Создается возможность рационально перераспределять ресурсы при изменении целей, задач и условий развития экономики в целом и отдельных ее звеньев. [c.118] Методы оптимизации производственной программы на нефтеперерабатывающих и нефтехимических предприятиях. [c.178]

Объективная необходимость и цели оптимизации. Методы оптимизации. Оптимизация портфеля по методу Г. Марковича. Основные положения теории Марковица. Эффективность рынка ценных бумаг как предпосылка оптимизации инвестиционного портфеля. Граница эффективных портфелей. Эффективный и оптимальный портфель. [c.334]

Изложенные выше методы оптимизации детальности разведки являются по существу методами оптимизации риска и могут рассматриваться в качестве составной части теории риска в освоении месторождений, в более широком смысле. [c.84]

Решение задач нормирования труда с использованием методов оптимизации может осуществляться как в виде отдельных изолированных задач, так и задач, решаемых в рамках автоматизированных систем управления- Метод решения может быть представлен различными алгоритмами, из которых выбирается наиболее эффективный. [c.166]

В настоящее время разработано несколько методов оптимизации сетевых моделей строительства промышленных объектов. [c.47]

Имеются и другие методы оптимизации сетевых графиков с применением ЭВМ. [c.48]

Недостатком такого метода оптимизации является односторонняя оценка результатов СПО только по затратам технологического времени, не учитывающая того существенного отрицательного влияния, которое оказывает интенсификация процесса на многие важнейшие показатели эффективности проводки скважин. К числу таких показателей можно отнести стоимость сменных элементов установки, расход которых зависит от режима СПО, а также связанное с этим ремонтное и вспомогательное время. Проведенные нами исследования показали, что при увеличении скорости спуска выше 3,0—3,5 м/с рост вспомогательного времени на замену только элементов ленточного тормоза значительно превышает ту экономию технологического времени спуска, которая получается за счет форсирования режима. [c.6]

ОСНОВНЫЕ ЗАКОНОМЕРНОСТИ, МЕТОДЫ ОПТИМИЗАЦИИ И РАСЧЕТА РЕЖИМОВ УПРАВЛЕНИЯ СПО [c.32]

Методы оптимизации режимов спуска [c.141]

Недостатком такого метода оптимизации является односторонняя оценка результатов операции, не учитывающая существенного отрицательного влияния, которое оказывает интенсификация режима спуска на другие показатели процесса. [c.143]

Построение фактического графика спуска бурильной колонны в скважину. В результате рассмотренных выше методов оптимизации находим среднее на скважину значение установившейся скорости спуска бурильной колонны (иу.з.с)опт. Этот режим можно реализовать двумя путями [c.151]

Выбор методов оптимизации СПО, оценка их эффективности не могут рассматриваться изолированно от главных задач, стоящих перед бурением в целом. Подчиненность целей и критериев оптимизации спуско-подъемных операций целям и критериям оптимизации всего цикла строительства скважин — необходимое условие, которое должно быть выполнено при разработке мероприятий по совершенствованию рассматриваемого процесса. [c.192]

Целью первого этапа является изучение основных закономерностей СПО, методов оптимизации отдельных подпроцессов, характерных ошибок управления, встречающихся на практике. Методической основой программы первого этапа могут послужить материалы, изложенные в главе II. Следует отметить, что обучение бурильщиков и инженерно-технических работников основным принципам оптимизации СПО должно проводиться независимо от того, какие-— сложные или простые —информационно-измерительные средства предполагается использовать в системе управления. Больше тоге, проведение такой учебы в полном объеме необходимо и в том случае, когда на буровом предприятии по тем или иным причинам не ставится задача комплексной оптимизации процесса СПО с использованием информационно-измерительных средств. Не исключена возможность, что именно в результате проведения технической учебы руководством УБР будет принято решение о комплексной постановке и реализации задач, связанных с совершенствованием СПО. Во всех случаях результаты учебы будут во многом зависеть от уровня методической и организационной подготовки занятий. В частности, очень полезно провести предварительную инструментальную регистрацию фактических режимов СПО на ряде буровых установок данного предприятия. Полученные таким образом материалы помогут на конкретных примерах проиллюстрировать те или иные теоретические положения, отметить характерные для местных условий нарушения режимов СПО и их влияние на эффективность проводки скважин. Все это повысит наглядность и действенность обучения. Наиболее целесообразной формой проведения первого этапа технической учебы для рабочих следует считать введение в программы учебно-курсовых комбинатов вопросов оптимизации режимов СПО. [c.247]

Описывается применение математических методов оптимизации сетевых моделей для определения численного и квалификационного состава рабочих бригад и минимальной продолжительности процесса строительства буровых при заданной численности вышкомонтажной бригады. [c.2]

ПРИМЕНЕНИЕ МАТЕМАТИЧЕСКИХ МЕТОДОВ ОПТИМИЗАЦИИ СЕТЕВЫХ МОДЕЛЕЙ [c.96]

Кондратьев В. П. Методы оптимизации сетевых планов работ. М., Экономика , 1970, 199 с. [c.108]

Метод оптимизации уровня качества [c.200]

Параллельно с выбором вида специализации и формы организации производства проводится анализ производственного процесса в пространстве с учетом характера и объемов намечаемых к выпуску изделий. Производятся расчеты потребного количества оборудования составляется планировка цеха или участка определяются потоки материалов, полуфабрикатов и готовой продукции. С применением различных методов оптимизации и имитационного моделирования рассматриваются возможные варианты организационных структур, планировок, маршрутов движения предметов труда и выбираются наиболее рациональные. [c.182]

Определение оптимальной интенсивности строительных процессов по сооружению линейной части нефтегазопроводов может осуществляться по методу, аналогичному предложенному в разделе 6. В качестве критерия оптимальности так же, как и при оптимизации сетевых моделей, может быть принят минимум затрат на передислокацию строительно-монтажных подразделений. По атому методу оптимизация матричной модели строительства линейной части трубопровода сводится к нахождению [c.66]

Смехов Б. М., Уринсон Я. М. Методы оптимизации народнохозяйственного плана. М. Экономика, 1976. [c.168]

Следует отметить, что методы оптимизации находят применение и в задачах текущего планирования. Так, ГВЦ Госплана СССР совместно с отделом легкой промышленности Госплана СССР в течение уже ряда лет решаются задачи оптимизации годовых планов производства тканей, тюлегардинных изделий, обуви. В этих задачах определяется такой вариант объема и структуры производства продукции данной подотрасли, который обеспечивает наиболее полное удовлетворение потребностей народного хозяйства и населения при заданных ограничениях по материальным ресурсам (прежде всего — исходному сырью) и производственным мощностям с учетом планируемого уровня их использования. [c.213]

Методы оптимизации развития мощности строительных организаций при развитии нефтедобывающих районов.— Нефтепромысловое строительство , 1972, № 10, с. 28—31. Авт. Г. Д. Соколов, П. С. Сапожников,. С. Н. Крашенинников и др. [c.218]

Загрузку исполнителей работ определяют путем построения карты проекта или графика потребности в исполнителях. Графический метод оптимизации позволяет проводить расчеты вручную или с помощью вычислительных машин. [c.43]

Одним из методов оптимизации является выявление возможного сокращения сроков выполнения работы и определение необходимых для этого затрат. Метод время — затраты заключается в установлении оптимального соотношения между продолжительностью и стоимостью работ. [c.43]

Для более комплексных методов оптимизации (и по времени, и по затра гам) разработаны алгоритмы и программы для ЭВМ. В некоторых случаях используются специализированные машины типа Ритм . [c.45]

ЭММ, применяемые при решении перечисленных задач, можно ус-лонно разделить на две категории 1) методы, позволяющие сформулировать, математически поставить и решить задачу 2) методы оптимизации решения этих задач. Под оптимизацией понимается процесс [c.306]

Основной метод исследования операций - изучение математических моделей операций. Сущность оперативного подхода заключается в следующем определение и математическая формулировка цели операции, критерия оптимальности (показателя качества процесса) и ограничений построение математической модели операции, выражающей эффективность исследуемой системы как функцию множества переменных, из которых, по крайней мере, хотя бы одна поддается управлению определение (а в случае необходимости прогнозирование) входной информации выбор метода оптимизации с помощью методов математического программирования нахождение оптимального решения проверка полученной модели путем сравнения с оригиналом операции и в случае необходимости корректировка модели и ее решения. [c.307]

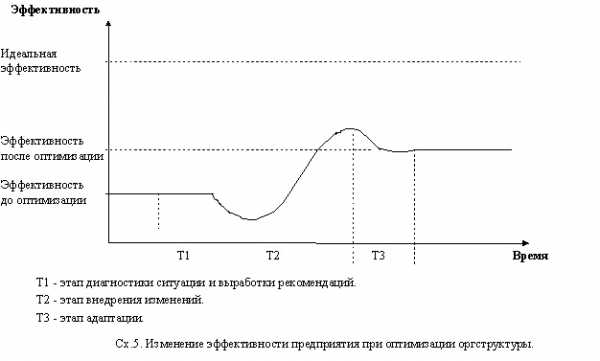
В конце шестидесятых годов методы оптимизации становятся одним из важнейших практических средств анализа экономических проблем. Фронт работ по применению электронной вычислительной техники в экономике стремительно расширяется, охватывая как чисто теоретические, так и прикладные задачи. Одновременно наступает известная переоценка ценностей идеи оптимизации оказались не столь всеобъемлющими, какими представлялись сначала. Прежде всего выяснилось, что представление о том, что такое хорошо, и что такое плохо , не так просто, для его анализа нужны глубокие исследования. Далее, даже если критерий оптимальности и сформулирован, то нахождение оптимального плана само по себе не решает все вопросы. Любой план, в том числе и оптимальный, для своей реализации требует хорошей организации структуры управления. Потери из-за плохо организованного управления могут во много раз превышать потери от неоптимальности плана разнообразные случайные обстоятельства, учесть которые заранее невозможно в принципе, могут привести к существенному отклонению результата от плана. [c.17]

Во-первых, это методы оптимизации производства. В их число входят методы определения производственных циклов, сокращения ненужных запасов, выравнивания загрузки производственных мощностей, обеспечения гибкости. Во-вторых, это методы сокращения подготовительно-заключительного времени для сокращения общего времени производства, нормирование операций, рациональное размещение производственного оборудования, обучение рабочих нескольким профессиям для проведения принципа гибкости и т. д. В-третьих, это способы обеспечения принципа авто-номизации. В его основе следующее. Каждый станок или линия оборудованы устройством автоматической остановки. На Тоёте все машины автономны, что позволяет предотвращать массовое производство брака. Что это значит Это значит, что рабочий, заметив дефект в детали, должен остановить станок или линию конвейера. Важными составными частями производственной системы Тоёта являются рационализаторская деятельность малых групп, а также функциональные системы управления. Основные идеи этих систем рассматриваются в гл. 5, 10, 12, 13. Это направлено на создание необходимых условий для производительного, качественного труда на каждом рабочем месте. Эта мысль встречается у многих японских авторов. Один из них выразился так Необходимо, чтобы именно условия, а не управляющие заставляли рабочих эффективно трудиться. Если создаются такие условия, сколь дорого бы они ни обходились, тогда и вложения в капитальное строительство, в передовую технологию оказываются не напрасными, а прибыль многократно увеличивается . [c.22]

Ткачев Ю. А. Критерии и методы оптимизации разведки месторождений нефти и газа. Сыктывкар, 1987. (Тр. X геол. конф. Коми АССР Вып. IV [c.164]

Анализ оптимизации показателей надежности сложной системы показал, что использование традиционных методов оптимизации поевосходит возможности существующих ЭВМ. Хорошие результаты дает использование принципов вычислительного метода группового учета аргументов (МГУА), [c.245]

В книге впервые делается попытка разработать единую методику, необходимую для решения задач, связанных с совершенствованием процесса спуско-нодъ-емных операций (СПО). Рассмотрены методика и технические средства проведения исследований СПО на буровых, методы обработки информации и детального анализа процесса. Изложены основные закономерности методов оптимизации г расчета режимов отдельных элементов СПО. Даны рекомендации по расчету и реализации оптимальных режимов СПО. Проанализированы дефекты нормативного, информационного п технического обеспечения системы управления СПО. Рассмотрены информационно-измерительные средства оптимизации СПО. Приведены методики анализа н управления СПО на уровне бурового предприятия. [c.2]

Методы оптимизации в организации и нормировании труда. М., НИИтруда, 1971, 97с. [c.108]

Одним из важнейших направлений конструкторской унификации является сокращение номенклатуры изделий, имеющих одинаковое или сходное эксплуатационное назначение. Оно реализуется в первую очередь путем создания параметрических рядов (гамм) изделий. Каждый ряд представляет собой совокупность изделий, аналогичных по кинематике, рабочему процессу, но различных по габаритным, мощностным или другим основным эксплуатационным параметрам (грузоподъемность грузового автомобиля или крана, рабочий объем двигателя, производительность компрессора и т. д.). Параметрический ряд, как правило, создается в соответствии с ГОСТ 8032—84 Предпочтительные числа и ряды предпочтительных чисел . Обычно пользуются четырьмя десятичными рядами R5 RIO , R20 R40 с соответствующими знаменателями геометрической прогрессии 1,6 1,25 1,12 1,06. Расчет параметрических рядов для выбора экономически рационального разрежения ряда производится по Типовым методикам оптимизации параметрического (типоразмерного) ряда и соответствующей типовой методике для многомерных рядов. Имеются экономико-математические модели их оптимизации, основанные как на классических методах в условиях непрерывности и дифференцируемости функции затрат и функции спроса и наличии экстремума общих затрат, так и неклассических методах оптимизации, разработанных, в частности, Институтом математики Сибирского отделения АН СССР. Параметрические ряды формируют в каждой отрасли перспективный типаж изделий, что весьма ограничивает их возможную номенклатуру. [c.107]

Имеются и другие метода оптимизации сетевых графиков с приме-ненией ЭШ, разработанный ЦШПИАСС Госстроя СССР, НИИ по строительству Госстроя ЭССР и 1ф. [c.56]

Карпов В. Г. Матричный метод оптимизации строительства линейной части магистральных трубопроводов // Постановка и методы решения задач планирования трубопроводного транспорта Сб. - Уфа БФАН СССР, 1978, с. 83 - 90. [c.72]

Экономические задачи, решаемые на макро- и микроуровне по своей сути являются многокритериальными. Свидетельством тому служит и многочисленная критика методов оптимизации (нахождения оптимального -точечного - критерия), и сложность, многофакторность процессов в экономике, особенно в производственных системах. Например, если решается вопрос об инвестициях, связанных с расширением основной деятельности, необходимо учесть ряд таких факторов, как возможность изменения положения фирмы на рынке товаров, доступность материальных, трудовых и финансовых ресурсов, возможность освоения новых рынков и пр. Например, при рассмотрении вариантов развития производства, последние сравниваются между собой по целому ряду показателей объем капиталовложений, ожидаемая прибыль, рентабельность, экологический ущерб и т.д. Как правило, критерии являются противоречащими друг другу, то есть, невозможно одновременно достичь наилучших результатов по каждому из рассматриваемых критериев. Отсутствие разработанных математических методов, позволяющих наиболее адекватно отображать экономические процессы приводит к тому, что при решении задач учитывают наиболее существенные факторы, что неизбежно приводит к искажению полученных результатов. Учесть влияние всех факторов в большинстве случаев не представляется возможным из-за увеличения сложности решаемой задачи. [c.44]

Рассмотренный метод оптимизации производственной программы. НПЗ в постановке (2)—(9)-реализован на ЭВМ М-22 . Ниже приводится общая схема вычисления по данному методу. Условия (4)—(8) формируются в виде отдельного. информационного массива. Он используется только при решении вспомогательной задачи (12). Основой предлагаемой вычислительной схемы является алгоритм мультипликативного симплекс-метода, к которому стыкуются алгоритмы решения вспомогательной задачи и усреднения. Для решения вспомогательнбй задачи может использоваться основная программа. Однако в связи/с ее небольшими размерами был разработан и реализован на ЭВМ более экономный прямой алгоритм симплекс метода с верхними ограничениями на переменные. Следует отметить, что предлагаемый подход может реализован и другой вычислительной схемой, отличной от приводимой ниже. Ее отличие состоит в том, что алгоритм решения вспомогательной задачи.подключается только после получения оптимального решения, основной задачи. Практическая проверка обеих вычислительных схем не показала существенного преимущества ни одной из них. [c.100]

economy-ru.info

МЕТОД ОПТИМИЗАЦИИ - это... Что такое МЕТОД ОПТИМИЗАЦИИ?

МЕТОД ОПТИМИЗАЦИИ

метод построения алгоритмов нахождения максимумов функции и точек, в которых они достигаются, при наличии ограничений или без них. Обычно рассматривается случай, когда функция задана в одномерном или многомерном пространстве; однако М.о. обобщены на функции, заданные в абстрактных пространствах. Существуют задачи нахождения глобального экстремума – соответственно максимуму или минимуму по всей допустимой области; локального экстремума – в произвольно малой окрестности точки этой области. Наиболее употребительные М.о. для случаев, когда ограничения отсутствуют, методы спуска. Они состоят в последовательности приближений к точке минимума, в которой каждое следующее получается смещением предыдущего в направлении градиента при поиске максимума или в противоположном направлении при поиске минимума. Имеются некоторые разновидности этого метода, различающиеся между собой правилом регулирования шага при переходе к следующему приближению и критерием остановки инерционного процесса. Более сложная задача нахождения условного экстремума. Многие методы основаны на правиле множителей Лагранжа.

Большой экономический словарь. — М.: Институт новой экономики. А.Н. Азрилиян. 1997.

МЕТОД НЬЮТОНА
МЕТОД ОРГАНИЗАЦИИ ТОРГОВОГО АППАРАТА СБЫТА

Смотреть что такое "МЕТОД ОПТИМИЗАЦИИ" в других словарях:

Теоретический метод оптимизации — Совокупность процедур построения или выбора математической модели оптимизации ПОС, проверки ее применимости, получения входных данных и вычисления оптимальных параметров Источник … Словарь-справочник терминов нормативно-технической документации
Метод Ньютона — Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном… … Википедия
Метод роя частиц — (МРЧ) метод численной оптимизации, для использования которого не требуется знать точного градиента оптимизируемой функции. МРЧ был доказан Кеннеди, Эберхартом и Ши[1] [2] и изначально предназначался для имитации социального поведения.… … Википедия
Метод одной касательной — Метод Ньютона (также известный как метод касательных) это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643 1727), под именем… … Википедия
Метод Гаусса — Ньютона — Метод Ньютона (также известный как метод касательных) это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643 1727), под именем… … Википедия
Метод Ньютона-Рафсона — Метод Ньютона (также известный как метод касательных) это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643 1727), под именем… … Википедия
Метод Ньютона — Рафсона — Метод Ньютона (также известный как метод касательных) это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643 1727), под именем… … Википедия
Метод касательной — Метод Ньютона (также известный как метод касательных) это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643 1727), под именем… … Википедия
Метод касательной (Метод Ньютона) — Метод Ньютона (также известный как метод касательных) это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643 1727), под именем… … Википедия
Метод касательных — Метод Ньютона (также известный как метод касательных) это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643 1727), под именем… … Википедия

big_economic_dictionary.academic.ru

Численные методы оптимизации - Энциклопедия по экономике

Решить ее можно с помощью численных методов оптимизации (так называемой экспериментальной оптимизации). [c.44] Процессы Р. моделей подразделяются на аналитические и численные. Метод аналитического Р. — последовательность математических преобразований, приводящих к заданному результату (напр., к формуле, выражающей зависимость экстремального значения фикция от ее аргументов). В этом случае численные значения переменных (см. Аналитические методы решения моделей) включаются лишь на последнем этапе. Численные методы получения Р., среди которых наибольшее значение имеют итеративные (см. Численные методы оптимизации), отличаются тем, что в них численные значения переменных участвуют в процессе Р. с самого начала и на каждом этапе проверяется, соответствуют ли они заданной цели в случае положительного ответа процесс Р. заканчивается, в случае отрицательного — продолжается. Полученное Р. обычно не является окончательным изменение условий и целей всегда может поставить вопрос о его корректировке, подстройке. Корректировка (иногда она также называется управлением Р.) — необходимое условие успешного внедрения моделей в практику. [c.310]

Численные методы оптимизации [c.391]

ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМИЗАЦИИ [c.391]

Черный ящик" 391 Человеческий капитал 391 Четная вершина 47 Четная функция 391 Численное представление модели 403 Численные методы оптимизации 391 Численные решения 310 Числовая модель 392 Числовая последовательность 269 Чистая (или технологическая) отрасль 392 Чистая прибыль 279 Чистая продукция 392 Чистая стратегия 392 Чистая экономическая рента 414 Чистое экономическое благосостояние 392 [c.495]

Другая трудность, с которой встретился автор, состоит в изложении вопросов вычислительной технологии. Вопросов, в сущности, мелких, но требующих достаточно ответственного решения. Без этого даже хорошая общая идея может не сработать. Попытки поднять эти вопросы до уровня науки и изложить их соответствующим образом (как это делается, например, в недавно переведенной монографии Э. П о л а к а Численные методы оптимизации М., Мир , 1974), представляются автору спорными. В книге реализован другой путь автор не пытался изложить технологию вычислений в самом общем и абстрактном виде, предпочитая показать, как решаются эти вопросы в конкретных зада-чах. При этом используются соображения здравого смысла. Поняв их в простом частном случае, читатель без труда сможет (если сочтет нужным) использовать аналогичные соображения в своей работе, соответствующим образом видоизменив их. [c.9]

Сравнивая описанные численные методы поиска оптимума,, можно сделать вывод, что в задачах оптимизации строительства линейной части магистральных трубопроводов-наиболее целесообразно применение параллельного метода. [c.51]

Наша дискуссия, однако, будет касаться лишь методов оптимизации, а не методов отыскания корней, как таковых. Сведения о последних можно почерпнуть в таком уникальном источнике, как Численные методы . [c.183]

Примерно со времени второй мировой войны для анализа больших и сложных систем стали использоваться некоторые математические методы, которые были объединены понятием "исследование операций". Эти методы оказались полезными для планирования, торговых операций, транспортных задач, при составлении расписаний самолетов для организации обработки материальных ценностей на складах и базах и для решения многих других подобных задач. Были разработаны методы оптимизации очередей, которые описывали возможные ситуации в сфере торговли и обслуживания и позволяли определить оптимальную численность обслуживающего персонала для переменного потока покупателей или клиентов. [c.9]

Для построения численных методов решения задач лексикографической оптимизации представляет интерес следующее утверждение [c.274]

Ф в правых частях этих определений считается заданной достаточно гладкой функцией своих аргументов. Не претендуя на исчерпывающую полноту, ограничимся пока этими конструкциями. Их, а также гладких функций от функционалов перечисленных типов, достаточно для постановки большинства прикладных задач. В дальнейшем будут использоваться и другие конструкции функционалов. В формулах (12)—(16) фазовая траектория х ( ) связана с управлением краевой задачей (11) и однозначно определяется им. Этим оправдывается обозначение выражений в правых частях определений через F [и ( ) . Фактическое вычисление F [ ( ) требует решения краевой задачи (11), для чего используются соответствующие приближенные методы, ориентированные, как правило, на использование ЭВМ. Выбор того или иного численного алгоритма определяется содержательным характером краевой задачи (И). Особых трудностей при этом не возникает, так как задача оптимизации какого-либо объекта обычно ставится после того, как расчет его функционирования при каком-то фиксированном управлении уже достаточно освоен, и подходящие численные методы разработаны и проверены. [c.26]

Если программа или номенклатура работ (например, типов локомотивов или видов их ремонта) изменяется без привлечения дополнительных капитальных вложений, а это изменение является следствием специализации предприятия на выполнении ограниченной номенклатуры работ, то для определения наиболее рационального сочетания между численностью и сроками ремонта (изготовления) машин, оборудования и других технических средств могут быть использованы методы оптимизации сетевых моделей. [c.136]

Если математическая модель непригодна для применения аналитических или численных методов, то для ее решения применяют метод экспериментальной оптимизации на ЭВМ. При этом методе нет необходимости в преобразовании математической модели в специальную систему уравнений. Как целевая функция, так и система ограничений могут быть заданы в виде алгоритма, позволяющего вычислять их значения в ходе моделирования. На рис.3.5.4 схематично показан вариант имитационного экспериментирования с применением метода экспериментальной оптимизации. [c.33]

Проведение имитационных экспериментов по принципу исследования влияния входных параметров системы на ее выходные параметры позволяет производить сравнение различных управленческих решений, однако при этом всегда возникает сомнение, оптимальным ли является выбранное решение и не существует ли других, более выгодных решений. Классический подход к решению задач оптимизации состоит в определении экстремальных значений целевой функции. При этом для моделей сложных социально-экономических систем наиболее распространены численные методы. Численные методы — это итерационные вычислительные процессы для определения экстремальных состояний модели. [c.99]

Если исследуемый объект настолько сложен, что его математическая модель непригодна для применения аналитических или численных методов, то для его исследования применяют метод экспериментальной оптимизации. При этом методе как целевая функция, так и система [c.99]

Предложен метод выбора вектора управления поликорпоративной системой с использованием аппроксимации множества Парето. Разработанный метод многокритериального выбора по сравнению с непосредственным применением принципа максимина позволяет избежать дифференцирования функции максимума (минимума) для выбора компромиссно-оптимального управления это преимущество особенно важно с учетом того, что функция максимума (минимума) непрерывно дифференцируема не на всей области определения. Применение данного метода в виде формирования минимизирующей последовательности управлений сводит решение многокритериальной задачи управления к последовательности решения скалярных задач оптимизации, для которых разработаны надежные численные методы решения. Использование предложенного метода наряду с получением конечного практически значимого результата - выбора минимаксно-оптимального управления - позволяет получить обширную информацию о структуре множества Парето ценность этой информации заключается в том, что сопоставление минимаксно-оптимального управления с другими элементами множества Парето является инструментом оценки качества этого [c.146]

Совершенствование организационной структуры управления нефтеперерабатывающими предприятиями возможно путем укрупнения цехов и участков, централизации и специализации работ, концентрации функций управления вспомогательными службами, оптимизации численности инженерно-технических работников и служащих, широкого применения экономико-математических методов, электронно-вычислительной техники, организационной техники н средств связи. Необходим системны подход к проектированию структур управления. [c.328]

Для реализации поставленных целей в курсе рассматриваются основные положения оптимизации налогов, изучаются численные балансовые методы бухгалтерского учета и налогового планирования, а также основные способы минимизации налоговых платежей. [c.250]

Значительное влияние на совершенствование методов и приемов труда оказывают рациональное разделение труда, оптимизация режима работы газоснабжающей системы, уточнение выполняемых функций, установление правильных соотношений численности рабочих, конструкторов и технологов, инженеров, техников и других категорий трудящихся. [c.143]

Основная задача в области совершенствования функционального разделения труда состоит в определении оптимального соотношения между численностью основных Ч0 и вспомогательных рабочих Ча. Принципиальный подход к ее решению состоит в отыскании такого значения указанного соотношения, которое обеспечивает максимальный удельный вес вес оперативного времени в составе его сменного фонда в среднем на одного рабочего, включая и основных и вспомогательных рабочих. Этот способ рекомендован в [1]. Однако будучи принципиально верным, он оставляет открытым вопрос о конкретном способе определения оптимального соотношения Ч0 и Чв. Конечно, можно найти его. прямым неупорядоченным перебором всех возможных вариантов, но это очень трудоемкая процедура. В связи с этим Е. С. Докучаевым в [2] разработан простой метод аналитического определения оптимальной численности вспомогательных рабочих Ч при известной численности основных рабочих Ч0. Критерием оптимизации служит максимум сменной выработки в среднем на на одного рабочего. Известно, что целевая для предприятия продукция создается в оперативное время основных рабочих. Поэтому критерий оптимальности запишется как [c.22]

Численное решение задачи оптимизации портфеля с учетом лимитов методом Монте-Карло. [c.231]

Организация труда опирается на познание и использование ряда точных наук, их законов, методов и принципов. Математические методы (теория вероятности, метод обратных связей, метод наименьших квадратов, графоаналитический метод и др.) нашли широкое применение при разработке нормативных материалов, используемых при расчете норм труда, в методиках изучения затрат рабочего времени, при оптимизации организации рабочих мест или определении численности работающих. Кроме того, [c.13]

Считать приоритетными направлениями государственной поддержки формирования трудовых ресурсов Севера оптимизацию численности населения, повышение адресности государственных гарантий и компенсаций с учетом складывающейся в регионе демографической ситуации и реальных миграционных потоков. В связи с этим Министерству труда и социального развития РФ, Министерству экономики РФ, Министерству природных ресурсов РФ, Государственному комитету по вопросам развития Севера с участием заинтересованных федеральных органов исполнительной власти и органов исполнительной власти субъектов РФ поручено разрабатывать до 1 июля 1998 г. концепцию формирования трудовых ресурсов с учетом потребностей северных районов, а также утвердить основные положения о вахтовом методе организации работ и рекомендации по заключению трудового договора (контракта), отражающие специфику регулирования социально-трудовых отношений в условиях Севера. [c.729]

Перевод части сотрудников на сокращенный рабочий день или рабочую неделю позволяет избежать увольнений и сохранить приобретенную работниками организации квалификацию при одновременном сокращении издержек на рабочую силу. Эти методы, так же как предоставление неоплачиваемых отпусков, широко используются в отраслях с сезонными колебаниями спроса - туризме, на транспорте, сельском хозяйстве. При переводе сотрудников на сокращенное рабочее время и предоставлении неоплачиваемого отпуска, руководству следует уделить особое внимание соблюдению требований трудового законодательства, чтобы избежать неприятных последствий в виде судебных разбирательств и финансовых санкций. Кроме того, оно должно четко представлять, когда вновь ожидается появление потребности в дополнительной рабочей силе, поскольку сокращенное рабочее время оказывает деморализующее влияние как на самих "пострадавших", так и на всю организацию и не может быть использовано в качестве долгосрочного средства оптимизации численности. [c.127]

Прогрессивность норматива Численность работников аппарата управления в расчете на 1 млн. руб. продукции обеспечивается также и тем, что группировка объединений (предприятий) при расчете норматива за последующие плановые периоды и определение объема выпуска продукции по отдельным группам предприятий производятся па основе нормативов Удельный вес производственных объединений нормативных размеров в общей производственной мощности и Рациональный уровень заводской концентрации производства . Ужесточение нормативов численности служащих отрасли (подотрасли) в последующие плановые периоды происходит в первую очередь за счет постепенной оптимизации производственной структуры отрасли. Таким образом, при расчете используется нормативно-целевой подход, предполагающий поэтапное достижение в перспективе оптимальных размеров и структуры производственных объединений п входящих в них хозяйственных единиц. Это позволит использовать опыт и методы работы передовых объединений (предприятий), имеющих оптимальные размеры и производственную структуру, для оптимизации размеров п структуры аппарата управления объединений (предприятий) всех типов. Оптимизация управляемой системы (производственной структуры отрасли) явится основным фактором оптимизации управляющей системы и относительного сокращения трудозатрат на управление. [c.193]

ДИХОТОМИЧЕСКИЙ ПОИСК [di hotomi sear h] — 1. В численных методах оптимизации — поиск оптимума путем последовательного деления пополам (дихотомии) пространства решений и проверки каждой половины на наличие в ней экстремальной точки. Оптимум отыскивается таким путем за конечное количество шагов (делений). [c.92]

ИМИТАЦИОННЫЕ (ЧИСЛЕННЫЕ) МЕТОДЫ РЕШЕНИЯ МОДЕЛЕЙ [numeri al simulation methods] — последовательное преобразование предварительно подготовленных численных значений исследуемых величин до получения искомого значения и его верификации. В частности, к ним относятся численные методы оптимизации. Ср. Аналитические методы решения моделей. [c.120]

Среди вычислительных алгоритмов Н.п. большое место занимают градиентные методы. Универсального же метода для нелинейных задач нет и, по-видимому, может не быть, поскольку они чрезвычайно разнообразны. Особенно трудно решаются многоэкстремалъпые задачи. Для некоторых типов задач выпуклого программирования (вид нелинейного) разработаны эффективные численные методы оптимизации. [c.222]

Проектирующие подсистемы, применяемые к конкретным объектам, часто называют объектно-ориентированными. Подобные подсистемы настолько многочисленны, что затруднительно привести даже их перечень. Остановимся для примера на подсистеме, связанной с проектированием гидропривода и названной САПР Гидрооборудование , сданной в промышленную эксплуатацию во ВНИИгидропривода [46]. Ее структурная схема приведена на рис. 1.5. Блок управления представляет собой управляющую программу (УП), обеспечивающую связь системы с пользователями, базой данных и блоком оптимизации. Работа УП начинается с обращения к блоку, содержащему базу данных. Устройством связи с оператором выдается список объектов проектирования, запрашивается код объекта, из базы данных выбирается модель, соответствующая указанному коду. Далее УП запрашивает дополнительную информацию, уточняющую модель, критерий эффективности, ограничения. Сформировав математическую модель, УП обращается к блоку оптимизации, сообщая пользователю список методов оптимального поиска. Пользователь указывает код метода оптимизации. В блок оптимизации включены методы Лагранжа, Шора, модифицированных функций Лагранжа с численным дифференцированием, Лагранжа—Мида, градиентный. Полученные по одному из указанных методов оптимизации параметры объекта выдаются УП в виде таблицы. Пользователь оценивает результаты и принимает решение о продолжении или окончании работы с системой. При необходимости могут быть уточнены математическая модель и исходная информация, выбран иной метод оптимизации. [c.39]

Последовательные методы экспериментального поиска чаще всего основаны на принципах построения численных методов, среди которых можно выделить симплекс-метод, метод покоординатной оптимизации, градиентный метод и его модификации. [c.104]

Численные методы условной оптимизации Ред Гилл Ф, Мюррей У М, Мир , 1977 [c.112]

Программный пакет SAS Neural Network Appli ation предназначен для обучения множества разновидностей нейронных сетей и включает в себя графический интерфейс пользователя. Данный пакет предусматривает возможность обучения на месте и настраивается с учетом потребностей пользователя. Основные функции пакета включают в себя многослойные перцептроны, сети радиального базиса, статистические версии обратного распространения ошибки и дискретизации обучаемого вектора, множество встроенных функций активации и ошибок, множественные скрытые слои, прямые связи между входами и выходами, обработку ситуаций с пропущенными данными, категориальные переменные, стандартизацию входных данных и целей и предварительную оптимизацию с помощью случайных начальных данных с целью избежать попадания в локальные минимумы. Обучение осуществляется с использованием стандартных численных алгоритмов оптимизации вместо более трудоемкого метода обратного распространения ошибки. [c.260]

Методы поиска оптимальной точки, рассмотренные в этом разделе, позволили решить многие задачи механики, а также наиболее простые экономические задачи. Необходимо, однако, заметить, что в случае достаточно сложных функций U(x) решение уравнений (4.11) и тем более (4.12) представляется крайне затруднительным. Поэтому даже для функций с единственным локальным максимумом проблему безусловной оптимизации нельзя считать решенной только на основе соотношений (4.11) и (4.12). Проблема еще более усложняется, если функция U(x) не является достаточно гладкой. f С появлением вычислительной техники широкое распространение получили так называемые градиентные методы, состоящие в определении направления наискорейшего роста функции U(x) и в переходе от некоторой исходной точки к другой, более предпочтительной. Затем новая точка берется за исходную и процесс повторяется. В настоящее время построены различные варианты градиентных методов и разработаны вычислительные системы, позволившие численно решить многие важные задачи безусловной оптимизации (см., например, [31]). Однако проблему многоэкстремальности (т. е. неединственности локального экстремума) до сих пор нельзя считать решенной. [c.45]

В Уфимском нефтяном институте проведены исследования экономических показателей работы 25 крупных перевалочных нефтебаз (трубопроводных, железнодорожных, морских, речных) и на этой основе разработаны прогрессивные нормативы эксплуатационных расходов и капитальных вложений на перевалку нефтепродуктов в указанных пунктах стыкования различных видов транспорта. Установление фактических затрат на перевалку нефтепродуктов с одного вида транспорта на другой произведено в соответствии с разработанной в процессе исследования методикой выделения издержек на перевалку этого рода грузов из общих затрат перевалочных нефтебаз. Исходными материалами для установления и анализа фактических затрат на перевалку нефтепродуктов послужили данные (стоимостные и натуральные), собранные по всем рассмотренным перевалочным нефтебазам. Метод исследования — экономико-математический анализ (сравнения, группировка, цепная подстановка, математическая статистика, в том числе корреляционный анализ с использованием ЭВМ). В исследовании путей повышения экономичности работы пунктов стыкования изучались возможности оптимизации резервуарной емкости, численности производственного персонала, автоматизации сливно-наливных эстакад и др. Установление типичных экономических показателей по перевалке нефтепродуктов основывалось на результатах анализа фактических затрат, выявленных путях повышения экономичности работы перевалочных нефтебаз, новых нормативных и проект-но-сметных материалов. [c.165]

Учет покрытия постоянных затрет с относительными прямыми затратами Постоянные затраты при необходимости можно разделить на группы (постоянные затраты изделия, группы изделий, центра ответственности, предприятия в целом) и рассчитать соответствующие суммы покрытия Возможны и другие варианты классификации затрат, например, на денежные и неденежные Разрабатывается иерархия объектов затрат, включающая в себя направления деятельности, центры ответственности, виды затрат, виды продукции, причем все затраты являются прямыми для какого-либо объекта Затраты подразделяют на следующие группы => прямые и косвенные для заданного объекта (например, продукция, центр затрат) => постоянные и переменные относительно объема деятельности = денежные и неденежные =>по факторам, определяющим размер затрат (например, численность персонала, производственные площади) Наличие информации для контроля, планирования затрат и результатов Нахождение критического объема производства (в краткосрочном и долгосрочном периодах) с целью оценки риска Уменьшение степени недооценки запасов по сравнению с простым ди-рект-костингом Нет необходимости распределять косвенные постоянные затраты Все затраты рассматриваются как прямые, что дает больше возможностей для контроля Наличие информации для оптимизации объема выпуска в условиях ограниченных ресурсов Наличие информации для оптимизации структуры выпуска в условиях ограниченных ресурсов Трудно проводить оценку запасов Не всегда можно найти объект, для которого затраты являются прямыми Сложность метода [c.58]

Васильев О.В., Терлецкий В.А., Болдонов А.В. К исследованию некоторых задач оптимального управления, возникающих в обратной проблеме цунами // В кн. Методы численного анализа и оптимизации. — Новосибирск Наука, 1987. С. 3-33. [c.414]

Плодотворность обоих методов была установлена экспериментально. Интересное свойство схемы заключается в таком изменении стандартной процедуры ( поиска образа в терминологии Хука и Дживса [13]), применяемой для оптимизации функции с численными значениями, чтобы стала возможна оптимизация GT4 путем рекурсивного обращения его к самому [c.390]

economy-ru.info

Методы локальной оптимизации - Энциклопедия по экономике

Методы локальной оптимизации [c.32]

Достоинством методов локальной оптимизации является простота со- [c.44]

В задачах календарного планирования метод локальной оптимизации [c.44]

Обобщением метода локальной оптимизации являются так называемые [c.47]

Второй подход основывается на методах локальной оптимизации (перебора составов АС из некоторой окрестности определенного состава). Используемые при этом эвристические методы в общем случае не дают оптимального решения и поэтому требуют оценивания их гарантированной эффективности. [c.10]

Таким образом, в предлагаемой модели расчета производственных мощностей используется метод локальной их оптимизации. Широкие группы оборудования рассчитываются по фактической загрузке по простым экономико-математическим моделям. [c.96]

Существуют несколько методов строгой оптимизации сетевых моделей, большинство из них разработано для локально размещенных объектов. При сооружении объектов нефтяной и газовой промышленности, обычно разбросанных на большой территории, значительную долю занимают затраты на передислокацию строительно-монтажных организаций. Поэтому в качестве критерия оптимальности задачи выбора оптимального варианта сетевых моделей реализации инвестиционных проектов в нефтяной, газовой, нефтеперерабатывающей и нефтехимической промышленности можно принять суммарные затраты на привлечение возобновляемых ресурсов. Под привлечением возобновляемых ресурсов может пониматься перемещение бригад и технологических звеньев к месту ра- [c.99]

Первая категория требований предполагает наличие у менеджера специальной подготовки в области теории управления, знания основ современной макро- и микроэкономики, общей теории принятия управленческих решений, умения применять экономико-математические методы для оптимизации решений, навыков работы на ПЭВМ как в локальном, так и в сетевых вариантах. [c.15]

Оптимизационные задачи для выпуклых функций. Общим недостатком рассмотренных выше методов безусловной оптимизации было, с одной стороны, то, что они позволяют отыскивать только точки, подозрительные на локальный экстремум, а с другой — то, что найденные решения могут существенно зависеть от начального приближения. Поиск глобального оптимума подразумевает перебор найденных точек, который, [c.89]

В тех случаях, когда все локальные критерии /,, /,,..., / , с точки зрения ЛПР, имеют одинаковую степень важности, решение задачи векторной оптимизации осуществляется с использованием принципа равномерности, метода идеальной" точки, принципа справедливого компромисса, оптимальности по Парето. [c.193]

Получение точного УКУ-решения на основе МДУ локального УКУ и метода моментов Н.Н. Красовского. В соответствии с шагами 1 и 2 алгоритма второго этапа алгоритма оптимизации приводим исходную постановку задачи к виду (1.113)-(1.118). [c.89]

При вычислительной реализации метода наименьших квадратов в нелинейном (по оцениваемым параметрам 0) случае приходится исследовать вопросы существования и единствен ности решения. Необходимо помнить, что используемые (в том числе все описанные выше) методы оптимизации приводят в лучшем случае лишь к локальному минимуму критериальной функции. Проверка того, является ли этот минимуму глобальным, является следующей, зачастую не менее трудоемкой, вычислительной операцией. [c.320]

Решение задач условной оптимизации методом Лагранжа. Одним из наиболее общих подходов к решению задачи поиска экстремума (локального максимума или минимума) функции при наличии связующих ограничений на ее переменные (или, как еще говорят, задачи условной оптимизации) является метод Лагранжа. Многим читателям он должен быть известен из курса дифференциального исчисления. Идея данного метода состоит в сведении задачи поиска условного экстремума целевой функции [c.84]

Градиентные методы решения задач безусловной оптимизации. Ведущее место среди прямых методов решения экстремальных задач занимает градиентный метод (точнее, семейство градиентных методов) поиска стационарных точек дифференцируемой функции. Напомним, что стационарной называется точка, в которой V/(jt) = 0 и которая в соответствии с необходимым условием оптимальности является подозрительной на наличие локального экстремума. Таким образом, применяя градиентный метод, находят множество то- [c.86]

Еще одна характеристика генетической оптимизации — то, что она хорошо работает на поверхностях с разрывами, плоскими участками и другими сложными неупорядоченными формами. Генетический метод делит это преимущество с другими неаналитическими методами — лобовым подходом, управлением пользователем и пр. При помощи генетического оптимизатора можно найти решения, максимизирующие такие показатели, как чистая прибыль, доходность, отношение Шарпа и подобные, для которых поверхность функции пригодности имеет сложную форму, с трудом поддающуюся анализу. Это не означает, что такой оптимизатор не применяется для задач с простыми поверхностями — уступая в скорости вычислительным методам, генетический оптимизатор защищен от влияния ловушек локальных экстремумов . [c.54]

Тем не менее низкая скорость оптимизации не является главным препятствием на пути аналитика. Гораздо сложнее справиться с так называемой проблемой локальных решений. Почти все аналитические методы, будь они простыми или сложными, легко попадаются в ловушку локальных максимумов при наличии множества впадин и выступов на поверхности они не могут найти наилучшее глобальное решение. Метод наименьших квадратов, моделирование нейронными сетями дают поверхности функции пригодности неправильной формы с большим количеством локальных экстремумов. Данные поверхности чрезвычайно сложны для стандартных аналитических методов, таких как метод сопряженных градиентов или алгоритм обратного распространения, применяемый в нейронных сетях. Впрочем, местные максимумы можно обойти, соединив аналитический метод с генетическим. Для поверхностей, которые можно исследовать аналитическими методами, такой двойной алгоритм может оказаться наилучшим решением он позволит быстро и с большой точностью найти глобальные оптимумы. [c.58]

Задачи принятия решений, в которых локальные критерии/,, /2,..., // могут быть упорядочены на основе отношения абсолютной предпочтительности, решаются с использованием метода лексикографической оптимизации. Алгоритм решения состоит из последовательно реализуемых однотипных процедур. На первом шаге выбирается подмножество альтернатив А, СА, имеющих наилучшие оценки по первому критерию. На втором шаге выбирается подмножество альтернатив Аг At, имеющих наилучшие оценки по второму критерию, и т. п. [c.193]

Главная вычислительная трудность при решении оптимизационных задач в моделях на основе решающих правил вызвана невыпуклостью. Затруднительно напрямую использовать стандартные алгоритмы нелинейного программирования, поскольку они ориентированы на поиск только точек локального оптимума. Обычно повторно запускают алгоритм из множества случайно выбранных точек и сравнивают полученные оптимальные значения. В качестве альтернативы можно пытаться использовать любые методы глобальной оптимизации, ограничиваясь решением задач с умеренным числом переменных. [c.25]

В последние годы уровень автоматизации процессов в нефтепереработке и нефтехимии значительно возрос. Разработаны и внедрены анализаторы качества продукции в потоке, уровнемеры, индикаторы составов, хроматографы, газоанализаторы, на многих предприятиях функционируют товарные парки с полной автоматизацией замера уровня и дистанционным управлением переключения, автоматизированы слив и налив сырья и продукции, разработаны и внедрены локальные системы автоматического регулирования различного назначения (системы автоматизации переключения контактных печей с контактирования на регенерацию, автоматического регулирования состава углеводородной шихты, оптимизации процессов дегидрирования бутана в бутилен и бутилена в бутадиен, автоматического управления процессом эмульсационной полимеризации и др.). На технологических установках (каталитического рифор-минга, пиролиза, полимеризации) внедряют управляющие вычислительные машины (УВМ). Внедрение УВМ знаменует переход к более высокому уровню автоматизации и обеспечивает дальнейший рост эффективности производства. Так, применение на одном из предприятий УВМ УМ-1 для оперативного управления и контроля процесса гидроочистки дизельного топлива дало 170 тыс. руб. годовой экономии. Использование экономико-математических методов и УВМ для компаундирования товарной продукции обеспечило 7 млн. руб. экономии. Коми- [c.109]

Решение задач многокритериальной или векторной оптимизации осуществляется с использованием принципов выделения главного критерия, скаляризации вектора целевых функций, равномерности, идеальной" точки, квазиоптимизации локальных критериев методом последовательных уступок, справедливого компромисса, оптимальности по Парето и ряда других. [c.192]

Базовой идеей всех алгоритмов обучения является учет локального градиента в пространстве конфигураций для выбора траектории быстрейшего спуска по функции ошибки. Функция ошибки, однако, может иметь множество локальных минимумов, представляющих суб-оптимальные решения. Поэтому градиентные методы обычно дополняются элементами стохастической оптимизации, чтобы предотвратить застревание конфигурации сети в таких локальных минимумах. Идеальный метод обучения должен найти глобальный оптимум конфигурации сети4. [c.45]

Использование того же метода наименьших квадратов, как и в линейной логопериодической формуле, позволяет отойти от линейных переменных А, В и С и образовать целевую функцию, зависящую только от ta ft, временные рамки от 1года до 20 лет. Как и прежде, нелинейность целевой функции приводит к возникновению множественных локальных минимумов, а предварительньш поиск по сетке данных используется для определения начальных точек оптимизации. [c.328]

В отличие от методов второго порядка, где веса изменяются пропорционально их вкладу в направление глобального поиска, в локальных методах оптимизации каждый вес меняется локально. В качестве примера таких методов можно назвать метод дельта-дельта (см. [151]),Кргор(см. [240]),Qui kProp( M. [104]). [c.32]

Глава 1. Модели и алгоритмы интеллектуальных систем 71 Этап 2. Алгоритм оптимизации управления ММС на основе модифицированных достаточных условий локальных УКУ и метода моментов Н.Н. Красовского. Общий вид достаточных условий локальных УКУ Э. Вайсборда и В. Жуковского [30]. В соответствии с общими принципами формирования коалиционной структуры [30] вводится коалиционное разбие- [c.71]

На совр. этапе в прикладных экономич. исследованиях возросла роль экономико-математич. методов. Особенно интенсивно развивается моделирование экономич. процессов, где используются макроэкономич. модели, аппарат призводств. функций, межотраслевой баланс, система нац. счетов и др. Ведутся работы в области оптимизац. моделей и решений, экономич. кибернетики. Закономерен переход экономико-математин. исследований от решений локальных к постановке нар.-хоз. задач, от статистич. к динамич. моделям, к учёту фактора неопределённости в процессе принятия решений, к включению в модели не только технико-эконо-мич., но и социальных переменных. Развитие и использование экономико-математич. методов может быть плодотворным только на основе марксистско-ленинской экономич. теории и методологии. [c.507]

economy-ru.info

Исследование методов оптимизации

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

«ХАРЬКОВСКИЙ ПОЛИТЕХНИЧЕСКИЙ ИНСТИТУТ»

Факультет информатики и управления

Кафедра экономической кибернетики и маркетингового менеджмента

КУРСОВАЯ РАБОТА

По математическому программированию

Исследование методов оптимизации

Харьков 2009

РЕФЕРАТ

Данная курсовая работа содержит : 41 страницу, 16 таблиц, 6 графиков.

В курсовой работе рассмотрены теоретические основы двух методов оптимизации математического программирования :

- метод Нелдера-Мида ;

- градиентный метод с дроблением шага.

Произведена минимизация исследуемой функции указанными методами. Выявлена зависимость числа итераций от заданной точности. Сопоставлена трудоемкость и эффективность оптимизации заданной функции различными методами (градиентным и методом Нелдера-Мида).

Ключевые термины:

Градиент – вектор первых частных производных функции.

Линии уровня – множества точек, в которых функция

принимает постоянные значения, т.е.

Методы нулевого порядка – методы, которые не предполагают вычисления производной для поиска оптимума.

Методы первого порядка – методы, в которых кроме вычисления функции в любой точке предлагается вычисление первых производных.

СОДЕРЖАНИЕ

1. Введение

2. Математическое описание методов оптимизации

2.1 Метод Нелдера-Мида

2.2 Градиентный метод с дроблением шага

3. Решение задачи минимизации для каждого из методов

3.1 Метод Нелдера-Мида

3.2 Градиентный метод с дроблением шага

4. Графическая интерпретация решения задачи

5. Аналитическое исследование методов

6. Заключение

7. Приложение

8. Список литературы

СПИСОК УСЛОВНЫХ ОБОЗНАЧЕНИЙ

- точка - длинна шага - вектор градиент

E - точность

N – количество итераций

Д – матрица координат симплекса

t – длинна ребра симплекса

1. ВВЕДЕНИЕ

Объектом исследования предмета математическое программирование являются задачи оптимизации.

Оптимизация подразумевает нахождение наилучшего варианта среди всех существующих. В любой практической оптимизационной задаче существует много совпадающих этапов. Наиболее важным этапом является моделирование рассматриваемой физической ситуации с целью получения математической функции, которую необходимо минимизировать, а также определения ограничений, если таковые существуют. Затем следует выбрать подходящую процедуру для осуществления минимизации. Эта процедура должна быть реализована на практике, что во многих реальных случаях вынуждает использовать ЭВМ для выполнения большого объема вычислений.

Универсальных методов, подходящих для поиска экстремума абсолютно любой функции не существует. Данная курсовая работа ставит себе целью исследовать метод оптимизации нулевого порядка – метод Нелдера-Мида, а также метод оптимизации первого порядка – градиентный метод с дроблением шага на примере конкретной функции. Таким образом, получив практические результаты, можно будет сравнить эффективность рассматриваемых методов, применяемых к исследуемой функции.

ПОСТАНОВКА ЗАДАЧИ ( Вариант задания 1)

Исследовать функцию типа :

Используемые методы минимизации

1. Метод: Нелдера-Мида.

2. Метод: Градиентный с дроблением шага.

Необходимо :

1. Решить задачу минимизации

, начав итерации из выбранной начальной точки x0=(1;1) заданными по варианту методами, необходимая точность решения . Привести таблицу результатов расчета типа: Итерация: - точка: значение: критерий: .

2. Рассчитать 3 линии уровня функции и изобразить их на графике.

3. Отобразить на графиках линий уровня для каждого из заданных методов траекторию движения по итерациям (траекторию спуска).

4. Выявить зависимость числа итераций N от заданной точности E, значения точности:

, , , , , . Привести таблицу результатов как в п.1 для каждого значения E.

5. Сравнить эффективность рассмотренных в варианте методов по числу итераций N, построить графики N=F(E).

2. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ МЕТОДОВ ОПТИМИЗАЦИИ

2.1 Метод Нелдера-Мида

Вводится симплекс, координаты вершин которого заданы таблицей (одна из вершин в начале координат).

t – некоторое выбранное число.

Если n = 2, то при t = 1 имеем

Расположение симплекса показано на рисунке 2.1

Рисунок 2.1- Начальное расположение симплекса

Легко убедиться в том, что если координаты вершин симплекса задать в соответствии с матрицей Д0 , то расстояние между двумя любыми вершинами симплекса всегда будет равно выбранной константе t независимо от размерности задачи n .

Действительно, расстояние между любой вершиной xj , j= 2,3,.., n+1, и вершиной x1 равно

С другой стороны, расстояние между любой парой вершин

, , , равно Зададим начальную точку процедуры поиска минимума вектором Перенесем исходный симплекс таким образом, чтобы вершина, находившаяся в начале координат, оказалась в точке . Получим матрицу

Вычислим значения оптимизируемой функции в точках

и переномеруем точки так, чтобы выполнялись неравенства : .

Найдем координаты центра тяжести фигуры , получающейся в результате удаления вершины

Осуществим отражение вершины

относительно центра тяжести. Получим точку .

Если a=1 , то получим зеркальное отражение. В одномерном случае процедура отражения, обеспечивающая получение точки

, симметричной точке относительно иллюстрируется рис. 2.2

Рисунок 2.2 - Построение точки

Сравним теперь между собой значения

Возможны следующие варианты

а)

. В этом случае выполняется растяжение симплекса и отыскивается точка

mirznanii.com

Методы поисковой оптимизации

1. Назначение и классификация методов поисковой оптимизации

В связи со сложностью объектов проектирования критерии качества и ограничения задачи параметрической оптимизации (1.5), как правило, слишком сложны для применения классических методов поиска экстремума. Поэтому на практике предпочтение отдается методам поисковой оптимизации. Рассмотрим основные этапы любого метода поиска.

Исходными данными в методах поиска являются требуемая точность метода и начальная точка поиска Х 0 .

Затем выбирается величина шага поиска h, и по некоторому правилу происходит получение новых точек Х k+1 по предыдущей точке Х k , при k = 0,1,2,… Получение новых точек продолжают до тех пор, пока не будет выполнено условие прекращения поиска. Последняя точка поиска считается решением задачи оптимизации. Все точки поиска составляют траекторию поиска.

Методы поиска могут отличаться друг от друга процедурой выбора величины шага h (шаг может быть одинаковым на всех итерациях метода или рассчитываться на каждой итерации), алгоритмом получения новой точки и условием прекращения поиска.

Для методов, использующих постоянную величину шага, h следует выбирать значительно меньше точности h » Öe). Если при выбранной величине шага h не удается получить решение с требуемой точностью, то нужно уменьшить величину шага и продолжить поиск из последней точки имеющейся траектории.

В качестве условий прекращения поиска принято использовать следующие:

все соседние точки поиска хуже, чем предыдущая;

çФ(Xk+1 ) - Ф(X k )ç£ e, то есть значения целевой функции Ф(Х) в соседних точках (новой и предыдущей) отличаются друг от друга на величину не больше, чем требуемая точность e;

то есть все частные производные в новой точке поиска практически равны 0 или отличаются от 0 на величину, не превышающую заданной точности e.

Алгоритм получения новой точки поиска Хk+1 по предыдущей точке Хk свой для каждого из методов поиска, но всякая новая точка поиска должна быть не хуже предыдущей: если задача оптимизации является задачей поиска минимума, то Ф(Хk+1 ) £ Ф(Хk ).

Методы поисковой оптимизации принято классифицировать по порядку производной целевой функции, используемой для получения новых точек. Так, в методах поиска нулевого порядка не требуется вычисления производных, а достаточно самой функции Ф(Х). Методы поиска первого порядка используют первые частные производные, а методы второго порядка используют матрицу вторых производных (матрицу Гессе).

Чем выше порядок производных, тем более обоснованным является выбор новой точки поиска и тем меньше число итераций метода. Но при этом возрастает трудоемкость каждой итерации из-за необходимости численного расчета производных.

Эффективность поискового метода определяют по числу итераций и по количеству вычислений целевой функции Ф(Х) на каждой итерации метода (N). Рассмотрим наиболее распространенные методы поиска, расположив их в порядке уменьшения числа итераций.

Для методов поиска нулевого порядка справедливо следующее: в методе случайного поиска нельзя заранее предсказать количество вычислений Ф(Х) на одной итерации N, а в методе покоординатного спуска N £ 2×n, где n- количество управляемых параметров X = ( x1, x2.,…,xn).

Для методов поиска первого порядка справедливы следующие оценки: в градиентном методе с постоянным шагом N=2×n; в градиентном методе с дроблением шага N = 2×n + n1 , где n1 – число вычислений Ф(Х), необходимых для проверки условия дробления шага; в методе наискорейшего спуска N=2×n+n2 , где n2 – число вычислений Ф(Х), необходимых для расчета оптимальной величины шага; а в методе Давидона – Флетчера - Пауэлла (ДФП) N = 2× n + n3 , где n3 – число вычислений Ф(Х), необходимых для расчета матрицы, приближающей матрицу Гессе ( для величин n1 , n2 , n3 справедливо соотношение n1 < n2 << n3 ).

И, наконец, в методе второго порядка - методе Ньютона N = 3×n2 . При получении данных оценок предполагается приближенное вычисление производных по формулам конечных разностей / 6 /:

то есть для вычисления производной первого порядка нужно знать два значения целевой функции Ф(Х) в соседних точках, а для второй производной – значения функции в трех точках.

На практике широкое применение нашли метод наискорейшего спуска и метод ДФП, как методы с оптимальным соотношением числа итераций и их трудоемкости.

2. Методы поиска нулевого порядка

2.1. Метод случайного поиска

В методе случайного поиска исходными данными являются требуемая точность метода e, начальная точка поиска Х0 = ( x10 , x2. 0 ,…,xn0 ) и величина шага поиска h. Поиск новых точек производится в случайном направлении, на котором и откладывается заданный шаг h (рис. 2.1), таким образом получают пробную точку Х^ и проверяют, является ли пробная точка лучшей, чем предыдущая точка поиска. Для задачи поиска минимума это означает, что

Ф(Х^ ) £ Ф(Хk ), k = 0,1,2… (2.4)

Если условие (2.4) выполнено, то пробную точку включают в траекторию поиска Х k+1 = Х^ . В противном случае, пробную точку исключают из рассмотрения и производят выбор нового случайного направления из точки Х k , k = 0,1,2,.

Несмотря на простоту данного метода, его главным недостатком является тот факт, что заранее неизвестно, сколько случайных направлений потребуется для получения новой точки траектории поиска Хk+1 , что делает затраты на проведение одной итерации слишком большими. Кроме того, поскольку при выборе направления поиска не используется информация о целевой функции Ф(Х), число итераций в методе случайного поиска очень велико.

В связи с этим метод случайного поиска используется для исследования малоизученных объектов проектирования и для выхода из зоны притяжения локального минимума при поиске глобального экстремума целевой функции /6/.

2.2. Метод покоординатного спуска

В отличие от метода случайного поиска, в методе покоординатного спуска в качестве возможных направлений поиска выбирают направления, параллельные осям координат, причем движение возможно как в сторону увеличения, так и уменьшения значения координаты.

Исходными данными в методе покоординатного спуска являются величина шага h и начальная точка поиска Х0 = ( x10 , x2. 0 ,…,xn0 ). Движение начинаем из точки Х0 вдоль оси x1 в сторону увеличения координаты. Получим пробную точку Х^ с координатами ( x10 +h, x20 ,…,xn0 ), при k = 0.

Сравним значение функции Ф(Х^ ) с значением функции в предыдущей точке поиска Хk . Если Ф(Х^ ) £ Ф(Хk ) (мы предполагаем, что требуется решить задачу минимизации целевой функции Ф(Х)), то пробную точку включают в траекторию поиска ( Х k+1 = Х^ ).

В противном случае, пробную точку исключаем из рассмотрения и получаем новую пробную точку, двигаясь вдоль оси x1 в сторону уменьшения координаты. Получим пробную точку Х^ = ( x1k -h, x2. k ,…,xnk ). Проверяем, если Ф(Х^ ) > Ф(Хk ), то продолжаем движение вдоль оси x2 в сторону увеличения координаты. Получим пробную точку Х^ = ( x1k , x2.k +h,…,xnk ) и т.д. При построении траектории поиска повторное движение по точкам, вошедшим в траекторию поиска, запрещено. Получение новых точек в методе покоординатного спуска продолжается до тех пор, пока не будет получена точка Хk , для которой все соседние 2×n пробных точек (по всем направлениям x1, x2.,…,xn в сторону увеличения и уменьшения значения каждой координаты) будут хуже, то есть Ф(Х^ ) > Ф(Хk ). Тогда поиск прекращается и в качестве точки минимума выбирается последняя точка траектории поиска Х* = Хk .

3. Методы поиска первого порядка

3.1. Структура градиентного метода поиска

В методах поиска первого порядка в качестве направления поиска максимума целевой функции Ф(Х) выбирается вектор градиент целевой функции grad (Ф(Хk )), для поиска минимума – вектор антиградиент -grad (Ф(Хk )). При этом используется свойство вектора градиента указывать направление наискорейшего изменения функции:

Для изучения методов поиска первого порядка важно также следующее свойство: вектор градиент grad (Ф(Хk )) направлен по нормали к линии уровня функции Ф(Х) в точке Хk (см. рис. 2.4). Линии уровня – это кривые, на которых функция принимает постоянное значение (Ф(Х) = соnst).

В данной главе мы рассмотрим 5 модификаций градиентного метода:

градиентный метод с постоянным шагом,

градиентный метод с дроблением шага,

метод наискорейшего спуска,

метод Давидона-Флетчера-Пауэлла,

двухуровневый адаптивный метод.

3.2. Градиентный метод с постоянным шагом

В градиентном методе с постоянным шагом исходными данными являются требуемая точность e, начальная точка поиска Х0 и шаг поиска h.

Получение новых точек производится по формуле:

Формула (2.7) применяется, если для функции Ф(Х) необходимо найти минимум. Если же задача параметрической оптимизации ставится как задача поиска максимума, то для получения новых точек в градиентном методе с постоянным шагом используется формула:

mirznanii.com