Постановка задачи оптимизации. Задачи оптимизации
Задачи оптимизации
РЯЗАНСКОЕ
ВЫСШЕЕ ВОЗДУШНО-ДЕСАНТНОЕ КОМАНДНОЕ
ДВАЖДЫ КРАСНОЗНАМЕННОЕ УЧИЛИЩЕ
ИМЕНИ ГЕНЕРАЛА АРМИИ МАРГЕЛОВА В.Ф.
Кафедра высшей математики и теоретической механики
КУРСОВАЯ РАБОТА
ЗАДАЧИ ОПТИМИЗАЦИИ
Выполнил курсант: Валуйкин Александр Владимирович
4 взвода 8 роты
Руководитель работы: Щукина Наталья Васильевна
Рязань – 2001 г.
СОДЕРЖАНИЕ
Введение................................................................................................................................. 3
§1. ПОСТАНОВКА ЗАДАЧ ОПТИМИЗАЦИИ.................................................................... 5
§2 ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ....................................................... 7
§3 АНАЛИТИЧЕСКИЙ МЕТОД ОПТИМИЗАЦИИ......................................................... 13
ЗАКЛЮЧЕНИЕ........................................................................................................................ 15
ЛИТЕРАТУРА.......................................................................................................................... 16
Каждый человек время от времени оказывается в ситуации, когда достижение некоторого результата может быть осуществлено не единственным способом. В таких случаях приходится отыскивать наилучший способ. Однако в различных ситуациях наилучшими могут быть совершенно разные решения. Все зависит от выбранного или заданного критерия. На практике оказывается, что в большинстве случаев понятие «наилучший» может быть выражено количественными критериями – минимум затрат, минимум времени, максимум прибыли и т.д. Поэтому возможна постановка математических задач отыскания оптимального (optimum – наилучший) результата, так как принципиальных различий в отыскании наименьшего или наибольшего значения нет. Задачи на отыскание оптимального решения называются задачами оптимизации. Оптимальный результат, как правило, находится не сразу, а в результате процесса, называемого процессом оптимизации. Применяемые в процессе оптимизации методы получили название методов оптимизации. Чтобы решить практическую задачу надо перевести ее на математический язык, то есть составить ее математическую модель.
Математическая модель представляет собой стройную и глубокую совокупность знаний о математических моделях со своими проблемами, с собственными путями развития, обусловленными внутренними и внешними причинами и задачами. Математика дает удобные и плодотворные способы описания самых разнообразных явлений реального мира и тем самым выполняет в этом смысле функцию языка. Эту роль математики прекрасно осознавал Галилей, сказавший: «Философия написана в грандиозной книге – Вселенной, которая открыта нашему пристальному взгляду. Но понять эту книгу может лишь тот, кто научился понимать ее язык и знаки, которыми она изложена. Написана же она на языке математики».
Итак, математика – это область человеческого знания, в которой изучаются математические модели.
Часто в математической модели требуется найти наибольшее или наименьшее значение некоторой функции на некотором множестве, то есть решить задачу оптимизации. Методов решения задач оптимизации достаточно много. Некоторые из них рассматривались при отыскании экстремальных значений функций одной и многих вещественных переменных. Кроме точных методов широко используются и приближенные, например, метод дихотомии и т.д.
Знание методов нахождения оптимального решения позволяет инженеру и офицеру выбирать наиболее эффективные и самые экономичные способы эксплуатации и ремонта машин, находить оптимальные решения тактических задач.
В курсовой работе по методам оптимизации предлагается две задачи: задача линейного программирования и общая задача оптимизации, решаемая аналитическим методом.
На протяжении всей своей эволюции человек, совершая те или иные деяния, стремился вести себя таким образом, чтобы результат, достигаемый как следствие некоторого поступка, оказался в определенном смысле наилучшим. Двигаясь из одного пункта в другой, он стремился найти кратчайший среди возможных путь. Строя жилище, он искал такую его геометрию, которая при наименьшем расходе топлива, обеспечивала приемлемо комфортные условия существования. Занимаясь строительством кораблей, он пытался придать им такую форму, при которой вода оказывала бы наименьшее сопротивление. Можно легко продолжить перечень подобных примеров.
Наилучшие в определенном смысле решения задач принято называть оптимальными . Без использования принципов оптимизации в настоящее время не решается ни одна более или менее сложная проблема. При постановке и решении задач оптимизации возникают два вопроса: что и как оптимизировать?
Ответ на первый вопрос получается как результат глубокого изучения проблемы, которую предстоит решить. Выявляется тот параметр, который определяет степень совершенства решения возникшей проблемы. Этот параметр обычно называют целевой функцией или критерием качества . Далее устанавливается совокупность величин, которые определяют целевую функцию. Наконец, формулируются все ограничения, которые должны учитываться при решении задачи. После этого строится математическая модель, заключающаяся в установлении аналитической зависимости целевой функции от всех аргументов и аналитической формулировки сопутствующих задаче ограничений. Далее приступают к поиску ответа на второй вопрос.
Итак, пусть в результате формализации прикладной задачи установлено, что целевая функция
, где множество Х – обобщение ограничений, его называют множеством допустимых решений. Существо проблемы оптимизации заключается в поиске на множестве Х – множестве допустимых решений такого решения , при котором целевая функция f достигает наименьшего или наибольшего значения.Впервые постановка задачи линейного программирования в виде предложения по составлению оптимального плана перевозок; позволяющего минимизировать суммарной километраж, была дана в работе советского экономиста А. Н. Толстого в 1930 году.
Систематические исследования задач линейного программирования и разработка общих методов их решения получили дальнейшее развитие в работах российских математиков Л. В. Канторовича, В. С. Немчинова и других математиков и экономистов. Также методам линейного программирования посвящено много работ зарубежных и прежде всего американских ученых.
Задача линейного программирования состоит в следующем: максимизировать (минимизировать) линейную функцию
, гдепри ограничениях
(*)
причем все
Замечание . Неравенства могут быть и противоположного смысла. Умножением соответствующих неравенств на (-1) можно всегда получить систему вида (*).
Если число переменных системы ограничений и целевой функции в математической модели задачи равно 2, то её можно решить графически.
Итак, надо максимизировать функцию
и удовлетворяющей системе ограничений.Обратимся к одному из неравенств системы ограничений.
С геометрической точки зрения все точки, удовлетворяющие этому неравенству, должны либо лежать на прямой
, либо принадлежать одной из полуплоскостей, на которые разбивается плоскость этой прямой. Для того, чтобы выяснить это, надо проверить какая из них содержит точку ().Замечание 2 . Если
, то проще взять точку (0;0).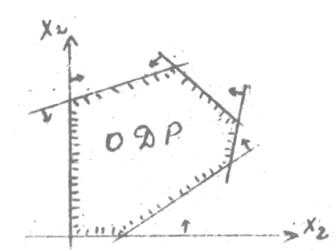 Условия неотрицательности также определяют полуплоскости соответственно с граничными прямыми . Будем считать, что система неравенств совместна, тогда полуплоскости, пересекаясь, образуют общую часть, которая является выпуклым множеством и представляет собой совокупность точек, координаты которых являются решением данной системы – это множество допустимых решений. Совокупность этих точек (решений) называется многоугольником решений. Он может быть точкой, лучом, многоугольником, неограниченной многоугольной областью. Таким образом, задача линейного программирования состоит в нахождении такой точки многоугольника решений, в которой целевая функция принимает максимальное (минимальное) значение. Эта точка существует тогда, когда многоугольник решений не пуст и на нем целевая функция ограничена сверху (снизу). При указанных условиях в одной из вершин многоугольника решений целевая функция принимает максимальное значение. Для определения данной вершины построим прямую (где h – некоторая постоянная). Чаще всего берется прямая . Остается выяснить направление движения данной прямой. Это направление определяется градиентом (антиградиентом) целевой функции
Условия неотрицательности также определяют полуплоскости соответственно с граничными прямыми . Будем считать, что система неравенств совместна, тогда полуплоскости, пересекаясь, образуют общую часть, которая является выпуклым множеством и представляет собой совокупность точек, координаты которых являются решением данной системы – это множество допустимых решений. Совокупность этих точек (решений) называется многоугольником решений. Он может быть точкой, лучом, многоугольником, неограниченной многоугольной областью. Таким образом, задача линейного программирования состоит в нахождении такой точки многоугольника решений, в которой целевая функция принимает максимальное (минимальное) значение. Эта точка существует тогда, когда многоугольник решений не пуст и на нем целевая функция ограничена сверху (снизу). При указанных условиях в одной из вершин многоугольника решений целевая функция принимает максимальное значение. Для определения данной вершины построим прямую (где h – некоторая постоянная). Чаще всего берется прямая . Остается выяснить направление движения данной прямой. Это направление определяется градиентом (антиградиентом) целевой функции Задачи оптимизации | Решение задач по математике и другим предметам!!!
Задача № 1. Решить графическим методом типовую задачу оптимизации.
Некоторая фирма выпускает два набора удобрений для газонов: обычный и улучшенный. В обычный набор входит 3 кг азотных, 4 кг фосфорных и 1 кг калийных удобрений, а в улучшенный – 2 кг азотных, 6 кг фосфорных и 3 кг калийных удобрений. Известно, что для некоторого газона требуется по меньшей мере 10 кг азотных, 20 кг фосфорных и 7 кг калийных удобрений. Обычный набор стоит 3 ден. ед., а улучшенный – 4 ден. ед. Какие и сколько наборов удобрений нужно купить, чтобы обеспечить эффективное питание почвы и минимизировать стоимость?
Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если решать задачу на максимум и почему?
Решение:
1. Введем переменные:
– количество обычных наборов;
– количество улучшенных наборов.
2. Зададим целевую функцию. Задача на минимизацию затрат. Запишем уравнение, описывающее затраты
3. Ограничения:
Найдем решение сформированной задачи, используя ее геометрическую интерпретацию. Сначала определим область допустимых решений. Для этого в неравенствах системы ограничений знаки неравенств заменим на знаки точных равенств, и найдем соответствующие прямые:
Выразим через
Для построения прямой достаточно двух точек, найдем их координаты:

Эти прямые изображены на рисунке 1. Условие неотрицательности показывает, что искомая область располагается в первой четверти.
Каждая из построенных прямых делит плоскость на две полуплоскости. Координаты точек одной полуплоскости удовлетворяют исходному неравенству, а другой – нет. Чтобы определить искомую полуплоскость, нужно взять какую-нибудь точку, принадлежащую одной из полуплоскостей, и проверить, удовлетворяют ли ее координаты данному неравенству. Если координаты взятой точки удовлетворяют данному неравенству, то искомой является та полуплоскость, которой принадлежит эта точка, в противном случае – другая полуплоскость.
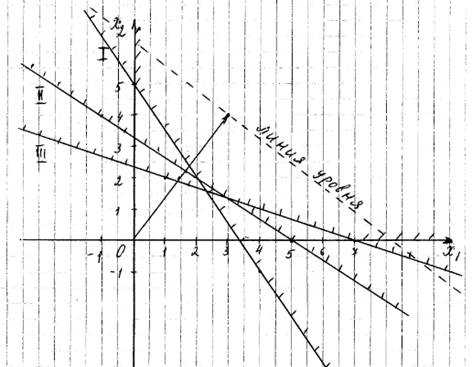
Рисунок 1. Графический метод решения
На рисунке 1, область допустимых решений не ограничена и отмечена штрихом. Координаты любой точки, принадлежащей этой области, удовлетворяют данной системе неравенств и условию неотрицательности переменных. Поэтому сформулированная задача будет решена, если мы сможем найти точку, принадлежащую области допустимых решений, в которой целевая функция принимает минимальное значение. Чтобы найти указанную точку, построим вектор и линию уровня, которая перпендикулярна этому вектору.
Так как задача на минимум, то линию уровня будем двигать по направлению вектора. Первая точка касания и будет оптимальным решением. Координаты этой точки и определяют оптимальные количества обычных и улучшенных наборов удобрений, при которых затраты являются минимальными.
В данном примере это точка пересечения прямых I и Следовательно, ее координаты удовлетворяют уравнениям этих прямых
Следовательно, если фирма купит 2 обычных и 2 улучшенных набора удобрений, то минимальные затраты составят
Если данную задачу решать на максимум, то линия уровня будет сдвигаться вправо до бесконечности (так область решений не ограничена). Таким образом, конечного решения не будет.
Задача № 2. Предложить оптимальное управленческое решение в следующих типовых хозяйственных ситуациях.
Металлургическому заводу требуется уголь с содержанием фосфора не более 0,03% и с долей зольных примесей не более 3,25%. Завод закупает три сорта угля , , с известным содержанием примесей. В какой пропорции нужно смешивать исходные продукты , , чтобы смесь удовлетворяла ограничениям на содержание примесей и имела минимальную цену? Содержание примесей и цена исходных продуктов приведены в таблице
Решение:
Введем следующие обозначения: – содержание угля в смеси; – содержание угля в смеси; – содержание угля в смеси. Тогда ограничения примут вид:
Целевая функция задачи:
Таким образом, ЭММ задачи имеет вид:
Решим данную задачу симплекс-методом. Преобразуем исходную модель. В ограничения типа добавим дополнительные переменные . В равенство добавим искусственную переменную Модель задачи будет выглядеть так:
При условиях:
Заполним первую симплекс-таблицу.
В среди оценок есть положительные значения, следовательно, план не является оптимальным. Среди значений находим наибольшее , столбец выбираем в качестве ведущего. Для положительных элементов ведущего столбца находим наименьшее из симплексных отношений – ведущая строка. Элемент 1 на пересечении ведущего столбца и ведущей строки – разрешающий элемент. После перехода к следующей симплексной таблице, в базисном плане отсутствует искусственная переменная.
В среди оценок есть положительные значения, следовательно, план не является оптимальным. Среди значений находим наибольшее , столбец выбираем в качестве ведущего. Для положительных элементов ведущего столбца находим наименьшее из симплексных отношений – ведущая строка. Элемент 1 на пересечении ведущего столбца и ведущей строки – разрешающий элемент. Переходим к следующей симплексной таблице.
В среди оценок есть положительное значение, следовательно, план не является оптимальным. Столбец выбираем в качестве ведущего. Для положительных элементов ведущего столбца находим наименьшее из симплексных отношений – ведущая строка. Элемент 0,06 на пересечении ведущего столбца и ведущей строки – разрешающий элемент. При переходе к следующей симплексной таблице, получаем оптимальное решение.
В среди оценок нет отрицательных, следовательно, план является оптимальным.
Полученное оптимальное решение означает, что для получения 1 т угля необходимо взять т первого компонента, т второго, т третьего. При этом его цена будет минимальной и составит Руб.
Задача № 3. Провести моделирование и решить специальную задачу линейного программирования.
Компания, занимающаяся ремонтом автомобильных дорог, в следующем месяце будет проводить ремонтные работы на пяти участках автодорог. Песок на участки ремонтных работ может доставляться из трех карьеров, месячные объемы предложений по карьерам известны. Из планов производства ремонтных работ известны месячные объемы потребностей по участкам работ. Имеются экономические оценки транспортных затрат (в у. е.) на перевозку 1тонны песка с карьеров на ремонтные участки.
Числовые данные для решения содержатся ниже в Матрице планирования. Требуется:
1) Предложить план перевозок песка на участки ремонта автодорог, который обеспечивает минимальные совокупные транспортные издержки.
2) Что произойдет с оптимальным планом, если изменятся условия перевозок: а) появится запрет на перевозки от первого карьера до второго участка работ?; б) по этой коммуникации будет ограничен объем перевозок 3 тоннами?
Матрица планирования:
| Участки работ Карьеры | Предложение | |||||
| 4 | 2 | 3 | 4 | 1 | 60 | |
| 2 | 4 | 3 | 5 | 6 | 90 | |
| 6 | 5 | 4 | 6 | 2 | 140 | |
| Потребности | 40 | 30 | 90 | 80 | 50 | 290 290 |
Решение:
Суммарные объемы предложений по карьерам равны суммарным объемам потребностей по участкам работ, т. е. выполняется условие общего баланса Следовательно, данная задача закрытого типа.
Построим начальный базисный план Методом минимальной стоимости. Назначение перевозок начинаем с клетки (1,5), имеющей минимальную стоимость перевозки (1). В клетку (1,5) записываем наименьшее из значений и и исключаем из дальнейшего рассмотрения пятый участок. Корректируем предложение первого карьера на величину
Следующая поставка осуществляется от первого карьера второму участку. В клетку (1,2) назначаем перевозку исключаем из дальнейшего рассмотрения первый карьер. Корректируем потребности второго участка С оставшейся матрицей поступаем аналогично предыдущему:
План перевозок, построенный методом минимальной стоимости:
Построенный начальный план перевозок является невырожденным, так как число назначенных перевозок равно Определим полную стоимость перевозок по найденному опорному плану:
Определим оптимальность полученного плана. С помощью Метода потенциалов вычислим потенциалы строк и столбцов по стоимости перевозок в загруженных клетках. Если известен , то если известен , то Положим, например, Тогда будут вычислены и остальные потенциалы строк и столбцов.
Для незагруженных клеток вычислим величины превышения стоимости
Полученный план не оптимален. Среди оценок имеются отрицательные значения. Потенциальной является клетка . От клетки строим замкнутый контур: Начиная с клетки разметим вершины контура попеременно знаками плюс «+», минус «-», обходя замкнутый контур в любом направлении. Из клеток, помеченных знаком «-», выбираем наименьшее значение объема перевозки Сформируем новый улучшенный план: на 20 увеличим перевозки в клетках, помеченных знаком «+», и уменьшим в клетках, помеченных знаком «-».
Определим полную стоимость перевозок по новому плану
Вычислим потенциалы и величины превышения стоимости для незагруженных клеток:
Полученный план не оптимален. Среди оценок имеется отрицательное значение. Потенциальной является клетка . От клетки строим замкнутый контур: Выбираем наименьшее значение объема перевозки Сформируем новый улучшенный план: на 30 увеличим перевозки в клетках, помеченных знаком «+», и уменьшим в клетках, помеченных знаком «-».
Определим полную стоимость перевозок по новому плану
Вычислим потенциалы и величины превышения стоимости для незагруженных клеток:
Характеристики свободных клеток не отрицательны, следовательно, текущий план оптимален.
Выясним, что произойдет с оптимальным планом, если появится запрет на перевозки от первого карьера до второго участка работ. В этом случае, будем считать, что транспортные затраты на перевозку от первого карьера до второго участка работ бесконечно большая . Составим начальный план методом минимальной стоимости в столбце.
Построенный начальный план перевозок является невырожденным, так как число назначенных перевозок равно Определим полную стоимость перевозок по найденному опорному плану:
Определим оптимальность полученного плана с помощью Метода потенциалов.
Для незагруженных клеток вычислим величины превышения стоимости
Полученный план не оптимален. Среди оценок имеется отрицательное значение. Потенциальной является клетка . От клетки строим замкнутый контур: Выбираем наименьшее значение объема перевозки Сформируем новый улучшенный план: на 60 увеличим перевозки в клетках, помеченных знаком «+», и уменьшим в клетках, помеченных знаком «-».
Определим полную стоимость перевозок по новому плану
Для незагруженных клеток вычислим величины превышения стоимости
Характеристики свободных клеток не отрицательны, следовательно, текущий план оптимален. Таким образом, при запрете на перевозку с первого карьера на второй участок, транспортные расходы вырастут на
Выясним, что произойдет с оптимальным планом, если перевозка от первого карьера до второго участка работ будет ограничена объемом 3 тонны. Составим начальный план произвольным образом, учитывая данное ограничение.
Построенный начальный план перевозок является невырожденным, так как число базисных клеток (без ограничений на перевозку) равно Определим полную стоимость перевозок по найденному опорному плану:
Определим оптимальность полученного плана с помощью Метода потенциалов.
Для незагруженных клеток вычислим величины превышения стоимости
Характеристики свободных клеток не отрицательны, следовательно, текущий план оптимален. Таким образом, при ограничении на перевозку с первого карьера на второй участок тремя тоннами, транспортные расходы вырастут на
Задача № 4. Рассчитать характеристики системы массового обслуживания. Поток требований является простейшим (пуассоновским), а продолжительность обслуживания распределена по экспоненциальному закону.
Поток клиентов, прибывающих в банк, имеет интенсивность 9 клиентов в час. Продолжительность обслуживания одного клиента в среднем длится 8 мин. Сколько операционистов должно обслуживать клиентуру, чтобы среднее число клиентов, ожидающих обслуживания, не превышало 3?
Решение:
Данная задача относится к многоканальным СМО с ограниченной длиной очереди.
Имеем
Тогда интенсивность обслуживания равна
Интенсивность нагрузки равна
Пусть количество операционистов тогда вероятность состояния :
Пусть количество операционистов тогда вероятность состояния :
Вычислим среднее число клиентов в очереди:
Таким образом, чтобы среднее число клиентов, ожидающих обслуживания, не превышало 3, достаточно двух операционистов.
Задача № 5. Построить диаграмму Ганта и найти критический путь задачи управления проектом организации выступления хора.
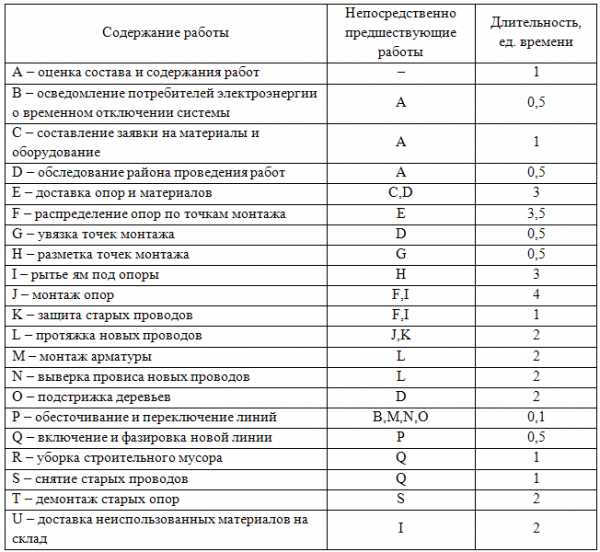
Решение:
Построим диаграмму Ганта с помощью Project Office и найдем его критический путь.

Таким образом, критический путь состоит из следующих работ:
Продолжительность пути составляет
| Следующая > |
matica.org.ua
Задача оптимизации - это... Что такое Задача оптимизации?
Задача оптимизацииЗадачей оптимизации в математике называется задача о нахождении экстремума (минимума или максимума) вещественной функции в некоторой области. Как правило, рассматриваются области, принадлежащие и заданные набором равенств и неравенств.
Постановка задачи оптимизации
Для того, чтобы корректно поставить задачу оптимизации необходимо задать:
- Допустимое множество — множество ;
- Целевую функцию — отображение ;
- Критерий поиска (max или min).
Тогда решить задачу означает одно из:
- Показать, что .
- Показать, что целевая функция не ограничена.
- Найти .
- Если , то найти .
Если минимизируемая функция не является выпуклой, то часто ограничиваются поиском локальных минимумов и максимумов: точек x0 таких, что всюду в некоторой их окрестности для минимума и для максимума.
Если допустимое множество , то такая задача называется задачей безусловной оптимизации, в противном случае — задачей условной оптимизации.
Классификация методов оптимизации
Методы, по средством которых решают задачи оптимизации, подразделяются на виды, соответствующие задачам, к которым они применяются:
- Локальные методы (задача оптимизации унимодальной целевой функции).
- Глобальные методы (имеют дело с многоэкстремальными целевыми функциями. При глобальном поиске основной задачей является выявление тенденций глобального поведения целевой функции.).
Существующие в настоящее время методы поиска можно разбить на три большие группы:
- детерминированные;
- случайные;
- комбинированные.
Некоторые детерминированные методы:
- Задачи оптимизации, в которых целевая функция и ограничения являются линейными функциями, разрешаются так называемыми методами линейного программирования.
- В противном случае имеют дело с задачей нелинейного программирования и применяют соответствующие методы. В свою очередь из них выделяют две частные задачи:
Помимо того, оптимизационные методы делятся на следующие группы:
Также они разделяются по критерию размерности допустимого множества на методы одномерной оптимизации и методы многомерной оптимизации.
Литература
- Акулич И.Л. Математическое программирование в примерах и задачах: Учеб. пособие для студентов эконом. пец. вузов. — М.: Высшая школа, 1986.
- Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. Пер. с англ. — М.: Мир, 1985.
- Коршунов Ю.М., Коршунов Ю.М. Математические основы кибернетики. — М.: Энергоатомиздат, 1972.
- Максимов Ю.А.,Филлиповская Е.А. Алгоритмы решения задач нелинейного программирования. — М.: МИФИ, 1982.
- Максимов Ю.А. Алгоритмы линейного и дискретного программирования. — М.: МИФИ, 1980.
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М.: Наука, 1970. — С. 575-576.
- Жиглявский А.А., Жилинкас А.Г. Методы поиска глобального экстремума. — М.: Наука, Физматлит, 1991.
- Растригин Л.А. Статистические методы поиска. — М.: 1968.
- Абакаров А.Ш., Сушков Ю.А. Статистическое исследование одного алгоритма глобальной оптимизации. — Труды ФОРА, 2004.
Ссылки
- MDOP — Поиск глобального оптимума для задач оптимального проектирования систем или определения оптимальных законов управления.
- Глобальная оптимизация, принятие решений — Программные системы поддержки принятия оптимальных решений. Глобальные алгоримы.
Wikimedia Foundation. 2010.
- Задача о четырёх красках
- Задача трех тел
Смотреть что такое "Задача оптимизации" в других словарях:
задача оптимизации надёжности — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN reliability optimization problem … Справочник технического переводчика
Задача о порядке перемножения матриц — Задача о порядке перемножения матриц классическая задача динамического программирования, в которой дана последовательность матриц и требуется минимизировать количество скалярных операций для вычисления их произведения. Матрицы… … Википедия
Задача о рюкзаке — Задача о ранце (рюкзаке) одна из задач комбинаторной оптимизации. Название это получила от максимизационной задачи укладки как можно большего числа нужных вещей в рюкзак при условии, что общий объём (или вес) всех предметов ограничен. Подобные… … Википедия
Задача о рюказаке — Задача о ранце (рюкзаке) одна из задач комбинаторной оптимизации. Название это получила от максимизационной задачи укладки как можно большего числа нужных вещей в рюкзак при условии, что общий объём (или вес) всех предметов ограничен. Подобные… … Википедия
Задача о коммивояжере — Задача коммивояжёра (коммивояжёр бродячий торговец) является одной из самых известных задач комбинаторной оптимизации. Задача заключается в отыскании самого выгодного маршрута, проходящего через указанные города хотя бы по одному разу с… … Википедия
Задача о коммивояжёре — Задача коммивояжёра (коммивояжёр бродячий торговец) является одной из самых известных задач комбинаторной оптимизации. Задача заключается в отыскании самого выгодного маршрута, проходящего через указанные города хотя бы по одному разу с… … Википедия
Задача коммивояжера — Задача коммивояжёра (коммивояжёр бродячий торговец) является одной из самых известных задач комбинаторной оптимизации. Задача заключается в отыскании самого выгодного маршрута, проходящего через указанные города хотя бы по одному разу с… … Википедия
Задача коммивояжёра — Оптимальный маршрут коммивояжёра через 15 крупнейших городов Германии. Указанный маршрут является самым коротким из всех возможных 43 589 145 600. Задача коммивояжёра (англ. Travelling salesman problem, TSP) (коммивояжёр … Википедия
Задача о ранце — Пример задачи о ранце: необходимо разместить ящики в рюкзак при условии на вместимость рюкзака 15 кг, так чтобы суммарная полезность предметов в рюкзаке была максимальной. Задача о ранце (рюкзаке) (англ. … Википедия
Задача о максимальном потоке — Максимальный поток в транспортной сети. Числа обозначают потоки и пропускные способности. В теории оптимизации и теории графов, задача о максимальном потоке заключается в нахождении такого потока по транспортной сети, что сум … Википедия
dic.academic.ru
Задачи оптимизации - часть 2
Вектор
в каждой точке перпендикулярной прямой , поэтому значение f будет возрастать при перемещении прямой в направлении градиента (убывать в направлении антиградиента). Для этого параллельно прямой проводим прямые, смещаясь в направлении градиента (антиградиента).Эти построения будем продолжать до тех пор, пока прямая не пройдет через последнюю вершину многоугольника решений. Эта точка определяет оптимальное значение.
Итак, нахождение решения задачи линейного программирования геометрическим методом включает следующие этапы:
1. Строят прямые, уравнения которых получаются в результате замены в ограничениях знаков неравенств на знаки точных равенств.
2. Находят полуплоскости, определяемые каждым из ограничений задачи.
3. Находят многоугольник решений.
4. Строят вектор
.5. Строят прямую
.6. Строят параллельные прямые
в направлении градиента или антиградиента, в результате чего находят точку, в которой функция принимает максимальное или минимальное значение, либо устанавливают неограниченность сверху (снизу) функции на допустимом множестве.7. Определяют координаты точки максимума (минимума) функции и вычисляют значение целевой функции в этой точке.
Пример 1. Два больших войсковых соединения
и к новому месту дислокации перевозятся по железной дороге. Для их погрузки выделяются три станции , с различными возможностями. Перевозка соединений осуществляется с соблюдением следующих ограничений:1. Количество перевозимых частей в соединении
равно 6, а в –9.2. Каждая станция может принять определенное количество частей:
.3. На погрузку одной части станции затрачивают различное время (в сутках), которое указано в таблице.
Определить оптимальный вариант распределения частей по станциям погрузки, исходя из минимума суммарных затрат времени на погрузку.
Решение.
Решение штабов соединений состоит в распределении частей по станциям погрузки. Обозначим через
число частей i - го соединения (i =1,2) на j - ой станции (j = 1, 2, 3).Мы можем записать:
количество частей соединений на станциях погрузки
соответственно. - количество частей соединения на местах погрузки. - количество частей соединения на местах погрузки.Общая сумма затрат времени (в сутках) на погрузку есть
В этой задаче 6 переменных, но мы можем свести к двум.
Пусть
Тогда
Целевая функция имеет вид
Итак, надо найти
при ограничениях:которая решается графически
Возьмем прямую
и начнем строить параллельные ей в направлении антиградиента, где .Последняя вершина многоугольника решений есть точка С , получаемая пересечением прямых (1) и (4). Решая, получим С (1;5).
Итак, оптимальные значения будут следующими:
, а общие затраты времени (суток).Пусть дана целевая функция
.Для нахождения наибольшего и наименьшего значения функции и (одной) вещественных переменных надо найти критические точки, в которых частные производные (производная) функции f по всем переменным обращается в 0. Кроме того, надо исследовать точки границы, если она принадлежит области определения. Среди них выбрать значения, где f принимает наибольшее и наименьшее значение.
 Пример 2. Определить оптимальный по времени маршрут выдвижения танкового подразделения из пункта А в пункт F, если допустимая скорость движения танков до дороги , по дороге , за дорогой . Удаление от дороге пункта А равно , пункта F. Расстояние между точками В и Е равно L = 90 км .
Пример 2. Определить оптимальный по времени маршрут выдвижения танкового подразделения из пункта А в пункт F, если допустимая скорость движения танков до дороги , по дороге , за дорогой . Удаление от дороге пункта А равно , пункта F. Расстояние между точками В и Е равно L = 90 км . Составим математическую модель, то есть найдем функцию цели. Нас интересует время. Время выдвижения из пункта А в пункт F.
ВС = х км ; DE = yкм ; АС =
CD = L – x – y; DF =
Составим функцию цели, которая зависит от двух переменных
Найдем критические точки
При данных условиях
Найдем значение t при полученных x и y
При вычислении значения t на границе, значения получаются больше, чем 4,24 часа. Следовательно, оптимальное решение будет при
х = 6,9 км , у = 24 км ,
.Развитие современного общества характеризуется повышением технического уровня, усложнением организационной структуры производства, управления войсками, углублением общественного разделения труда, предъявлением высоких требований к методам планирования хозяйственного и военного руководства. В этих условиях только научный подход к руководству хозяйственной жизнью общества позволит обеспечить высокие темпы развития народного хозяйства. Научного подхода требует и решение тактических и стратегических задач, руководство военными операциями.
mirznanii.com
Задачи оптимизации
Геометрия в задачах оптимизации
Содержание
1. Введение……………………………………………………………………с.2
2. Задание выпуклых многоугольников с помощью неравенств……..с.3
3. Задачи оптимизации на плоскости……………………………………с.4-6
4. Задание выпуклых многогранников с помощью неравенств……с.7
5. Задача оптимизации в пространстве………………………………..с.8-9
6. Заключение ………………………………………………………………...с.9
7. Список используемой литературы и Интернет-ресурсов……………c.10
Введение
Среди прикладных задач, решаемых с помощью математики, выделяются так называемые задачи оптимизации. Среди них:
- транспортная задача о составлении оптимального способа перевозок грузов;
- задача о диете, то есть о составлении наиболее экономного рациона питания, удовлетворяющего определенным медицинским требованиям;
- задача о наилучшем использовании ресурсов;
- задача о смесях, то есть о получении продукции с заданными свойствами при наименьших затратах;
- задача составления оптимального плана производства;
- задача рационального использования посевных площадей и т.д.
Несмотря на различные содержательные ситуации в этих задачах, математические модели, их описывающие, имеют много общего, и все они решаются одним и тем же методом, разработанным отечественным математиком Л. В. Канторовичем (1912 – 1986). Несколько слов о разработчике метода.
Леонид Витальевич Канторович (6 (19) января 1912, Санкт-Петербург — 7 апреля 1986, Москва) — советский математик и экономист, лауреат Нобелевской премии по экономике 1975 года «За вклад в теорию оптимального распределения ресурсов». Пионер и один из создателей линейного программирования.

Леонид Витальевич впервые применил функциональный анализ к вычислительной математике, развил общую теорию приближённых методов, построил эффективные методы решения операторных уравнений. Также развил идею оптимальности в экономике. Установил взаимозависимость оптимальных цен и оптимальных производственных и управленческих решений.
Л. В. Канторович — представитель петербургской математической школы П. Л. Чебышева, ученик Г. М. Фихтенгольца и В. И. Смирнова. Канторович разделял и развивал взгляды П. Л. Чебышева на математику как на единую дисциплину, все разделы которой взаимосвязаны, взаимозависимы и играют особую роль в развитии науки, техники, технологии и производства. Л. В. Канторович выдвигал тезис взаимопроникновения математики и экономики и стремился к синтезу гуманитарных и точных технологий знания. Творчество Канторовича стало образцом научного служения, базирующегося на универсализации математического мышления.
Задание выпуклых многоугольников с помощью неравенств
Пусть прямая задана уравнением и проходит через точку (. Ее вектор нормали имеет координаты и определяет полуплоскость. Точка A(x; y) принадлежит этой полуплоскости в случае, если угол между векторами и не превосходит 90˚, т.е. в том случае, если скалярное произведение этих векторов больше или равно нулю, т.е. = a(x ) + b(y ) 0. При этом Следовательно, точка A(x; y) принадлежит этой полуплоскости, если выполняется неравенство ax + by +c
Аналогично точка A(x; y) принадлежит другой полуплоскости по отношению к данной прямой, если выполняется неравенство ax + by +c .
Для того, чтобы определить, какой из двух полуплоскостей принадлежит точка A (x; y), достаточно подставить ее координаты в левую часть уравнения прямой и найти знак получившегося значения.
Покажем, как с помощью неравенств можно задавать выпуклые многоугольники.
Действительно, пусть стороны выпуклого многоугольника лежат на прямых, задаваемых уравнениями:
……………………,
Тогда сам многоугольник является пересечением соответствующих полуплоскостей, и, следовательно, для его точек должна выполняться система неравенств вида
которая и определяет этот многоугольник.
Например, неравенства которые можно переписать в виде системы
определяют единичный квадрат.
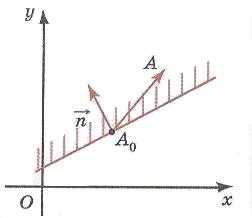


Если к этим неравенствам добавить еще одно неравенство
то соответствующий многоугольник получается из квадрата отсечением треугольника.
Задачи оптимизации на плоскости
В качестве примера задач оптимизации рассмотрим следующие задачи.
Задача 1. На трех складах хранится сырье одинакового вида в количестве соответственно 10 т, 20 т, 30 т. На завод нужно завести 35 т сырья. Найдите наиболее выгодный вариант перевозок, если расстояния от складов равны соответственно 7 км, 5 км, 8 км.
Р е ш е н и е. Составим математическую модель. Для этого обозначим через х и у количество тонн сырья, которое нужно перевезти соответственно с первого и второго складов на завод. Тогда с третьего склада нужно будет перевезти 35 – (x + y) тонн сырья. Занесем данные в таблицу, где склады.
Склад
Количество сырья (т)
10
20
30
Расстояние до завода (км)
7
5
8
Количество сырья, перевезенное на завод (т)
x
y
35 – (x + y)
Все величины, входящие в эту таблицу, должны быть неотрицательны. Поэтому имеем систему неравенств:
Систему можно переписать иначе:
Эта система определяет многоугольник ABCDE. Найдем на нем наименьшее значение функции
F = 7x + 5y + 8(35 – x – y), или F = – x – 3y + 280.
Найдем координаты вершин многоугольника: А(5;0), В(0;5), С(0;20), D(10;20) , E(10;0). Тогда
Таким образом, наименьшее значение функция принимает в точке D(10;20). Следовательно, наиболее выгодно с первого склада перевезти на завод 10 т сырья, со второго – 20 т и с третьего – 5 т.
Задача 2. Установка собирается из трех различных деталей – А, Б, В. На одном станке можно за смену изготовить либо 12 деталей типа А, 18 – Б, 30 –В. (первый режим), либо 20 деталей типа А, 15 – Б, 9 – В (второй режим). Хватит ли 100 станков, чтобы изготовить за смену детали для 720 установок? Какое наименьшее количество станков (и с какими режимами работы) нужно для выполнения заказа?
Режим
Кол-во станков
детали
А
Б
В
I
x
12
18
30
II
y
20
15
9
Р е ш е н и е. Пусть х, у – количество станков, работающих в первом и втором режимах соответственно. Для изготовления 720 деталей нужно, чтобы выполнялись неравенства
Кроме того, поскольку количество деталей должно быть неотрицательно, нужно, чтобы выполнялись неравенства Перепишем все эти неравенства в виде системы:
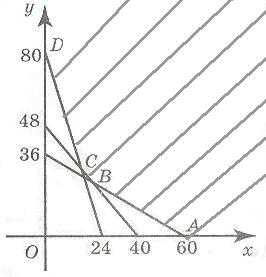
Эта система неравенств определяет фигуру на плоскости.
Вершины A и D имеют координаты (60;0) и (0;80) соответственно. Для нахождения координат вершин B и C нужно решить системы уравнений
В: C:
В результате имеем В(20;24), С(15;30).
Для нахождения наименьшего значения функции F = x + y, вычислим ее значения в вершинах: Наименьшее значение принимается в вершине В, и оно равно 44.
Таким образом, для выпуска 720 деталей достаточно 44 станка, из которых 20 работает в первом режиме, а 24 – во втором.
Задача 3. Для изготовления двух видов продукции используют три вида сырья: Запасы сырья, количество единиц сырья, затрачиваемых на изготовление единицы продукции, а так же величина прибыли, получаемая от реализации единицы продукции, приведены в таблице.
Вид сырья
Запас сырья
Количество единиц сырья, идущих на изготовление единицы продукции
20
2
5
40
8
5
30
5
6
Прибыль от единицы продукции, руб.
50
40
Необходимо составить такой план выпуска продукции, чтобы при ее реализации получить максимальную прибыль.
Р е ш е н и е. Обозначим через x количество единиц продукции , а через y - количество единиц продукции . Тогда количество единиц сырья, расходуемое на изготовление продукции, а так же запасы сырья, получим систему ограничений:
которая показывает, что количество сырья, расходуемое на изготовление продукции, не может превысить имеющихся запасов. Если продукция не выпускается, то То же самое получаем и для второго вида продукции. Таким образом, на наши неизвестные должно быть наложено ограничение неотрицательности.
Конечную цель решаемой задачи – получение максимальной прибыли – выразим как функцию переменных x и y. Реализация единиц продукции даст 50x и 40y руб. прибыли, суммарная прибыль Z = 50x + 40 y (руб.).
Неделимость продукции в условии не оговорена, поэтому переменные
могут быть и дробными числами.
Требуется найти такие х и y, при которых функция Z достигнет максимума, т.е. найти максимальное значение линейной функции
Z = при ограничениях:
Построим многоугольник решений. Для этого в системе координат изобразим граничные прямые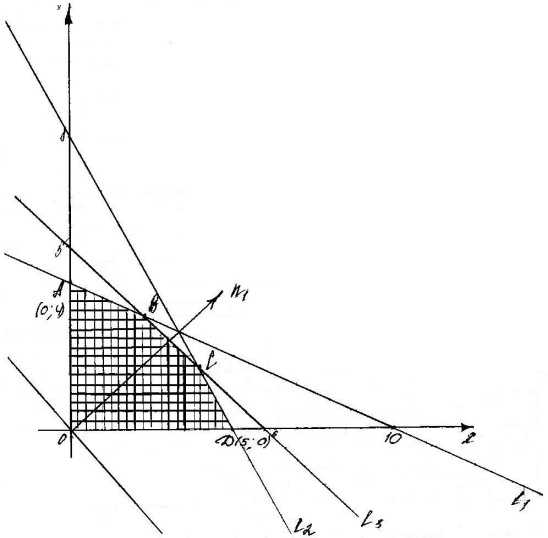
Взяв какую-нибудь точку, например, начало координат, установим, какую полуплоскость определяет соответствующее неравенство. Многоугольником решений данной задачи является ограниченный пятиугольник OABCD.
Для построения прямой 50x + 40 y = 0 строим радиус-вектор и через точку О проводим прямую, перпендикулярную ему. Построенную прямую Z = 0 перемещаем параллельно самой себе в направлении вектора . Из рисунка следует, что опорной по отношению к многоугольнику решений эта прямая становится в точке С, где функция Z принимает максимальное значение. Точка С лежит на пересечении прямых и . Для определения ее координат решим систему уравнений
Оптимальный план задачи: = 3,9; Подставляя значения в линейную функцию, получаем, что максимальная прибыль равна 260,3 руб., и чтобы ее заработать надо запланировать производство 3,9 ед. продукции и 1,7 ед. продукции
Задание выпуклых многогранников с помощью неравенств
Плоскость в пространстве задается уравнением 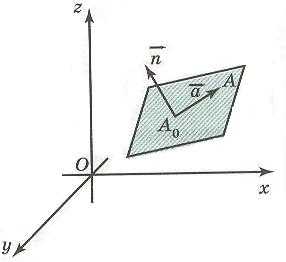
ax + by + cz + d = 0, (*),
где a, b, c, d – действительные числа, причем a,b,c не равны нулю и составляют координаты вектора , перпендикулярного этой плоскости и называемого вектором нормали.
4 частных случая расположения плоскости:
ax + by + cz = 0 (d = 0) – плоскость проходит через начало координат;
ax + by + d = 0 (с = 0) – параллельно ;
ax + by = 0 (с = d = 0) – пересекает ;
ax + d = 0 (b = с = 0) – .
A( точки пересечения плоскости с осью абсцисс, осью ординат и осью аппликат соответственно. Если уравнение плоскости разделить на d, то получим уравнение плоскости в отрезках
.
Заметим, что если плоскость задана уравнением (*), то неравенства
ax + by + cz + d ax + by + cz + d определяют полупространства, на которые эта плоскость разбивает пространство. Для того, чтобы определить, какому из двух полупространств принадлежит точка А (x; y. z), достаточно подставит ее координаты в левую часть уравнения плоскости и найти знак получившегося значения.
Поменяв знаки чисел a, b, c, d, второе неравенство всегда можно свести к первому.
Покажем, как с помощью таких неравенств в пространстве можно задавать выпуклые многогранники.
Например, неравенства которые можно переписать в виде системы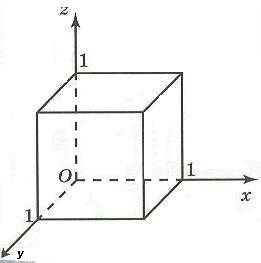
определяют единичный куб в пространстве.
Если к этим неравенствам добавить еще одно неравенство
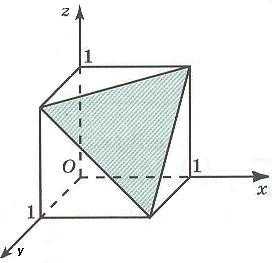
то соответствующий многогранник получается из куба отсечением пирамиды.
Задача оптимизации в пространстве
Задача. Пусть на четыре завода , требуется завезти сырье одинакового вида, которое хранится на двух складах , . Потребность данных заводов в сырье каждого вида указана в таблице , а расстояние от склада до завода – в таблице 2. Требуется найти наиболее выгодный вариант перевозок.
Таблица 1
Наличие сырья на складе (т)
Потребность завода в сырье (т)
С1
С2
З1
З2
З3
З4
20
25
8
10
12
15
Таблица 2
Склад
Расстояние от склада до завода (км)
З1
З2
З3
З4
С1
5
6
4
10
С2
3
7
3
7
Для решения этой задачи в первую очередь проанализируем ее условие и переведем его на язык математики, то есть составим математическую модель. Для этого количество сырья, которое нужно перевезти со склада С1 на заводы З1, З2, З3, обозначим через x, y, z. Тогда на четвертый завод с этого склада нужно перевезти 20 – x – y – z сырья в тоннах, а со второго нужно перевезти 8 – x, 10 – y, 12 – z, x + y + z – 5 сырья в тоннах. Запишем эти данные в таблицу 3.
Таблица 3
Склад
Количество сырья, перевезенное на завод (т)
З1
З2
З3
З4
С1
x
y
z
20 – x – y – z
С2
8 - x
10 - y
12 - z
x + y + z - 5
Поскольку все величины, входящие в эту таблицу, должны быть неотрицательными, получим следующую систему неравенств:
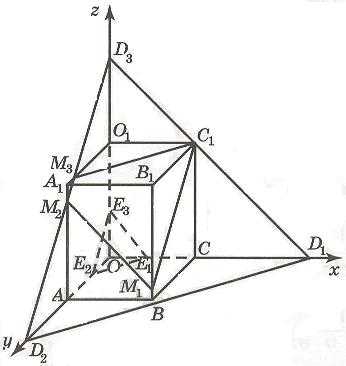
Эта система неравенств определяет некоторый многогранник. Для того чтобы его построить, изобразим сначала многогранник, определяемый первой и второй строкой данной системы. На рисунке это параллелепипед OABCO1A1B1C1. Уравнение 20 - x - y - z = 0 определяет плоскость D1D2D3, которая, пересекает параллелепипед, образуя многоугольник M1M2M3C1. Уравнение x + y + z - 5 = 0 определяет плоскость, которая пересекает параллелепипед и образует в нем треугольник E1E2E3. На многограннике M1M2M3C1CBAE1E2E3O1, где M1(8,10,2), M2(0,10,10), M3(0,8,12), C1(8,0,12), C(8,0,0), B(8,10,0), A(0,10,0), E1(5,0,0), E2(0,5,0), E3(0,0,5), O1(0,0,12), выполняются все условия данной системы. Назовем его многогранником ограничений.
Для нахождения общего числа тонно-километров умножим расстояния от складов до заводов на перевозимое количество сырья и полученные результаты сложим. Общее число тонно-километров выражается формулой:
5x + 6y + 4z + 10(20 - x - y - z) + 3(8 - x) + 7(10 - y) + + 3(12 - z) + 7(x + y + z - 5) = 295 - x - 4y - 2z.
Таким образом, задача сводится к отысканию наименьшего значения функции F = 295 - x - 4y - 2z на многограннике ограничений. Для этого достаточно найти наибольшее значение функции f = x + 4y + 2z. Тогда Fmin = 295 - fmax.
Вычислим значение функции f = x + 4y + 2z в вершинах многогранника ограничений: f(M1) = 52, f(M2) = 60, f(M3) = 56,f(C1) = 32, f(C) = 8, f(B) = 48, f(A) = 40, f(E1) = 5, f(E2) = 20, f(E3) = 10, f(O1) = 24.
Легко видеть, что максимальное значение функции f равно 60. Тогда Fmin = 295 - 60 = 235. Это значение функция F принимает в точкеM2(0,10,10). Таким образом, наиболее выгодный вариант перевозок задается таблицей 4.
Таблица 4
Склад
Количество сырья (в т), перевезенное на заводы
З1
З2
З3
З4
С1
0
10
10
0
С2
8
0
2
15
Заключение
Закончив работу над темой «Геометрия в задачах оптимизации», мы сделали следующие выводы:
- основополагающим свойством в задачах оптимизации является следующий факт: наибольшее и наименьшее значения линейная функция достигает в вершинах многоугольников или многогранников ограничений;
- если число переменных равно 2-м, то в процессе решения задачи получится многоугольник, а если число переменных равно 3-м – многогранник;
- в реальных задачах число независимых переменных значительно больше трех, и для получения геометрической интерпретации этих задач требуется рассмотрение n-мерного пространства и n-мерных многогранников с очень большим n. При решении таких задач используются ЭВМ.
Таким образом, хотя пространственные свойства окружающего нас мира хорошо описываются геометрическим трехмерным пространством, потребности практической деятельности человека приводят к необходимости рассмотрения пространств большей размерности, которые изучаются в специальном разделе математики – многомерной геометрии.
Список используемой литературы и Интернет-ресурсов
Ефимов Н.В. Краткий курс аналитической геометрии. Москва: Издательство «Наука», 1975 год
Смирнова И.М., Смирнов В.А. Геометрия 7-9 классы. Москва: Издательство «Мнемозина», 2009 год
Смирнова И.М., Смирнов В.А. Геометрия 10-11 классы. Москва: Издательство «Мнемозина», 2009 год
Волков В.А. Элементы линейного программирования. Москва: Издательство «Просвещение», 1975 год
Беляева Е.С., Монахов В.М. Экстремальные задачи. Москва: Издательство «Просвещение», 1977 год
www.wikipedia.ru
infourok.ru
Постановка задачи оптимизации — Мегаобучалка
Постановка задачи оптимизации предполагает существование конкурирующих свойств процесса, например:
- количество продукции - расход сырья";
- количество продукции - качество продукции".
Выбор компромиссного варианта для указанных свойств и представляет собой процедуру решения оптимизационной задачи.
При постановке задачи оптимизации необходимо:
1. Наличие объекта оптимизации и цели оптимизации. При этом формулировка каждой задачи оптимизации должна требовать экстремального значения лишь одной величины, т.е. одновременно системе не должно приписываться два и более критериев оптимизации, т.к. практически всегда экстремум одного критерия не соответствует экстремуму другого.
Типичный пример неправильной постановки задачи оптимизации: "Получить максимальную производительность при минимальной себестоимости". Ошибка заключается в том, что ставится задача поиска оптимума 2-х величин, противоречащих друг другу по своей сути.
Правильная постановка задачи могла быть следующая:
а) получить максимальную производительность при заданной себестоимости;
б) получить минимальную себестоимость при заданной производительности.
В первом случае критерий оптимизации – производительность, а во втором - себестоимость.
2. Наличие ресурсов оптимизации, под которыми понимают возможность выбора значений некоторых параметров оптимизируемого объекта. Объект должен обладать определенными степенями свободы - управляющими воздействиями.
3. Возможность количественной оценки оптимизируемой величины, поскольку только в этом случае можно сравнивать эффекты от выбора тех или иных управляющих воздействий.
4. Учет ограничений.
Обычно оптимизируемая величина связана с экономичностью работы рассматриваемого объекта (аппарат, цех, завод). Оптимизируемый вариант объекта или его работы должен оцениваться какой-то количественной мерой -критерием оптимальности.
Критерием оптимальности называется количественная оценка оптимизируемого качества объекта.
На основании выбранного критерия оптимальности составляется целевая функция, представляющая собой зависимость критерия оптимальности от параметров, влияющих на ее значение. Вид критерия оптимальности или целевой функции определяется конкретной задачей оптимизации.
Таким образом, задача оптимизации сводится к нахождению экстремума целевой функции.
Наиболее общей постановкой оптимальной задачи является выражение критерия оптимальности в виде экономической оценки (производительность, себестоимость продукции, прибыль, рентабельность). Однако в частных задачах оптимизации, когда объект является частью технической системы или технологического процесса, не всегда удается или не всегда целесообразно выделять прямой экономический показатель, который бы полностью характеризовал эффективность работы рассматриваемого объекта. В таких случаях критерием оптимальности может служить техническая или технологическая характеристика, косвенно оценивающая экономичность работы агрегата (время контакта, выход продукта, степень превращения, температура). Но в любом случае любой критерий оптимальности имеет экономическую природу.
Критерий оптимальности должен иметь ясный физический смысл, отражать наиболее существенные стороны системы или процесса, должен иметь количественную оценку.
В том случае, когда случайные возмущения невелики и их воздействие на объект можно не учитывать, критерий оптимальности может быть представлен как функция входных, выходных и управляющих параметров: R=R(X1, X2,...,XN, Y1,Y2,...,YN, U1,U2,..., UN).
Так как Y=f(U), то при фиксированных Х можно записать: R=R(U1,U2,..., UN).
При этом всякое изменение значений управляющих параметров двояко сказывается на величине R:
- прямо, так как управляющие параметры непосредственно входят в выражение критерия оптимизации;
- косвенно, через изменение выходных параметров системы или процесса, которые зависят от управляющих.
Как правило, для конкретных задач оптимизации технических систем критерий оптимальности не может быть записан в виде аналитического выражения.
В принципе, для оптимизации вместо математической модели можно использовать и сам объект, однако оптимизация опытным путем имеет ряд существенных недостатков:
а) необходим реальный объект;
б) необходимо изменять параметры технической системы в значительных пределах, что не всегда возможно;
в) длительность испытаний и сложность обработки данных.
Наличие математической модели (при условии, что она достаточно надежно описывает систему) позволяет значительно проще решить задачу оптимизации аналитическим либо численным методами.
Итак, для решения задачи оптимизации необходимо:
а) составить математическую модель объекта оптимизации;
б) выбрать критерий оптимальности и составить целевую функцию;
в) установить возможные ограничения, которые должны накладываться на переменные;
г) выбрать метод оптимизации, который позволит найти экстремальные значения искомых величин.
Методы оптимизации
При решении конкретной задачи оптимизации исследователь прежде всего должен выбрать математический метод, который приводил бы к конечным результатам с наименьшими затратами на вычисления или же давал возможность получить наибольший объем информации об искомом решении. Выбор того или иного метода в значительной степени определяется постановкой задачи оптимизации, а также используемой математической моделью объекта оптимизации.
В настоящее время для решения оптимальных задач применяют в основном следующие методы:
- методы исследования функций классического анализа;
- методы, основанные на использовании неопределенных множителей Лагранжа;
- вариационное исчисление;
- динамическое программирование;
- принцип максимума;
- линейное программирование;
- нелинейное программирование.
В последнее время разработан и успешно применяется для решения определенного класса задач метод геометрического программирования.
Как правило, нельзя рекомендовать какой-либо один метод, который можно использовать для решения всех без исключения задач, возникающих на практике. Одни методы в этом отношении являются более общими, другие - менее общими. Наконец, целую группу методов (методы исследования функций классического анализа, метод множителей Лагранжа, методы нелинейного программирования) на определенных этапах решения оптимальной задачи можно применять в сочетании с другими методами, например динамическим программированием или принципом максимума.
Отметим также, что некоторые методы специально разработаны или наилучшим образом подходят для решения оптимальных задач с математическими моделями определенного вида. Так, математический аппарат линейного программирования, специально создан для решения задач с линейными критериями оптимальности и линейными ограничениями на переменные и позволяет решать большинство задач, сформулированных в такой постановке. Так же и геометрическое программирование предназначено для решения оптимальных задач, в которых критерий оптимальности и ограничения представляются специального вида функциями позиномами.
Динамическое программирование хорошо приспособлено для решения задач оптимизации многостадийных процессов, особенно тех, в которых состояние каждой стадии характеризуется относительно небольшим числом переменных состояния. Однако при наличии значительного числа этих переменных, т. е. при высокой размерности каждой стадии, применение метода динамического программирования затруднительно вследствие ограниченных быстродействия и объема памяти вычислительных машин.
Пожалуй, наилучшим путем при выборе метода оптимизации, наиболее пригодного для решения соответствующей задачи, следует признать исследование возможностей и опыта применения различных методов оптимизации. Ниже дана краткая характеристика наиболее распространненых методов и областей их применения, что до некоторой степени может облегчить выбор того или иного метода для решения конкретной оптимальной задачи.
Методы исследования функций классического анализа представляют собой наиболее известные методы решения несложных оптимальных задач, с которыми известны из курса математического анализа. Обычной областью использования данных методов являются задачи с известным аналитическим выражением критерия оптимальности, что позволяет найти не очень сложное, также аналитическое выражение для производных. Полученные приравниванием нулю производных уравнения, определяющие экстремальные решения оптимальной задачи, крайне редко удается решить аналитическим путем, поэтому, как, правило, применяют вычислительные машины. При этом надо решить систему конечных уравнений, чаще всего нелинейных, для чего приходится использовать численные методы, аналогичные методам нелинейного программирования.
Дополнительные трудности при решении оптимальной задачи методами исследования функций классического анализа возникают вследствие того, что система уравнений, получаемая в результате их применения, обеспечивает лишь необходимые условия оптимальности. Поэтому все решения данной системы (а их может быть и несколько) должны быть проверены на достаточность. В результате такой проверки сначала отбрасывают решения, которые не определяют экстремальные значения критерия оптимальности, а затем среди остающихся экстремальных решений выбирают решение, удовлетворяющее условиям оптимальной задачи, т. е. наибольшему или наименьшему значению критерия оптимальности в зависимости от постановки задачи.
Методы исследования при наличии ограничений на область изменения независимых переменных можно использовать только для отыскания экстремальных значений внутри указанной области. В особенности это относится к задачам с большим числом независимых переменных (практически больше двух), в которых анализ значений критерия оптимальности на границе допустимой области изменения переменных становится весьма сложным.
Метод множителей Лагранжа применяют для решения задач такого же класса сложности, как и при использовании обычных методов исследования функций, но при наличии ограничений типа равенств на независимые переменные. К требованию возможности получения аналитических выражений для производных от критерия оптимальности при этом добавляется аналогичное требование относительно аналитического вида уравнений ограничений.
В основном при использовании метода множителей Лагранжа приходится решать те же задачи, что и без ограничений. Некоторое усложнение в данном случае возникает лишь от введения дополнительных неопределенных множителей, вследствие чего порядок системы уравнений, решаемой для нахождения экстремумов критерия оптимальности, соответственно повышается на число ограничений. В остальном, процедура поиска решений и проверки их на оптимальность отвечает процедуре решения задач без ограничений.
Множители Лагранжа можно применять для решения задач оптимизации объектов на основе уравнений с частными производными и задач динамической оптимизации. При этом вместо решения системы конечных уравнений для отыскания оптимума необходимо интегрировать систему дифференциальных уравнений.
Следует отметить, что множители Лагранжа используют также в качестве вспомогательного средства и при решении специальными методами задач других классов с ограничениями типа равенств, например, в вариационном исчислении и динамическом программировании. Особенно эффективно применение множителей Лагранжа в методе динамического программирования, где с их помощью иногда удается снизить размерность решаемой задачи.
Методы вариационного исчисления обычно используют для решения задач, в которых критерии оптимальности представляются в виде функционалов и решениями которых служат неизвестные функции. Такие задачи возникают обычно при статической оптимизации процессов с распределенными параметрами или в задачах динамической оптимизации.
Вариационные методы позволяют в этом случае свести решение оптимальной задачи к интегрированию системы дифференциальных ' уравнений Эйлера, каждое из которых является нелинейным дифференциальным уравнением второго порядка с граничными условиями, заданными на обоих концах интервала интегрирования. Число уравнений указанной системы при этом равно числу неизвестных функций, определяемых при решении оптимальной задачи. Каждую функцию находят в результате интегрирования получаемой системы.
Уравнения Эйлера выводятся как необходимые условия экстремума функционала. Поэтому полученные интегрированием системы дифференциальных уравнений функции должны быть проверены на экстремум функционала.
При наличии ограничений типа равенств, имеющих вид функционалов, применяют множители Лагранжа, что дает возможность перейти от условной задачи к безусловной. Наиболее значительные трудности при использовании вариационных методов возникают в случае решения задач с ограничениями типа неравенств.
Заслуживают внимания прямые методы решения задач оптимизации функционалов, обычно позволяющие свести исходную вариационную задачу к задаче нелинейного программирования, решить которую иногда проще, чем краевую задачу для уравнений Эйлера.
Динамическое программирование служит эффективным методом решения задач оптимизации дискретных многостадийных процессов, для которых критерий оптимальности задается как аддитивная функция критериев оптимальности отдельных стадий. Без особых затруднений указанный метод можно распространить и на случай, когда критерий оптимальности задан в другой форме, однако при этом обычно увеличивается размерность отдельных стадий.
По существу метод динамического программирования представляет собой алгоритм определения оптимальной стратегии управления на всех стадиях процесса. При этом закон управления на каждой стадии находят путем решения частных задач оптимизации последовательно для всех стадий процесса с помощью методов исследования функций классического анализа или методов нелинейного программирования. Результаты решения обычно не могут быть выражены в аналитической форме, а получаются в виде таблиц.
Ограничения на переменные задачи не оказывают влияния на общий алгоритм решения, а учитываются при решении частных задач оптимизации на каждой стадии процесса. При наличии ограничений типа равенств иногда даже удается снизить размерность этих частных задач за счет использования множителей Лагранжа. Применение метода динамического программирования для оптимизации процессов с распределенными параметрами или в задачах динамической оптимизации приводит к решению дифференциальных уравнений в частных производных. Вместо решения таких уравнений зачастую значительно проще представить непрерывный процесс как дискретный с достаточно большим числом стадий. Подобный прием оправдан особенно в тех случаях, когда имеются ограничения на переменные задачи и прямое решение дифференциальных уравнений осложняется необходимостью учета указанных ограничений.
При решении задач методом динамического программирования, как правило, используют вычислительные машины, обладающие достаточным объемом памяти для хранения промежуточных результатов решения, которые обычно получаются в табличной форме.
Принцип максимума применяют для решения задач оптимизации процессов, описываемых системами дифференциальных уравнений. Достоинством математического аппарата принципа максимума является то, что решение может определяться в виде разрывных функций; это свойственно многим задачам оптимизации, например задачам оптимального управления объектами, описываемыми линейными дифференциальными уравнениями.
Нахождение оптимального решения при использовании принципа максимума сводится к задаче интегрирования системы дифференциальных уравнений процесса и сопряженной системы для вспомогательных функций при граничных условиях, заданных на обоих концах интервала интегрирования, т. е. к решению краевой задачи. На область изменения переменных могут быть наложены ограничения. Систему дифференциальных уравнений интегрируют, применяя обычные программы на цифровых вычислительных машинах.
Принцип максимума для процессов, описываемых дифференциальными уравнениями, при некоторых предположениях является достаточным условием оптимальности. Поэтому дополнительной проверки на оптимум получаемых решений обычно не требуется.
Для дискретных процессов принцип максимума в той же формулировке, что и для непрерывных, вообще говоря, несправедлив. Однако условия оптимальности, получаемые при его применении для многостадийных процессов, позволяют найти достаточно удобные алгоритмы оптимизации.
Линейное программирование представляет собой математический аппарат, разработанный для решения оптимальных задач с линейными выражениями для критерия оптимальности и линейными ограничениями на область изменения переменных. Такие задачи обычно встречаются при решении вопросов оптимального планирования производства с ограниченным количеством ресурсов, при определении оптимального плана перевозок (транспортные задачи) и т. д.
Для решения большого круга задач линейного программирования имеется практически универсальный алгоритм - симплексный метод, позволяющий за конечное число итераций находить оптимальное решение подавляющего большинства задач. Тип используемых ограничений (равенства или неравенства) не сказывается на возможности применения указанного алгоритма. Дополнительной проверки на оптимальность для получаемых решений не требуется. Как правило, практические задачи линейного программирования отличаются весьма значительным числом независимых переменных. Поэтому для их решения обычно используют вычислительные машины, необходимая мощность которых определяется размерностью решаемой задачи.
Методы нелинейного программирования применяют для решения оптимальных задач с нелинейными функциями цели. На независимые переменные могут быть наложены ограничения также в виде нелинейных соотношений, имеющих вид равенств или неравенств. По существу методы нелинейного программирования используют, если ни один из перечисленных выше методов не позволяет сколько-нибудь продвинуться в решении оптимальной задачи. Поэтому указанные методы иногда называют также прямыми методами решения оптимальных задач.
Для получения численных результатов важное место отводится нелинейному программированию и в решении оптимальных задач такими методами, как динамическое программирование, принцип максимума и т. п. на определенных этапах их применения.
Названием “методы нелинейного программирования” объединяется большая группа численных методов, многие из которых приспособлены для решения оптимальных задач соответствующего класса. Выбор того или иного метода обусловлен сложностью вычисления критерия оптимальности и сложностью ограничивающих условий, необходимой точностью решения, мощностью имеющейся вычислительной машины и т.д. Ряд методов нелинейного программирования практически постоянно используется в сочетании с другими методами оптимизации, как, например, метод сканирования в динамическом программировании. Кроме того, эти методы служат основой построения систем автоматической оптимизации - оптимизаторов, непосредственно применяющихся для управления производственными процессами.
Геометрическое программирование есть метод решения одного специального класса задач нелинейного программирования, в которых критерий оптимальности и ограничения задаются в виде позиномов - выражений, представляющих собой сумму произведений степенных функций от независимых переменных. С подобными задачами иногда приходится сталкиваться в проектировании. Кроме того, некоторые задачи нелинейного программирования иногда можно свести к указанному представлению, используя аппроксимационное представление для целевых функций и ограничений.
Специфической особенностью методов решения оптимальных задач (за исключением методов нелинейного программирования) является то, что до некоторого этапа оптимальную задачу решают аналитически, т. е. находят определенные аналитические выражения, например, системы конечных или дифференциальных уравнений, откуда уже отыскивают оптимальное решение. В отличие от указанных методов при использовании методов нелинейного программирования, которые, как уже отмечалось выше, могут быть названы прямыми, применяют информацию, получаемую при вычислении критерия оптимальности, изменение которого служит оценкой эффективности того или иного действия.
Важной характеристикой любой оптимальной задачи является ее размерность n, равная числу переменных, задание значений которых необходимо для однозначного определения состояния оптимизируемого объекта. Как правило, решение задач высокой размерности связано с необходимостью выполнения большого объема вычислений. Ряд методов (например, динамическое программирование и дискретный принцип максимума) специально предназначен для решения задач оптимизации процессов высокой размерности, которые могут быть представлены как многостадийные процессы с относительно невысокой размерностью каждой стадии.
В таблице дана характеристика областей применения различных методов оптимизации, при этом за основу положена сравнительная оценка эффективности использования каждого метода для решения различных типов оптимальных задач. Классификация задач проведена по следующим признакам:
- вид математического описания процесса;
- тип ограничений на переменные процесса
- число переменных.

Предполагается, что решение оптимальной задачи для процессов, описываемых системами конечных уравнений, определяется как конечный набор значений управляющих воздействий (статическая оптимизация процессов с сосредоточенными параметрами), а для процессов, описываемых системами обыкновенных дифференциальных уравнений, управляющие воздействия характеризуются функциями времени (динамическая оптимизация процессов с сосредоточенными параметрами) или пространственных переменных (статическая оптимизация процессов с распределенными параметрами).
Классификация задач по группам с числом независимых переменных, большим и меньшим трех или равным трем как характеристика размерности задач с большим и малым числом переменных, разумеется, весьма условна и в данном случае выбрана скорее из соображений наглядности графического изображения пространства изменения переменных задачи - фазового пространства (при числе переменных большем трех графическое изображение фазового пространства обычными приемами отсутствует). Тем не менее, такая классификация до некоторой степени все же отражает действительные трудности, возникающие при решении задач с размерностью выше трех.
megaobuchalka.ru
3. Классификация задач оптимизации.
1. По наличию ограничений.
Если область допустимых решений 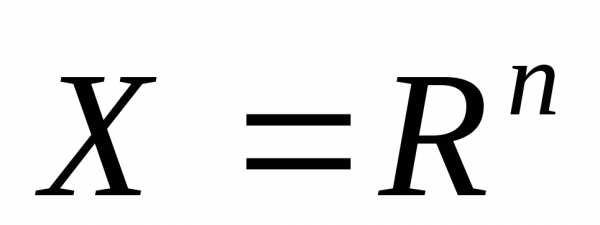 , то задача не является задачей оптимизации без ограничений или задачей безусловной оптимизации. При этом для характеристики экстремума целевой функции используют термин «безусловный».
, то задача не является задачей оптимизации без ограничений или задачей безусловной оптимизации. При этом для характеристики экстремума целевой функции используют термин «безусловный».
Если 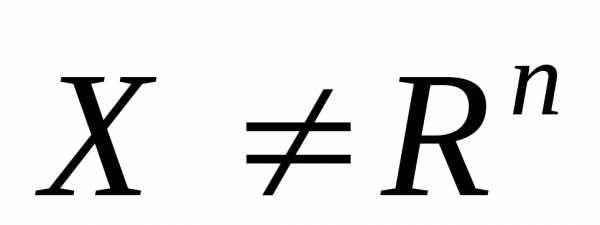 , то имеет место задача оптимизации с ограничениями или задача условной оптимизации. При этом говорят об «условном экстремуме», а множество допустимых решений ограничивается системой уравнений вида или системой неравенств .
, то имеет место задача оптимизации с ограничениями или задача условной оптимизации. При этом говорят об «условном экстремуме», а множество допустимых решений ограничивается системой уравнений вида или системой неравенств .
2. По количеству управляющих параметров 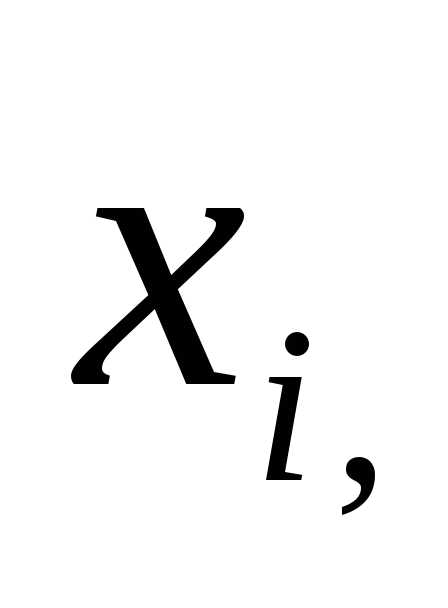
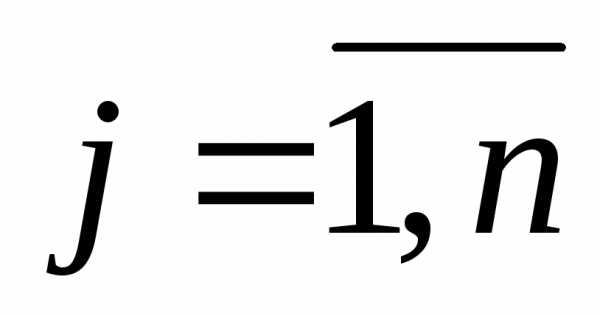 , принадлежащих множеству допустимых решений - приn=1 задача одномерной оптимизации.
, принадлежащих множеству допустимых решений - приn=1 задача одномерной оптимизации.
Здесь поиск экстремума целевой функции производится на некоторой кривой 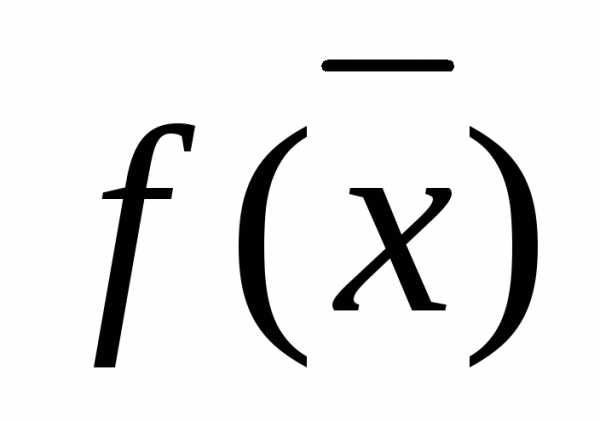 в интервале
в интервале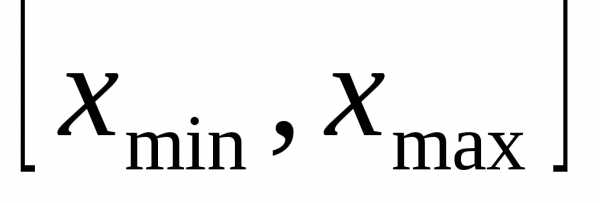 , т. е.
, т. е.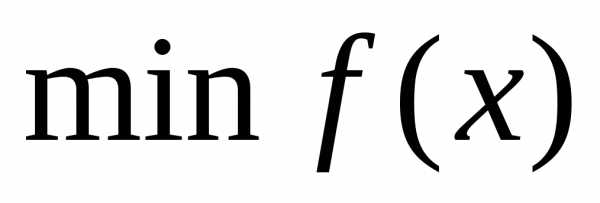 ,или,- приn>1 задача многопараметрической или многомерной оптимизации. Здесь производится поиск экстремума функции, определяемой на некотором множестве допустимых решений
,или,- приn>1 задача многопараметрической или многомерной оптимизации. Здесь производится поиск экстремума функции, определяемой на некотором множестве допустимых решений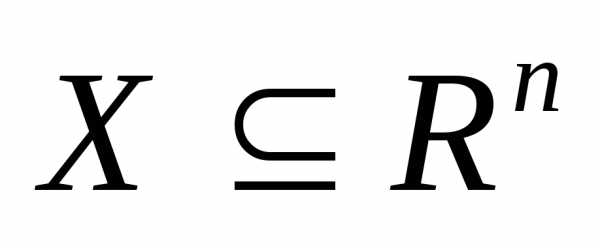 , т. е.
, т. е.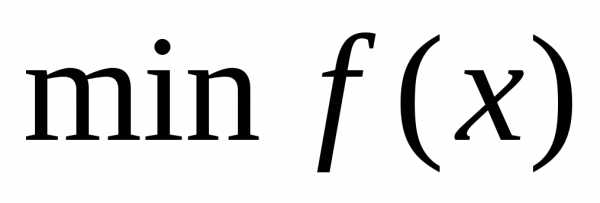 ,
,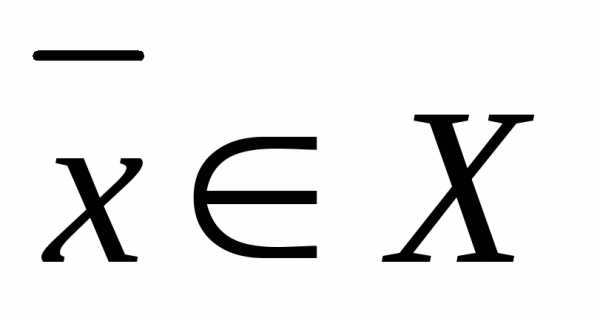 или,
или, .
.
3. По количеству экстремумов целевой функции различают задачи унимодальной (одноэкстремальной ) и многоэкстремальной оптимизации.
Поясним эти понятия. В зависимости от вида целевой функции 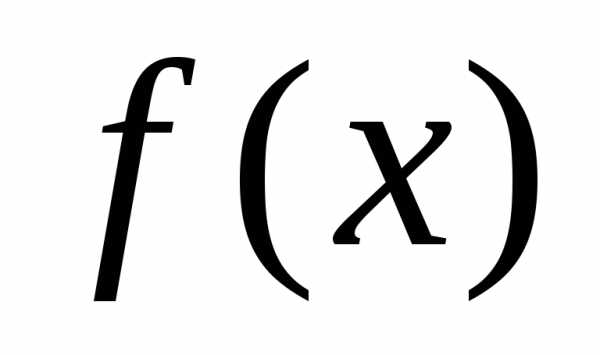 оптимальное решение
оптимальное решение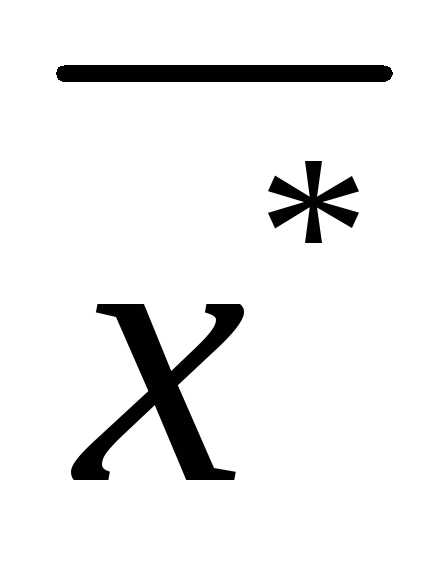 может быть точкой локального или глобального минимума (максимума).
может быть точкой локального или глобального минимума (максимума).
Вектор  называется точкой локального (относительного) минимума, если для всех точек
называется точкой локального (относительного) минимума, если для всех точек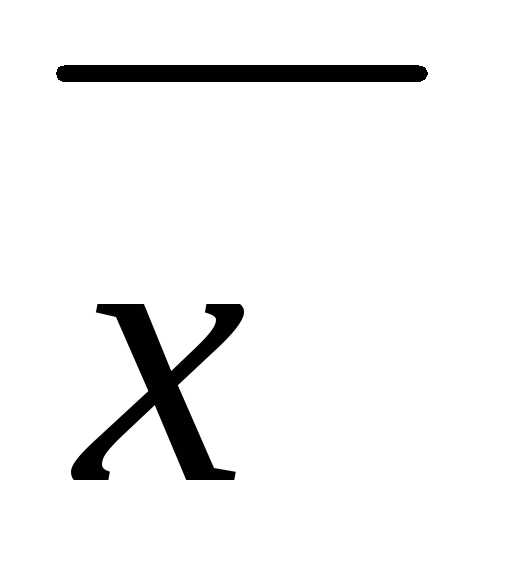 , принадлежащих
, принадлежащих - окрестности
- окрестности точки
точки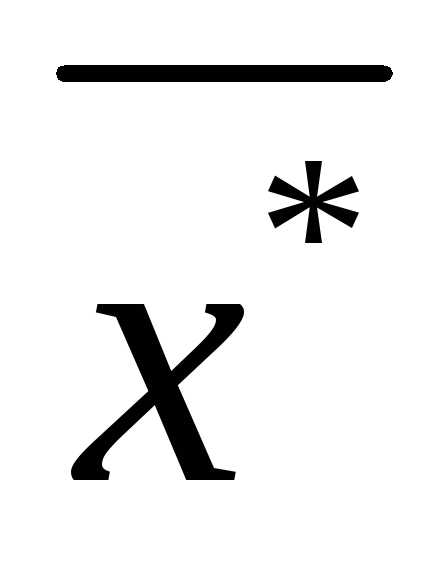 , функция
, функция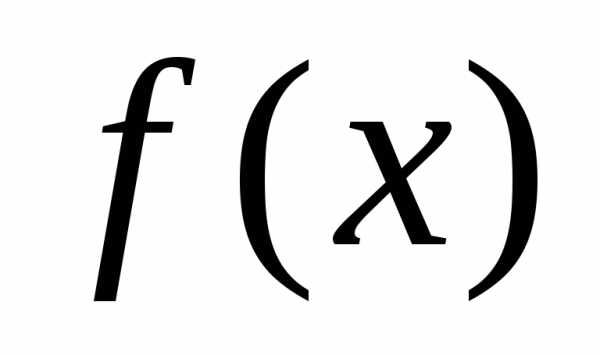 не принимает меньшего значения:
не принимает меньшего значения:
для всех.
Замечание:  - окрестностью точки
- окрестностью точки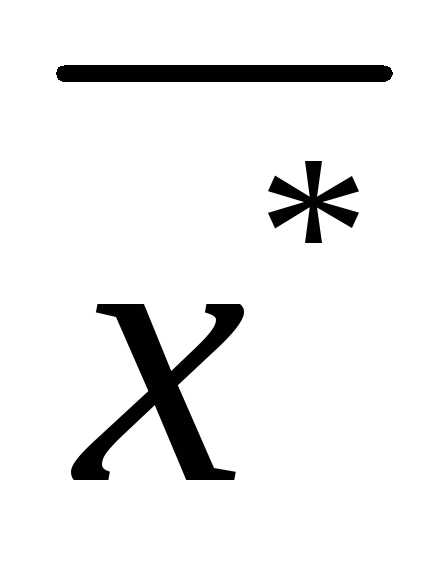 называется множество точек вида:, где расстояние между точками евклидова пространства:
называется множество точек вида:, где расстояние между точками евклидова пространства:
.
Вектор 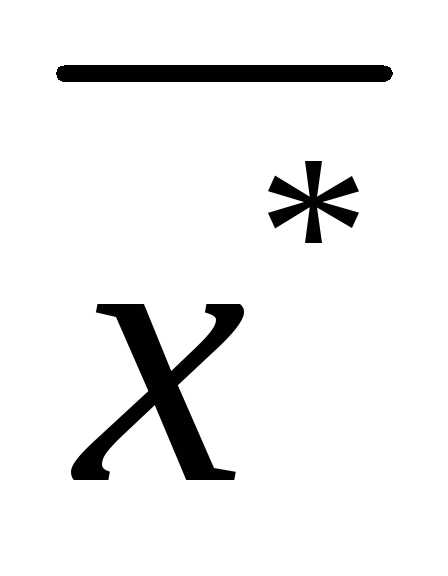 является точкой глобального (абсолютного) минимума, если ни в какой другой точке
является точкой глобального (абсолютного) минимума, если ни в какой другой точке допустимой области функция
допустимой области функция не принимает меньшего значения:
не принимает меньшего значения:
для всех .
.
Таким образом, глобальный минимум- это наименьший из всех локальных минимумов.
Например:
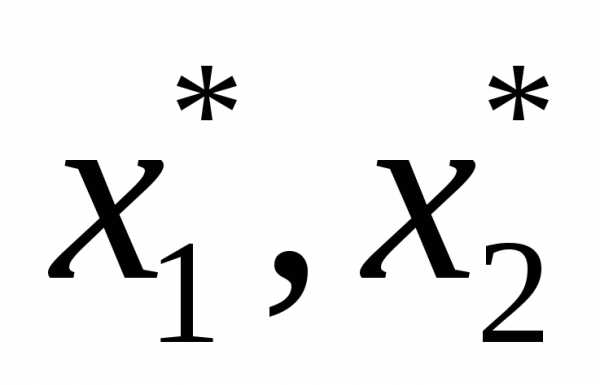 - точки локального минимума,
- точки локального минимума,
 - точка глобального минимума.
- точка глобального минимума.
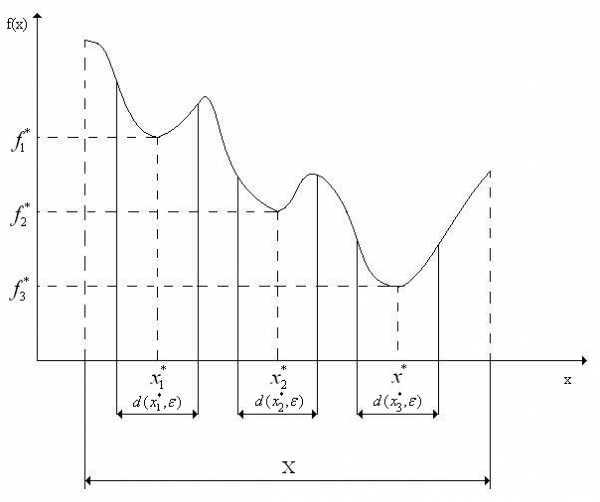
Понятия локального и глобального максимума выводятся аналогично.
Задачей унимодальной оптимизации является задача оптимизации вида 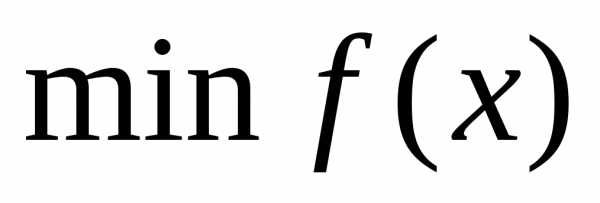 ,
,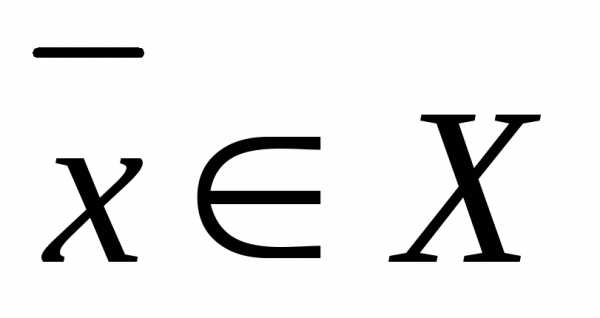 или,
или,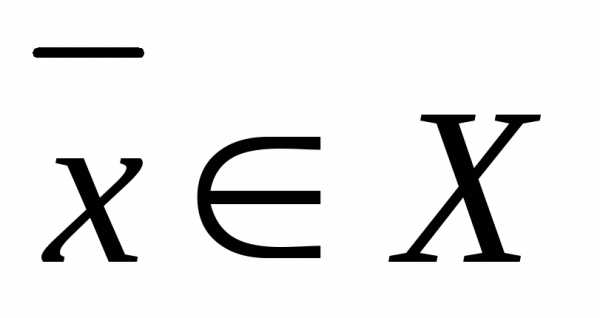 , для которой целевая функцияимеет в области Х единственный локальный экстремум.
, для которой целевая функцияимеет в области Х единственный локальный экстремум.
Если целевая функция имеет несколько локальных экстремумов, то это многозадачная задача оптимизации.
4. По количеству критериев оптимизации.
Различают задачи однокритериальной и многокритериальной (векторной) оптимизации.
В первом случае целевая функция единственна и имеет скалярный характер, во втором случае для совместного учета совокупности частных критериев обычно вводится векторный критерий оптимальности.
При этом минимизация 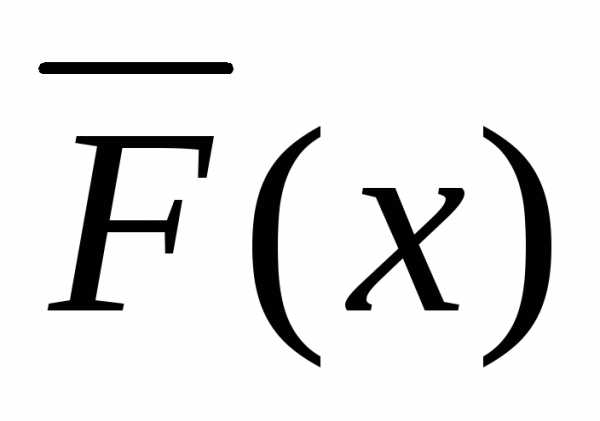 эквивалентна одновременной минимизации
эквивалентна одновременной минимизации
Поскольку частные критерии носят противоречивый характер, то оптимальное решение 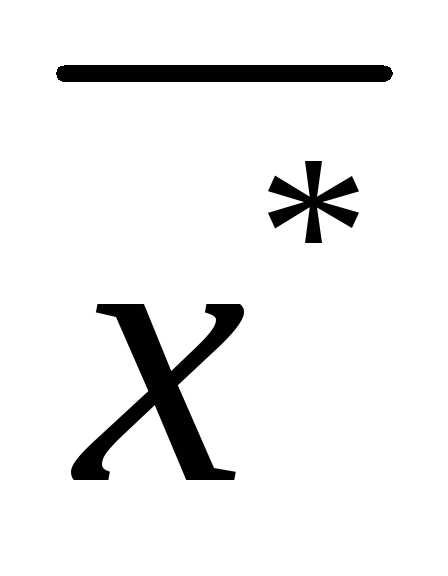 задачи векторной оптимизации в общем случае не является оптимальным ни для одного из частных критериев, но должно быть компромиссным для векторного критерия в целом.
задачи векторной оптимизации в общем случае не является оптимальным ни для одного из частных критериев, но должно быть компромиссным для векторного критерия в целом.
Возможным подходом к поиску компромиссного решения задачи векторной оптимизации является ее сведение к задаче многопараметрической оптимизации с единственной целевой функцией, учитывающей влияние всех частных критериев на решение.
4. Выбор критериев оптимизации.
Целевая функция в задаче оптимизации обязательно должна быть скалярной, т. е. оптимизация конструкции или технологического процесса может выполняться только по одному критерию.
Однако задачи конструкторско- технологического проектирования обычно носят многоцелевой характер, т. е. имеется большое число частных показателей, характеризующих качество проекта (надежность, стоимость, быстродействие, потребляемая мощность и т. д.)
Поэтому обоснованный выбор критериев оптимизации представляет важную задачу. Рассмотрим математические методы , позволяющие учитывать многоцелевой характер задач оптимизации. Все эти методы выполняют свертывание векторного критерия в скалярный.
1. Метод обобщенного критерия.
Пусть имеется совокупность частных критериев качества , .
.
На ее основе вводится скалярная функция от частных показателей вида .
Если все показатели 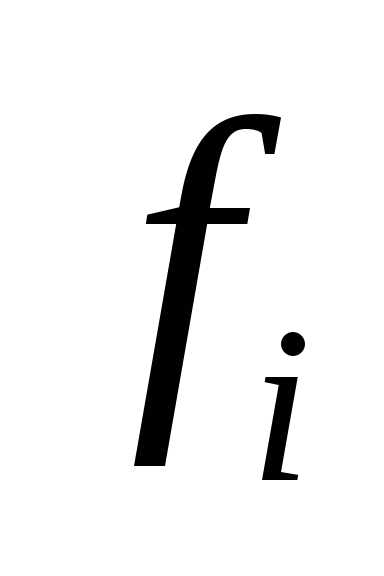 измеряются по одной шкале, то возможно использовать аддитивный или мультипликативный критерий:
измеряются по одной шкале, то возможно использовать аддитивный или мультипликативный критерий:
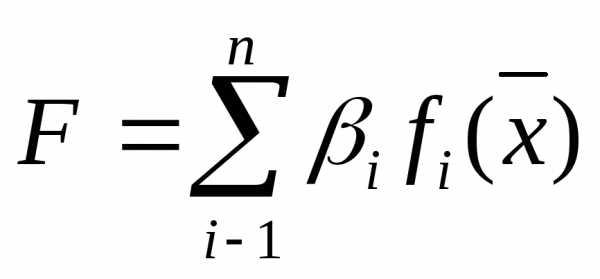 - аддитивный,
- аддитивный,
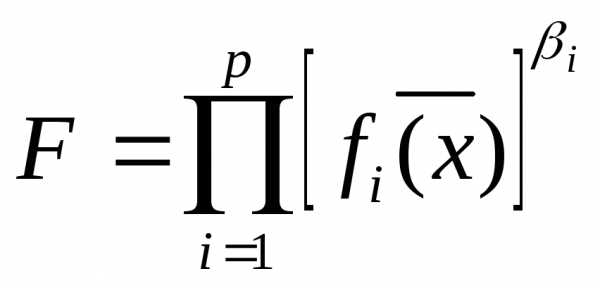 - мультипликативный,
- мультипликативный,
где  - вес (степень влияния) соответствующего критерия, устанавливаемый, например, в результате экспертных оценок.
- вес (степень влияния) соответствующего критерия, устанавливаемый, например, в результате экспертных оценок.
После формирования обобщенного критерия задача оптимизации ставится как  ,
,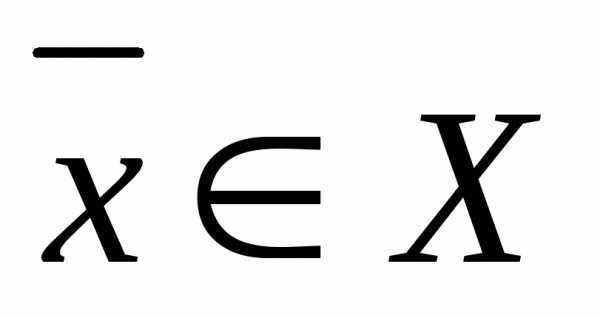 или
или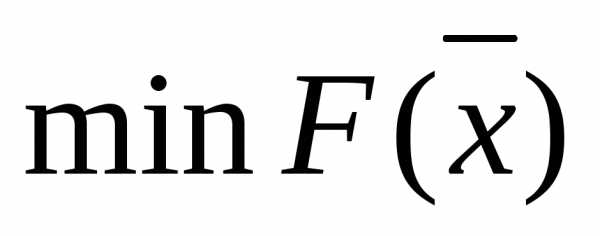 ,
, .
.
Если частные показатели качества 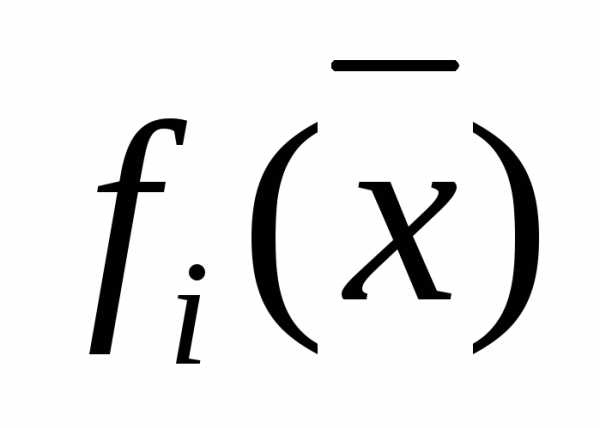 измеряются по разным шкалам, то формируется обобщенный критерий, приведенный к единой шкале измерений (для случая):
измеряются по разным шкалам, то формируется обобщенный критерий, приведенный к единой шкале измерений (для случая):
, где.
Для такого критерия решение задачи минимизации обеспечивает максимизацию всех частных критериев, т. к. функция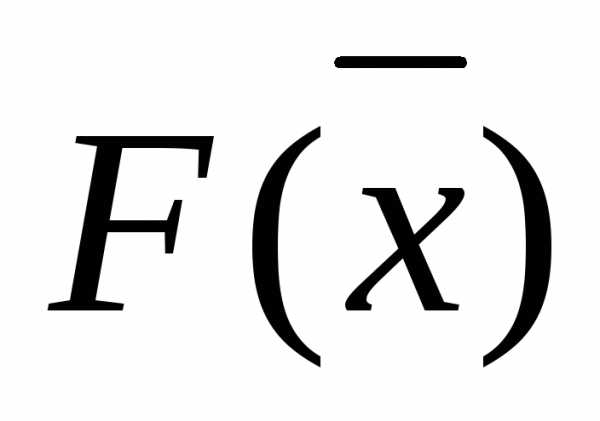 задает относительные отклонения частных критериев от их максимально- возможных значений
задает относительные отклонения частных критериев от их максимально- возможных значений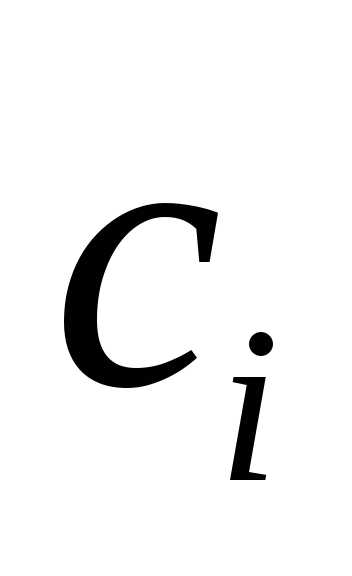
Основной недостаток такого метода выбора критерия оптимизации заключается в субъективном определении значений  , что может привести к улучшению одних частных показателей за счет ухудшения других.
, что может привести к улучшению одних частных показателей за счет ухудшения других.
2. Метод главного критерия.
Предполагается, что среди всех частных показателей можно выделить один, наиболее важный, который определяется обычно показателем ЭВС. Например, для бортовой аппаратуры - это надежность, для суперЭВМ- быстродействие, для микроЭВМ- стоимость и т. д.
Остальные частные критерии выступают в роли ограничений, т. е. Их значения не должны быть больше или меньше их предельно-допустимых значений.
Математически задача оптимизации формулируется следующим образом: найти при ограничениях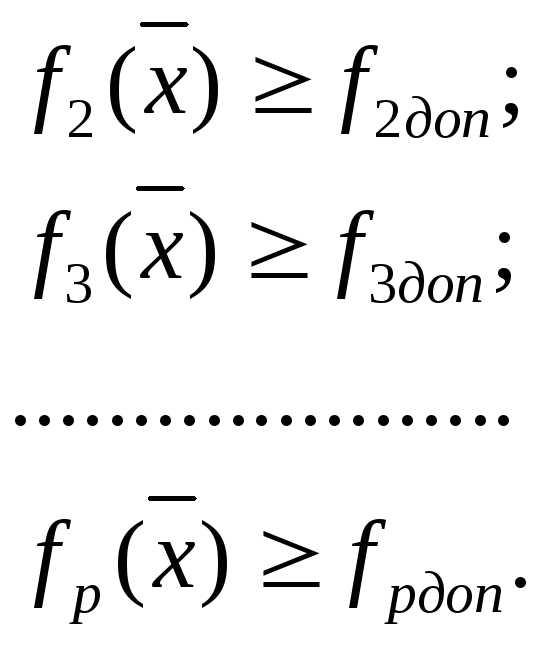
Такая задача оптимизации всегда корректна и является наиболее распространенной. Она называется однокритериальной задачей оптимизации.
3. Метод минимального (максимального) критерия.
В качестве функции 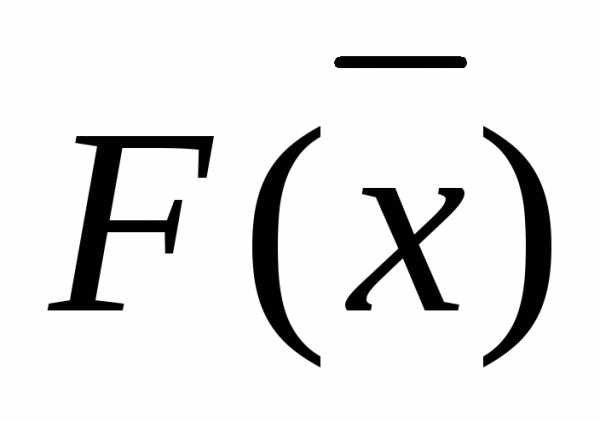 выбирается худшее значение из частных критериев и решается задача максимизации, т. е.
выбирается худшее значение из частных критериев и решается задача максимизации, т. е.
- максимальный критерий.
Другими словами, для нескольких максимизируемых параметров выбирается наихудший, который должен быть максимальным.
Для максимального критерия наоборот- минимизируется наибольшее значение из всех частных показателей: .
4. Метод последовательных уступок.
Используется в том случае, если нельзя выделить главный критерий, но можно некоторым образом упорядочить показатели по степени их важности.
Предположим, что частные критерии расположены по убыванию важности.
Тогда сначала решается задача ; результат которой обозначается через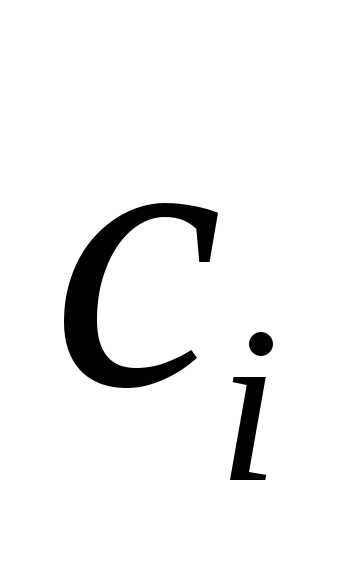 .
.
Затем вводится некоторая уступка (ухудшение)  в первом показателе и решается задачапри ограничении (дополнительном).
в первом показателе и решается задачапри ограничении (дополнительном).
Максимальное значение показателя  обозначаем через
обозначаем через и назначаем уступку
и назначаем уступку Решаем задачу:
Решаем задачу:
при дополнительных ограничениях .
.
Процесс продолжается для всех pкритериев качества.
Окончательный вариант решения находится как при ограничениях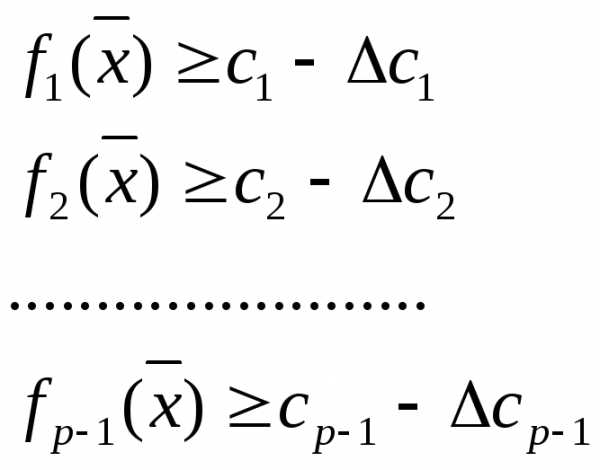 .
.
Сложность данного метода заключается в выборе значений 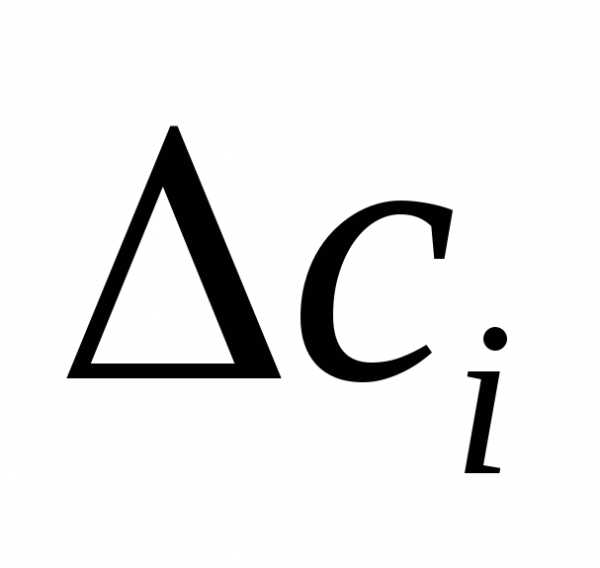 , а также в определении степени важности критериев качества (порядка их следования при решении).
, а также в определении степени важности критериев качества (порядка их следования при решении).
В качестве выводов укажем способы выбора критериев при автоматизированном проектировании ЭВС.
1. Если в т3 на проектирование сформулировано условие, что необходимо оптимизировать один из параметров проектируемого объекта при соблюдении ограничений на остальные параметры, то необходимо использовать метод главного критерия.
2. При наличии в т3 нескольких критериев оптимальности выбор аддитивного критерия целесообразен в тех случаях, когда существенные значения имеют абсолютные значения частных критериев при выбранном векторе решения
3. Если существенное значение имеет взаимное изменение абсолютных значений критериев при вариации вектора 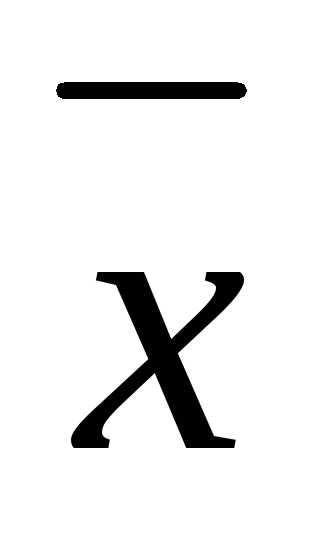 , то в этом случае рекомендуется применять мультипликативный критерий оптимизации.
, то в этом случае рекомендуется применять мультипликативный критерий оптимизации.
4. Если задача предполагает достижение примерного равенства конфликтующих частных критериев, то оптимальное проектирование следует проводить по минимаксному или максиминному критерию.
studfiles.net