Автоматизация многодисциплинарных инженерных расчетов с помощью потока работ. Александр А. Прохоров (докладчик) Алексей М. Многодисциплинарная оптимизация
Решение задачи многодисциплинарной оптимизации силовых конструкций на основе многоуровневого подхода Текст научной статьи по специальности «Механика»
Механика деформируемого твердого тела Вестник Нижегородского университета им. Н.И. Лобачевского, 2011, № 4 (4), с. 1847-1849 1847
УДК 629.7.015.4
РЕШЕНИЕ ЗАДАЧИ МНОГОДИСЦИПЛИНАРНОЙ ОПТИМИЗАЦИ И СИЛОВЫХ КОНСТРУКЦИЙ НА ОСНОВЕ МНОГОУРОВНЕВОГО ПОДХОДА
© 2011 г. В.В. Чедрик
Центральный аэрогидродинамический институт им. Н.Е. Жуковского, г Жуковский
Поступила в редакцию 15.06.2011
Представлена многоуровневая процедура решения задач оптимизации конструкций с учетом ограничений по прочности, жесткости, устойчивости и аэроупругости, реализованная в рамках программного обеспечения многодисциплинарного проектирования. Процедура опробована на решении ряда задач проектирования элементов авиационных конструкций.
Ключевые слова: многодисциплинарная оптимизация конструкций, многоуровневый подход, метод ко -нечных элементов, метод заданных форм, напряжение, потеря устойчивости, аэроупругость.
Для синтеза рациональных конструктивно-силовых схем летательных аппаратов необходим комплексный подход к задаче проектирования силовых конструкций, который бы учитывал совокупность требований прочности, аэроупругости и ресурса. Такой многодисциплинарный подход реализован в системе аналитического сопровождения проектирования конструкций АРГОН. В общем виде задача многодисциплинарной оптимизации формулируется так же, как задача нелинейного программирования, и для ее решения применяются методы оптимизации, представленные в [1, 2]. При этом функциональные ограничения, накладываемые на поведение конструкции, обычно рассчитываются отдельными программами, представляющими различные технические дисциплины. Расчет характеристик конструкции может проводиться на моделях различного уровня. Глобальный метод конечных элементов (МКЭ) используется для определения напряжений и перемещений конструкции. Метод заданных форм и расчет аэродинамического обтекания на основе панельного метода применяются для вычисления характеристик статической и динамической аэроупругости. Локальные подробные МКЭ модели необходимо использовать для анализа напряженно-деформированного состояния отдельных элементов конструкции при анализе ресурса и устойчивости конструкции. Чтобы объединить ограничения, вытекающие из различных дисциплин, в одну задачу проектирования предлагается многоуровневая процедура оптимизации. Она может быть условно разделена на три этапа.
Первый этап многодисциплинарной оптимизации может трактоваться как этап многодисцип-
линарного анализа конструкции. На нем проводится расчет рассматриваемой конструкции с использованием моделей различного уровня. Многие случаи могут быть включены на этом этапе для определения функциональных характеристик конструкции в каждой из рассматриваемых дисциплин. На втором этапе вычисляются градиенты этих ограничений по отношению к проектным параметрам. Так как реальная задача имеет большое количество ограничений, то производится процедура отсеивания для выбора ограничений, которые могут играть важную роль при проектировочном пересчете проектных параметров. Отметим, что для вычисления градиентов необходимо пройти по всем дисциплинам, в которых имеются активные нарушенные ограничения. На третьем этапе оптимизации, рассматривается задача минимизации целевой функции при редуцированном наборе активных ограничений. Для решения задачи многодисциплинарной оптимизации используется метод последовательного квадратичного программирования и модифицированный метод Пшеничного [1]. Отметим, что при решении задач оптимизации в рамках одной дисциплины (например, статический анализ) реализованы более эффективные процедуры оптимизации.
Поскольку этап расчета конструкции является наиболее затратным по времени, важным является минимизации количества полных расчетов конструкции. Целесообразно проводить пересчет конструкции в оптимизационной процедуре в предположении, что градиенты не меняются при изменении проектных переменных. На основе известных производных строятся явные аппрок-
1848
В.В. Чедрик
симации ограничений, и формируется явное выражение для целевой функции. Полученная приближенная задача математического программирования передается в блок оптимизации. Эта задача дополняется ограничениями на изменение проектных переменных, в рамках которого остается корректной аппроксимация. Эта задача может быть легко решена с использованием одного из алгоритмов оптимизации (внутренний цикл оптимизации). Далее полученное решение аппрок-симационной задачи берется в качестве нового приближения в процессе оптимизации конструкции (внешний цикл оптимизации). Многошаговая оптимизационная процедура обычно завершается при удовлетворении критериям сходимости по целевой функции и удовлетворении ограничениям.
Приведены два примера многодисциплинарной оптимизации. Оптимизация конструкции лонжерона (рис. 1) была проведена с помощью систем АРГОН двумя способами: последовательно и одновременно.
мизации на последующем этапе. В рамках второго способа все ограничения рассматривались од -новременно. Спроектированная конструкция, полученная последовательным подходом, оказалась на 3% тяжелее конструкции, найденной по второму методу.
Разработанная процедура оптимизации использовалась при поиске рациональной конструктивно-силовой схемы композиционного кессона крыла средне-магистрального самолета. Проектные переменные кессона показаны на рис. 2. Процедура многодисциплинарного проектирования включала в себя анализ аэродинамических и инерционных нагрузок с использованием упругой пла-стинно-балочной модели (два случая нагружения (А) и (А')) и оптимизацию распределения толщин композиционного пакета на модели МКЭ.
На рис. 3 показано полученное распределение приведенных толщин верхней и нижней обшивки вдоль размаха крыла. Анализ напряжен-но-де формированного состояния оптимизированной конструкции показал, что если не учитывать
А
7
8
9
10
11
12
'М
1 2 3 4 5 6 1
13 <- 14 15 16 17 18 ->
6 м
Р2 А Р2
Л
б)
Р2
I Р2 " Р2
Р1
т, кг
300 250 200 150 100 50
10
15
Итерации
Рис. 1
При последовательном подходе сначала была осуществлена оптимизация с учетом только ограничений по напряжениям, затем фигурировали только ограничения по перемещениям, после чего рассматривались только условия по частоте. При этом значения проектных переменных, полученные на предыдущей стадии, служили минимально допустимыми величинами для них при опти-
упругость конструкции, то толщины практически всех элементов определяются нагрузками второго случая нагружения (А'). Оптимальная масса для конструкции с «упругими» нагрузками существенно меньше (1007 кг), чем для «жестких» нагрузок (1271 кг).
Отметим, что сброс нагрузки во втором случае (А') значительно больше, чем в случае А, так
Распределение приведенных толщин верхней и нижней обшивки по размаху крыла
Рис. 2
2500 5000 7500 10000 12500 15000 17500 Размах крыла, мм
Рис. 3
0
3
0
5
2
2
0
Решение задачи многодисциплинарной оптимизации силовых конструкций
1849
что при учете упругости конструкции оба случая являются определяющими.
Таким образом, разработанная многоуровневая процедура оптимизации обладает высокой гибкостью и позволяет решать широкий класс исследовательских и практических задач проектирования силовых конструкций. Многоуровневая оптимизация, при которой задача распадается на ряд отдельно решаемых задач, обеспечивает практическое осуществление оптимизации со многими проектными переменными и ограниче-
ниями из различных дисциплин.
Список литературы
1. Никифоров А.К., Чедрик В.В. О методах и алгоритмах многодисциплинарной оптимизации силовых конструкций // Уч. зап. ЦАГИ. 2007. Т. XXXVIII, №1-2. С. 129-142.
2. Ishmuratov F.Z., Chedrik VV. ARGON code: structural aeroelastic analysis and optimization // International Forum on Aeroelasticity and Structural Dynamics, 2003. Amsterdam, IFASD-2003.
SOLVING THE MULTIDISCIPLINARY STRUCTURAL OPTIMIZATION PROBLEM BASED
ON MULTILEVEL APPROACH
V.V. Chedrik
A multilevel flowchart for solving optimization problems of design of composite and metallic structures under strength, stiffness, buckling and aero-elasticity constraints is presented. It has been implemented in the framework of the software for multidisciplinary structural optimization. A set of test problems has been solved and the multilevel approach has been used in design studies of advanced aircraft structures.
Keywords: multidisciplinary design optimization, multilevel approach, finite element method, prescribed forms method, stress, buckling, aeroelasticity.
cyberleninka.ru
Программное обеспечение Многодисциплинарная параметрическая оптимизация
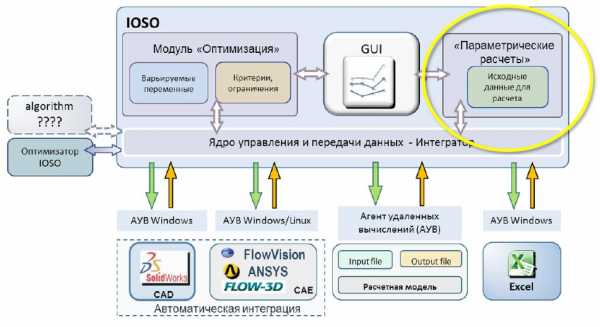
Программная платформа IOSO - эффективный инструментарий решения инженерных и оптимизационных расчетов, хранения и анализа данных в едином информационном пространстве, основанном на интеграции программных и аппаратных средств предприятия.
В программе реализованы уникальные высокоэффективные алгоритмы нелинейной оптимизации с возможностью решения многокритериальных (до 20 критериев) многопараметрических (до 100 переменных и ограничений) задач нелинейной оптимизации, эффективность которых подтверждена тестированием на нескольких тысячах тестовых примеров.
Стркутура программного комплекса IOSO
- Реализована возможность интеграции с расчетными моделями, имеющими текстовые файлы ввода/вывода данных произвольного формата, в том числе XML-файлы;
- Интегрированы модули с различными алгоритмами оптимизации;
- Обеспечены кросплатформенные вычисления.
Инструментальные средства IOSO разработаны для решения широкого спектра задач нелинейной оптимизации и состоят из нескольких независимых алгоритмов. Элементы IOSO-технологии созданы в рамках единой концепции по постановке задач оптимизации, анализу полученных результатов, обмену данными с программным продуктом пользователя и заданием исходных данных на начальном этапе.
Отличительные особенности IOSO-алгоритмов оптимизации:
- Быстрое решение сложных многопараметрических задач с наличием ограничений, зон невычисляемости и многоэкстремальностью целевой функции;
- Высокая эффективность решения многопараметрических (до 100 переменных и 100 ограничений) многокритериальных (до 20 критериев) задач оптимизации. До 7 раз быстрее традиционных методов, в том числе и генетического алгоритма, что позволяет существенно сократить сроки решения этих задач;
- Простота использования процедур оптимизации. Реализованные адаптивные алгоритмы не требуют предварительных настроек и задания параметров, что позволяет их использовать специалистам не владеющими специальными знаниями в теории оптимизации;
- Процедуры распараллеленной оптимизации для кластеров и многопроцессорных вычислительных систем позволяют использовать эти возможности для значительного сокращения времени решения задач.
Программное обеспечение Многодисциплинарная параметрическая оптимизация
Программная платформа IOSO - эффективный инструментарий решения инженерных и оптимизационных расчетов, хранения и анализа данных в едином информационном пространстве, основанном на интеграции программных и аппаратных средств предприятия.
В программе реализованы уникальные высокоэффективные алгоритмы нелинейной оптимизации с возможностью решения многокритериальных (до 20 критериев) многопараметрических (до 100 переменных и ограничений) задач нелинейной оптимизации, эффективность которых подтверждена тестированием на нескольких тысячах тестовых примеров.
Стркутура программного комплекса IOSO
- Реализована возможность интеграции с расчетными моделями, имеющими текстовые файлы ввода/вывода данных произвольного формата, в том числе XML-файлы;
- Интегрированы модули с различными алгоритмами оптимизации;
- Обеспечены кросплатформенные вычисления.
Инструментальные средства IOSO разработаны для решения широкого спектра задач нелинейной оптимизации и состоят из нескольких независимых алгоритмов. Элементы IOSO-технологии созданы в рамках единой концепции по постановке задач оптимизации, анализу полученных результатов, обмену данными с программным продуктом пользователя и заданием исходных данных на начальном этапе.
Отличительные особенности IOSO-алгоритмов оптимизации:
- Быстрое решение сложных многопараметрических задач с наличием ограничений, зон невычисляемости и многоэкстремальностью целевой функции;
- Высокая эффективность решения многопараметрических (до 100 переменных и 100 ограничений) многокритериальных (до 20 критериев) задач оптимизации. До 7 раз быстрее традиционных методов, в том числе и генетического алгоритма, что позволяет существенно сократить сроки решения этих задач;
- Простота использования процедур оптимизации. Реализованные адаптивные алгоритмы не требуют предварительных настроек и задания параметров, что позволяет их использовать специалистам не владеющими специальными знаниями в теории оптимизации;
- Процедуры распараллеленной оптимизации для кластеров и многопроцессорных вычислительных систем позволяют использовать эти возможности для значительного сокращения времени решения задач.
advengineering.ru
Автоматизация многодисциплинарных инженерных расчетов с помощью потока работ. Александр А. Прохоров (докладчик) Алексей М.
Технологии разработки
Технологии разработки Методологии программирования Императивное пошаговое изменение состояния вычислителя. Архитектура фон Неймана. Языки: Fortran, Pascal, C. Объектно-ориентированное. Методология основана
ПодробнееМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ Государственное образовательное учреждение высшего профессионального образования "Ижевский государственный технический университет" ГЛАЗОВСКИЙ ИНЖЕНЕРНО-ЭКОНОМИЧЕСКИЙ
ПодробнееВведение в нейронные сети [M.160]
Введение в нейронные сети [M.160] Ранее отмечалось, что такие популярные инструменты Data Mining, как регрессия и деревья решений, широко используемые для решения задач классификации и прогнозирования,
ПодробнееРазбор задачи «Автобусы»
Разбор задачи «Автобусы» Прежде всего, определим, в каких случаях требуется конечное число автобусов. Построим ориентированный граф, вершинами которого будут города, а ребрами рейсы автобусов. Чтобы автобусы
ПодробнееРЕАЛИЗАЦИЯ ПРЕЦЕДЕНТОВ
ПРОГРАММНАЯ ИНЖЕНЕРИЯ РЕАЛИЗАЦИЯ ПРЕЦЕДЕНТОВ РАДЧЕНКО Г.И., КАФЕДРА СП ЮУРГУ АНАЛИЗ ПРЕЦЕДЕНТА Аналитическая модель классов это статическая структура системы, а реализация прецедентов показывает, как взаимодействуют
ПодробнееЕстественные и технические науки, 2005 (4). ISSN
О ПРОБЛЕМАХ СИНТЕЗА ИЗОМОРФНЫХ АВТОМАТОВ В.В. Стрижов, Вычислительный центр РАН Аннотация При синтезе автомата требуется определить такую его структуру, которая была бы оптимальна в пространстве трех параметров:
ПодробнееЛекция 31. Программное обеспечение САПР
Лекция 31 Программное обеспечение САПР Программное обеспечение САПР (ПО) представляет собой совокупность программ, необходимых для обработки исходной информации по проектным алгоритмам, управления вычислительным
ПодробнееБаза нормативной документации:
М Е Ж Г О С У Д А Р С Т В Е Н Н Ы Й С Т А Н Д А Р Т Единая система программной документации Р-СХЕМЫ АЛГОРИТМОВ И ПРОГРАММ Обозначения условные графические и правила выполнения Unified system for program
ПодробнееПередаточная функция сети Петри
Опубликовано: Искусственный интеллект. - 00. - С. -0. Передаточная функция сети Петри Д.А.Зайцев ВВЕДЕНИЕ В [] показано что произвольная сеть Петри [] может рассматриваться как функциональная сеть по отношению
ПодробнееДИСКРЕТНЫЕ ФУНКЦИИ И АВТОМАТЫ
ВЕСТНИК ТОМСКОГО ГОСУДАРСТВЕННОГО УНИВЕРСИТЕТА 2011 Управление, вычислительная техника и информатика 3(16) ДИСКРЕТНЫЕ ФУНКЦИИ И АВТОМАТЫ УДК 519.7 А.Д. Закревский АЛГОРИТМ МАТРИЧНОГО ОТОБРАЖЕНИЯ ГРАФА
ПодробнееОпределение 1: Определение 2:
РАЗРАБОТКА ИС Жизненный цикл ИС Определение 1: Жизненный цикл ИС это процесс ее построения и развития. Определение 2: Жизненный цикл ИС период времени, который начинается с момента принятия решения о необходимости
ПодробнееЛекция 4. Задача коммивояжера
Лекция 4. Задача коммивояжера Екатерина Алексеева Новосибирский Государственный Университет Механико-математический факультет http://math.nsc.ru/ alekseeva/ 30 сентября, 2012 Содержание лекции Постановка
ПодробнееЛекция 4: Эйлеров и гамильтонов цикл
Уральский федеральный университет, Институт математики и компьютерных наук, кафедра алгебры и дискретной математики Эйлеров цикл Определение Цикл, содержащий все ребра графа, называется эйлеровым. Граф
ПодробнееТема 8. Гамильтоновы графы
Тема 8. Гамильтоновы графы 8.1. Определение гамильтонова графа и достаточные условия гамильтоновости Определение. Если граф имеет простой цикл, содержащий все вершины графа по одному разу, то такой цикл
ПодробнееТема 6. Эйлеровы графы
Тема 6. Эйлеровы графы 6.1. Эйлеровы графы, необходимые и достаточные условия эйлеровости Определение. Если граф имеет цикл (не обязательно простой), содержащий все ребра графа по одному разу, то такой
ПодробнееА.С. Тяхти. Вариант 11
Санкт-Петербургский государственный университет информационных технологий, механики и оптики Факультет информационных технологий и программирования Кафедра «Компьютерные технологии» А.С. Тяхти Отчет по
Подробнее2 Основы алгоритмизации
2 Основы алгоритмизации 2.1 Основные определения и понятия 2.1.1 Алгоритм и алгоритмизация Понятие алгоритма такое же основополагающее для информатики, как и понятие информации. Термин «алгоритм» обязан
Подробнееdocplayer.ru