7.3. Примеры статистических моделей и гипотез, ранги и ранжирование. Ранжирование в статистике это
Атрибутивные и вариационные ряды распределения. Ранжирование данных.
В результате сводки статистических материалов образуются ряды статистических данных, которые показывают либо изменение объемов совокупностей в динамике, либо распределение совокупностей по тем или иным признакам в статике.
Распределение может быть по признакам, не имеющим количественной меры (атрибутивным), и по признакам, в которых изменяется их количественная мера (вариационные ряды).
Атрибутивные ряды распределения. Примерами таких распределений являются распределение населения на городское и сельское, мужское и женское, товарооборота на продовольственные и непродовольственные товары, занятого населения по отраслям и профессиям.
Вариационные ряды. Примерами служат распределение рабочих по размеру среднемесячной заработной платы, предприятий по объемам производства или численности работающих.
Вариационные ряды по способу построения бывают интервальными и дискретными. Интервальные вариационные ряды – ряды, в которых значения вариант даны в виде интервалов (например, численность населения по возрастам). Дискретные вариационные ряды - ряды, в которых значения вариант имеют значения целых чисел (например, общее число семей по числу человек)
Характер вариационного ряда (интервальный или дискретный) определяется характером вариации. Вариация может быть непрерывной и прерывной (дискретной). Примерами непрерывной вариации служат урожайность сельскохозяйственных культур, заработная плата, объемы производства.
Примерами дискретной вариации могут служить число членов семьи, тарифный разряд рабочего, число комнат в квартире, число рабочих на предприятии.
Если дискретная вариация проявляется в широких пределах (например, численность рабочих на предприятии), то строятся интервальные вариационные ряды.
Ранжированный ряд - это распределение отдельных единиц совокупности в порядке возрастания или убывания исследуемого признака. Ранжирование позволяет легко разделить количественные данные по группам, сразу обнаружить наименьшее и наибольшее значения признака, выделить значения, которые чаще всего повторяются.
www.ekonomstat.ru
Ранжирование • ru.knowledgr.com
Ранжирование - отношения между рядом пунктов, таким образом, что для любых двух пунктов первое или 'оценивается выше, чем', 'оцениваемый ниже, чем' или 'занял место равный' второму.
В математике это известно как слабый заказ или полный предварительный заказ объектов. Это - не обязательно полный заказ объектов, потому что у двух различных объектов может быть то же самое ранжирование. Сам рейтинг полностью заказан. Например, материалы полностью предварительно заказаны твердостью, в то время как степени твердости полностью заказаны.
Уменьшая подробные меры до последовательности порядковых числительных, рейтинг позволяет оценить сложную информацию согласно определенным критериям. Таким образом, например, интернет-поисковая система может оценить страницы, которые она находит согласно оценке их уместности, позволяющей пользователю быстро выбрать страницы, которые они, вероятно, захотят видеть.
Анализ данных, полученных, занимая место обычно, требует непараметрической статистики.
Стратегии назначения рейтинга
Не всегда возможно назначить рейтинг уникально. Например, в гонке или соревновании два (или больше) участники могли бы связать для места в ранжировании. Когда вычисление порядкового измерения, два (или больше) оцениваемых количеств могло бы иметь размеры равный. В этих случаях может быть принята одна из стратегий, показанных ниже для назначения рейтинга.
Общий способ стенографии отличить эти стратегии ранжирования занимающими место числами, которые были бы произведены для четырех пунктов с первым пунктом, оцениваемым перед вторым и третьим (которые выдерживают сравнение равный), которые оба оцениваются перед четвертым. Эти имена также показывают ниже.
Стандартное ранжирование соревнования («1224» ранжирование)
В ранжировании соревнования пункты, которые выдерживают сравнение равный, получают то же самое число ранжирования, и затем промежуток оставляют в занимающих место числах. Число занимающих место чисел, которые не учтены в этом промежутке, является тем меньше, чем число пунктов, которые выдержали сравнение равный. Эквивалентно, число ранжирования каждого пункта 1 плюс число пунктов, ставивших выше его. Эта стратегия ранжирования часто принимается для соревнований, как это означает, что, если два (или больше) конкуренты связывают для положения в ранжировании, положения всех, оцениваемые ниже их незатронуты (т.е., конкурент только приходит вторым, если точно очки человека лучше, чем они, треть, если точно два человека выигрывают лучше, чем они, четвертый, если точно три человека выигрывают лучше, чем они, и т.д.).
Таким образом, если разряды перед B и C (которые выдерживают сравнение равный), которые оба оцениваются перед D, тогда A получает занимающий место номер 1 («сначала»), B добирается, занимающий место номер 2 («соединяют второй»), C также добирается, занимающий место номер 2 («соединяют второй»), и D получает занимающий место («четвертый») номер 4.
Измененное ранжирование соревнования («1334» ранжирование)
Таким образом, если разряды перед B и C (которые выдерживают сравнение равный), которые оба оцениваются перед D, тогда A получает занимающий место номер 1 («сначала»), B добирается, занимающий место номер 3 («соединяют треть»), C также добирается, занимающий место номер 3 («соединяют треть»), и D получает занимающий место («четвертый») номер 4. В этом случае никто не получил бы занимающий место («второй») номер 2, и это оставят как промежуток.
Плотное ранжирование («1223» ранжирование)
В плотном ранжировании пункты, которые выдерживают сравнение равный, получают то же самое число ранжирования, и следующий пункт (ы) получает немедленно после занимающего место числа. Эквивалентно, число ранжирования каждого пункта 1 плюс число пунктов, ставивших выше его, которые отличны относительно занимающего место заказа.
Таким образом, если разряды перед B и C (которые выдерживают сравнение равный), которые оба оцениваются перед D, тогда A получает занимающий место номер 1 («сначала»), B добирается, занимающий место номер 2 («соединяют второй»), C также добирается, занимающий место номер 2 («соединяют второй»), и D получает занимающий место номер 3 («треть»).
Порядковое ранжирование («1234» ранжирование)
В порядковом ранжировании все пункты получают отличные порядковые числительные, включая пункты, которые выдерживают сравнение равный. Назначение отличных порядковых числительных к пунктам, которые выдерживают сравнение равный, может быть сделано наугад, или произвольно, но вообще предпочтительно использовать систему, которая произвольна, но последовательна, поскольку это дает стабильные результаты, если ранжирование сделано многократно. Пример произвольной, но последовательной системы должен был бы включить другие признаки в занимающий место заказ (такие как буквенный заказ имени конкурента), чтобы гарантировать, чтобы никакие два пункта точно не соответствовали.
С этой стратегией, если разряды перед B и C (которые выдерживают сравнение равный), которые и оцениваются перед D, тогда добирается A, занимающий место номер 1 («сначала») и D получают занимающий место («четвертый») номер 4, и или B получает занимающий место («второй») номер 2, и C добирается, занимающий место номер 3 («треть») или C получает занимающий место («второй») номер 2, и B получает занимающий место номер 3 («треть»).
В компьютерной обработке данных порядковое ранжирование также упоминается как «ряд, нумерующий»....
Фракционное ранжирование («1 2.5 2.5 4» ранжирования)
Пункты, которые выдерживают сравнение равный, получают то же самое число ранжирования, которое является средним из того, что они имели бы при порядковом рейтинге. Эквивалентно, занимающее место число 1 плюс число пунктов, ставивших выше его плюс половина числа пунктов, равняется ему. У этой стратегии есть собственность, которой сумма занимающих место чисел совпадает с при порядковом ранжировании. Поэтому это используется в вычислении количества Борды и в статистических тестах (см. ниже).
Таким образом, если разряды перед B и C (которые выдерживают сравнение равный), которые и оцениваются перед D, тогда A получает занимающий место номер 1 («сначала»), B и C, каждый получает занимающий место номер 2.5 (среднее число «сустава, второго/третьего»), и D получает занимающий место («четвертый») номер 4.
Вот пример: Предположим, что у Вас есть набор данных 1 1 2 3 3 4 5 5 5
Есть 5 различных чисел, таким образом, было бы пять различных разрядов.
Если бы 1 и 1 были фактически различные числа, то они заняли бы разряды 1 и 2. Так как они - то же самое число, Вы находите их разряд, находя среднее число следующим образом: (разряд) 1 + (разряд) 2 / 2 общих количества чисел = 1.5 (средний разряд).
Следующему числу в наборе данных, 2, таким образом назначают разряд 3 (среднее число поднимает 1 и 2 в первых двух 1's).
Два 3's в наборе заняли бы разряды 4 и 5, если бы они были различными числами, таким образом, средний разряд был бы вычислен следующим образом: (4 + 5) / 2 = 4.5.
4 получил бы разряд 6 (потому что Ваше среднее число приняло во внимание разряд 4 и 5 в среднем числе).
есть 3 5's в наборе данных. Их средний разряд вычислен как (7+8+9)/3 = 8
Ваши разряды были бы: 1.5 1.5 3 4.5 4.5 6 8 8 8
Ранжирование в статистике
В статистике «ранжирование» относится к преобразованию данных, в котором числовые или порядковые ценности заменены их разрядом, когда данные сортированы. Например, числовые данные 3.4, 5.1, 2.6, 7.3 наблюдаются, разряды этих элементов данных были бы 2, 3, 1 и 4 соответственно. Например, порядковые данные, горячие, холодные, теплые, были бы заменены 3, 1, 2. В этих примерах разряды назначены на ценности в порядке возрастания. (В некоторых других случаях используются спускающиеся разряды.) Разряды связаны с индексируемым списком статистики заказа, которая состоит из оригинального набора данных, перестроенного в порядок по возрастанию.
Некоторые виды статистических тестов используют вычисления, основанные на разрядах. Примеры включают:
- Тест Фридмана
- Тест Краскэл-Уоллиса
- Коэффициент корреляции разряда копьеносца
- Сумма разряда Wilcoxon проверяет
- Написанный разряд Wilcoxon проверяет
некоторых разрядов могут быть ценности нецелого числа для связанных значений данных. Например, когда есть четное число копий того же самого значения данных, вышеупомянутого описанного фракционного статистического разряда связанных концов данных в ½.
Функция разряда в Excel
Функция разряда в Microsoft Excel назначает разряды соревнования («1224»), как описано выше. В некоторых статистических целях, который не является желаемым результатом - например, это означает, что сумма разрядов для списка данной длины изменяется в зависимости от числа связей. Поттель описал пользователя, определенного, оценив функцию, которая поручает фракционным разрядам на связи сохранять сумму последовательной.
Примеры ранжирования
- В политике, внимании рейтинга на сравнение экономических, социальных, экологических и исполнения управления стран, см. Список международного рейтинга
- На многих спортивных состязаниях людям или командам дает рейтинг, обычно руководство спорта
- В футболе национальные сборные оцениваются в Классификациях сильнейших спортсменов мира ФИФА и, неофициально, в Мировом Футболе Рейтинги Elo.
- На Олимпийских Играх каждое государство-член (NOC) оценивается основанное на золоте, количестве серебряной и бронзовой медали в Олимпийском рейтинге медали.
- В снукере игроки оцениваются, используя Снукерные классификации сильнейших спортсменов мира
- В хоккее с шайбой национальные сборные оцениваются в Классификации сильнейших спортсменов мира ИИХФ
- В баскетболе национальные сборные оцениваются в Классификациях сильнейших спортсменов мира FIBA
- В гольфе главные гольфисты мужского пола оцениваются, используя Официальный Мировой Рейтинг Гольфа
- В гэльском футболе команды графства оцениваются, используя гэльскую футбольную систему рейтинга
- Относительно положения кредита относится ранжирование безопасности туда, где та особая безопасность стояла бы на ветру эмиссионной компании, т.е., ее старшинство в структуре капитала компании. Например, капитальные примечания - подчиненные ценные бумаги; они заняли бы место позади старшего долга на ветру. Другими словами, держатели старшего долга были бы выплачены, прежде чем подчиненные долговые держатели получили любые фонды.
- Поисковые системы оценивают веб-страницы своим ожидаемым отношением к вопросу пользователя, используя комбинацию зависимых от вопроса и независимых от вопроса методов. Независимые от вопроса методы пытаются измерить предполагаемую важность страницы, независимой от любого рассмотрения того, как хорошо это соответствует определенному вопросу. Независимое от вопроса ранжирование обычно основано на анализе связи; примеры включают алгоритм ХИТОВ, PageRank и TrustRank. Зависимые от вопроса методы пытаются измерить степень, которой страница соответствует определенному вопросу, независимому от важности страницы. Зависимое от вопроса ранжирование обычно основано на эвристике, которые рассматривают число и местоположения матчей различных слов вопроса на самой странице в URL или в любом якорном тексте, относящемся к странице.
- В Webometrics возможно оценить учреждения согласно их присутствию в сети (число интернет-страниц) и воздействие этого содержания (внешние inlinks=site цитаты), такие как Ранжирование Webometrics Мировых университетов
- В видео играх игрокам можно дать ранжирование. «Занимать место» означает достигнуть более высокопоставленного относительно других игроков, особенно со стратегиями, которые не зависят от умения игрока.
- Система ранжирования TrueSkill - умение, базируемое, оценивая систему для Xbox Live, разработанного в Microsoft Research
- bibliogram оценивает фразы имени нарицательное в части текста.
- На языке, статусе пункта (обычно через то, что известно как «downranking» или «перемена разряда») относительно высшего разряда в пункте; например, в предложении «Я хочу съесть пирог, который Вы сделали сегодня», «поешьте», находится на высшем разряде, но «сделанный» downranked как часть именной группы «пирог, который Вы сделали сегодня»; эта именная группа ведет себя, как будто это было единственное существительное (т.е., я хочу съесть его), и таким образом глагол в пределах («сделанного») оценивается по-другому от, «едят».
- Академические журналы иногда оцениваются согласно фактору воздействия; число более поздних статей, которые цитируют статьи в данном журнале.
См. также
- Сравнительная таблица
- Порядковое измерение
- Рейтинг (разрешения неоднозначности)
Внешние ссылки
- Ронен Перри, относительное значение американских юридических журналов: критическая оценка занимающих место методов
- Ронен Перри, относительное значение американских юридических журналов: обработка и внедрение
- Комплект инструментов MATLAB для вычислительного рейтинга, используя пять различных методологий
- Система ранжирования TrueSkill
- Ранжирование Библиотеки, написанной в Руби
- Список глобальных индексов развития и рейтинга
ru.knowledgr.com
|
Ранги. Во многих случаях имеющиеся в нашем распоряжении числовые данные (например, значения элементов выборки) носят в той или иной мере условный характер. Например, эти данные могут быть тестовыми баллами, экспертными оценками, данными о вкусовых или политических предпочтениях опрошенных людей и т. д. Анализ таких данных требует особой осторожности, поскольку многие предпосылки классических статистических методов (например, предположения о каком-либо конкретном, скажем нормальном, законе распределения) для них не выполняются. Твердую основу для выводов здесь дают только соотношения между наблюдениями типа «больше-меньше», так как они не меняются при изменении шкалы измерений. Например, при анализе анкет с данными о симпатиях избирателей к политическим деятелям мы можем сказать, что политик, получивший больший балл в анкете, более симпатичен отвечавшему на вопросы человеку (респонденту), чем политик, получивший меньший балл. Но на сколько (или во сколько раз) он более симпатичен, сказать нельзя, так как для предпочтений нет объективной единицы измерения. В подобных случаях (которые мы будем более подробно рассматривать в последующих главах), имеет смысл вообще отказаться от анализа конкретных значений данных, а исследовать только информацию об из взаимной упорядоченности. Для этого от исходных числовых данных осуществляют переход к их Рангам. Определение. Рангом наблюдения называют тот номер, который получит это наблюдение в упорядоченной совокупности всех данных — после их упорядочения по определенному правилу (например, от меньших значений к большим или наоборот). Чаще всего упорядочение чисел (набор которых составляют упомянутые выше данные) производят по величине — от меньших к большим. Именно такое упорядочение и связанное с ним ранжирование (присвоение рангов) мы будем иметь в виду в дальнейшем. Пример. Пусть выборка состоит из чисел 6, 17, 14,5, 12. Тогда рангом числа 6 оказывается 2, рангом 17 будет 5 и т. д. Определение. Процедура перехода от совокупности наблюдений к последовательности их рангов называется ранжированием. Результат ранжирования называется ранжировкой. Статистические методы, в которых мы делаем выводы о данных на основании их рангов, называются ранговыми. Они получили широкое распространение, так как надежно работают при очень слабых предположениях об исходных данных (не требуя, например, чтобы эти данные имели какой-либо конкретный закон распределения). В последующих главах этой книги мы рассмотрим применение ранговых методов в наиболее распространенных практических задачах. Средние ранги. Трудности в назначении рангов возникают, если среди элементов выборки встречаются совпадающие. (Так часто бывает, когда данные регистрируются с округлением.) В этом случае обыкновенно используют Средние ранги. Средние ранги вводятся так. Предположим, что наблюдение , имеет ту же величину, что и некоторые другие из общего числа П Наблюдений. (Эту совокупность одинаковых наблюдений из набора называют Связкой, количество таких одинаковых наблюдений в данной связке называют ее размером.) Средний ранг , в ранжировке наблюдений есть среднее арифметическое тех рангов, которые были бы назначены и всем остальным элементам связки, если бы одинаковые наблюдения оказались различны. В качестве примера рассмотрим выборку 6, 17, 12, 6, 12. Ее ранжировка равна . Покажем на примерах, как может проходить математическая формализация практических задач и как сформулированные на естественном языке вопросы превращаются в статистические гипотезы. Тройной тест. Рассмотрим распространенный в психологии тройной тест (его другое название — тест дегустатора). Он состоит из серии одинаковых опытов, в каждом из которых испытуемому предъявляют одновременно три стимула. Два из них идентичны, а третий несколько отличается. Испытуемый, ориентируясь на свои ощущения, должен указать этот отличающийся стимул. Например, испытуемому могут быть предложены три стакана с жидкостью: два с чистой водой, а третий — со слабым раствором сахара, либо наоборот — два стакана подслащенных, а третий — с чистой водой. Задание для испытуемого — указать стакан, отличающийся от двух других. Опыты стараются организовать так, чтобы они проходили в одинаковых условиях и чтобы в каждом из них испытуемый мог полагаться только на свои ощущения. В результате подобного однократного эксперимента можно получить как правильный, так и неправильный ответ. При слабой концентрации раствора, когда его трудно отличить от воды, из одного ответа нельзя сделать определенного заключения о способности испытуемого чувствовать данную концентрацию. Испытуемый может случайно ошибиться, даже если в целом он способен отличать данную концентрацию сахара от чистой воды. С другой стороны, правильный ответ не исключает того, что испытуемый его просто угадал, не отличая раствора от воды. Эти свойства эксперимента мы можем перечислить в виде следующих допущений: • в каждом испытании ответ испытуемого случаен; • существует вероятность правильного ответа, которая неизменна во все время испытаний; • результаты отдельных испытаний статистически независимы. Коротко это выражается так: статистической моделью эксперимента служит схема Бернулли. Сформулировав математическую модель явления, перейдем к выдвижению статистических гипотез. Интересующая нас способность испытуемого характеризуется вероятностью правильного ответа, которую мы обозначим Р. В этом опыте она нам неизвестна. Естественно, эта вероятность зависит от степени концентрации сахара. Если концентрация очень мала и не воспринимается, то у испытуемого нет оснований для выбора. Он «наудачу» будет указывать один из трех стаканов. В этих условиях вероятность правильного ответа . Предположим, что экспериментатора интересует, начиная с каких концентраций испытуемый отличает раствор от воды. Тогда для данной концентрации экспериментатор может выдвинуть предположение, что испытуемый ее ощутить не в состоянии. В изложенной модели это предположение превращается в статистическую гипотезу о том, что . Примем следующую форму записи статистической гипотезы: . Если же экспериментатор предполагает, что испытуемый может ощутить наличие сахара, то соответствующая статистическая гипотеза состоит в том, что , т. е. . Возможна и гипотеза о том, что , она соответствует тому, что испытуемый способен отличить раствор от воды, но принимает одно за другое. Экспериментатор может выдвигать и другие гипотезы о способности испытуемого к различению концентраций. Например, возможна такая гипотеза: испытуемый способен ощутить присутствие сахара, ошибаясь один раз из десяти. В этом случае вероятность правильного ответа равна 0.9 и гипотеза примет вид: Н : р = 0.9. Заметим, что с чисто математической точки зрения гипотеза вида проще, чем или . Действительно, при мы имеем дело с одним (полностью заданным) биномиальным распределением, а в других случаях перед нами семейство распределений. Ясно, что с одним распределением иметь дело проще. Сейчас мы не будем рассматривать процесс проверки этих гипотез (он описан в п. 4), а вместо этого приведем еще один пример перевода естественнонаучной задачи на статистический язык, т. е. построения статистической модели явления и выдвижения гипотезы для проверки. Парные наблюдения. На практике часто бывает необходимо сравнить два способа действий по их результатам. Речь может идти о сравнении двух методик обучения, эффективности двух лекарств, производительности труда при двух технологиях и т. д. В качестве конкретного примера рассмотрим эксперимент, в котором выясняется, на какой из сигналов человек реагирует быстрее: на свет или на звук. Эксперимент был организован следующим образом. Каждому из семнадцати испытуемых в случайном порядке поочередно подавались два сигнала: световой и звуковой. Интенсивность сигналов была неизменна в течение всего эксперимента. Увидев или услышав сигнал, испытуемый должен был нажать на кнопку. Время между сигналом и реакцией испытуемого регистрировал прибор. Результаты эксперимента приведены в табл. 1. Таблица 1 Время реакции на свет и на звук, в миллисекундах
I — номер испытуемого, I = 1,..., 17; Xi — время его реакции на звук, YI — время его реакции на свет. Вместо поставленного выше вопроса о том, на какой из сигналов человек отвечает быстрее, выдвинем другой: можно ли считать, что время реакции человека на свет и на звук одинаковы? Логически эти вопросы тесно связаны: если мы отвечаем отрицательно на второй из них, мы тем самым признаем, что различия есть. После этого уже не трудно понять, когда время реакции меньше. Если же на второй вопрос мы отвечаем положительно, то первый после этого просто снимается. С математической же точки зрения второй вопрос проще, как мы увидим из дальнейшего обсуждения. Итак, время реакции на звук, X, и время реакции на свет, Y, различно у разных людей, несмотря на то, что во время опыта они находились в одинаковых условиях. Ясно, что наблюдаемый разброс во времени реакции не связан с изучаемым явлением (различием двух действий). По-видимому, этот разброс можно объяснить различиями между испытуемыми и/или нестабильностью времени отклика на сигнал у каждого испытуемого. Как бы то ни было, эти колебания не имеют отношения к той закономерности, что нас интересует. Поэтому мы объявляем их случайными. Так сделан первый шаг к статистической модели: переменные Xi и Yi признаны реализациями случайных величин, скажем Xi и Yi. Поскольку каждый испытуемый решал свои задачи самостоятельно, не взаимодействуя с другими испытуемыми и не испытывая с их стороны влияния, мы будем считать случайные величины X1, Y1,..., Х17, Y17 Независимыми (в теоретико-вероятностном смысле). Выбор статистической модели. Дальнейшее уточнение статистической модели в подобных задачах может идти различными путями, в зависимости от природы эксперимента и наших знаний о ней. Один путь связан с предположением о том, что случайные величины XI и Yi имеют некоторые конкретные законы распределения. Например, мы можем предположить, что Xi и Yi — независимы и имеют нормальные распределения с одной и той же дисперсией (обозначим ее ). Тогда, если ввести для средних значений обозначения: где I = 1,..., 17, то можно сформулировать наши допущения так: случайные величины Xi, Yi подчиняются нормальным распределениям Соответственно, где параметры нам неизвестны. При этих обозначениях выдвинутый вопрос о равном времени реакции на свет и на звук может быть сформулирован как статистическая гипотеза: Если экспериментатор уверен, что группа испытуемых достаточно однородна, он может дополнительно предположить, что и . Если обозначить общие значения параметров через A и B соответственно, то статистическую модель в этом случае можно сформулировать так: случайные величины независимы и распределены по закону ; случайные величины тоже независимы, не зависят от и распределены по закону . Параметры A, B и неизвестны. Тогда гипотезу о равном времени реакции можно записать следующим образом: Ясно, что задача с меньшим числом неопределенных параметров, как во второй постановке, в принципе должна давать более точные ответы. При проверке гипотез это означает, что мы сможем принять или отвергнуть проверяемую гипотезу с большей степенью уверенности. Но следует помнить, что уменьшение количества параметров в модели является следствием принятия дополнительных предположений об имеющихся данных. Так, в приведенном выше примере мы предположили, что и , что и дало нам возможность уменьшить количество параметров в модели с 35 до 3. Но если сделанные дополнительные предположения являются неправомерными, то использование полученной математической модели может привести к неверному заключению. Например, при обработке наших данных по однородной схеме можно получить неверный ответ, если фактически эти данные однородными не являются. Итак, при построении статистической модели постоянно приходится вводить упрощающие математические предположения и одновременно оценивать, насколько они приемлемы с содержательной точки зрения. И часто надо быть готовым к тому, чтобы отказаться от недопустимых предположений или заменить их чем-то другим. Другой путь построения статистической модели — так называемый Непараметрический. Здесь мы не делаем предположений о том, что наблюдаемые случайные переменные имеют какой-либо параметрический закон распределения. В этом случае мы делаем меньше математических допущений, а значит, здесь меньше опасности принять неоправданное предположение. Зато при этом мы используем не всю информацию об имеющихся данных, а только ту ее часть, которая не зависит от конкретного вида распределения исходных данных. Например, при проверке гипотезы о равном времени реакции на свет и звук мы должны будем использовать не сами значения времен реакций Xi и Yi, а их Ранги В объединенной выборке Xi и Yi. По сравнению с параметрическим методом (если предположения о параметрическом характере случайных событий справедливы), мы получим при этом несколько менее точные выводы, но зато непараметрический метод имеет гораздо более широкую область применимости. Итак, при построении статистической модели приходится делать ряд предположений. Большую часть этих предположений мы не проверяем (и часто даже и не можем проверить). Некоторые предположения мы Выбираем для проверки их совместимости со статистическим материалом и называем такие предположения статистическими гипотезами. НиЖе Мы расскажем, как осуществляется проверка статистических гипотез.
|
matica.org.ua
Задача №1 Работа двадцати предприятий пищевой промышленности В отчетном периоде характеризуется следующими данными: Таблица 1
H=Xmax-Xmin/n 2. Определите по каждой группе: – число заводов; – стоимость ОПФ-всего и в среднем на один завод: – стоимость ТП-всего и в среднем на один завод. Результаты представьте в табличном виде, проанализирйте их и сделайте выводы H=20–10/5=2 где xmax, xmin – максимальное и минимальное значения кредитных вложений Определим теперь интервалы групп (xi, xi+1): 1 группа: 10–12 млн. руб. 2 группа: 12–14 млн. руб. 3 группа: 14–16 млн. руб. 4 группа: 16–18 млн. руб. 5 группа: 18–20 млн. руб. Далее упорядочим исходную таблицу по возрастанию ОФ
P=(0,34*52,1+0,48*45,7+0,53*23,8)/(52,1+45,7+23,8)= 0,4298=0,43 ч Вывод: средние затраты времени на производство продукции в базисном и отчетном году отличаются на (0,43–0,427)*100%= 0,003*100%=0,3% Задача №9 В результате контрольной выборочной проверки расфасовки чая осуществлена 25% механическая выборка по способу бесповторного отбора, в результате которой получено следующее распределение пачек чая по массе:
РешениеПриведем группировку к стандартному виду с равными интервалами и найдем середины интервалов для каждой группы. Результаты представлены в таблице:
Подставив в последнюю формулу известные значения, получим дисперсию: sІ=((48,5–49,77)І*17+(49,5–49,77)І*52+(50,5–49,77)І*21+(51,5–49,77)І*7+(52,5–49,77)І)/100=85,71/100=0,8571 г.І Среднее квадратическое отклонение равно: S=√sІ=√0,8571=0,93 г. Коэффициент вариации определяется по формуле: V=s/y=0,93/49,77= 0,019*100%=1,9% Рассчитаем сначала предельную ошибку выборки. Так при вероятности p = 0,997 коэффициент доверия t = 3. Поскольку дана 25%-ная случайная бесповторная выборка, то n/N=0,25 где n – объем выборочной совокупности, N – объем генеральной совокупности. Считаем также, что дисперсия sІ=0,8571. Тогда предельная ошибка выборочной средней равна: Δy=t*√σІ/n*(1-n/N)=3*√0,8571/100*(1–0,25)=0,24 г. Определим теперь возможные границы, в которых ожидается средняя масса чая на 1 пакетик чая y – Δy≤my≤y+ Δy 49,77–0,8571≤my≤49,77+0,8571 48,9129≤my≤50,6271 Т.е., с вероятностью 0,997 можно утверждать, что масса чая на 1 пакетик находится в пределах 48,9129 до 50,6271 Выборочная доля w удельного веса пачек чая с массой до 49 г. и свыше 52 г. во всей продукции с вероятностью 0,954 равна. W=(48+3)/100=0,51=51 г. Учитывая, что при вероятности p = 0,954 коэффициент доверия t = 2, вычислим предельную ошибку выборочной доли: Δw= t*√(w*(1-w)/n) *(1-n/N)=2*√(0,51*(1–0,51)/100)*(1–0,25)=0,086г или Пределы доли признака во всей совокупности: 51–8,6≤d≤51+8,6 42,4≤d≤59,6 Таким образом, с вероятностью 0,954 можно утверждать, что границы удельного веса пачек чая находятся в пределах42,4г до 59,6г во всей продукции. Выводы: 1. Так как коэффициент вариации меньше 33%, то исходная выборка однородная. Задача №14 Урожайность пшеницы характеризуется следующими данными. Интервальный ряд динамики «А»
1993=34*0,01=0,34 1994=34,8*0,01=0,348 1995=36,6*0,01=0,366 1996=39,3*0,01=0,393 1997=42,8*0,01=0,428 Результаты приведены в таблице:
| ||||||||
www.referatnatemu.com
Задача №1 Работа двадцати предприятий пищевой промышленности В отчетном периоде характеризуется следующими данными: Таблица 1
H=Xmax-Xmin/n 2. Определите по каждой группе: – число заводов; – стоимость ОПФ-всего и в среднем на один завод: – стоимость ТП-всего и в среднем на один завод. Результаты представьте в табличном виде, проанализирйте их и сделайте выводы H=20–10/5=2 где xmax, xmin – максимальное и минимальное значения кредитных вложений Определим теперь интервалы групп (xi, xi+1): 1 группа: 10–12 млн. руб. 2 группа: 12–14 млн. руб. 3 группа: 14–16 млн. руб. 4 группа: 16–18 млн. руб. 5 группа: 18–20 млн. руб. Далее упорядочим исходную таблицу по возрастанию ОФ
P=(0,34*52,1+0,48*45,7+0,53*23,8)/(52,1+45,7+23,8)= 0,4298=0,43 ч Вывод: средние затраты времени на производство продукции в базисном и отчетном году отличаются на (0,43–0,427)*100%= 0,003*100%=0,3% Задача №9 В результате контрольной выборочной проверки расфасовки чая осуществлена 25% механическая выборка по способу бесповторного отбора, в результате которой получено следующее распределение пачек чая по массе:
РешениеПриведем группировку к стандартному виду с равными интервалами и найдем середины интервалов для каждой группы. Результаты представлены в таблице:
Подставив в последнюю формулу известные значения, получим дисперсию: sІ=((48,5–49,77)І*17+(49,5–49,77)І*52+(50,5–49,77)І*21+(51,5–49,77)І*7+(52,5–49,77)І)/100=85,71/100=0,8571 г.І Среднее квадратическое отклонение равно: S=√sІ=√0,8571=0,93 г. Коэффициент вариации определяется по формуле: V=s/y=0,93/49,77= 0,019*100%=1,9% Рассчитаем сначала предельную ошибку выборки. Так при вероятности p = 0,997 коэффициент доверия t = 3. Поскольку дана 25%-ная случайная бесповторная выборка, то n/N=0,25 где n – объем выборочной совокупности, N – объем генеральной совокупности. Считаем также, что дисперсия sІ=0,8571. Тогда предельная ошибка выборочной средней равна: Δy=t*√σІ/n*(1-n/N)=3*√0,8571/100*(1–0,25)=0,24 г. Определим теперь возможные границы, в которых ожидается средняя масса чая на 1 пакетик чая y – Δy≤my≤y+ Δy 49,77–0,8571≤my≤49,77+0,8571 48,9129≤my≤50,6271 Т.е., с вероятностью 0,997 можно утверждать, что масса чая на 1 пакетик находится в пределах 48,9129 до 50,6271 Выборочная доля w удельного веса пачек чая с массой до 49 г. и свыше 52 г. во всей продукции с вероятностью 0,954 равна. W=(48+3)/100=0,51=51 г. Учитывая, что при вероятности p = 0,954 коэффициент доверия t = 2, вычислим предельную ошибку выборочной доли: Δw= t*√(w*(1-w)/n) *(1-n/N)=2*√(0,51*(1–0,51)/100)*(1–0,25)=0,086г или Пределы доли признака во всей совокупности: 51–8,6≤d≤51+8,6 42,4≤d≤59,6 Таким образом, с вероятностью 0,954 можно утверждать, что границы удельного веса пачек чая находятся в пределах42,4г до 59,6г во всей продукции. Выводы: 1. Так как коэффициент вариации меньше 33%, то исходная выборка однородная. Задача №14 Урожайность пшеницы характеризуется следующими данными. Интервальный ряд динамики «А»
1993=34*0,01=0,34 1994=34,8*0,01=0,348 1995=36,6*0,01=0,366 1996=39,3*0,01=0,393 1997=42,8*0,01=0,428 Результаты приведены в таблице:
| ||||||||
referatnatemu.com
Ранжирование и группировка данных в статистике
Ранжирование и группировка данных в статистике
Задача №1
Работа двадцати предприятий пищевой промышленности
В отчетном периоде характеризуется следующими данными:
Таблица 1
| № | 1 | 2 |
| 1 | 10 | 11,8 |
| 2 | 11 | 12,4 |
| 3 | 12,6 | 13,8 |
| 4 | 13 | 15,1 |
| 5 | 14,2 | 16,4 |
| 6 | 15 | 17 |
| 7 | 15,5 | 17,3 |
| 8 | 16,3 | 18,1 |
| 9 | 17,7 | 19,6 |
| 10 | 19,3 | 23,1 |
| 11 | 10,8 | 12 |
| 12 | 12,2 | 13 |
| 13 | 12,8 | 12,9 |
| 14 | 13,5 | 15,6 |
| 15 | 14,6 | 16,8 |
| 16 | 15,3 | 18,2 |
| 17 | 16 | 17,9 |
| 18 | 17,1 | 10 |
| 19 | 18 | 18 |
| 20 | 20 | 27,2 |
1-Среднегодовая стоимость промышленно-производственных ОФ, млн. руб.
2-Товарная продукция в сопоставимых оптовых ценах предприятия, млн. руб.
1. Проведите ранжирование исходных данных по размеру ОФ и их группировку, образовав 5 групп с равновеликими интервалами. Приведите расчет равновеликого интервала группировки по формуле:
H=Xmax-Xmin/n
2. Определите по каждой группе:
– число заводов;
– стоимость ОПФ-всего и в среднем на один завод:
– стоимость ТП-всего и в среднем на один завод.
Результаты представьте в табличном виде, проанализирйте их и сделайте выводы
H=20–10/5=2
где xmax, xmin – максимальное и минимальное значения кредитных вложений
Определим теперь интервалы групп (xi, xi+1):
1 группа: 10–12 млн. руб.
2 группа: 12–14 млн. руб.
3 группа: 14–16 млн. руб.
4 группа: 16–18 млн. руб.
5 группа: 18–20 млн. руб.
Далее упорядочим исходную таблицу по возрастанию ОФ
| № | Группа | Среднегодовая стоимость промышленно – производственных ОФ в группе, млн. руб. | Товарная продукция в сопоставимых оптовых ценах предприятия, млн. руб. |
| 1 | 10,1–12 | 10 | 11,8 |
| 11 | 12,4 | ||
| 10,8 | 12 | ||
| 2 | 12,1–14 | 12,6 | 13,8 |
| 13 | 15,1 | ||
| 12,2 | 13 | ||
| 12,8 | 12,9 | ||
| 13,5 | 15,6 | ||
| 3 | 14,1–16 | 14,2 | 16,4 |
| 15 | 17 | ||
| 15,5 | 17,3 | ||
| 14,6 | 16,8 | ||
| 15,3 | 18,2 | ||
| 16 | 17,9 | ||
| 4 | 16,1–18 | 16,3 | 18,1 |
| 17,7 | 19,6 | ||
| 17,1 | 10 | ||
| 18 | 18 | ||
| 5 | 18,1–20 | 19,3 | 23,1 |
| 20 | 27,2 |
На основе полученной таблицы определим требуемые показатели. Результаты представим в виде групповой таблицы:
Таблица 1.2
| Группа | Количество заводов в группе, шт. | Среднегодовая стоимость промышленно – производственных ОПФ, млн. руб. | Стоимость промышленно – производственных ОПФ, млн. руб. | Товарная продукция в сопоставимых оптовых ценах предприятия, млн. руб. | ||
| 1 | 3 | 10–12 | Всего | 31,8 | Всего | 36,2 |
| В среднем на один завод | 10,6 | В среднем на один завод | 12,067 | |||
| 2 | 5 | 12,1–14 | Всего | 64,1 | Всего | 70,4 |
| В среднем на один завод | 12,82 | В среднем на один завод | 14,08 | |||
| 3 | 6 | 14,1–16 | Всего | 90,6 | Всего | 103,6 |
| В среднем на один завод | 15,1 | В среднем на один завод | 17,27 | |||
| 4 | 4 | 16,1–18 | Всего | 69,1 | Всего | 65,7 |
| В среднем на один завод | 17,275 | В среднем на один завод | 17,275 | |||
| 5 | 2 | 18,1–20 | Всего | 39,3 | Всего | 50,3 |
| В среднем на один завод | 19,65 | В среднем на один завод | 25,15 | |||
Задача №4
Имеются данные по трем предприятиям, вырабатывающие однородную продукцию:
| № | Базисный год | Отчетный год | ||
| Затрата времени на ед. продукции, час | Выпущено продукции, тыс. ед. | Затраты времени на ед. продукции, тыс. ед. | Затраты времени на всю продукцию, ч | |
| 1 | 0,34 | 52,1 | 0,34 | 19975 |
| 2 | 0,48 | 45,7 | 0,48 | 22248 |
| 3 | 0,53 | 23,8 | 0,53 | 13462 |
Обоснуйте выбор формул средней и по этим формулам определите средние затраты времени на продукцию по трем предприятиям в базисном и отчетном годах, сравните полученные результаты и сделайте выводы.
Решение
Средние затраты времени определяются по формуле:
,
где V – затраты времени на единицу продукции; S – затраты времени на всю продукцию. Определим средние затраты времени на 3 предприятиях. Т.к. заданы затраты времени на единицу продукции и затраты времени на всю продукцию то:
Данная формула называется средней гармонической взвешенной.
Подставив в последнюю формулу известные значения, получим средние затраты времени на производство на предприятиях в отчетном году:
P=19975+22248+13462/(19972/0,34+22248/0,48+13462/0,53)= 0,427 ч
Определим средние затраты времени на производства продукции в базисном году:
Данная формула называется средней арифметической взвешенной.
Подставив в последнюю формулу известные значения, получим затраты времени на производство продукции в базисном году:
P=(0,34*52,1+0,48*45,7+0,53*23,8)/(52,1+45,7+23,8)= 0,4298=0,43 ч
Вывод: средние затраты времени на производство продукции в базисном и отчетном году отличаются на (0,43–0,427)*100%= 0,003*100%=0,3%
Задача №9
В результате контрольной выборочной проверки расфасовки чая осуществлена 25% механическая выборка по способу бесповторного отбора, в результате которой получено следующее распределение пачек чая по массе:
| Масса пачки чая, г | Число пачек чая, шт. |
| До 49 | 17 |
| 49–50 | 52 |
| 50–51 | 21 |
| 51–52 | 7 |
| 52 и выше | 3 |
| ИТОГО | 100 |
По результатам выборочного обследования определите:
1. Среднюю массу пачки чая;
2. Дисперсию и среднее квадратичное отклонение;
3. Коэффициент вариации;
4. С вероятностью 0,997 возможные пределы средней массы пачки чая во всей партии продукции;
5. С вероятностью 0,954 возможные пределы удельного веса пачек чая с массой до 49 г. и свыше 52 г. во всей продукции.
Решение
Приведем группировку к стандартному виду с равными интервалами и найдем середины интервалов для каждой группы. Результаты представлены в таблице:
| Масса пачки чая, г | Масса пачки чая, г | Средняя масса пачки чая, г | Число пачек чая, шт |
| До 49 | 48–49 | 48,5 | 17 |
| От 49 до 50 | 49–50 | 49,5 | 52 |
| От 50 до 51 | 50–51 | 50,5 | 21 |
| От 51 до 52 | 51–52 | 51,5 | 7 |
| Свыше 52 | 52–53 | 52,5 | 3 |
| Итого | 100 | ||
Среднюю массу пачки чая находим по формуле средней арифметической взвешенной:
Подставив в последнюю формулу известные значения, получим среднюю массу пачки чая:
Y=(48.5*17+49.5*52+50.5*21+51.5*7+52.5*3)/100=49.77 г.
Дисперсия определяется по формуле:
.
Подставив в последнюю формулу известные значения, получим дисперсию:
s²=((48,5–49,77)²*17+(49,5–49,77)²*52+(50,5–49,77)²*21+(51,5–49,77)²*7+(52,5–49,77)²)/100=85,71/100=0,8571 г.²
Среднее квадратическое отклонение равно:
S=√s²=√0,8571=0,93 г.
Коэффициент вариации определяется по формуле:
V=s/y=0,93/49,77= 0,019*100%=1,9%
Рассчитаем сначала предельную ошибку выборки. Так при вероятности p = 0,997 коэффициент доверия t = 3. Поскольку дана 25%-ная случайная бесповторная выборка, то
n/N=0,25
где n – объем выборочной совокупности, N – объем генеральной совокупности.
Считаем также, что дисперсия s²=0,8571. Тогда предельная ошибка выборочной средней равна:
Δy=t*√σ²/n*(1-n/N)=3*√0,8571/100*(1–0,25)=0,24 г.
Определим теперь возможные границы, в которых ожидается средняя масса чая на 1 пакетик чая
y – Δy≤my≤y+ Δy
49,77–0,8571≤my≤49,77+0,8571
48,9129≤my≤50,6271
Т.е., с вероятностью 0,997 можно утверждать, что масса чая на 1 пакетик находится в пределах 48,9129 до 50,6271
Выборочная доля w удельного веса пачек чая с массой до 49 г. и свыше 52 г. во всей продукции с вероятностью 0,954 равна.
W=(48+3)/100=0,51=51 г.
Учитывая, что при вероятности p = 0,954 коэффициент доверия t = 2, вычислим предельную ошибку выборочной доли:
Δw= t*√(w*(1-w)/n) *(1-n/N)=2*√(0,51*(1–0,51)/100)*(1–0,25)=0,086г
или
Пределы доли признака во всей совокупности:
51–8,6≤d≤51+8,6
42,4≤d≤59,6
Таким образом, с вероятностью 0,954 можно утверждать, что границы удельного веса пачек чая находятся в пределах42,4г до 59,6г во всей продукции.
Выводы:
1. Так как коэффициент вариации меньше 33%, то исходная выборка однородная.
Задача №14
Урожайность пшеницы характеризуется следующими данными.
Интервальный ряд динамики «А»
| года показатель | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 |
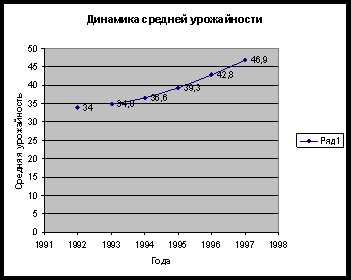
| Средняя урожайность, ц/га | 34 | 34,8 | 36,6 | 39,3 | 42,8 | 46,9 |
На основе имеющихся данных:
1. Определите все аналитические показатели ряда динамики «А»
2. Покажите взаимосвязь цепных и базисных темпов роста
3. Приведите графическое изображение динамики средней урожайности
Моментальный ряд динамики» Б»
| дата показатель | На 1.1 | На 1.2 | На 1.3 | На 1.4 |
| Списочная численность рабочих, чел. | 402 | 406 | 403 | 408 |
4. Приведите расчет среденесписочной численности работников предприятия за квартал по данным моментального ряда динамики» Б» по формуле средней хронологической для моментального ряда.
Решение
1. Определим показатели, характеризующие рост урожайности пшеницы: абсолютные приросты, темпы роста и прироста по годам. Формулы для расчета следующие.
Определим абсолютный прирост цепным способом:
Δy=yi-yi-1
1993=34,8–34=0,8
1994=36,6–34,8=1,8
1995=39,3–36,6=2,7
1996=42,8–39,3=3,5
1997=46,9–42,8=4,1
Базисным способом
Δy=yi-y0
1993=34,8–34=0,8
1994=36,6–34=2,6
1995=39,3–34=5,3
1996=42,8–34=8,8
1997=46,9–34=12,9
Определим темпы прироста цепным способом
Tр.ц= yi/ yi-1*100%
1993=34,8/34*100%=102,36%
1994=36,6/34,8*100%=105,17%
1995=39,3/36,6*100%=107,38%
1996=42,8/39,3*100%=108,91
1997=46,9/42,8*100%=109,58%
Базисным способом
1993=34,8/34*100%=102,36%
1994=36,6/34*100%=107,65%
1995=39,3/34*100%=115,59%
1996=42,8/34*100%=125,88%
1997=46,9/34*100%=137,94%
Определим темпы прироста цепным способом
Тпр.ц=Трц-100%
1993=102,36%-100%=2,36%
1994=105,17%-100%=5,17%
1995=107,38%-100%=7,38%
1996=108,91%-100%=8,91%
1997=109,58%-100%=9,58%
Базисным способом
Тпр б=Тр б-100%
1993=102,36%-100%=2,36%
1994=107,65%-100%=7,65%
1995=115,59%-100%=15,59%
1996=125,88%-100%=25,88%
1997=137,94%-100%=37,94%
Определим абсолютное значение 1%
1993=34*0,01=0,34
1994=34,8*0,01=0,348
1995=36,6*0,01=0,366
1996=39,3*0,01=0,393
1997=42,8*0,01=0,428
Результаты приведены в таблице:
| Годы | Средняя урожайность пшеницы, ц/га | Абсолютный прирост, млрд. руб. | Темпы роста, % | Темпы прироста, % | Абсолютное содержание 1% прироста | |||
| по годам | по годам | по годам | ||||||
| 1992 | 34 | цепной | базисный | цепной | базисный | цепной | базисный | |
| - | - | - | ||||||
| 1993 | 34,8 | 0,8 | 0,8 | 102,36 | 102,35 | 2,36 | 2,36 | 0,34 |
| 1994 | 36,6 | 1,8 | 2,6 | 105,17 | 107,52 | 5,17 | 7,65 | 0,348 |
| 1995 | 39,3 | 2,7 | 5,3 | 107,38 | 114,9 | 7,38 | 15,59 | 0,366 |
| 1996 | 42,8 | 3,5 | 8,8 | 108,91 | 123,5 | 8,91 | 25,88 | 0,393 |
| 1997 | 46,9 | 4,1 | 12,9 | 109,58 | 133,08 | 9,58 | 37,94 | 0,428 |
| ||||||||
Среднегодовую урожайность пшеницы определим по формуле средней арифметической взвешенной:
Х=(34+34,8+36,6+39,3+42,8+46,9)/6=234,4/6=39,066
Для моментального ряда «Б» с равностоящими уровнями средний уровень ряда можно вычислить по формуле средней хронологической:
Y=(1/2Y0+Y1+Y2+…1/2Yn)/n-1
Y=(1/2*402+406+403+1/2408)/4–1=405 человек
Среднесписочная численность рабочих за 1 квартал составила 405 человек.
Задача №19
Себестоимость и объем производства Советского шампанского характеризуется следующими данными:
| Марка шампанского | Себестоимость 100 бутылок, руб. | Выработано продукции, тыс. бутылок | ||
| ноябрь | декабрь | ноябрь | декабрь | |
| Полусладкое | 2233 | 2222 | 1835 | 1910 |
| Сладкое | 1725 | 1716 | 1404 | 1415 |
Определите:
1. Индивидуальные и общие индексы себестоимости продукции.
2. Общий индекс затрат на продукцию (издержек производства)
3. Использую взаимосвязь индексов, определите, на сколько% увеличивается объем производства продукции
Решение
Общий индекс себестоимости продукции:
Iz=(∑Z1*q1)/(∑Z0q1)
Где Z1, Z0 – себестоимость единицы продукции в ноябре и декабре;
Где q1, q0 – физический объем продукции в ноябре и декабре.
Iz=(2222*1910+1415*1716)/(2233*1910+1725*1415)= 0,994968
Общий индекс физического объема продукции:
Iq=(∑Z0* q1)/ (∑Z0q0)
Iq=(2233*1910+1725*1415)/(2233*1835+1725*1404)= 1,028599
Общий индекс затрат на производство продукции:
Izq= (∑Z1*q1)/(∑Z0q0)=(2222*1910+1415*1716)/(2233*1835+1725*1404)= 1,023423
Взаимосвязь индексов: Izq= Iz* Iq 1,023423=1,028599*0,994968
Задача №24
Имеются следующие данные по хлебозаводу:
| Виды продукции | Себестоимость за 1 т, руб. | Продано продукции, т | ||
| Базисный | Отчетный | Базисный | Отчетный | |
| Батоны столовые в/с – 0,3 кг | 38,8 | 40,1 | 1254 | 1210 |
| Батоны нарезные в/с – 0,5 кг | 35,6 | 36,85 | 2565 | 2632 |
Вычислите:
1. Индекс цен переменного состава
2. Индекс цен постоянного состава
3. Индекс структурных сдвигов
4. Покажите взаимосвязь между исчисленными индексами.
5. Поясните полученные результаты.
Решение
Индекс переменного состава:
Iсп=P1:P0=∑Р1q1/∑q1:∑ Р0q0/∑q0=∑Р1q1/∑q1*∑q0/∑ Р0q0
Где P1 и P0-соответсвенно средняя цена в отчетном и базисном периодах.
Iсп=(40,1*1210+36,85*2565)*(3842/38,8–1254+35,6*2565)=1,033
Повышение средней цены в отчетном периоде составило 3,3%, повышение средней
Цены может быть вызвано повышением цен на отдельные виды продукции и ростом удельного веса продукции с более высокой ценой.
Индекс цен постоянного (фиксированного) состава:
Iфс=∑Р1q1/∑q1: ∑ Р0q1/∑q1=∑Р1q1/∑q1*∑q1/∑ Р0q1
Iфс=(40,1*1210+36,85*2632)/3842*(3842/38,8*1210+35,6*2632)=1,035
Индекс структурных сдвигов:
Iстр=∑Р0q1/∑q1:∑ Р0q0/∑q0=(∑Р0q1/∑q1)*(∑q0/∑ Р0q0)
Iстр=(38,8*1210+35,6*2632)/3842*(3819/38,8*1254+35,6*2565)=0,998
Взаимосвязь трех индексов:
Iсп= Iфс* Iстр
1,033=0,998*1,035
В среднем цены на батоны в отчетном периоде повысились на 3,3%, за счет повышения цен на отдельные виды батонов средние цены повысились на 3,5%, за счет изменения структуры производства продукции по разным видам батонов цены снизились на 0,2%
Задача №29
Стоимость фактически выпущенной продукции в действующих ценах составила:
| Вид продукции | Стоимость произведенной продукции, тыс. руб. | Изменение цен в отчетном по сравнению с базисным, % | |
| Базисная | Отчетная | ||
| Макароны | 104 | 106 | +10 |
| Вермишель | 1616 | 1611 | -5 |
| Лапша | 1038 | 1044 | Без изменения |
Исчислите:
1. Общий индекс стоимость продукции
2. Индивидуальные и общие индексы цен и абсолютную сумму экономии (или перерасхода) от изменения цен
3. Общий индекс физического объема продукции, используя взаимосвязь всех трех индексов
4. Поясните полученные результаты.
Iq=∑qi*p0/∑q0*p0
q1=ip*q0, тогда Iq= ip*q0*р0/∑q0*p0
Где Р0q0 – стоимость продукции в базисном периоде, руб.;
Ip-индивидуальный индекс объема продукции;
| Виды продукции | Изменение количества произведенной продукции в отчетном периоде по сравнению с базисным, % | Индивидуальный индекс цен |
| Макароны | +10 | Iq=(100+10)/100=1,1 |
| Вермишель | -5 | Iq=(100–5)/100=0,95 |
| Лапша | Без изменения | Iq=(100–0)/100=1 |
Общий индекс товарооборота в фактических ценах равен
(106+1611+1044)/(104+1616+1038)=1,001
Общий индекс цен равен
2761/(106/1,1*1)+(1611/0,95*1)+(1044/1*1)=0,97
Общий индекс физического объема товарооборота, используя взаимосвязь индексов, определим как:
=1,001/0,97=1,032=103,2%
Выводы.
За отчетный год цены снизились на 3%.
За отчетный год физический объем товарооборота вырос на 3,2%.
За отчетный год товарооборот в фактических ценах вырос на 0,1%.
diplomba.ru
 Для моментального ряда «Б» с равностоящими уровнями средний уровень ряда можно вычислить по формуле средней хронологической: Y=(1/2Y0+Y1+Y2+…1/2Yn)/n-1 Y=(1/2*402+406+403+1/2408)/4–1=405 человек Среднесписочная численность рабочих за 1 квартал составила 405 человек. Задача №19 Себестоимость и объем производства Советского шампанского характеризуется следующими данными:
Для моментального ряда «Б» с равностоящими уровнями средний уровень ряда можно вычислить по формуле средней хронологической: Y=(1/2Y0+Y1+Y2+…1/2Yn)/n-1 Y=(1/2*402+406+403+1/2408)/4–1=405 человек Среднесписочная численность рабочих за 1 квартал составила 405 человек. Задача №19 Себестоимость и объем производства Советского шампанского характеризуется следующими данными: 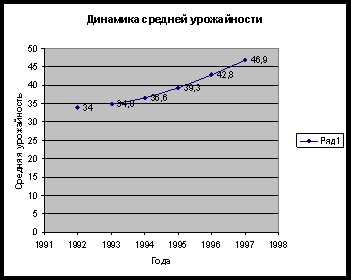 Для моментального ряда «Б» с равностоящими уровнями средний уровень ряда можно вычислить по формуле средней хронологической: Y=(1/2Y0+Y1+Y2+…1/2Yn)/n-1 Y=(1/2*402+406+403+1/2408)/4–1=405 человек Среднесписочная численность рабочих за 1 квартал составила 405 человек. Задача №19 Себестоимость и объем производства Советского шампанского характеризуется следующими данными:
Для моментального ряда «Б» с равностоящими уровнями средний уровень ряда можно вычислить по формуле средней хронологической: Y=(1/2Y0+Y1+Y2+…1/2Yn)/n-1 Y=(1/2*402+406+403+1/2408)/4–1=405 человек Среднесписочная численность рабочих за 1 квартал составила 405 человек. Задача №19 Себестоимость и объем производства Советского шампанского характеризуется следующими данными: