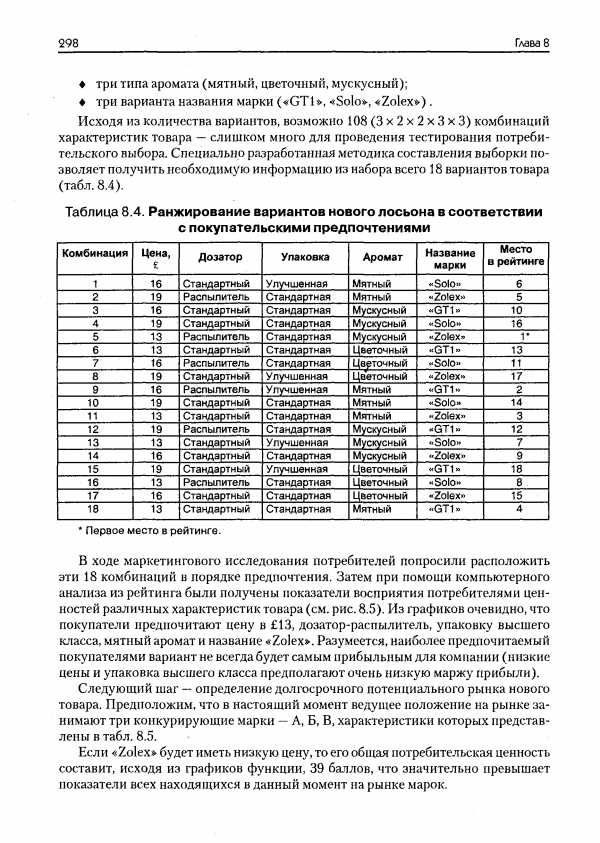
5.6. Построение вариационного ряда. Виды рядов. Ранжирование данных. Ранжирование это в статистике
5.6. Построение вариационного ряда. Виды рядов. Ранжирование данных
Первым этапом статистического изучения вариации являются построение вариационного ряда — упорядоченного распределения единиц совокупности по возрастающим (чаще) или по убывающим (реже) значениям признака и подсчет числа единиц с тем или иным значением признака.
Существуют три формы вариационного ряда: ранжированный, дискретный, интервальный. Вариационный ряд часто называют рядом распределения. Этот термин употребляется при изучении вариации как количественных, так и неколичественных признаков. Ряд распределения представляет собой структурную группировку (гл. 6).
Ранжированный ряд — это перечень отдельных единиц совокупности в порядке возрастания (убывания) изучаемого признака.
Ниже приведены сведения о крупных банках Санкт-Петербурга,ранжированных по размерам собственного капитала на
01.10.1999 г. |
|
|
Название банка | Собственный капитал, млн руб. | |
Балтонэксим банк |
| 169 |
Банк «Санкт-Петербург» | 237 | |
Петровский |
| 268 |
Балтийский |
| 290 |
Промстройбанк |
| 1007 |
Если численность единиц совокупности достаточно велика, ранжированный ряд становится громоздким, а его построение, даже с помощью компьютера, занимает длительное время. В таких случаях вариационный ряд строится с помощью группировки единиц совокупности по значениям изучаемого признака.
Определение числа групп
Число групп в дискретном вариационном ряду определяется числом реально существующих значений варьирующего признака. Если признак принимает дискретные значения, но их число очень велико (например, поголовье скота на 1 января года в разных сельскохозяйственных предприятиях может составить от нуля до десятков тысяч голов), то строится интервальный вариационный ряд. Интервальный вариационный ряд строится и для изучения признаков, которые могут принимать любые, как целые, так и дробные значения в области своего существования. Таковы, например, рентабельность реализованной продукции, себестоимость единицы продукции, доход на одного жителя города, доля лиц с высшим образованием среди населения разных территорий и вообще все вторичные признаки, значения которых рассчитываются путем деления величины одного первичного признака на величину другого (см. гл. 3).
Интервальный вариационный ряд представляет собой таблицу, состоящую из двух граф (или строк) — интервалов признака, вариация которого изучается, и числа единиц совокупности, попадающих в данный интервал (частот), или долей этого числа от общей численности совокупности (частостей).
Наиболее часто используются два вида интервальных вариационных рядов: равноинтервальный и равночастотный. Равноинтервальный ряд применяется, если вариация признака не очень сильна, т.е. для однородной совокупности, распределение которой по данному признаку близко к нормальному закону. (Такой ряд представлен в табл. 5.6.) Равночастотный ряд применяется, если вариация признака очень сильна, однако распределение не является нормальным, а, например, гиперболическим (табл. 5.5).
При построении равноинтервального ряда число групп выбирается так, чтобы в достаточной мере отразились разнообразие значений признака в совокупности и в то же время закономерность распределения, его форма не искажалась случайными колебаниями частот. Если групп будет слишком мало, не проявится закономерность вариации; если групп будет чрезмерно много, случайные скачки частот исказят форму распределения.
143

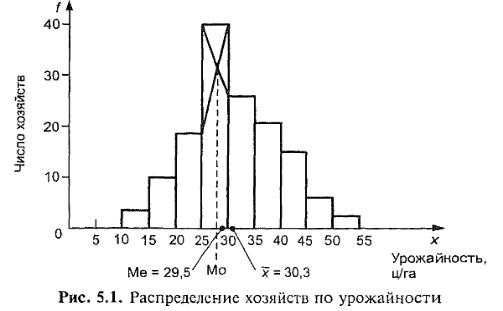
Границы интервалов могут указываться разным образом: верхняя граница предыдущего интервала повторяет нижнюю границу следующего, как показано в табл. 5.5, или не повторяет.
В последнем случае второй интервал будет обозначен как 15,1—20,третий — как20,1—25и т.д., т.е. предполагается, что все значения урожайности обязательно округлены до одной десятой. Кроме того, возникает нежелательное осложнение с серединой интервала15,1—20,которая, строго говоря, уже будет равна не 17,5, а 17,55; соответственно при замене округленного интервала40—60на40,1—60вместо округленного значения его середины 50 получим 50,5. Поэтому предпочтительнее оставить интервалы с повторяющейся округленной границей и договориться, что единицы совокупности, имеющие значение признака, равное границе интервала, включаются в тот интервал, где это точное значение впервые указывается. Так, хозяйство, имеющее урожайность, равную 15 ц/га, включается в первую группу, значение 20 ц/га
— во вторую и т.д.
Равночастотный вариационный ряд необходим при очень сильной вариации признака потому, что при равноинтервальном распределении большая часть единиц совокупности ока-
145

Таблица 5.5 Распределение 100 банков России по балансовой оценке активов на 01.01.2000 г.
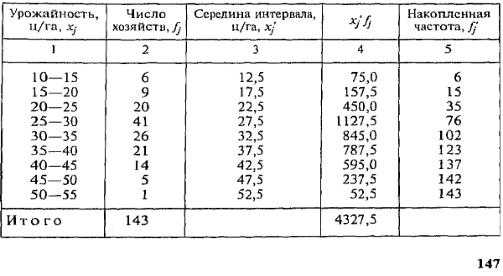
Границы интервалов при равночастотном распределении — это фактические величины активов первого, десятого, одиннадцатого, двадцатого и так далее банков.
Графическое изображение вариационного ряда
Существенную помощь в анализе вариационного ряда и его свойств оказывает графическое изображение. Интервальный ряд изображается столбиковой диаграммой, в которой основания столбиков, расположенные на оси абсцисс, — это интервалы значений варьирующего признака, а высота столбиков — частоты, соответствующие масштабу по оси ординат. Графическое изображение распределения хозяйств области по урожайности зерновых культур приведено на рис. 5.1. Диаграмма этого рода часто называется гистограммой (гр. histos — ткань).
Данные табл. 5.6 и рис. 5.1 показывают характерную для многих признаков форму распределения: чаще встречаются значения средних интервалов признака, реже — крайние, малые и большие значения признака. Форма этого распределения близка к рассматриваемому в курсе математической статистики закону нормального распределения. Великий русский математик А. М. Ляпунов (1857—1918)доказал, что норТаблица 5.6 Распределение хозяйств области по урожайности зерновых культур

мальное распределение образуется, если на варьирующую переменную влияет большое число факторов, ни один из которых не имеет преобладающего влияния. Случайное сочетание множества примерно равных факторов, влияющих на вариации урожайности зерновых культур, как природных, так и агротехнических, экономических, создает близкое к нормальному закону распределения распределение хозяйств области по урожайности.
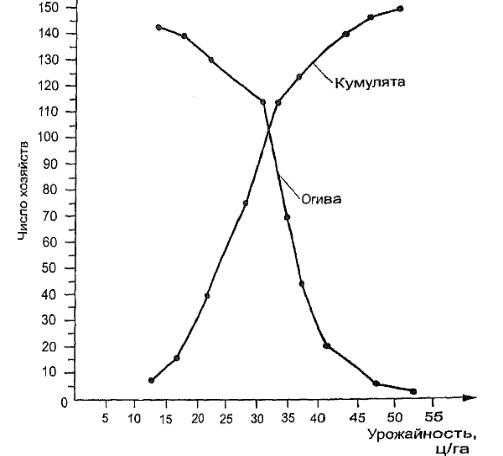
Рис. 5.2. Кумулята и огива распределения хозяйств по урожайности Такой ряд называется кумулятивным. Можно построить
кумулятивное распределение «не меньше, чем», а можно «больше, чем». В первом случае график кумулятивного распределения называется кумулятой, во втором — огивой (рис. 5.2).
Плотность распределения
Если приходится иметь дело с вариационным рядом с неравными интервалами, то для сопоставимости нужно частоты, или частости, привести к единице интервала. Полученное отношение называется плотностью распределения:
149
studfiles.net
Ранжирование и группировка данных в статистике
Задача №1
Работа двадцати предприятий пищевой промышленности
В отчетном периоде характеризуется следующими данными:
Таблица 1
1-Среднегодовая стоимость промышленно-производственных ОФ, млн. руб.
2-Товарная продукция в сопоставимых оптовых ценах предприятия, млн. руб.
H=Xmax-Xmin/n
2. Определите по каждой группе:
– число заводов;
– стоимость ОПФ-всего и в среднем на один завод:
– стоимость ТП-всего и в среднем на один завод.
Результаты представьте в табличном виде, проанализирйте их и сделайте выводы
H=20–10/5=2
где xmax , xmin – максимальное и минимальное значения кредитных вложений
Определим теперь интервалы групп (xi , xi +1 ):
1 группа: 10–12 млн. руб.
2 группа: 12–14 млн. руб.
3 группа: 14–16 млн. руб.
4 группа: 16–18 млн. руб.
5 группа: 18–20 млн. руб.
Далее упорядочим исходную таблицу по возрастанию ОФ
На основе полученной таблицы определим требуемые показатели. Результаты представим в виде групповой таблицы:
Таблица 1.2
Задача №4
Имеются данные по трем предприятиям, вырабатывающие однородную продукцию:
Обоснуйте выбор формул средней и по этим формулам определите средние затраты времени на продукцию по трем предприятиям в базисном и отчетном годах, сравните полученные результаты и сделайте выводы.
Решение
Средние затраты времени определяются по формуле:
,где V – затраты времени на единицу продукции; S – затраты времени на всю продукцию. Определим средние затраты времени на 3 предприятиях. Т.к. заданы затраты времени на единицу продукции и затраты времени на всю продукцию то:
Данная формула называется средней гармонической взвешенной.
Подставив в последнюю формулу известные значения, получим средние затраты времени на производство на предприятиях в отчетном году:
P=19975+22248+13462/(19972/0,34+22248/0,48+13462/0,53)= 0,427 ч
Определим средние затраты времени на производства продукции в базисном году:
Данная формула называется средней арифметической взвешенной.
Подставив в последнюю формулу известные значения, получим затраты времени на производство продукции в базисном году:
P=(0,34*52,1+0,48*45,7+0,53*23,8)/(52,1+45,7+23,8)= 0,4298=0,43 ч
Вывод: средние затраты времени на производство продукции в базисном и отчетном году отличаются на (0,43–0,427)*100%= 0,003*100%=0,3%
Задача №9
В результате контрольной выборочной проверки расфасовки чая осуществлена 25% механическая выборка по способу бесповторного отбора, в результате которой получено следующее распределение пачек чая по массе:
По результатам выборочного обследования определите:
1. Среднюю массу пачки чая;
2. Дисперсию и среднее квадратичное отклонение;
3. Коэффициент вариации;
4. С вероятностью 0,997 возможные пределы средней массы пачки чая во всей партии продукции;
5. С вероятностью 0,954 возможные пределы удельного веса пачек чая с массой до 49 г. и свыше 52 г. во всей продукции.
Решение
Приведем группировку к стандартному виду с равными интервалами и найдем середины интервалов для каждой группы. Результаты представлены в таблице:
Среднюю массу пачки чая находим по формуле средней арифметической взвешенной:
Подставив в последнюю формулу известные значения, получим среднюю массу пачки чая:
Y=(48.5*17+49.5*52+50.5*21+51.5*7+52.5*3)/100=49.77 г.
Дисперсия определяется по формуле:
.Подставив в последнюю формулу известные значения, получим дисперсию:
s²=((48,5–49,77)²*17+(49,5–49,77)²*52+(50,5–49,77)²*21+(51,5–49,77)²*7+(52,5–49,77)²)/100=85,71/100=0,8571 г.²
Среднее квадратическое отклонение равно:
S=√s²=√0,8571=0,93 г.
Коэффициент вариации определяется по формуле:
V=s/y=0,93/49,77= 0,019*100%=1,9%
Рассчитаем сначала предельную ошибку выборки. Так при вероятности p = 0,997 коэффициент доверия t = 3. Поскольку дана 25%-ная случайная бесповторная выборка, то
n/N=0,25
где n – объем выборочной совокупности, N – объем генеральной совокупности.
Считаем также, что дисперсия s²=0,8571. Тогда предельная ошибка выборочной средней равна:
Δy=t*√σ²/n*(1-n/N)=3*√0,8571/100*(1–0,25)=0,24 г.
Определим теперь возможные границы, в которых ожидается средняя масса чая на 1 пакетик чая
y – Δy≤my≤y+ Δy
49,77–0,8571≤my≤49,77+0,8571
48,9129≤my≤50,6271
Т.е., с вероятностью 0,997 можно утверждать, что масса чая на 1 пакетик находится в пределах 48,9129 до 50,6271
Выборочная доля w удельного веса пачек чая с массой до 49 г. и свыше 52 г. во всей продукции с вероятностью 0,954 равна.
W=(48+3)/100=0,51=51 г.
Учитывая, что при вероятности p = 0,954 коэффициент доверия t = 2, вычислим предельную ошибку выборочной доли:
Δw= t*√(w*(1-w)/n) *(1-n/N)=2*√(0,51*(1–0,51)/100)*(1–0,25)=0,086г
или
Пределы доли признака во всей совокупности:
51–8,6≤d≤51+8,6
42,4≤d≤59,6
Таким образом, с вероятностью 0,954 можно утверждать, что границы удельного веса пачек чая находятся в пределах42,4г до 59,6г во всей продукции.
mirznanii.com
Правила ранжирования
"-//W3C//DTD HTML 3.2 Final//RU\">
-
Меньшему значению начисляется меньший ранг.
Наименьшему значению начисляется ранг 1.
Наибольшему значению начисляется ранг, соответствующий количеству ранжируемых значений. Например, если n=7, то наибольшее значение получит ранг 7, за возможным исключением для тех случаев, которые предусмотрены правилом 2.
-
В случае, если несколько значений равны, им начисляется ранг, представляющий собой среднее значение из тех рангов, которые они получили бы, если бы не были равны.
Например, 3 наименьших значения равны 10 секундам.
Если бы мы измеряли время более точно, то эти значения могли бы различаться и составили бы, скажем, 10.2 сек; 10.5 сек; 10.7 сек. В этом случае они получили бы ранги, соответственно, 1, 2 и 3. Но поскольку полученные нами значения равны, каждое из них получает средний ранг:
Допустим, следующие 2 значения равны 12 сек. Они должны были бы получить ранги 4 и 5, но, поскольку они равны, то получают средний ранг:
и т.д. -
Общая сумма рангов должна совпадать с расчетной, которая определяется по формуле:
где N - общее количество ранжируемых наблюдений (значений).Несовпадение реальной и расчетной сумм рангов будет свидетельствовать об ошибке, допущенной при начислении рангов или их суммировании. Прежде чем продолжить работу, необходимо найти ошибку и устранить ее.
Источник: Сидоренко Е. В. Методы математической обработки в психологии - CПб.: ООО "Речь", 2001, с.52.
© Куксов А. Ю., 2005
qxov.narod.ru
Статистическая сводка и группировка. Статистический ряд распределения. Примеры решения задач
Важнейшим этапом исследования социально-экономических явлений и процессов является систематизация первичных данных и получение на этой основе сводной характеристики всего объекта при помощи обобщающих показателей, что достигается путем сводки и группировки первичного статистического материала.
Статистическая сводка - это комплекс последовательных операций по обобщению конкретных единичных фактов, образующих совокупность, для выявления типичных черт и закономерностей, присущих изучаемому явлению в целом. Проведение статистической сводки включает следующие этапы:
- выбор группировочного признака;
- определение порядка формирования групп;
- разработка системы статистических показателей для характеристики групп и объекта в целом;
- разработка макетов статистических таблиц для представления результатов сводки.
Статистической группировкой называется расчленение единиц изучаемой совокупности на однородные группы по определенным существенным для них признакам. Группировки являются важнейшим статистическим методом обобщения статистических данных, основой для правильного исчисления статистических показателей.
Различают следующие виды группировок: типологические, структурные, аналитические. Все эти группировки объединяет то, что единицы объекта разделены на группы по какому-либо признаку.
Группировочным признаком называется признак, по которому проводится разбиение единиц совокупности на отдельные группы. От правильного выбора группировочного признака зависят выводы статистического исследования. В качестве основания группировки необходимо использовать существенные, теоретически обоснованные признаки (количественные или качественные).
Количественные признаки группировки имеют числовое выражение (объем торгов, возраст человека, доход семьи и т. д.), а качественные признаки группировки отражают состояние единицы совокупности (пол, семейное положение, отраслевая принадлежность предприятия, его форма собственности и т. д.).
После того, как определено основание группировки следует решить вопрос о количестве групп, на которые надо разбить исследуемую совокупность. Число групп зависит от задач исследования и вида показателя, положенного в основание группировки, объема совокупности, степени вариации признака.
Например, группировка предприятий по формам собственности учитывает муниципальную, федеральную и собственность субъектов федерации. Если группировка производится по количественному признаку, то тогда необходимо обратить особое внимание на число единиц исследуемого объекта и степень колеблемости группировочного признака.
Когда определено число групп, то следует определить интервалы группировки. Интервал - это значения варьирующего признака, лежащие в определенных границах. Каждый интервал имеет свою величину, верхнюю и нижнюю границы или хотя бы одну из них.
Нижней границей интервала называется наименьшее значение признака в интервале, а верхней границей - наибольшее значение признака в интервале. Величина интервала представляет собой разность между верхней и нижней границами.
Интервалы группировки в зависимости от их величины бывают: равные и неравные. Если вариация признака проявляется в сравнительно узких границах и распределение носит равномерный характер, то строят группировку с равными интервалами. Величина равного интервала определяется по следующей формуле:
где Хmax, Хmin - максимальное и минимальное значения признака в совокупности; n - число групп.
Простейшая группировка, в которой каждая выделенная группа характеризуется одним показателем представляет собой ряд распределения.
Статистический ряд распределения - это упорядоченное распределение единиц совокупности на группы по определенному признаку. В зависимости от признака, положенного в основу образования ряда распределения, различают атрибутивные и вариационные ряды распределения.
Атрибутивными называют ряды распределения, построенные по качественным признакам, то есть признакам, не имеющим числового выражения (распределение по видам труда, по полу, по профессии и т.д.). Атрибутивные ряды распределения характеризуют состав совокупности по тем или иным существенным признакам. Взятые за несколько периодов, эти данные позволяют исследовать изменение структуры.
Вариационными рядами называют ряды распределения, построенные по количественному признаку. Любой вариационный ряд состоит из двух элементов: вариантов и частот. Вариантами называются отдельные значения признака, которые он принимает в вариационном ряду, то есть конкретное значение варьирующего признака.
Частотами называются численности отдельных вариант или каждой группы вариационного ряда, то есть это числа, которые показывают, как часто встречаются те или иные варианты в ряду распределения. Сумма всех частот определяет численность всей совокупности, ее объем. Частостями называются частоты, выраженные в долях единицы или в процентах к итогу. Соответственно сумма частостей равна 1 или 100%.
В зависимости от характера вариации признака различают три формы вариационного ряда: ранжированный ряд, дискретный ряд и интервальный ряд.
Ранжированный вариационный ряд - это распределение отдельных единиц совокупности в порядке возрастания или убывания исследуемого признака. Ранжирование позволяет легко разделить количественные данные по группам, сразу обнаружить наименьшее и наибольшее значения признака, выделить значения, которые чаще всего повторяются.
Дискретный вариационный ряд характеризует распределение единиц совокупности по дискретному признаку, принимающему только целые значения. Например, тарифный разряд, количество детей в семье, число работников на предприятии и др.
Если признак имеет непрерывное изменение, которые в определенных границах могут принимать любые значения («от - до»), то для этого признака нужно строить интервальный вариационный ряд. Например, размер дохода, стаж работы, стоимость основных фондов предприятия и др.
Примеры решения задач по теме «Статистическая сводка и группировка»
Задача 1. Имеется информация о количестве книг, полученных студентами по абонементу за прошедший учебный год.
Построить ранжированный и дискретный вариационные ряды распределения, обозначив элементы ряда.
Решение
Данная совокупность представляет собой множество вариантов количества получаемых студентами книг. Подсчитаем число таких вариантов и упорядочим в виде вариационного ранжированного и вариационного дискретного рядов распределения.
Задача 2. Имеются данные о стоимости основных фондов у 50 предприятий, тыс. руб.
Построить ряд распределения, выделив 5 групп предприятий (с равными интервалами).
Решение
Для решения выберем наибольшее и наименьшее значения стоимости основных фондов предприятий. Это 30,0 и 10,2 тыс. руб.
Найдем размер интервала: h = (30,0-10,2):5= 3,96 тыс. руб.
Тогда в первую группу будут входить предприятия, размер основных фондов которых составляет от 10,2 тыс. руб. до 10,2+3,96=14,16 тыс. руб. Таких предприятий будет 9. Во вторую группу войдут предприятия, размер основных фондов которых составит от 14,16 тыс. руб. до 14,16+3,96=18,12 тыс. руб. Таких предприятий будет 16. Аналогично найдем число предприятий, входящих в третью, четвертую и пятую группы.
Полученный ряд распределения поместим в таблицу.
Задача 3. По ряду предприятий легкой промышленности получены следующие данные:
Произведите группировку предприятий по числу рабочих, образуя 6 групп с равными интервалами. Подсчитайте по каждой группе:
1. число предприятий 2. число рабочих 3. объем произведенной продукции за год 4. среднюю фактическую выработку одного рабочего 5. объем основных средств 6. средний размер основных средств одного предприятия 7. среднюю величину произведенной продукции одним предприятием
Результаты расчета оформите в таблицы. Сделайте выводы.
Решение
Для решения выберем наибольшее и наименьшее значения среднесписочного числа рабочих на предприятии. Это 43 и 256.
Найдем размер интервала: h = (256-43):6 = 35,5
Тогда в первую группу будут входить предприятия, среднесписочное число рабочих на которых составляет от 43 до 43+35,5=78,5 человек. Таких предприятий будет 5. Во вторую группу войдут предприятия, среднесписочное число рабочих на которых составит от 78,5 до 78,5+35,5=114 человек. Таких предприятий будет 12. Аналогично найдем число предприятий, входящих в третью, четвертую, пятую и шестую группы.
Полученный ряд распределения поместим в таблицу и вычислим необходимые показатели по каждой группе:
Вывод: Как видно из таблицы, вторая группа предприятий является самой многочисленной. В нее входят 12 предприятий. Самыми малочисленными являются пятая и шестая группы (по два предприятия). Это самые крупные предприятия (по числу рабочих).
Поскольку вторая группа самая многочисленная, объем произведенной продукции за год предприятиями этой группы и объем основных средств значительно выше других. Вместе с тем средняя фактическая выработка одного рабочего на предприятиях этой группы наибольшей не является. Здесь лидируют предприятия четвертой группы. На эту группу приходится и довольно большой объем основных средств.
В заключении отметим, что средний размер основных средств и средняя величина произведенной продукции одного предприятия прямо пропорциональны размерам предприятия (по числу рабочих).
Другие статьи по данной теме:
Список использованных источников
- Белобородова С.С. и др. Теория статистики: Типовые задачи с контрольными заданиями. Екатеринбург: Изд-во Урал. гос. экон. ун-та, 2001;
- Минашкин В.Г. и др. Курс лекций по теории статистики. / Московский международный институт эконометрики, информатики, финансов и права. - М., 2003;
- Сизова Т.М. Статистика: Учебное пособие. – СПб.: СПб ГУИТМО, 2005;
- Фёдорова Л.Н., Фёдорова А.Е. Методические указания по написанию контрольной работы по курсу «Статистика» для студентов экономических специальностей: УрГЭУ, 2007;
www.ekonomika-st.ru
Построение вариационного ряда. Виды рядов. Ранжирование данных
⇐ ПредыдущаяСтр 13 из 38Следующая ⇒
Первым этапом статистического изучения вариации являются построение вариационного ряда — упорядоченного распределения единиц совокупности по возрастающим (чаще) или по убывающим (реже) значениям признака и подсчет числа единиц с тем или иным значением признака.
Существуют три формы вариационного ряда: ранжированный, дискретный, интервальный. Вариационный ряд часто называют рядом распределения. Этот термин употребляется при изучении вариации как количественных, так и неколичественных признаков. Ряд распределения представляет собой структурную группировку (гл. 6).
Ранжированный ряд — это перечень отдельных единиц совокупности в порядке возрастания (убывания) изучаемого признака.
Ниже приведены сведения о крупных банках Санкт-Петербурга, ранжированных по размерам собственного капитала на 01.10.1999 г.
Название банка Собственный капитал, млн руб.
Балтонэксим банк 169
Банк «Санкт-Петербург» 237
Петровский 268
Балтийский 290
Промстройбанк 1007
Если численность единиц совокупности достаточно велика, ранжированный ряд становится громоздким, а его построение, даже с помощью компьютера, занимает длительное время. В таких случаях вариационный ряд строится с помощью группировки единиц совокупности по значениям изучаемого признака.
142
Определение числа групп
Число групп в дискретном вариационном ряду определяется числом реально существующих значений варьирующего признака. Если признак принимает дискретные значения, но их число очень велико (например, поголовье скота на 1 января года в разных сельскохозяйственных предприятиях может составить от нуля до десятков тысяч голов), то строится интервальный вариационный ряд. Интервальный вариационный ряд строится и для изучения признаков, которые могут принимать любые, как целые, так и дробные значения в области своего существования. Таковы, например, рентабельность реализованной продукции, себестоимость единицы продукции, доход на одного жителя города, доля лиц с высшим образованием среди населения разных территорий и вообще все вторичные признаки, значения которых рассчитываются путем деления величины одного первичного признака на величину другого (см. гл. 3).
Интервальный вариационный ряд представляет собой таблицу, состоящую из двух граф (или строк) — интервалов признака, вариация которого изучается, и числа единиц совокупности, попадающих в данный интервал (частот), или долей этого числа от общей численности совокупности (частостей).
Наиболее часто используются два вида интервальных вариационных рядов: равноинтервальный и равночастотный. Равноинтервальный ряд применяется, если вариация признака не очень сильна, т.е. для однородной совокупности, распределение которой по данному признаку близко к нормальному закону. (Такой ряд представлен в табл. 5.6.) Равночастотный ряд применяется, если вариация признака очень сильна, однако распределение не является нормальным, а, например, гиперболическим (табл. 5.5).
При построении равноинтервального ряда число групп выбирается так, чтобы в достаточной мере отразились разнообразие значений признака в совокупности и в то же время закономерность распределения, его форма не искажалась случайными колебаниями частот. Если групп будет слишком мало, не проявится закономерность вариации; если групп будет чрезмерно много, случайные скачки частот исказят форму распределения.
Границы интервалов могут указываться разным образом: верхняя граница предыдущего интервала повторяет нижнюю границу следующего, как показано в табл. 5.5, или не повторяет.
В последнем случае второй интервал будет обозначен как 15,1—20, третий — как 20,1—25 и т.д., т.е. предполагается, что все значения урожайности обязательно округлены до одной десятой. Кроме того, возникает нежелательное осложнение с серединой интервала 15,1—20, которая, строго говоря, уже будет равна не 17,5, а 17,55; соответственно при замене округленного интервала 40—60 на 40,1—60 вместо округленного значения его середины 50 получим 50,5. Поэтому предпочтительнее оставить интервалы с повторяющейся округленной границей и договориться, что единицы совокупности, имеющие значение признака, равное границе интервала, включаются в тот интервал, где это точное значение впервые указывается. Так, хозяйство, имеющее урожайность, равную 15 ц/га, включается в первую группу, значение 20 ц/га — во вторую и т.д.
Равночастотный вариационный ряд необходим при очень сильной вариации признака потому, что при равноинтерваль-ном распределении большая часть единиц совокупности ока-
Таблица 5.5
Распределение 100 банков России по балансовой оценке активов на 01.01.2000 г.

Границы интервалов при равночастотном распределении — это фактические величины активов первого, десятого, одиннадцатого, двадцатого и так далее банков.
Графическое изображение вариационного ряда
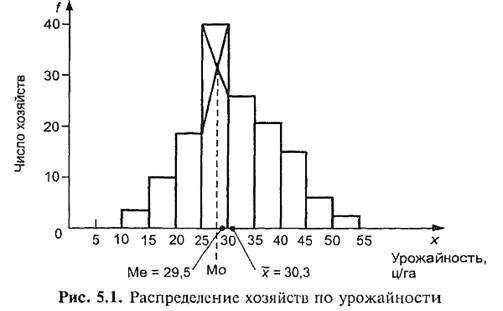
Существенную помощь в анализе вариационного ряда и его свойств оказывает графическое изображение. Интервальный ряд изображается столбиковой диаграммой, в которой основания столбиков, расположенные на оси абсцисс, — это интервалы значений варьирующего признака, а высота столбиков — частоты, соответствующие масштабу по оси ординат. Графическое изображение распределения хозяйств области по урожайности зерновых культур приведено на рис. 5.1. Диаграмма этого рода часто называется гистограммой (гр. histos — ткань).
Данные табл. 5.6 и рис. 5.1 показывают характерную для многих признаков форму распределения: чаще встречаются значения средних интервалов признака, реже — крайние, малые и большие значения признака. Форма этого распределения близка к рассматриваемому в курсе математической статистики закону нормального распределения. Великий русский математик А. М. Ляпунов (1857—1918) доказал, что нор-
Таблица 5.6 Распределение хозяйств области по урожайности зерновых культур

мальное распределение образуется, если на варьирующую переменную влияет большое число факторов, ни один из которых не имеет преобладающего влияния. Случайное сочетание множества примерно равных факторов, влияющих на вариации урожайности зерновых культур, как природных, так и агротехнических, экономических, создает близкое к нормальному закону распределения распределение хозяйств области по урожайности.

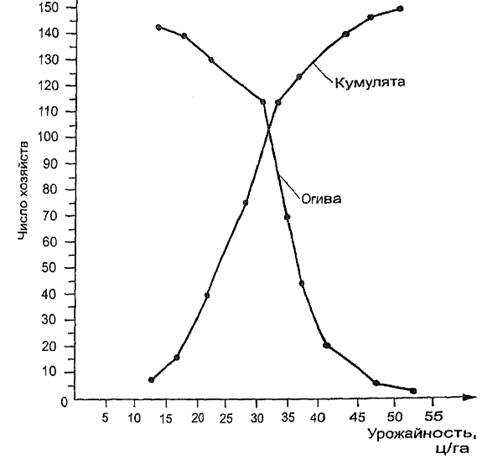 Рис. 5.2. Кумулята и огива распределения хозяйств по урожайности
Рис. 5.2. Кумулята и огива распределения хозяйств по урожайности
Такой ряд называется кумулятивным. Можно построить кумулятивное распределение «не меньше, чем», а можно «больше, чем». В первом случае график кумулятивного распределения называется кумулятой, во втором — огивой (рис. 5.2).
Плотность распределения
Если приходится иметь дело с вариационным рядом с неравными интервалами, то для сопоставимости нужно частоты, или частости, привести к единице интервала. Полученное отношение называется плотностью распределения:
Плотность распределения используется как для расчета обобщающих показателей, так и для графического изображения вариационных рядов с неравными интервалами.
Читайте также:
lektsia.com
1.4 Ранжирование выборочных данных, вычисление моды и медианы. Основные понятия математической статистики
Похожие главы из других работ:
Анализ интервального вариационного ряда "Численность экономически активного населения по субъектам Российской Федерации в 2012 году"
1.1 Ранжирование исходных данных, определение наличия выбросов
Первым этапом статистического изучения вариации являются построение вариационного ряда - упорядоченного распределения единиц совокупности по возрастающим (чаще) или по убывающим (реже) значениям признака и подсчет числа единиц с тем или иным...
Выборочное наблюдение
3 Распространение выборочных данных на генеральную совокупность
Выборочное наблюдение проводится в целях распространения выводов, полученных по данным выборки, на генеральную совокупность. Пределы, в которых находятся значения характеристик в генеральной совокупности при заданном уровне вероятности...
Исследование государственных служащих МНС РФ №3 по Ярославской области
4.1 Расчет средней величины, моды и медианы показателей ряда распределения, построенного по вариационному признаку
1) Средняя величина: X= (?Xi*Fi)/?Fi, где ?Xi - сумма значений; Fi - частота повтора Xi. Найдем середины интервалов Xс1 = (18+22)/2=20; Xc2= (22+30)/2=26; Xc3= (30+40)/2=35; Xc4= (40+50)/2=45; Xc5= (50+60)/2=55. X= (20*7+26*8+35*16+45*14+55*5)/50=36...
Исследование государственных служащих МНС РФ №3 по Ярославской области
4.3 Расчет средней величины, моды и медианы показателей ряда распределения, построенного по вариационному признаку
Ряд распределения опрошенных по стажу работы № группы Стаж работы Количество человек % к итогу накопленные частоты I нет стажа 7 14 7 II 1-3 лет 9 18 16 III 3-5 лет 7 14 23 IV 5-10 лет 15 30 38 V 10-15...
Основные понятия математической статистики
1.2 Вычисление основных числовых характеристик выборочных наблюдений
1.Среднее арифметическое случайной величины Х i = = 4,06 2. Среднее линейное отклонение d = = = 0,79 3. Смещённая оценка дисперсии случайной величины Х 4. Несмещённая оценка дисперсии случайной величины Х D[X] = ??2 = 2 = = 0,97 5...
Применение статистических методов при проведении качественного анализа выборочной совокупности по данным показателям деятельности банков Российской Федерации
4.5Оценка параметров генеральной совокупности на основе выборочных данных
Рассчитаем среднюю ошибку для выборки по объему вложений в ценные бумаги: (млн.руб.) Найдем предельную ошибку для выборки по объемам вложений в ценные бумаги, принимая вероятность равной 0,95. По таблице находим коэффициент доверия t, равный 1,96...
Проведение качественного анализа выборочной совокупности банков
1.5 Оценка параметров генеральной совокупности на основе выборочных данных
совокупность банк корреляция регрессия Расхождения между выборочной и генеральной совокупностей измеряется средней ошибки выборки () характеризует меру отклонения выборочных показателей от аналогичных показателей генеральной совокупности...
Расчет и моделирование статистических данных
1.1.4 Расчет моды и медианы
Особым видом средних величин являются структурные средние. Они применяются для изучения внутреннего строения и структуры рядов распределения значений признака. К таким показателям относятся мода и медиана...
Ряды распределения: виды, графическое изображение, формы распределения
1.4 Расчет моды и медианы
Особым видом средних величин являются структурные средние. Они применяются для изучения внутреннего строения и структуры рядов распределения значений признака. К таким показателям относятся мода и медиана...
Статистика
Оценка параметров генеральной совокупности на основе выборочных данных
В реальных условиях для наблюдения какого-то признака практически никогда не анализируется вся совокупность в целом. Вместо этого применяют выборочное наблюдение...
Статистическая обработка данных
4. Результаты ранжирования выборочных данных и вычисление моды и медианы
Используя исходные данные, записываем все заданные значения выборки в виде неубывающей последовательности значений случайной величины Х, которые представлены в таблице 4.1. Таблица 4.1 Ранжированный ряд 6,9275 9,5319 10,6512 11,7579 12,4240 13,3734 7...
Статистическая обработка данных. Статистика денежного обращения
1.2 Вычисление основных выборочных характеристик по заданной выборке
1. Среднее арифметическое случайной величины X - представляет собой обобщенную количественную характеристику признаков статистической совокупности в конкретных условиях места и времени 16,0515 2...
Статистическая обработка данных. Статистика денежного обращения
1.4 Результаты ранжирования выборочных данных вычисления моды и медианы
Используя исходные данные, записываем все заданные значения выборки в виде неубывающей последовательности значений случайной величины Х. Таблица 1.4.1 Ранжированный ряд 1 14,4 11 15,15 21 15,61 31 15,88 41 16,4 51 17,02 2 14,44 12 15,15 22 15,64 32 15...
Статистический анализ данных выборочного наблюдения по объему инвестиций
2.3 Нахождение моды и медианы ряда
Мода - это варианта с наибольшей частотой. В нашем случае наибольшую частоту имеет интервал (500 - 57), где mi =27 (см табл. 2). Рассчитываем моду ряда по формуле: , где xi-1 - нижняя граница модального интервала, h - шаг интервала...
Статистическое изучение затрат на рабочую силу
2.1 Нахождение моды и медианы полученного интервального ряда распределения графическим методом и путем расчетов
Мода и медиана являются структурными средними величинами, характеризующими (наряду со средней арифметической) центр распределения единиц совокупности по изучаемому признаку. Мода Мо для дискретного ряда - это значение признака...
econ.bobrodobro.ru
4.1. Правила ранжирования
А. Ранжирование качественных признаков
Пример 1.
Испытуемому предлагается задание, в котором семь личностных качеств необходимо упорядочить (проранжировать) в двух столбцах: в левом столбце в соответствии с особенностями его «Я реального», а в правом столбце в соответствии с особенностями его «Я идеального». Результаты ранжирования даны в таблице 2.
Таблица 2.
| Я реальное | Качества личности | Я идеальное |
| 7 | ответственность | 1 |
| 1 | общительность | 5 |
| 3 | настойчивость | 7 |
| 2 | энергичность | 6 |
| 5 | жизнерадостность | 4 |
| 4 | терпеливость | 3 |
| 6 | решительность | 2 |
Б. Ранжирование количественных признаков
Пример 2.
В результате диагностики невроза у пяти испытуемых по методике К.Хека и Х. Хесса были получены следующие баллы: 24, 25, 37, 13, 12. Этому ряду чисел можно проставить ранги двумя способами:
большему числу в ряду ставится больший ранг, в этом случае получится: 3, 4, 5, 2, 1;
большему числу в ряду ставится меньший ранг: в этом случае получится: 3, 2, 1, 4, 5.
4.2. Проверка правильности ранжирования
А. Формула для подсчета суммы рангов по столбцу (строчке)
Если ранжируется N чисел, то сумма рангов расчитывается по формуле (1.1):
1+2+3+...+N=N(N+1)/2 (1.1)
В случае примера 1 число ранжируемых признаков было равно N =7, поэтому сумма рангов, подсчитанная по формуле (1.1), должна равняться 7(7+1)/2=28.
Сложим величины рангов отдельно для левого и правого столбца таблицы:
7 + 1 + 3+ 2 + 5 + 4 + 6 = 28 — для левого столбца и
1 + 5+ 7+ 6 + 4 + 3 + 2 = 28 — для правого столбца.
Суммы рангов совпали.
Б. Формула для расчета суммы рангов в таблице
Ранжирование по столбцам.
Пример 3. Результаты тестирования двух групп испытуемых по 5 человек в каждой по методике дифференциальной диагностики депрессивных состояний В. А. Жмурова представлены в таблице 3.
Таблица 3.
| Номер испытуемого | Группа 1 | Группа 2 |
| 1 | 15 | 26 |
| 2 | 45 | 67 |
| 3 | 44 | 23 |
| 4 | 14 | 78 |
| 5 | 21 | 3 |
Задача: проранжировать обе группы испытуемых как одну, т. е. объединить выборки и проставить ранги объединенной выборке, сохраняя, однако различие между группами. Сделаем это в таблице 4, причем так, что максимальной величине будем ставить минимальный ранг.
Таблица 4.
| Номер испытеумого | Группа 1 | Ранги | Группа 2 | Ранги |
| 1 | 15 | 8 | 26 | 5 |
| 2 | 45 | 3 | 67 | 2 |
| 3 | 44 | 4 | 23 | 6 |
| 4 | 14 | 9 | 78 | 1 |
| 5 | 21 | 7 | 3 | 10 |
| Сумма | 31 | 24 |
Поскольку у нас получены суммы ранга по столбцам, то общую сумму рангов можно получить, сложив эти суммы: 31+24= 55.
Чтобы применить формулу (1.1), нужно подсчитать общее количество испытуемых — это 5+5=10.
Тогда по формуле (1.1) получаем: 10(10+1)/2=55.
Ранжирование прведено правильно.
Если в таблице имеется большое число строк и столбцов, то можно использовать модификацию формулы (1.1)
Сумма рангов в таблице
= (kc+1)kc/2 , (1.2)
где k — число строк, с — число столбцов.
Вычислим сумму рангов по формуле (1.2.) для нашего примера. В таблице 2 имеется 5 строк и 2 столбца, сумма рангов = ((5·2+1)·5·2)/2=55
Ранжирование по строкам
Пример 4.
В предыдущем примере добавили еще одну группу испытуемых 5 человек
.
Таблица 5. Проведем ранжирование по строчкам.
| Номер испытуемого | Группа 1 | Ранги | Группа 2 | Ранги | Группа 3 | Рагни |
| 1 | 15 | 1 | 26 | 2 | 37 | 3 |
| 2 | 45 | 2 | 67 | 3 | 24 | 1 |
| 3 | 44 | 3 | 23 | 1 | 55 | 3 |
| 4 | 14 | 1 | 78 | 3 | 36 | 2 |
| 5 | 21 | 2 | 3 | 1 | 33 | 1 |
| Суммы по столбцам | 8 | 10 | 12 |
В этой таблице минимальному по величине числу ставится минимальный ранг. Сумма рангов по каждой строчке должна быть равна 6, поскольку у нас ранжируется три величины: 1+2+3= 6. В нашем случае так оно и есть. Теперь просуммируем ранги по каждому столбцу отдельно и сложим их.
Расчетная формула общей суммы рангов для ранжирования по строчкам для таблицы определяется по формуле:
Сумма рангов = nc(c+1)/2, (1.3.)
где n – количество испытуемых в столбце, с — количество столбцов (групп).
Проверим правильность ранжирования для нашего примера.
Реальная сумма рангов в таблице 8+10+12= 30
По формуле (1.3): 5·3·(3+1)/2=30.
Следовательно, ранжирование проведено правильно.
Случай одинаковых рангов
Ранжирование качественных признаков
А. Ранжирование качественных признаков
Модифицируем пример 1. и перепишем его в табл. 6. Предположим, что при оценке особенностей «Я реального» испытуемый считает, что такие качества, как «настойчивость» и «энергичность», должны иметь один и тот же ранг. При проведении ранжирования (столбец 1 табл. 6) этим качествам необходимо проставить мысленные ранги (М.Р.), как числа, обязательно идущие по порядку друг за другом, и отметить эти ранги круглыми скобками — ( ). Однако поскольку эти качества, по мнению испытуемого, должны иметь одинаковые ранги, то во втором столбце табл. 6, относящемуся к «Я реальному», следует поместить среднее арифметическое рангов, проставленных в скобках, т.е. (2 + 3)/2 = 2,5. Таким образом, второй столбец табл. 6 и будет окончательным итогом ранжирования особенностей «Я реального», данным испытуемым, а проставленные в этом столбце ранги будут носить название — реальные ранги (P.P.).
Аналогично при ранжировании «Я идеального» испытуемый считает, что такие качества, как «общительность», «энергичность» и «жизнерадостность», должны иметь один и тот же ранг. Тогда при проведении ранжирования (см. столбец 5 табл. 6) этим качествам необходимо проставить мысленные ранги, как числа, обязательно идущие по порядку друг за другом, и отметить эти ранги круглыми скобками — ( ). Однако поскольку эти качества, по мнению испытуемого, должны иметь одинаковые ранги — то в четвертом столбце табл. 6, относящемся к «Я идеальному», следует поместить среднее арифметическое рангов, проставленных в скобках, т.е. (4 + 5 + 6)/3 = 5. Таким образом, четвертый столбец таблицы 6 и будет окончательным итогом ранжирования особенностей «Я идеального», данным испытуемым, а проставленные в этом столбце ранги будут носить название — реальные ранги. Подчеркнем еще раз, что мысленные (условные) ранги, как числа, должны располагаться друг за другом по порядку, несмотря на то что ранжируемые качества в таблице данных не находятся рядом друг с другом.
Таблица 6.
| Я реальное | Качества личности | Я идеальное | ||
| М.Р. | P.P. | P.P. | М.Р. | |
| 7 | 7 | Ответственность | 1 | 1 |
| 1 | 1 | Общительность | 5 | (4) |
| (2) | 2,5 | Настойчивость | 7 | 7 |
| (3) | 2,5 | Энергичность | 5 | (5) |
| 5 | 5 | Жизнерадостность | 5 | (6) |
| 4 | 4 | Терпеливость | 3 | 3 |
| 6 | 6 | Решительность | 2 | 2 |
Обозначения: М.Р. — мысленные, или условные, ранги; P.P. — реальные ранги.
Проверим правильность ранжирования во втором столбце табл. 6, т.е. реальные ранги, относящиеся к «Я реальному»:
1 + 2,5 + 2,5 + 5 + 4 + 6 = 28.
По формуле (1.1) сумма рангов также равняется 28. Следовательно, ранжирование проведено правильно.
Проверим правильность ранжирования в четвертом столбце табл. 6, т.е. реальные ранги, относящиеся к «Я идеальному»:
1 + 2 + 3 + 5 + 5 + 5 + 7 = 28.
По формуле (1.1) сумма рангов также равняется 28. Следовательно, ранжирование проведено правильно.
Б. Ранжирование количественных характеристик (чисел)
Ранжирование чисел рассмотрим на примере.
Пример. Психолог получил у 11 испытуемых следующие значения показателя невербального интеллекта: 113,102,123,122, 117, 117, 102, 108, 114, 102, 104. Необходимо проранжировать эти показатели, и лучше всего это сделать в таблице 7.
Таблица 7
| Номер испытуемых | Показатели интеллекта | Мысленные ранги (М.Р.) | Реальные ранги (P.P.) |
| 1 | 113 | 6 | 6 |
| 2 | 102 | (1) | 2 |
| 3 | 123 | 11 | 11 |
| 4 | 122 | 10 | 10 |
| 5 | 117 | [8] | 8,5 |
| 6 | 117 | [9] | 8,5 |
| 7 | 102 | (2) | 2 |
| 8 | 108 | 5 | 5 |
| 9 | 114 | 7 | 7 |
| 10 | 102 | (3) | 2 |
| 11 | 104 | 4 | 4 |
В примере встретились две группы из равных чисел (102, 102 и 102; 117 и 117), поскольку числа в группах различны, то и скобки, проставленные этим группам чисел, также различны.
Проверим правильность ранжирования по формуле (1.1). Подставив исходные значения в формулу, получим: 11·12/2 = 66. Суммируя реальные ранги, получим:
6 + 2 + 11 + 10 + 8,5 + 8,5 + 2 + 5 + 7 + 2 + 4 = 66.
Поскольку суммы совпали, следовательно, ранжирование проведено правильно.
Правила ранжирования чисел таковы.
1. Наименьшему (наибольшему) числовому значению приписывается ранг 1.
2. Наибольшему (наименьшему) числовому значению приписывается ранг, равный количеству ранжируемых величин.
3. Одинаковым по величине числам должны проставляться одинаковые ранги.
4. Если в ранжируемом ряду несколько чисел оказались равными, то им приписывается реальный ранг, равный средней арифметической величине тех рангов, которые эти числа получили бы, если бы стояли по порядку друг за другом.
5. Если в ранжируемом ряду имеется две и больше групп равных между собой чисел, то для каждой такой группы применяется правило 4, и мысленные ранги каждой группы заключаются в разные скобки.
6. Общая сумма реальных рангов должна совпадать с расчетной, определяемой по формуле (1.1).
7. Не рекомендуется ранжировать более чем 20 величин (признаков, качеств, свойств и т.п.), поскольку в этом случае ранжирование в целом оказывается малоустойчивым.
При необходимости ранжирования достаточно большого числа объектов следует объединять их по какому-либо признаку в достаточно однородные классы (группы), а затем уже ранжировать полученные классы (группы).
Наиболее часто к измерениям, полученным в ранговой шкале, применяются коэффициенты корреляции Спирмена и Кэндалла, и, кроме того, используются разнообразные критерии различий.
studfiles.net