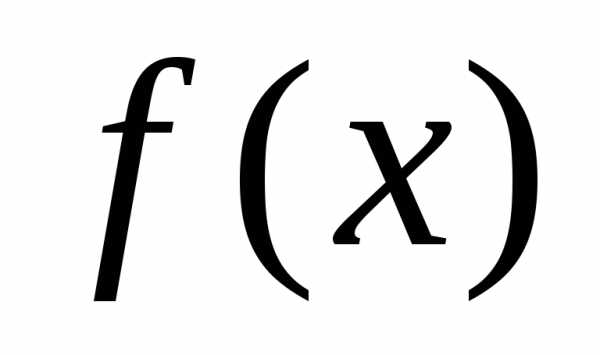3.2. Задачи условной оптимизации и методы их решений. Задача условной оптимизации

Задача условной оптимизации ( линейного программирования).Целевая функция и ограничения. Способы решения задачи условной оптимизации. Компьютерная технология решения задачи условной оптимизации

Линейные задачи являются элементом более широкого класса задач – задач принятия решений при наличии ограничений, которые называются задачами условной оптимизации.

Линейное программирование - это раздел математического программирования, в котором рассматриваются методы решения экстремальных задач с линейным функционалом и линейными ограничениями, которым должны удовлетворять искомые переменные.

Задачи линейной оптимизации - это тип экстремальных задач, формирующихся линейными функциями и линейными соотношениями. Так или иначе базовой задачей такого рода является задача линейного программирования, т.е. задача поиска экстремума (максимума или минимума) линейной функции при ограничениях в форме линейных неравенств.

Выбор оптимального решения или сравнение двух альтернативных решений проводится с помощью некоторой зависимой величины (функции), определяемой проектными параметрами. Эта величина называется целевой функцией (или критерием качества). В процессе решения задачи оптимизации должны быть найдены такие значения проектных параметров, при которых целевая функция имеет минимум (или максимум). Таким образом, целевая функция — это глобальный критерий оптимальности в математических моделях, с помощью которых описываются инженерные или экономические задачи.

Набор количественных соотношений между переменными, выражающие определенные требования экономической задачи в виде уравнений или неравенств. Называется системой ограничений.

Модели линейного программирования применяются для нахождения оптимального решения в ситуации распределения дефицитных ресурсов при наличии конкурирующих потребностей. Например, с помощью модели линейного программирования управляющий производством может определить оптимальную производственную программу, т.е. рассчитать, какое количество изделий каждого наименования следует производить для получения наибольшей прибыли при известных объемах материалов и деталей, фонде времени работы оборудования и рентабельности каждого вида изделий. Большая часть разработанных для практического применения оптимизационных моделей сводится к задачам линейного программирования. Однако с учетом характера анализируемых операций и сложившихся форм зависимости факторов могут применяться и модели других типов. При нелинейных формах зависимости результата операции от новых факторов - модели нелинейного программирования; при необходимости включения в анализ фактора времени - модели динамического программирования; при вероятностном влиянии факторов на результат операции - модели математической статистики.

Линейное программирование имеет дело с оптимизацией моделей, в которых целевая функция линейно зависит от переменных решения. Ограничения также представляют собой линейные неравенства или уравнения относительно переменных решения. Требование линейности означает, что и целевая функция, и ограничения могут представлять собой только суммы произведений постоянных коэффициентов на переменные решения. Искусство математического моделирования состоит в том, чтобы учесть как можно больше факторов по возможности простыми средствами. Именно в силу этого процесс моделирования часто носит итеративный характер. На первой стадии строится относительно простая модель и проводится ее исследование, позволяющее понять, какие из существенных свойств изучаемого объекта не улавливаются данной формальной схемой. Затем происходит уточнение, усложнение модели.

В большинстве случаев первой степенью приближения к реальности является модель, в которой все зависимости между переменными, характеризующими состояние объекта, предполагаются линейными. Здесь имеется полная аналогия с тем, как весьма важна и зачастую исчерпывающая информация о поведении произвольной функции получается на основе изучения ее производной -- происходит замена этой функции в окрестности каждой точки линейной зависимостью. Значительное количество экономических, технических и других процессов достаточно хорошо и полно описывается линейными моделями.

Можно выделить два типа задач оптимизации — безусловные и условные. Безусловная задача оптимизации состоит в отыскании максимума или минимума действительной функции от действительных переменных и определении соответствующих значений аргументов на некотором множестве а n-мерного пространства.

Условные задачи оптимизации,илизадачи с ограничениями, — это такие, при формулировке которых задаются некоторые условия (ограничения) на множестве а. Эти ограничения задаются совокупностью некоторых функций, удовлетворяющих уравнениям или неравенствам.

Ограничения равенства выражают зависимость между проектными параметрами, которая должна учитываться при нахождении решения. Эти ограничения отражают законы природы, наличие ресурсов, финансовые требования и т. п.

cyberpedia.su

Задача - условная оптимизация - Большая Энциклопедия Нефти и Газа, статья, страница 2

Задача - условная оптимизация

Cтраница 2

Разбиение графа относится к задачам дискретной условной оптимизации из-за прерывности ее ЦФ и наличия множества ограничений на переменные. Однако применительно к задаче разбиения большинство из вышеприведенных методов не может быть использовано в связи с ее дискретностью, которая приводит к существенному росту трудностей при поиске оптимума. Поэтому данные задачи выделяют в особый класс оптимизационных комбинаторных задач на графах. [16]

Вопросы теории и методы решения задач условной оптимизации рассматриваются в области математики, называемой математическим программированием. [17]

Лагранжа): Метод решения задачи условной оптимизации ( constrained optimization), при котором ограничения ( constraints), записываемые как неявные функции ( implicit functions), объединяются с целевой функцией ( objective function) в форме нового уравнения, называемого лагранжианом. [18]

Важным и полезным для исследования задач условной оптимизации является понятие о расширении экстремальной задачи. Оно позволяет подчеркнуть взаимосвязь таких различных подходов, как метод Лагранжа, метод штрафов, переход к оеред-ненной постановке и др. Основное внимание будет уделено изложению и пояснению методики перехода от условий задачи ( критерия оптимальности, связей и ограничений) к условиям, выделяющим оптимальные решения. Конструкции, которые будут приведены, позволяют провести такой переход по определенным правилам для произвольной задачи из очень широкого класса задач оптимизации. Важно и то обстоятельство, что изменения в постановке задачи легко учесть при составлении условий оптимальности решения. [19]

Лагранжа для того и служит, чтобы от задачи условной оптимизации перейти к задаче безусловной оптимизации по расширенному ( за счет множителей Лагранжа) набору аргументов оптимизации. [20]

В этом случае на каждом шаге алгоритма удается перейти от задачи условной оптимизации к безусловной и вместо двух условно-оптимальных зависимостей запоминать только одну. Рассмотрим алгоритм динамического программирования применительно к частным формам связи. [21]

Итак, решение задачи условной оптимизации при нескольких ограничениях сведено к многократному решению задачи условной оптимизации с одним ограничением. Здесь же возникает задача оптимального изменения симплекса Р, например, правило выбора изменения Р и выбор шага изменения АР. [22]

В заключение отметим, что, используя идею проектирования, можно модифицировать применительно к задачам условной оптимизации и другие методы безусловной оптимизации, в том числе метод Ньютона и метод сопряженных направлений, изложенные в § § 2, 3 гл. [23]

Как следует из анализа соотношений, входящих в модели, решаемая задача относится к группе задач условной оптимизации с нелинейной целевой функцией и нелинейными ограничениями. Учет ограничений при использовании этого метода производится путем введения штрафов. [24]

Если X - подмножество R, заданное с помощью некоторых ограничений, то задачу оптимизации на X называют задачей условной оптимизации. [25]

Большинство методов оптимизации разработано для поиска безусловного экстремума. Обычно задачи условной оптимизации сводят к задачам безусловной оптимизации с помощью штрафных функций или множителей Лагранжа. [26]

Ясно, что критерий (2.12) относится лишь к задачам безусловной оптимизации. В задаче условной оптимизации критерий (2.12) следует заменить на критерий е-стацио-нарности, соответствующий данной задаче. [27]

При решении задач условной оптимизации целесообразно использовать методы безусловной оптимизации, учитывая большое количество разработанных по этим методам программ. С этой целью задача условной оптимизации сводится к задаче безусловной оптимизации устранением ограничений путем преобразования параметра xt, на значения которого наложены ограничения, в неограничиваемый. [28]

Задачи проектирования технических объектов характеризуются большим количеством оптимизируемых параметров и наличием ограничений, накладываемых на параметры. Они формулируются как задачи многопараметрической условной оптимизации. [29]

При наличии нескольких критериев возможны два класса задач оптимизации: задачи условной оптимизации по одному критерию и задачи векторной оптимизации. При условной оптимизации отыскивается наибольшее или наименьшее значение одного из критериев при условии, что остальные критерии имеют заданные значения. [30]

Страницы: 1 2 3

www.ngpedia.ru

Условия оптимальности для задачи условной оптимизации

Сформулируем теперь условия оптимальности для задачи условной оптимизации (1.32).

Предположим, что ограничения gi (х) являются непрерывными дифференцируемыми функциями и уравнения связи gi(х) =bi, i = 1,2,…, m первых компонент x1, х2,…, хn). Для того чтобы выполнялось последнее условие, необходимо, чтобы ранг матрицы Якоби для функций gi (х), i = 1, 2,…, m, равнялся m, т. е. определитель этой матрицы, составленной из производных по первым m аргументам, не равнялся нулю:

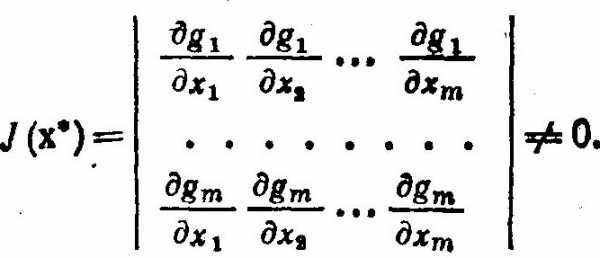
Для того чтобы точка х* ∈ D являлась оптимальным решением задачи условной оптимизации (1.32), она должна удовлетворять системе из (n + m) уравнений вида:

∂Q/∂xj|x=x* + ∑λk∂gk/∂xj|x=x* = 0, j=1, 2, …, n;

gi (x*) = bi, i = 1, 2, …, m. (1.60)

По теореме о неявных функциях, если в точке х* выполняется условие (1.59), то из уравнений связи gi (х) = bi, i = 1, 2, …, m, можно выразить зависимые переменные через независимые!

xi = φi (xm+1, xm+2, …, n), i = 1, 2, …, m (1.61)

где φi (xm+1, xm+2, …, n) — непрерывные дифференцируемые функции. Подставляя (1.61) в функцию Q (х), получаем для любых значений х ∈ d (х*, ε) следующее выражение:

Q (φ1(xm+1, xm+2, …, n), …. φ1(xm+1, xm+2, …, n), xm+1, xm+2, …, n = Q* (xm+1, xm+2, …, n). (1.62)

Точка х* является локальным минимумом функции Q* (xm+1, xm+2, …, n). если выполняется условия оптимальности (1.55) для многопараметрической задачи безусловной оптимизации:

∂Q*/∂xj |x=x* = 0, j = m+1, m+2, …, n. (1.63)

По правилу дифференцирования сложных функций, учитывая (1,62), вместо (1.63) можем записать:

∂Q*/∂xj |x=x* = ∑∂Q*/∂xi ∂φi/ ∂xj + ∂Q*/∂xj =0, j = m+1, …, n, (1.64)

где производные ∂φi/ ∂xj, i — 1, 2, …, m, для каждого j представляют собой единственное решение системы уравнений;

∑∂g*/∂xi ∂φi/∂xj + ∂g*/∂xj = 0, k = m+1, …, n,

Вместо того чтобы решать систему уравнений (1.65), поступим следующим образом. Рассмотрим совокупность чисел λi, i = 1, 2, …, m, являющихся решениями системы линейных уравнений:

∑λi∂gi/∂xj + ∂Q/∂xj =0, j = 1, …, m, (1.66)

Решение системы (1.66) существует и единственно в силу предположения (1.59). Умножим k-ое уравнение (1.65) на λk и просуммируем по k от 1 до m. Тогда для каждого j = m + 1, …, n, если поменять порядок суммирования, справедливо соотношение

∑ ( ∑ λi ∂gi/∂xj)∂φi∂xj + ∑λi ∂gi/∂xj = 0.

Прибавляя (1.67) к (1.64), имеем:

∑[ ∂Q/∂xi + ∑λi ∂gi/∂xj]∂φi/∂xj + [ ∂Q/∂xj + ∑λi ∂gi/∂xj] = 0

откуда, учитывая (1.66), получаем, что для выполнения соотношений (1.63), необходимо, чтобы выполнялась система уравнений:

∂Q/∂xj + ∑λi ∂gi/∂xj = 0, j=m + 1,…, n. (1.69)

Объединяя эту систему с системой уравнений (1.66) и уравнениями связи gi (х) — bi, i = 1, …, m, получаем, что точка х* является оптимальным решением задачи условной оптимизации (1.32), если она удовлетворяет системе (n+m) уравнений (1.60).

Условия оптимальности (1.60) для задачи условной оптимизации (1.32) могут быть получены при помощи следующего приема, называемого методом множителей Лагранжа.

Составляется функция (n + m) переменных х = (х1, х2,…, хn) и λ = (λ1, λ2,…, λn), которые считаются независимыми:

L(x, λ) = Q(x) + ∑λi(gi(x) — bi),

по каждой из компонент векторов х и λ, вычисляются частные производные от функции L (х, λ) и приравниваются нулю:

∂L/∂xj = ∂Q/∂xj + ∑λi ∂gi/∂xj, j = 1, 2, …, m;

∂L/∂λi = gi(x) — bi, i = 1,2,…, n.

Функция L (х, λ) называется функцией Лагранжа, а числа λi, которые могут иметь любой знак, множителями Лагранжа.

Представляет интерес ответить на вопрос: какова в терминологии рассматриваемой задачи оптимизации (1.32) интерпретация искусственно введенных множителей Лагранжа λi, i = 1, 2,…, m. С этой целью рассмотрим поведение минимального значения критерия оптимальности Q* = Q (х*) при изменении правых частей bi, i = 1, …, m, уравнений связи:

gi (х) = bi, i = 1, 2, …, m. (4.70)

Пусть х* — оптимальное решение задачи условной оптимизации (1.32), а λ*— множители Лагранжа, соответствующие точке х*. Очевидно, что х* и λ* являются функциями правых частей уравнений связи (1.70):

х* = х* (b), λ* = λ* (b). (1.71)

Предположим, что зависимости (1.71) являются непрерывно дифференцируемыми функциями вектора b = (b1, b2,…, bn), и вычислим частные производные критерия оптимальности Q (х*) и уравнений связи (1.70) по bi в точке х*:

∂Q/∂bi|x=x* = ∑∂Q/∂xj∂xj/∂bi, j = 1, 2, …, m; (1.72)

∂gk/∂bi|x=x* = ∑∂gk/∂xj∂xj/∂bi — δik, i, k = 1, 2, …, m; (1.73)

где

δik = 1, если i=k0 — в противном случае.

Умножим k-e уравнение (1.73) на λ*k, просуммируем по k от 1 до m и прибавим его к правой части выражения (1.72). Тогда, меняя порядок суммирования, можем записать

∂Q/∂bi = ∑(∂Q/∂xj + ∑λ*k∂gk/∂xj)∂xj/∂bi — ∑λ*kδik, i = 1, 2, …, m.

Так как х* и λ* удовлетворяют условиям оптимальности (1.60), то, учитывая (1.74), получим, что

∂Q/∂bi | x=x* = — λ*i, i = 1, 2, …, m.

Таким образом, множители Лагранжа λ*i, i = 1, 2, …, m, можно интерпретировать как коэффициенты чувствительности минимального значения критерия оптимальности Q (х*) к малым изменениям правых частей уравнений связи (1.70).

Практическое значение полученного результата заключается в том, что, не решая задачи оптимизации (1.32) при новых значениях правых частей уравнений связи (1.70), мы можем оценить, как изменится оптимальное значение критерия оптимальности при малых изменениях вектора b.

При выводе условий оптимальности для задачи выпуклого программирования (1.30) необходимо допустить, что выпуклая допустимая область D имеет внутренние точки. Наличие таких точек гарантирует, что существует хотя бы одна точка х ∈ D, в которой все ограничения могут быть разделены на два типа: активные ограничения, в которых неравенства выполняются как равенства (gi (х) = bi i ∈ J—), и неактивные ограничения, являющиеся строгими неравенствами (gk (х) > 0, k ∈ J+, J+ ≠ ∅). Существование внутренних точек множества D можно определить также следующим образом.

Будем называть направление S возможным направлением в точке х ∈ D если можно двигаться вдоль направления S, оставаясь в D. Область D имеет внутренние точки, если возможное направление S в точке х для любого активного ограничения удовлетворяет следующим условиям, называемым условиями регулярности:

(∇giT(x), S) ≥ 0, i∈J—. (1.75).

Пусть допустимая область D = {x|gi(x) ≥ 0, i = 1, 2, …, m} удовлетворяет условиям регулярности (1.75). Тогда для того, чтобы точка х* ∈ D была оптимальным решением задачи выпуклого программирования (1.30), необходимо существование таких чисел u* = (u1*, u2*,…, um*), что

gi(x*) ≥ 0, i = 1, 2, … m; (1.76)ui* ≥ 0, i = 1, 2,…, m; (1.77)ui*gi(х*) = 0, i = 1, 2, …, m; (1.78)

∇Q(x*) — ∑ui*∇gi(x*) = 0.

all4study.ru

3.2. Задачи условной оптимизации и методы их решений.

В общем случае задача условной оптимизации имеет вид:

F= f(xj) →min;

gi (xj) = 0;

aj ≤ xj ≤ bj.

Рассмотрим один из способов решения подобных задач, называемый методом штрафных функций, суть которого заключается в следующем. От задачи целевой оптимизации переходят к такой задаче, минимизируется новая целевая функция, включающая, кроме заданной целевой функции f(xj) , заданные ограничения gi (xj). Новая целевая функция записывается следующим образом

Ф(xj) = f(xj)+ ψ[gi(xj)]→min, где ψ[gi(xj)] –штрафная функция.

Вводимая штрафная функция ψ[gi(xj)] должна удовлетворять следующим требованиям:

ψ[gi(xj)] = 0, если xj находится в области допустимых значений.

ψ[gi(xj)] > 0, если xj находится в области допустимых решений.

Штрафная функция может иметь следующий вид :

ψ[gi(xj)] = M ∑ gi2 (xj), где M – большое число

i=1

(например, если ожидаемое оптимальное значение целевой функции порядка единицы, то можно принять М=1000).

Если xj находится в области допустимых решений, то выполняются все ограничения, значит,

gi(xj) = 0. При этом штрафная функция равняется нулю, и новая целевая функция оказывается равной заданной, т.е Ф(xj) = f (xj)→min.

Если xj не находится в области допустимых решений, то ограничения не выполняются, т.е. gi(xj)≠ 0 . Значит, gi2 (xj)> 0, а большое число M приводит к тому, что в новой целевой функции штрафная функция оказывается существенно больше заданной целевой функции f (xj). Поэтому в ходе минимизации сначала уменьшается до нуля штрафная функция, а затем уже и сама целевая функция.

Примеp: решить задачу условной оптимизации вида: F =X2→min;

X2 = 2(x1-2)2+1;

(x1-3)2+(x2-0,5)2 ≥ 4;

0 ≤ x1 ≤ 4; 0 ≤ x2 ≤3.

Решение: Первое ограничение представляет собой параболу с координатами вершины A(2;1) , второе – часть плоскости, находящуюся вне окружности радиуса R=2, центр которой имеет координаты O (3; 0.5). Без наложения второго ограничения минимум находился бы в вершине параболы и имел бы значение F1=1. Наложение привело к тому, что минимум переместился в точку B с координатой х1=1.4. При этом F2= x2= 1.8, то есть его значение ухудшилось.

Решение этой задачи методом штрафных функций предусматривает следующий алгоритм.

1. Записывается условие задачи в виде системы

F= x2 – min;

x2 – 2(x1-2)2-1=0;

(x1-3)2 + (x2-0.5)2 – y1 – 4=0;

0 ≤ x1≤ 4; 0 ≤ x2 ≤ 3;

y1≥0

Составляется новая целевая функция, включающая штрафную функцию с число M=1000. Получим F=x2+100 [x2-2(x1-2)2+1+(x1-3)2+(x2-0.5)2 –y1-4] →min; 0 ≤ x1≤ 4; 0 ≤ x2 ≤ 3;

y1≥0.

Далее проводится решение полученной системы.

studfiles.net

Условная оптимизация - Большая Энциклопедия Нефти и Газа, статья, страница 3

Условная оптимизация

Cтраница 3

Таким образом, решение управленческой задачи состоит в условной оптимизации управленческих решений в рамках человеко-машинной интерактивной процедуры. [32]

Рациональность выбираемого варианта системы или комплекса достигают его условной оптимизацией, означающей минимизацию затрат на реализацию при заданной эксплуатационной надежности. [33]

Книга представляет собой отредактированный сборник трудов конференции по методам условной оптимизации, проведенной Национальной физической лабораторией ( Великобритания, Тэддингтон) в январе 1974 г., и содержит практически все существующие в настоящее время методы решения задач оптимизации при наличии ограничений. Выделяются две основные группы методов: методы спуска по возможным направлениям и методы штрафных функций. В первых поиск точки минимума функции ведется на последовательности точек, удовлетворяющих ограничениям задачи. Известно, что задачи оптимизации при линейных ограничениях хорошо решаются такими методами. Если же в задаче имеются нелинейные ограничения, то каждый раз приходится корректировать направление спуска, поскольку постоянно нарушаются криволинейные ограничения. В этих случаях, по-видимому, заранее стоит отказаться от построения последовательности точек, удовлетворяющих ограничениям, и допустить к конкурсу все точки соответствующего пространства. На этой идее основаны методы второй группы. [35]

Таким образом, приходится отказаться от абсолютной оптимизации и ограничиться условной оптимизацией в заданном классе фильтров. Такие фильтры выбираются из условия минимальной сложности и реализуемости на практике. Теория УОФ дает возможность получать фильтры более низких порядков, а также фильтры, равноценные по сложности любому данному субоптимальному фильтру, но обладающие более высокой точностью. Расчеты, необходимые для проектирования таких фильтров, не опираются на результаты текущих измерений и могут быть выполнены по априорным данным в процессе проектирования. [36]

В рамках рассматриваемого подхода к системному анализу возможны и другие варианты условной оптимизации. Один из таких вариантов реализуется в способе уступок, другой 197 в установлении граничных значений всех частных критериев без исключения. [37]

W, называются условными оптимальными управлениями, а процесс их нахождения - условной оптимизацией. [39]

Основная идея методов первой группы состоит в том, чтобы аппроксимировать исходную задачу условной оптимизации некоторой вспомогательной задачей, решение которой менее сложно, чем решение исходной. [40]

Если X - подмножество R, заданное с помощью некоторых ограничений, то задачу оптимизации на X называют задачей условной оптимизации. [44]

Эквивалентная задача ( впрочем, как и исходная) представляет собой задачу на условный экстремум, для решения которой использовалась условная оптимизация: метод уровней и метод модифицированной функции Лагранжа. [45]

Страницы: 1 2 3 4

www.ngpedia.ru

Задача условной оптимизации - Энциклопедия по машиностроению XXL

Задачи, в которых экстремум ищут в пределах неограниченного пространства переменных проектирования, относятся к задачам б е з у с л о в и о й оптимизации. Найденные при этом экстремумы называют безусловными. Наличие ограничений любого вида приводит к задачам условной оптимизации, решение которых дает условный экстремум. [c.277]

Методы условной оптимизации. Задачи условной оптимизации, заключающиеся в минимизации некоторого критерия оптимальности с ограничениями на область существования переменных проектирования, относятся к классу задач математического программирования. [c.290]

В задачах условной оптимизации, в которых ограничения заданы только в виде неравенств, возможно построение обобщенного критерия оптимальности с помощью барьерных функций. Значения, принимаемые барьерной функцией, неограниченно возрастают при приближении к границе допустимой области. [c.291]

Объясните общность и различие методов штрафных и барьерных функций в задачах условной оптимизации. [c.329]

При решении задач условной оптимизации целесообразно использовать методы безусловной оптимизации, учитывая большое количество разработанных по этим методам программ. С этой целью задача условной оптимизации сводится к задаче безусловной оптимизации устранением ограничений путем преобразования параметра XI, на значения которого наложены ограничения, в не-ограничиваемый. [c.319]

Сведение исходной задачи условной оптимизации к последовательности задач безусловной оптимизации может быть выполнено с помощью функций штрафа. [c.167]

Метод отжига - метод поисковой оптимизации, в котором для увеличения вероятности выхода из областей притяжения локальных минимумов допускается переход в точки с худшим значением целевой функции с некоторой вероятностью Метод распространения ограничений - метод решения задач условной оптимизации, основанный на сокращении интервалов значений управляемых переменных (или мощности множеств значений этих переменных) благодаря учету исходных ограничений. Сокращенные интервалы в явном виде определяют подмножество допустимых решений [c.312]

Для задачи о максимальной вписанной окружности соответствующая задача условной оптимизации будет выглядеть следующим образом [c.193]

Различают методы условной и безусловной оптимизации по наличию или отсутствию ограничений. Для реальных задач характерно наличие ограничений, однако методы безусловной оптимизации также представляют интерес, поскольку задачи условной оптимизации с помощью специальных методов могут быть сведены к задачам без ограничений. [c.158]

Суть метода заключается в преобразовании задачи условной оптимизации (4.19) в задачу безусловной оптимизации с помощью образования новой целевой функции [c.166]

Важная идея методов штрафных функций - преобразование задачи условной оптимизации в задачу безусловной оптимизации путем формирования новой целевой функции Ф(Х), за счет введения в исходную целевую функцию F(X) специальным образом выбранной функции штрафа S(X) [c.167]

Если периоды слабо связаны (то есть существует единственное ограничение, связывающее действия, или множества допустимых действий, или затраты, или доходы, или вознаграждения и т.д. - см. аналогии в задачах стимулирования в многоэлементных АС со слабо связанными АЭ [59]), то задача (4) превращается в задачу условной оптимизации (изменяется множество действий, по которому ищется максимум). [c.1204]

Беллмана (см. примеры 3 и 4), что качественно отличает их от модели ДАС с несвязанными или со слабо связанными периодами, в которых применение принципа компенсации затрат сводило задачу управления к стандартной задаче условной оптимизации. [c.1204]

В случае наличия общих ограничений на целевые функции, допустимые множества, параметры механизма стимулирования и т.д., при несвязанных периодах функционирования, задача стимулирования в динамической системе, по аналогии с задачей стимулирования в системе со слабо связанными элементами, может быть сведена к стандартной задаче условной оптимизации [52, 56-58]. [c.1204]

В основу алгоритмов минимизации гладких функций на ограниченных множествах положены следующие идеи. Общая задача математического программирования может быть преобразована в задачу либо последовательность задач безусловной оптимизации. Такие алгоритмы основаны на использовании метода центров [225], замены независимых переменных [211], применении различных вариантов штрафных функций и модифицированных функций Лагранжа [215, 217, 218]. Можно отметить также метод [225], позволяющий перейти к безусловной минимизации функции максимума. Задача условной оптимизации может быть аппроксимирована последовательностью задач линейного или квадратичного программирования. К этой группе относятся методы возможных направлений [228], линеаризации [215], линейной аппроксимации [96], проектирования [218]. [c.148]

При описании комплексной целевой функции нелинейными зависимостями от внутренних параметров задача оптимизации решается методами линейного программирования если же целевая функция является линейной функцией от внутренних параметров, то имеет место задача линейного программирования. В общем случае целевая функция может иметь несколько экстремумов, отличающихся по абсолютной величине. В зависимости от типа экстремума, в котором заканчивается поиск оптимального решения, различают методы поиска локального и глобального экстремума. Если на значение определяемых параметров наложены некоторые ограничения, то решение задачи синтеза механизмов осуществляется методами условной оптимизации. В противном случае (при отсутствии ограничений) при синтезе механизмов для поиска значений определяемых параметров используют методы безусловной оптимизации. [c.316]

Конечно, возможны иные критерии оптимизации периода предупредительных замен. Так, могут быть заданы не стоимости проведения предупредительной и аварийной замен, а их длительности, что приведет к необходимости минимизировать коэффициент простоя элемента (математическая постановка задачи в данном случае сохранится с точностью до обозначений), или может быть оптимизирована вероятность выполнения задачи заданной длительности. Могут быть сформулированы задачи на условную оптимизацию. Например, необходимо добиться заданных эксплуатационных характеристик при минимальных экономических затратах (или добиться максимально возможных эксплуатационных характеристик при заданных экономических затратах). [c.359]

Условная оптимизация. Имеется система, рассмотренная в предыдущем пункте, однако необходимо учесть и экономическую сторону проведения ТО. В этом случае можно сформулировать задачу на условную оптимизацию типа [c.366]

Иначе говоря, это - задачи на условную оптимизацию. Обе эти задачи решаются обычными способами дискретного программирования как задачи на условную оптимизацию. Как и в первом случае, здесь рассмотрены только варианты очень упрощенной постановки задачи. Но и в этом случае практическое решение подобных задач приводит к большим трудностям. [c.395]

Существенно отличается подход к решению задач с единственным и несколькими экстремумами. Во втором случае обычно требуется найти главный из них (так называемый глобальный). Наличие или отсутствие ограничений на искомые переменные относит задачу к области условной или безусловной оптимизации. В свою очередь линейность целевой функции или ограничений обуславливает использование методов линейного или нелинейного программирования. При постановке задачи существенное значение имеет то, что исходная информация не полностью определена и характеризуется определенными вероятностными свойствами. Такую задачу следует решать методами стохастического программирования. Наконец, подход к решению оптимизационной задачи значительно изменяется, если целевая функция приобретает не скалярный, а векторный вид. Тогда возникает необходимость оптимизации по нескольким независящим критериям. После этой краткой общей классификации остановимся более подробно на типах оптимизационных задач, наиболее подходящих для разработки приборов квантовой электроники. К таким задачам прежде всего относятся задачи параметрической оптимизации. [c.121]

Совокупность методов НЛП, в зависимости от ограничений в математических моделях оптимизации, делится на две группы методы безусловной оптимизации и методы условной оптимизации. Первые используют для решения задач без ограничений на оптимизируемые параметры, вторые — для задач с ограничениями. Следует отметить, что методы безусловной оптимизации (см. описание методов штрафных функций) можно использовать и при решении задач с ограничениями, предварительно приведенных к задачам без ограничений. [c.152]

Методы условной оптимизации. Метод штрафных функций основан на преобразовании исходной задачи (3.3) с ограничениями к задаче без ограничений с применением к последней методов безусловной оптимизации. Преобразование проводится по формуле Ф(Х) =/ (Х)+0(Х), где Ф(Х) и F )—соответственно новая и первоначальная целевые функции, 0(Х) —функция штрафа, учитывающая нарушенные ограничения. В методе штрафных функций, называемом методом внешней точки, функция штрафа [c.75]

Рассмотренный алгоритм обеспечивает решение задачи безусловной минимизации целевой функции. Однако, как уже отмечалось, при оптимизации АФАР область изменения варьируемых параметров часто бывает ограничена, что формально приводит к задаче условной минимизации (т. е. к задаче вида (7.1) с ограничениями [c.198]

Еще более проблематичным представляется применение аналитических методов при отыскании условных экстремумов функции цели, что характерно для реальных задач оптимизации ЭМУ при наличии многочисленных ограничений. Ограничения, накладываемые на область определения функции цели, приводят к возможному несовпадению условных и локальных экстремумов, а поэтому уравнения (5.38) в данном случае вообще нельзя рассматривать в качестве необходимых условий для определения точек экстремума. [c.149]

Остальные параметры системы (они обозначаются yij I Уп) условимся называть параметрами состояния. Разделение параметров на две группы является условным и определяется постановкой задачи оптимизации, особенностями работы элемента и узлов и др. [c.555]

Разработаны многочисленные методы рещения задачи оптимизации при различных видах целевой функции, уравнений связи и типах ограничений, которые условно можно подразделить на две группы а) классические (метод дифференциального исчисления, метод множителей Лагранжа, вариационное исчисление) б) метод математического программирования (методы линейного и нелинейного программирования, метод динамического программирования, принцип максимума Понтрягина и др.). [c.555]

Структуру сезонных запасов в предлагаемой детерминированной постановке задачи будут определять режимы завоза топлива, накопления и сработки его запасов, обусловленные неравномерностью и рассогласованием процессов добычи и потребления топлива, а также транспортными ограничениями. Таким образом, в содержательном плане задача состоит в получении ответа на вопрос, как в течение года накапливать и срабатывать запасы топлива в отдельных районах, чтобы обеспечить решение, полученное в масштабе годовых объемов при оптимизации развития ЭК [64]. При этом система топливоснабжения страны должна быть представлена в достаточно агрегированном виде [64], а получаемые решения должны быть детализированы в рамках отдельных районов с помощью специальных моделей, условно говоря, районного уровня. [c.413]

Одна из главнейших задач оптимизации — выбор критерия качества технологической системы. Условно критерии можно разделить на четыре группы [15], каждая из которых объединяет следующие качественные характеристики АЛ [c.163]

Решение задачи связано с нахождением условного экстремума. Для нахождения безусловного экстремума задачу необходимо преобразовать так, чтобы она стала задачей на безусловный минимум. Это преобразование может осуществляться различными способами, выбор которых зависит от сложности и трудоемкости вычислений. Одним из эффективных способов является метод неопределенных множителей Лагранжа. Практические приемы преобразования и методы оптимизации решений достаточно подробно освещены в работах [21, 66]. [c.85]

Вторым важным обстоятельством является то, что реализация рассмотренных алгоритмов значительно усложняется, если задача сводится к нахождению условного экстремума, т. е. экстремума, находящегося на границе допустимой области. Такая ситуация может возникнуть при решении задачи оптимизации параметров тепло- [c.202]

Б. Камера распределения. Ширина приемного сопла йпв. При проектировании струйных элементов возникает задача оптимизации величины проходного сечения приемного сопла с целью максимального использования энергии потока питания. Сложность решения этой задачи заключается в том, что расход и давление в приемном канале во время работы струйного элемента с различными нагрузками — величины переменные и взаимозависимые. Критерии оптимизации могут быть самыми различными в зависимости от назначения струйного элемента. Наиболее общим критерием оптимальности является обеспечение условного максимального КПД (или максимального коэффициента передачи энергии) элемента [c.291]

Задачу оптимизации соотношения толщин и /ij двухслойной термоизоляции можно поставить в данном случае двояким образом. Во-первых, при заданном значении т (массы или стоимости термоизоляции) оптимальное соотношение hj и можно подобрать из условия максимума термического сопротивления R. Во-вторых, при заданном значении R оптимальным следует считать соотношение hi и hj, которое обеспечивает минимум величины т (массы термоизоляции или ее стоимости). Оба варианта оптимизационной задачи соответствуют математической формулировке задачи на условный экстремум функции двух переменных с заданным ограничением в форме равенства. В первом случае нужно найти максимум функции R(hi, hj) при ограничении m(hi, hj) = mg, а во втором - минимум функции m hi, hj) при ограничении jR(/ij, hj) = где Щ - заданные значения. [c.138]

Существует и используется большое число математических методов численного решения задач условной оптимизации (см., например, [18]). Эти методы, так же как ih разработанные на их основе алгаритмы и программы, различаются требованиями к начальному приближению решения, скоростью сходимости процесса, чувствительностью к погрешностям в задаваемых параметрах, точностью локализации координат экстремума, объемом необходимой оперативной памяти и требованиями к быстродействию ЭВМ, удобством работы и другими характеристиками. В некоторых случаях экстремум функции (22.8) иш ется непосредственно в заданной допустимой области, другие методы основаны на решении с + с( > +... +нелинейных уравнений [c.187]

Вообщ,е задачи условной оптимизации более сложны, чем задачи безусловной оптимизации. Для их решения используют специально разработанные методы программирования с ограничениями. Одним из таких методов, которые относятся к методам поиска глобального экстремума, является метод сканирования, состоящий в том, что допустимая область поиска, определяемая системой ограничений, разбивается на к подобластей, в центре каждой из которых определяется значение целевой функции. Если целевая функция зависит от п параметров, необходимо выполнить вариантов расчета. Для надежного определения глобального минимума необходимо увеличивать число к подобластей, что приводит к большим затратам машинного времени. [c.319]

Изложение различных методов решения задач минимизации (в том числе задач условной оптимизации, линейного проп аммирования, дискретной оптимизации) можно найти в [6, 11, 14, 22, 66, 78]. [c.143]

Таким образом, задача условной оптимизации (3.24) сведена к задаче безусловной оптимизации квадратичной функции (3.27). Производная Фрегпе функции (3.27) есть 1 х (ЛТ — 1) -матрица [c.66]

В соответствии с делением экстремумов на условные и безусловные различают методы условной и безусловной оптимизации. Методы безусловной оптимизации могут быть применены к поиску условных экстремумов. Основным методом сведения задач условной оптимизации к безусловной является метод штрафных функций [49], та же цель достигается и при использовании максиминного критерия. В последнем случае каждое из ограничений на управляемые параметры представляется как условие работоспособности с соответствующим запасом. [c.155]

Задача оптимизации сложной теплоэнергетической установки является многоэкстремальной, имеющей ряд локальных экстремумов. Для поиска среди них глобального экстремума используются комбинации методов случайного поиска с методами направленного поиска. По существу это заключается в том, что спуск производится из разных подобластей с последующим анализом кривых, соединяющих экстремальные и особые точки. Наличие ограничений превращает задачу поиска безусловного экстремума в задачу условного экстремума (возможность нахождения условного экстремума на границе). [c.58]

Третий этап — формирование модели (либо совокупности моделей) взаимодействия разрабатываемой конструкции и внешней среды, т. е. модели функционирования, построенной для всех этапов жизненного цикла изделия с учетом зависимостей, отража-10ЩИХ реальные физические процессы и трансформации объекта проектирования в процессе эксплуатации. Основная цель этого этапа — исследование моделей функционирования по всем параметрам, определяющим качество искомого технического решения. Именно на этом этапе разработки целесообразно привлечь методы оптимизации с целью выявления наилучшего варианта конструкции. Наиболее существенные принципиальные трудности, возникающие при реализации решения многокритериальная природа задачи необходимость учета большого числа факторов многообразие критериев условной оптимизации отсутствие простых и достаточно отработанных способов вычисления условных функционалов, задания конструктивных и технологических ограничений при моделировании реальных физических процессов и др. В связи с этим многовариантное исследование прочности конструкций на основании анализа моделей функционирования для получения рациональных, надежных и всесторонне обоснованных конструкторских решений следует признать более целесообразным, чем глобальная оптимизация разрабатываемых конструкций (что, конечно, не исключает возможности локального использования методов оптимизации конструкций на отдельных этапах проектирования). [c.288]

Методы условной оптимизации можно разделить на следующие три группы ориентированные на решение задач НЛП определенных классов (задачи сепарабельного, квадратичного, геометрического программирова- [c.157]

В качестве важной особенности ЭМУ как объекта оптимизации необходимо отметить большое количество ограничений как основных, так и вспомогательных. Это приводит к сложной конфигурации допустимой области изменения параметров, а также к существенным трудностям попада1ШЯ в нее, что в совокупности значительно усложняет поиск экстремума функции цели. При этом часто лучшим вариантам проекта соответствуют точки в пространстве параметров, лежащие на границе допустимой области. При этом задача оптимизации ЭМУ сводится к отысканию лишь условного зкстремума функции цели. Примеры такой ситуации показаны на рис. 5.15 и 5.16, где представлены области поиска соответственно при минимизации времени разгона асинхронного гиродвигателя с короткозамкнутой беличьей клеткой в пространстве параметров к(кратность максимального момента) и при оптимизации на максимум КПД (р) асинхронного конденсаторного микродвигателя [19] в пространстве параметров к — коэффициента трансформации и Хном номинального скольжения. [c.147]

Транспорт газа — одно из самых энергоемких производств, в связи с этим экономное расходование топливно-энергетических ресурсов (ТЭР) составляет одну из основных задач. Главтюменгазпром вопросам планирования, анализа и рационального расхода газа на собственные нужды уделяет постоянное внимание. Мероприятия по экономии ТЭР и материально-технических ресурсов (МТР) условно можно разбить на три группы первая — устранение прямых потерь газа и электроэнергии вторая — оптимизация загрузки компрессорных станций и агрегатов третья — оптимизация тепловых, водных, санитарных и технологических процессов в обслуживании и подготовке к работе газотранспортных систем. [c.64]

Трудоемкость решения задачи оптимизации компоновки поверхностей нагрева котлоагрегата по изложенному алгоритму вполне приемлема для реализации на ЭЦВМ среднего класса. Вместо рассмотрения нескольких миллионов (при п = 10) вариантов возможных компоновок поверхностей нагрева котлоагрегата при использовании изложенного алгоритма требуется найти и сопоставить несколько сот (на одном из средних участков максимум 252) условно оптимальных компоновок. При этом единичная поверхность нагрева, на которую расходуется подавляюш ая часть машинного времени, рассчитывается примерно пять тысяч раз вместо десяти миллионов раз при переборе всех вариантов. Учет указанных выше ограничений по компоновке поверхностей нагрева уменьшит приведенную цифру еш,е примерно вдвое. [c.47]

mash-xxl.info

Образовательный портал | ЗАДАЧА УСЛОВНОЙ ОПТИМИЗАЦИИ Методы оптимизации

Задача оптимизации (минимизации) f (x) ^ min, x е X называется задачей условной оптимизации, если X - собственное подмножество пространства Rn (X с Rn , X ф Rn). На практическом занятии рассматривается так называемая классическая задача на условный экстремум. Это задача оптимизации с допустимым множеством X, заданным системой конечного числа уравнений: X = {x е Rn : gt (x) = 0, i = 1m}. Здесь предполагается, что m Обычно эта задача записывается в виде f (x) ^ min, (2.1) gi(x) = 0, i =1,m . Для решения задачи (2.1) используется метод множителей Лагранжа. Основная идея метода заключается в переходе от задачи на условный экстремум исходной функции f (x) к задаче на безусловный экстремум некоторой специально построенной функции Лагранжа L( x, Я) m L( x, Я) = f (x) + (x), i=1 где xе Rn, Я = ( Я, Я2,..., Яm)е Rm.

МЕТОД АППРОКСИМИРУЮЩЕГО ПРОГРАММИРОВАНИЯзадач условной оптимизации. Наиболее простой и хорошо изученной задачей условной оптимизации является задача линейного программирования (ЛП). МАП является одним из методов решения задач нелинейного программирования. В данном случае исходная задача нелинейного программирования преобразуется в последовательность задач ЛП с помощью процедур линеаризации. Рассмотрим задачу условной минимизации вида
МЕТОД ШТРАФНЫХ ФУНКЦИЙзадач условной оптимизации. В данном случае ис-ходная задача условной оптимизации преобразуется в последова-тельность задач безусловной оптимизации путем введения штрафных функций. Рассмотрим задачу условной минимизации вида f (x) ^ min, xе X = {xе Rn : gt(x) задача безусловной минимизации P( x, R) = f (x) + Q(R, g (x)) ^ min, x е Rn, где P( x, R) -
методы внешней точкизадачу условной оптимизации. Рассмотрим в качестве иллюстрации аналитического решения следующий пример. Пример. Дана задача условной минимизации f (x) = x ^ min, x > 2. Легко видеть, что решением данной задачи является точка x =2, при этом f=2. Рассмотрим аналитическое решение задачи: а) методом внешней точки, б) методом внутренней точки (логарифмическая штрафная функция), в) методом
2. Задача условной оптимизацииусловный ло- 22 ' .А' 2 , 2 = {х е R : х1 + х2 = 1} имеет в точке х = условный ло- кальный максимум, а в точке х = кальный минимум. 2. Функция f (х) = х^2 + х22 + х3 в допустимой области X = {хе R3:4хj2 + х^ + 2х3 = 14} имеет в точках х = (2,2,1) и f a a ал x = (2, - 2,1) условные локальные минимумы. 3. Точка x = 3 3 3 является точкой условного максимума функции f (x) = x1x2 x3 в
Условие согласованностизадачи определения оптимального числа нанимаемых работников при учете только ограничения участия и фиксированных стратегиях центра, затем появились работы, посвященные методам решения задач управления (задач синтеза оптимальных контрактов), сфор-мулированных с учетом и ограничения участия, и условия согласо-ванности, затем акцент сместился на изучение более сложных моделей, описывающих
4.1. Принципы и методы оценки эффективности предпринимательской деятельностизадача максимизировать результат, приходящийся на единицу затрат. Предпринимательская деятельность всегда направлена на достижение цели и обязательно заканчивается результатом, даже если он не запланирован или является отрицательным (рис. 4.1). Если конечный результат совпадает с целью, деятельность можно считать рациональной, если же такое совпадение отсутствует, то деятельность является
12.4. УСЛОВИЯ ТРУДА НА ПРЕДПРИЯТИИзадач, ухудшаются общие результаты работы. Задача установления рационального режима труда и отдыха состоит в том, чтобы обеспечить быструю врабатываемость людей, максимально увеличить период устойчивой высокой работоспособ-ности и сократить'фазу утомления. На предприятиях нередко используется функциональная му зыка - музыка, сопровождающая процессы труда в производствен ной обстановке для
7.2. Методологические подходы к задачам краткосредне- и долгосрочного прогнозирования мировых товарных рынковзадач. Это находит свое конкретное выражение по меньшей мере в четырех основных содер жательных составляющих общего процесса разработки внешнеэкономи ческого прогноза в зависимости от заданного горизонта (периода) предви-дения. Во-первых, каждая из задач с позиции пользователя прогноза имеет свою целевую функциональную направленность. Краткосрочный (конъ-юнктурный) прогноз рынка имеет в первую
14.3. Мировой рынок услуг аутсорсингазадачам стратегического характера и спо собен принципиально изменить будущее организации, выстраивающей отношения со своими партнерами в долгосрочной перспективе. Развитие идеи аутсорсинга приводит к созданию организации нового типа - виртуальной и также к формированию нового типа производственных отношений, гармонично сочетающихся с процессами глобализации миро вой экономики. По расчетам,
4.3. Межотраслевые связи и межотраслевой баланс. Модель В. Леонтьева лзатраты-выпуск.задачу. Например, поставлена задача увеличить на 10 % выпуск автомо билей. Необходимо проанализировать, какие отрасли будут по ставщиками при увеличении объема производства (металлургия, машиностроение, химическая промышленность). Все эти отрасли должны направить в автомобилестроение на 10 % больше своих ресурсов. Коэффициенты прямых и косвенных затрат в каждый мо мент показывают национальную

geum.ru