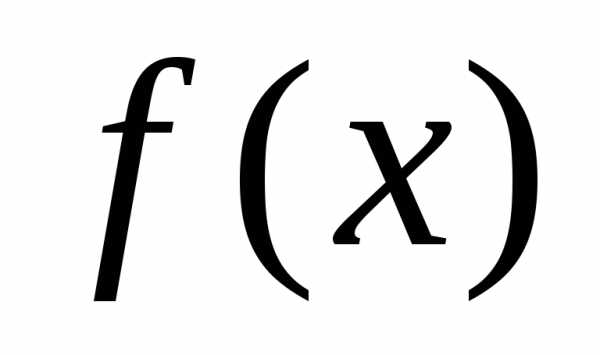численные методы / метод ньютона. Метод оптимизации ньютона
Моделирование в электроэнергетике - Безусловная оптимизация. Метод Ньютона
Безусловная оптимизация. Метод Ньютона
Метод Ньютона – это итерационный численный метод (второго порядка) решения оптимизационных задач, который позволяет определить экстремум (минимум или максимум) целевой функции:
- это значения аргумента функции (управляемые параметры), которые определены на вещественной области.
При поиске экстремума целевой функции используется информация о функции и её производных: первого и второго порядка. Итерационная формула для вычисления аргумента функции по методу Ньютона получается при квадратичной аппроксимации целевой функции, т. е. при разложении функции в ряд Тейлора (с отбрасыванием членов третьего и более высоких порядков).
где - матрица Гессе, которая представляет собой симметричную квадратную матрицу вторых частных производных целевой функции в точке
Необходимым условием экстремума функции многих переменных в точке является равенство нулю ее производной (градиента) в этой точке:
Продифференцируем функцию, разложенную в ряд Тейлора, по компоненте
Таким образом, целевая функция имеет экстремум функции при следующем значении ее аргумента:
В общем случае процесс нахождения экстремума функции является итерационной процедурой, поэтому выражение преобразуют к следующему виду:
- вектор столбец управляемых параметров, которые определяются в задаче оптимизации (размерность: 1xn)
- квадратная матрица вторых частных производных (размерность: nxn)
- вектор столбец градиента целевой функции по управляемым параметрам (размерность: 1xn).
Итерационный процесс расчета продолжается до тех пор, пока не будут выполнены некоторые критерии останова:
- траектория поиска остается в малой окрестности текущей точки поиска:
- приращение целевой функции не меняется:
- градиент целевой функции в точке локального минимума обращается в нуль:
Метод Ньютона обладает квадратичной скоростью сходимости, в отличие от других методов первого порядка (Градиентные методы), которые обладают линейной скоростью сходимости. Применение метода Ньютона оказывается очень эффективным при условии, что выполняются необходимые и достаточные условия его сходимости. Условием, гарантирующим сходимость метода Ньютона в предположении, что функция дважды дифференцируема, заключается в том, что матрица Гессе должна быть положительно определенной.
В аналитической геометрии поверхности второго порядка описываются как: эллиптический параболоид, гиперболоид, гиперболический параболоид (седло) и эллипсоид. В задачах поиска минимума квадратичной функции с положительной матрицей вторых производных метод Ньютона дает решение за одну итерацию независимо от выбора начальной точки.

Рис.1. Поиск минимума квадратичной функции по методу Ньютона
При увеличении количества переменных и усложнением функции возникают сложности с вычислением матрицы Гессе, поэтому в настоящее время разработаны квазиньютоновские алгоритмы, основанные на приближённых выражениях для матрицы Гессе. Тем не менее, многие компьютерные программы, решающие задачу оптимизации, построены на основе метода Ньютона. Роль метода Ньютона велика: большинство наиболее эффективных методов в линейном и нелинейном программировании строятся на его основе.
Методика расчета
• 1 шаг: Определяем аналитические выражения (в символьном виде) для вычисления градиента рассматриваемой функции и квадратной матрицы Гессе:
градиент рассматриваемой функции:
квадратная матрица Гессе:
• 2 шаг: Задаем начальное приближение
Далее выполняется итерационный процесс.
• 3 шаг: Определяем новые значения аргументов функции после выполнения k-го шага расчета методом по следующей формуле:
• 4 шаг: проверяем критерии останова итерационного процесса. Вычислительный процесс заканчивается, когда будет достигнута точка, в которой оценка градиента будет равна нулю (коэффициенты функции отклика становятся незначимыми). В противном случае возвращаемся к шагу 3 и продолжаем итерационный расчет.
Для того, чтобы добавить Ваш комментарий к статье, пожалуйста, зарегистрируйтесь на сайте.
simenergy.ru
метод ньютона
Метод Ньютона
Материал из Википедии — свободной энциклопедии
Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) — это итерационный численный методнахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономомИсааком Ньютоном (1643—1727). Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации. Метод обладает квадратичной сходимостью. Улучшением метода является метод хорд и касательных. Также метод Ньютона может быть использован для решения задач оптимизации, в которых требуется определить нуль первой производной либо градиента в случае многомерного пространства.
Описание метода
Обоснование
Чтобы численно решить уравнение методом простой итерации, его необходимо привести к следующей форме: , где — сжимающее отображение.
Для наилучшей сходимости метода в точке очередного приближения должно выполняться условие . Решение данного уравнения ищут в виде , тогда:
В предположении, что точка приближения «достаточно близка» к корню , и что заданная функция непрерывна , окончательная формула для такова:
С учётом этого функция определяется выражением:
Эта функция в окрестности корня осуществляет сжимающее отображение[1], и алгоритм нахождения численного решения уравнения сводится к итерационной процедуре вычисления:
По теореме Банаха последовательность приближений стремится к корню уравнения .
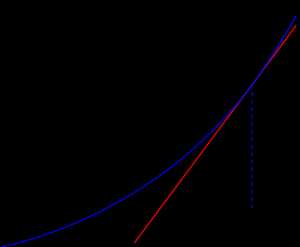
Иллюстрация метода Ньютона (синим изображена функция , нуль которой необходимо найти, красным — касательная в точке очередного приближения ). Здесь мы можем увидеть, что последующее приближение лучше предыдущего .
Геометрическая интерпретация
Основная идея метода заключается в следующем: задаётся начальное приближение вблизи предположительного корня, после чего строится касательная к исследуемой функции в точке приближения, для которой находится пересечение с осью абсцисс. Эта точка и берётся в качестве следующего приближения. И так далее, пока не будет достигнута необходимая точность.
Пусть — определённая на отрезке идифференцируемая на нём вещественнозначная функция. Тогда формула итеративного исчисления приближений может быть выведена следующим образом:
где — угол наклона касательной в точке .
Следовательно искомое выражение для имеет вид:
Итерационный процесс начинается с некоего начального приближения (чем ближе к нулю, тем лучше, но если предположения о нахождении решения отсутствуют, методом проб и ошибок можно сузить область возможных значений, применив теорему о промежуточных значениях).
Алгоритм
Задается начальное приближение .
Пока не выполнено условие остановки, в качестве которого можно взять или (то есть погрешность в нужных пределах), вычисляют новое приближение: .
Пример
| Иллюстрация применения метода Ньютона к функции с начальным приближением в точке . | |
|
График последовательных приближений. |
График сходимости. |
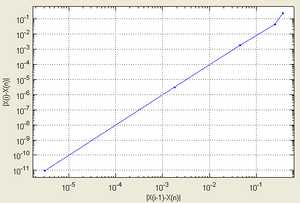
| Согласно способу практического определения скорость сходимости может быть оценена как тангенс угла наклона графика сходимости, то есть в данном случае равна двум. | |
Рассмотрим задачу о нахождении положительных , для которых . Эта задача может быть представлена как задача нахождения нуля функции . Имеем выражение для производной . Так как для всех и для , очевидно, что решение лежит между 0 и 1. Возьмём в качестве начального приближения значение , тогда:

Подчёркиванием отмечены верные значащие цифры. Видно, что их количество от шага к шагу растёт (приблизительно удваиваясь с каждым шагом): от 1 к 2, от 2 к 5, от 5 к 10, иллюстрируя квадратичную скорость сходимости.
[править]Условия применения
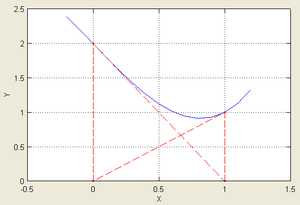
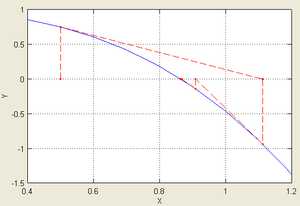
Иллюстрация расхождения метода Ньютона, применённого к функции с начальным приближением в точке .
Рассмотрим ряд примеров, указывающих на недостатки метода.
Контрпримеры
Пусть
Тогда
Возьмём нуль в качестве начального приближения. Первая итерация даст в качестве приближения единицу. В свою очередь, вторая снова даст нуль. Метод зациклится и решение не будет найдено. В общем случае построение последовательности приближений может быть очень запутанным.
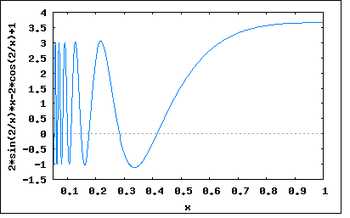
График производной функции при приближении к нулю справа.
Рассмотрим функцию:
Тогда и всюду, кроме 0.
В окрестности корня производная меняет знак при приближении к нулю справа или слева. В то время, как для .
Таким образом не ограничено вблизи корня, и метод будет расходиться, хотя функция всюду дифференцируема, её производная не равна нулю в корне, бесконечно дифференцируема везде, кроме как в корне, а её производная ограничена в окрестности корня.
Если не существует вторая производная в точке корня, то скорость сходимости метода может быть заметно снижена.
Рассмотрим пример:
Тогда и за исключением , где она не определена.
На очередном шаге имеем :
Скорость сходимости полученной последовательности составляет приблизительно 4/3. Это существенно меньше, нежели 2, необходимое для квадратичной сходимости, поэтому в данном случае можно говорить лишь о линейной сходимости, хотя функция всюду непрерывно дифференцируема, производная в корне не равна нулю, и бесконечно дифференцируема везде, кроме как в корне.
Если производная в точке корня равна нулю, то скорость сходимости не будет квадратичной, а сам метод может преждевременно прекратить поиск, и дать неверное для заданной точности приближение.
Пусть
Тогда и следовательно . Таким образом сходимость метода не квадратичная, а линейная, хотя функция всюду бесконечно дифференцируема.
Ограничения
Пусть задано уравнение , где и надо найти его решение.
Ниже приведена формулировка основной теоремы, которая позволяет дать чёткие условия применимости. Она носит имя советского математика и экономиста Леонида Витальевича Канторовича (1912—1986).
Теорема Канторовича.
Если существуют такие константы , что:
- на , то есть существует и не равна нулю;
на , то есть ограничена;
на , и ;
Причём длина рассматриваемого отрезка . Тогда справедливы следующие утверждения:
на существует корень уравнения ;
если , то итерационная последовательность сходится к этому корню: ;
погрешность может быть оценена по формуле .
Из последнего из утверждений теоремы в частности следует квадратичная сходимость метода:
Тогда ограничения на исходную функцию будут выглядеть так:
функция должна быть ограничена;
функция должна быть гладкой, дважды дифференцируемой;
её первая производная равномерно отделена от нуля;
её вторая производная должна быть равномерно ограничена.
studfiles.net
Реферат Метод Ньютона
скачатьРеферат на тему:
План:
- Введение
- 1 Описание метода
- 1.1 Обоснование
- 1.2 Геометрическая интерпретация
- 1.3 Алгоритм
- 1.4 Пример
- 2 Условия применения
- 2.1 Контрпримеры
- 2.2 Ограничения
- 3 Историческая справка
- 4 Обобщения и модификации
- 4.1 Метод одной касательной
- 4.2 Многомерный случай
- 4.3 Применительно к задачам оптимизации
- 4.4 Метод Ньютона — Рафсона
- 4.5 Применительно к задачам о наименьших квадратах
- 4.6 Метод Гаусса — Ньютона
- 4.7 Обобщение на комплексную плоскость
ЛитератураПримечания
Введение
Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643—1727), под именем которого и обрёл свою известность. Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации. Метод обладает квадратичной сходимостью. Улучшением метода является метод хорд и касательных. Также метод Ньютона может быть использован для решения задач оптимизации, в которых требуется определить нуль первой производной либо градиента в случае многомерного пространства.
1. Описание метода
1.1. Обоснование
Чтобы численно решить уравнение методом простой итерации, его необходимо привести к следующей форме: , где — сжимающее отображение.
Для наилучшей сходимости метода в точке очередного приближения должно выполняться условие . Решение данного уравнения ищут в виде , тогда:
В предположении, что точка приближения «достаточно близка» к корню , и что заданная функция непрерывна , окончательная формула для такова:
С учётом этого функция определяется выражением:
Эта функция в окрестности корня осуществляет сжимающее отображение[1], и алгоритм нахождения численного решения уравнения сводится к итерационной процедуре вычисления:
По теореме Банаха последовательность приближений стремится к корню уравнения .
1.2. Геометрическая интерпретация
Основная идея метода заключается в следующем: задаётся начальное приближение вблизи предположительного корня, после чего строится касательная к исследуемой функции в точке приближения, для которой находится пересечение с осью абсцисс. Эта точка и берётся в качестве следующего приближения. И так далее, пока не будет достигнута необходимая точность.
Пусть — определённая на отрезке и дифференцируемая на нём вещественнозначная функция. Тогда формула итеративного исчисления приближений может быть выведена следующим образом:
где α — угол наклона касательной в точке .
Следовательно искомое выражение для имеет вид:
Итерационный процесс начинается с некоего начального приближения x0 (чем ближе к нулю, тем лучше, но если предположения о нахождении решения отсутствуют, методом проб и ошибок можно сузить область возможных значений, применив теорему о промежуточных значениях).
1.3. Алгоритм
- Задается начальное приближение x0.
- Пока не выполнено условие остановки, в качестве которого можно взять или (то есть погрешность в нужных пределах), вычисляют новое приближение: .
1.4. Пример
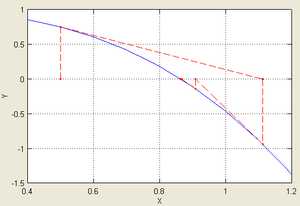 График последовательных приближений. | 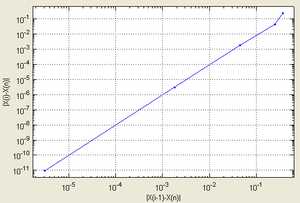 График сходимости. |
| Согласно способу практического определения скорость сходимости может быть оценена как тангенс угла наклона графика сходимости, то есть в данном случае равна двум. | |
Рассмотрим задачу о нахождении положительных x, для которых cosx = x3. Эта задача может быть представлена как задача нахождения нуля функции f(x) = cosx − x3. Имеем выражение для производной f'(x) = − sinx − 3x2. Так как для всех x и x3 > 1 для x > 1, очевидно, что решение лежит между 0 и 1. Возьмём в качестве начального приближения значение x0 = 0,5, тогда:

Подчёркиванием отмечены верные значащие цифры. Видно, что их количество от шага к шагу растёт (приблизительно удваиваясь с каждым шагом): от 1 к 2, от 2 к 5, от 5 к 10, иллюстрируя квадратичную скорость сходимости.
2. Условия применения
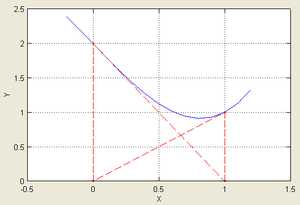 Иллюстрация расхождения метода Ньютона, применённого к функции с начальным приближением в точке .
Иллюстрация расхождения метода Ньютона, применённого к функции с начальным приближением в точке . Рассмотрим ряд примеров, указывающих на недостатки метода.
2.1. Контрпримеры
- Если начальное приближение недостаточно близко к решению, то метод может не сойтись.
Пусть
Тогда
Возьмём нуль в качестве начального приближения. Первая итерация даст в качестве приближения единицу. В свою очередь, вторая снова даст нуль. Метод зациклится и решение не будет найдено. В общем случае построение последовательности приближений может быть очень запутанным.
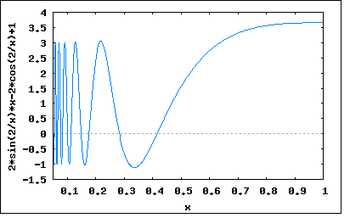 График производной функции при приближении к нулю справа.
График производной функции при приближении к нулю справа. - Если производная не непрерывна в точке корня, то метод может расходиться в любой окрестности корня.
Рассмотрим функцию:
Тогда и всюду, кроме 0.
В окрестности корня производная меняет знак при приближении x к нулю справа или слева. В то время, как для .
Таким образом не ограничено вблизи корня, и метод будет расходиться, хотя функция всюду дифференцируема, её производная не равна нулю в корне, бесконечно дифференцируема везде, кроме как в корне, а её производная ограничена в окрестности корня.
- Если не существует вторая производная в точке корня, то скорость сходимости метода может быть заметно снижена.
Рассмотрим пример:
Тогда и за исключением , где она не определена.
На очередном шаге имеем :
Скорость сходимости полученной последовательности составляет приблизительно 4/3. Это существенно меньше, нежели 2, необходимое для квадратичной сходимости, поэтому в данном случае можно говорить лишь о линейной сходимости, хотя функция всюду непрерывно дифференцируема, производная в корне не равна нулю, и бесконечно дифференцируема везде, кроме как в корне.
- Если производная в точке корня равна нулю, то скорость сходимости не будет квадратичной, а сам метод может преждевременно прекратить поиск, и дать неверное для заданной точности приближение.
Пусть
Тогда и следовательно . Таким образом сходимость метода не квадратичная, а линейная, хотя функция всюду бесконечно дифференцируема.
2.2. Ограничения
Пусть задано уравнение , где и надо найти его решение.
Ниже приведена формулировка основной теоремы, которая позволяет дать чёткие условия применимости. Она носит имя советского математика и экономиста, лауреата Нобелевской премии по экономике 1975 года «за вклад в теорию оптимального распределения ресурсов» Леонида Витальевича Канторовича (1912—1986) и является одной из многочисленных теорем, ставших результатами его научных изысканий.
Теорема Канторовича.
Если существуют такие константы , что:
- на , то есть существует и не равна нулю;
- на , то есть ограничена;
- на , и ;
Причём длина рассматриваемого отрезка . Тогда справедливы следующие утверждения:
- на существует корень уравнения ;
- если , то итерационная последовательность сходится к этому корню: ;
- погрешность может быть оценена по формуле .
Из последнего из утверждений теоремы в частности следует квадратичная сходимость метода:
Тогда ограничения на исходную функцию будут выглядеть так:
- функция должна быть ограничена;
- функция должна быть гладкой, дважды дифференцируемой;
- её первая производная равномерно отделена от нуля;
- её вторая производная должна быть равномерно ограничена.
3. Историческая справка
Метод был описан Исааком Ньютоном в рукописи «Об анализе уравнениями бесконечных рядов» (лат. «De analysi per aequationes numero terminorum infinitas»), адресованной в 1669 году Барроу, и в работе «Метод флюксий и бесконечные ряды» (лат. «De metodis fluxionum et serierum infinitarum») или «Аналитическая геометрия» (лат. «Geometria analytica») в собраниях трудов Ньютона, которая была написана в 1671 году. В своих работах Ньютон вводит такие понятия, как разложение функции в ряд, бесконечно малые и флюксии (производные в нынешнем понимании). Указанные работы были изданы значительно позднее: первая вышла в свет в 1711 году благодаря Уильяму Джонсону, вторая была издана Джоном Кользоном в 1736 году уже после смерти создателя. Однако описание метода существенно отличалось от его нынешнего изложения: Ньютон применял свой метод исключительно к полиномам. Он вычислял не последовательные приближения xn, а последовательность полиномов и в результате получал приближённое решение x.
Впервые метод был опубликован в трактате «Алгебра» Джона Валлиса в 1685 году, по просьбе которого он был кратко описан самим Ньютоном. В 1690 году Джозеф Рафсон опубликовал упрощённое описание в работе «Общий анализ уравнений» (лат. «Analysis aequationum universalis»). Рафсон рассматривал метод Ньютона как чисто алгебраический и ограничил его применение полиномами, однако при этом он описал метод на основе последовательных приближений xn вместо более трудной для понимания последовательности полиномов, использованной Ньютоном. Наконец, в 1740 году метод Ньютона был описан Томасом Симпсоном как итеративный метод первого порядка решения нелинейных уравнений с использованием производной в том виде, в котором он излагается здесь. В той же публикации Симпсон обобщил метод на случай системы из двух уравнений и отметил, что метод Ньютона также может быть применён для решения задач оптимизации путём нахождения нуля производной или градиента.
В 1879 году Артур Кэли в работе «Проблема комплексных чисел Ньютона — Фурье» (англ. «The Newton-Fourier imaginary problem») был первым, кто отметил трудности в обобщении метода Ньютона на случай мнимых корней полиномов степени выше второй и комплексных начальных приближений. Эта работа открыла путь к изучению теории фракталов.
4. Обобщения и модификации
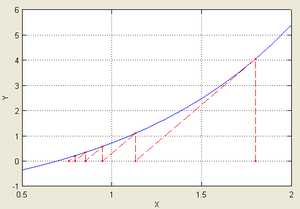 Иллюстрация последовательных приближений метода одной касательной, применённого к функции с начальным приближением в точке .
Иллюстрация последовательных приближений метода одной касательной, применённого к функции с начальным приближением в точке . 4.1. Метод одной касательной
В целях уменьшения числа обращений к значениям производной функции применяют так называемый метод одной касательной.
Формула итераций этого метода имеет вид:
Суть метода заключается в том, чтобы вычислять производную лишь один раз, в точке начального приближения , а затем использовать это значение на каждой последующей итерации:
При таком выборе в точке выполнено равенство:
и если отрезок, на котором предполагается наличие корня и выбрано начальное приближение , достаточно мал, а производная непрерывна, то значение будет не сильно отличаться от и, следовательно, график пройдёт почти горизонтально, пересекая прямую , что в свою очередь обеспечит быструю сходимость последовательности точек приближений к корню.
Этот метод можно также рассматривать, как модернизацию метода хорд (секущих), где число следует выбрать равным
4.2. Многомерный случай
Обобщим полученный результат на многомерный случай.
Пускай необходимо найти решение системы:
Выбирая некоторое начальное значение , последовательные приближения находят путём решения систем уравнений:
где .
4.3. Применительно к задачам оптимизации
Пусть необходимо найти минимум функции многих переменных . Эта задача равносильна задаче нахождения нуля градиента . Применим изложенный выше метод Ньютона:
где — гессиан функции .
В более удобном итеративном виде это выражение выглядит так:
Следует отметить, что в случае квадратичной функции метод Ньютона находит экстремум за одну итерацию.
Нахождение матрицы Гессе связано с большими вычислительными затратами, и зачастую не представляется возможным. В таких случаях альтернативой могут служить квазиньютоновские методы, в которых приближение матрицы Гессе строится в процессе накопления информации о кривизне функции.
4.4. Метод Ньютона — Рафсона
Метод Ньютона — Рафсона является улучшением метода Ньютона нахождения экстремума, описанного выше. Основное отличие заключается в том, что на очередной итерации каким-либо из методов одномерной оптимизации выбирается оптимальный шаг:
где Для оптимизации вычислений применяют следующее улучшение: вместо того, чтобы на каждой итерации заново вычислять гессиан целевой функции, ограничиваются начальным приближением и обновляют его лишь раз в шагов, либо не обновляют вовсе.
4.5. Применительно к задачам о наименьших квадратах
На практике часто встречаются задачи, в которых требуется произвести настройку свободных параметров объекта или подогнать математическую модель под реальные данные. В этих случаях появляются задачи о наименьших квадратах:
Эти задачи отличаются особым видом градиента и матрицы Гессе:
где — матрица Якоби вектор-функции , — матрица Гессе для её компоненты .
Тогда очередное направление определяется из системы:
4.6. Метод Гаусса — Ньютона
Метод Гаусса — Ньютона строится на предположении о том, что слагаемое доминирует над . Это требование не соблюдается, если минимальные невязки велики, то есть если норма сравнима с максимальным собственным значением матрицы . В противном случае можно записать:
Таким образом, когда норма близка к нулю, а матрица имеет полный столбцевой ранг, направление мало отличается от ньютоновского (с учётом ), и метод может достигать квадратичной скорости сходимости, хотя вторые производные и не учитываются. Улучшением метода является алгоритм Левенберга — Марквардта, основанный на эвристических соображениях.
4.7. Обобщение на комплексную плоскость
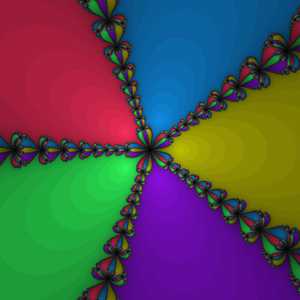 Бассейны Ньютона для полинома пятой степени . Разными цветами закрашены области притяжения для разных корней. Более тёмные области соответствуют большему числу итераций.
Бассейны Ньютона для полинома пятой степени . Разными цветами закрашены области притяжения для разных корней. Более тёмные области соответствуют большему числу итераций. До сих пор в описании метода использовались функции, осуществляющие отображения в пределах множества вещественных значений. Однако метод может быть применён и для нахождения нуля функции комплексного переменного. При этом процедура остаётся неизменной:
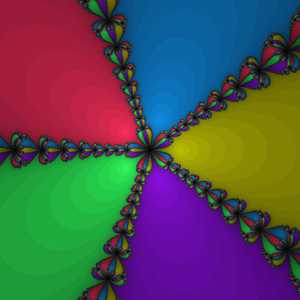
Особый интерес представляет выбор начального приближения . Ввиду того, что функция может иметь несколько нулей, в различных случаях метод может сходиться к различным значениям, и вполне естественно возникает желание выяснить, какие области обеспечат сходимость к тому или иному корню. Этот вопрос заинтересовал Артура Кейли ещё в 1879 году, однако разрешить его смогли лишь в 70-х годах двадцатого столетия с появлением вычислительной техники. Оказалось, что на пересечениях этих областей (их принято называть областями притяжения) образуются так называемые фракталы — бесконечные самоподобные геометрические фигуры.
Ввиду того, что Ньютон применял свой метод исключительно к полиномам, фракталы, образованные в результате такого применения, обрели название фракталов Ньютона или бассейнов Ньютона.
Литература
- Акулич И. Л. Математическое программирование в примерах и задачах: Учеб. пособие для студентов эконом. спец. вузов. — М.: Высш. шк., 1986.
- Амосов А. А., Дубинский Ю. А., Копченова Н. П. Вычислительные методы для инженеров. — М.: Мир, 1998.
- Бахвалов Н. С., Жидков Н. П., Кобельков Г. Г. Численные методы. — 8-е изд.. — М.: Лаборатория Базовых Знаний, 2000.
- Вавилов С. И. Исаак Ньютон. — М.: Изд. АН СССР, 1945.
- Волков Е. А. Численные методы. — М.: Физматлит, 2003.
- Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. Пер. с англ. — М.: Мир, 1985.
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М.: Наука, 1970. — С. 575-576.
- Коршунов Ю. М., Коршунов Ю. М. Математические основы кибернетики. — Энергоатомиздат, 1972.
- Максимов Ю. А.,Филлиповская Е. А. Алгоритмы решения задач нелинейного программирования. — М.: МИФИ, 1982.
- Морозов А. Д. Введение в теорию фракталов. — МИФИ, 2002.
Примечания
wreferat.baza-referat.ru
Метод Ньютона.
- один постоянный член любой точки данной функции является оптимальным – тривиальный случай;
линейная функция (двучлен)
(возможно бесконечное уменьшение и увеличение)
1 И 2 не подходят для оптимизации.
трехчлен
;
без ограничения общности можно положить что матрица q– симметричная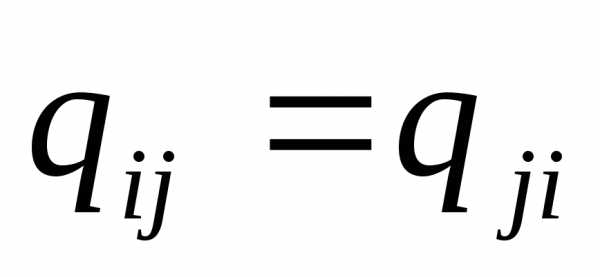
Разложим функцию в ряд Тейлора (должно быть 3 члена). Чтобы найти линейный член квадратичной функции, надо взять grad.
;
;С =0
Найдем матрицу Гесса (матрица вторых частных производных)
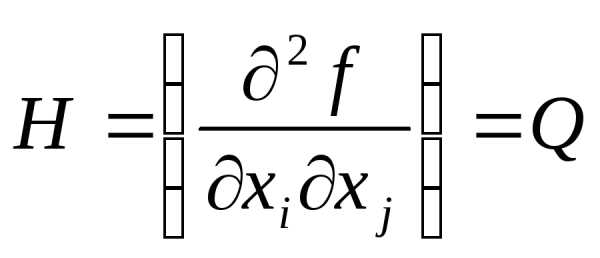
элемент матрицы Гесса является элементом функции Q.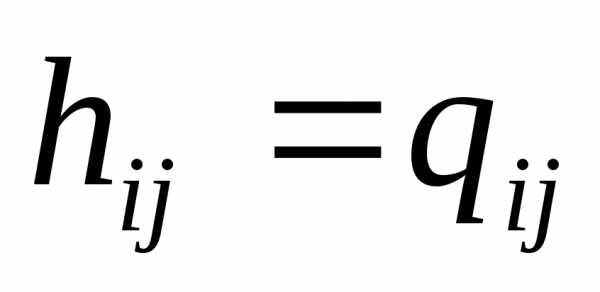 (все частные производные высших порядков равны 0).
(все частные производные высших порядков равны 0).
Функция экстремальна, если gradв данной точке равен 0,следовательно условие экстремальности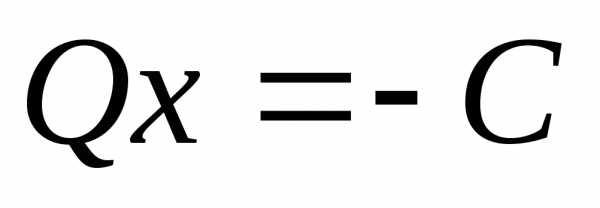 - система.
- система.
Необходимое условие оптимальности:
Если  решение данной системы существует и оно единственное (совместная система).
решение данной системы существует и оно единственное (совместная система).
Если 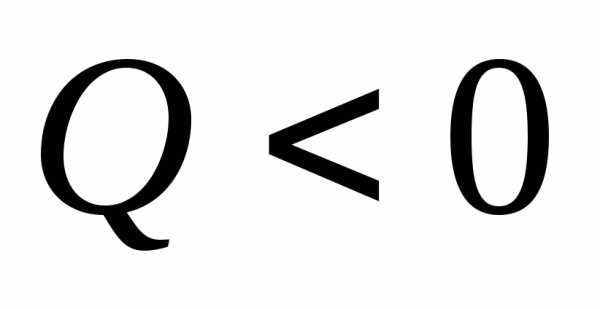 решение данной системы существует и оно единственное, т.е. еслиQзнакоопределена, то существует решение и оно единственное.
решение данной системы существует и оно единственное, т.е. еслиQзнакоопределена, то существует решение и оно единственное.
Если имеем квадратичную функцию и матрица положительно определена, то линии уровня – эллипсы.
Собственные значения определяют оси эллипсов.
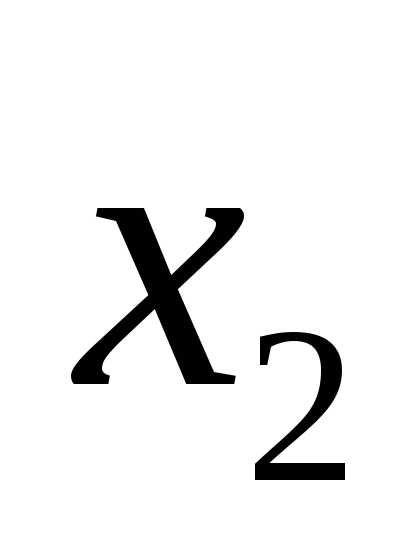
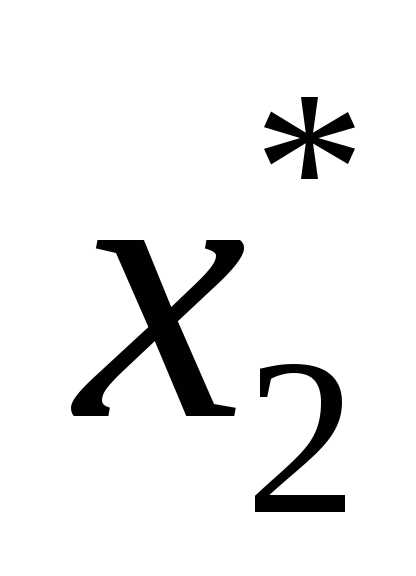
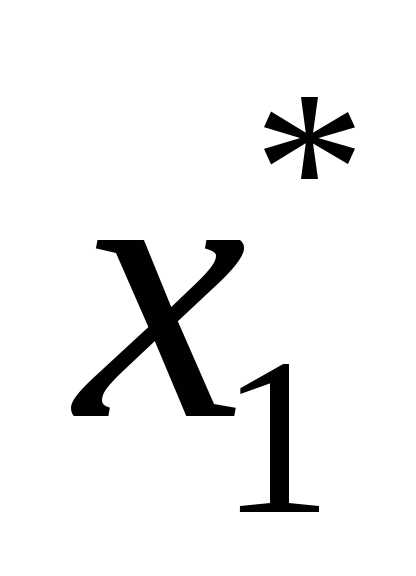
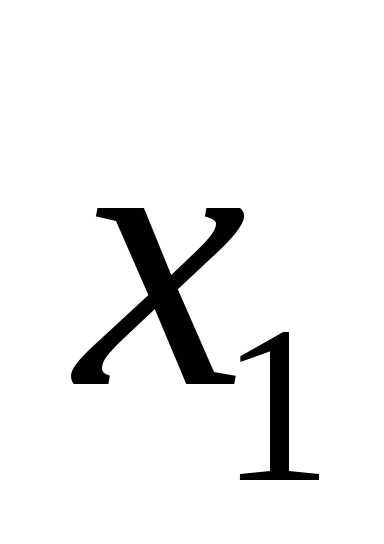
Чтобы определить координаты точки локального минимума, нужно решить систему 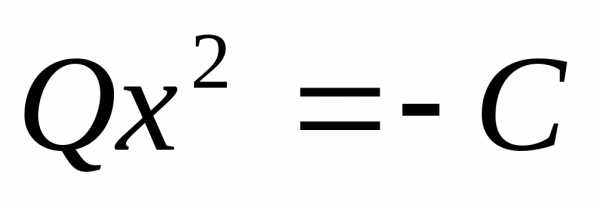 .
.
Пусть f(x)– произвольная функция и надо найти точку локального минимума. Разложим функцию в ряд Тейлора в окрестности точки.
Пусть функция не квадратичная, эллипсы примерно отражают кривизну линий уровня и находятся в окрестности точки 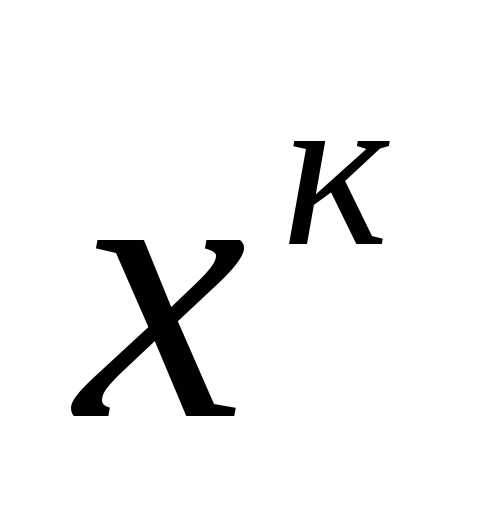 . В окрестности точки
. В окрестности точки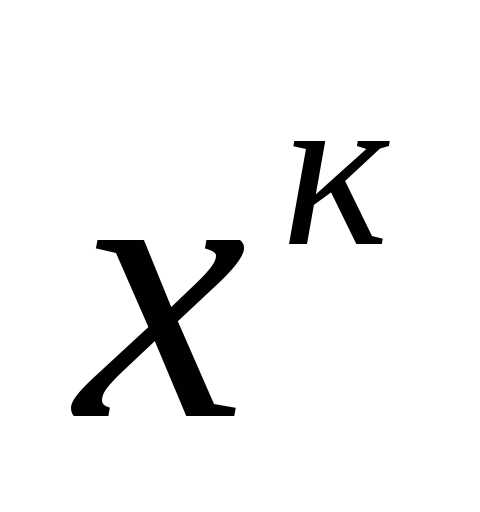 находим приближение и заменяем эту функцию квадратичной функцией, которая получается из разложения в ряд Тейлора. Далее решаем задачу минимизации.
находим приближение и заменяем эту функцию квадратичной функцией, которая получается из разложения в ряд Тейлора. Далее решаем задачу минимизации.
Находим точку минимума и рассматриваем эту точку как следующее приближение и т.д.
Для нахождения точки минимума квадратичной функции (зависит от 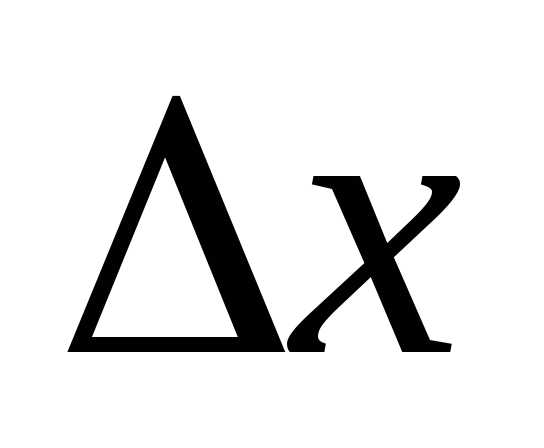 )необходимо решить систему:
)необходимо решить систему:
Окончательно следующее приближение .
- формула Ньютона
(обобщение формулы минимизации одной переменной)
Выполнение метода останавливается когда  , т.е. когда
, т.е. когда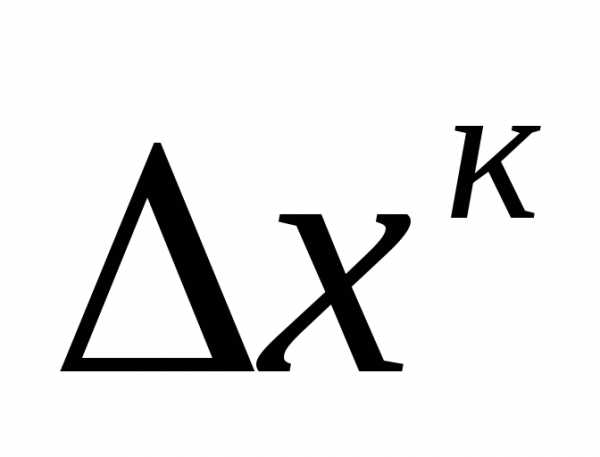 очень мало. Для получения практической точности достаточно выполнить 4 итерации метода Ньютона.
очень мало. Для получения практической точности достаточно выполнить 4 итерации метода Ньютона.
Если f– хороша, то метод Ньютона подходит, еслиf– квадратичная функция, то метод Ньютона приводит к минимальной точке за 1 шаг, из любой точки.
Недостатки:
на каждом шаге итерации надо находить решение системы ;
С ростом числа итераций Н– разрежается, т.е. большое число членов становится равными 0.
Все формулы безусловной минимизации можно записать в общую схему:
выбор направления;
выбор шага.
|
|
|
Допустим, требуется f(x)min;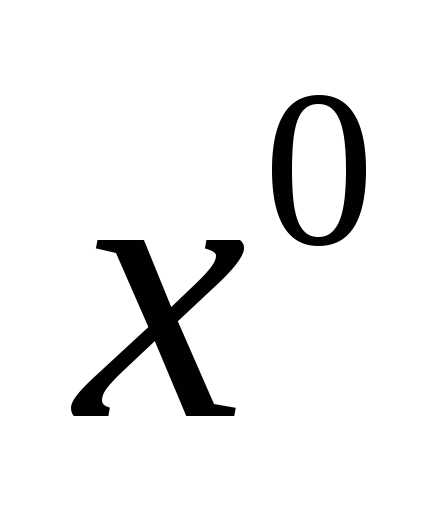 - начальное приближение;
- начальное приближение;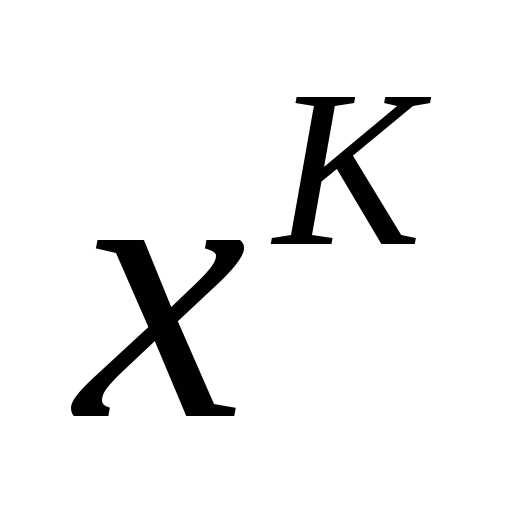 - текущее приближение
- текущее приближение
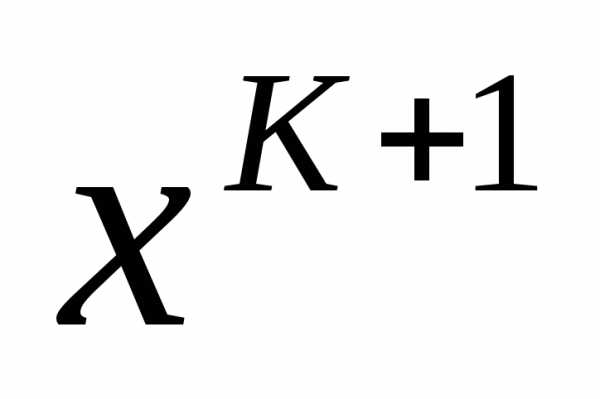
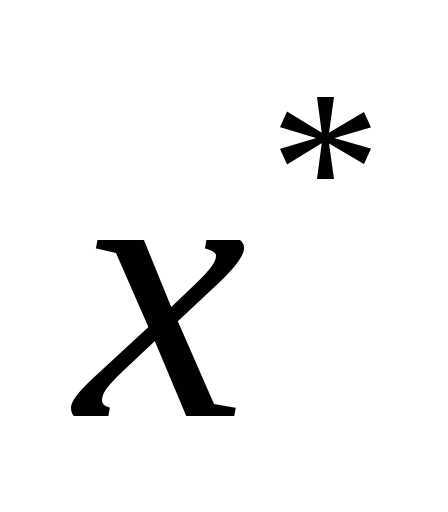
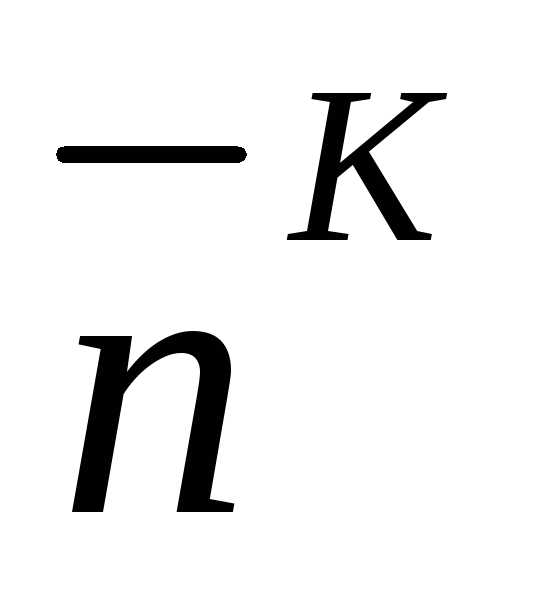
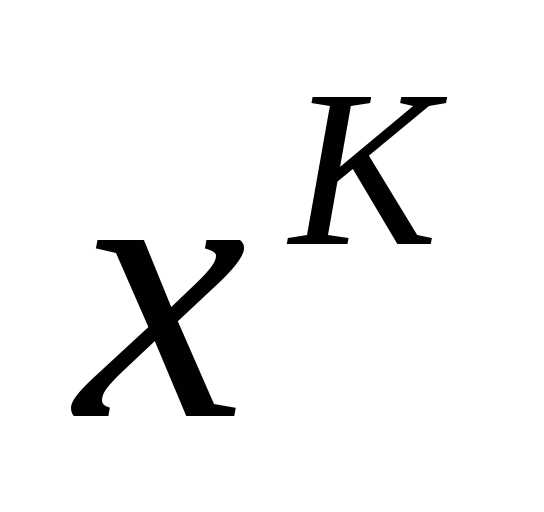
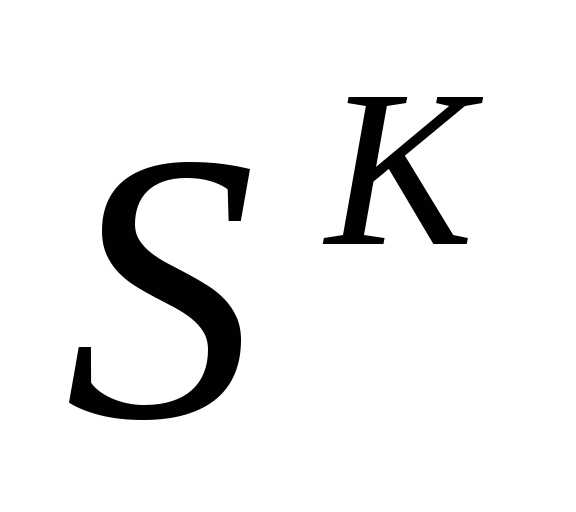
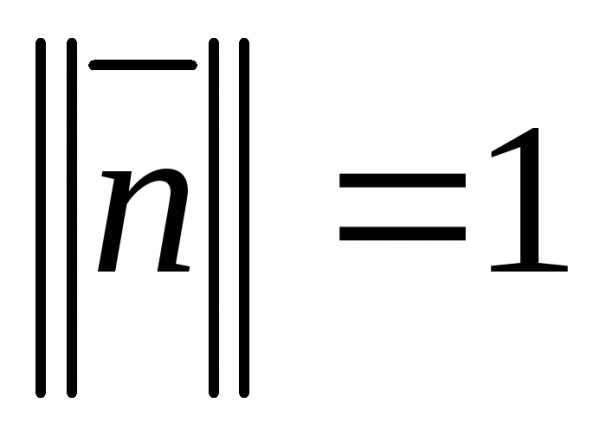
а) выбор направления ;
б) движение вдоль выбранного направления
studfiles.net
Модифицированный метод Ньютона
Обратная связь
ПОЗНАВАТЕЛЬНОЕ
Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса - ваш вокал
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший "Салат из свеклы с чесноком"
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
При поиске экстремума неквадратных функций метод Ньютона не очень надежен, при неудачном выборе начального приближения шаг поиска окажется слишком большим и итерации не сойдутся. Для устранения этого недостатка используют модифицированный метод Ньютона. Он реализуется такими итерациями:
, .
Коэффициент (параметр шага) выбирают на каждом шаге так, чтобы , (как в методе Коши), это гарантирует, что .
Метод эффективный и надежный, если вычисление первых и вторых производных не связано с трудностями. Недостаток состоит в необходимости построения и решения линейного уравнения, содержащего элементы матрицы Гессе (для вычисления ).
Метод Марквардта
Метод Марквардта (1963 г.) является комбинацией методов Коши и Ньютона, сочетает положительные свойства обоих методов. Итерации выполняются по формуле
.
Направление поиска на каждой итерации определяется как
,
где – матрица Гессе; – единичная матрица.
В начале поиска значение >>1 (например, ), тогда
,
и направление поиска:
.
Если после первого шага получается точка с меньшим значением целевой функции , следует выбрать < и продолжить. Иначе принять , и вновь реализовать предыдущий шаг.
Преимущества алгоритма: простота, высокая скорость сходимости в окрестности минимума .
Недостаток алгоритма: необходимость вычисления матрицы Гессе и обращения матрицы .
Метод хорошо работает в задачах с целевой функцией вида
(например, задачи регрессионного анализа).
Квазиньютоновские методы
Квазиньютоновские методы оптимизации обладают положительными чертами метода Ньютона, но используют только первые производные. Все квазиньютоновские методы используют итерационную процедуру (4.1), в которой направление поиска задается в виде
,
где – положительно определенная симметрическая матрица, которая называется метрика. Матрица аппроксимирует обратную матрицу Гессе и обновляется на каждой итерации, поэтому квазиньтоновские методы называются методами переменной метрики. Метрика обновляется с помощью рекуррентного соотношения
,
где – корректирующая матрица, и в пределе становится равной обратному гессиану.
Метод Дэвидона-Флетчера-Пауэлла (ДФП). Один из наиболее широко применяемых градиентных методов – метод Дэвидона-Флетчера-Пауэлла (ДФП). Используются следующие обозначения
, или
Упрощенно алгоритм можно представить такими шагами
1. Задать начальную точку и начальную матрицу (обычно единичная матрица)
2. Минимизировать
3. Вычислить .
4. Обновить метрику
5. Вычислить
6. Если не выполнены условия окончания поиска, то присвоить , перейти на 2.
7. Конец алгоритма.
Метод ДФП использует идеи метода Ньютона-Рафсона и свойство сопряженных направлений. Для минимизации квадратичной функции переменных метод ДФП сходится не более чем за итераций. Это весьма мощная оптимизационная процедура, очень эффективная при оптимизации большинства функций независимо от того, квадратичны они или нет.
megapredmet.ru
Метод Ньютона - это... Что такое Метод Ньютона?
Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643—1727). Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации. Метод обладает квадратичной сходимостью. Улучшением метода является метод хорд и касательных. Также метод Ньютона может быть использован для решения задач оптимизации, в которых требуется определить нуль первой производной либо градиента в случае многомерного пространства.
Описание метода
Обоснование
Чтобы численно решить уравнение методом простой итерации, его необходимо привести к следующей форме: , где — сжимающее отображение.
Для наилучшей сходимости метода в точке очередного приближения должно выполняться условие . Решение данного уравнения ищут в виде , тогда:
В предположении, что точка приближения «достаточно близка» к корню , и что заданная функция непрерывна , окончательная формула для такова:
С учётом этого функция определяется выражением:
Эта функция в окрестности корня осуществляет сжимающее отображение[1], и алгоритм нахождения численного решения уравнения сводится к итерационной процедуре вычисления:
По теореме Банаха последовательность приближений стремится к корню уравнения .
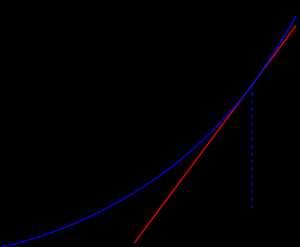
Геометрическая интерпретация
Основная идея метода заключается в следующем: задаётся начальное приближение вблизи предположительного корня, после чего строится касательная к исследуемой функции в точке приближения, для которой находится пересечение с осью абсцисс. Эта точка и берётся в качестве следующего приближения. И так далее, пока не будет достигнута необходимая точность.
Пусть — определённая на отрезке и дифференцируемая на нём вещественнозначная функция. Тогда формула итеративного исчисления приближений может быть выведена следующим образом:
где — угол наклона касательной в точке .
Следовательно искомое выражение для имеет вид:
Итерационный процесс начинается с некоего начального приближения (чем ближе к нулю, тем лучше, но если предположения о нахождении решения отсутствуют, методом проб и ошибок можно сузить область возможных значений, применив теорему о промежуточных значениях).
Алгоритм
- Задается начальное приближение .
- Пока не выполнено условие остановки, в качестве которого можно взять или (то есть погрешность в нужных пределах), вычисляют новое приближение: .
Пример
Рассмотрим задачу о нахождении положительных , для которых . Эта задача может быть представлена как задача нахождения нуля функции . Имеем выражение для производной . Так как для всех и для , очевидно, что решение лежит между 0 и 1. Возьмём в качестве начального приближения значение , тогда:
Подчёркиванием отмечены верные значащие цифры. Видно, что их количество от шага к шагу растёт (приблизительно удваиваясь с каждым шагом): от 1 к 2, от 2 к 5, от 5 к 10, иллюстрируя квадратичную скорость сходимости.
Условия применения
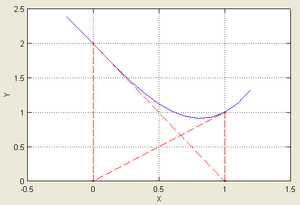 Иллюстрация расхождения метода Ньютона, применённого к функции с начальным приближением в точке .
Иллюстрация расхождения метода Ньютона, применённого к функции с начальным приближением в точке . Рассмотрим ряд примеров, указывающих на недостатки метода.
Контрпримеры
- Если начальное приближение недостаточно близко к решению, то метод может не сойтись.
Пусть
Тогда
Возьмём нуль в качестве начального приближения. Первая итерация даст в качестве приближения единицу. В свою очередь, вторая снова даст нуль. Метод зациклится и решение не будет найдено. В общем случае построение последовательности приближений может быть очень запутанным.
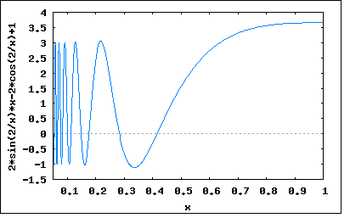 График производной функции при приближении к нулю справа.
График производной функции при приближении к нулю справа. Рассмотрим функцию:
Тогда и всюду, кроме 0.
В окрестности корня производная меняет знак при приближении к нулю справа или слева. В то время, как для .
Таким образом не ограничено вблизи корня, и метод будет расходиться, хотя функция всюду дифференцируема, её производная не равна нулю в корне, бесконечно дифференцируема везде, кроме как в корне, а её производная ограничена в окрестности корня.
Рассмотрим пример:
Тогда и за исключением , где она не определена.
На очередном шаге имеем :
Скорость сходимости полученной последовательности составляет приблизительно 4/3. Это существенно меньше, нежели 2, необходимое для квадратичной сходимости, поэтому в данном случае можно говорить лишь о линейной сходимости, хотя функция всюду непрерывно дифференцируема, производная в корне не равна нулю, и бесконечно дифференцируема везде, кроме как в корне.
- Если производная в точке корня равна нулю, то скорость сходимости не будет квадратичной, а сам метод может преждевременно прекратить поиск, и дать неверное для заданной точности приближение.
Пусть
Тогда и следовательно . Таким образом сходимость метода не квадратичная, а линейная, хотя функция всюду бесконечно дифференцируема.
Ограничения
Пусть задано уравнение , где и надо найти его решение.
Ниже приведена формулировка основной теоремы, которая позволяет дать чёткие условия применимости. Она носит имя советского математика и экономиста Леонида Витальевича Канторовича (1912—1986).
Теорема Канторовича.
Если существуют такие константы , что:
- на , то есть существует и не равна нулю;
- на , то есть ограничена;
- на , и ;
Причём длина рассматриваемого отрезка . Тогда справедливы следующие утверждения:
- на существует корень уравнения ;
- если , то итерационная последовательность сходится к этому корню: ;
- погрешность может быть оценена по формуле .
Из последнего из утверждений теоремы в частности следует квадратичная сходимость метода:
Тогда ограничения на исходную функцию будут выглядеть так:
- функция должна быть ограничена;
- функция должна быть гладкой, дважды дифференцируемой;
- её первая производная равномерно отделена от нуля;
- её вторая производная должна быть равномерно ограничена.
Историческая справка
Метод был описан Исааком Ньютоном в рукописи «Об анализе уравнениями бесконечных рядов» (лат. «De analysi per aequationes numero terminorum infinitas»), адресованной в 1669 году Барроу, и в работе «Метод флюксий и бесконечные ряды» (лат. «De metodis fluxionum et serierum infinitarum») или «Аналитическая геометрия» (лат. «Geometria analytica») в собраниях трудов Ньютона, которая была написана в 1671 году. В своих работах Ньютон вводит такие понятия, как разложение функции в ряд, бесконечно малые и флюксии (производные в нынешнем понимании). Указанные работы были изданы значительно позднее: первая вышла в свет в 1711 году благодаря Уильяму Джонсону, вторая была издана Джоном Кользоном в 1736 году уже после смерти создателя. Однако описание метода существенно отличалось от его нынешнего изложения: Ньютон применял свой метод исключительно к полиномам. Он вычислял не последовательные приближения , а последовательность полиномов и в результате получал приближённое решение .
Впервые метод был опубликован в трактате «Алгебра» Джона Валлиса в 1685 году, по просьбе которого он был кратко описан самим Ньютоном. В 1690 году Джозеф Рафсон опубликовал упрощённое описание в работе «Общий анализ уравнений» (лат. «Analysis aequationum universalis»). Рафсон рассматривал метод Ньютона как чисто алгебраический и ограничил его применение полиномами, однако при этом он описал метод на основе последовательных приближений вместо более трудной для понимания последовательности полиномов, использованной Ньютоном. Наконец, в 1740 году метод Ньютона был описан Томасом Симпсоном как итеративный метод первого порядка решения нелинейных уравнений с использованием производной в том виде, в котором он излагается здесь. В той же публикации Симпсон обобщил метод на случай системы из двух уравнений и отметил, что метод Ньютона также может быть применён для решения задач оптимизации путём нахождения нуля производной или градиента.
В 1879 году Артур Кэли в работе «Проблема комплексных чисел Ньютона — Фурье» (англ. «The Newton-Fourier imaginary problem») был первым, кто отметил трудности в обобщении метода Ньютона на случай мнимых корней полиномов степени выше второй и комплексных начальных приближений. Эта работа открыла путь к изучению теории фракталов.
Обобщения и модификации
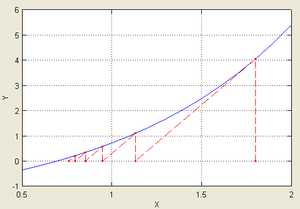 Иллюстрация последовательных приближений метода одной касательной, применённого к функции с начальным приближением в точке .
Иллюстрация последовательных приближений метода одной касательной, применённого к функции с начальным приближением в точке . Метод одной касательной
В целях уменьшения числа обращений к значениям производной функции применяют так называемый метод одной касательной.
Формула итераций этого метода имеет вид:
Суть метода заключается в том, чтобы вычислять производную лишь один раз, в точке начального приближения , а затем использовать это значение на каждой последующей итерации:
При таком выборе в точке выполнено равенство:
и если отрезок, на котором предполагается наличие корня и выбрано начальное приближение , достаточно мал, а производная непрерывна, то значение будет не сильно отличаться от и, следовательно, график пройдёт почти горизонтально, пересекая прямую , что в свою очередь обеспечит быструю сходимость последовательности точек приближений к корню.
Этот метод можно также рассматривать, как модернизацию метода хорд (секущих), где число следует выбрать равным
Многомерный случай
Обобщим полученный результат на многомерный случай.
Пусть необходимо найти решение системы:
Выбирая некоторое начальное значение , последовательные приближения находят путём решения систем уравнений:
где .
Применительно к задачам оптимизации
Пусть необходимо найти минимум функции многих переменных . Эта задача равносильна задаче нахождения нуля градиента . Применим изложенный выше метод Ньютона:
где — гессиан функции .
В более удобном итеративном виде это выражение выглядит так:
Следует отметить, что в случае квадратичной функции метод Ньютона находит экстремум за одну итерацию.
Нахождение матрицы Гессе связано с большими вычислительными затратами, и зачастую не представляется возможным. В таких случаях альтернативой могут служить квазиньютоновские методы, в которых приближение матрицы Гессе строится в процессе накопления информации о кривизне функции.
Метод Ньютона — Рафсона
Метод Ньютона — Рафсона является улучшением метода Ньютона нахождения экстремума, описанного выше. Основное отличие заключается в том, что на очередной итерации каким-либо из методов одномерной оптимизации выбирается оптимальный шаг:
где Для оптимизации вычислений применяют следующее улучшение: вместо того, чтобы на каждой итерации заново вычислять гессиан целевой функции, ограничиваются начальным приближением и обновляют его лишь раз в шагов, либо не обновляют вовсе.
Применительно к задачам о наименьших квадратах
На практике часто встречаются задачи, в которых требуется произвести настройку свободных параметров объекта или подогнать математическую модель под реальные данные. В этих случаях появляются задачи о наименьших квадратах:
Эти задачи отличаются особым видом градиента и матрицы Гессе:
где — матрица Якоби вектор-функции , — матрица Гессе для её компоненты .
Тогда очередное направление определяется из системы:
Метод Гаусса — Ньютона
Метод Гаусса — Ньютона строится на предположении о том, что слагаемое доминирует над . Это требование не соблюдается, если минимальные невязки велики, то есть если норма сравнима с максимальным собственным значением матрицы . В противном случае можно записать:
Таким образом, когда норма близка к нулю, а матрица имеет полный столбцевой ранг, направление мало отличается от ньютоновского (с учётом ), и метод может достигать квадратичной скорости сходимости, хотя вторые производные и не учитываются. Улучшением метода является алгоритм Левенберга — Марквардта, основанный на эвристических соображениях.
Обобщение на комплексную плоскость
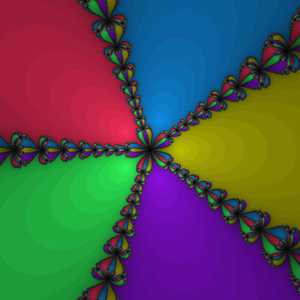 Бассейны Ньютона для полинома пятой степени . Разными цветами закрашены области притяжения для разных корней. Более тёмные области соответствуют большему числу итераций.
Бассейны Ньютона для полинома пятой степени . Разными цветами закрашены области притяжения для разных корней. Более тёмные области соответствуют большему числу итераций. До сих пор в описании метода использовались функции, осуществляющие отображения в пределах множества вещественных значений. Однако метод может быть применён и для нахождения нуля функции комплексного переменного. При этом процедура остаётся неизменной:
Особый интерес представляет выбор начального приближения . Ввиду того, что функция может иметь несколько нулей, в различных случаях метод может сходиться к различным значениям, и вполне естественно возникает желание выяснить, какие области обеспечат сходимость к тому или иному корню. Этот вопрос заинтересовал Артура Кейли ещё в 1879 году, однако разрешить его смогли лишь в 70-х годах двадцатого столетия с появлением вычислительной техники. Оказалось, что на пересечениях этих областей (их принято называть областями притяжения) образуются так называемые фракталы — бесконечные самоподобные геометрические фигуры.
Ввиду того, что Ньютон применял свой метод исключительно к полиномам, фракталы, образованные в результате такого применения, обрели название фракталов Ньютона или бассейнов Ньютона.
Литература
- Акулич И. Л. Математическое программирование в примерах и задачах: Учеб. пособие для студентов эконом. спец. вузов. — М.: Высш. шк., 1986.
- Амосов А. А., Дубинский Ю. А., Копченова Н. П. Вычислительные методы для инженеров. — М.: Мир, 1998.
- Бахвалов Н. С., Жидков Н. П., Кобельков Г. Г. Численные методы. — 8-е изд.. — М.: Лаборатория Базовых Знаний, 2000.
- Вавилов С. И. Исаак Ньютон. — М.: Изд. АН СССР, 1945.
- Волков Е. А. Численные методы. — М.: Физматлит, 2003.
- Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. Пер. с англ. — М.: Мир, 1985.
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М.: Наука, 1970. — С. 575-576.
- Коршунов Ю. М., Коршунов Ю. М. Математические основы кибернетики. — Энергоатомиздат, 1972.
- Максимов Ю. А.,Филлиповская Е. А. Алгоритмы решения задач нелинейного программирования. — М.: МИФИ, 1982.
- Морозов А. Д. Введение в теорию фракталов. — МИФИ, 2002.
Примечания
См. также
Ссылки
dic.academic.ru
Метод Ньютона - это... Что такое Метод Ньютона?
Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643—1727). Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации. Метод обладает квадратичной сходимостью. Улучшением метода является метод хорд и касательных. Также метод Ньютона может быть использован для решения задач оптимизации, в которых требуется определить нуль первой производной либо градиента в случае многомерного пространства.
Описание метода
Обоснование
Чтобы численно решить уравнение методом простой итерации, его необходимо привести к следующей форме: , где — сжимающее отображение.
Для наилучшей сходимости метода в точке очередного приближения должно выполняться условие . Решение данного уравнения ищут в виде , тогда:
В предположении, что точка приближения «достаточно близка» к корню , и что заданная функция непрерывна , окончательная формула для такова:
С учётом этого функция определяется выражением:
Эта функция в окрестности корня осуществляет сжимающее отображение[1], и алгоритм нахождения численного решения уравнения сводится к итерационной процедуре вычисления:
По теореме Банаха последовательность приближений стремится к корню уравнения .
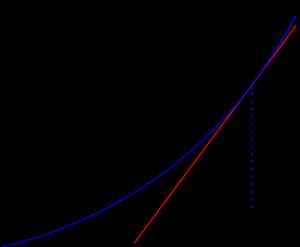
Геометрическая интерпретация
Основная идея метода заключается в следующем: задаётся начальное приближение вблизи предположительного корня, после чего строится касательная к исследуемой функции в точке приближения, для которой находится пересечение с осью абсцисс. Эта точка и берётся в качестве следующего приближения. И так далее, пока не будет достигнута необходимая точность.
Пусть — определённая на отрезке и дифференцируемая на нём вещественнозначная функция. Тогда формула итеративного исчисления приближений может быть выведена следующим образом:
где — угол наклона касательной в точке .
Следовательно искомое выражение для имеет вид:
Итерационный процесс начинается с некоего начального приближения (чем ближе к нулю, тем лучше, но если предположения о нахождении решения отсутствуют, методом проб и ошибок можно сузить область возможных значений, применив теорему о промежуточных значениях).
Алгоритм
- Задается начальное приближение .
- Пока не выполнено условие остановки, в качестве которого можно взять или (то есть погрешность в нужных пределах), вычисляют новое приближение: .
Пример
Рассмотрим задачу о нахождении положительных , для которых . Эта задача может быть представлена как задача нахождения нуля функции . Имеем выражение для производной . Так как для всех и для , очевидно, что решение лежит между 0 и 1. Возьмём в качестве начального приближения значение , тогда:
Подчёркиванием отмечены верные значащие цифры. Видно, что их количество от шага к шагу растёт (приблизительно удваиваясь с каждым шагом): от 1 к 2, от 2 к 5, от 5 к 10, иллюстрируя квадратичную скорость сходимости.
Условия применения
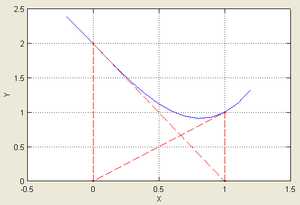 Иллюстрация расхождения метода Ньютона, применённого к функции с начальным приближением в точке .
Иллюстрация расхождения метода Ньютона, применённого к функции с начальным приближением в точке . Рассмотрим ряд примеров, указывающих на недостатки метода.
Контрпримеры
- Если начальное приближение недостаточно близко к решению, то метод может не сойтись.
Пусть
Тогда
Возьмём нуль в качестве начального приближения. Первая итерация даст в качестве приближения единицу. В свою очередь, вторая снова даст нуль. Метод зациклится и решение не будет найдено. В общем случае построение последовательности приближений может быть очень запутанным.
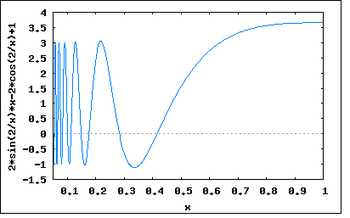 График производной функции при приближении к нулю справа.
График производной функции при приближении к нулю справа. Рассмотрим функцию:
Тогда и всюду, кроме 0.
В окрестности корня производная меняет знак при приближении к нулю справа или слева. В то время, как для .
Таким образом не ограничено вблизи корня, и метод будет расходиться, хотя функция всюду дифференцируема, её производная не равна нулю в корне, бесконечно дифференцируема везде, кроме как в корне, а её производная ограничена в окрестности корня.
Рассмотрим пример:
Тогда и за исключением , где она не определена.
На очередном шаге имеем :
Скорость сходимости полученной последовательности составляет приблизительно 4/3. Это существенно меньше, нежели 2, необходимое для квадратичной сходимости, поэтому в данном случае можно говорить лишь о линейной сходимости, хотя функция всюду непрерывно дифференцируема, производная в корне не равна нулю, и бесконечно дифференцируема везде, кроме как в корне.
- Если производная в точке корня равна нулю, то скорость сходимости не будет квадратичной, а сам метод может преждевременно прекратить поиск, и дать неверное для заданной точности приближение.
Пусть
Тогда и следовательно . Таким образом сходимость метода не квадратичная, а линейная, хотя функция всюду бесконечно дифференцируема.
Ограничения
Пусть задано уравнение , где и надо найти его решение.
Ниже приведена формулировка основной теоремы, которая позволяет дать чёткие условия применимости. Она носит имя советского математика и экономиста Леонида Витальевича Канторовича (1912—1986).
Теорема Канторовича.
Если существуют такие константы , что:
- на , то есть существует и не равна нулю;
- на , то есть ограничена;
- на , и ;
Причём длина рассматриваемого отрезка . Тогда справедливы следующие утверждения:
- на существует корень уравнения ;
- если , то итерационная последовательность сходится к этому корню: ;
- погрешность может быть оценена по формуле .
Из последнего из утверждений теоремы в частности следует квадратичная сходимость метода:
Тогда ограничения на исходную функцию будут выглядеть так:
- функция должна быть ограничена;
- функция должна быть гладкой, дважды дифференцируемой;
- её первая производная равномерно отделена от нуля;
- её вторая производная должна быть равномерно ограничена.
Историческая справка
Метод был описан Исааком Ньютоном в рукописи «Об анализе уравнениями бесконечных рядов» (лат. «De analysi per aequationes numero terminorum infinitas»), адресованной в 1669 году Барроу, и в работе «Метод флюксий и бесконечные ряды» (лат. «De metodis fluxionum et serierum infinitarum») или «Аналитическая геометрия» (лат. «Geometria analytica») в собраниях трудов Ньютона, которая была написана в 1671 году. В своих работах Ньютон вводит такие понятия, как разложение функции в ряд, бесконечно малые и флюксии (производные в нынешнем понимании). Указанные работы были изданы значительно позднее: первая вышла в свет в 1711 году благодаря Уильяму Джонсону, вторая была издана Джоном Кользоном в 1736 году уже после смерти создателя. Однако описание метода существенно отличалось от его нынешнего изложения: Ньютон применял свой метод исключительно к полиномам. Он вычислял не последовательные приближения , а последовательность полиномов и в результате получал приближённое решение .
Впервые метод был опубликован в трактате «Алгебра» Джона Валлиса в 1685 году, по просьбе которого он был кратко описан самим Ньютоном. В 1690 году Джозеф Рафсон опубликовал упрощённое описание в работе «Общий анализ уравнений» (лат. «Analysis aequationum universalis»). Рафсон рассматривал метод Ньютона как чисто алгебраический и ограничил его применение полиномами, однако при этом он описал метод на основе последовательных приближений вместо более трудной для понимания последовательности полиномов, использованной Ньютоном. Наконец, в 1740 году метод Ньютона был описан Томасом Симпсоном как итеративный метод первого порядка решения нелинейных уравнений с использованием производной в том виде, в котором он излагается здесь. В той же публикации Симпсон обобщил метод на случай системы из двух уравнений и отметил, что метод Ньютона также может быть применён для решения задач оптимизации путём нахождения нуля производной или градиента.
В 1879 году Артур Кэли в работе «Проблема комплексных чисел Ньютона — Фурье» (англ. «The Newton-Fourier imaginary problem») был первым, кто отметил трудности в обобщении метода Ньютона на случай мнимых корней полиномов степени выше второй и комплексных начальных приближений. Эта работа открыла путь к изучению теории фракталов.
Обобщения и модификации
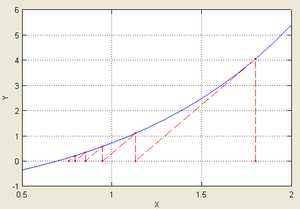 Иллюстрация последовательных приближений метода одной касательной, применённого к функции с начальным приближением в точке .
Иллюстрация последовательных приближений метода одной касательной, применённого к функции с начальным приближением в точке . Метод одной касательной
В целях уменьшения числа обращений к значениям производной функции применяют так называемый метод одной касательной.
Формула итераций этого метода имеет вид:
Суть метода заключается в том, чтобы вычислять производную лишь один раз, в точке начального приближения , а затем использовать это значение на каждой последующей итерации:
При таком выборе в точке выполнено равенство:
и если отрезок, на котором предполагается наличие корня и выбрано начальное приближение , достаточно мал, а производная непрерывна, то значение будет не сильно отличаться от и, следовательно, график пройдёт почти горизонтально, пересекая прямую , что в свою очередь обеспечит быструю сходимость последовательности точек приближений к корню.
Этот метод можно также рассматривать, как модернизацию метода хорд (секущих), где число следует выбрать равным
Многомерный случай
Обобщим полученный результат на многомерный случай.
Пусть необходимо найти решение системы:
Выбирая некоторое начальное значение , последовательные приближения находят путём решения систем уравнений:
где .
Применительно к задачам оптимизации
Пусть необходимо найти минимум функции многих переменных . Эта задача равносильна задаче нахождения нуля градиента . Применим изложенный выше метод Ньютона:
где — гессиан функции .
В более удобном итеративном виде это выражение выглядит так:
Следует отметить, что в случае квадратичной функции метод Ньютона находит экстремум за одну итерацию.
Нахождение матрицы Гессе связано с большими вычислительными затратами, и зачастую не представляется возможным. В таких случаях альтернативой могут служить квазиньютоновские методы, в которых приближение матрицы Гессе строится в процессе накопления информации о кривизне функции.
Метод Ньютона — Рафсона
Метод Ньютона — Рафсона является улучшением метода Ньютона нахождения экстремума, описанного выше. Основное отличие заключается в том, что на очередной итерации каким-либо из методов одномерной оптимизации выбирается оптимальный шаг:
где Для оптимизации вычислений применяют следующее улучшение: вместо того, чтобы на каждой итерации заново вычислять гессиан целевой функции, ограничиваются начальным приближением и обновляют его лишь раз в шагов, либо не обновляют вовсе.
Применительно к задачам о наименьших квадратах
На практике часто встречаются задачи, в которых требуется произвести настройку свободных параметров объекта или подогнать математическую модель под реальные данные. В этих случаях появляются задачи о наименьших квадратах:
Эти задачи отличаются особым видом градиента и матрицы Гессе:
где — матрица Якоби вектор-функции , — матрица Гессе для её компоненты .
Тогда очередное направление определяется из системы:
Метод Гаусса — Ньютона
Метод Гаусса — Ньютона строится на предположении о том, что слагаемое доминирует над . Это требование не соблюдается, если минимальные невязки велики, то есть если норма сравнима с максимальным собственным значением матрицы . В противном случае можно записать:
Таким образом, когда норма близка к нулю, а матрица имеет полный столбцевой ранг, направление мало отличается от ньютоновского (с учётом ), и метод может достигать квадратичной скорости сходимости, хотя вторые производные и не учитываются. Улучшением метода является алгоритм Левенберга — Марквардта, основанный на эвристических соображениях.
Обобщение на комплексную плоскость
 Бассейны Ньютона для полинома пятой степени . Разными цветами закрашены области притяжения для разных корней. Более тёмные области соответствуют большему числу итераций.
Бассейны Ньютона для полинома пятой степени . Разными цветами закрашены области притяжения для разных корней. Более тёмные области соответствуют большему числу итераций. До сих пор в описании метода использовались функции, осуществляющие отображения в пределах множества вещественных значений. Однако метод может быть применён и для нахождения нуля функции комплексного переменного. При этом процедура остаётся неизменной:
Особый интерес представляет выбор начального приближения . Ввиду того, что функция может иметь несколько нулей, в различных случаях метод может сходиться к различным значениям, и вполне естественно возникает желание выяснить, какие области обеспечат сходимость к тому или иному корню. Этот вопрос заинтересовал Артура Кейли ещё в 1879 году, однако разрешить его смогли лишь в 70-х годах двадцатого столетия с появлением вычислительной техники. Оказалось, что на пересечениях этих областей (их принято называть областями притяжения) образуются так называемые фракталы — бесконечные самоподобные геометрические фигуры.
Ввиду того, что Ньютон применял свой метод исключительно к полиномам, фракталы, образованные в результате такого применения, обрели название фракталов Ньютона или бассейнов Ньютона.
Литература
- Акулич И. Л. Математическое программирование в примерах и задачах: Учеб. пособие для студентов эконом. спец. вузов. — М.: Высш. шк., 1986.
- Амосов А. А., Дубинский Ю. А., Копченова Н. П. Вычислительные методы для инженеров. — М.: Мир, 1998.
- Бахвалов Н. С., Жидков Н. П., Кобельков Г. Г. Численные методы. — 8-е изд.. — М.: Лаборатория Базовых Знаний, 2000.
- Вавилов С. И. Исаак Ньютон. — М.: Изд. АН СССР, 1945.
- Волков Е. А. Численные методы. — М.: Физматлит, 2003.
- Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. Пер. с англ. — М.: Мир, 1985.
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М.: Наука, 1970. — С. 575-576.
- Коршунов Ю. М., Коршунов Ю. М. Математические основы кибернетики. — Энергоатомиздат, 1972.
- Максимов Ю. А.,Филлиповская Е. А. Алгоритмы решения задач нелинейного программирования. — М.: МИФИ, 1982.
- Морозов А. Д. Введение в теорию фракталов. — МИФИ, 2002.
Примечания
См. также
Ссылки
dvc.academic.ru


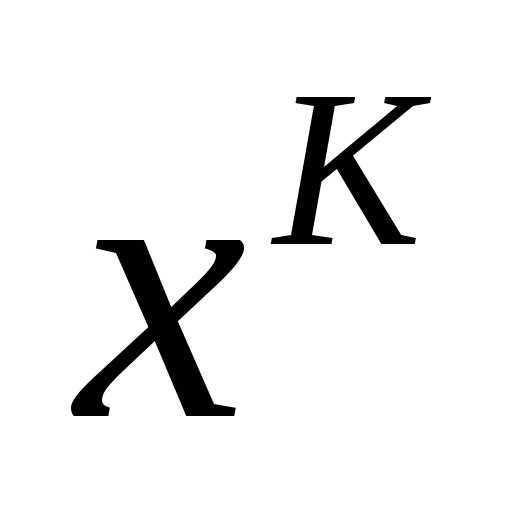
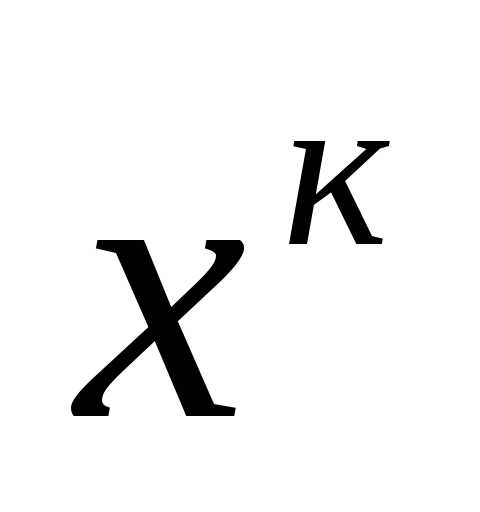 - приближение в точке локального минимума, чтобы приблизиться к искомой точке
- приближение в точке локального минимума, чтобы приблизиться к искомой точке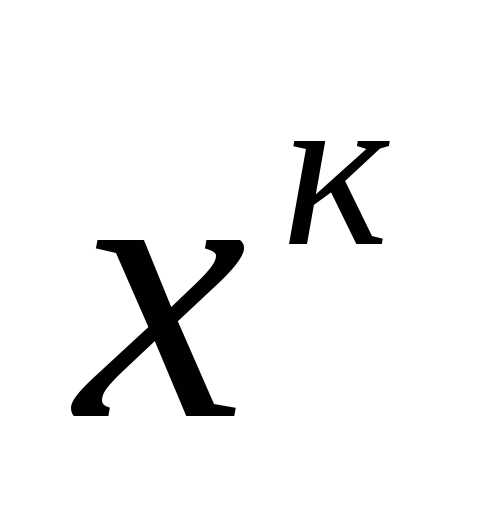 . Мы должны выбрать направление, в конце получим локальную линию.
. Мы должны выбрать направление, в конце получим локальную линию.