Задача безусловной оптимизации. Метод самого быстрого спуску. Задача безусловной оптимизации
Решение задачи безусловной оптимизации функции многих переменных с использованием необходимых и достаточных условий экстремума
Необходимые и достаточные условия безусловного экстремума
Пусть дана дважды непрерывно дифференцируемая функция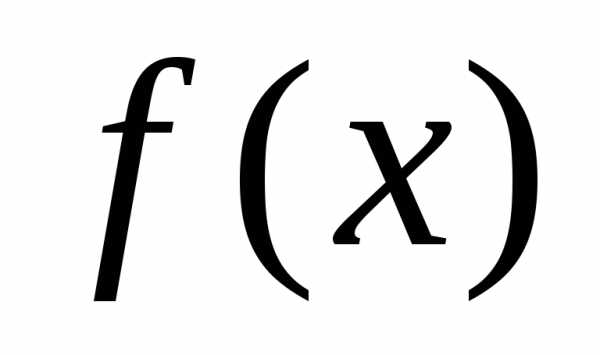 
, определенная на множестве
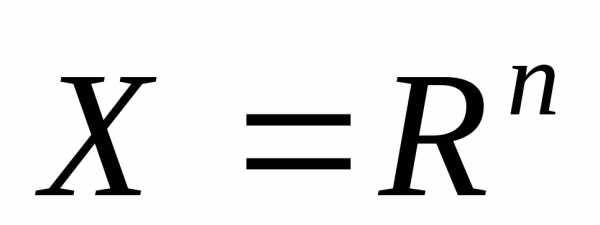. Требуется исследовать функцию
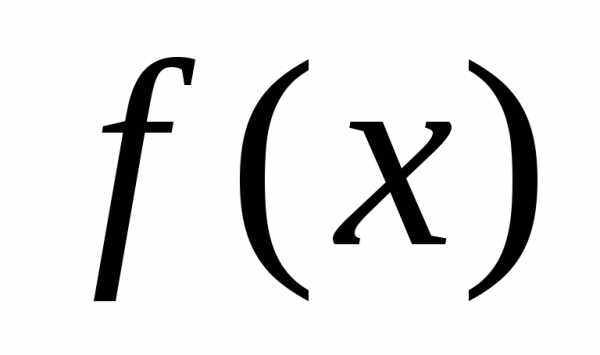на экстремум, т.е. определить точки
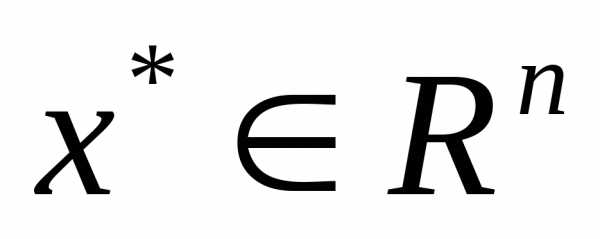ее локальных минимумов и максимумов на
:
, .
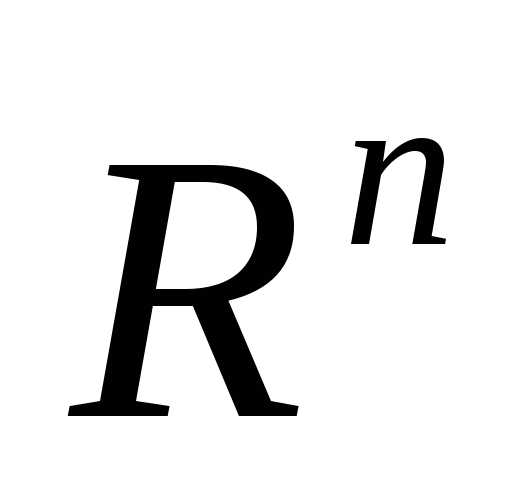Необходимые условия экстремума первого порядка
Пусть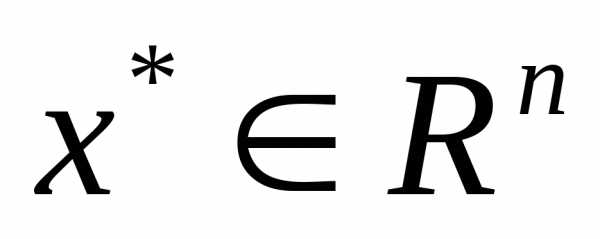 
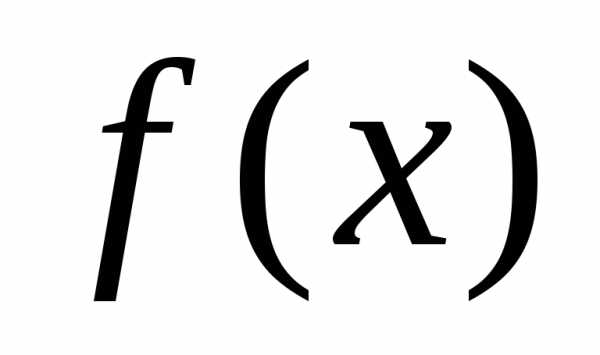на множестве
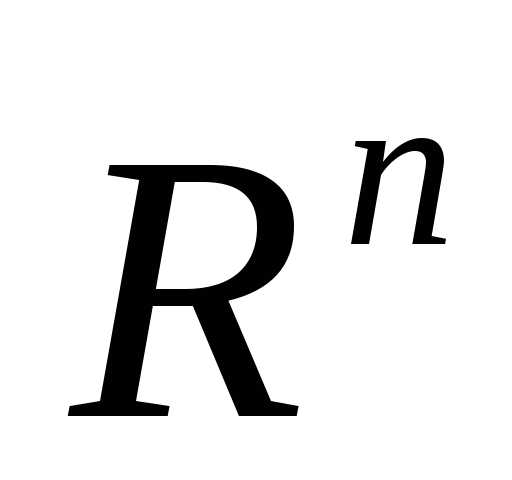и
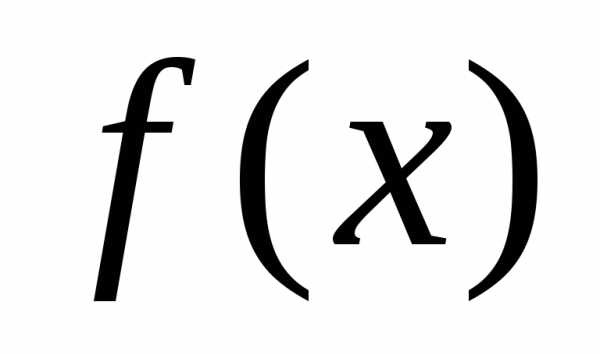дифференцируема в точке
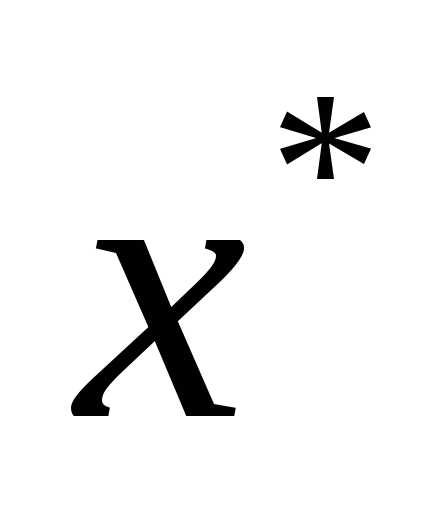. Тогда градиент функции
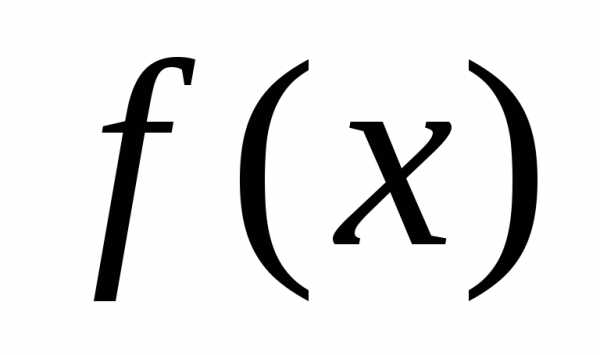в точке
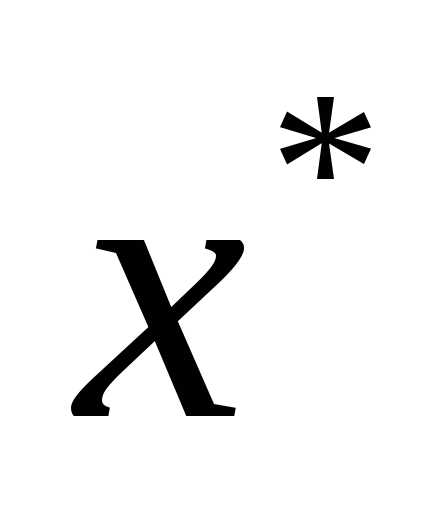равен нулю, т.е.:, или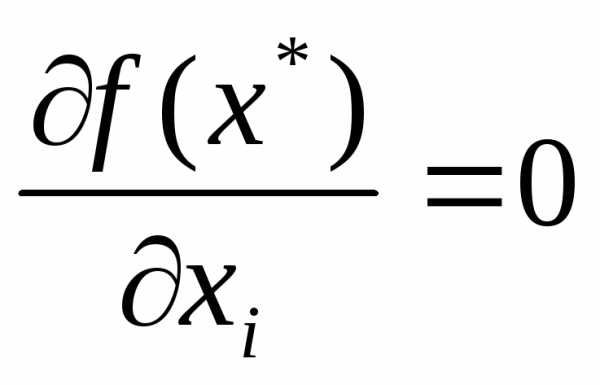 
,
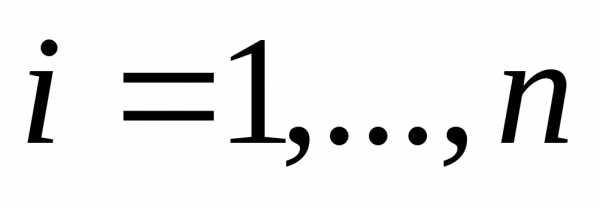
Точки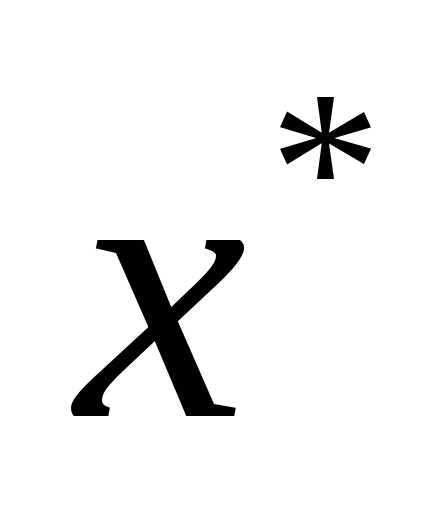 
, удовлетворяющие этому условию называются стационарными.
Необходимые условия экстремума второго порядка
Пусть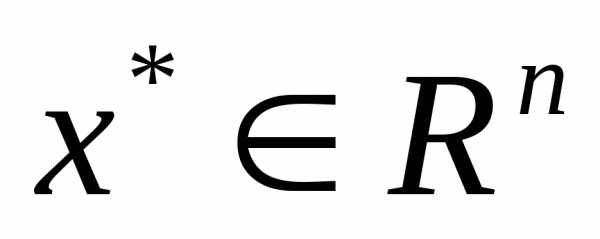 
есть точка локального минимума (максимума) функции
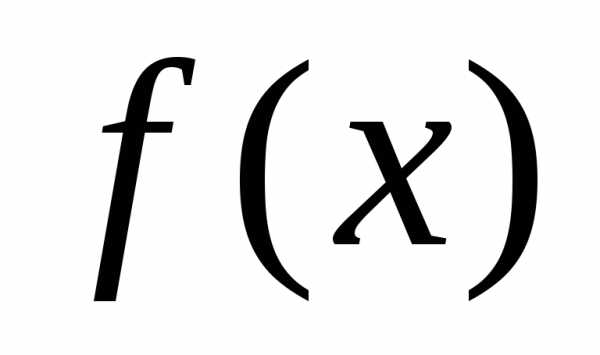на множестве
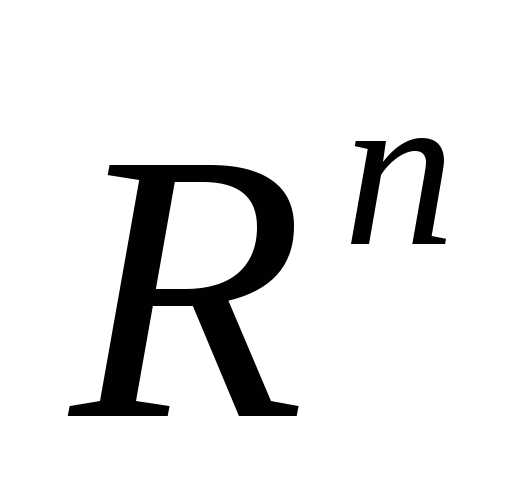и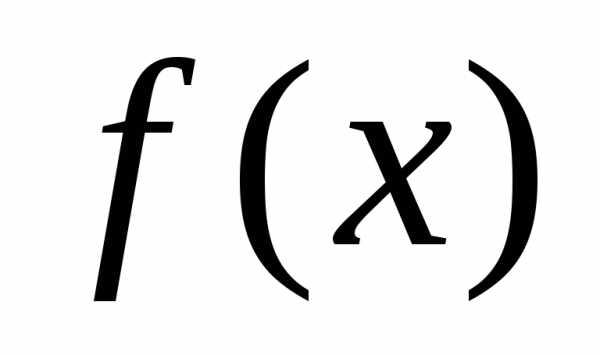
дважды дифференцируема в точке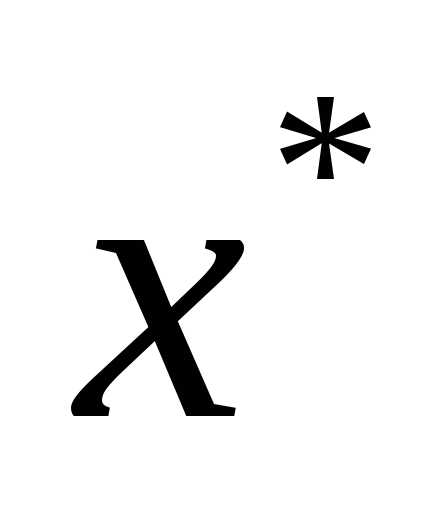
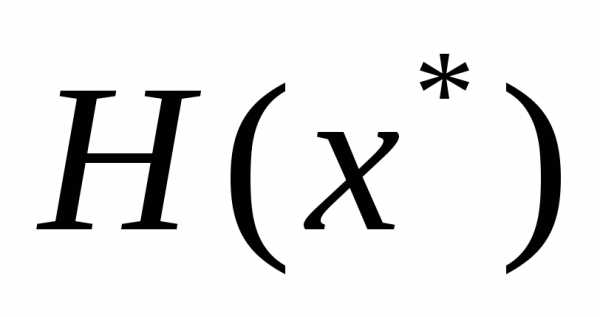функции
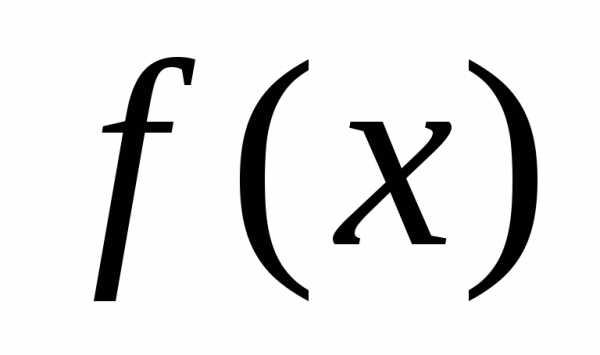, вычисленная в точке
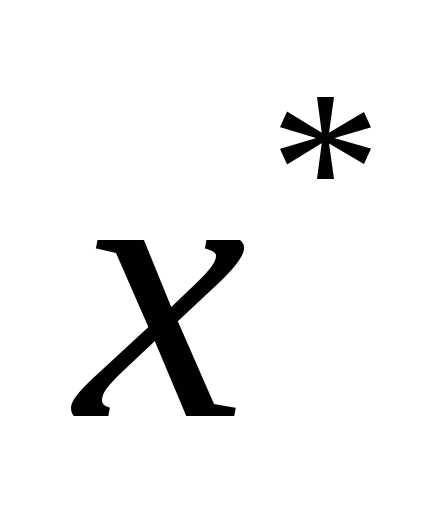, является положительно полуопределенной (отрицательно полуопределенной), т.е..
Достаточные условия экстремума
Пусть функция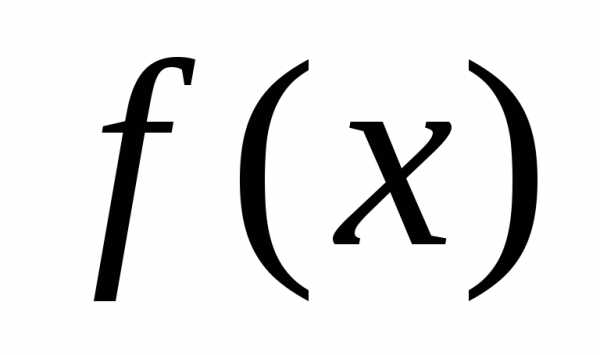 
в точке дважды дифференцируема, ее градиент равен нулю, а матрица Гессе является положительно определенной (отрицательно определенной), т.е.:
,
Тогда точка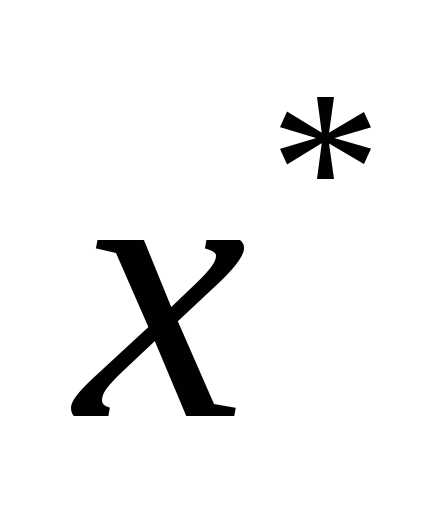 
есть точка локального минимума (максимума) функции
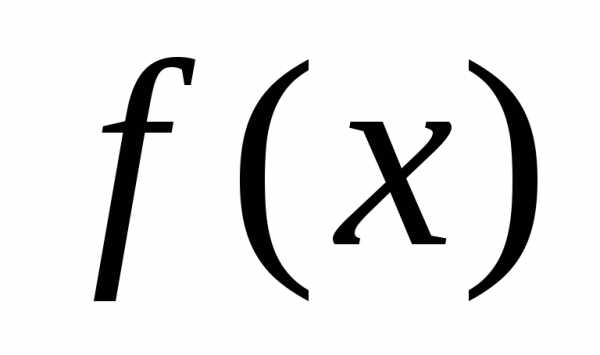на множестве
.
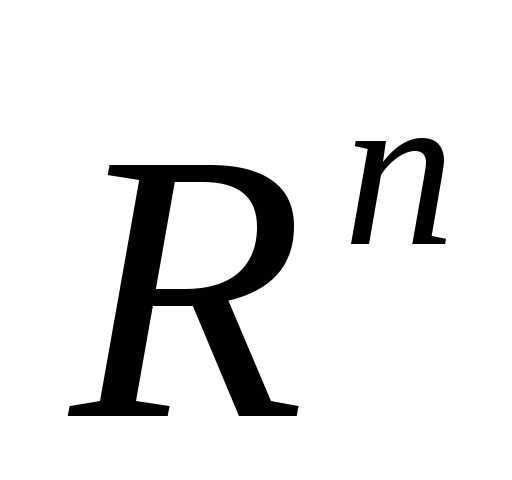Алгоритм решения задачи нахождения безусловного экстремума функции многих переменных с помощью необходимых и достаточных условий
Записать необходимые условия экстремума первого порядка и найти стационарные точки
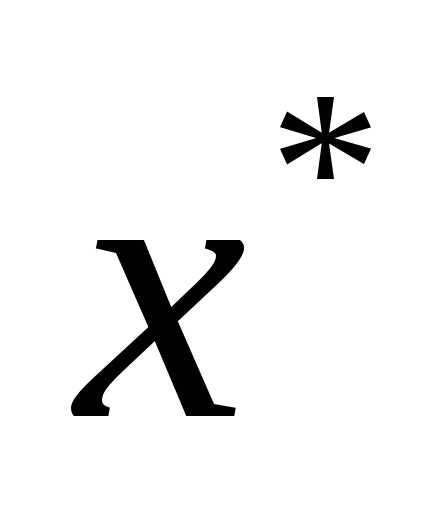
В найденных стационарных точках
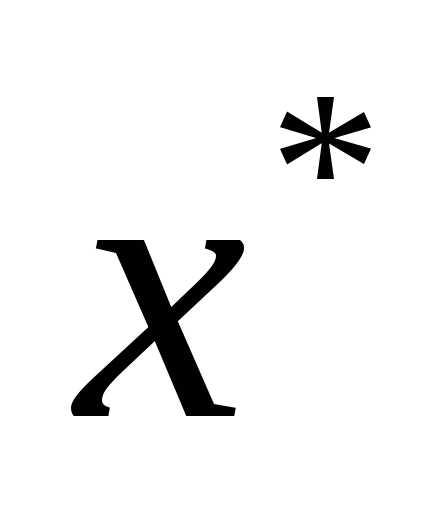проверить выполнение достаточных, а если они не выполняются, то необходимых условий второго порядка.Вычислить значение
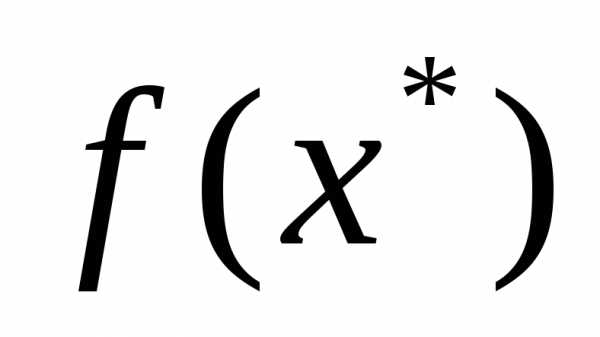в точках экстремума.
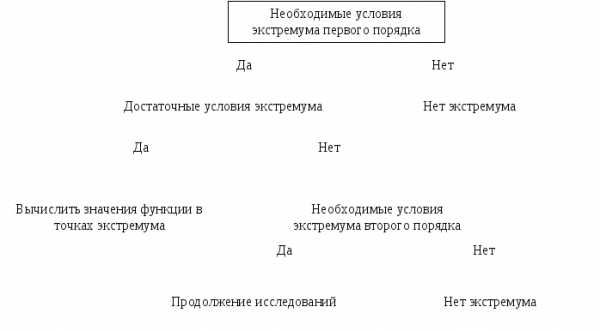
Примеры решения задачи нахождения безусловного экстремума функции многих переменных с использованием необходимых и достаточных условий
Найти экстремум функции на множестве
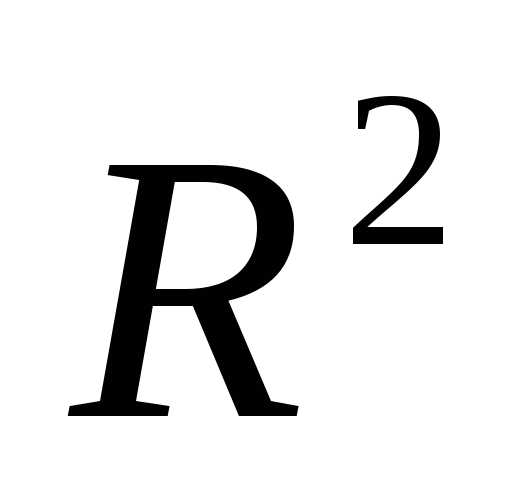
Запишем необходимые условия экстремума первого порядка
, 
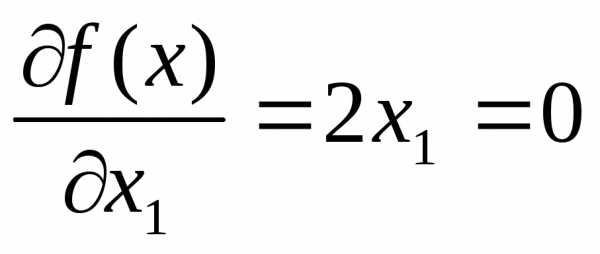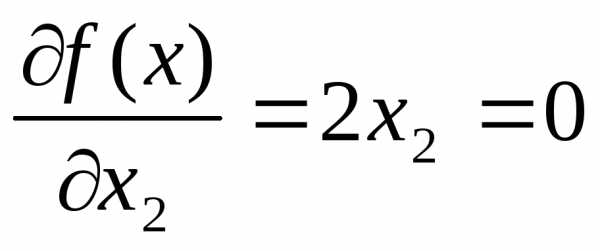
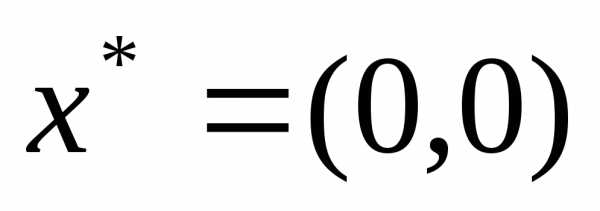
Проверим выполнение достаточных условий
, ,
.
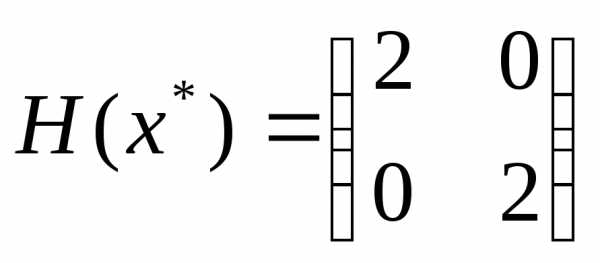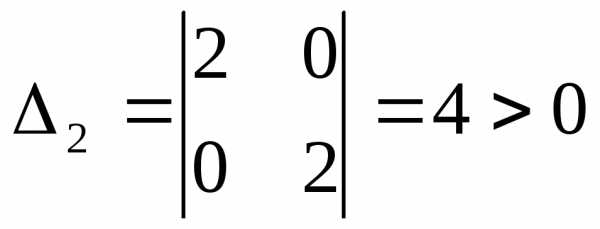Все угловые миноры матрицы Гессе положительны, следовательно матрица Гессе положительно определена
Значит в точке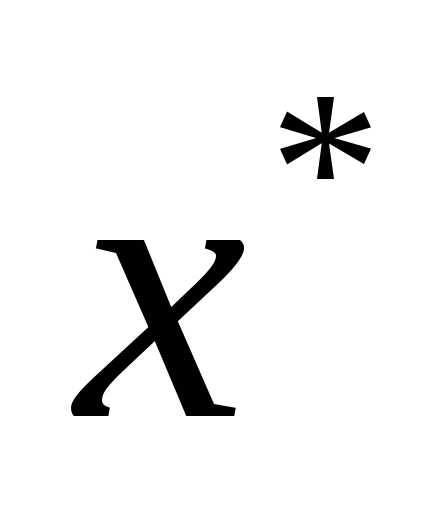 
локальный минимум. Т.к. функция является строго выпуклой на множестве
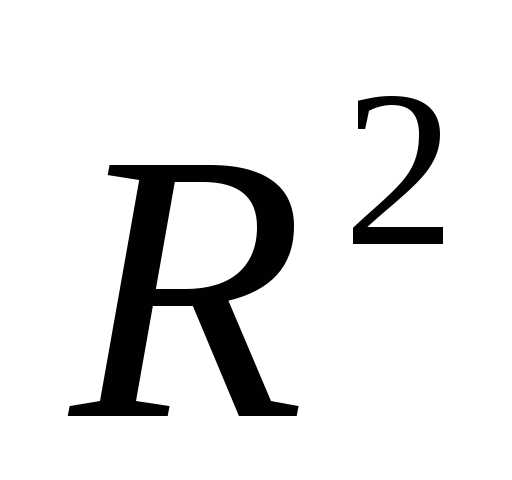, то точка локального минимума является точкой глобального минимума.
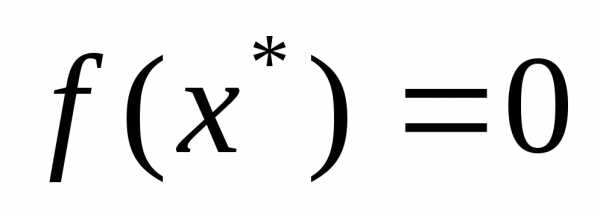
Найти экстремум функции на множестве
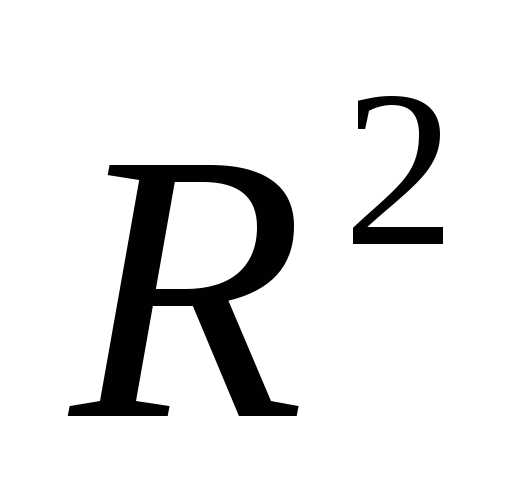
Запишем необходимые условия экстремума первого порядка
, 
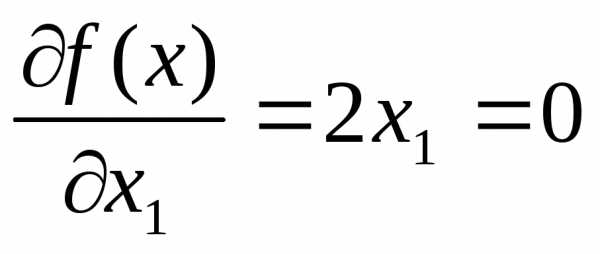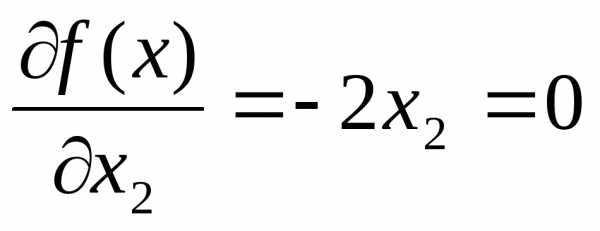
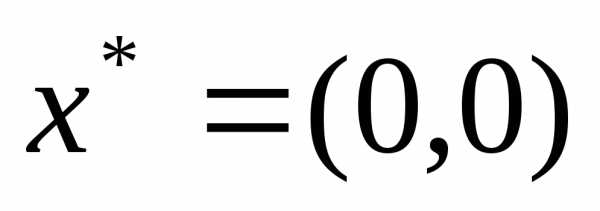
Проверим выполнение достаточных условий
, ,.
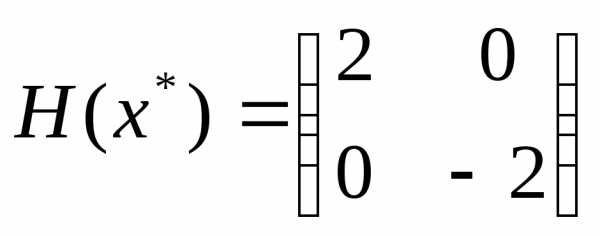Матрица Гессе не является положительно определенной, а значит достаточные условия экстремума не выполняются.
Проверим выполнение необходимого условия экстремума второго порядка.
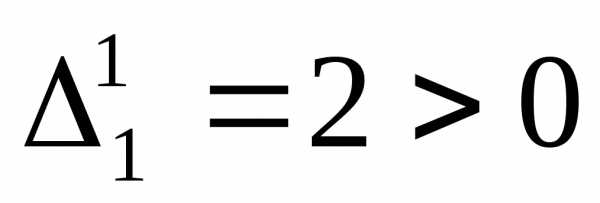, ,, Т.к. главные миноры матрицы Гессе имеют как положительные, так и отрицательные значения, то матрица Гессе не является ни положительно полуопределенной ни отрицательно полуопределенной, а значит необходимое условие второго порядка не выполняется. Значит, в точке
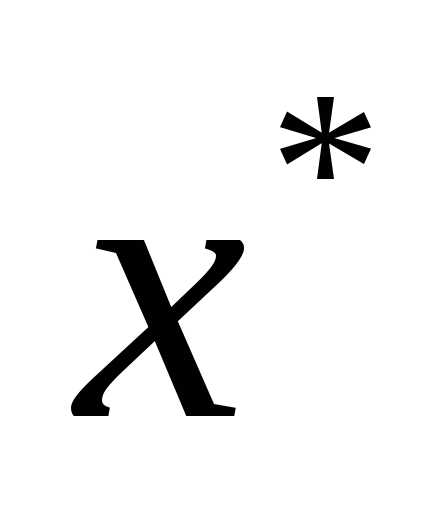нет экстремума. Точка
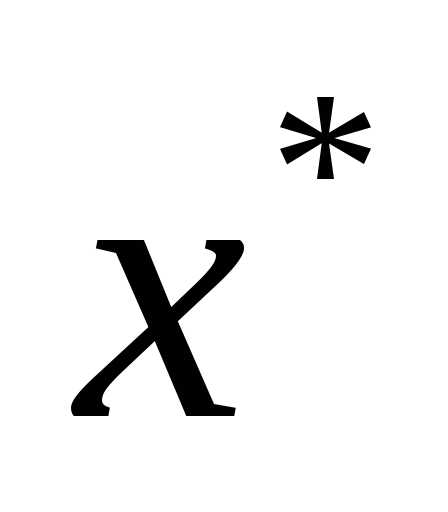является седловой точкой.
Найти экстремум функции на множестве
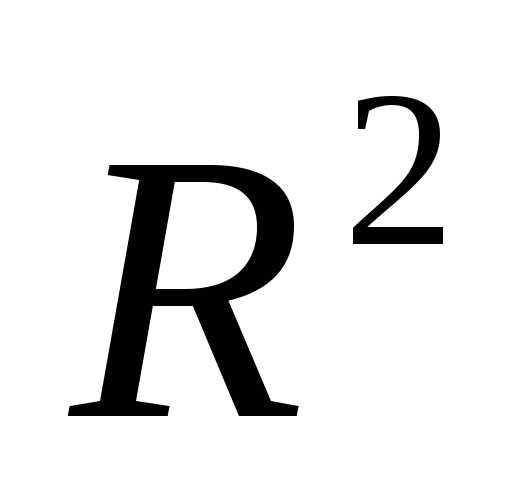
Запишем необходимые условия экстремума первого порядка
, 
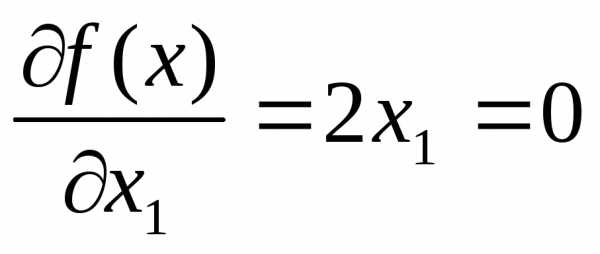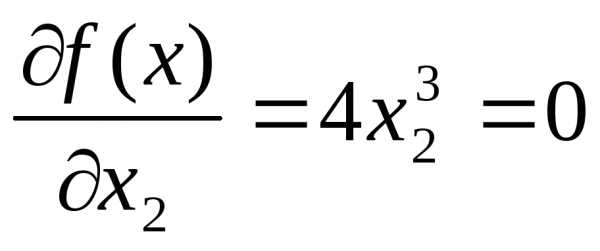
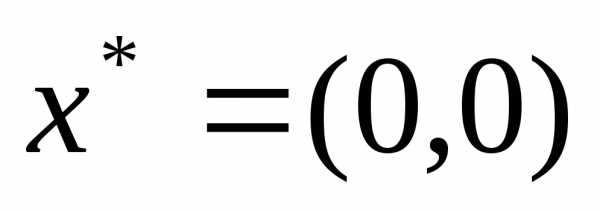
Проверим выполнение достаточных условий
, ,
.
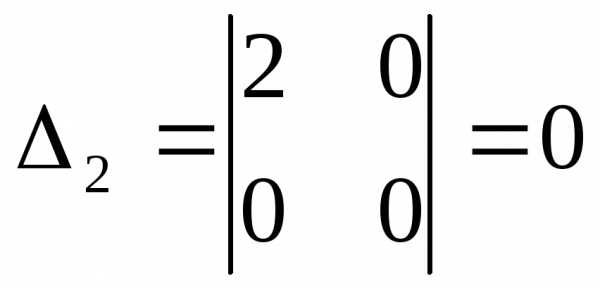Матрица Гессе не является положительно определенной, а значит достаточные условия экстремума не выполняются.
Проверим выполнение необходимого условия экстремума второго порядка.
, 
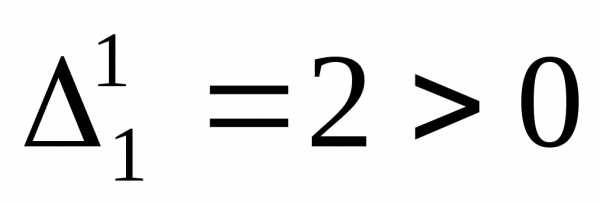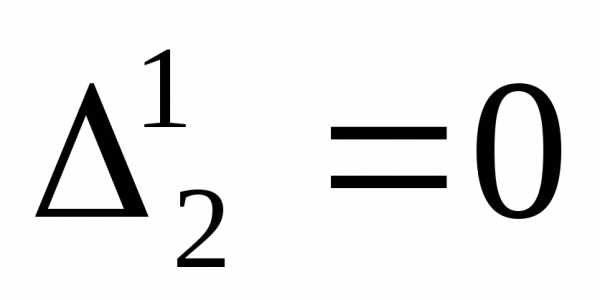,. Т.к. все главные миноры неотрицательны, значит матрица Гессе положительно полуопределена, и в точке
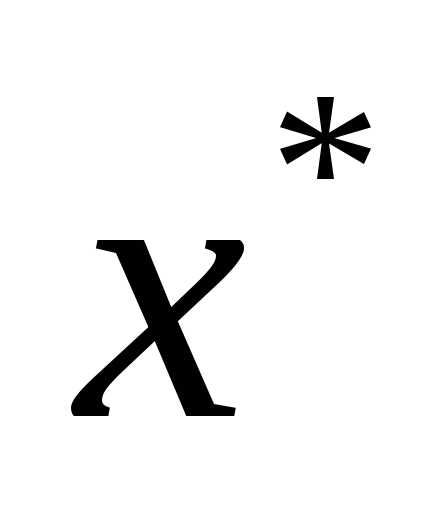может быть минимум, но требуется дополнительное исследование.
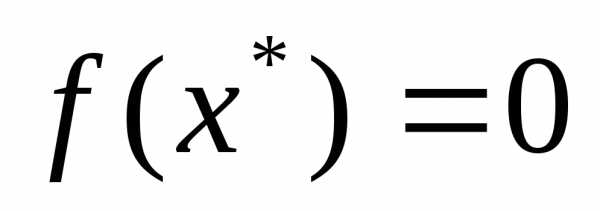. Рассмотрим 
-окрестность точки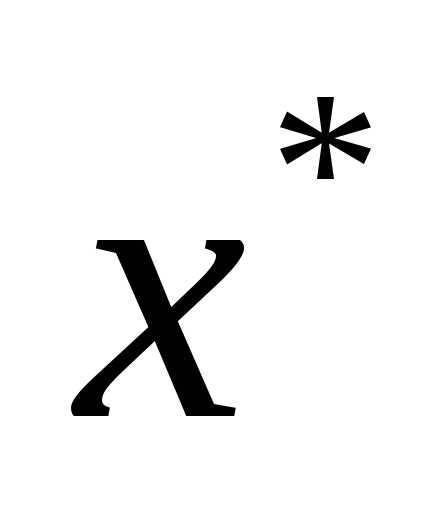
, а также поведение функции
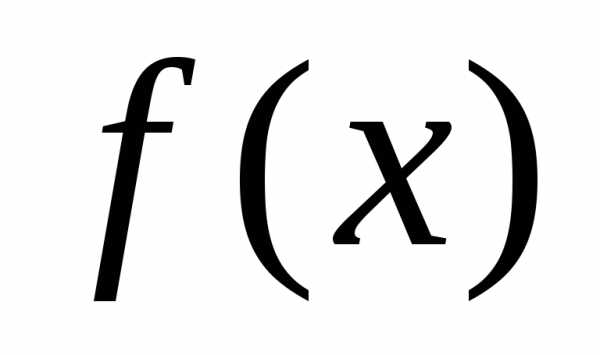на множестве
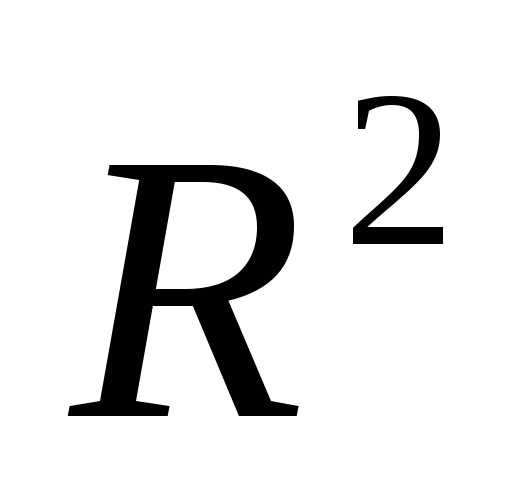. При любых
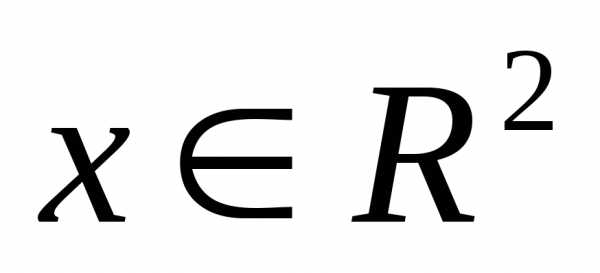имеем:, поэтому точка
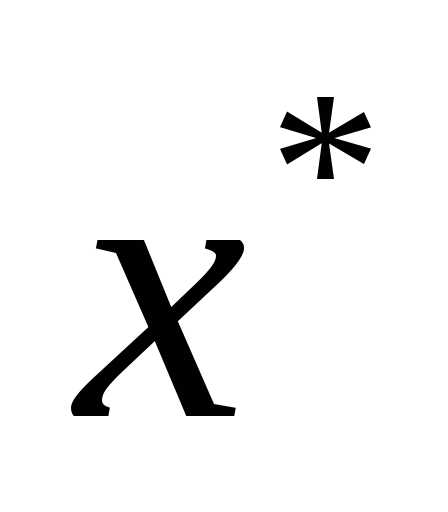является точкой глобального оптимума.
studfiles.net
Задача безусловной оптимизации. Метод самого быстрого спуску
Постановка задачи безусловной оптимизации.
Найти вектор x=(x1...,xn), что минимизирует (максимизирует) функцию
F(x)=F(x1...,xn).
Градиентные методы безусловной оптимизации.
Для задачи безусловной минимизации метод заключается в вычислении последовательности приближений x[s] по правилу
x[s+1]= x[s] – [s] F(x[s])
где F(.) — градиент функции F(.), который задается соотношением
[s]>0 — шаг, величина которого определяется конкретным градиентным методом. Начальное решение x[0] выбирается произвольно. Итерации прекращают, если на некотором шаге s выполняется неравенство
||F(x[s])|| < ,
где норма градиента определяется формулой
а >0 — некоторая заранее заданная величина, что определяет точность решения.
Метод самого быстрого спуска.
Метод самого быстрого спуска представляет собой градиентный метод, в котором величина шага [s] выбирается по правилу
F(x[s]– [s]F(x[s])) = min(F(x[s]–F(x[s])))
где минимум берется по всем >0.
При некоторых условиях x[s] следует к стационарной точке функции F(x), если s следует к бесконечности.
Программное обеспечение.
Обучающий модуль, с помощью которого задача безусловной оптимизации решается в диалоге с пользователем методом самого быстрого спуска, вызывается из раздела «НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ» главного меню пакета.
Задание.
Решить методом самого быстрого спуска задачи безусловной оптимизации, условия которых задаются модулем с помощью команды «Данные» главного меню (задачи №1–№9).
Лiтература
1. Ю.М.Ермольев, И.И.Ляшко, В.С.Михалевич, В.И.Тюптя. Математические методы исследования операций. Киев, «Высшая школа», 1979.
2. Ю.Д.Попов. Линейное и нелинейное программирование. Киев, УМК ВО, 1988.
3. Ф.П.Васильев. Численные методы решения экстремальных задач. Москва, «Наука», 1980.
4. И.Л.Калихман. Сборник задач по математическому программированию. Москва, «Высшая школа», 1975.
5. В.Ф.Капустин. Практические занятия по курсу математического программирования. Издательство Ленинградского университета, 1976.
6. Ю.П.Зайченко, С.А.Шумилова. Исследование операций, сборник задач. Киев, «Высшая школа», 1990.
7. В.Э.Фигурнов. IBM PC для пользователя. Москва, «Финансы и статистика», 1992.
studfiles.net
Одномерная задача оптимизации
Рассмотрим задачу поиска минимума одномерной функции (), определенной на интервале :
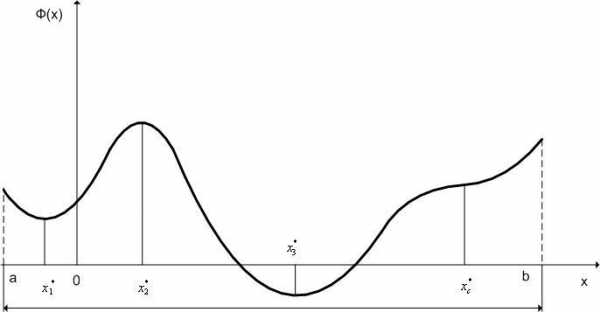
Как известно из курса математического анализа, внутренние точки локального и глобального минимума функции () являются стационарными точками критерия оптимальности () (см. рис. 1) или, что то же самое, решениями уравнения
| (1) |
|
|
Рис. 1. Локальные минимумы(x1*,x3*), локальный максимум (x2*) и точка перегиба (xc*) функции Φ(x).
Но, решениями уравнения (1) являются не только точки минимума, но и точки максимума и точки перегиба функции () (см. рис. 1). Следовательно, уравнение (1) является только необходимым условием минимума, но не является достаточным условием.
Если существует вторая производная функции (), то для отыскания достаточных условий минимума () можно привлечь эту производную. Из курса математического анализа известно, что если в точке значение первой производной функции () равно нулю, а второй производной – положительно, то в этой точке функция () имеет минимум (локальный или глобальный).
Таким образом, имеем следующую теорему:
Теорема 1. Если функция () определена и дважды непрерывно дифференцируема на интервале [,], то необходимыми и достаточными условиями минимума этой функции в точке являются условия
Приведем доказательство справедливости последнего условия. Для этого рассмотрим разложение функции () в ряд Тейлора в окрестности точки :
| (2) |
Здесь – некоторая достаточно малая величина.
Для того, что в точке достигался минимум функции (), необходимо, чтобы разность была положительной. Поскольку , то из (2) следует, что для выполнения этого условия необходимо, чтобы имело место неравенство
Точками, в которых функция () принимает наименьшее на интервале значение, могут быть либо ее стационарные точки, лежащие внутри интервала , либо ее точки недифференцируемости (критические точки критерия оптимальности), к которым следует отнести также концы интервала .
Поэтому точку, в которой функция принимает наименьшее на интервале значение, нужно искать, сравнивая значения этой функции во всех стационарных и критических точках.
Многомерная задача безусловной оптимизации
Многие методы решения многомерной задачи нелинейного программирования основаны на сведении этой задачи к задаче безусловной оптимизации. Поэтому рассмотрим -мерную задачу оптимизации без ограничений
| (1) |
По аналогии с одномерной задачей, для того, чтобы точка являлась минимумом функции () необходимо выполнение условия стационарности функции () в точке или, что то же самое, необходимо, чтобы точка была стационарной точкой функции ():
| (2) |
Положим, что функции () дважды непрерывно дифференцируема в окрестности точки . Для поиска достаточного условия достижения этой функцией в точке минимума, разложим () в окрестности точки в ряд Тейлора:
| (3) |
Здесь -мерный вектор-столбец достаточно малых величин , – -матрица Гессе.
По аналогии с одномерной задачей, для того, что в точке достигался минимум функции (), необходимо, чтобы разность была положительной. Поскольку , то из (3) следует, что для выполнения этого условия необходимо, чтобы матрица Гессе () была положительно определена в точке .
Таким образом, справедлива
Теорема 1. Если функция () дважды непрерывно дифференцируема в окрестности точки Rn, то необходимыми и достаточными условиями минимума этой функция в точке являются условия:
| (4) |
() - положительно определена
Таким образом, теорема 1 определяет необходимые и достаточные условия минимума в многомерная задача безусловной оптимизации.
Заметим, что условие ()=0 является только необходимым условием минимума в многомерной задаче безусловной оптимизации.
По аналогии с одномерной задачей точками, в которых функция () достигает своего наименьшего значения, могут быть либо ее стационарные точки функции, либо критические точки функции (точки недифференцируемости).
Поэтому так же, как в одномерной задаче, точку, в которой функция () принимает наименьшее значение нужно искать, сравнивая значения этой функции во всех стационарных и критических точках.
studfiles.net
Задача безусловной оптимизации (задача без ограничений) — МегаЛекции
(6)
Задача условной оптимизации (задача с ограничениями или задача математического программирования)
(7)
Задача безусловной оптимизации
Постановка и схема решения задачи
Данные: ;
Модель: ;
- управляющие переменные;
Задача безусловной оптимизации имеет вид:
(6)
Предполагается, что функция дважды непрерывно дифференцируема всюду на , т.е. в точке имеет градиент
и матрицу Гессе
.
Схема решения задачи оптимизации может выглядеть следующим образом:
1. Находятся все точки локальных минимумов;
2. Вычисляются значения функции во всех найденных точках и выбирается точка с наименьшим значением функции. Это и есть решение задачи.
Необходимые и достаточные условия наличия локального экстремума
Теорема 1 Необходимое условие наличия локального экстремума
Пусть - непрерывно дифференцируемая функция в точке . Если - точка локального минимума (максимума) функции , то
(7)
Точка , удовлетворяющая условию (7), называется стационарной точкой функции или задачи (1).
Для выявления искомой точки на множестве стационарных используется условие локальной оптимальности второго порядка
Теорема 2
Пусть - дважды непрерывно дифференцируемая функция в некоторой окрестности точки .Если - точка локального минимума функции , то матрица Гессе неотрицательно определена, т.е. ,(8) где
Теорема 3 Достаточное условие локальной оптимальности
Пусть - дважды непрерывно дифференцируемая функция в некоторой окрестности точки . Если удовлетворяет условию (2), а матрица Гессе положительно определена, т.е.
, (9)
то - точка строгого локального минимума функции
Знакоопределенность матрицы. Критерий Сильвестра
Для установления знакоопределенности квадратной матрицы предлагается следующая схема:
1. Если знаки всех угловых миноров матрицы положительны, то она является положительно определенной ;
2. Если знаки угловых миноров чередуются, начиная с минуса, то матрица отрицательно определена ;
2.4. Одномерная минимизация
Для функции одной переменной необходимые условия локальной оптимальности определяется следующими соотношениями:
(1)
Достаточное условие
Модель спроса на наличные деньги
Согласно этой модели определяются размеры необходимой суммы наличных денег. Предполагается, что годовая потребность (годовой спрос) в наличных деньгах субъекта, которые находятся на банковском счете под процент , известна - . При необходимости субъект посещает банк и снимает со счета определенную сумму денег - , которую он использует для покрытия своих расходов. Его запас наличности становится , а затем начинает уменьшаться с интенсивностью . Когда денежный запас исчерпан , следует новое обращение в банк и т.д. Графически эту процедуру можно представить следующим образом
Средний уровень денег на руках
- комиссионные расходы, связанные с однократным заказом денег в банке
- число посещений банка в год
Годовые затраты на банковские операции
Альтернативные потери от хранения денег «на руках» (недополучение банковского процента)
- формула Баумоля – Тобина
2.5. Алгоритмы многомерной оптимизации
(1)
Градиентные методы поиска
Методы используют информацию о градиенте целевой функции и относятся к методам первого порядка.
(3)
дифференцируема на
(4)
(5)
Поскольку , то
(6)
(7)
Из свойства скалярного произведения
(8)
(9)
градиентные методы
,
(10)
Методы спуска
1. Простейший градиентный метод ;
2. Метод наискорейшего спуска
(11)
Из (11) следует:
3. Градиентный метод с дроблением шага
3.1. часто ;
3.2. к следующей итерации
Вычислительная процедура
1. ,
2. ,
3. ,
4.
5. Проверка условий останова: если выполняются ;иначе к п. 2
Особенности методов:
- относятся к локальным методам оптимизации;
- используются для решения как одномерных, так и многомерных экстремальных задач;
- выпуклая ЦФ – метод сходится к точке минимума;
сильно выпуклая ЦФ - метод сходится к точке минимума с линейной скоростью;
невыпуклая ЦФ - метод сходится ко множеству стационарных точек
· градиентные методы относятся к методам спуска ;
низкая скорость сходимости в окрестности точки минимума; метод чувствителен к ошибкам вычислений; градиентные методы целесообразно применять на начальном этапе оптимизационной процедуры.
Метод Ньютона
(1)
Процедура поиска
(2)
Из (1) имеем
, (3)
(3) в (2)
(4)- оптимизационный метод Ньютона
Особенности метода Ньютона
1. Трудоемкость, обусловленная вычислением и обращением матрицы Гессе на каждой итерации;
2. Выбор ;
3. Метод Ньютона сходится к точке минимума произвольной ЦФ с квадратичной скоростью, если матрица Гессе положительно определена, а располагается «достаточно близко» к .
Метод Ньютона с регулировкой шага:
(5)
, ,
Скорость сходимости – сверхлинейная;
квадратичная
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
Задача - безусловная оптимизация - Большая Энциклопедия Нефти и Газа, статья, страница 1
Задача - безусловная оптимизация
Cтраница 1
Задачи безусловной оптимизации, которым мы уделили внимание в этом разделе, довольно редко встречаются в экономических исследованиях, основной особенностью которых является ограниченность используемых ресурсов. [1]
Таким образом, для задачи безусловной оптимизации ( X Rn) теорема 1.2 не дает ничего нового в сравнении со знакомыми результатами ( теоремы 1.2 и 1.9 гл. [2]
Исходную задачу приводим к задаче безусловной оптимизации. [3]
Как правило, при решении задач безусловной оптимизации для достаточно гладких выпуклых или вогнутых функций F () методы, использующие первые и вторые производные, сходятся быстрее, чем методы нулевого порядка. Однако при оптимизации схем в условиях сложного непредсказуемого рельефа целевых функций F ( X), их алгоритмического, неявного способа задания, например посредством решения системы дифференциальных уравнений, а также при сложной форме ограничений использование методов нулевого порядка часто предпочтительнее. Кроме того, при неявном задании / 7 ( Х) ее производные приходится определять численно, а возникающие при этом ошибки, особенно в окрестности экстремума, создают значительные трудности для точного определения точки оптимума. [4]
С помощью естественного обобщения получим задачу безусловной оптимизации, охватывающую весь блок ВПБ. [5]
Квазиньютоновские методы являются эффективным средством решения задач безусловной оптимизации. Их отличает высокая скорость сходимости, в то же время при реализации квазиньютоновских алгоритмов не приходится выполнять такие трудоемкие операции, как вычисление матрицы вторых производных или обращение матрицы. Однако при большой размерности пространства необходимость хранения и пересчета на каждом шаге матриц Hk обусловливает высокие требования к объему занимаемой памяти ЭВМ. Этот недостаток не присущ изучаемому в следующем параграфе методу сопряженных градиентов. [6]
В этом случае мы говорим о задаче безусловной оптимизации. [7]
Там же были приведены соответствующие результаты для задачи безусловной оптимизации и классической задачи на условный экстремум. В данной главе излагается общая теория необходимых и достаточных условий оптимальности в задачах математического программирования, включающая указанные результаты как частные случаи. [8]
Рассмотрим один из вариантов симплексного метода решения задачи безусловной оптимизации. [9]
Сведение исходной задачи условной оптимизации к последовательности задач безусловной оптимизации может быть выполнено с помощью функций штрафа. [10]
Задача поиска Е ( W) является задачей безусловной оптимизации. [11]
Теория необходимых и достаточных условий оптимальности в задачах безусловной оптимизации излагается в любом курсе математического анализа. [12]
Задача условной оптимизации (3.16) может быть сформулирована как задача безусловной оптимизации с помощью методов Лагранжа или штрафных функций. Тогда применяются методы безусловной оптимизации. [14]
Вообще задачи условной оптимизации более сложны, чем задачи безусловной оптимизации. Для их решения используют специально разработанные методы программирования с ограничениями. Одним из таких методов, которые относятся к методам поиска глобального экстремума, является метод сканирования, состоящий в том, что допустимая область поиска, определяемая системой ограничений, разбивается на k подобластей, в центре каждой из которых определяется значение целевой функции. Если целевая функция зависит от п параметров, необходимо выполнить kK вариантов расчета. Для надежного определения глобального минимума необходимо увеличивать число k подобластей, что приводит к большим затратам машинного времени. [15]
Страницы: 1 2 3
www.ngpedia.ru
Задача - безусловная оптимизация - Большая Энциклопедия Нефти и Газа, статья, страница 3
Задача - безусловная оптимизация
Cтраница 3
Переход к усредненной постановке предполагает, что решение задачи повторяют многократно и в качестве значения задачи принимают среднее значений функции fo ( x), полученных при каждом единичном решении. Естественно, что такой переход в задаче безусловной оптимизации неэффективен, так как среднее значение / о не может быть больше ее максимального значения. В задачах условной оптимизации переход к усредненной постановке может быть эффективен, если для каждого единичного решения не требовать, чтобы х принадлежало D, а вместо этого потребовать, чтобы ограничения задачи выдерживались в среднем на множестве решений. [32]
Большинство методов оптимизации разработано для поиска безусловного экстремума. Обычно задачи условной оптимизации сводят к задачам безусловной оптимизации с помощью штрафных функций или множителей Лагранжа. [33]
Второе свойство выпуклых задач можно высказать в виде следующего общего принципа: необходимые условия оптимальности в том или ином классе задач оптимизации при соответствующих предположениях выпуклости оказываются и достаточными. Ограничимся здесь обоснованием этого принципа применительно к задаче безусловной оптимизации ( ср. Другими его подтверждениями служат теоремы 1.2 и 2.2 гл. [34]
При решении задач условной оптимизации целесообразно использовать методы безусловной оптимизации, учитывая большое количество разработанных по этим методам программ. С этой целью задача условной оптимизации сводится к задаче безусловной оптимизации устранением ограничений путем преобразования параметра xt, на значения которого наложены ограничения, в неограничиваемый. [35]
Функциональные ограничения устраняются путем конструирования обобщенной функции оптимизации с учетом типа ограничений. Так, если все ограничения представлены в аналитическом виде и являются функциональными зависимостями типа равенств (3.11), то переход к задаче безусловной оптимизации часто осуществляется с помощью метода неопределенных множителей Лагранжа. [36]
В этом случае реализация алгоритма завершается. Как несложно показать, в силу того что функция f ( x X2) является вогнутой, найденная точка является решением задачи безусловной оптимизации. [37]
При втором подходе ( блок DII) задачу оптимизации с ограничениями посредством того или иного приема ( метод штрафов, метод неопределенных множителей Лагранжа) сводят к задачам безусловной оптимизации. [38]
Использование алгоритмов стохастической аппроксимации в задачах на условный экстремум функции регрессии или задачах, где ограничения носят регрессионный характер, может основываться на сведении этих задач к задаче безусловной оптимизации с помощью штрафных функций или на стохастических аналогах градиентных алгоритмов детерминированных задач. [39]
Правда, расчет предотвращенного ущерба по Временной типовой методике / 1 /, как правило, дает результаты, намного превышающие затраты, что заведомо их оправдывает практически в каждом случае. В большой мере это происходит из-за учета внеэкономической составляющей в расчетных формулах ( например из-за учета скорости оседания частиц и радиуса их рассеивания), что завышает размер предотвращенного ущерба подобно тому, как это происходит при переводе задачи оптимизации с ограничениями в задачу безусловной оптимизации. Однако при этом предотвращенный ущерб теряет свое экономическое содержание, а следовательно, сопоставление его с затратами не будет иметь смысла. Например, затраты, направленные на снижение загрязнения какого-либо уникального природного ландшафта ( заповедника) вряд ли смогут быть оправданы реальным предотвращенным ущербом, поскольку природные компоненты этого ландшафта не имеют адекватной стоимостной оценки. [40]
В первом подходе учитывается, что большинство развитых методов оптимизации ориентировано на поиск безусловного экстремума. Поэтому их применение к решению задачи условной оптимизации требует, чтобы эта задача была предварительно сведена к задаче безусловной оптимизации. Во втором подходе используются методы, специально разработанные для решения задач нелинейного программирования с ограничениями. [41]
При малых значениях параметра 0 вне области D функция F ( x / 3) сильно возрастает. Поэтому ее минимум может быть либо внутри D, либо снаружи вблизи границ этой области. В первом случае минимумы функций F ( xj / 3) и / ( х) совпадают, поскольку дополнительные члены в (6.20) равны нулю. Если минимум функции F ( x, / 3) находится вне D, то минимум целевой функции / ( х) лежит на границе D. Таким образом, задача оптимизации для целевой функции / ( х) с ограничениями (6.19) свелась к последовательности задач безусловной оптимизации для вспомогательной функции (6.20), решение которых может быть проведено с помощью методов спуска. [43]
В данной главе будут рассмотрены алгоритмы отыскания экстремума нелинейной функции при нелинейных ограничениях. С простейшим из них, предназначенным для решения задач, ограничения которых имеют вид равенств, мы уже познакомились ранее. Надо сказать, что в своем большинстве алгоритмы такого сорта представляют собой различные способы воплощения двух подходов к организации поиска условного экстремума. Первый состоит в том, чтобы, непосредственно контролируя соблюдение ограничений задачи, двигаться к ее оптимуму по последовательности допустимых или почти допустимых точек с монотонно убывающими либо монотонно возрастающими ( это зависит от того, что ищется - минимум или максимум) значениями целевой функции Соответствующие алгоритмы называются методами спуска. Два из них представлены в первом параграфе этой главы. Второй подход заключается в сведении задачи на экстремум при наличии ограничений к последовательности задач безусловной оптимизации конструируемых специальным образом вспомогательных функций. Эти функции принято называть штрафными, а использующие их алгоритмы - методами штрафных функций. Им посвящен второй параграф. [44]
Страницы: 1 2 3
www.ngpedia.ru
| Задача оптимизации формулируется следующим образом: заданы множество Х (допустимое множество задачи) и функция f(x) (целевая функция), определенная на Х; требуется найти точки минимума или максимума функции f на Х. Задача оптимизации, в которой целевая функция подлежит минимизации, имеет вид f (х) ^ min (1 1) х е X. В курсе рассматриваются задачи, допустимое множество nn которых лежит в евклидовом пространстве R . Точка х* е X называется точкой глобального минимума f(x) на множестве X, или глобальным решением задачи (1.1), если f (х*) Точка х* е X называется точкой локального минимума ^х) на множестве X, или локальным решением задачи (1.1), если f (х*) 0 с центром в точке х (? - окрестность точки х ). Ясно, что глобальное решение является и локальным; обратное неверно. Задача (1.1) называется задачей безусловной оптимизации, если X=Rn. На практических занятиях рассматриваются аналитические методы решения задач безусловной оптимизации, базирующиеся на условиях оптимальности. Различают необходимые условия оптимальности, т. е. условия, которым должна удовлетворять точка, являющаяся решением задачи, и достаточные условия оптимальности, т. е. условия, из которых следует, что данная точка является решением задачи. |
|
geum.ru
