Оптимизация сетевых моделей по критерию «время- затраты». Оптимизация сетевых моделей
2. Оптимизация сетевых моделей по критерию "минимум исполнителей"
Графики привязки и загрузки для исходных данных из табл.2.1, представлены на рис.2.1.
Таблица 2.1
Исходные данные для оптимизации загрузки (Вариант 3)
| Код работ | Продолжительность работ | Количество исполнителей |
| (1,2) | 4 | 4 |
| (1,3) | 3 | 4 |
| (1,7) | 12 | 6 |
| (2,5) | 5 | 4 |
| (3,6) | 2 | 2 |
| (5,7) | 8 | 1 |
| (6,7) | 7 | 3 |
| (6,8) | 3 | 4 |
| (7,8) | 6 | 6 |
| (8,9) | 5 | 5 |
| N=10 человек | ||
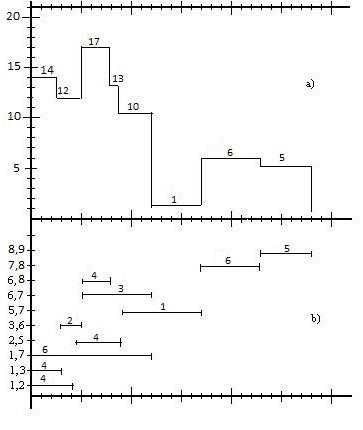
Рис.2.1. Графики загрузки (а) и привязки (b) до оптимизации
Допустим, что организация, выполняющая проект, имеет в распоряжении только исполнителей. Но в соответствии с графиком загрузки (рис.2.1), в течении интервала времени с 1 по 9 день для выполнения проекта требуется работа одновременно 14, 12, 17 и затем 13 человек. Таким образом, возникает необходимость снижения максимального количества одновременно занятых исполнителей с 17 до 10 человек.Для лучшего понимания последующего описания процесса оптимизации загрузки вручную вносите изменения в графики привязки и загрузки работ.
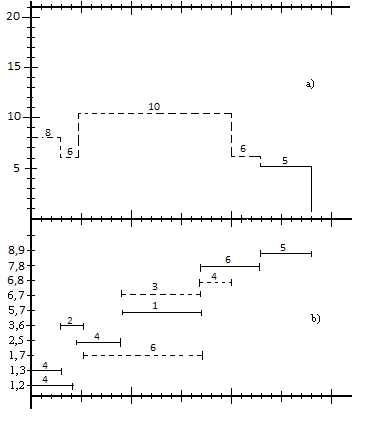
Рис.2. Графики загрузки (а) и привязки (b) после оптимизации
Проанализируем возможность уменьшения загрузки (14 и 12 человек) с 1 по 5-ый день. Используя , сдвинем работуна 5 дней, что снизит загрузку с 1 по 5-ый день до 8 и 6 человек. Также с 5 по 8-ой день загрузка остается 17 человек, проанализируем возможность уменьшения загрузки человек с 5 по 8-ой день т.е. в течении интервала 3-ёх дней. Так работы (6,7) и (6,8) являются единственными, которые можно сдвинуть, таким образом, чтобы они не выполнялись в указанные 3 дня с 5 по 8 день. Для этого, используя, сдвинем работу (6,7) на 5 дней, после чего она будет начинаться в 9-ый день, а работу (6,7) сдвинем на 11 дней используяи будет она начинаться в 17-ый день.
В результате произведенных сдвигов максимальная загрузка сетевой модели уменьшилась с 17 до 10 человек, что и являлось целью проводимой оптимизации. Окончательные изменения в графиках привязки и загрузки показаны на рис.2.2 пунктирной линией.
Проведенная оптимизация продемонстрировала следующее различие использования свободных и полных резервов работ. Так сдвиг работы на время в пределах ее свободного резерва не меняет моменты начала последующих за ней работ. В то же время сдвиг работы на время, которое находится в пределах ее полного резерва, но превышает ее свободный резерв, влечет сдвиг последующих за ней работ.
3. Оптимизация сетевых моделей по критерию "время-затраты"
Проведем максимально возможное уменьшение сроков выполнения проекта при минимально возможных дополнительных затратах для следующих исходных данных (табл.3.1, рис. 3.2).
Таблица 3.1
Исходные данные для оптимизации "Время -затраты"( Вариант 3)
Нормальный режим | Ускоренный режим | |||||
| (1,2) | 4 | 15 | 2 | 17 | ||
| (1,3) | 3 | 8 | 2 | 10 | ||
| (1,7) | 12 | 18 | 6 | 25 | ||
| (2,5) | 5 | 13 | 1 | | ||
| (3,6) | 2 | 9 | 1 | 10 | ||
| (5,7) | 8 | 14 | 3 | 18 | ||
| (6,7) | 7 | 14 | 4 | 15 | ||
| (6,8) | 3 | 5 | 1 | 7 | ||
| (7,8) | 6 | 16 | 1 | 29 | ||
| (8,9) | 5 | 11 | 2 | 13 | ||
| руб./день | руб. | |||||
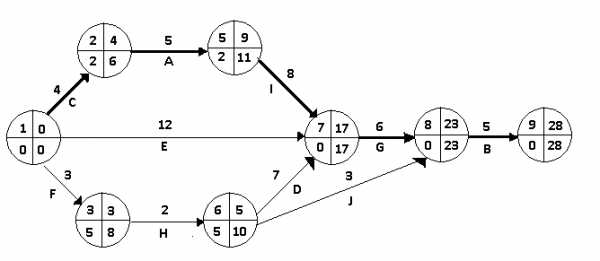
Рис.3.2. Исходная сетевая модель
Исходя из нормальных длительностей работ получаем следующие характеристики сетевой модели.
Кроме того, вычислим коэффициенты нарастания затрат и максимальные запасы времени сокращения работ сетевой модели (табл. 3.2).
Таблица 3.2
Коэффициенты нарастания затрат работ сети
| [дни] | [руб./день] | |
| (1,2) | 2 | 1,00 |
| (1,3) | 1 | 2,00 |
| (1,7) | 6 | 1,20 |
| (2,5) | 4 | 0,25 |
| (3,6) | 1 | 1,00 |
| (5,7) | 5 | 0,80 |
| (6,7) | 3 | 0,35 |
| (6,8) | 2 | 1,00 |
| (7,8) | 5 | 2,60 |
| (8,9) | 3 | 0,70 |
I шаг. Для сокращения выбираем критическую работу с минимальным коэффициентомруб./день. Текущий запас сокращения времени работына данном шаге равендня. Разность между продолжительностью критического и подкритического путейдней. Также для сокращения выбираем еще одну критическую работу (5,7) с коэффициентомk(5,7)=0,80 руб./день. Поэтому согласно п.3.2 оптимизации сокращаем работу на 4 дня, а (5,7) на 1день. Новая текущая длительность работыдень,, а запас их дальнейшего сокращения сокращается додня,дня. Измененный сетевой график представлен на рис.3.3
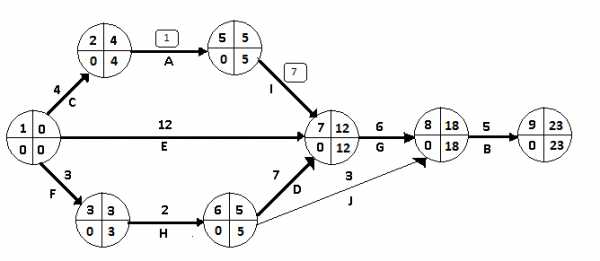
Рис.3.3. Сетевая модель после первого шага оптимизации
После ускорения работы и (5,7) возникли следующие изменения.
II шаг. Одновременное сокращение трех критических путей можно провести либо ускорив работу , принадлежащую трем путям, либо одновременно ускорив различные работы из каждого пути. Наиболее дешевым вариантом является ускорение работ (5,7), (1,7) и (6,7) - 2,35 руб./день за три работы, тогда как ускорение работыобошлось бы в 2,60 руб./день. Поскольку, то сокращаем работы (5,7), (1,7) и (6,7) по 3 дня на каждый путь. Запасы дальнейшего сокращения времени работ сокращаются до,идней. Измененный сетевой график представлен на рис.3.4.
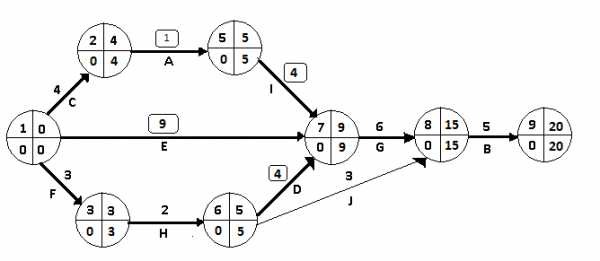
Рис.3.4. Сетевая модель после второго шага оптимизации
После ускорения работ (5,7), (1,7) и (6,7) возникли следующие изменения.
руб.
III шаг. Поскольку на данном шаге работа (6,7) исчерпала свой запас ускорения, то единственным сокращением трех критических путей является ускорение работы (7,8) - 2,60 руб./день. Сокращаем работы (7,8) на 5 дней. Измененный сетевой график представлен на рис.3.5.
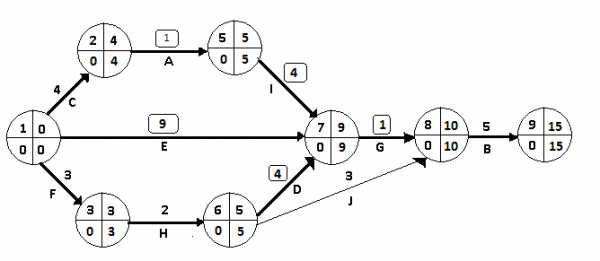
Рис.3.5. Сетевая модель после третьего шага оптимизации
После ускорения работ (7,8) возникли следующие изменения.
руб.
IV шаг. Сокращением трех критических путей возможно только при условии сокращения подкретического пути. Таким образом мы сможем сократить длительность всего проекта. Сократим следующие работы (8,9) на 3 дня, (1,7) на 2 дня, (1,2),(5,7),(1,3),(3,6) на 1день, этим шагом сможем максимально сократить длительность всего проекта, при условии не имея ограничения на затрату средств. Измененный сетевой график представлен на рис.3.6.
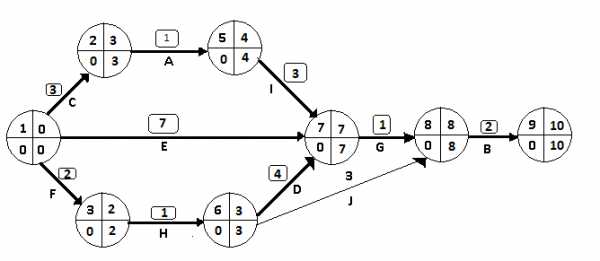
Рис.3.6. Сетевая модель после четвертого шага оптимизации
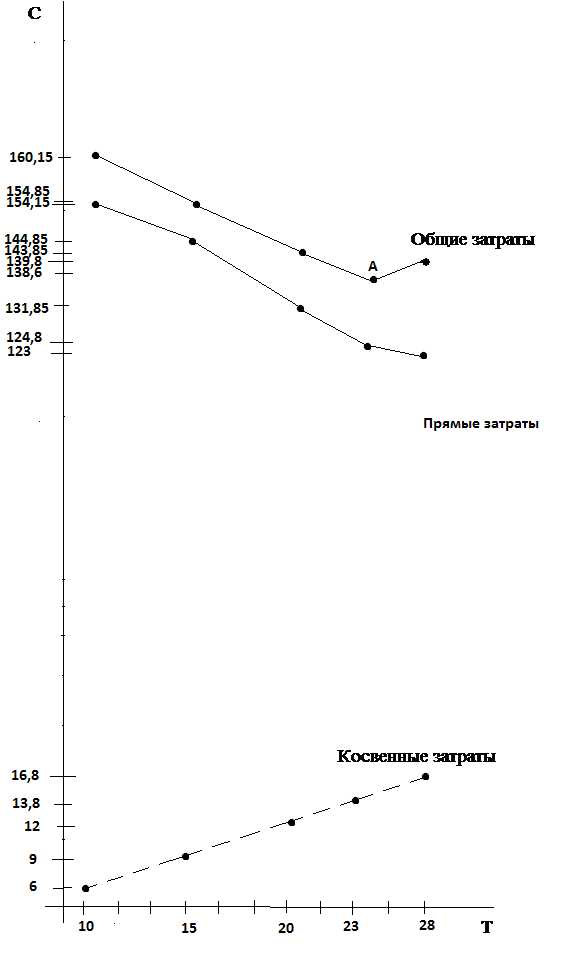
Рис.3.7 "Время - затрат"
После ускорения работ (8,9) на 3 дня (1,7)на 2 дня, (1,2),(5,7),(1,3),(3,6) возникли следующие изменения.
Дальнейшая оптимизация стала невозможной, поскольку все работы критических путей исчерпали свой запас времени ускорения, а значит проект не может быть выполнен меньше, чем за дней.
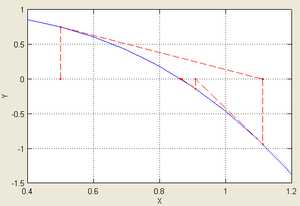
Таким образом, при отсутствии ограничений на затраты минимально возможная длительность проекта составляет 10 дней. Сокращение длительности проекта с 28 до 10 дней потребовало 31,15 рублей прямых затрат. В отличие от прямых затрат при уменьшении продолжительности проекта косвенные затраты (руб./день) убывают, что показано на графике (см. рис.3.7). Минимум общих затрат (точка А) соответствует продолжительности проекта 23 дня.
Если же учитывать ограничение по средствам, выделенным на выполнение проекта, рубля, то оптимальным является выполнение проекта за 23 дня (точка А).
studfiles.net
44. Оптимизация сетевых моделей по ресурсам.
С каждой работой, имеющей определенный неизменный объем, связаны затраты на ее выполнение. Как правило, затраты на выполнение работы с неизменным ее объемом возрастают с уменьшением ее продолжительности и снижаются при увеличении ее продолжительности.
В связи с этим возможны варианты организации комплекса работ, отличающиеся продолжительностью его выполнения и затратами на его выполнение.
Для выбора наилучшего варианта служит оптимизация. Оптимальным считается тот вариант, который отвечает заданному критерию.
Оптимизация сетевого графика может осуществляться по следующим двум критериям:
- минимизация времени выполнения комплекса работ при заданных затратах на это выполнение;
- минимизация затрат на выполнение комплекса работ при заданном времени этого выполнения.
Таким образом, нельзя добиться выполнения комплекса работ одновременно в минимальные сроки и с наименьшими затратами.
Целью оптимизации по критерию является сокращение времени выполнения проекта в целом. Эта оптимизация имеет смысл только в том случае, когда длительность выполнения работ может быть уменьшена за счет дополнительных ресурсов, что влечет к повышению затрат на выполнение работ. Для оценки величины дополнительных затрат, связанных с ускорением выполнения той или иной работы, используются либо нормативы, либо данные о выполнении аналогичных работ в прошлом.
Исходными данными для проведения оптимизации являются:
нормальная длительность работы;
ускоренная длительность;
затраты на выполнение работы в нормальный срок;
затраты на выполнение работы в ускоренный срок.
Требуется оптимизировать по критерию минимизации затрат сетевой график при заданной продолжительности выполнения всего комплекса работ за 19 суток.
Оптимизировать сетевой график по критерию минимизации затрат при заданной продолжительности выполнения всего комплекса работ можно двумя способами. Первый способ заключается в уменьшении продолжительности выполнения работ, начиная с тех, которые дают наименьший прирост затрат. Второй способ заключается в увеличении продолжительности выполнения работ, начиная с тех, которые дают наибольший прирост затрат. Определяемые любым из указанных способов оптимальные затраты должны иметь одинаковую величину.
45. Оптимизация сетевых моделей по времени и стоимости
если сокращается продолжительность строительства, то при одновременном снижении накладных расходов прямые расходы возрастают. Функциональная зависимость между продолжительностью работ и их стоимостью пока точно не определена. Поэтому рассмотрим зависимость «время—стоимость» (с учетом прямых затрат), которая может быть определена условно.
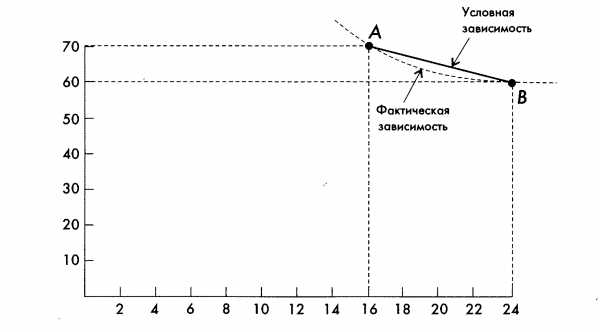
Как видно из рисунка, точка А соответствует наикратчайшему сроку выполнения данного проекта, т.е. сроку, при котором все работы проводятся в предельно сжатые сроки.
Точка В соответствует нормальной продолжительности работ.
Затраты в точке А, так же как срок, считаются предельными: их дальнейшее увеличение лишь в очень незначительной степени повлияет на сокращение сроков. Затраты в точке В являются нормальными.
Прямая линия, соединяющая точки А и В, точнее степень наклона этой прямой, и является характеристикой изменения величины прямых затрат при изменении продолжительности работ на единицу времени. Величина наклона для каждой единицы времени является величиной постоянной, так как мы приняли линейную зависимость между продолжительностью и стоимостью работ. (В действительности эта величина является условной. Фактическая зависимость изображена на рис. 7.10 кривой, соединяющей точки А и В.)
Величина наклона прямой определяется дробью, в числителе которой — разность между затратами в предельном и нормальном режимах, а в знаменателе — разность между продолжительностью работ в нормальном и предельном режимах. Для прямой, изображенной на рис. 7.10, эта величина составит:
(70 - 60) : (24 - 16) = 1,25 (тыс. руб./день).
Для проведения оптимизации необходимо по каждой работе определить предельные и нормальные сроки выполнения, а также предельные и нормальные величины затрат. После этого методом последовательного приближения достичь заданного предельного срока за счет сокращения продолжительность.
46.Коридорные сетевые графики
Коридорный сетевой график представляет собой сетевой график, стрелки (работы) которого расположены в горизонтальных коридорах, соответствующих отдельным исполнителям работ или отдельным комплексам работ.
Коридор — горизонтальная зона сетевой модели, объединяющая работы, выполняемые одним исполнителем или относящиеся к одному комплексу (очереди, блоку)
Принадлежность работы к тому или иному коридору определяется горизонтальным участком стрелки, обозначающим эту работу.
Иногда наглядность коридорного графика можно значительно повысить, показав на нем одновременно и комплексы работ и их исполнителей.
Для этого начальные события работ, выполняемых различными исполнителями, изображают в виде различных фигур (кружков, квадратов, треугольников и др.)
Коридорный сетевой график несет значительно больше информации, чем обычный сетевой график. Это позволяет использовать коридорные сетевые графики в тех случаях, когда простых сетевых графиков для управленческих функций бывает недостаточно.
studfiles.net
ОПТИМИЗАЦИЯ СЕТЕВЫХ МОДЕЛЕЙ ПО КРИТЕРИЮ — Студопедия.Нет
ПОСТРОЕНИЕ И РАСЧЕТ МОДЕЛЕЙ СЕТЕВОГО ПЛАНИРОВАНИЯ И УПРАВЛЕНИЯ
Исходные данные варианта расчетно-графической работы включают название и продолжительность каждой работы (табл. 1.1), а также описание упорядочения работ.
Исходные данные (Вариант 3)
Таблица 1.1
| Название работы | Продолжительность работы |
| A | 5 |
| B | 5 |
| C | 4 |
| D | 7 |
| E | 12 |
| F | 3 |
| G | 6 |
| H | 2 |
| I | 8 |
| J | 3 |
Упорядочение работ
1) Работы C, E, F являются исходными работами проекта, которые могут выполняться одновременно.
2) Работа A начинается сразу по окончании работы C.
3) Работа H следует за работой F.
4) Работы I следуют за A, а работы D и J - за Н .
5) Работа G следует за работой E, но не может начаться, пока не завершены D и I.
6) Работа B следует за G и J.
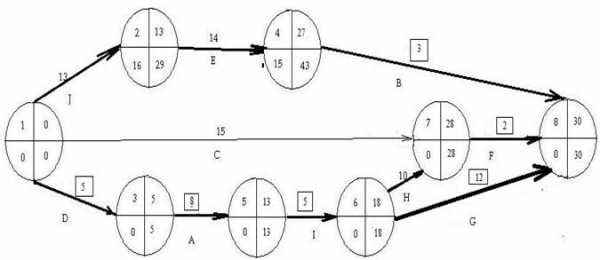
На рис.1.4 представлена сетевая модель, соответствующая данному упорядочению работ. Каждому событию присвоен номер, что позволяет в дальнейшем использовать не названия работ, а их коды (см. табл. 1.2). Численные значения временных параметров событий сети вписаны в соответствующие секторы вершин сетевого графика, а временные параметры работ сети представлены в табл. 1.3.
- Для исходного события И .
- Для всех остальных событий i , где максимум берется по всем работам , входящим в событие i.
- Поздние сроки свершения событий рассчитываются от завершающего к исходному событию.
- Для завершающего события З .
- Для всех остальных событий , где минимум берется по всем работам , выходящим из события i.
- .
Таблица 1.2
Описание сетевой модели с помощью кодирования работ
| Номера событий | Код работы | Продолжительность | |
| начального | конечного | работы | |
| 1 | 2 | (1,2) | 4 |
| 1 | 3 | (1,3) | 3 |
| 1 | 4 | (1,7) | 12 |
| 2 | 5 | (2,5) | 5 |
| 3 | 6 | (3,6) | 2 |
| 5 | 4 | (5,7) | 8 |
| 6 | 4 | (6,7) | 7 |
| 6 | 7 | (6,8) | 3 |
| 4 | 7 | (7,8) | 6 |
| 7 | 8 | (8,9) | 5 |
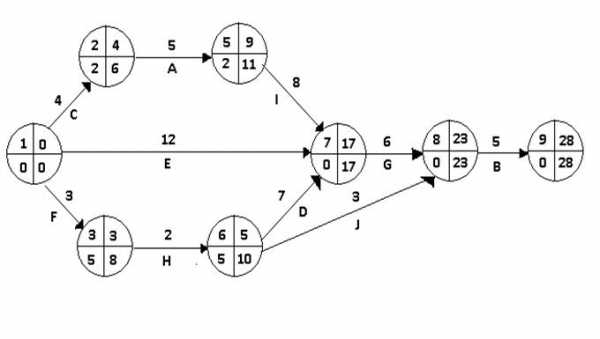Рис.1.4. Сетевая модель
К наиболее важным временным параметрам работ относятся:
· - ранний срок начала работы;
· - поздний срок начала работы;
· - ранний срок окончания работы;
· - поздний срок окончания работы;
1) ;
2) или ;
3) ;
4) или ;
5) ;
6) .
Таблица 1.3
Временные параметры работ
| (1,2) | 4 | 0 | 4 | 2 | 6 | 2 | 0 |
| (1,3) | 3 | 0 | 3 | 5 | 8 | 5 | 0 |
| (1,7) | 12 | 0 | 12 | 5 | 17 | 5 | 5 |
| (2,5) | 5 | 4 | 9 | 6 | 11 | 2 | 0 |
| (3,6) | 2 | 3 | 5 | 8 | 10 | 5 | 0 |
| (5,7) | 8 | 9 | 17 | 9 | 17 | 0 | 0 |
| (6,7) | 7 | 5 | 12 | 10 | 17 | 5 | 5 |
| (6,8) | 3 | 5 | 8 | 20 | 23 | 15 | 14 |
| (7,8) | 6 | 17 | 23 | 17 | 23 | 0 | 0 |
| (8,9) | 5 | 23 | 28 | 23 | 28 | 0 | 0 |
ОПТИМИЗАЦИЯ СЕТЕВЫХ МОДЕЛЕЙ ПО КРИТЕРИЮ
"МИНИМУМ ИСПОЛНИТЕЛЕЙ"
Графики привязки и загрузки для исходных данных из табл.2.1, представлены на рис.2.1.
Таблица 2.1
Исходные данные для оптимизации загрузки (Вариант 3)
| Код работ | Продолжительность работ | Количество исполнителей |
| (1,2) | 4 | 4 |
| (1,3) | 3 | 4 |
| (1,7) | 12 | 6 |
| (2,5) | 5 | 4 |
| (3,6) | 2 | 2 |
| (5,7) | 8 | 1 |
| (6,7) | 7 | 3 |
| (6,8) | 3 | 4 |
| (7,8) | 6 | 6 |
| (8,9) | 5 | 5 |
| N=10 человек | ||
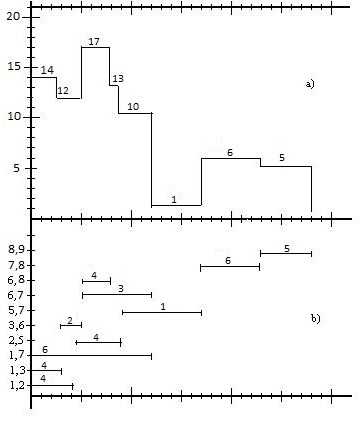
Рис.2.1. Графики загрузки (а) и привязки (b) до оптимизации
Допустим, что организация, выполняющая проект, имеет в распоряжении только исполнителей. Но в соответствии с графиком загрузки (рис.2.1), в течении интервала времени с 1 по 9 день для выполнения проекта требуется работа одновременно 14, 12, 17 и затем 13 человек. Таким образом, возникает необходимость снижения максимального количества одновременно занятых исполнителей с 17 до 10 человек. Для лучшего понимания последующего описания процесса оптимизации загрузки вручную вносите изменения в графики привязки и загрузки работ.
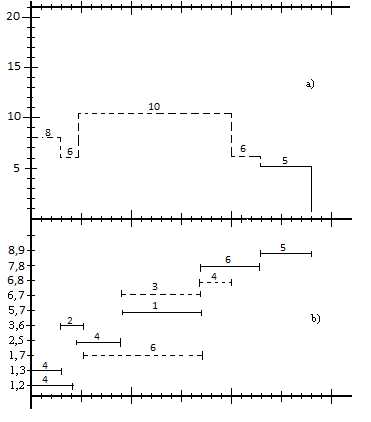
Рис.2. Графики загрузки (а) и привязки (b) после оптимизации
Проанализируем возможность уменьшения загрузки (14 и 12 человек) с 1 по 5-ый день. Используя , сдвинем работу на 5 дней, что снизит загрузку с 1 по 5-ый день до 8 и 6 человек. Также с 5 по 8-ой день загрузка остается 17 человек, проанализируем возможность уменьшения загрузки человек с 5 по 8-ой день т.е. в течении интервала 3-ёх дней. Так работы (6,7) и (6,8) являются единственными, которые можно сдвинуть, таким образом, чтобы они не выполнялись в указанные 3 дня с 5 по 8 день. Для этого, используя , сдвинем работу (6,7) на 5 дней, после чего она будет начинаться в 9-ый день, а работу (6,7) сдвинем на 11 дней используя и будет она начинаться в 17-ый день.
В результате произведенных сдвигов максимальная загрузка сетевой модели уменьшилась с 17 до 10 человек, что и являлось целью проводимой оптимизации. Окончательные изменения в графиках привязки и загрузки показаны на рис.2.2 пунктирной линией.
Проведенная оптимизация продемонстрировала следующее различие использования свободных и полных резервов работ. Так сдвиг работы на время в пределах ее свободного резерва не меняет моменты начала последующих за ней работ. В то же время сдвиг работы на время, которое находится в пределах ее полного резерва, но превышает ее свободный резерв, влечет сдвиг последующих за ней работ.
ОПТИМИЗАЦИЯ СЕТЕВЫХ МОДЕЛЕЙ ПО КРИТЕРИЮ
"ВРЕМЯ-ЗАТРАТЫ"
Проведем максимально возможное уменьшение сроков выполнения проекта при минимально возможных дополнительных затратах для следующих исходных данных (табл.3.1, рис. 3.2).
Таблица 3.1
Исходные данные для оптимизации "Время -затраты"(Вариант 3)
| Нормальный режим | Ускоренный режим | ||||
| (1,2) | 4 | 15 | 2 | 17 | |
| (1,3) | 3 | 8 | 2 | 10 | |
| (1,7) | 12 | 18 | 6 | 25 | |
| (2,5) | 5 | 13 | 1 | 14 | |
| (3,6) | 2 | 9 | 1 | 10 | |
| (5,7) | 8 | 14 | 3 | 18 | |
| (6,7) | 7 | 14 | 4 | 15 | |
| (6,8) | 3 | 5 | 1 | 7 | |
| (7,8) | 6 | 16 | 1 | 29 | |
| (8,9) | 5 | 11 | 2 | 13 | |
| руб./день | руб. | ||||
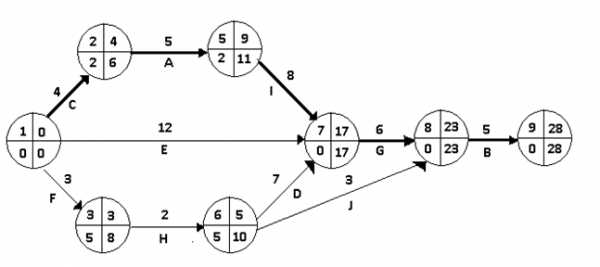
Рис.3.2. Исходная сетевая модель
Исходя из нормальных длительностей работ получаем следующие характеристики сетевой модели.
· Общие затраты на проект руб.
· Длительность проекта дней.
· Критический путь или .
· Подкритический путь или , дня.
Кроме того, вычислим коэффициенты нарастания затрат и максимальные запасы времени сокращения работ сетевой модели (табл. 3.2).
Таблица 3.2
Коэффициенты нарастания затрат работ сети
| [дни] | [руб./день] | |
| (1,2) | 2 | 1,00 |
| (1,3) | 1 | 2,00 |
| (1,7) | 6 | 1,20 |
| (2,5) | 4 | 0,25 |
| (3,6) | 1 | 1,00 |
| (5,7) | 5 | 0,80 |
| (6,7) | 3 | 0,35 |
| (6,8) | 2 | 1,00 |
| (7,8) | 5 | 2,60 |
| (8,9) | 3 | 0,70 |
I шаг. Для сокращения выбираем критическую работу с минимальным коэффициентом руб./день. Текущий запас сокращения времени работы на данном шаге равен дня. Разность между продолжительностью критического и подкритического путей дней. Также для сокращения выбираем еще одну критическую работу (5,7) с коэффициентом k(5,7)=0,80 руб./день. Поэтому согласно п.3.2 оптимизации сокращаем работу на 4 дня, а (5,7) на 1день. Новая текущая длительность работы день, , а запас их дальнейшего сокращения сокращается до дня, дня. Измененный сетевой график представлен на рис.3.3
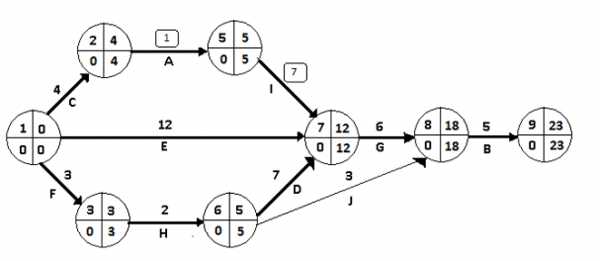
Рис.3.3. Сетевая модель после первого шага оптимизации
После ускорения работы и (5,7) возникли следующие изменения.
· Затраты на работу возросли на , (5,7) возросли на 0,80 руб./день * 1 день =0,80 руб. и общие затраты на проект составили руб.
· Длительность проекта дней.
· Три критических пути ; и .
· Подкритический путь , дней.
II шаг.Одновременное сокращение трех критических путей можно провести либо ускорив работу , принадлежащую трем путям, либо одновременно ускорив различные работы из каждого пути. Наиболее дешевым вариантом является ускорение работ (5,7), (1,7) и (6,7) - 2,35 руб./день за три работы, тогда как ускорение работы обошлось бы в 2,60 руб./день. Поскольку , то сокращаем работы (5,7), (1,7) и (6,7) по 3 дня на каждый путь. Запасы дальнейшего сокращения времени работ сокращаются до , и дней. Измененный сетевой график представлен на рис.3.4.
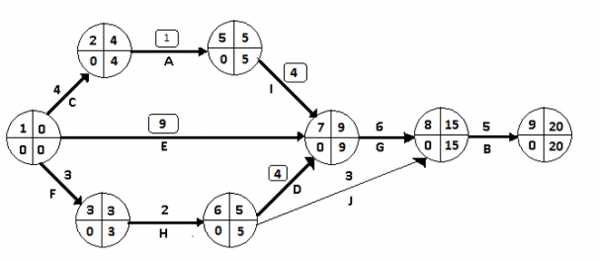
Рис.3.4. Сетевая модель после второго шага оптимизации
После ускорения работ (5,7), (1,7) и (6,7) возникли следующие изменения.
· Общие затраты на проект составили
руб.
· Длительность проекта дней.
· Три критических пути ; и .
· Подкритический путь , дней.
III шаг. Поскольку на данном шаге работа (6,7) исчерпала свой запас ускорения, то единственным сокращением трех критических путей является ускорение работы (7,8) - 2,60 руб./день. Сокращаем работы (7,8) на 5 дней. Измененный сетевой график представлен на рис.3.5.
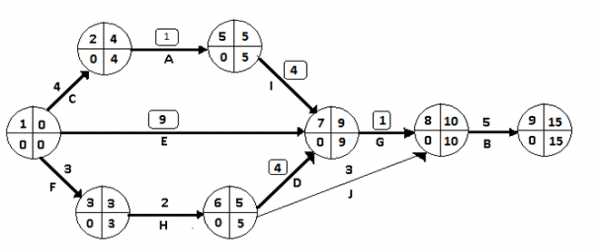
Рис.3.5. Сетевая модель после третьего шага оптимизации
После ускорения работ (7,8) возникли следующие изменения.
· Общие затраты на проект составили
руб.
· Длительность проекта дней.
· Три критических пути ; и .
· Подкритический путь , дней.
IV шаг. Сокращением трех критических путей возможно только при условии сокращения подкретического пути. Таким образом мы сможем сократить длительность всего проекта. Сократим следующие работы (8,9) на 3 дня, (1,7) на 2 дня, (1,2),(5,7),(1,3),(3,6) на 1день, этим шагом сможем максимально сократить длительность всего проекта, при условии не имея ограничения на затрату средств. Измененный сетевой график представлен на рис.3.6.
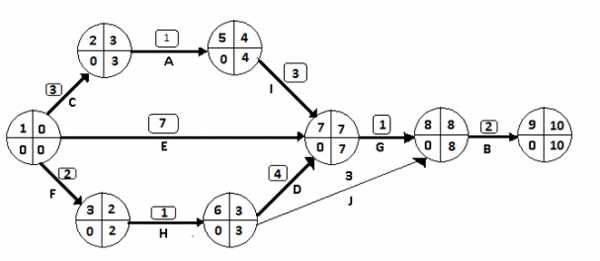
Рис.3.6. Сетевая модель после четвертого шага оптимизации
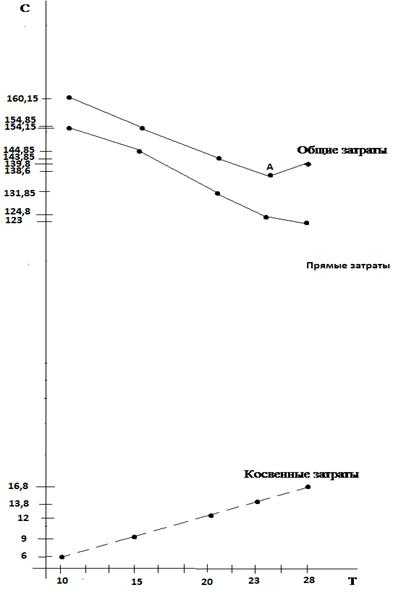
Рис.3.7 "Время - затрат"
После ускорения работ (8,9) на 3 дня (1,7)на 2 дня, (1,2),(5,7),(1,3),(3,6) возникли следующие изменения.
· Общие затраты на проект составили руб.
· Длительность проекта дней.
· Три критических пути ; и .
· Подкритический путь , дней.
Дальнейшая оптимизация стала невозможной, поскольку все работы критических путей исчерпали свой запас времени ускорения, а значит проект не может быть выполнен меньше, чем за дней.
Таким образом, при отсутствии ограничений на затраты минимально возможная длительность проекта составляет 10 дней. Сокращение длительности проекта с 28 до 10 дней потребовало 31,15 рублей прямых затрат. В отличие от прямых затрат при уменьшении продолжительности проекта косвенные затраты ( руб./день) убывают, что показано на графике (см. рис.3.7). Минимум общих затрат (точка А) соответствует продолжительности проекта 23 дня.
Если же учитывать ограничение по средствам, выделенным на выполнение проекта, рубля, то оптимальным является выполнение проекта за 23 дня (точка А).
ЛИТЕРАТУРА
1. Сетевое планирование и управление. Под ред. Д.И. Голенко. - М.: Экономика, 1967.
2. Н.М. Губин, А.С. Добронравов, Б.С. Дорохов. Экономико-математические методы и модели в планировании и управлении в отрасли связи. - М.: Радио и связь, 1993.
3. Сетевые графики в планировании. Под ред. И.М. Разумова. - М.: Высшая школа, 1975.
4. Х. Таха. Введение в исследование операций. - М.: Мир, 1985.
5. М. Эддоус, Р. Стенсфилд. Методы принятия решений. - М.: Аудит, ЮНИТИ, 1997.
studopedia.net
Оптимизация сетевых моделей
Содержание
| Введение | 2 |
| 1. Основные методические положения | 3 |
| 2. Практическая часть | 11 |
| Вычисление параметров сетевого графика графическим методом | 12 |
| Вычисление параметров сетевого графика табличным методом | 14 |
| Оптимизация сетевого графика по времени | 16 |
| Оптимизация сетевого графика по ресурсам | 21 |
| Заключение | 22 |
| Приложение 1 – Карта сетевого проекта | 23 |
| Приложение 2 – Карта сетевого проекта после оптимизации по времени | 24 |
| Приложение 3 – Карта сетевого проекта после оптимизации по ресурса | 25 |
ВведениеЦелью данной работы является развитие навыков построения, расчета, анализа и оптимизации сетевого графика.
Работа включает в себя:
1. расчет ожидаемой продолжительности выполнения работ
2. построение топологической модели сетевого графика
3. расчет параметров сетевого графика одним из предложенных методов
4. построение карты проекта сетевого графика
5. расчет показателей КH i, j, X
6. оптимизация сетевого графика по времени
7. расчет параметров оптимизированного по времени сетевого графика
8. построение карты проекта оптимизированного сетевого графика
9. расчет показателей КH i, j, X для оптимизированного графика
10. оптимизация сетевого графика по ресурсам1.Основные методические положенияДля планирования и управления комплексами работ применяются системы сетевого планирования и управления (СПУ). СПУ основано на построении графического изображения определенного комплекса работ, отражающего их логическую последовательность, взаимосвязь и длительность, с последующим анализом и оптимизацией разработанного графика.
Сетевая модель (график, сеть) представляет собой графическую модель, в которой изображаются взаимосвязи и результаты всех работ планируемого комплекса.
Основными элементами графика являются события и работы.
Событие – это результат выполнения одной или нескольких работ. Событие – это свершившийся факт, оно занимает лишь один момент во времени и не имеет продолжительности. Оно указывает на начало каких-либо работ и может быть одновременно итогом завершения других работ. Различают две группы событий: для всей группы работ – исходное I и завершающие J, а для каждой работы – начальное i и конечное j.
В сетевом графике событие изображается геометрической фигурой (кружком, квадратом и т.д.), в котором указывается порядковый номер или шифр события, а иногда и название события.
Работами называются любые процессы, действия, приводящие к достижению определенных результатов (событий).
Работа может быть действительной или фиктивной. Действительная работа – это процесс, требующий затрат времени и исполнителей. Графически действительная работа изображается сплошной линией со стрелкой, которая означает затрату времени, необходимого для выполнения данной работы. Затрачиваемое на работу время обозначается над стрелкой, а число исполнителей под стрелкой. Фиктивная работа устанавливает только логическую связь между работами, она не требует затрат времени и исполнителей, на сетевом графике изображается пунктирной линией.
Любая последовательность в сетевом графике, в которой конечное событие одной работы совпадает с начальным событием следующей за ней работы, называет путем. В сетевом графике следует различать несколько видов путей:
а) от исходного события до завершающего события – полный путь
б) от исходного события до данного – путь, предшествующий данному событию
в) от данного события до завершающего – путь, последующий за данным событием
г) между двумя какими-либо промежуточными событиями i и j – путь между событиями i и j
д) путь между исходным и завершающим событием, имеющий наибольшую продолжительность – критический путь.
Сетевое планирование и управление включает семь этапов:
1. составление перечня работ, которые надлежит выполнить по объекту разработки для получения конечной цели.
2. установление топологии сети
3. построение сетевого графика
4. определение продолжительности работ
5. расчет параметров сети
6. анализ сети и оптимизация сетевого графика
7. функционирование сетевой модели.Правила построения сетевого графика:
1. При построении сетевого графика необходимо соблюдать технологическую последовательность выполняемых работ планируемого комплекса.
2. В сетевом графике не должно быть пересекающихся стрелок.
3. Направление стрелок в сетевом графике должно быть слева на право.
4. В сетевом графике не должно быть событий, которым не предшествует ни одна работа (кроме исходной).
5. В построенном сетевом графике должно быть одно начальное и одно завершенное событие.
6. В сетевом графике необходимо соблюдать последовательность в нумерации событий от исходного, которому обычно присваивается нулевой номер, к завершающему. При этом для любой работы i-j одним из условий правильного построения сетевого графика является обязательным выполнение неравенства i<j.Основные параметры сетевого графика.
К основным параметрам сетевого графика относятся критический путь, резервы времени событий и работ. Эти параметры являются исходными для получения ряда дополнительных характеристик, а так же для анализа сети.
1. Критическим путем называют наибольший по продолжительности из всех путей сетевого графика от исходного события до завершающего. В сетевом графике имеются и другие пути, опирающиеся на исходное и завершающее события (полные пути), которые могут либо полностью проходить вне критического пути, либо частично совпадать с критической последовательностью работ. Эти пути называются не напряженными. Ненапряженные пути – это полные пути сетевого графика, которые по продолжительности меньше критического пути.
Ненапряженные пути обладают важным свойством: на участках, не совпадающих с критической последовательностью работ, они имеют резервы времени. Это означает, что задержка в совершении событий, не лежащих на критическом пути, до определенного момента не влияет на срок завершения разработки в целом. Критические пути резервами времени не располагают.
2. Резервы времени события – это такой промежуток времени, на который может быть отсрочено совершение этого события без нарушения сроков завершения разработки в целом.
Резерв времени события Ri определяет как разность между поздним Тпi и ранним Трi сроками наступления события:
Ri = Тпi - Трi (1)
3. Поздний срок Тпi – это такой срок завершения i-го события, превышение которого вызовет задержку завершения события.
Ранний из возможных сроков совершения i-го события Трi – минимальный срок, необходимый для выполнения всех работ, предшествующих данному событию.
Ранний срок совершения события i определяется как продолжительность во времени максимального из путей Lmax, ведущих от исходного события I до данного события i:
Трi = t [ L (I – i)max ] (2)
Поздний срок события I определяется по следующей формуле:
Тпi = t (Lкр) – t [ L ( i – C)max ] (3)
Путь, соединяющий события с нулевыми резервами времени, является критическим.
4. Резервами времени так же располагают работы. Зная ранние и поздние сроки наступления событий, можно для любой работы (i,j) определить ранние и поздние сроки начала и окончания работ.
Ранний срок начала работ:
Tрн i,j = Трi (4)
Поздний срок начала этой работы:
Tпн i,j = Тпσ – t i,j (5)
Ранний срок окончания работ:
Tро i,j = Трi + t i,j (6)
Поздний срок окончания работ:
Tпо i,j = Тпj (7)
5. Разница во времени между длиной критического пути t ( Lкр ) и длиной любого другого пути t ( Li ) называется полным резервом времени пути. Он равен:
R (Li) = t ( Lкр ) – t ( Li ) (8)
Полный резерв пути показывает, насколько могут быть увеличены продолжительности всех работ, принадлежавших пути Li.
6. Полный резерв времени работы Rп i,j показывает, сколько имеется в запасе времени для выполнения данной работы, на которое можно увеличить продолжительность данной работы, не изменяя при этом продолжительности данного пути:
Rп i,j = Тпj - Трi - t i,j (9)
7. У отдельных видов работ помимо полного резерва времени имеется свободный резерв времени Rс i,j, являющийся частью резерва. На время этого резерва можно увеличить продолжительность работы, не изменяя ранних сроков начала последующих работ.
Rс i,j = Трj - Трi - t i,j (10)
Резервы времени работ, особенно свободный, позволяют маневрировать сроками начала и окончания работ, их продолжительностью.Определение продолжительности работ.При построенной сетевой модели для каждой работы определяется ожидаемая продолжительность ее выполнения, которая проставляется над соответствующей стрелкой в графике. Для определения продолжительности работ пользуются установленными нормами времени, при их отсутствии используют систему вероятностных оценок. В таких случаях ожидаемое время выполнения работ ti,j определяют на основе экспертных оценок по формуле
(11)
Дисперсия, или мера разброса для принятого в СПУ закона распределения:
(12)
Для двух оценок:
(13)
(14)
где tmin – минимально возможное время выполнения работ;
tmax – максимально возможное время выполнения работ;
tнв – наиболее вероятное время выполнения работ.
Расчет параметров сетевого графика графическим методом.
Существует несколько методов расчета сетевых графиков: графический, табличный, матричный, метод Форда и др.
Графический метод можно применять в тех случаях, когда число событий невелико (до 15-20). При этом каждый кружок, изображающий событие, делится на четыре сектора (рис.1).
en.coolreferat.com
Оптимизация сетевых моделей
Содержание
Введение
Целью данной работы является развитие навыков построения, расчета, анализа и оптимизации сетевого графика.
Работа включает в себя:
1. расчет ожидаемой продолжительности выполнения работ
2. построение топологической модели сетевого графика
3. расчет параметров сетевого графика одним из предложенных методов
4. построение карты проекта сетевого графика
5. расчет показателей КHi, j , X
6. оптимизация сетевого графика по времени
7. расчет параметров оптимизированного по времени сетевого графика
8. построение карты проекта оптимизированного сетевого графика
9. расчет показателей КHi, j , X для оптимизированного графика
10. оптимизация сетевого графика по ресурсам
1.Основные методические положения
Для планирования и управления комплексами работ применяются системы сетевого планирования и управления (СПУ). СПУ основано на построении графического изображения определенного комплекса работ, отражающего их логическую последовательность, взаимосвязь и длительность, с последующим анализом и оптимизацией разработанного графика.
Сетевая модель (график, сеть) представляет собой графическую модель, в которой изображаются взаимосвязи и результаты всех работ планируемого комплекса.
Основными элементами графика являются события и работы.
Событие – это результат выполнения одной или нескольких работ. Событие – это свершившийся факт, оно занимает лишь один момент во времени и не имеет продолжительности. Оно указывает на начало каких-либо работ и может быть одновременно итогом завершения других работ. Различают две группы событий: для всей группы работ – исходное Iи завершающие J, а для каждой работы – начальное i и конечное j.
В сетевом графике событие изображается геометрической фигурой (кружком, квадратом и т.д.), в котором указывается порядковый номер или шифр события, а иногда и название события.
Работами называются любые процессы, действия, приводящие к достижению определенных результатов (событий).
Работа может быть действительной или фиктивной. Действительная работа – это процесс, требующий затрат времени и исполнителей. Графически действительная работа изображается сплошной линией со стрелкой, которая означает затрату времени, необходимого для выполнения данной работы. Затрачиваемое на работу время обозначается над стрелкой, а число исполнителей под стрелкой. Фиктивная работа устанавливает только логическую связь между работами, она не требует затрат времени и исполнителей, на сетевом графике изображается пунктирной линией.
Любая последовательность в сетевом графике, в которой конечное событие одной работы совпадает с начальным событием следующей за ней работы, называет путем. В сетевом графике следует различать несколько видов путей:
а) от исходного события до завершающего события – полный путь
б) от исходного события до данного – путь, предшествующий данному событию
в) от данного события до завершающего – путь, последующий за данным событием
г) между двумя какими-либо промежуточными событиями iи j – путь между событиями iи j
д) путь между исходным и завершающим событием, имеющий наибольшую продолжительность – критический путь.
Сетевое планирование и управление включает семь этапов:
1. составление перечня работ, которые надлежит выполнить по объекту разработки для получения конечной цели.
2. установление топологии сети
3. построение сетевого графика
4. определение продолжительности работ
5. расчет параметров сети
6. анализ сети и оптимизация сетевого графика
7. функционирование сетевой модели.
Правила построения сетевого графика:
1. При построении сетевого графика необходимо соблюдать технологическую последовательность выполняемых работ планируемого комплекса.
2. В сетевом графике не должно быть пересекающихся стрелок.
3. Направление стрелок в сетевом графике должно быть слева на право.
4. В сетевом графике не должно быть событий, которым не предшествует ни одна работа (кроме исходной).
5. В построенном сетевом графике должно быть одно начальное и одно завершенное событие.
6. В сетевом графике необходимо соблюдать последовательность в нумерации событий от исходного, которому обычно присваивается нулевой номер, к завершающему. При этом для любой работы i-j одним из условий правильного построения сетевого графика является обязательным выполнение неравенства i<j.
Основные параметры сетевого графика.
К основным параметрам сетевого графика относятся критический путь, резервы времени событий и работ. Эти параметры являются исходными для получения ряда дополнительных характеристик, а так же для анализа сети.
1. Критическим путем называют наибольший по продолжительности из всех путей сетевого графика от исходного события до завершающего. В сетевом графике имеются и другие пути, опирающиеся на исходное и завершающее события (полные пути), которые могут либо полностью проходить вне критического пути, либо частично совпадать с критической последовательностью работ. Эти пути называются не напряженными. Ненапряженные пути – это полные пути сетевого графика, которые по продолжительности меньше критического пути.
Ненапряженные пути обладают важным свойством: на участках, не совпадающих с критической последовательностью работ, они имеют резервы времени. Это означает, что задержка в совершении событий, не лежащих на критическом пути, до определенного момента не влияет на срок завершения разработки в целом. Критические пути резервами времени не располагают.
2. Резервы времени события – это такой промежуток времени, на который может быть отсрочено совершение этого события без нарушения сроков завершения разработки в целом.
Резерв времени события Ri определяет как разность между поздним Тпi и ранним Трi сроками наступления события:
Ri = Тпi - Трi (1)
3. Поздний срок Тпi – это такой срок завершения i-го события, превышение которого вызовет задержку завершения события.
Ранний из возможных сроков совершения i-го события Трi – минимальный срок, необходимый для выполнения всех работ, предшествующих данному событию.
Ранний срок совершения события iопределяется как продолжительность во времени максимального из путей Lmax , ведущих от исходного события Iдо данного события i:
Трi = t [ L (I – i)max ] (2)
Поздний срок события Iопределяется по следующей формуле:
Тпi = t (Lкр ) – t [ L ( i – C)max ] (3)
Путь, соединяющий события с нулевыми резервами времени, является критическим.
4. Резервами времени так же располагают работы. Зная ранние и поздние сроки наступления событий, можно для любой работы (i,j) определить ранние и поздние сроки начала и окончания работ.
Ранний срок начала работ:
Tрн i,j = Трi (4)
Поздний срок начала этой работы:
Tпнi,j = Тпσ – t i,j (5)
Ранний срок окончания работ:
Tро i,j = Трi + ti,j (6)
Поздний срок окончания работ:
Tпо i,j = Тпj (7)
5. Разница во времени между длиной критического пути t ( Lкр ) и длиной любого другого пути t ( Li ) называется полным резервом времени пути. Он равен:
R (Li ) = t ( Lкр ) – t ( Li ) (8)
Полный резерв пути показывает, насколько могут быть увеличены продолжительности всех работ, принадлежавших пути Li .
6. Полный резерв времени работы Rп i,j показывает, сколько имеется в запасе времени для выполнения данной работы, на которое можно увеличить продолжительность данной работы, не изменяя при этом продолжительности данного пути:
Rпi,j = Тпj - Трi - t i,j (9)
7. У отдельных видов работ помимо полного резерва времени имеется свободный резерв времени Rс i,j , являющийся частью резерва. На время этого резерва можно увеличить продолжительность работы, не изменяя ранних сроков начала последующих работ.
Rсi,j = Трj - Трi - t i,j (10)
Резервы времени работ, особенно свободный, позволяют маневрировать сроками начала и окончания работ, их продолжительностью.
Определение продолжительности работ.
При построенной сетевой модели для каждой работы определяется ожидаемая продолжительность ее выполнения, которая проставляется над соответствующей стрелкой в графике. Для определения продолжительности работ пользуются установленными нормами времени, при их отсутствии используют систему вероятностных оценок. В таких случаях ожидаемое время выполнения работ ti,j определяют на основе экспертных оценок по формуле
(11)Дисперсия, или мера разброса для принятого в СПУ закона распределения:
mirznanii.com
Оптимизация сетевых моделей по критерию «время- затраты» — КиберПедия
Целью оптимизации по критерию "время - затраты" является сокращение времени выполнения проекта в целом. Эта оптимизация имеет смысл только в том случае, когда длительность выполнения работ может быть уменьшена за счет задействования дополнительных ресурсов, что влечет повышение затрат на выполнение работ. Для оценки величины дополнительных затрат, связанных с ускорением выполнения той или иной работы, используются либо нормативы, либо данные о выполнении аналогичных работ в прошлом.
Исходными данными для проведения оптимизации являются:
· - нормальная длительность работы;
· - ускоренная длительность;
· - затраты на выполнение работы в нормальный срок;
· - затраты на выполнение работы в ускоренный срок.
Т.о. каждая работа имеет некоторый максимальный запас времени для сокращения своей длительности .
,
Для анализа сетевой модели в данном виде оптимизации используется коэффициент нарастания затрат (коэффициент ускорения)
,
который имеет смысл затрат денежных средств для сокращения длительности выполнения работ (i,j) на один день.
Проведем максимально возможные уменьшения сроков выполнения проекта при минимальных возможных дополнительных затратах.
| Нормальный режим | Ускоренный режим | ||||
| (1,2) | 3,5 | ||||
| (1,3) | 3,25 | ||||
| (1,7) | 4,6 | ||||
| (2,4) | |||||
| (3,5) | 1,75 | ||||
| (4,8) | 3,4 | ||||
| (5,6) | |||||
| (6,7) | 4,33 | ||||
| (6,8) | 1,8 | ||||
| (7,8) | 1,57 |
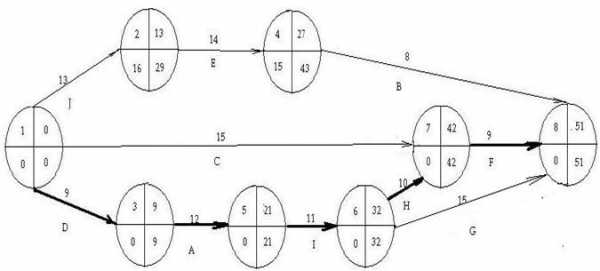Сетевая модель
1. Исходя из нормальных длительностей работ получаем следующие характеристики сетевой модели.
· Общие затраты на проек руб.
· Длительность проекта = 51дней.
· Критический путь = 1-3-5-6-7-8 или =(1,3),(3,5),(5,6),(6,7),(7,8).
· Подкритический путь =1-3-5-6-8 или = (1,3),(3,5),(5,6),(6,8), 47 дней.
2. Для ускорения выбираем работу (7,8) с руб./день. Текущий запас сокращения или предел сокращения работы (7,8) на данный момент равен. дней.Разность между продолжительностью критического и подкритического путей дня. Поэтому согласно сокращаем работу (7,8) на дня. Новое текущее значение дней, а запас ее дальнейшего сокращения, т.е. . Новый сетевой график имеет вид
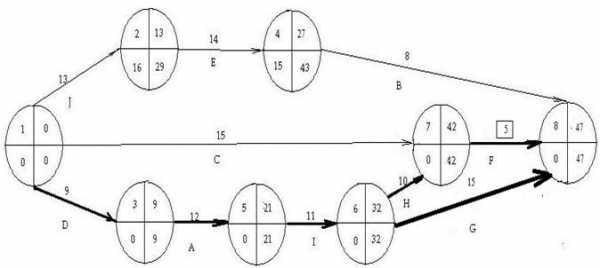
3. Исходя из новой длительности работы (7,8) получаем:
· Затраты на работу (7,8) выросли на =1,57·4=6,28 рублей, поэтому общие затраты составляют =114+6,28=120,28
· Длительность проекта = 47дней.
· Критический путь =1-3-5-6-7-8 и =1-3-5-6-8 или
· =(1,3),(3,5),(5,6),(6,7),(7,8) и =(1,3),(3,5),(5,6),(6,8).
· Подкритический путь =1-2-4-8 или = (1,2),(2,4),(4,8), 35 дней.
4. Появляется несколько критических путей. Говорят о том, что для дальнейших сокращений длительности проекта необходимо уменьшить длину всех критических путей одновременно. Из первого критического пути =(1,3),(3,5),(5,6),(6,7),(7,8) можно сократить работу (7,8)с предельным сокращением (7,8)= 3руб/день, а во втором критическом пути работу (6,8) с k(6,8)= 1,8 и предельным сокращением (6,8)=8-3=5дней дней. Сокращаем работы (7,8) и (6,8) на дня,где первые два элемента при выборе минимума это (6,8) =5 и Новое текущие значение дней, а запас ее дальнейшего сокращения полностью исчерпан, т.е. . Новое текущие значение дней, а запас ее дальнейшего сокращения, т.е. Новый сетевой график имеет вид
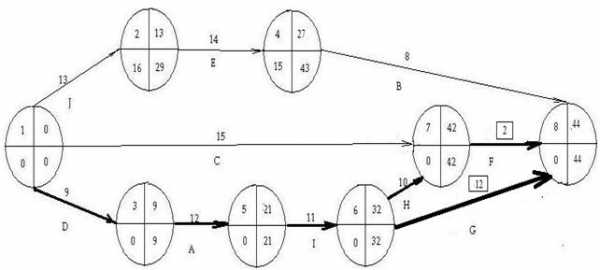
5.Исходя из новой длительности работы (7,8) и (6,8) получаем:
· Затраты на работу (7,8) выросли на =1,57·3=4,71 рублей, а затраты на работу (6,8) выросли на =1,8·3=5,4 рублей, поэтому общие затраты составляют 120,28+4,71+5,4=130,39 рублей
· Длительность проекта = 44 дней.
· Критический путь =1-3-5-6-7-8 и =1-3-5-6-8 или
· =(1,3),(3,5),(5,6),(6,7),(7,8) и =(1,3),(3,5),(5,6),(6,8).
· Подкритический путь =1-2-4-8 или = (1,2),(2,4),(4,8), 35 дней.
6. Для ускорения выбираем работу (3,5) с руб./день. Текущий запас сокращения или предел сокращения работы (3,5) на данный момент равен. дней . Разность между продолжительностью критического и подкритического путей дня. Поэтому согласно сокращаем работу (3,5) на дня. Новое текущее значение дней, а запас ее дальнейшего сокращения полностью исчерпан, т.е. . Новый сетевой график имеет вид
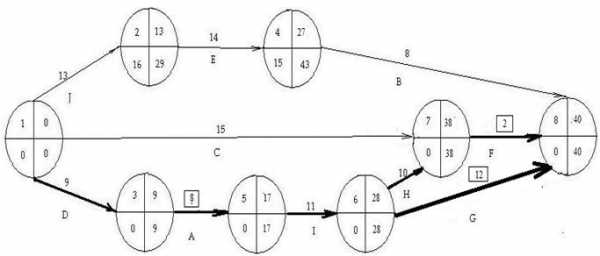
7.Исходя из новой длительности работы (3,5) получаем:
· Затраты на работу (3,5) выросли на 1,75·4= 7 рублей, поэтому общие затраты составляют =130,39+7= 137,39 рублей.
· Длительность проекта = 40дней.
· Критический путь =1-3-5-6-7-8 и =1-3-5-6-8 или
=(1,3),(3,5),(5,6),(6,7),(7,8) и =(1,3),(3,5),(5,6),(6,8).
· Подкритический путь =1-2-4-8 или = (1,2),(2,4),(4,8), 35 дней.
8. . Для ускорения выбираем работу (5,6) с руб./день. Текущий запас сокращения или предел сокращения работы (3,5) на данный момент равен. дней . Разность между продолжительностью критического и подкритического путей дней. Поэтому согласно сокращаем работу (5,6) на дня. Новое текущее значение дней, а запас ее дальнейшего сокращения, т.е. . Новый сетевой график имеет вид
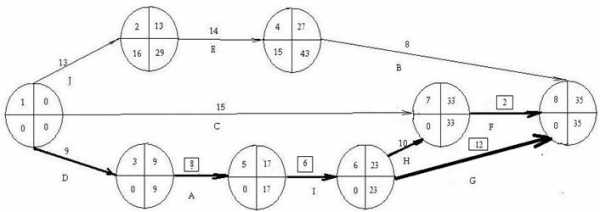
9.Исходя из новой длительности работы (5,6) получаем:
· Затраты на работу (5,6) выросли на 3·5= 15 рублей, поэтому общие затраты составляют =137,39+15= 142,38 рублей.
· Длительность проекта = 35дней.
Критический путь =1-3-5-6-7-8 и =1-3-5-6-8 и =1-2-4-8 или =(1,3),(3,5),(5,6),(6,7),(7,8) и =(1,3),(3,5),(5,6),(6,8) и =(1,2),(2,4),(4,8).
· Подкритический путь =1-7-8 или = (1,7),(7,8), 17 дней.
10.Для ускорения выбираем работу (5,6) и (4,8) с руб./день. Работа первого критиеского с предельным сокращением (5,6)= 1день, а во втором критическом пути работа (4,8) и предельным сокращением (4,8)=8-3=5дней дней. Сокращаем работы (4,8) и (5,6) на дня,где первые два элемента при выборе минимума это (4,8) =5 и Новое текущие значение дней, а запас ее дальнейшего сокращения полностью исчерпан, т.е. . Новое текущие значение дней, а запас ее дальнейшего сокращения, т.е. Новый сетевой график имеет вид
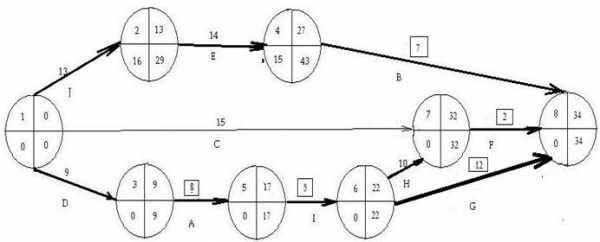
11. Исходя из новой длительности работы (5,6) и (4,8) получаем:
· Затраты на работу (5,6) выросли на 3·1= 3 рубля, а затраты на работу (4,8) выросли на 3,4·1= 3,4 рубля, поэтому общие затраты составляют =142,38+3+3,4= 148,68 рублей.
· Длительность проекта = 34дней.
Критический путь =1-3-5-6-7-8 и =1-3-5-6-8 и =1-2-4-8 или =(1,3),(3,5),(5,6),(6,7),(7,8) и =(1,3),(3,5),(5,6),(6,8) и =(1,2),(2,4),(4,8).
· Подкритический путь =1-7-8 или = (1,7),(7,8), 17 дней.
12.Для ускорения выбираем работу (1,3) и (4,8) с руб./день. Работа второго критического с предельным сокращением (4,8)= 4 деня, а в первом критическом пути работа (1,3) и предельным сокращением (1,3) = 9 -5=4 дня дней. Сокращаем работы (1,3) и (4,8) на дня,где первые два элемента при выборе минимума это (1,3) =4 и Новое текущие значение дней, а запас ее дальнейшего сокращения полностью исчерпан, т.е. . Новое текущие значение дней, а запас ее дальнейшего сокращения полностью исчерпан, т.е. Новый сетевой график имеет вид
13. Исходя из новой длительности работы (1,3) и (4,8) получаем:
· Затраты на работу (1,3) выросли на 3,4·4= 13 рублей, а затраты на работу (4,8) выросли на 3,4·4= 13,6 рубля, поэтому общие затраты составляют =148,68+13+13,6=175,28 рублей.
· Длительность проекта = 30дней.
Критический путь =1-3-5-6-7-8 и =1-3-5-6-8 и =1-2-4-8 или =(1,3),(3,5),(5,6),(6,7),(7,8) и =(1,3),(3,5),(5,6),(6,8) и =(1,2),(2,4),(4,8).
· Подкритический путь =1-7-8 или = (1,7),(7,8), 17 дней.
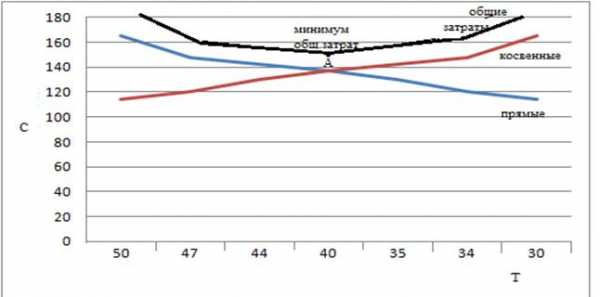
График «время-затраты»
cyberpedia.su
Оптимизация сетевых моделей по ресурсам
Менеджмент Оптимизация сетевых моделей по ресурсам
просмотров - 385
Практика осуществления проектов показывает, что зачастую недостаточно упорядочить систему управления только по времени. Важным фактором в управлении любым проектом является правильное распределение материальных и трудовых ресурсов, которыми располагают исполнители работ. По этой причине при планировании сложных проектов огромное значение приобретает рациональное распределение всех видов имеющихся ресурсов. Одним из важнейших вопросов при разработке проекта является обеспечение соответствия между установленными сроками выполнения работ и имеющимися ресурсными возможностями.
Следует иметь в виду, что к оптимизации по различным видам ресурсов приступают после проведения оптимизации сетевых графиков по времени. Последовательность проведения оптимизации по отдельным видам ресурсов устанавливается в зависимости от пределов ограничения каждого из них в конкретных условиях. Практика показывает, что чаще всего лимитирующими оказываются трудовые ресурсы.
Оптимизация сетевых моделей по трудовым ресурсам. При осуществлении любого проекта͵ а особенно при осуществлении проектов на постоянной основе в рамках одной организации, огромное значение имеет непрерывность и равномерность использования трудовых ресурсов.
Оптимизация сетевых графиков по этому параметру осуществляется последовательно в пределах имеющихся частных резервов времени.
Рассмотрим пример.
На предприятии, реализующем проект, работают 70 человек (см. рисунок 41). Необходимо оптимизировать данный график, чтобы ежедневно на работах были заняты все 70 человек.
0 1 2 3 4 5 6 7 8 9 10 11 12
1020 45
3050 20 20 5
40 5040
| Численность по графику |
Рисунок 41 - Сетевой график до оптимизации
Подсчитав на сетевом графике количество работников, ежедневно занятых на проекте, можно увидеть, что только в первые два дня планируемая численность работников соответствует заданному ограничению, а во все последующие дни она либо больше, либо меньше фактической.
Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, в третий день, когда плановая численность работников превышает фактическую, многие работы бывают не выполнены в заданные сроки, ᴛ.ᴇ. пойти с опозданием. Известно, что, если срыв сроков произошел на критических работах, в дальнейшем ликвидировать его последствия довольно сложно. Следовательно, если полученная расчетная (плановая) численность не соответствует заданным ограничениям, необходимо оптимизировать график выполнения проекта.
Для того чтобы уменьшить число людей, занятых на работах в третий день, и увеличить число людей, занятых на работах в четвертый день, нужно продлить срок выполнения работы 1—2 с одного до двух дней за счет имеющегося на этой работе частного резерва времени и вдвое сократить численность занятых на ней работников. Аналогично следует поступить с работами 2—5 и 5—6. В данной ситуации трудоемкость работ рассматривается как величина неизменная.
После оптимизации по трудовым ресурсам сетевой график будет выглядеть так, как показано на рисунке 42.
0 1 2 3 4 5 6 7 8 9 10 11 12
1020 45
3050 10 20 5
40 2520
| Численность после оптимизации |
Рисунок 42 - Сетевой график после оптимизации по трудовым ресурсам
Как видно, в результате оптимизации ежедневная численность работающих составляет 70 человек. Появились новые критические пути, так как по некоторым работам полностью использованы резервы времени.
В случае если оптимизация не дала положительного результата͵ крайне важно изменить продолжительность отдельных работ, выйдя за пределы резервов времени, потому что при сохранении прежней продолжительности многие работы в заданные сроки выполнены не будут.
Оптимизация сетевых моделей по материальным ресурсам. Оптимизация по материальным ресурсам осуществляется последовательно по каждому виду ресурса в пределах имеющихся частных резервов времени.
В первую очередь оптимизацию следует проводить по тому виду ресурсов, который является определяющим для выполнения данного комплекса работ по проекту.
Допустим, на строительную площадку для выполнения работ по проекту еженедельно может поступать не более 500 м3 бетона. Параметры сетевого графика данного проекта представлены в таблице 17. Необходимо оптимизировать сетевой график проекта͵ чтобы эти ограничения не привели к увеличению продолжительности проекта.
Таблица 17 – Исходные параметры сетевого графика
| Коды работ | Параметры графика до оптимизации | Потребность в бетоне, м3 | ||
| i | j | |||
Для определения расхода бетона в ходе выполнения работ по проекту в таблице с исходными параметрами справа добавим расчетные графы (таблица 18).
Заполним таблицу по каждой работе дробными числами (таблица 18), в которых числитель будет показывать еженедельную потребность (расход бетона) на протяжении всего времени выполнения данной работы, а знаменатель — оставшуюся после исполнения данной работы часть от объема возможной поставки бетона. Полученный остаток будем направлять для использования на следующей работе, для которой в числителе опять будем записывать потребность (расход), а в знаменателе — новый остаток, и так до полного использования объема поставки.
Таблица 18 – Использование бетона в ходе выполнения работ по проекту
Из приведенной таблицы видно, что бетоном в первую очередь необходимо обеспечивать работы 0—1, 1—2, 2—3 и 3—4, причем в точно установленные сроки, так как эти работы являются критическими. Другие работы имеют частные резервы времени, в связи с этим можно либо отодвигать их начала, либо увеличивать их продолжительность.
Работа 0—2 не может закончиться за одну неделю в связи с тем, что в первую неделю свободный остаток бетона составляет 200 м3, а потребность — 400 м3. По этой причине, используя частный резерв времени, нужно увеличить продолжительность работы до двух недель, распределив ее потребность в бетоне на две недели, ᴛ.ᴇ. по 200 м3 еженедельно.
Работа 1—3 не может начаться сразу после окончания предшествующей работы — работы 0—1, так как бетон, поступающий во вторую неделю, полностью распределяется между работами 1—2 и 0—2. Вместе с тем, работа 1—3 не может быть выполнена за одну неделю, как это определено ее продолжительностью, потому что в третью неделю из 500 м3 поставляемого бетона крайне важно выделить 200 м3 на критическую работу 2—3. Следовательно, мы вынуждены помимо смещения начала работы 1—3 на одну неделю увеличить ее продолжительность до двух недель, равномерно распределив потребность этой работы в бетоне — 600 м3 — на две недели: третью и четвертую.
Работа 2—4 не может выполняться ни в третью, ни в четвертую недели, так как в данный период общее количество поставляемого бетона уже полностью распределено между работами 2—3 и 1—3. В связи с этим отодвигаем срок выполнения работы 2—4 на пятую неделю.
Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, сетевой график оптимизирован с учетом данных ограничений.
Процесс оптимизации сетевого графика по ресурсам можно выполнить также при помощи масштабного сетевого графика, аналогично тому, как это было сделано при оптимизации по трудовым ресурсам. Воспользуемся теми же самыми исходными данными (см. таблицу 17).
В сетевом графике до оптимизации по материальным ресурсам (рисунок 43) над стрелками указано крайне важное для каждой работы количество бетона.
0 1 2 3 4 5
600300
200300 100
400 200
400| Еженедельная потребность в бетоне |
Рисунок 43 - Сетевой график до оптимизации по материальным ресурсам
Как видно из графика, первые три недели крайне важное количество бетона постоянно превышает поставляемое количество. Так, в первую неделю потребность превышает поставку на 200 м3, во вторую неделю — на 400 м3, в третью неделю — на 100 м3.
После оптимизации по материальным ресурсам сетевой график будет выглядеть следующим образом (рисунок 44).
После оптимизации еженедельная потребность в бетоне стала равна еженедельной поставке. При этом следует иметь в виду, что в случае, когда все резервы времени использованы на всех работах, а потребность в ресурсах в единицу времени превышает их поступление, возникает крайне важность изменить либо технологию работ, либо увеличить общую продолжительность критического пути.
0 1 2 3 4 5
300 300 300 200300 100
200 400| Еженедельная потребность в бетоне после оптимизации |
Рисунок 44 - Сетевой график после оптимизации по материальным ресурсам
Оптимизация сетевых моделей по денежным ресурсам. При планировании денежных ресурсов, необходимых для реализации проекта͵ как правило, стремятся к их равномерному распределению в течение года. В связи с этим возникает вопрос: как увязать планы в денежном выражении с объемами работ по сетевым графикам? Этот вопрос может быть решен в процессе оптимизации сетевых графиков по денежным ресурсам.
Заменим в таблицах 17 и 18 данные по бетону на данные по денежным средствам, необходимым для выполнения работ, ᴛ.ᴇ. физические объемы работ переведем в денежный эквивалент, к примеру в рубли. В качестве ограничения примем ту же величину — 500. Это будет означать, что еженедельный плановый объем работ составляет 500 руб. Оптимизация по денежным ресурсам осуществляется аналогично оптимизации по материальным ресурсам.
Исключением может оказаться случай, когда проект не вписывается в бюджетные ограничения организации на определенный период. К примеру, на год по плану отпущено 2,0 млн руб., а подсчет объемов работ по сетевому графику показывает, что для осуществления проекта крайне важно 2,3 млн руб. Задача оптимизации будет сводиться к тому, чтобы из графика выбрать ряд работ, которые можно будет перенести на следующий год без изменения общей величины продолжительности критического пути.
Читайте также
Практика осуществления проектов показывает, что зачастую недостаточно упорядочить систему управления только по времени. Важным фактором в управлении любым проектом является правильное распределение материальных и трудовых ресурсов, которыми располагают... [читать подробенее]
oplib.ru
