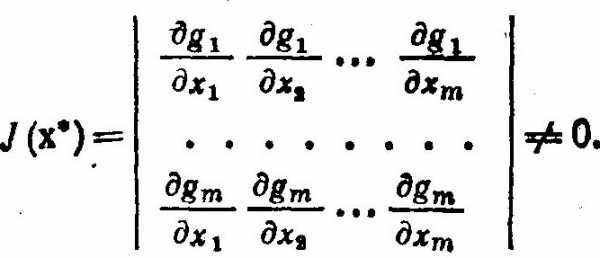6.2. Принцип оптимальности Парето. Оптимизация по парето

Многокритериальная оптимизация - это... Что такое Многокритериальная оптимизация?

Многокритериальная оптимизация или программирование (англ. Multi-objective optimization),[1][2] — это процесс одновременной оптимизации двух или более конфликтующих целевых функций в заданной области определения.

Задача многокритериальной оптимизации встречаются во многих областях науки, техники и экономики.

Определение

Задача многокритериальной оптимизации формулируется следующим образом:[3]

где это () целевых функций. Векторы решений относятся к непустой области определения .

Задача многокритериальной оптимизации состоит в поиске вектора целевых переменных, удовлетворяющего наложенным ограничениям и оптимизирующего векторную функцию, элементы которой соответствуют целевым функциям. Эти функции образуют математическое описание критерия удовлетворительности и, как правило, взаимно конфликтуют. Отсюда, «оптимизировать» означает найти такое решение, при котором значение целевых функций были бы приемлемыми для постановщика задачи.[4]

Эталонные точки

Для возможности оценки качества найденных решений обычно рассматривают такие точки в области значения целевой функции:

идеальная точка ,
утопическая точка ,
надир .

В некоторых случаях эти точки могут быть решениями.

Идеальная точка определяется как вектор , каждая из координат которого имеет оптимальное значение соответствующей составляющей целевой функции:[5]

Точка надир определяется как вектор:

Утопическую точку вычисляют на основе идеальной:[6]

где , — единичный вектор.

Критерий Парето

Вектор решения называется оптимальным по Парето, если не существует , такого, что для всех и для хотя бы одного . Множество оптимальных по Парето решений можно обозначить как . Целевой вектор является оптимальным по Парето, если соответствующий ему вектор из области определения также оптимален по Парето. Множество оптимальных по Парето целевых векторов можно обозначить как .

Множество оптимальных по Парето векторов является подмножеством оптимальных по Парето в слабом смысле векторов. Вектор является слабым оптимумом по Парето тогда, когда не существует вектора такого, что для всех .

Диапазон значений оптимальных по Парето решений в области допустимых значений дает полезную информацию об исследуемой задаче, если целевые функции ограничены областью определения. Нижние границы оптимального по Парето множества представлены в «идеальном целевом векторе» . Его компоненты получены путем минимализации каждой целевой функции в пределах области определения.

Множество оптимальных по Парето решений также называют Парето-фронтом (англ. Pareto-frontier).

Лексикографический порядок

Если одни целевые функции важнее других, критерий оптимальности можно определить по лексикографическому порядку.

Отношение лексикографического порядка между векторами и выполняется, если , где . То есть, первая компонента вектора меньше компоненты вектора , а компоненты — уровни (если есть). Лексикографический порядок для случая действительных чисел является линейным.

Вектор является лексикографическим решением, если не существует вектора , такого, что .

Поскольку отношение лексикографического порядка является линейным, можно доказать, что вектор является лексикографическим решением, если для всех выполняется:

Основной особенностью решений по лексикографическому порядку является существование выбора между критериями. Лексикографическая упорядоченность требует ранжирования критериев в том смысле, что оптимизация по критерию возможна лишь тогда, когда был достигнут оптимум для предыдущих критериев. Это означает, что первый критерий имеет наибольший приоритет, и только в случае существования нескольких решений по этому критерию будет поиск решений по второму и остальным критериям.

Существование иерархии среди критериев позволяет решать лексикографические задачи последовательно, шаг за шагом минимизируя по каждому следующему критерию, и используюя оптимальные значения предварительных критериев как ограничения.

Скаляризация

Для получения оптимальных по Парето решений часто используют методы скаляризации. Поскольку целевая функция задачи многокритериальной оптимизации имеет векторные значения, ее превращают в функцию со скалярным значением. Таким образом, задача многокритериальной оптимизации сводится к задаче оптимизации с одной скалярной целевой функцией. Функция скаляризации должна удовлетворять следующим условиям.

Пусть - функция скаляризации, что превращает векторную функцию в скалярную. Если сохраняет упорядоченность по Парето , то есть, если для произвольных выполняется:

тогда решение , что минимизирует до , является решением по Парето.[7] Если сохраняет отношение порядка в , то есть, если для произвольных выполняется:

тогда решение , что минимизирует до , является слабым по Парето. Если непрерывна на и единственная точка минимума на , тогда является решением по Парето.

Взвешенная сумма

Приведенная функция сохраняет упорядоченность по Парето для . Поэтому решения, минимизирующие до для произвольных являются оптимальными по Парето. Однако не сохраняет упорядоченность по Парето для , а сохраняет лишь отношение , поэтому решения, минимизирующие на для являются слабыми по Парето.[7]

Недостатком метода взвешенных сумм в случае выпуклого множества значений целевых функций является невозможность охватить все оптимальные по Парето точки из множества Парето-фронта. В задачах комбинаторной многокритериальной оптимизации множество целевых значений не является выпуклым, поэтому метод взвешенных сумм не подходит для скаляризации целевых функций для этих задач.

Функция скаляризации Чебышева

Взвешенная функция скаляризации Чебышева сохраняет отношения и поэтому минимум является слабым по Парето.[7]

Метод изменения ограничений (ε-ограничения)

По методу изменения ограничений одну из целевых функций оставляют в качестве целевой, а остальные превращают в ограничения. То есть, пусть будет целевой, а остальные представим как ограничение неравенства:

при условиях

Значения могут рассматриваться как допустимые уровни для .

Методы решения

Интерактивность

Часто решение задачи многокритериальной оптимизации происходит с участием эксперта — человека, который выбирает и принимает решения на основе информации, представленной системой поддержки принятия решений. Возможно участие группы из нескольких экспертов. В случае участия человека в поиске решения алгоритмы и методы называют интерактивными.[3]

Эволюционные методы

Упоминания о применении генетических алгоритмов для решения задачи многокритериальной оптимизации относятся к концу 1960-х [8].

Примечания

↑ Steuer R.E. Multiple Criteria Optimization: Theory, Computations, and Application. — New York: John Wiley & Sons, Inc. — ISBN 047188846X

↑ Sawaragi Y. Theory of Multiobjective Optimization (vol. 176 of Mathematics in Science and Engineering). — Orlando, FL: Academic Press Inc. — ISBN 0126203709
↑ 1 2 Jürgen Branke, Kalyanmoy Deb, Kaisa Miettinen та Roman Slowinski Multiobjective Optimization: Interactive and Evolutionary Approaches (Lecture Notes in Computer Science). — Springer. — ISBN 3-540-88907-8
↑ A. Osyzka. «Multicriteria optimization for engineering design». Design Optimization (Academic Press): 193-227.
↑ (Ehrgott, c. 34)
↑ (Jürgen et al, с. XI)
↑ 1 2 3 Sequential Approximate Multiobjective Optimization Using Computational Intelligence (Vector Optimization). — Springer. — ISBN 978-3-540-88909-0
↑ R. S. Rosenberg Simulation of genetic populations with biochemical properties. — University of Michigan, 1967.

См. также

Литература

Кини Р.Л., Райфа Х. Принятие решений при многих критериях: предпочтения и замещения. — М: Радио и связь, 1981. — 560 с.
Matthias Ehrgott Multicriteria Optimization. — Springer. — ISBN 3-540-21398-8

M. Ehrgott and X. Gandibleux (2004). «Approximative Solution Methods for Multiobjective Combinatorial Optimization». TOP (Sociedad de Estadística e Investigación Operativa) 12 (1).

Ресурсы интернета

dal.academic.ru

6.2. Принцип оптимальности Парето.

Неулучшаемые (оптимальные по Парето) решения

Рассмотрим проблемную ситуацию, решения которой оцениваются по некоторой совокупности показателей (под может пониматься, например, целевая функция, описывающая какую-либо характеристику производственного процесса, показатель функционирования предприятия и т.п.). Для наглядности можно представлять, что в выборе решения участвуют сторон, каждая из которых заинтересована в максимизации соответствующего («своего») показателя. При этом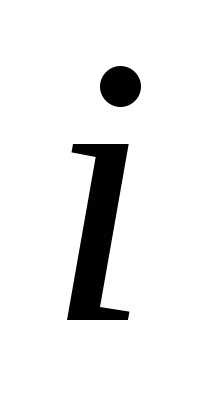-я сторона может выбрать любое допустимое для нее решение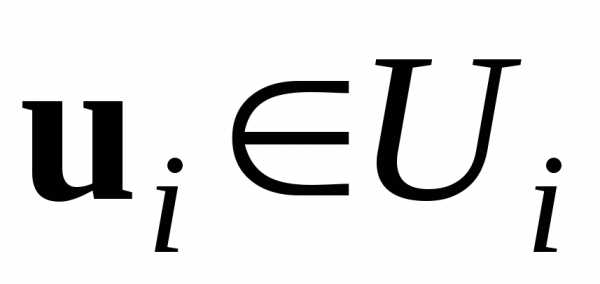. Чрезвычайно важно, что решение, выбранное этой стороной, влияет на эффективность всех остальных. Это означает, что показатель эффективности любой стороны зависит от совокупности допустимых решений всех сторон, т.е. .

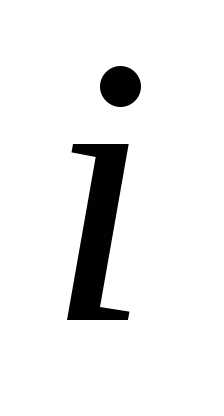Решение стороны предпочтительнее ее решения, если

На основании вышесказанного (учитывая наличие сторон, самостоятельно выбирающих свои решения) можно сформулировать принцип единогласия, известный как принцип оптимальности Парето).

Если для всех сторон допустимые решения предпочтительнее решений , то последние не будут приняты (единогласно отвергнуты).

Как правило, на практике совокупность решений { } оказывается неединственной и образует некоторое множество U решений, оптимальных по Парето. Любой набор решений из этого множества не может быть улучшен сразу по всем показателям . В силу этого решения, оптимальные по Парето, называются также неулучшаемыми. Следует отметить, что задачи, в которых имеется единственная совокупность неулучшаемых решений, встречаются исключительно редко. Любое решение из множества U является неулучшаемым. Изменением этого решения невозможно добиться увеличения какого-либо показателя эффективности, не уменьшая при этом хотя бы одного из остальных. Выбор конкретного решения из множества оптимальных по Парето может быть осуществлен лишь на основе компромисса на основе переговоров ЛПР всех заинтересованных сторон.

Хотя до сих пор мы считали, что в выборе решения участвуют S различных сторон, рассмотренные понятия и вся формулировка в целом совершенно аналогичны и в том случае, когда выбор решения осуществляет одна сторона, руководствующаяся не единственным, а некоторой совокупностью S показателей эффективности. Принятие какого-либо конкретного решения { } из множества Парето является при этом прерогативой исключительно ЛПР и осуществляется, как правило, на основе его субъективных предпочтений.

6.3. Принцип равновесия по Нэшу

Пусть все стороны выбрали решения, оптимальные по Парето (назовем эту ситуацию оптимальной по Парето). Согласно принципу оптимальности Парето все стороны, действуя совместно, не могут увеличить эффективность своих решений. Однако любая сторона, уклонившись от ситуации, оптимальной по Парето, при определенных условиях может добиться большего значения «своего» показателя эффективности. Иными словами, ситуации, оптимальные по Парето, не обладают устойчивостью по отношению к отклонениям от них какой-либо стороны. В то же время желательно, чтобы ни одна из сторон, действуя в одиночку, не могла увеличить эффективность выбираемых ею решений, т.е. необходим поиск таких ситуаций, отклонение от которых было бы невыгодным ни для одной из сторон по отдельности.

Существование ситуаций, являющихся устойчивыми в смысле невыгодности отклонения от них ни одной из сторон, приводит к принципу равновесия по Нэшу.

Ситуацию, характеризующуюся набором решений , называют равновесной по Нэшу, если для всех 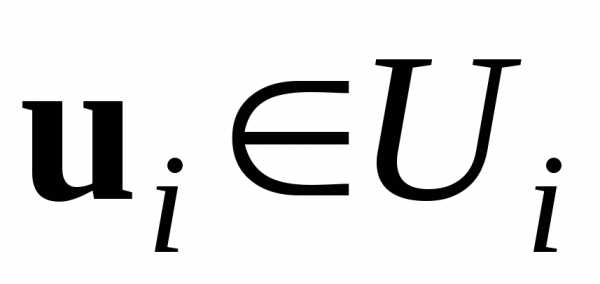имеет место неравенство

Если прочитать эти неравенства справа налево, то можно видеть, что замена какого-либо одного решения, входящего в равновесную ситуацию, любым другим из множества допустимых уменьшает соответствующий показатель эффективности. Если под понимать показатели эффективности сторон, то из определения ситуации равновесия по Нэшу следует, что ни одна из них не заинтересована в изменении решения, входящего в ситуацию равновесия, если все остальные стороны сохраняют решения, соответствующие этой ситуации.

Таким образом, если стороны предварительно договариваются о выборе решений, образующих равновесную ситуацию, то индивидуальное нарушение этого договора невыгодно нарушителю. Отметим некоторые особенности равновесных ситуаций.

Ситуация равновесия может оказаться не единственной.
Ситуации равновесия часто оказываются в разной степени предпочтительными для различных сторон. Иначе говоря, показатели эффективности решений сторон имеют неодинаковые значения в различных равновесных ситуациях. В связи с этим какая-то равновесная ситуация, выгодная для одной стороны, может оказываться невыгодной для других. Поэтому решение i-й стороны, соответствующее какой-либо равновесной ситуации, не следует трактовать как оптимальное для этой стороны. Равновесность как принцип оптимальности имеет смысл только для набора равновесных решений всех сторон.
Ситуации равновесия могут совпадать или не совпадать с ситуациями, оптимальными по Парето.

studfiles.net

Презентация на тему: РЕШЕНИЕ

МНОГОКРИТЕРИАЬНЫХ

ЗАДАЧ

Оптимальность по Парето Методы сверток критериев

Методы, использующие ограничения на критерии

Оптимальность по Парето

Большинство реально возникающих задач оптимизации являются многокритериальными. То есть, нужно оптимизировать одновременно не одну, а целое множество функций (критериев оптимальности).

Пусть имеются критерии оптимальности (эффективности): f1(X ),..., fk (X ) ,

где	X (x	,..., x	) Rn
	1	n		D : gi (X) bi ,i1,m
удовлетворяют ограничениям				D : gi (X) bi ,i1,m

Тогда задача оптимизации примет вид:

F {f1 (X ),...,fk (X )} min,X D Rn

Оптимальность по Парето

Функции (критерии) могут быть согласованными,

нейтральными, конфликтующими.

Критерии являются согласованными, если улучшение одного из них приводит к улучшению другого. Критерии являютсянейтральными, если изменение одного из них не влияет на другие.

Критерии являются конфликтующими, когда улучшение одного из них приводит к ухудшению других.

В последнем случае решение возможно только на основе компромисса, для чего используется понятиемножества

Парето - множества точек несравнимых по предпочтению.

Оптимальность по Парето

Определение 1. РешениеX 0 D называется оптимальным по Парето, если во множестве допустимых решений не существуют решения, которое по целевым функциям было бы не хуже, и по крайней мере по одной целевой функции было бы строго лучше чемX 0 .

Определение 2. Множество всех допустимых, оптимальных по Парето, точек называется множеством Парето в пространстве переменных.

Определение 3. Множество Парето в критериальном пространстве – это множествоfi (X ) ,i 1,k , гдеX – множество точек, оптимальных по Парето, в пространстве переменных.

Оптимальность по Парето

Из определения следует, что решение

многокритериальной задачи оптимизации целесообразно выбирать из множества Парето, так как любое другое может быть улучшено некоторой точкой Парето как минимум по одному критерию без ухудшения других.

Оптимальность по Парето

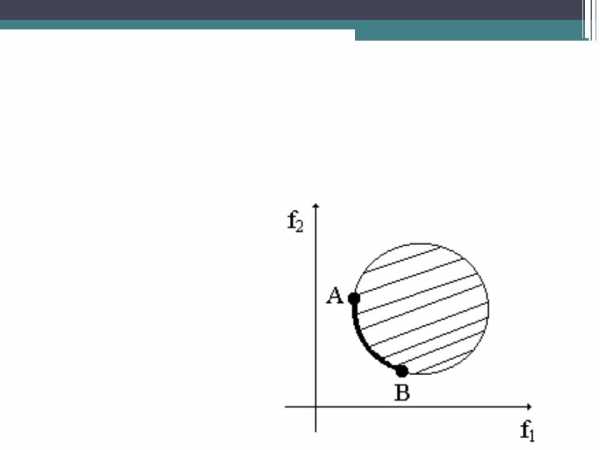
Рассмотрим простейшую ситуацию. Заштрихованная область изображает значения двух критериев оптимизации f1 и f2, которые соответствуют переменным X в допустимой области.

Множество точек, оптимальных по Парето, лежит между точками минимума (если задача на минимум), полученных при решении многокритериальной задачи отдельно по каждому критерию. Точками Парето является множество контурных точек между точками А и В.

Оптимальность по Парето

Точек оптимальных по Парето, даже в простейших задачах может быть много.

Чем больше точек Парето, тем хуже, так как с формальных позиций они равноценны между собой.

Очевидно, что с точки зрения практики надо выйти на одну или несколько точек, оптимальными по Парето, для чего после построения множества Парето осуществляют его сужение.

Оптимальность по Парето

Для построения множества Парето могут быть использованы следующие методы:

1)методы свертки критериев,

2)методы, основанные на наложении ограничений на критерии,

3)методы, основанные на отыскании компромиссного решения,

4)методы целевого программирования и др.

Методы сверток

критериев

Задача многокритериальной оптимизации сводится к задаче однокритериальной оптимизации введением одного

обобщенного критерия	k
F 0 1 f1(x) ...k	fk (x)i fi (x) min,x D
где (1,...,k )	i 1
где (1,...,k )	– вектор весовых

коэффициентов критериев, характеризующий относительную важность соответствующего критерия. Обычно, весовые коэффициенты используются в нормированном виде и удовлетворяют условиям

Методы сверток критериев

Функция F 0 называетсяаддитивной сверткой.

В результате оптимизации аддитивной свертки может быть получена точка, оптимальная по Парето.

Задача должна решаться многократно, с изменением весовых коэффициентов, чтобы сгенерировать

множество точек Парето.

Кроме того, при изменении коэффициентов во всем диапазоне может получаться одна и та же точка.

studfiles.net

Оптимальность по Парето

Выгоды от конкуренции были, в общем, понятны со времен А.Смита, и, вероятно, даже раньше. Однако точный смысл принципа «совершенная конкуренция эффективно распределяет ресурсы» был формально определен выдающимся итальянским экономистом Вильфредо Парето (1848-1923). Воспользуемся его определением эффективности, называемой оптимальностью по Парето. Говорят, что ресурсы распределены оптимально по Парето, когда никто не может улучшить положение без того, чтобы в результате для кого-нибудь оно не ухудшилось. В ситуации, оптимальной по Парето, не существует нерационального расходования ресурсов. Оптимальность по Парето предлагает критерий, подсказывающий, имеет ли место в данной конкретной ситуации растрата ресурсов или нет. Но сам по себе этот критерий не говорит нам о том, как следует распределять ресурсы, что справедливо, а что несправедливо.

Проиллюстрируем сказанное графическим примером (см. рис.1).

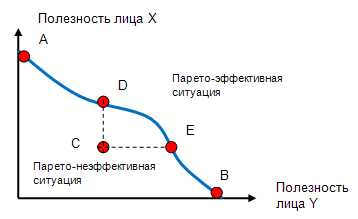Рис.1. Граница достижимой полезности.

Из графика, представленного на рис.1 видно, что в точке А все ресурсы общества отдаются лицу Х и его полезность максимальна. В точке В максимизируется полезность лица Y. При перемещении из точки А в точку В имеет место компромисс, когда блага передаются от лица Х к лицу Y. Обе точки А и В эффективны по Парето, так как ни в одной, ни в другой ситуации нельзя улучшить положение одной из сторон, не сделав хуже другой. Они, конечно, несправедливы, но оптимальны по Парето.

Рассмотрим далее точки C, D и E. Точка С не является оптимальной по Парето. Двигаясь в направлении вправо вверх, можно улучшать полезность и лица Х и лица Y.

Основное ограничение концепции оптимальности по Парето состоит в том, что она не дает нам никакого способа проранжировать точки на границе достижимой полезности. Здесь должны применяться иные способы.

Эффективность и оценочные суждения. Рынки совершенной конкуренции являются эффективными по Парето в части распределения ресурсов. Другими словами, совершенно конкурентные рынки гарантируют, что экономика автоматически достигнет точки на графике достижимой полезности – точки, в которой ничье положение нельзя улучшить без того, чтобы не ухудшить положение кого-то другого. Но означает ли это, что конкурентные, эффективные по Парето распределения являются в известном смысле социально оптимальными? Совпадает ли экономический оптимум с оптимумом социальным? Ответ будет отрицательным – эти оптимумы чаще всего не совпадают.

Каждый член общества может согласиться, например, с тем, что более равномерное распределение дохода предпочтительнее менее равномерного. Таким образом, такие точки, как точка D на рис.1 в целом предпочтительнее точек, соответствующих крайнему неравенству (точек А и В). Но конкурентной экономике ничто не мешает порождать крайне неравномерное распределение дохода. В этом случае распределение ресурсов было бы оптимальным по Парето, но необязательно социально оптимальным в силу того, что общество предпочло бы находиться в некой другой точке на границе достижимой полезности.

Например, в российском обществе имеется довольно значительная дифференциация населения по доходам и собственности. Политические партии левой ориентации предлагают выравнивать существующее неравенство с точки зрения справедливости, под которой понимается более равномерное распределение дохода. Сделать это предлагается за счет введения прогрессивной шкалы налогообложения, социальных трансфертов и выравнивания ставок заработной платы. За основу предлагается взять скандинавский опыт.

Но тогда, возражают правые партии, порождается уравнительность в экономических отношениях, угасают стимулы к эффективному труду (мы уже рассматривали выше, например, работу М.Фридмена «Свобода, равенство и эгалитаризм», «Капитализм и свобода» и др.). Таким образом, формируется конфликт между социальной справедливостью и экономической эффективностью.

Переводя выявленное противоречие, на язык математической формализации, построим следующую модель. Обозначим за Р1(х) параметр социального развития, а за Р2(х) – экономического. Допустим, что функционирование такой экономико-социальной системы зависит от значений вектора управляемых параметров Х, а значения обоих критериев необходимо максимизировать. Область допустимых значений зададим отрезком Х, принадлежащим интервалу[a, b] (см. рис.2).

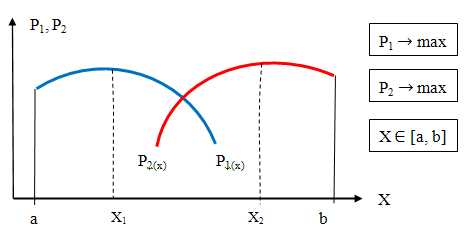Рис.2. Система конфликтующих критериев Р1 и Р2.

Оптимумы (максимумы) по каждому из критериев достигаются в точках Х1 и Х2 соответственно для Р1(х) и Р2(х). До максимума Х1 и после Х2 критерии Р1(х) и Р2(х) ведут себя согласованно, одновременно увеличиваясь, а затем уменьшаясь. С точки зрения поставленной задачи эти области интереса не представляют (т.е., например, увеличение экономической эффективности вызывает некоторый подъем в социальной жизни и общественных настроениях. И напротив, снижение экономической эффективности ведет к определенному снижению социальных показателей).

Рассматривая теперь область между Х1 и Х2, видим, что увеличение значения критерия Р1(х) (параметра экономического развития) ведет к снижению уровня жизни широких слоев населения и социальным протестам Р2(х), то есть критерии конфликтуют. Этот конфликт отображается в определенную область в пространстве критериев Р1(х) и Р2(х), которая представляет собой совокупность конфликтных решений – множество Парето (см. график на рис.3).

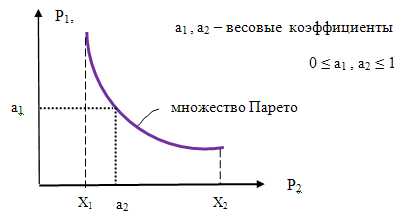Рис.3. Множество Парето в системе критериев Р1 и Р2.

Взаимосвязь между экономическим и социальным оптимумом может иметь вид обратно пропорциональной зависимости. Выразить количественные соотношения между данными двумя параметрами можно при помощи весовых коэффициентов а1 и а2, придавая им соответствующий «вес» (важность):

Р = а1Р1 + а2Р2, 0 ≤ а1 , а2 ≤ 1.

Проводя, таким образом, линейную свертку критерия, получим некоторый глобальный критерий Р. Выбор соответствующих значений весовых коэффициентов а1 и а2 эквивалентен выбору каких-либо точек на множестве Парето. Количественные оценки весовых коэффициентов могут быть определены экспертами или населением в ходе голосования или опросов.

21biz.ru

Понятие оптимальности по Парето — МегаЛекции

Принятие управленческих решений в условиях многокритериальности

Источники многокритериальности.

Понятие оптимальности по Парето

В специальной литературе можно встретить термин «методы решения многокритериальных задач», иногда говорят даже о методах «преодоления многокритериальности». Необходимо иметь в виду, что какого-либо формального математического метода «преодоления» многокритериальности не может быть в принципе. Все без исключения методы решения многокритериальных задач представляют собой различные способы организации взаимодействия (диалога) с лицом, принимающим решение, и, по существу, отличаются друг от друга формой вопросов, которые ему «задаются» компьютерной программой.

Отдельного внимания заслуживает вопрос, почему задача принятия решения в условиях рыночной экономики является многокритериальной. Ведь доходность в краткосрочной и долгосрочной перспективе, казалось бы, исчерпывает возможный набор критериев принятия решений свободным участником рынка. В то же время в работах советского периода многокритериальность связывалась с существованием сложной системы так называемых оценочных показателей предприятий. Известно, что на протяжении длительного времени конструирование таких показателей, как, например, удельный вес продукции высшей категории качества, нормативно-чистая, товарная, реализованная продукция и т.п., рассматривалось в качестве чуть ли не главной прикладной задачи экономической науки. Возникает вопрос: а нужны ли в условиях рынка все эти методы, и если да, то зачем? На первую половину вопроса можно легко ответить, обратившись к опыту развитых стран с рыночной экономикой. Есть ли там такие методы? Да, есть. Попробуем понять, почему. Действительно, генеральная цель фирмы на рынке — максимизация дохода владельца. Но достигается она не непосредственно, а через частные цели более низкого уровня.

Рассмотрим пример. Фирма анализирует возможности организации рекламной кампании. Решается задача оптимального распределения рекламного бюджета между вложениями в печатную рекламу и рекламу в электронных СМИ. Если у фирмы нет достоверных данных об эффективности рекламы в печатных и электронных средствах информации, то в качестве результативного показателя целесообразно использовать показатель охвата целевой аудитории рекламным сообщением. В итоге мы получаем два показателя охвата для каждого варианта использования СМИ, которые нельзя просто суммировать. В этих условиях задача принятия решения становится задачей с двумя критериями.

Как уже отмечалось, анализ решений при многих критериях в значительной степени сводится к организации в той или иной форме взаимодействия с ЛПР, которое одно только и может разрешить проблему соизмерения различных критериев. Тем не менее, существует довольно ограниченная область, в которой применение сугубо формального анализа без обращения к ЛПР оказывается весьма полезным. Речь идет о выделении так называемого множества эффективных, или оптимальных по Парето, альтернатив.

Эффективной (оптимальной по Парето) называется такая альтернатива, для которой не существует другой допустимой, не уступающей ей по всем критериям и хотя бы по одному критерию превосходящей ее.

Альтернатива, не являющаяся эффективной, ни при каких условиях не может рассматриваться в качестве решения задачи. Для неэффективной альтернативы существует другая, превосходящая ее по всем критериям. (Такая альтернатива называется доминирующей первую).

Отсюда вытекает важнейший принцип рациональности процесса разработки решения: выбираемый вариант должен быть эффективным.

Как же отыскивать эффективные решения?

Главное здесь состоит в том, что, после того как сформулированы критерии, задача отыскания множества эффективных решений на заданном множестве альтернатив является, хоть и сложной, но вполне формальной задачей, не требующей для своего решения обращения к ЛПР. Особенно простой задача отыскания эффективных решений является в дискретном случае, т.е. тогда, когда имеется заданный набор вариантов решения, из которых надо сделать выбор.

Пусть для каждого из критериев, учитываемых при принятии решения, предпочтительнее большее значение. Тогда альтернатива а доминирует альтернативу b, если оценки у альтернативы а по всем критериям не меньше (больше, или равны) оценок альтернативы b.

Таким образом, можно построить матрицу сравнения альтернатив, в которой в i-й строке, j-м столбце будем ставить 1, если i-я альтернатива доминирует j-ю, и 0 - в противном случае.

Приведем пример. Пусть у нас есть 6 альтернатив, каждая из которых оценена по 5 критериям. Они представлены в таблице 1.

Таблица 1

	Критерий 1	Критерий 2	Критерий 3	Критерий 4	Критерий 5
Альтернатива 1
Альтернатива 2
Альтернатива 3
Альтернатива 4
Альтернатива 5
Альтернатива 6

По результатам попарного сравнения 6 альтернатив между собой у нас получится следующая матрица 6х6 (таблица 2), где i=1,2,…,6, j=1,2,…,6.

Доминируется 3

Доминируется 3,6

Таблица 2

	А1 (j=1)	А 2 (j=2)	А 3	А 4	А 5	А 6
А1 (i=1)
А 2 (i=2)
А 3
А 4
А 5
А 6

В таблице 2 получилось два столбца, в которых есть единицы: первый и четвертый. Это значит, что первая и четвертая альтернативы доминируются какими-то другими (первая – третьей, а четвертая – третьей и шестой). Поэтому они не являются эффективными. Парето-оптимальные альтернативы в нашем примере - вторая, третья, пятая, шестая.

Во многих случаях множество эффективных альтернатив можно найти, решая задачу с интегральным критерием оптимальности, представляющим собой сумму отдельных, частных критериев с переменными весами. При этом, какие веса брать для начала процесса, значения не имеет. Все равно перебираются все возможные комбинации на отрезке от 0 до 1 с каким-то заданным шагом. Сразу же предостережем читателя от грубой ошибки. После того как выделено множество эффективных альтернатив, ЛПР может выбрать одну из них, но строить из них комбинации, даже в тех случаях, когда такая комбинированная альтернатива имеет смысл, нельзя. Она может оказаться неэффективной и не должна рассматриваться в качестве решения задачи.

Выделение множества Парето можно рассматривать лишь как предварительный этап оптимизации, и налицо проблема сокращения этого множества.

Дальнейший поиск во множестве эффективных решений может быть осуществлен только на основе применения принципов принятия решений. Рассмотрим некоторые из них. При этом полагаем, что все критерии являются нормализованными, т.е. приведенными к одному, часто безразмерному виду.

Принцип равномерности.

Он состоит в стремлении к равномерному и гармоничному улучшению решения по всем локальным критериям. Имеются следующие его разновидности:

1. Принцип равенства. Наилучшим решением является такое, при котором достигается равенство всех локальных критериев. Данный принцип очень «жесткий» и может приводить к решениям вне множества эффективных решений и даже не иметь их, особенно в дискретных случаях.

2. Принцип максимина. Идея равномерности состоит в стремлении повышать уровень всех критериев за счет максимального «подтягивания» наихудшего из критериев (имеющего наименьшее значение).

3. Принцип квазиравенства. Решение считается наилучшим, если значения отдельных критериев отличаются друг от друга не более, чем на величину d.

Рекомендуемые страницы:

Воспользуйтесь поиском по сайту:

megalektsii.ru

Оптимальность по Парето — Словарь Лопатникова

Оптимальность по Парето [Pareto optimum]. Выдающийся итальянский экономист В.Парето в начале XX в. математически сформулировал один из самых распространенных критериев оптимальности, предназначенный для того, чтобы проверить, улучшает ли предложенное изменение в экономике общий уровень благосостояния.

Критерий Парето формулируется им просто: «Следует считать, что любое изменение, которое никому не причиняет убытков и которое приносит некоторым людям пользу (по их собственной оценке), является улучшением». Этот критерий имеет весьма широкий смысл. Он применяется при решении таких задач, когда оптимизация означает улучшение одних показателей при условии, чтобы другие не ухудшались, а также таких, когда реализуется композиционный подход к построению плана развития экономической системы, учитывающий интересы составляющих ее подсистем (групп экономических объектов).

Приведенное выше определение можно формализовать следующим утверждением: cостояние экономики S* считается лучшим по Парето, чем другое состояние S1, если хотя бы один экономический субъект предпочитает S*, а все остальные по меньшей мере не делают различий между этими состояниями, но в то же время нет таких, кто предпочитает S1; состояние S* безразлично по Парето состоянию S1, если все экономические субъекты не делают между ними различий; наконец, оно оптимально по Парето, если не существует такого допустимого состояния экономики, которое было бы лучше, чем это.

Критерий Парето неприменим к весьма распространенным ситуациям, при которых экономическая мера, приносящая пользу одним, в то же время наносит ущерб другим. На рис. O.7а показано точкой А исходное состояние экономической системы, состоящей из двух подсистем (группы X и Y). Улучшают его лишь те решения, которые приводят систему в любую точку, лежащую в заштрихованной области и на ее границах (например, точки B, C, D). Решение, обозначенное точкой E, не удовлетворяет требованию Парето, несмотря на значительный рост удовлетворения потребностей членов группировки Y: он достигается за счет снижения уровня благосостояния группировки X.

Если x1 и y1 соответственно отображают максимальные значения целевых функций подсистем X и Y при их независимом друг от друга функционировании, то участок FF1 множества Парето (недостижимый для каждой из них в отдельности) заинтересовывает их в совместной деятельности. Этот участок называется ядром экономической системы. Чем теснее взаимозависимы подсистемы, тем меньше различия между множеством Парето («оптимумом по Парето») и ядром системы. Выбор при планировании единственного наилучшего плана (например, точки g) — вопрос согласования или, как говорят, «устройства» экономического механизма. Например, такой точкой может быть точка равновесия по Нэшу.

Таким образом, оптимумов по Парето может быть много, но существенно меньше, чем вообще вариантов развития системы; оптимумов по Парето, входящих в ядро, — еще меньше, и все это, в частности, позволяет сужать выбор вариантов, подлежащих рассмотрению в процессе оптимального композиционного планирования. (Те же рассуждения применимы и к анализу некооперативных игр.)

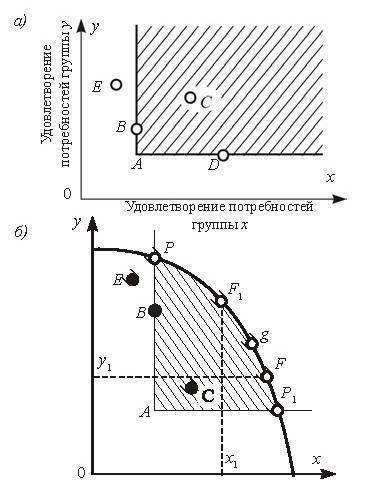
Рис. О.7 Оптимальность по Парето

lopatnikov.pro

Оптимальность по Парето - это... Что такое Оптимальность по Парето?

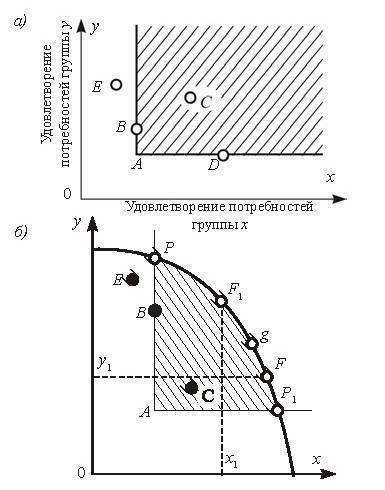
Рис. О.7 Оптимальность по Парето

Экономико-математический словарь: Словарь современной экономической науки. — М.: Дело. Л. И. Лопатников. 2003.

economic_mathematics.academic.ru