10 Линейные модели оптимизации в управлении. Оптимизации модели

Модели оптимизации - Энциклопедия по экономике

Экономико-математическое моделирование является важным инструментом планового управления. Различаются группы моделей графические, корреляционные (регрессионные), балансовые, модели оптимизации экономики. [c.72] Модели оптимизации экономики имеют целью добиться наибольшей результативности (эффективности) использования имеющегося потенциала и ресурсов. Любая экономико-математическая модель — это воспроизведение связей между экономическими явлениями и процессами. Критерии оптимального плана могут быть разными, поэтому в общей форме подразумевается оптимальное сочетание цели и средств социалистического производства за счет интенсивного использования всех имеющихся возможностей. Целевая функция и ограничения выражаются в математическом виде, и решение их методами линейного программирования позволяет найти оптимальный вариант. [c.73]

В подтверждение достаточной сложности математической формализации ряда оптимизационных задач ниже приведена линейная модель для расчета производственной программы предприятия . Подобного рода модель оптимизации текущего заводского планирования характерна для предприятий химической, нефтехимической и нефтеперерабатывающей промышленности, имеющих принципиальное сходство в построении технологических процессов (для непрерывных производств). [c.407]

В отрасли выполнены и внедрены в практику экономико-математические модели оптимизации и размещения производства асинхронных низковольтных электродвигателей, силовых трансформаторов, кабельной техники, источников света и светотехнических изделий, электрокерамических изделий, объем производства которых составляет около 40% отраслевого выпуска. За основу принимались динамические производственно-транспортные модели в вариантной постановке с дискретными переменными. Вместе с тем в каждом конкретном случае учитывалась специфика электротехнических производств. [c.27]

Модели оптимизации производственной программы [c.131]

Б2.2 — модели оптимизации производственной программы [c.135]

Б2.3 — модели оптимизации распределения и использования ресурсов. [c.135]

BIV — комплекс моделей оптимизации народнохозяйственного планирования. При различной комбинации отдельных моделей типа Б1 и Б2 получаются различ- [c.136]

Нелинейная модель выбора рациональной суточной производительности комплекса установок не противопоставляется и не препятствует применению известной линейной модели оптимизации производственной программы НПЗ. Она формирует лишь экономически обоснованные ограничения на значения суточной производительности установок АВТ, КК, КР. В их пределах возможна реализация экономических возможностей оптимизации производственной программы всего шлейфа сопутствующих установок специфическими средствами линейной модели. [c.43]

ВНИИОЭНГом разработана модель оптимизации развития строительных организаций 1 [29], учитывающая влияние на увеличение мощности строительной организации многочисленных факторов, основными из которых являются фондоотдача баз строительной индустрии (Р=1/Ф), изменения мощности строительной организации вследствие роста производительности труда (у) при совершенствовании технологии строительного процесса (без изменения структуры работ и местных условий). [c.68]

Агрегированная модель оптимизации строительной программы разбития нефтяного района [c.117]

В соответствии с изложенным была сформирована модель оптимизации топливного производства НПЗ. Размеры модели характеризуются следующими данными число ограничений — 211, число основных переменных — 272, число дополнительных переменных — 211. В сформированной модели 44 установки представлены векторами с переменными коэффициентами выпуска и затрат. Об эффективности предлагаемого подхода с точки зрения размерности моделей можно судить на основании сравнения с эквивалентной моделью, сформированной с помощью обычных методов (например, метод замены переменных). Такая модель имела бы размерность 938 ограничений и 1153 переменных. [c.102]

Как показывает практика, число предложений по совершенствованию производств, содержащихся в портфеле технической службы предприятия, обычно превышает его возможности па их финансированию. В связи с этим возникает проблема оптимизации распределения капитальных вложений между возможными объектами и направлениями их использования. В соответствии с положениями Типовой методики определения экономической эффективности капитальных вложений и новой техники в качестве критерия оптимальности принимается минимум приведенных затрат. Однако выбор критерия оптимальности еще не решает задачи оптимального использования капитальных вложений в целях интенсификации производства. В завершенном виде модель оптимизации должна включать ограничения на переменные и целевую функцию. В рассматриваемом случае наибольшую трудность, представляет формулировка целевой функции. Она должна быть [c.132]

Результаты работ, изложенные в [1], [2], позволяют считать твердо доказанным тот факт, что с ростом капиталоемкости продукции до определенного уровня себестоимость ее снижается, а затем начинает вновь повышаться в связи с увеличением доли. амортизации. Однако для построения модели оптимизации рас-.пределения капитальных вложений недостаточно представления рассматриваемой зависимости в общем виде, как функции С = [c.134]

Основой предлагаемой системы формирования модели оптимизации производственной программы является тщательно разработанный словарь терминов. Не останавливаясь на всех принципах организации словаря отметим лишь, что одним из основных требований к нему является отсутствие одинаковых терминов с различными шифрами. [c.169]

Мартынов А. П. и др. Автоматизированная подготовка модели оптимизации производственной программы НПЗ Автоматизация и контрольно-измерительные приборы , М., ЦНИИТЭнефтехим, № 9, 1975. [c.170]

Речь идет о том, чтобы, оставаясь в рамках концепции приведенных затрат, найти способ построения логически замкнутой модели оптимизации распределения капитальных вложений, [c.98]

ЭКОНОМИКО-СТАТИЧЕСКАЯ МОДЕЛЬ ОПТИМИЗАЦИИ РАЗВИТИЯ ГАЗОСНАБЖАЮЩИХ СИСТЕМ [c.28]

Неучет внутренних свойств информации и ее замена детерминированной (например, усреднением) может привести к неправильным решениям, которые рассмотрены в работах [l,2J. Сооружение же системы, рассчитанной на маловероятный и наименее благоприятный вариант условий, приведет к дополнительным капиталовложениям и, в конечном счете, к народнохозяйственному ущербу. Поэтому актуальной задачей является разработка методов и моделей оптимизации развития газоснабжающих систем, учитывающих случайный характер исходной информации. [c.28]

С этой целью в данной работе предложена модель оптимизации развития газоснабжающих систем, в которой необходимая исходная информация принимается вероятностно-определенной. Учитывая, что затраты на сооружение объектов системы зависят от принимаемых реше -ний линейно, для учета случайного характера затрат достаточно ввести расчет усредненными значениями. [c.29]

Предложена математическая модель оптимизации развития газоснабжающих систем, учитывающих вероятностный характер исходной информации. Рассмотрены способы реализации модели. [c.85]

В западных компаниях часто обсуждается, должен ли управленческий учет в большей степени быть связанным с управлением и всеми его функциями или должен быть сосредоточен на теории, статистических показателях и моделях оптимизации. Успешно работающие западные компании способны сочетать оба эти подхода. Сами по себе количественные данные и модели не улучшают процесс управления. Только при использовании количественных методов высококвалифицированным руководителем могут появиться прекрасные результаты. Покажем это на следующем примере. Врач поехал на выходной со своими друзьями на дачу. Один из них заболел. Было установлено, что ему нужно удалить аппендикс. Не имея острого хирургического скальпеля, врач решил воспользоваться кухонным ножом. Управленческий учет подобен тупому ножу. Сам по себе он только орудие, хотя острый скальпель был бы лучше, но и он может оказаться смертоносным орудием, если не знать, как им пользоваться. На Западе управленческий учет представляет собой лишь набор средств. Он не может заменить квалифицированного руководителя. В данной главе рассматриваются несколько основных количественных методов, успешно применяемых западными компаниями. Наши цели в данной главе состоят в следующем [c.204]

В теории управления запасами на основании минимизации рассмотренных выше затрат разработана целая система моделей оптимизации запасов. В основе их лежит простейшая одно-продуктовая модель (модель Уилсона, предложенная им еще в 1914 г.). Оптимальный запас на складе Q определяют по формуле [c.292]

Это особый вид экономико-математических моделей, описывающих варианты решения определенной проблемы. Нормативные модели оптимизации включают переменные для выбора варианта решения и его оценки. Модели оптимизации содержат уравнения взаимосвязи переменных и критерий для выбора — функционал или целевую функцию. Целевая функция принимает значения в области, ограниченной условиями задачи. В состав целевой функции входят управляемые переменные, параметры задается форма функции. Для решения оптимизационных задач применяются методы математического программирования. [c.435]

Рассмотрим условия постановки задачи управления маневренностью в терминах наиболее простых модификаций линейной модели оптимизации перспективного плана. [c.8]

Один из основных недостатков используемого комплекса моделей оптимизации перспективных планов развития газовой промышленности состоит в отсутствии связи между уровнями. Большинство моделей нижнего и верхнего уровня разрабатывались вне ресурсных ограничений на трубы, агрегаты и пр. [c.62]

Необходимо отметить, что сказанное ранее об известной ограниченности описываемых моделей оптимизации кратности запасов газа относится и к предложенной модели оптимизации соотношения газа тюменских п европейских месторождений в газовом балансе. Однако учет в поставленной задаче (хотя и в ограниченной форме) вероятностной ситуации, возникающей в газодобывающих районах европейской части СССР, позволит более обоснованно подойти к перспективному планированию добычи газа на еще не разведанные месторождения. [c.79]

Для решения этой задачи разрабатывается специальная модель оптимизации инвестиционной программы предприятия при заданной [c.265]

Книга посвящена разработке и исследованию методов и моделей оптимизации нефтеперерабатывающих производств. Обобщен опыт применения вероятностных, в том числе и энтропийных моделей для решения задач текущего и оперативно-календарного планирования. Рассмотрены основные предпосылки и особенности применения диалогового и лингвистического подходов для анализа производственных ситуаций и принятия плановых решений. [c.2]

Раздельное решение задач не обеспечивает нахождения оптимальных плановых решений, и это нашло отражение в структуре системы моделей оптимального текущего планирования нефтеперерабатывающего производства [1], включающей отраслевую модель оптимизации производства и распределения нефтепродуктов, модель линейного программирования комплекса НПП и модель линейного программирования НПП, обеспечивающих расчет производственной программы отдельных предприятий, распределение плановых заданий между комплексами предприятий. [c.12]

В настоящее время нефтеперерабатывающей и нефтехимической промышленности принадлежит ведущая роль во внедрении в производственную практику современных методов управления, моделей оптимизации и средств вычислительной техники. [c.13]

СРАВНИТЕЛЬНЫЙ АНАЛИЗ СВОЙСТВ ОСНОВНЫХ ТИПОВ МОДЕЛЕЙ ОПТИМИЗАЦИИ ПЛАНИРОВАНИЯ НЕФТЕПЕРЕРАБАТЫВАЮЩИХ ПРОИЗВОДСТВ [c.41]

В условиях функционирования АСУ принятие оптимальных плановых и управленческих решений основывается на результатах расчетов, проводимых на ЭВМ с помощью экономико-математических моделей соответствующих задач. Моделирование позволяет осуществлять эффективный выбор решений и прогнозировать последствия их реализации. В связи с этим математическая модель оптимизации календарного планирования основного производства НПП является центральным звеном подсистемы и блока принятия плановых решений. [c.75]

Принятие решений на базе экономико-математических моделей оптимизации основного производства НПП представляет собой итеративный процесс, отдельными этапами которого являются решение исходной задачи с использованием оптимизационных методов, анализ конкретных результатов, уточнение данных, а иногда и самой формулировки задачи, и переход к новому решению. [c.76]

Применение стохастической модели оптимизации календарного планирования основного производства НПП позволяет повысить степень обоснованности и надежности плановых расчетов и снижает вероятность потерь ожидаемой прибыли, возникающих из-за корректировок первоначально принятых плановых заданий. [c.178]

Экономико-математическая модель оптимизации развития судоремонтной базы позволяет проводить систематические расчеты плана, обеспечивающего потребность флота в ремонте при минимальных затратах на ремонт и сокращение простоев судов в ремонте с учетом ограничений по производстйенным мощностям, грузоподъемности доков, длине причала и др. При этом определяется схема расстановки флота на ремонт по предприятиям, обеспечивающая максимально эффективную загрузку действующих судоремонтных предприятий, что, в свою очередь, позволяет уменьшить имеющиеся дефициты производственных мощностей, а следовательно, и необходимый объем капитальных вложений на развитие предприятий. [c.212]

Переход от общетеоретической структуры модели оптимизации суточной производительности к ее уточненному варианту основывается на предварительном анализе фактических соотношений затрат и выхода целевой продукции. Он проведен на основе данных трех НПЗ Уфимской группы АО "УНПЗ", АО "Уфанефтехим" и АО "НУНПЗ". [c.42]

Расчеты на основе моделей оптимизации производительности установок конкретного НПЗ (АО "УНПЗ") привели к выводу об относительности принципа максимизации уровней интенсивного использования технологического оборудования. Если локально-оптимальные решения применительно к отдельным установкам требуют их работы на максимальном технически обусловленном пределе, то модель взаимосвязанной оптимизации комплекса АВТ, каталитического крекинга и каталитического реформинга устанавливает другие пропорции между их суточной производительностью, обеспечивающие максимум чистой прибыли от реализации продукции всего технологического комплекса. Взаимосвязанная оптимизация производительности центрального технологического комплекса (АВТ, КК, КР) позволяет выявить несопряженность мощностей составляющих его установок и устанавливать рациональный путь выхода из нее анализом альтернатив на основе принципа максимизации прибыли. [c.43]

При такой постановке задачи оптимизации плана производства НПЗ модель (2)— (9) является нелинейной. Аналогичные постановки имели место в работах [2, 3, 4,. Б]. Пути решения указанных задач в основном связываются с различными методами линеаризации, предложенными в работе Дж, Данцига 16]. Подробное обоснование этих методов в отношении моделей оптимизации плана производства НПЗ рассматривается в работах [3, 4]. Недостатками методов линеаризации является, во-первых, значительное увеличение размерности моделей, а во-вторых, усложнение подготов-.ки исходной информации для решения. [c.98]

Эквиваленты денежных средств. Этим термином описываются ликвидные рыночные ценные бумаги, которые с минимальным временным лагом могут быть трансформированы в денежные средства. Живые деньги нужны любому предприятию вместе с тем, поскольку перечисленные выше модели оптимизации остатка денежных средств весьма теоретизированы, на практике обычно руководствуются здравым смыслом, выбирая, какую часть мобильных активов держать на расчетном счете, а какую временно разместить в ценных бумагах. В результате такой политики у предприятия на балансе формируются краткосрочные финансовые вложения. [c.375]

Достигнутый прогресс в разработке частных моделей оптимизации и в их численной реализации не означает, однако, что становление моделирования нефтяной отрасли дюжно считать завершенным. Особенно это касается нефтедобывающей продшшленности, представляющей собой сложную систему, включающую подготовку запасов, добычу (разработку нефтяных месторождений) и транспортировку нефти от районов добычи к пунктад потребления. [c.94]

Стратегическое управление позволяет руководству фирмой представить ситуационное поле в прогнозных моделях, определить степень необходимости намеченных изменений, конкретные этапы их проведения и, что немаловажно, предвидеть возможное их поведение. Поиск путей обновления фирмы, выработка масштабной и гибкой политики непрерывного продвижения вперед - вот главная составляющая долговременного успеха. Это особенно актуально сейчас для российских предприятий. Привычные способы развития ушли в прошлое, достижение успеха простым изменением факторов производства уже невозможно, существовавшая система государственной защиты субъектов производства демонтирована. Традиционный подход к разработке стратегии развития у нас в стране, как правило, ограничен кругом моделей оптимизации ресурсного потенциала и организационных структур ( взгляд вовнутрь ), оторван от интересов потребителей (рынка), владельцев (акционеров) предприятия и персонала. А в итоге - низкий рыночный потенциал и высокая конфликтогенность в маркетинговой среде характеризуется напряженностью взаимоотношений между менеджерами и акционерами, с одной стороны, и внутри персонала, с другой. [c.38]

Формализация математических моделей связана с рядом технических трудностей, успешное преодоление которых и определяет в конечном счете как адекватность описания моделирующего объекта, так и оптимальность принятых решений. К их числу относятся 1) выделение из значительного числа особенностей варьируемых параметров технологических процессов исследуемого объекта основных, причем в приемлемом для намеченного к применению метода оптимизации количестве 2) условная классификация выделенного множества параметров на определяющие и определяемые. Например, в аппроксимационной модели комплекса НПП (2.48) —(2.52) определяемыми параметрами являются переменные xkr, остальные параметры — определяющие. Нетрудно понять, что в зависимости от способа осуществления этого процесса модель оптимизации примет тот или иной вид. [c.46]

economy-ru.info

Модель оптимизации - это... Что такое Модель оптимизации?

Модель оптимизации - математическая модель, характеризующаяся предположением, что некоторые переменные в данном процессе или ситуации максимизируются или минимизируются.

Социологический словарь Socium. 2003.

Модель ожидаемой полезности
Модель

Смотреть что такое "Модель оптимизации" в других словарях:

Универсальная математическая модель оптимизации — Базовая или рабочая модель оптимизации, годная для решения не только поставленной задачи оптимизации ПОС, но и более общей задачи. Для решения каждой конкретной задачи с помощью универсальной модели оптимизации эту модель, как правило, следует… … Словарь-справочник терминов нормативно-технической документации
Базовая математическая модель оптимизации — Модель оптимизации большого класса комплексов объектов стандартизации данной отрасли или нескольких отраслей, предназначенная для составления рабочих математических моделей оптимизации конкретных объектов. В базовой математической модели… … Словарь-справочник терминов нормативно-технической документации
Рабочая математическая модель оптимизации — Модель оптимизации, содержащая всю исходную и входную информацию, необходимую для оптимизации объекта (по ГОСТ 18.401 77) Источник … Словарь-справочник терминов нормативно-технической документации
МОДЕЛЬ ВАЛЬРАСА — модель показывает роль трансакционных издержек, применяя эффект их отсутствия. Вальрас предлагает идеальную модель рынка с трансакционными издержками, равными нулю. Роль координирующей силы, направляющей и удерживающей рынок в состоянии… … Большой экономический словарь
модель линейного программирования — Модель, используемая для оптимизации распределения дефицитных ресурсов между конкурирующими потребностями. [http://tourlib.net/books men/meskon glossary.htm] Тематики менеджмент в целом EN linear programming model … Справочник технического переводчика
модель управления запасами — Модель, используемая для оптимизации графика размещения и размера заказов на ресурсы, а также размера необходимых запасов. [http://tourlib.net/books men/meskon glossary.htm] Тематики менеджмент в целом EN model inventory … Справочник технического переводчика
Модель — 9. Модель Изделие, являющееся трехразмерным упрощенным изображением предмета в установленном масштабе Модель является составной частью макета Источник … Словарь-справочник терминов нормативно-технической документации
Модель регрессионного анализа — 28. Модель регрессионного анализа Регрессионная модель Зависимость отклика от количественных факторов и ошибок наблюдения отклика Источник: ГОСТ 24026 80: Исследовательские испытания. Планирование эксперимента. Термины и определения … Словарь-справочник терминов нормативно-технической документации
Модель акторов — В компьютерных науках модель акторов представляет собой математическую модель параллельных вычислений, которая трактует понятие «актор» как универсальный примитив параллельного численного расчёта: в ответ на сообщения, которые он получает, актор… … Википедия
Модель регрессионного анализа первого порядка — 31. Модель регрессионного анализа первого порядка Линейная модель Модель регрессионного анализа, задаваемая полиномом первого порядка по факторам Источник: ГОСТ 24026 80: Исследовательские испытания. Планирование эксперимента. Термины и… … Словарь-справочник терминов нормативно-технической документации

socium.academic.ru

10 Линейные модели оптимизации в управлении » СтудИзба

Линейные модели оптимизации в управлении

Сначала рассмотрим задачи линейной оптимизации (или оптимизационные задачи линейного программирования), математические модели которых содержат лишь линейные зависимости от переменных.

Как уже отмечалось, оптимизация, включающая теорию и методы решения задач, в которых критерий оптимальности (целевая функция) линейно зависит от параметров задачи, является наиболее разработанным разделом информационных технологий оптимальных решений. Линейные модели широко используются в теории и практике принятия управленческих решений.

Современные информационные технологии оптимизации решений широкого класса практических задач включают их формулировку (построение математической модели), математические методы и компьютерные программы решения этих задач, а также методы экономико-математического анализа оптимальных решений.

Общая задача линейной оптимизации заключается в нахождении максимума (минимума) линейной целевой функции

, (2.1)

при ограничениях

, (2.2)

, (2.3)

. (2.4)

Функция называется целевой функцией, критерием оптимальности или линейной формой.

Вектор значений неизвестных , удовлетворяющих условию задачи (2.1)-(2.4), называется допустимым решением или допустимым планом задачи линейной оптимизации. Совокупность всех допустимых планов называется множеством допустимых планов. Допустимое решение называется оптимальным, если оно обеспечивает максимальное (или, в зависимости от условий задачи, - минимальное) значение целевой функции.

Решение задач линейной оптимизации может быть получено без особых затруднений (естественно, при корректной формулировке проблемы). Классическим методом решения задач данного типа является симплекс-метод. В случае лишь двух переменных успешно может использоваться также графический метод решения, обладающий преимуществом наглядности. Очевидно, в случае применение графического метода невозможно.

При решении ряда оптимизационных задач требуется, чтобы значения неизвестных выражались в целых числах. Естественно, к задачам подобного типа относятся те, в которых требуется определить необходимые для принятия решений значения физически цельных объектов (машин, агрегатов различного типа, людей, транспортных единиц и т.д. и т.п.). Такие задачи относятся к задачам целочисленной оптимизации. Математическая модель задачи линейной целочисленной оптимизации также определяется формулами (2.1)-(2.4), но в данном случае налагается дополнительное требование целочисленности всех (или части) неизвестных. Если требование целочисленности распространяется лишь на часть неизвестных величин задачи, то такая задача называется частично целочисленной.

Процесс построения математической модели для решения задачи начинается, как правило, с ответов на следующие вопросы:

· Для определения каких величин должна быть построена модель, т.е. как идентифицировать переменные задачи?

· Какие ограничения должны быть наложены на переменные, чтобы выполнялись условия, характерные для моделируемой системы?

· В чем состоит цель задачи, для достижения которой из всех допустимых значений переменных нужно выбрать те, которые будут соответствовать оптимальному (наилучшему) решению задачи?

После ответа на данные вопросы для построения модели остается только идентифицировать переменные и представить цель и ограничения в виде математических функций этих переменных.

Надлежащий анализ вопросов подобного рода и корректная формулировка математической модели являются центральным звеном решения задач линейной (и не только линейной) оптимизации.

Эффективным средством решения задач линейной оптимизации является MS Excel. Входящий в состав данного программного продукта пакет Поиск решения (Solver) позволяет проводить решения задач подобного рода с большим (свыше 200) числом переменных и ограничений.

Отметим, что применительно к задачам оптимизации производственной программы предприятия наиболее типичными задачами линейной оптимизации являются оптимизация дохода, прибыли, себестоимости, номенклатуры производимой продукции, затрат станочного времени и т.п.

Рассмотрим использование информационных технологий решения задач линейной оптимизации на ряде конкретных примеров, имеющих непосредственное отношение к практике принятия управленческих решений.

Пример 1. Определение оптимального ассортимента продукции.

Предприятие изготавливает два вида продукции П1 и П2 , которая поступает в оптовую продажу. Для производства используются два вида сырья и . Максимально возможные запасы сырья в сутки составляют 9 и 13 единиц соответственно. Расход сырья на единицу продукции приведен в таблице.

Таблица 2.1

Сырье	Расход сырья на единицу продукции		Запас сырья, ед.
Сырье	П1	П2	Запас сырья, ед.
	2	3	9
	3	2	13

Маркетинговые исследования показали, что суточный спрос на продукцию П1 не превышает спрос на продукцию П2 более чем на 1 ед. Кроме того, известно, что спрос на продукцию П2 не превышает 2 единиц в сутки.

Оптовые цены единицы продукции равны для П1 3 д.е., для П2- 4 д.е. Какое количество продукции каждого вида должно производить предприятие, чтобы доход от реализации продукции был максимальным?

Решение. Очевидно, фирме требуется определить объемы производства каждого вида продукции в тоннах, максимизирующие доход в д.е. от реализации продукции, с учетом ограничений на спрос и расход исходных продуктов. Предположим, что предприятие изготовит единиц продукции П1 и единиц продукции П2. Поскольку производство продукции ограничено имеющимся в распоряжении предприятия сырьем каждого вида и спросом на данную продукцию, а также учитывая, что количество изготовляемых изделий не может быть отрицательным, получим следующую систему ограничений:

Доход от реализации продукции (целевая функция) составит . Таким образом, данная простая задача сводится к максимизации целевой функции при учете вышеприведенных ограничений.

Проведем решение задачи в Excel.

Введем данные на рабочий лист так, как показано на Рис 2.1.

Искомые значения переменных будут располагаться в ячейках A10 и B10 соответственно, целевая функция – в ячейке E10.

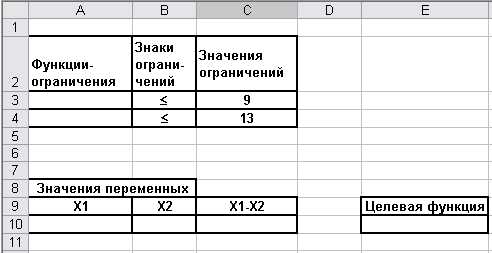
Рис. 2.1.

В ячейки A3, A4 введем левые части функций – ограничений: =2*A10+3*B10 и = 3*A10+2*B10 соответственно. В ячейку C10 введем левую часть третьей функции-ограничения: =A10-B10.

Далее, запускаем пакет Поиск решения (Сервис ® Поиск решения) и устанавливаем целевую и изменяемые ячейки, а также вводим ограничения (Рис.2.2):

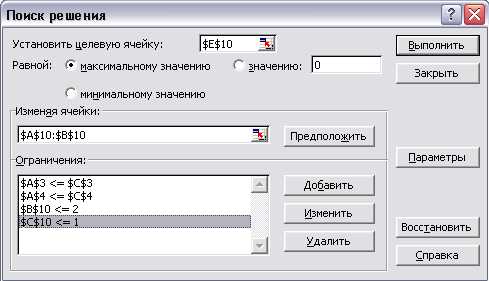
Рис. 2.2. Окно диалога Поиск решения.

Поиск решения дает ответ

Пример 2 .Использование мощностей оборудования.

Предприятие имеет моделей машин различных мощностей. Задан план по времени и номенклатуре: - время работы каждой машины; продукции - го вида должно быть выпущено не менее единиц.

Необходимо составить такой план работы оборудования, чтобы обеспечить минимальные затраты на производство, если известны производительность каждой - машины по выпуску - го вида продукции и стоимость единицы времени, затрачиваемого -й машиной на выпуск - го вида продукции .

Другими словами, задача для предприятия состоит в следующем: требуется определить время работы время работы - машины по выпуску - го вида продукции , обеспечивающее минимальные затраты на производство при соблюдении ограничений по общему времени работы машин и заданному количеству продукции .

Решение. По условию задачи машины работают заданное время , поэтому данное ограничение можно представить в следующем виде:

Ограничение по заданному количеству продукции имеет вид:

Задача решается на минимум затрат на производство:

В данной постановке задачи предполагается, что количество выпускаемой продукции должно быть, по крайней мере, не менее . В некоторых случаях не допускается превышение плана по номенклатуре; очевидно в этом случае в ограничениях по количеству продукции необходимо использовать знак равенства.

Проведем решение задачи в Excel. Введем данные на рабочий лист так, как показано на Рис 2.3.

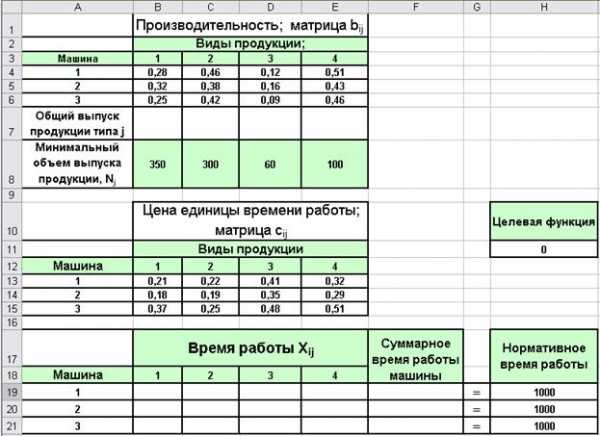
Рис. 2.3. Данные для решения примера 2.

В ячейки B7:E7 введем формулы для ограничений по объему выпускаемой продукции (), в диапазон ячеек F19:F21 – формулы для ограничений по времени работы машин (). В качестве целевой ячейки выберем h21 и введем в нее формулу минимизируемой функции.

С помощью Поиска решения получим следующий ответ:

	Время работы Xij
Машина	1	2	3	4
1	803,92	0	0	196,07
2	625	0	375	0
3	0	1000	0	0

Искомое значение минимальных затрат на производство составляет 725,32 д.е.

Следующие два рассматриваемых нами примера относятся к области целочисленной оптимизации.

Пример 3. Оптимизация производственной программы.

Автомобилестроительный завод выпускает три модели автомобилей, которые изготавливаются последовательно в трех цехах. Мощность цехов составляет 300, 250 и 200 человеко-дней в декаду. В первом цехе для сборки одного автомобиля первой модели требуется 6 человеко-дней, второй модели – 4 и третьей модели – 2 человеко-дня в неделю соответственно. Во втором цехе трудоемкость равна 3, 4 и 5 человеко-дней соответственно, в третьем – по 3 человеко-дня на каждую модель. Прибыль, получаемая от продажи автомобиля каждой модели, составляет соответственно 15, 13 и 10 тыс. д.е. Требуется построить модель оптимального плана и определить оптимальные количества моделей каждого типа, т.е. такие, при которых прибыль завода будет максимальной.

Решение. Пусть - количество выпускаемых автомобилей -й модели в течение декады (). Модель может быть описана следующей целевой функцией и системами ограничений:

(2.5)

Решение.

Введем данные на рабочий лист так, как показано на Рис. 2.4.

Искомые значения переменных будут размещаться в ячейках A10:B10, целевая функция – в ячейке E10.

В ячейки A3:A5 введем левые части функций – ограничений, соответствующих второму, третьему и четвертому соотношению из (n.5).

С помощью Поиска решения получим ответ

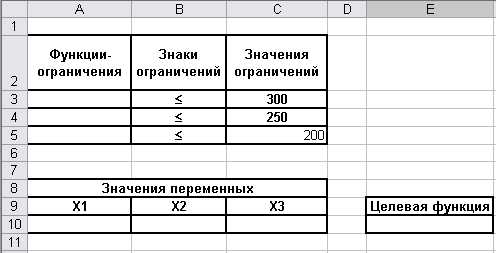
Рис. 2.4. Данные для решения примера 3.

Пример 4. Размещение проектов на предприятиях.

Имеется инвестиционных возможностей (вариантов проектов), которые можно реализовать на (предприятиях). Эффективность реализации каждой инвестиции на каждом из объектов задана в таблице 2.2.

Таблица 2.2.

Инвестици-онные проекты ()	Объекты ()
Инвестици-онные проекты ()	I	II	III	IV	V
1	0.12	0.02	0.50	0.43	0.15
2	0.71	0.18	0.81	0.05	0.26
3	0.84	0.76	0.26	0.37	0.52
4	0.22	0.45	0.83	0.81	0.65
5	0.49	0.02	0.50	0.25	0.27

Целевой функцией, подлежащей оптимизации, является функция:

где - искомые распределения инвестиций по объектам.

Таким образом, по смыслу величина есть ожидаемый результат от осуществления всех инвестиционных проектов. Ограничениями в данном случае являются:

означающие, что на каждом объекте может быть реализован лишь один проект, и

означающие, что должны быть реализованы все проекты. Необходимо распределить проекты по объектам таким образом, чтобы суммарная эффективность от реализации всех проектов была максимальной.

Решение. Введем данные на рабочий лист (Рис.2.5.).

В ячейку B17 введем формулу =СУММ(B12:B16) и скопируем эту формулу в диапазон C17:F17. Аналогично, введем формулу =СУММ(B12:F12) в ячейку G12 и скопируем ее в диапазон G13:G16. Введем в ячейку для целевой функции (I13) формулу

=СУММПРОИЗВ(B4:F8;B12:F16).

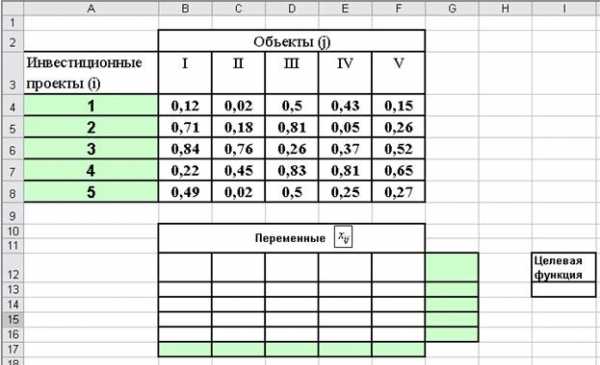
Рис. 2.5. Данные для решения примера 4.

Для решения задачи с помощью Поиска решения необходимо ввести ограничения в соответствии с приведенным ниже рисунком.

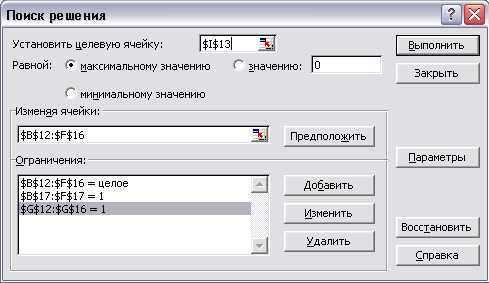
Поиск решения дает ответ (остальные ), .

studizba.com

Оптимизация модель - Справочник химика 21

Если в ходе процесса происходит задержка в выполнении каких-либо работ, не лежащих на критическом пути, то она не создает угрозы для выполнения работ по объекту в целом. Любая задержка ла критическом пути не допустима. Если расчет критического пути показывает, что сроки работ не укладываются в заданные, то производят оптимизацию модели с целью сокращения продолжительности критического пути. Для этого анализируют модель и определяют, с каких участков некритической зоны сети можно переместить рабочих и технику на работы, лежащие на критическом пути. В этом случае выявляют новый критический путь с продолжительностью меньше или равной директивной (заданной). В результате оптимизации модели принимают конечный ее вариант,который и утверждают. На его основе устанавливают и доводят до ответственных исполнителей календарные сроки выполнения закрепленных за ними работ. [c.362] Пример 3.2. Решение задач оптимизации модели на основе уравнения регрессии методами классического аналитического поиска экстремума и Гаусса-Зейделя [c.76]

ОПТИМИЗАЦИЯ МОДЕЛИ ПРОИЗВОДСТВА [c.277]

Оптимизация модели производства 279 [c.279]

Оптимизация модели производства [c.281]

Оптимизация Модели производства [c.287]

Оптимизация модели производства 293 [c.293]

Оптимизация. Существуют две возможности при оптимизации моделей первая заключается в сохранении всех первоначально выбранных реакций в схеме, вторая — в предварительном отборе только наиболее существенных реакций в целях экономии машинного времени. В любом случае, если оптимизация приводит к величинам параметров, лежащим за пределами области, рассмотренной ранее при анализе чувствительностей, весь анализ чувствительностей следует повторить снова, и, если спектр чувствительностей заметно изменился, модель необходимо еще раз оптимизировать, [c.395]

Примерная структура САПР технологического проектирования приведена на рис. 2.2. Ее основу составляют банк данных (БД) — информационное обеспечение, содержащее данные о свойствах перерабатываемых и получаемых веществ, параметрах оборудования и схем, экономические и технико-экономические показатели последних, информационно-справочные данные и т. д. пакеты прикладных программ (ППП) общего и специали-зпрованного назначения (алгоритмы решения задач оптимизации, модели аппаратов и технологических схем) алгоритмы синтеза технологических схем алгоритмы конструкционного расчета и выбора оборудования, размещения оборудования алгоритмы синтеза систем управления. Организационно САПР технологического проектирования состоит из ряда взаимосвязанных подсистем, принципы разработки, структура и состав которой подробно изложены во второй части книги. [c.44]

В ряде курсов, таких как Вычислительная математика , Математическая зконо.мика , Математические основы кибернетики , Моделирование и опти--мизация систем управления можно выделить три грз ппы задач построение математической модели статистическими и аналит гческими методами исследование математической. модели метода1Ми прикладной математики оптимизация моделей для решения которых удобно использовать пакет MATH AD. [c.215]

Пример 3 2 Решение задач оптимизации модели на основе уравнения регрессии методами классического аналитического поиска экстремума и Гаусса-Зейделя 76 Пример 3. 3 Расчет оптимальных размеров слоя катализатора в реакторе термокаталитической очистки отходящих газов от пргшесей углеводородов методом неопределенных множителей Лагранжа 79 Пример 3.4. Выбор рациональной схемы взаимного расположения аппаратов на базе [c.162]

Когда речь идет об оптшшзации действующего производства с помощью системы с обратной связью, иначе говоря, о том, чтобы по результатам анализа качества потоков установить новые задания регуляторам процесса, то, казалось бы, модель не может найти дальнейшее применение ввиду эмпирического характера системы с обратной связью. Впрочем, если бы модель была исчерпывающе полной и точной, не было бы никакой надобности в оптимизации, основанной на обратной связи, — производство сразу начало бы работать в оптимальном режиме. Однако на практике эта идеальная ситуация встречается крайне редко в тех же случаях, когда отклонение от оптамального режима всего на несколько процентов грозит существенными убытками, может оказаться целесообразным комбинированное использование модели для предваряющего управления и оптимизации по схеме с обратной связью. При таком подходе модель укажет оператору наилучпше начальные значения регулируемых переменных, а также рациональные величины одноразовых изменений (шагов) крутого восхождения (метода оптимизации). Модель призвана обеспечить выбор таких шагов, которые представляли бы собой существенные, но не опасные изменения. [c.240]

chem21.info

Модель - оптимизация - Большая Энциклопедия Нефти и Газа, статья, страница 1

Модель - оптимизация

Cтраница 1

Модель оптимизации под готовки запасов и добычи нефти S i - м районе ( операционный, уровень. [2]

Модели оптимизации, которые могут быть использованы для оптимизации некоторых действий. [3]

Модели оптимизации в этом случае получаются достаточно сложными. [4]

Модели оптимизации по этим критериям входят в общую задачу оптимизации ОУ следующим образом. До возникновения отказа или другого возмущения система МН характеризуется некоторым базовым набором режимов НП. После снижения пропускной способности НП вырабатывается решение об оптимальном использовании имеющихся резервов в целях минимизации ограничений с учетом приоритетов поставщиков и потребителей. [5]

Модели оптимизации оболочек, подкрепленных ребрами жесткости ( шпангоутами и стрингерами), в сравнении с аналогичными моделями для гладких оболочек имеют некоторые особенности. Во-вторых, если оптимизируется схема подкрепления оболочки, то в число оптимизируемых параметров следует включить существенно дискретный параметр - число элементов подкрепления, вследствие чего модель оптимизации оболочки, подкрепленной ребрами жесткости, приобретает поливариантный характер. [6]

Модель оптимизации региона также должна включать ограничения на свои параметры и целевую функцию в виде функции, отражающей минимум затрат на единицу производимой продукции. Таким образом, на этапе региональной оптимизации при заданных входных и выходных параметрах региона ( определяемых при глобальной оптимизации и оптимальных в смысле всего ХТК) находятся оптимальные в смысле самого региона показатели всех его элементов. [7]

Модели оптимизации экономики имеют целью добиться наибольшей результативности ( эффективности) использования имеющегося потенциала и ресурсов. [8]

Модели оптимизации надежности при проектировании нефтепровода обеспечивают его структурный синтез. [9]

Модели оптимизации надежности при прогнозировании развития сети призваны решать комплекс вопросов по обоснованию резервов пропускных способностей линий, объемов ре-зервуарных парков и их расстановки, размещения баз технического обслуживания и центров диагностики, построения системы управления. [10]

Модель оптимизации размера ( объема) заказанной партии материальных средств - алгоритм, позволяющий оптимизировать средний размер заказа и соответственно размер запаса материальных средств, входящих в состав оборотных активов. Входными исходными данными для этой модели являются показатели объема потребностей в материальных средствах ( например, их суточный расход), удельных затрат на завоз и хранение единицы рассматриваемых материалов, представительских затрат на осуществление одного заказа. [11]

Модели оптимизации прибыли или издержек большого предприятия могут содержать очень много переменных. Поэтому попытки наугад или с помощью простого перебора вариантов изменить те или иные параметры, чтобы улучшить функционирование управляемой системы, обречены на неудачу. В этой ситуации только использование концепции теневых цен и интервалов устойчивости, выдаваемых в отчете об устойчивости оптимального решения, позволяет нащупать наиболее эффективные рычаги управления. [12]

Модели оптимизации несущих конструкций из композитов являются достаточно сложным объектом для численного анализа даже при условии применения самых современных его средств и методов. Развитие этих методов, составляющих самостоятельный раздел современной математики - нелинейное математическое программирование, в значительной мере стимулируется потребностями разработки практических приемов решения конкретных задач ОПК, в частности задач оптимизации конструкций из композитов. [13]

Модели оптимизации тонкостенных оболочек из слоистых композитов / / Теоретична и прилежна механика. [14]

Модель оптимизации запасов нефти в РП (6.2) получена при предположении, что резерв производительности нефтепровода таков, что вероятность восстановления запасов нефти в РП, перераспределенных в результате отказа, близка к единице и затраты на восстановление запасов гораздо меньше суммарных ущербов от простоев поставщика, нефтепровода и потребителя. [15]

Страницы: 1 2 3 4

www.ngpedia.ru

Модели оптимизации структуры производства - Энциклопедия по экономике

Из моделей первой группы можно назвать модели долгосрочного прогноза сводных показателей экономического развития, межотраслевые модели, отраслевые модели оптимального планирования и размещения производства, а также модели оптимизации структуры производства в отраслях. [c.404] Модели календарного планирования 54 Модели качественного отклика 202 Модели леонтьевского типа 83 Модели магистрального типа 203 Модели мировой динамики 203 Модели непрерывной длительности 203 Модели объектов планирования 243 Модели оптимизации структуры производства 404 Модели поэтапного расчета объемов [c.474]

Широкое применение находят в отраслевом планировании модели типа оптимизации, в которых определяется наилучшая система экономических показателей с точки зрения реализации какого-либо избранного на перспективу критерия. Например, модели оптимизации структуры производства и применения того или иного продукта мощности и последовательности строительства отдельных производств размещения отдельных видов производства по экономическим районам и др. [c.220]

В планировании развития химической промышленности используются модели оптимизации структуры производства и распределения продукции, развития и размещения важнейших отраслей химической промышленности, структуры капитальных вложений и их распределения по годам строительства, экономико-статистические модели расчета технико-экономических показателей развития отрасли и другие модели. [c.252]

Во-первых, базовая модель анализа, изображенная на рис. 1, решает задачу нахождения оптимальной величины физического объема сбыта и уровня цен реализации для одного вида продукции. При ограниченных ресурсах предприятия и наличии широкого ассортимента сбыта на практике часто необходимо решать задачи оптимизации структуры производства и сбыта, исходя из сравнения планируемого дохода от реализации различных видов продукции. Это в достаточной степени усложняет алгоритм СКР-анализа. [c.45]

Модель планирования ассортимента путем оптимизации ключевых финансовых показателей (Модель 4) [128]. Данная методика предполагает несколько этапов планирования и основывается на определении ключевых финансовых показателей при наилучшем из имеющихся вариантах структуры производства, оценке влияния производственных факторов на финансовые показатели и определении себестоимости единицы каждого вида продукции. Расчеты проводятся по следующим этапам [c.32]

Заметным явлением в сфере трудовых отношений и мотивации труда в развитых странах стало развитие экономической демократии как процесса, с одной стороны, продолжающего многолетние усилия по оптимизации управленческих моделей в экономике, а с другой стороны, имеющего целью гармонизацию социальных отношений на производстве и в обществе. Экономическая демократия может быть охарактеризована как система, включающая демократизацию собственности фирмы в форме привлечения работников к ее владению, а также участия работников в управлении фирмой в форме как предоставления им значительной произвол- ственной автономии, так и представительства рядовых работников (или профсоюзов, где они имеются) в руководящих структурах фирмы контроль (по крайней мере, в определенных пределах) со [c.315]

Абстрактно-исследовательские модели. Как следует из названия, модели разрабатываются с целью исследования природы систем качества, выявления в них общих и специфических структур, обусловленных характером продукции, типом производства, масштабом предприятий, отраслевой спецификой или общих закономерностей функционирования и формирования систем качества. При помощи таких моделей удается в предварительном порядке определять конфигурации возможных структур систем качества, возможную степень их упрощения, подходы к оптимизации, разрабатывать варианты схем прямых и обратных связей и их информационного наполнения. [c.136]

Не всё во внедрении моделей для оптимизации управления проходит гладко. Так, на одном крупном уральском заводе, купившем популярный на Западе пакет управленческого программного обеспечения и вложившем большие деньги в обучение своих специалистов, выяснилось, что для нормальной работы программ предприятию нужно стать прозрачной бизнес-структурой — платить налоги, пройти международный аудит и т.д. В результате завод установил у себя программы отечественного производства, позволяющие вести одновременно белую и черную бухгалтерию. [c.160]

Сформулировав принципы создания рациональной модели трудовых отношений, в рамках которой становится возможным реализовать ту самую предпосылку научного управления - добиться совпадения интересов в виде их тождества, мы тем самым фактически реабилитируем традиционные управленческие концепции. А ведь не секрет, что правильность последних все чаще подвергается сомнению и ведется интенсивный поиск новых чудодейственных рецептов создания гибких организационных структур и подходов к управлению. Целью этого поиска является выход из кризисного тупика и нахождение ответов "на животрепещущие проблемы современности, перед которыми традиционная теория оказалась бессильной" [87]. Но, как известно, традиционные рационалистические концепции управления базируются в первую очередь на измерениях и точных расчетах, без которых говорить о рациональной организации индивидуальной и групповой работы, о налаживании гибкого производства с низким уровнем запасов, о какой-либо оптимизации производственного процесса и рациональном использовании всех ресурсов организации просто немыслимо. [c.249]

Следующий тип оптимальных моделей, по которым уже начались практические исследования, охватывает расчеты планов для комплекса отраслей. Наибольшие результаты получены при разработке топливно-энергетического баланса, оптимизирующего производство и потребление угля, нефти, газа и других ресурсов топлива и энергетики. Расчеты по этому балансу дали ряд ценных выводов как относительно пропорций и темпов развития отдельных отраслей, бассейнов и месторождений, входящих в комплекс, так и относительно установления цен на топливо. Еще один комплекс отраслей, где для планирования производства применяются оптимальные модели,— сельское хозяйство. Расчеты по таким моделям уже показали, что в этом экономическом комплексе оптимизация позволяет достигнуть значительного эффекта, например прийти к практически полезным результатам относительно улучшения структуры сельскохозяйственного производства. Следует иметь в виду, что все это только первые шаги в деле разработки и использования многоотраслевых моделей оптимального планирования. [c.211]

Вариантные расчеты могут осуществляться при постоянной структуре самой модели (постоянном составе неизвестных, способов производства, ограничений задачи и одинаковом критерии оптимизации), но с изменением величины конкретных показателей модели или при варьировании элементов самой модели изменении критерия оптимизации, добавлении новых ограничений на ресурсы или на способы производства, расширении множества вариантов и т.д. [c.17]

Исторически развитие тренажерных технологий шло бок о бок с совершенствованием средств управления [1], поскольку, с одной стороны, стимулировалось появлением новых СУ, а с другой - основывалось на тех же теоретических и прикладных достижениях разнообразных ответвлений науки об управлении. Тем не менее, последнее обстоятельство не нашло необходимого осмысления в свете наблюдаемой конвергенции средств управления, инжиниринга и обучения в рамках современной концепции производственной автоматизации ( оптимизация реального времени [2]). Действительно, динамические модели ТП в современном КТ не только не уступают по детальности и точности описания процессов моделям для систем управления и инжиниринга, но зачастую могут служить базой для построения последних. Компьютерные интерфейсы обучаемого в тренажерных системах либо являются репликами операторских интерфейсов реальных систем управления производством (микропроцессорных распределенных СУ, программируемых логических контроллеров и пр.), либо на высокоточном уровне эмулируют указанные интерфейсы или централизованные управляющие пульты. Наконец, в основе методики КТ в современных тренажерных системах лежит воссоздание структуры реальной деятельности оператора по управлению ТП. В этих условиях рассмотрение всех аспектов построения и использования компьютерных тренажеров в отрыве от многообразной проблематики автоматизированного управления производством представляется непродуктивным. В настоящей работе предпринимается попытка преодолеть указанный разрыв и обозначить общность задач управления и обучения в рамках комплексной автоматизации производства. [c.197]

Оптимизационные модели основаны на выборе критерия оптимальности, на основе которго путем сравнения различных вариантов выбирается лучший (оптимальный) вариант. Оптимизационная экономико-математическая модель состоит из целевой функции и системы ограничений. Целевая функция описывает цель оптимизации и отражает зависимость показателя, по которому ведется оптимизация, от независимых переменных (ограничений). Система ограничений отражает объективные экономические связи и зависимости и представляет собой систему равенств и неравенств, например, между потреблением ресурсов или величинами технико-экономических показателей и установленными лимитами, а также пределами выпуска продукции. Влияние каждой из переменных на величину целевой функции выражается коэффициентом-показателем, экстремум которого выступает критерием оптимальности. Примеры оптимизационных моделей в планировании и прогнозировании модели оптимизации развития и размещения производств, модели оптимизации структуры производства продукции отраслей промышленности, модели АПК, модели транспортных задач, с помощью которых осуществляется рациональное прикрепление поставщиков к потребителям и определяются минимальные транспортные затраты, и другие. [c.165]

К середине 60-х годов в результате глубоких научных исследований было показано, что предпринимавшиеся ранее попытки построить модель оптимального народнохозяйственного плана с целевой функцией, выражающей требования основного экономического закона социализма, и системой ограничений, описывающей условия и технологию расширенного воспроизводства, яе принесут желаемых результатов. И дело здесь не только в гигантской размерности такой модели, делающей ее необозримой для пользователя и нереализуемой даже на самых мощных ЭВМ, но и в том, что, во-первых, в одной целевой функции нельзя выразить все многообразие социально-экономических интересов общества во-вторых, в одной системе ограничений невозможно достаточно полно и конкретно описать различные по масштабам, временным и пространственным параметрам, характеру управляемых переменных процессы развития социально-экономической системы социалистического государства в-третьих, функционирование такой модели предполагает, что управление всеми воспроизводственными процессами и элементами народного хозяйства осуществляется из единого центра, что противоречит принципу демократического централизма и действующей иерархической структуре социалистического управления. Поэтому в теории построения АСПР развился подход к оптимизации народнохозяйственного плана посредством построения такой системы моделей, в которой они дифференцированы прежде всего по уровням народнохозяйственной иерархии модели центра, региона, отрасли, объединения, предприятия. Каждой из этих моделей присущ свой уровень агрегирования и конкретности описания планируемых объектов. Этот вертикальный разрез системы моделей дополняется ее горизонтальными разрезами формализованное описание объектов каждого уровня охватывается не одной, а целым рядом моделей. Так, например, на верхнем уровне могут строиться модель технологии общественного производства (на основе межотраслевого баланса), модель формирования и удовлетворения конечных общественных потребностей (на основе дифференцированного баланса доходов и потребления населения), модели элементов ресурсного потенциала (демографиче- [c.124]

Итак, каждому этажу планирования присуща своя оптимальная модель. Следуя этому принципу, советские экономисты создали математические модели оптимизации оперативно-календарного планирования, матричные модели техпромфинплана предприятия (планирование на уровне предприятия), модели размещения производства и оптимального плана перевозок (отраслевые задачи), оптимальные модели экономического района (региональное, районное планирование). Особое место среди всех названных занимает модель статического межотраслевого баланса, позволяющая планировать межотраслевую структуру народного хозяйства страны1. [c.19]

Наиболее предпочтительны линейные многофакторные регрессионные модели. При использовании же нелинейных многофакторных моделей увеличение числа параметров ведет к снижению точности оценок и сложности интерпретации возникают сложности и при их оптимизации. Однако практически наиболее употребимые непрерывные (линейные и нелинейные) регрессионные модели предполагают наличие качественной однородности рассматриваемой совокупности, что наблюдается далеко не всегда. Неизбежны и различия в уровне техники, технологии и организации производства на отдельных объектах исследуемой совокупности, вызванные различиями в возрасте объектов (или отдельных единиц оборудования), их мощности, структуре выпуска продукции и ее назначении, природных условиях и т. д. Эти различия могут быть таковы, что внутри общей совокупности четко выделяются особые подсовокупности с различными характеристиками интересующих нас зависимостей. В этих условиях применение непрерывных моделей неправомерно, что вынуждает переходить к построению дискретных и дискретно-непрерывных моделей. [c.40]

Для определения воздействия производства и потребления химической продукции на конечные народнохозяйственные показатели развития экономики разрабатывают оптимизационную полудинамическую натурально-стоимостную модель межотраслевого баланса. Составная часть расчетов рассматриваемой модели (наряду с другими факторами оптимизации) - выявление эффективной структуры потребления мате-308 [c.308]

Лит. В о л к о в Ю. И., Макаров В. Л., Динамическая модель для расчета оптимального перспективного топливно-энергетического баланса СССР. [Доклад на конференции по применению математики и вычислительной техники в планировании], Новосибирск, октябрь 1962 (ротапринт) Кузнецов Ю. А., Мелентьев Л. А., Некрасов А. С., М е р е н к о в А. П., Определение оптимальной структуры перспективного энергетического баланса с использованием электронных вычислительных машин, Теплоэнергетика , 1962, № 5 М е л е н т ь е в Л. А., С т ы р и-кович М. А. и Штейнгауз Е. О., Топливно-энергетический баланс СССР, М.—Л., 1962 Маш В. А., Оптимизация топливно-энергетического баланса. Доклад на конференции по применению математики и вычислительной техники в планировании, Новосибирск, октябрь 1962 (ротапринт) Смерти н А., О расчетах эффективности капитальных вложений в производство взаимозаменяемой продукции, Плановое хозяйство , 1961, К> 12, стр. 45—54 его же, Линейное программирование в расчетах топливного баланса, М., 1963. [c.213]

Как уже упоминалось, в наиболее общем виде прибыль Р может быть представлена как разность между суммами доходов (R) и затрат (Ех), формируемыми в привязке к периоду, за который исчисляется прибыль, и логически соотносимыми друг с другом. Оба выделенных фактора (R и Ех) в определенных рамках являются регулируемыми со стороны управленческого персонала. В особенности это относится к фактору затраты именно этим объясняется тот факт, что затраты (издержки) производства и обращения, выступая одним из основных факторов прибыли, безусловно находятся под пристальным вниманием и контролем руководства предприятия. Информация о структуре затрат и способах ее оптимизации является конфиденциальной, однако укрупненные элементы совокупных затрат являются общедоступными и приводятся в отчете о прибылях и убытках. Несложно понять, что данный отчет являет собой табличное Lпредставление жестко детерминированной факторной модели [c.301]

economy-ru.info

Оптимизация моделей процессов производства

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Кафедра менеджмента

РЕФЕРАТ

на тему:

«ОПТИМИЗАЦИЯ МОДЕЛЕЙ ПРОЦЕССОВ ПРОИЗВОДСТВА»

МИНСК, 2008

В условиях оживления и развития отечественной промышленности существенно возрастает интерес к проблемам организации производства, и в частности, к задачам оперативно-календарного планирования.

Календарные планы работы отдельных производственных ячеек предприятия представляют собой расписания изготовления всех изделий, загрузки оборудования и рабочих мест. Производственная ячейка - часть производственного пространства (станки, участок), на котором соответствующим образом организованы производственные ресурсы и процессы.

Основными параметрами календарных графиков являются: приоритетность работ (очередность запуска изделий в обработку), размер партий запуска и время опережения начала обработки изделий на связанных рабочих местах, размер незавершенного производства. Результатом составления оптимального календарного графика является определение наименьшей длительности производственного цикла, оказывающей существенное влияние на улучшение экономических результатов деятельности предприятия. В этом случае происходит снижение объема оборотных средств в незавершенном производстве, уменьшаются простои оборудования и рабочих.

В производственных подразделениях машиностроительных предприятий календарное планирование в настоящее время основано главным образом на моделировании, позволяющем обеспечить пропорциональность, непрерывность, устранить «узкие места» и правильно установить приоритеты работ. Следует отметить, что установление очередности запуска изделий в производство является одной из основных задач, которую необходимо решить при составлении оптимального календарного графика.

В силу этого, в качестве критерия оптимальности моделей целесообразно использовать минимизацию длительности совокупного производственного цикла. Под моделью производственного процесса понимается его пространственное построение, отражающее технолого-организационную суть последнего через организационную структуру. Под моделью плана производства - количественно-временная организация предметов труда в ходе производственного процесса. Под моделью оперативного управления (части управляющей системы - надстройки) - функциональное выделение той части управляющей системы, которая предназначена для удержания существующих переменных управляемого объекта в заданных планом пороговых значениях.

Все существующие методы решения задач календарного планирования по степени достижения экстремального результата подразделяются на две четко выраженные подгруппы - точных и приближенных решений.

К числу опробованных точных методов решения задачи моделирования относятся методы линейного и динамического программирования, комбинаторные методы дискретного программирования и др.

Метод линейного программирования удачно использован С.М. Джонсоном для решения задачи нахождения оптимального по календарному времени плана обработки m деталей на двух станках. Алгоритм Джонсона чрезвычайно прост. Выбирается самое короткое операционное время, и если оно относится к первому станку, планируют выполнение задания первым на первом станке, а если ко второму - то последним. Затем процедура повторяется до полного перебора всех заданий на обоих станках. Имеются многочисленные обобщения правила Джонсона для различных случаев трехстадийной обработки деталей. Однако этот алгоритм неприменим для случаев обработки деталей на большем количестве станков.

Метод динамического программирования удачно использован Р. Беллманом для однооперационного производства. Он дал частное решение задачи оптимального календарного планирования обработки совокупности изделий, имеющих одинаковый процесс производства, но различных по длительности операций обработки. Запуск изделий в производство необходимо осуществлять, соблюдая условие: min(t11 , t 22 ) < min( t12 , t 21 ), где: t11 - трудоемкость выполнения первой операции над изделием, первым запускаем в производство; t 22 - трудоемкость выполнения второй операции над изделием, вторым запускаем в производство, а t12 и t 2 l - соответственно наоборот.

Метод «ветвей и границ», являющийся комбинаторным методом дискретного программирования, предполагает уменьшение множества допустимых решений, вплоть до получения конечного множества, при котором оказывается возможным применение метода перебора. В этом методе происходит последовательный выбор пары номеров деталей для получения оптимальной последовательности. Составление последовательности номеров деталей для запуска в производство происходит в процессе работы итерационного алгоритма. На каждой итерации выбираются две детали и помещаются на позиции: (n+ 1) и (d– n), где n - номер итерации, ad- количество наименований деталей, участвующих в производственном процессе. Эффективность метода «ветвей и границ» зависит от уровня, на котором происходит «отсечение» ветви. В общем случае этот метод не исключает полный перебор всех возможных вариантов.

Типичные модели линейного, линейного целочисленного и квадратичного целочисленного программирования свидетельствуют о том, что в них могут быть отражены многие ограничения задачи календарного планирования. В частности, в этих моделях, в форме ограничений на переменные, могут быть выражены требования, накладываемые на сроки выпуска этих деталей. Допускается обработка деталей партиями, но для этого необходимо некоторое предварительное преобразование исходной информации.

Данные модели имеют ограниченное применение при моделировании производственных процессов. Главным недостатком является быстрый рост размеров моделей с ростом задачи календарного планирования. Точные методы оптимизации применимы лишь для частных и небольших по размеру задач. На машиностроительных предприятиях составление оптимального календарного графика усложняется широтой номенклатуры выпускаемых изделий и является динамической, вероятностной задачей большой размерности. Поэтому наряду с разработкой точных методов интенсивно развиваются приближенные методы.

К числу приближенных методов оптимизации задач календарного планирования относятся: частичный и направленный перебор, метод Монте-Карло, аналитико-приоритетные, эвристические и др. методы.

Метод Монте-Карло аналогичен методу перебора и оценки вариантов с той разницей, что оценивается некоторое ограниченное подмножество вариантов, выбор которых производится некоторым случайным образом. Решение задачи календарного планирования методом Монте-Карло можно рассматривать как некоторую задачу статистического моделирования производственного процесса. Метод Монте-Карло имеет ограниченное применение, так как может потребовать перебора и оценки достаточно большого количества вариантов.

В последнее время к решению задач календарного планирования стала привлекаться теория массового обслуживания. Такая возможность появилась в связи с развитием специальной теории очередей с приоритетом. Однако если в задачах массового обслуживания поток требований на обслуживание является свободным процессом, то в задачах календарного планирования требования поступают в детерминированном порядке. Вместе с тем при прохождении требований (партии деталеопераций) через большое количество обрабатывающих устройств (производственных ячеек) происходят задержки в обслуживании, и поступление требования на следующее обрабатывающее устройство может быть рассмотрено как случайное событие. В таком плане эта связь теории расписаний с задачами теории очередей с приоритетом обслуживания может быть использована как средство приближенного решения теории расписаний.

Многие задачи календарного планирования относятся к классу задач, для которых трудна конкретная аналитическая постановка, неярко выражена величина критерия эффективности и отсутствуют эффективные алгоритмы численного решения. Последнее связано с тем, что минимизируемые функции комбинаторных задач лежат не в непрерывной области переменных, а на различных дискретных перестановках элементов. Следовательно, применение приближенных методов, основанных на сочетании аналитических принципов и моделировании календарных планов с использованием правил предпочтительности, является наиболее перспективным направлением практического решения данного класса задач.

Среди приближенных методов различают большую группу аналитико-приоритетных методов. Аналитико-приоритетные методы не следует смешивать с эвристическими. В аналитико-приоритетных методах имеется математическая модель с соответствующей функцией - критерием, что позволяет приблизить решение к оптимальному, тогда как в эвристических методах такая функция отсутствует, либо имеется в неявно выраженной форме или же задается как локальная функция приоритета. Эвристические методы строятся на использовании установленных свойств и приемов решения задач других смежных групп, а также интуитивных свойств и приемов поиска.

Можно выделить семь наиболее удачных правил предпочтительности для формирования приоритетов календарного планирования последовательности работ1 .

1. FCFS (Fist - Come, Fist - Served) - первым вошел - первым обслужен. Работы выполняются в порядке поступления в подразделение.

2. SOT (Short'sOperatingTime) - по кратчайшему времени выполнения. Сначала выполняется работа с самым коротким временем выполнения, затем процедура повторяется для оставшихся работ.

mirznanii.com