Методы одномерной минимизации. Обычно в процессе применения методов одномерной оптимизации
текст(all) - Стр 5
Шаг 5. Если b | a | , то | x* a | k 1 | ;b | , конец. |
k 1 | k 1 |
|
| k 1 |
|
Шаг 6. k k 1, прейти к шагу 2.
Как было отмечено выше, на каждой итерации метода золотого сечения производится лишь одно вычисление значения функции. При этом длина полученного в результате одной итерации отрезка составит1 , где – длина исходного интервала.
Если сравнить методы дихотомического поиска и золотого сечения,
используя в качестве критерия эффективности F n – относительное
уменьшение интервала после n вычислений значений функцииf (x) , гдеn – длина интервала, полученного послеn вычислений, то
(0,5)n / 2 | для дихотомитрического | поиска |
|
|
|
F |
|
|
(0, 6181)n | для метода золотого | сечения |
|
|
|
т.е. метод золотого сечения оказывается более эффективным.
Пример. Найти точку максимума функцииf x sinx на отрезке1,5;1,6 методом золотого сечения,0,02 .
Решение. 1,6180 ;a1 1,5 ;b1 1,6 .
y0,61801,5 0,38201,6 1,5382 .
z0,3820 1,5 0,6180 1,6 1,5618 .
A siny 0,99947 ;B sinz 0,99996 .
Итерация 1. Так какA B , тоa2 y 1,5382 ; | b2 | b1 | 1,6 . |
y z 1,5618 ;A B 0,99996 ; |
|
|
|
z 0,3820 1,5382 0,6180 1,6 1,5764; |
|
|
|
B sinz 0,999984 ; |
|
|
|
b2 a2 0,0618 . |
|
|
|
Итерация 2. Так как A B , тоa3 y 1,5618 ; | b3 | b2 | 1,6 . |
y z 1,5764 ;A B 0,99998 ; |
|
|
|
z 0,3820 1,5618 0,6180 1,6 1,5854;
B sinz 0,99989 ;b3 a3 0,0382 .
Итерация 3. Так как A B , тоa4 a3 1,5618 ;b4 z 1,5854 .z y 1,5764 ;B A 0,99998 ;
y 0,61801,5618 0,38201,5854 1,5708 ;
A 1,00000;
studfiles.net
Методы одномерной минимизации.
24
Основные понятия
Постановка задачи.
- числовая функция вещественной переменной . Под задачей одномерной минимизации на отрезкепонимается поисктакого, что
(3.1.0 )
- наименьшее значение на ;
 , удовлетворяющее ( 3.1 .0 ) называется точкой минимума на ;
, удовлетворяющее ( 3.1 .0 ) называется точкой минимума на ;

 может быть пустым, содержать конечное или бесконечное число точек.
может быть пустым, содержать конечное или бесконечное число точек.
Замечание. Задача поиска максимума сводится к задаче поиска минимума :
Задача одномерной минимизации состоит из двух частей:
локализации точек минимума, то есть указания отрезков, содержащих единственную точку минимума;
поиска точки минимума на заданном отрезке при наличии информации о том, что на этом отрезке заведомо существует единственный минимум.
Задача локализации минимума обычно решается с помощью классического метода, основанного на дифференциальном исчислении.
Кроме того, существуют и некоторые вычислительные процедуры, позволяющие в определенных условиях такую задачу решать.
В основном, ниже рассматриваются численные методы, позволяющие решать локализованные задачи.
Классический подход.
Напомним 2 важные для данного рассмотрения теоремы из классического анализа.
Теорема Вейерштрасса. Если непрерывна на , то существует.
Теорема Ферма. Пусть дифференцируема в точке . Если доставляет локальный минимум , то
Определение.  называется точкой локального минимума, если существует > 0 такое, что для выполняется
называется точкой локального минимума, если существует > 0 такое, что для выполняется
Пусть кусочно-непрерывная и кусочно-гладкая на функция. Это означает, что наможет существовать лишь конечное число точек, где терпит разрыв I-го рода, либо непрерывна, но не имеет производной.
Тогда точками минимума могут быть такие точки, в которых:
- терпит разрыв;
- непрерывна, но не существует;
-
- либо , либо.
Рисунки ниже иллюстрируют эти 4 случая.
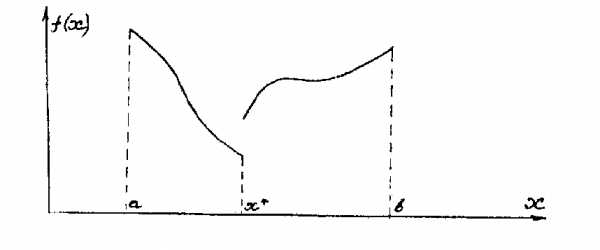
Рисунок 3.2.1
терпит разрыв в точке .
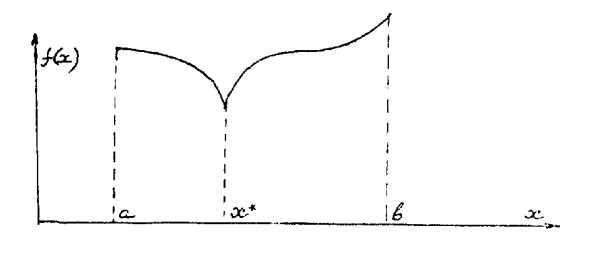
Рисунок 3.2.2
непрерывна, но производной не существует.
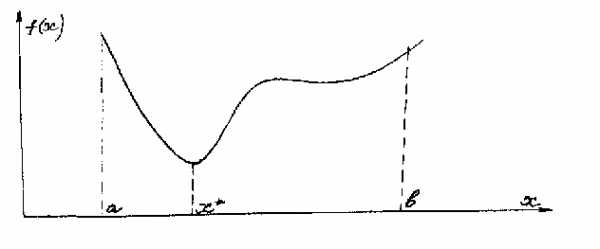
Рисунок 3.2.3
.

Рисунок 3.2.4
.
Методы решения задачи минимизации для унимодальных функций.
Понятие унимодальной функции.
Определение. унимодальна на , если существуют такие, что
строго монотонно убывает на ,
строго монотонно возрастает на,
для
Если ,то строго унимодальна.
Унимодальная функция не обязательно должна быть непрерывной и дифференцируемой. Ниже представлены примеры унимодальных функций.
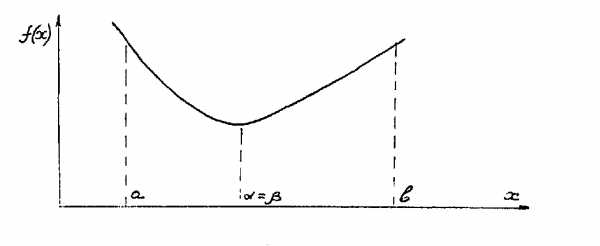
Рисунок 3.3.5
Строго унимодальная, непрерывная, дифференцируемая функция.
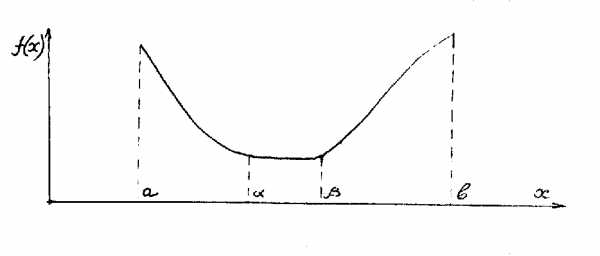
Рисунок 3.3.6
Нестрого унимодальная, непрерывная, дифференцируемая функция.
Рисунок 3.3.7
При имеет разрывI- го рода, при , производной у не существует.
Общие сведения о численных методах оптимизации, их классификация.
Определение 1. Под численным методом одномерной минимизации понимается процедура получения числовой последовательности приближений к точному решению задачи минимизации.
Определение 2. Под численным методом одномерной минимизации понимается процедура получения вложенных отрезков, покрывающих точное решение:
.
Порядок метода.
Метод имеет порядок k, если он использует информацию о производных до k - порядка включительно. Обычно применяются методы 0-го, 1-го и 2-го порядков.
Сходимость метода.
Численный метод сходится, если последовательность сходится к точному решению, то есть (скорость сходимости характеризуется ) или метод сходится, если ; (скорость сходимости характеризуется разностью ).
studfiles.net
Методы одномерной оптимизации - Энциклопедия по машиностроению XXL
В начале вычислений нужно задаться произвольной положительно определенной матрицей Но, в частности Но может быть единичной матрицей. Шаг hk выбирают по методу одномерной оптимизации. [c.288]Оцените эффективность методов одномерной оптимизации. [c.329]
Величина шага для каждого метода или алгоритма поиска может определяться по-разному. В простейших случаях шаг выбирается постоянным или изменяется пропорционально модулю градиента Яо. Максимальная величина шага (до достижения границы или наилучшего в данном направлении значения Нд) выбирается с помощью методов одномерной оптимизации, рассмотренных в [43]. [c.131]
Наиболее эффективными численными методами одномерной оптимизации являются методы Фибоначчи и золотого сечения, основанные на построении последовательности отрезков, стягивающихся в точку оптимума [80]. В качестве примера рассмотрим схему метода золотого сечения (рис. П.2, г). Произвольно выберем начальный интеграл изменения Х в виде (Хтш, Яшах). С помощью чисел Фибоначчи [c.243]Время поиска существенно уменьшается при стремлении к локальному оптимуму. В этом случае соотношение (П.43) принципиально сохраняет свою силу, однако значения N существенно уменьшаются и не являются постоянными. Количество расчетов Но на каждом этапе определяется принятым методом одномерной оптимизации и начальной точкой, с которой начинается поиск на данном этапе. Поэтому N изменяется при повторной оптимизации на данном этапе. На основе стратегии динамического программирования построены алгоритмы локальной оптимизации, обеспечивающие значительно меньшее время поиска по сравнению с глобальной оптимизацией [4, 8]. [c.255]
В зависимости от числа управляемых параметров различают методы одномерной и многомерной оптимизации, в первых из них управляемый параметр единственный, во вторых размер вектора X не менее двух. Реальные задачи в САПР многомерны, методы одномерной оптимизации играют вспомогательную роль на отдельных этапах многомерного поиска. [c.158]
Методы одномерной оптимизации [c.159]
К методам одномерной оптимизации относятся методы дихотомического деления, золотого сечения, чисел Фибоначчи, полиномиальной аппроксимации и ряд их модификаций. [c.159]
Методы нелинейного программирования в зависимости от способа задания шага Анг подразделяются на три основных класса 1) градиентные методы 2) безградиентные методы 3) методы случайного поиска. Некоторые методы организуются как комбинированные алгоритмы, использующие достоинства методов различных классов. Кроме того различают методы одномерной оптимизации (м-скаляр) и многомерной оптимизации (и-вектор). [c.24]
МЕТОДЫ ОДНОМЕРНОЙ ОПТИМИЗАЦИИ Задача поиска экстремума функции одной переменной возникает при оптимизации целевой функции, зависящей от одной скалярной переменной. Такие задачи входят составной частью во многие итерационные методы решения задач многомерной оптимизации. [c.26]
Методы поиска экстремума классифицируются по следующим признакам в зависимости от характера экстремума существуют методы условной и безусловной, локальной и глобальной оптимизации по числу переменных проектирования различают методы одномерного и многомерного поиска, а по характеру информации о виде целевой функции — методы нулевого, первого и второго порядков, причем в методах первого порядка используют градиент целевой функции, поэтому эти методы называются градиентными, в методах второго порядка применяют вторые производные, а в методах нулевого порядка производные не используют. [c.281]
Поисковые методы динамического программирования основаны на численных методах решения уравнения (3.75). Общая вычислительная схема на первом этапе сводится к решению задачи одномерной оптимизации ДЯо по параметру Azi, при фиксированной точке Zo и заданной функции /p-i(Zi). Аналитический вид этой функции, как правило, неизвестен, но для численных [c.254]
Таким образом, методы рещения граничных обратных задач должны учитывать высокую чувствительность результатов к различного рода погрешностям. В противном случае легко получить решение, весьма далекое от истинного. Одним из перспективных направлений в решении ОЗТ является приведение их к экстремальным постановкам и использование численных методов теории оптимизации. Рассмотрим обратную задачу для одномерного нелинейного уравнения теплопроводности [c.285]
Метод покоординатного спуска характеризуется выбором направлений поиска поочередно вдоль всех п координатных осей, шаг рассчитывается на основе одномерной оптимизации, критерий окончания поиска Х , - [c.160]
Если ограничения на параметры модели отсутствуют, то для минимизации квадратичной формы (8 16) можно применять методы многомерной d> 1) или одномерной d = 1) безусловной оптимизации (см, пп. 5.1.10, 5.1.11 книги 1 настоящей справочной серии, а также [13, 19]). Если же ограничения на параметры существуют и их нужно учитывать, то следует использовать методы условной оптимизации [13]. [c.471]
Градиентный метод расчета бинарных решеток, рассмотренный в пункте 2.8.4, является эффективным лишь в задачах расчета одномерных решеток. Методы стохастической оптимизации в общем двумерном случае требуют больших вычислительных затрат и оказываются малопригодными при фокусировке в области, размер которых на порядок превышает размер дифракционного пятна. [c.123]
Метод конфигураций включает выполнение циклов из п шагов покоординатного спуска. После каждого цикла делается один дополнительный шаг, определяемый с помощью одномерной оптимизации (3.14), вдоль направления и, —и п, где к=п,2п,Ъп,. .., т. е. по линии, проходящей через конечные точки двух смежных циклов шагов. На рис. 3.8 показан поиск по методу конфигураций точки Х[ и Хг получены из начальной Хо с помощью покоординатного спуска, точка Хд — результат дополнительного шага. [c.73]
ПК ПА9 имеет библиотеку методов одномерной и многомерной оптимизации. В состоянии поставки ПК ПА9 библиотека содержит методы полного перебора, половинного деления, золотого сечения, квадратичной интерполяции, случайного поиска, метод Нел дера-Мида. [c.501]
К понятию реентерабельности подпрограмм близко (но не тождественно) понятие рекурсивности. Рекурсивная подпрограмма — подпрограмма, которая вызывает сама себя (либо непосредственно, либо через цепочку модулей). Многие алгоритмы автоматизированного проектирования в области структурного синтеза и параметрической оптимизации по сути рекурсивные. Самым простым примером здесь может служить метод половинного деления, используемый для одномерного поиска экстремума функций. Однако не все алгоритмические языки [c.23]
Изложенные здесь результаты оптимизации формы тел, обтекаемых плоскопараллельным или осесимметричным сверхзвуковым потоком совершенного газа, а также оптимизации формы сверхзвуковых сопел были обобщены на случай несовершенного газа Крайко [17]. В дальнейшем Крайко [39] развил обладающий своими достоинствами метод неопределенного контура, позволяющий, как вариант метода контрольного контура, сводить определенные вариационные задачи с двумя независимыми переменными к одномерным задачам. [c.174]
К выбору коэффициента Xk для градиентных методов можно подойти двояко. Если учесть локальный характер аппроксимации (П.15), то шаг Д2),, а следовательно, Хк надо выбирать достаточно малым. Это приводит к увеличению количества шагов в процессе поиска и снижает его эффективность. Поэтому часто ki, выбирают из условия оптимизации АНок, решая одномерную зада- [c.245]
Для оптимизации объектов проектирования, в которых происходят одномерные процессы, предлагаются методы [2], основанные на анализе знака и значения соответствующих производных от целевой функции, а также на анализе градиента целевой ф /нкции. [c.30]
Отдельную группу детерминированных методов поиска составляют покоординатные методы, в связи с тем что человек, работающий в диалоговой системе оптимизации, обычно выбирает пошаговый покоординатный принцип работы с поочередным варьированием переменных. Покоординатное изменение параметров сводит поиск к одномерному, и наибольшими возможностями в однопараметрическом поиске обладают известные итерационные приемы, такие, как методы дихотомии, метод золотого сечения, сходимость которых проверена на многих задачах. [c.120]
Симплексный метод. Симплексный метод планирования эксперимента был разработан для автоматической оптимизации объекта с помощью ЭВМ. Его сущность состоит в том, что, начиная восхождение в целях определения экстремума целевой функции, планируют исходную серию опытов таким образом, чтобы точки, соответствующие условиям проведения этих опытов, образовывали правильный симплекс в многомерном факторном пространстве. Под правильным симплексом понимают совокупность k равноудаленных друг от друга точек в fe-мерном пространстве. В одномерном пространстве симплексом является отрезок прямой. Для двухмерного пространства симплексом служит равносторонний треугольник, а для трех параметров — правильная треугольная пирамида. [c.195]
Наилучшими критериями сравнения пяти методов поиска, описанных выше, являются их эффективность и универсальность. Под эффективностью алгоритма обычно понимают число вычислений функции, необходимое для достижения требуемого сужения интервала неопределенности. Из табл. 6.2 следует, что лучшим в этом отношении является метод Фибоначчи, а худшим — метод общего поиска. Конструктор иной раз неохотно прибегает к методу Фибоначчи, так как при его применении требуется заранее задать число вычислений значений функции. Однако он может воспользоваться методом золотого сечения. Как правило, оказывается, что методы Фибоначчи и золотого сечения, обладающие высокой эффективностью, наиболее подходят для решения одномерных унимодальных задач оптимизации. [c.152]
В настоящей главе изучение движения простейшей модели снаряда в виде одномерного движения материальной точки обобщено на случай двух- и трехмерного движения. Отсюда естественно возникает проблема оптимизации траектории, которая оказывается тесно связанной с целым рядом смежных проблем. Простейшей задачей из этого круга проблем является задача определения оптимального управления, когда динамические характеристики снаряда заданы и требуется найти такую траекторию, которая оптимизирует некоторую заданную величину. Для случаев, когда поле сил зависит от скорости и координат снаряда, дана общая постановка задачи оптимизации траектории, а в случаях, когда силовое поле однородно или когда сила зависит от расстояния линейно, оказывается возможным получить решение в замкнутой форме. Это особенно важно в применении к баллистическим снарядам (нанример, снарядам дальнего радиуса действия класса земля — земля или носителям спутников), где расстояние, проходимое за время выгорания топлива, мало по сравнению с земным радиусом. Простой и в то же время почти оптимальной траекторией в этих случаях оказывается траектория гравитационного разворота при движении снаряда в плотной атмосфере и затем переход на траекторию, определяемую соотношением (2.6). Хотя точного решения уравнений движения по траектории гравитационного разворота не существует, все же можно построить ряд графиков, позволяющих во многих случаях подбирать требуемые значения параметров. Если ограничиться лишь получением решений, удовлетворяющих условию стационарности, то обычными методами вариационного исчисления можно исследовать те задачи оптимизации, в которых масса снаряда, программа скорости истечения и время выгорания, так же как и программа управления, являются варьируемыми функциями. Для того чтобы найти решения, являющиеся действительно максимальными или минимальными в определенном смысле, нужно проводить специальное исследование каждого отдельного случая, так как не всегда решение, удовлетворяющее требованию стационарности, является оптимальным, и наоборот. В тех задачах, где скорость истечения есть известная функция времени, как, например, это имеет место в жидкостных ракетных двигателях, из анализа следует лишь то, что оптимальной программой для М ( ) будет, как правило, программа импульсного сжигания топлива. Поэтому для получения практически интересных результатов необходимо проводить более глубокий анализ, с учетом таких факторов, как параметры двигателя, топливных баков и т. д., при одновременном учете характера траектории полета снаряда. Для выполнения такого рода анализа используется схема расчета, где анализ различных элементов Конструкции и групп уравнений (одной [c.63]
Однако для практических задач такой подход обычно неприменим из-за отсутствия аналитических выражений функции АНок Хк), незнания свойств диффе-ренцируемости и т. п. Поэтому для выбора Хц обычно пользуются численными методами одномерной оптимизации, реализуемыми на ЭВМ. Наиболее простыми среди них являются методы перебора, описанные ниже и позволяющие приближенно с желаемой точностью определить оптимальное Хк. Однако с повышением точности количество вычислений АНок Хк) возрастает, и поэтому такой путь не всегда приемлем, хотя он дает возможность определения абсолютного оптимума (рис, П.2, б). [c.242]
Таким образом, методы покоординатного поиска могут иметь различную модификацию в зависимости от выбора последовательности координатных осей, способов преодоления оврагов ( гребней ) и т. п. Используя эти модификации, а также возможные вариации методов одномерной оптимизации, можно построить ряд эффе1 тивных алгоритмов направленного поиска, изложенных в [79, 80]. [c.244]
Сходимость метода Ньютона гарантируется при условии выпуклости минимизируемой функции и ее непрерывной дифференци-руемости до второго порядка [218]. Величину а можно определить либо путем одномерной минимизации вдоль направления задаваемого (5.36), либо более просто в результате проверки соотношения givh+Pk 2Ч—g(vkXfiPkg i Vk) 2 , 0Сравнительная оценка методов безусловной оптимизации гладких функций имеется в [96, 216], там же приведены результаты численных экспериментов. [c.148]
В многозтапных методах каждый щаг поиска осуществляется изменением одного или нескольких параметров из полного их числа и. К таковым относится группа методов покоординатного поиска, основанных на использовании одномерного поиска экстремума Q по каждому параметру х., и метод динамического программирования, в соответствии с которым функция цели разбивается на составляющие, которые последовательно оптимизируются на различных этапах расчета, чем и достигается решение задачи оптимизации в целом. [c.152]
Работа с моделью. В рассматриваемой задаче для на- хождения оптимального варианта конструкции теплообменника варьируют два параметра 1 и гакв Дв программе соответственно Ш и/02). В связи с этим говорят о двумерной задаче оптимизации. Простейшим методом решения таких многомерных задач является алгоритм покоординатного спуска. Его идея заключается в последовательном циклическом применении одномерного поиска для каждого варьируемого параметра. Проще всего проиллюстрировать метод покоординатного спуска с помощью распечатки, полученной на ЭВМ (рис. 5.21). Поиск был начат с начальной (базовой) точки 01 ==0,08 02=0,04. Сначала осуществлялся спуск вдоль координаты 02 при фиксированном значении 01 = 0,08, и в точке 02 = 0,06 было достигнуто наименьшее значение целевой функции 2=212. Затем спуск проводился вдоль координаты 01 при фиксированном значении 02 = 0,06. [c.249]
Хотя задача одномерной оптимизацип является частью более общей задачи многомерной оптимизации, она так часто встречается в процессе конструирования и обладает столь ярко выраженной спецификой, что мы сочли целесообразным рассмотреть ее отдельно. В следующей главе рассматриваются более сложные методы многомерного поиска оптимальных решений. [c.159]
Оптимизация одномерного параметрического ряда методом динамического программирования. Метод построения оптимального одномерного параметрического ряда методами динамического профаммирования разработан Э. X. Шмади и В. Т. Дементьевым [32]. Математическая модель оптимизации параметрического ряда сводится к следующему. [c.438]
FREDOM — пакет автоматизированного проектирован 1я на основе классических методов (FREquen y DOMain), предназначенный для анализа и синтеза одномерных систем управления. В пакете предусмотрены средства для моделирования, исследования устойчивости, графических методов расчета на основе логарифмических частотных характеристик, корневых годографов и годографов Найквиста, синтеза корректирующих устройств, понижения порядка модели и оптимизации, а также вспомогательные методы линейной алгебры и теории преобразования [c.321]
mash-xxl.info