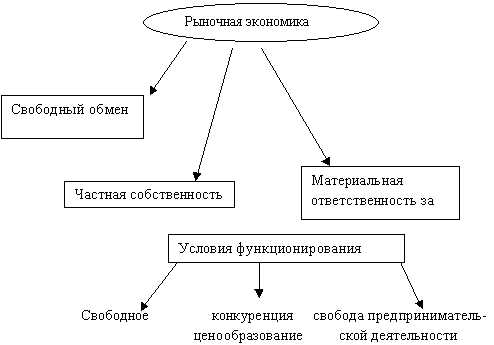
3.2.2. Оптимизация сетевого графика по временным параметрам. Оптимизация размеров и времени выполнения разработки по
6. Оптимизация сетевого графика
Разработанная сетевая модель может быть оптимизирована, то есть, - возможно сокращение продолжительности критического пути.
Основными критериями оптимизации являются:
минимизация стоимости всего комплекса работ при заданном времени выполнения проекта;
сокращение величины критического пути за счет перераспределения ресурсов;
уменьшение пиковых значений потребляемых ресурсов за счет изменения начальных сроков некритических путей.
Наиболее распространенным способом оптимизации является сокращение критического пути за счет параллельного (одновременного), где это возможно, выполнения некоторых работ по проекту.
Такая оптимизация, конечно, не снижает общей трудоемкости, однако будут удовлетворены требования по срокам разработки и за счет уменьшения времени реализации проекта будут снижены расходы, непосредственно связанные с продолжительностью работ (например, затраты на аренду, коммунальные и другие услуги временного характера). Таким образом, сокращение времени выполнения работ (критического пути) является одним из способов уменьшения затрат на проект.
Анализ сетевого графика позволяет перераспределять трудовые ресурсы. Так, например, изменяя сроки начала работ, не входящих в критический путь, можно обеспечить загрузку свободных на этот момент исполнителей. Этим осуществляется более равномерное по численности участие сотрудников в течение всего времени выполнения проекта.
Таким образом, формируют новый сетевой график (после оптимизации) проекта и определяют новое значение времени его выполнения.
Разработка календарного плана выполнения назначенных работ
Для иллюстрации последовательности проводимых работ проекта применяют ленточный график (календарно-сетевой график или диаграмму Гантта). На диаграмме Гантта на оси Х показывают календарные месяцы от начала проекта до его завершения. По оси Y - выполняемые этапы работ. Вариант изображения диаграммы Гантта представлен на рис.2.
Рис. 2. Вариант изображения диаграммы Гантта
Если отдельные этапы проекта могут выполняться параллельно различными исполнителями, то они отображается в виде нескольких нумерованных отрезков (или прямоугольников), размещенных на временных интервалах, как показано на рис. 2.
Анализ структуры затрат на реализацию проекта и расчет его целевых экономических показателей
В рамках выполнения организационно-экономической части дипломного проекта студентам предлагается на выбор два варианта определения структуры затрат проекта и расчета его ключевых экономических показателей.
1 Вариант – агрегатный метод расчета (проводится в условиях ограниченной информации)
Расчет стоимости разработки продукта проекта (системы, конструкции).
Стоимость разработки продукта в наукоемких промышленных отраслях традиционно включает затраты на следующие этапы, проводимые в рамках ОКР:
Разработка технического и эскизного проектов.
Технологическая подготовка производства.
Разработка и выпуск конструкторской и эксплуатационной документации.
Изготовление стендового оборудования для проведения испытаний.
Автономные и комплексные испытания.
Изготовление/поставка необходимых КИ.
Изготовление опытных образцов и корректировка конструкторской документации по результатам испытаний.
При выборе данного метода рекомендуется использовать метод оценки затрат на ОКР по базовым техническим параметрам. Для этого потребуется следующая исходная информация:
целевое назначение продукта проекта;
его масса;
год начала испытаний;
сведения о степени преемственности вновь создаваемого опытного образца разрабатываемой конструкции от аналога.
В этом случае затраты на ОКР определяют по формуле:
где - коэффициент, учитывающий увеличение стоимости ОКР за счет повышения конструктивно-технологической сложности конструкции, применения новых более эффективных материалов и комплектующих изделий, ужесточения требований отработке при сохранении современных направлений и темпов совершенствования создаваемого образца;
- коэффициент новизны, учитывающий снижение затрат за счет преемственности конструктивных элементов создаваемого образца от аналога;
- удельная стоимость разработки конструкции;
- масса готового продукта.
Указанные данные предоставляются студенту предприятием– производителем продукции заданного типа.
Этот метод использует коэффициенты, полученные на основе статистических данных. Метод не раскрывает оценки составляющих затрат и поэтому, он может быть использован для расчетов в условиях ограниченного объема информации.
Расчет стоимости изготовления продукта проекта (системы, конструкции).
Этот расчет рекомендуется проводить методом удельных стоимостей. Для этого необходима информация по массам систем/подсистем изготавливаемого продукта (массы систем, составляющих основу конструкции) и удельным стоимостям работ по их изготовлению, полученная на основании статистических данных (данные предоставляются предприятием – производителем). Стоимость изготовления рассчитывается арифметическим сложением стоимостей разработки всех составляющих систем/подсистем с учетом корректировки итоговой стоимости на поправочные коэффициенты, установленные производителем.
Расчет стоимости подготовительных мероприятий для выведения вновь созданного продукта на рынок.
Для случаев отсутствия прямой реализации готового продукта проекта заказчику – при создании, например, спутниковых систем/космических аппаратов (КА) – рассчитывается стоимость работ по подготовке КА к пуску (технических, монтажных и др.) и стоимости запуска (расчет включает определение суммарной стоимости работ по осуществлению реального запуска спроектированного производителем КА).
В общем же случае данный расчет включает определение суммарных затрат по статьям на необходимые дополнительные (маркетинговые) мероприятия для успешного выведения вновь созданного продукта на отраслевой рынок.
Расчет суммарных затрат по проекту и оценка их экономической целесообразности с точки зрения текущего состояния финансовой платежеспособности производителя.
studfiles.net
Оптимизация сетевых моделей
Содержание
| Введение | 2 |
| 1. Основные методические положения | 3 |
| 2. Практическая часть | 11 |
| Вычисление параметров сетевого графика графическим методом | 12 |
| Вычисление параметров сетевого графика табличным методом | 14 |
| Оптимизация сетевого графика по времени | 16 |
| Оптимизация сетевого графика по ресурсам | 21 |
| Заключение | 22 |
| Приложение 1 – Карта сетевого проекта | 23 |
| Приложение 2 – Карта сетевого проекта после оптимизации по времени | 24 |
| Приложение 3 – Карта сетевого проекта после оптимизации по ресурса | 25 |
ВведениеЦелью данной работы является развитие навыков построения, расчета, анализа и оптимизации сетевого графика.
Работа включает в себя:
1. расчет ожидаемой продолжительности выполнения работ
2. построение топологической модели сетевого графика
3. расчет параметров сетевого графика одним из предложенных методов
4. построение карты проекта сетевого графика
5. расчет показателей КH i, j, X
6. оптимизация сетевого графика по времени
7. расчет параметров оптимизированного по времени сетевого графика
8. построение карты проекта оптимизированного сетевого графика
9. расчет показателей КH i, j, X для оптимизированного графика
10. оптимизация сетевого графика по ресурсам1.Основные методические положенияДля планирования и управления комплексами работ применяются системы сетевого планирования и управления (СПУ). СПУ основано на построении графического изображения определенного комплекса работ, отражающего их логическую последовательность, взаимосвязь и длительность, с последующим анализом и оптимизацией разработанного графика.
Сетевая модель (график, сеть) представляет собой графическую модель, в которой изображаются взаимосвязи и результаты всех работ планируемого комплекса.
Основными элементами графика являются события и работы.
Событие – это результат выполнения одной или нескольких работ. Событие – это свершившийся факт, оно занимает лишь один момент во времени и не имеет продолжительности. Оно указывает на начало каких-либо работ и может быть одновременно итогом завершения других работ. Различают две группы событий: для всей группы работ – исходное I и завершающие J, а для каждой работы – начальное i и конечное j.
В сетевом графике событие изображается геометрической фигурой (кружком, квадратом и т.д.), в котором указывается порядковый номер или шифр события, а иногда и название события.
Работами называются любые процессы, действия, приводящие к достижению определенных результатов (событий).
Работа может быть действительной или фиктивной. Действительная работа – это процесс, требующий затрат времени и исполнителей. Графически действительная работа изображается сплошной линией со стрелкой, которая означает затрату времени, необходимого для выполнения данной работы. Затрачиваемое на работу время обозначается над стрелкой, а число исполнителей под стрелкой. Фиктивная работа устанавливает только логическую связь между работами, она не требует затрат времени и исполнителей, на сетевом графике изображается пунктирной линией.
Любая последовательность в сетевом графике, в которой конечное событие одной работы совпадает с начальным событием следующей за ней работы, называет путем. В сетевом графике следует различать несколько видов путей:
а) от исходного события до завершающего события – полный путь
б) от исходного события до данного – путь, предшествующий данному событию
в) от данного события до завершающего – путь, последующий за данным событием
г) между двумя какими-либо промежуточными событиями i и j – путь между событиями i и j
д) путь между исходным и завершающим событием, имеющий наибольшую продолжительность – критический путь.
Сетевое планирование и управление включает семь этапов:
1. составление перечня работ, которые надлежит выполнить по объекту разработки для получения конечной цели.
2. установление топологии сети
3. построение сетевого графика
4. определение продолжительности работ
5. расчет параметров сети
6. анализ сети и оптимизация сетевого графика
7. функционирование сетевой модели.Правила построения сетевого графика:
1. При построении сетевого графика необходимо соблюдать технологическую последовательность выполняемых работ планируемого комплекса.
2. В сетевом графике не должно быть пересекающихся стрелок.
3. Направление стрелок в сетевом графике должно быть слева на право.
4. В сетевом графике не должно быть событий, которым не предшествует ни одна работа (кроме исходной).
5. В построенном сетевом графике должно быть одно начальное и одно завершенное событие.
6. В сетевом графике необходимо соблюдать последовательность в нумерации событий от исходного, которому обычно присваивается нулевой номер, к завершающему. При этом для любой работы i-j одним из условий правильного построения сетевого графика является обязательным выполнение неравенства i<j.Основные параметры сетевого графика.
К основным параметрам сетевого графика относятся критический путь, резервы времени событий и работ. Эти параметры являются исходными для получения ряда дополнительных характеристик, а так же для анализа сети.
1. Критическим путем называют наибольший по продолжительности из всех путей сетевого графика от исходного события до завершающего. В сетевом графике имеются и другие пути, опирающиеся на исходное и завершающее события (полные пути), которые могут либо полностью проходить вне критического пути, либо частично совпадать с критической последовательностью работ. Эти пути называются не напряженными. Ненапряженные пути – это полные пути сетевого графика, которые по продолжительности меньше критического пути.
Ненапряженные пути обладают важным свойством: на участках, не совпадающих с критической последовательностью работ, они имеют резервы времени. Это означает, что задержка в совершении событий, не лежащих на критическом пути, до определенного момента не влияет на срок завершения разработки в целом. Критические пути резервами времени не располагают.
2. Резервы времени события – это такой промежуток времени, на который может быть отсрочено совершение этого события без нарушения сроков завершения разработки в целом.
Резерв времени события Ri определяет как разность между поздним Тпi и ранним Трi сроками наступления события:
Ri = Тпi - Трi (1)
3. Поздний срок Тпi – это такой срок завершения i-го события, превышение которого вызовет задержку завершения события.
Ранний из возможных сроков совершения i-го события Трi – минимальный срок, необходимый для выполнения всех работ, предшествующих данному событию.
Ранний срок совершения события i определяется как продолжительность во времени максимального из путей Lmax, ведущих от исходного события I до данного события i:
Трi = t [ L (I – i)max ] (2)
Поздний срок события I определяется по следующей формуле:
Тпi = t (Lкр) – t [ L ( i – C)max ] (3)
Путь, соединяющий события с нулевыми резервами времени, является критическим.
4. Резервами времени так же располагают работы. Зная ранние и поздние сроки наступления событий, можно для любой работы (i,j) определить ранние и поздние сроки начала и окончания работ.
Ранний срок начала работ:
Tрн i,j = Трi (4)
Поздний срок начала этой работы:
Tпн i,j = Тпσ – t i,j (5)
Ранний срок окончания работ:
Tро i,j = Трi + t i,j (6)
Поздний срок окончания работ:
Tпо i,j = Тпj (7)
5. Разница во времени между длиной критического пути t ( Lкр ) и длиной любого другого пути t ( Li ) называется полным резервом времени пути. Он равен:
R (Li) = t ( Lкр ) – t ( Li ) (8)
Полный резерв пути показывает, насколько могут быть увеличены продолжительности всех работ, принадлежавших пути Li.
6. Полный резерв времени работы Rп i,j показывает, сколько имеется в запасе времени для выполнения данной работы, на которое можно увеличить продолжительность данной работы, не изменяя при этом продолжительности данного пути:
Rп i,j = Тпj - Трi - t i,j (9)
7. У отдельных видов работ помимо полного резерва времени имеется свободный резерв времени Rс i,j, являющийся частью резерва. На время этого резерва можно увеличить продолжительность работы, не изменяя ранних сроков начала последующих работ.
Rс i,j = Трj - Трi - t i,j (10)
Резервы времени работ, особенно свободный, позволяют маневрировать сроками начала и окончания работ, их продолжительностью.Определение продолжительности работ.При построенной сетевой модели для каждой работы определяется ожидаемая продолжительность ее выполнения, которая проставляется над соответствующей стрелкой в графике. Для определения продолжительности работ пользуются установленными нормами времени, при их отсутствии используют систему вероятностных оценок. В таких случаях ожидаемое время выполнения работ ti,j определяют на основе экспертных оценок по формуле
(11)
Дисперсия, или мера разброса для принятого в СПУ закона распределения:
(12)
Для двух оценок:
(13)
(14)
где tmin – минимально возможное время выполнения работ;
tmax – максимально возможное время выполнения работ;
tнв – наиболее вероятное время выполнения работ.
Расчет параметров сетевого графика графическим методом.
Существует несколько методов расчета сетевых графиков: графический, табличный, матричный, метод Форда и др.
Графический метод можно применять в тех случаях, когда число событий невелико (до 15-20). При этом каждый кружок, изображающий событие, делится на четыре сектора (рис.1).
coolreferat.com
3.2.2. Оптимизация сетевого графика по временным параметрам.
Если первоначальный вариант сетевого графика не обеспечивает соблюдение директивного срока, следует изменить планируемые параметры сетевой модели, т.е. оптимизировать его.
Рассчитаем вероятность свершения конечного события в заданный срок Рк; при этом 0,35 ≤ Рк≤ 0,б5. Если Рк< 0,35, то опасность нарушения срока настолько велика, что необходимо повторное планирование с перераспределением ресурсов. При Рк >0,65 работы критического пути имеют избыточные ресурсы, что вызывает необходимость проведения повторного расчета сетевого графика. Этот расчет сводится к вычислению вероятности попадания в область кривой нормального распределения при заданном математическом ожидании и дисперсии некоторой случайной величины, представляющей длину критического пути (рис. 4.3.).
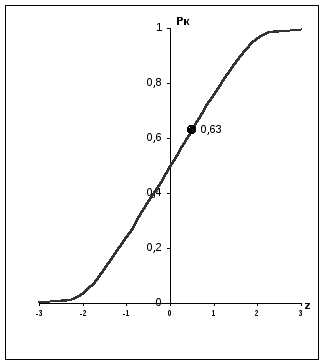
Рис. 3.3. Кривая нормального распределения.
Вероятность рассчитывается через меру разброса ожидаемого времени выполнения работы (т.е. дисперсию работы, лежащей на критическом пути), определяемую по формуле:
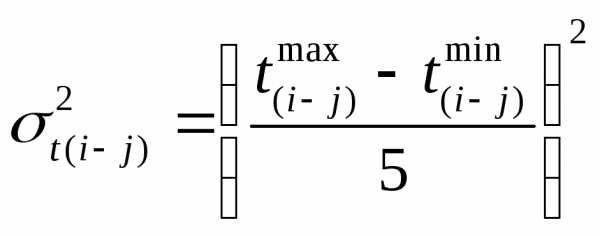
Вычислим дисперсии всех работ, лежащих на критическом пути:
| σ0-12= 0,04 σ1-22= 0,04 σ2-32= 0,04 σ2-42= 0,04 σ2-52= 0,36 | σ5-72= 1,96 σ2-62= 1 σ6-72= 0,64 σ7-82= 1 σ8-92= 1 | σ9-102= 0,64 σ10-112= 0,64 σ11-122= 4 σ12-172= 0,36 σ3-132= 0,36 | σ13-142= 0,36 σ4-152= 0,64 σ15-162= 0,36 σ17-182= 0,64 σ17-202= 0,64 | σ18-192= 0,16 σ20-212= 0,16 σ19-222= 0,16 σ22-232= 0,16 σ23-242= 0,04 σ24-252= 0 |
Аргумент нормальной функции распределения вероятностей определяется по формуле:
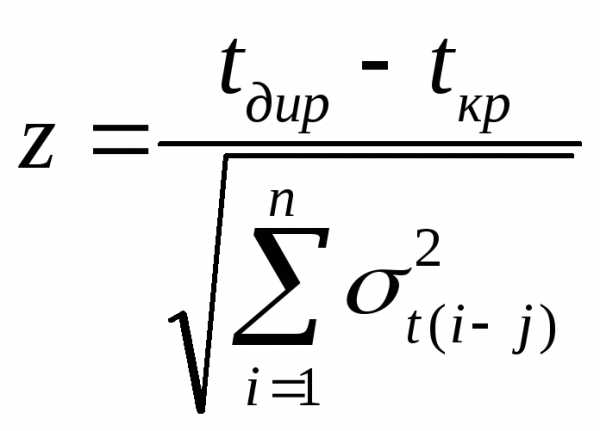
В соответствии с временем, отведенным на дипломное проектирование, директивный срок, за который должно быть выполнено проектирование задаем как Lдир = 105 дней.
Z= (105-103)/3,93 = 0,51
Найдя Z, по графику функции нормального распределения (рис.4.3.) определим вероятность свершения завершающего события в заданный срокРк =0,63. Первоначальный вариант сетевого графика обеспечивает соблюдение директивного срока, поэтому в изменении параметров сетевой модели нет необходимости.
3.2.3. Оптимизация сетевого графика по трудовым ресурсам.
При оптимизации анализируем структуру графика, трудоемкость и длительность выполнения каждой работы, вероятность завершения разработки в заданный срок и загрузку исполнителей. Распределение ресурсов (исполнителей) , связанное со сроками работ, определим путем построения "карты проекта" или графика потребности в исполнителях.
Линейная диаграмма и график ежедневной потребности в исполнителях - "карта проекта" до оптимизации приведены на рис.4.4. Работы критического пути расположены на одной линии. Из графика видно, что без проведения оптимизации выполнение проекта на некоторых этапах требует до семи исполнителей, причем с неравномерной загрузкой. Путем использования имеющихся резервов времени работ можно снизить число необходимых исполнителей до трех.
Линейная диаграмма и "карта проекта" после оптимизации приведены на рис.3.5. График оптимизированной сетевой модели приведен на рис.3.6.
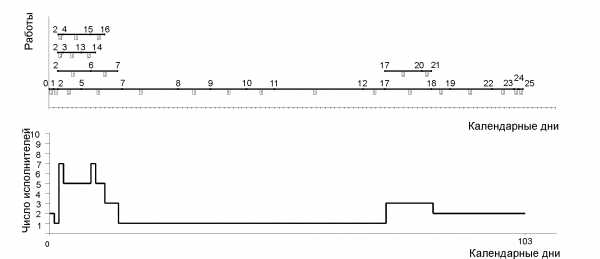
Рис. 3.4. Линейная диаграмма и график ежедневной потребности
studfiles.net
Часть 1. Построение и расчет моделей сетевого планирования и управления 4
| Министерство общего и профессионального образования Российской Федерации Таганрогский государственный радиотехнический университет |

Таганрог 1999
ББК
Составитель:Т.В. Алесинская
Методические указания к лабораторной работе Моделирование систем сетевого планирования и управления по курсу "Экономико-математические модели и методы":Таганрог:Изд-во ТРТУ, 1999. 36с.
В методических указаниях к лабораторным работам рассмотрены вопросы построения, расчета и оптимизации сетевых моделей, приведены конкретные примеры реализации рассмотренных методик.
Предлагаемые лабораторные работы рекомендуются для использования в курсе Экономико-математические методы и модели. Для студентов экономических специальностей.
Табл. 13. Ил. 13. Библиогр.:5 назв.
Рецензент Непомнящий Е.Г., доцент кафедры менеджмента, экономики и маркетинга ТРТУ.
Содержание
1.1. ЦЕЛЬ РАБОТЫ 4
1.2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 4
1.3. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ 4
1.3.1. Введение 4
1.3.2. Основные понятия и определения 5
1.3.3. Временные параметры событий 7
1.3.4. Временные параметры работ и путей 8
1.3.5. Пример построения и расчета сетевой модели 9
1.4. КОНТРОЛЬНЫЕ ВОПРОСЫ 12
1.4.1. Зачетный минимум 12
1.4.2. Дополнительные вопросы 12
Часть 2. ОПТИМИЗАЦИЯ СЕТЕВЫХ МОДЕЛЕЙ ПО КРИТЕРИЮ "МИНИМУМ ИСПОЛНИТЕЛЕЙ" 13
2.1. ЦЕЛЬ РАБОТЫ 13
2.2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 13
2.3. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ 13
2.3.1. Методика оптимизации загрузки сетевых моделей 13
2.3.2. Пример проведения оптимизации сетевой модели по критерию "Минимум исполнителей" 14
2.4. КОНТРОЛЬНЫЕ ВОПРОСЫ 17
2.4.1. Зачетный минимум 17
2.4.2. Дополнительные вопросы 17
Часть 3. ОПТИМИЗАЦИЯ СЕТЕВЫХ МОДЕЛЕЙ ПО КРИТЕРИЮ "ВРЕМЯ-ЗАТРАТЫ" 17
3.1. ЦЕЛЬ РАБОТЫ 17
3.2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 18
3.3. ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ 18
3.3.1. Методика оптимизации сетевых моделей по критерию "Время - затраты 18
3.3.2. Пример проведения оптимизации сетевой модели по критерию "Время - затраты" 20
3.4. КОНТРОЛЬНЫЕ ВОПРОСЫ 26
3.4.1. Зачетный минимум 26
3.4.2. Дополнительные вопросы 26
Часть 4. ВОЗМОЖНОСТИ ПРОГРАММЫ РАСЧЕТА И ОПТИМИЗАЦИИ СЕТЕВЫХ МОДЕЛЕЙ ON_BEST 27
5. ВАРИАНТЫ 27
ЛИТЕРАТУРА 35
Часть 1. ПОСТРОЕНИЕ И РАСЧЕТ МОДЕЛЕЙ СЕТЕВОГО ПЛАНИРОВАНИЯ И УПРАВЛЕНИЯ
1.1. ЦЕЛЬ РАБОТЫ
Приобретение навыков построения и расчета временных параметров моделей сетевого планирования и управления.
1.2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Согласно номеру своего варианта получите следующие исходные данные: - время нормальной длительности каждой работы сетевой модели и описание упорядочения этих работ.
2. В соответствии с правилами построения сетевых графиков и на основе исходных данных Вашего варианта постройте сетевую модель (см. п.1.3.2), затем пронумеруйте события полученной сети.
3. В соответствии с методиками, описанными в п.1.3.3 и п.1.3.4.
рассчитайте и отобразите на сетевом графике временные параметры событий: ранний и поздний срок свершения события, резерв события;
рассчитайте и представьте в таблице временные параметры работ: время раннего и позднего начала работ; время раннего и позднего окончания работ; полный и свободный резервы работ.
4. Покажите преподавателю результаты своих построений и расчетов, после чего проведите аналогичные расчеты с помощью компьютера (см. п.4). Сравните результаты ручного и компьютерного расчета, а при необходимости, выявите и устраните причины ошибок в Ваших расчетах.
5. Отчет по лабораторной работе должен содержать:
номер варианта;
исходные данные варианта;
сетевой график с отображенными на нем временными параметрами событий;
таблицу с кодами и временными параметрами работ.
1.3. Теоретическая часть
1.3.1. Введение
Сетевое Планирование и Управление - это комплекс графических и расчетных методов, организационных мероприятий, обеспечивающих моделирование, анализ и динамическую перестройку плана выполнения сложных проектов и разработок, например, таких как: строительство и реконструкция каких-либо объектов; выполнение научно-исследовательских и конструкторских работ; подготовка производства к выпуску продукции; перевооружение армии; развертывание системы медицинских или профилактических мероприятий.
Характерной особенностьютаких проектов является то, что они состоят из ряда отдельных, элементарныхработ. Они обуславливают друг друга так, что выполнение некоторых работ не может быть начато раньше, чем завершены некоторые другие. Например, укладка фундамента не может быть начата раньше, чем будут доставлены необходимые материалы; эти материалы не могут быть доставлены раньше, чем будут построены подъездные пути; любой этап строительства не может быть начат без составления соответствующей технической документации и т.д.
Сетевое Планирование и Управление включает три основных этапа:
Структурное планирование;
Календарное планирование;
Оперативное управление.
Структурное планированиеначинается с разбиения проекта на четко определенные операции, для которых определяется продолжительность. Затем строится сетевой график, который представляет взаимосвязи работ проекта. Это позволяет детально анализировать все работы и вносить улучшения в структуру проекта еще до начала его реализации.
Календарное планированиепредусматривает построение календарного графика, определяющего моменты начала и окончания каждой работы и другие временные характеристики сетевого графика. Это позволяет, в частности, выявлять критические операции, которым необходимо уделять особое внимание, чтобы закончить проект в директивных срок. Во время календарного планирования определяются временные характеристики всех работ с целью проведения в дальнейшемоптимизациисетевой модели, которая позволит улучшить эффективность использования какого-либо ресурса.
В ходе оперативного управленияиспользуются сетевой и календарный графики для составления периодических отчетов о ходе выполнения проекта. При этом сетевая модель может подвергаться оперативной корректировке, вследствие чего будет разрабатываться новый календарный план остальной части проекта.
studfiles.net
Оптимизация – ваш злейший враг
Автор: Dr. Joseph M. NewcomerПеревод: Андрей ЛягусскийИсточник: "Optimization - your worst enemy"Материал предоставил: RSDN Magazine #6-2004
Опубликовано: 25.06.2005Исправлено: 30.06.2005Версия текста: 1.0Для начала позвольте привлечь ваше внимание к моей персоне. Я серьезно!
Немного общей информации: моя докторская работа была одной из первых работ по автоматической генерации оптимизирующих компиляторов из формального машинного описания («Машинно-независимая генерация оптимального кода», университет Карнеги-Меллона (в дальнейшем CMU – прим. перев.), кафедра информатики, 1975). После защиты докторской я провел три года в CMU в качестве ведущего исследователя многопроцессорной компьютерной системы Cmmp, использовавшей нашу местную операционную систему Hydra, безопасную и высокопроизводительную. Затем я вернулся к исследованию компиляторов на проекте PQCC (компилятор компиляторов промышленного уровня), который, в конечном счете, привел к основанию лабораторий Tartan (сейчас поглощены Texas Instruments) – компании по разработке компиляторов, в которой я работал в инструментальной группе. Я провел полтора десятка лет за написанием и использованием инструментов измерения производительности.
Это эссе состоит из нескольких частей и представляет по большей части мой собственный опыт. Истории, которые я рассказываю, произошли на самом деле. Имена не изменялись, правда, парочку из них пришлось изъять.
Оптимизация: Что и Когда
Достаточно квалифицированный программист вряд ли напишет очень неэффективный код. По крайней мере, неосознанно. Оптимизация – это то, чем вы занимаетесь, когда текущая производительность вас не устраивает. Иногда оптимизировать легко, иногда сложно. Иногда оптимизация является частью оригинального дизайна, иногда приходится попирать все ваши красивые абстракции, заложенные в классовой иерархии. Но всегда, я повторюсь, всегда мой опыт показывал, что не сыскать программиста, который был бы способен предсказать или проанализировать узкие места в производительности без всякой информации. Не имеет значения, что вы думаете, будто знаете, где проблемы с производительностью. Вы будете весьма удивлены, узнав, что они спрятаны в совсем другом месте.
Итак, вы оптимизируете потому, что у вас проблемы с производительностью. Иногда это оптимизация вычислений: манипуляция картинкой слишком медленна. Иногда это оптимизация доступа к данным: слишком много времени нужно для загрузки данных. А иногда это оптимизация алгоритмов: вы ошиблись в алгоритмической основе. Если вы не понимаете разницу между квадратичной сложностью сортировки, и сложностью n log n, у вас наверняка проблемы, хотя само по себе такое знание совершенно бесполезно.
Пару лет назад я работал над сложной программой, которая должна была выполнять семантические кросс-проверки между «выражениями» в коде программы и «объявлениями». Я обнаружил, что вычисления имеют сложность n3 (вообще-то m*n2, но в большинстве случаев m было сравнимо с n). И здесь у вас три пути:
- Наивный подход. Вы даже не осознаете, что у вас проблема с n3-сложностью. Скорее всего, вы столкнетесь с определенными трудностями, потому что если это действительно узкое место, вы даже не будете знать об этом.
- Формальный академический подход. Вы осознаете, что у вас проблема с n3-сложностью, вы знаете, что такая сложность – это сущее зло, и поэтому переписываете свои алгоритмы.
- Инженерный подход. Вы осознаете, что у вас проблема с n3-сложностью, но вы берете подходящий инструмент и начинаете исследовать, как обнаруженная сложность вычислений сказывается на производительности системы.
Единственный верный путь при оптимизации – это инженерный подход. Я исследовал производительность, и на самом большом «реальном» примере, который у нас был, я обнаружил, что практически всегда n равнялось 1, иногда 2, редко 3, и только один раз 4. И это были слишком маленькие значения, чтобы проявлять беспокойство. Конечно, сложность алгоритма равнялась n3, но при этом значения n были столь малы, что необходимости переписывать код не возникло. Переписывание кода являло собой сложную задачу, задержало бы весь проект на пару недель и потребовало бы дополнительно по нескольку указателей в каждом узле дерева в и без того тесном адресном пространстве миникомпьютера.
Также я написал распределитель памяти, который все использовали. И я провел кучу времени, оттачивая его производительность - чтобы это был самый быстрый распределитель в своем классе. Все эти приключения детально описаны в книге «IDL: The Language and its Implementation», в настоящий момент, увы, уже вышедшей из печати (Nestor, Newcomer, Gianinni and Stone, Prentice-Hall, 1990). Одна группа, использовавшая этот распределитель, также использовала специальный инструмент для измерения производительности на Unix. Эта программа определяла, где в данный момент крутится счетчик выполнения (program counter), и через достаточное время предоставляла «гистограмму плотности», показывающую, сколько времени профилированная программа проводила в каждом блоке кода. И этот инструмент показал, что львиную долю своего времени выполнения программа проводила в распределителе памяти. Для меня это не имело значения, но все пальцы указывали в моем направлении.
Тогда я написал небольшую зацепку в распределителе, которая подсчитывала количество его вызовов. И этот счетчик показал, что распределитель вызывался более 4 000 000 раз. Ни один вызов не занимал больше времени, чем минимальный измеримый интервал в 10 микросекунд (приблизительно десять инструкций на нашей 1-MIPS машине), но 40 000 000 микросекунд – это 40 секунд. Конечно, общее время было еще больше, потому что надо учесть 4 000 000 операций освобождения памяти, которые были, конечно, быстрее, но все-таки распределитель занимал более 50% времени выполнения всей программы.
Почему такое происходило? Потому что, по неизвестным для программистов причинам, критическая функция, которую они вызывали во внутреннем цикле своих алгоритмов, выделяла блок памяти в 5-10 байт, делала свою работу и освобождала его. Когда мы изменили это поведение на 10-байтовый локальный стековый буфер, время, занимаемое распределителем по отношению к общему времени выполнения всей программы снизилось до 3%.
Без дополнительной информации мы не смогли бы определить, почему распределитель вызывался так много раз. Профилирующие инструменты, основанные на счетчике выполнения – это очень слабый класс инструментов. Выдаваемые ими результаты часто бывают подозрительными. Вы можете обратиться к моей статье «Профилирование производительности» в Dr.Dobb’s Journal за январь 1993. (только для зарегистрированных пользователей – прим. перев.)
Классический случай грубой ошибки при оптимизации несколько лет назад допустила одна из крупнейших компаний разработки программного обеспечения. Мы имели дело с их первой интерактивной системой, работающей в режиме разделения времени, и эта работа позволила нам набраться нового опыта различными способами. Одна из таких возможностей выпала на долю группы, работавшей с компилятором FORTRAN. Сейчас любой разработчик компиляторов в курсе, что чем большую хэш-таблицу он использует для поиска символов, тем значительнее будет производительность при поиске. Когда вы разрабатываете многопроходный компилятор на мэйнфрейме с 32 килобайтами памяти, в результате вы придете к относительно маленькой таблице символов, но будете использовать очень, очень хороший алгоритм хеширования, так что вероятность коллизии при хешировании уменьшается (в отличие от двоичного поиска, который имеет сложность log n, хорошая хэш-таблица имеет константное время доступа относительно некоторой плотности таблицы, так что пока вы держите плотность ниже этого порога, можно ожидать, что стоимость доступа к символу или его добавления в среднем будет равна 1 или 2. Отличная хэш-таблица (которая обычно вычисляется заранее для константных символов) имеет константное время доступа в районе 1.0 или 1.3; когда достигается значение 1.5, хеширование нужно переработать).
И вот, эта группа, работавшая с компилятором, обнаружила, что у них теперь не 32 килобайта памяти, и не 128, и даже не 512. Вместо этого у них появилось 4 гигабайта виртуального адресного пространства. «Эй, а давайте-ка сделаем действительно большую хэш-таблицу!» - завопили они от радости. «Например, как насчет таблицы в 1 мегабайт?». Сказано – сделано. Однако кроме этого у них еще был чрезвычайно изощренный компилятор, разработанный специально для маленьких, густозаселенных хэш-таблиц. В результате, так как символы были равномерно распределены по 256 4-килобайтовым страницам в этом одном мегабайте, каждая операция обращения к символу из таблицы приводила к ошибке отсутствия страницы в памяти. Компилятор оказался той еще сволочью. Когда же наконец группа решила вернуться к 64-килобайтной таблице, несмотря на то, что алгоритм стал хуже по «абсолютной» производительности с чисто алгоритмической точки зрения (больше машинных инструкций требовалось для поиска символа), он не вызывал так много ошибок при обращении к отсутствующей странице памяти, и поэтому стал работать на порядок быстрее. Так что эффекты третьей стороны имеют значение.
Кроме того, избегайте С. Нет, не скорости света. Когда мы говорим об эффективности, с алгоритмической точки зрения это записывается как C * f(n). Так, квадратичный алгоритм формально будет обозначен как C * n2, что значит «константа умноженная на квадрат количества обрабатываемых элементов». Это сокращается до O(n2), или «квадратичной сложности», а в обиходе принято опускать слово «сложность». Но никогда не забывайте, что у вас еще есть C. Когда-то давно я выполнял проект, который на выходе выдавал набор отчетов, сортированных разными способами. Для начала (а дело было еще до языка С и qsort) я просто сделал обычную пузырьковую сортировку, алгоритм со сложностью O(n2). После первичного тестирования я скормил ему немного реальных данных. Через десять минут после того, как сообщение «Обработка отчетов» появилось на консоли, все еще не было никаких результатов. Парочка простых проверок показала, что все это время программа занималась сортировкой. Ну что же, я был наказан за свою лень. Пришлось откопать доверенный алгоритм сортировки в куче (n log n), и потратить час времени, чтобы реализовать его рабочую версию в моей программе (как вы помните, еще никакого qsort не было и в помине). Закончив с реализацией, я снова запустил тест. Через семь минут после начала фазы обработки отчетов результатов еще не было. Проверки вскрыли кое-что любопытное: теперь программа большую часть времени была занята выполнением эквивалента функции strcmp, сравнивая строки. Решая проблемы с О, я просто проигнорировал С. Поэтому сначала я сделал отдельную сортировку таблицы символов, представляющих имена, и ассоциировал каждую запись с целым числом. Затем, когда нужно было сортировать подструктуры, я уже имел дело с простыми целочисленными идентификаторами. Этот прием уменьшил константу C до того порога, при котором для полной сортировки отчетов требовалось менее 30 секунд. Вторичный эффект, но весьма значимый.
Некоторые инструменты профилирования измеряют только время процессов, проведенное в пользовательском режиме выполнения, а время выполнения в режиме ядра не учитывают. Это может замаскировать ту ударную нагрузку, которую приложение перекладывает на плечи процессов в режиме ядра. К примеру, однажды мне довелось разбираться с программой, производительность которой была просто на нуле. В терминах затраченного времени никаких узких мест c помощью профайлера обнаружено не было. Однако, когда я взглянул на отладочную информацию, то увидел что процедура считывания данных вызывалась около миллиона раз, что не является исключительным при обработке мегабайтов данных, но меня это насторожило. Посмотрев на выполнение кода при отладке, я обнаружил что каждый раз когда процедура вызывалась, она обращалась к ядру чтобы прочитать один байт из файла! Заменив такое поведение на работу с 8-килобайтным буфером, я получил 30-кратное увеличение производительности. Вывод из этого такой: время выполнения в режиме ядра имеет значение. Не случайно графический интерфейс пользователя начиная с NT 4.0 больше не является пользовательским процессом, а интегрирован в ядро. Процессы ядра диктуют уровень производительности.
Поэтому ответ на вопрос «что оптимизировать?» очень прост: оптимизировать надо то, что забирает слишком много времени. В то же время локальные оптимизации, игнорирующие общие проблемы с производительностью абсолютно бесполезны. И эффекты первого порядка (например, время выполнения, занятое распределителем) могут быть побочны. Семь раз отмерь – один раз отрежь.
Процветающая жизнь – лучшее отмщение
Вообще-то это просто небольшое отступление, немного приправленное личными воспоминаниями. Можете сразу переходить к следующей части, если не хотите читать это. Я вас предупредил.
Когда-то, во времена зарождения языка C, его распределитель памяти был самым слабым из существующих. Это был алгоритм «первый попавшийся», то есть он работал следующим образом: распределитель просматривал все узлы в списке блоков памяти, и первый же попавшийся свободный блок, который был не меньше нужного размера, разбивался на две части – одна возвращалась по запросу, вторая (общий размер блока минус запрошенный размер) возвращалась в список свободных узлов. «Преимущества» этого очевидны – очень низкая скорость работы и дикая фрагментация памяти. В действительности это хуже, чем вы можете себе представить. При выделении памяти приходилось пробегать весь список блоков, игнорируя уже выделенные. Поэтому при увеличении числа блоков производительность падала, а блоки становились все меньше и были непригодны к использованию. Они отнимали время без всякой реальной пользы.
Я как-то работал в CMU по годичному контракту. И мое первое впечатление от использования среды Unix выражалось в желании пойти к кому-нибудь из окружающих и спросить – «как вы вообще можете жить при таком раскладе вещей?» Технологии ПО в 1990 были в точности теми же, что и за десять лет до этого, когда я заканчивал CMU, за исключением того, что в современном случае компилятор не работал (он генерировал неправильный код даже для простейших конструкций), отладчик не работал, отслеживание вызовов (которое целиком состояло из шестнадцатеричных адресов безо всяких символов) было бесполезным, линковщик не работал, и не было ничего даже отдаленно похожего на подходящую систему документирования. Не принимая во внимание эти мелочи, я ожидал хотя бы нормальной пользовательской среды. Используя до этого Microsoft C вместе с CodeView, и даже ранние версии среды Visual C, я установил для себя достаточно высокие стандарты относительно инструментария, от которых Unix (особенно в то время) отстала очень далеко. На целые мили. И пару раз я чистосердечно выразился на эту тему.
В один из дней мы обсуждали какой-то алгоритм, требовавший распределения памяти. Я был убежден, что это решение неприемлемо, так как распределение памяти обошлось бы слишком дорого. Я произнес что-то вроде «ну конечно, если вы будете использовать этот тупоголовый распределитель памяти из Unix, то вы обречены на проблемы с производительностью. Нормальный распределитель снял бы все вопросы.». Один человек из присутствовавших на обсуждении сразу же набросился на меня: «Мне неприятно слышать, как вы опускаете Unix. И вообще, что вы знаете о распределителях памяти?». На что мой ответ был – «задержитесь на этой мысли, я сейчас вернусь». Я сходил в свой кабинет, где лежала копия книги IDL, принес ее с собой назад, и открыл главу «Распределение памяти». «Видите это?» - «Да». «Как называется эта глава?» - «Распределение памяти». Я закрыл книгу и указал на обложку – «Это имя вам знакомо?» - «Да, это ваше имя». «Отлично. Я написал эту главу, в которой рассказывается о разработке высокопроизводительного, минимально фрагментирующего распределителя памяти. Итак, вы спрашивали, что я знаю о распределителях памяти? Вообще-то, я написал на эту тему книгу».
Больше никто не набрасывался на меня, когда я опускал Unix.
В качестве небольшого замечания. Распределитель памяти в NT работает весьма схожим образом с тем, что я описал в книге IDL, и основан на алгоритме «быстрого совпадения», разработанном Чаком Вейнстоком для его докторской в CMU около 1974 года.
Когда не нужно оптимизировать
Не занимайтесь «продвинутой» оптимизацией, которая в действительности не имеет смысла. Например, есть люди, которые пытаются «оптимизировать» графический интерфейс пользователя. Константы в виде «магических чисел» и супернавороченные алгоритмы. В результате получается нечто, что сложно разрабатывать, еще сложнее отлаживать и абсолютно невозможно поддерживать. В данном случае оптимизация бессмысленна. И вот почему.
Нужно принимать во внимание человеческий фактор. Компьютерная мышь находится приблизительно в 60 сантиметрах от уха. Звук распространяется со скоростью около 330 м/с. Это значит, что звук от щелчка мышью или нажатия клавиши доходит до уха за 2 миллисекунды. Цепочка нервных клеток от мозга до кончиков пальцев в длину составляет около 90 сантиметров. Распространение сигнала по нервным клеткам имеет скорость около 100 м/с, то есть факт нажатия кнопки мыши или клавиатуры принимается мозгом приблизительно через 10 миллисекунд. Плюс, задержка восприятия сигнала в мозгу может составить от 50 до 250 миллисекунд.
Как много инструкций процессор Pentium успеет выполнить за 2, или за 10, или за 100 миллисекунд? За 2 миллисекунды 500 MHz процессор выполняет 1 000 000 тактов, так что за это время вы сможете выполнить много инструкций. Даже на таком хламе как 120 MHz Pentium ощутимой задержки при обработке графических элементов управления нет.
Однако этот факт не помешал Microsoft полностью проигнорировать объектную модель для обработки событий; если вы обращаетесь к процедуре CWnd::OnWhatever(…), вместо того чтобы напрямую вызвать DefWindowProc с нужными параметрами, MFC повторно использует параметры последнего сообщения для вызова ::DefWindowProc. Целью этого было «уменьшение размера библиотеки MFC», как будто пара лишних строк кода в массивной библиотеке может иметь значение! Даже я могу сообразить, как вместо CWnd::OnWhatever(…) можно сделать inline-подстановку для вызова DefWindowProc.
Оптимизация – ваш враг
Когда-то, много лет назад, я работал на большой (16 процессоров) многопроцессорной системе. Использовались специальным образом модифицированные миникомпьютеры PDP-11, в целом относительно медленные. Мы программировали их с помощью Bliss-11, который, как я могу сказать, до сих пор находится в списке мировых лидеров среди сильно оптимизирующих компиляторов (несмотря на то, что я видел действительно впечатляющие оптимизации в Microsoft C/C++). Сделав несколько замеров уровня производительности, мы обнаружили, что алгоритм страничного доступа представляет собой узкое место. Поэтому естественным предположением было проверить алгоритм на наличие изъянов. После анализа кода человек, ответственный за этот алгоритм, переписал его, принимая во внимание наши новые пожелания насчет производительности. Через неделю у нас уже была новая, более быстро работающая версия алгоритма.
Между тем, в MIT (Массачусетский технологический университет), все еще работала операционная система MULTICS. И они указали на серьезную проблему с производительностью, которая упиралась в алгоритм страничного доступа. Из-за того, что реализация алгоритма была выполнена на PL/1-подобном языке, EPL, они предположили неоптимальность реализации ввиду использования языка высокого уровня. Поэтому были приложены усилия для переписывания алгоритма целиком на ассемблере. Через год, когда вся система была готова и вышла в промышленную эксплуатацию, потери производительности составили 5%. После детальной инспекции выяснился факт наличия ошибки в одном из фундаментальных алгоритмов. С использованием языка EPL, замена старой версии алгоритма исправленной была выполнена через пару недель. Вывод: не оптимизируйте что-то, не представляющее собой проблему. Для начала постарайтесь эту проблему обнаружить. И только после этого можно думать об оптимизации. В противном случае вся ваша оптимизация будет пустой тратой времени и может даже ухудшить производительность.
В компиляторе Bliss атрибут переменной register был равнозначен приказу для компилятора – «Ты действительно сохранишь эту переменную в регистре процессора». В языке С такой атрибут значит совсем другое – «Я бы хотел, чтобы ты сохранил эту переменную в регистре процессора». Множество программистов полагают, что они должны размещать свои переменные в регистрах для получения оптимального по производительности кода. Компилятор Bliss действительно очень хорош, и реализует очень сложную схему распределения регистров под переменные, и при отсутствии указаний от программиста обладает свободой выбора при размещении переменной в регистре, если такое действие улучшает производительность. Однако явное указание на сохранение переменной в регистре процессора делала этот регистр недоступным для более общих вычислений, в частности при доступе к структурам данных. После нескольких добросовестных экспериментов было обнаружено, что в подавляющем большинстве случаев добавление атрибута register к переменной порождало значительно худший код, чем если бы компилятор сам занимался переменными и регистрами. Многочасовые усилия при разработке какого-нибудь вложенного цикла могут привести к небольшому улучшению производительности, но в целом было совершенно ясно, что без изучения сгенерированного машинного кода и серии откалиброванных экспериментов любая попытка оптимизации ведет к худшему коду.
Если вы слышали об эталонных тестах производительности группы SPEC, то наверняка имеете представление о том, как эти тесты обыгрываются. В частности, IBM написала программу, которая берет базовую программу на FORTRAN (которая, к примеру может выполнять один из эталонных тестов – вроде умножения матриц), и преобразует ее с учетом оптимизации для архитектуры кэша системы, на которой программа будет работать. Небольшое количество параметров описывает все стратегии кэширования для модельной линии RISC 6000. Исходная программа показывает на какой-то системе результат в 45 очков по классификации SPEC. После соответствующей «оптимизирующей» модификации та же программа показывает результат в 900 очков. Это 20-кратное увеличение производительности основано целиком на сторонних эффектах четвертого порядка – стратегии кэширования для частной архитектуры. Если вы занимаетесь преобразованием изображений, особенно изображений больших размеров, то знание о кэшировании (пусть даже машинно-независимое) может принести вам прирост производительности на порядок.
Наивный подход к оптимизации на уровне строк кода не так эффективен, как высокоуровневая оптимизация. Оптимизация страничного доступа, кэширования и распределения памяти приносит обычно более ощутимые результаты, чем построчная оптимизация кода. Алгоритмическая оптимизация – следующий кандидат на рассмотрение, особенно если ваша проблема не поддается только что перечисленным способам оптимизации. И только после того, как все это было выполнено, вы можете переходить на уровень строк кода. И если ваша предметная область потребует, то можно даже запрограммировать внутренние циклы (особенно это касается алгоритмов свертки и цифровой обработки сигналов) на ассемблере, чтобы использовать все возможности специализированных инструкций вроде MMX или потоковой обработки мультимедиа.
Возможно, самый лучший пример чисто программистской глупости при «оптимизации» я видел, когда занимался переносом большой библиотеки в исследовательском проекте. Представьте себе, что это был перенос с 16-битной платформы на 32-битную (в действительности это было 18-бит на 36-бит портирование, и язык был совсем не С, но это неважно – устрашающий код можно написать на любом языке, и я видел программистов на С, совершающих те же ошибки). В основном все работало, но иногда возникала странная проблема, проявлявшаяся при редком совпадении условий, и приводила эта проблема к краху программы. Я начал разбираться. Память в куче была повреждена. Когда я обнаружил, как это происходило, оказалось, что память в куче повреждалась при использовании неверного указателя, который приводил к затиранию случайного места в этой же куче. О’кей, а как этот указатель стал испорченным? Четыре уровня вложенности вниз при использовании указателей, и через 12 непрерывных часов отладки я нашел источник проблемы. Но почему это произошло? Еще через 5 часов я обнаружил что программист написал конструктор для структуры данных, похожей на struct, в виде { char* p1; char* p2; } где указатели были сначала 16-битными, а потом стали 32-битными. Когда я посмотрел на код инициализации, вместо ожидаемых конструкций вроде something->p1 = NULL; something->p2 = NULL; я увидел код эквивалентный (*(DWORD*)&something.p1) = 0! На очной ставке программист пытался оправдаться тем, что он смог обнулить два указателя одной машинной инструкцией (хотя это был не x86-компьютер, а мэйнфрейм), и преподносил это действие как умную оптимизацию. Конечно, когда указатели стали 32-битными, такая оптимизация приводила к тому, что обнулялся только один из двух указателей, а второй оставался заполненным каким-то случайным значением. Я заметил что такая оптимизация срабатывала только один раз, при создании объекта; и что среднее приложение, использовавшее эту библиотеку создавало в среднем шесть таких объектов; и что я потратил в предшествующий день 17 часов личного времени и 6 часов машинного времени на отладку; и что если бы программа не содержала ошибки и запускалась бы непрерывно сразу после своего завершения в течение 14 часов, то время, сэкономленное этой «умной оптимизацией» просто рассеивается как пыль! Пару лет спустя этот программист все еще выкидывал подобные трюки – есть люди, которые никогда ничему не учатся.
Выводы
Оптимизация имеет смысл только тогда, когда она имеет смысл. И если это происходит, то смысл оптимизации действительно значим; но не увлекайтесь ею чрезмерно. Даже если вы знаете что есть смысл в оптимизации, сначала найдите, где есть место в коде для применения оптимизации. Без дополнительной информации о производительности вы не будете точно знать, что оптимизировать, поэтому все ваши усилия могут быть направлены не в то русло. В результате вы получите невразумительный код, который нельзя ни поддерживать, ни сопровождать, ни отлаживать, и который к тому же не решает ваших проблем. Такие последствия выражаются, во-первых, в увеличении стоимости разработки и сопровождения кода, а во-вторых, в отсутствии всякого реального улучшения производительности.
Тяжело справиться с такими последствиями! Теперь вы понимаете, в чем смысл заголовка статьи?
Эта статья опубликована в журнале RSDN Magazine #6-2004. Информацию о журнале можно найти здесьrsdn.org
Оптимизация в OpenMP / Хабрахабр
Постепенное развитие проекта шло своим чередом.На часть полученных по гранту средств было произведено обновление парка личной вычислительной техники. В итоге расчёты сейчас осуществляются не на многострадальном ноутбуке, а на вполне приемлемой машине с псевдовосьмиядерным Intel Core i7-2600 и 8 Gb оперативной памяти на борту. А разработка производится под Visual Studio 2005 (получена по программе DreamSpark) с подключенной триал-версией Intel FORTRAN Compiler 12 / Intel Parallel Studio XE 2011 (всё это крутится под Win 7). В качестве параллельного API задействован OpenMP.
Ввиду явно заметного роста доступных мощностей, обнаружились и новые негативные особенности написанного ранее алгоритма. Прежде всего, с марта месяца была проведена глубокая оптимизация вычислительной части кода, что позволило выиграть в производительности около 70%. Такой прирост обеспечила прежде всего ликвидация операций деления, а также увеличение количества предвычисляемых переменных.
upd: Пост, в общем-то, о серой рабочей повседневности, и никаких открытий в себе не содержит.
Мелкие пакости
Программа исправно использовалась и выдавала хорошие результаты, пока в один прекрасный день не было решено проверить, насколько эффективно выполнено распараллеливание. И, скорее даже ожидаемо, чем удивительно, исполнение в один поток оказалось в среднем вдвое быстрее многопоточных запусков, причём независимо от количества потоков.Ответ, в общем-то, лежит на поверхности. Алгоритм с математической точки зрения оказался оптимизирован настолько, что его узким местом стал обмен данными между отдельными потоками, что подтвердилось даже при беглом анализе в Intel Vtune Amplifier. Наибольших временных затрат потребовала инициализация потоков и их локальных переменных, а также обращение к общим переменным и массивам. Немалую роль в заметности проявившейся пакости сыграл и тот факт, что до сих пор применялась грубая расчётная сетка, всего 3х200 пространственных узлов (своего рода имитация одномерной задачи), и время вычислений оказалось относительно малым.
Мелкие исправления
Что же было сделано для оптимизации?В первую очередь, подкорректированы директивы и разделение переменных по классам. В частности, основные рабочие массивы, в которых хранятся величины, являющиеся целью расчёта, из SHARED были превращены в THREADPRIVATE посредством задания атрибута COMMON (что попутно оптимизировало их размещение в памяти) и директивы COPYIN. Предвычисляемые переменные были оставлены в виде SHARED, т.к. применение к ним FIRSTPRIVATE или COPYIN заметного эффекта не только не давали, но и ухудшали результаты. Итого, директива перед основными рабочими циклами приняли примерно такой вид:
!$OMP PARALLEL DO NUM_THREADS(Threads_number) SCHEDULE(DYNAMIC) & !$OMP PRIVATE(...) & !$OMP COPYIN(...) & !$OMP DEFAULT(SHARED) Здесь опущены списки переменных, т.к. с ними код занимает около десятка строчек.Всего же таких мест в коде девять. Девять бутылочных горлышек, через которые программа, цитируя М. Евдокимова, «Пищит, но лезет».
Перекидывание разных переменных туда-сюда продолжалось пару вечеров, однако об оптимальности работы не могло быть и речи. Запуск на полной загрузке процессора показывал, что в среднем одновременно существуют только 2.1 — 2.3 потока. Процессорное время же расходовалось исправно в восьмикратном размере. Для наглядности, гистограммы из VTune Amplifier для сетки 3х200: Для 100х100: Для 200х200:
Очевидно, что по мере увеличения доли вычислений, результаты улучшаются, однако высокой эффективностью называть такое желания нет.
Применение к потокам принудительного лишения сна посредством увеличения значения KMP_BLOCKTIME с 200 мс до 10 с точно так же помогло лишь чуточку.
Глупости мелкими бывают редко
Неожиданно был брошен суровый взгляд на «пространственно-временную» структуру, образуемую в алгоритме потоками. И всё сразу встало на свои места. Слабым местом оказалась директива!$OMP PARALLEL DO NUM_THREADS(Threads_number) SCHEDULE(DYNAMIC) Ключевое слово PARALLEL отвечает, как известно, за границы параллельной и последовательной области кода. По её достижении, происходит создание новых нитей, перераспределение локальных переменных в их памяти и прочие процедуры, требующие немалого времени. Таких мест, как уже говорилось, было девять. Соответственно, девять раз потоки создавались и уничтожались, а при этом между ними кое-где даже не было последовательных участков. Схематически, это можно представить на такой картинке:Была проведена полная реорганизация структуры параллельной части программы. Теперь схема потоков выглядит так: Вертикальные штриховые линии условно показывают границы параллельных циклов, а ближе к концу использована директива SINGLE — там осуществляется запись результатов расчёта на диск, для чего работа всех потоков, кроме одного, приостанавливается. Распараллелить её как минимум затруднительно, хотя есть идея записывать в одном потоке и выполнять дальнейший цикл в остальных, т.к. он от записи на диск не зависит, либо переставить их местами. Но это уже детали, к делу отношения не имеющие.
А в исходном тексте структура директив выглядит так:
Time_cycle: do n = 0, Nt, 1 !$OMP PARALLEL NUM_THREADS(Threads_number) & !$OMP PRIVATE(...) & !$OMP COPYIN(...) & !$OMP DEFAULT(SHARED) !$OMP DO SCHEDULE(DYNAMIC) ... !$OMP END DO ... ещё 7 таких параллельных циклов !$OMP SINGLE ... запись на диск !$OMP END SINGLE !$OMP DO SCHEDULE(DYNAMIC) ... !$OMP END DO !$OMP END PARALLEL enddo Tyme_Cycle Т.е., всё тело цикла по времени (программа производит прямое численное моделирование эволюции гидродинамической системы) теперь находится в параллельной области, потоки создаются в начале итерации и уничтожаются только при её завершении, а не воскрешаются неоднократно. Обёртывать в параллельную область и временной цикл уже не представляется возможным, поскольку каждая его итерация, естественно, полностью зависит от предыдущей (прошу поправить, ежели не так — моя логика здесь даёт определённый сбой).Финальным улучшением, направленным на ускорение работы, явилось отключение барьерной синхронизации между потоками в некоторых циклах, где это не повлияет на последующие вычисления.
В результате, время действительно параллельного исполнения кода как будто бы увеличивается. На сетке 3х200 узел VTune изображает такой результат:
На сетке 100х100 — такой:
Наконец, на 200х200 — такой:
Таким образом, подтверждаем давнюю истину, что на больших сетках, когда вычислений реально много, они занимают большую часть времени и параллелизм эффективен. На маленьких же сетках требуется оптимизировать обмен между процессами, иначе результаты оказываются не радостными. Да и несмотря на это, последовательные этапы занимают преобладающую часть рабочего времени.
Возникает вопрос, стоит ли проделанная работа по оптимизации потраченного времени и сил? Проверим реальную скорость выполнения программы. Запуск осуществлён на тех же трёх разных сетках с восемью потоками, и измерено время до некоторой контрольной точки. Контрольные точки во всех случаях разные, посему проводить сравнение по абсолютным величинам между разными сетками будет некорректно — 1 млн. итераций для 3 х 200, 500 тыс. для 100 х 100 и 200 тыс. для 200 х 200 узлов. Во второй строчке в скобках приводится относительное различие времени исполнения двумя вариантами программы.
| 3 х 200, до оптимизации | 94.4 |
| 3 х 200, оптимизировано | 70.0 (-26 %) |
| 100 х 100, до оптимизации | 352 |
| 100 х 100, оптимизировано | 285 (-19 %) |
| 200 х 200, до оптимизации | 543 |
| 200 х 200, оптимизировано | 436 (-19 %) |
Попутно сравним качество распараллеливания, определив таким же способом прирост производительности по мере увеличения числа потоков. Сразу следует оговориться, что на одном потоке вычисления могут оказаться быстрее, чем на двух-трёх, в силу, во-первых, отсутствия необходимости обмениваться данными с соседями, а во-вторых, работы TurboBoost, поднимающей тактовую частоту на 400 МГц. Также напомним, что физических ядер у упомянутого в начале процессора всего 4, и ускорение на 8 потоках — результат работы Hyper-Threading.
Сетка 3х200, 1 млн. итераций:
| 1 | 80.9 |
| 2 | 88.7 |
| 3 | 84.4 |
| 4 | 83.7 |
| 8 | 94.4 |
| 1 | 87.9 |
| 2 | 145 |
| 3 | 113 |
| 4 | 97.8 |
| 8 | 70.0 |
| 1 | 918 |
| 2 | 736 |
| 3 | 536 |
| 4 | 431 |
| 8 | 352 |
| 1 | 845 |
| 2 | 528 |
| 3 | 434 |
| 4 | 381 |
| 8 | 285 |
Выводы? Основной вывод один — следите за тем, как рождаются и умирают потоки в программе. Продление их жизни может оказаться полезным.
Реализованная перекомпоновка пространственно-временной структуры потоков описана, в частности, здесь:Эффективное распределение нагрузки между потоками с помощью OpenMP*. Вот только прочитано оно было уже после придумывания решения. Сэкономил бы пару дней, эх.
habr.com