Задачи оптимизации и методы их решения. Общая постановка задачи оптимизации
симплекс-метод и его применение для решения задач оптимизации
«Методы оптимизации»
1 Общая постановка задачи оптимизации. Необходимые и достаточные условия существования безусловного экстремума функции одной и нескольких переменных.
2 Численные методы поиска безусловного экстремума: методы нулевого порядка (методы одномерной минимизации).
3 Численные методы поиска безусловного экстремума: методы первого порядка.
4 Линейное программирование: симплекс-метод и его применение для решения задач оптимизации.
1 Общая постановка задачи оптимизации. Необходимые и достаточные условия существования безусловного экстремума функции одной и нескольких переменных.
Оптимизация – это целенаправленная деятельность, которая заключается в получении наилучших результатов при соответствующих условиях.
Задача безусловной оптимизации состоит в нахождении минимума или максимума функции в отсутствие каких-либо ограничений.
Функция у=f(x) имеет локальный min (локальный max) в точке х0, если существует некоторая положительная величина δ, при которой выполняется неравенство: /х-х0/<δ, а также выполняется условие f(x)≥f(x0)- для задач минимизации; f(x)≤ f(x0)-для задач максимизации.
Функция у=f(x) имеет глобальный min в точке х* если для всех х выполняется условие f(x)≥f(x*), где f(x*) –точка глобального max.
Необходимым условием существования экстремума G(x) при отсутствии ограничений на диапазон изменения переменной x могут быть получены из анализа первой производной:
Достаточные условия существования экстремума:
сравнение значений функций, сравнение знаков производных, исследование знаков высших производных.
Если G(xk-e) и G(xk+e) одновременно больше или меньше G(xk), то в точке xk – экстремум.
Если знак производной меняется при переходе через точку xk, то это экстремум. Меняется с (+) на (–), то max; с (–) на (+), то min.
Если порядок первой необращающейся в нуль в точке xk производной четный, то в данной точке есть экстремум функции G(x), который будет max или min в зависимости от знака этой производной: < 0 – max; > 0 – min.
Функция нескольких переменных G = G(x1, x2, …, xn).
Необходимое:
Достаточное: D1 = а11 > 0;
2 Численные методы поиска безусловного экстремума: методы нулевого порядка (методы одномерной минимизации).
Безградиентные методы – это методы, которые использую в процессе поиска экстремума информацию, полученную от сравнительной оценки критерия оптимальности в результате выполнения очередного шага.
Метод золотого сечения.
Задача состоит в определения положения экстремума функции одного переменного G(x) на некотором интервале [a,b]. Для решения этой задачи весь исходный интервал разбивается на части в определенном пропорциональном отношении.
Значения функции G(x) на концах исходного интервала, в некоторых внутренних точках в точках Х1 и Х2 известны, выбираем один из 2-х подынтервалов [Х0; Х2] или [Х1; Х3]. В одном из этих интервалов локализуется экстремум функции G(x).
Отношение , называется золотым сечением: если в интервале [Х0; Х3] внутренние точки Х1 и Х2 отстоят от концов интервала на величину z, в любом из образующихся подинтевалов можно так выбрать положение новой точки Х4 , которая будет отстоять от концов своего подинтервала на величину z.
Одним вычислением на каждом этапе локализуем положение экстремума внутри интервала, длина которого составляет 1-z=0.62 от длины исходного интервала.
Алгоритм:
1). Вычисляем значения функции G(x) на концах исходного интервала т. е. значения G(Х0) и G(Х3).
2). Вычисляем значения функции в точке Х1 = Х0 +0,38(Х3 - Х0 )
3). Вычисляем значения функции в точке Х2 = Х3 -0,38(Х3 - Х0 )
4). Сравниваем полученные значения G(Х1) и G(Х2) и по результатам сравнения выбирают подинтервал в котором локализуется экстремум.
Эти новые 2-а подинтервала состоят из 2-х участков l1 и l2.
5). Внутри большого отрезка (l1) есть точка отстоящая от концов отрезка (l1+l2) на 0,38. В этой точке рассчитываем значения функции G(x) и снова определяем подинтервал внутри интервала (l1+l2) и т. д.
Методы с использованием чисел Фибоначчи.
Свойство чисел Фибоначчи можно использовать для поиска экстремума функции одной переменной G(x). Последовательность чисел Фибоначчи: Fк = Fk-1 + Fk-2 , где F0 = F1 =1.
Ряд чисел Фибоначчи 1, 2,3,5,8,13,21,34,55,89
Алгоритм поиска min:
1). По заданной точности ε находим количество шагов , где a,b – границы интервала.
2). Для N находим из таблицы такое число для которого выполняется условие Fs-1 <N< Fs .
3). Определяем минимальный шаг поиска экстремума по найденному числу
4). Считаем значения функции в точках начала и конца интервала.
5). Определяем следующую точку из интервала, в ней считаем значение функции G(x): .
6). Рассчитываем значение функции G(x) в этой найденной новой точке G().
Сравниваем G(x) и G(). Если шаг оказался удачным G()<G(x), то определяется новая точка [a,b] по выражению: .
7). Выполняют расчет в новый точке G() и т. д. до тех пор пока шаг окажется неудачным.
В случае неудачного шага расчет новой точки выполняется по выражению например, для
8). Последующие шаги выполняются с уменьшающейся величиной шага, которую определяют по выражению: , где i=0, 1, 2,…- номер шага.
Метод дихотомии.
Дихотомия – половина деления. Из N экспериментов находят интересующий интервал [Х1; Х2], Х1 и Х2 – это два значения отрезка, которые рассматриваются как единичный отрезок. Значения Х1 и Х2 располагаются симметрично относительно центра исходного интервала на расстоянии ε/2 (ε – заданная точность)
В т. Х1 и Х2 вычисляется значения целевой функции, и их сравнивают, определяют гарантируемый интервал неопределенности G1=(1±ε)/2.
Допустим этот интервал неопределенности смещен влево. В результате получаем интервал отрезка между точками [0; Х2].
Далее рассматривается отрезок [0; Х2] внутри этого отрезка относительно центра находят новые точки Х3 и Х4 , которые располагаются симметрично относительно центра на величину ε/2.
vunivere.ru
Задачи оптимизации и методы их решения
Общие сведения
Методы оптимизации относятся к разделу прикладной математики – математическое программирование. Математическое программирование - раздел прикладной математики, изучающий способы оптимизации – совершенствование и повышение эффективности организации, планирования и управления в различных системах на основе вычислительных методов. Таким образом, в основе математического программирования лежит математический аппарат решения задач оптимизации.
Можно указать некоторые приложения математического программирования в исследовании операций:
оптимизация технико-экономических систем
транспортные задачи
задачи управления
автоматика (распознавание систем, фильтрация, управление технологическими процессами, роботы)
техника (управление размерами, оптимизация информационных систем, компьютерных сетей)
математическая экономика (решение макроэкономических задач, оптимизация моделей предпринимательства)
теория принятия решений и игр
Постановка любой задачи оптимизации начинается с определения набора независимых переменных, определении области допустимых значений для этих переменных (ограниченные задачи). Обычно оптимизируется скалярная мера качества, которая зависит от переменных (целевая функция). Решение оптимизационной задачи – это приемлемый набор значений переменных, которому отвечает оптимальное решение целевой функции. Под оптимальным решением понимают максимальность или минимальность целевой функции.
Общая постановка задач оптимизации
Найти ,
где 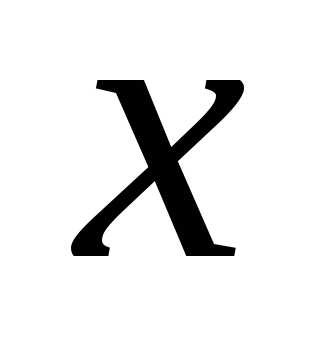 – векторный аргумент, по которому ведется оптимизация,
– векторный аргумент, по которому ведется оптимизация,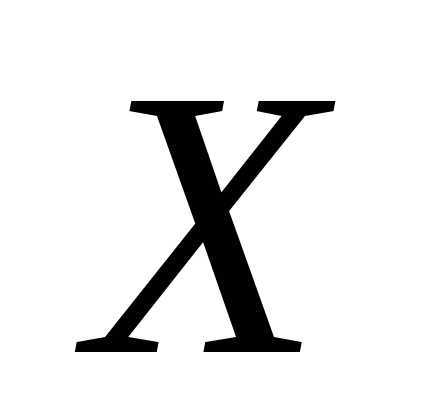 – область допустимых значений
– область допустимых значений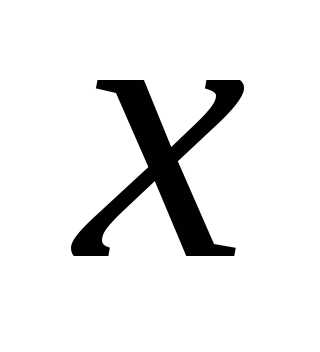 ,
,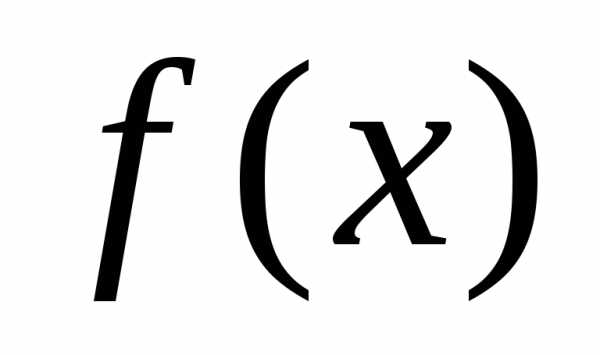 – целевая функция.
– целевая функция.
Введем обозначения:
,
где 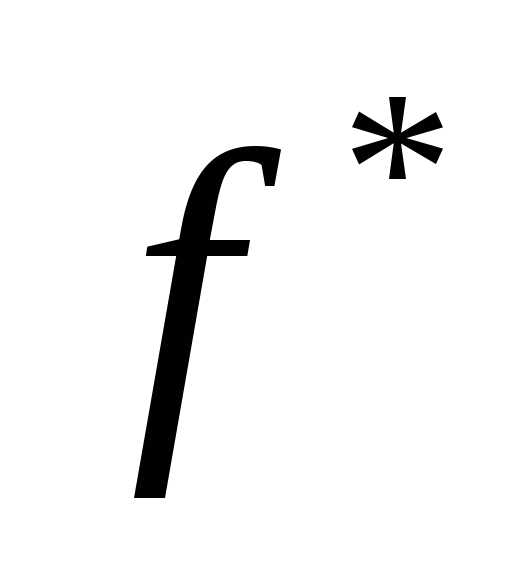 - оптимальное значение целевой функции,
- оптимальное значение целевой функции,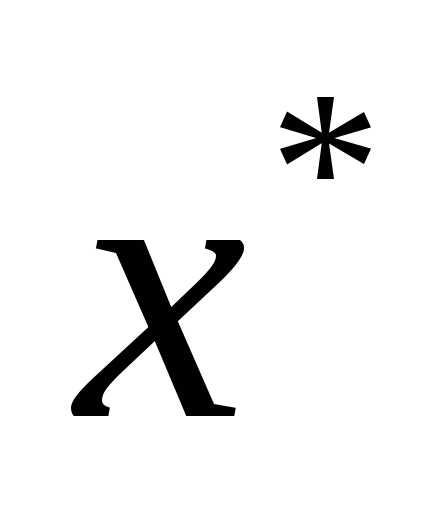 - значение аргумента, при котором определяется
- значение аргумента, при котором определяется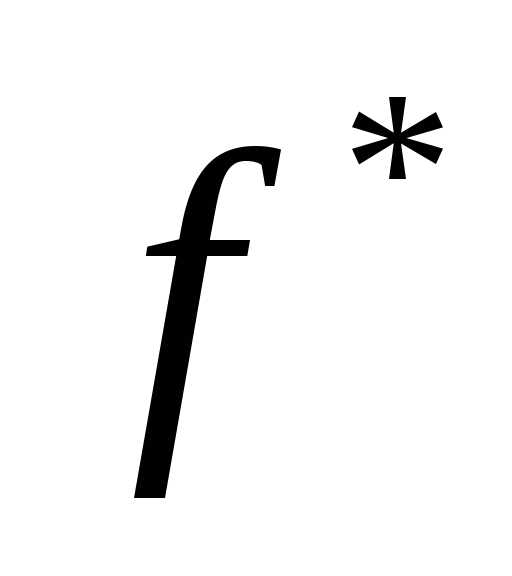 .
.
Постановка задачи минимизации или максимизации не нарушает общности:
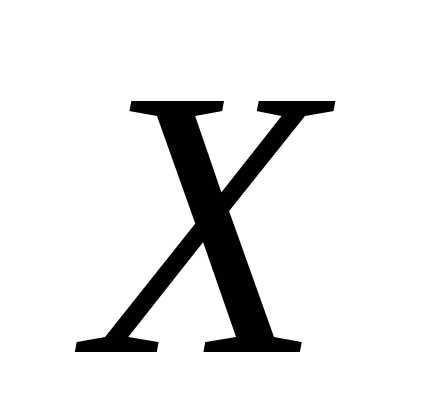
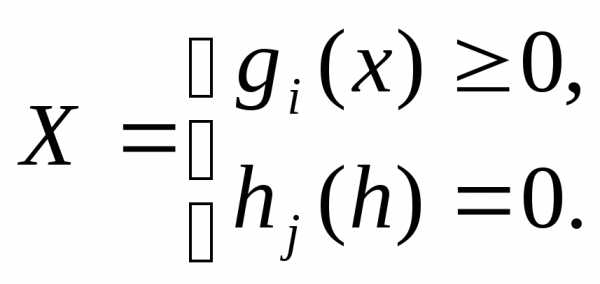 ,
,
где 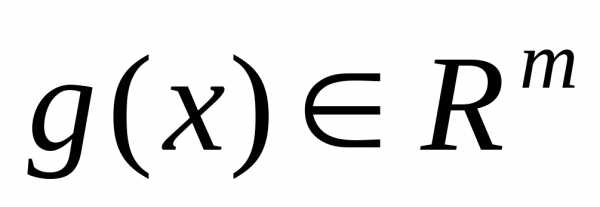 - ограничения неравенства, а
- ограничения неравенства, а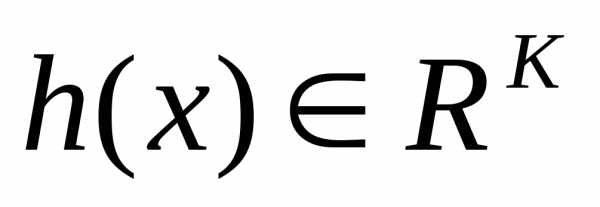 - ограничения равенства.
- ограничения равенства.
Классификация разделов математического программирования
По виду решаемой задачи можно выделить следующие разделы математического программирования:
Линейное программирование (ЛП) – раздел математического программирования, изучающий задачу поиска минимальной (максимальной) линейной функции при линейных ограничениях в виде равенств или неравенств.
Нелинейное программирование – раздел математического программирования, изучающий методы решения и характер экстремума в задачах оптимизации с нелинейной целевой функцией и (или) нелинейными ограничениями.
Стохастическое программирование - раздел математического программирования, изучающий модели выбора оптимальных решений в ситуациях, характеризуемых случайными величинами.
Существуют также методы, которые при решении задач оптимизации учитывают специфику этих задач. Такие методы превосходят по эффективности общие алгоритмы и их выделяют в отдельный класс методов для решения задач специальной структуры.
Разделы математического программирования
Можно выделить следующие разделы:
Целочисленное программирование - решает задачи оптимизации, в которых на значения переменных наложено требование целочисленности.
Квадратичное программирование - решает задачи оптимизации с квадратичной целевой функцией и линейными ограничениями.
Геометрическое программирование – решает задачи оптимизации, в которых целевая функция и ограничения представляют собой обобщенные многочлены с положительными коэффициентами.
Сепарабельное программирование - решает задачи оптимизации с сепарабельной целевой функцией и сепарабельными ограничениями.
Дробно-линейное программирование - решает задачи оптимизации с дробно-линейной целевой функцией и линейными ограничениями.
IV. Общая постановка задач оптимизации.
Приведённые постановки однокритериальных задач оптимизации распределения функций , процесса функционирования и сложности алгоритма являются частными случаями двух общих задач оптимизации АСОИУ как системы Ч-М-С, которые могут быть сформулированы с введением следующих понятий и обозначений :
Мс - модель структуры системы; Мф - модель функционирования системы; Мр - модель ресурсов, требуемых для обеспечения функционирования системы; Мц - модель цели функционирования системы ; Gц(Мц) - векторный функционал, характеризующий степень достижения функционирования системы; Gр(Мр)- векторный функционал, характеризующий степень использования ресурсов для обеспечения функционирования системы.
Формулировка первой общей задачи:
найти вариант <Мс , Мф> , такой ,что Gр(Мр) min при Gц(Мц) Gц.доп
Формулировка второй общей задачи :
найти вариант <Мс , Мф> , такой ,что Gц(Мц) max при Gр(Мр) Gр.доп
В такой широкой формулировке эти оптимизационные задачи могут быть решены методом диалогового программирования с использованием систем интеллектуальной поддержки разработчика или экспертных систем.
Указанное обстоятельство обусловлено рядом причин , основными из которых являются :
--- многокритериальность целей функционирования АСОИУ ;
--- размытость обобщённых критериев оценки как системы в целом , так и отдельных её частей ;
--- недостаток и недостоверность исходных данных для решения задач оптимизации ,особенно на ранних стадиях проектирования ;
--- размерность и динамичность самих моделей Мс , Мф , Мц и Мр .
Однако пока ещё далека от решения проблема автоматизации эргономического обеспечения проектирования АСОИУ, что затрудняет решение задач её оптимизационного проектирования и что частично компенсируется использованием эвристических приёмов и метода экспертных оценок .
12
studfiles.net