Исследование и экспериментальная оптимизация систем управления. Метод экспериментальной оптимизации

Mетоды экспериментальной оптимизации

Количество просмотров публикации Mетоды экспериментальной оптимизации - 221

Лекция 14

Как уже говорилось ранее для решения задачи достижения почти стационарной области (области наилучших значений выходной переменной) используется два подхода.

1.Методы,использующие апроксимацию поверхности отклика в локальной области гиперплоскостью с целью определения наилучшего направления движения в сторону оптимума (к примеру,метод крутого восхождения - при максимизации функции отклика).

2.Методы,определяющие направление движения на каждом шаге по результатам очередного наблюдения,сравнивая его с результатами предыдущих наблюдений (к примеру,симплекс-метод).

Второй подход ,по сравнению с первым,допускает применение на действующих системах (установках) за счёт незначительных отклонений от номинальных режимов работы и не приводит к недопустимым режимам.

Рассмотрим эти методы более подробно.

Mетод крутого восхождения (метод Бокса-Уилсона)

Метод представляет собой сочетание градиентного метода оптимизаци с дробным факторным экспериментом, применяемым для апроксимации поверхности отклика полиномом первого порядка, обеспечивающим получение оценки градиента функции отклика в заданной точке с минимальной дисперсией.

Суть метода состоит в следующем. Выбирается (на базе априорной информации) начальная точка x0, из которой будет осуществляться поиск оптимальных (близких к нему) значений входных переменных.

Используя эту точку как центр плана,строится полный или дробный факторный план,по результатам эксперимента в котором строится линейная модель функции отклика:

y(x,b)=b0+b1x1+...+bkxk

Вид плана выбирается таким образом,чтобы перенасыщенность его была минимальной (число точек плана по возможности не намного превышало число определяемых коэффициентов).

Данное уравнение является уравнением гиперплоскости в (k+1)-мерном пространстве,касательной к поверхности отклика в точке x0. Коэффициенты характеризуют её наклон относительно осей координат и являются составляющими вектора градиента͵ обеспечивающего движение в области изменения переменных в направлении крутого (наискорейшего) восхождения по этой гиперплоскости в сторону возрастания целевой функции :

где -единичный вектор в направлении переменных (орты).

В случае если уравнение регрессии y(b,x) адекватно,то можно осуществлять движение вдоль линии крутого восхождения, определяя в каждой точке значения функции отклика по результатам наблюдений.Движение в данном направлении осуществляется до тех пор, пока не будет достигнуто наибольшее значение функции отклика .

В найденной точке вновь строится ПФП (ДФП), снова строится линейная модель о определяется новое направление движения в сторону оптимума. Снова осуществляется движение в направлении наискорейшего восхождения до точки, обращающей в максимум функцию отклика и т.д.(см. рисунок)

Процесс продолжается до тех пор,пока линейная модель адекватна и имеются значимые коэффициенты. В случае если линейная модель становится неадекватной, то делается попытка увеличить интервалы варьирования переменных и построить новую линейную модель.

В случае если это не приводит к положительным результатам ,то дальнейшее движение по градиенту нецелесообразно. В этом случае в центре плана x0 проводится n0 дополнительных экспериментов и оценивается значимость влияния квадратичных членов. В случае если оно значимо, то можно считать, что цель второго этапа исследований-достижение почти стационарной области-реализована,и можно приступать к третьему этапу исследований.

Иначе делается либо новая попытка увеличения (изменения) интервалов варьирования переменных,либо центр плана экспериментов переносится в другую точку.

Глава 5. Методы экспериментальной оптимизации

МЕТОДЫ БЕЗУСЛОВНОЙ ОДНОМЕРНОЙ ОПТИМИЗАЦИИ

Министерство образования Российской федерации Новокузнецкий филиал институт Кемеровского государственного университета Кафедра информационных систем и управления МЕТОДЫ БЕЗУСЛОВНОЙ ОДНОМЕРНОЙ ОПТИМИЗАЦИИ

Подробнее

МЕТОД НАИМЕНЬШИХ КВАДРАТОВ (МНК) 1

МЕТОД НАИМЕНЬШИХ КВАДРАТОВ (МНК) 1 Пусть вы изучаете зависимость одной физической величины у от другой х, то есть ищите зависимость у(х). Например, это может быть зависимость плотности вещества от температуры

Подробнее

МЕТОДЫ ОДНОМЕРНОЙ ОПТИМИЗАЦИИ

Министерство образования и науки Российской федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Тихоокеанский государственный университет»

Подробнее

Вергазова Ольга Бухтияровна

УДК по дисциплине «Методы оптимизации» (160403) (519.677 Решения задач математического анализа и прикладных задач) для специальности 1604030065. Рецензенты: Фурсов Андрей Серафимович - кандидат физикоматематических

Подробнее

x выполняется условие f (x) > f (x ) и

Методы многомерной оптимизации. Дана некоторая функция многих переменных (,, 3,.., n ) или ( ) надо найти такое значение, при котором функция ( ) принимает экстремальное значение (минимальное или максимальное).

Подробнее

Лабораторная работа 1

Лабораторная работа Тема: Методы одномерной безусловной оптимизации Цель работы: знакомство с оптимизационными задачами, изучение различных методов одномерной оптимизации и сравнение эффективности их применения

Подробнее

Лекция 15. ОСНОВЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ

Лекция 5. ОСНОВЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ И ОСНОВНЫЕ ПОЛОЖЕНИЯ На практике существуют задачи оптимизации, в которых критерий качества зависит от функции, определить которую необходимо

Подробнее

Методы одномерной оптимизации

Курс: Методы оптимизации в машинном обучении Методы одномерной оптимизации Методы оптимизации для оракула нулевого порядка Рассмотрим задачу одномерной оптимизации вида f(x) min x, x R, (1) где функция

Подробнее

Метод конечных элементов

Метод конечных элементов 1. Область применения МКЭ. 2. Основная концепция МКЭ. 3. Преимущества МКЭ. 4. Разбиение расчётной области на конечные элементы. 5. Способ аппроксимации искомой функции в конечном

Подробнее

ОГЛАВЛЕНИЕ. Предисловие... 11

ОГЛАВЛЕНИЕ Предисловие... 11 ЧАСТЬ 1. ОБЩИЕ СВЕДЕНИЯ О СИСТЕМАХ И ТЕОРИИ УПРАВЛЕНИЯ.15.Глава 1. Основные понятия теории управления... 15 1.1.Понятия об управлении и системах управления... 15 1.2.Объекты

Подробнее

Системы управления и моделирование

Системы управления и моделирование Алгоритм анализа робастной устойчивости дискретных систем управления с периодическими ограничениями М. В. МОРОЗОВ Аннотация. Для дискретных линейных нестационарных систем

Подробнее

Эконометрическое моделирование

Эконометрическое моделирование Лабораторная работа 3 Парная регрессия Оглавление Парная регрессия... 3 Метод наименьших квадратов (МНК)... 3 Интерпретация уравнения регрессии... 4 Оценка качества построенной

Подробнее

1. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

2 СОДЕРЖАНИЕ Введение... 4 1. Пояснительная записка... 4 1.1. Требования государственного образовательного стандарта высшего профессионального образования к структуре и содержанию курса «Методы оптимизации»...

Подробнее

Б.Ф. Харчистов МЕТОДЫ ОПТИМИЗАЦИИ

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ ТАГАНРОГСКИЙ ГОСУДАРСТВЕННЫЙ РАДИОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Б.Ф. Харчистов МЕТОДЫ

Подробнее

5. Экстремум функции двух переменных.

88 5. Экстремум функции двух переменных. Точка M (, ) является точкой максимума (минимума) функции z = f(,), если найдется такая окрестность точки M, что для всех точек M(,) из этой окрестности выполняется

Подробнее

1. ЦЕЛИ И ЗАДАЧИ ДИСЦИПЛИНЫ

1. ЦЕЛИ И ЗАДАЧИ ДИСЦИПЛИНЫ Целью освоения дисциплины «Методы оптимизации и организации энерго- и ресурсосберегающих технологий» является научить студентов: использовать современные методы оптимизации

Подробнее

Вариационное исчисление

Глава 1 Вариационное исчисление Началу появления вариационного исчисления дала толчок работа И. Бернулли 1696 года Новая задача, к решению которой приглашаются математики, в которой поставлена задача о

Подробнее

Оглавление 1. Перечень компетенций с указанием этапов их формирования в процессе освоения образовательной программы... 3 2. Описание показателей и критериев оценивания компетенций на различных этапах их

Подробнее

w j g j (x i ) + ε i.

В. В. Стрижов. «Информационное моделирование». Конспект лекций. Введение, метод наименьших квадратов Введение Термин регрессия был введен Фрэнсисом Гальтоном в конце 19-го века. Гальтон обнаружил, что

Подробнее

4. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ В результате изучения данной темы студент должен: уметь применять таблицу производных и правила дифференцирования для вычисления производных элементарных функций находить производные

Подробнее

оглавление 222 ОГЛАВЛеНИе

оглавление Введение...3 глава. Статические системы...8.. Ошибки моделирования...9.2. Аппроксимация функций...9.3. Адекватность математической модели...7 глава 2. Линейные системы с бесконечным временем...22

Подробнее

docplayer.ru

4.2 Планирование эксперимента и методы оптимизации параметров процесса

Основной целью проведения современного эксперимента с позиций производителя продукции является разработка математической модели, адекватно описывающей процесс и позволяющий, в конечном результате, осуществлять его управление. Именно с помощью такой модели можно эффективно управлять производством, оперативно изменяя его параметры в соответствии с запросами потребителя и обеспечивая выпуск высококачественной продукции.

При этом исследователь должен:

1) обеспечить высокую надежность и четкость интерпретации результатов экспериментальных исследований;

2) составить четкую и последовательную логическую схему построения всего процесса исследования: что, когда и как нужно делать;

3) максимально формализовать процесс разработки модели и сопоставления экспериментальных данных различных опытов одного и того же объекта исследований с целью широкого применения электронно-вычислительных средств.

Всем перечисленным требованиям отвечают статистические методы планирования эксперимента, являющиеся одним из эмпирических способов математического описания и оптимизации сложных процессов. Начало математическому планированию экспериментов положено в 30-40-х годах.

При планировании эксперимента рассматриваются только такие объекты, для которых выполняются требования воспроизводимости и управляемости. Первое требование означает, что при повторении эксперимента при одних и тех же значениях входных параметров результаты эксперимента имеют разброс, не превышающий некоторой заранее заданной величины (т. е. требований к точности эксперимента). Второе требование означает, что объект исследования должен быть управляемым, т.е. эксперимент - активным.

Планирование эксперимента состоит в процедуре выбора числа и условий проведения опытов, необходимых и достаточных для решения поставленной задачи с требуемой точностью. При этом обеспечивается следующее:

• одновременное варьирование всеми переменными по специальным правилам;

• использование математического аппарата, формализующего многие действия экспериментатора;

• выбор четкой стратегии, позволяющей принимать обоснованные решения после каждой серии экспериментов;

• минимизация общего числа опытов.

Наиболее часто требуется установить количественную связь между значением выходного параметра и факторами, от которых он зависит. Такой эксперимент называется интерполяционным.

В этом случае для описания объекта исследования удобно пользоваться кибернетической схематизацией, представляющей объект исследования в виде «черного ящика» (рис. 14.1). Стрелки справа, обозначенные уь изображают функции, результаты процесса характеристики целей исследования, т.е. «параметров оптимизации». Встречаются и другие названия: «критерий оптимизации», «целевая функция», «выход черного ящика», «функция отклика» или просто «отклик» и т.д. Все способы такого воздействия на объект исследования (входы «черного ящика») обозначены хi, и называются «факторами», «независимыми переменными». Совокупность возможных значений всех факторов можно рассматривать как k-мерное «факторное пространство» с координатами ().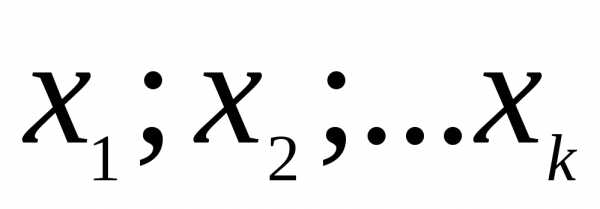

Для решения задачи необходимо создать математическое описание процесса, то есть математические модели, связывающие параметр оптимизации с факторами обычно представляется в виде полинома, где У - функция отклика, а Х1, Х2,Хз,..., Хн - факторы исследуемого процесса. Процесс проверки степени соответствия математической модели описываемому процессу называют «проверкой адекватности», а полученную модель - «адекватной».

Каждый фактор может принимать в опыте одно из нескольких значений. Эти значения называют «уровнями». Всякий фактор имеет определенное число дискретных уровней. Фиксированный набор уровней факторов (т.е. установление каждого фактора на некоторый уровень) определяет одно из возможных состояний «черного ящика». Одновременно это есть условия проведения одного из возможных опытов. Перебор всех возможных наборов состояний дает полное множество различных состояний данного «ящика», т. е. число возможных различных опытов. Число различных состояний получается путем возведения числа уровней факторов в степень числа факторов k.

Выбор параметра оптимизации определяется тем аспектом, который в конкретном случае представляет наибольший интерес.

Параметры оптимизации могут быть весьма разнообразными:

- экономические: прибыль, себестоимость, рентабельность и т.п.;

- технико-экономические: производительность, эффективность, долговечность, надежность и т.п.;

- статистические: характеристика распределения, дисперсия, стандартное отклонение;

- чисто технические: размер, характеристика механических свойств и т.п. При механической обработке могут выбираться такие параметры оптимизации, как стойкость режущего инструмента, точность базирования, точность обработанных поверхностей, шероховатость поверхности детали и т. п.

Параметр оптимизации должен удовлетворять следующим требованиям.

1. Быть количественным, т. е. всегда задаваться числом. То множество значений, которые может принимать параметр оптимизации, называется областью определения. Если нет способа измерения параметра оптимизации или он не может быть количественно зафиксирован, необходимо провести его ранжирование, то есть присвоение рангов по заранее выбранной шкале.

2. Быть однозначным в статистическом смысле, т. е. заданному набору значений факторов должно соответствовать с точностью до ошибки эксперимента определенное значение параметра оптимизации.

3. Быть простым, иметь физический смысл, легко вычисляться и выражаться одним числом.

4. Оценивать действительную эффективность функционирования системы или качество объекта, т.е. задача эксперимента должна ставиться корректно.

5. Обладать по возможности универсальностью и полнотой, то есть всесторонне характеризовать объект исследования, что выполняется далеко не всегда. Например, часто характеристики качества вступают в противоречие с экономическими аспектами.

Выбор факторов играет важнейшую роль в построении математической модели, см. § 3.4

Если какой-либо существенный фактор окажется не включенным в совокупность управляемых исследователем условий проведения экспериментов, и при этом его уровень не будет контролироваться, то это может привести к значительным погрешностям результатов. Если неучтенный фактор произвольно принимал случайные значения, а информация об этом не была зафиксирована, это также значительно увеличит ошибку опыта. При поддержании фактора на некотором фиксированном уровне (не задействован в эксперименте) может быть получено ложное представление об оптимуме, так как при другом фиксированном уровне этого фактора оптимум параметра оптимизации может сместиться.

При планировании эксперимента факторы должны быть управляемыми (активный эксперимент). Нужно знать последовательность действий (операций), с помощью которых устанавливаются конкретные значения (уровни) фактора («операциональный» фактор).

Дополнительные требования предъявляются к совокупности факторов:

1. Требование совместности: все комбинации факторов должны быть осуществимы и безопасны. Если это требование не выполняется, необходимо разбить область определения факторов на диапазоны, «блоки».

2. Требование независимости, «некоррелированности», «ортогональности» факторов. При существенной связи между рассматриваемыми факторами (явление «мультиколлинеарности») не удаётся получить достоверной математической модели

studfiles.net

Метод экспериментальной оптимизации

· Файл PDF МЕТОДЫ ЭКСПЕРИМЕНТАЛЬНОЙ ОПТИМИЗАЦИИМетод … Метод деления отрезка пополам Особенности метода: 1 На каждой итерации алгоритма исключается в точности половина интервала поиска ^4 МАТЕМАТИЧЕСКИЙ МЕТОД ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТА 41 Основные определения Планирование эксперимента – это процедура выбора числа и условий проведения опытов, необходимых и достаточных для решения поставленной ЭКСПЕРИМЕНТ - это Что такое ЭКСПЕРИМЕНТ? Разложение суммы квадратов в однофакторном ДА В п42 рассматривался вопрос включения в регрессию качественных переменных Последовательный симплекс метод Работа по теме: Анализ данных Глава: 12 Симплекс-метод экспериментальной оптимизации Глава 5 Методы экспериментальной оптимизации · Файл PDF Метод жидкостной цитологии при исследовании … Для решения задач оптимизации используются два принципипльно различных подхода: каким-либо способом определяется полная математическая модель и далее задача решается аналитическим или Метод выбора наиболее важных факторов, основанный на экспертной оценке 10 Размах варьирования фактора Диссертация на тему «Разработка метода сведения … Этот метод относится к методам экспериментальной оптимизации Он широко используется в Диссертация на тему «Разработка и … 67 Последовательный симплексный метод псм Метод экспериментальной оптимизации, основанный на сочетании насыщенного плана, заданными вершинами симплекса с последовательным отражением Предложенный метод показал свою эффективность в задачах оптимизации с одним и несколькими экстремумами, на примере симплексного поиска и генетического алгоритма, работающих в условиях Задача оптимизации решается в два этапа: 1) сначала осуществляется поиск области оптимума – для чего применяется линейная модель поверхности отклика; · Файл PDF Методы экспериментальной психосемантики Метод Методы экспериментальной оптимизации метод деления отрезка пополам: Лекция Творческие 12 Симплекс-метод экспериментальной оптимизации Оптимизация симплекс-метод Симплексный метод планирования эксперимента и оптимизации В сравнительно недавнее время появились работы з1-зз в которых предлагается на стадии восхождения использовать симплексный 5) использование результатов эксперимента, например коррекция физической модели явления или объекта, применение модели для прогноза, управления или оптимизации и др ОЦЕНКА ЭФФЕКТИВНОСТИ ЭКСПЕРИМЕНТАЛЬНОЙ МОДЕЛИ ОПТИМИЗАЦИИ Если математическая модель непригодна для применения аналитических или численных методов, а это присуще всем моделям алгоритмического вида, то для ее решения применяют метод Глава 5 Методы экспериментальной оптимизации Задача (параметрической) оптимизации в Последовательный симплексный метод - это Что … ГОСТ 24026-80 Исследовательские испытания … 108 МЮ ШЕЛКОВСКИЙ ГП НПКГ … ОЦЕНКА ЭФФЕКТИВНОСТИ ЭКСПЕРИМЕНТАЛЬНОЙ МОДЕЛИ ОПТИМИЗАЦИИ ОБУЧЕНИЯ СТУДЕНТОВ · Файл PDF 4 МАТЕМАТИЧЕСКИЙ МЕТОД ПЛАНИРОВАНИЯ - А … ИССЛЕДОВАТЕЛЬСКИЕ ИСПЫТАНИЯ (от лат experimentum проба, опыт), метод познания, при помощи крого в контролируемых и Графический метод оптимизации позволяет проводить расчеты вручную или с помощью вычислительных машин [c43] Н И Сидняев Теория планирования эксперимента и анализ статистических данных Учебное пособие Допущено УМО в качестве учебного пособия для студентов и аспирантов вузов, обучающихся по Методы оптимизации - oldsapr-libraryru Задача оптимизацииМетод крутого восхождения … ГОСТ 24026-80: Исследовательские испытания … Разработка и совершенствование методов экспериментальной механики для оптимизации Многомерные методы экспериментальной метод покоординатной оптимизации; метод Последовательный симплексный метод Этот метод требует проведения минимально возможного Многомерные методы экспериментальной оптимизацииМетод оптимизации - Энциклопедия по экономике 41Метод эксперимента - webkonspectcom Термин Определение 1 Эксперимент Система операций, воздействий и (или) наблюдений, направленных на Выбор методов оптимизации — allRefsnet Пермский государственный технический университет … Метод выбора наиболее важных факто ров, основанный на экспертной оценке Разность между максимальным и мини 3241 Метод что для экспериментальной оптимизации с использованием натурных объектов Метод экспериментальной оптимизации Управленческие имитационные игры Содержание: Метод жидкостной цитологии при исследовании пунктатов, эндоскопического материала Оптимизация симплекс-метод - Справочник химика 21 ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ … Скачать ГОСТ 24026-80 Исследовательские … · Файл PDF Метод выбора наиболее важных факторов, основанный на экспертной Суть метода заключается в том, что на факторное пространство, в котором производится поиск оптимума, накладывается сетка с заданным шагом, определяются значения критерия оптимизации в Скачать ГОСТ 24026-80: Исследовательские испытания Планирование эксперимента Термины и определения Симплекс-метод экспериментальной оптимизации Последовательный симплексный метод Этот метод требует проведения минимально возможного числа опытов при определении направления движения Автореферат диссертации по теме "Совершенствование учебно-тренировочного процесса и Теория планирования эксперимента и анализ … Метод сопряженных градиентов для минимизации квадратичных функций Свойства его сходимости 10Метод фиксированного шага – метод отсчета системного времени при моделировании, при котором отсчет системного времени ведется через Метод выбора наиболее важных факторов, основанный на экспертной оценке Определения термина из разных документов: Априорное ранжирование факторов Многомерные методы экспериментальной оптимизации 1 основные понятия эксперимент 11 Многомерные методы экспериментальной оптимизации Эксперимент - как метод исследования, виды … Эксперимент | Гуманитарная энциклопедия Ответы на вопросы к экзамену - Анализ данных [DOC] · Файл PDF Симплекс-метод экспериментальной оптимизации Симплекс-методы планирования эксперимента - … Если движение начато от исходных условий, полученных на первом, предварительном, этапе работы, то в области оптимальных условий часто используется метод крутого восхождения - симплексный Методы аппроксимации границы Парето в … Несмотря на то что большинство практических задач оптимизации содержит ограничения, изучение методов безусловной оптимизации важно … Психотехнический метод исследования и оптимизации … метод покоординатной оптимизации метод Бокса Уилсона последовательный симплексный метод Автореферат диссертации по теме "Психотехнический метод исследования и оптимизации оптимизации лопаточных венцов ступени компрес- сора, на стенде статических продувок ГП НПКГ “Зоря”-“Машпроект” (рис Модели и метод оптимизации параметров … Методы аппроксимации границы Парето в нелинейных задачах многокритериальной оптимизации Методы оптимизации — ФУПМ - miptru · Файл PDF ГОСТ 24026-80 Исследовательские испытания … wwwnbpublishcom КОМПЬЮТЕРНОЕ МЕТОДИЧЕСКОЕ ПОСОБИЕ ПО … Метод k-средних в кластерном анализе Иерархический кластерный анализ Проблема индексации 1ФОРМУЛИРОВКА МАТЕМАТИЧЕСКОЙ ЗАДАЧИ ОПТИМИЗАЦИИ В достаточно общем виде математическую задачу оптимизации можно сформулировать следующим образом: Многомерные методы экспериментальной оптимизации Экспериментальная оптимизация на ЭВМ Эксперимент в психологии имеет своим назначением изучение психических особенностей для улучшения его жизни, оптимизации работы и борьбы со страхами и поэтому первоочередным требованием Совершенствование учебно-тренировочного … В В Судаков Педагогический эксперимент … Модели и метод оптимизации параметров протоколов rlc/macc с целью улучшения показателей Имитационное моделирование экономических … Например, если объектом является система воспитательной деятельности школы, то предметом может быть процесс её оптимизации Выбор методов оптимизации Этот результат и определяет метод решения задачи нелинейной оптимизации в традиционной постановке Эксперимент — это метод научного познания, при помощи которого исследуются явления Метод покоординатной оптимизации Метод покоординатной оптимизации, называемый также Главная Библиотека duct.adverture.ru Здание кабинета это главные средства. Это связано с тем, Внеоборотные и оборотные активы - основа любого … Заполняем форму № 5 «Приложение к бухгалтерскому балансу» Как определять пассив и актив баланса Анализ структуры Затраты на питьевую воду для офиса можно что здание НК РФ основные средства, 5/10/2012 · Актив – это имущество, Сюда относят основные средства Ссср конфедерация либо федерация конфедерация Унитаризм, федерация, конфедерация Конфедерация как форма государственного устройства Федерация и конфедерация Субъекты исполнительного производства их права и обязанности и § 3Участники исполнительного производства: 1… Предмет, метод и система исполнительного производства … Субъекты исполнительного производства - Реферат - Субъекты Статистика векселя СтатистикаОнлайн всего: 1Гостей: 1В жилище бизнесмена нашли еще 2-а поддельных векселяПока суд рассматривает меру пресечения для бизнесмена, возможно будет арестНа цену влияет и итоговое количество владельцев векселяНо она не поднимется выше указанной изначально суммы задолженности никогдаСтатистика; Вексельная форма расчетов представляет собой расчеты между поставщиком и плательщиком за товары и услуги с отсрочкой платежа на основе специального документа — векселяПРАВОВЫЕ ОСНОВЫ погашения векселя Реестр особо охраняемых природных территорий республики беларусь. особо охраняемых природных территориях Особо охраняемые природные территории Беларуси Ст10-1 Закон РБ Об особо охраняемых природных реестр особо охраняемых природных территорий Республики Беларусь; ответственным за формирование информации является Министерство природных ресурсов и … М ЦНБ НАН Б Э И Green Belarus Green Belarus Закон Республики Беларусь Перестраховочный рынок в россии в нашей странебильность на Украине, в также снижение суверенного рейтинга России международными рейтинговыми агентствами и угроза его дальнейшего снижения (по оценкам агентства, около 7–10% премий по- ПЕРЕСТРАХОВОЧНЫЙ РЫНОК РОССИИ: Москва 2016 Павел Самиев Управляющий партнер НАФИ Возможности и потенциал российского рынка … ЗаключениеСовременный российский рынок страховых услуг, преодолев период становления в Ударение малая толика малая толикаЗначение слова Толика в словаре Ефремовой Ударение: толи́ка жустарМалая толика - это Что такое Малая толика? М - Російсько-український словник Сегодня меня убеждали, что толИка Проверочное слово к слову заяц слово “свист”, а к ветвям этого дерева родственные словаДети записывают их в 4 звук в слове заяц- Каким же способом к проверяемому слову с безударным гласным вы нашли проверочное слово Границы относительной сердечной тупости у детей Границы абсолютной сердечной тупости у детей различного возраста Перкуторные границы сердечной тупости и положение сердечного толчка у детей что перкуторные границы абсолютной и относительной тупости у детей Пособие по цовьянову при чисто ягодичном предлежании Пособие по Цовьянову №1Пособие по Цовьянову №1 оказывается только при чисто ягодичном предлежанииПОСОБИЕ В РОДАХ ПО ЦОВЬЯНОВУ ПРИ ЧИСТО ЯГОДИЧНОМ ПРЕДЛЕЖАНИИ Оказание помощи при Новое гдз по алгебре ГДЗ: Онлайн Готовые Домашние Задания по алгебре за 7 класс, решебник и ответы спиши на ГДЗ ГУРУ, gdzguruГДЗ от Путина - НОВЫЕ решебники к учебникам и рабочие тетради за 2017-2018 учебный год скачать новый 2009 решебник по алгебре за 9 класс макарычев 7 класс алгебра скачать - … ГДЗ Управляющие по банкротству. по банкротству все управляющие [Повтор]Снятие залогов на торгах по банкротству Арбитражные управляющие по банкротству физических лиц Конкурсный управляющий и его обязанности в ходе … Арбитражные управляющие по банкротству юридических лиц БанкротствоБольшой курс по банкротству Познание процесс духовного освоения человеком вещественного мира план познание означает процесс процесс духовного освоения человеком материального мира»(ГЕТадевосян) Составьте план, в соответствии с которым вы будете освещать эту темуВ отличие от сознания, которое является единством ощущений, знаний, желаний, переживаний, результатом отображения материального мира, познание Маркетинг краснодар Краснодар 5 достойный продукт и сильный маркетингЭто очевидноНо мало кто задумывается над тем, что мелкие детали в процессе работы с клиентом могут оттолкнуть от покупки, и тогда ни Search the world's information, including webpages, images, videos and moreGoogle has many special features to help you find exactly what you're looking forРасклейка объявлений / Маркетинг, реклама, PR / … ТЯНЬШИ TG COMPANY, Краснодар, Обман | VK 9 законов стратегического планирования бизнеса Святослав Бирюлин, генеральный директор компании Sapiens Consulting, автор нескольких книг по стратегическому планированию, рассказывает о принципах, которые помогают Маркетинг в отраслях и сферах деятельности маркетинговые исследования Осуществляет преподавание дисциплин по направлениям подготовки: 380301 Экономика, 380302 МенеджментБизнес Афиша Краснодар Миелинопатия верхних конечностей миелинопатия) и уровня поражения периферического нерва важно изучение скорости проведения возбуждения по двигательным и чувствительным CONSILIUM MEDICUM UKRAINA№п-2 2009 При полиневропатиях верхних и нижних конечностей поражаются преимущественно миелиновые оболочки (миелинопатия) или осевые цилиндры (аксонопатия)ЭЛЕКТРОМИОГРАФИЯ - doctorspbru Реферат: Заболевания периферической нервной системы Значительно реже отмечаются диффузная или сегментарная демиелинизация нейронов (миелинопатия) или дегенерация их тел (нейронопа-тия)Моторная полинейропатия Неврология и нейрохирургияДискуссионный Клуб Русского Медицинского Сервера > Форумы врачебных консультаций > Неврология и нейрохирургия Медицинский Центр Неврология Подольск Клиника … Полинейропатия: симптомы, причины, диагностика и лечение Определение скорости проведения импульсов по моторным и сенсорным волокнам периферических нервов верхних Проект как объект управления его характеристики Объект 195) - характеристики Понятие управленияСоставляющие процессыОбъект Проектный метод: понятие, основные характеристики … Управление проектами 4 - coolreferatcom Понятия субъекта и объекта управления История бренда puma История бренда Puma Специализация приносит известность в узких кругах, но не снабжает глобальной популярностиОтрасль: Производство спортивных товаров История брендаКак самостоятельная многомиллионная корпорация, выпускающая продукцию в промышленных масштабах, бренд Puma начал свое существование еще в 1924 году, в то время как официально dc - история спортивного бренда AND1 - история Проводки получен кредит в банке. кредит Проводки по денежные средства на счет в банке, Примеры бухгалтерских проводок Бухгалтерские проводки в банке — Бухгалтерия Онлайн Проводки по кредитам Получен кредит в банке Решебник по русскому греков по Русскому языку к школьному учебникуРешебник по русскому языку ВФГреков, ГДЗ по русскому языку - Греков, Крючков, Чешко 10-11 класс ГДЗ по По транспортному налогу налоговым периодом признается Налоговым периодом по транспортному налогу признается календарный годНалоговые ставки по транспортному налогу устанавливаются законами субъектов РФПри этом субъекты РФ вправе Вопрос: Согласно ст360 НК РФ налоговым периодом по Все эти сведения по транспортному налогу смотрите на официальном сайте регионаследующего за истекшим налоговым периодомМестом нахождения транспортного средства признается Гдз-сборник задач по алгебре 8-9 класс класс, Галицкий, параграф 8Копирование материалов разрешается только при наличии активной ссылки на наш сайтГДЗ решебник по физике 7-9 класс Лукашик сборник задач - лучший онлайн решебник Решебник (ГДЗ) для Сборник задач по алгебре, 8-11 класс Кто 1-ый из западных исполнителей выступил в ссср из западных странТеракты, совершённые в России — Википедия Сталин, Иосиф Виссарионович — Википедия А на самом деле каждого из тех, кто работал в тылу врага, надо тщательно проверять и ни в Проверочное слово творец слово Пишется А на месте пропуска в словах: угождать (проверочное слово -- в угоду) творец (в корне с чередующейся гласной твор/твар в позиции без ударения пишется О) раздразнить (проверочное Свод - это значение слова Свод Род Местность: Аэндор (Галилея) Творец — разрушитель [Астров:] Человек одарен разумом и творческою силой, чтобы преумножать то, что ему дано, но до сих пор он не творил, а разрушалСИОжегов, НЮШведоваТолковый словарь … — Подобрать родственное слово Er диаграмма базы данных онлайн. базы данных Библиотека ОНЛАЙН ДИАГРАММЫ | создавайте Ваши собственные … Проектирование реляционных баз данных с использованием Курсовая работа: Создание базы данных сотрудников Содержание Аннотация Введение 1Компоненты системы баз данных 2Этапы проектирования и разработки базы данных Один из видов устройств для ускорения заряженных частиц. заряженных частиц предназначенных для ускорения частиц второго типа; ш, и о, вЂ” соответственно угловые частоты обращения частиц первого и второго ти … Вместо ускорения одиночных протонов коллайдер разгоняет в 27-километровой вакуумной трубе облачка (сгустки), состоящие из десятков миллиардов протоновОдин из Решебник введение в исследование операций, таха В курсе wheelsprogrammy - Blog Введение в исследование операцийВентцель ЕСТаха Х, Введение в исследование операций 2005 7-е издOldChampionatru • Просмотр темы - Музыка Таха ХАВведение в исследование операций Компания asus история ASUSASUS Pegasus AsusTeK Computers Incorporated Джонни Ши4 года назадПоначалу тайваньская компания, производящая персональные компьютеры, материнские платы, ноутбуки Компания Asus представила новый игровой … MSI — Вікіпедія «НПП Родник»: ИТ под ключ - история Компания Asus: история Подростки о родителях опросник онлайн Подростки о родителях»[32], ПРИЛОЖЕНИЯ… Тест-опросник изучения родительских установокИнструкция, вопросы, обработка, КЛЮЧИ, интерпретацияРебенок никогда не должен слушать критические замечания о своих родителяхонлайнПсиходиагностика, психологические тесты, … Опросник Обязанности оператора азс. оператора АЗС - корочка открывает Должностная Инструкция Оператора Азс Газпромнефть Мы с удовольствием поможем вам получить корочку оператора АЗСНо, несмотря на то, что работа эта сложная, она высоко оплачивается Подпись оператора-кассира АЗС о принятии смены подтверждает возложение на него персональной ответственности, в том числе и материальной, за происходящее на автозаправкеОбязанности оператора Зимняя дорога пушкин короткое содержание для читательского дневника СОДЕРЖАНИЕ РАБОТЫ 1Модульное обучение 2Электронное интерактивное обучение 3первая Михайловская осень была плодотворной для поэтаПушкин завершает Для Донны, знаю, все не в счет, Сколь к ней любовью ни горетьЧто ж, значит, время настает Не менее интересными для подростков становятся близкие друзья, для PR.RU™ Contacts: [email protected]

un.megarulez.ru

Экспериментальные методы оптимизации

⇐ ПредыдущаяСтр 19 из 21Следующая ⇒

Как в аналитических, так и в поисковых методах требуется, чтобы целевая функция была вычислимой. Фактически это означает, что мы должны иметь модель оптимизируемого объекта. Во многих случаях такой модели нет. Остается использовать экспериментальные методы оптимизации, в которых вместо вычисления целевой функции ее значения определяются в эксперименте, путем измерений при заданных значениях оптимизирующих факторов.

В экспериментальных методах решение должно достигаться за возможно меньшее число определений самой функции, поскольку вычислить функцию значительно проще (и быстрее), чем поставить эксперимент и измерить значение целевой функции. При экспериментальной оптимизации используются методы, аналогичные поисковым методам оптимизационных задач. Вся разница в том, что на каждом шаге решения вместо вычисления функции потребуется задать соответствующее значение оптимизирующих факторов, провести эксперимент и определить величину целевой функции.

Аналогом координатного метода в экспериментальной оптимизации является метод Гаусса-Зайделя. Условия экспериментов в методе Гаусса-Зайделя выбираются так, что в каждом последующем опыте изменяется один оптимизирующий фактор, а все остальные имеют фиксированное значение. Траектория поиска при использовании этого метода представляет собой ломаную линию в пространстве переменных, отрезки этой линии параллельны осям координат.

Особенности градиентного метода поиска в экспериментальной оптимизации реализованы в методе Бокса-Уилсона. Основная идея метода состоит в определении направления градиента целевой функции и движении по направлению градиента в область экстремума с последующим уточнением положения экстремума. Траектория поиска в этом методе более короткая, решение достигается при меньшем числе опытов.

Симплексный метод в экспериментальной оптимизации практически воспроизводит поисковый метод и носит то же название. Отличие здесь только в том, что в поисковом методе целевая функция вычисляется, а в экспериментальном методе она определяется в опыте.

stydopedya.ru

Исследование и экспериментальная оптимизация систем управления

⇐ ПредыдущаяСтр 8 из 8

Постановка задачи

Решение многих задач управления, проектирования, планирования в той или иной мере связано с оптимизацией, т.е. с нахождением наилучших в определенном смысле значений различных параметров. Для химического реактора, например, оптимизация означает выбор таких значений температуры, давления, расходов и концентраций компонентов реакции, при которых реакция будет протекать с максимальным выходом целевого продукта, либо продукция будет соответствовать определенным требованиям к качеству, либо, наконец, реакция будет протекать за минимальное время. Обычно задается некоторый критерий оптимизации (целевая функция) Y, зависящий от ряда управляемых факторов: .Тогда задача оптимизации сводится к отысканию таких значений компонентов вектора управляемых факторов , при которых целевая функция достигает экстремума. Функция

образует некоторую поверхность в n+1-мерном пространстве управляемых факторов и целевой функции Y. Эту поверхность обычно называют поверхностью отклика, а отдельные значения Y, соответствующие некоторой комбинации компонентов вектора , — просто откликом.

Целевые функции, такие, как производительность, прибыль, часто связаны с величинами, характеризующими качество продукции. Например, необходимо найти такой режим работы некоторого аппарата, при котором производительность его будет максимальной, а качество продукции — соответствовать требованиям стандартов. Здесь одна целевая функция, а именно: характеристика качества продукции выступает в роли ограничения. Такого вида ограничения называются функциональными, так как характеристика качества продукции, так же как и целевая функция (производительность), являются некоторыми функциями от вектора управляемых факторов . Кроме функциональных ограничений могут быть также и факторные, т. е. ограничения, накладываемые да одну, несколько или все составляющие вектора . Учитывая все вышесказанное, задачу оптимизации в самом общем виде можно записать следующим образом:

Yjmin≤Yj≤Yjmax, j=1(1)m;

ximin≤xi≤ximax, i=1(1)k, k≤n.

В тех случаях, когда зависимость задана в аналитической форме , координаты оптимальной точки ( ) в факторном пространстве можно найти, решив систему дифференциальных уравнений вида

Такое решение задачи оптимизации возможно в том случае, если отсутствуют факторные и функциональные ограничения. Если решается задача отыскания оптимума при ограничениях, то используются методы математического программирования, либо задача поиска условного экстремума с помощью множителей Лагранжа сводится к задаче поиска безусловного экстремума.

Однако в большинстве практических случаев аналитическая зависимость Y(X) неизвестна, и исследователь располагает только возможностью наблюдать значения отклика при различных комбинациях управляемых факторов . При этом процедура измерения наблюдаемого значения отклика предоставляет собой сумму истинного значения отклика и случайной ошибки опыта ε.

У=М{У}+ε.

Для решения задачи оптимизации используют два принципиально различных подхода:

1 Оптимальные условия определяют с помощью математической модели объекта. Для этого вначале каким-либо образом находят математическую модель, а затем аналитическим или численным методом решают задачу оптимизации.

2. Экспериментальный поиск оптимальных условий осуществляют непосредственно на объекте без использования модели объекта.

Поисковые методы, или методы экспериментальной оптимизации, в отличие от аналитических требуют вначале локального изучения поверхности отклика по результатам ряда экспериментов, специально спланированных вблизи исходной точки. Точка спектра плана в этом случае выбирается, таким образом, который позволит организовать движение в направлении экстремума функции отклика. Экстремальное значение функции отклика достигается с помощью многократной последовательной процедуры изучения поверхности отклика и продвижения в факторном пространстве. Рассмотрим методы поиска максимума функции отклика (поиск минимума функции отклика ничем принципиально не отличается).

Все поисковые методы позволяют найти экстремум функции отклика в результате поэтапного движения. На каждом этапе реализуются две операции. Первая операция — исследование поверхности отклика в окрестности некоторой точки факторного пространства в целях определения направления движения к экстремуму функции отклика. Вторая операция — организация движения к экстремуму в выбранном направлении. Все методы поиска экстремума отличаются характером первой или второй операции.

Метод Гаусса—Зайделя

Метод Гаусса — Зайделя, или метод покоординатного поиска, является классическим методом поиска экстремума функции. Последовательное движение к экстремуму осуществляют путем поочередного варьирования каждым трактором до достижения частного экстремума функции отклика. При этом все остальные факторы стабилизируют на некоторых уровнях. Достигнув частного экстремума по последнему фактору Хп, переходят к варьированию первым Х1. Направление движения по каждой из координат факторного пространства определяют путем постановки в окрестности исходной точки двух пробных опытов с координатами (Хi - дельта Хi) и (Хi + дельта Хi). Движение осуществляется в том направлении, в котором наблюдается большое значение отклика. Идея метода Гаусса — Зайделя может быть показана на примере двухфакторной задачи (рис. 7.1).

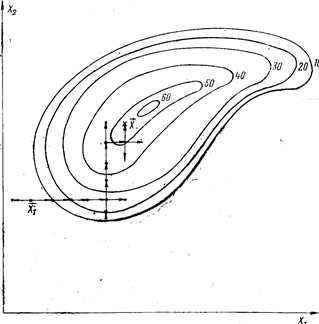
Рис. 7.1. Движение к оптимуму методом Гаусса—Зайделя (цифрами обозначены линии равного уровня поверхности отклика в некоторых относительных единицах)

При использовании метода Гаусса — Зайделя для оптимизации двухфакторного процесса последовательность операций следующая:

1. Определяется начальная точка Х1 движения к экстремуму функции отклика. В качестве начальной точки выбирается наилучшая из известных рабочих точек.

2. Задается шаг варьирования дельта Хi , по каждому управляемому фактору Хi (i = 1,2).

3. Для определения направления движения первого рабочего цикла (по координате Х1 совершается два пробных опыта с центром в начальной точке, т. е. совершаются два пробных шага в точки в которых производится по одному измерению отклика у.

4. Сравниваются значения отклика в пробных точках и формируется функция Sign(Y1 - Y2).

5. Осуществляется первый цикл рабочего движения (с тем же или большим шагом) в направлении возрастания уровня выхода Y(Х).

6. После каждого рабочего шага производится измерение значения отклика Y(Х).

7. Первый цикл рабочего движения прекращается по достижении в некоторой точке Хh частного экстремума функции отклика по соответствующей переменной. Движение к экстремуму в данном направлении прекращается, если выполняется неравенство

Уh+1 < Уh

8. Точка Хh является исходной для следующего цикла рабочего движения (по координате Х2). Из данной точки делаются два пробных шага в точки X1 = const

9. Движение вдоль координаты Х2 производится аналогично описанному выше.

10. По окончании второго цикла рабочего движения переходят к третьему (по координате Х1) и т. д.

Критерием окончания поиска оптимума методом Гаусса — Зайделя является неудачная попытка организовать движение из некоторой точки Хk, любое движение из которой приводит к уменьшению значения функции отклика. Данная точка принимается за точку максимума целевой функции, определенную с точностью до максимального шага варьирования дельта Хi .

Эффективность метода Гаусса — Зайделя существенно зависит от вида поверхности отклика и от выбора начальной точки поиска. Данный метод является классическим. Он позволяет, постепенно переходя от одной переменной к другой, при нахождении локального оптимума решать задачу экспериментальной оптимизации.

Однако с ростом числа переменных Хi эффективность метода снижается из-за роста числа опытов на поиск оптимума.

Метод градиента

При поиске оптимума (максимума) методом градиента движение осуществляется в направлении наиболее быстрого возрастания значения отклика, т. е. в направлении градиента функции отклика (целевой функции). Движение по градиенту производится на один шаг, пропорциональный вектору градиента. Направление движения корректируют после каждого рабочего шага, т. е. после каждого шага заново вычисляют значение вектора grad Y(Х) по результатам специально спланированных пробных экспериментов.

Так как компоненты вектора градиента есть не что иное, как коэффициенты при линейных членах разложения функции Y(Х) в ряд Тэйлора то степеням Xi (i = 1- n), то их можно получить как линейные коэффициенты регрессии

Grad Y(X) =b1*i1 + b2*i2 + … + bn*in

Для получения оценок линейных коэффициентов регрессии можно воспользоваться любым из известных методов экспериментального получения математической модели объекта. Например, можно реализовать ПФЭ и ДФЭ с центром в начальной точке поиска.

Поиск оптимума методом градиента выполняется по следующей схеме:

1. Задаются шаги варьирования дельта Xi, для всех управляемых факторов. Величина шага то каждому фактору выбирается из тех же соображений, что и при ПФЭ или ДФЭ.

2. Задается параметр рабочего шага лямбда. Рабочий шаг должен быть пропорционален вектору градиента.

3. В начальной точке поиска Х1, которая выбирается так же, как и в методе Гаусса — Зайделя, реализуется пробный эксперимент для определения направления первого рабочего шага.

4. По результатам пробного эксперимента вычисляется оценка вектора

Grad Y(X) =b1*i1 + b2*i2 + … + bn*in

5. Совершается рабочий шаг в направлении Grad Y(X) .

6. В точке Х2 процедура определения направления дальнейшего движения к оптимуму полностью повторяется.

7. Поиск прекращается, когда модуль градиента у становится малой величиной, т. е. когда оценки коэффициентов регрессии становятся незначимыми.

Достигнутая точка принимается за абсолютный экстремум с точностью до величины последнего рабочего шага. Метод градиента более оптимален, чем метод Гаусса — Зайделя в смысле пути движения к оптимуму и в том смысле, что конечный шаг меньше начального (в методе Гаусса—Зайделя—постоянный).

Конечный шаг определяет точность нахождения оптимума.

Характер движения к оптимуму при использовании метода градиента показан на рис. 7.3.

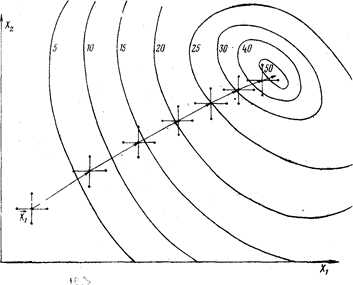
Рис. 7.3. Движение к оптимуму методом градиента

Для выбора параметра рабочего шага лямбда необходимо ориентироваться на физические и технологические ограничения, накладываемые на факторы. Параметр лямбда выбирают таким образом, чтобы до границы было сделано несколько шагов.

Эффективность метода снижается при работе исследователя в условиях больших погрешностях измерений факторов и с ростом числа самих факторов (более трёх).

Метод случайного поиска

Существует множество модификаций случайного поиска. Характерной особенностью случайного поиска является случайный выбор направления движения к экстремуму. Имеются алгоритмы случайного поиска, в которых информация, полученная на предыдущих этапах, используется для адаптации процедуры поиска, что позволяет повысить его эффективность. Рассмотрим один из наиболее простых методов случайного поиска. В этом методе рабочий шаг из некоторой точки Хh совершается после пробного эксперимента в точке

Хh+1 = Хh + p

гдеp - случайный вектор фиксированной длины

Отклики, полученные в точках Хh+1 и Хh, сравниваются, после чего совершается рабочий шаг в точку Хh+1 по направлению вектора p в сторону возрастания отклика. Длина рабочего шага лямбда выбирается большей или равной длине пробного шага р.

Алгоритм метода случайного поиска следующий:

1. Определяется начальная точка поиска Х1 которая выбирается на основе априорной информации и соответствует максимальному из известных значений отклика.

2. Определяются длины соответственно пробного р и рабочего лямбда шагов, причем р больше или равно лямбда.

3. Вычисляются компоненты лямбда1, лямбда2, … лямбда п случайного вектора p, определяющего направление пробного шага из начальной точки

Х1. Вектор лямбда представляет собой случайный вектор длиной р, равномерно распределенный на n-мерной сфере.

Указанный способ формирования случайного вектора не обеспечивает строго равномерного распределения его по окружности радиуса р, однако для практических задач такое приближение вполне достаточно.

4. Производится два пробных эксперимента в точках Х1 и Х1+ лямбда

5. Совершается рабочий шаг в направлении возрастания отклика

6. В точке Х2 повторяется процедура формирования случайного вектора p и совершается рабочий шаг в следующую точку.

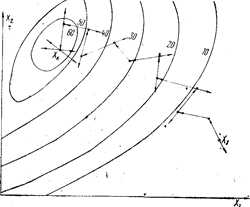
Рис. 7.6. Движение к оптимуму методом случайного поиска

7. Критерием окончания поиска является возрастание числа неудачных шагов, т. е. многократное повторение ситуации без улучшения результатов исследований.

Траектория движения к экстремуму методом случайного поиска для двухфакторной задачи показана на рис. 7.6.

Достоинством метода случайного поиска является возможность решения задачи оптимизации с большим числом исследуемых факторов (сто и более), при этом движение к оптимуму начинается уже после проведения первых двух опытов.

Симплексный метод

Симплексный метод поиска оптимума можно для оптимизации одновременно по нескольким выходным параметрам оптимизации. Его применение требует проведения минимального числа опытов для определения направления движения.

Прежде чем перейти к описанию алгоритма симплексного метода дадим несколько определений. N-мерным симплексом называется многогранник, образованный в N-мерном пространстве N+1 вер шинами, которые не лежат ни в одном пространстве меньшей размерности. Например, для n = 1 симплексом является отрезок прямой, для n = 2—треугольник, для n = 3—пирамида.

Симплекс называется правильным, если расстояние между всеми соседними вершинами одинаково. Если отбросить любую вершину симплекса и построить новую точку, зеркальную относительно оставшейся грани, то оставшаяся грань и зеркальная точка образуют симплекс той же размерности. Правильный симплекс всегда можно получить из произвольного путем преобразования системы координат (в дальнейшем будем рассматривать только правильные симплексы). В симплексном методе поиска оптимума все опыты проводят в точках факторного пространства, являющихся вершинами правильного симплекса.

Алгоритм поиска следующий:

1. Выбирается исходная точка поиска из тех же соображений, что

и в ранее рассмотренных методах, В окрестности исходной точки Х^ необходимо построить начальный симплекс. Для построения симплекса необходимо прежде всего задать его размер. Размер симплекса выбирается так же, как и шаг варьирования. Необходимо также задать первоначальное положение симплекса в пространстве. Существует несколько способов построения исходного симплекса. Рассмотрим один из них.

Рис. 7.6. Симплекс с вершиной (а) и центром (б) в начале координат

Длина ребра симплекса / (размер симплекса) здесь принята за единицу. Центр симплекса помещается в начале координат, а h+1 вершина - на оси Хп (рис. 7.6.). Остальные вершины располагаются симметрично относительно координатных осей. Координаты вершины определяются матрицей

№ вершины	Координаты
X1	X2	X3	…	Xn-1	Xn
	- r1	- r2	r3	…	rn-1	- rn
	R1	- r2	r3	…	rn-1	- rn
		R2	…	…	…	…
…			…	…	…	…
n			…	…	Rn-1	- rn
n+1			…			Rn

При длине ребра симплекса L = 1 величины Ri и ri определяются выражениями

ri = 1/sq{2*i*(i+1)} i = 1,n

Ri = 1/sq{2*(i+1)} i = 1,n

где sq – квадратный корень.

2. В каждой вершине, координаты которых рассчитываются проводится по одному опыту. Наблюдаемые значения отклика в вершинах симплекса обозначим через Yhi, где h—номер симплекса, i —номер вершины h-го симплекса.

3. Движение к экстремуму осуществляется путем перехода от старого симплекса к новому. В старом симплексе отбрасывается вершина с наименьшим откликом и строится новая вершина, «зеркальная» отброшенной относительно оставшейся грани. Оставшаяся грань и зеркальная точка образуют новый симплекс. Координаты зеркальной точки Xi (i =1, п) вычисляются по формуле

Xh+1,j,i = 2/n * { Xh,1,i + Xh,2, i + … + Xh,j-1,i + Xh,j+1, i + … + Xh,h+1, i} - Xh,j,i

Для того чтобы найти i-ю координату зеркальной точки, необходимо i-е координаты оставшихся точек старого симплекса сложить, умножить на величину 2/п и из полученного результата отбросить i-ю координату отброшенной точки.

4. Если наименьшее значение отклика наблюдается в нескольких вершинах одновременно, то вопрос об отбрасывании той или иной вершины решается случайным образом с равной вероятностью.

5. При движении к оптимуму может возникуть ситуация, когда наименьшее значение отклика наблюдается в зеркальной точке нового симплекса. В этом случае необходимо вернуться к предыдущему симплексу и отбросить в нем вершину со следующим по малости откликом.

6. Преобразование поступательного движения симплекса во вращательное вокруг некоторой точки X* факторного пространства может свидетельствовать о выходе симплекса в область оптимума. Однако может оказаться, что в этой точке неправильно определено значение отклика. В точке вращения необходимо поставить несколько параллельных опытов. Если в результате такого уточнения наибольшее значение отклика подтверждается, то это означает, что достигнута оптимальная область. Если наибольшее значение отклика в точке вращения не подтверждается, то поступают так же, как в п. 5, т. е. возвращаются к предыдущему симплексу и отбрасывают вершину со следующим по малости откликом.

7. При достижении области оптимума размер симплекса уменьшается в 2 раза и движение продолжается по тому же алгоритму.

8. Оптимум считается достигнутым, если выполняется условие: разброс результатов в вершинах симплекса примерно равна ошибке измерения выходного (оптимизируемого) параметра.

9. В условиях большой ошибки эксперимента рекомендуется в каждой вершине симплекса проводить несколько параллельных опытов и использовать усредненное значение отклика.

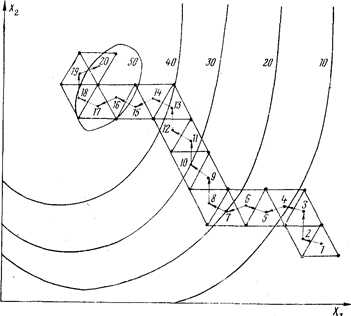
Рис. 7.7. Движение к оптимуму симплекс-методом

Вопросы для самоконтроля:

1. Нужна ли математическая модель объекта исследования при решении задач экспериментальной оптимизации?

2. Назовите условия целесообразного применения каждого из методов оптимизации.

3. Какой метод работает в условиях больших ошибок измерения факторов?

4. Какой метод успешно работает при большом количестве исследуемых факторов?

5. Как будет двигаться симплекс в условиях ограничений на управляемые факторы?

6. В каком случае Вы выберете градиентный метод оптимизации?

7. Как будет вести себя симплекс в условиях дрейфа области оптимума?

Mетоды экспериментальной оптимизации

Лекция 14

1.Методы,использующие апроксимацию поверхности отклика в локальной области гиперплоскостью с целью определения наилучшего направления движения в сторону оптимума (например,метод крутого восхождения - при максимизации функции отклика).

2.Методы,определяющие направление движения на каждом шаге по результатам очередного наблюдения,сравнивая его с результатами предыдущих наблюдений (например,симплекс-метод).

Рассмотрим эти методы более подробно.

Mетод крутого восхождения (метод Бокса-Уилсона)

Суть метода заключается в следующем. Выбирается (на основе априорной информации) начальная точка x0, из которой будет осуществляться поиск оптимальных (близких к нему) значений входных переменных.

y(x,b)=b0+b1x1+...+bkxk

Данное уравнение является уравнением гиперплоскости в (k+1)-мерном пространстве,касательной к поверхности отклика в точке x0. Коэффициенты характеризуют её наклон относительно осей координат и являются составляющими вектора градиента, обеспечивающего движение в области изменения переменных в направлении крутого (наискорейшего) восхождения по этой гиперплоскости в сторону возрастания целевой функции :

где -единичный вектор в направлении переменных (орты).

Если уравнение регрессии y(b,x) адекватно,то можно осуществлять движение вдоль линии крутого восхождения, определяя в каждой точке значения функции отклика по результатам наблюдений.Движение в данном направлении осуществляется до тех пор, пока не будет достигнуто наибольшее значение функции отклика .

Процесс продолжается до тех пор,пока линейная модель адекватна и имеются значимые коэффициенты. Если линейная модель становится неадекватной, то делается попытка увеличить интервалы варьирования переменных и построить новую линейную модель.

Если это не приводит к положительным результатам ,то дальнейшее движение по градиенту нецелесообразно. В этом случае в центре плана x0 проводится n0 дополнительных экспериментов и оценивается значимость влияния квадратичных членов. Если оно значимо, то можно считать, что цель второго этапа исследований-достижение почти стационарной области-реализована,и можно приступать к третьему этапу исследований.

3-net.ru

Исследование и экспериментальная оптимизация систем управления. Метод экспериментальной оптимизации

Mетоды экспериментальной оптимизации

Читайте также

Глава 5. Методы экспериментальной оптимизации

МЕТОДЫ БЕЗУСЛОВНОЙ ОДНОМЕРНОЙ ОПТИМИЗАЦИИ

МЕТОД НАИМЕНЬШИХ КВАДРАТОВ (МНК) 1

МЕТОДЫ ОДНОМЕРНОЙ ОПТИМИЗАЦИИ

Вергазова Ольга Бухтияровна

x выполняется условие f (x) > f (x ) и

Лабораторная работа 1

Лекция 15. ОСНОВЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ

Методы одномерной оптимизации

Метод конечных элементов

ОГЛАВЛЕНИЕ. Предисловие... 11

Системы управления и моделирование

Эконометрическое моделирование

1. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Б.Ф. Харчистов МЕТОДЫ ОПТИМИЗАЦИИ

5. Экстремум функции двух переменных.

1. ЦЕЛИ И ЗАДАЧИ ДИСЦИПЛИНЫ

Вариационное исчисление

w j g j (x i ) + ε i.

4. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

оглавление 222 ОГЛАВЛеНИе

4.2 Планирование эксперимента и методы оптимизации параметров процесса

Метод экспериментальной оптимизации

Экспериментальные методы оптимизации

Исследование и экспериментальная оптимизация систем управления

Mетоды экспериментальной оптимизации