Оптимизация сетевого графика по времени. Оптимизация сетевых графиков
4. Оптимизация сетевых графиков
Оптимизация сетевого графика представляет процесс улучшения организации выполнения комплекса работ с учетом срока его выполнения. Она проводится с целью сокращения длины критического пути, рационального использования ресурсов.
4.1. Перераспределение средств
Оптимизация основана на перераспределении ресурсов из резервной зоны в критическую так, чтобы время выполнения всего комплекса стало минимальным. Переброска ресурсов возможна только между работами, у которых время их выполнения полностью или в большей своей части перекрывается. Снимая часть персонала и других ресурсов с резервной работы и направляя их на критическую работу, мы удлиняем продолжительность выполнения первой работы и сокращаем продолжительность второй.
При выполнении перераспределения ресурсов необходимо учитывать, что из-за ограниченности фронта работ численность исполнителей по отдельно взятой работе не должна возрастать или уменьшаться более чем в 1.5... 2 раза.
4.2. Привлечение дополнительных средств
Оптимизация основана на привлечении дополнительных средств на работы критического пути так, чтобы общий срок выполнения работ был равен директивному, а расход дополнительных средств минимален.
Ход оптимизации следующий. Выбирается работа критического пути, у которой коэффициент роста затрат минимален и производится сокращение ее продолжительности до большей из следующих величин:
своего минимально-возможного значения;
того промежуточного значения, при котором в сетевом графике параллельно данной работе появляется еще одна ветвь критического пути.
Во втором случае дальнейшее сокращение продолжительности одной работы не ведет к сокращению продолжительности критического пути, так как прежняя ветвь критического пути, проходившая через эту работу, исчезает.
Теперь придется сокращать одновременно продолжительности двух работ, лежащих на старой и новой ветвях, критического пути, если окажется, что сумма их коэффициентов роста затрат минимальна.
Можно принять за правило, что претендентами на сокращение продолжительностей являются:
одиночные работы, если параллельно им не появляются новые критические пути в ходе самого сокращения;
две и большее число работ одновременно, лежащие на параллельных ветвях критического путей, существующих до начала сокращения работ или появляющихся в ходе такого сокращения.
В этом случае претендентов на сокращение продолжительности подбирают по минимуму коэффициентов роста затрат одиночных работ и сумм коэффициентов работ, лежащих на параллельных ветвях критических путей.
4.3. Выравнивание занятости работников
В ходе выполнения комплекса работ занятость работников различной категории оказывается неравномерной. Это приводит к завышению потребности в них с одновременным снижением среднего уровня занятости и, как следствие, к перерасходу заработной платы. Оптимизация основана на сдвиге работ в пределах имеющихся у них резервов времени, чтобы, не изменяя общей продолжительности комплекса работ, обеспечить наиболее равномерную занятость работников.
Для приближенного решения этой задачи составляется карта проекта (график перераспределения ресурсов). Каждая работа вычерчивается в масштабе, причем работы критического пути вытягиваются в одну горизонтальную линию. Под стрелкой, изображающей работу, помещается в виде висящего флажка набор чисел, указывающих численность работников каждой категории, занятых выполнением данной работы. Резерв времени работы некритического пути показывается пунктирной линией. В исходной карте проекта все работы начинаются в свои ранние сроки.
Под картой проекта в масштабе строятся диаграммы занятости работников соответствующих категорий, причем части графиков, изображающие занятость на работах критического пути, заштриховываются.
Перемещая те или иные резервные работы вправо по оси времени на некоторую часть или полную величину их резерва времени, следует добиться максимального сглаживания пиков численности работающих каждой категории на всех диаграммах и тем самым получить более равномерную занятость работников.
studfiles.net
Оптимизация сетевого графика по времени
Расчет параметров сетевого графика проекта позволяет выявить критические работы, определяющие ход выполнения всего комплекса работ, продолжительность его реализации, резервы времени событий и работ и проанализировать можно ли его использовать в качестве плана выполнения работ. Чаще всего требуется улучшение сетевого графика с учетом сроков выполнения работ и рационального использования материальных, трудовых и денежных ресурсов, т. е. требуется его оптимизация. Рассмотрим одну из математических моделей оптимизационных задач на сетевых графиках, т.е. оптимизацию проекта по времени.
Пусть задан срок выполнения проекта t0, а расчетное tкр > t0. В этом случае оптимизация комплекса работ сводится к сокращению продолжительности критического пути, которое может быть осуществлено либо за счет перераспределения внутренних резервов, либо за счет привлечения дополнительных средств.
Сокращение времени завершения проекта, как правило, связано с привлечением дополнительных средств (количество рабочих, сверхурочное время). Рассмотрим два примера постановки задачи оптимизации проекта по времени с привлечением дополнительных средств.
Пример решения задачи 1
Постановка задачи 1.Проект представлен сетевым графиком. Для каждой работы известна ее продолжительность tij и минимально возможное время выполнения dij. Пусть задан срок выполнения проекта to, а расчетное tкр > tо. Продолжительность выполнения работы (i, j) линейно зависит от суммы дополнительно вложенных средств хij и выражается соотношением: t’ij = tij - kjjxij. Технологические коэффициенты kij известны.
Требуется найти такие tнij, tоij, хij, чтобы:
- срок выполнения всего комплекса работ не превышал заданной величины tо;
- суммарное количество дополнительно вложенных средств было минимальным;
- продолжительность выполнения каждой работы t’ij была не меньше заданной величины dij.
При выполнении работы используйте данные, приведенные в таблице 6.6.
Таблица 6.6 – Исходные данные по вариантам
| Параметры | Работы | Срок выполнения проекта tо | |||||||||
| 1,2 | 1,3 | 1,4 | 2,4 | 2,5 | 3,4 | 3,6 | 4,5 | 4,6 | 5,6 | ||
| tij | |||||||||||
| dij | |||||||||||
| kij | 0,1 | 0,3 | 0,2 | 0,05 | 0,25 | 0,2 | 0,12 | 0,5 | 0,08 | 0,02 |
Решение задачи
1 Запишем все данные на сетевой график (рисунок 6.4) и рассчитаем сроки свершения событий.
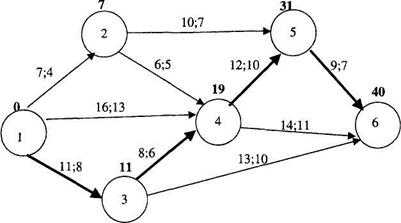
Рисунок 6.4 – Исходный сетевой график
Расчеты показали, что срок выполнения проекта tкр = 40, т.е. превышает директивный срок to = 34.
2 Составление математической модели задачи
Целевая функция имеет вид
f = х12 + х13 + х14 + х24 + х25 + х34 + х36 + х45 + х46 + х56 (min).
Запишем ограничения задачи:
а) срок выполнения проекта не должен превышать tо = 34
t°36< 34; t°46< 34; t°56< 34;
б) продолжительность выполнения каждой работы должна быть не меньше минимально возможного времени:
; ; ; ; ;
; ; ; ; ;
в) зависимость продолжительности работ от вложенных средств:
; ; ; ; ; ;
; ; ; ;
г) время начала выполнения каждой работы должно быть не меньше времени окончания непосредственно предшествующей ей работы:
; ; ; ; ;
; ; ; ;
; ; ; ; ;
д) условие неотрицательности неизвестных:
; ; ; .
3 Технология решения задачи в Excel.
Сделать форму и ввести данные математической модели на рабочем листе Excel в ячейках А1:АЕ40 (таблица 6.7).
Решить данную задачу средствами Excel как оптимизационную с помощью инструмента Поиск решения (рисунок 6.5). В параметрах Поиска решения установить флажки «Линейная модель» и «Неотрицательные значения».
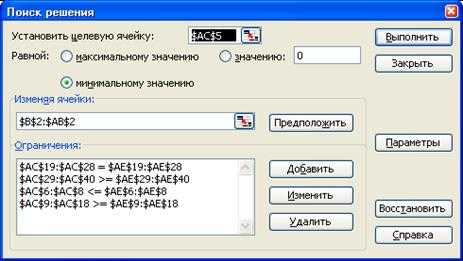
Рисунок 6.5 – Решение задачи с помощью инструмента Поиск решения
Для нашего примера получаем следующие результаты:
; ; ; ; ; ;
; ; ; ; ; ;
; ; ; ; ; ; ; ; ; ; ; ;
; ; ; ; ; ;
.
Результаты оптимизации представим на сетевом графике (рисунок 6.6).
Рисунок 6.6 – Сетевой график в результате оптимизации
4 Анализ полученных результатов.
Чтобы выполнить работы проекта за директивное время to = 34, необходимо дополнительно вложить 24 ден. ед. При этом средства распределятся следующим образом: 10 ден. ед. - в работу (1,3), 5 ден. ед. - в работу (1,4), 5 ден. ед. - в работу (3,4) и 4 ден. ед. - в работу (4,5), что приведет к сокращению продолжительности работы (1,3) на 3 дня, работ (1,4) и (3,4) - на 1 день и работы (4,5) - на 2 дня. Сокращение срока реализации проекта за счет вложения дополнительных средств составит 6 ед. времени.
Пример решения задачи 2
Постановка задачи 2. Проект представлен сетевым графиком. Для каждой работы известна ее продолжительность tij и минимально возможное время выполнения dij. Для сокращения срока реализации проекта выделено В ден. ед. Вложение дополнительных средств хij в работу (i, j) сокращает время ее выполнения до t’ij = tij - kijxij. Технологические коэффициенты kij известны.
Требуется найти такие tнij, tоij, хij, чтобы:
- время выполнения всего комплекса работ было минимальным;
- количество используемых дополнительных средств не превышало В ден. ед.;
- продолжительность выполнения каждой работы tij была не меньше заданной величины dij.
При выполнении заданий воспользуйтесь данными, приведенными в таблице 6.8.
Таблица 6.8 – Исходные данные для решения задачи
| Параметры | Работы | Сумма средств, В | ||||||
| (1,2) | (1,3) | (1,4) | (2,3) | (3,4) | (3,5) | (4,5) | ||
| tij | ||||||||
| dij | ||||||||
| kij | 0,5 | 0,2 | 0,3 | 0,25 | 0,4 | 0,2 | 0,1 |
Решение задачи
1 Запишем все данные на сетевой график и рассчитаем сроки свершения событий (рисунок 6.7).
Рисунок 6.7 – Исходный сетевой график
Видим, что по первоначальному условию tкр = 22, т.е. проект может быть выполнен за 22 ед. времени.
2 Составление математической модели задачи.
Чтобы однозначно записать целевую функцию, добавим на сетевом графике (рисунок 6.8) фиктивную работу (5,6).
Рисунок 6.8 – Измененный сетевой график
Целевая функция имеет вид tкр = t°56 (min).
Запишем ограничения задачи:
а) сумма вложенных средств не должна превышать их наличного количества:
х12 + х13 + х14 + х23 + х34 + х35 + х45< 47;
б) продолжительность выполнения каждой работы должна быть не меньше минимально возможного времени:
; ; ; ;
; ; ; ;
в) зависимость продолжительности работ от вложенных средств:
; ; ; ; ; ; ;
г) время начала выполнения каждой работы должно быть не меньше времени окончания непосредственно предшествующей ей работы:
; ; ; ; ; ; ; ; ; ; ; ;
д) условие неотрицательности неизвестных:
; ; ; .
3 Технология решения задачи средствами Excel.
Сделать форму и ввести данные математической модели на рабочем листе Excel в ячейках А1:АЕ40 (таблица 6.9).
Решить данную задачу средствами Excel как оптимизационную с помощью инструмента Поиск решения (рисунок 6.9). В параметрах Поиска решения установить флажки «Линейная модель» и «Неотрицательные значения».
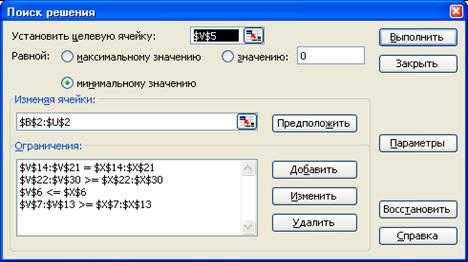
Рисунок 6.9 – Решение задачи с помощью инструмента Поиск решения
Решив данную задачу средствами Excel, получаем следующие результаты:
; ; ; ; ; ;
; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; .
Результаты решения представим на сетевом графике (рисунок 6.10).
Рисунок 6.10 - Сетевой график в результате оптимизации
4 Анализ полученных результатов.
При дополнительном вложении 47 ден. ед. проект может быть выполнен за 12 ед. времени. При этом средства распределятся следующим образом: 4 ден. ед. - в работу (1,2), 5 ден. ед. - в работу (1,3), 8 ден. ед. - в работу (2,3), 10 ден. ед. - в работу (3,4) и 20 ден. ед. - в работу (4,5), что приведет к сокращению продолжительности работ (1,2), (2,3) и (4,5) на 2 дня, работы (1,3) на 1 день, работы (3,4) на 4 дня. Сокращение срока реализации проекта за счет вложения дополнительных средств составит 10 ед. времени.
Задачи для самостоятельного решения
Задача 1
Проект представлен сетевым графиком. Для каждой работы известна ее продолжительность tij и минимально возможное время выполнения dij. Пусть задан срок выполнения проекта to, а расчетное tкр > tо. Продолжительность выполнения работы (i, j) линейно зависит от суммы дополнительно вложенных средств хij и выражается соотношением: t’ij = tij - kjjxij. Технологические коэффициенты kij известны.
Требуется найти такие tнij, tоij, хij, чтобы:
- срок выполнения всего комплекса работ не превышал заданной величины tо;
- суммарное количество дополнительно вложенных средств было минимальным;
- продолжительность выполнения каждой работы t’ij была не меньше заданной величины dij.
При выполнении работы используйте данные, приведенные в таблице 6.10.
Таблица 6.10 – Исходные данные по вариантам
| Номер варианта | Параметры | Работы | Срок выполнения проекта tо | |||||||||
| 1,2 | 1,3 | 1,4 | 2,4 | 2,5 | 3,4 | 3,6 | 4,5 | 4,6 | 5,6 | |||
| tij | ||||||||||||
| dij | ||||||||||||
| kij | 0,05 | 0,2 | 0,25 | 0,08 | 0,15 | 0,1 | 0,06 | 0,05 | 0,1 | 0,5 | ||
| tij | ||||||||||||
| dij | ||||||||||||
| kij | 0,08 | 0,25 | 0,1 | 0,15 | 0,3 | 0,2 | 0,08 | 0,4 | 0,2 | 0,1 | ||
| tij | ||||||||||||
| dij | ||||||||||||
| kij | 0,05 | 0,25 | 0,3 | 0,07 | 0,15 | 0,1 | 0,05 | 0,03 | 0,14 | 0,5 | ||
| tij | ||||||||||||
| dij | ||||||||||||
| kij | 0,25 | 0,07 | 0,1 | 0,2 | 0,13 | 0,15 | 0,06 | 0,4 | 0,2 | 0,1 | ||
| tij | ||||||||||||
| dij | ||||||||||||
| kij | 0,07 | 0,2 | 0,3 | 0,1 | 0,05 | 0,1 | 0,04 | 0,05 | 0,15 | 0,5 |
Задача 2
Проект представлен сетевым графиком. Для каждой работы известна ее продолжительность tij и минимально возможное время выполнения dij. Для сокращения срока реализации проекта выделено В ден. ед. Вложение дополнительных средств хij в работу (i, j) сокращает время ее выполнения до t’ij = tij - kijxij. Технологические коэффициенты kij известны.
Требуется найти такие tнij, tоij, хij, чтобы:
- время выполнения всего комплекса работ было минимальным;
- количество используемых дополнительных средств не превышало В ден. ед.;
- продолжительность выполнения каждой работы tij была не меньше заданной величины dij.
При выполнении заданий воспользуйтесь данными, приведенными в таблице 6.11.
Таблица 6.11 – Исходные данные для решения задачи
lektsia.com
Оптимизация сетевого графика по времени.
Оптимизация сетевого графика по стоимости.
Оптимизация сетевого графика по критериям «время – стоимость»
В реальных проектах каждая работа характеризуется не только временем, но и стоимостью выполнения. В этом случае полная стоимость проекта будет равна сумме стоимостей всех входящих в него работ. Могутбыть поставлены и решены следующие две задачи оптимизации сетевого графика по критериям «время-стоимость»:
1. Минимизация стоимости проекта при сохранении времени его выполнения tkp.
2. Минимизация времени выполнения tkp при заданной стоимости проекта.
При оптимизации сетевого графика предполагается:
1) уменьшение продолжительности работ ведет к увеличению их стоимости;
2) для каждой работы (i, j) ее продолжительность t(i, j) лежит в пределах
a(i, j) ≤ t (i, j) ≤ b(i, j) , где а(i, j) – минимально возможная продолжительность
работы; b(i, j)– максимально допустимая продолжительность выполнения
работы;
3) стоимость С(i,j) работы заключена в пределах Cmax(i, j) и Cmin(i, j).
C(t)
Cmax(i,j)
C(i,j)
Cmin(i,j)
∆C(i,j)
α
a(i,j)
t(i,j)
b(i,j) t
Рис. 3.3. Зависимость стоимости от времени выполнения проекта
Обычно применяют линейную модель зависимости затрат от времени (рис. 3.3). Тогда изменение стоимости работы ∆С(i, j) при увеличении ее продолжительности на величину ∆t(i, j) определяется соотношением
∆С(i, j) = h(i, j) ⋅∆t(i, j), (3.1)
где h(i, j) показывает изменение затрат при изменении времени выполнения
работы (i, j) на единицу и вычисляется по формуле
h (i, j) = tgα =
Cmax (i, j) - Cmin (i, j)
b(i, j) - a(i, j)
. (3.2)
Более точной будет нелинейная модель вида
C ( i , j ) = a⋅t − b
ij
или линейная логарифмическая модель
(3.3)
ln C ( i , j ) = ln a −bln t ij . (3.4)
Ниже будет использоваться линейная модель (3.1).
Задача минимизации стоимости проекта
Минимизация стоимости проекта при сохранении tkp достигается увеличением продолжительности выполнения некритических работ на основе использования их свободных резервов времени, т.к. они не влияют на ранние сроки начала последующих работ. Увеличение продолжительности работы
(i, j) осуществляется на величину
∆tij
до тех пор, пока не будет исчерпан весь
свободный резерв времени, или не будет достигнуто максимально допустимое значение продолжительности работы в (i, j), т.е.
∆t ij
= min{ b ij
− t ij
, R c
( i , j )},
(3.5)
∆C ij
= h ij
⋅∆t ij .
Полная стоимость проекта С = ∑С(i, j) увеличивается на величину
∆С = ∑∆Cij.
Пример 3. Провести минимизацию стоимости проекта, сетевой график которого при заданных значениях продолжительности а(i, j), tij, b(i, j), стоимости С(i, j) и коэффициентов затрат на ускорение hij представлен на рис. 3.4. Первоначальная стоимость проекта 1216 усл. р.
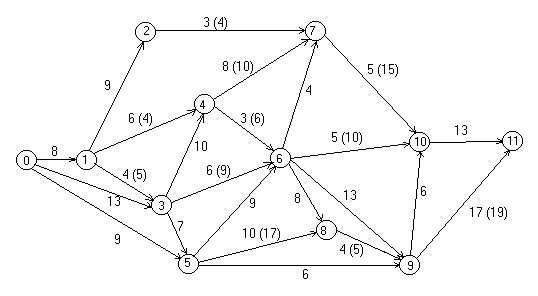
Рис. 3.4. Сетевой график проекта
Решение. Исходные и расчетные значения представлены в табл. 3.3. Заметим, что в таблице приводятся только те работы, для которых Rс(i, j) > 0. В результате оптимизации стоимость нового проекта при том же времени выполнения снизилась на 293 единицы и стала равна 923, т.е. уменьшилась почти на 25%. В результате снижения стоимости проекта появились новые критические пути с tкр = 61: 0-1-3-4-7-10-11, 0-3-5-8-9-11, 0-1-3-4-6-7-10-11,
0-3-5-6-8-9-11 и т.д. В новом графике из 64 полных путей 28 путей будут
критическими.
Таблица 3.3
| Работа (i, j) | aij | tij | bij | Rc(ij) | Cij | hiJ | ∆tij | ∆Cij | tнij = tij + ∆tij | ||||
| 0, 5 | 5 | 9 | 14 | 11 | 60 | 8 | 5 | 40 | 14 | ||||
| 1, 4 | 4 | 6 | 10 | 9 | 28 | 4 | 4 | 16 | 10 | ||||
| 1, 3 | 3 | 4 | 6 | 1 | 37 | 12 | 1 | 12 | 5 | ||||
| 2, 7 | 2 | 3 | 7 | 13 | 86 | 6 | 4 | 24 | 7 | ||||
| 3, 6 | 4 | 6 | 9 | 10 | 92 | 10 | 3 | 30 | 9 | ||||
| 4, 7 | 3 | 8 | 14 | 2 | 48 | 5 | 2 | 10 | 10 | ||||
| 4, 6 | 1 | 3 | 6 | 3 | 64 | 12 | 3 | 36 | 6 | ||||
| 5, 8 | 5 | 10 | 18 | 7 | 15 | 1 | 7 | 7 | 17 | ||||
| 5, 9 | 3 | 6 | 12 | 16 | 86 | 7 | 6 | 42 | 12 | ||||
| 6, 10 | 2 | 5 | 10 | 14 | 44 | 5 | 5 | 25 | 10 | ||||
| 7, 10 | 1 | 5 | 15 | 10 | 74 | 4 | 10 | 40 | 15 | ||||
| 8, 9 | 2 | 4 | 8 | 1 | 20 | 3 | 1 | 3 | 5 | ||||
| 9, 11 | 11 | 17 | 23 | 2 | 40 | 4 | 2 | 8 | 19 | ||||
| Итого | 694 | 293 | |||||||||||
Задача минимизации времени выполнения проекта
Минимизация времени выполнения проекта возможна только за счет сокращения продолжительности выполнения работ, лежащих на критическом пути Lkp. При этом стоимость этих работ и всего проекта увеличится согласно соотношениям (3.1) и (3.6). Для решения этой задачи проводится расчет исходного сетевого графика, а затем выполняется его оптимизация. В начальном сетевом графике продолжительность всех работ может считаться равной максимальному значению (tij = bij). Далее выполняются следующие действия.
10. Составляется список всех полных путей ( алгоритм перебора).
20. Определяется длительность каждого полного пути.
30. Начиная с критических путей, строятся линейные графы всех полных путей с упорядочиванием по убыванию их длительности:
Tkp = T1 > T2 > T3 > … > Tn–1 > Tn.
Сверху над каждой работой записывается hij, а снизу – (tij – aij)
(возможное сокращение ее длительности).
40. Начиная с k = 1, на каждом шаге k составляется список всех
критических путей {Lkkp}. Обозначается их длительность через Tк , а
kp
стоимость сетевого графика обозначается через Ск. Если все tij = aij, то расчеты на данном шаге закончены. Переход к 60.
50. Для путей списка {Lkkp} определяются работы, подлежащие сокращению по двум возможным вариантам 5.1 и 5.2.
Вариант 5.1. Есть работы, общие для всех путей {Lkkp}. В этом случае выбирается одна общая работа для всех путей в {Lkkp}, для которой
минимальна величина hij и продолжительность ее выполнения не равна минимальному сроку:
* = min h ,
h
pq
ij
k
(3.7)
( i , j )∈{ I L
kp ,t ij
> a ij }.
Определяется время сокращения длительности выбранной общей работы
(р,q) в каждом пути {Lkkp}по формуле
∆t = min {tрq – aрq; Тк
кр
– T2}, (3.8)
т.е. сокращение длительности работы не больше ее минимального времени
выполнения и не превышает длительности ближайшего к критическому пути
T2 (шаг 30), не вошедшего в список{Lkkp}. Определяется новая
продолжительность tн
рq
tн
выбранной работы:
рq = tрq – ∆t. (3.9)
Согласно (3.9), длительность всех путей {Lkkp}, содержащих работу (р,q),
снизится на величину ∆t. Определяется новая длина Т к + 1
кр
Т к + 1
к
путей в {Lk
kp}:
кр = Т
кр – ∆t. (3.10)
С учетом изменения времени выполнения работ проводится пересчет
длин всех полных путей:
(Tк + 1 1
kp =T
> T2
> T3
> … > T
n–1
> Tn).
Определяется новая стоимость сетевого графика
Ск + 1 = Ск + hpq ∆t. (3.11)
Зависимость стоимости сетевого графика от длительности критического
пути определяется по формуле
С(t) = C + hpq (Tkp – t), (3.12)
Тк + 1
кр < t < Т
к
кр.
Если новая продолжительность tн
рq
= apq, то при решении задач (3.7)
исключается работа (p, q), поскольку она не имеет больше резерва снижения.
Увеличиваем шаг на единицу, т.е. полагаем k равным k + 1 и
осуществляем переход к шагу 40 до тех пор, пока k ≠ n. Иначе идем к 60.
Вариант 5.2. В списке {Lkkp} нет общих работ. В каждом пути {Lkkp}
выбирается по одной работе с минимальным значением hij;
* = min h
h
pq
ij
, ( i , j )∈{ L kkp
,t ij
> a ij }.
(3.13)
Список этих работ обозначим через Q = {(p, q)}.Определяется длительность сокращения выбранных работ ∆t по формуле (3.8) для всего списка Q.
Определяется новая продолжительность выбранных работы tн по
рq
формуле (3.9) и новое время Тк + 1
кр
для путей {Lk
kp} по формуле (3.10).
Осуществляется пересчет длин всех полных путей (Тк + 1
кр
= T1 > T2 > T3 > … >
> Tn–1 > Tn) с учетом изменения времени выполнения работ. Определяется новая стоимость сетевого графика
Сk +1 = Ck + ∆t ⋅∑ h pq , (3.14)
pq
где сумма берется по всем выбранным работам. Зависимость стоимости сетевого графика от длительности критического пути определяется по формуле
С (t) = C
+ (T k
− t) ⋅∑ h pq , где Т
кр < t < Т
к + 1
кр. (3.15)
к
k kp
pq
Работы, у которых новая продолжительность tн
рq
= apq, исключаются при
решении задачи (3.13), поскольку они не имеют больше резерва снижения.
Увеличиваем шаг k на 1 (k + 1) и осуществляем переход к 40 до тех пор,
пока k ≠ n. Иначе идем к 60.
60. На основе формул (3.12) и (3.15) строится график зависимости
стоимости сетевого графика от длительности критического пути С = С(t).
70. Для определения минимального времени выполнения t* по заданной стоимости С* проекта решается уравнение вида C(t*) = С*.
Сделаем ряд замечаний к данному алгоритму. Дополнительные затраты, связанные с сокращением времени выполнения проекта с t1 до t2, равны C(t2) – C(t1). Для учета шагов алгоритма следует вести таблицу длительности и стоимости работ и длительности полных путей.
Другим вариантом данного алгоритма является случай, когда начальный сетевой график построен при минимальных сроках выполнения каждой работы, а затем последовательно увеличивают длину критического пути, увеличивая сроки выполнения некритических, а затем и критических работ по критерию максимума коэффициента напряженности hij.
Пример 4. Провести минимизацию времени выполнения проекта при
заданных затратах на его осуществление и построить зависимость стоимости от критического времени С = С(t). Исходные данные задачи сведены в табл. 3.4.
Таблица 3.4.
| № п/п | Работы | Продолжительность работ | hij | Стоимость работ при tij = bij | ||
| аij | bij | |||||
| 1 2 3 4 5 6 7 8 9 10 11 | (0, 1) (0, 2) (1, 2) (1, 3) (2, 7) (3, 4) (3, 5) (4, 6) (5, 6) (6, 7) (7, 8) | 10 12 2 2 2 16 8 12 20 8 6 | 20 32 12 7 7 26 13 22 25 13 11 | 6 3 3 8 3 2 6 4 4 5 9 | 35 50 15 10 10 50 15 40 30 25 20 | |
| Итого | 300 | |||||
Находим все полные пути сетевого графика и их длины:
L1: 0 – 1 – 3 – 4 – 6 – 7 – 8, t(L1) = tкр = 99;
L2: 0 – 1 – 3 – 5 – 6 – 7 – 8, t(L2) = 89;
L3: 0 – 1 – 2 – 7 – 8, t(L3) = 50;
L4: 0 – 2 – 7 – 8, t(L4) = 50.
Для удобства дальнейших расчетов представим эти пути графически в
виде цепочек, в которых цифры над каждой работой показывают коэффициенты затрат на ускорение работ hij, а под стрелками – максимально
возможные величины уменьшения продолжительности работ ∆tij = bij – aij.
hij
i j
bij – aij
Ниже построены схемы всех полных путей.
 10. Первоначальная стоимость проекта С = 300. Критическим является путь L2, его длина tкр = 99. Уменьшение продолжительности выполнения комплекса можно только за счёт сокращения продолжительности работ пути L2. Из работ критического пути L2 наименьший коэффициент hij имеет работа (3, 4): h44 = 2. Продолжительность работы (3, 4) можно сократить не более чем
10. Первоначальная стоимость проекта С = 300. Критическим является путь L2, его длина tкр = 99. Уменьшение продолжительности выполнения комплекса можно только за счёт сокращения продолжительности работ пути L2. Из работ критического пути L2 наименьший коэффициент hij имеет работа (3, 4): h44 = 2. Продолжительность работы (3, 4) можно сократить не более чем
на 10 суток. Действительно, ∆ t = min{b34 – a34, Tkp – T1} = min{10,
99 – 89} = 10. При этом изменяется длина только критического пути L2 (с 99 до
89 суток), единственного пути, проходящего через работу (3, 4). Стоимость
всего проекта за счет ускорения работы (3, 4) возрастет на 2⋅10 = 20 единиц и
станет равной 300 + 20 = 320.
Итак, согласно (3.15) получаем
С(t) = 300 + 2(99 − t),89 ≤ t ≤ 99.
Новые длины
путей равны t(L1) = t(L2) = 89, t(L3) = t(L4) = 50, tкр = 89.
20. Есть два критических пути L1 и L2 и сократить срок выполнения проекта можно за счет одновременного сокращения их продолжительности, изменяя продолжительность работ, лежащих на этих путях: либо (0, 1), либо
(1, 3), либо (6, 7), либо (7, 8). Остановимся на работе (6, 7), поскольку при этом обеспечивается минимум затрат на ускорение. Действительно, из работ критических путей L1 и L2 наименьший коэффициент h67 = 5 имеет работа (6, 7).
Продолжительность работы (6,7) можно уменьшить не более чем на
5 дней. Действительно , ∆ t = min{b67 – a67, Tkp – T2} = min{5, 89 – 50} = 5. На
эту величину уменьшатся длины критических путей t(L1) и t(L2), а
следовательно, и срок выполнения проекта. При этом стоимость работы (6, 7)
возрастет на 5⋅5 = 25 усл. единиц, а для всего проекта она увеличится с 320 до
345 усл.ед. Согласно (3.15), получаем С (t) = 320 + 5(89 − t),84 ≤ t ≤ 89.
30. С = 345; t(L2) = t(L1) = 84; t(L3) = t(L4) = 50; tкр = 84. Критическими
являются пути L1 и L2, tкр = 84, {Lkkp} = {L1, L2 }. Из работ на критических путях L1 и L2 наименьший коэффициент hij имеет работа (0, 1): h01 = 6.
Действительно,
hmin(i, j) = min(h(0, 1), h(1, 3), h(7, 8)) = min(6, 8, 9) = 6.
Продолжительность общей работы (0, 1) на этих путях можно сократить
на 10 дней:
∆t = min{b01 – a01, Tkp – T2} = min{10, 84 – 50} = 10.
Согласно (3.15) получаем С(t) = 345 + 6(84 − t),74 ≤ t ≤ 84.
Стоимость работы (0, 1) и всего проекта возрастет на 6⋅10 = 60 единиц,
С01 = 35 + 60 = 95. Новые значения стоимости проекта и длин критических
путей: С = 345 + 6⋅10 = 405, t(L1) = t(L2) = 74.
40. С = 405, t(L1) = t(L2) = 74, t(L3) = 40, t(L4) = 50. Критическими
являются пути L1 и L2. tкр = 74, {Lkkp} = {L1, L2}. hmin(i, j) = min(h(1, 3),
h(7, 8)) = min(8, 9) = 8, hmin = h(1, 3) = 8. Продолжительность общей работы
(1, 3) сокращается на 5 дней:
∆t = min{b13 – a13, Tkp – T2} = min{5, 74–50} = 5.
Согласно (3.15) получаем С(t) = 405 + 8(74 − t),69 ≤ t ≤ 74.
Стоимость работы (1, 3) и всего проекта возрастет на 8⋅5 = 40 единиц,
С13 = 10 + 40 = 50. Новое значение С = 405 + 8⋅5 = 445, t(L1) = t(L2) = 69.
50. С = 445, t(L1) = t(L2) = 69, t(L3) = 40, t(L4) = 50. Критическим являются
пути L1 и L2. tкр = 69, {Lkkp} = {L1, L2}. hmin(i, j) = h(7, 8) = 9. Продолжительность общей работы (7, 8) сокращается на 5 дней:
∆t = min{b78 – a78, Tkp – T2} = min{5, 69–50} = 5.
Согласно (3.15) получаем С(t) = 445 + 9(69 − t),64 ≤ t ≤ 69.
Стоимость работы (7, 8) и всего проекта возрастет на 9⋅5 = 45 единиц,
С78 = 20 + 45 = 65. Новое значение С = 445 + 9⋅5 = 490, t(L1) =t(L2) = 64.
60. С = 490, t(L1) = t(L2) = 64, t(L3) = 35, t(L4) = 45. Критическими
являются пути L1 и L2. tкр = 64, {Lkkp} = {L1, L2}. Общих работ на этих путях нет. Можно сократить работы (3,5) и (5,6) пути L1 на 5 дней и работу (4, 6)
пути L2 на 10 дней. Одновременно можно сократить на 5 дней продолжительность работы (5, 6) пути L1 и работы (4, 6) пути L2.
Действительно, ∆t = min{b46 – a46, b56 – a56, Tkp – T2} = min{10, 5, 64 – 50} = 5.
Коэффициенты напряженности этих работ равны соответственно h(5, 6) = 4,
h(4, 6) = 4. Коэффициент затрат на ускорение работ равен h(5, 6) +
+ h(4, 6) = 4 + 4 = 8.
Согласно (3.15) получаем С(t) = 490 + 8(64 − t ),59 ≤ t ≤ 64.
Стоимость работы (4, 6) возрастет на 4⋅5 = 20, а работы (5, 6) на 4⋅5 = 20
единиц: С46 = 40 + 20 = 60, С56 = 30 + 20 = 50. Новые значения С = 490 + 8⋅5 =
= 530, t(L1) = t(L2) = 59.
70. С = 530, t(L1) = t(L2) = 59, t(L3) = 35, t(L4) = 45. Критическими являются пути L1 и L2. tкр = 59, {Lkkp} = {L1, L2 }.
Общих работ нет. Теперь можно одновременно сократить на 5 дней
продолжительность работы (3, 5) пути L1 и работы (4, 6) пути L2:
∆t = min{b35 – a35, b46 – a46 , Tkp – T2} = min{5, 5, 59–50} = 5.
Коэффициенты напряженности этих работ равны h(3, 5) = 6, h(4, 6) = 4
соответственно. Коэффициент затрат на ускорение обеих работ будет равен
h(3, 5) + h(4, 6) = 6 + 4 = 10. Следовательно,
С(t) = 530 + 10(59 − t),54 ≤ t ≤ 59.
Стоимость работы (3,5) возрастет на 6⋅5 = 30, а работы (4, 6) – на 4⋅5 = 20
единиц: С35 = 15 + 30 = 45, С46 = 60 + 20 = 80. Новые значения С = 530 + 10⋅5 =
= 580, t(L1) = t(L2) = 54. Алгоритм продолжается до тех пор, пока есть tij > aij.
Шаги алгоритма представим в табл. 3.5.
Таблица длительности / стоимости работ
Таблица 3.5
| № п/п | Работа | Шаг алгоритма | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
| 1 | (0, 1) | 20/35 | 10/95 | |||||
| 2 | (0, 2) | 32/50 | ||||||
| 3 | (1, 2) | 12/15 | ||||||
| 4 | (1, 3) | 7/10 | 2/50 | |||||
| 5 | (2, 7) | 7/10 | ||||||
| 6 | (3, 4) | 26/50 | 16/70 | |||||
| 7 | (3, 5) | 13/15 | ||||||
| 8 | (4, 6) | 22/40 | 17/60 | |||||
| 9 | (5, 6) | 25/30 | 20/50 | |||||
| 10 | (6, 7) | 13/25 | 8/50 | |||||
| 11 | (7, 8) | 11/20 | 6/65 | |||||
| Стоимость проекта | 300 | 320 | 345 | 405 | 445 | 490 | 530 | |
Ниже представлены длительности полных путей на различных шагах алгоритма (табл. 3.6.)
Таблица длительности полных путей
Таблица 3.6
| Длительность полных путей | Шаг алгоритма | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| T(L1) | 99 | 89 | 84 | 74 | 69 | 64 | 59 |
| T(L2) | 89 | 89 | 84 | 74 | 69 | 64 | 59 |
| T(L3) | 50 | 50 | 50 | 40 | 40 | 35 | 35 |
| T(L4) | 50 | 50 | 50 | 50 | 50 | 45 | 45 |
Теперь, построив функцию С(t), можно определить время выполнения проекта t* для любых затрат С* и наоборот.
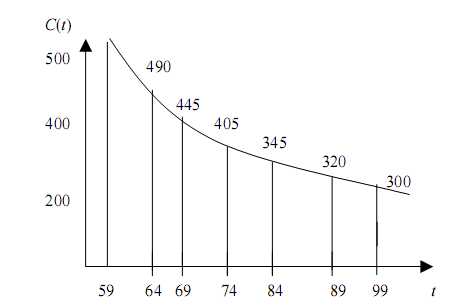
59 64 69 74 84 89 99 t
Например, из шага 30 следует, что при стоимости проекта С* = 375 усл. р.
минимальная продолжительность проекта будет равна t* = 79 дней, а из шага
70 видно, что при стоимости С* = 540 усл. р. t* = 55 дней.
С помощью функции С(t) можно оценить и дополнительные затраты, связанные с сокращением сроков завершения проекта. Так, сокращение продолжительности проекта с 79 до 55 дней потребует дополнительно 540 –
– 375 = 165 усл. р.
В заключение сделаем следующее замечание. При линейной зависимости стоимости работ от их продолжительности задача оптимизации сетевого графика может быть поставлена в виде задачи линейного программирования, в которой необходимо минимизировать стоимость проекта при двух группах ограничений. Первая группа ограничений- ограничения на время выполнения работ, вторая группа ограничений показывает, что продолжительность всех полных путей не должна превышать заданного времени выполнения проекта. Однако решать такие задачи линейного программирования классическими методами неэффективно.
studfiles.net
Методы оптимизации сетевых графиков
В практике планирования руководящие органы часто еще до составления и анализа сетевого графика КР устанавливают директивный срок его окончания Tд. После составления и анализа сетевого графика КР возможно получения трех результатов:
Ткр=Тд (приведенный сетевой график)
Ткр<Тд (приемлемый сетевой график)
Ткр >Тд (неприемлемый сетевой график). В этом случае необходимо оптимизировать сетевой график с целью сокращения Ткр до выполнения условия Ткр Тд
Сокращение Ткр может быть достигнуто путем:
замены последовательного выполнения работ параллельным там, где это допускается характером работ и организационных условий
перераспределения ресурсов между работами, не принадлежащими критической зоне КР, и работами критического пути.
При оптимизации сетевых графиков с вероятностными оценками продолжительности работ необходимо рассчитать вероятность выполнения всего комплекса работ и наступления его событий в заданные сроки.
Для таких графиков Tкрявляется математическим ожиданием срока завершения всей разработки, а сам этот срок подчиняется нормальному закону распределения.
(t) - Критическая продолжительность
TД
TфкрTКР. t
Если задано Tд(директивный срок), то вероятность того, что работа будет выполнена заTд определяется площадьюP(TфкрTд), гдеTфкр- фактическая продолжительность выполнения КР.
Принято считать, что выполнение КР уложится в директивный срок, если значение P(TфкрTд) находится в пределах 0,35-0,65.
Оптимизация сетевого графика методом «время - затраты».
Данный метод состоит в установлении оптимального соотношения между продолжительностью и стоимостью выполнения КР и основан на использовании имеющихся для работ каждого вида зависимостей «время - затраты».
C
cmax
cmin
tmin tmax
Зависимость имеет нелинейный характер, причем с сокращением продолжительности работы стоимость ее возрастает за счет снижения эффективности использования ресурсов и труда исполнителей при увеличении их количества на данной работе. Для каждой работы имеется свой график «время - затраты» и установлены пределы изменения ее продолжительности:tmin- практически возможное минимальное время выполнения работы,tmaх - практически допустимое максимальное время выполнения работы, превышение которого снова приводит к возрастанию стоимости работы за счет чрезмерно низкой интенсивности ее выполнения.Для упрощения расчетов осуществляется линейная аппроксимация и определяется коэффициент приростастоимости каждой работы, характеризующий величину приращения ее стоимости при сокращении времени ее выполнения на единицу:
Возможны два варианта оптимизации сетевых графиков методом «время - затраты»
Получение минимальной стоимости КР без увеличения его общей продолжительности. Для этого на графике выделяют работы, имеющие свободные резервы времени, в их пределах увеличивают продолжительности этих работ, получая при этом уменьшение стоимости их выполнения .
Сокращение продолжительности выполнения КР за счет некоторого увеличения его стоимости. В данном случае за счет некоторого увеличения стоимости работ критического и подкритических путей сокращают время выполнения этих работ, а следовательно, и продолжительность критического пути.
Оптимизация по численности
Во многих случаях численность работников, участвующих в разработке, фиксирована и не может превышать списочную численность работников подразделения, но график распределения занятости работников во времени таков, что в отдельные периоды времени требуемая численность превышает списочную. Для устранения этого начало и окончание некоторых работ могут сдвигаться в сторону увеличения сроков выполнения, таким образом, чтобы получить более равномерную загрузку работников и уложиться в списочную численность подразделения. Такой сдвиг сроков выполнения может оставаться в пределах резервов времени этих работ.
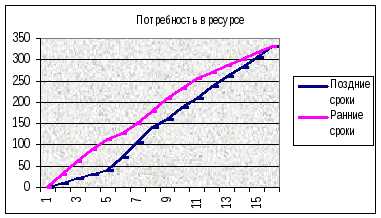
В целях такой оптимизации возможно использование временных диаграмм, выражающих степень занятости персонала в некоторый момент времени:
В приведенной ниже табл. представлен ленточный график выполнения данного комплекса работ (график построен при условии, что все работы комплекса начинаются в наиболее ранние сроки). Символом “x” отмечены резервы времени по каждой из работ комплекса.
Используя ленточный график можно определить потребность в ресурсах на каждую неделю, путем суммирования ресурсов, задействованных на работах.
Таблица
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | ||||
| 0-1 | Сбор и обработка заказов на прибор | 3 | 20 | 20 | 20 | 20 | x | x | x | x | x | x | ||||||
| 0-2 | Подготовка производства | 5 | 10 | 10 | 10 | 10 | 10 | 10 | ||||||||||
| 1-3 | Уточнение спецификации по заказам | 2 | 5 | 5 | 5 | x | x | x | x | x | x | |||||||
| 1-4 | Оформление договоров | 1 | 7 | 7 | x | x | x | x | x | x | x | x | x | x | ||||
| 2-3 | Установление требований | 1 | 8 | 8 | x | x | x | x | x | |||||||||
| 2-5 | Производство приборов | 10 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | |||||
| 3-4 | Рассылка заказчикам спецификации | 2 | 6 | 6 | 6 | x | x | x | x | x | x | |||||||
| 3-5 | Подготовка технической документации по приборам | 4 | 8 | 8 | 8 | 8 | 8 | x | x | x | x | x | ||||||
| 4-5 | Подготовка комплекта ЗИП | 1 | 2 | 2 | x | x | x | x | x | x | ||||||||
|
| Потребность в ресурсе (трудовые ресурсы) |
|
| 30 | 30 | 30 | 22 | 15 | 23 | 29 | 29 | 25 | 23 | 15 | 15 | 15 | 15 | 15 |
По такой диаграмме видно, в какие моменты времени требуемая численность превышает списочную. С учетом резервов времени можно сдвигать некоторые работы, добиваясь минимизации требуемой численности работников.
studfiles.net
39. Оптимизация сетевых графиков
Процесс корректировки сетевого графика (оптимизация) - это последовательное улучшение сети с целью достижения заданного срока или равномерного распределения различных видов ресурсов (трудовых, материально-технических, финансовых и др.) с учетом имеющихся ограничений.
Первоначально сеть корректируется по критерии «время» без учета ограничений по другим видам ресурсов. По достижении заданного срока приступают к корректировке распределения других критичных видов ресурсов. Очередность корректировки по отдельным видам ресурсов устанавливается в зависимости от значения каждого из них в конкретных условиях. Чаще всего лимитирующими являются: время, людские и финансовые ресурсы.
После каждой оптимизации производится проверочный расчет всех временных параметров сети, заново определяются: критический путь, количество критических работ, возрастающее с каждой оптимизацией, и резервы времени ненапряженных работ, которые используются для последующей корректировки.
Уплотнение сетевого графика (перепланирование) производится обычно несколько раз методом последовательных приближений, т.е. многократным сжатием очередного критического пути, пока не будет достигнут удовлетворительный результат.
Существует несколько методов приведения сетевого графика в соответствие с заданными сроками:
• изменение временных оценок путем замены нормальной продолжительности выполнения работ сокращенной;
• изменение топологии сети вследствие пересмотра технологии выполнения работ;
• расчленение работ и их совмещение во времени.
Корректировка сети по критерию «людские ресурсы»
В практике работы менеджеров сферы малого и среднего бизнеса нередко возникает проблема острой нехватки трудовых ресурсов, которая зачастую приводит к отказу от перспективных, выгодных проектов. Однако в большинстве случаев, используя методы оптимизации сети, потребность в них можно существенно уменьшить без изменений критического пути.
Существуют несколько аналитических и графоаналитических методов оптимизации сетевых графиков по ресурсам. Наиболее часто используется на практике графоаналитический способ оптимизации сетевого графика. В случае оптимизации по критерию «людские ресурсы» порядок корректировки будет следующий.
На первом этапе осуществляется расчет параметров сети: продолжительность критического пути, ранних и поздних сроков начала и окончания работ, полных и частных резервов работ. Если полученные расчетные параметры удовлетворяют поставленным требованиям и не требуется проведение корректировки сетевой модели по критерию «время», то возможен переход ко второму этапу.
На втором этапе на основе сети строится линейный график выполнения работ с выделением работ, принадлежащих критическому пути, резервов времени и указанием ежедневной потребности численности персонала, необходимого для выполнения каждой работы. Численность персонала определяется либо по нормативам, либо путем экспертных оценок. Далее, путем суммирования, определяется ежедневная потребность в персонале для выполнения всех работ.
Третий этап - это использование частного резерва времени, который может быть использован для увеличения продолжительности работы и одновременного уменьшения численности занятых на ней исполнителей. На этом этапе определяется число исполнителей работ (ЛГ.) путем деления трудоемкости работы на сумму ее продолжительности и частного резерва времени. Полученный результат округляется до целого.
studfiles.net
Оптимизация сетевого график - Энциклопедия по экономике
Оптимизация сетевого графика. Если первоначальный вариант сетевого графика не обеспечивает соблюдения заданного (директивного) срока, то следует изменить планируемые параметры сетевой модели, т. е. оптимизировать сетевой график. Необходимо определить наиболее целесообразные способы сокращения и достижения оптимальных сроков выполнения комплекса работ. Для решения этой проблемы могут быть перераспределены имеющиеся или привлечены дополнительные трудовые и материальные ресурсы. При сокращении времени выполнения одной или более работ, лежащих на критическом пути, за счет перераспределения ресурсов производится анализ ненапряженных путей. [c.75] При оптимизации сетевого графика вычисляется коэффициент напряженности работы, который позволяет судить о том, насколько свободно можно располагать имеющимися резервами. [c.75]Имеются и другие методы оптимизации сетевых графиков с применением ЭВМ. [c.48]
Анализ результатов расчета (оптимизация сетевого графика и распределение ресурсов). [c.23]
Операции по составлению расписаний производства работ с решением указанных задач называются оптимизацией сетевых графиков. [c.54]
Оптимизация сетевых графиков [c.54]
Для решения задачи необходимо построить сетевой график строительно-монтажных работ. При построении графика проводятся процедуры, аналогичные описанным в упомянутой методике. Так как процесс строительства буровых хорошо отработан практически, то оптимизация сетевого графика по времени приводится к расчету минимальной продолжительности строительства, которая равна длине критического пути. После определения продолжительности строительства буровой требуется так разместить работы и людские ресурсы, чтобы потребление ресурсов было оптимальным. [c.98]
На рис. 7.6 показан сетевой график, в котором пути, проходящие через работы 0,2 и 2,6 0,1 и 1,3 0,1—1,4— 4,5, имеют одинаковый полный резерв времени (30 дней). Однако коэффициенты напряженности путей, проходящих через эти работы, будут совершенно различными. Соответственно /z,u= 150/180 = 0,833 /г 2 = 30/60 = 0,5 kn3 = = 90/120 = 0,75. Поэтому в случае последующей оптимизации сетевого графика (при прочих равных условиях, например одинаковом составе ресурсов) в первую очередь целесообразно изъять резервы с пути 0,1 и 1,3 как менее напряженного (Ан2 = 0,5). Уменьшение резерва, допустим, на 20 дней сделает первый и третий пути совсем близкими к критическому ( = 170/180=0,944 kB3 110/120— = 0,917), а второй — еще имеющим довольно ощутимые резервы ( П2=50/60=0,833). [c.234]
Для величины рк имеются вполне определенные границы допустимого риска. При pf >0,65 можно утверждать, что на работах критического пути имеются избыточные ресурсы, следовательно, общая продолжительность работ может быть сокращена. При ркперераспределением ресурсов, т. е. оптимизация сетевого графика. [c.235]
Оптимизация сетевого графика в зависимости от полноты решаемых задач может быть разделена на частную и комплексную. Примерами частной оптимизации сетевого графика являются 1) минимизация времени подготовки производства при фиксированных затратах [c.236]
Комплексная оптимизация сетевого графика технической подготовки производства может заключаться в нахождении оптимальных соотношений затрат и сроков выполнения ее стадий и этапов. Здесь многое будет зависеть от конкретных условий (ограничения в людских, денежных и материальных ресурсах или, наоборот, допустимость повышенных затрат при сжатых директивных сроках подготовки). [c.239]
Проведением оптимизации сетевого графика стадия составления исходного плана заканчивается. [c.239]
Оптимизация сетевого графика 236 [c.315]
Седьмой этап - корректировка и оптимизация сетевого графика, построение графика движения ресурсов. [c.50]
Специально организуемые службы СПУ при руководстве всех уровней, а также при вычислительном центре. Это совещательные органы, осуществляющие сбор, обработку и анализ информации, разработку и оптимизацию сетевых графиков, хранение материалов и т. д. Они не вправе давать команды управления, хотя и участвуют в их формировании. [c.170]
Исходные данные, порядок составления, расчет и оптимизация сетевых графиков [c.91]
Оптимизация сетевых графиков позволяет найти пути для своевременного, а в ряде случаев досрочного ввода объекта в эксплуатацию. В свою очередь, досрочный ввод объектов транспорта, хранения п распределения нефти, нефтепродуктов и газа создает условия для более быстрого вытеснения замыкающих менее экономичных видов топлив. [c.95]
Поэтому оптимизация сетевых графиков наряду с сокращенном стоимости строительства должна учитывать изменения в стоимости затрат на замыкающее топливо. [c.95]
Анализ и оптимизация сетевого графика [c.42]
Сетевой график следует проанализировать с целью сокращения критического пути, затрат ресурсов, уменьшения ненужных резервов. Этот процесс предшествует оптимизации сетевого графика. Анализ позволяет оценить целесообразность структуры графика, определить степень сложности выполнения каждой работы, вероятность наступления событий в заданный (директивный) срок, загрузку исполнителей работ на всех этапах выполнения проекта. [c.42]
С учетом выявленных резервов времени производят оптимизацию сетевого графика, направленную на сокращение продолжительности первоначально установленного критического пути. [c.360]
Для расчета критического пути и оптимизации сетевых графиков широко используют электронно-вычислительную технику. [c.362]
Оптимизация сетевых графиков осуществляется на стадии планирования посредством сокращения критического пути, т. е. минимизации сроков выполнения строительных работ при заданных уровнях ресурсов, минимизации уровня потребления материальных, трудовых и финансовых ресурсов при фиксированных сроках выполнения строительных работ. Возможен и смешанный подход для одной части работ (более дорогостоящих) — минимизировать уровень потребления ресурсов при фиксированных сроках выполнения работ, для другой — минимизировать сроки при фиксированном уровне ресурсов. [c.155]
Определение временных параметров работ сетевого графика. Лри этом следует учитывать, что для оптимизации сетевого графика по каждой работе (стрелке) сетевой модели необходимо знать следующие параметры [c.60]
Оптимизация сетевого графика. Привязка работ сетевого графика к календарю. . . [c.62]
Типовые технологические карты в настоящее время составлены на следующие виды работ подготовительные (в нормативных условиях проложения трассы), погрузочно-разгрузочные, сборочно-сварочные (на полевой трубосварочной базе и трассе), гнутье звеньев труб, изоляционно-укладочные, балластировку трубопровода и установку узлов линейных кранов и задвижек. В технологических картах, кроме описания работ, графика их выполнения в нормальных условиях, калькуляции стоимости и правил техники безопасности, дается состав комплексных звеньев и перечень используемых машин и механизмов. Таким образом, технологические карты содержат основную исходную информацию для оптимизации сетевых графиков. [c.78]
Разработка, расчет параметров и оптимизация сетевого графика выполняются на ЭВМ. Для этого можно воспользоваться -стандартным ППП. Технологический процесс создания САПР должен включать операции сообщения сведений в автоматизированную систему сетевого планирования о текущей ситуации на каждой технологической линии процесса с тем, чтобы корректировать его ход с учетом возникающих изменений (первоначально планировавшейся длительности отдельных работ, числа исполнителей и их квалификации, характера работ и взаимосвязей и др.). Автоматизированное планирование и управление процессом создания САПР на основе ППП СПУ позволяет улучшить его характеристики при небольших дополнительных затратах. [c.43]
Она основана на графическом изображении комплекса взаимосвязанных работ, отражающем последовательность и длительность их выполнения, их взаимоувязку и представляющем, таким образом, как бы логическую модель всего процесса создания данного комплекса. Система предусматривает последующую оптимизацию сетевых графиков и их использование для текущего планирования и управления указанными работами. [c.361]
ОПТИМИЗАЦИЯ СЕТЕВОГО ГРАФИКА [c.369]
Оптимизация сетевого графика заключается главным образом в сокращении продолжительности критического пути. [c.369]
В отдельных случаях, главным образом при недостаточности ресурсов, результаты оптимизации сетевого графика могут явиться обоснованным доказательством невозможности уложиться в установленный срок. В таких случаях должен быть решен вопрос о наращивании ресурсов или пересмотре общего объема работ, либо об изменении директивного срока их выполнения. [c.369]
Если расчет сетевой модели показал временные затраты на выполнение задания (в данном [c.99]
Модель оптимизации сетевого графика с учетом налоговых [c.21]
Чем выше значение коэффициента напряженности, тем более жесткими являются временные оценки отдельных работ, а резервы времени на рассматриваемом пути в меньшей степени можно использовать для оптимизации сетевого графика. [c.153]
При анализе и оптимизации сетевых графиков по времени следует учитывать, что концентрация ресурсов на любых работах имеет определенные технологические ограничения - по фронту работ, технологии, технике безопасности и другим соображениям. Кроме того, не следует допускать, чтобы в результате перераспределения ресурсов полностью исчерпывались резервы времени, так как в этом случае возникает большое количество критических путей, график становится напряженным и трудно выполнимым. [c.154]
Важным этапом сетевого планирования является оптимизация сетевого графика. [c.208]
Наиболее часто применяются следую приемы оптимизации сетевых графиков пересмотр перечня работ, перераспределение ресурсов, перенесение их с некритических путей на критический, пересмотр оценок длительности работ, в том числе благодаря повышению уровня оснащенности техническими средствами и повышению степени параллельности выполнения работ. [c.209]
При составлении и оптимизации сетевых графиков всегда следует иметь в виду, что любая работа не может быть начата раньше, чем свершится ее начальное событие. [c.108]
Специально организуемые службы СПУ при руководстве всех уровней, а также при вычислительном центре. Это совещательные органы СПУ, осуществляющие сбор, обработку и анализ информации, разработку и оптимизацию сетевых графиков, хранение документации и др. [c.139]
Большое значение имеет оптимизация сетевого графика, которая представляет собой процесс улучшения организации выполнения комплекса (работ с учетом срока выполнения и использования ресурсов. Она осуществляется путем перераспределения всех видов ресурсов, интенсификации и параллельного выполнения работ критического пути, изменения структуры комплекса работ. Комплексная оптимизация сетевого графика— это нахождение варианта, наилучшего по соотношению затрат и сроков выполнения работ в зависимости от конкретных целей. Критериями оптимизации обычно служат время и затраты. При их использовании устанавливают зависимость между продолжительностью и стоимостью работ. Кроме того, рассчитывают трудоемкость и общую стоимость работ. [c.68]
Оптимизация сетевого графика [c.209]
Оптимизация сетевого графика осуществляется прежде всего за счет свободных резервов времени. Если технология ведения работ и сам характер работ позволяют, изменяя число рабочих, получать разную продолжительность этих работ, то часть рабочих снимается с работ, имеющих резервы времени, и ставится на работы, лежащие на критических и подкритиче-ских путях. При этом продолжительность отдельных работ может увеличиваться на величину их резерва времени, но общая продолжительность процесса уменьшается за счет сокращения продолжительности работ, лежащих на критическом пути. [c.55]
Имеются и другие метода оптимизации сетевых графиков с приме-ненией ЭШ, разработанный ЦШПИАСС Госстроя СССР, НИИ по строительству Госстроя ЭССР и 1ф. [c.56]
Учитывая, что изменение численности работающих по линейным работам при оптимизации может осуществляться только дискретно на величину комплексного технологического звена, при решении вопроса создания нормативной базы для оптимизации сетевых графиков могут быть использованы типовые технологические карты на комплекс работ по строительству линейной части магистральных трубопроводов, составленные ВНИИСТом и Орг-газстроем . [c.78]
economy-ru.info
Оптимизация сетевых графиков
Оптимизация сетевых графиков может производиться по двум направлениям.
1. Оптимизация по времени
Директивное ограничение по времени итоговой продолжительности (Тдир.), определяемой расчетом сетевого графика, связано с сокращением продолжительности критического пути. Это, в свою очередь, влечет за собой сокращение продолжительности отдельных работ, лежащих на этом пути. Однако такое изменение может привести к образованию новых путей, мало отличающихся по продолжительности от прежнего.
Пути графика, отличающиеся по продолжительности критического пути на величину, не превышающую некоторое заданное положительное число 8, называются подкритических
Заполнение оконных и дверных проёмов
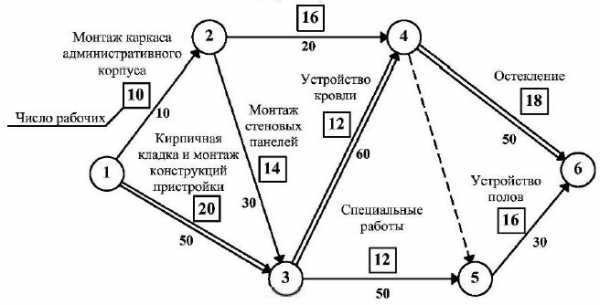
Рис. 18.21 Определение подкритических работ
Определим подкритические пути сетевого графика, изображённого на рис. 18.21, при условии, что б=15 дням.
Мерой критичности работы сетевого графика является полный резерв времени работы. Чем меньше этот резерв, тем больше путь, проходящий через работу. Подкритические пути могут быть определены как состоящие из подкритических и критических работ. Однако не все пути, состоящие только из этих работ, являются подкритическими. В нашем случае подкритическим путём является путь l-2-3-4-6. В нём Tокр.= 150 дням. Пути l-2-3-4-5-6 (Т=130 дн.) и l-3-4-5-6 (Т=140 дн.) не являются подкритическими.
Подкритические работы обозначаются следующим образом (рис. 18.22).
Рис. 18.22 Изображение подкритических работ
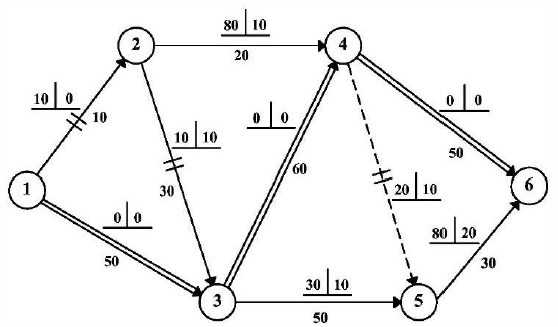
Рис. 18.23 Обозначение подкритических работ графика
Очевидно, что некоторые работы принадлежат и критическим и подкритическим путям сетевого графика. Допустим, что выставлено ограничение на максимальную продолжительность выполнения работ по графику (рис. 18.23) и она не может превышать 140 дн. Эrо на 20 дней меньше расчетной критической продолжительности (Ткр.=160 дней). Существует несколько методов оптимизации сетевых графиков во времени:
I метод предусматривает перераспределение ресурсов с некритических однородных работ на критические.
В примере, приведенном на рис. 18.24, выполнено перераспределение трудовых ресурсов с работы 2-3 на работу 1-3, с работы 2-4 на работу 3-4 и с работы 5-6 на работу 4-6.
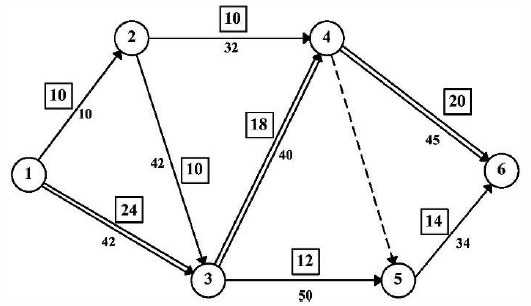
Рис. 18.24 Перераспределение трудовых ресурсов на работах
При этом меняется не только направление критического пути (1-2-3-4-6), но и его продолжительность (Т1кр=10+42+40+45=137 дн. < Тдир=140 дн.).
Ткр=160 дн., Тдир.=140 дн.
II метод предусматривает расчленение и запараллеливание критических работ.
Эти меры продемонстрированы на рис. 18.25. Изменению подлежали работы 3-4 и4-6.
Работа 3'-4 является фиктивной. Работы 3 1-4 1 и 4-4 1 выполняются практически параллельно.
В результате направление критического пути будет 1-3-3 1-4'-6. А его продолжительность Т2кр=50+30+30+25 =135 дн. < Тдuр=140 дн.
III метод предусматривает изменение последовательности и взаимосвязи выполнения отдельных работ (если это возможно)-изменение тополог1Ш сети.
IV метод предусматривает привлечение дополнительных ресурсов извне.
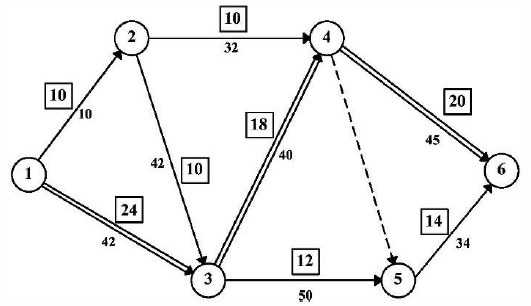
Рис. 18.25 Расчленение и запараллеливание критических работ
2. Оптимизация по ресурсам
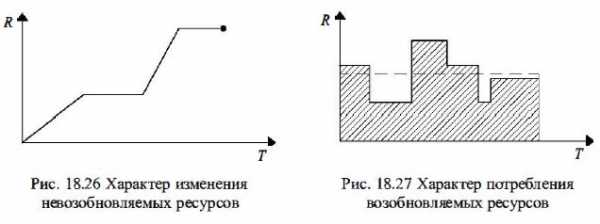
Прежде всего следует заметить, что ресурсы делятся на невознобляемые (финансовые средства, материалы, конструкции) и возобновляемые (людские ресурсы, строительные машины, оборудование).
Как показано на рис. 18.26, потребление невознобляемых ресурсов R во времени Т развивается специфическим образом.
Характер потребления возобновляемых ресурсов во времени приведен на рис. 18.27.
Существует несколько алгоритмов оптимизации графика по ресурсам. Далее приводится один из них.
Алгоритм и рационального распределения ресурсов с постоянной интенсивностью
Алгоритм сводится к отысканию рационального распределения ограниченных ресурсов посредством снижения пиковых суммарных интенсивностей потребления до заданной величины. При решении не всегда можно выдержать ограничение в ресурсах при заданном сроке строительства. Тогда критический путь увеличивают на минимальную величину. Пусть в рассматриваемом примере (для оптимизации выбираем сетевой график на рис. 18.17) имеет место ограничение по рабочим ресурсам. На графике рис. 18.28 над каждой работой (стрелкой) показано число занятых рабочих.
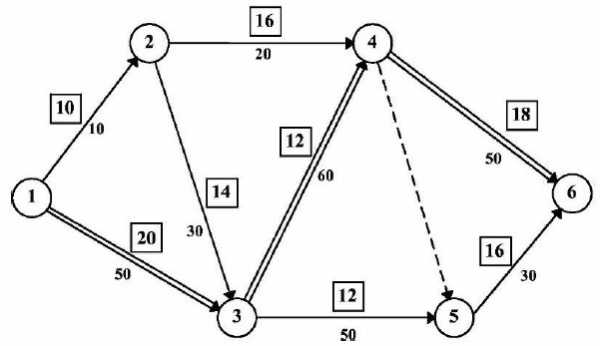
Рис. 18.28 Исходный график для оптимизации по рабочим ресурсам
Пусть максимально возможное число рабочих 36, т.е. max R = 36. Составим линейный график выполнения работ по ранним их началам с обозначением и использованием частных резервов времени. Возможно использование полных резервов времени, но это повлекло бы изменение ранних начал последующих работ (рис. 18.29, а). Построим эпюру потребности в рабочих (рис. 18.29, 6).
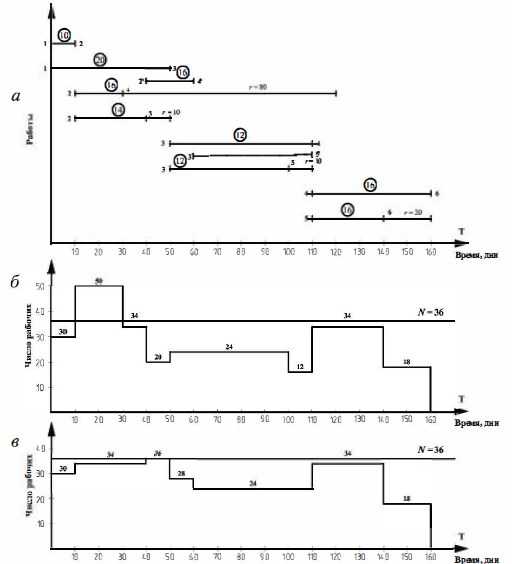
Рис. 18.29 Эпюра потребности в рабочих
Выясняется, что максимум потребности в рабочих равен 50 чел. Рассмотрим последовательно проекции работ в единицу времени. В первый промежуток времени 0-1 число рабочих 30 < max R =36. Во второй промежуток времени
1-2 число рабочих 50. Определим порядок работ в этом промежутке. Он присваивается в последовательности возрастания резервов времени, а при равных резервах- в последовательности убывания интенсивности работ, т.е. работе 1-3 присваиваем 1-й порядок, работе 2-3 2-й и работе 2-4 - 3-й. Складывая последовательно ресурсы на работах, получаем, что суммарный ресурс первых двух работ (34) удовлетворяет заданному ограничению, а в сумме с ресурсом 3-й работы - не удовлетворяет. Следовательно, 3-ю работу за счет её резерва необходимо передвинуть вправо до момента, когда суммарное потребление ресурса станет не больше заданного. Повторяя таким образом обозначенные операции, можно прийти к варианту (рис. 18.29, в), при котором максимальное количество ресурса не превышает заданного (36 чел.).
honneur.ru