ГлавнаяОптимизацияКритерии оптимизации

Критерии оптимизации и ограничения. Критерии оптимизации


Критерии оптимизации

 

Важная сторона оптимизации – это выбор критерия, по которому определяются свойства объекта и который позволяет количественно оценить какое из устройств данного класса является наилучшим.

Критерии в зависимости от назначения устройства могут быть самыми разными.

Так при проектировании фильтра критерий может относиться к его амплитудно-частной характеристике, минимуму потерь в полосе прозрачности и максимуму – в полосе заграждения.

В случае усилителя высокочастотных колебаний такой критерий может быть связан с получением максимального КПД, с соблюдением требования по нелинейным искажениям сигнала.

Несмотря на все разнообразие критериев их можно свести к единой математической записи – функции цели, которая в концентрированной форме отражает смысл решаемой задачи по оптимизации устройства – в наилучшем приближении его характеристик к требуемым согласно определенным признакам.

Все действия в такой программе оптимизации в конечном итоге направлены на получение экстремального значения функции цели – максимального или минимального, в зависимости от поставленной задачи.

Поскольку, как правило, качество устройства определяют несколько критериев (например, в приводимом выше примере с фильтром – максимум в одной полосе, минимум – в другой), то целевая функция является суммой определенного числа членов и по своему виду является взвешенно-аддитивно цифровой, отражающей требование минимального отличия желаемых (иногда идеальных) характеристик от реально получаемых. Составим в обобщенном виде функцию цели.

При исследовании в частотной области для целевой функции, определяемой K критериями, запишем:

 

(6.5)

 

где Фk – частная целевая функция для k-й характеристики;

ψkT – функция, определяющая требуемую k-ю частотную характеристику;

ψkP – функция, определяющая реально полученную k-ю частотную характеристику, зависящую от параметров устройства;

Vk – весовой множитель для k-й характеристики.

Мерой расхождения между требуемой и реальной характеристиками могут являться или минимум суммы квадратов уклонений, или минимаксный критерий. При них функция цели примет вид:

 

(6.6)

 

(6.7)

Кроме того возможен вариант, когда требуется получить максимальное отношение параметров устройства, например Ak к Bk. Тогда функция цели примет вид:

(6.8)

 

Путем определенной процедуры следует найти или минимальное при (6.6) и (6.7), или максимальное при (6.8) значение функции цели. Для определенности рассмотрим первый случай, связанный с получением минимального значения.

Разделим все параметры устройства, определяющие его реальную характеристику ψkP, на две группы: варьируемые (x1,x2,…,xn) и неизменные (y1,y2,…,ym). Соберем варьируемые параметры (их еще называют переменными) в вектор-столбец, который затем преобразуем в транспонированную матрицу:

 

(6.9)

 

Аналогичным образом поступим с постоянными или неизменными параметрами устройства:

(6.10)

Будем рассматривать вектор x как точку или элемент n-мерного действительного пространства Rn. Совокупность объектов x произвольного содержания (точки, векторы, функции и т.д.) составляют множество X, а сами объекты есть элементы этого множества. Совместив понятия точечного множества, составленного из точек х, и n-мерного пространства Rn, можно утверждать, что множество X представляет собой совокупность точек х в многомерном пространстве Rn.

В процессе поиска среди множества векторов x следует найти такой вектор Xопт в пространстве Rn, при котором функция цели (6.6) или (6.7) минимальна:

 

, где x Є Rn (6.11)

 

При этом на вектор х могут накладываться определенные ограничения. Точка xопт соответствует наилучшему в соответствии с выбранными критериями варианту проектируемого устройства. Поиск xопт относится к классу задач, объединяемых теорией нелинейного программирования. При этом вектор х во всех рассматриваемых ниже задачах ограничен определенным пространством Rn, что можно следующим образом представить в развернутом виде:

 

x1мин ≤ x1 ≤ x1макс, ……….xn.мин ≤ xn.макс (6.12)

 

При функции цели в виде (6.8) выражение (6.11) примет вид:

 

Fц (xопт,y)=maxF(x,y), где x Є Rn (6.13)

 

Перейдем к рассмотрению путей нахождения xопт.

 

Похожие статьи:

poznayka.org

Критерии оптимизации

В зависимости от вида подынтегральной функции 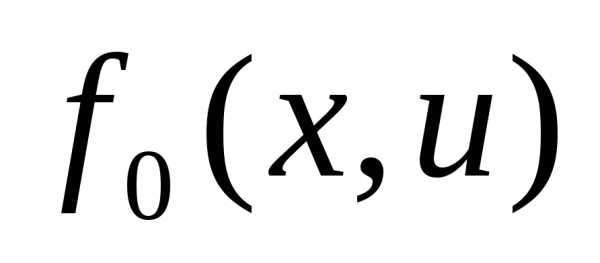функционала:

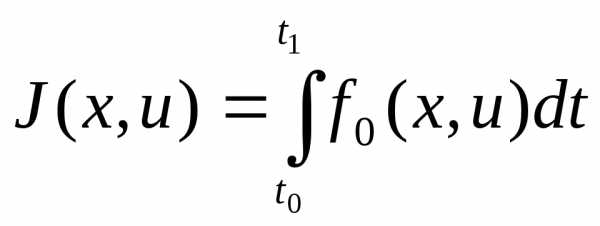(1)

могут быть получены различные критерии применяемой проектируемой автоматической системой.

Одним из наиболее распространенных критериев является время переходного процесса объекта управления из заданного начального состояния 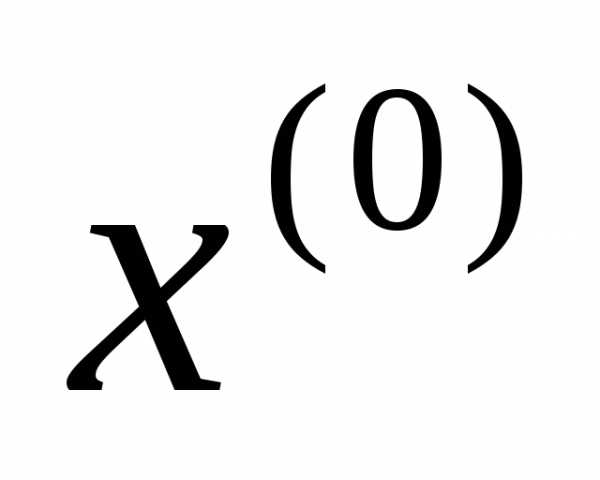в конечное состояния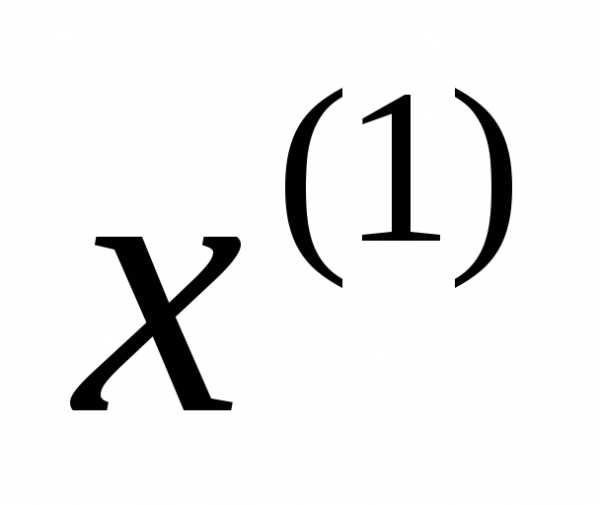. Чтобы получить критерий, нужно положить подынтегральную функцию:

Тогда мы получим следующий критерий оптимизации:

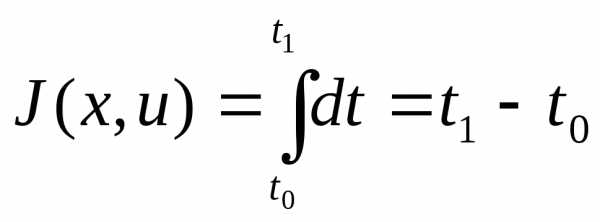(2)

Другой широко распространенный критерий оптимальности – это квадратичный критерий:

(3)

Здесь:

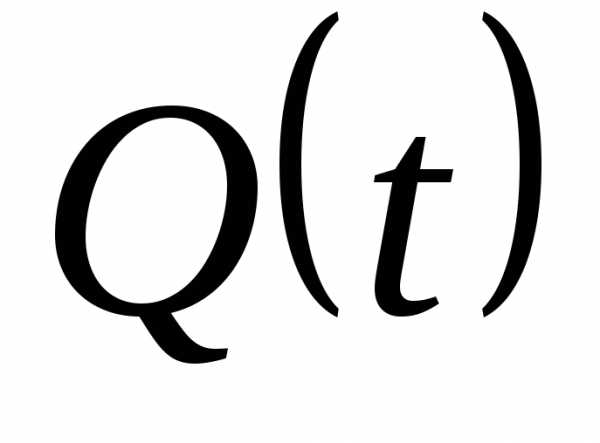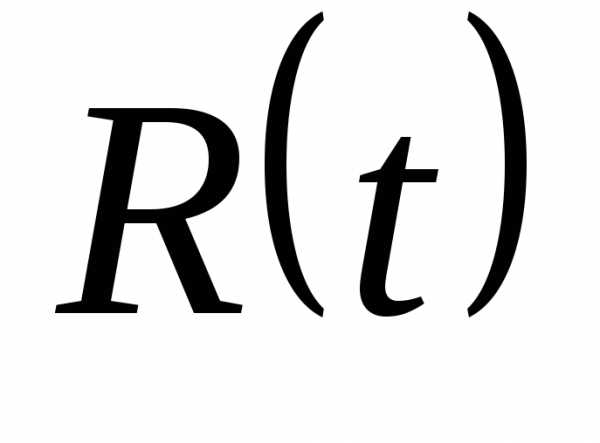,и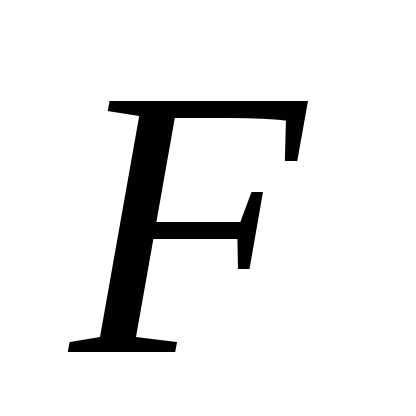- симметричные матрицы соответствующих размерностей,,;

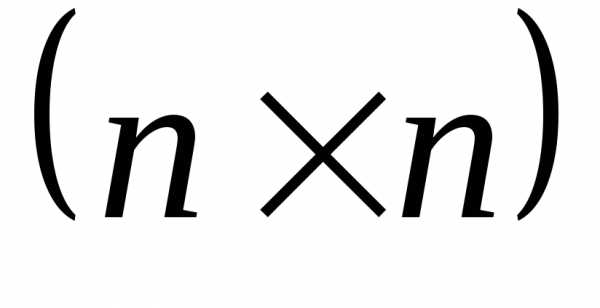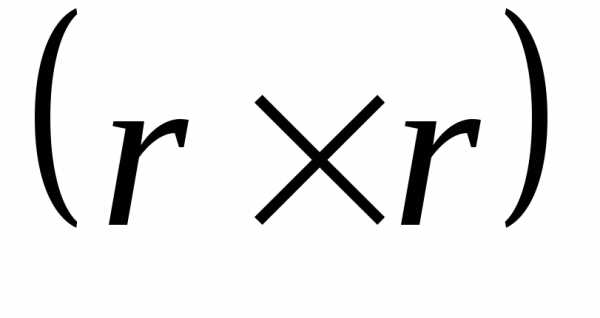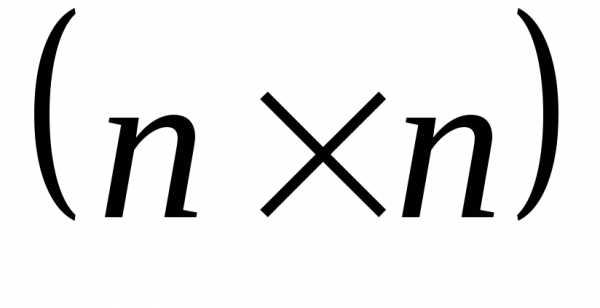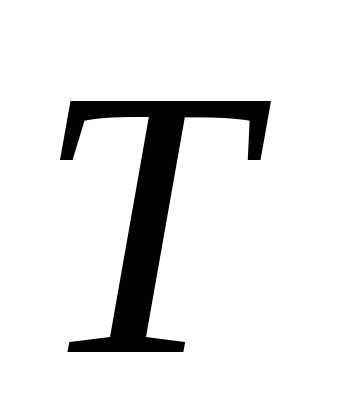- символ транспонирования.

Другой функционал:

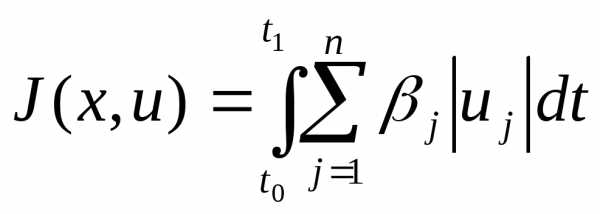(4)

Здесь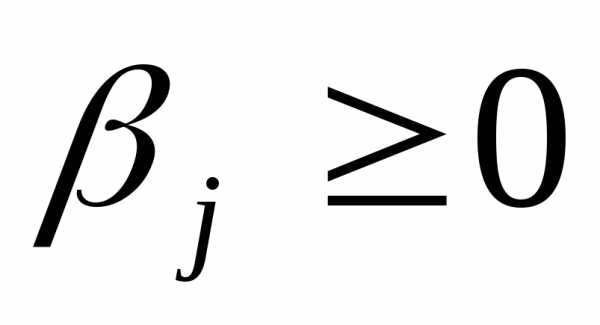,- это весовые координаты. Эти координаты позволяют учесть расход рабочего тела на управление. Задачи, решение которой минимизировалось в процесс (4), называются задачами САУ по расходу топлива. Такие задачи возникают, например, при управлении космическими аппаратами, когда существенной является экономия расходования горючего на борту аппарата.

Иногда в практике проектирования рассматривается функционал:

(5)

Здесь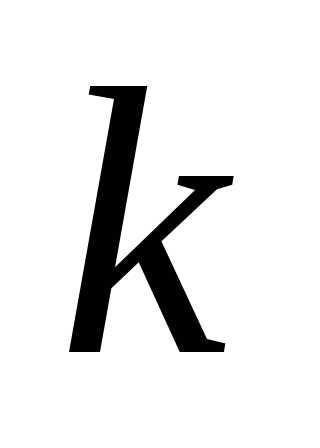

иудовлетворяют неравенствам.

Этот функционал является комбинацией функционалов (2) и (4) и позволяет учесть как время переходного процесса, так и расход топлива.

Выбор того или иного функционала определяется и техническими показателями и условиями работы проектируемой САУ, а также во многом определяется от интуиции практических навыков проектировщика. К этому относится также и выбор весовых коэффициентов.

Синтез оптимальных систем с помощью вариационного исчисления. Задача Лагранжа

Эта задача на условный экстремум, и нас будет интересовать случай, когда условия представляют собой систему дифференциальных уравнений.

Имеется функционал:

(1)

При этом допустимые кривые , среди которых ищется экстремум функционала, должны удовлетворять граничным условиям:

(2)

И условиям вида:

(3)

При этом . Мы предполагаем, что условия (3) являются независимыми, а это значит, что для всех

, которые удовлетворяют условиям (3), справедливо:

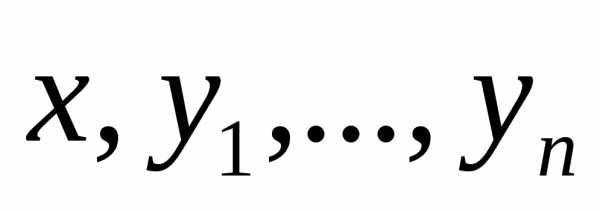
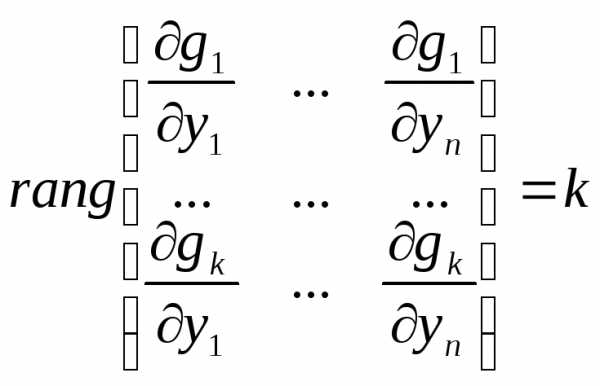
Таким образом, функционал (1) рассматривается не на всех допустимых кривых, удовлетворяющих граничным условиям (2), а только на тех кривых, которые удовлетворяют системе уравнений (3). Важно, чтобы условия (2) и (3) были согласованными, то есть начальные и конечные точки должны удовлетворять - мерному многообразию, которая задается системой уравнений (3).

Следует отметить, что граничные условия можно задать следующим образом:

А недостающее условие определяется из уравнений связи (3).

Это задача на условный экстремум называется задачей Лагранжа с голономными связями .

Введем в рассмотрение новый функционал:

(4)

Здесь 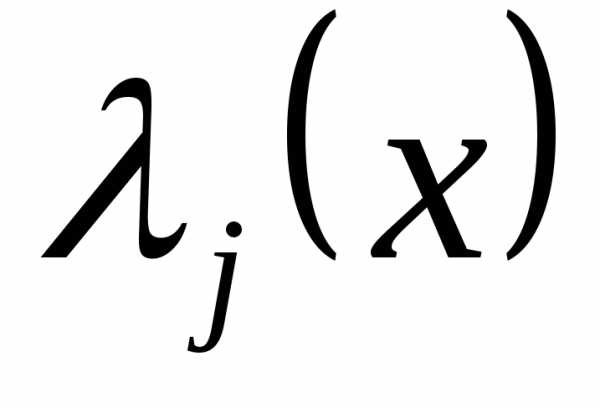- функции, подлежащие определению.

Относительно функционала (4) решается задача на безусловный экстремум, при чем подлежащие определению функции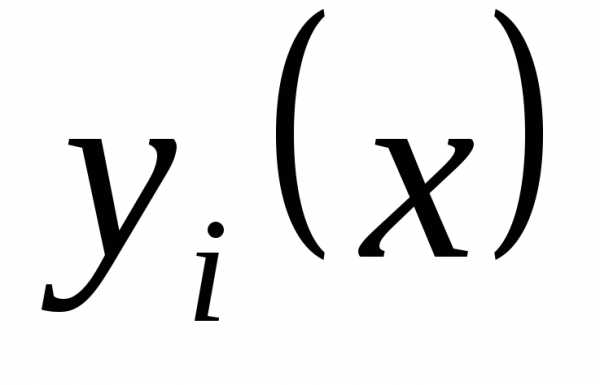

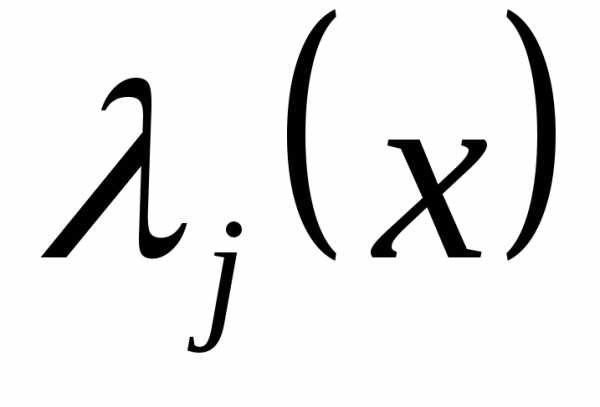и. Система уравнений Эйлера-Лагранжа для функционала (4) принимает вид:

(5)

Система (5) состоит из 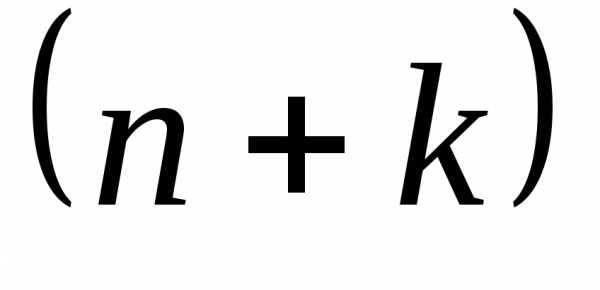уравнений, которые совпадают с числом искомых функцийи. Общее решение системы (5) содержит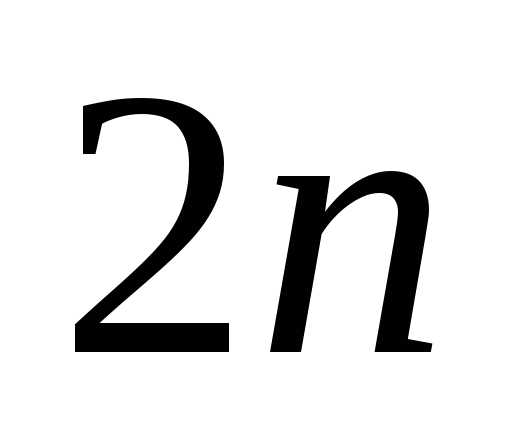произвольных постоянных, для определения которых используются граничные условия (2).

Если кривая доставляет безусловный экстремум функционалу (4), то на ней достигается и условный экстремум функционала (1). В самом деле, если на кривой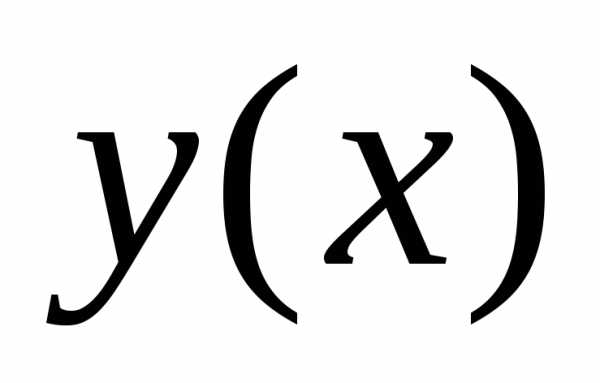достигается безусловный экстремум функционала (4), то эта кривая доставляет экстремум функционалу (5).

Тогда , и если кривая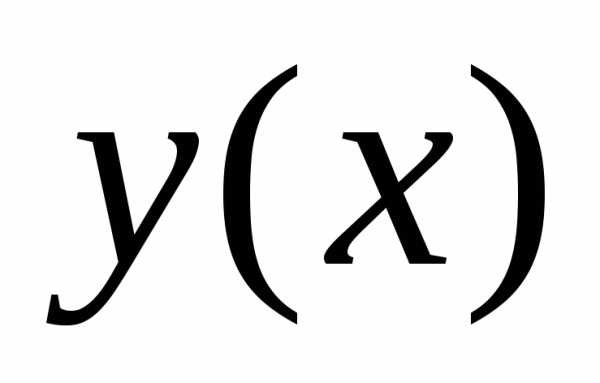доставляет безусловный экстремум функционалу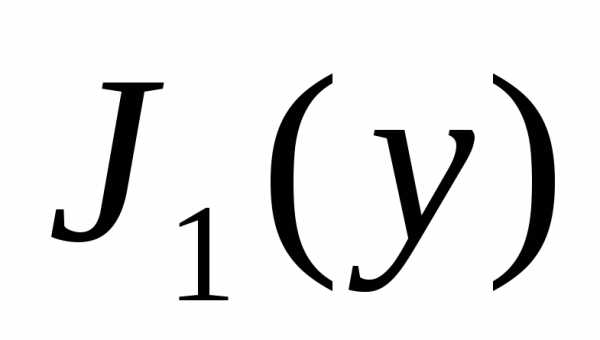, то, в частности, она будет доставлять экстремум и в более узком классе кривых, удовлетворяющих уравнениям связи.

Докажем следующую теорему:

studfiles.net

Критерии оптимизации конструкций машин — Мегаобучалка

Введение

Конспект лекций по дисциплине «Оптимальное проектирование» для подготовки специалистов по динамике и прочности машин соответствует Федеральному государственному образовательному стандарту высшего профессионального образования по направлению 151600 «Прикладная механика». Программа курса разработана на основе учебного плана направления «Прикладная механика» для очной формы обучения. В структуре учебного плана дисциплина имеет 72 час. аудиторных занятий, из них 36 час. лекций, 36 час. практических занятий, и 72 час. самостоятельной работы.

Целью настоящей дисциплины является изучение методов и критериев оптимального проектирования механизмов и силовых конструкций машин, приборов и аппаратуры. Внимание акцентируется на актуальных проблемах, связанных с оптимизацией несущей способности и функциональных свойств проектируемых изделий машиностроения.

Учебная дисциплина предусматривает изучение критериев оптимизации и основных ограничений, корректной постановки многокритериальных задач, анализ чувствительности, вычислительные алгоритмы и программы оптимального проектирования. Изучаются типовые задачи оптимального проектирования, в том числе постановка задач оптимизации и обоснованный выбор средств их решения.

Программой учебной дисциплины предусмотрено чтение лекций, проведение практических занятий, выполнение семестровой расчетно-графической работы. Практические занятия выполняются на основе соответствующих рекомендаций методической базы кафедры.

ТЕМА 1. Введение в оптимальное проектирование

Понятие оптимального и рационального проектирования

Задача проектирования конструкций машин состоит в выборе конструктивно-силовой схемы, кинематической схемы механизма, выборе материала и конструктивных размеров. Конструктор имеет свободу в выборе решений, но эта свобода ограничена тем, что проектируемое изделие должно быть, во-первых, работоспособно, а во-вторых – быть конкурентоспособным. Последнее качество определяется тем, насколько эффективно применение данного изделия по сравнению с его аналогами.

Для обеспечения конкурентоспособности конструктор задается целью создать устройство, наилучшее (в некотором смысле) из всех возможных аналогов, т.е. создать оптимальный проект. Оптимизация – это нахождение наилучшего (оптимального) решения какой-либо задачи (набора параметров) при заданных критериях.

Как правило, решение оптимизационной задачи распадается на следующие этапы:

анализ ситуации и формулировка задачи,

определение параметров решения, подлежащих оптимизации (то есть тех, которые могут быть изменены в ходе решения),

установление допустимой области существования параметров, то есть ограничений, налагаемых на параметры и их сочетания,

выбор и оценка влияния внешних факторов, учитываемых в ходе решения,

выбор критериев оптимальности,

построение целевой функции (математической модели), которая выдавала бы показатели, соответствующие выбранным критериям,

выбор математического метода оптимизационных расчётов,

проведение расчётов и оценка полученных решений по выбранным критериям,

окончательное принятие решения с учетом неопределённости и риска.

Следует подчеркнуть, что оптимизация в отличие от обычного сравнения вариантов предполагает рассмотрение всех решений, попадающих в область допустимых значений параметров. Те решения, в процессе поиска которых не проводился полный просмотр возможных вариантов, обычно называют «рациональными».

Критерии оптимизации конструкций машин

Два аналогичных технических устройства могут сравниваться по различным критериям.

Характеризуя объект, сложно выбрать такой один критерий, который бы обеспечил всю полноту требований. А стремление к всеобъемлющему решению и назначение большого числа критериев сильно усложняет задачу. Поэтому в разных задачах количество критериев может быть различным. Задачи однокритериальной оптимизации (с одним критерием оптимизации) иногда называют скалярными, а многокритериальной — векторной оптимизации. Кроме того, количество параметров, характеризующих оптимизируемый объект (задачу), также может быть различным, причём параметры могут меняться непрерывно или дискретно (дискретная оптимизация).

В предельном случае решение практических задач можно свести к задаче двухкритериальной оптимизации, критериями в которой являются «цена» и «качество» (т. н. «цена-качество»). Это наглядно позволяет учесть и экономические (цена), и производственно-технические (качество продукции) требования. Сведение задачи к однокритериальной требует введения существенных допущений, но облегчает окончательный выбор.

Оптимизационные задачи активно используются там, где важно получение высокоэффективного результата, например, в экономике, технике, информатике. Простейшим примером технико-экономической оптимизационной задачи может быть выбор диаметра трубопровода, по которому насосом перекачивается жидкость. При уменьшении диаметра трубы снижается её стоимость, но увеличиваются затраты энергии на перекачку жидкости из-за возросшего гидравлического сопротивления.

Примером задачи многопараметрической (двухпараметрической) оптимизации будет задача выбора диаметра трубопровода с горячей жидкостью или паром, так как одновременно выбирается диаметр трубопровода и толщина тепловой изоляции при постоянстве остальных. При этом оба параметра дискретны, так как существуют как сортамент труб, так и типовые параметры готовых теплоизоляционных сегментов.

Оптимизации подлежат параметры многих технологических процессов, объемы производства предприятий, уровни надежности продукции и мн. др.

Экономические критерии часто являются слишком глобальными для практического применения. Оптимальное проектирование отдельных устройств основывается на более частных критериях: максимальной производительности, максимального коэффициента полезного действия, минимальной массы, максимальной прочности и т.п. Использование частных критериев оптимизации требует одновременного учета тех требований к проектируемому изделию, которые не входят в критерий. Эти дополнительные требования выступают как ограничения, накладываемые на проект. Например, при проектировании конструкции минимальной массы ограничениями могут быть требования по прочности и производительности.

megaobuchalka.ru

Критерий оптимизации - Энциклопедия по экономике

Ткачев Ю. А. Экономические критерии оптимизации геологоразведочных работ. М. ВИНИТИ, 1973. № 7499-73-Деп. (РЖ Геология . 1974. № 3. Реферат ЗД4).  [c.164] Выбор методов оптимизации СПО, оценка их эффективности не могут рассматриваться изолированно от главных задач, стоящих перед бурением в целом. Подчиненность целей и критериев оптимизации спуско-подъемных операций целям и критериям оптимизации всего цикла строительства скважин — необходимое условие, которое должно быть выполнено при разработке мероприятий по совершенствованию рассматриваемого процесса.  [c.192]

В общем виде, т.е. безотносительно к конкретным значениям параметров (П, а, в, с, /7),критерий оптимизации  [c.13]

Показатели назначения. Показатели этой группы играют основную роль в оценке уровня качества, их часто используют как критерии оптимизации при нахождении наилучших решений в управлении качеством.  [c.30]

Поскольку действующий фонд нефтяных скважин образуют как рентабельные, так и нерентабельные скважины, то критерием оптимизации фонда является значение требуемой для Компании величины прибыли и рентабельности производства.  [c.25]

Очевидно, что существуют такие экономические задачи, в которых преобладают неопределенные факторы одного типа (Pi), но в то же время присутствуют и неопределенные факторы другого (или других) типов (Р ). В этом случае, если ЛПР (лицо, принимающее решение) сочтет возможным не учитывать влияние неопределенных факторов (Pi), то их влиянием можно либо пренебречь вообще, либо, пренебрегая ими, внести определенную поправку в критерий оптимизации. Первый подход, на наш взгляд, ведет к большим погрешностям в решении, в то время как второй позволяет получить более точное решение с помощью перехода к нечеткой задаче математического программирования. Способы решения задач нечеткого математического программирования приведены в [4, 5].  [c.49]

Основная задача в области совершенствования функционального разделения труда состоит в определении оптимального соотношения между численностью основных Ч0 и вспомогательных рабочих Ча. Принципиальный подход к ее решению состоит в отыскании такого значения указанного соотношения, которое обеспечивает максимальный удельный вес вес оперативного времени в составе его сменного фонда в среднем на одного рабочего, включая и основных и вспомогательных рабочих. Этот способ рекомендован в [1]. Однако будучи принципиально верным, он оставляет открытым вопрос о конкретном способе определения оптимального соотношения Ч0 и Чв. Конечно, можно найти его. прямым неупорядоченным перебором всех возможных вариантов, но это очень трудоемкая процедура. В связи с этим Е. С. Докучаевым в [2] разработан простой метод аналитического определения оптимальной численности вспомогательных рабочих Ч при известной численности основных рабочих Ч0. Критерием оптимизации служит максимум сменной выработки в среднем на на одного рабочего. Известно, что целевая для предприятия продукция создается в оперативное время основных рабочих. Поэтому критерий оптимальности запишется как  [c.22]

Для рассмотрения таких сложных проблем, как создание и освоение новой техники, используется системный подход, который основан на комплексном рассмотрении входящих в проблему процессов и задач, предусматривает постановку цели, требует выявления содержания входных и выходных потоков информации, установления критериев оптимизации. Реализация системного подхода невозможна без знания прогнозирования, информатики, математического моделирования. Особенно важными являются методы моделирования, которые позволяют исследовать сложные процессы в режиме опережающего анализа.  [c.29]

В первую очередь требуется указать критерий оптимизации. Будем для начала считать, что мы можем единице продукции каждой отрасли сопоставить число, которое отражает важность этого вида конечного продукта. Для i-й отрасли такое число обозначим через t (i — 1,. .., п). Конечно, С > 0. Тогда вектор конечного продукта можно оценить показателем  [c.138]

Поскольку описываемые здесь модели планирования экономических объектов предназначены для выбора наилучшего плана, под которым обычно понимается план, оптимальный в смысле некоторого критерия, то модели стараются сформулировать в таком виде, чтобы воспользоваться уже существующими методами решения задач оптимизации. Наиболее развитыми методами решения оптимизационных задач являются методы линейного программирования, т. е. методы оптимизации на основе моделей, состоящих из линейных равенств и неравенств, причем критерий оптимизации является линейной функцией от переменных задачи. Это — одна из причин того, что линейные модели получили наиболее широкое распространение в практических экономических расчетах.  [c.150]

Существует бесконечное число вариантов перевозок Хц, удовлетворяющих всем сформулированным здесь условиям. Естественно попытаться найти те из них, которые соответствуют минимальным затратам. Предположим, что затраты пропорциональны тонно-километрам перевезенного груза. Тогда критерием оптимизации может служить величина  [c.154]

Критерий оптимизации 31, 40, 43, 13S Критический путь 188  [c.301]

Широкое использование экономико-математических методов на практике привело к пониманию многих принципиальных, трудностей, возникающих при их внедрении. Прежде всего выяснилось, что вопрос о том, что такое хорошо и что такое плохо , не так прост. Часто, его не удается решить путем формулировки некоторой математической функции — критерия оптимизации. Оказалось, что ЛПР при принятии решения учитывает огромное число разнообразных показателей, представить которые-в виде единственного критерия удается только в редких случаях.  [c.17]

Оптимизационная задача для модели народного хозяйства с критерием оптимизации (7.2) ставится так найти допустимые управления st(t) и sz(t) (t = О, 1,. . ., Т), на которых критерий (7.2) принимает максимальное значение.  [c.150]

Это — задача линейного программирования общего типа, т. е. рациональное распределение площадей с помощью модели (2.25) — (2.28) с критерием оптимизации (2.24) также может быть найдено с помощью систем линейного программирования.  [c.172]

Можно было бы привести много других критериев оптимизации, использующихся в многоотраслевых динамических моделях народного хозяйства. Каждый из них имеет определенные преимущества, но ни один не лишен недостатков. До настоящего времени попытки построить единственный критерий, который можно было бы использовать на практике для выбора наиболее рационального плана развития народного хозяйства, к успеху не привели,  [c.275]

Одним из интересных подходов к анализу динамических многоотраслевых моделей является анализ их магистральных свойств. Магистральные свойства, которые уже упоминались в предыдущей главе при описании методов анализа сильно агрегированных моделей народного хозяйства, состоят в том, что при достаточно больших периодах времени вне зависимости от критерия оптимизации (принадлежащего к некоторому определенному классу разумных критериев) основная часть оптимальной траектории находится вблизи магистрали — такой структуры экономики, при которой достигается ее максимальный рост. Начальный участок траектории состоит в выходе на магистраль наискорейшим образом (или приближении к ней) и также не зависит от критерия оптимизации. Критерий связан только с моментом схода с магистрали и особенностями заключительного участка траектории. Поскольку в задачах планирования нас интересует прежде всего начальный подход, то магистральные свойства могли бы быть использованы для планирования развития народного хозяйства. На практике применение магистральных теорем сдерживается тем, что они доказаны для относительно простых моделей и, что самое главное, применимы обычно при достаточно больших интервалах планирования, значительно превышающих периоды времени, рассматриваемые при планировании народного хозяйства и составляющие 10—15 лет.  [c.276]

Рыночная стоимость облигаций в результате их последующей продажи на вторичном рынке может отличаться и от стоимости их размещения, и от номинальной стоимости. Учитывая, что купонный процент зафиксирован к номиналу облигации, его размер не будет являться основным критерием оптимизации выбора инвестора при покупке облигации.  [c.357]

Оптимизация решений по привлечению капитала — это процесс исследования множества факторов, воздействующих на ожидаемые результаты, в ходе которого на основе ранее установленных критериев оптимизации менеджерами-аналитиками осуществляется осознанный (рациональный) выбор наиболее эффективного варианта привлечения капитала. В качестве критериев оптимизации могут выступать прирост обобщающих показателей рентабельности капитала, а разработанные на их основе факторные модели зависимости рентабельности собственного или заемного капитала от других частных показателей-факторов позволяют выявить степень количественного воздействия каждого из них на изменение (+, — ) результативных показателей.  [c.215]

В качестве критерия оптимизации для моделей среднего уровня принимается минимизация интегральных производственно-транспортных затрат в районе. Каждая модель района состоит из трех взаимосвязанных блоков производственного, геологического, транспортного.  [c.207]

Основа построения экономико-математической модели ГДП — выбор критерия оптимизации, являющийся одним из наиболее важных этапов экономико-математического моделирования, который характеризует всю деятельность ГДП за определенный отрезок времени. Известно, что для количественной оценки эксплуатации ГДП можно использовать различные технико-экономические показатели объемы добычи природного газа и конденсата, себестоимость добываемой из газоносного пласта продукции, удельные капитальные вложения, прибыль,, получаемую ГДП от эксплуатации технологических объектов,, качество добываемого природного газа и т. д.  [c.51]

В качестве критерия оптимизации ГДП можно принять удельные приведенные затраты. Этот показатель позволяет определять сравнительную экономическую эффективность капи-  [c.51]

При выборе источников финансирования для расширения деятельности предприятия собственники бывают заинтересованы втом, чтобы средневзвешенная цена капитала увеличивалась при условии опережающего роста, во-первых, показателя EPS и, во-вторых, стоимости предприятия. Только такое финансирование отвечает долговременным целям развития предприятия, а поэтому сформулированное выше условие служит основным критерием оптимизации структуры капитала.  [c.174]

В качестве критерия оптимизации выступает требование минимизации суммарных приведенных. затрат, которое записывается в такой форме  [c.78]

В качестве критерия оптимизации для моделей среднего уровня принимается минимизация интегральных производственно-транспортных затрат в районе.  [c.99]

Особого внимания заслуживает критерий оптимизации. В наибольшей мере целям планирования соответствует минимум интегральных затрат на выявление структур в количестве, достаточном для заданного прироста запасов газа. Задание либо устанавливается директивно, либо, как было отмечено выше, получается из решения по расширенной модели межотраслевого межрайонного баланса.  [c.153]

Выбор оптимального плана геофизических исследований по этому критерию должен осуществляться итеративным методом, а именно путем многократного решения задачи среднего уровня каждый раз после направленного обновления вариантов развития отдельных баз ц всего перспективного задания экспедиции. Такое обновление осуществляется на основе вспомогательных моделей верхнего и нижнего уровней. Алгоритм согласования [2] обеспечивает последовательное улучшение перспективного плана по значению выбранного критерия оптимизации.  [c.153]

Для экспедиции выявлено (и на отдельном этапе решения считается незыблемым) производственное задание по важнейшим показателям на перспективу, а также сформулирована количественная оценка деятельности, подлежащая максимизации,— критерий оптимизации.  [c.154]

Согласованно с ограничениями введен критерий оптимизации — максимальная расчетная прибыль экспедиции, измеряемая разностью объемов расчетного финансирования и ожидаемых затрат. Такой критерий в отличие, например, от минимума приведенных затрат не способствует свертыванию работ до минимально допустимых объемов. Если сопоставить его с максимумом выпускаемой продукции (в нашем случае количество информации), то и здесь преимущество предлагаемого критерия проявляется в возможном недоиспользовании (экономии) средств.  [c.155]

Критериями оптимизации в задачах выбора очередности могут быть  [c.82]

Решение не может быть оптимальным вообще, во всех смыслах, а только в одном-единственном смысле, определяемом выбранным критерием. Критерий оптимизации называют целевой функцией, функцией цели, функционалом.  [c.103]

Массовое применение ПТК НАСОС на нефтепромыслах показало, что резерв для повышения эффективности существует на любой стадии разработки месторождений, при различных геологических и технологических условиях. Преимущества автоматизированного подбора оборудования максимально выражаются при использовании экономического критерия оптимизации.  [c.52]

Формально оптимизация в любой области возможна на базе количественных критериев оптимизации. В проектировании организационных структур приходится считаться с противоречивым характером локальных показателей эффективности структур, поскольку чем глубже обеспечивается технологическая специализация, тем больше, в общем случае, организационно-технологическая напряженность структуры. В предельном случае можно представить такое комплексное управление, которое проводит все работы своими силами — в этом случае, очевидно, показатель технологической специализации будет весьма низок. Наоборот, можно представить структуру с чрезмерно углубленной специализацией — здесь следует опасаться возрастания организационно-технологической напряженности. Интегральный эффект должен получиться от  [c.15]

Критерии оптимизации технологических процессов бурения определены минимальная стоимость проводки скважин в заданные (плановые) сроки и заданное сохранение коллекторских -свойств продуктивных пластов.  [c.86]

В настоящее время программа усовершенствуется с целью обеспечения оптимизации расчетов доразработки объектов для определения экономически оправданного срока эксплуатации и конечного коэффициента нефтеотдачи. При этом в качестве критерия оптимизации за период доразра— ботки используется максимальное значение денежной оценки за этот  [c.53]

Наиболее распространенным методом моделирования сложного процесса строительства КС и НС являются сетевые графики. Учитывая большую рассредоточенность площадочных объектов вдоль трассы, в качестве критерия оптимизации сетевых моделей могут быть приняты затраты на передислокацию строительно-монтажных подразделений. Общая величина расходов на передислокацию включает в себя затраты на передислокацию трудовых ресурсов, затраты на перемещение механизмов и оборудования, сумму амортизационных отчислений на реновацию и платы за основные фонды [2]. В связи с освоением месторож-  [c.65]

В качестве критериев оптимизации системы, цикла и процессов СОН " могут быть выбраны уровень технических параметров (технический уровень) новых изделий сроки (цикл) их создания и освоения увеличение объемов новой продукции, выпускаемой на стадии освоения увеличение числа наименований (номенклатуры) отрабатываемых в системе СОНТ новых изделий повышение эффективности выполнения входящих в процессы работ экономия денежных затрат и трудовых ре-  [c.29]

Указанный недостаток оптимизации носит технический характер и преодолевается с разработкой новых, более эффективных методов оптимизации и с повышением мощности ЭВМ. Более принципиальное значение имеет другой недостаток оптимизации — необходимость построения единственного критерия оптимизации. Оказалось, что в большинстве задач заказчик не может сформулировать такой критерий и соизмерить тем самым различные показатели. Искусственное объединение различных показателей в один часто приводило к тому, что заказчик отказывал- ся использовать решение, найденное с помощью математических моделей и такого критерия. Для преодоления подобных трудностей наряду с имитационными методами, для которых многокри-териальность помехой не является, стали разрабатываться многокритериальные методы. Основными понятиями многокритериальных методов (см. 4 гл. 1) являются понятия множества всех достижимых значений показателей и множества их эффективных значений. Пусть для модели народного хозяйства выбраны два  [c.151]

Анализ воздействия хозяйственного механизма на показатели работы предприятия. Проанализируем возможности исследования влияния хозяйственного механизма на эффективность деятельности предприятия на основе альтернативного подхода, в котором поведение производственной единицы не описывается вообще. Вместо этого иследователи анализируют вопрос о том, каково было бы рациональное поведение предприятия при различных целях, в том числе и совпадающих с целями вышестоящих организаций. При этом удается оценить рассогласование возможных интересов предприятий и Центра. Можно также попытаться выявить те критерии оптимизации, которые приводят к результатам, наиболее близким к реальности. Проиллюстрируем возможности подобного подхода на примере стандартной модели производственной единицы (4.1). Поскольку будет рассматриваться единственная единица, то индекс i будем опускать. Цены на ресурс и продукцию будем считать фиксированными (р = 1). Выясним, какой объем ресурсов потребовала бы производственная единица и какой объем продукции был бы выпущен при разных критериях выбора решения, если бы ресурсы выдавались в любом количестве без ограничений.  [c.372]

Obje tive fun tion — целевая функция в моделях линейного программирования выраженный в математическом виде критерий оптимизации (максимизация прибыли, минимизация затрат), принятый для определенной задачи.  [c.325]

АИС и АИТ реализуют решение функциональных задач управления, совокупность которых составляет так называемую, функциональную часть деятельности экономического объекта как системы. Состав, порядок и принципы взаимодействия функциональных подсистем, задач и их комплексов устанавливаются исходя и с учетом достижения стоящей перед экономическим объектом цели функционирования. Основными принципами декомпозиции — выделения самостоятельных функциональных подсистем комплексов задач — являются относительная самостоятельность каждой из них, т.е. наличие конкретного объекта управления наличие соответствующего набора функций и функциональных задач с четко выраженной локальной целью функционирования минимизация состава включенных в подсистему элементов наличие одного или нескольких локальных критериев, способствующих оптимизации режима работы подсистемы и согласующихся с глобальным критерием оптимизации функциойирования АИС и системы в целом.  [c.52]

Использование суммарной прибыли как критерия оптимизации производственной деятельности экспедиции на перспективу способствует, во-первых, разумному наращиванию объема работ сверх предусмотренного заданием, во-вторых, рациональному расходованию бюджетных ассигнований (при бесприбыльном производстве выделенные деньги недоиспользуются) и, в-третьих, применению наиболее эффективных (по технологии и организации производства) способов геофизических исследований в отдельных партиях.  [c.155]

economy-ru.info

Выбор критериев оптимальности

Поиск Лекций

На разных этапах проектирования встает задача выбора наилучшего варианта из множества допустимых проектных решений, удовлетворяющих предъявленным требованиям.

Процесс принятия решения при оптимальном проектировании характеризуют следующие основные черты: наличие цели (критериев оптимальности) и альтернативных вариантов проектируемого объекта, и учет существенных факторов при проектировании.

Понятие «оптимальное решение» при проектировании имеет вполне определенное толкование — лучшее в том или ином смысле проектное решение, допускаемое обстоятельствами. В подавляющем большинстве случаев одна и та же техническая задача может быть решена несколькими способами, приводящими не только к различным выходным характеристикам, схемам и конструкциям, но даже и к физическим принципам, положенным в основу построения объекта. При этом одно из решений может превосходить другое по одним свойствам и уступать ему по другим. В этих условиях часто чрезвычайно трудно сказать, не только какая из систем оптимальна, но даже какая из них предпочтительнее.

Если выделяют один параметр, который характеризует свойства, то этот параметр принимается за целевую функцию. При этом другие параметры подпадают под категорию ограничений. При решении однокритериальных задач применяется математический аппарат исследования операций. При создании вычислительной сети в большинстве случаев однокритериальные задачи не удовлетворяют полученному решению. Сложные ВС характеризуются многими параметрами (емкость памяти, время счета, пропускная способность каналов и т. п.), определяющими ее качество. Среди этих параметров есть такие, значения которых желательно всемерно увеличивать, но есть и такие, которые желательно минимизировать.

Таким образом, ограничения и связи между отдельными параметрами ВС приводят к необходимости идти на компромисс и выбирать для каждой характеристики не максимально возможное в принципе значение, а мень­шее, но такое, при котором и другие важные характеристики тоже будут иметь приемлемые значения. Поэтому необходимо принимать во внимание всю совокупность характеристик ВС. Задачи проектирования, проводимые по нескольким критериям оптимизации, носят название многокритериальных, или задач векторной оптимизации.

Известные методы векторной оптимизации прямо или косвенно сводят решаемые задачи к задачам скалярной оптимизации, т. е. частные критерии тем или иным способом объединяются в составной критерий, который затем максимизируется (или минимизируется). Если составной критерий отражает физическую суть ВС и вскрывает объективную связь между частными критериями и составным критерием, то оптимальное решение является объективным.

На практике из-за сложности обычно составной критерий объединяет частные, что ведет к субъективности решения; такой критерий является обобщенным, или интегральным. В зависимости от того, каким образом частные критерии объединяются в обобщенный критерий, различают критерии аддитивные, мультипликативные и минимаксные (максиминные).

Если оптимизация ведется без учета статистического разброса характеристик, то соответствующий критерий оптимальности называют детерминированным критерием; если разброс параметров учитывается, то имеем критерий статистический. Статистический критерий оптимальности наиболее полно отражает качество ВС, но его использование требует больших затрат машинного времени.

Рассмотрим способы выбора критериев оптимальности.

Частные критерии

При проектировании по частным критериям в качестве целевой функции F(X) принимается наиболее важный выходной параметр проектируемой ВС, все остальные параметры в виде соответствующих условий работоспособности относятся к ограничениям. В этом случае задача оптимального проектирования является однокритериальной задачей математического программирования: максимизировать (или минимизировать) значение целевой функции при наличии ограничений на параметры ВС.

Из постановки задачи вытекает, что параметры, для которых выполняются ограничения в виде строгих неравенств, имеют определенный запас по сравнению с заданными техническими требованиями. Ряд параметров, для которых условия работоспособности имеют вид неравенств, запасов вообще не имеет, и любые изменения технических требований для этих параметров приводят как к изменению характеристик и структуры проектируемого объекта, так и к изменению значения целевой функции.

Частные критерии используются при проектировании ВС различного назначения.

Аддитивные критерии

В этих критериях целевая функция образуется путем сложения нормированных значений частных критериев. Частные критерии имеют различную физическую природу и в соответствии с этим — различную размерность. Поэтому при образовании обобщенного критерия следует оперировать не с «натуральными» критериями, а с их нормированными значениями. Нормированные критерии представляют собой отношение «натурального» частного критерия к некоторой нормирующей величине, измеренной в тех же единицах, что и сам критерий. При этом выбор нормирующего делителя должен быть логически обоснован. Возможны несколько подходов к выбору нормирующего делителя.

Первый подход предлагает принимать в качестве нормирующего делителя директивные значения параметров, заданные заказчиком. Логически слабым моментом такого подхода является негласное предположение того, что в ТЗ на проектируемую ВС заданы оптимальные значения параметров объекта, и что совокупность заданных значений критериев рассматривается как образцовая.

Второй подход предполагает выбор в качестве нормирующих делителей максимальных значений критериев, достигаемых в области существования проектных решений (в области компромисса). Возможен подход, при котором в качестве нормирующих делителей выбирают разность между максимальным и минимальным значениями критерия в области компромисса.

Выбор подхода к формированию безразмерной формы частных критериев носит иногда субъективный характер и должен обосновываться в каждом конкретном случае. Пусть при проектировании ВС существует п частных критериев. Тогда целевая функция задачи оптимизации в случае применения аддитивного критерия определяется

где — весовой коэффициент частного критерия;

— нормирующий делитель;

— нормированное значение частного критерия.

Такая целевая функция позволяет осуществить компромисс, при котором улучшение значения одного нормированного частного критерия компенсирует ухудшение значений других.

Введение весовых коэффициентов должно учитывать различную значимость частных критериев при формировании аддитивного критерия. Определение весовых коэффициентов сталкивается с серьезными трудностями и обычно сводится либо к использованию формальных процедур, либо к применению экспертных оценок. С появлением обобщенного критерия исчезают логические проблемы, связанные с установлением взаимосвязей между частными критериями различной размерности и выбором наилучшего варианта ВС, и остаются лишь вычислительные трудности. Но аддитивный критерий имеет ряд недостатков, главный из которых состоит в том, что он не вытекает из объективной роли частных критериев в функционировании ВС и выступает поэтому как формальный математический прием, придающий задаче удобный для решения вид.

Другой недостаток заключается в том, что в аддитивном критерии может происходить взаимная компенсация частных критериев. Это значит, что значительное уменьшение одного из критериев вплоть до нулевого значения может быть покрыто возрастанием другого критерия. Для ослабления этого недостатка следует вводить ограничения на минимальные значения частных критериев и их весовых коэффициентов.

Несмотря на слабые стороны, обобщенный аддитивный критерий позволяет в ряде случаев успешно решать многокритериальные задачи и получать полезные результаты.

poisk-ru.ru

критерий оптимизации - это... Что такое критерий оптимизации?

 критерий оптимизации мат. optimization criterion

Большой англо-русский и русско-английский словарь. 2001.

Смотреть что такое "критерий оптимизации" в других словарях:

dic.academic.ru

Критерии оптимизации и ограничения | Бесплатные курсовые, рефераты и дипломные работы

 

В качестве критерия оптимизации могут выбираться различные экономические и технико-экономические параметры (КПД, прибыль, расход энергии, средств и т.д.).

Для сложных технологических процессов и производств при их оптимизации часто разрабатывают автоматизированные системы управления производством (АСУП). Ее можно рассматривать как четырехуровневую систему, в которой функции разделены по уровню.

1. Оптимальное планирование.

2. Оперативное управление.

3. Оптимизация технологических процессов (определяется, при каких оптимальных переменных получается наилучшее качество выпускаемой продукции).

4. Оптимизация режимов работы оборудования (технологических установок).

Подсистемы 1 и 2 уровней решают задачу управления предприятием в целом, т.е. административно-хозяйственные задачи: распределение запасов, учета, планирования, анализа деятельности предприятия. Эти системы нуждаются в техническом персонале. … Выбор критерия эффективности определяется экономическими требованиями, в качестве критерия оптимизации используются технико-экономические критерии.

При оптимизации статики и установившихся режимов работы многомерных объектов критерии оптимизации формулируются как некоторая функция, характеризующая качество работы объекта.

, где – функция, характеризующая эффективность работы предприятия.

В качестве критерия оптимизации (на высших уровнях АСУТП) может применяться:

1) функция пользы, которая представляет собой некоторую сумму:

X – вектор координат состояний объекта

Y – вектор выходных состояний объекта

U – вектор управляющих воздействий

2) максимум прибыли

g – цена

П – производительность

S – затраты

Критерий максимум прибыли не всегда согласуется с глобальными критериями производства. Поэтому используются ограничения.

3) минимум потерь

à

– реализуемая переменная технологического процесса;

– стоимость потерь от нестабильности i-ой переменной.

Во многих случаях качество работы АСУТП оценивается несколькими критериями, часть из которых противоречива. Тогда либо формируют векторный критерий, либо используют один показатель качества, а на остальные накладывают ограничения.

Векторный критерий оптимизации:

От векторного критерия переходят к обобщенному скалярному:

– коэффициент, отражающий вклад частного критерия в общий скалярный

Для объектов, работающих в переходных режимах, что характерно для систем 3-го уровня, в качестве критерия оптимизации используются известные критерии оценки точности и качества переходного процесса.

Максимальное быстродействие:

.

Максимальная точность:

.

При использовании в качестве функционала этого критерия в системе возникают процессы с большим перерегулированием, поэтому используют улучшенный критерий оптимизации:

λ – коэффициент, ограничивающий скорость переходного процесса, т.е. величину перерегулирования.

Если система подвержена случайным воздействиям, она относится к классу стохастических. Для стохастических систем в качестве критерия оптимизации можно использовать среднее значение квадрата ошибки

.

В качестве критерия оптимизации можно выбрать расход энергии на управление

.

если используются механические источники энергии

U(t) – управляющее воздействие

– скорость изменения выходного сигнала

Если на объект управления действуют возмущения (контролируемые и неконтролируемые), то в качестве критерия принят функционал, характеризующий взаимную корреляцию между выходом и возмущением:

.

Таким образом, критерий оптимизации зависит от того, в каком режиме работает объект, и от целей оптимизации. В общей постановке задачи оптимизации минимизируемый функционал детерминированных систем можно записать в следующем виде:

– функция, характеризующая качество в конечный момент времени, т.е. в установившемся состоянии – после завершения переходного процесса.

F – функционал, характеризующий качество работы объекта в переходных режимах (характеризует динамику).

 

refac.ru

Prostoy-Site | Все права защищены © 2018 | Карта сайта