Правила принудительного ранжирования. Правила ранжирования
Правила ранжирования
1. Меньшему значению начисляется меньший ранг. Наименьшему значению начисляется ранг 1.
Наибольшему значению начисляется ранг, соответствующий количеству ранжируемых значений. Например, если n=7, то наибольшее значение получит ранг 7, за возможным исключением для тех случаев, которые предусмотрены правилом 2.
2. В случае, если несколько значений равны, им начисляется ранг, представляющий собой среднее значение из тех рангов, которые они получили бы, если бы не были равны.
Например, 3 наименьших значения равны 10 секундам. Если бы мы измеряли время более точно, то эти значения могли бы различаться и составляли бы, скажем, 10,2 сек; 10,5 сек; 10,7 сек. В этом случае они получили бы ранги, соответственно, 1, 2 и 3. Но поскольку полученные нами значения равны, каждое из них получает средний ранг:
3. Общая сумма рангов должна совпадать с расчетной, которая определяется по формуле:
где N - общее количество ранжируемых наблюдений (значений). Несовпадение реальной и расчетной сумм рангов будет свидетельствовать об ошибке, допущенной при начислении рангов или их суммировании. Прежде чем продолжить работу, необходимо найти ошибку и устранить ее.
При подсчете критерия U легче всего сразу приучить себя действовать по строгому алгоритму.
Алгоритм 4 Подсчет критерия u Манна-Уитни.
1. Перенести все данные испытуемых на индивидуальные карточки.
2. Пометить карточки испытуемых выборки 1 одним цветом, скажем красным, а все карточки из выборки 2 - другим, например синим.
3. Разложить все карточки в единый ряд по степени нарастания признака, не считаясь с тем, к какой выборке они относятся, как если бы мы работали с одной большой выборкой.
5. Вновь разложить карточки на две группы, ориентируясь на цветные обозначения: красные карточки в один ряд, синие - в другой.
6. Подсчитать сумму рангов отдельно на красных карточках (выборка 1) и на синих карточках (выборка 2). Проверить, совпадает ли общая сумма рангов с расчетной.
7. Определить большую из двух ранговых сумм.
8. Определить значение U по формуле:
где n1 - количество испытуемых в выборке 1;
n2 - количество испытуемых в выборке 2;
Тх - большая из двух ранговых сумм;
nх - количество испытуемых в группе с большей суммой рангов.
9. Определить критические значения U по Табл. II Приложения 1. Если Uэмп.>Uкp005, Но принимается. Если Uэмп≤Uкp_005, Но отвергается. Чем меньше значения U, тем достоверность различий выше.
Теперь проделаем всю эту работу на материале данного примера. В результате работы по 1-6 шагам алгоритма построим таблицу.
Таблица 2.4
Подсчет ранговых сумм по выборкам студентов физического и психа-логического факультетов
| Студенты-физики (n1=14) | Студенты-психологи (n2=12) | |||
| Показатель невербального интеллекта | Ранг | Показатель невербального интеллекта | Ранг | |
| 127 | 26 | |||
| 123 | 25 | |||
| 122 | 24 | |||
| 117 | 23 | |||
| 116 | 22 | |||
| 115 | 20,5 | |||
| 115 | 20,5 | |||
| 114 | 19 | |||
| 113 | 18 | |||
| 112 | 17 | |||
| 111 | 15,5 | 111 | 15.5 | |
| 108 | 14' | |||
| 107 | 11.5 | 107 | 11,5 | |
| 107 | 11,5 | |||
| 107 | 11,5 | |||
| 106 | 9 | |||
| 105 | 8 | |||
| 104 | 6.5 | 104 | 6,5 | |
| 102 | 4,5 | 102 | 4,5 | |
| 99 | 3 | |||
| 95 | 2 | |||
| 90 | 1 | |||
| Суммы | 1501 | 165 | 1338 | 186 |
| Средние | 107,2 | 111,5 | ||
Общая сумма рангов: 165+186=351. Расчетная сумма:
Равенство реальной и расчетной сумм соблюдено.
Мы видим, что по уровню невербального интеллекта более "высоким" рядом оказывается выборка студентов-психологов. Именно на эту выборку приходится большая ранговая сумма: 186.
Теперь мы готовы сформулировать гипотезы:
H0: Группа студентов-психологов не превосходит группу студентов-физиков по уровню невербального интеллекта.
Н1: Группа студентов-психологов превосходит группу студентов-физиков по уровню невербального интеллекта.
В соответствии со следующим шагом алгоритма определяем эмпирическую величину U:
Поскольку в нашем случае п\Фп2, подсчитаем эмпирическую величину U и для второй ранговой суммы (165), подставляя в формулу соответствующее ей пх:
Такую проверку рекомендуется производить в некоторых руководствах (Рунион Р., 1982; Greene J., D'Olivera M., 1989). Для сопоставления с критическим значением выбираем меньшую величину U: Uэмп=60.
По Табл. II Приложения 1 определяем критические значения для n1=14, n2=12.
Мы помним, что критерий U является одним из двух исключений из общего правила принятия решения о достоверности различий, а именно, мы можем констатировать достоверные различия, если Uэмп≤Uкp
Построим "ось значимости".
Uэмп=60
Uэмп>Uкp
Ответ: H0 принимается. Группа студентов-психологов не превосходит группы студентов-физиков по уровню невербального интеллекта.
Обратим внимание на то, что для данного случая критерий Q Розенбаума неприменим, так как размах вариативности в группе физиков шире, чем в группе психологов: и самое высокое, и самое низкое значение невербального интеллекта приходится на группу физиков (см. Табл. 2.4).
studfiles.net
Правила ранжирования
Психология Правила ранжирования
Пример
Ограничения критерия U
1. В каждой выборке должно быть не менее 3 наблюдений: n1•n2≥3; допускается, чтобы в одной выборке было 2 наблюдения, но тогда во второй их должно быть не менее 5.
2. В каждой выборке должно быть не более 60 наблюдений; n1•n2≤60. При этом уже при n1•n2>20 ранжирование становиться достаточно трудоемким.
На наш взгляд, в случае, если n1•n2>20, лучше использовать другой критерий, а именно угловое преобразование Фишера в комбинации с критерием λ,, позволяющим выявить критическую точку, в которой накапливаются максимальные различия между двумя сопоставляемыми выборками (см. п. 5.4). .Формулировка звучит сложно, но сам метод достаточно прост. Каждому исследователю лучше попробовать разные пути и выбрать тот, который кажется ему более подходящим.
Вернемся к результатам обследования студентов физического и психологического факультетов Ленинградского университета с помощью методики Д. Векслера для измерения вербального и невербального интеллекта. С помощью критерия Q Розенбаума мы в предыдущем параграфе смогли с высоким уровнем значимости определить, что уровень вербального интеллекта в выборке студентов физического факультета выше. Попытаемся установить теперь, воспроизводится ли данный результат при сопоставлении выборок по уровню невербального интеллекта. Данные приведены в Табл. 2.3.
Можно ли утверждать, что одна из выборок превосходит другую по уровню невербального интеллекта?
Таблица 2.3
Индивидуальные значения невербального интеллекта в выборках студентов физического (щ=\4) и психологического (п2=12) факультетов
| Студенты-физики | Студенты-психологи | ||||
| Код имени испытуемого | Показатель невербального интеллекта | Код имени испытуемого | Показатель невербального интеллекта | ||
| 1. | И.А. | 1. | Н.Т. | ИЗ | |
| 2. | К.А. | 2. | О.В. | ||
| 3. | К.Е. | 3. | Е.В. | ||
| 4. | П.А. | 4. | Ф.О. | ||
| 5. | С.А. | 5. | И.Н. | ||
| 6. | Ст.А. | 6. | И.Ч. | ||
| 7. | Т.А. | 7. | И.В. | ||
| 8. | Ф.А. | 8. | К.О. | ||
| 9. | Ч.И. | 9. | P.P. | ||
| 10. | ЦА. | 10. | Р.И. | ||
| 11. | См.А. | 11. | O.K. | ||
| 12. | К.Ан. | 12. | Н.К. | ||
| 13. | Б.Л. | ||||
| 14. | Ф.В. |
Критерий U требует тщательности и внимания. Прежде всего, крайне важно помнить правила ранжирования.
1. Меньшему значению начисляется меньший ранᴦ. Наименьшему значению начисляется ранг 1.
Наибольшему значению начисляется ранг, соответствующий количеству ранжируемых значений. К примеру, если n=7, то наибольшее значение получит ранг 7, за возможным исключением для тех случаев, которые предусмотрены правилом 2.
2. В случае, если несколько значений равны, им начисляется ранг, представляющий собой среднее значение из тех рангов, которые они получили бы, если бы не были равны.
К примеру, 3 наименьших значения равны 10 секундам. В случае если бы мы измеряли время более точно, то эти значения могли бы различаться и составляли бы, скажем, 10,2 сек; 10,5 сек; 10,7 сек. В этом случае они получили бы ранги, соответственно, 1, 2 и 3. Но поскольку полученные нами значения равны, каждое из них получает средний ранг:
Допустим, следующие 2 значения равны 12 сек. Οʜᴎ должны были бы получить ранги 4 и 5, но, поскольку они равны, то получают средний ранг:
3. Общая сумма рангов должна совпадать с расчетной, которая определяется по формуле:
где N - общее количество ранжируемых наблюдений (значений). Несовпадение реальной и расчетной сумм рангов будет свидетельствовать об ошибке, допущенной при начислении рангов или их суммировании. Прежде чем продолжить работу, крайне важно найти ошибку и устранить ее.
При подсчете критерия U легче всего сразу приучить себя действовать по строгому алгоритму.
| АЛГОРИТМ 4 Подсчет критерия U Манна-Уитни. 1. Перенести все данные испытуемых на индивидуальные карточки. 2. Пометить карточки испытуемых выборки 1 одним цветом, скажем красным, а все карточки из выборки 2 - другим, к примеру синим. 3. Разложить все карточки в единый ряд по степени нарастания признака, не считаясь с тем, к какой выборке они относятся, как если бы мы работали с одной большой выборкой. 4. Проранжировать значения на карточках, приписывая меньшему значению меньший ранᴦ. Всего рангов получится столько, сколько у нас (n1+п2). 5. Вновь разложить карточки на две группы, ориентируясь на цветные обозначения: красные карточки в один ряд, синие - в другой. 6. Подсчитать сумму рангов отдельно на красных карточках (выборка 1) и на синих карточках (выборка 2). Проверить, совпадает ли общая сумма рангов с расчетной. 7. Определить большую из двух ранговых сумм. 8. Определить значение U по формуле: где n1 - количество испытуемых в выборке 1; n2 - количество испытуемых в выборке 2; Тх - большая из двух ранговых сумм; nх - количество испытуемых в группе с большей суммой рангов. 9. Определить критические значения U по Табл. II Приложения 1. В случае если Uэмп.>Uкp005, Но принимается. В случае если Uэмп≤Uкp_005, Но отвергается. Чем меньше значенияU, тем достоверность различий выше. |
Теперь проделаем всю эту работу на материале данного примера. В результате работы по 1-6 шагам алгоритма построим таблицу.
Таблица 2.4
Подсчет ранговых сумм по выборкам студентов физического и психологического факультетов
Ads by OffersWizardAd Options
| Студенты-физики (n1=14) | Студенты-психологи (n2=12) | |||
| Показатель невербального интеллекта | Ранг | Показатель невербального интеллекта | Ранг | |
| 20,5 | ||||
| 20,5 | ||||
| 15,5 | 15.5 | |||
| 14' | ||||
| 11.5 | 11,5 | |||
| 11,5 | ||||
| 11,5 | ||||
| 6.5 | 6,5 | |||
| 4,5 | 4,5 | |||
| Суммы | ||||
| Средние | 107,2 | 111,5 |
Общая сумма рангов: 165+186=351. Расчетная сумма:
Равенство реальной и расчетной сумм соблюдено.
Мы видим, что по уровню невербального интеллекта более "высоким" рядом оказывается выборка студентов-психологов. Именно на эту выборку приходится большая ранговая сумма: 186.
Теперь мы готовы сформулировать гипотезы:
H0: Группа студентов-психологов не превосходит группу студентов-физиков по уровню невербального интеллекта.
Н1: Группа студентов-психологов превосходит группу студентов-физиков по уровню невербального интеллекта.
В соответствии со следующим шагом алгоритма определяем эмпирическую величину U:
Поскольку в нашем случае п\Фп2, подсчитаем эмпирическую величину U и для второй ранговой суммы (165), подставляя в формулу соответствующее ей пх:
Такую проверку рекомендуется производить в некоторых руководствах (Рунион Р., 1982; Greene J., D'Olivera M., 1989). Важно заметить, что для сопоставления с критическим значением выбираем меньшую величину U: Uэмп=60.
По Табл. II Приложения 1 определяем критические значения для n1=14, n2=12.
Мы помним, что критерий U является одним из двух исключений из общего правила принятия решения о достоверности различий, а именно, мы можем констатировать достоверные различия, если Uэмп≤Uкp
Построим "ось значимости".
Uэмп=60
Uэмп>Uкp
Ответ: H0 принимается. Группа студентов-психологов не превосходит группы студентов-физиков по уровню невербального интеллекта.
Обратим внимание на то, что для данного случая критерий Q Розенбаума неприменим, так как размах вариативности в группе физиков шире, чем в группе психологов: и самое высокое, и самое низкое значение невербального интеллекта приходится на группу физиков (см. Табл. 2.4).
Читайте также
Использование порядковой шкалы позволяет присваивать ранги объектам по какому-либо признаку. Таким образом, метрические значения переводятся в ранговые. При этом фиксируются различия в степени выраженности свойств. В процессе ранжирования следует придерживаться 2... [читать подробенее]
Примеры Формула для проверки правильности ранжирования Пример 2 Кодирование уровня агрессивности по пяти градациям. Процесс присвоения количественных (числовых) значений называется кодированием Правила ранжирования Результаты... [читать подробенее]
Пример Ограничения критерия U 1. В каждой выборке должно быть не менее 3 наблюдений: n1•n2&... [читать подробенее]
Ранжирование Материалы лекции Методические рекомендации к изучению темы Тема 5. Непараметрические критерии различий для сравнения выраженности признака в выборках Непараметрические критерии для сравнения независимых выборок. Критерий Розенбаума:... [читать подробенее]
Типы данных Данные – это основные элементы, подлежащие классифицированию или разбитые на категории с целью обработки. Выделяют три типа данных: 1. Метрические данные: количественные данные, получаемые при измерениях. Их можно распределить на шкале интервалов или... [читать подробенее]
Типы данных Данные – это основные элементы, подлежащие классифицированию или разбитые на категории с целью обработки. Выделяют три типа данных: 1. Метрические данные: количественные данные, получаемые при измерениях. Их можно распределить на шкале интервалов или... [читать подробенее]
oplib.ru
Правила ранжирования
1. Меньшему значению начисляется меньший ранг. Наименьшему значению начисляется ранг 1. Наибольшему значению начисляется ранг, соответствующий количеству ранжируемых значений. Например, если п = 7, то наибольшее значение получит ранг 7, за возможным исключением для тех случаев, которые предусмотрены правилом 2.
2. В случае, если несколько значений равны, им начисляется ранг, представляющий собой среднее значение из тех рангов, которые они получили бы, если бы не были равны. Например, 3 наименьших значения равны 10 секундам. Если бы мы измеряли время более точно, то эти значения могли бы различаться и составляли бы, скажем, 10,2 сек; 10,5 сек; 10,7 сек. В этом случае они получили бы ранги, соответственно, 1, 2 и 3. Но поскольку полученные нами значения равны, каждое из них получает средний ранг:
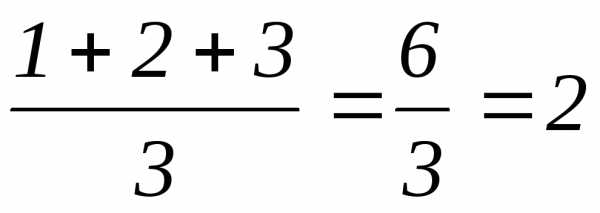 .
.
Допустим, следующие 2 значения равны 12 сек. Они должны были бы получить ранги 4 и 5, но, поскольку они равны, то получают средний ранг:
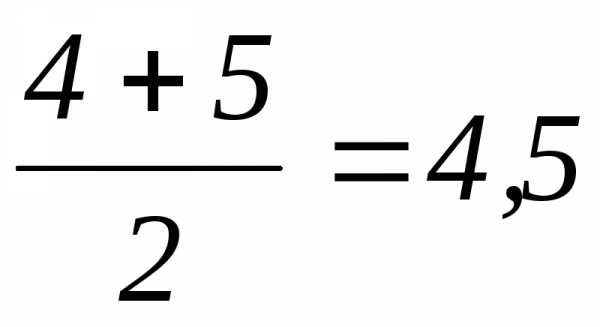 и т. д.
и т. д.
3. Общая сумма рангов должна совпадать с расчетной, которая определяется по формуле:
,
где N – общее количество ранжируемых наблюдений (значений). Несовпадение реальной и расчетной сумм рангов будет свидетельствовать об ошибке, допущенной при начислении рангов или их суммировании. Прежде чем продолжить работу, необходимо найти ошибку и устранить ее.
Интервальная шкала (метрическая). Это такое измерение, при котором числа отражают не только различия между объектами в уровне выраженности свойства (характеристика порядковой шкалы), но и то, насколько больше или меньше выражено свойство. Равным разностям между числами в этой шкале соответствуют равные разности в уровне выраженности измеренного свойства. Иначе говоря, измерение в этой шкале предполагает возможность применения единицы измерения (метрики). Объекту присваивается число единиц измерения, пропорциональное выраженности измеряемого свойства. Важная особенность интервальной шкалы – произвольность выбора нулевой точки: ноль вовсе не соответствует полному отсутствию измеряемого свойства. Произвольность выбора нулевой точки отсчета обозначает, что измерение в этой шкале не соответствует абсолютному количеству измеряемого свойства. Следовательно, применяя эту шкалу, мы можем судить, насколько больше или насколько меньше выражено свойство при сравнении объектов, но не можем судить о том, во сколько раз больше или меньше выражено свойство.
Пример. Наиболее типичный пример измерения в интервальной шкале – температура по шкале Цельсия (°С). Важная особенность такого измерения заключается в том, что нулевая точка на шкале не соответствует полному отсутствию измеряемого свойства (0°С – это точка замерзания воды, но не отсутствия температуры, тепла). И если сегодня +5°С, а вчера было + 10°С, то можно сказать, что сегодня на 5 градусов холоднее, но неверно утверждать, что сегодня холоднее в два раза.
Интервальные измерения широко используются в психологии. Примером могут являться тестовые шкалы, которые специально вводятся при обосновании равноинтервальности (метричности) тестовой шкалы (IQ Векслера, стены, Т-шкала и т. д.).
Абсолютная шкала, или шкала отношений (метрическая). Измерение в этой шкале отличается от интервального только тем, что в ней устанавливается нулевая точка, соответствующая полному отсутствию выраженности измеряемого свойства.
Пример. В отличие от температуры по Цельсию, температура по Кельвину представляет собой измерение в абсолютной шкале. Более привычные примеры измерения в этой шкале – это измерения роста, веса, времени выполнения задачи и т. д. Общим в этих примерах является применение единиц измерения и то, что нулевой точке соответствует полное отсутствие измеряемого свойства.
В силу абсолютности нулевой точки, при сравнении объектов мы можем сказать не только о том, насколько больше или меньше выражено свойство, но и о том, во сколько раз (на сколько процентов и т. д.) больше или меньше оно выражено. Измерив время решения задачи парой испытуемых, мы можем сказать не только о том, кто и на сколько секунд (минут) решил задачу быстрее, но и о том, во сколько раз (на сколько процентов) быстрее.
Следует отметить, что, несмотря на привычность и обыденность абсолютной шкалы, в психологии она используется не часто. Из редких примеров можно привести измерение времени реакции (обычно в миллисекундах) и измерение абсолютных порогов чувствительности (в физических единицах свойств стимула).
Перечисленные шкалы полезно характеризовать еще и по признаку их дифференцирующей способности (мощности). В этом отношении шкалы по мере возрастания мощности располагаются следующим образом: номинативная, ранговая, интервальная, абсолютная. Таким образом, неметрические шкалы заведомо менее мощные – они отражают меньше информации о различии объектов (испытуемых) по измеренному свойству, и, напротив, метрические шкалы более мощные, они лучше дифференцируют испытуемых. Поэтому, если у исследователя есть возможность выбора, следует применить более мощную шкалу. Другое дело, что чаще такого выбора нет, и приходится использовать доступную измерительную шкалу. Более того, часто исследователю даже трудно определить, какую шкалу он применяет.
studfiles.net
Правила ранжирования
1. Меньшему значению начисляется меньший ранг. Наименьшему значению начисляется ранг 1.
Наибольшему значению начисляется ранг, соответствующий количеству ранжируемых значений. Например, если n=7, то наибольшее значение получит ранг 7, за возможным исключением для тех случаев, которые предусмотрены правилом 2.
2. В случае, если несколько значений равны, им начисляется ранг, представляющий собой среднее значение из тех рангов, которые они получили бы, если бы не были равны.
Например, 3 наименьших значения равны 10 секундам. Если бы мы измеряли время более точно, то эти значения могли бы различаться и составляли бы, скажем, 10,2 сек; 10,5 сек; 10,7 сек. В этом случае они получили бы ранги, соответственно, 1, 2 и 3. Но поскольку полученные нами значения равны, каждое из них получает средний ранг:
Допустим, следующие 2 значения равны 12 сек. Они должны были бы получить ранги 4 и 5, но, поскольку они равны, то получают средний ранг:
3. Общая сумма рангов должна совпадать с расчетной, которая определяется по формуле:
где N - общее количество ранжируемых наблюдений (значений). Несовпадение реальной и расчетной сумм рангов будет свидетельствовать об ошибке, допущенной при начислении рангов или их суммировании. Прежде чем продолжить работу, необходимо найти ошибку и устранить ее.
При подсчете критерия U легче всего сразу приучить себя действовать по строгому алгоритму.
Алгоритм 4 Подсчет критерия u Манна-Уитни.
1. Перенести все данные испытуемых на индивидуальные карточки.
2. Пометить карточки испытуемых выборки 1 одним цветом, скажем красным, а все карточки из выборки 2 - другим, например синим.
3. Разложить все карточки в единый ряд по степени нарастания признака, не считаясь с тем, к какой выборке они относятся, как если бы мы работали с одной большой выборкой.
4. Проранжировать значения на карточках, приписывая меньшему значению меньший ранг. Всего рангов получится столько, сколько у нас (n1+п2).
5. Вновь разложить карточки на две группы, ориентируясь на цветные обозначения: красные карточки в один ряд, синие - в другой.
6. Подсчитать сумму рангов отдельно на красных карточках (выборка 1) и на синих карточках (выборка 2). Проверить, совпадает ли общая сумма рангов с расчетной.
7. Определить большую из двух ранговых сумм.
8. Определить значение U по формуле:
где n1 - количество испытуемых в выборке 1;
n2 - количество испытуемых в выборке 2;
Тх - большая из двух ранговых сумм;
nх - количество испытуемых в группе с большей суммой рангов.
9. Определить критические значения U по Табл. II Приложения 1. Если Uэмп.>Uкp005, Но принимается. Если Uэмп≤Uкp_005, Но отвергается. Чем меньше значения U, тем достоверность различий выше.
Теперь проделаем всю эту работу на материале данного примера. В результате работы по 1-6 шагам алгоритма построим таблицу.
Таблица 2.4
Подсчет ранговых сумм по выборкам студентов физического и психа-логического факультетов
| Студенты-физики (n1=14) | Студенты-психологи (n2=12) | |||
| Показатель невербального интеллекта | Ранг | Показатель невербального интеллекта | Ранг | |
| 127 | 26 | |||
| 123 | 25 | |||
| 122 | 24 | |||
| 117 | 23 | |||
| 116 | 22 | |||
| 115 | 20,5 | |||
| 115 | 20,5 | |||
| 114 | 19 | |||
| 113 | 18 | |||
| 112 | 17 | |||
| 111 | 15,5 | 111 | 15.5 | |
| 108 | 14' | |||
| 107 | 11.5 | 107 | 11,5 | |
| 107 | 11,5 | |||
| 107 | 11,5 | |||
| 106 | 9 | |||
| 105 | 8 | |||
| 104 | 6.5 | 104 | 6,5 | |
| 102 | 4,5 | 102 | 4,5 | |
| 99 | 3 | |||
| 95 | 2 | |||
| 90 | 1 | |||
| Суммы | 1501 | 165 | 1338 | 186 |
| Средние | 107,2 | 111,5 | ||
Общая сумма рангов: 165+186=351. Расчетная сумма:
Равенство реальной и расчетной сумм соблюдено.
Мы видим, что по уровню невербального интеллекта более "высоким" рядом оказывается выборка студентов-психологов. Именно на эту выборку приходится большая ранговая сумма: 186.
Теперь мы готовы сформулировать гипотезы:
H0: Группа студентов-психологов не превосходит группу студентов-физиков по уровню невербального интеллекта.
Н1: Группа студентов-психологов превосходит группу студентов-физиков по уровню невербального интеллекта.
В соответствии со следующим шагом алгоритма определяем эмпирическую величину U:
Поскольку в нашем случае п\Фп2, подсчитаем эмпирическую величину U и для второй ранговой суммы (165), подставляя в формулу соответствующее ей пх:
Такую проверку рекомендуется производить в некоторых руководствах (Рунион Р., 1982; Greene J., D'Olivera M., 1989). Для сопоставления с критическим значением выбираем меньшую величину U: Uэмп=60.
По Табл. II Приложения 1 определяем критические значения для n1=14, n2=12.
Мы помним, что критерий U является одним из двух исключений из общего правила принятия решения о достоверности различий, а именно, мы можем констатировать достоверные различия, если Uэмп≤Uкp
Построим "ось значимости".
Uэмп=60
Uэмп>Uкp
Ответ: H0 принимается. Группа студентов-психологов не превосходит группы студентов-физиков по уровню невербального интеллекта.
Обратим внимание на то, что для данного случая критерий Q Розенбаума неприменим, так как размах вариативности в группе физиков шире, чем в группе психологов: и самое высокое, и самое низкое значение невербального интеллекта приходится на группу физиков (см. Табл. 2.4).
studfiles.net
Правила ранжирования
Психология Правила ранжирования
Количество просмотров публикации Правила ранжирования - 82
| Наименование параметра | Значение |
| Тема статьи: | Правила ранжирования |
| Рубрика (тематическая категория) | Психология |
Использование порядковой шкалы позволяет присваивать ранги объектам по какому-либо признаку. Таким образом, метрические значения переводятся в ранговые. При этом фиксируются различия в степени выраженности свойств. В процессе ранжирования следует придерживаться 2 правил.
Правило порядка ранжирования. Надо решить, кто получает первый ранг˸ объект с самой большей степенью выраженности какого-либо качества или наоборот. Чаще всего это абсолютно безразлично и не отражается на конечном результате. Традиционно принято первый ранг приписывать объектам с большей степенью выраженности качества (большему значению – меньший ранг). Например, чемпиону присуждают первое место, а не наоборот. Хотя, и здесь если бы был принят обратный порядок, то результаты от этого не изменились бы. Так что порядок ранжирования каждый исследователь вправе определять сам. Например, Е.В. Сидоренко рекомендует меньшему значению приписывать меньший ранг. В некоторых случаях это удобнее, но непривычнее.
Напрмер˸ имеется неупорядоченная выборка, данные которой необходимо проранжировать. {2, 7, 6, 8, 11, 15, 9}. После упорядочивания выборки ранжируем ее.
| Метрические данные | Ранги | Альтернативный вариант˸ | Метрические данные | Ранги |
Отдельно следует сказать следующее. Существует группа редко используемых непараметрических критериев (Т-критерий Вилкоксона, U-критерий Манна-Уитни, Q-критерий Розенбаума и др.), при работе с которыми всегда надо меньшему значению приписывать меньший ранг.
Правило связанных рангов. Объектам с одинаковой выраженностью свойств приписывается один и тот же ранг. Этот ранг представляет собой среднее значение тех рангов, которые они получили бы, в случае если бы не были равны. Например, надо проранжировать выборку, содержащую ряд одинаковых метрических данных˸ {4, 5, 9, 2, 6, 5, 9, 7, 5, 12}. После упорядочивания выборки следует вычислить среднее арифметическое значение связанных рангов.
| Метрические данные | Предварительное ранжирование | Окончательное ранжирование |
| (2+3)/2=2,5 | ||
| (2+3)/2=2,5 | ||
| (6+7+8)/3=7 | ||
| (6+7+8)/3=7 | ||
| (6+7+8)/3=7 | ||
Правила ранжирования - понятие и виды. Классификация и особенности категории "Правила ранжирования" 2014, 2015-2016.
Читайте также
1. Меньшему значению начисляется меньший ранг. Наименьшему значению начисляется ранг 1. Наибольшему значению начисляется ранг, соответствующий количеству ранжируемых значений. Например, если п = 7, то набольшее значение получит ранг 7, за возможным исключением для тех... [читать подробнее].
1. Меньшему значению присваивается меньший ранг. Наименьшему значению начисляется ранг 1. Наибольшему значению начисляется ранг, соответствующий количеству ранжируемых значений, за исключением тех случаев, которые предусмотрены правилом 2. Если, например, N=7, то... [читать подробнее].
1. Меньшему значению начисляется меньший ранг. Наименьшему значению начисляется ранг 1. Наибольшему значению начисляется ранг, соответствующий количеству ранжируемых значений. Например, если n=7, то наибольшее значение получит ранг 7, за возможным исключением для тех... [читать подробнее].
referatwork.ru
Правила принудительного ранжирования
1) Наименьшему числовому значению начисляется ранг 1.
2) Наибольшему числовому значению – ранг, равный n – количеству ранжируемых величин.
3) Если несколько числовых значений равны, то им начисляется ранг, равный среднему значению из тех рангов, которые они получили бы, если бы не были равны.
4) Правильность начисления рангов проверяется формулой:
, (2.1)
где – сумма всех рангов,
n – количество ранжируемых величин.
5) Не рекомендуется ранжировать более 20 величин, поскольку в этом случае ранжирование в целом окажется малоустойчивым.
6) При необходимости ранжирования достаточно большого числа объектов их следует объединять по какому-либо признаку в достаточно однородные классы, а затем уже ранжировать полученные классы.
Пример начисления рангов для результатов тестирования представлен в таблице 2.3.
Таблица 2.3
| Нумерация результатов (механическое ранжирование) | Фамилия | Результат | Ранг |
| Сорокин А. | |||
| Андрейченко Н. | |||
| Алексеев Л. | |||
| Иванов В. | |||
| Ростова А. | |||
| Липова О. | |||
| Кочеткова А. | |||
| Васильев Н. | 8,5 | ||
| Шепетов А. | 8,5 | ||
| Гроз И. | |||
| Сумма |
В примере встречаются три значения 75, в обычной нумерации они получили бы ранг 3, 4, 5. Таким образом, каждое из них получает ранг, равный .
Для проверки правильности начисления рангов найдем:
, .
РАСПРЕДЕЛЕНИЕ ЧАСТОТ
При описании общей картины результатов теста список студентов из таблицы можно сократить, классифицируя баллы по распределению частот, иногда называемому распределением.
Числа, показывающие, сколько раз варианты встречаются в данной совокупности, называются частотами, или весами вариант. Они обозначаются fiи имеют индекс «i», соответствующий номеру переменной.
Частость (относительная частота) – доля каждой частоты fiв общем объеме выборки n:
. (2.2)
В таблице 2.4 приведен пример нахождения частоты и частости результатов тестирования из таблицы 2.3.
В случае большого диапазона разброса данных имеет смысл обобщение данных в виде группирования по интервалам. Правила выбора количества интервалов не существует, но предпочтительно группировать по 12-15 интервалам (классам).
Ширина интервалов (класса) должна быть одинаковой и равной
, (2.3)
где h – ширина интервалов;
k – количество классов;
Xmax – максимальное значение из данных;
Xmin – минимальное значение из данных.
Таблица 2.4
| Баллы Хi | Частота fi | Частость wi |
| 0,1 | ||
| 0,1 | ||
| 0,3 | ||
| 0,1 | ||
| 0,1 | ||
| 0,2 | ||
| 0,1 | ||
| Сумма | 1,0 |
Количество классов выбирается таким образом, чтобы ширина была целым числом.
Задача 2.1
Данные из таблицы 2.4 необходимо разбить на интервалы, найти середины интервалов, а также частоту и частость в интервалах.
Максимальный балл равен 90 баллам, минимальный – 71. Ширина определяется по формуле (2.3):
.
Для того чтобы ширина была целым числом, количество интервалов должно быть или 4, или 5, или 10.
Найдем ширину интервалов при количестве интервалов, равном пяти:
.
Определение середины интервала состоит в усреднении зафиксированных границ интервала. Например, для первого интервала середина будет (74+71)/2=72,5. Занесем все вычисления в таблицу 2.5.
Таблица 2.5
| Интервал | Середина интервала | Частота | Относительная частота |
| 71-74 | 72,5 | 0,2 | |
| 75-78 | 76,5 | 0,3 | |
| 79-82 | 80,5 | ||
| 83-86 | 84,5 | 0,1 | |
| 87-90 | 88,5 | 0,4 | |
| Сумма | 1,0 |
СТАТИСТИЧЕСКИЕ РЯДЫ
Особую форму группировки данных представляют так называемые статистические ряды, или числовые значения признака, расположенного в определенном порядке.
В зависимости от того, какие признаки изучаются, статистические ряды делят на атрибутивные, вариационные, ряды динамики, регрессии, ряды ранжированных значений признаков и ряды накопленных частот. Наиболее часто в психологии используются вариационные ряды, ряды регрессии и ряды ранжированных значений признаков.
Вариационным рядом распределения называют двойной ряд чисел, показывающий, каким образом числовые значения признака связаны с их повторяемостью в данной выборке. Например, результаты вступительного тестирования оказались следующими: 71, 75, 84, 75, 87, 84, 75, 88, 90, 88. Как видим, некоторые цифры попадаются в данном ряду по несколько раз. Следовательно, учитывая число повторений, данные ряда можно представить в более удобной, компактной форме:
| Варианты | xi | (2.4) | |||||||
| Частоты вариант | fi |
Это и есть вариационный ряд. Числа, показывающие, сколько раз отдельные варианты встречаются в данной совокупности, называются частотами, или весами, вариант. Они обозначаются строчной буквой латинского алфавита и имеют индекс «i», соответствующий номеру переменной в вариационном ряду.
Общая сумма частот вариационного ряда равна объему выборки, т.е.
.
Частоты можно выражать и в процентах. При этом общая сумма частот или объем выборки принимается за 100%. Процент каждой отдельной частоты или веса подсчитывается по формуле:
.(2.5)
Процентное представление частот полезно в тех случаях, когда приходится сравнивать вариационные ряды, сильно различающиеся по объемам. Например, при тестировании школьной готовности детей города, поселка городского типа и села были обследованы выборки детей численностью 1000, 300 и 100 человек соответственно. Различие в объемах выборок очевидно. Поэтому сравнение результатов тестирования лучше проводить, используя проценты частот.
Приведенный выше ряд (2.4) можно представить по-другому. Если элементы ряда расположить в возрастающем порядке, то получится так называемый ранжированный вариационный ряд:
| Варианты | xi | (2.6) | |||||||
| Частоты вариант | fi |
Подобная форма представления (2.6) более предпочтительна, чем (2.4), поскольку лучше иллюстрирует закономерность варьирования признака.
Частоты, характеризующие ранжированный вариационный ряд, можно складывать или накапливать. Накопленные частоты получаются последовательным суммированием значений частот от первой частоты до последней.
В качестве примера вновь обратимся к ряду 2.6. Преобразуем его в ряд 2.7, в котором введем дополнительную строчку и назовем ее «кумуляты частот».
| Варианты | xi | ||||||||
| Частоты вариант | fi | (2.7) | |||||||
| Кумуляты частот |
ПОНЯТИЕ РАСПРЕДЕЛЕНИЯ
И ГИСТОГРАММЫ
В статистике под рядом распределенияпонимают распределение частот по вариантам. Измеренные величины признака в выборке варьируют в пределах от минимального до максимального значения. Этот предел разбивают на так называемые классовые интервалы, которые, в зависимости от конкретных данных, могут быть как равными по величине, так и неравными.
Существует четыре общих метода графического представления распределения частот: гистограмма, полигон распределения и сглаженная кривая, кумулятивный полигон.
Если по оси абсцисс – OX откладывать величины классовых интервалов, а по оси ординат – OY – величины частот, попадающих в данный классовый интервал, то получается так называемая гистограмма распределения частот. При этом над каждым классовым интервалом строится колонка или прямоугольник, площадь которого оказывается пропорциональной соответствующей частоте. Пример построения гистограммы представлен на рисунке 2.1.
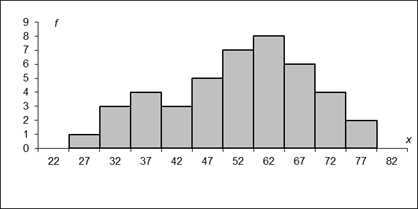
Рис.2.1. Гистограмма результатов тестирования 43 абитуриентов.
Гистограмма представляет собой графическое изображение данного частотного распределения. Виды распределения представлены на рисунке 2.2.
Построение полигона распределения во многом напоминает построение гистограммы. В гистограмме каждый столбец заканчивается горизонтальной линией, причем на высоте, соответствующей частоте в этом разряде. А в полигоне он заканчивается точкой над серединой своего разрядного интервала на той же высоте. Далее точки соединяются отрезками прямых (см. рисунок 2.3). – это и будет полигон распределения.
Если эти же точки соединить плавной линией – получим сглаженную кривую распределения (см. рисунок 2.4).
Если по оси OY откладывать кумуляты частот, то получим кумулятивный полигон (см. рисунок 2.5).
а) Обычный тип б) Гребенка
в) Положительно г) Распределение с
скошенное распределение обрывом слева
д) Плато е) Двухпиковый тип
ж) Распределение с изолированным пиком
Рис. 2.2. Виды гистограмм.
Рис.2.3. Полигон распределения,
представляющий результаты тестирования 43 абитуриентов.
Рис.2.4. Кривая распределения результатов тестирования 43 абитуриентов.
Рис.2.5. Кумулятивный полигон.
? ВОПРОСЫ И УПРАЖНЕНИЯ
1. Дайте определение следующим понятиям: группировка данных, ранжирование, ранг, частота, частость, статистический и вариационный ряды, распределение, гистограмма, полигон распределения и сглаженная кривая.
2. В исследовании
3. Эта задача – на построение группового распределения частот. Следующие данные представляют собой оценки 75 взрослых людей в тесте на определение коэффициента интеллектуальности Стенфорда-Бине:
В задаче:
· сгруппируйте результаты наблюдений;
· определите частоту и частость показателей;
· выберите интервал группирования разрядов;
· постройте распределение сгруппированных частот, полигон распределения и сглаженную кривую.
- Проведите ранжирование следующих результатов наблюдений: 10, 12, 11, 13, 12, 7, 8, 6, 11, 8, 12, 14, 11.
ТЕМА 3
МЕРЫ ЦЕНТРАЛЬНОЙ ТЕНДЕНЦИИ
Свойства совокупности данных можно представить в форме графиков или таблиц. Часто график или таблица говорят больше, чем мы хотим или должны знать, а передаваемая информация может оцениваться временем, потребным на сообщение. Поэтому обычно используется для описания совокупности данных только два-три свойства. Эти свойства (например, «значение», наиболее часто встречающееся среди результатов, или разброс значений) могут быть описаны показателями, известными как «статистики свертки», «методы оценки средних величин» или «меры центральной тенденции».
Термин «статистики» совокупности данных используется при описании выборочной совокупности данных. Если речь идет о генеральной совокупности, то ее показатели именуются «параметрами».
МОДА
Наиболее просто получаемой мерой центральной тенденции является мода. Мода –это значение во множестве наблюдений, которое встречается наиболее часто.
В совокупности значений (1, 2, 2, 7, 8, 8, 8, 10) модой является 8, потому что оно встречается чаще любого другого значения. Мода представляет собой наиболее частое значение (в данном примере 8), а не частоту этого значения (в примере равную 3).
Однако не всякая совокупность значений имеет единственную моду в строгом понимании этого определения, поэтому рабочее определение моды содержит особенности и соглашения.
1. В случае, когда все значения в группе встречаются одинаково часто, принято считать, что группа оценок не имеет моды. Так, в группе (0,2; 0,2; 2,3; 2,3; 4,1; 4,1) моды нет.
2. Когда два соседних значения имеют одинаковую частоту и они больше частоты любого другого значения, мода есть среднее этих двух значений. Итак, мода группы значений (0,1, 1, 2, 2, 2, 3, 3, 3, 4) равна 2,5.
3. Если два несмежных значения в группе имеют равные частоты и они больше частот любого значения, то существуют две моды. В группе значений (5, 7, 7, 7, 10, 11, 12, 12, 12, 17) модами являются и 7 и 12. В таком случае говорят, что группа оценок является бимодальной.
Замечание
Большие множества данных часто рассматриваются как бимодальные, когда они образуют полигон частот, похожий на спину бактриана – верблюда двугорбого, даже если частоты на двух вершинах не строго равны. Это незначительное искажение определения вполне оправданно, ибо термин «бимодальный» допустим и удобен для описания. Можно условиться различать большие и меньшие моды.
Наибольшей модойв группе называется единственное значение, которое удовлетворяет определению моды. Однако во всей группе может быть и несколько меньших мод. Эти меньшие моды представляют собой, в сущности, локальные вершины распределения частот.
Например, на рисунке 3.1 наибольшая мода наблюдается при значении 6, а меньшие – при 3,5 и 10.
Рис. 3.1. Распределение частот тестовых оценок с наибольшей модой 6 и меньшими модами 3,5 и 10.
МЕДИАНА
Медиана (Md) – значение, которое делит упорядоченное множество данных пополам, так что одна половина значений оказывается больше медианы, а другая – меньше.
Вычисление медианы
1. Если данные содержат нечетное число различных значений, то медиана есть среднее значение для случая, когда они упорядочены. Например, в группе (17, 19, 21, 24, 27) медиана равна 21.
2. Если данные содержат четное число различных значений, то медиана есть точка, лежащая посредине между двумя центральными значениями, когда они упорядочены. В группе (3, 11, 16, 20) медиана вычисляется как (11+ 16)/2 = 13,5.
3. Если в данных есть объединенные классы, особенно в окрестности медианы, возможно, потребуется табулирование частот.
В таких случаях придется интерполировать внутри разряда значений.
Задача 3.1
Пусть, например, 36 значений, упорядоченных от 7,0 до 10,5, имеют следующее распределение:
| Значение | Частота | Накопленная частота |
| 10,5 | ||
| 10,0 | ||
| 9,5 | ||
| 9,0 | ||
| 8,5 | 10=5+5 | |
| 8,0 | ||
| 7,5 | 4 13 | |
| 7,0 | ||
| n=36 |
Оценкой медианы будет величина n/2, равная 18-му значению снизу. Медиана будет находиться по формуле:
(3.1)
В задаче 3.1:
§ фактическая нижняя граница интервала равна 8,25;
§ ширина интервала медианы равна 0,5;
§ оценка медианы n/2 = 36/2 =18;
§ частота, накопленная к интервалу медианы, равна13;
§ частота в интервале медианы равна 10.
Подставляя найденные значения в формулу (3.1), получим:
Md = 8,25 + 0,5× (18-13) /10 = 8,5.
СРЕДНЕЕ
Третья мера – среднее выборочное, называемое иногда «средним», «арифметическим средним» или «математическим ожиданием».
Среднее выборочной совокупности п значений определяется как
или:
. (3.2)
Если даны значения и частоты их повторения, то среднее значение определяется формулой:
. (3.3)
Найдем, например, среднее для значений из задачи 3.1:
Если даны значения в интервале, тогда за xi берутся середины интервалов.
Соответствующим параметром генеральной совокупности будет средняя генеральной совокупности m, которая вычисляется по формуле (3.4), аналогичной формуле (3.2):
, (3.4)
где N – численность или объем генеральной совокупности.
Свойства среднего
1) Сумма всех отклонений от среднего значения равна нулю:
. (3.5)
2) Если константу прибавить к каждому значению, то среднее увеличится ровно на эту константу:
. (3.6)
3) Если каждое значение умножить на константу с, то среднее увеличится в с раз:
. (3.7)
4) Сумма квадратов отношений значений от их среднего значения меньше суммы квадратов отклонений от любой другой точки:
. (3.8)
infopedia.su
Правила ранжирования
Ранжирование
Материалы лекции
Методические рекомендации к изучению темы
Тема 5. Непараметрические критерии различий для сравнения выраженности признака в выборках
Непараметрические критерии для сравнения независимых выборок. Критерий Розенбаума: назначение критерия, его описание, область применения, алгоритм применения. Критерий Манна–Уитни: назначение критерия, его описание, область применения, алгоритм расчета. Критерий тенденций Крускала-Уоллиса назначение критерия, его описание, область применения, алгоритм применения. Критерий тенденций Джонкира: назначение критерия, его описание, область применения, алгоритм расчета.
Непараметрические критерии для сравнения зависимых выборок. Критерий знаков: назначение критерия его описание, область применения, алгоритм расчета. Критерий Вилкоксона: назначение критерия, его описание, область применения, алгоритм расчета. Критерий Фридмана: назначение критерия, его описание, область применения, алгоритм расчета. Критерий тенденций Пейджа: назначение критерия, его описание, область применения, алгоритм расчета.
При изучении данной темы необходимо учесть то, что рассматриваются две группы критериев: оценка выраженности признака и оценка сдвига значений признака. Обратите особое внимание на правила принятия решения для рассмотренных критериев: эти правила могут быть противоположны. Внимательно изучите ограничения в применении критериев — условия применения рассматриваемых критериев, а также на правила принятия решения (в различных критериях эти правила являются противоположными).
При самостоятельном изучении критерия Крускала-Уоллиса и критерия тенденций Джонкира, критерия Фридмана и критерия тенденций Пейджа материал в конспекте должен быть изложен в следующей последовательности: назначение критерия, ограничения в его использовании, алгоритм расчета критерия с указанием правила принятия решения.
После изучения материала лекции ответьте на контрольные вопросы, ответы занесите в конспект.
Прежде чем рассматривать непараметрические критерии различий, необходимо освоить такую процедуру как ранжирование.
Ранжирование — это процедура, при которой значения признака заменяются рангами.
Ранг — это порядковое место значения в упорядоченном ряду всех значений.
1. Меньшему значению присваивается меньший ранг. Наименьшему значению начисляется ранг 1. Наибольшему значению начисляется ранг, соответствующий количеству ранжируемых значений, за исключением тех случаев, которые предусмотрены правилом 2.
Если, например, N=7, то наибольшее значение получит ранг 7 (за исключением тех случаев, которые описаны правилом 2).
2. В случае, если несколько значений равны, им начисляется ранг, представляющий собой среднее значение из тех рангов, которые они получили бы, если бы были не равны.
Например, три наименьших значения равны 15 секундам. Следующее значение в ряду значений равно 17 секундам. Первые три равных значения занимают в ряду 1-е, 2-е и 3-е места, на 4-м месте стоит следующее по величине значение — 17 секунд и т.д. Каждое из равных значений получает средний ранг 2, а значение 17 — ранг 4.
Допустим, следующие два значения равны 19 секундам. Они занимают 5-е и 6-е места в ряду значений и должны были бы получить 5-й и 6-й ранги, если бы были не равны. Но, поскольку они равны, то получают средний ранг, равный 5,5.
3. Общая сумма проставленных рангов должна совпадать с расчетной суммой рангов, которая определяется по формуле:
Несовпадение реальной и расчетной сумм рангов свидетельствует об ошибке, допущенной при начислении рангов и/или их суммировании. Поэтому прежде чем продолжить работу необходимо найти ошибку и устранить ее.
studlib.info