ГлавнаяПоведенческиеПоведенческих паттернов

Паттерн. Поведенческих паттернов


Поведенческие паттерны - Интересные вопросы социальной психологии

Слово «паттерн» (от английского pattern, что можно перевести как «шаблон», «модель», «система», «структура») применяется в различных научных дисциплинах и сферах деятельности. В одной только психологии паттерны используются в нескольких разделах, в том числе в когнитивной психологии, гипнологии и некоторых других сферах.

В общем и целом паттерн обозначает определенный набор, шаблон поведенческих реакций или последовательностей стереотипических действий, поэтому относительно любой области, где человек применяет шаблоны (а это почти все сферы), можно говорить о паттернах. Например, гипнотический паттерн — это текст, который использует гипнолог, чтобы ввести человека в транс. Словесные паттерны — это речевые приемы, которые мы сознательно или бессознательно применяем в речи. Паттерны мышления — мыслительные шаблоны, в частности обобщения. В данном тексте пойдет речь об общей характеристике поведенческих паттернов.

Людям в принципе свойственна стереотипизация поведения, мы вырабатываем определенные способы взаимодействия с окружающим миром. Это объясняется принципом рациональности — вместо того чтобы каждый раз придумывать новые способы реагирования на то или иное явление, проще воспользоваться готовой моделью. Поведенческие паттерны формируются в процессе обучения, воспитания, а также наблюдения за окружающими — какие модели применяют другие люди в различных ситуациях?

Зная о том, как определенный человек вел себя в тех или иных ситуациях, какие у него имеются паттерны поведения, вы сможете определить его действия и поступки в схожих ситуациях. Правда, прежде чем делать выводы, надо хорошо изучить саму личность и ее поведенческие паттерны. Самый простой пример — если ваш друг с легкостью раздает обещания направо и налево, но еще ни одно не выполнил (или по крайней мере мало какие), каков шанс, что он сделает то, что пообещает вам? То же касается вечно занимающих и не возвращающих долги знакомых.

Выработанные в детстве паттерны если и меняются, то с трудом. Именно поэтому девушке, выбирающей жениха, стоит обратить внимание на его отношение к матери. Дело в том, что через несколько лет после брака, когда пройдет стадия влюбленности, у мужчин зачастую (но не всегда) проявляются такие же поведенческие алгоритмы к супруге, которые от выработал по отношению к матери.

Важно и то, что, как правило, для близкого общения мы выбираем людей со схожими паттернами. Поэтому про некоторых девушек говорят, что у них, например, талант к поиску подлецов. На самом деле такие представительницы прекрасного пола просто ищут человека, подходящего под реализацию их паттерна. И, видимо, в данном случае мы имеем дело с моделью поведения, при которой мужчина должен обманывать женщину, не уважать ее, он король — она никто и так далее. И тут снова можно вернуться к тому, что все идет из детства.

Иными словами, не мужчине «везет» на чрезмерно ветреных подруг, а он подсознательно ищет девушек-изменниц. И когда его бросит одна из них, он будет искать другую, на подсознательном уровне, с таким же поведением, подходящим под паттерн. Хотя на уровне сознания личности может казаться, что следующая дама сердца будет совсем другой. У использования паттернов есть и еще одна сторона, которую порой используют в НЛП, школах успеха и др. Зная шаблон поведения, при котором несколько людей добились успеха, вы можете повторить эту модель, чтобы добиться успеха самому.

psifactory.livejournal.com

Паттерн — Википедия

плитка — пример использования паттернов в дизайне помещений

Па́ттерн (англ. pattern «образец, шаблон; форма, модель; схема, диаграмма») — схема-образ, действующая как посредствующее представление, или чувственное понятие, благодаря которому в режиме одновременности восприятия и мышления выявляются закономерности, как они существуют в природе и обществе.

Паттерн понимается в этом плане как повторяющийся шаблон или образец. Элементы паттерна повторяются предсказуемо. Так, из графических паттернов складываются красивые узоры.

Каждый из органов восприятия (чувств) воспринимает паттерны в соответствии со своими особенностями.

В науке, в том числе в математике и языкознании, паттерны выявляются путём исследования.

Прямое наблюдение может выявлять визуальные паттерны, как они формируются в природе и в искусстве. Визуальные паттерны в природе часто хаотичны. Они не копируют друг друга и часто являются фрактальными.

Паттерны в природе включают спирали, меандры, волны, пену, трещины, а также паттерны, созданные благодаря симметрии поворота и отражения. Все подобные паттерны имеют математически описываемую структуру, которая может быть выражена формулами, тем не менее математика сама по себе является поиском регулярностей, и любой конечный продукт применения функций является математическим паттерном.

Когда научные теории исследуют и предсказывают синхронно существующие регулярности в природе и обществе, то это и есть выявление паттернов.В искусстве и архитектуре для получения определенного устойчивого воздействия декорации и различные визуальные элементы могут комбинироваться и повторяться, образуя паттерны.В компьютерных науках шаблоны проектирования являются широко используемым решением большого класса проблем программирования.

Под паттерном в медицине понимают устойчивую комбинацию результатов исследований или других признаков (например, симптомов) при сходных жалобах пациента или у больных одной нозологии. Понятие «паттерн» включает несколько признаков (симптомов). Синдром включает один или несколько паттернов. Болезнь включает один или несколько синдромов.

Паттерны в природе

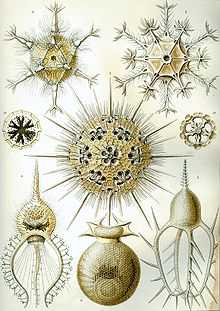рисунки морских животных Эрнста Геккеля, демонстрирующие различные виды симметрии

Ранние греческие философы, такие как Платон, Пифагор, Эмпедокл, исследовали паттерны, пытаясь объяснить порядок в природе. Современное понимание визуальных паттернов формировалось постепенно с развитием наук.

В XIX веке бельгийский физик Жозеф Плато, изучая мыльные пузыри, сформулировал концепцию минимальной поверхности. Немецкий биолог и художник Эрнст Геккель нарисовал сотни морских организмов, подчёркивая их симметрию. Шотландский биолог Дарси Томпсон первым начал изучение паттернов роста как растений, так и животных, показав, что спиральный рост можно описать простыми уравнениями. В XX веке британский математик Алан Тьюринг предсказал механизмы морфогенеза, которые ответственны за образование пятен и полос. Венгерский биолог Аристид Линденмайер и французско-американский математик Бенуа́ Мандельбро́т показали, как математика фракталов может объяснить паттерны роста растений.

Математика, физика и химия объясняют паттерны в природе на различных уровнях. Паттерны в живых организмах могут быть объяснены биологическими процессами естественного и полового отбора. Изучение формирования паттернов использует компьютерное моделирование для симуляции широкого спектра паттернов.

Видео по теме

Виды паттернов в природе

Симметрия

Симметрия для живых организмов является практически всеобщей. У большинства животных наблюдается зеркальная, или билатеральная, симметрия, она также присутствует в листьях растений и некоторых цветах, например орхидеях.[1] Растения часто имеют круговую, или вращательную, симметрию, как у многих цветов и некоторых животных, например у медуз. Пятилучевая симметрия встречается у иглокожих, таких как морские звёзды, морские ежи и морские лилии[2].

В неживой природе снежинка имеет красивую шестилучевую симметрию, каждая снежинка уникальна, но один и тот же паттерн повторяется на всех шести её лучах[3]. Кристаллы обычно имеют разные виды симметрии и габитусы, они могут быть кубическими, шестигранными, восьмигранными, но настоящие кристаллы никогда не имеют пятилучевую симметрию (чего нельзя сказать о квазикристаллах).[4] Вращательная симметрия встречается в различных явлениях неживой природы, например при всплеске, когда капля падает в водоём,[5] а также в сферических формах и кольцах планет, таких как Сатурн.[6]

Деревья, фракталы

самоподобие фрактального листа

Фракталы бесконечно самоподобны.[7][8][9] Бесконечные повторения в природе невозможны, поэтому 'фрактальные' паттерны фрактальны лишь приблизительно. Например, листья папоротников и зонтичных (Apiaceae) самоподобны на 2-м, 3-м или 4-м уровне. Схожие с папоротником паттерны самоподобия встречаются также у животных, включая мшанки, кораллы, гидроидные, а также в неживой природе, преимущественно в электрических разрядах.

Фракталоподобные паттерны широко встречаются в природе, в таких распространённых феноменах, как облака, речные сети, геологические разломы, горы, береговые линии,[10] окрас животных, снежинки,[11]кристаллы,[12] разветвления кровеносных сосудов[13] и морские волны.[14]

Спирали

Спирали часто встречаются у растений и некоторых животных, преимущественно моллюсков. Например у наутилусов, головоногих моллюсков, каждая камера его раковины является приблизительной копией предыдущей камеры, увеличенной на определённый коэффициент и представленной в виде логарифмической спирали.[15] Исходя из современного понимания фракталов, растущая спираль является частным случаем самоподобия.[16]

Среди растений спирали образуют некоторые виды алоэ, спиралевидным является распределение листьев на стебле, а также других частей у иных растений, например: соцветья астровых, семянные головки подсолнечника или фрукты вроде ананаса[17]:337 и салака, а также паттерн на шишках, где многочисленные спирали располагаются как по часовой, так и против часовой стрелки.

Спираль произрастания листьев может быть выведена из последовательности чисел Фибоначчи: 1, 1, 2, 3, 5, 8, 13… (каждое следующее число является суммой двух предыдущих). Например, при росте листьев из ствола, один поворот спирали равен двум листьям, поэтому паттерн или соотношение равно 1/2. У орешника соотношение 1/3; у абрикоса 2/5; у груши 3/8; у миндаля оно составляет 5/13.[18]

Хаос, потоки, меандры

хаос в окраске ракушки Вид на Николаев из космоса. Синусоидальный паттерн, образованный реками — пример меандра

В математике динамическая система является хаотической, если она слишком чувствительна к начальным условиям (так называемый эффект бабочки[19]).

Теория хаоса считается одним из самых важных факторов, влияющих на возникновение паттернов в природе. Существует связь между хаосом и фракталами — странные аттракторы в хаотических системах имеют фрактальную размерность.[20]

Турбулентность в газах и жидкостях при преодолении твердого препятствия образует характерные паттерны кручения.

Меандры — это синусообразные изгибы в реках и других каналах, формируемые жидкостью, обычно водой, текущей вдоль изгибов. Если русло не является ровным, размеры и неровность изгибов увеличивается за счёт того, что течение переносит твёрдый материал, обычно песок и гальку к внутренней стороне изгиба. Внешняя часть изгиба остаётся незащищённой, поэтому эрозия усиливается, увеличивая темпы меандрирования.[21]

Волны, дюны

Под влиянием ветра на поверхности воды и песка в природе образовываются схожие по строению хаотические паттерны, оставляющие рябь, называемые волнами на воде и дюнами на песке. Под действием ветра происходит неравномерное распределение, возвышенные участки чередуются с понижениями уровня.

Частным случаем дюн являются барханы.

Пузыри, пена

Мыльные пузыри образуют пену

Замощение

Замощение — разбиение без каких-либо накладок и без пробелов. Наиболее известным примером замощения в природе являются пчелиные соты, где шестиугольный паттерн многократно дублируется, заполняя всё пространство улья.

Трещины

Пятна и полосы

Паттерны в архитектуре

Паттерны в дизайне

Паттерны (повторяющиеся элементы) широко используются для украшения среды обитания человека — от лепнины, тротуарной плитки, обоев, паркета и кафеля до орнаментов в одежде, раскраски тканей и использования узоров в оформлении всевозможной печатной продукции. Наиболее популярные паттерны имеют имена, Клетка, Гусиные лапки, Бута, Турецкие огурцы, Алагрек, Меандр.

Паттерны часто употребляются в исламском мире. Искусствоведы подразделяют исламские узоры на стилизованные растительные, которые называются Арабеска, и геометрические, называемые Мореска.[22]

Паттерны для детей

Простым инструментом для создания паттернов является спирограф.

Наблюдать причудливые паттерны можно с помощью калейдоскопа.

Паттерны в медицине

В медицине термин «паттерн» употребляют при анализе, например, кардиограмм, энцефалограмм и результатов других исследований, понимая под ним[23] одинаковую последовательность колебаний биопотенциалов, повторяющуюся в одном или нескольких отведениях при одинаковых состояниях и условиях[24]

Термин паттерн используется для обозначения последовательности нервных импульсов, имеющей определённое информационное значение[25], например, «паттерны боли при биомеханических нарушениях суставов краниовертебрального перехода и шейного отдела позвоночника»[26] или «паттерны двигательных и чувствительных расстройств при патологии нервных структур в дистальных отделах верхней конечности»[27].

Паттерны широко представлены в глоссарии мануальных терапевтов (например паттерн ходьбы), рефлексотерапевтов (например, паттерн сырости-жара) и прикладных кинезиологов (например, паттерн дыхания).

Паттерны вязания

В вязании часто используются схемы рисунков, которые повторяются через определенное количество столбцов и рядов. Один такой рисунок, предназначенный для многократного повторения в вязаном изделии, и называется паттерном. Паттерн может состоять из различных видов петель, в результате получается объемный узор, или образовываться повторением узора из пряжи различных цветов, например стилизованные цветы или олени на свитерах.

Примечания

  1. ↑ Stewart, Ian. 2001. Pages 48-49.
  2. ↑ Stewart, Ian. 2001. Pages 64-65.
  3. ↑ Stewart, Ian. 2001. Page 52.
  4. ↑ Stewart, Ian. 2001. Pages 82-84.
  5. ↑ Stewart, Ian. 2001. Page 60.
  6. ↑ Stewart, Ian. 2001. Page 71.
  7. ↑ Mandelbrot, Benoît B. The fractal geometry of nature. — Macmillan, 1983.
  8. ↑ Falconer, Kenneth. Fractal Geometry: Mathematical Foundations and Applications. — John Wiley, 2003.
  9. ↑ Briggs, John. Fractals:The Patterns of Chaos. — Thames and Hudson, 1992. — P. 148.
  10. ↑ Batty, Michael (1985-04-04). «Fractals – Geometry Between Dimensions». New Scientist (Holborn Publishing Group) 105 (1450).
  11. ↑ Meyer, Yves; Roques, Sylvie. Progress in wavelet analysis and applications: proceedings of the International Conference "Wavelets and Applications," Toulouse, France – June 1992. — Atlantica Séguier Frontières, 1993. — P. 25.
  12. ↑ Carbone, Alessandra; Gromov, Mikhael; Prusinkiewicz, Przemyslaw. Pattern formation in biology, vision and dynamics. — World Scientific, 2000. — P. 78. — ISBN 9789810237929.
  13. ↑ Hahn, Horst K.; Georg,Manfred; Peitgen, Heinz-Otto. Fractal aspects of three-dimensional vascular constructive optimization // Fractals in biology and medicine / Losa, Gabriele A.; Nonnenmacher, Theo F.. — Springer, 2005. — P. 55–66.>
  14. ↑ Addison, Paul S. Fractals and chaos: an illustrated course. — CRC Press, 1997. — P. 44–46.
  15. ↑ Maor, Eli. e: The Story of a Number. Princeton University Press, 2009. Page 135.
  16. ↑ Ball, 2009. Shapes pp 29-32.
  17. ↑ Kappraff, Jay (2004). «Growth in Plants: A Study in Number». Forma 19: 335–354.
  18. ↑ Coxeter, H. S. M. Introduction to geometry. — Wiley, 1961. — P. 169.
  19. ↑ Lorenz, Edward N. (March 1963). «Deterministic Nonperiodic Flow». Journal of the Atmospheric Sciences 20 (2): 130–141. DOI:10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2. ISSN 1520-0469. Bibcode: 1963JAtS...20..130L. Проверено 3 June 2010.
  20. ↑ Ruelle, David. Chance and Chaos. Princeton University Press, 1991.
  21. ↑ Lewalle, Jacques. Flow Separation and Secondary Flow: Section 9.1 // Lecture Notes in Incompressible Fluid Dynamics: Phenomenology, Concepts and Analytical Tools. — Syracuse, NY : Syracuse University, 2006..
  22. ↑ Информация из справочника интерьерных идей 4living.ru. Архивировано 3 декабря 2012 года.
  23. ↑ Ciaccio E. J., Dunn S.M., Akay M. Biosignal pattern recognition and interpretation systems. Part 4 of 4: Review of applications // IEEE Engineering in Medicine and Biology Magazine. — 1994. — Vol. 13, 2006, Issue 2. — P. 269—273.
  24. ↑ Гапонова О .В. Электроэнцефалографические паттерны синдрома Веста // Медицинский совет. — 2008.- № 1-2.
  25. ↑ Малая меди цинская энциклопедия. — М.: Медицинская энциклопедия. 1991-96 гг.
  26. ↑ Небожин А. И., Ситель А. Б. Паттерны боли при биомеханических нарушениях шейного отдела позвоночника // Мануальная терапия. — 2007. — № 1 (25). — С. 2-8.
  27. ↑ Паттерны двигательных и чувствительных расстройств при патологии нервных структур в дистальных отделах верхней конечности // Медицинский портал для врачей и студентов doctorspb.ru. 2010. Источник в Интернет: http://doctorspb.ru/articles.php?article_id=1477

wiki2.red

Паттерн — WiKi

плитка — пример использования паттернов в дизайне помещений

Па́ттерн (англ. pattern «образец, шаблон; форма, модель; схема, диаграмма») — схема-образ, действующая как посредствующее представление, или чувственное понятие, благодаря которому в режиме одновременности восприятия и мышления выявляются закономерности, как они существуют в природе и обществе.

Паттерн понимается в этом плане как повторяющийся шаблон или образец. Элементы паттерна повторяются предсказуемо. Так, из графических паттернов складываются красивые узоры.

Каждый из органов восприятия (чувств) воспринимает паттерны в соответствии со своими особенностями.

В науке, в том числе в математике и языкознании, паттерны выявляются путём исследования.

Прямое наблюдение может выявлять визуальные паттерны, как они формируются в природе и в искусстве. Визуальные паттерны в природе часто хаотичны. Они не копируют друг друга и часто являются фрактальными.

Паттерны в природе включают спирали, меандры, волны, пену, трещины, а также паттерны, созданные благодаря симметрии поворота и отражения. Все подобные паттерны имеют математически описываемую структуру, которая может быть выражена формулами, тем не менее математика сама по себе является поиском регулярностей, и любой конечный продукт применения функций является математическим паттерном.

Когда научные теории исследуют и предсказывают синхронно существующие регулярности в природе и обществе, то это и есть выявление паттернов.В искусстве и архитектуре для получения определенного устойчивого воздействия декорации и различные визуальные элементы могут комбинироваться и повторяться, образуя паттерны.В компьютерных науках шаблоны проектирования являются широко используемым решением большого класса проблем программирования.

Под паттерном в медицине понимают устойчивую комбинацию результатов исследований или других признаков (например, симптомов) при сходных жалобах пациента или у больных одной нозологии. Понятие «паттерн» включает несколько признаков (симптомов). Синдром включает один или несколько паттернов. Болезнь включает один или несколько синдромов.

Паттерны в природе

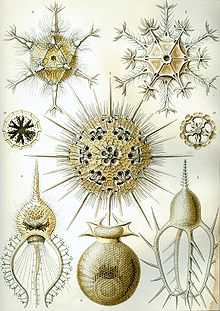  рисунки морских животных Эрнста Геккеля, демонстрирующие различные виды симметрии

Ранние греческие философы, такие как Платон, Пифагор, Эмпедокл, исследовали паттерны, пытаясь объяснить порядок в природе. Современное понимание визуальных паттернов формировалось постепенно с развитием наук.

В XIX веке бельгийский физик Жозеф Плато, изучая мыльные пузыри, сформулировал концепцию минимальной поверхности. Немецкий биолог и художник Эрнст Геккель нарисовал сотни морских организмов, подчёркивая их симметрию. Шотландский биолог Дарси Томпсон первым начал изучение паттернов роста как растений, так и животных, показав, что спиральный рост можно описать простыми уравнениями. В XX веке британский математик Алан Тьюринг предсказал механизмы морфогенеза, которые ответственны за образование пятен и полос. Венгерский биолог Аристид Линденмайер и французско-американский математик Бенуа́ Мандельбро́т показали, как математика фракталов может объяснить паттерны роста растений.

Математика, физика и химия объясняют паттерны в природе на различных уровнях. Паттерны в живых организмах могут быть объяснены биологическими процессами естественного и полового отбора. Изучение формирования паттернов использует компьютерное моделирование для симуляции широкого спектра паттернов.

Виды паттернов в природе

Симметрия

Симметрия для живых организмов является практически всеобщей. У большинства животных наблюдается зеркальная, или билатеральная, симметрия, она также присутствует в листьях растений и некоторых цветах, например орхидеях.[1] Растения часто имеют круговую, или вращательную, симметрию, как у многих цветов и некоторых животных, например у медуз. Пятилучевая симметрия встречается у иглокожих, таких как морские звёзды, морские ежи и морские лилии[2].

В неживой природе снежинка имеет красивую шестилучевую симметрию, каждая снежинка уникальна, но один и тот же паттерн повторяется на всех шести её лучах[3]. Кристаллы обычно имеют разные виды симметрии и габитусы, они могут быть кубическими, шестигранными, восьмигранными, но настоящие кристаллы никогда не имеют пятилучевую симметрию (чего нельзя сказать о квазикристаллах).[4] Вращательная симметрия встречается в различных явлениях неживой природы, например при всплеске, когда капля падает в водоём,[5] а также в сферических формах и кольцах планет, таких как Сатурн.[6]

Деревья, фракталы

  самоподобие фрактального листа

Фракталы бесконечно самоподобны.[7][8][9] Бесконечные повторения в природе невозможны, поэтому 'фрактальные' паттерны фрактальны лишь приблизительно. Например, листья папоротников и зонтичных (Apiaceae) самоподобны на 2-м, 3-м или 4-м уровне. Схожие с папоротником паттерны самоподобия встречаются также у животных, включая мшанки, кораллы, гидроидные, а также в неживой природе, преимущественно в электрических разрядах.

Фракталоподобные паттерны широко встречаются в природе, в таких распространённых феноменах, как облака, речные сети, геологические разломы, горы, береговые линии,[10] окрас животных, снежинки,[11]кристаллы,[12] разветвления кровеносных сосудов[13] и морские волны.[14]

Спирали

Спирали часто встречаются у растений и некоторых животных, преимущественно моллюсков. Например у наутилусов, головоногих моллюсков, каждая камера его раковины является приблизительной копией предыдущей камеры, увеличенной на определённый коэффициент и представленной в виде логарифмической спирали.[15] Исходя из современного понимания фракталов, растущая спираль является частным случаем самоподобия.[16]

Среди растений спирали образуют некоторые виды алоэ, спиралевидным является распределение листьев на стебле, а также других частей у иных растений, например: соцветья астровых, семянные головки подсолнечника или фрукты вроде ананаса[17]:337 и салака, а также паттерн на шишках, где многочисленные спирали располагаются как по часовой, так и против часовой стрелки.

Спираль произрастания листьев может быть выведена из последовательности чисел Фибоначчи: 1, 1, 2, 3, 5, 8, 13… (каждое следующее число является суммой двух предыдущих). Например, при росте листьев из ствола, один поворот спирали равен двум листьям, поэтому паттерн или соотношение равно 1/2. У орешника соотношение 1/3; у абрикоса 2/5; у груши 3/8; у миндаля оно составляет 5/13.[18]

Хаос, потоки, меандры

  хаос в окраске ракушки   Вид на Николаев из космоса. Синусоидальный паттерн, образованный реками — пример меандра

В математике динамическая система является хаотической, если она слишком чувствительна к начальным условиям (так называемый эффект бабочки[19]).

Теория хаоса считается одним из самых важных факторов, влияющих на возникновение паттернов в природе. Существует связь между хаосом и фракталами — странные аттракторы в хаотических системах имеют фрактальную размерность.[20]

Турбулентность в газах и жидкостях при преодолении твердого препятствия образует характерные паттерны кручения.

Меандры — это синусообразные изгибы в реках и других каналах, формируемые жидкостью, обычно водой, текущей вдоль изгибов. Если русло не является ровным, размеры и неровность изгибов увеличивается за счёт того, что течение переносит твёрдый материал, обычно песок и гальку к внутренней стороне изгиба. Внешняя часть изгиба остаётся незащищённой, поэтому эрозия усиливается, увеличивая темпы меандрирования.[21]

Волны, дюны

Под влиянием ветра на поверхности воды и песка в природе образовываются схожие по строению хаотические паттерны, оставляющие рябь, называемые волнами на воде и дюнами на песке. Под действием ветра происходит неравномерное распределение, возвышенные участки чередуются с понижениями уровня.

Частным случаем дюн являются барханы.

Пузыри, пена

  Мыльные пузыри образуют пену

Замощение

Замощение — разбиение без каких-либо накладок и без пробелов. Наиболее известным примером замощения в природе являются пчелиные соты, где шестиугольный паттерн многократно дублируется, заполняя всё пространство улья.

Трещины

Пятна и полосы

Паттерны в архитектуре

Паттерны в дизайне

Паттерны (повторяющиеся элементы) широко используются для украшения среды обитания человека — от лепнины, тротуарной плитки, обоев, паркета и кафеля до орнаментов в одежде, раскраски тканей и использования узоров в оформлении всевозможной печатной продукции. Наиболее популярные паттерны имеют имена, Клетка, Гусиные лапки, Бута, Турецкие огурцы, Алагрек, Меандр.

Паттерны часто употребляются в исламском мире. Искусствоведы подразделяют исламские узоры на стилизованные растительные, которые называются Арабеска, и геометрические, называемые Мореска.[22]

Паттерны для детей

Простым инструментом для создания паттернов является спирограф.

Наблюдать причудливые паттерны можно с помощью калейдоскопа.

Паттерны в медицине

В медицине термин «паттерн» употребляют при анализе, например, кардиограмм, энцефалограмм и результатов других исследований, понимая под ним[23] одинаковую последовательность колебаний биопотенциалов, повторяющуюся в одном или нескольких отведениях при одинаковых состояниях и условиях[24]

Термин паттерн используется для обозначения последовательности нервных импульсов, имеющей определённое информационное значение[25], например, «паттерны боли при биомеханических нарушениях суставов краниовертебрального перехода и шейного отдела позвоночника»[26] или «паттерны двигательных и чувствительных расстройств при патологии нервных структур в дистальных отделах верхней конечности»[27].

Паттерны широко представлены в глоссарии мануальных терапевтов (например паттерн ходьбы), рефлексотерапевтов (например, паттерн сырости-жара) и прикладных кинезиологов (например, паттерн дыхания).

Паттерны вязания

В вязании часто используются схемы рисунков, которые повторяются через определенное количество столбцов и рядов. Один такой рисунок, предназначенный для многократного повторения в вязаном изделии, и называется паттерном. Паттерн может состоять из различных видов петель, в результате получается объемный узор, или образовываться повторением узора из пряжи различных цветов, например стилизованные цветы или олени на свитерах.

Примечания

  1. ↑ Stewart, Ian. 2001. Pages 48-49.
  2. ↑ Stewart, Ian. 2001. Pages 64-65.
  3. ↑ Stewart, Ian. 2001. Page 52.
  4. ↑ Stewart, Ian. 2001. Pages 82-84.
  5. ↑ Stewart, Ian. 2001. Page 60.
  6. ↑ Stewart, Ian. 2001. Page 71.
  7. ↑ Mandelbrot, Benoît B. The fractal geometry of nature. — Macmillan, 1983.
  8. ↑ Falconer, Kenneth. Fractal Geometry: Mathematical Foundations and Applications. — John Wiley, 2003.
  9. ↑ Briggs, John. Fractals:The Patterns of Chaos. — Thames and Hudson, 1992. — P. 148.
  10. ↑ Batty, Michael (1985-04-04). «Fractals – Geometry Between Dimensions». New Scientist (Holborn Publishing Group) 105 (1450).
  11. ↑ Meyer, Yves; Roques, Sylvie. Progress in wavelet analysis and applications: proceedings of the International Conference "Wavelets and Applications," Toulouse, France – June 1992. — Atlantica Séguier Frontières, 1993. — P. 25.
  12. ↑ Carbone, Alessandra; Gromov, Mikhael; Prusinkiewicz, Przemyslaw. Pattern formation in biology, vision and dynamics. — World Scientific, 2000. — P. 78. — ISBN 9789810237929.
  13. ↑ Hahn, Horst K.; Georg,Manfred; Peitgen, Heinz-Otto. Fractal aspects of three-dimensional vascular constructive optimization // Fractals in biology and medicine / Losa, Gabriele A.; Nonnenmacher, Theo F.. — Springer, 2005. — P. 55–66.>
  14. ↑ Addison, Paul S. Fractals and chaos: an illustrated course. — CRC Press, 1997. — P. 44–46.
  15. ↑ Maor, Eli. e: The Story of a Number. Princeton University Press, 2009. Page 135.
  16. ↑ Ball, 2009. Shapes pp 29-32.
  17. ↑ Kappraff, Jay (2004). «Growth in Plants: A Study in Number». Forma 19: 335–354.
  18. ↑ Coxeter, H. S. M. Introduction to geometry. — Wiley, 1961. — P. 169.
  19. ↑ Lorenz, Edward N. (March 1963). «Deterministic Nonperiodic Flow». Journal of the Atmospheric Sciences 20 (2): 130–141. DOI:10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2. ISSN 1520-0469. Bibcode: 1963JAtS...20..130L. Проверено 3 June 2010.
  20. ↑ Ruelle, David. Chance and Chaos. Princeton University Press, 1991.
  21. ↑ Lewalle, Jacques. Flow Separation and Secondary Flow: Section 9.1 // Lecture Notes in Incompressible Fluid Dynamics: Phenomenology, Concepts and Analytical Tools. — Syracuse, NY : Syracuse University, 2006..
  22. ↑ Информация из справочника интерьерных идей 4living.ru (недоступная ссылка — история). Проверено 4 апреля 2013. Архивировано 3 декабря 2012 года.
  23. ↑ Ciaccio E. J., Dunn S.M., Akay M. Biosignal pattern recognition and interpretation systems. Part 4 of 4: Review of applications // IEEE Engineering in Medicine and Biology Magazine. — 1994. — Vol. 13, 2006, Issue 2. — P. 269—273.
  24. ↑ Гапонова О .В. Электроэнцефалографические паттерны синдрома Веста // Медицинский совет. — 2008.- № 1-2.
  25. ↑ Малая меди цинская энциклопедия. — М.: Медицинская энциклопедия. 1991-96 гг.
  26. ↑ Небожин А. И., Ситель А. Б. Паттерны боли при биомеханических нарушениях шейного отдела позвоночника // Мануальная терапия. — 2007. — № 1 (25). — С. 2-8.
  27. ↑ Паттерны двигательных и чувствительных расстройств при патологии нервных структур в дистальных отделах верхней конечности // Медицинский портал для врачей и студентов doctorspb.ru. 2010. Источник в Интернет: http://doctorspb.ru/articles.php?article_id=1477

ru-wiki.org

Prostoy-Site | Все права защищены © 2018 | Карта сайта