К организационно-плановым характеристикам процесса изготовления деталей относится. Задача оптимизации порядка запуска деталей в производство решается

К организационно-плановым характеристикам процесса изготовления деталей относится

1. Объектом изучения производственной логистики являются... (*ответ к тесту*) промышленные предприятия; оптовые предприятия; пункты розничной торговли; грузовые станции.2. Тянущие системы обеспечивают... (*ответ к тесту*) удовлетворение рыночного спроса; пополнение запаса готовой продукции на складе; ускорение транспортных операций.3. Толкающие системы обеспечивают... удовлетворение рыночного спроса; (*ответ к тесту*) пополнение запаса готовой продукции на складе; ускорение транспортных операций.4. Правило золотого сечения применяется... в закупочной логистике; (*ответ к тесту*) в производственной логистике; в коммерческой логистике; в информационной логистике; в сбытовой логистике.5. Задача оптимизации порядка запуска деталей в производство решается... (*ответ к тесту*) с помощью графика Ганта; методом условного центра масс; (*ответ к тесту*) с помощью обобщений алгоритма Джонсона; методом "дворника-стеклоочистителя".6. Логистическая концепция организации производства включает... (*ответ к тесту*) отказ от избыточных запасов; (*ответ к тесту*) отказ от изготовления серий деталей, на которые нет заказа; изготавливать продукцию большими партиями; никогда не останавливать основное оборудование; (*ответ к тесту*) устранение простоев оборудования.7. Принципы производственной логистики: (*ответ к тесту*) однонаправленность; разносторонность; (*ответ к тесту*) гибкость; жесткость; (*ответ к тесту*) синхронизация потоков; (*ответ к тесту*) интеграция потоков.8. Объектом изучения производственной логистики являются... (*ответ к тесту*) внутрипроизводственные логистические системы; требования к качеству производства; программа регулирования сбыта на рынке; (*ответ к тесту*) внутрипроизводственные связи.9. К организационно-плановым характеристикам процесса изготовления деталей относится... (*ответ к тесту*) трудоемкость; габариты; (*ответ к тесту*) объем выпуска; производительность.

www.soloby.ru

1. Объектом изучения производственной логистики являются... (*ответ к тесту*) промышленные предприятия;

1. Объектом изучения производственной логистики являются... (ответ к тесту) промышленные предприятия;

Ответов: 1 | Категория вопроса: Экономические дисциплины

abiturient24.com

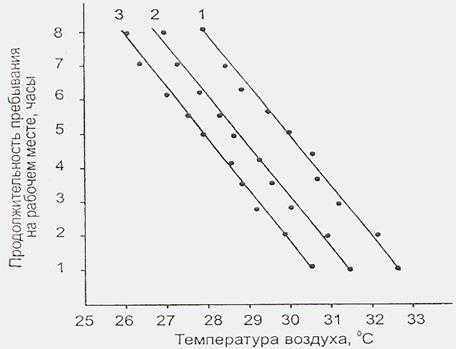
12 Определение оптимальной последовательности при запуске деталей в мебельном производстве

Задача календарного планирования о трех и более станках

Постановка задачи Имеется n деталей, каждая из которых должна последоват. пройти обраб. сначала на m станках. Известно время обраб. каждой детали на каждом из станков (tij, i=1-m, j=1-n). Требуется опр-ть порядок запуска деталей, при котором общая продолж-ть их обраб. на двух станках минимальна.

Алгоритм р-ния Для р-ния задачи определяют 4 различных варианта последов-ти запуска деталей в обработку в соответствии с 4-мя изложенными ниже правилами. Для каждой из последов-ей вычерчивают график Ганта и определяют соответствующее суммарное время обработки. Затем из четырех вариантов принимают тот, в к-м это время минимально.

Правила запуска деталей в обработку:

- пр 1: детали запускаются в порядке возрастания времени их обраб. на первом станке;

- пр 2: детали запускаются в порядке убыв. времени их обраб. на последнем станке;

- пр. 3: детали запускаются в порядке убыв. времени их обраб. на станке, который является «узким местом» процесса (это станок, суммарное время обработки на котором всех деталей максимально;

- пр 4: детали запускаются в порядке убывания суммарного времени их обработки на всех станках

13 Методы отыскания экстремума для функции двух переменных. Необходимое и достаточное условие экстремума. У=f(x1;x2)

Необходимое

1)Необходимое условие экстремума. Если у - функция от х1 и х2, и в точке с координатами достигает своего экстремума, то ее частные в этой точке превращаются в «0».

Среди найденных значений находятся точки экстремума (критич).

2)Достаточное условие экстремума. Для проверки: действительно ли в данной точке достигается экстремум, вычисляются вторые производные.

1D = AC -D>0, A>0 – min

2D>0, A<0 – max

3D<0 эктремум отсутствует

4D=0 т.е. нужны дополнительные условия.

ПРИМЕР: Оптимизация размеров тарного ящика. Предположим, что ящик имеет форму прямоугольника. Все его стенки имеют одинаковую толщину и изготовлены из одного и того же материала. Требуется найти оптимальные размеры ящика без крышки при заданной его вместимости V. И состоящие из x,y,Z – ширина, длина, толщина.

С учетом принятых предположений, количество материалов, необходимых для создания ящика, пропорционально площади всех его стенок.

f=xy+2xZ+2yZ min

V=xyZ, Z=

f =

Воспользуемся необходимыми условиями экстремума:

Воспользуемся достаточным условием экстремума для подтверждения, что при данном количестве сторон достигается оптимальный раскрой. Зная, что

15 Распределительная задача. Постановка, методы решения. С математической точки зрения данные задачи – это частный случай транспортной задачи. В таких задачах от каждого поставщика к каждому потребителю поставляется одна единица груза.

Например. Только одного рабочего можно назначить для выполнения данной работы, или одна операция может выполнятся только на одном из станков. Поэтому все “запасы” и все “заказы” =1. Все переменные решения в таких задачах могут принимать значения только 1 или 0. Эффективным методом решения явл-ся алгоритм транспортной задачи.

На п-станках (і) различных типов можно выполить п-операций (ј).

За каждым из станков м.б. закреплена лишь одна операция и одна и та же операция м. выполниться только одним из станков. Время выполнения каждой из операций на каждом из станков задается матрицей:

Составив такое распределение выполняемых операций м-ду станками, при кот. суммарные затраты времени на обработку детали является минимальным.

Ограничения:

закрепление за каждым станком i только одной операции j:

(i=1÷n)

Закрепление каждой из операций только за одним станком :

(j=1÷n)

или

studfiles.net

6Задача нелинейного программирования. Методы решения и оптимизации.

Задачи отыскания наибольшего или наименьшего значения целевой функции на множестве допустимых планов носят название экстремума задач. Такие задачи называются задачами нелинейного программирования. При линейном программировании принимают, что производство каждой детали приносит определённые одинаковые издержки. На самом деле – чем больше деталей, тем меньше издержек, то есть затраты на каждое изделие, это некая функция. Решения данных задач проводиться по необходимым и достаточным условиям экстремума. Если одна переменная, то по методам: градиентный, метод дихотомии (половины деления), метод золотого сечения. Если функция нескольких переменных: метод покоординатного поиска, градиентный метод, необходимое и достаточное условие экстремума.

7 Многокритериальные задачи исследования операцийЗадачи исследования операций, решения которых направлены на оптимизацию нескольких показателей, наз-ся многокритериальными (МК)

Вар-ты формирования критериев МК задач:

1Из всех рассматриваемых критериев выделяется важнейший, по которому решается задача. На остальные критерии накладываются ограничения в тех пределах, в которых хотел бы иметь разработчик, исполнитель, заказчик.

Пример:W1, W2, W3, ….. Wn . W1 → max; W2≥W20, W3≥W30, Wn≥Wn0.

2Формируется обобщенный критерий, представляющий собой функцию от частных критериев. Предполагается, что все критерии имеют одну размерность и диапазоны измнения. Обобщен. критерий представляют в виде дроби. Числитель в ней – все частн. Критерии, кот-е надо обратить в МАХ-м, а в знаменателе – произведение MIN-х критериев. W=W1W2W3/W4W5. Недостаток: м.б. достигнуто приемлемое значение обобщенных критериев при неудовлетворительных значениях некот-х частных критериев.

1Формируется обобщенный критерий W в виде взвешенной суммы частных критериев:

λi – коэф-т значимости соотв-го критерия Wi. Он берется с «+», если частный критерий Wi обращается в МАХ-м, с минусом – в MIN-м. Абсолютные величины коэф-та λi берутся пропорциональными важности соответствующего частного критерия с учетом требован6ия их нормированности : . Оценка ведется экспертным методом.

2Формируется критерий при оценке качественных показателей: эстетич. требования к внешнему виду, технологичность конструкции, удобство эксплуатации.

Пример:требуется рекомендовать производству один из нескольких имеющихся проектов корпусной мебели. При определении лучшего варианта учит-т все показатели качества. Для перехода к количественному показателю Wi противопоставляется количественный показатель di, изменяющийся от 0 до 1. Если, напрмер, качеств. Критерий приеимает 3 значения: «плохо», «удовл.», «хорошо», то соответствующий этим оценкам количествен. показатель будет:

; ;.

Совокупный показатель

«+» расчета: область значений совокупного показателя D измен-ся от 0 до 1. Если хоть один из показ-лей di =0, то D=0.

8 Симплекс-метод в задачах линейного программирования. Признак оптимальности опорного решения.Идея метода:

1) указывает способ вычисления исходной программы;

2)Устанавливаем признак позволяющий проверять данную программу на оптимальность;

3)указывает способ, позволяющей на данной программе выбрать другую, более близкую к оптимальной.

Сj- коэф. Целевой функции; Сi- коэф. Целевых функций при базисных неизвестных; Р – наименование базисных неизвестных; В – неотрицательные значения ограничений; β – симплексное отношение, показывающее величину отношения значений ограничений в столбце В к элементам аij в разрешающем столбце; W – значение целевой функции; ∆ij – двойственная оценка. Для решения необходимо:

1) заполнить первую симплекс-таблицу.

2) рассчитать в каждом столбце двойственные оценки.

3) если на макс то разрешающий столбец отрицательная оценка, если мин то положительная,

4) найти симплексное отношение в каждом ряду. Выбрать наименьшую Экономический смысл: в столбце В представлены ресурсы, в разрешающем столбце – нормы их расхода. В результате деления В на разр получаем количество продукции, которое можно изготовить из данных ресурсов.

5) выбирают разрешающий элемент

6) пересчёт таблицыПризнаком оптимальности опорного решения является отсутствие отрицательных двойственных оценок при решении задач максимизации или отсутствие положительных двойственных оценок при решении задач минимизации.

9 Математическая модельПо форме представления информации делятся на детерминированные и вероятностные. Детерминир. модели предсказывают значние выходной величины при заданных значениях входных параметров. Они строятся на основе фундаментальных теоретических законов и закономерностей. Это з-ны термодинамики, химич. кинетики и т.д. Вероятностные модели содержат случайные параметры, поэтому рез-тат расчета по такой модели это либо вероятность наступления определен. События, либо статистическая оценка некот-х случайных величин. Все регрессион. модели явл-ся вероятностными, т.к. для них выходной величиной явл-ся статистическая оценка условного математ. ожидания некот. параметра.

По способу получения информации дел-ся на аналитические и эмпирические. Аналитические модели получают теорет. путем, но при построении их используют константы, значения кот-х определяют по рез-там эксперимента. Эмпирические модели получ-т по рез-там обработки экспериментальных данных.

По фактору времени: статические, динамические. Статич. модели включают описание связи между основными процесса в установившихся режимах, т.е. в равновесн. состоянии без изменения во времени. Динамические модели характеризуются множеством переменных состояния системы, кот-е изменяются во времени.

studfiles.net

Методы оптимизации запуска партий

Деталей в обработку

В описываемой ситуации управляющим (изменяемым) параметром является порядок запуска партий деталей в обработку, а функцией — совокупное время обработки на участке всех партий Tсц, которое следует минимизировать. Простой и точный способ отыскания оптимального порядка запуска партий деталей в обработку по критерию Тсц ⇒ min существует только для двухоперационных ПЗУ. Он предложен английским ученым С. М. Джонсоном в 1954 г. Для трехоперационных ПЗУ также имеется точный метод, однако он очень сложен (Р. Беллман, 1957). Для многооперационных ПЗУ (К > 3) доказано, что точного метода вообще не существует. Для них разработано большое число приближенных методов, среди которых общеизвестны методы, предложенные учеными С. А. Соколицыным и В. А. Петровым.

Приближенные методы позволяют множество вариантов порядка запуска свести к нескольким вариантам, среди которых с большой долей вероятности находится оптимальный. Наиболее простым и распространенным из них является метод Петрова-Соколицына (1951). Лучшие результаты (вероятность отыскания оптимума - до 90%) дает метод Петрова, разработанный позднее. Постановка задачи оптимизации запуска партий деталей в обработку предполагает также, что время переналадки оборудования с одной партии на другую невелико и примерно одинаково. Если это допущение не выполняется, то указанные методы не работают.

Метод Джонсона. Так как метод применяется только для двухоперационных участков, исходная матрица времени обработки партий имеет всего два столбца. Алгоритм нахождения оптимальной последовательности запуска - итерационный, каждая итерация включает два шага.

Шаг 1. В матрице времени обработки отыскивается минимальный элемент. Если минимум достигается в первом столбце, то соответствующую ему (по строке) партию деталей следует запускать в обработку первой (последующей). Если во втором столбце, то партию следует обрабатывать последней (предыдущей). Строка, где найден минимум, из дальнейшего рассмотрения исключается (вычеркивается).

Шаг 2. Если в матрице остались невычеркнутые строки, то необходимо перейти к шагу 1.

Пример 11.3

Работу алгоритма рассмотрим, используя данные табл. 11.6 (в таблице выделены найденные минимумы). Получены две оптимальные последовательности: E-B-D-A-C-F и E-D-B-A-C-F.Проверим равенство Tсц для них построением графических моделей (рис. 11.3 и 11.4).

Таблица 116

Деталь	Время обработки партии по операциям, часов
1	2
А	[2,3]	6,1
В	[1,2]	2,2
С	4,8	[1,0]
	[1,2]	5,7
Е	[0,8]	4,3
F	9,2	[0,6]

Рис. 11.3. График обработки партий деталей на ПЗУ в последовательности E-B-D-A-C-F

Рис. 11.4. График обработки партий деталей на ПЗУ в последовательности E-D-B-A-C-F

Если элементы одной строки одинаковы или в столбце несколько одинаковых элементов, то порядок их включения в план произволен, а в результате получается соответствующее число оптимальных последовательностей.

Метод Петрова — Соколицына. Исходная матрица та же, что и в методе Джонсона, но снято ограничение на число операций (столбцов). Алгоритм предполагает расчет двух промежуточных сумм и их разности. Затем определяется несколько последовательностей запуска партий в обработку по следующим правилам:

1) в порядке убывания первой суммы

2) в порядке возрастания второй суммы

3) в порядке убывания разности

4) в порядке убывания абсолютной величины этой разности.

Таким образом, множество вариантов запуска партий в обработку сводится к четырем вариантам, среди которых, скорее всего, и находится оптимальный. Если среди упорядочиваемых элементов находятся одинаковые, то число вариантов возрастает. Поиск лучшего варианта из отобранных производится прямым перебором. С этой целью для каждой последовательности запуска должно быть найдено время Tсц и произведен выбор последовательности, минимизирующей эту величину. Оптимальных последовательностей может быть несколько с равными значениями Tсц.

Пример 11.4

Используя данные примера 11.1, рассчитаем матрицу вспомогательных сумм для метода Петрова—Соколицына (табл. 11.7). Для удобства здесь же повторена исходная таблица

Таблица 11. 7

Деталь	Операции	Вспомогательные суммы
1	2		4	5	T1i	T2i	T3i	T4i
А	18,52	19,42		19,05	19,80	58,27	56,99	1,28	1,28
В	7,41	11,65	16,82			28,47	35,88	-7,41	7,41
С	22,22	8,74	22,42	11,43	2,97	45,56	64,81	-19,25	19,25
D	2,77	6,55		8,57	3,71	18,83	17,89	0,94	0,94
Е	13,88	21,84	21,03		29,70	72,87	56,75	15,82	15,82

Согласно четырем правилам метода, партии деталей запускаются в обработку:

1) в порядке убывания суммы T1i, т. е. в последовательности Е—А—С—-B - D;

2) в порядке возрастания суммы T2i, т. е. D-B-E-A-C;

3) в порядке убывания разности T3i, т. е. E-A-D—B—C;

4) в порядке убывания разности T4i, т. е. C—E-B-A-D.

Для выбора лучшей последовательности из четырех полученных необходимо рассчитать для них Tсц и выбрать ту, которая имеет минимальное значение этой величины. Сделать это можно, как уже отмечалось, путем построения графических или аналитических моделей процессов обработки. График для последовательности E-A-C-B-Dпоказан на рис. 11.2. Tсц= 118 ч Цепным методом в табл. 11.5 рассчитано значение Tсц= 122 ч Для последовательности D-B-E-A-C.Для последовательности E-A-D- В-Свремя Tсц- 130ч; для C-E-B-A-D время Tсц= 142 ч. Таким образом, лучшим является вариант E—A—C-B-D.

Контрольные задания

1. Дайте полную характеристику предметно-замкнутых участков, укажите их преимущества и недостатки, области применения.

2. Укажите все возможные технологические маршруты, если на участке выполняется следующая последовательность операций:

а) фрезерная-токарная-круглошлифовальная;

б) разметочная-сверлильная-фрезерная-резьбонарезная.

3. Укажите все возможные варианты порядка запуска партий в обработку на ПЗУ, если за участком закреплены следующие типоразмеры деталей (обозначены латинскими буквами): а) А, В, С; б) А, В, С, D.

4. Оптимизируйте порядок запуска партий деталей в обработку на ПЗУ методом Джонсона для исходных данных, представленных в табл. 11.8. Постройте график (графики) оптимальной последовательности запуска.

Таблица 11.8

Типоразмер детали	Штучное время обработки детали на операциях 1 и 2, мин	Размер партии деталей, шт.
1	2
А В С D Е

5. Оптимизируйте порядок запуска партий деталей в обработку методом Петрова—Соколицына для наборов данных, приведенных в табл. 11.9 и 11.10.

Таблица 11.9

Типоразмер детали	Штучное время обработки детали на операциях 1-4, мин	Размер партии деталей, шт
1	2	3	4
А		-	-	в
В				-
С	-	-
D
Е		-
Число рабочих мест

Таблица 11.10

Типоразмер детали	Норма штучного времени обработки детали на операциях 1-5, нормо-часов/шт.	Размер партии деталей, шт.
1	2	3	4
А	1,2	0,3	-	-	1,3
В	-	0,5	-	0,2	0,7
С	-	0,1	1,1	0,6	0,9
D	1,6	0,4	1,4	-	-
Е	0,8	-	-	0,4	-
F	0,6	-	0,5	0,8	0,9
Число рабочих мест
Выполнение норм, %

6. Предметно-замкнутый участок работает в две смены. Плановый период — один месяц (19 рабочих дней). На участке выполняются три операции. Производственная программа участка на планируемый период включает четыре типоразмера деталей. Планируются четыре запуска партий деталей в обработку. Плановая загрузка оборудования — 85%. Определите число рабочих мест, необходимых для выполнения производственной программы, их реальную загрузку, а также оптимальный порядок запуска партий в обработку методом Петрова—Соколицына. Исходные данные для расчета сведены в табл. 11.11.

Таблица 11.11

Типоразмер детали	Норма штучного времени обработки детали на операциях 1-3, нормо-минут/шт.	Программа, шт /мес
1	2	3
А В С D	6,1 2,8 7,1	4,6 7,4 9,2	9,9 4,9 3,2 8,5
Выполнение норм, %

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:

zdamsam.ru

Задача 5.1 Фирма «Фасад»

Задание 5 Линейная оптимизация в условиях полной определенности

Постановка задачи

Фирма «Фасад» производит двери для продажи местным строительным компаниям. Репутация фирмы позволяет ей продавать всю производимую продукцию. На фирме работает 10 рабочих в одну смену (8 рабочих часов), 5 дней в неделю, что дает 400 часов в неделю. Рабочее время поделено между двумя существенно различными технологическими процессами: собственно производством и конечной обработкой дверей. Из 400 рабочих часов в неделю 250 отведены под собственно производство и 150 под конечную обработку.

«Фасад» производит 3 типа дверей: стандартные, полированные и резные. В таблице 5-1 приведены временные затраты и прибыль от продажи одной двери каждого типа.

			Таблица 5-1

Тип дверей	Время на	Время на обработку	Прибыль ($)
	производство (мин.)	(мин.)
Стандартные	30	15	45
Полированные	30	30	90
Резные	60	30	120

a. Сколько дверей различных типов нужно производить, чтобы максимизировать прибыль?

b. Оптимально ли распределение рабочего времени между двумя технологическими процессами (производство и конечная обработка)? Как изменится прибыль, если распределить рабочее время между этими процессами оптимально?

c. На предстоящей неделе «Фасад» должен выполнить контракт на поставку 280 стандартных, 120 полированных и 100 резных дверей. Для выполнения заказа «Фасад» может закупить некоторое количество полуфабрикатов дверей у внешнего поставщика. Эти полуфабрикаты «Фасад» может использовать только для производства стандартных и полированных, но не резных дверей. При этом изготовление стандартной двери требует лишь 6 мин. процесса обработки, а полированной – 30 мин. обработки (процесс собственно производства для этих полуфабрикатов не требуется). Полученная таким образом стандартная дверь приносит $15 прибыли, а полированная – $50. Предполагая, что попрежнему 250 часов в неделю отведено под производство и 150 под обработку, определите сколько и каких дверей «Фасад» должен произвести самостоятельно, и сколько полуфабрикатов закупить для изготовления стандартных и полированных дверей?

d. Как изменится оптимальный план, полученный при выполнении предыдущего пункта, если правильно распределить время между собственно производством и обработкой дверей? Каково будет правильное распределение в данном случае?

Решение задачи

a. Прежде всего, определим цель задачи и вид целевой функции. В данном случае мы хотим максимизировать прибыль, следовательно, целевая функция должна вычислять полную прибыль. В задаче не приводится сведений об издержках и выручке, а задана прибыль, которую приносит каждая произведенная дверь. Поэтому полная прибыль (P) будет определяться этой прибылью и тем, сколько дверей произведено.

Эти соображения приводят к выводу, что в качестве переменных задачи следует выбрать количества дверей каждого типа, которые следует произвести. Значит, в задаче будет 3 переменных: Х1 – количество стандартных, Х2 – количество полированных и Х3 – количество резных дверей. При этом целевая функция запишется следующим образом:

P = X1*45 + X2*90 + X3*120 ($).

Лучше всего организовать данные на листе Excel следующим образом (рис. 5-1).

Рисунок 5-1

Удобно выделить ячейки, в которых будут располагаться переменные цветом, (в данном случае серым), т.к. начальные значения переменных неизвестны, а ссылаться на переменные при вычислениях необходимо. Целевая функция задана с помощью стандартной функции Excel =СУММПРОИЗВ(E3:E5;D3:D5), которая и вычисляет приведенное выше выражение для прибыли P.

На следующем этапе решения следует выяснить, при каких ограничениях нужно найти максимальную прибыль. В данном случае из условия следует, что можно затратить на производственную стадию не больше 250 часов в неделю, а на обработку не больше 150 часов. Других существенных ограничений в задаче нет. Так как в надстройке «Поиск решения» нельзя задавать ограничения в виде формул, все необходимые расчеты для задания ограничений следует сделать на листе Excel.

Итак, следует подсчитать, сколько времени на каждой стадии потребуется для реализации произвольного плана производства дверей. Для стадии производства это время будет равно

t1=X1*30+X2*30+X3*60 (мин.),

а для стадии обработки

t2=X1*15+X2*30+X3*30 (мин.).

По условию

t1<=250*60 (мин.), а t2<=150*60 (мин.).

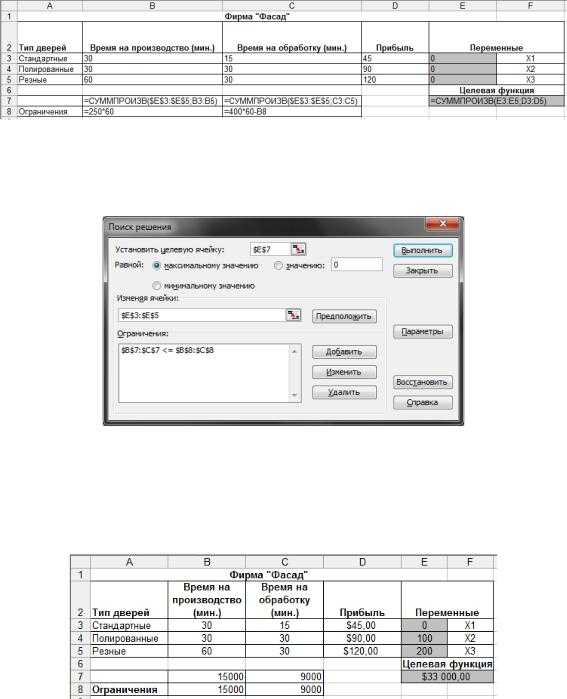
Добавим эти данные на лист с данными задачи (рис. 5-2).

Рисунок 5-2

Теперь имеется вся информация, необходимая надстройке «Поиск решения» для определения оптимального по прибыли плана производства (рис. 5-3).

Рисунок 5-3

До запуска надстройки на поиск нужно еще указать в параметрах поиска решений, что задача соответствует линейной модели и что переменные неотрицательны.

В результате работы надстройки будет найдено решение (рис. 5-4).

Рисунок 5-4

В данном случае оказывается, что максимально возможная прибыль равна $33000 и получена она будет, если производить за неделю 100 полированных дверей и 200 резных.

b. В первой части задачи мы полагали, что суммарное рабочее время покаким-топричинам (не упоминаемым в условии задачи) жестко разбито на 250 часов производства и 150 часов обработки. Возможно, что это связано со специализацией рабочих.

Тем не менее, можно попробовать выяснить, каково оптимальное распределение рабочего времени между стадиями? Ведь если выигрыш от некоторого, возможного на

практике, изменения условий значителен, будет иметь смысл приложить определенные усилия и реорганизовать работу.

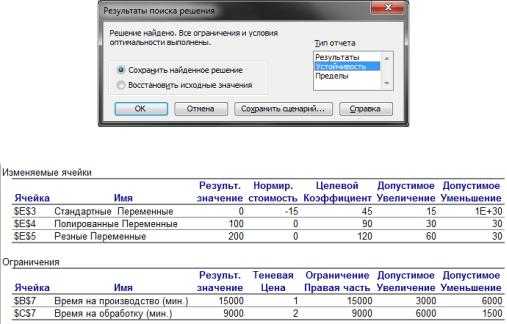
Сначала взглянем на отчет об устойчивости. Чтобы получить его для предыдущего решения задачи, нужно в итоговом окне Результаты поиска решения (рис.5-5),прежде чем нажать кнопкуОК, отметить пунктТип отчета –Устойчивость. При этом к книге Excel

добавится лист Отчет по устойчивости 1 (рис.5-6).

Рисунок 5-5

Рисунок 5-6

Отчет по устойчивости состоит из 2 таблиц.

1. Изменяемые ячейки. Кроме имени переменных и адресов ячеек в ней присутствуют столбцы:

Результирующее значение – это оптимальный план.

Нормированная стоимость – показывает, на сколько изменится целевая функция после принудительного включения единицы этой продукции в оптимальный план. Если продукт рентабелен, то нормированная стоимость будет равна 0.

Целевой коэффициент – значения коэффициентов целевой функции.

Допустимое увеличение, допустимое уменьшение– показывает границы изменений коэффициентов целевой функции, при которых сохраняется набор переменных, входящих в оптимальное решение.

2. Ограничения. Кроме имени переменных и адресов ячеек в ней присутствуют столбцы:

Результирующее значение – значение левой части ограничения при оптимальном плане.

Теневая цена – изменение целевой функции при изменении дефицитного ресурса на 1 единицу. Теневая цена недефицитного ресурса будет равна 0.

Ограничение Правая часть – правая часть ограничения.

Допустимое увеличение, допустимое уменьшение– показывает, на сколько можно изменить правую часть ограничения до того момента пока это будет влиять на целевую функцию.

В данном случае нас интересует теневая цена ресурсов. Так как теневая цена Времени на обработку выше, чемВремени на производство, очевидно, что следует перераспределить рабочее время в пользу обработки. Руководствуясь отчетом об устойчивости можно подобрать нужное распределение времени, но удобнее изменить задачу.

Чтобы модифицировать задачу в соответствии с изменившимися условиями, достаточно отказаться от ограничения по рабочему времени каждой из стадий и потребовать, чтобы суммарное рабочее время не превышало 400*60 (мин).

Оставим действующим решение задачи (а), и для модифицированной задачи создадим новый лист. Имеет смысл создать копию листа, щелкнув правой кнопкой по ярлычку листа и

отметив пункт Переместить/Скопировать, а затем поставив флажокСоздавать копию. При

этой процедуре копируется и скрытый лист с установками для надстройки «Поиск решения».

Для изменения условий добавим в ячейки D7 и D8 формулы:

соответственно, а из ячеек B8 и C8 удалим формулы. После этого нужно немного модифицировать задание надстройке. Удалим из ограничений условие

$B$7:$C$7 <= $B$8:$C$8,

и добавим вместо него условие

D7 <= D8.

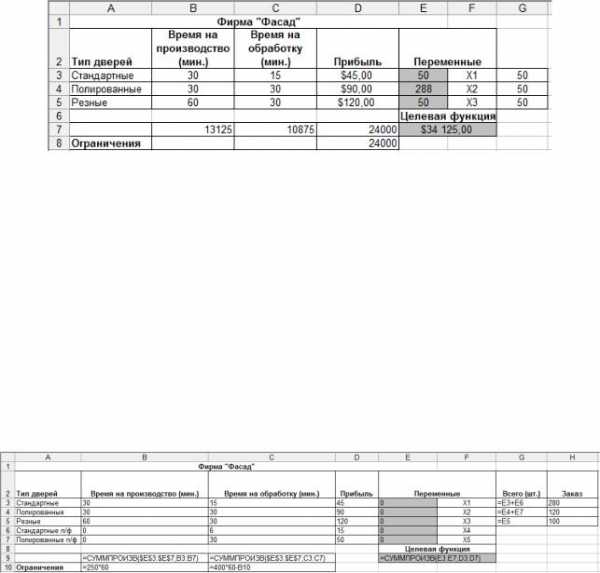
Получим следующее решение (рис. 5-7).

Рисунок 5-7

Распределение времени на производство и на обработку изменилось. Кроме того отметим, во-первых,что максимальная общая прибыль выросла на $3000 в неделю. Вовторых, оптимальный план рекомендует выпускать только полированные двери в количестве 400 штук.

Применительно к реальной ситуации вызывает некоторые подозрения рекомендация совсем не выпускать двери первого и третьего типов. Понятно, что условия задачи отвечают ситуации, когда рынок дверей сильно не насыщен, но при этом существуют другие поставщики дверей разных типов. Сужение ассортимента может осложнить позиции фирмы в конкурентной борьбе, особенно при условии ограниченных производственных возможностях фирмы (суммарное время на производство и обработку ограниченно).

Поэтому имеет смысл посмотреть, что меняется, если потребовать выпускать все двери. Конечно, здесь нужно задать некоторое конкретное число, которое мы вынуждены «взять с потолка». Положим, что следует выпускать не менее 50 штук дверей каждого типа. Введем в ячейки G3:G5 число 50 и добавим в надстройку «Поиск решения» ограничение

E3:E5 >= G3:G5.

Получим новое решение задачи (рис. 5-8).

Рисунок 5-8

Введенное ограничение, как любое новое ограничение задачи, уменьшает итоговую прибыль. Тем не менее, она оказывается выше, чем прибыль в базовом решении (а). Кроме того, ведь в базовом решении тоже не предполагалась к выпуску стандартная дверь.

Конечно, только что проведенное исследование задачи не требуется по условию, но зачастую такой анализ очень интересен и полезен для принятия разумного управленческого решения при использовании той или иной математической модели.

c. Новые условия, описанные в пункте с, усложняют задачу. Чтобы их учесть следует ввести две новые переменные: количество стандартных дверей и количество полированных дверей, изготовленных из полуфабрикатов стороннего поставщика. Кроме этого нужно учесть размер заказа и потребовать безусловного его выполнения.

Организация данных на листе Excel в этом случае представлена на рисунке 5-9.

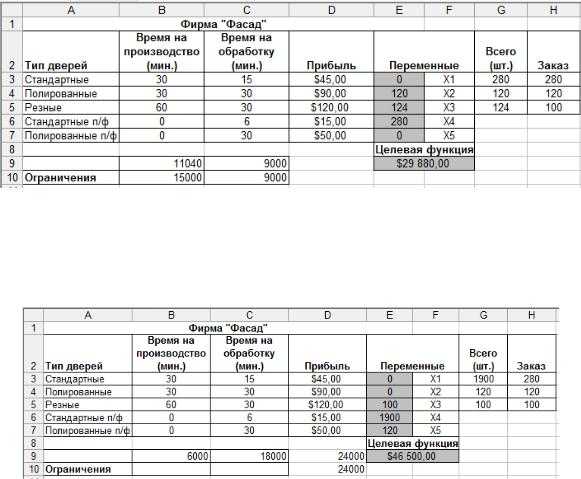
Вячейках G3:G5 подсчитываем полное количество дверей каждого типа, а в надстройке «Поиска решения» сравниваем результаты с заказом (G3:G5>=h4:H5). Что касается общего времени на обработку и производство, то вернемся к первоначальным условиям: 150 и 250 часов соответственно.

Врезультате получим новое решение (рис. 5-10).

Рисунок 5-10

d. Для решения этой задачи нужно изменить только одно условие – так же как делали при анализе части, ограничим только суммарное время двух стадий. Результат представлен на рисунке5-11.

Рисунок 5-11

Целевая функция в этом варианте задачи сильно выросла, больше чем в 1.5 раза в сравнении со случаем неоптимального разделения времени. Однако оптимальный план производства наводит на новые вопросы о путях развития данного бизнеса. Например:

-Общее количество дверей, которые можно изготовить с использованием полуфабрикатов, гораздо больше, чем в начальном плане. Можно ли обеспечить сбыт такого количества стандартных дверей?

-Если продать 1900 стандартных дверей невозможно (а возможно, допустим, 600), то, при добавлении соответствующего ограничения, возрастет производство дверей других типов. А сколько их можно продавать за неделю?

-А нельзя ли увеличить сбыт, сбросив отпускные цены (и уменьшив тем самым прибыльность)? Принесет ли это дополнительные деньги?

Впрочем, это уже совершенно выходит за рамки первоначальной задачи.

studfiles.net

Оптимизация моделей процессов производства

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ Кафедра менеджмента РЕФЕРАТ на тему: «ОПТИМИЗАЦИЯ МОДЕЛЕЙ ПРОЦЕССОВ ПРОИЗВОДСТВА» МИНСК, 2008

В условиях оживления и развития отечественной промышленности существенно возрастает интерес к проблемам организации производства, и в частности, к задачам оперативно-календарного планирования. Календарные планы работы отдельных производственных ячеек предприятия представляют собой расписания изготовления всех изделий, загрузки оборудования и рабочих мест. Производственная ячейка - часть производственного пространства (станки, участок), на котором соответствующим образом организованы производственные ресурсы и процессы. Основными параметрами календарных графиков являются: приоритетность работ (очередность запуска изделий в обработку), размер партий запуска и время опережения начала обработки изделий на связанных рабочих местах, размер незавершенного производства. Результатом составления оптимального календарного графика является определение наименьшей длительности производственного цикла, оказывающей существенное влияние на улучшение экономических результатов деятельности предприятия. В этом случае происходит снижение объема оборотных средств в незавершенном производстве, уменьшаются простои оборудования и рабочих. В производственных подразделениях машиностроительных предприятий календарное планирование в настоящее время основано главным образом на моделировании, позволяющем обеспечить пропорциональность, непрерывность, устранить «узкие места» и правильно установить приоритеты работ. Следует отметить, что установление очередности запуска изделий в производство является одной из основных задач, которую необходимо решить при составлении оптимального календарного графика. В силу этого, в качестве критерия оптимальности моделей целесообразно использовать минимизацию длительности совокупного производственного цикла. Под моделью производственного процесса понимается его пространственное построение, отражающее технолого-организационную суть последнего через организационную структуру. Под моделью плана производства - количественно-временная организация предметов труда в ходе производственного процесса. Под моделью оперативного управления (части управляющей системы - надстройки) - функциональное выделение той части управляющей системы, которая предназначена для удержания существующих переменных управляемого объекта в заданных планом пороговых значениях. Все существующие методы решения задач календарного планирования по степени достижения экстремального результата подразделяются на две четко выраженные подгруппы - точных и приближенных решений. К числу опробованных точных методов решения задачи моделирования относятся методы линейного и динамического программирования, комбинаторные методы дискретного программирования и др. Метод линейного программирования удачно использован С.М. Джонсоном для решения задачи нахождения оптимального по календарному времени плана обработки m деталей на двух станках. Алгоритм Джонсона чрезвычайно прост. Выбирается самое короткое операционное время, и если оно относится к первому станку, планируют выполнение задания первым на первом станке, а если ко второму - то последним. Затем процедура повторяется до полного перебора всех заданий на обоих станках. Имеются многочисленные обобщения правила Джонсона для различных случаев трехстадийной обработки деталей. Однако этот алгоритм неприменим для случаев обработки деталей на большем количестве станков. Метод динамического программирования удачно использован Р. Беллманом для однооперационного производства. Он дал частное решение задачи оптимального календарного планирования обработки совокупности изделий, имеющих одинаковый процесс производства, но различных по длительности операций обработки. Запуск изделий в производство необходимо осуществлять, соблюдая условие: min (t11, t22) < min (t12, t21), где: t11- трудоемкость выполнения первой операции над изделием, первым запускаем в производство; t22 - трудоемкость выполнения второй операции над изделием, вторым запускаем в производство, а t12 и t2l - соответственно наоборот. Метод «ветвей и границ», являющийся комбинаторным методом дискретного программирования, предполагает уменьшение множества допустимых решений, вплоть до получения конечного множества, при котором оказывается возможным применение метода перебора. В этом методе происходит последовательный выбор пары номеров деталей для получения оптимальной последовательности. Составление последовательности номеров деталей для запуска в производство происходит в процессе работы итерационного алгоритма. На каждой итерации выбираются две детали и помещаются на позиции: (n + 1) и (d – n), где n - номер итерации, a d- количество наименований деталей, участвующих в производственном процессе. Эффективность метода «ветвей и границ» зависит от уровня, на котором происходит «отсечение» ветви. В общем случае этот метод не исключает полный перебор всех возможных вариантов. Типичные модели линейного, линейного целочисленного и квадратичного целочисленного программирования свидетельствуют о том, что в них могут быть отражены многие ограничения задачи календарного планирования. В частности, в этих моделях, в форме ограничений на переменные, могут быть выражены требования, накладываемые на сроки выпуска этих деталей. Допускается обработка деталей партиями, но для этого необходимо некоторое предварительное преобразование исходной информации. Данные модели имеют ограниченное применение при моделировании производственных процессов. Главным недостатком является быстрый рост размеров моделей с ростом задачи календарного планирования. Точные методы оптимизации применимы лишь для частных и небольших по размеру задач. На машиностроительных предприятиях составление оптимального календарного графика усложняется широтой номенклатуры выпускаемых изделий и является динамической, вероятностной задачей большой размерности. Поэтому наряду с разработкой точных методов интенсивно развиваются приближенные методы. К числу приближенных методов оптимизации задач календарного планирования относятся: частичный и направленный перебор, метод Монте-Карло, аналитико-приоритетные, эвристические и др. методы. Метод Монте-Карло аналогичен методу перебора и оценки вариантов с той разницей, что оценивается некоторое ограниченное подмножество вариантов, выбор которых производится некоторым случайным образом. Решение задачи календарного планирования методом Монте-Карло можно рассматривать как некоторую задачу статистического моделирования производственного процесса. Метод Монте-Карло имеет ограниченное применение, так как может потребовать перебора и оценки достаточно большого количества вариантов. В последнее время к решению задач календарного планирования стала привлекаться теория массового обслуживания. Такая возможность появилась в связи с развитием специальной теории очередей с приоритетом. Однако если в задачах массового обслуживания поток требований на обслуживание является свободным процессом, то в задачах календарного планирования требования поступают в детерминированном порядке. Вместе с тем при прохождении требований (партии деталеопераций) через большое количество обрабатывающих устройств (производственных ячеек) происходят задержки в обслуживании, и поступление требования на следующее обрабатывающее устройство может быть рассмотрено как случайное событие. В таком плане эта связь теории расписаний с задачами теории очередей с приоритетом обслуживания может быть использована как средство приближенного решения теории расписаний. Многие задачи календарного планирования относятся к классу задач, для которых трудна конкретная аналитическая постановка, неярко выражена величина критерия эффективности и отсутствуют эффективные алгоритмы численного решения. Последнее связано с тем, что минимизируемые функции комбинаторных задач лежат не в непрерывной области переменных, а на различных дискретных перестановках элементов. Следовательно, применение приближенных методов, основанных на сочетании аналитических принципов и моделировании календарных планов с использованием правил предпочтительности, является наиболее перспективным направлением практического решения данного класса задач. Среди приближенных методов различают большую группу аналитико-приоритетных методов. Аналитико-приоритетные методы не следует смешивать с эвристическими. В аналитико-приоритетных методах имеется математическая модель с соответствующей функцией - критерием, что позволяет приблизить решение к оптимальному, тогда как в эвристических методах такая функция отсутствует, либо имеется в неявно выраженной форме или же задается как локальная функция приоритета. Эвристические методы строятся на использовании установленных свойств и приемов решения задач других смежных групп, а также интуитивных свойств и приемов поиска. Можно выделить семь наиболее удачных правил предпочтительности для формирования приоритетов календарного планирования последовательности работ1. 1. FCFS (Fist - Come, Fist - Served) - первым вошел - первым обслужен. Работы выполняются в порядке поступления в подразделение. 2. SOT (Short's Operating Time) - по кратчайшему времени выполнения. Сначала выполняется работа с самым коротким временем выполнения, затем процедура повторяется для оставшихся работ. 3. D date (Due Date) - по установленным срокам окончания. Первой выполняется работа с самой ранней датой начала выполнения. 4. SD - по ранней дате начала выполнения, определяемой как установленная дата выполнения работы, минус время выполнения работы. 5. STR (Slack Time Remaining) - по наименьшему оставшемуся запасу времени, который вычисляется как разность между временем, остающимся до установленной даты выполнения, и временем выполнения работы. 6. STR/OP (Slack Time Remaining per Operation) - по наименьшему оставшемуся запасу времени на одну операцию, которое определяется как разность времени, оставшегося до установленной даты выполнения работ, минус время оставшихся операций, деленная на количество оставшихся операций. Заказы с самым коротким STR/OP выполняются первыми. 7. LCFS (Last - Come, First - Served) - последним вошел - первым обслужен. Первой выполняется работа, поступившая последней в подразделение. Иногда используют различные комбинации функций предпочтения, но это требует многовариантного перебора. В результате отработки информации, полученной при выполнении на модели серии экспериментов каждый раз с новым правилом очередности, были выявлены законы распределения и другие оценки наиболее вероятных длительностей производственных циклов, ________________________ 1 Donald W. Fogarty, Yohn H. Blackstone, Yr. And Thomas R. Hoffman. Production and Inventory management (Cincinnati: South - Western Publishing, 1991). P. 452 - 453. опозданий в выполнении работ по сравнению с плановыми сроками, объемом незавершенного производства, простоев оборудования и т.д. Однако при проведении оптимизации метод не учитывает взаимного влияния моментов начала и окончания смежных операций на разных станках, что значительно снижает степень оптимальности полученного результата. В условиях многопредметных автоматизированных производственных систем задача построения календарных графиков существенно усложняется. Решение задачи формирования графика производства деталей (парий деталей), имеющих произвольное число и очередность выполнения операций и запланированных к изготовлению на одном и том же технологическом оборудовании является комбинаторной задачей большой размерности. В этих условиях наиболее удачным методом является аналитический метод, учитывающий взаимное влияние пооперационных трудоемкостей обработки деталей на совокупный цикл их обработки. Метод предполагает оптимизацию длительности совокупного цикла обработки партий (групп) деталей путем анализа и минимизации величин смещения. При этом суммарное время опережения запуска деталей в обработку на каждой технологически связанной паре рабочих мест дифференцируется на две составляющие, первая из которых учитывает несинхронность операций технологических процессов обработки деталей, а вторая - время обработки передаточных партий деталей. В этом случае задача моделирования сводится к тому, чтобы время опережения начала и окончания обработки партий деталей каждого наименования на передающем и получающем детали рабочих местах обеспечивало непрерывную обработку партий деталей с максимальной параллельностью. Длительность производственного цикла обработки партий деталей в рассматриваемой постановке решения задачи может быть определена по формуле (1) где - номер рабочего места, начинающего процесс обработки деталей данной группы; k - номер рабочего места, на котором заканчивается процесс обработки деталей данной группы; m - количество групп деталей; d - количество деталей в группе; - величина смещения на j-м рабочем месте, на котором начинается процесс обработки i-й партии деталей; - величина смещения на j-м рабочем месте, на котором заканчивается процесс обработки i-й партии деталей; - время обработки групп деталей на рабочем месте, завершающем процесс обработки, следующих за r-й группой; - время обработки деталей групп, предшествующих r-й группе деталей на рабочем месте, начинающем процесс обработки; - время обработки партий деталей, предшествующих i-й партии деталей на рабочем месте, начинающем процесс обработки; - время обработки партий деталей, обработка которых следует за обработкой партии деталей i-ro наименования на рабочем месте, завершающем процесс обработки. Поскольку время обработки передаточных партий от очередности их обработки не зависит, критерием оптимизации является: В первую очередь следует запускать в обработку партию деталей, которая обеспечивает наименьшую составляющую в общем смещении. Метод предполагает проведение пошаговой оптимизации: на каждом шаге ищется для партий деталей, очередность которых еще не определена. Величина зависит от , которое определяется как сумма положительных разностей (). Здесь - соответственно время обработки партии деталей на передающем и получающем рабочих местах связанной пары. Следует учитывать, что положительная разность () времени обработки детали n-й очереди запуска компенсируется лишь тогда, когда модуль отрицательной разности времени обработки детали (n + 1)-й очереди равен или больше разности ()детали n-й очереди запуска. Таким образом, при определении любой n-й очереди запуска необходимо проводить анализ знака разности времени обработки всех оставшихся деталей на всех парах связанных рабочих мест. Связи, у которых эти разности имеют знак плюс, из дальнейшего анализа следует исключать. Это же относится к связям, у которых все разности имеют только отрицательные значения. На основании анализа разностей () на технологически связанных парах рабочих мест и учитывая то, что эти разности со знаком минус являются компенсаторами, т.е. способны «гасить» положительные разности () деталей следующей очереди обработки, можно сформулировать правила, позволяющие улучшить полученные результаты оптимизации. 1. Если при очередной итерации окажется несколько минимальных значений , то в первую очередь запускается деталь, у которой сумма отрицательных разностей () по модулю наибольшая, так как она имеет большее значение компенсаторов. 2. Если при очередной итерации у i-й детали на данной связанной паре рабочих мест разность () со знаком плюс по модулю больше суммы разностей () со знаком минус, то в этом случае в значении найденной суммы следует учитывать только абсолютную величину суммы отрицательных разностей. 3. Если при очередной итерации определения очередности запуска деталей в обработку оказывается, что i-я деталь имеет у всех связей только положительные разности (), то такую деталь следует запускать в последнюю очередь, так как у этой детали нет компенсаторов. Исследование большого объема статистических данных автоматизированного решения задачи показывает, что использование приведенных правил, улучшающих алгоритм поиска оптимальной очередности запуска деталей в обработку, приводит к уменьшению длительности производственного цикла на 40-50 %. Результатом моделирования является формирование календарного расписания рабочих мест производственной системы, в котором учитывается информация о затратах времени на наладку и переналадку оборудования, принятый размер партии запуска и время смещений запуска деталей в обработку относительно первого рабочего места системы. Для оптимизации размера партий, запускаемых в обработку деталей, может быть предложена следующая формула: , (2) где р - размер партии запуска деталей в обработку, компл.; Е - коэффициент эффективности капиталовложений; Sобj - стоимость оборудования j-ro наименования, р.; tпз - подготовительно-заключительное время по каждому j-му виду оборудования на весь комплект обрабатываемых на нем деталей, ч.; k - количество единиц оборудования производственной системы, шт.; tштj - штучное время обработки всего комплекта деталей на данном j-м оборудовании, ч./компл.; М - затраты материалов (заготовок) на комплект деталей, р./компл.; Зк - заработная плата рабочих за изготовление комплекта деталей, обрабатываемых производственной системой, р./компл.; КТ - коэффициент технической готовности незавершенного производства; Зч - среднечасовая зарплата рабочих, р./ч. Литература 1. Михайлова Л.В., Парамонов Ф.И., Чудин А.В. Формирование и оперативное управление производственными системами на базе поточно-группового производства в автоматизированном режиме. М.: ИТЦ МАТИ, 2002.- 60 с.

coolreferat.com