Однокритериальная оптимизация. Основные методы оптимизации, используемые при синтезе детерминированных сложных технических систем. Задача однокритериальной оптимизации

Однокритериальная оптимизация. Основные методы оптимизации, используемые при синтезе детерминированных сложных технических систем

1. Постановка и методы решения задач математического программирования. Линейное программирование

Формальная постановка задачи математического программирования (м п).

В рамках задач однокритериальной оптимизации наибольший интерес представляют методы, относящиеся к группе оптимального планирования, при ограниченных ресурсах. Данными методами учитываются разнообразные задачи создания новой техники. Множество задач в том или ином виде может быть сведено к постановке задачи математического программирования. С формальной точки зрения данная задача относится к задачам математического программирования (термин программирование, здесь понимается в смысле составления плана, либо программы действий).

Задача оптимизации состоит в выборе наилучших планов.

Не смотря на смысловое разнообразие задач, все они формально сводятся к одной общей постановке.

Найти значение переменных обращающих в максимум, либо минимум значение целевой функции:

min(max)←Z=f(x1,…,xn),

при условиях: gi(x1,…,xn)≤≥bi,i=1,m

Замечание: в случае, когда Zесть множество действительных чисел (используемых на практике), функцияZ=f(x1,…,xn), называетсяскалярной.Условияgi(x1,…,xn)≤≥bi,i=1,mпредполагающие, что в каждой изnстрок может присутствовать одно из рассмотренных ограниченийgi(x1,…,xn)≤≥bi,i=1,m, называютсяобластью определения(U) задачи.

Функция Zназываетсяцелевойфункцией, которая может представлять собой критерий оптимальности при синтезе какой-либо системы. Таким образом, целевая функцияZдостигает экстремального значения в одной или нескольких точек U, которые требуется отыскать.

Обычно в постановке задачи выбора оптимального решения, вид функций Zиgi,известны, константыbiопределены ,специально оговариваются ограничения, выраженные в требованиях к неотрицательности, либо к целочисленности переменных.

Краткая запись условия задачи математического программирования(М П) имеет вид:

XєU→max(min){Z=f(x)}

Два основных класса задач МП - это задачи линейного и нелинейного программирования. К задачам линейного программирования (ЛП)относятся те, в которых и целевая функцияZ, и все функцииgiлинейны.

Задачи, в которых присутствуют какие-либо нелинейности, соответственно называются задачами нелинейного программирования.

В данном курсе лекций мы ограничимся рассмотрением задач линейного программирования, которые наиболее часто требуется решать в нашей предметной области знаний.

Линейное программирование. Постановка задачи.

Задача ЛП в общей постановке состоит в отыскании переменных x1,…,xn ,обращающих в

экстремум функцию: max←Z=Σ СjXjпри ограничениях:

j=1

a11 x1 + a12 x2 +…+ a1n xn ≤ b1

…

am1 x1 + am2 x2 +…+ amn xn ≤ bm

Обычно, кроме того, на практике добавляют требования не отрицательности(xj>0ij=1,n)

Пример постановки задачи: Ферма производит откорм скота. Допустим, что имеется 4 вида продуктов (П1,П2,П3,П4). Стоимость единицы каждого продукта (С1,С2,С3,С4). Из этих продуктов требуется составить пищевой рацион, который должен содержать: белков не менееb1 единиц, углеродов не менееb2 единиц, жиров не менееb3 единиц. Для продуктов (П1,П2,П3,П4) содержание белков, жиров и углеродов в единицах на единицу продукта приведено в таблице.

продукты	Элемент
продукты	белки	углероды	жиры
П1	а11	а12	а13
П2	а21	а22	а23
П3	а31	а32	а33
П4	а41	а42	а43

Где аijнекоторые числа иi– продуктj– элемент.

Задача: составить такой пищевой рацион, то есть определить количество продуктов (П1,П2,П3,П4) входящих в рацион, что при минимальной стоимости рациона, при условии выполнения ограничения белков, жиров и углеродов.

Z=C1x1+C2x2+C3x3+C4x4→minздесь мы заx1…x2обозначили количество продуктов которые должны входить в рацион.

a11 x1 + a12 x2 +a13 x3 + a14 x4 ≥ b1

a12 x1 + a22 x2 +a32 x3 + 242 x4 ≥ b2

a13 x1 + a23 x2 +a33 x3 + a43 x4 ≥ b3

x ≥ 0

Замечание.Измените физический смысл параметров в данной задаче, и вы получите задачу оптимизации загрузки ресурсов (планирование загрузки) многомашинной вычислительной системы и множество иных задач из нашей предметной области.

studfiles.net

1.5.1. Однокритериальные задачи принятия решений.

Критерию q(x) может придаваться различный смысл, но почти всегда его можно интерпретировать как выигрыш или проигрыш, который получает лицо, выбравшее альтернативу х из множества альтернатив Х. Если последствия выбора альтернативы х известны точно, т.е. выбор детерминированный, то сравнение альтернатив в этом случае сводится к сравнению соответствующих чисел. Заметим, что введенное соответствие задает функцию q(x) на множестве альтернатив Х.

В этом случае принятие решения сводится к выбору оптимальной (наилучшей) альтернативы х из множества альтернатив Х.

Определение 1: Наилучшей (оптимальной) альтернативой xX называется такая альтернатива, которая обеспечивает минимальное значение критерия (проигрыша) при выборе альтернативы х:

x = argmin q(x), xX

Если по своему содержанию критерий q(x) характеризует выигрыш, то наилучшей должна быть альтернатива, которая обеспечивает максимум критерия выигрыша.

Такие задачи принятия решений называются оптимизационными. Для их решения разработано множество различных методов одномерной и многомерной оптимизации, которые достаточно подробно описаны в литературе. Укажем наиболее распространенные из них. Среди методов одномерной оптимизации к самым распространенным относятся методы бисекции, золотого сечения, ломаных. При решении задач многомерной оптимизации обычно используют методы линейного программирования (в том числе различные модификации симплекс-метода), различные варианты градиентных методов, вариационные методы, методы динамического программирования. Все эти методы математически формализованы. Их разработкой и обоснованием занимается специальный раздел математики, который называют обычно “методами решения экстремальных задач” или “методами оптимизации”.

В случае, если последствия выбора альтернативы х из множества альтернатив Х точно не известны, но известны вероятности их появления p(x), то принятие решений обычно сводится к выбору альтернативы х, удовлетворяющей принципу «наименьшего гарантированного проигрыша» или «наибольшего гарантированного выигрыша». Разработкой методов принятия решений в таких ситуациях занимаются в разделах математики, называемых «теорией игр» и «исследованием операций».

1.5.2. Многокритериальные задачи принятия решения.

В случае многокритериальной задачи принятия решения совсем не тривиально определить, что есть «оптимальное» решение. Поясним это на примере. Пусть мы покупаем подарок, который характеризуется тремя критериями: ценой, временем, затрачиваемым на его покупку, полезностью. Естественно, что нам хотелось бы, чтобы цена и время были минимальными, а полезность - максимальной. Но в случае многокритериальных задач, критерии могут быть противоположны друг другу (как в нашем случае, например, время – деньги). Поэтому бессмысленно принимать за оптимальное решение ту альтернативу, на которой достигается экстремальное значение всех критериев.

К сожалению, единой трактовки термина «оптимальное» решение в случае многокритериальных задач не существует. Однако существует четыре основных подхода к введению понятия «оптимальный» в этом случае.

Разделим все задачи многокритериального выбора на два класса: задачи принятия решений с равнозначными критериями и задачи принятия решений с неравнозначными критериями (т.е. существует некоторый приоритет одних критериев над другими).

Рассмотрим вначале более простой в некотором отношении случай - неравнозначных критериев.

Метод суперкритерия.

Предположим, что есть n критериев: q1,...qn. Эти критерии можем упорядочить. Причём каждому критерию мы можем приписать не только порядковый номер, но и вес, т.е. некоторое числовое значение, определяющее превосходство этого критерия над остальными. В этом случае на основе существующих критериев мы можем ввести новый критерий q0, который принято называть суперкритерием. Самым распространенным способом введения суперкритерия является аддитивный:

Здесь i– вес критерия qi(x), а i- коэффициент, снимающий размерность (чтобы можно было складывать «землекопов» с «лопатами»).

Пример.В задаче выбора подарка оставим два критерия:q1- цена подарка, главный критерий;q2- время. Договоримся, что 1 час = 60 руб. В нашем случаеq0(x) =q1(x)/руб. + 60q2(x)/час. Допустим, что нам надо выбрать наилучший из трех подарков: цена первого, второго и третьего соответственно 300 руб., 350 руб. и 400 руб.; время, затрачиваемое на их приобретение, 2 часа, 1 час и 30 мин. Посчитаем значение суперкритерия для каждого из подарков:

q0(x1) = 300 + 60*2 = 420;

q0(x2) = 350 + 60*1 = 410;

q0(x3) = 400 + 60*0,5 = 430

Из сравнения суперкритериев видно, что наилучшим будет второй подарок.

После введения суперкритерия многокритериальная задача стала фактически однокритериальной задачей. Примеры введения суперкритерия мы часто можем наблюдать в спортивных состязаниях. Например, лыжные двоеборцы сначала прыгают на лыжах с трамплина (результат меряется в метрах, а потом в баллах), а потом бегут на лыжах дистанцию 15 км. (результат меряется в сек.) При определении победителя приравнивают 1 балл к 1 сек. У биатлонистов в гонке на 20 км. у мужчин 1 промах (критерий точности стрельбы) приравнивается к 1 мин. штрафа в беге по дистанции (критерий – скорость). Можно встретиться с таким подходом при определении, например, лучшего ученого года в Оренбургской области: 1 изданный учебник приравнивается в баллах к 3 защищенным под руководством данного ученого кандидатским диссертациям или к 1 докторской диссертации.

Достоинства метода:

Недостатки метода:

этот метод и само оптимальное решение существенно зависят от точности определения весовых коэффициентов i;
вводится дополнительный критерий – суперкритерий, который иногда сложно интерпретировать содержательно.

Последнее легко пояснить на рассмотренном выше примере. Если бы мы оценили 1 час времени в 40 руб., то значение суперкритериев было бы следующим:

q0(x1) = 300 + 40*2 = 380;

q0(x2) = 350 + 40*1 = 390;

q0(x3) = 400 + 40*0,5 = 420

Как видно, в этом случае наилучшим был бы первый подарок. А если бы 1 час времени оценивался в 100 руб., то наилучшим был бы третий подарок.

Метод условной оптимизации.

Этот метод, также как и метод суперкритерия, предполагает, что критерии не равнозначны. Мы можем выбрать самый значимый для нас критерий, но не можем оценить вес каждого критерия численно (не можем сказать, сколько рублей стоит 1 час). В этом случае в качестве единственного критерия мы оставляем самый значимый для нас критерий, а остальные критерии считаем ограничениями (условиями). Далее различают два случая введения ограничений: типа равенств и типа неравенств. Первый случай проще осуществляется технически, но менее адекватен реальности. Второй более адекватен реальности, но труднее осуществляется технически.

Пример. Как и в предыдущем примере будем выбирать лучший подарок по двум критериям: q1 - цена подарка, главный критерий; q2 - время, затрачиваемое на его приобретение. Допустим, что цена первого, второго и третьего соответственно 300 руб., 350 руб. и 400 руб.; время, затрачиваемое на их приобретение, 2 часа, 1 час и 30 мин.

Рассмотрим случай ограничений типа равенств. Зададим ограничение по времени (так как это не главный для нас критерий): время, затрачиваемое на приобретение подарка q2 = 1 час. 20 мин. Выберем теперь из всех подарков такие, у которых q2 = 1 час. 20 мин. Видим, что таких подарков в нашем списке нет. Таким образом, далее мы осуществляем выбор на пустом множестве альтернатив. Это значит, что мы отвергли все предложенные альтернативы.

Естественно, что в реальных ситуациях принятия решений ограничения типа равенств встречаются не часто. Более адекватный случай – ограничения типа неравенств. Зададим в нашем примере ограничения типа неравенств. Будем считать, что нам надо купить подарок не ровно за 1 час. 20 мин. (как это было в ограничении типа равенств), а не более, чем за 1 час 20 мин., т.е. 0 мин. q2 1 час 20 мин. Выбираем из всего множества подарков те, которые покупаются не более, чем за 1 час 20 мин. В это множество вошли второй и третий подарок. Теперь мы выбираем из них наилучший на основании только главного критерия – цены. Наилучшим будет второй подарок, т.к. у него меньшая цена (350 руб.)

Достоинства метода:

не вводится никаких новых критериев;
выявляется только самый значимый критерий, но численные значения весов не определяются.

Недостатки метода:

ограничения типа равенств часто являются неадекватными реальным ситуациям принятия решений;
с ограничениями типа неравенств часто технически сложно решать задачу принятия решений.

Метод уступок.

На практике при решении многокритериальных задач выбора при неравнозначных критериях часто пользуются методом уступок. Как и в методе условной оптимизации, выбирают главный критерий. Далее задают значение вспомогательного критерия. После этого при фиксированном значении вспомогательного критерия ищут альтернативу с оптимальным значением главного критерия. Если значение главного критерия удовлетворяет лицо, принимающее решение, то найденная альтернатива принимается. Если значение главного критерия не удовлетворяет лицо, принимающее решение, то он пытается «уступить», т.е. снизить значение второстепенного критерия в надежде получить выигрыш в значении главного критерия. Если при сделанной уступке лицо, принимающее решение не выигрывает в значении главного критерия, то он либо продолжает процесс уступок, либо принимает какое-то решение из предыдущих, либо отвергает все альтернативы.

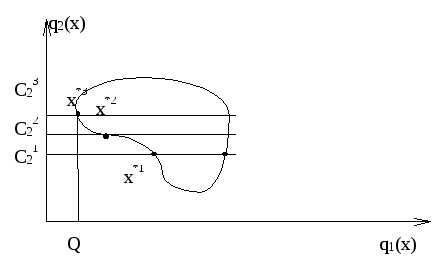
Поясним суть этого метода на рисунке. Пусть q1(x) - главный критерий. Зафиксируем значение второстепенного критерия q2(x) = C21. При данном фиксированном значении этого критерия (на рисунке это нижняя из горизонтальных прямых) найдем альтернативу с минимальным значением критерия q1(x). Это точка x1*1. Предположим, что значение главного критерия q1(x1*1) нас не удовлетворяет.

Мы делаем уступку в значении второстепенного критерия q2(x), полагая его значение q2(x) = C22 > C21. Далее при этом значении критерия q2(x) (на рисунке это средняя из горизонтальных прямых) найдем альтернативу с минимальным значением критерия q1(x). Это точка x1*2. Предположим, что значение главного критерия q1(x1*1) нас не удовлетворяет.

Мы готовы сделать еще уступку в значении второстепенного критерия q2(x), полагая его значение q2(x) = C23 > C22. Далее при этом значении критерия q2(x) (на рисунке это верхняя из горизонтальных прямых) найдем альтернативу с минимальным значением критерия q1(x). Это точка x1*3. Значение главного критерия q1(x1*3) = Q нас теперь удовлетворяет. На этом процесс поиска решения прекращается. Найденная альтернатива x1*3 считается принятой.

Пример. Выбираем лучший подарок по двум критериям: q1 - цена подарка, главный критерий; q2 - время, затрачиваемое на его приобретение. Допустим, что цена первого, второго и третьего подарков соответственно 300 руб., 350 руб. и 400 руб.; время, затрачиваемое на их приобретение 2 часа, 1 час и 30 мин.

Зафиксируем значение второстепенного критерия q2(x) = 20 мин. При этом значении второго критерия выберем подарок с наименьшей ценой. Это множество пусто. Такое положение нас не удовлетворяет. Сделаем уступку по времени. Положим q2(x) = 30 мин. При этом значении второго критерия выберем подарок с наименьшей ценой. Это подарок третий. Посмотрим значение главного критерия – цену. Допустим, что его цена 400 руб. нас не устраивает. Вновь делаем уступку по времени. Положим q2(x) = 1 час. При этом значении второго критерия выберем подарок с наименьшей ценой. Это подарок второй. Посмотрим значение главного критерия – цену. Допустим, что его цена 350 руб. нас устраивает, т.е. мы считаем цену нашей уступки по времени (30 мин.) адекватной цене нашего выигрыша в главном критерии (50 руб.). Тогда процесс выбора окончен. Мы выбираем второй подарок.

Достоинства метода:

Недостатки метода:

метод не гарантирует, что за достаточно большое число шагов найдётся удовлетворяющее решение. Это возможно из-за того, что цена уступок не будет адекватной цене нашего выигрыша.

Метод Парето.

Все предыдущие методы относились к случаю, когда критерии были неравнозначные. Остановимся теперь на случае равнозначных критериев. В этом случае критерии нельзя не только упорядочить между собой, но даже выделить главный среди них. В этой ситуации оптимальные решения образуют паретовское множество (множество оптимальных по Парето решений), т.е. множество альтернатив, не сравнимых между собой.

Альтернативы x, y называются несравнимыми между собой, если по одному критерию q1 первая альтернатива хуже второй (q1(x) > q1(y)), а по другому критерию q2 первая альтернатива лучше второй (q2(x) < q2(y)).

На приведенном ниже рисунке множество оптимальных по Парето альтернатив содержит 2 альтернативы: альтернативу с минимальным значением q1 = q1min и альтернативу с минимальным значением критерия q2 = q2min.

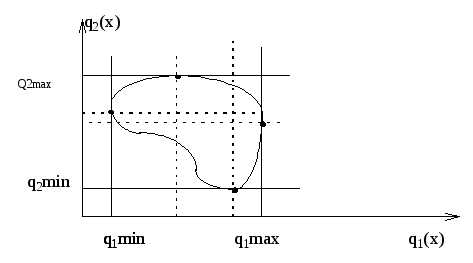
Как правило, Парето оптимальное множество содержит достаточно много альтернатив. Поэтому встаёт задача дальнейшего выбора из этого множества альтернатив. Дальнейший выбор может быть осуществлён только путём введения новых критериев.

Пример. Вновь будем выбирать лучший подарок по двум критериям: q1 - цена подарка, q2 - время, затрачиваемое на его приобретение. Допустим, что цена первого, второго и третьего подарков соответственно 300 руб., 350 руб. и 400 руб.; время, затрачиваемое на их приобретение, 2 часа, 1 час и 30 мин. Предположим, что критерии равнозначны. Выберем парето-оптимальное множество альтернатив. В него войдут первая альтернатива (самая низкая цена) и третья альтернатива (самое маленькое время). Далее, чтобы осуществить выбор на этом множестве альтернатив, необходимо ввести новый критерий. Допустим, что этим критерием будет оригинальность подарка. Если первый подарок оригинальнее третьего, то мы выберем первый подарок.

Заключение. Принятие решения в случае наличия нескольких критериев основано на том, что многокритериальная задача тем или иным способом сводится к однокритериальной задаче. Существует 4 метода сведения многокритериальных задач принятия решений к однокритериальным: суперкритерия, условной оптимизации, уступок, Парето.

Критериальный язык описания задач принятия решений существенно опирается на следующие предположения: 1) каждую альтернативу из множества альтернатив можно оценить численно; 2) эта оценка не зависит от наличия других альтернатив в множестве исходных альтернатив.

В реальных ситуациях принятия решений такие предположения часто не работают. Например, мы не можем оценить каждую альтернативу численно. Или результат оценки каждой альтернативы зависит от того, какие ещё альтернативы присутствуют в этом множестве. В этой ситуации можно описывать задачу принятия решения на языке бинарных отношений.

studfiles.net

Задачи многокритериальной оптимизации - более сложные задачи, чем задачи однокритериальной оптимизации

Системы массового обслуживания (СМО) могут быть трех видов: (*ответ*) нет даСитуационный анализ денежных потоков является динамическим процессом, использующим методы оптимизации и критерии оптимальности: (*ответ*) да нетТеория игр - теория, используемая исключительно для анализа игр: (*ответ*) нет даТеория систем массового обслуживания - область прикладной математики, использующая методы математической логики: (*ответ*) нет даФункция полезности является качественной характеристикой результата принятого решения: (*ответ*) нет даАддитивный критерий - обобщенный критерий, представляющий собой сумму исходных критериев с заданными весами: (*ответ*) да нетВ задачах многокритериальной оптимизации могут присутствовать как качественные, так и количественные критерии: (*ответ*) да нетВ мультипликативном критерии происходит сложение критериев с учетом их весов: (*ответ*) нет даВесовые множители в определении интегрального критерия имеют ту же размерность, что и сам критерий: (*ответ*) нет даВозникновение дисциплины "Исследование операций" связано с активным использованием достижений математики в различных областях, связанных с принятием управленческих решений: (*ответ*) да нетВсе слагаемые в мультипликативном критерии должны иметь одинаковую размерность: (*ответ*) нет даЗадача "достичь максимальной производительности при наименьших затратах" относится к задачам однокритериальной оптимизации: (*ответ*) нет даЗадачи многокритериальной оптимизации - более сложные задачи, чем задачи однокритериальной оптимизации: (*ответ*) да нетИнтегральный критерий - единственный критерий, построенный на базе всех остальных: (*ответ*) да нетКритерии оптимальности в задачах многокритериальной оптимизации всегда имеют одинаковую значимость: (*ответ*) нет даЛюбое решение, принадлежащее множеству Парето, можно улучшить по всем критериям: (*ответ*) нет даМножество Парето - множество точек неулучшаемых решений: (*ответ*) да нетНаходя множество Парето, всегда получается одно оптимальное решение: (*ответ*) нет даНормирующие множители делают критерии оптимальности безразмерными: (*ответ*) да нетРешение в задачах многокритериальной оптимизации чаще всего является единственным: (*ответ*) нет даРешение, принадлежащее множеству Парето, можно улучшить сразу по всем критериям: (*ответ*) нет да

www.soloby.ru

Однокритериальная оптимизация. Основные методы оптимизации, используемые при синтезе детерминированных сложных технических систем

1. Постановка и методы решения задач математического программирования. Линейное программирование

Формальная постановка задачи математического программирования (м п).

Задача оптимизации состоит в выборе наилучших планов.

Не смотря на смысловое разнообразие задач, все они формально сводятся к одной общей постановке.

Найти значение переменных обращающих в максимум, либо минимум значение целевой функции:

min(max)←Z=f(x1,…,xn),

при условиях: gi(x1,…,xn)≤≥bi,i=1,m

Краткая запись условия задачи математического программирования(М П) имеет вид:

XєU→max(min){Z=f(x)}

Линейное программирование. Постановка задачи.

Задача ЛП в общей постановке состоит в отыскании переменных x1,…,xn ,обращающих в

экстремум функцию: max←Z=Σ СjXjпри ограничениях:

j=1

a11 x1 + a12 x2 +…+ a1n xn ≤ b1

…

am1 x1 + am2 x2 +…+ amn xn ≤ bm

Обычно, кроме того, на практике добавляют требования не отрицательности(xj>0ij=1,n)

продукты	Элемент
продукты	белки	углероды	жиры
П1	а11	а12	а13
П2	а21	а22	а23
П3	а31	а32	а33
П4	а41	а42	а43

Где аijнекоторые числа иi– продуктj– элемент.

Z=C1x1+C2x2+C3x3+C4x4→minздесь мы заx1…x2обозначили количество продуктов которые должны входить в рацион.

a11 x1 + a12 x2 +a13 x3 + a14 x4 ≥ b1

a12 x1 + a22 x2 +a32 x3 + 242 x4 ≥ b2

a13 x1 + a23 x2 +a33 x3 + a43 x4 ≥ b3

x ≥ 0

studfiles.net

3. Однокритериальные задачи исследования операций.

Будем предполагать, что необходимо найти решение, доставляющее наилучшее значение одному критерию. Остальные критерии переводятся в разряд ограничений в форме равенств и неравенств по отношению к каким-то конкретным числовым значениям.

Пример: найти минимум себестоимости продукции при ограничениях: производительность больше заданной, запасы сырья меньше (или равны) имеющихся.

Имеем некоторый технологический объект (процесс) управления. Это м. б. задача оптимально проектирования этого ТП или задача управления, решаемая либо на стадии проектирования либо на стадии действующего производства.

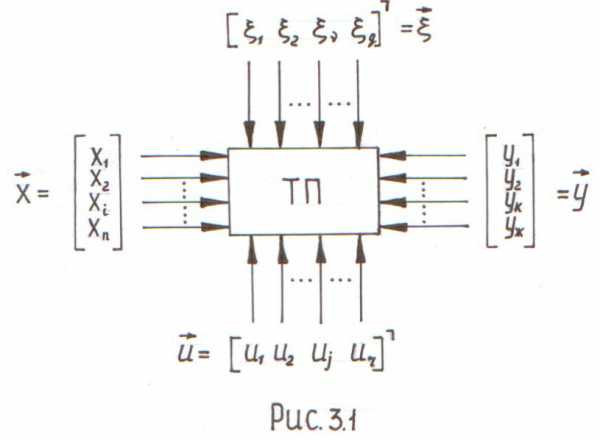
Классификация параметров ХТП как объектов оптимизации.

С точки зрения постановки и решения задач однокритериальной оптимизации, параметры ТП или ОУ удобно классифицировать: (рис. 3.1), где вектор 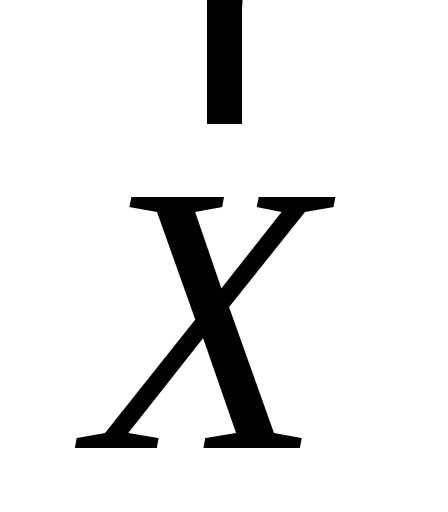– вектор переменных, значения которых известны (заданы) в задаче или они поступают с объекта как измеренные, но измерить их мы не можем; вектор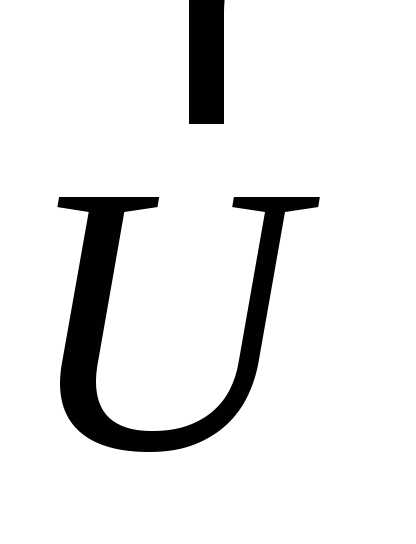– вектор управляющих воздействий; вектор– вектор неконтролируемых возмущений, значение не изменяется; вектор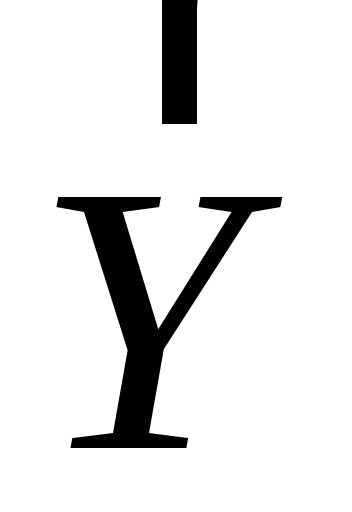– вектор выходных параметров (координат). Вектор управлений контролируется, измеряется и, изменяя значение этих параметров можно изменить значения выходных параметров.

4. Понятия и определения.

В сфере деятельности (химической технологии, химическом производстве) является определение аппаратурно-технологического оформления процесса, определение наилучших параметров процесса и обеспечение высокой точности поддержания (регулирования) найденных значений этих параметров. Другой сферой деятельности хим. технологии является организация и проведение оптимального эксперимента по изучению закономерности процесса, по созданию аппаратурного оформления. Эти эксперименты исследуются в химической технологии с целью формирования исходных данных для проектирования как вновь действующих ХП (создания новых технологий), так и данных для реконструкции действующих процессов. Целью эксперимента является сокращение времени эксперимента и стоимости, выбор наилучших и оптимальных вариантов. Оптимум – наилучшее условие, совокупность наилучших условий. Оптимизация – процесс достижения оптимума, т.е. определение наилучших условий. Применительно к технологическому процессу – это определение условий и значений параметров.

Введение ТП наилучшей организации технологической системы – закон о принятии наилучших условий значений технологических параметров, введение ТП в реальном времени. Любая оптимизация представляет: наличие множества вариантов, оценка которых по некоторым показателям позволяет выявить какой вариант из нескольких сравниваемых лучше, т.е. оптимизация дает возможность выбора. При постановке задачи оптимизации необходимо иметь возможность вариации состояния оптимизируемой технологические схемы, причем возможность вариации зависит от вида и числа степеней свободы оптимальной мат. системы. Число степеней свободы = числу параметров(координат) объекта оптимизации, которые позволяют менять состояние системы и влиять на значения критерия. Эти параметры называются управляющими воздействиями или управлениями. Иногда эти параметры называют оптимизирующими факторами (переменными). Для того, чтобы сравнить различные варианты состояния оптимизируемой системы, д.б. разработаны количественные оценки для сравнения этих состояний, которые называются критериями.

Обычно если критериев несколько, задача становится многокритериальной и для решения разрабатывается схема нахождения компромиссов между различными критериями. Простейшая схема – 1 критерий выбирается за основной, ищут его макс. и мин., остальные критерии переводятся в ограничения в виде равенств и неравенств. Равенство – критерий имеет 1 заданное значение. Неравенство – критерий либо меньше, либо больше заданного значения. Независимо от схемы компромиссов решение задачи оптимизации сводится к решению задачи с одним критерием - однокритериальная оптимизация.

studfiles.net

3. многокритериальные задачи принятия решений математическая модель многокритериальной оптимизации

3. многокритериальные задачи принятия решений математическая модель многокритериальной - страница №1/1

3. МНОГОКРИТЕРИАЛЬНЫЕ ЗАДАЧИ ПРИНЯТИЯ РЕШЕНИЙ 3.1. Математическая модель многокритериальной оптимизации В теории многокритериальной оптимизации (МКО) решаются задачи принятия решений одновременно по нескольким критериям. Задача МКО ставится следующим образом: требуется найти числа , удовлетворяющие системе ограничений

, , (3.1)

для которых функции

, , (3.2)

достигают максимального значения.

Множество точек , удовлетворяющих системе (3.1), образует допустимую область . Элементы множества называются допустимыми решениями или альтернативами, а числовые функции , – целевыми функциями, или критериями, заданными на множестве D. В формулировке задаче (3.1)-(3.2) присутствует целевых функций. Эти функции отображают множество в множество , которое называется множеством достижимости.

В векторной форме математическую модель МКО (3.1)-(3.2) можно записать следующим образом:

при . (3.3)

Здесь – вектор-функция аргумента .

Впервые проблема МКО возникла у итальянского экономиста В.Парето в 1904 г. при математическом исследовании товарного обмена. В дальнейшем интерес к проблеме МКО усилился в связи с разработкой и использованием вычислительной техники, и уже позднее стало ясно, что многокритериальные задачи возникают также и в технике, например, при проектировании сложных технических систем.

В отличие от задач оптимизации с одним критерием в МКО имеется неопределенность целей. Действительно, существование решения, максимизирующего несколько целевых функций, является редким исключением, поэтому с математической точки зрения задачи МКО являются неопределенными и решением может быть только компромиссное решение. Например, при поиске плана предприятия, макимизирующего прибыль и минимизирующего затраты очевидна невозможность достижения обеих целей одновременно, так как чем больше затраты, тем больше должно быть продукции и тем больше прибыль.

Ввиду этого в теории МКО понятие оптимальности получает различные толкования, и поэтому сама теория содержит три основных направления:

1. Разработка концепции оптимальности.

2. Доказательство существования решения, оптимального в соответствующем смысле.

3. Разработка методов нахождения оптимального решения.

3.2. Оптимальность по Парето Если функции достигают максимум в одной и той же точке , то говорят, что задача (3.3) имеет идеальное решение.

Случаи существования идеального решения в многокритериальной задаче крайне редки. Поэтому основная проблема при рассмотрении задачи (3.3) – формализация принципа оптимальности, т.е. определение того, в каком смысле «оптимальное» решение лучше других. В случае отсутствия «идеального решения» в задаче (3.3) ищется компромиссное решение.

Для всякой альтернативы вектор из значений целевых функций является векторной оценкой альтернативы. Векторная оценка альтернативы содержит полную информацию о ценности (полезности) этой альтернативы для главного конструктора системы, или, как принято говорить в системном анализе, лица, принимающего решение (ЛПР). Сравнение любых двух исходов заменяется сравнением их векторных оценок.

Пусть . Если для всех критериев имеют место неравенства , , причем хотя бы одно неравенство строгое, то говорят, что решение предпочтительнее решения . Условие предпочтительности принято обозначать в виде .

Определение (оптимальность по Парето). В задаче МКО точка называется оптимальной по Парето, если не существует другой точки , которая была бы предпочтительнее, чем .

Точки, оптимальные по Парето, образуют множество точек, оптимальных по Парето (множество неулучшаемых или эффективных точек) .

Оптимальные решения многокритериальной задачи следует искать только среди элементов множества альтернатив . В этой области ни один критерий не может быть улучшен без ухудшения хотя бы одного из других. Важным свойством множества Парето является возможность «выбраковывать» из множества альтернатив заведомо неудачные, уступающие другим по всем критериям. Обычно решение многокритериальной задачи должно начинаться с выделения множества . При отсутствии дополнительной информации о системе предпочтений ЛПР должно принимать решение именно из множества Парето .

В векторной оптимизации кроме множества Парето в общем случае нет общих правил, по которому варианту отдается предпочтение по сравнению с другим вариантом .

Часто решение многокритериальной задачи состоит в построении множества Парето-оптимальных точек и дальнейшем выборе одной из них на основе «здравого смысла» или с помощью какого-либо другого критерия.

Во всех случаях задача многокритериальной оптимизации каким-то способом сводится к задаче с одним критерием. Существует много способов построения такого окончательного критерия, однако ни одному из них нельзя заранее отдать наибольшее предпочтение. Для каждой задачи этот выбор должен делаться ЛПР.

Заметим, что целевые функции отображают множество точек, оптимальных по Парето в множество , которое называется множеством Парето.

3.3. Построение эффективной области для двух критериев

Пример 3.1. Пусть математическая модель задачи МКО с двумя критериями имеет вид:

при ограничениях:

Требуется определить множество точек, оптимальных по Парето.

Допустимая область представляет собой четверть круга радиуса 10 с центром в начале координат, расположенную в 1-ом квадранте (рис. 3.1).

Рис. 3.1. Множество Парето-оптимальных точек

Найдем точки, оптимальные по критериям и в отдельности. Для этого построим векторы, имеющие направления векторов и , и перпендикулярно им – линии уровня. По линиям уровня определяются оптимальные точки и , расположенные на окружности.

Проверим произвольную точку на Парето-оптимальность. Через неё проведём линии уровня целевых функций и рассмотрим конус, образованный пересечением полуплоскостей, ограниченных этими линиями и лежащих в направлении увеличения соответствующих целевых функций (конус доминирования для альтернативы ). На рис. 3.1 этот конус закрашен. Очевидно, что точку можно улучшить по обоим критериям, и поэтому она не является эффективной. Множество эффективных точек (точек, оптимальных по Парето) расположено на дуге окружности . Таким образом, эффективные точки лежат только между точками оптимума, полученными при решении многокритериальной задачи отдельно по каждому из критериев.

Найдем координаты точки . Нормальный вектор к окружности имеет координаты , а к линии уровня 1-ой целевой функции – . Из условия коллинеарности векторов следует, что их координаты пропорциональны, то есть . Значит, координаты точки удовлетворяют системе уравнений

Из решения системы следует, что точка имеет координаты . Аналогично найдем, что точка имеет координаты .

Пример 3.2. Для задачи, сформулированной в примере 3.1, определить множество достижимости и множество Парето.

Рассмотрим, что происходит в пространстве критериев для отображения с помощью вектора целевых функций.

Составим табл. 3.1, в которой поместим характерные точки допустимой области и соответствующие им образы в пространстве критериев.

Таблица 3.1

Для двух заданных критериев на рис. 3.2 представлено множество достижимости и множество Парето , являющееся образом множества , оптимальных по Парето точек. Эти множества получены на основе данных табл. 3.1.

Рис. 3.2. Множество достижимости и множество Парето

Множество на рис. 3.2 представляет собой дугу . Для двух критериев это множество образует «северо-восточную» границу множества достижимости.

Таким образом, решением задачи МКО является множество точек, оптимальных по Парето . Окончательный выбор всегда остается за ЛПР.

3.4. Проблемы и классификация методов решения задач многокритериальной оптимизации При решении задач МКО приходится решать специфические вопросы, связанные с неопределенностью целей и несоизмеримостью критериев. Перечислим основные проблемы, возникающие при разработке методов МКО.

1. Проблема нормализации критериев, то есть приведение критериев к единому (безразмерному) масштабу измерения.

2. Проблема выбора принципа оптимальности, то есть установление, в каком смысле оптимальное решение лучше всех остальных решений.

3. Проблема учета приоритетов критериев, возникающая в тех случаях, когда из физического смысла ясно, что некоторые критерии имеют приоритет над другими.

4. Проблема вычисления оптимума задачи МКО. Речь идет о том, как использовать методы линейной, нелинейной, дискретной оптимизации для вычисления оптимума задач с определенной спецификой.

При решении многокритериальной задачи часто возникает необходимость нормализации (нормирования) критериев , то есть приведение всех критериев к единому масштабу и безразмерному виду. В дальнейшем будем считать, что все критерии неотрицательны, то есть для всех .

Наиболее часто используется замена критериев их безразмерными относительными величинами: , где . Нормализованные критерии обладают двумя важными свойствами: во-первых, они являются безразмерными величинами, и, во-вторых, они удовлетворяют неравенству для любого . Эти свойства позволяют сравнивать критерии между собой.

Основные методы, применяемые при решении задач МКО, представлены на рис. 3.3.

Рис. 3.3. Классификация методов решения многокритериальных задач

В следующих пунктах приведенные здесь методы рассматриваются более подробно. 3.5. Методы, основанные на свертывании критериев Вместо частных критериев рассматривается один скалярный критерий, полученный путем комбинации частных критериев. Различают аддитивный и мультипликативный методы свертывания критериев. 3.5.1. Метод аддитивной свертки критериев

Пусть критерии соизмеримы, например, нормированы и определен вектор весовых коэффициентов критериев , характеризующих важность соответствующего критерия. Это значит, что , если критерий имеет приоритет над критерием . При этом

, .

Для аддитивного метода строится новая целевая функция

и решается задача оптимизации скалярного критерия

при условии .

Можно доказать, что решение задачи со скалярным критерием является эффективным для задачи (3.3).

Пример 3.3. Рассмотрим задачу МКО с двумя критериями

при ограничениях

Решим задачу оптимизации по каждому критерию в отдельности. Используя графический метод (рис. 3.4а), получим оптимальное решение по первому критерию и оптимальное решение по второму критерию .

Рис. 3.4. Решение задачи оптимизации по двум критериям

На рис. 3.4б изображено множество достижимости F и указаны значения и . Выполним свертку критериев:

где .

Целевая функция является линейной, поэтому в зависимости от и оптимальными будут угловые точки допустимой области , или , или все точки отрезка . Полагая, например, , получим оптимальное решение . 3.5.2. Метод мультипликативной свертки критериев

Для мультипликативного метода подход к решению аналогичен, только целевая функция имеет вид

, причем .

Основной и очень существенный недостаток методов свертывания критериев состоит в субъективности выбора коэффициентов .

3.6. Метод главного критерия Выбирается основной (главный) среди критериев. Пусть это, например, . Все остальные целевые функции переводятся в разряд ограничений по приведенному ниже правилу.

В соответствии с требованиями ЛПР на все критерии накладываются определенные ограничения, которым они должны удовлетворять. Вводится система контрольных показателей , относительно которых по всем критериям должны быть достигнуты значения, не меньше заданных значений :

, .

После выбора основного критерия и установления нижних границ для остальных критериев решается задача однокритериальной оптимизации:

при условиях

Этот способ наиболее употребителен в инженерной практике.

Пример 3.4. Методом главного критерия решить задачу из примера 3.3.

Назначим значения контрольных показателей: , , и пусть первый критерий выбран в качестве основного. Тогда получим задачу с одним критерием:

при условиях

Из рис. 3.4а ясно, что оптимальным решением является , . Заметим, что решение, полученное этим методом может не быть эффективным.

3.7. Метод последовательных уступок Другой способ носит название метода последовательных уступок. В этом методе критерии нумеруются в порядке убывания важности. Пусть критерии записаны в порядке уменьшения их важности. Тогда должны быть выполнены следующие действия.

1-й шаг. Решается однокритериальная задача по 1-му критерию:

2-й шаг. Назначается разумная с инженерной точки зрения уступка , составляется и решается новая задача оптимизации по 2-му критерию:

3-й шаг. Назначается уступка для 2-го критерия , составляется и решается задача оптимизации по 3-му критерию:

Процесс назначения уступок по каждому критерию и решения однокритериальных задач продолжается, пока не дойдем до последнего – го шага.

-й шаг. Назначается уступка для – го критерия , составляется и решается задача оптимизации по последнему – му критерию:

Основной недостаток методов, использующих ограничения на критерии, состоит в субъективности выбора контрольных показателей и в субъективности выбора уступок. При использовании метода последовательных уступок следует помнить, что уступки могут быть несоизмеримы между собой, поэтому надо предварительно организовать нормализацию критериев. Кроме того, в общем случае уже со 2-го шага решение может оказаться не оптимальным по Парето.

Пример 3.5. В примере 2.5 была рассмотрена задача по критерию максимизации общей прибыли от реализации готовой продукции. Математическая модель была сформулирована в виде целевой функции (2.5) и ограничений (2.6)-(2.7). Согласно оптимальному плану предприятие должно изготовить 12 шкафов и 32 стола, и наибольшая прибыль составит 320 ден.ед.

Дополнительно предположим, что предприятие заинтересовано в эффективном использовании оборудования. При этом известны цены за 1 час простоя оборудования каждого вида: для строгальных станков – 3 ден.ед., для фрезерных станков – 9 ден.ед., для шлифовальных станков – 2 ден.ед.

Требуется составить задачу оптимизации с двумя критериями и решить ее методом уступок.

Обозначим через суммарные издержки предприятия за простой оборудования. Поскольку время простоя равно

– для строгальных станков,

– для фрезерных станков,

– для шлифовальных станков,

то суммарные издержки равны

или

. (3.4)

Система ограничений (2.6)-(2.7) при этом не изменяется:

, (3.5)

, . (3.6)

Задача оптимизации по второму критерию (3.4)-(3.6) решается в Excel с использованием процедуры «Поиск решения» аналогично п.2.3.3. Исходные данные и результаты оптимизации показаны на рис. 3.5.

Рис. 3.5. Исходные данные и результаты решения задачи (3.4)-(3.6)

Заметим, что целевая функция (3.4) содержит свободный член, поэтому в ячейку D6 помещается одна из формул табл. 3.2.

Таблица 3.2

= B6*B4+C6*C4+1248

или

=СУММПРОИЗВ(B6:C6;B4:C4)+1248

На рис. 3.5 представлен оптимальный план выпуска мебели по критерию минимизации издержек за простой оборудования: предприятие должно изготовить 24 шкафа и 16 столов. При этом минимальные издержки составят ден.ед. Как видим, этот план существенно отличается от оптимального плана по критерию общей прибыли.

Решим теперь задачу с двумя критериями методом уступок. Для первого критерия назначим уступку , и в математическую модель (3.4)-(3.6) добавим еще одно ограничение . Тогда получим новую задачу оптимизации по второму критерию:

(3.7)

при ограничениях

, (3.8)

, . (3.9)

Организация исходных данных задачи (3.7)-(3.9) на листе Excel приведена на рис. 3.6.

Рис. 3.6. Исходные данные и результаты решения задачи МКО

В результате получен компромиссный план выпуска мебели, состоящий в изготовлении 18 шкафов и 24 столов. Издержки за простой оборудования составят ден.ед., а общая прибыль предприятия будет равна ден.ед. 3.8. Методы целевого программирования Название этой группы методов связано с тем, что ЛПР задает определенные цели для каждого критерия. Задача МКО в этом случае преобразуется в задачу минимизации суммы отклонений с некоторым показателем :

, при XÎD, (3.10)

где – некоторые весовые коэффициенты, характеризующие важность того или иного критерия.

Задачу (3.10) можно конкретизировать в зависимости от значений параметра и заданных целей. В частности, при и получим задачу минимизации суммы квадратов отклонений:

при XÎD,

в которой минимизируется евклидово расстояние от множества достижимости F до «абсолютного максимума» в пространстве критериев. Здесь .

Осложнения, обусловленные несоизмеримостью величин , можно преодолеть с помощью нормализации критериев, рассматривая следующую задачу оптимизации:

при XÎD. (3.11)

Пример 3.6. Методом целевого программирования решить задачу МКО из примера 3.3.

В условиях примера 3.3 имеем , , поэтому задача (3.11) принимает вид

при условиях

При постоянном значении линии уровня целевой функции представляют собой эллипсы с центром в точке и полуосями и . Необходимо найти минимальное значение , для которого соответствующий эллипс будет иметь общие точки с областью D. На рис. 3.7 показано графическое решение данной задачи.

Рис. 3.7. Решение задачи методом целевого программирования

Оптимальной является точка . 3.9. Методы гарантированного результата Рассматриваются методы, которые дают наилучший результат даже для самого наименьшего из критериев, а именно, компромиссное решение находится путем решения следующей задачи оптимизации:

при .

Это есть максиминная задача. С учетом нормализации критериев методы гарантированного результата образуют наиболее перспективное направление в решении задач МКО.

Для нормализованных критериев , где , максиминная задача формулируется в виде:

при . (3.12)

Остановимся на рассмотрении двух случаев, когда критерии равнозначны и неравнозначны (с заданным приоритетом).

3.9.1. Равнозначные критерии

Задача (3.12) эквивалентна задаче

(3.13)

при условиях

. (3.14)

Задача (3.13)-(3.14) называется -задачей. Она имеет линейную целевую функцию и ограничений. Если все функции и линейны, то -задача относится к линейному программированию. В этом случае доказано, что оптимальное решение -задачи оптимально по Парето.

Пример 3.7. Требуется решить задачу из примера 3.3 методом гарантированного результата с равнозначными критериями. Составим -задачу:

при условиях

Оптимальное решение этой задачи есть , .

3.9.2. Критерии с заданным приоритетом

Рассмотрим только два критерия и , и пусть и – соответствующие нормализованные критерии. Разобьем допустимую область на две части так, что в области выполняется неравенство , то есть первый критерий имеет приоритет над вторым, а в области выполняется неравенство , то есть второй критерий имеет приоритет над первым.

Для числовой характеристики приоритета вводится коэффициент связи : , который показывает, во сколько раз относительная оценка больше . Если – оптимальная точка для равнозначных критериев, то .

Если – точка оптимума по 1-му критерию, то , , то есть , и значит . Аналогично, если – точка оптимума по 2-му критерию, то , , и значит .

Предположим, что первый критерий имеет приоритет над вторым. Тогда коэффициент необходимо задать в интервале , а затем составить и решить -задачу, включив в систему ограничений равенство . В результате получим точку , которая будет принадлежать множеству , где 1-ый критерий имеет приоритет над 2-ым.

Доказано, что для выпуклых задач МКО точка , являющаяся решением -задачи, единственная и оптимальна по Парето.

Пример 3.8. Требуется решить задачу из примера 3.3 методом гарантированного результата с неравнозначными критериями при условии, что 1-ый критерий имеет приоритет над 2-ым.

Так как , то , , следовательно, . В интервале зададим коэффициент связи . Тогда , или . Составим -задачу:

при условиях

В результате решения задачи получим оптимальное решение , .

Недостаток рассмотренного метода состоит в субъективности задания коэффициента связи .

Решение задачи МКО методом гарантированного результата, как правило, проходит следующие этапы.

Разработка математической модели системы на основе заданных целей и ограничений; при этом часто используется мнение экспертов.
Предварительный анализ системы отдельно по каждому критерию; используются методы и программные средства оптимизации с одним критерием.
Нормализация критериев.
Решение задачи МКО при равнозначных критериях.
Задание приоритетов критериев и решение задачи МКО с назначенными приоритетами.

umotnas.ru

Постановки задач однокритериальной оптимизации

Задачи однокритериальной оптимизации делятся на задачи безусловной (когда ищется оптимальное решение, удовлетворяющее целевой функции) и условной (ищется оптимальное решение, удовлетворяющее некоторым ограничениям и целевой функции) оптимизации.

Среди задач условной однокритериальной оптимизации наиболее изучены следующие линейные задачи:

задача линейного программирования

; (1)

задача целочисленного линейного программирования

; (2)

задача частично-целочисленного линейного программирования

(3)

задача булевого линейного программирования

, где векторы , матрицы - заданы, а - -мерные векторы переменных.

Если целевая функция и/или ограничения являются нелинейными, то описанные выше модели являются нелинейными.

Будем далее рассматривать задачи линейного программирования. Любую задачу линейного программирования (1) можно привести к виду:

, (4)

где --мерный вектор.

Задача (4) называется задачей линейного программирования в канонической форме.

Для получения такой формы в ограничения ≤задачи (1) вводятся дополнительные переменные со знаком «+».

Если в ограничениях задачи (1) стоит знак «», то дополнительные переменные вводятся со знаком «-».

Если необходимо решить задачу на минимум, то делаются следующие простые преобразования:

Задача (1) в координатной форме запишется следующим образом:

найти

на множестве векторов х=( х1,х2, …хn), удовлетворяющих условиям:

1. хj ³0 для j=1,...,n

2. (5)

Используя знак суммирования, задача (5) запишется в следующем виде:

найти

на множестве векторов х=( х1,х2, …хn), удовлетворяющих условиям:

10. хj ³0 для j=1,...,n

20. (6)

Приведя ограничения 20 в задаче (6) к равенствам, получим задачу в канонической форме:

найти

на множестве векторов х=( х1,х2, …хn), удовлетворяющих условиям:

10. хj ³0 для j=1,...,n,

20, (7)

где - это дополнительная переменная, .

Пример 1 . Привести к канонической форме следующую задачу линейного программирования:

найти максимум функции

на множестве векторов х = (х1, х2,х3), удовлетворяющих условиям:

10 ., ,

20.

Для приведения ограничений 20 к каноническому виду, введем дополнительные неотрицательные переменные :

studlib.info