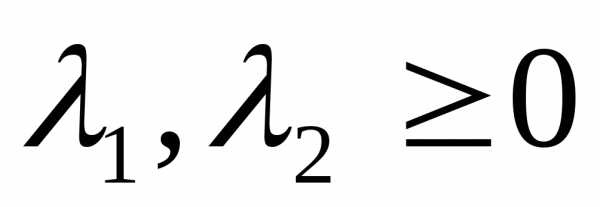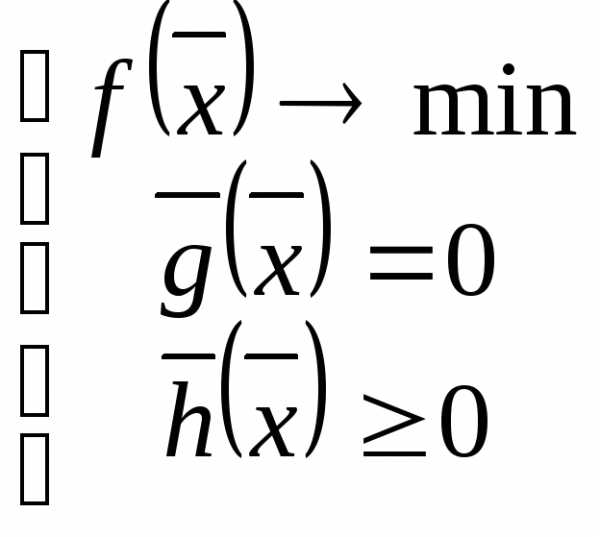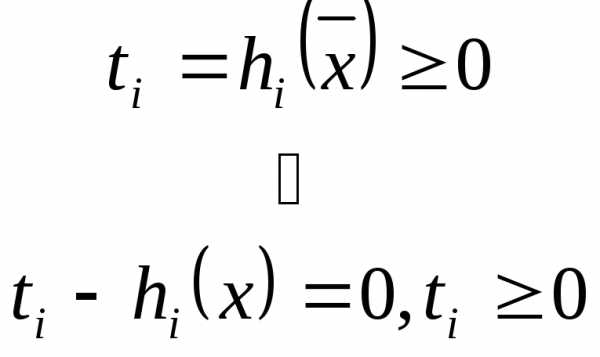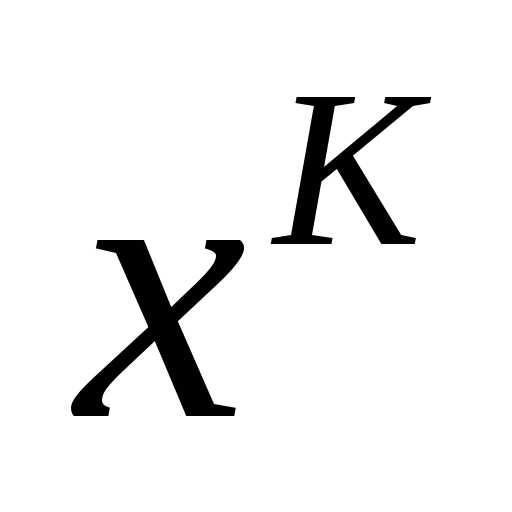Оптимизация модели энергосистемы методом множителей Лагранжа. Основные выражения. Оптимизация метод лагранжа
4. Классическая задача условной оптимизации и методы ее решения
Переобозначим переменные согласно [1]. Классическая задача условной оптимизации в новых обозначениях имеет вид:
(3)
(4)
Итак, область допустимых решений (ОДР) 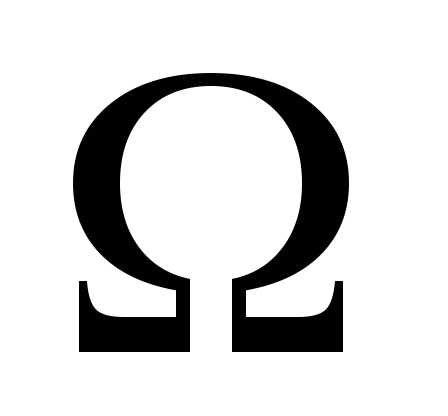 в рассматриваемой задаче представляет собой некоторое многообразие коразмерностиm.
в рассматриваемой задаче представляет собой некоторое многообразие коразмерностиm.
Задачу можно решить методом исключения (подстановки), решив уравнение (4) относительно (базисных) переменных  i, i=1,…m, и подставляя найденное решение в (3). Например, . Исходная задача (3), (4), таким образом, преобразована в задачу безусловной оптимизации функции
i, i=1,…m, и подставляя найденное решение в (3). Например, . Исходная задача (3), (4), таким образом, преобразована в задачу безусловной оптимизации функции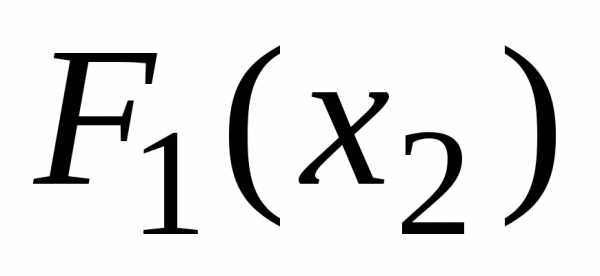 . Такая операция для нелинейных функций из (4) не всегда выполнима, и всегда трудоемка.
. Такая операция для нелинейных функций из (4) не всегда выполнима, и всегда трудоемка.
Метод множителей Лагранжа (ммл). Необходимые условия в классической задаче условной оптимизации. Функция Лагранжа
ММЛ позволяет исходную задачу классической условной оптимизации (3), (4) преобразовать в задачу безусловной оптимизации для специально "сконструированной" функции, называемой функцией Лагранжа:
, (5)
где - множители Лагранжа;. (6)
Читатель уже знакомился с понятием функции Лагранжа в других курсах, поэтому кратко изложим лишь основные факты.
Пусть задача (3), (4) имеет локальное решение 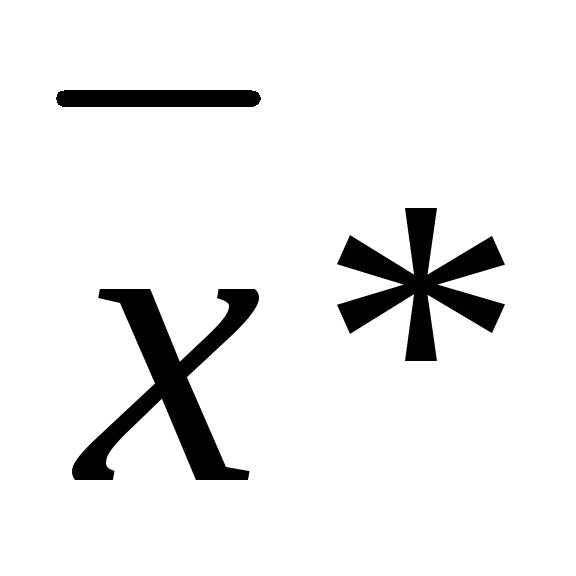 , и вектор-функция (6) удовлетворяетусловию Якоби, то есть
, и вектор-функция (6) удовлетворяетусловию Якоби, то есть 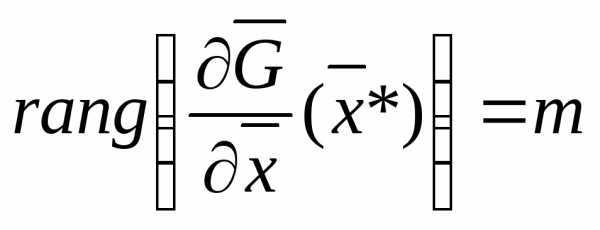 - числу строк в матрице Якоби и числу ограничений в (6). Это часто называют условиемрегулярности. В противном случае, в L(x,) присутствует множитель при F(x).
- числу строк в матрице Якоби и числу ограничений в (6). Это часто называют условиемрегулярности. В противном случае, в L(x,) присутствует множитель при F(x).
Перенумеруем переменные x так, чтобы последний минор матрицы Якоби был ненулевым и разобьем вектор инструментальных переменных на две части, размерности n-m и m, соответственно: 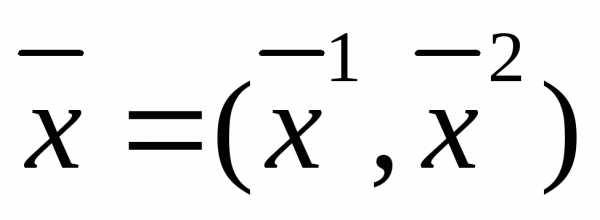
По теореме о неявной функции в окрестности 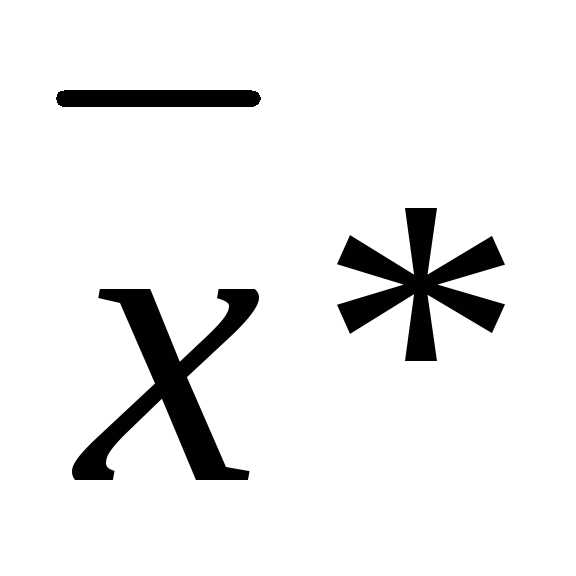 систему (4) можно разрешить относительно
систему (4) можно разрешить относительно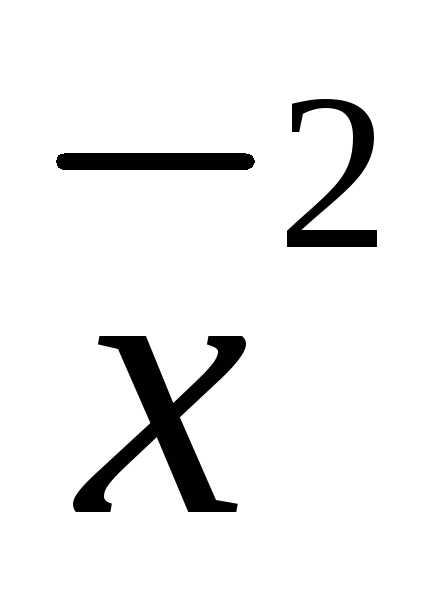 :
: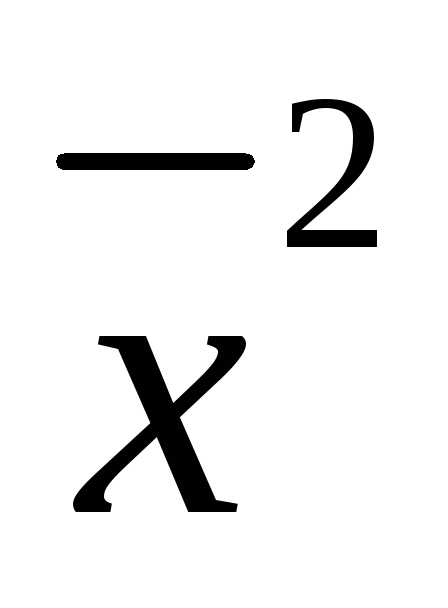 =f(
=f(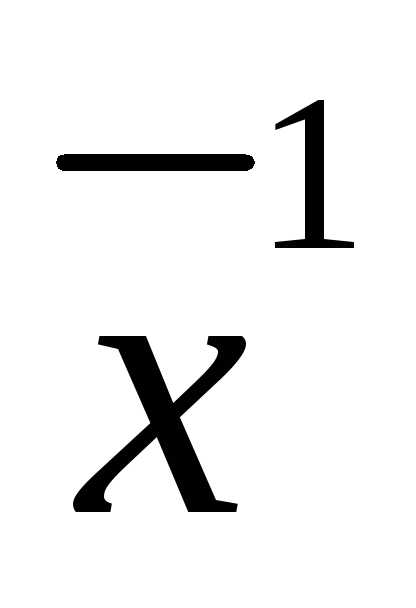 ), гдеf – вектор столбец из m функций. Тогда исходная задача сводится к задаче оптимизации без ограничений: max Ф(
), гдеf – вектор столбец из m функций. Тогда исходная задача сводится к задаче оптимизации без ограничений: max Ф(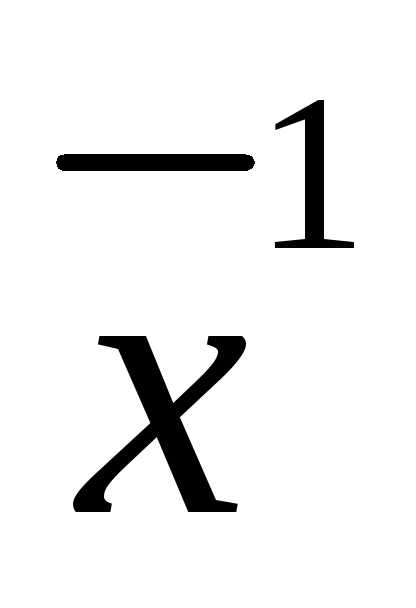 )= maxF(
)= maxF(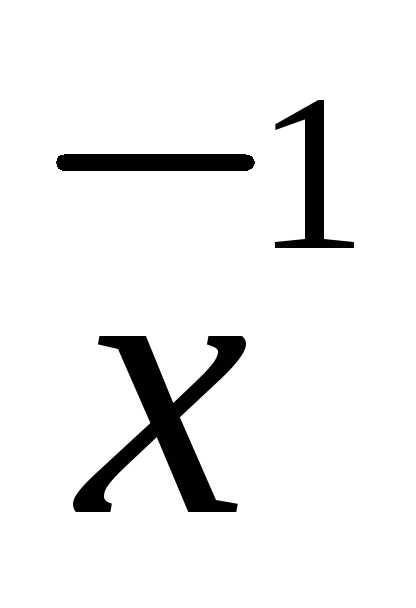 ,f(
,f(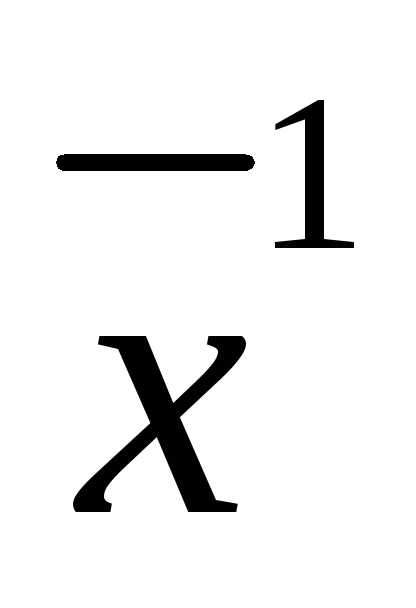 )), необходимое условие (1) для которой состоит в следующем:
)), необходимое условие (1) для которой состоит в следующем:
, (7)
где ,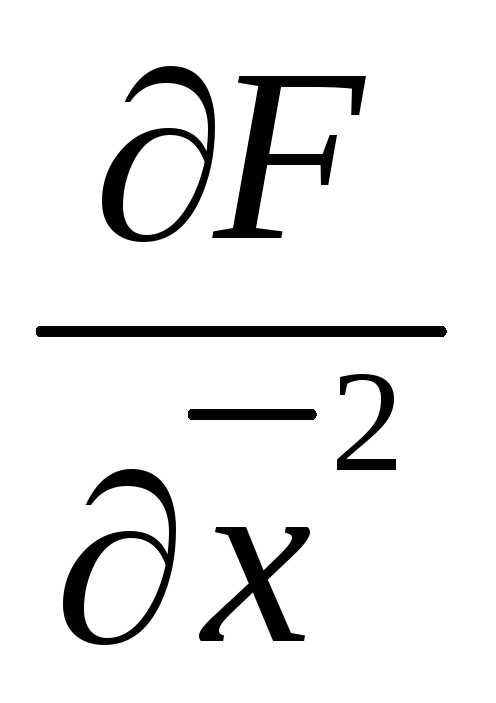 ,
,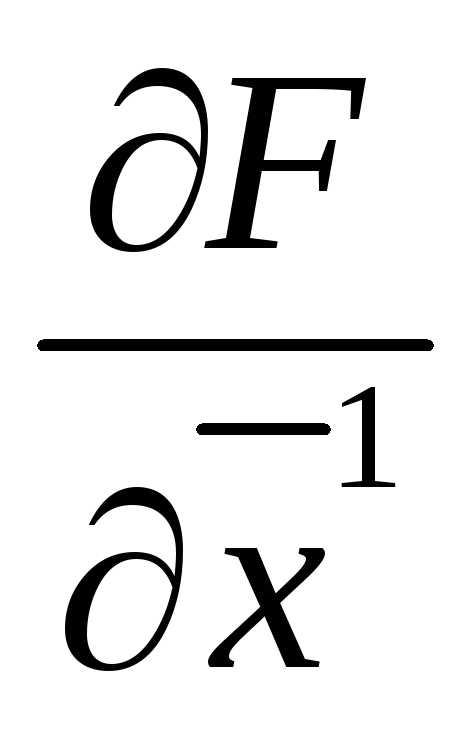 - вектор-строки градиентов, а
- вектор-строки градиентов, а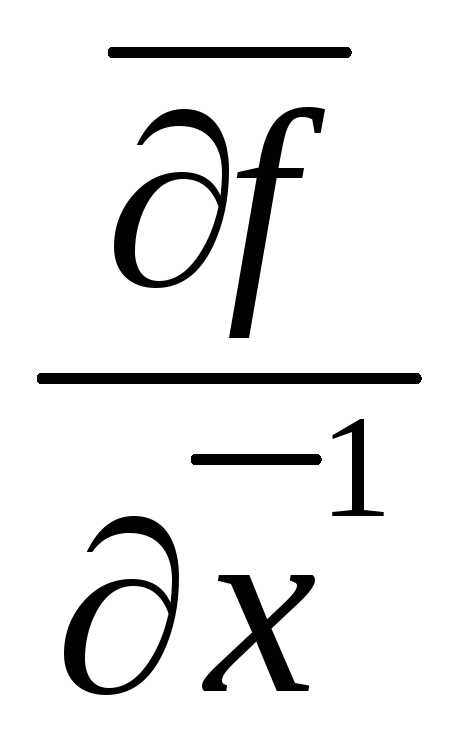 - матрица Якоби размерностиn(n-m). После исключения базисных переменных
- матрица Якоби размерностиn(n-m). После исключения базисных переменных 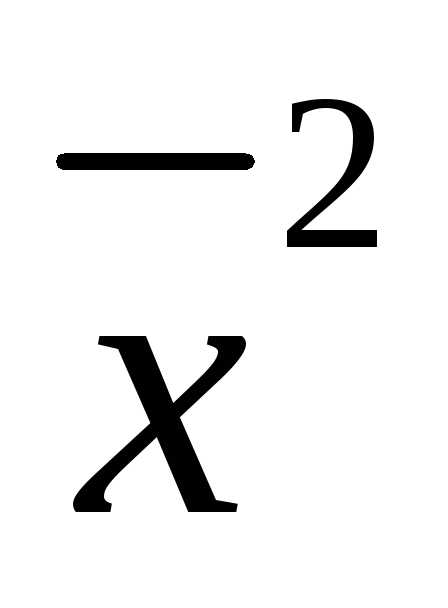 ограничения (4) станут тождествами от
ограничения (4) станут тождествами от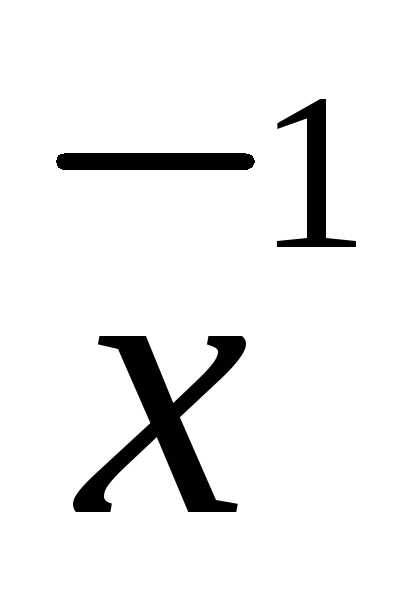 . Продифференцируем их. («Полная» производная по
. Продифференцируем их. («Полная» производная по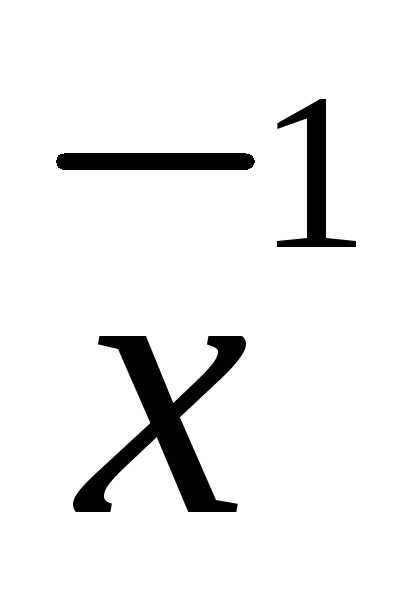
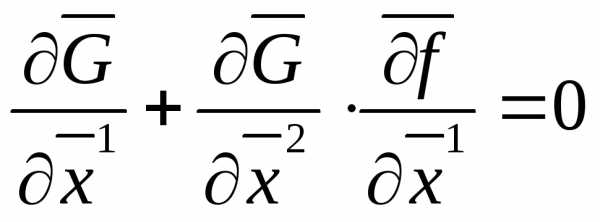 , (8)
, (8)
где 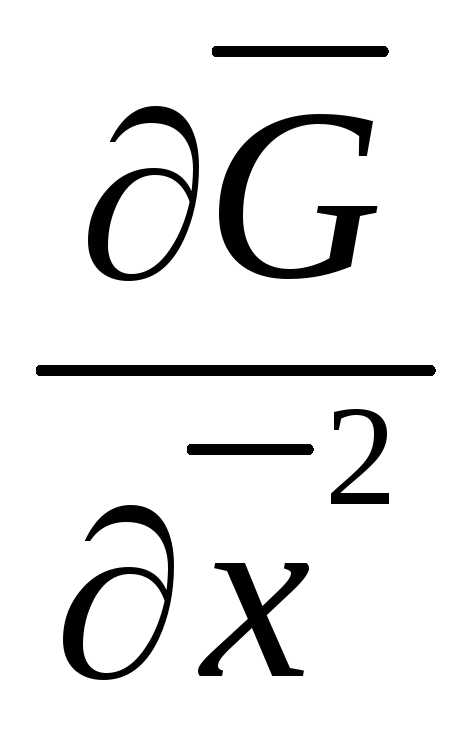 , по условию Якоби, невырожденная (mm) матрица. Тогда из (8)
, по условию Якоби, невырожденная (mm) матрица. Тогда из (8)
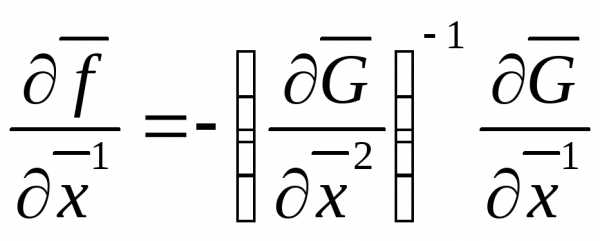
Условия (7) запишем в виде:
(9)
Очевидно, верно тождество (10)
Полагая 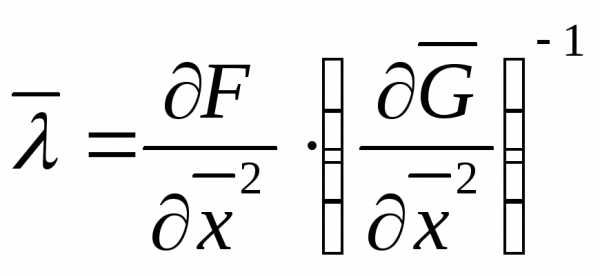 , из (9) и (10) получим аналог необходимых условий (7) экстремума в виде
, из (9) и (10) получим аналог необходимых условий (7) экстремума в виде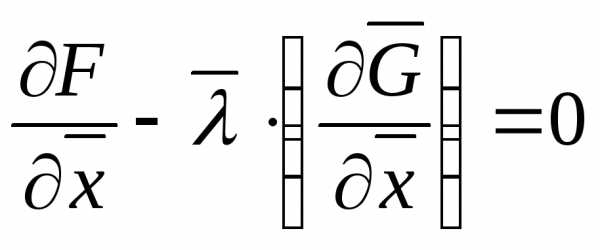 (11)
(11)
Полученный результат составляет основное содержание ММЛ.
Систему уравнений (11) можно получить формально, вводя в рассмотрение специально сконструированную выше функцию Лагранжа (5).
Действительно,
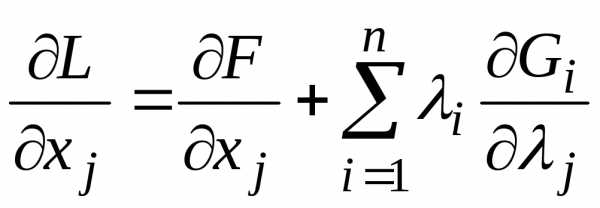 ,
, 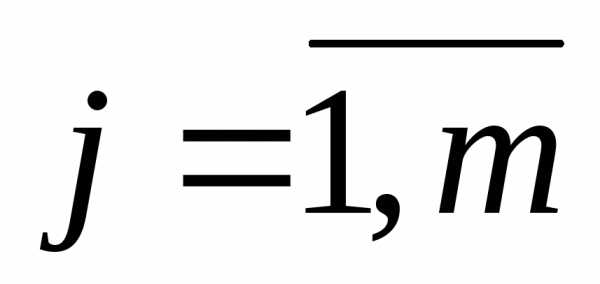 ;
;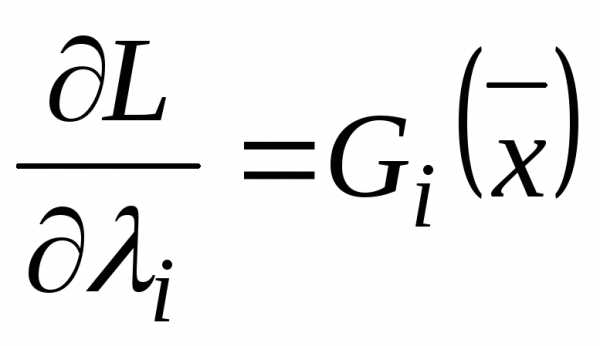 ,
,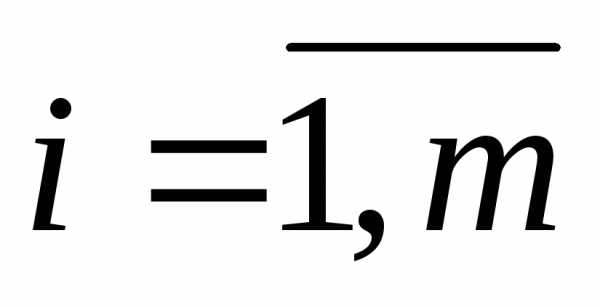 ,
,
и система уравнений (11) представлена в виде:
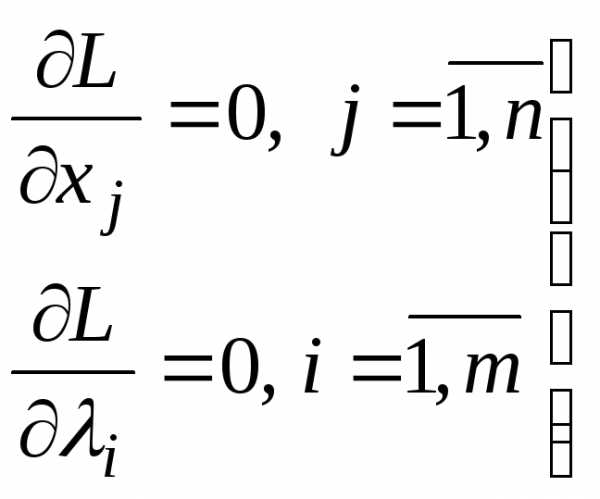 (12)
(12)
Система уравнений (12) представляет необходимое условие в классической задаче условной оптимизации.
Найденное в результате решения этой системы значение вектора 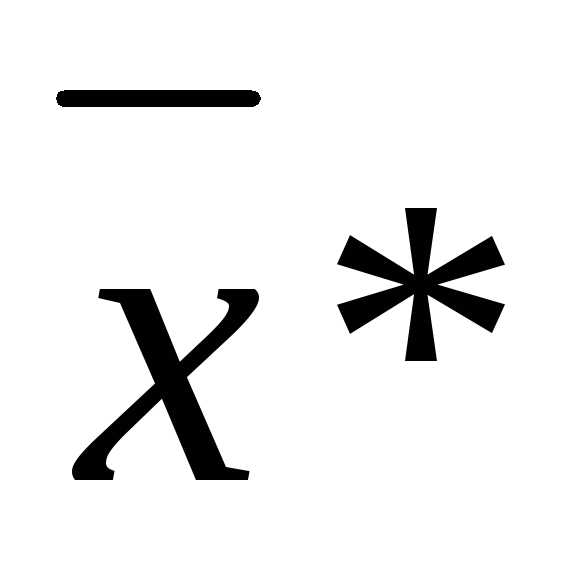 называетсяусловно-стационарной точкой.
называетсяусловно-стационарной точкой.
Для того, чтобы выяснить характер условно-стационарной точки 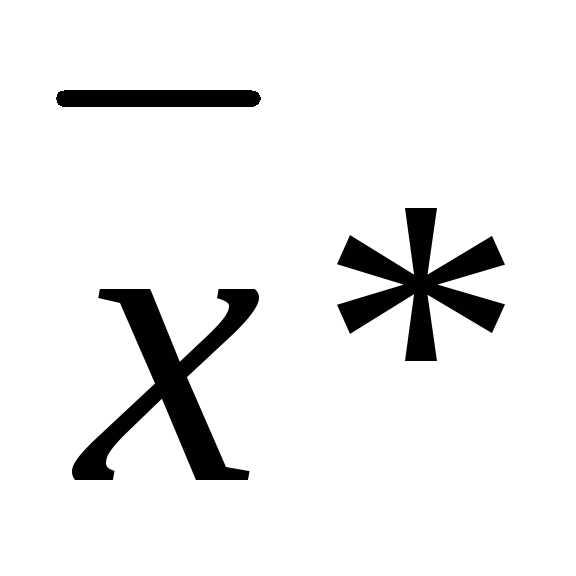 необходимо воспользоваться достаточными условиями.
необходимо воспользоваться достаточными условиями.
Достаточные условия в классической задаче условной оптимизации
Эти условия позволяют выяснить, является ли условно-стационарная точка 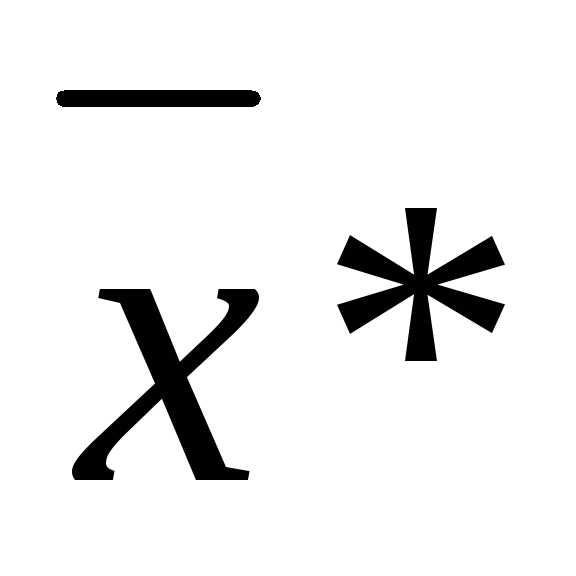 точкой локального условного минимума, или точкой локального условного максимума. Они получены подобно тому, как были получены достаточные условия в задаче на безусловный экстремум.
точкой локального условного минимума, или точкой локального условного максимума. Они получены подобно тому, как были получены достаточные условия в задаче на безусловный экстремум.
Результат следующий:
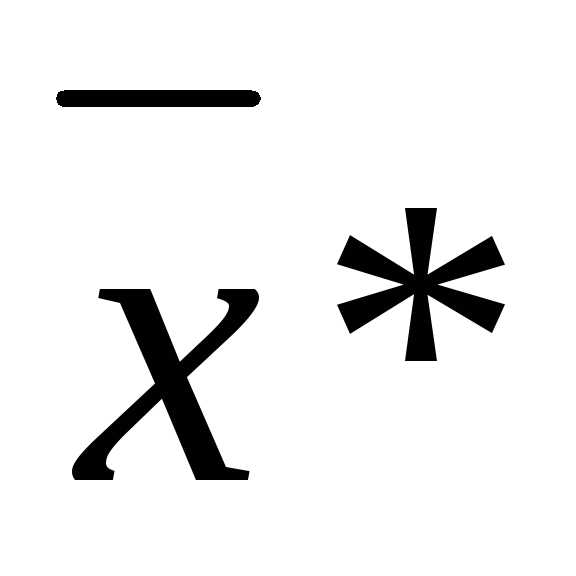 - точка локального условного минимума, если ;
- точка локального условного минимума, если ;
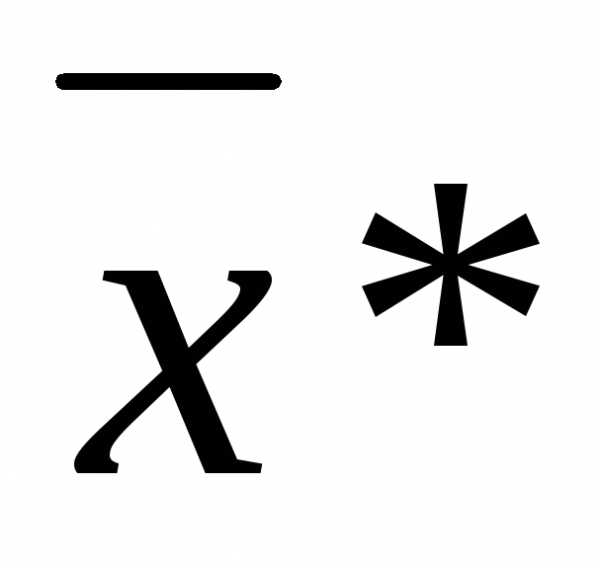
где 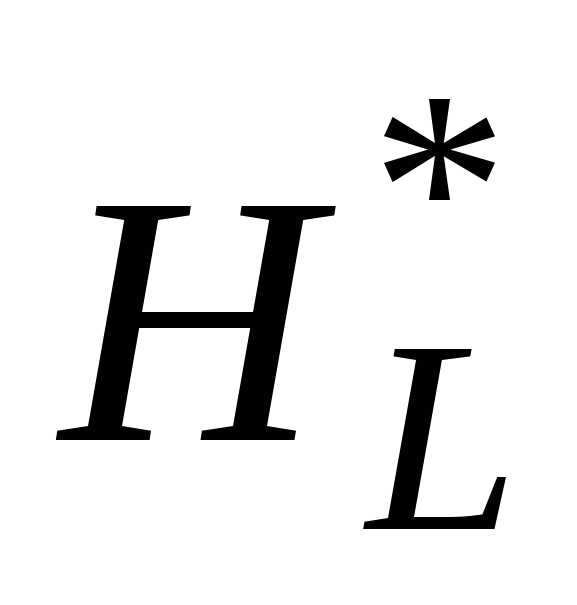 - матрица Гессе размерности
- матрица Гессе размерности с элементами
с элементами 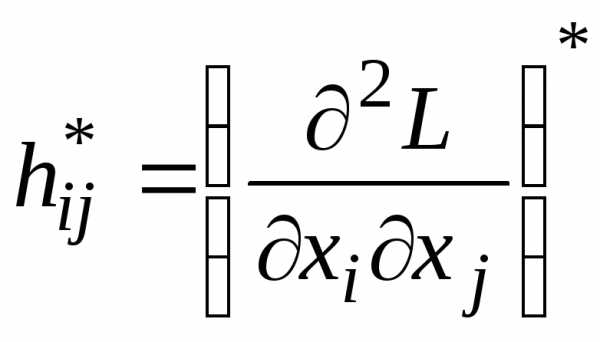 ,
,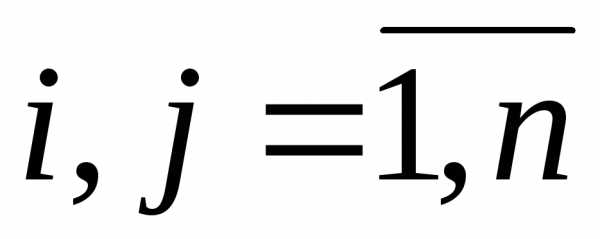 для функцииL(
для функцииL(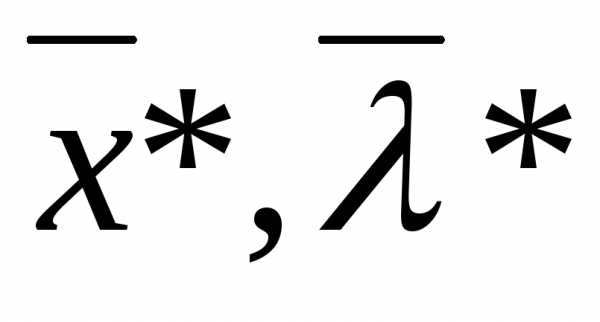 ) в стационарной точке
) в стационарной точке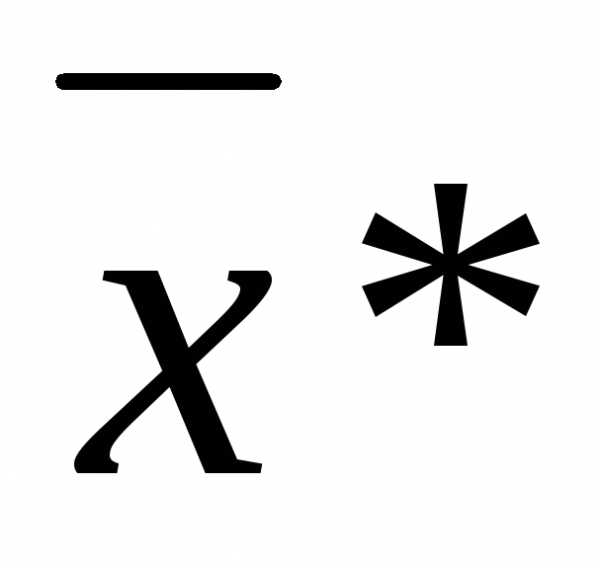 . Здесь производные отL берутся только по x*, а не по всем её аргументам.
. Здесь производные отL берутся только по x*, а не по всем её аргументам.
Размерность матрицы Гессе 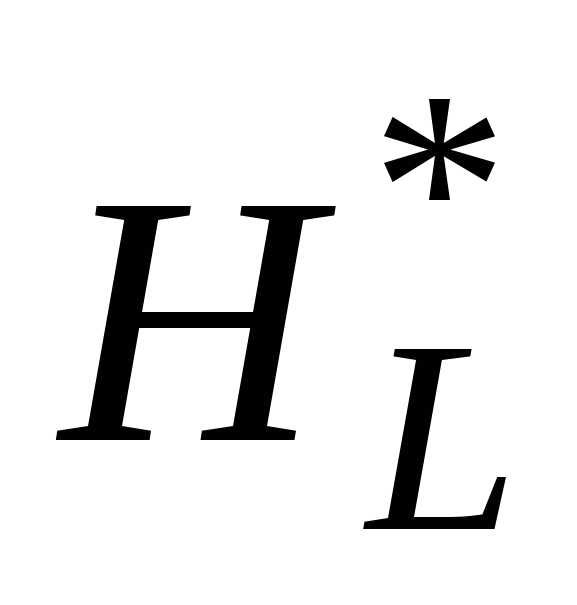 можно уменьшить, используя условие неравенства нулю якобиана:
можно уменьшить, используя условие неравенства нулю якобиана: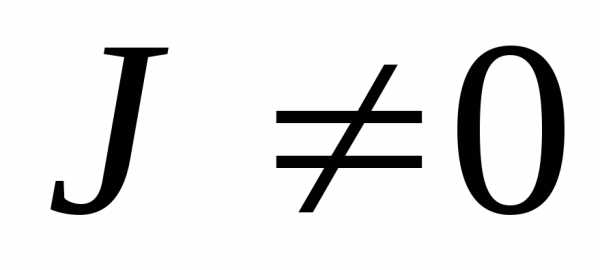 . При этом условии можно зависимые переменные (пусть здесь они стоят первыми)выразить через независимые переменные. Матрица Гессе дляLN, полученной в результате подстановки, будет иметь размерность , т.е. необходимо говорить о матрице
. При этом условии можно зависимые переменные (пусть здесь они стоят первыми)выразить через независимые переменные. Матрица Гессе дляLN, полученной в результате подстановки, будет иметь размерность , т.е. необходимо говорить о матрице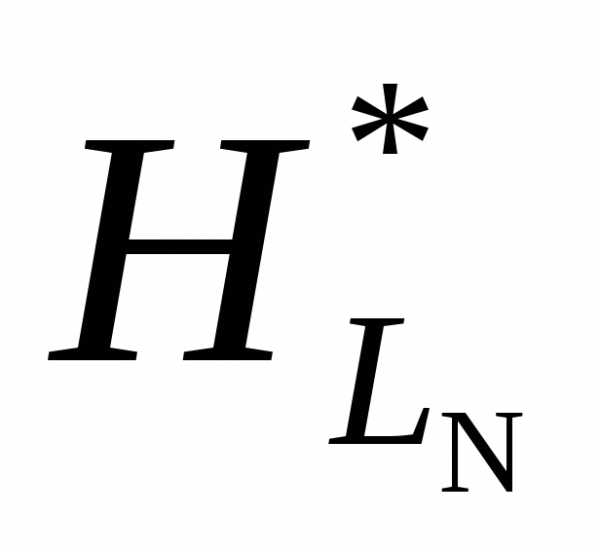 с элементами
с элементами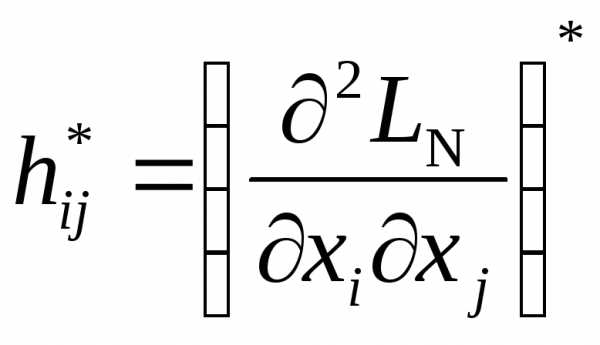 ,, тогда достаточные условия будут иметь вид:
,, тогда достаточные условия будут иметь вид:
, для точки локального условного минимума.
, для точки локального условного максимума.
studfiles.net
Метод оптимизации Лагранжа — контрольная работа
Федеральное государственное образовательное бюджетное учреждение
высшего профессионального образования
«Финансовый университет при Правительстве Российской Федерации»
(Финуниверситет)
Архангельский филиал Финуниверситета
Факультет «Финансово-кредитный»
Специальность «Бакалавр экономики»
КОНТРОЛЬНАЯ РАБОТА
по дисциплине
«Экономико-математические методы и прикладные модели».
студента | |
Номер личного дела | |
Курс | |
Поток | |
Форма обучения | периферия |
Руководитель | Доцент Тутыгин А.Г. |
Архангельск
2012
Задание 1.15
«Метод оптимизации Лагранжа».
Лагранжиа́н, функция Лагранжа динамической системы, названа в честь Жозефа Луи Лагранжа, является функцией обобщённых координат и описывает эволюцию системы. Например уравнения движения (для классической механики) в этом подходе получаются из принципа наименьшего действия, записываемого как:
где действие — функционал
а — обобщённые координаты (например, координаты частиц или полевые переменные), обозначает множество параметров системы, в случае классической механики — независимые пространственные координаты и время, а более широком еще электрические или другие физические параметры.
Уравнения, полученные посредством приравнивания нулю функциональной производной функционала по всем направлениям, идентичны обычным уравнениям Эйлера-Лагранжа. Динамические системы, чьи уравнения могут быть получены посредством принципа наименьшего действия для удобно выбранной функции Лагранжа, известны как лагранжевые динамические системы.
Метод множителей Лагранжа.
Рассмотрим общую задачу оптимизации, содержащую несколько ограничений в виде равенств: минимизировать f(x) при ограничениях gi (x)=0, j=1,...,k.
Эта задача в принципе может быть решена как задача безусловной оптимизации, полученная путем исключения из целевой функции k независимых переменных с помощью заданных равенств. Наличие ограничений в виде равенств фактически позволяет уменьшить размерность исходной задачи с n до n-k. В качестве иллюстрации рассмотрим следующий пример.
Минимизировать f(x)= x1 . x2 + x3 при ограничении:
g(x)= x1 +x 2+ x3 - 1 = 0.
Исключив переменную x3 с помощью уравнения g(x)=0, получим оптимизационную задачу с двумя переменными без ограничений:
f(x1 , x2) = x1 . x2 + (1 - x1 - x2) .
Метод исключения переменных применим лишь в тех случаях, когда уравнения, представляющие ограничения, можно разрешить относительно некоторого конкретного набора независимых переменных. При наличии большого числа ограничений в виде равенств, процесс исключения переменных становится весьма трудоемкой процедурой. Кроме того, возможны ситуации, когда уравнения не удается разрешать относительно переменной. В частности, если в приведенном примере ограничения g(x)=0 задать в виде g(x)= + + , то получить аналитическое выражение какой-либо из переменных через другие не представляется возможным. Таким образом, при решении оптимизационных задач, содержащих сложные ограничения в виде равенств, целесообразно использовать метод множителей Лагранжа. С помощью этого метода находят необходимые условия, позволяющие идентифицировать точки оптимума в задачах оптимизации с ограничением в виде равенств. При этом задача с ограничением в виде равенств, преобразуется в эквивалентную задачу безусловной оптимизации.
Рассмотрим задачу, имеющую несколько ограничений в виде равенств:
минимизировать f(x) при ограничениях (x)=0, при j=1,2,....,k.
В соответствии с методом множителей эта задача преобразуется в следующую задачу безусловной оптимизации:
минимизировать L(x)=f (x)- ,
где L(x, ) - функция Лагранжа, - множители Лагранжа.
На знак никаких требований не накладывается.
Приравниваем частные производные L(x, ) по x к нулю, получаем следующую систему n уравнений с n неизвестными:
... ,
Если найти решение приведенной выше системы в виде функций вектора оказывается затруднительным, то можно расширить систему путем включения в нее ограничений в виде равенств:
g1(x)=0,
g2(x)=0,
.........
gk(x)=0.
Решение расширенной системы, состоящей из n+k неизвестными, определяет стационарную точку функции L.
Пример.
Минимизировать при ограничении .
Соответствующая задача безусловной оптимизации записывается в следующем виде.
Минимизировать
Приравняв две компоненты градиента L к нулю, получим:
Поставив полученные значения в уравнение , получим, т.е. . Следовательно,
Задание 2.9
Условие.
При производстве двух видов продукции используется четыре типа ресурсов. Норма расхода ресурсов на производство единицы продукции, общий объем каждого ресурса отражены в таблице 1.
Таблица 1
|
Ресурсы | Норма затрат ресурсов на товары | Общее количество ресурсов | |
|
1-го вида |
2-го вида | ||
1 | 2 | 2 | 12 |
2 | 1 | 2 | 8 |
3 | 4 | 0 | 16 |
4 | 0 | 4 | 12 |
Прибыль от реализации одной единицы продукции первого вида составляет 2 ден. ед., второго вида – 3 ден. ед.
Задача состоит в формировании производственной программы выпуска продукции, обеспечивающей максимальную прибыль от её реализации.
Построить экономико-математическую модель задачи, дать необходимые комментарии к её элементам и получить решение графическим методом. Что произойдёт, если решить задачу на минимум и почему?
Решение.
Пусть необходимо изготовить единиц продукции первого вида и единиц продукции второго вида. Тогда прибыль, получаемая от реализации продукции, будет задаваться целевой функцией:
Ограничения по использованию ресурсов имеют вид:
Ресурс 1:
Ресурс 2:
Ресурс 3:
Ресурс 4:
Экономико-математическая модель задачи имеет вид:
Для получения решения графическим методом строим прямые:
Рис. 1
Область допустимых решений: ОАВС
Строим прямую:
И вектор (2;3)
Максимум ищем в точке области допустимых решений наиболее удаленной от прямой по направлению вектора . Он достигается либо в точке А, либо в точке В. Найдем их координаты:
Теперь найдем значение целевой функции в каждой точке:
Таким образом, максимум функции достигается в точке В.
Для того чтобы получить максимум прибыли 14 ден.ед. необходимо произвести 4 ед. продукции первого вида и 3 ед. продукции второго вида.
Если решать задачу на минимум, то необходимо найти такое решение, при котором предприятие получит наименьшую функцию. Минимум функции необходимо искать в точке области допустимых решений самой близкой к прямой по направлению вектора . Очевидно, что он достигается либо в точке 0 (0; 0). Тогда полученная прибыль будет равна 0.
Решение данной задачи линейного программирования на минимум лишено экономического смысла, так как выручку от реализации продукции стремятся получить наибольшей, а не наименьшей.
Задание 4.9
Условие.
Затраты на заказ партии посуды равны 200руб., затраты на хранение продукции 10 руб. в сутки, интенсивность потребления товара 5 шт.в день, цена товара-120 руб.за штуку. Определите оптимальный размер заказа, цену покупки и совокупные затраты на заказ и хранение. Постройте график циклов изменения запаса товара.
Решение.
Параметры:
М=10 руб./сут. (затраты на хранение),
К=200 руб. (затраты на заказ),
h=5шт/сут. (интенсивность потребления),
С=120 руб./шт. (цена товара)
Оптимальный размер заказа:
Qопт=√(2К*М/h)
Qопт =√(2*200*10/5)≈28,28 (шт.)
Длительность цикла:
Т=С/М
Т=120/10=12 (сут.)
Интенсивность потребления товара за цикл:
S=h*Т
S=5*12=60 (шт./цикл)
Цена покупки:
Р= Qопт*С
Р= 28,28*120=3393,6 (руб.)
Совокупные затраты:
Z(Q)=(K*M)/Q+(h(S-M)*Q)/2S+C*M=1329.64 руб.
При условии, что исходные данные мы оставим, а Qопт возьмем произвольно, график циклов изменения запаса товара (Рис.2) будет выглядеть так:
Рис.2
Список используемой литературы:
- ЭММ и ПМ. Практикум для студентов бакалавриата обучающихся на третьем курсе по направлениям 080500.62 «Менеджмент», 080100.62 «Экономика». – М.: ВЗФЭИ, 2011
- ЭММ и ПМ. Учеб. пособие для вузов/ В.В. Федосеев, А.Н. Гармаш, Д.М. Дайитбегов и др.; Под ред. В.В. Федосеева. – М.: ЮНИТИ, 1999. – 391с.
- http://www.rae.ru/monographs/57-2325
student.zoomru.ru
Лагранжа метод множителей оптимизация - Справочник химика 21
Недостатком метода множителей Лагранжа является введение дополнительных переменных, которые должны быть исключены с помощью дополнительных уравнений. Если учесть, что при решении задачи комплексной оптимизации параметров адсорбционных установок число уравнений связи между оптимизируемыми параметрами велико, то станет очевидной важность этого недостатка. Кроме отмеченного для метода множителей [c.124] Рассмотренные в настоящей главе примеры использования метода множителей Лагранжа для решения задач оптимизации с ограничениями типа равенств или задач, сводимых к этому классу, показывают, что данный метод представляет собой достаточно удобный математический аппарат, позволяющий ставить и решать довольно сложные оптимальные задачи для процессов с сосредоточенными и распределенными параметрами. Как отмечено ниже (см. главу VII), метод множителей Лагранжа при отсутствии ограничений на переменные процесса типа неравенств приводит к уравнениям, которые иногда совпадают с основными уравнениями методов, специально созданных для решения широкого класса задач оптимизации, таких, например, как принцип максимума. [c.200]Для сложных реальных ситуаций метод множителей Лагранжа позволяет лишь сформулировать аналитически задачу оптимизации, а для нахождения оптимальных значений параметров необходимо применение поисковых методов. [c.178]
Аналитический метод оптимизации предусматривает аналитическое задание соответствующих функций и определение производных от них. На значения переменных, однако, могут накладываться ограничения, связанные с конструкцией, характером работы, стоимостью и т. п. В случае наличия таких ограничений, касающихся переменных величин, полезным может оказаться хорошо известный в математике метод множителей Лагранжа, [c.362]
В простейших случаях, когда целевая функция задана аналитически, используют классические методы нахождения экстремума методами дифференциального исчисления. При наличии ограничений типа равенств, наложенных на независимые переменные, используют метод множителей Лагранжа. В более сложных случаях, когда критерий оптимальности представлен в виде функционалов, используют методы вариационного исчисления-, при оптимизации процессов, описываемых системами дифференциальных уравнений, применяют принцип максимума Понтрягина. Используют также динамическое, линейное программирование и другие методы оптимизации. [c.38]
В настоящее время для решения оптимальных задач применяют в основном следующие методы 1) исследование функций классического анализа 2) метод множителей Лагранжа 3) вариационное исчисление 4) динамическое программирование 5) принцип максимума 6) линейное программирование. Однако общего метода, пригодного для решения всех без исключения задач, возникающих на практике, нет. Вместе с тем каждый из перечисленных выше методов имеет предпочтительные области применения. Так, метод динамического программирования наилучшим образом приспособлен для решения задач оптимизации многостадийных процессов. Такие задачи чаще всего возникают при проектировании процессов ООС и СК, осуществляемых либо в многоступенчатых реакторах, либо в каскадах реакторов. Поэтому мы в сжатой форме рассмотрим основные положения метода динамического программирования. [c.191]
Решение этой задачи можно провести непосредственно по (2.49), но при этом следует иметь в виду, что вариация величины, оптимум которой ищется, приводит к изменению значений Яei потоков, т. е. необходимо совместное решение (2.49) и (2.25). Значительно проще можно решить задачу оптимизации методом множителей Лагранжа [33], если исследовать на экстремум функцию [c.43]
Для нахождения решения по модели с ограничениями в виде равенств и небольшого числа управляемых переменных может быть использовано дифференциальное исчисление, например, метод множителей Лагранжа. В других случаях применяют методы зкспериментальной оптимизации метод случайного поиска, метод многофакторного анализа, одношаговый метод и метод наискорейшего спуска. [c.158]
Для построения декомпозиционных методов оптимизации мы используем методы множителей Лагранжа и штрафов . [c.228]
Пример. Проиллюстрируем метод множителей Лагранжа на примере простой схемы, изображенной на рис. 72. Положим, все входные переменные 1-го блока варьируемыми, а все выходные переменные 4-го блока свободными. Критерий оптимизации для этой схемы имеет вид [c.181]
На 1-ом уровне при использовании метода множителей Лагранжа большинство блоков приходится оптимизировать при условии, что их выходные переменные являются свободными, в то время как в методе закрепления входные и выходные переменные блоков считаются фиксированными, что усложняет оптимизацию. [c.189]
При оптимизации А -го блока методом закрепления необходимо искать только максимумы функции В случае же применения метода множителей Лагранжа ищутся экстремальные точки функции что, конечно, значительно труднее. [c.189]
Без существенных усложнений метод множителей Лагранжа можно применить для оптимизации процессов со сложной топологической структурой, т. е. не только многостадийных, а также распространить на процессы, математические описания которых, наряду с конечными уравнениями, содержат и дифференциальные. Разумеется, что во всех перечисленных случаях метод множителей Лагранжа дает лишь самые общие соотношения оптимальности, и наиболее трудной частью решения задачи становится решение получаемых конечных и дифференциальных уравнений для переменных процесса и вспомогательных переменных. Однако сейчас уже разработаны в достаточной мере удобные приемы и алгоритмы решения [4], позволяющие, как правило, получать конечные результаты на вычислительных машинах для процессов высокой степени сложности. [c.201]
I. Группа аналитических методов оптимизации объединяет аналитический поиск экстремума функций, заданных без ограничений, метод множителей Лагранжа, вариационные методы и принцип максимума. [c.247]
Прежде чем перейти к изложению отдельных задач оптимального проектирования, необходимо хотя бы коротко коснуться основных. математических методов оптимизации. К классическим методам решения экстремальных задач относятся методы дифференциального и вариационного исчислений. С помощью дифференциального исчисления можно решать дискретные задачи (т. е. задачи с конечным числом параметров) как при отсутствии ограничений, так и при наличии ограничений типа равенств (метод множителей Лагранжа) . [c.129]
Отметим еще здесь связь цен хР и ор с множителями Лагранжа (см. стр. 87). Рассмотрим снова задачу оптимизации сложной схемы. Критерий оптимизации пусть имеет вид (11,15). Между входными и выходными переменными различных блоков должны при этом выполняться соотношения (1,11). Используя метод множителей Лагранжа, получим, что в данном случае необходимо искать минимум функции [c.300]
Иногда при использовании этого метода не учитывается одно важное обстоятельство. Можно показать, что этот метод эквивалентен описанному здесь методу, использующему множители Лагранжа, которым при этом соответствуют промежуточные цены. Как было указано, при фиксированных Хг надо искать стационарные точки функции Лагранжа. Отсюда следует, что в данном декомпозиционном методе при оптимизации каждого блока следует искать не минимум функционала, а стационарную точку. В противном случае может быть получен неправильный результат. [c.377]
Задачи оптимизации могут быть решены при использовании метода множителей Лагранжа. Рассмотрим использование этого метода на примере. [c.72]
С помощью метода множителей Лагранжа и путем введения вспомогательных переменных [163], необходимых для учета ограничений типа неравенств на независимые переменные, задачу оптимизации представим в виде [c.117]
Следует также отметить, что множители Лагранжа часто применяют и в других методах оптимизации в качестве вспомогательного средства, позволяющего упростить решение более сложных задач (подробно см. главы, посвященные изложению вариационного исчисления и динамического программирования). [c.139]
Здесь индекс О относится к условиям на входе в слой-Сформулируем критерий оптимизации. Разумеется, можно максимизировать разность X — Хо, но нужно учитывать необходимость ограничения общего объема (или условного времени контакта т. ). Тогда целевую функцию можно записать по методу Лагранжа-Можно однако придать и физический смысл множителю Лагранжа. Если б — коэффициент, учитывающий затраты на единицу времени контакта, то критерий оптимизации имеет вид [c.210]
Для решения указанной задачи оптимизации можно применить метод неопределенных множителей Лагранжа. [c.108]
Метод неопределенных множителей Лагранжа, который подробно рассмотрен в разделе 8.2.2, прост и удобен для решения задач оптимизации резервирования ХТС с использованием ЭВх 1. Однако он имеет следующие существенные недостатки. Во-первых, в процессе решения как прямой, так и обратной задачи оптимизации резервирования могут получиться нецелочисленные значения Х1. Поэтому возникает необходимость округления этих значений до ближайших целых чисел. При таком округлении возможны многочисленные варианты составов поэлементного резерва ХТС, перебор которых для выявления наилучшего варианта оказывается трудоемким процессом, требующим больших затрат времени [126, 237]. [c.205]
Для решения задачи I уровня оптимизации—для определения оптимального варианта поэлементного резервирования — используется метод неопределенных множителей Лагранжа, отличающийся от других возможных методов (наискорейшего спуска, динамического программирования и других) сравнительной простотой реализации на ЭВМ. Для решения задачи II уровня оптимизации— выбора оптимальной величины надежности БТС — применяется метод сканирования по ряду предварительно задаваемых значений надежности системы. Математической моделью, устанавливающей влияние изменений в технологической топологии БТС за счет ввода резервных элементов на величину ее надежности, является параметрический граф надежности (п. г. н.) [c.174]
Основная идея в применении метода неопределенных множителей для оптимизации рассмотренного выше многостадийного процесса состоит в том, что при решении задачи оптимизации соотношения (IV, 90), характеризующие связь входных и выходных параметров и управляющих воздействий на всех стадиях процесса, принимаются как ограничивающие условия, имеющие вид равенств, наложенные на переменные процесса д , часть из которых входит в выражение критерия оптимальности (IV, 88). Это, в свою очередь, позволяет использовать для решения оптимальной задачи математический аппарат метода неопределенных множителей Лагранжа (см. стр. 148). [c.165]
Определим оптимальные мощности перемешивания для получения однородного кристаллического продукта с заданным средним размером в каскаде кристаллизаторов типа MSMPR. Задача нахождения оптимальных мощностей перемешивания для получения однородного кристаллического продукта с заданным средним размером была решена авторами совместно с Ле Суан Хаем с помощью метода множителей Лагранжа. Критерием оптимизации выбрана дисперсия размеров (объемов) кристаллов относительно среднего размера (объема), которая служит оценкой однородности, [c.351]
Итак, общий алгоритм оптимизации схемы на базе метода множителей Лагранжа выглядит следующим образом. Вначале задаются какими-то значениями В соответствии с формулой (VIII,10) [c.179]
Остановимся теперь на экономической интерпретации метода множителей Лагранжа. Для этого обратимся еще раз к критерию [см. выражение (VIII,7)], применяемому при оптимизации /с-го блока. Если формально считать (х[c.179]
Пусть А ЫЙ блок включает только один аппарат, модель которого имеет вид формулы (VIII,1). Пусть также в данном блоке величины л и г/,- приняли соответственно значения и г/ (Z — номер итерации в центральном алгоритме). Оптимизация к-го блока при этих значениях входных и выходных переменных, которая проведена с использованием метода множителей Лагранжа, дает искомые производные вида (V,71) и (V,73). Ограничения типа равенств (V,66) в данном случае будут иметь вид уравнения (VHI,29). Роль констант 6,- в соотношениях (VHI,29) играют величины а роль констант а ,. . ., — величины Отсюда соотноше- [c.186]
Бертсекас Д. Условная оптимизация и методы множителей Лагранжа Пер. с англ. М. Радио и связь, 1987. 399 с. [c.557]
Вкратце идея такова вычислительная машина состоит из большого числа параллельно работающих автоматов - нейронов, связанных между собой. Обучение состоит в оптимизации связей градиентным методом или его модификациями. Сдвиги за шаг обучения вычисляются самой сетью автоматов в акте двойственного функционирования (также в параллельном режиме). Обыкновенная двойственность (метод множителей Лагранжа) удачно ложится на структуру параллельных самооптимизирующихся сетей. В Красноярске такие сети существуют в виде программных имитаторов на обычных ЭВМ, решают при этом задачу коммивояжера, играют в простые игры, распознают образы. Машины второго царства - это еще не техносфера № 2, но они могут породить ее. [c.164]
Метод максимального элемента имеет преимущества по сравнению с другими методами оптимизации, применяемыми для определения оптимального состава резерва ХТС (например, метод неопределенных множителей Лагранжа, градиентный метод и др.), так как позволяет декомпозировать задачу поиска опти- [c.228]
Функция желательности. Задачу оптимизации процессов, ха-ракгеризующихся несколькими откликами, обычно сводят к задаче оптимизации по одному критерию с ограничениями в виде равенств или неравенств. В зависимости от вида поверхности отклика и ха-ракгера ограничений для оптимизации предлагается использовать методы неопределенных множителей Лагранжа, линейного и нелинейного программирования, ридж-анализ [10] и др. К недостаткам этих способов решения задачи оптимизации следует отнести вычислительные трудности. В частности, при описании поверхности отклика полиномами второго порядка решение задачи на условный экстремум с применением неопределенных множителей Лагранжа приводит к необходимости решать систему нелинейных уравнений. Поэтому одним из наиболее удачных способов решения задачи оптимизации процессов с большим количеством откликов является использование предложенной Харрингтоном [23] в качестве обобщенного критерия оптимизации так называемой обобщенной функции желательности О. Для построения обобщенной функции желательности О предлагается преобразовать измеренные значения от- [c.207]
Не вдаваясь в теоретические основы метода, ог етим, что воли функция оптимизации при некоторых оптимальных значениях пара> метров стремиться к экстремуму, то очевидно, что добавление к функции оптимизации нулевых ( по 5.19 ) функций ограничения на изменит значения критерия оптимальности в экстремальной точке. Координаты экстремума находется из условия равенства нулю первых производных функции Лагранжа по параметрам процесса и неопределенным множителям [c.55]
chem21.info
Методы одномерной оптимизации. Методы одномерной оптимизации на основе преобразования задач. Поисковые методы одномерной оптимизации, страница 4
В этом случае число связей (5.14) m меньше размерности n вектора искомых переменных хί. Требования m<n связано с тем, что в противном случае множество допустимых решений задачи представляет собой либо набор изолированных точек, являющихся корнями системы уравнений (5.14), либо вообще пусто. При m=n, если система (5.14) совместна, может оказаться, что система (2.14) имеет единственное решение и задача оптимизации не имеет смысла.
Если ранг матрицы Якоби равен m, т.е.
, (2.15)
то m уравнений связи можно в простейших случаях разрешить относительно m переменных (например, х1, х2, …, хm), выразив их через n-m остальных. Подстановка их в целевую функцию приводит к задаче на безусловный экстремум функции n-m переменных. Условие (2.12) является условием регулярности типа линейной независимости для задач на условный экстремум.
Выразим х1, х2, …, хm через остальные n-m переменных
(2.16)
Подставляя (2.16) в (2.10), получаем задачу безусловной оптимизации без ограничений:
(2.17)
Решая задачу (2.17) находим и подставляя их в (2.16), находим оптимальные значения остальных переменных: х*1, х*2, …, х*m
При наличии нескольких ограничений в виде нелинейных уравнений практически затруднено и даже невыполнимо решение системы (2.14) относительно m переменных с целью их выражения через остальные n-m переменных и исключение таким образом ограничивающие условия. Поэтому данный метод имеет ограниченное применение и уступает по эффективности методам Лагранжа и штрафных функций.
2.3 Метод множителей Лагранжа
Рассмотрим задачу условной оптимизации с ограничением в виде равенств
(2.18)
при условии
(2.19)
Предположим, что условие регулярности (2.12) выполняется, т.е.
Метод множителей Лагранжа заключается в следующем: составляют вспомогательную функцию, в которую входит уравнение связей (2.19)
(2.20)
Функция L называется нормальной функцией Лагранжа, а коэффициент λ – неопределённым множителем Лагранжа (λ пока неизвестная величина).
Если в точке функция достигает максимума (или минимума) при условии (2.19), то функция так же достигает минимума (или максимума) по х в этой точке. При этом по переменной λ функция достигает максимума (или минимума), т.е. точка является Седловой точкой функции .
Поэтому для решения задачи оптимизации определяем точку, в которой частные произведения равны нулю:
(2.21)
Решив систему уравнений (2.21), определяем
, (2.22)
зависящие от неопределённого множителя λ. Чтобы определить значение λ, найдём и приравняем нулю частную производную по λ:
(2.23)
Подставим выражение (2.22) в уравнение (2.23)
(2.24)
Отсюда определяем λ и подставляем его в выражение (2.22), окончательно находим экстремальную точку. Подставляя в (2.18), можно вычислить экстремальное значение критериев.
Если имеется несколько ограничений в виде равенств, то каждому из этих ограничений соответствует свой множитель λі Лагранжа. Так, для решения задачи
(2.25)
при условиях
, (2.26)
при выполнении условия нормальная функция Лагранжа имеет вид
(2.27)
Для определения условного экстремума составляем систему уравнений
(2.28)
Из (m+n) уравнений (2.28) определяем n переменных , и m множителей λj , .
Если условия (2.26) таковы, что не выполняется условие регулярности (2.12), то правило множителей с нормальной функцией Лагранжа в этом случае не справедливо. Для перехода к задаче на безусловный экстремум составляют функцию Лагранжа вида
, (2.29)
где, – неопределённые множители Лагранжа, и решают задачу таким же образом, как и при составлении нормальной функции Лагранжа.
Следует особо отметить, что метод множителей Лагранжа позволяет найти лишь необходимые условия существования условного экстремума для конкретных функций, имеющих к тому же непрерывные производные. Полученные значения, , могут и не давать экстремального значения функции, что точно так же как и в задачах на безусловный экстремум, рассмотренный выше. Поэтому найденный при решении системы уравнений (2.28) значение переменных , , должны быть проверенны на экстремум с помощью анализа производных более высокого порядка или какими либо другими методами.
Часто в примерах оптимальных задач анализ условного экстремума требует довольно сложных выкладок при исследовании высших производных. Поэтому по возможности характер найденного экстремума определяется исходя из физического смысла решаемой задачи.
2.4 Пример применения метода множителей Лагранжа
Оптимизация распределения нагрузок между параллельно работающими агрегатами.
В пищевой, химической промышленности, энергетике и других отраслях часто используются системы, состоящие из параллельно включённых объектов. Это связанно с расширением производства путём ввода дополнительных мощностей. Кроме того, при этом повышается надёжность системы, так как вывод из строя части объектов не делает её неработоспособной; при переменных нагрузках отключение части объектов позволяет оставшимся работать в более экономичном режиме.
Система из n таких параллельных объектов изображена на рис. 2.1
Сделаем два важных допущения:
1. Состав работающих объектов определён, т.е. каждый объект включён и должен потреблять сырья не менее хi min.
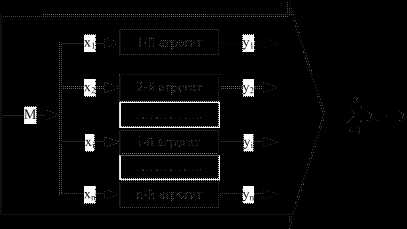
Рисунок 2.1 – система параллельных объектов
2. Нагрузочные характеристики yi = ƒi(xi) – выпуклые функции. Возможный вид такой характеристики показан на рисунке 5.2
Рисунок 2.2 Нагрузочная характеристика объекта
Сформулируем задачу об оптимальном распределении нагрузок как задачу о таком выборе расходов сырья xi на каждый объект, чтобы общая производительность у всех n объектов была максимальна при заданном расходе сырья на всю систему М. При этом будут предлагать расходы сырья скалярными величинами, т.е. не учитывать, например его состав.
vunivere.ru
1.5.3. Метод неопределенных множителей Лагранжа
Решение задачи лежит там, где 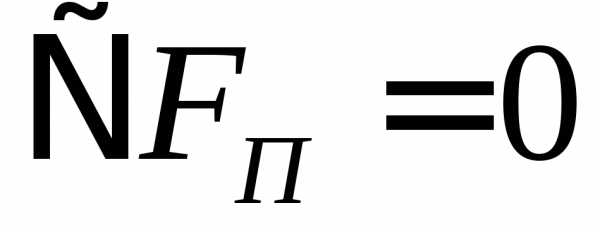 , то есть условием минимума является равенство:
, то есть условием минимума является равенство:
Введем обозначение:
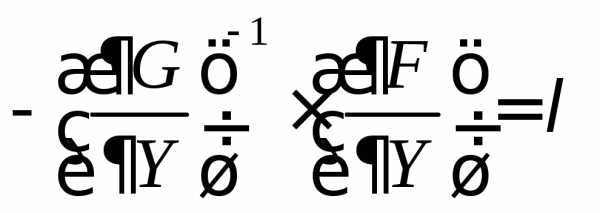 ,
,
где = {1,…,m} образуют вектор некоторых множителей.
С учетом этого условие минимума можно представить в виде следующей системы:
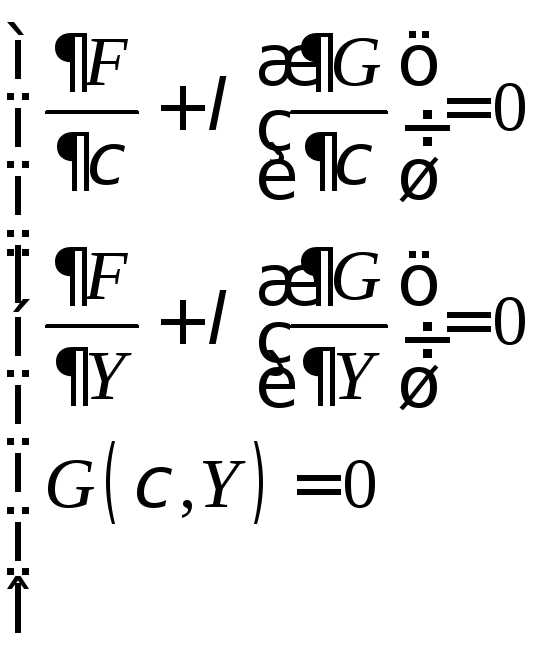
Система (2) тождественна условию 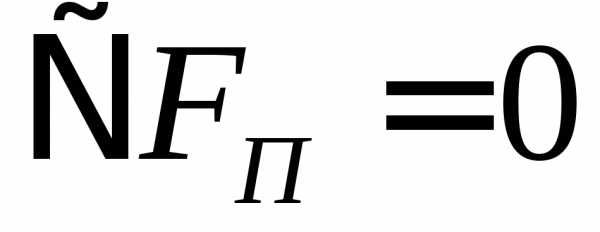 и определяет решение задачи. Эту систему можно составить формально как условие минимума некоторой функции Лагранжа L(,Y,)
и определяет решение задачи. Эту систему можно составить формально как условие минимума некоторой функции Лагранжа L(,Y,)
L(,Y,) = F(,Y) + G(,Y)min.
Функцию Лагранжа можно составить, не разделяя X на зависимые и независимые составляющие:
L(Х,) = F(Х) + G(Х)= F(Х) + Σjgj (X) min.
.
Условие минимума:
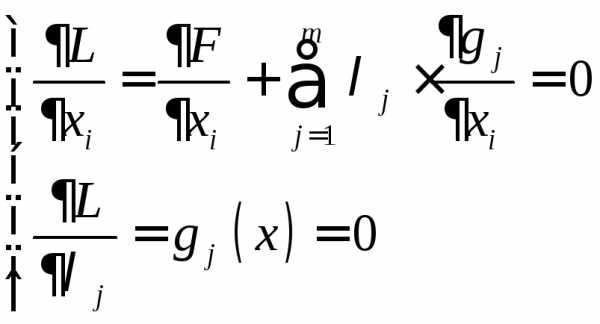 .
.
Эта система из (m + n) уравнений позволяет найти все неизвестные xi и неопределенные множители j.
1.6. Оптимизация с учетом ограничений в форме неравенств
Общая задача нелинейного программирования содержит ограничения в форме неравенств
F(Х) min;
G(Х) ≥ 0.
Учет таких ограничений является наиболее сложным. Простейший подход, заключающийся в последовательном решении задачи без учета ограничений с последующей проверкой ограничений и закреплении вышедших за допустимую область переменных на границе, далеко не всегда дает правильное решение.
На рис.1.12 показан такой случай F(x) min; g1(x) ≥ 0; g2(x) ≥ 0.
Решение без учета ограничений определяет точку A(x`1,x`2), в которой нарушены оба ограничения
g1(x) = x1max – x1 < 0;
g2(x) = x2max – x2 < 0;
Закрепление переменных на границе определяет точку В предполагаемого решения, для которой x1ОПТ = x1max, x2ОПТ = x2max.
Фактически же решение лежит в точке C. В этой точке только x2ОПТ лежит на границе и ограничение g2(x) называют активным. Переменная x1ОПТ < x1max, и ограничение g1(x) называют пассивным.
Таким образом, при решении могут возникнуть самые разные ситуации, в которых надо определять тип ограничений (активные или пассивные). При учете активных ограничений нужно использовать проекции градиента, если антиградиент выводит за допустимую область и т.п.
Поэтому для учета ограничений в форме неравенств существует много методов. Большинство основано на идее проектирования градиента и называются проективными. В последнее время начинают использовать методы, основанные на линеаризации, т.е. замене нелинейностей в исходной точке Х(0)разложением в ряд Тейлора с учетом первых двух членов разложения, линеаризации задачи и поиска минимума симплекс- методом.
Критерием окончания такого итерационного процесса является небольшая разница между значениями, полученными на смежных итерациях.
Наиболее простой метод учета ограничений – метод штрафных функций. Здесь допускается любое значение неизвестных, но при выходе за допустимую область к F(X) добавляется штрафная функция. Величина штрафа зависит от степени нарушения ограничений.
Формируемая функция имеет вид ,
где ;
.
На рис. 1.13 показана оптимизация для функции с одной переменной:
f(x)min;
g1(x) = xmax – x 0;
g2(x) = x – xmax 0;
Решение по методу всегда лежит за допустимой областью, но вблизи границы.
Жесткость ограничения зависит от величины коэффициента штрафа kШ. Сочетание метода штрафных функций с методами нулевого порядка позволяет строить надежные алгоритмы решения общей задачи нелинейного программирования.
studfiles.net
Оптимизация модели энергосистемы методом множителей Лагранжа. Основные выражения.
Порядок построения расчетной модели ТЭС. Основные выражения.
В рассмотренной методике до формулы (1) вставляются характерис-тики работающих турбин:
Gпараi = Spl_6(Wi, Qi),
где Gпара =Σ Gпараi
при условии: WТЭЦ =Σ Wi
QТЭЦ =Σ Qi
А сама формула (1) «переворачивается» и дополняется формулой (2):
(9)
Получаем ожидаемую (прогнозируемую) величину сожженного топлива.
Потери электроэнергии на привод питательных, циркуляционных, теплофикационных насосов и вентиляционных установок тяги и дутья (основных потребителей электроэнергии на ТЭС) вычисляем также по нормативным характеристикам, представленным в модели в виде кубических сплайнов.
Порядок построения и оптимизации насосной станции. Основные выражения.
Обычно любая насосная станция представляет собой несколько центро-бежных (или диагональных) насосов, работающих на общий коллектор.
Расход воды из коллектора регулируется дроссельными клапанами потребителей. Сами насосы регуляторов расхода не имеют.
Поэтому будет справедлива система n+1 уравнений, содержащая n+1 неизвестных - Q1, Q2, …, Qn, Н:
H = Spl_4(Q1),
H = Spl_4(Q2),
… (10)
H = Spl_4(Qn),
Q = Σ Qn
После решения этой системы уравнений определяется величина требуемой электрической мощности насосной станции:
W1 = Spl_4(Q1),
W2 = Spl_4(Q2),
… (11)
Wn = Spl_4(Qn),
W = Σ Wn.
Согласно такой схеме включения для некоторых насосов расход Q может быть предельным (нулевым или даже отрицательным).
Оптимизация модели энергосистемы методом множителей Лагранжа. Основные выражения.
Оптимизация параметров работы тепловых электростанций (ТЭС) и энергосистемы (ЭС) в целом позволяют обеспечить существенную экономию топлива практически без дополнительных капитальных вложений, что является весьма актуальным.
Для каждой ТЭС имеется своя зависимость расхода топлива от выраба-тываемой активной мощности Bi = f(Pген,i), которая называется расходной характеристикой ТЭС.
В качестве топлива для ТЭС может использоваться уголь, газ, щепа и другие виды органического топлива, поэтому при определении расходной характеристики ТЭС в энергетике РБ и РФ используется понятие «условного топлива», равного по теплотворной способности 1 килограмму каменного угля или 29,3 МДж (7000 Ккал).
Если бы расходные характеристики были линейны и одинаковы для всех станций, то суммарный расход условного топлива не зависел бы от распределения активных мощностей между ТЭС. В действительности эти характеристики нелинейны и различны. Поэтому изменение распределения генерируемых активных мощностей между ТЭС в энергосистеме приводит и к изменению расхода условного топлива.
Существует оптимальное распределение активных мощностей, соответствующее минимуму расхода условного топлива при выработке заданной активной мощности.
При оптимизации режимов электроэнергетических систем наибольшее распространение получили метод множителей Лагранжа и градиентные методы.
Также используется метод динамического программирования (метод Беллмана), метод эквивалентирования групп ТЭС с условно одинаковыми расходными характеристиками, и некоторые другие. В настоящее время разрабатываются также альтернативные алгоритмы оптимизации режимов, в частности, с использованием методов нечеткой логики и эволюционных алгоритмов.
Эти методы основаны на предположении, что расходные характеристики ТЭС имеют определенные аналитические выражения и минимальное количество ограничений, что вполне приемлемо, например, для ТЭС с конденсационными турбинами.
В качестве критерия оптимизации выберем расход условного топлива на выработку электроэнергии в энергосистеме регионального уровня, например, уровня Витебскэнерго.
Соответствующая целевая функция оптимизации имеет вид:
, (12)
где Вi – расход условного топлива на i–й ТЭС на выработку активной электрической мощности,
под (m+1)-й ТЭС понимается балансирующий узел энергосистемы, расходная характеристика которого известна.
В энергосистеме РУП Витебскэнерго и Белорусской энергосистеме в целом таким балансирующим узлом является Лукомльская ГРЭС, имеющая эквивалентную характеристику замещающей конденсационной электростанции 0,320 кг/кВтч.
Баланс активных мощностей в энергосистеме можно записать:
13
где Pген,i – активная мощность, генерируемая i-й ТЭС в энергосистему;
Pн – активная нагрузка в электросети;
PΣ – суммарные потери активной мощности в сети.
Уравнение оптимизации в виде функции Лагранжа будет иметь вид:
14
Активная мощность нагрузок считается постоянной величиной, а потери – функцией генерируемых мощностей, за исключением мощности балансирую-щего узла.
Так как выражение для баланса мощности равно нулю (13), то минимумы функции Лагранжа (14) будут совпадать с минимумами целевой функции (12).
Для поиска глобального оптимума продифференцируем функцию Лагранжа по переменным Рген,i и приравняем производные нулю.
Получим систему уравнений:
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
Метод множителей Лагранжа.
Применяется для нахождения точки локального минимума для точек исходной задачи . Экстремальными точками локального минимума являются седловые.
Пример:
Найти расстояние от точки до прямой в 3-х мерном пространстве.
Плоскость :
y
Пересечение плоскостей – линия
5 Условий дают систему линейных уравнений Нелинейное программирование (нлп).
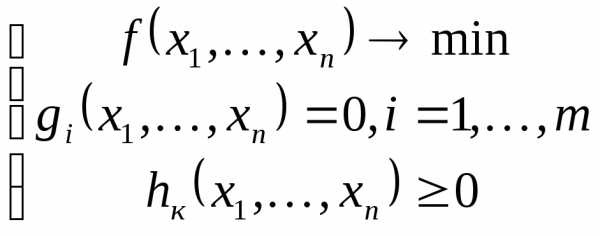
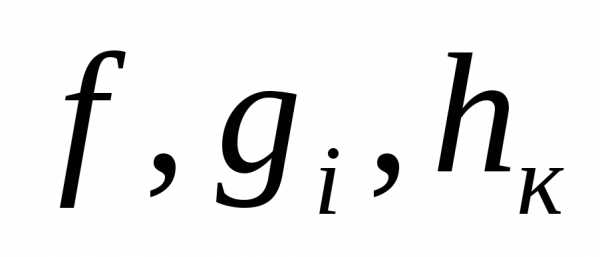 - заданные функции нелинейные
- заданные функции нелинейные
НЛП 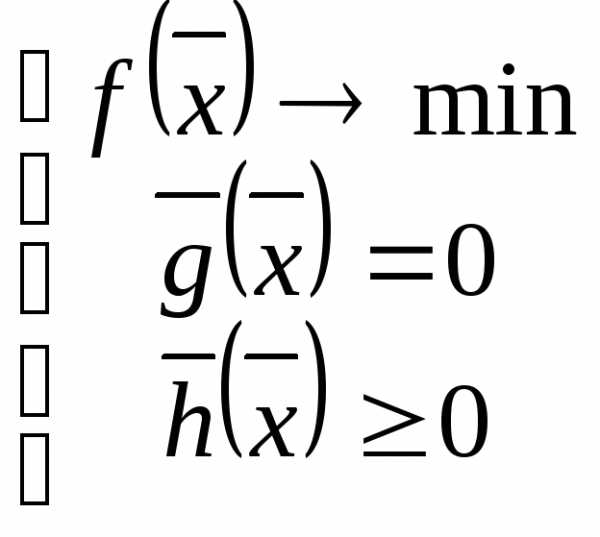
Рассмотрим
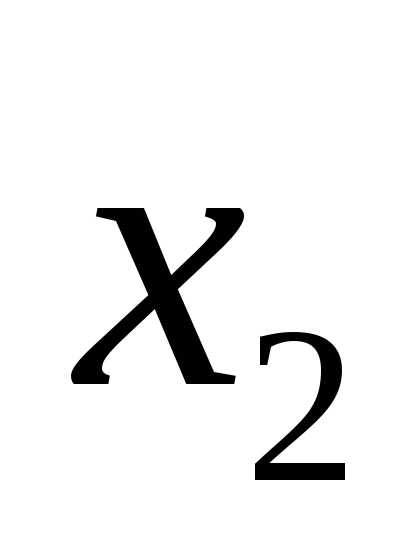
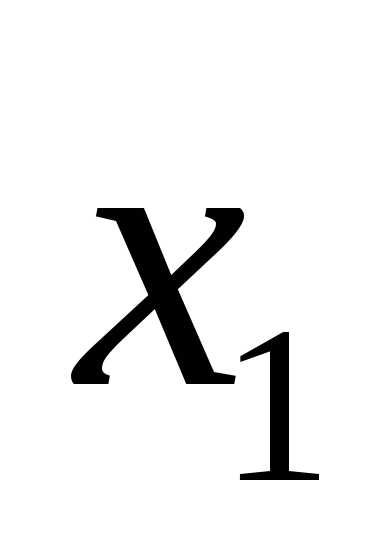
Пример:
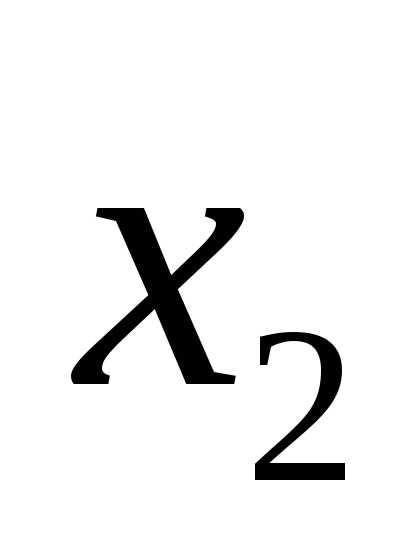
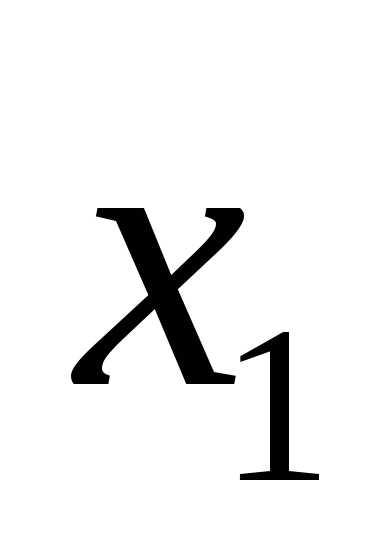
В случае системы неравенств пересечение всех областей. Если g > 0, то ограничение неравенства – неактивно (точку можно смещать).
Если точка точно на границе, то говорят, что ограничение активно.
Рассмотрим случай:
|
| Если задано линейное ограничивающее неравенство, то вектор |
Если 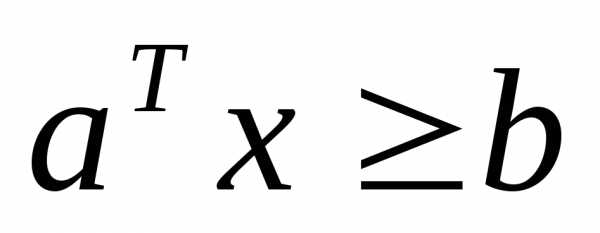 , то граница проходит не через начало координат.
, то граница проходит не через начало координат.
Необходимые условия:
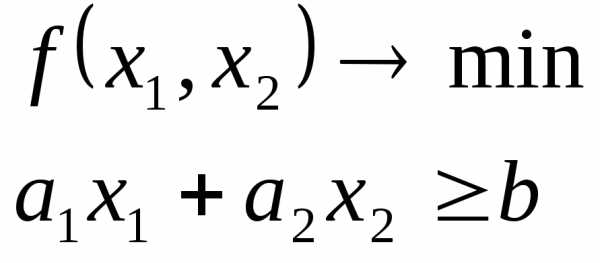

Если локальный минимум внутри допустимой области, то ;
Если точка локального минимума точно на границе, то , точка является точкой локального, еслии
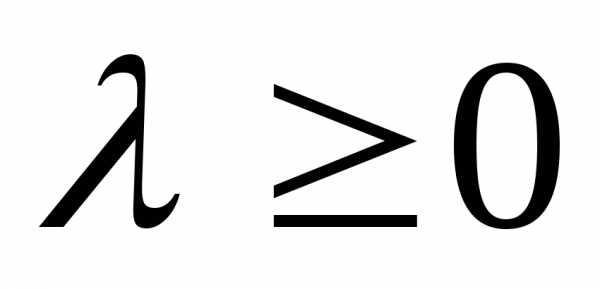
| |
|
В общем случае:
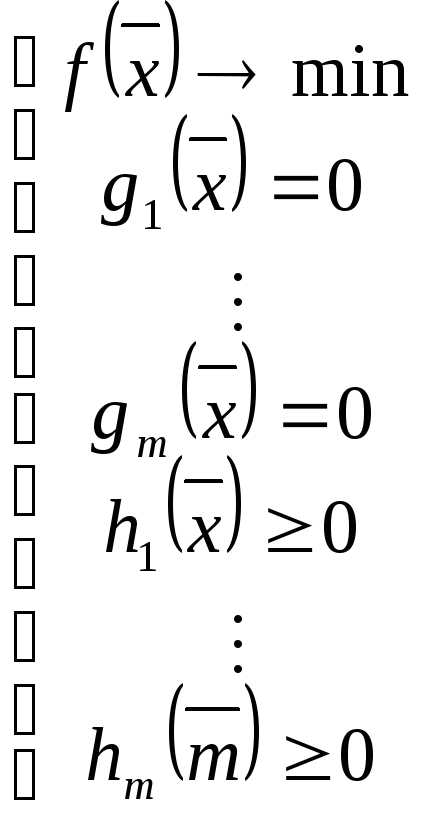
а) ;
б) 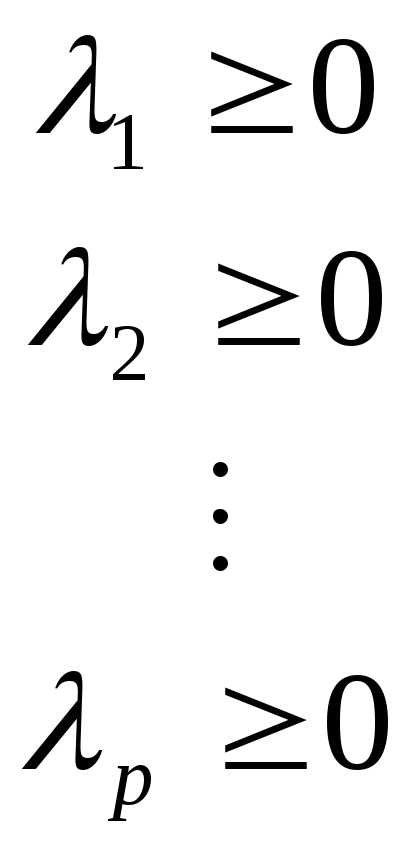 ;
;
в) Если 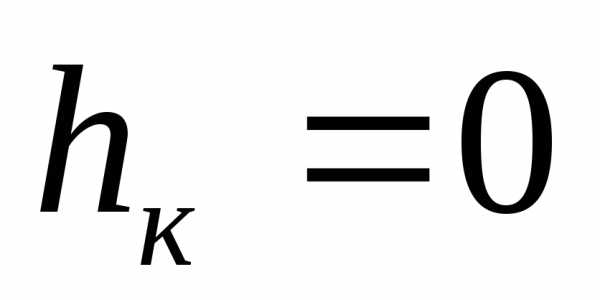 , то
, то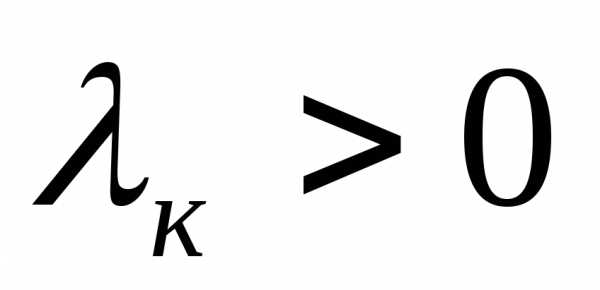 . Если
. Если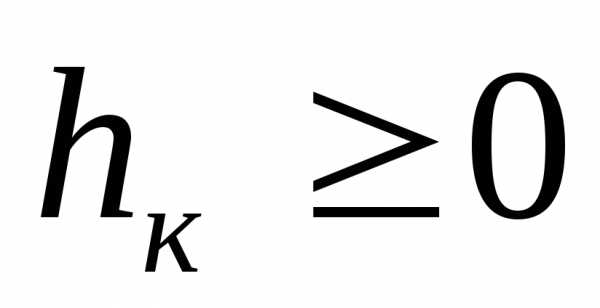 , то
, то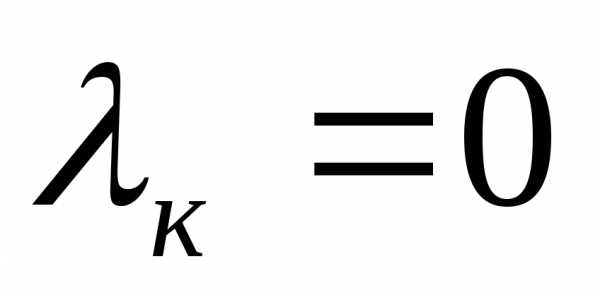 . Т.е.. Условие дополняющей нежесткости.
. Т.е.. Условие дополняющей нежесткости.
Все 3 условия в совокупности называются условиями Куна-Таккера (условия оптимальности первого порядка).
|
| Ограничения неравенства
|
Можно записать и так:
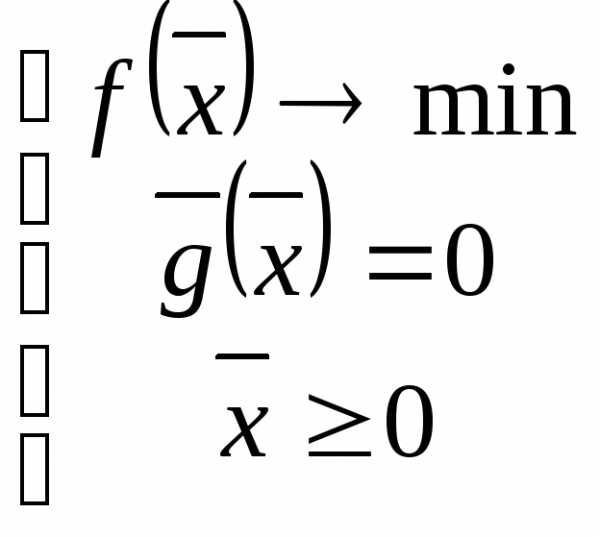
Поскольку постановка задачи 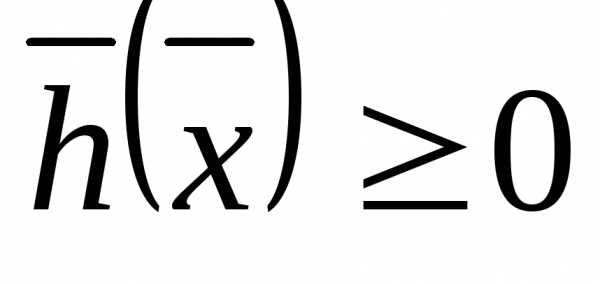
Основные результаты:
Область п-мерного пространства называется выпуклой если вместе с 2-ми точками, она содержит весь отрезок, соединяющий эти 2 точки.
Пример:
Функция нескольких переменных 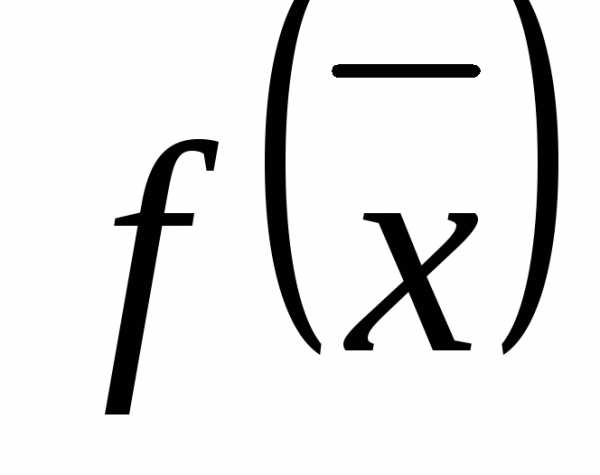 называется выпуклой если ее матрица Гесса положительно определена.
называется выпуклой если ее матрица Гесса положительно определена.
;
Если мы рассматриваем неравенство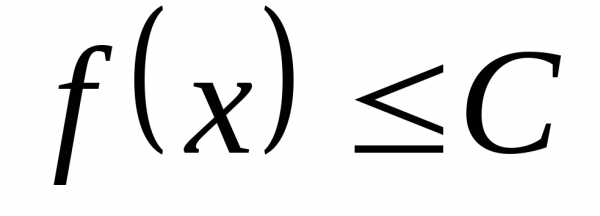 , то данное неравенство определяет выпуклую область.
, то данное неравенство определяет выпуклую область.
область будет выпуклой
Th: Пусть дана задача НЛП, если целевая функция этой задачи – выпуклая, и область целевых решений так же выпукла, то локальный оптимум совпадает с ее глобальным оптимумом задачи (задачи выпуклого программирования).
случай – когда все ограничительные неравенства являются не активными.
случай – когда точка лежит на границе.
| Методы решения НЛП. | ||
| Нулевого порядка– поисковые методы (безусловные ориентиры похожи на это). Используется только значение целевой функции (Z). | Первого порядка– аналогичны градиентным методам. Условно градиентные методы. Используется иZи вектор градиента (grad Z). | Второго порядка. Ньютоновские методы. Они являются специальными вариантами методов Ньютона для оптимизации. ИспользуетсяZ,grad Zи матрица Гесса (Н) |
| (*) | (**) | (***) |
(**)
случай – вектор gradнаправлен по нормали;
случай – идет под углом (надо спроецировать поверхность следовательно она будет показывать направление)
Если мы внутри, двигаемся как в (*), а далее (**). Это более эффективный метод.
(***)
Рассмотреть отрезок, это может дать нам еще один отрезок.
studfiles.net

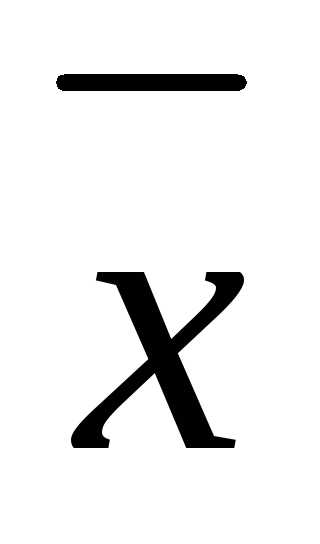
 направлен внутрь допустимой области. Если
направлен внутрь допустимой области. Если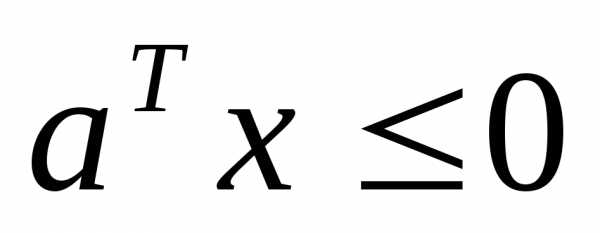 , то вектор
, то вектор будет направлен из допустимой области.
будет направлен из допустимой области.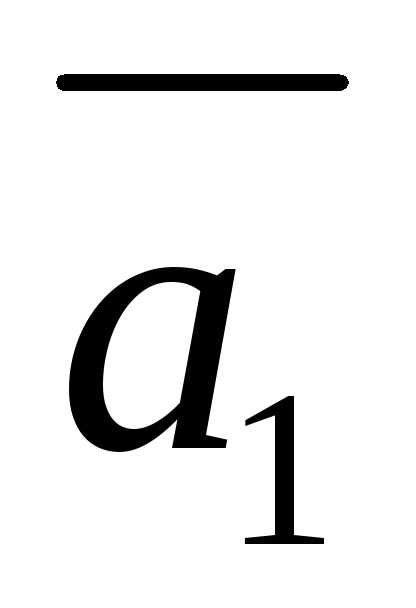
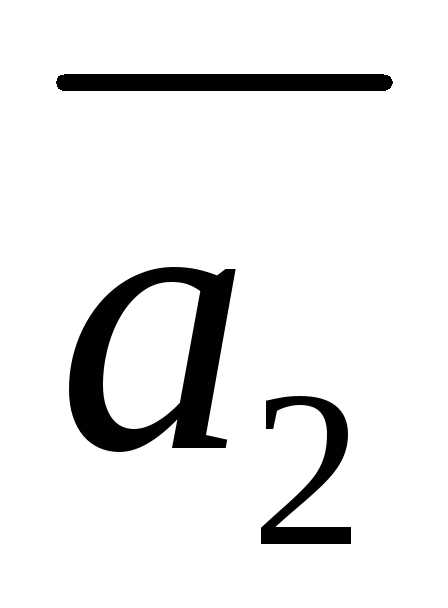
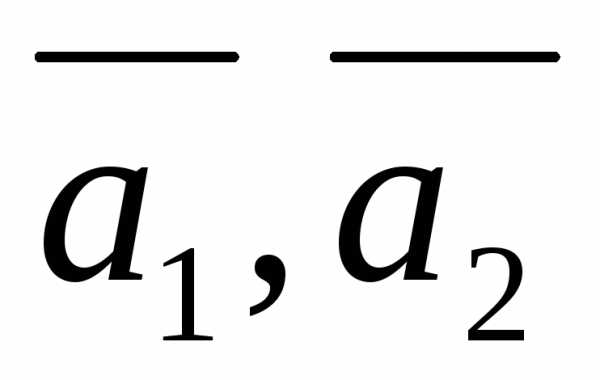 - вектора нормали к соответствующей плоскости.
- вектора нормали к соответствующей плоскости.