Большая Энциклопедия Нефти и Газа. Векторной оптимизации

Задачи векторной оптимизации.

114

1. Основные понятия и определения.

Напомним, что классической задачей оптимизации или задачей математического программирования является следующая:

найти минимум функции нескольких переменных при ограничениях, или обычно такая задача записывается в векторной форме :

(11.1.0 )

- векторная функция с компонентами

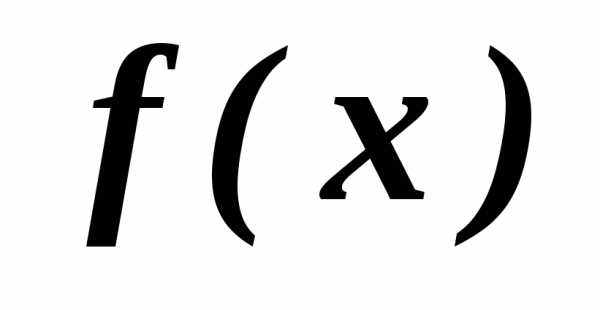- обычно называется целевой функцией,

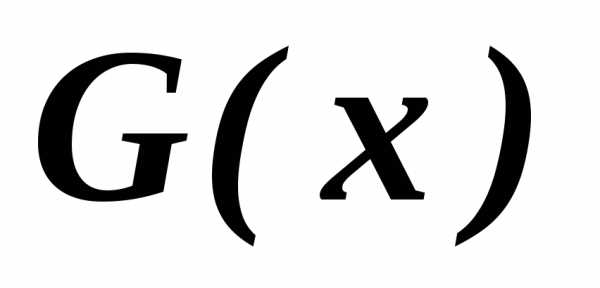- векторная функция ограничений.

Множество называетсядопустимым , то есть допустимое множество – это части пространства 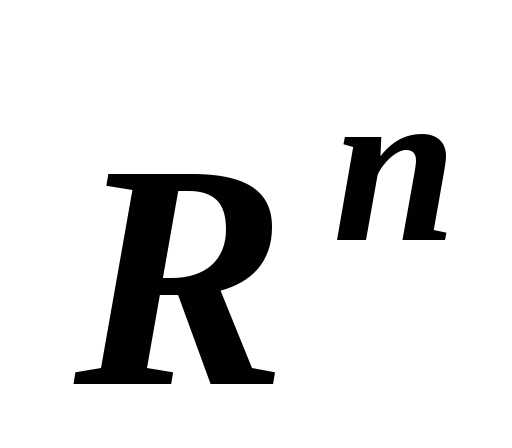, где выполнены ограничения :.

Множество 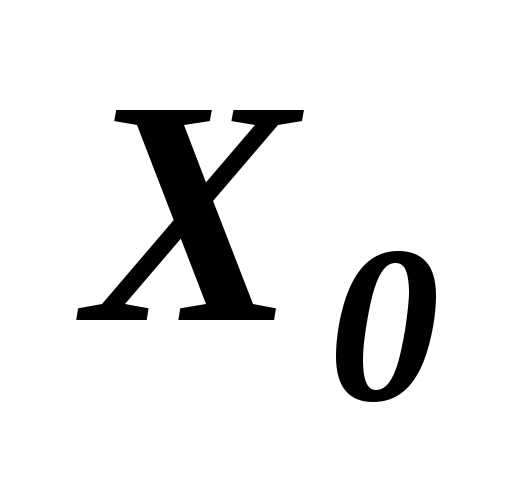называетсяоптимальным , если оно допустимо и кроме того, на этом множестве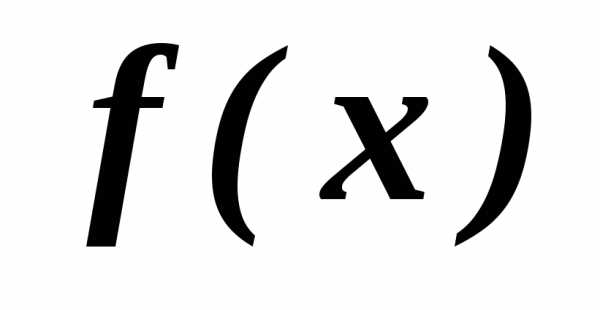

принимает минимальное значение.

Такую задачу еще можно назвать задачей скалярной оптимизации, так как 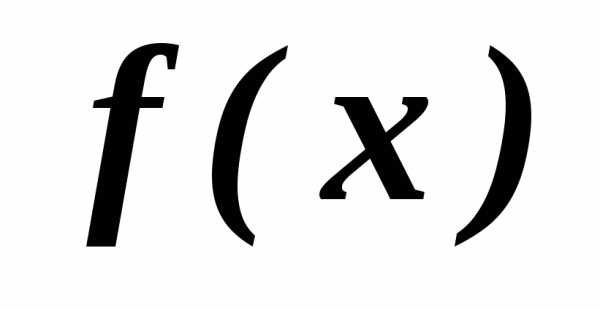- скалярная функция переменной. Поскольку в дальнейшем нам придётся на некоторых этапах обращаться к решению задачи ( 11.1 .0 ), кратко напомним основные моменты : задача ( 11.1 .0 ) может не иметь решения, может иметь одно решение, может иметь более одного решения.

Работы по скалярной оптимизации имеют два основных направления:

выявление условий единственности решения задачи ( 11.1 .0 ) , либо условий отсутствия решений;
разработка численных методов решения задачи ( 11.1 .0 ).

Эти два направления тесно связаны, так как разработка численных методов обычно предполагает выполненными определенные условия ,следующие из 1-го направления.

С другой стороны, существуют численные методы, которые в ходе своей реализации выявляют отсутствие решения или его не единственность.

Напомним, что основными численными методами решения задачи ( 11.1 .0 ) являются:

методы штрафных функций ;
прямые методы, использующие только значения функций;
градиентные методы ;
метод случайного поиска.

И, наконец, в заключение напоминания о задаче скалярной оптимизации, заметим, что в настоящее время существуют самые разнообразные пакеты прикладных программ, решающих задачу ( 11.1 .0 ) . Это пакеты на самых распространенных языках / FORTRAN, BASIC, PASCAL, C/ и для различных вычислительных машин /ЕС, СМ, ПЭВМ/.

Задача, решению которой посвящена данная работа, состоит в нахождении минимума векторной функции

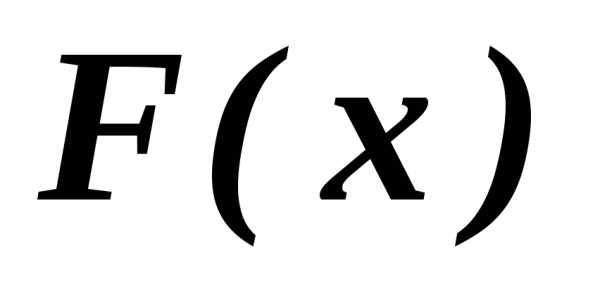при некоторых ограничениях и может быть записана так :

(11.1.0 )

- компоненты векторной функции 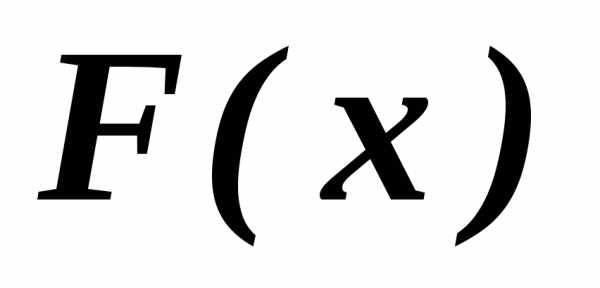, часто их называют частными критериями, поэтому и задачу ( 1.2 ) называют многокритериальной.

В задаче ( 11.1 .0 ) функцию мы называли целевой, поэтому задачу ( 11.1 .0 ) еще называют и задачей многоцелевой оптимизации. Заметим, что в общем случае, для реализации одной цели можно использовать много критериев. Поэтому задачу ( 11.1 .0 ) можно называть задачей многоцелевой оптимизации, предполагая, что одной цели соответствует один критерий.

Итак, мы будем заниматься задачей ( 11.1 .0 ), которая в разных источниках может называться как :

задача векторной оптимизации;
многокритериальная задача оптимизации;
задача многоцелевой оптимизации.

Дело в том, что реальные задачи , а особенно задачи , связанные с созданием АСУ, САПР, задачи системного анализа, теории больших систем и так далее, в основном многокритериальные, поэтому сама жизнь требует умения их решать, что подчеркивает актуальность проблемы.

В настоящее время существуют отдельные исследования как в теоретическом аспекте, так и в сфере создания алгоритмов.

Целью данной работы является попытка обобщения этих исследований, ориентированная в основном на практическое применение, то есть использование конкретных алгоритмов решения с минимальным их теоретическим обоснованием.

С математической точки зрения, задача ( 11.1 .0 ) может иметь решение только в том случае, если оно совпадает со всеми решениями скалярных задач:

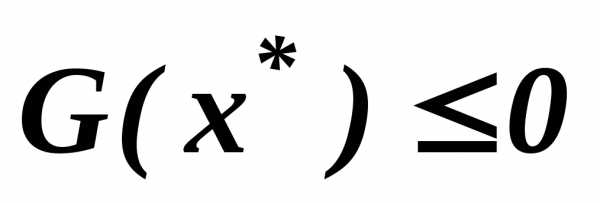
Однако, этот вариант, как правило не представляет интереса для практических задач, поскольку в реальных задачах уменьшение одного критерия приводит часто к увеличению другого и возникает проблема сравнимости критериев.

Действительно, какое решение / 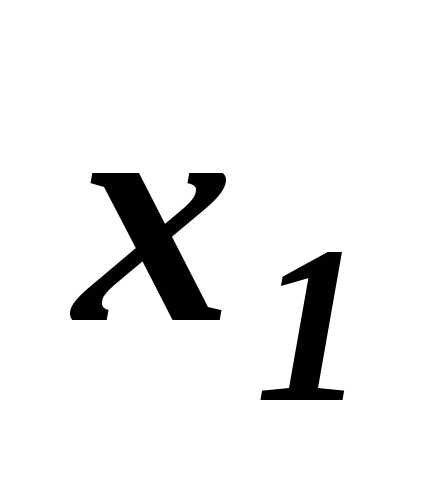или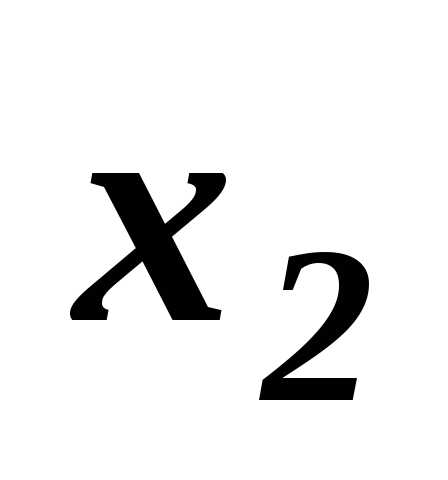/ лучше, например, для двухкритериальной задачи :

По-видимому, в данном случае, решения несравнимы.

В дальнейшем будем использовать следующие понятия и определения.

Назовем область -допустимой областью, а -допустимой точкой. - область, где выполнены все ограничения. Критерииназываютупорядоченными по важности, если каждый

предыдущий критерий важнее всех последующих , то есть 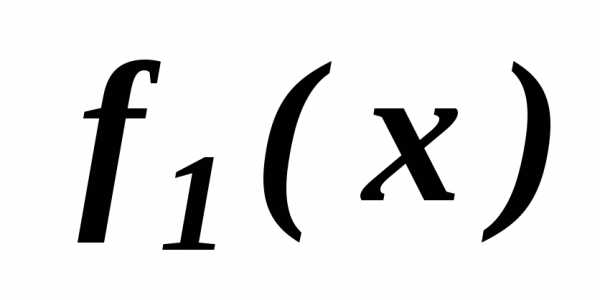- самый важный, следующий за ним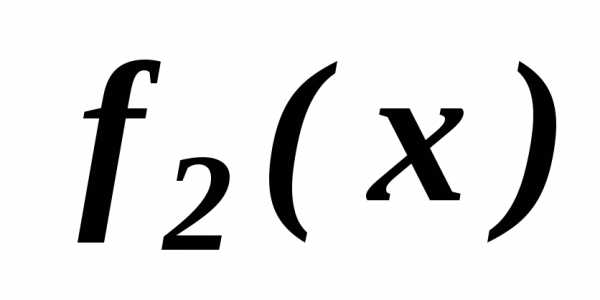и так далее.

Определение 1.

Из двух точек точка

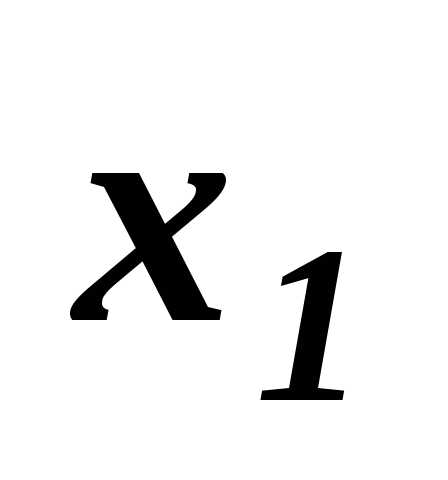называетсядоминирующей по отношению к

(

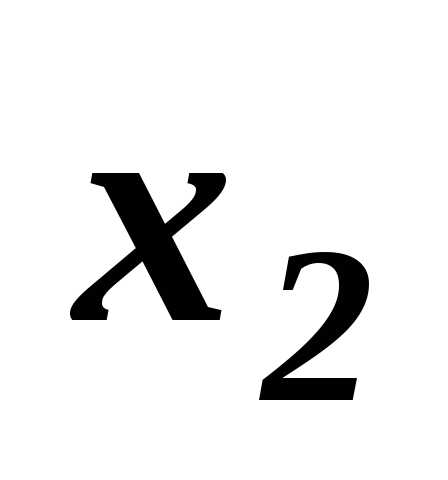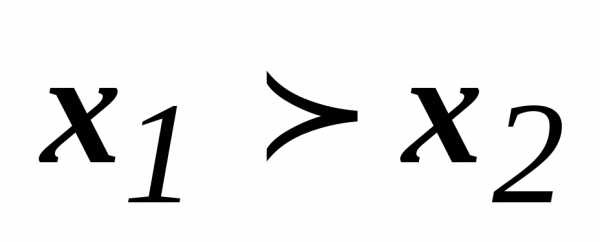), если для всех

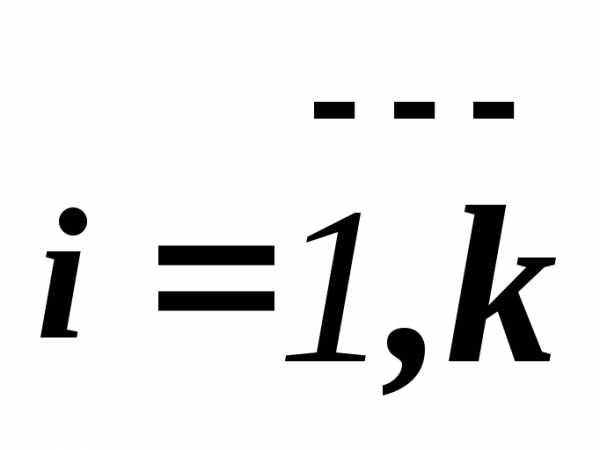выполняетсяи, кроме того , по крайней мере для одного

Определение 2.

Точка 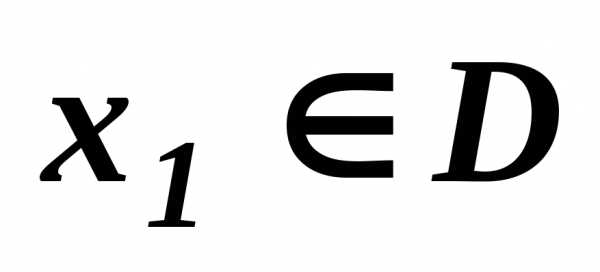называетсяулучшаемой, если существует хотя бы одна точка , такая, что,

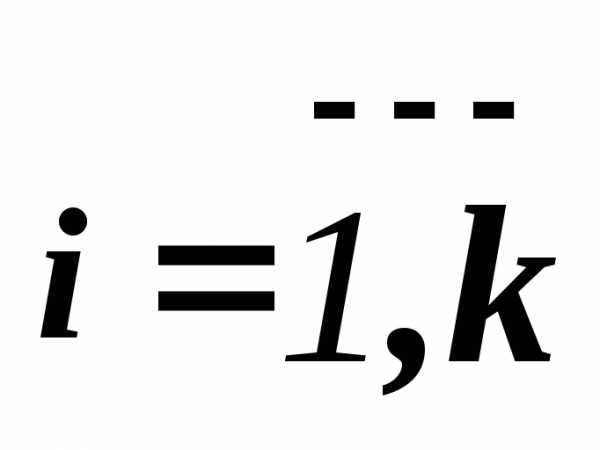и хотя бы для одного 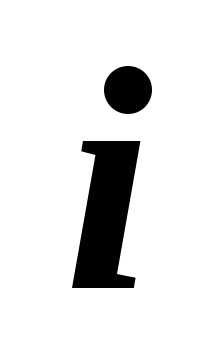:, в противном случае точкане улучшаемая или эффективная.

Определение 3.

Множество , состоящее из эффективных точек называетсямножеством решений, оптимальных по Парето.

( В. Парето / 1848-1923 / - итальянский экономист, социолог, математик. Впервые ввел понятие " эффективная точка множества ". )

Множество является решением задачи ( 11.1 .0 ), с формальной точки зрения этим можно завершить рассмотрение задачи ( 11.1 .0 ) . Множество

строится затем, чтобы из него, привлекая неформальные критерии можно было бы выбрать некоторое решение. Однако обычно выбор делается в пространстве критериев, а затем в силу взаимно-однозначного соответствия выбирается элемент из

. В задаче ( 11.1 .0 )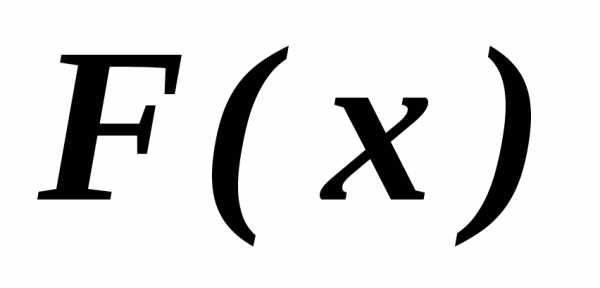

задает отображение области

в некоторую область

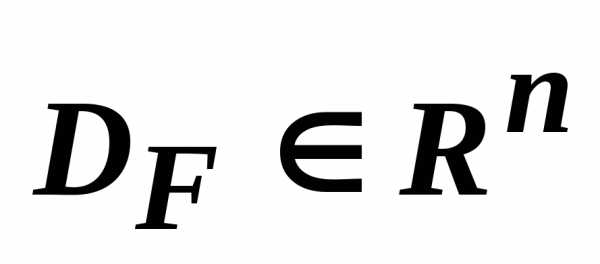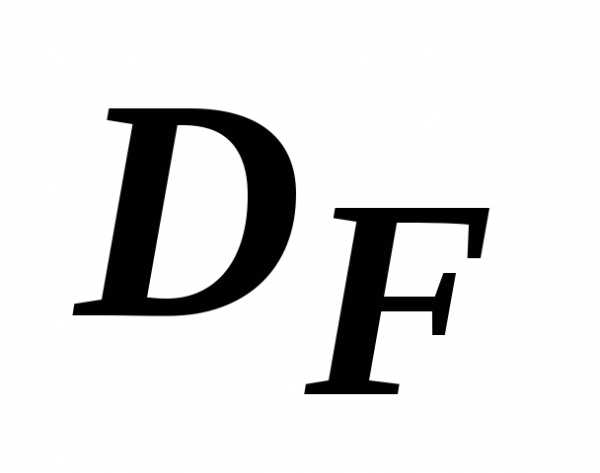называетсяобластью критериев.

Определение 1.

Доминирование остается в силе и для точек из 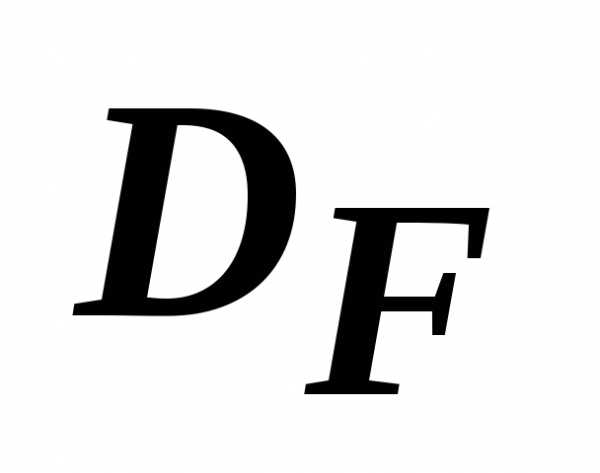.- элемент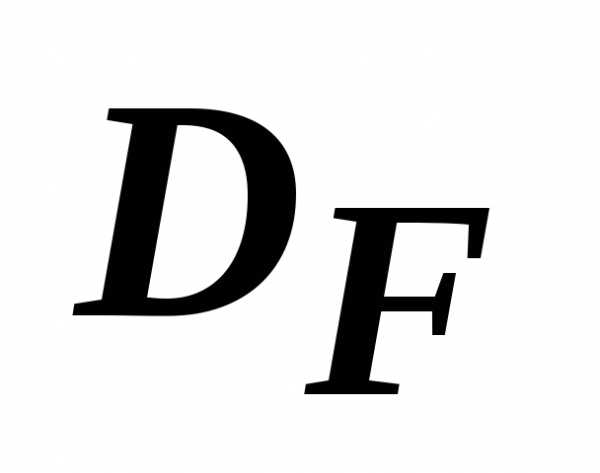. Область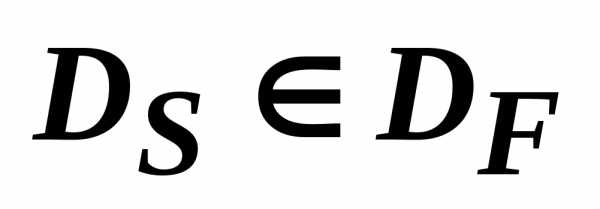называетсяобластью согласия, если из любых двух точек этой области одна будет доминирующей по отношению к другой. Если 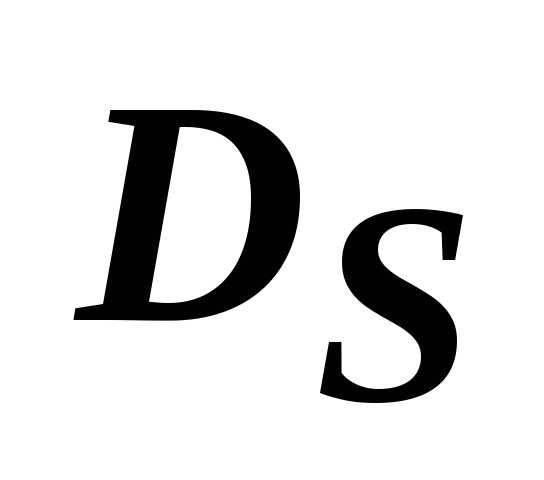совпадает с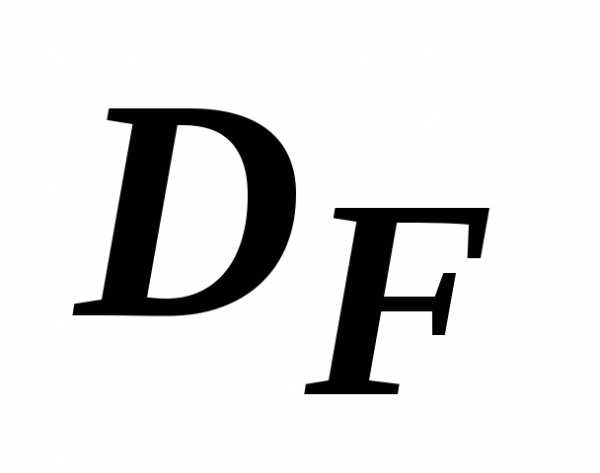

, тогда существует единственная точка

, являющаяся доминирующей по отношению ко всем другим точкам из

, то есть

- оптимальное решение задачи ( 11.1 .0 ) .

Определение 2.

Точка 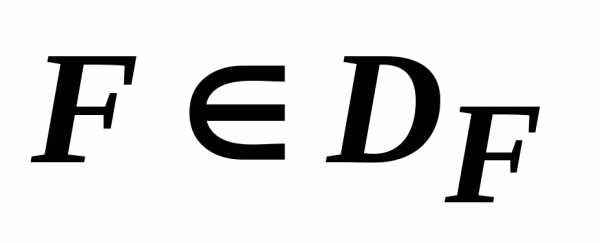называется неулучшаемой, если не существует ни одной точки из 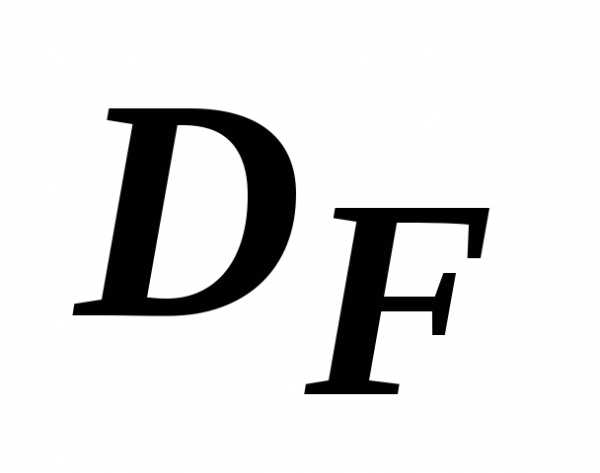, компоненты которой были бы не более компонент неулучшаемой точки / хотя бы по одной компоненте необходимо выполнение строгого неравенства /. Область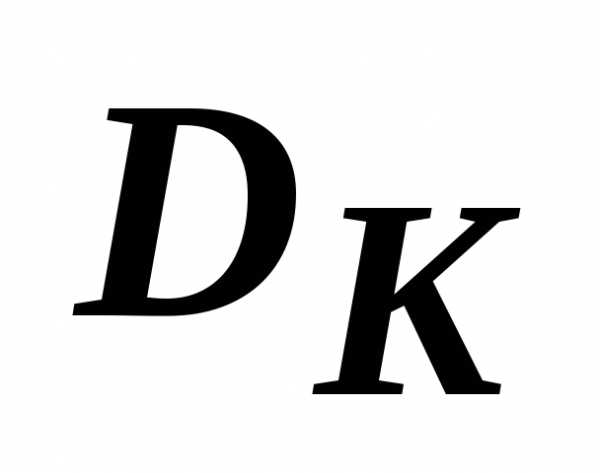, вложенная либо равная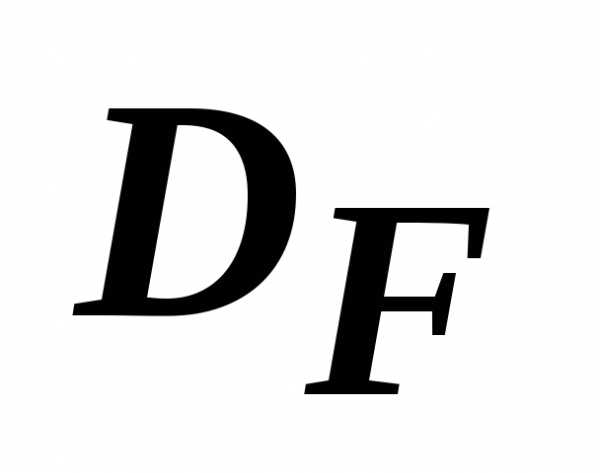называетсяобластью неулучшаемых точек.

Давайте рассмотрим следующую задачу :

(11.1.0 )

Графически она представлена следующем рисунке

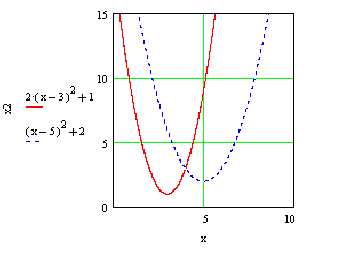
Рисунок 11‑1

На этом рисунке видно, что для

, а также для

оба критерия возрастают, следовательно точки из полуинтервала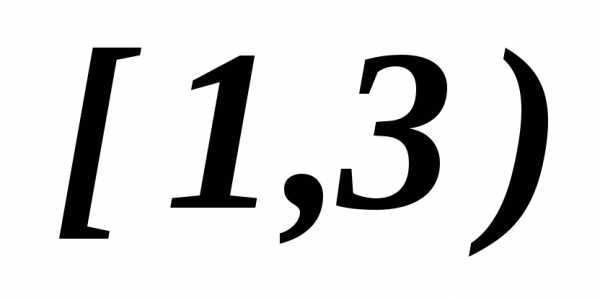

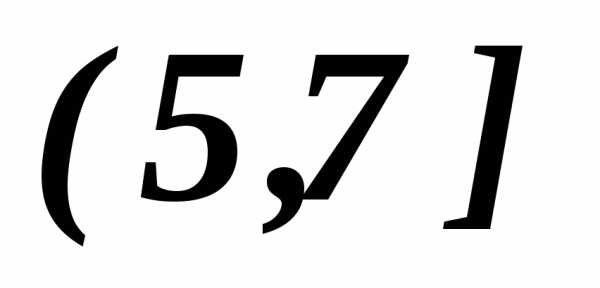улучшаемы : дляточка

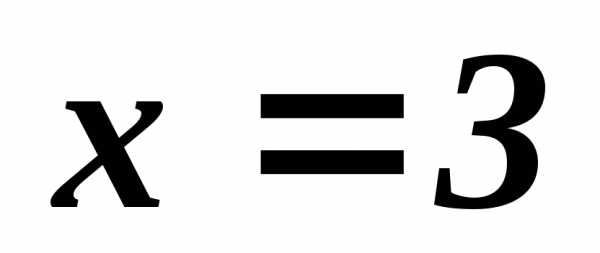дает меньшее значение критериев, аналогично ведет себя

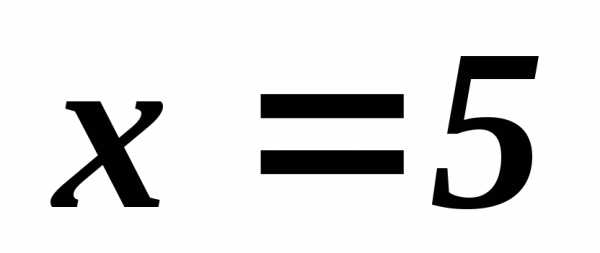для.

Мы видим, что внутри отрезка 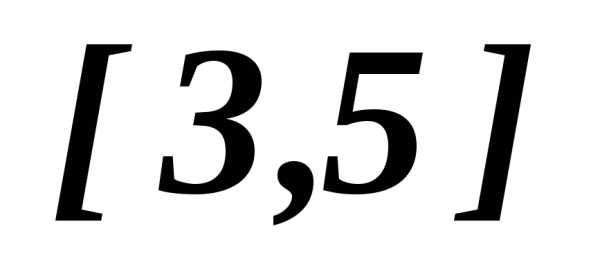до точки пересечения графиков обеих функций, т.е. на отрезке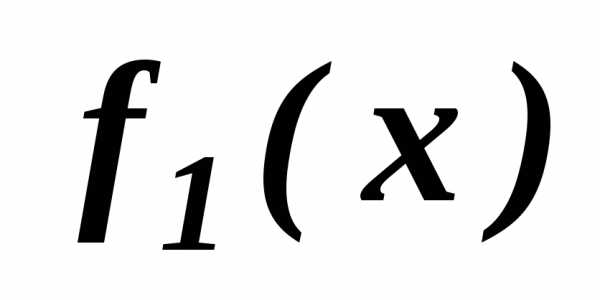убывает, а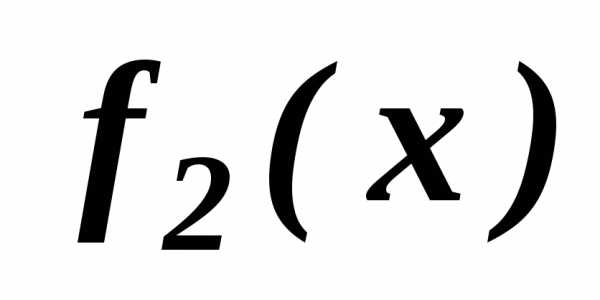возрастает, на отрезке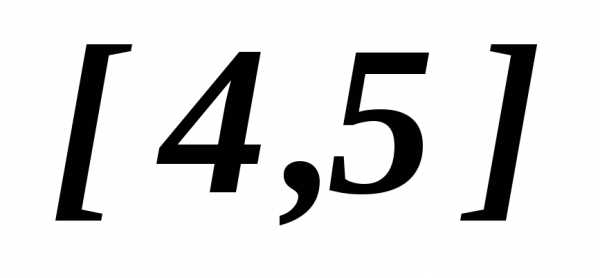наоборот: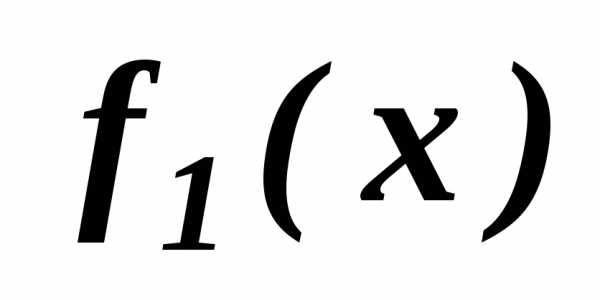возрастает, а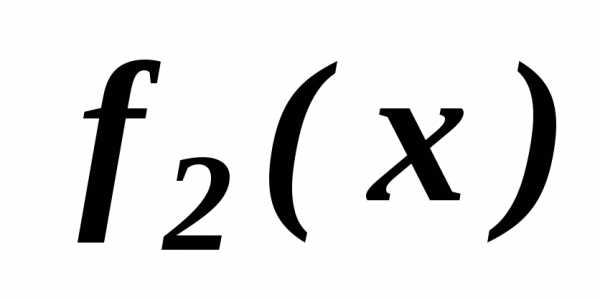убывает, следовательно, согласно введенным выше определениям - отрезок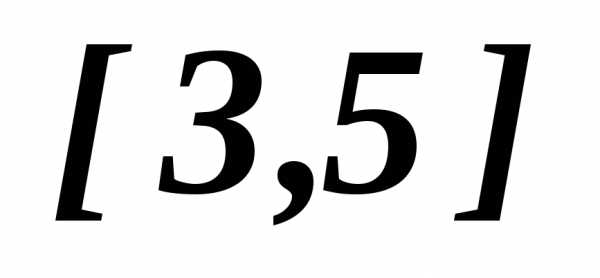для данной задачи является множеством решений, оптимальных по Парето.

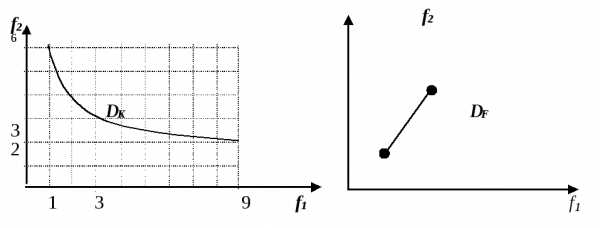
На следующем рисунке в пространстве 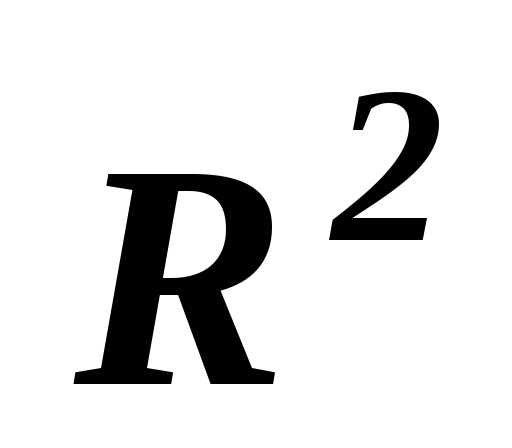, для этой же задачи представлены области согласия и компромиссов, являющиеся плоскими кривыми, полученными в результате отображения области

/ отрезок

/ в области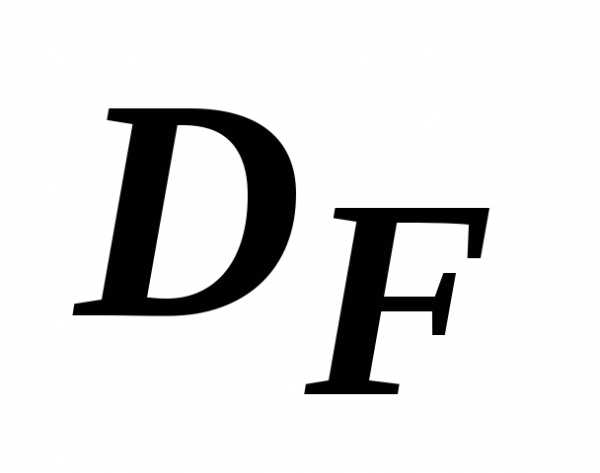

Такое представление является наглядным пособием и удобным для того, кому предстоит сделать выбор элемента из 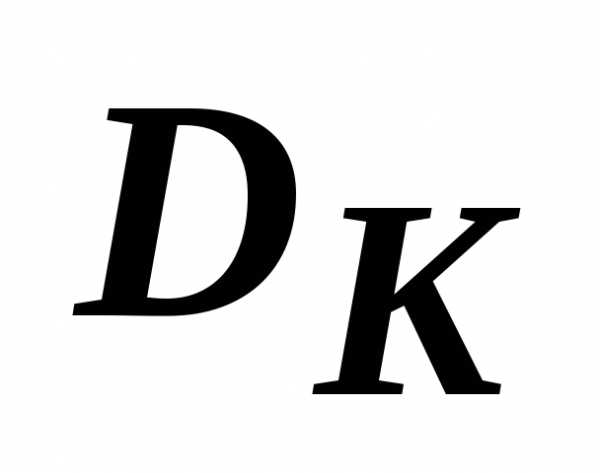. С увеличением числа частных критериев оптимальности наглядность теряется.

x	f1(x)	f2(x)
3	1	6
4	3	3
5	9	2

исунок11‑2

studfiles.net

Задача - векторная оптимизация - Большая Энциклопедия Нефти и Газа, статья, страница 1

Задача - векторная оптимизация

Cтраница 1

Задачи векторной оптимизации типичны для объектов, в которых протекает химическая реакция, когда наряду с целевым продуктом получается целая гамма побочных продуктов и возникает необходимость поиска компромиссного режима, обеспечивающего максимум выпуска целевого продукта и минимум - побочных. В настоящем параграфе осуществлена реализация алгоритма векторной оптимизации на примере моделей реакторов димеризации ацетилена и хлорирования бутадие1 на, в которых получается основной мономер для производства хлоро-преновых каучуков и латексов. [1]

В задачах векторной оптимизации принцип оптимальности определяет свойства оптимального решения и дает ответ на главный вопрос - в каком смысле оптимальное решение превосходит все остальные допустимые решения и дает правило поиска этого оптимального решения. [2]

Каким образом задача векторной оптимизации сводится к задаче скалярной оптимизации. [3]

Рассмотрим постановку задачи векторной оптимизации. Практика автоматического управления технологическими процессами в химии, металлургии, машиностроении и других производствах показала, что оптимальное управление должно опираться на несколько критериев. В качестве критериев оптимальности одновременно могут выступать такие показатели качества и эффективности ведения технологического процесса, как объем переработанного сырья, количество полученных продуктов, чистота готового продукта, степень переработки сырья и извлечение из него ценных компонентов, себестоимость отдельных видов продукции, прибыль предприятия и др. Управление с применением только одного критерия, например количества получаемого продукта, может привести к неудовлетворительным показателям по другим критериям: завышенная себестоимость, содержание примесей, недостаточное извлечение ценных составляющих из сырья. [4]

Рассмотрим постановку задачи векторной оптимизации, содержательно интерпретируемую и с точки зрения принятия плановых решений. [5]

Для решения задач векторной оптимизации с аддитивными критериями в системе CHOISE реализованы все три алгоритма ( см. параграф 4.7), причем скалярные задачи и задачу выбора с обобщенной матрицей можно решать любым из перечисленных выше шести методов скалярной оптимизации. [6]

В формулировке задач векторной оптимизации важно построение функционала, который оценивает выбираемые решения. В процессе его построения не меньшее значение имеет лицо, принимающее решение. Поэтому методы, входящие в рассматриваемую группу, называют человеко-машинными процедурами. [7]

Неполная определенность решения задачи векторной оптимизации ( множественный характер решения) обусловлена неопределенностью постановки задачи. При формализации пожеланий проектировщика не установлены предпочтения и приоритеты. Уменьшение неопределенности решения связано с привлечением дополнительной информации. [9]

Второй этап решения задачи векторной оптимизации обычно осуществляется с помощью экспертных оценок разработчиков аналитических приборов. [10]

В третьей главе излагаются задачи векторной оптимизации и векторных уравновешиваний на основе коалиционного равновесия при отсутствии угроз. Сравнительный анализ методов векторной оптимизации позволяет выбрать гибкий интерактивный подход на основе конусов доминирования. Данный метод применяется для решения задачи коалиционного перехвата соединением ЛА подвижной цели с учетом противодействия на основе программно-корректируемого управления ( как фрагмента конфликта ЛС ПВО - ЛС СВН) с анализом способов увеличения быстродействия для его реализации. [11]

Многоцелевые задачи ( или задачи векторной оптимизации) и отвечающие им экономико-математические модели успешно применяют в условиях, когда необходимо учитывать несколько критериев - натуральных и денежных показателей. Приведение нескольких критериев к одному может противоречить идее построения наилучшего плана работы ТСК. Здесь же рассмотрим другие подходы векторной оптимизации. [12]

Существует несколько способов сведения задачи векторной оптимизации к задаче оптимизации скалярного критерия и получения, тем самым, единственного решения. Отметим, что все способы, которые рассматриваются ниже, удовлетворяют необходимому условию: минимизация скалярного критерия дает решение из области Парето. [13]

По определению, решением задачи векторной оптимизации является множество значений параметров, в котором изменение любого параметра с целью улучшения одного из частных критериев обязательно ухудшает хотя бы один другой. [15]

Страницы: 1 2 3 4

www.ngpedia.ru

Постановка задачи векторной оптимизации. Принципы оптимальности — МегаЛекции

Н.Б. Баева, Ю.В. Бондаренко, Т.В. Азарнова, И.Л. Каширина

ТЕОРИЯ И ПРАКТИКА ВЕКТОРНОЙ ОПТИМИЗАЦИИ

Учебное пособие

Издательский дом ВГУ

Утверждено учебно-методическим советом факультета прикладной математики, информатики и механики 10 января 2017 г., протокол № 5

Рецензент: декан математического факультета ВГУ, доктор физико-математических наук, профессор А.Д. Баев

В пособии излагается теоретический и практический материал, затрагивающий основные разделы векторной оптимизации. Приведены различные алгоритмы решения задач векторной оптимизации, обоснованные доказательством теорем и проиллюстрированные примерами.

Учебное пособие подготовлено на кафедре математических методов исследования операций факультета ПММ Воронежского государственного университета. Рекомендуется для студентов, обучающихся по направлениям: "Прикладная математика и информатика" , "Бизнес-информатика"

СОДЕРЖАНИЕ

§1. Постановка задачи векторной оптимизации. Принципы оптимальности
§2. Графический метод проверки эффективности точки задач векторной оптимизации
§3.Классификация методов решения ЗВО
§4. Методы решения ЗВМ, основанные на свертывании (скаляризации) критериев
§5.Принцип максимальной эффективности и принцип гарантированного результата
5.1. Принцип максимальной эффективности и принцип гарантированного результата в случае равнозначных критериев
5.2. Принцип максимальной эффективности и принцип гарантированного результата при заданном приоритете критериев
§6. Методы решения ЗВМ, основанные на лексикографическом принципе оптимальности
§7. Методы, использующие ограничения на критерии
7.1. Метод ограничений
7.2. Метод последовательных уступок
§8. Целевое программирование
§9. Методы решения ЗВМ произвольной структуры
9.1. Дискретизация множеств
9.2. Фильтрация множеств
Список литературы

Постановка задачи векторной оптимизации. Принципы оптимальности

Рассмотрим задачу принятия решений, в которой качество альтернатив множества ( – непрерывные выпуклые функции) оценивается набором критериев – непрерывных функций Если цель решения задачи заключается в отыскании такой альтернативы , в которой каждый из критериев принимает наибольшее или наименьшее значение, то в этом случае задача математически записывается следующим образом:

(1)

и называется задачей векторной оптимизации (ЗВО), а каждая из функций - частным критерием.

Если в исходной задаче критерии однонаправлены, т.е. все критерии, например, стремятся к максимуму (или к минимуму), то задача называется однородной. В противном случае исходная задача – неоднородная задача оптимизации.

Если – непрерывные, вогнутые функции, а – непустой компакт (замкнутое, выпуклое множество), задача (1) называется задачей выпуклой векторной оптимизации. Именно такие задачи мы преимущественно и будем рассматривать.

Если и линейны, то задача (1) называется задачей линейной векторной оптимизации. Теория решения таких задач разработана наиболее полно.

С учетом того, что каждая оптимизированная задача может быть переписана в эквивалентной постановке как задача максимизации критериев, будем для удобства рассматривать задачу векторной максимизации (ЗВМ), записывая её в следующем виде:

. (2)

Введем в рассмотрение ряд определений, связанных с понятием решения ЗВО.

Определение 1. Вектор называется идеальным решением задачи векторной оптимизации, если для любого выполнены неравенства:

Другими словами, идеальное решение задачи (2) является одновременно решением всех M частных задач:

(3)

Требования, предъявленные к функциям и естественное предположение о том, что не пусто, обеспечивают существование решения частных задач. Причем, если через обозначить множество оптимальных точек каждой из частных задач, то

–

множество решений исходной задачи.

Однако на практике критерии оказываются, как правило, противоречивыми, что приводит к пустому пересечению множеств решений (3) и отсутствию идеального решения. Поэтому формальная запись задачи векторной максимизации не может быть основой для решения. В результате этого считается, что задача векторной оптимизации реализует так называемые априорные рациональные принципы оптимальности, которые полностью определяются описанием множества , отображениями и предпочтительными направлениями изменения оценок (в нашем случае - максимизация). К таким принципам оптимальности относятся принципы Слейтера и Парето.

1.Принцип Слейтера

Определение 2. Точка называется оптимальной по Слейтеру в задаче векторной максимизации, если не существует другой точки для которой

Множество оптимальных по Слейтеру точек Sl называют множеством слабо эффективных точек.

Другими словами, если ввести множество

то

Замечание 1. Любое решение каждой частной задачи (3) является точкой, оптимальной по Слейтеру.

2. Принцип Парето

Определение 3. Точка называется оптимальной по Парето в задаче векторной максимизации, если не существует другой точки для которой и существует такой индекс , что

Множество Парето – оптимальных точек Pr называют множеством эффективных точек.

Другими словами, если ввести множество

то

Замечание 2. Отметим, что в множестве решений каждой частной задачи (3) существует непустое подмножество точек, являющихся Парето – оптимальными, что обеспечивает существование решение задачи выбора с принципом Парето. Более того, если решение каждой частной задачи единственно, то Таким образом,

С понятием решения ЗВО связано понятие доминирования.

Доминирование. Недоминируемые критериальные векторы

Рассмотрим задачу векторной максимизации (2).

Каждой точке может быть поставлена в соответствие точка где Тогда Z – элемент из M – мерного евклидова пространства , которое принято называть критериальным, а его элементы – критериальными векторами.

Множество называется достижимым множеством.

Таким образом, каждой задаче векторной максимизации (2) может быть поставлена в соответствие задача:

(4)

Для установления аналогий между решениями задач (2) и (4) введем в рассмотрение следующие определения.

Пусть – критериальные векторы.

Определение 4. Вектор слабо доминирует вектор , если (т. е. и по крайней мере, для одного k).

Определение 5.Вектор сильно доминирует вектор , если , т. е.

Определение 6. Критериальный вектор называется недоминируемым, если не существует другого вектора такого, что

Иначе называется доминируемым.

Определение 7. Критериальный вектор называется недоминируемым сильно, если не существует другого вектора такого, что

В рамках введенных определений Парето – оптимальное множество задачи (2) состоит из таких точек , критериальные векторы которых являются недоминируемыми, а множество Слейтера включает точки, критериальные векторы которых недоминируются сильно.

Замечание 3. Соотношения понимаются выполняемыми покоординатно.

Рассмотрим следующие примеры.

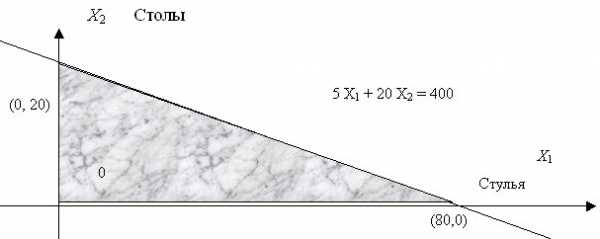
Пример 1.Представить графически достижимую область в пространстве критериев для задачи:

Решение. Допустимое множество задачи представлено на рисунке 1.

Вершинами многогранника являются следующие точки:

Каждая точка X множества является выпуклой линейной комбинацией вершин т.е.

где

Рассмотрим отображение определяемое правилом:

где

Отображение F является линейным оператором, и поэтому образ любой точки является линейной комбинацией образов вершин допустимого множества, т.е. где т.е. является выпуклым многогранником, вершины которого находятся среди точек

Найдем координаты точки т.е.

Аналогично:

Достижимое множество в пространстве критериев Q изображено на рисунке 2.

Пример2. Вектор сильно доминирует вектор и слабо доминирует вектор

Пример 3. Рассмотрим задачу:

Найти множество оптимальных по Парето и по Слейтеру точек.

Решение. Допустимая область задачи и векторы – градиенты целевых функций представлены на рисунке 3.

Точка является оптимальной по Парето, так как в допустимом множестве не существует точек X таких, что причем одно из неравенств – строгое. (ABC) – множество оптимальных по Слейтору точек.

Упражнения к § 1

№ 1. Представьте графически достижимую область в пространстве критериев для задач:

№ 2. Для каждого из перечисленных векторов определите слабо и сильно доминирующие векторы:

№ 3. Определите, какие точки из таблицы эффективны.

Рекомендуемые страницы:

Воспользуйтесь поиском по сайту:

megalektsii.ru

Решение векторной задачи оптимизации методом

Таким образом, в настоящее время разработаны мощные методы решения оптимизационных задач как для статических, так и для динамических систем. Эти методы интенсивно используются в экономико-математических исследованиях. В то же время массовое использование оптимизационных методов на практике выявило их определенную ограниченность, связанную с необходимостью заранее формулировать единственный критерий. Часто проблема соизмерения различных показателей и построения единственного критерия оказывается чрезвычайно сложной, во многих случаях — неразрешимой. Это привело к принципиально новому этапу в развитии методов оптимизации — появлению методов многокритериальной (векторной) оптимизации. [c.59] Принятие решения в рамках указанных моделей в большинстве случаев удается свести к решению одной или нескольких задач математического программирования. В тех случаях, когда существует множество критериев оценки качества решения, как правило, осуществляется свертка векторного критерия в скалярный, используются методы лексикографической оптимизации, методы последовательных уступок или иные эвристические человеко-машинные процедуры. [c.186]

Все эти методы объединяет общий прием поиска наилучшего решения векторный критерий тем или иным способом превращается в скалярную целевую функцию, а затем решается задача оптимизации. [c.190]

В тех случаях, когда все локальные критерии /,, /,,..., / , с точки зрения ЛПР, имеют одинаковую степень важности, решение задачи векторной оптимизации осуществляется с использованием принципа равномерности, метода идеальной" точки, принципа справедливого компромисса, оптимальности по Парето. [c.193]

Векторная оптимизация — комплекс методов решения задач математического программирования, в которых критерий оптимальности представляет собой вектор, компонентами которого являются, в свою очередь, несводимые друг к другу скалярные критерии оптимальности подсистем, входящих в данную систему. [c.211]

Анализ таких ситуаций осложняется, когда число объектов велико и аналогичные расчеты приходится проводить многократно, в связи с чем возникает задача автоматизации этих расчетов для лица, принимающего решения (ЛПР). Автоматизация расчетов, как правило, связана с попыткой свести многокритериальную задачу к однокритериалыюй, что соответственно приводит к ряду субъективных допущений. Обычно методы решения векторных задач оптимизации построены таким образом, чтобы выйти на одну из оптимальных точек по Парето, учитывая важность (приоритет) того или иного критерия. [c.202]

ВЕКТОРНАЯ ОПТИМИЗАЦИЯ [ve tor optimization] — комплекс методов решения задач математического программирования, в которых критерий оптимальности представляет собой вектор, компонентами которого являются, в свою очередь, несводимые друг к другу скалярные критерии оптимальности подсистем, входящих в данную систему (напр., критерии роста благосостояния разных социальных групп в социально-экономическом планировании). При этом задача оптимизации существенно видоизменяется по сравнению с теми задачами, которые рассматриваются в большинстве статей словаря. В них она сводится к тому, чтобы, зная условия и ограничения, найти такой план, который бы максимизировал или минимизировал единственный заданный критериальный показатель. Это называется "скалярная оптимизация". [c.43]

Другая важная проблема, тесно связанная с согласованием решений,— формирование и согласование целей (критериев оптимальности) различных уровней. При декомпозиционном подходе к построению С. о.-м. м., используемом гл. обр. для разработки моделей планирования, общая цель для всей системы задана, а целевые функции составных частей формируются исходя из этой общей цели. Методика декомпозиции целей хорошо разработана для моделей оптимального планирования, базирующихся на методах блочного программирования. При синтотич. подходе, более универсальном и реалистичном, целевые функции частей (напр., групп населения) являются исходными, заданными. Задача состоит в определении такого взаимодействия частей внутри системы и такого порядка функционирования, при к-ром вся система в целом достигла бы решения, соответствующего глобальной цели. Проблемы синтеза общем цели на основе частных ставятся и решаются в теории игр, моделях векторной оптимизации, моделях экономич. равновесия, теории принятия групповых решений, а также методами имитационного моделирования. В имитационных моделях, понимаемых достаточно широко, переменными или варьируемыми параметрами могут выступать алгоритмы принятия решений отд. подмоделями, а также алгоритмы согласования решений. Следовательно, задача состоит в нахождении такого набора алгоритмов, имитирующих функционирование экономич. системы, при к-ром получаемое общее решение наилучшим образом соответствует глобально] цели системы. [c.558]

Работа реальных транспортных систем оценивается, как правило, не по одному показателю, а по целому набору критериев. Таким образом, показатель качества системы является векторной величиной. Современные методы оптимизации позволяют решать лишь однокритериальные задачи. Поэтому результатом решения является набор различных вариантов построения или управления транспортной системой, соответствующих различным критериям. В зависимости от реально сложившейся ситуации лицо, принимающее решения, или группа экспертов выбирают тот или другой вариант найденного оптимального решения. Таким образом, окончатель- [c.180]

Решение задач многокритериальной или векторной оптимизации осуществляется с использованием принципов выделения главного критерия, скаляризации вектора целевых функций, равномерности, идеальной" точки, квазиоптимизации локальных критериев методом последовательных уступок, справедливого компромисса, оптимальности по Парето и ряда других. [c.192]

СКАЛЯРНАЯ ОПТИМИЗАЦИЯ [s alar optimization] — совокупность методов решения задач математического программирования, целевая функция которых представляет собой скаляр. Большинство задач, рассматриваемых в словаре (см. Линейное программирование, Нелинейное программирование, Дискретное программирование и др.), принадлежит к этому классу. Ср. Векторная оптимизация, Многокритериальная оптимизация. [c.330]

economy-ru.info

Векторная оптимизация - Большая Энциклопедия Нефти и Газа, статья, страница 3

Векторная оптимизация

Cтраница 3

В этой главе аксиоматика векторной оптимизации, разработанная в гл. Такие многокритериальные задачи имеют в своей основе сложные нелинейные функции, и решение их по одному критерию затруднительно, а тем более решение Х - зада-чи, в основе которой лежат все критерии, входящие в модель. [31]

Решение задач многокритериальной или векторной оптимизации осуществляется с использованием принципов выделения главного критерия, скаляризации вектора целевых функций, равномерности, идеальной точки, квазиоптимизации локальных критериев методом последовательных уступок, справедливого компромисса, оптимальности по Парето и ряда других. [34]

Для решения такого класса задач векторной оптимизации используются алгоритмы, решения, представленные в разд. [39]

Вторая тенденция в развитии методов векторной оптимизации базируется на хорошо развитом аппарате теории оптимального управления и математического программирования. В рамках этих направлений разработаны многочисленные методы скалярной оптимизации, максимально учитывающие специфику решаемых задач, которая проявляется, прежде всего, в форме математического описания объекта управления, форме критерия, фазовых ограничений, ограничений на управление. Поскольку при решении задач векторной оптимизации так или иначе приходится решать одну или большее число задач скалярной оптимизации, то вполне естественно попытаться использовать математический аппарат, разработанный для решения задач скалярной оптимизации. [43]

Согласно последней, общую задачу векторной оптимизации (2.1) можно решать с помощью алгоритмов, которые условно разбиты на две группы. [45]

Страницы: 1 2 3 4

www.ngpedia.ru

Оптимизация векторная - Энциклопедия по машиностроению XXL

Сущность оптимизации при выбранной комплексной целевой функции сводится к отысканию при наложенных ограничениях таких значений параметров механизма, которые дают максимум (минимум) целевой функции, характеризующей комплексную эффективность проектируемой машины. При этом используются математические методы оптимизации, позволяющие осуществить непрерывный поиск направления улучшения внутренних параметров механизма за счет количественного изменения их значений. Так как комплексная целевая функция, получаемая сверткой векторных критериев, определяется неявным образом от внутренних параметров синтеза, что не позволяет оценить ее свойства (выпуклость, вогнутость и т. д.), то решение задач оптимизации ведется с помощью поисковых методов, получивших название методов математического программирования. В настоящее время нет экономичного, универсального метода, дающего высокую гарантию получения наилучшей совокупности внутренних параметров машины и механизма, пригодного для решения любой задачи оптимизации. В зависимости от класса решаемых задач из имеющихся в наличии программ, входящих в программное обеспечение методов оптимизации, выбирают такую, которая дает наиболее высокую вероятность отыскания оптимальной совокупности определяемых параметров с наименьшими затратами машинного времени. [c.316] Непрерывная оптимизация системы, заключающаяся в автоматическом определении для каждого момента времени t оптимального значения вектора настраиваемых параметров (t), осуществляется посредством изменения настраиваемых параметров согласно векторному уравнению [c.5]

Применение метода векторной оптимизации дает компромиссные решения, которые заранее трудно предсказать, но правильно отражающие логику выбора оптимальных параметров. Так, например, оптимизация по вектору (Л1к, Ук, Фев (вариант 7) по сравнению с вариантом 5 (критерий (Л1к, Фев ) приближает переменные и Х4 к оптимальным для вариантов минимизации Л4 и Ук (варианты 1 и 3), поскольку в векторе Мц, Ук, Фев удельный вес составляющей Л4к (или Ук) выше, чем в Л4к, Фев , ввиду непротиворечивости критериев Л1к и Ук- [c.222]

Вначале рассмотрим задачу анализа. Пусть заданы критерии качества Ф-f (a/Gv), 7 = 2,. . р, которые по параметрам могут быть противоречивыми (задача векторной оптимизации). Необходимо найти компромиссный критерий, к примеру, типа [c.46]

Входными данными для оптимизации ПОС служат векторные и скалярные функции. [c.125]

Скалярное объединение противоречивых критериев в единый критерий качества редко приводит к результатам, удовлетворяющим исследователя. Поэтому появились методы векторной оптимизации, когда противоречивые критерии объединяются в единый критерий на векторной основе [2, 30]. [c.189]

Рассмотрены варианты постановок задач оптимизации с несколькими локальными критериями эффективности проекта конструкции. Для задач с формализуемыми критериями показана взаимосвязь между векторной и скалярной моделями оптимизации, реализуемая с помощью методов редукции. [c.7]

Векторные модели оптимизации, несмотря на компактную обобщенную форму записи (4.1), в зависимости от содержания проектной ситуации могут иметь различную, иногда достаточно сложную структуру. В частности, если проектирование конструкции осуществляется на множестве, состоящем из Ус>1 различных конструкционных материалов Сг ( =1,1 с), то для каждого из этих материалов, очевидно, можно сформулировать частную модель оптимизации М типа (4.1). В этом случае общая формулировка модели оптимизации конструкции в форме (4.1) может быть сохранена, если рассматривать поливариантную модель оптимизации [c.166]

На третьем этапе процесса ОПК, как следует из изложенного, осуществляется численная реализация модели оптимизации. При этом в случае многокритериальной задачи оптимизации исходная векторная модель оптимизации должна быть предварительно преобразована к скалярному виду, в котором по определенному правилу вектору эффективности ё ставится в соответствие некоторый интегральный показатель эффективности, так называемый целевой функционал, или целевая функция. [c.167]

Преобразование векторных моделей оптимизации [c.203]

ПРЕОБРАЗОВАНИЕ ВЕКТОРНЫХ МОДЕЛЕЙ ОПТИМИЗАЦИИ К СКАЛЯРНОМУ ВИДУ [c.203]

Проблема оптимума векторной модели оптимизации. [c.203]

Действительно, конфликтность локальных критериев эффективности означает недостижимость так называемой утопической точки х у, т. е. некоторого идеального проекта, обладающего экстремальными значениями всех локальных показателей эффективности. Недостижимость утопической точки является следствием того, что х у не принадлежит D или же вообще не существует, что возможно в тех случаях, когда функции локальных критериев проекта или часть из них определены на ограниченных множествах. Поскольку идеальное решение задачи оптимизации оказывается, таким образом, невозможным, то очевидно, что оптимальный проект конструкции может быть определен только в итоге некоторого компромисса, являющегося результатом согласования несовместимых требований к показателям эффективности проекта на основе регулируемого снижения уровней их взаимной конфликтности. Отсюда следует, что формулировке принципа оптимальности в векторных задачах оптимизации предшествует выделение области компромиссов (области решений, оптимальных по Парето [16]). [c.204]

Выполнение неравенств (4.100) и (4.101) означает, что в области компромиссов Р ни одна из возможных реализаций проекта конструкции не может быть улучшена одновременно по всем его локальным показателям эффективности. Отсюда следует важный вывод о том, что независимо от выбора принципа оптимальности оптимум векторной модели оптимизации всегда принадлежит Р. [c.205]

По определению множества Р и смыслу векторного критерия эффективности проекта, любая точка х Р реализует оптимум векторной модели оптимизации, соответствующей выбранному принципу оптимальности. [c.205]

Рассмотренный пример наглядно показывает, что проблема выбора оптимума векторной модели оптимизации сводится к нетривиальной задаче математически строгого определения отношения порядка между элементами векторного множества — области ком- [c.205]

Общая форма математической модели объекта управления для решения задя динамической оптимизации — векторное дифференциальное уравнение [c.546]

Оптимизация векторных критериев (4) или (6) позволяет найти области Парето (см., например, [4]), т. е. такое множество стратегий управления, для которого невозможно одновременное улучшение всех скалярных критериев. Выбор единственного решения из множества Парето осуществляется путем скаляризации вектора эффективности [4, 6]. Для систем производственного типа широко используется метод скаляризации (так называемая пороговая оптимизация [1]), состоящий в выборе единственного критерия и преобразовании остальных в систему ограничений [c.174]

В предыдущих разделах были рассмотрены возможности решения проблем векторной оптимизации в иерархических структурах производственного типа. В конечном счете решение поставленной проблемы сведено к скалярной оптимизации в одноуровневых системах. Хотя такая оптимизация существенно проще оптимизации векторной, трудности ее реализации (в основном вычислительные) полностью еще не преодолены. В данном и последующих разделах будут рассмотрены возможности и эффективность использования для этих целей принципа сложности. Иерархичность структуры решения задач и декомпозиция будут играть при этом первостепенную роль. Начнем рассмотрение с нелинейных распределительных задач. [c.181]

Все известные методы векторной оптимизации непосредственно или косвенно сводят решаемые задачи к задачам скалярной оптимизации. Иначе говоря, частные критерии Fi(X), i=l, п, тем или иным способом объединяются в составной критерий F(X) =ф( 1(Х),. .., f (X)), который затем максимизируется (или минимизируется). Если составной критерий получается в результате проникновения в физическую суть функционирования системы и вскрытия объективно существующей взаимозависимости между частными критериями и составным критерием, то оптимальное решение является объективным. Однако отыскание подобной взаимозависимости чрезвычайно сложно, а может быть, и не всегда возможно. Поэтому на практике составной критерий обычно образуют путем формального объединения частных критериев, что неизбежно ведет к субъективности получаемого оптимального решения. Составной критерий иногда называют обобщенным или интегральным критерием. [c.16]

Минимаксные критерии. В теории векторной оптимизации особое место занимает принцпп компромисса, осиовап-ный на идее равномерности. На базе этого прннп.ипа работают минимаксные (максиминные) критерии. [c.22]

Для постановки и решения задачи параметрического синтеза необходимо формирование целевой функции F ), отражающей качество функционирования проектируемой системы или объекта. Векторный характер критериев оптимальности (многокритериальность) в задачах проектирования обусловливает сложность проблемы постановки задач оптимизации. [c.273]

Трудности сведения векторной оптимизации к скалярной приводят к попыткам упростить задачу в исходной постановке. Например, наиболее часто на практике все критерии, кроме основного, переводят в разряд ограничений и решают обычную однокритериальную задачу. Основная трудность такого подхода состоит в невозможности однозначного и обоснованного задания ограничений на неосновные критерии. [c.211]

Отметим, что задача (15.4) относится к классу задач векторной оптимизации, характеризующихся необходимостью выбора наилучшего решения при наличии нескольких критериев эффективности, которыми являются компоненты вектора Кя, v В этом случае возможно большое число принципов оптимальности, которые приводят к выбору различных оптимальных решений, В общем случае задача векторной оптимизации отличается значительной сложностью, причем в математическом плане она идентична задаче упорядочения векторных множеств, а выбор принципа оптимальности-выбору отношения порядка [12]. В прикладных задачах динамического синтеза машинных агрегатов проблема выбора принципа оптимальности сводится обычно к задаче скаляри-зации вектора эффективности Кд, v и заключается в выборе на основе некоторой схемы компромисса обобщенного скалярного критерия эффективности А (целевой апироксиыациониой функции). [c.254]

При динамическом синтезе машинных агрегатов компонентами вектора эффективности служат динамические нагрузки, динамические критерии качества, характеризующие работоспособность элементов силовой цепи или системы управления, и пр. В качестве принципа оптимальности при скаляризации векторного критерия эффективности в большинстве практически решаемых задач динамического синтеза машинных агрегатов принимается принцип чебышевской, равномерной оптимизации, что приводит к минимаксной трактовке оптимизационных задач (17.1) (см. 15) [c.273]

Постановка задачи такова по измеренным значениям смещения спектра собственных частот найти смещение упругодиссипативных параметров. В качестве предварительных этапов предусматривается решение задачи о собственных значениях и задачи идентификации. Вводится матрица чувствительности и линейная связь между частотным и параметрическим возмущением. Далее решается вариационная задача оптимизации скалярного функционала качества. В результате получено векторно-матричное алгебраическое уравнение, в котором с целью сжатия информации используются матрицы Грама. Имея в распоряжении экспериментальные данные о смещении частот, можно вычислить параметрические возмущения. Аналогичная процедура оценки параметрических возмущений может быть построена по измеренному смещению фазы механического импеданса [5]. [c.139]

Однако далеко не всегда удается определить и обосновать весовые коэффициенты. Существует принципиально иной подход к поставленной проблеме — векторная оптимизация, который наиболее детально разработан М. Е. Салуквадзе для широкого круга задач оптимального управления (программирования оптимальных траекторий, аналитического конструирования оптимальных регуляторов, исследования операций и др.) [5.47]. Указанный подход был применен для оптимизации параметров теплообменных аппаратов по нескольким критериям качества [5.48]. Сущность метода заключается в определении идеальной (утопической) точки в пространстве критериев качества и введении нормы в этом пространстве, с помощью которой находится реальная точка в пространстве оптимизируемых параметров, характеризующаяся наибольщей близостью критериев качества к своим наилучщим значениям. [c.218]

Таким образом, процесс оптимального управления безопасностью с помощью МОПЗ нельзя рассматривать как стремление к оптимизации одного скалярного параметра, и он должен быть дополнен соблюдением определенных ограничений. Другими словами, проблема управления безопасностью сводится к часто обсуждаемой [15, 16] проблеме поиска векторного критерия качества . В этом случае процесс управления безопасностью представляет собой не задачу оптимизации, а скорее задачу нахождения удовлетворительной траектории развития социально-экономической системы. Такой концептуальный подход к проблеме управления социальными системами впервые был сформулирован в [15, 16]. Отметим здесь же, что управление безопасностью с помощью векторного критерия качества требует соответственно введения и дополнения в принятое в данной работе определение термина безопасность . Если ранее постулировалось, что безопасность есть защита человека, то в рамках рассмотренной концепции следует определить безопасность уже как защиту не только человека, но и окружающей его среды от чрезмерной опасности. [c.102]

Оптимизация многоэкстремальных функций осуществляется методами случайного поиска [36]. Методы многокритериальной (векторной) оптимизации рассмотрены в [39]. [c.133]

Различают задачи однокритериальные, проводимые по одному обобщенному или доминирующему критерию (например, массе), и многокритериальные (задаад векторной оптимизации), проводимые одновременно по нескольким частным критериям. [c.16]

В книге рассматриваются современные модели расчета и методы параметрической оптимизации несущей способности оболочек вращения из композитов двумерной и пространственной структур армирования. Основное внимание при этом уделено оболочкам, работающим на статическую устойчивость или в режиме колебаний, эффективные деформативные характеристики которых определяются методами теории структурного моделирования композита. В задачах, содержащих оценки предельных состояний оболочек по прочности, используется феноменологическая структурная модель прочностных характеристик слоистого композита, параметры которой получены экспериментально. Подробно анализируются особенности постановки задач пара.метрической оптимизации оболочек из композитов. Показана взаимосвязь векторной и скалярной моделей задач оптимизации в случае формализуемых локальных критериев качества проекта. Значительное место отведено изложению и примерам приложения нового метода решения задач оптимизации оболочек из. многослойных композитов — метода обобщенных структурных параметров, применение которого позволяет получить наиболее полную информацию об опти.чальных проектах широкого класса практически важных задач оптимизации. Содержащиеся в книге результаты могут быть использованы для инженерного проектирования оболочек из волокнистых композитов. Табл. 23, ил. 58, библиогр. 181 назв. [c.4]

Различие между частными векторными моделями оптимизации, вообще говоря, не сводится к различию только числовых значений физико-механических характеристик соответствующих им вариантов конструкционного материала. В том случае, когда среди набора допустимых по проектной ситуации конструкцнон- [c.166]

Методы скаляризации моделей. Преобразование векторных моделей оптимизации к скалярному виду [c.206]

mash-xxl.info

Векторная оптимизация - Большая Энциклопедия Нефти и Газа, статья, страница 2

Векторная оптимизация

Cтраница 2

Известные результаты теории векторной оптимизации позволяют предложить различные координирующие функции. Рассмотрим некоторые из этих функций, опуская для простоты обозначений индекс /, указывающий номер элемента. [16]

В приложении к векторной оптимизации самоочевидным принципом [61] является сравнение относительных оценок или их относительных отклонений. Только при первоначальном условии, что они равны ( равнозначны) возможно в дальнейшем построение принципа оптимальности и вытекающих из него алгоритмов решения векторных задач математического программирования. [18]

Несомненно, метод векторной оптимизации еще ждет своего применения. Наиболее ощутимых результатов здесь следует ожидать при рассмотрении комплексных задач. [19]

Все известные методы векторной оптимизации непосредственно или косвенно сводят решаемые задачи к задачам скалярнойоптимизации. Если составной критерий получается в результате проникновения в физическую суть функционирования системы и вскрытия объективно существующей взаимозависимости между частными критериями и составным критерием, то оптимальное решение является объективным. Однако отыскание подобной взаимозависимости чрезвычайно сложно, а может быть, и не всегда возможно. Поэтому на практике составной критерий обычно образуют путем формального объединения частных критериев, что неизбежно ведет к субъективности получаемого оптимального решения. Составной критерий иногда называют обобщенным или интегральным критерием. [20]

Каким образом задача векторной оптимизации сводится к задаче скалярной оптимизации. [21]

Рассмотрим постановку задачи векторной оптимизации, содержательно интерпретируемую и с точки зрения принятия плановых решений. [23]

Реализация нового алгоритма векторной оптимизации, описанного в предыдущей главе, осуществлена на примере таких распространенных типовых процессов химической технологии, как химическая реакция и ректификация. [25]

Второй этап решения задачи векторной оптимизации обычно осуществляется с помощью экспертных оценок разработчиков аналитических приборов. [28]

Парето в дискретной задаче векторной оптимизации. [29]

Страницы: 1 2 3 4

Большая Энциклопедия Нефти и Газа. Векторной оптимизации

Задачи векторной оптимизации.

Основные понятия и определения.

Задача - векторная оптимизация - Большая Энциклопедия Нефти и Газа, статья, страница 1

Постановка задачи векторной оптимизации. Принципы оптимальности — МегаЛекции

Решение векторной задачи оптимизации методом

Векторная оптимизация - Большая Энциклопедия Нефти и Газа, статья, страница 3

Векторная оптимизация

Оптимизация векторная - Энциклопедия по машиностроению XXL

Векторная оптимизация - Большая Энциклопедия Нефти и Газа, статья, страница 2

Векторная оптимизация