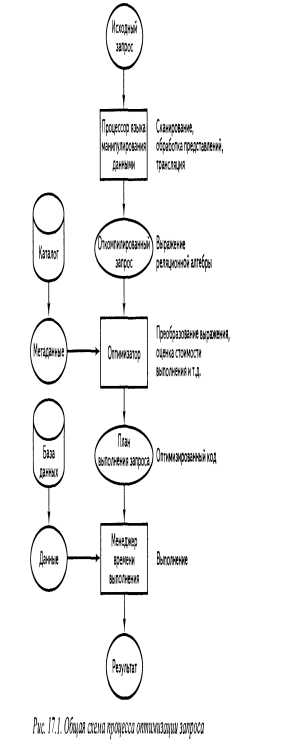
Лекции в doc. Лекция 1 Постановка задачи оптимизации Модель оптимизируемого объекта. Оптимизация лекции

НОУ ИНТУИТ | Лекция | Методы оптимизации

Аннотация: На экономических примерах рассматривается задача линейного программирования, в том числе двойственная к ней, а также графический и симплекс-метод ее решения. Даются постановки транспортной задачи и задачи о ранце. Вводится понятие графа, дается понятие о задачах коммивояжера, кратчайшего пути, максимального потока.

В настоящее время менеджер может использовать при принятии решения различные компьютерные и математические средства. В памяти компьютеров держат массу информации, организованную с помощью баз данных и других программных продуктов, позволяющих оперативно ею пользоваться. Экономико-математические и эконометрические модели позволяют просчитывать последствия тех или иных решений, прогнозировать развитие событий. Методы экспертных оценок, о которых пойдет речь ниже, также весьма математизированы и используют компьютеры.

Наиболее часто используются оптимизационные модели принятия решений. Их общий вид таков:

Здесь - параметр, который менеджер может выбирать (управляющий параметр). Он может иметь различную природу - число, вектор, множество и т.п. Цель менеджера - максимизировать целевую функцию , выбрав соответствующий .. При этом он должен учитывать ограничения на возможные значения управляющего параметра - он должен лежать в множестве . Ряд примеров оптимизационных задач менеджмента приведен ниже.

Линейное программирование

Среди оптимизационных задач менеджмента наиболее известны задачи линейного программирования, в которых максимизируемая функция является линейной, а ограничения задаются линейными неравенствами. Начнем с примера.

Производственная задача. Цех может производить стулья и столы. На производство стула идет 5 единиц материала, на производство стола - 20 единиц (футов красного дерева). Стул требует 10 человеко-часов, стол - 15. Имеется 400 единиц материала и 450 человеко-часов. Прибыль при производстве стула - 45 долларов США, при производстве стола - 80 долларов США. Сколько надо сделать стульев и столов, чтобы получить максимальную прибыль?

Обозначим: - число изготовленных стульев, - число сделанных столов. Задача оптимизации имеет вид:

В первой строке выписана целевая функция - прибыль при выпуске стульев и столов. Ее требуется максимизировать, выбирая оптимальные значения переменных и При этом должны быть выполнены ограничения по материалу (вторая строчка) - истрачено не более 400 футов красного дерева. А также и ограничения по труду (третья строчка) - затрачено не более 450 часов. Кроме того, нельзя забывать, что число столов и число стульев неотрицательны. Если , то это значит, что стулья не выпускаются. Если же хоть один стул сделан, то положительно. Но невозможно представить себе отрицательный выпуск - не может быть отрицательным с экономической точки зрения, хотя с математической точки зрения такого ограничения усмотреть нельзя. В четвертой и пятой строчках задачи и констатируется, что переменные неотрицательны.

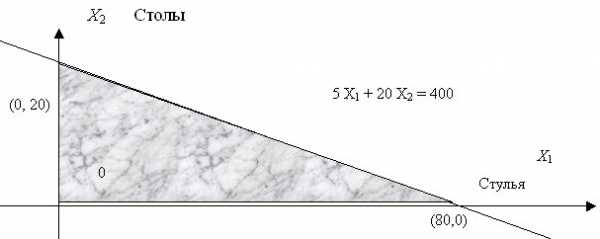Условия производственной задачи можно изобразить на координатной плоскости. Будем по горизонтальной оси абсцисс откладывать значения а по вертикальной оси ординат - значения . Тогда ограничения по материалу и последние две строчки оптимизационной задачи выделяют возможные значения объемов выпуска в виде треугольника (рис.12.1).

Рис. 12.1. Ограничения по материалу

Таким образом, ограничения по материалу изображаются в виде выпуклого многоугольника, конкретно, треугольника. Этот треугольник получается путем отсечения от первого квадранта примыкающей к началу координат зоны. Отсечение проводится прямой, соответствующей второй строке исходной задачи, с заменой неравенства на равенство. Прямая пересекает ось , соответствующую стульям, в точке (80,0). Это означает, что если весь материал пустить на изготовление стульев, то будет изготовлено 80 стульев. Та же прямая пересекает ось , соответствующую столам, в точке (0,20). Это означает, что если весь материал пустить на изготовление столов, то будет изготовлено 20 столов. Для всех точек внутри треугольника выполнено неравенство, а не равенство - материал останется.

Аналогичным образом можно изобразить и ограничения по труду (рис.12.1).

Таким образом, ограничения по труду, как и ограничения по материалу, изображаются в виде треугольника. Этот треугольник также получается путем отсечения от первого квадранта примыкающей к началу координат зоны. Отсечение проводится прямой, соответствующей третьей строке исходной задачи, с заменой неравенства на равенство. Прямая пересекает ось , соответствующую стульям, в точке (45,0). Это означает, что если все трудовые ресурсы пустить на изготовление стульев, то будет сделано 45 стульев. Та же прямая пересекает ось , соответствующую столам, в точке (0,30). Это означает, что если всех рабочих поставить на изготовление столов, то будет сделано 30 столов. Для всех точек внутри треугольника выполнено неравенство, а не равенство - часть рабочих будет простаивать.

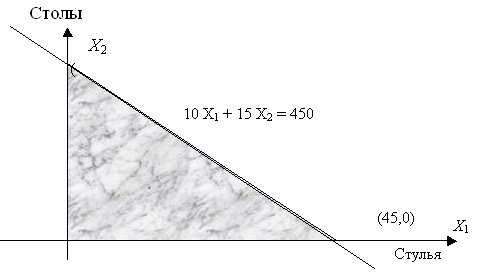Рис. 12.2. Ограничения по труду

Мы видим, что очевидного решения нет - для изготовления 80 стульев есть материал, но не хватает рабочих рук, а для производства 30 столов есть рабочая сила, но нет материала, Значит, надо изготавливать и то, и другое. Но в каком соотношении?

Чтобы ответить на этот вопрос, надо "совместить" рис.12.1 и рис.12.2, получив область возможных решений, а затем проследить, какие значения принимает целевая функция на этом множестве (рис.12.3).

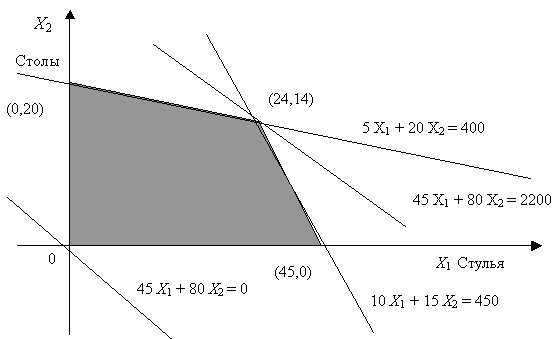Рис. 12.3. Основная идея линейного программирования

Таким образом, множество возможных значений объемов выпуска стульев и столов , или, в других терминах, множество , задающее ограничения на параметр управления в общей оптимизационной задаче, представляет собой пересечение двух треугольников, т.е. выпуклый четырехугольник, показанный на рис.12.1. Три его вершины очевидны - это (0,0), (45,0) и (0,20). Четвертая - это пересечение двух прямых - границ треугольников на рис.12.1 и рис.12.2, т.е. решение системы уравнений

Из первого уравнения: . Подставляем во второе уравнение:

следовательно, , откуда . Итак, четвертая вершина четырехугольника - это (24, 14).

Надо найти максимум линейной функции на выпуклом многоугольнике. (В общем случае линейного программирования - максимум линейной функции на выпуклом многограннике, лежащем в конечномерном линейном пространстве.) Основная идея линейного программирования состоит в том, что максимум достигается в вершинах многоугольника. В общем случае - в одной вершине, и это - единственная точка максимума. В частном - в двух, и тогда отрезок, их соединяющий, тоже состоит из точек максимума.

Целевая функция принимает минимальное значение, равное 0, в вершине (0,0). При увеличении аргументов эта функция увеличивается. В вершине (24,14) она принимает значение 2200. При этом прямая проходит между прямыми ограничений и , пересекающимися в той же точке. Отсюда, как и из непосредственной проверки двух оставшихся вершин, вытекает, что максимум целевой функции, равный 2200, достигается в вершине (24,14).

Таким образом, оптимальный выпуск таков: 24 стула и 14 столов. При этом используется весь материал и все трудовые ресурсы, а прибыль равна 2200 долларам США.

Двойственная задача. Каждой задаче линейного программирования соответствует так называемая двойственная задача. В ней по сравнению с исходной задачей строки переходят в столбцы, неравенства меняют знак, вместо максимума ищется минимум (или, наоборот, вместо минимума - максимум). Задача, двойственная к двойственной - эта сама исходная задача. Сравним исходную задачу (слева) и двойственную к ней (справа):

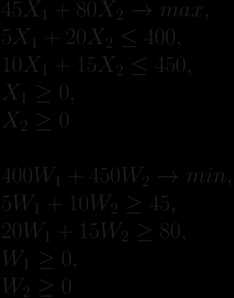
Почему двойственная задача столь важна? Можно доказать, что оптимальные значения целевых функций в исходной и двойственной задачах совпадают (т.е. максимум в исходной задаче совпадает с минимумом в двойственной). При этом оптимальные значения и показывают стоимость материала и труда соответственно, если их оценивать по вкладу в целевую функцию. Чтобы не путать с рыночными ценами этих факторов производства, и называют "объективно обусловленными оценками" сырья и рабочей силы.

Линейное программирование как научно-практическая дисциплина. Из всех задач оптимизации задачи линейного программирования выделяются тем, что в них ограничения - системы линейных неравенств или равенств. Ограничения задают выпуклые линейные многогранники в конечном линейном пространстве. Целевые функции также линейны.

Впервые такие задачи решались советским математиком Л.В. Канторовичем (1912-1986) в 1930-х годах как задачи производственного менеджмента с целью оптимизации организации производства и производственных процессов, например, процессов загрузки станков и раскройки листов материалов. После второй мировой войны аналогичными задачами занялись в США. В 1975 г. Т. Купманс (1910-1985, родился в Нидерландах, работал в основном в США) и академик АН СССР Л.В. Канторович были награждены Нобелевскими премиями по экономике.

Рассмотрим несколько типовых задач линейного программирования .

Задача о диете (упрощенный вариант). Предположим для определенности, что необходимо составить самый дешевый рацион питания цыплят, содержащий необходимое количество определенных питательных веществ (для простоты, тиамина Т и ниацина Н).

Таблица 12.1. Исходные данные в задаче об оптимизации смеси Содержание в 1 унции К Содержание в 1 унции С Потребность

Вещество Т	0,10 мг	0,25 мг	1,00 мг
Вещество Н	1,00 мг	0,25 мг	5,00 мг
Калории	110,00	120,00	400,00
Стоимость 1 унции, в центах	3,8	4,2

Пищевая ценность рациона (в калориях) должна быть не менее заданной. Пусть для простоты смесь для цыплят изготавливается из двух продуктов - К и С. Известно содержание тиамина и ниацина в этих продуктах, а. также питательная ценность К и С (в калориях). Сколько К и С надо взять для одной порции куриного корма, чтобы цыплята получили необходимую им дозу веществ Н и Т и калорий (или больше), а стоимость порции была минимальна? Исходные данные для расчетов приведены в табл.12.1.

Задача линейного программирования имеет вид:

Ее графическое решение представлено на рис.4. Ради облегчения восприятия четыре прямые обозначены номерами (1) - (4). Прямая (1) - это прямая 1,00 К + 0,25 С = 5,00 (ограничение по веществу Н). Она проходит, как и показано на рисунке, через точки (5,0) на оси абсцисс и (0,20) на оси ординат. Обратите внимание, что допустимые значения параметров (К, С) лежат выше прямой (1) или на ней, в отличие от ранее рассмотренных случаев в предыдущей производственной задаче линейного программирования.

Рис. 12.4. Графическое решение задачи об оптимизации смеси

Прямая (2) - это прямая 110,00 К + 120,00 С = 400,00 (ограничение по калориям). Обратим внимание, что в области неотрицательных С она расположена всюду ниже прямой (1). Действительно, это верно при К = 0, прямая (1) проходит через точку (0,20), а прямая (2) - через расположенную ниже точку (0, 400/120). Точка пересечения двух прямых находится при решении системы уравнений

Из первого уравнения . Подставим во второе: , откуда . Следовательно, , т.е. решение достигается при отрицательном С. Это и означает, что при всех положительных С прямая (2) лежит ниже прямой (1). Значит, если выполнено ограничения по Н, то обязательно выполнено и ограничение по калориям. Мы столкнулись с новым явлением - некоторые ограничения с математической точки зрения могут оказаться лишними. С точки зрения менеджера они необходимы, отражают существенные черты постановки задачи, но в данном случае внутренняя структура задачи оказалась такова, что ограничение по калориям не участвует в формировании допустимой области параметров и нахождении решения.

Прямая (4) - это прямая (ограничение по веществу Т). Она проходит, как и показано на рисунке, через точки (10,0) на оси абсцисс и (0,4) на оси ординат. Обратите внимание, что допустимые значения параметров (К, С) лежат выше прямой (4) или на ней, как и для прямой (1).

Следовательно, область допустимых значений параметров (К, С) является неограниченной сверху. Из всей плоскости она выделяется осями координат (лежит в первом квадранте) и прямыми (1) и (4) (лежит выше этих прямых, а также включает граничные отрезки). Область допустимых значений параметров, т.е. точек (К, С), можно назвать "неограниченным многоугольником". Минимум целевой функции может достигаться только в вершинах этого "многоугольника". Вершин всего три. Это пересечения с осями абсцисс (10,0) и ординат (0,20) прямых (1) и (4) (в каждом случае из двух пересечений берется то, которое удовлетворяет обоим ограничениям). Третья вершина - это точка А пересечения прямых (1) и (4), координаты которой находятся при решении системы уравнений

Из второго уравнения , из первого , откуда и . Итак, .

Прямая (3) на рис.4 - это прямая, соответствующая целевой функции Она проходит между прямыми (1) и (4), задающими ограничения, и минимум достигается в точке А, через которую и проходит прямая (3). Следовательно, минимум равен . Задача об оптимизации смеси полностью решена.

Двойственная задача, построенная по описанным выше правилам, имеет приведенный ниже вид (мы повторяем здесь и исходную задачу об оптимизации смеси, чтобы наглядно продемонстрировать технологию построения двойственной задачи):

Минимальное значение в прямой задаче, как и должно быть, равно максимальному значению в двойственной задаче, т.е. оба числа равны . Интерпретация двойственных переменных: - "стоимость" единицы вещества , а - "стоимость" единицы вещества , измеренные "по их вкладу" в целевую функцию. При этом , поскольку ограничение на число калорий никак не участвует в формировании оптимального решения. Итак, - это т.н. объективно обусловленные оценки (по Л.В. Канторовичу) ресурсов (веществ Т и Н, калорий).

Планирование номенклатуры и объемов выпуска. Вернемся к организации производства. Предприятие может выпускать автоматические кухни (вид кастрюль), кофеварки и самовары. В табл.12.2 приведены данные о производственных мощностях, имеющихся на предприятии (в штуках изделий).

Таблица 12.2. Производственные мощности (в шт.) Кухни Кофеварки Самовары

Штамповка	20000	30000	12000
Отделка	30000	10000	10000
Сборка	20000	12000	8000
Объем выпуска
Удельная прибыль (на одно изделие)	15	12	14

При этом штамповка и отделка проводятся на одном и том же оборудовании. Оно позволяет штамповать за заданное время или 20000 кухонь, либо 30000 кофеварок, либо и то, и другое, не в меньшем количестве. А вот сборка проводится на отдельных участках.

Задача линейного программирования имеет вид:

Здесь:

(0) - обычное в экономике условие неотрицательности переменных,

(1) - ограничение по возможностям штамповки (выраженное для облегчения восприятия в процентах),

(2) - ограничение по возможностям отделки,

(3) - ограничение по сборке для кухонь,

(4) - то же для кофемолок,

(5) - то же для самоваров (как уже говорилось, все три вида изделий собираются на отдельных линиях).

Наконец, целевая функция F - общая прибыль предприятия.

Заметим, что неравенство (3) вытекает из неравенства (1), а неравенство (4) - из (2). Поэтому неравенства (3) и (4) можно из формулировки задачи линейного программирования исключить.

Отметим сразу любопытный факт. Как будет установлено, в оптимальном плане , т.е. самовары выпускать невыгодно.

www.intuit.ru

Лекция 10 Оптимизация технологических процессов в сапр тп

Задачи проектирования технологических процессов (ТП) являются многовариантными. К многовариантным относятся, например, задачи выбора оборудования, режущего инструмента, расчета режимов резания и т.д. В разрабатываемом ТП число возможных комбинаций переходов, схем базирования, методов обработки и компоновок операций даже для простых деталей значительно, а для более сложных возрастает чрезвычайно.

Разные варианты ТП изготовления одной и той же детали вследствие различий в структуре, применяемом оборудовании, инструменте, режимах резания и т.д. имеют различные выходные показатели: производительность, себестоимость, расход металла, загрузку оборудования и др.

Наличие нескольких вариантов решения задачи (вариантов ТП) естественным путем приводит к задаче выбора наилучшего варианта. В нашем случае таковым будет вариант ТП, обеспечивающий выполнение в конкретных производственных условиях все требования чертежа детали и дающий наилучшее значение выходных показателей. Такой технологический процесс носит названиеоптимального. Таким образом, задача проектирования ТП по своей природе является оптимизационной.

Постановка задачи проектирования оптимального ТП

Технологический процесс называется оптимальным, если он обеспечивает:

Выполнение системы ограничений, отражающих условия протекания ТП и требования, предъявляемые к нему и детали.
Экстремум целевой функции.

ТП, оптимальный по одному критерию, может быть далеко не оптимальным по другому. Например, максимум производительности операции может не соответствовать минимуму ее себестоимости. Поэтому при постановке задачи проектирования оптимального ТП весьма важным является выбор критерия оптимальности.

Известен и применяется ряд различных критериев оптимальности, используемых для оптимизации как ТП в целом, так и при решении отдельных частных технологических задач. Наиболее часто используются следующие критерии оптимальности ТП:

Штучное время - (целевая функция).
Производительность (целевая функция).</P.< li>
Себестоимость детали (целевая функция).

В целом же для постановки задачи оптимизации ТП (как и любой другой задачи оптимизации) необходимо сформировать математическую модель процесса обработки детали (сборки изделия), которая должна включать в себя:

Критерий (критерии) оптимальности ТП.
Целевую функцию.
Систему ограничений.
Четко определенные входные, выходные и внутренние параметры.
Управляемый (варьируемый) параметр или управляемые (варьируемые) параметры, которые выделяются из числа внутренних параметров.

После формирования математической модели необходимо определить (выбрать, разработать) метод решения задачи оптимизации.

Различают три вида оптимизации ТП:

Структурную.
Параметрическую.</P.< li>
Структурно – параметрическую.

Структурная оптимизация– это определение оптимальной структуры ТП (вида заготовки, технологического маршрута, модели оборудования, типоразмера инструмента и т.д.).

Параметрическая оптимизацияТП заключается в расчете оптимальных припусков и межпереходных размеров, режимов резания и т.д.

Структурно – параметрическаяоптимизация представляет собой комбинацию двух первых.

Параметрическая оптимизация ТП на примере расчета оптимальных режимов резания представлена подробно в дисциплине «Математическое моделирование процессов в машиностроении» в курсе лабораторных работ и здесь не рассматривается.

Структурная оптимизация ТП

Принципиальное отличие структурной оптимизации от параметрической оптимизации состоит в сущности оптимизируемых параметров. При структурной оптимизации они по своей природе являются неупорядоченными переменными. В параметрической оптимизации параметры представляют собой переменные, для которых существует понятие больше или меньше и которые естественным образом могут быть размещены в координатной системе. В структурной же оптимизации эти параметры не являются по существу числовыми. Параметрами структурной оптимизации являются, например, модели станков, типы инструментов, схемы базирования, т.е. варианты типовых решений.

Структурная оптимизация рассматривает последовательно каждую задачу технологического проектирования. Таким образом, весь процесс проектирования расчленяется на несколько взаимосвязанных уровней. Процесс проектирования на каждом уровне представляет собой многовариантную процедуру. В результате проектирования на всех уровнях образуется граф допустимых вариантов ТП, отвечающих заданным ограничениям – рис.10.1.

Задача структурной оптимизациисостоит в поиске ветви графа, обеспечивающей экстремум целевой функции. В силу неупорядоченности параметров основной метод структурной оптимизации состоит в последовательном переборе возможных вариантов. Чтобы выбрать один оптимальный вариант, необходимо до конца спроектировать очень большое количество допустимых техническими и технологическими ограничениями вариантов ТП.

Для реального ТП изготовления деталей даже средней сложности таких вариантов может быть огромное множество. Перебор всех вариантов даже при помощи современных быстродействующих компьютеров занимает очень большое время. Для уменьшения времени проектирования используются следующие приемы.

Прием 1. Эффективность процесса проектирования можно резко повысить, если организовать отбор рациональных вариантов проектных решений на каждом уровне проектирования. Однако при этом возникает проблема формирования критериев промежуточного отбора наиболее рациональных вариантов на различных уровнях. Например, на уровне (этапе) выбора заготовки анализ вариантов можно производить по критерию «себестоимость заготовки». Данный критерий можно достоверно рассчитать на этом этапе. Но указанный критерий не является до конца объективным. «Дешевая» заготовка (например, круглый прокат для изготовления ступенчатого вала) даст «дорогую» механическую обработку. А «дорогая» заготовка (например, штамповка для изготовления такого же вала) обеспечит более «дешевую» механическую обработку. Целесообразно, поэтому, использовать в качестве критерия суммарную стоимость заготовки и механической обработки. Однако стоимость механической обработки можно рассчитать только после разработки всего ТП. Следовательно, пропадает смысл «поэтапной оптимизации».

Но, все – таки, если удачно назначить критерии на каждом уровне проектирования, такой подход имеет смысл. При его применении может оказаться несколько равнозначных вариантов ТП, но среди них уже гораздо легче выбрать оптимальный вариант. Общая модель процесса технологического проектирования с поэтапным отсечением решений на каждом уровне может быть представлена следующим образом – см. рис.10.2.

Прием 2. «Предпроектная оптимизация».Рассмотрим этот прием на примере выбора модели круглошлифовального станка. Множествовозможных вариантов моделей круглошлифовальных станков определяется с помощью таблиц соответствий. Фрагмент такой таблицы приведен ниже в табл. 10.1.

Таблица 10.1

Левая часть таблицы, обозначающая ее строки, представляет собой множество типовых решений. Верхняя часть таблицы, обозначающая ее столбцы, - условия применимости и их числовые значения. Центральная часть таблицы – булева матрица соответствий, в которой зафиксированы связи между решениями и определяющими их применимость значениями условий. Наличие связи обозначают единицей, отсутствие – нулем. Иногда вместо единицы применяют штриховку соответствующей клетки, вместо нуля клетку оставляют незаштрихованной.

По имеющемуся комплексу исходных данных из таблицы соответствий принимаются те решения, в строках которых булева матрица имеет единицы для всех значений факторов, входящих в условия применимости.

На базе таблиц соответствий строятся алгоритмы, позволяющие выбирать множестводопустимых решений, из которых путем последовательного перебора выбираются наилучшие решения согласно тому или иному критерию оптимальности.

Но и при локализованной структурной оптимизации перебор и анализ всех допустимых решений, выбираемых из таблиц соответствий, занимает большое время. Для сокращения времени счета при структурной оптимизации с использованием таблиц соответствий производят так называемую предпроектную оптимизациюна стадии разработки информационного обеспечения. Для этого используютграфики соответствий.

Построим график соответствий для одного из условий применимости, например, для первого – см. табл. 10.1. Критерий оптимизации – себестоимость , соответственно, целевая функция. Примем- типовые решения (здесь – модели станков),- диапазоны условий применимости. Пусть количество типовых решений (моделей станков) равняется не трем, а семи, количество диапазонов в первом условии применимости – пять.

График соответствий показан на рис. 10.3.

Соединяя линией решения, имеющие минимальную себестоимость, получаем линию минимальной себестоимости. Решения, лежащие на этой линии, называют предпочтительными.

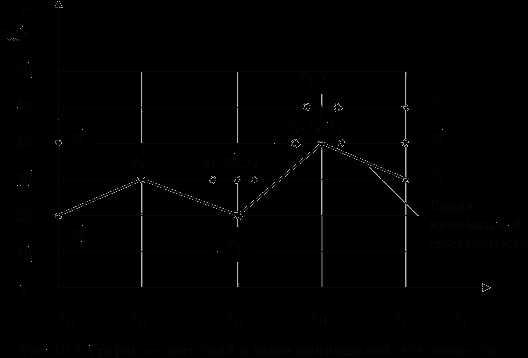
Построим теперь таблицу соответствий, в которой единицы заменены штриховкой и предпочтительные решения выделены звездочками – см. табл. 10.2.

Таблица 10.2

Другими словами в таблице штриховкой показаны технически возможные решения, звездочками – экономически эффективные решения.

Поиск решений в таблице соответствий сначала осуществляется по предпочтительным решениям. В случае отсутствия подходящего предпочтительного решения поиск производится по оставшимся допустимым.

Такой подход эффективен для случаев наличия экстремума целевой функции. Но в ряде случаев решение получается неопределенным. Так, например, в нашем случае для диапазона условия применимости имеется несколько эффективных решений.

Прием 3.Следующим шагом в развитии предпроектной оптимизации является переход от булевых матриц соответствий к оценочным матрицам. В этом случае в соответствующих клетках матрицы соответствий проставляются значения себестоимости с графика соответствий – см. табл.10.3.

Таблица 10.3

Подобные матрицы заполняются для всех условий применимости.

Алгоритм поиска оптимального решения по оценочной матрице состоит в поиске одноименной строки в оценочных матрицах для всех диапазонов условий применимости, обеспечивающей наименьшую сумму затрат для данного условия задачи.

Рассмотренная процедура повторяется для каждого уровня проектирования, приводя в конечном итоге к варианту с оптимальной структурой.

studfiles.net

Лекции по методам оптимизации [DOC]

Добавлен пользователем Ксения Хазова, дата добавления неизвестна
Отредактирован 26.10.2016 02:22

Линейное программирование. Задача линейного программирования (ЗЛП) Симплекс – метод (решение ЗЛП) Задача минимизации. Метод искусственного базиса. Решение общей ЗЛП. Двойственные ЗЛП. Несимметричные двойственные задачи. Теорема двойственности. Симметричные двойственные задачи. Соотношения между решениями двойственной и исходной задачи. Нелинейное программирование. Задачи нелинейного программирования (ЗНП).Задачи оптимизации на безусловный экстремум. Задачи на условный экстремум. Задача выпуклого программирования (ЗВП). Теорема Куна - Таккера. Частная теорема Куна – Таккера. Задача квадратичного программирования (ЗКП). Вспомогательная задача линейного программирования. Решение задачи оптимизации (ЗВП) с ограничениями типа неравенств. Алгоритм градиентной процедуры. Метод возможных направлений (метод Зонтендейка). Сходимость метода возможных направлений. Численные методы поиска оптимального решения ЗНП с ограничениями типа равенств. Теорема Люстерника.Необходимое условие оптимальности задачи с ограничениями типа равенств. Алгоритм решения задачи с ограничениями типа равенств. Решение общей задачи нелинейного программирования. Алгоритм. Решение ЗНП методом линеаризации. Алгоритм построения последовательности, сходящейся к оптимальному решению исходной задачи. Метод штрафных функций. Методы случайного поиска. Методы оптимизации теории оптимальных процессов. Задача оптимального управления (ЗОУ). Задание граничных условий. Решение ЗОУ с ограничениями типа неравенств. Алгоритм. Оптимизация систем с ограничениями типа равенств. Алгоритм. Оптимизация систем со смешанными ограничениями типа равенств и неравенств. Алгоритм. Оптимизация систем с подвижными границами (концами).

Чтобы скачать этот файл зарегистрируйтесь и/или войдите на сайт используя форму сверху.
Регистрация

www.twirpx.com

Оптимизация сапр Лекция №1 Постановка задачи оптимизации

Модель оптимизируемого объекта.

1) Анализ модели:определ. вект. вых. хар-к.

2) Изменение модели: → структурные: кол-во переменных, кас. Ф (измен.)

→ параметрические: изм. пар-ров

–обычно фиксирован.

В обычно выделяют: подмножество коэф.наз-ся вектор варьируемого коэф.

Будем считать, что . Обычно на значения коэф.накладываются ограничения, определ. услов. их физ. реализуемости.

Скорее всего в этой последовательностинаилучший вариант.

Задача. Найти такое значение обеспеч. наилучшие вых. хар-ки (чаще всего встреч.)

Свойства модели (влияющие на нахождение наилучш. вых. хар-ки.):

Аналит. зависимость, анал. выр. исп. теорет. зн. < 1%

Алгорит. завис-ть, вычисл. задача (система ур-й), 99%

Дискрет. или непрерыв. хар-р зависимость вых. хар-к от варьир. параметров.

Если хар-р зав. непр., то ф-ии бывают гладкие или нет (это можно оценить) и порядок гладкости.

Наклад. ограничения на вар. парам. или нет? Можно ли их классифицировать, если есть?
Трудоемкость процесса анализа, вычисл. производных.

Эти свойства модели очень важны.

Пример:

Смысл ур-й менять нельзя, но можно менять коэффициент.

Будем рассматривать параметр. изменения.

Постановка задач оптимизации.

Дано:

Мат. модель.
D – это ограничение на , вытекающее из специфики решения задачи.
- то, к чему должны стремиться
- целевая функция, критерий качества, функционал качества (разница между желаемым и действительным).

Замечание. Построению F будет посвящена отдельная тема.

Функционал отображает вектор в скаляр.

Не всегда функционал отображает разницу между жел. и действит., но иногда и занимается поиском max и min и т.д.

Смысл F:

А) «как можно больше» (обратная задача)

Б) «как можно меньше»

В) «как можно ближе» (min разности между желаемым и действительным)

Во всех трех случаях речь идет о поиске min.

Найти:

Обсуждение основных подходов к решению задач.

Аналитический – исп. ан. мет. для поиска min значений. Недостаток: треб. аналит. зав. (1%), которая чаще всего отсутствует., треб. высокая квалификация человека, задачи могут оказаться очень сложными.
Сканирование

Если сотни параметров, то этот подход не подходит.

Нас интересует время решения этой задачи

Нам нужно уменьшить Т.

Типовой алгоритм:

Начало

Синтез структ. мод.

Задание N, i=0

Анализ мод.

Вычисл.

конец

Задача математического программирования

Если целевая функция или ограничения не линейны, то это задача нелинейного математического программирования.

Если целевая функция или ограничения линейны, то это задача линейного математического программирования.

В течение ближайших 6 тем не обращаем внимания на F.

В зависимости от вида целевой функции и ограничений задачу можно классифицировать.

Если ограничения заданы, то задача условной оптимизации, иначе безусловной оптимизации.

studfiles.net

Лекции. Оптимизация систем управления. Оптимальное управление и оптимальные мехатронные системы

Лекции. Оптимизация систем управления. Оптимальное управление и оптимальные мехатронные системыскачать (1529.3 kb.)

Доступные файлы (22):

содержание

ЛЕКЦИЯ 10.doc

Реклама MarketGid: ЛЕКЦИЯ 10 План лекции

Математическая модель объекта третьего порядка.
Уравнение для расчета поверхности переключения.
Формы задания поверхности переключения.
Структурная схема оптимальной по быстродействию САР.

4. Пример. 2. Рассмотрим применение изложенной выше теории для синтеза оптимальной системы третьего порядка.

Пусть движение объекта задаётся уравнением

. (3.15)

На управляющий параметр наложено ограничение

Задающее воздействие имеет вид

где , , - произвольные числа.

Введём ошибку

. (3.16)

Из равенства (3.16) следует, что

Тогда уравнение (3.15) можно записать в виде

. (3.17)

В соответствии с теоремой о числе переключений оптимальное по быстродействию управление релейно и в переходном процессе допускается не более двух переключений реле. Так как уравнение (3.17) имеет третий порядок, то в фазовом пространстве системы с декартовыми координатами , , существует поверхность переключения , по одну сторону от которой - оптимальное управление , а по другую - .

В обратном времени уравнение (3.17) принимает вид

. (3.18)

Найдём решение уравнения (3.18), предполагая, что :

■ ,

, □ (3.19)

где , и - константы интегрирования.

Перейдём в уравнениях (3.19) к производным по прямому времени:

, ,

Константы , , определяются из условий

, , .

Окончательно получим

■

□ (3.20)

Уравнения (3.20) позволяют рассчитать любую траекторию, входящую в совокупность (см. рис. 3.4).

Назовём полутраекторией траекторию движения системы (3.17) (или (3.18)), соответствующую постоянному знаку управления . Будем предполагать, что обратное время вводится отдельно для каждой полутраектории. Структура оптимальной поверхности переключения представлена на рис. 3.4.

Положим в уравнениях (3.20) . Уравнения

, , . (3.21)

при задают (в функции параметра ) линию , а при - линию . Отметим, что параметр необходимо изменять от нуля в положительную сторону.

В результате численных расчётов, выполненных с помощью уравнений (3.21), линия задаётся совокупностью дискретных точек. На рис. 3.7 представлена проекция линии на плоскость . Если над каждой расчётной точкой записать соответствующее ей значение координаты , то с помощью рис. 3.7 можно задать линию .

Поверхность переключения образуют полутраектории, примыкающие к линии . Для определения, например, полутраектории (рис. 3.8), примыкающей с управлением к линии , необходимо в уравнениях (3.20) положить , а в качестве начальных значений , , взять координаты точки . Параметр при этом по-прежнему отсчитывается от нуля в положительную сторону. Аналогичным образом строятся другие полутраектории, образующие совокупность .

Рис. 3.7.

Полутраектории, входящие в совокупность , характеризуются управлением и примыкают к линии . Каждая из этих полутраекторий может быть рассчитана по уравнениям (3.20). Для этого в уравнениях (3.20) следует положить , а начальные значения должны совпадать с координатами соответствующей точки линии . Легко видеть, что полутраектории, входящие в совокупность , симметричны относительно начала координат полутраекториям, входящим в совокупность .

На рис. 3.8 изображены проекции образующих поверхность переключения траекторий на плоскость . Рис. 3.8 позволяет задать поверхность переключения. Для этого над каждой расчётной точкой необходимо записать соответствующее ей значение координаты . Отметим, что с практической точки зрения результаты расчётов целесообразно оформлять в виде рис. 3.8.

Рис. 3.8.

Поверхность переключения часто задают в виде таблицы с двумя входами. Для получения такой таблицы необходимо на рис. 3.8 наложить координатную сетку и с помощью интерполяции определить значения координаты в узлах этой сетки. В верхней строке таблицы записываются значения координаты , в левом столбце - значения координаты , а на пересечении строки и столбца - соответствующее им значение координаты .Таблица 3.1.

Положим, что - уравнение поверхности переключения. Нетрудно установить, что выше поверхности переключения , а ниже поверхности переключения . Оптимальный закон управления, таким образом, можно записать в виде

На рис. 3.9 представлена структурная схема оптимальной по быстродействию системы управления.

Рис. 3.9.

Скачать файл (1529.3 kb.)

gendocs.ru

Лекции в doc - Лекция 1 Постановка задачи оптимизации Модель оптимизируемого объекта

Оптимизация САПРЛекция №1Постановка задачи оптимизации

Модель оптимизируемого объекта.

1) Анализ модели: определ. вект. вых. хар-к.

2) Изменение модели: → структурные: кол-во переменных, кас. Ф (измен.)

→ параметрические: изм. пар-ров

– обычно фиксирован.

В обычно выделяют: подмножество коэф. наз-ся вектор варьируемого коэф.

Будем считать, что . Обычно на значения коэф. накладываются ограничения, определ. услов. их физ. реализуемости.

Скорее всего в этой последовательности наилучший вариант.

Задача. Найти такое значение обеспеч. наилучшие вых. хар-ки (чаще всего встреч.)

Свойства модели (влияющие на нахождение наилучш. вых. хар-ки.):

Аналит. зависимость, анал. выр. исп. теорет. зн.

Алгорит. завис-ть, вычисл. задача (система ур-й), 99%

Дискрет. или непрерыв. хар-р зависимость вых. хар-к от варьир. параметров.

Если хар-р зав. непр., то ф-ии бывают гладкие или нет (это можно оценить) и порядок гладкости.

Наклад. ограничения на вар. парам. или нет? Можно ли их классифицировать, если есть?
Трудоемкость процесса анализа, вычисл. производных.

Эти свойства модели очень важны.

Пример:

Смысл ур-й менять нельзя, но можно менять коэффициент.

Будем рассматривать параметр. изменения.

Постановка задач оптимизации.

Дано:

Мат. модель.
D – это ограничение на , вытекающее из специфики решения задачи.
- то, к чему должны стремиться
- целевая функция, критерий качества, функционал качества (разница между желаемым и действительным).

Замечание. Построению F будет посвящена отдельная тема.

Функционал отображает вектор в скаляр.

Не всегда функционал отображает разницу между жел. и действит., но иногда и занимается поиском max и min и т.д.

Смысл F:

А) «как можно больше» (обратная задача)

Б) «как можно меньше»

В) «как можно ближе» (min разности между желаемым и действительным)

Во всех трех случаях речь идет о поиске min.

Найти:

Обсуждение основных подходов к решению задач.

Аналитический – исп. ан. мет. для поиска min значений. Недостаток: треб. аналит. зав. (1%), которая чаще всего отсутствует., треб. высокая квалификация человека, задачи могут оказаться очень сложными.
Сканирование

Если сотни параметров, то этот подход не подходит.

Поисковые методы оптимизации

Нас интересует время решения этой задачи

Нам нужно уменьшить Т.

Типовой алгоритм:

НачалоСинтез структ. мод.Задание N, i=0Анализ мод.Вычисл.

конец

Задача математического программирования

Если целевая функция или ограничения линейны, то это задача линейного математического программирования.

В течение ближайших 6 тем не обращаем внимания на F.

В зависимости от вида целевой функции и ограничений задачу можно классифицировать.

Если ограничения заданы, то задача условной оптимизации, иначе безусловной оптимизации.

Лекция №2

{Если нелинейная целевая функция и нелин. }

Дальнейшая классификация будет производиться последовательно.

Задача нелинейного программирования.

Условие существования экстремума целевой функции

(задача безусловной оптимизации)Формулировка задачи:

– n-мерное Евклид. пространство

Все точки допустимы.

I

Обоснование необходимости изучения темы.
1. Задача проще, лучше начинать с нее.
2. Такие задачи редко, но на практике.
3. переход от задачи условной оптимизации к безусловной.
Зачем нужны условия экстремума.
1. Для оценки задачи ( или нет min)
2. Нужны критерии как для построения методов решения задач, так и для остановки процесса поиска.

Основное внимание на теоремы, док-ва которых имеют конструктивный характер.

II. Определение min целевой функции

Определение: Скалярная функция n переменных : , т.е. вектор в скаляр наз-ся нормой вектора, если она удовлетворяет следующим трем условиям:

Нормированное пространство.

В рамках данного определения переход от вектора к скаляру определяется не единственным образом.

Евклидова норма вектора

;

Определение.

Т. х наз. точка локации min ф-ии, если справедливо следующее:

Если в определении поменять знак на противоположный, то это будет определение лок. max.

Т. min и max называются экстремальными точками.

Для использования в алгоритмах это определение не годится по очевидным причинам. Поэтому такое определение будет использоваться только в теоретических выкладках.

Определение. Функция наз-ся унимодальной, если она в области определения имеет единственный min.

Если много экстремумов, то мультимодальной.

Min наз-ся глобальным, если внем ф-ия принимает наименьшее значение.

В унимодальной ф-ии локальные и глобальные min совпадают.

Поиску глобального min будет посвящена отдельная тема.III.  экстремума.

Теорема Вейерштрасса.

Если ф-ия непрерывна и ограничена на , то она там имеет глобальный min.

Результат имеет слишком общий характер, практически ничего не дает для построения методов.

1) Условие  экстремума гладкой функции одной переменной.

Потребуем, чтобы функция была гладкой, чем выше порядок гладкости, тем лучше.

Гладкая в некоторой окрестности, если есть производная в этой окрестности.

Если первый порядок гладкости.

Мы считаем, что - т. min в необход. Все зависит от .

Пусть ф-ия имеет 2-й порядок гладкости.

Необходимое условие 1-го пор. формул в виде след. теоремы (Th. Ферма):

Пусть т. min и ф-ия диф. в этой точке ( хотя бы 1-я производная), тогда 1-я производная в т. min =0.

Док-во Th:

Получено противоречие, заключающееся в том, что в окрестности т.  т. с меньшим значением ф-ии, чем в т. min. Это противоречие устраняется, если производная равна 0.

Теорема доказана.

Обратим внимание на конструктивный характер доказательства Th.

В док-ве показан способ перехода из текущей точки в точку с меньшим значением ф-ии.

Производная в т. , не равна 0.

, р надо выбирать очень маленьким.

Это лежит в основе построения градиентных методов оптимизации.Основные задачи при нахождении min:

Выбрать направление.
Выбрать шаг.

Необходимое условие 2-го порядка:

Пусть т. min и в этой т. ф-ия 2 раза диф., тогда 2-я произв. ф-ии неотрицательна.

Определение. Т. наз-ся стационарной, если произв. ф-ии в этой точке равна 0.

Задача док-ть (на след. лекции)

Теорема достаточное условие экстремума.

Пусть стационарная точка и 2-я производная положительна в т. , тогда т. лок. min.

Док-во:

Геометрическая иллюстрация этих теорем.

Лекция №3

2) Условие экстремума гладкой ф-ии многих переменных.

Док-во (необх. 2-го порядка):

Это и док. необ. усл. 2-го порядка.

Th. доказана.

Далее идет обощение полученных результатов одном. ф-и на многом. случай.

Теорема Ферма.

Пусть - т. min и дифференцируема в окрестности этой точки.

Тогда градиент в = 0.

Если градиент в какой-либо точке равен 0, то эта точка наз-ся стационарной.

Док-во:

А это противоречит 1). Значит предположение о том, что не верно.

Th. доказана.

Определение:

Матрица А наз-ся положительно определенной, если

квадратичная форма

Такое определение для вычислительной практики не подходит.

Теорема (необходимое условие 2-го порядка).

Пусть - т. min и градиент в ней не равен 0, тогда Гессиан ф-ии явл-ся не отрицательно определенной матрицей.

Док-во:

Отсюда вытекает, что , что и доказывает теорему.

Определение.

Т. будет наз-ся седловой, если

Теорема (дост. усл-е экстремума)

max или min седл. т.

Линии постоянного уровня в седловой т. не замкнуты.

Пусть

Тогда т. явл-ся т. локального min.

Док-во:

Всегда можно выбрать , когда второе слагаемое будет > третьего.

Что и доказывает теорему.

Условие экстремума и количественные оценки положительной определенности ГессианаTh. Ферма имеет конструктивный характер.

Пусть G – Гессиан.

Если все соб. значения >0, то G полож. определено.

Можно рассмотреть следующие случаи соб. значений:

. Матрица положительно определена. Если рассматривать стационарные точки, то это точки min (локальн.).
. Матрица отрицательно определена. Если стац. т. – т. max (локальный).
- знаконеопределенная матрица. Т. седловая.
. Матрица неотриц. определен. (полуопределенная матрица). Недостаток информации. Т. стационарна.

Обусловленность экстремумаЗамечание. Вывод числа обусл. Матрицы смотри в дисциплине алгоритмизация вычислений.

Норма матрицы.

ставит в соответствие матрице скаляр.

Замечание.  много способов определения нормы матрицы. Большинство из них будут рассматриваться в АВ.

Покажем как организуется вычисление нормы матрицы на практике.

Спектральная норма матрицы

использ. Евклидову норму вектора

Утверждение. Значение отношения Релея на всех ненулевых векторах совпадает со значением квадратичной формы.

(определенных на мн-ве векторов единичной длины)

Доказать самостоятельно!

Максимальное значение квадрата нормы матрицы равно собственному значению матрицы В.

Лекция №4

Задача. Показать, что

число обусловленности

Чем оно больше, тем хуже, тем сложнее решение задачи.

Частный случай:

Числа обусловленности – мера искажения окружности.

В целевых ф-ях имеют место гребни и овраги.

Если есть узкий и извилистый овраг, резко увеличивается кол-во шагов поиска.

Хорошо обусловленная матрица – число обусловленности не велико.

Плохо обусловленная матрица – число обусловленности велико.

Выводы:

Получены необх. и дост. условия экстремума гладкой ф-ии.
Отмечен подход к построению(нахождению) т. min ф-ии . Док-во Th. Ферма.
Услов. экстремума легко проверяется.
Отмечена важная характеристика экстрем., определяемая через число обуслов.

Условие существования экстремума гладкой функции многих переменных

(условная оптимизация с ограничениями типа равенств)

Формулировка задачи.

функциональные ограничения

прямые

ограничения равенства неравенства

n-мерная зад. гиперпараллелепипед.

Обычно эти ограничения формируются физическими параметрами.

Прямые ограничения будут рассмотрены в отдельной теме.

- ограничения типа равенств

- ограничения типа неравенств

- ограничение типа равенств

В нашем случае:

Такая система имеет бесчисленное мн-во решений.

Обоснование необходимости изучения этой темы

Практические задачи
Для построения оптимальных методов

1.Основные подходы к решению задач

Замена переменных.
Множители Лагранжа.
Поисковые методы. (Изложены будут позже)

Метод замены переменных

Из системы уравнений необходимо определить:

Пример:

Характеристики метода:

Для использования этого метода нужна аналитическая зависимость от х услов. функции и огранич. (скорее всего будет алгоритм. зав.)
если будет такое ограничение, то нельзя разделить на зависимые и независимые переменные.
Даже если можно разделить на зависимые и независимые переменные, то нужна квалификация для решения системы.

Вывод: для практики такой подход не применим, а только для решения учебных задач.Метод множителей Лагранжа

Позволяет:

Сформулировать необходимые условия  экстремума целевой функции при ограничениях типа равенств.
Свести задачу услов. оптим. к задаче безуслов. оптимизации.

Ф-я Лагранжа зависит от переменных.

Пусть при некотором найдено значение целевой ф-ии для такое, что ф-я Лагранжа принимает min значение.

Если т.  обл. огранич., видим, что min ф-ии Лагранжа будет совпадать с min ф-ии .

Аналитический метод решения задачи (для оптимальных методов оптимизации)
Численный (для решения практических задач)

Аналитический метод

- буквы

Найти
Подставить найденное значение в ограничения и найти числовое значение для всех 
Подставить найденные в и найти числовые значения .

Пример:

Теоретически можно построить численный метод:

построить ф-ию Лагранжа. используя  методы (Ньютона), найти все стационарные точки. Провести исследование всех стационарных точек, в том числе и седловых (седло может быть разделено по перем.  и х, из всех min по х выбрать наименьший.Теорема (необходимое условие экстремума)

Пусть

Матрица якобы не вырождена.

Для того чтобы была т. min, необходимо, чтобы было решением следующей системы уравнений:

Лекция №5

Док-во:

Считаем, что - т. min должны получить .

В производной огранич. исп. правило дифференцирования сложной функции.

Если матрица не вырожд., то имеет одно решение.

Из  что могут быть определены однозначно.

Суммируем все ограничения при этом i-е ограничение умножаем на .

Изменим порядок суммирования в последнем выражении. Вынесем эл-ты типа

Прибавим к последнему выражению необх. условие экстремума из формулы .

Подставим , определяемые из системы .

= 0

Утверждение доказано (Th.)Интерпретация множителей Лагранжа

Выводы по теме:

Отмечены 2 подхода к решению задач (зам. пер. и мн-ли Лагранжа).
Получены необх. условия экстремума для зад. услов. min с огран. типа равенства.
Приведена интерпрет. мн-й Лагранжа.

Лекция №6Минимизация однопараметрической унимодальной функции

Формулировка задачи

Обоснование необходимости изучения темы.

а) такие задачи имеют место;

б) минимиз. многопараметр. ф-и сводится к решению последовательности задач минимиз. однопарам. ф-и.

Лекция №7

Особенности этой задачи:

1) Высокая вероятность того, что унимодальна.

Высокая трудоемкость, а иногда и не возможность вычисления производной:

а) может быть не диф.

б) если диф., то трудоемкость вычисл. производной очень высока (диф. по всем парам.)

Вывод: эта задача очень часто решается на практике. Надо изучать специфические методы (без использования производных) отыскания min.

Постановка задачи

Необходимо за конечное число шагов m или с точностью, локализовать т. min.

Можно установить связь между .

Основа рассматриваемого метода

Предполагая, что функция унимодальна, можно отбросить одну из частей (заведомо не содержащую т. min).

Общая характеристика метода

Методы делятся на 2 группы:

пассивная стратегия поиска min.
последовательная стратегия поиска:

выбираются порциями в процессе min ф-и. Выбор зависит от результата min на предыдущем шаге. Основная опер. выбор и вычисление . Облад. лучшей гибкостью и дают лучшие результаты.

Общее для 2-ой группы методов:

Отличие: в правилах генерации точек, трудоемкостью вычисления .

Можно классифицировать по исп. :

1 группа: нужны качественные оценки .

- узел интерполяцииМетод последовательного дихотомического поискаНа каждом шаге генерируются две точки, и в этих точках вычисляется значение функций. Наиболее трудоемкая операция – вычисление значения ф-й.

Точки генерируются по специальному правилу:

 - малое число, сравнимое с компьютерной погрешностью, генерируются близко к середине.

Если считать, что функция на каждом шаге вычисляется два раза, то

Если целевая функция вычисляется очень быстро, то можно применять этот метод.

Алгоритм:

Основная цель: обеспечить наиболее быстрое убывание отрезка неопредел. при min количестве вычислений целевой функции. Для достижения этой цели предлагается: на 1-ом шаге вычислить 2 значения целевой функции, на всех остальных – только 1 раз. Эта идея реализуется в методе Фибоначчи и в методе золотого сечения.Методы Фибоначчи и золотого сечения

Общая часть

Будем задавать точки параметрически.

Завис. от пар. на котор.

При таком выборе точек справедливо следующее

Лекция №8

Утверждение:

Для того, чтобы или , необходимо

Док-во:

Рассмотрим первый случай:

Что и требовалось доказать.

Рассмотрим другую ситуацию:

Утверждение доказано.

Эта задача решается по разному при методе Фибоначчи и методе золотого сечения.Метод Фибоначчи

Основные этапы:

Задача.

Выражаем все через

В результате получим:

Подставляем в ограничение для

Оказывается, что в этой системе неравенств  одно наиболее жесткое, которое гарантирует выполнение всех неравенств одновременно.

записывается через числа Фибоначчи в целевой функции:

Оптимальное решение имеет следующий вид:

Наиболее быстрый метод.Получим аналитическое выражение для вычисления n-го числа Фибоначчи.

Используется для вычисления n-го числа Фибоначчи.
Используется для оценки скорости работы метода Фибоначчи.

Предположим , то

Замечание. при больших N метод Фибоначчи может оказаться численно неустойчивым (найденный отрезок не будет содержать т. min). Это будет происходить всегда, рано или поздно. Но нужно сделать много шагов. Тем позже будет проявляться численная неустойчивость, чем точнее .

Метод Золотого Сечения

Говорят, что х провод. зол. сеч. отрезка, если выполняется следующее условие:

Имеется две точки, проводящие зол. сеч. и . и симметричны относительно центра.

проводит золотое сечение отрезка .

historich.ru

Лекция №5 – Оптимизация бизнес-процессов

Перед тем как проводить оптимизацию, надо четко выделить бизнес-процессы. Оптимизировать хаос невозможно. Уже задание неких формальных норм к результатам процедур само по себе является улучшением, поскольку это переход от хаоса к порядку. Существуют два принципиальных направления: снижение уровня выполнения операций и повышение эффективности деятельности. Приемов по оптимизации бизнес-процессов существует великое множество. Рассмотрим лишь некоторую часть из них, которые являются низкобюджетными и которые можно применять сразу.

Прежде чем говорить о методах оптимизации, важно понять ее принципы.

Принцип первый: у оптимизации должна быть основа.Суть этого принципа заключается в том, что перед тем как проводить оптимизацию, надо четко выделить бизнес-процессы. Сначала надо «увидеть» ход протекания процессов, т. е. зафиксировать процессы в виде моделей «как есть». Ведь если не удается описать процессы, происходящие в настоящее время (например, из-за их высокой изменчивости), то и оптимизировать будет нечего (в данной ситуации можно выстраивать процессы заново, оценивать их оптимальность и улучшать уже новые).

Принцип второй: при оптимизации «рыбу чистят с хвоста».Данный принцип означает, что оценивать оптимальность надо от частного к общему, выявляя отдельные недостатки, объединяя их в группы и оперативно устраняя. Если лично вам ближе подход от общего к частному, то вам нужен реинжиниринг, т. е. комплексное, системное, «до основания» изменение деятельности.

Принцип третий: решения по оптимизации неоднозначны. Другими словами, велика вероятность того, что, устраняя неоптимальность по одному критерию, мы ухудшаем процесс по другому. Причем недостаточно просто знать об этом, надо еще и уметь выявлять такие последствия, оценивать преимущества и недостатки и делать обоснованный выбор.

Принцип четвертый: сотрудники не любят оптимальных процессов.Неизбежным следствием настоящей оптимизации процессов является усиление эксплуатации исполнителей, поэтому неизбежно явное и неявное, часто даже не осознаваемое людьми, сопротивление.

Из данных принципов достаточно логично следуют условия и шаги проведения оптимизации:

1. Перед тем как начинать работу по оптимизации, необходимо описать существующие в компании бизнес-процессы «как есть» (создать их модели). Описания должны быть четкими, однозначными и затрагивать уровень, на котором видна конкретная работа сотрудников. Объем моделей может быть разным: как по отдельно выделенному бизнес-процессу, так и по группе взаимосвязанных бизнес-процессов. Безусловно, чем больше процессов описано в модели, тем лучше и шире можно оценить их оптимальность.

2. Оценивая оптимальность, в первую очередь надо анализировать каждую часть бизнес-процесса, выполняемую конкретным исполнителей(далее мы будем называть ее процедура). Оценивая ее, надо проверять, к каким результатам приводит правильное выполнение, какие данные или материалы исполнитель получает в итоге, что он с ними делает, насколько оптимальны его действия, а также время работы и продолжительность выполнения процедуры.

3. Проанализировав каждую процедуру и определив ее явные недостатки, можно оценить оптимальность управления бизнес-процессом и оптимальность группы процессов. Результатами оценки оптимальности должны стать выявленные недостатки в процессе и/или группе процессов.

4. Затем надо разработать предложения по исправлению выявленных недостатков, перестроить модель процесса («как будет»), учитывая данные предложения, пересмотреть действия исполнителей и кандидатуры самих исполнителей (если это необходимо), а самое главное — улучшить средства труда. Улучшение средств труда заключается, конечно, не в разработке экспертных систем (осуществляемой в процессе реинжиниринга), а в усовершенствовании форм фиксации, хранения и первичной обработки данных, используемых при выполнении конкретной процедуры. Например, когда полномочия устанавливать правила предоставления скидок делегируются менеджеру по продажам, можно вставить в электронную форму бланка-заказа поля, при заполнении которых расчет скидки будет производиться автоматически (при этом может использоваться обычный Microsoft Excel).

5. На завершающем шаге надо оценить возможные ухудшения от предлагаемых улучшений в других местах процесса, в том числе и возможное сопротивление сотрудников.

Приемов по оптимизации бизнес-процессов существует великое множество. Рассмотрим лишь некоторую часть из них, которую можно применять сразу. К тому же предлагаемые методы являются низкобюджетными.

К таким методам оптимизации бизнес-процессов относятся:

- усовершенствование/разработка форм документов;

- фиксация оснований для принятия управленческих решений;

- изменение состава и последовательности процедур процесса;

- определение областей ответственности за выполнение процедур;

- изменение требований к конечному результату.

Усовершенствование/разработка форм документов.Часто бывает так, что информация в бизнес-процессе передается в неформализованном виде: либо устно, либо в какой-то свободной форме. Соответственно информация может быть утрачена либо искажена при передаче («испорченный телефон»), и сотрудники тратят много времени на ее получение/восстановление. Чтобы избежать этого, необходимо использовать какую-то структурированную форму представления информации. Это нужно как для структурирования собственно данных, так и для планирования хода выполнения процесса и последующего учета. Кроме того, в формах документов полезно использовать всевозможные классификаторы данных для облегчения последующей обработки информации, в том числе компьютеризованной.

Так, например, в одном реальном случае при разработке проектно-сметной документации руководитель зачастую не знал, в какой стадии находится процесс разработки. При малейшей проблеме исполнители спихивали вину друг на друга и концов было не найти. Мы предложили четко структурировать последовательность разработки проектно-сметной документации, и при передаче информации от исполнителя исполнителю они фиксировали этот факт в специальной форме документа, висевшей прямо на стене офиса, и заверяли это своими подписями. Таким образом, руководитель проекта в любой момент мог подойти и посмотреть, на какой стадии находится разработка документации.

Фиксация оснований для принятия управленческих решений. По сути, это четкая алгоритмизация принятия управленческих решений на основе структурирования условий, при «срабатывании» которых принимается то или иное решение. Прежде всего надо выявить типовые решения, которые могут приниматься в процессе (поставка товара в кредит или по предоплате, например). Затем определяем исходные данные, на основе которых принимается решение (например, объем задолженности, срок сотрудничества, и т. п.) Далее определяем правила принятия решения в том или ином варианте и разграничиваем зоны ответственности за результат (например, до 50 тыс. руб. решение принимает менеджер, свыше этой суммы — начальник отдела). В итоге такой стандартизации мы можем разгрузить высокооплачиваемых сотрудников от «текучки», которую могут выполнять менее квалифицированные работники. А это, в свою очередь, тоже благотворно отразится на издержках.

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:

zdamsam.ru