Методы оптимизации (Введение к учебному пособию). Предмет методы оптимизации
1.Оптимизационные задачи, их классификация 7
Содержани
Введение 5
1.1Классификация задач оптимизации 7
1.2Классификация методов оптимизации 12
2. Постановка задачи линейного программирования 13
2.1 Общая задача линейного программирования (ЗЛП) 13
2.2 Математические модели задач линейного программирования 14
2.3 Формы записи задач линейного программирования: общая, каноническая и стандартная 17
3. Графический метод решения задачи линейного программирования 20
4. Симплекс- метод решения задач линейного программирования 25
4.1 Метод Жордана – Гаусса - метод решения систем линейных уравнений 25
4.2. Симплексные таблицы. Нахождение начального опорного решения 31
4.3. Критерий оптимальности 34
4.4. Невырожденные ЗЛП, алгоритм их решения 34
4.5. Альтернативный оптимум, алгоритм нахождения всех оптимальных решений 41
4.6. Вырожденные ЗЛП, алгоритм их решения 46
5. Двойственные задачи 48
5.1 Постановка двойственной задачи 48
5.2 Основное неравенство двойственности 53
5.3 Критерий Канторовича 54
5.4 Первая теорема двойственности 55
5.5. Вторая теорема двойственности 55
(необходимое и достаточное условия оптимальности решения). 55
5.6. Третья теорема двойственности 56
5.7. Двойственный симплекс-метод 59
6. Транспортная задача 63
6.1 Экономическая постановка и математическая модель транспортной задачи 63
6.2 Методы нахождения начального плана перевозок 66
6.3 Метод потенциалов решения транспортной задачи 68
6.4 Открытая модель транспортной задачи 78
7. Матричные игры, их применение к решению оптимизационных задач 82
7.1 Основные понятия теории матричных игр 82
7.2 Решение матричных игр в чистых стратегиях 85
7.3 Решение матричной игры в смешанных стратегиях 88
7.4 Сведение матричной игры к задаче линейного программирования 93
7.5 Статистические игры 97
8. Графы, их применение в решение оптимизационных задач 105
8.1 Определение графа 105
8.2 Путь и цикл в графе 107
8.3 Связность графа, деревья 109
8.4 Виды графов 110
8.5 Сети. Критический путь 115
Вопросы к экзамену 121
Индивидуальные задания 124
ТЕСТЫ 145
Библиографический список 151
Введение 4
1. Оптимизационные задачи, их классификация 6
1.1 Классификация задач оптимизации 6
1.2 Классификация методов оптимизации 10
2. Постановка задачи линейного программирования 11
2.1 Общая задача линейного программирования (ЗЛП) 11
2.2 Математические модели задач линейного программирования 12
2.3 Формы записи задач линейного программирования: общая, каноническая и стандартная 15
3. Графический метод решения задачи линейного программирования 17
4. Симплекс- метод решения задач линейного программирования 23
4.1 Метод Жордана – Гаусса - метод решения систем линейных уравнений 23
4.2. Симплексные таблицы. Нахождение начального опорного решения 28
4.3. Критерий оптимальности 31
4.4. Невырожденные ЗЛП, алгоритм их решения 32
4.5. Альтернативный оптимум, алгоритм нахождения всех оптимальных решений 38
4.6. Вырожденные ЗЛП, алгоритм их решения 42
5. Двойственные задачи 44
5.1 Постановка двойственной задачи44
5.2 Основное неравенство двойственности49
5.3 Критерий Канторовича 50
5.4 Первая теорема двойственности 50
5.5. Вторая теорема двойственности 50
(необходимое и достаточное условия оптимальности решения). 50
5.6. Третья теорема двойственности 51
5.7. Двойственный симплекс-метод 53
6. Транспортная задача 57
6.1 Экономическая постановка и математическая модель транспортной задачи57
6.2 Методы нахождения начального плана перевозок 60
6.3 Метод потенциалов решения транспортной задачи 62
6.4 Открытая модель транспортной задачи 70
7. Матричные игры, их применение к решению оптимизационных задач72
7.1 Основные понятия теории матричных игр72
7.2 Решение матричных игр в чистых стратегиях76
7.3 Решение матричной игры в смешанных стратегиях79
7.4 Сведение матричной игры к задаче линейного программирования84
7.5 Статистические игры87
8. Графы, их применение в решение оптимизационных задач95
8.1 Определение графа95
8.2 Путь и цикл в графе 97
8.3 Связность графа, деревья98
8.4 Виды графов100
8.5 Сети. Критический путь105
Вопросы к экзамену 111
Индивидуальные задания 114
ТЕСТЫ 131
Библиографический список 138
Введение
Данное учебное пособие является первой частью учебно-методического комплекса дисциплины «Методы оптимизации» и содержит разделы :
Классификация задач и методов оптимизации.
Постановка задачи линейного программирования.
Графический метод решения задач линейного программирования.
Симплексный метод решения задач линейного программирования.
Двойственные задачи, основные теоремы двойственности.
Транспортные задачи, их решение методом потенциалов.
Матричные игры, применение к решению оптимизационных задач.
Графы, их применение к решению оптимизационных задач.
Целью данного учебно-методического комплекса является оказание помощи студентам всех форм обучения в организации самостоятельной работы при изучении курса «Методы оптимизации».
Настоящее учебное пособие предназначено для студентов второго курса специальности 080801.65 «Прикладная информатика в экономике». Пособие написано на основе курса лекций, который авторы читают для студентов всех форм обучения, оно рассчитано как для самостоятельной работы студентов, так и для обучения в аудитории.
Учебное пособие содержит контрольные задания (приложение А), которые необходимо выполнить, чтобы получить допуск к экзамену. Решения типовых задач рассмотрены подробно во всех разделах учебного пособия.
Предмет «Методы оптимизации» включает в себя изучение методов решения задач на отыскание оптимальных решений.
В настоящем учебном пособии рассматриваются линейные оптимизационные задачи, которые традиционно называют задачами линейного программирования. Термин «программирование» следует понимать как планирование и не смешивать с программированием,
обучающим составлению программы, осуществляющей заданный вычислительный процесс на ЭВМ.
Систематическое исследование линейных оптимизационных задач и разработка общих методов их решения начаты в работах советского математика, лауреата Нобелевской премии по экономике (1972), Л. В. Канторовича, который предложил в 1939 г. метод разрешающих множителей и применил его к решению ряда практических задач.
Впервые постановка задачи линейного программирования по составлению оптимального плана перевозок дана в работе советского экономиста А. Н. Толстого в 1930 г.
Л. В. Канторович в 1949 г. совместно с М. К. Гавуриным разработал метод потенциалов для транспортной задачи линейного программирования, которая была поставлена в 1941 г. американским ученым Ф. Хичкоком, предложившим и метод последовательного улучшения для этой задачи.
Основным методом решения задач линейного программирования является симплексный метод Дж. Данцига, опубликованный в 1949 г.
Большой толчок для интенсификации разработок методов линейного программирования дала концепция двойственности, разработанная в 1947 г. основателем теории игр (и одним из отцов кибернетики) американским ученым Дж. Фон Нейманом.
Великий математик Леонард Эйлер 2,5 века тому назад написал: «В мире не происходит ничего, где не виден был бы смысл какого-нибудь минимума или максимума».
За рамками учебного пособия остались методы и алгоритмы многих более сложных задач оптимизации. Это алгоритмы векторной и дискретной оптимизации, алгоритмы многоэкстремальной оптимизации и генетические алгоритмы, и другие.
Классические и численные методы безусловной оптимизации рассматриваются в дисциплинах: математика и численные методы.
Задача оптимизации, в которой целевая функция задана функцией одной переменной, относится к наиболее простому типу оптимизационных задач. Одномерные методы оптимизации часто используются и при решении задач с несколькими переменными при подходящем выборе направления и последующей минимизации вдоль этого направления. Методы решения задач одномерной оптимизации: методы дихотомии, золотого сечения, Фибоначчи, квадратичной интерполяции также рассматриваются при изучении численных методов.
В настоящем учебном пособии рассматривается условная оптимизация. Все практические задачи могут быть выполнены в пакетах численных расчетов, например, MATHCAD.
| 1. Общая постановка задачи математического программирования. Задача формулируется таким образом: среди элементов , образующих множество X, найти такой элемент, который доставляет минимальное значение заданной функции . Для корректной постановки задачи требуется задать допустимое множество X (с помощью ограничений), целевую функцию , а также критерий поиска (минимум/максимум). Тогда решить задачу означает либо найти такое , при котором . В случае, если множество X является множеством всех возможных значений, то это задача безусловной оптимизации, в обратном случае – условной. Порядок поиска решений: 1. Поиск всех точек стационарности 2. Выбор тех, что принадлежат области допустимых решений 3. Проверка граничных точек. Сложность решения зависит от размерности. Например, может потребоваться проверить условие на границе, заданной линией, т.е. в бесконечном количестве точек. Задача на условный экстремум включает ограничения: - это ограничение типа равенство. Этап поиска условий экстремума – обычно аналитический, а вычисления оптимальных решений – инженерный. Найти наибольшее и наименьшее значения y при ограничениях: ,i=1,2,…,k; , j=1,2,…,l; Ограничения бывают типа равенств и неравенств. | 2.1 Метод неопределенных множителей Лагранжа при поиске максимальных значений функций. Требуется найти экстремум функции , которая зависит от n переменных и эти переменные связаны m соотношениями , причем m<n, иначе решение было бы тривиальным. Для решения методом неопределенных множителей Лагранжа составим функцию . Составим систему из n+m уравнений, приравняв нулю частные производные функции Лагранжа по и . Если полученная система имеет решения относительно своих параметров, то точка x может быть решением исходной задачи, то есть условным экстремумов. На картинке изображены линии уровня при условии . Данное уравнение задает кривую S. | 2.2 Пример. Найти экстремум функции при ограничении . Составляем функцию Лагранжа , откуда Правда, можно было решить проще: выразить из ограничений одну переменную через другую, подставить в функцию и найти экстремум функции одной переменной: например . | 3. Линейный функционал. Функционалом называют отображение, аргументов которого является функция вещественной переменной, а результатом – вещественное число. Функционал обозначим . Функционал является линейным, если он удовлетворяет принципу суперпозиции: . Другое определение: функционалами называются величины, значение которых определяются выбором одной или нескольких функций. Пример: длина дуги пространственной кривой, соединяющей заданные точки. Исторические предпосылки введения функционалов: 1. Геодезические линии. Найти линию минимальной длины между двумя точками при некотором условии. 2. Изометрическая задача. Найти замкнутую линию заданной длины, ограничивающей максимальную площадь. Условие на постоянство длины кривой называется изопараметрическим. 3. Задача о брахистохроне. На плоскости, требуется попасть из одной точки в другую без начальной скорости и только за счет силы тяжести за минимальное время. Функционал непрерывен, если малому изменению соответствует малое изменение функционала. Функции можно считать близкими, если мал модуль их разности при любом x из области определений. Но так как часто функционал зависит еще от производных, желательно считать близкими функции, также близкие по своим производным (1-й порядок близости). | 4. Понятие вариации функционала. Вариация функционала позволяет определить экстремум функционала. Вариация функционала обозначается как и выглядит как приращение к «точке» (то есть функции, так как у нас исходная часть – не функция, а функционал) . Такое приращение называется вариацией аргумента и оно должно принадлежать тому же выбранному линейному нормированному пространству. Необходимое условие экстремума заключается в равенстве нулю вариации функционала. Проще говоря – как бы мы не толкали наши функцию, она в любом случае будет иметь один и тот же знак, то есть будет сидеть в экстремуме. | 5. Вычисление вариации функционала. Для вычисления вариации функционала запишем: где – линейный функционал относительно второго аргумента, – бесконечно малая величина высокого порядка. Учитывая свойство линейности функционала L, можно записать При переходе получаем при . |
studfiles.net
Методы оптимизации
Определения
Под оптимизацией понимают процесс выбора наилучшего варианта из всех возможных. С точки зрения инженерных расчётов методы оптимизации позволяют выбрать наилучший вариант конструкции, наилучшее распределение ресурсов и т.п.
В процессе решения задачи оптимизации обычно необходимо найти оптимальные значения некоторых параметров, определяющих данную задачу. В инженерных задачах их называют проектными параметрами, в экономических задачахпараметрами плана.В качестве проектных параметров могут быть:значения линейных размеров объекта, массы объекта, температуры и т.п.
Число проектных параметров 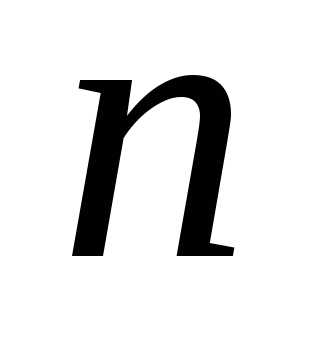
характеризует размерность и степень сложности задачи оптимизации.
Выбор правильного решения или сравнивание двух альтернативных решений проводиться с помощью некоторой зависимой величины (функции), определяемой проектными параметрами. Эта величина называется целевой функцией (или критерием качества).
В процессе решения задачи оптимизации должны быть найдены такие значения проектных параметров, при которых целевая функция имеет экстремум: минимум или максимум.
Целевую функцию можно записать в виде
(8.1)
Примеры целевых функций, встречающихся в экономических и инженерных расчетах: прочность или масса конструкции, мощность установки, объём выпуска продукции, стоимость перевозок грузов, прибыль и т.п.
При 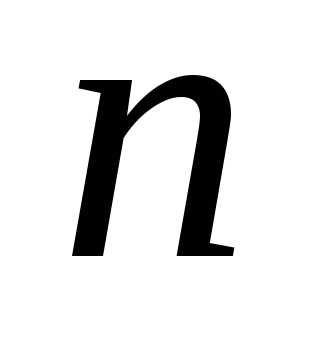 =1 целевая функция-функция одной переменной, её график - кривая на плоскости.
=1 целевая функция-функция одной переменной, её график - кривая на плоскости.
При 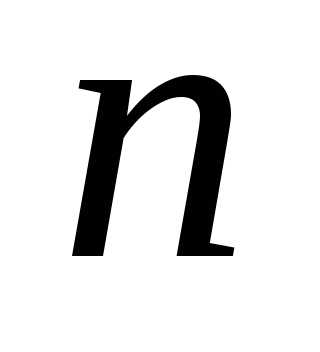 =2 целевая функция-функция двух переменных, её график - поверхность в трёхмерном пространстве.
=2 целевая функция-функция двух переменных, её график - поверхность в трёхмерном пространстве.
Целевая функция не всегда может быть представлена в виде формулы. Иногда она может принимать некоторые дискретные значения, задаваться в виде таблицы и т.п. В любом случае, она должна быть однозначной функцией проектных параметров.
Целевых функций может быть несколько.
Например, при проектировании изделий машиностроения одновременно требуется обеспечить  надёжность,
надёжность, материалоёмкость,
материалоёмкость,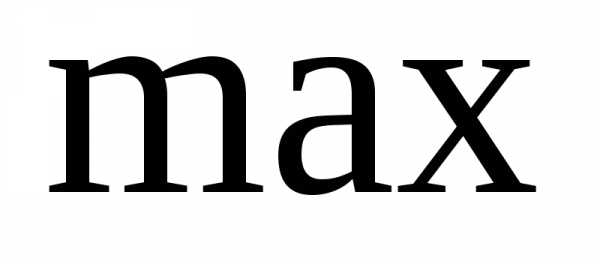 полезный объём или грузоподъёмность. Некоторые целевые функции могут оказаться несовместимыми. В таких случаях, необходимо вводить приоритет той или иной функции.
полезный объём или грузоподъёмность. Некоторые целевые функции могут оказаться несовместимыми. В таких случаях, необходимо вводить приоритет той или иной функции.
Задачи оптимизации можно классифицировать различными способами.
Пирумов: на 3 группы (см. стр. 57)
Турчак: на 2 типа: условные и без условные.
Безусловная задача оптимизации
Состоит в отыскании 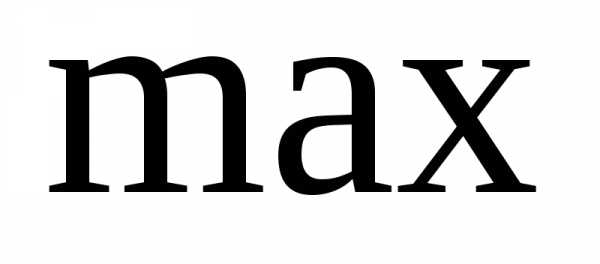 и
и действительной функции
действительной функции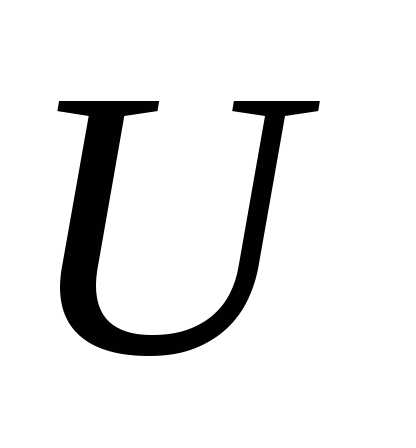 (8.1) от
(8.1) от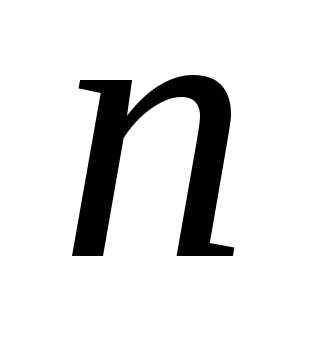 действительных переменных определении соответствующих значений аргументов на некотором подмножестве
действительных переменных определении соответствующих значений аргументов на некотором подмножестве
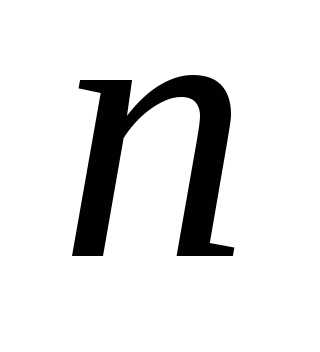 - мерного пространства.
- мерного пространства.
Обычно рассматриваются задачи минимизации; задачи на поиск 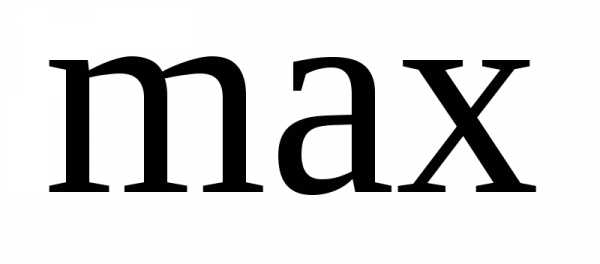 к ним легко сводится путём замены знака целевой функции на противоположный.
к ним легко сводится путём замены знака целевой функции на противоположный.
Условные задачи оптимизации или задачи с ограничениями - это задачи, при формулировке которых задаются некоторые условия (ограничения) на множестве  . Эти ограничения задаются совокупностью некоторых функций, удовлетворяющих уравнениям или неравенствам.
. Эти ограничения задаются совокупностью некоторых функций, удовлетворяющих уравнениям или неравенствам.
Ограничения- равенства выражают зависимость между проектными параметрами, отражают законы природы, наличие ресурсов, финансовые требования и т.п.
В результате ограничений область проектирования  , определяемая всеми проектными параметрами, может быть существенно уменьшена в соответствии с физической сущностью задачи. Число ограничений – равенство
, определяемая всеми проектными параметрами, может быть существенно уменьшена в соответствии с физической сущностью задачи. Число ограничений – равенство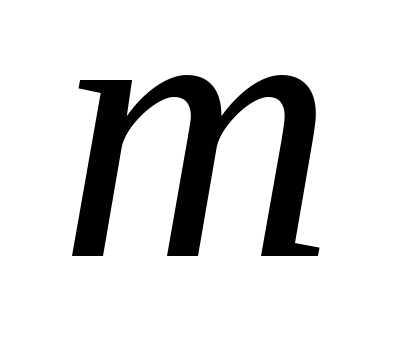 может быть произвольным.
может быть произвольным.
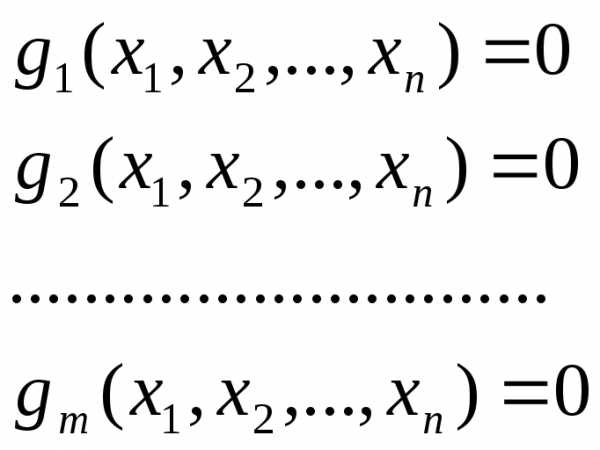 (8.2)
(8.2)
В ряде случаев из этих соотношений можно выразить одни проектные параметры через другие, что, в свою очередь, может уменьшить размерность задачи и облегчить её решение.
Аналогично можно вводить ограничения-неравенства:
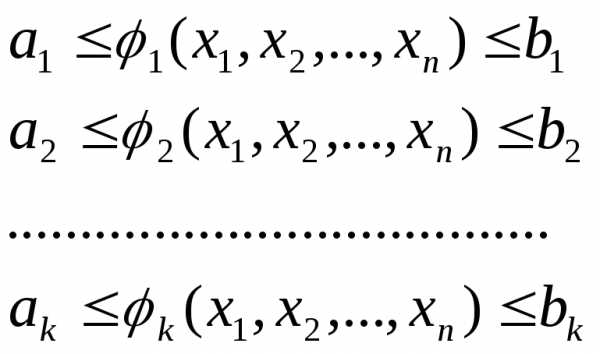 (8.3)
(8.3)
Особенность отыскания решения при наличии ограничений: оптимальное решение может соответствовать либо локальному экстремуму функции внутри области проектирования, либо значению целевой функции на границе области.
Если же ограничений нет, то ищется оптимальное решение на всей области проектирования, т.е. глобальный экстремум. Теория и методы решения задач оптимизации при наличии ограничений составляют предмет исследования одного из разделов прикладной математики, математического - программирования.
Пример постановки задачи:
Пусть требуется спроектировать контейнер в форме прямоугольного параллелепипеда объёмом 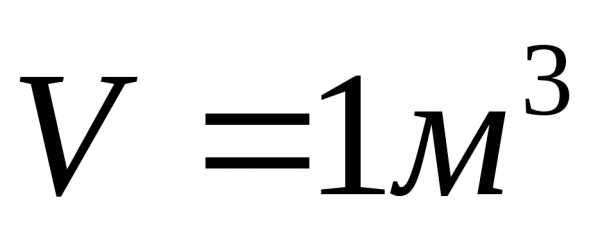 ; желательно израсходовать как можно меньше материала. При постоянной толщине стенок условие уменьшения расходов материала означает, что площадь полной поверхности контейнера должна быть
; желательно израсходовать как можно меньше материала. При постоянной толщине стенок условие уменьшения расходов материала означает, что площадь полной поверхности контейнера должна быть .
.
Обозначим 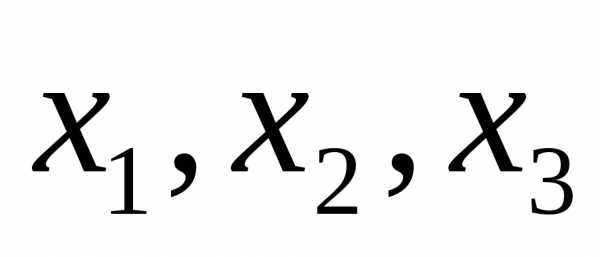 - рёбер контейнера. Следовательно, задача сводится к минимизации функции
- рёбер контейнера. Следовательно, задача сводится к минимизации функции
(8.4)
Эта функция в данном случае является целевой. Условие 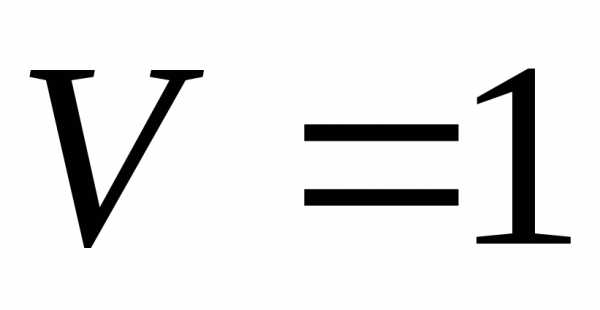 - ограничение – равенство. Оно позволяет исключить один параметр
- ограничение – равенство. Оно позволяет исключить один параметр
(8.5)
Свели задачу к минимизации функции двух переменных. В результате решения будут найдены значения проектных параметров 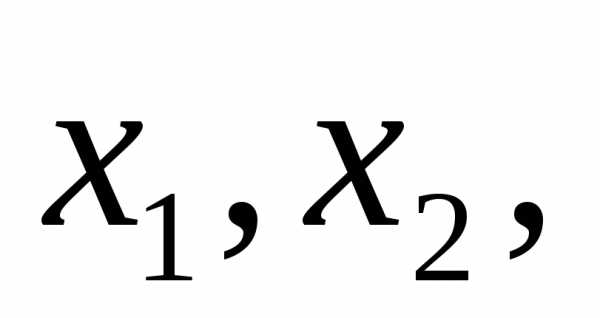 а потом
а потом 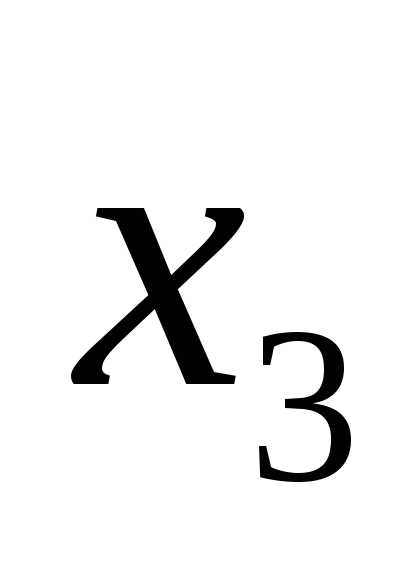 .
.
Фактически получилась задача безусловной оптимизации для целевой функции (8.5), так как ограниченное равенство было использовано для исключения параметра 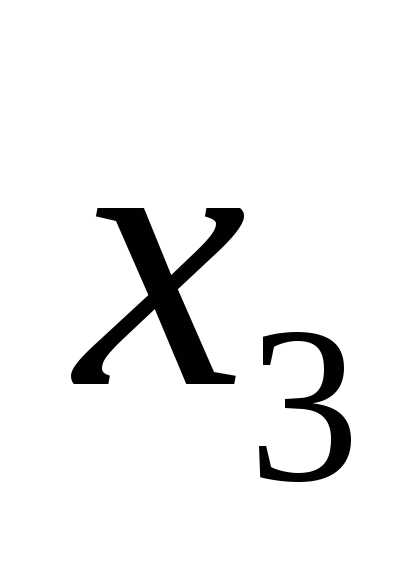 .
.
Можно усложнить задачу, добавив дополнительные условия. Например, потребуем, чтобы данный контейнер имел длину не менее 2 метров.
Получим ограничение-нераенство на один из параметров
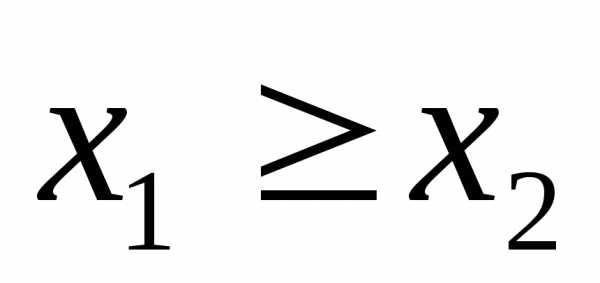 (8.5)
(8.5)
Таким образом, получаем условную задачу оптимизации: необходимо минимизировать функцию (8.4), учитывая ограничение-неравенство (8.5), найти оптимизацию значения параметров  .
.
studfiles.net
Методы оптимизации Предмет методов оптимизации.
Работа добавлена на сайт samzan.ru: 2016-03-13ВОПРОСЫ
для подготовки к экзамену по дисциплине «Методы оптимизации»
- Предмет методов оптимизации. Постановка задачи оптимизации.
- Классификация задач оптимизации. Примеры.
- Постановка задачи линейного программирования (ЛП). Виды задач ЛП.
- Векторная форма записи основной задачи ЛП. Свойства основной задачи ЛП.
- Общая идея симплекс-метода. Построение начального опорного плана.
- Симплекс-метод при известном опорном плане. Теорема о признаке оптимальности опорного плана.
- Симплекс-таблица. Правила вычисления элементов симплекс-таблицы.
- Симплекс-метод при неизвестном опорном плане. Метод искусственного базиса. Теорема об оптимальном плане расширенной задачи.
- Признак бесконечности множества оптимальных планов ЗЛП. Признак неограниченности целевой функции ЗЛП.
- Признак несовместности системы ограничений ЗЛП. Понятие о вырождении. Монотонность и конечность симплекс-метода.
- Постановка двойственной задачи ЛП. Правила составления двойственной задачи.
- Взаимосвязь между решениями прямой и двойственной задач ЛП.
- Постановка классической транспортной задачи. Закрытая и открытая модели транспортной задачи.
- Транспортная таблица. Теорема о необходимом и достаточном условии разрешимости транспортной задачи (ТЗ).
- Определение опорного плана ТЗ. Метод северо-западного угла.
- Определение оптимального плана ТЗ. Метод потенциалов.
- Постановка и методы решения целочисленной задачи линейного программирования. Идея метода ветвей и границ. Идея метода отсечений.
- Метод ветвей и границ. Ветвление задачи ЛП с ослабленными ограничениями. Порожденные задачи. Понятие границы для целевой функции.
- Метод Гомори последовательных отсечений.
- Постановка задачи нелинейного программирования в общем виде. Геометрическая интерпретация задачи.
- Минимизация при ограничениях типа равенств. Необходимые условия условного локального экстремума функции.
- Обобщенное правило множителей Лагранжа. Метод множителей Лагранжа.
- Постановка задачи выпуклого программирования. Теорема о свойстве области допустимых решении задачи. Теорема об экстремумах задачи.
- Функция Лагранжа задачи выпуклого программирования. Седловая точка функции Лагранжа.
- Условие регулярности области допустимых решений задачи выпуклого программирования. Теорема Куна-Таккера.
- Постановка задачи динамического программирования, ее графическая интерпретация. Понятия условно оптимального управления, оптимального управления.
- Особенности задачи динамического программирования.
- Принцип оптимальности Беллмана. Многошаговая процедура нахождения решения в задачах динамического программирования.
- Основное функциональное уравнение Беллмана.
- Постановка задачи одномерной безусловной оптимизации. Унимодальная функция. Методы прямого поиска наименьшего значения функции.
- Методы последовательного поиска решения задач одномерной оптимизации. Интервал неопределенности. Теорема о процедуре исключения отрезка.
- Метод дихотомии.
- Метод «золотого сечения».
- Эффективность, простота реализации метода. Сравнение методов прямого поиска по точности.
Ст. преподаватель И.Е. Кривцова
Кафедра БИТ, 2013 г.
samzan.ru
3. Методы оптимизации решений
управленческое решение менеджмент оптимизация
Оптимизация решения — это процесс перебора множества факторов, влияющих на результат. Оптимальное решение — это выбранное по какому-либо критерию оптимизации наиболее эффективное из всех альтернативных вариантов решение. Поскольку процесс оптимизации дорогостоящий, то ее целесообразно применять при решении стратегических и тактических задач любой подсистемы системы менеджмента. Оперативные задачи должны решаться с применением, как правило, простых, эвристических методов.
Методы оптимизации:
1) анализ;
2) прогнозирование;
3) моделирование, которое, в свою очередь, делится на логическое, физическое и экономико-математическое моделирование. Рассмотрим подробнее методы моделирования.
Пример логического моделирования приведен на рис.4 (диаграмма Исикавы). В представленной логической модели анализа факторов снижения качества продукции имеется только два уровня моделирования: на первом уровне — машины, человек, материалы, методы; на втором уровне — факторы, влияющие на первый уровень. Подобные модели могут иметь больше уровней, и ориентированы на любой результат (положительный — улучшение показателей или отрицательный — их снижение, ухудшение).
Физические модели представляют собой пропорционально уменьшенные в 10 и более раз и изготовленные из различных материалов (металл, дерево, пенопласт, пластилин и др.) натуральные объекты. Они изготавливаются в уменьшенном виде с целью экономии материалов для проверки аэродинамических, эстетических, компоновочных и других характеристик объекта.
Экономико-математическое моделирование представляет собой процесс выражения экономических явлений математическими моделями. Экономическая модель — это схематичное представление экономического явления или процесса с использованием научной абстракции, отражение их характерных черт. Математические модели — основное средство решения задач оптимизации любой деятельности. По сути, эти модели — средство плановых расчетов. Ценность их для экономического анализа и оптимизации решений состоит в том, что они позволяют оценить напряженность плановых заданий, определить лимитирующую группу оборудования, видов ресурсов, получать оценки их дефицитности и т. п. Математическое моделирование экономических явлений и процессов дает возможность получить четкое представление об исследуемом объекте, охарактеризовать и количественно описать его внутреннюю структуру и внешние связи. Модель — условный образ объекта управления.
Экономико-математическая модель должна быть адекватной действительности, отражать существенные стороны и связи изучаемого объекта. Отметим принципиальные черты, характерные для построения экономико-математической модели любого вида.
Процесс моделирования можно условно подразделить на три этапа:
1) анализ теоретических закономерностей, свойственных изучаемому явлению или процессу и эмпирических данных о его структуре и особенностях; на основе такого анализа формируются модели;
2) определение методов, с помощью которых можно решить задачу;
3) анализ полученных результатов.
Важнейшим моментом первого этапа моделирования является четкая формулировка конечной цели построения модели, а также определение критерия, по которому будут сравниваться различные варианты решения. Такими критериями в системе менеджмента могут быть:
а) максимизация полезного эффекта товара при ограничении совокупности затрат;
б) максимизация прибыли фирмы при условии, что качество товара не снизится;
в) снижение себестоимости товара при условии, что его качество не снизится и затраты у потребителя не увеличатся;
г) рост производительности труда, улучшение использования оборудования или материалов, повышение оборачиваемости оборотных средств при условии, что качество товара не снизится и другие критерии не ухудшатся. Таким образом, в качестве критерия оптимизации может быть какой-либо показатель или компонент прибыли, эффективности товара, объема рынка при условии, что другие компоненты при этом не ухудшатся. Не для всякой экономической задачи нужна собственная модель. Некоторые процессы с математической точки зрения однотипны и могут описываться одинаковыми моделями. Например, в линейном программировании, теории массового обслуживания и других существуют типовые модели, к которым приводится множество конкретных задач.
Вторым этапом моделирования экономических процессов является выбор наиболее рационального математического метода для решения задачи. Так, для решения задач линейного программирования известно много методов (симплексный, потенциалов и др.). Лучшей моделью является не самая сложная и самая похожая на реальное явление, а та, которая позволяет получить самое рациональное решение и наиболее точные экономические оценки. Излишняя детализация затрудняет построение модели, а излишнее укрупнение модели приводит к потере существенной экономической информации, к неадекватному отражению реальности.
Третьим этапом моделирования является всесторонний анализ результата, полученного при изучении экономического явления. Окончательным критерием достоверности и качества модели являются практика, соответствие полученных результатов и выводов реальным условиям, экономическая содержательность полученных оценок. Если результаты не соответствуют реальным условиям, то необходим анализ причин несоответствия, в качестве которых могут быть недостоверность информации, несоответствие модели экономическим условиям и др. По результатам анализа причин несоответствия экономико-математическая модель корректируется, и решение задачи повторяется.
studfiles.net
Методы оптимизации (Введение к учебному пособию)
"В мире не происходит ничего, в чем
не был бы виден смысл какого-либо
максимума или минимума" - Л. Эйлер
Введение
Целью учебного пособия является знакомство с основными методами поиска решений различных экстремальных задач. Математические методы оптимизации применялись и применяются в настоящее время в конечном счете для улучшения конструирования и управления техническими и организационными системами.
|
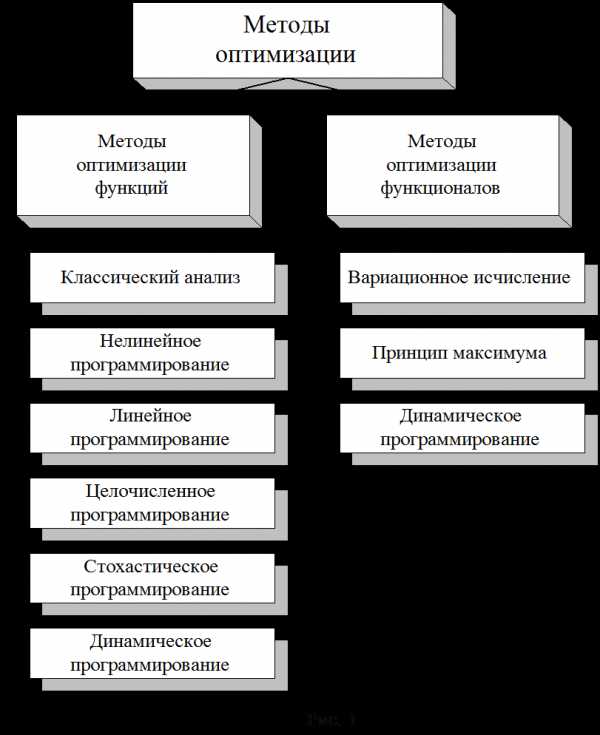
|
Обратимся к рис. 1. Все методы оптимизации можно условно разделить на две группы: методы минимизации функций конечного числа переменных и методы оптимизации динамических систем (методы минимизации функционалов).
К первой группе отнесем классические методы анализа функций, методы нелинейного, линейного, целочисленного, стохастического и динамического программирования.
Рассмотрим несколько примеров. Однако, прежде заметим, что общий путь решения задач, в которых используются методы оптимизации, следующий:
1) осуществляется общая постановка задачи: описывается объект исследования и хотя бы в описательной форме формулируются желания исследователя на выбор наилучшей стратегии;
2) составляется математическая модель объекта;
3) математически формулируются желания исследователя, т.е. составляется функция качества; иногда удается математическую модель подставить в функцию качества и получить явную зависимость функции качества от управляющих воздействий, т.е. от возможных стратегий управления объектом; в остальных случаях математическая модель выступает в роли ограничений на управления;
4) составляется критерий оптимальности, который, как правило, заключается в требовании минимума или максимума функции качества по управляющим воздействиям при наличии ограничений;
5) решается экстремальная задача с помощью метода оптимизации.
|
|
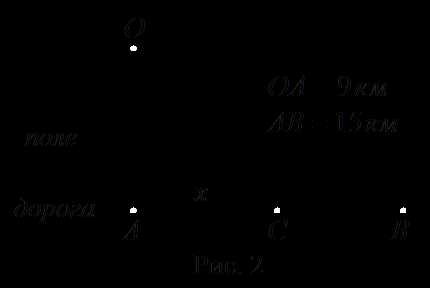
Пример. Необходимо попасть из поселка в районный центр , находящийся на дороге. Считаем, что дорога прямая, а из т. до дороги можно двигаться только по прямой линии. Известно, что: 1) кратчайшее расстояние от т. до дороги 9 км; 2) расстояние от т. до т. - 15 км; 3) скорость движения из т. до дороги (т.е. по полям) 4 км в час; 4) скорость движения по дороге - 5 км в час.
Необходимо выбрать такой путь движения , т.е. найти такое , чтобы время движения из т. в т. было минимальным. Управляющим воздействием в этой задаче является , который имеет естественное ограничение . Управление, лежащее за этими пределами приводит к явно худшим решениям.
Рассчитаем теперь время движения по ломанной
. (1)Получили функцию качества и нам необходимо решить экстремальную задачу
. (2)
Так как - нелинейная функция от управляющего воздействия , то (2) - это задача нелинейного программирования. Однако, функция настолько проста, что найти экстремум можно, используя классические методы анализа, которые были полностью развиты уже в XIX в.
В течение длительного времени в экономической науке использовался весьма ограниченный арсенал математических моделей. В частности, широко применялись модели, использующие простейшие алгебраические соотношения и обозначения (см., например, “Капитал” К. Маркса). С помощью них выражены основные экономические закономерности капиталистического хозяйства. Делались также попытки использовать дифференциальное и интегральное исчисление при изучении экономических проблем. Но этот подход в то время (в начале двадцатого столетия) не нашел применения. Основная причина заключалась в том, что исследователи не могли представить всей проблемы в целом: 1) создание адекватной математической модели объекта; 2) решение экстремальных задач с целью получения оптимальных стратегий управления.
Впервые научный подход к решению оптимизационных экономических задач был указан советским математиком ( в последствии академиком) Леонидом Витальевичем Канторовичем. Началом послужило решение в 1938 г. задачи о наилучшей производительной программе загрузки группы лущильных станков в фанерном тресте. После этого в 1938-1939 гг. была решена еще группа задач, например, о раскрое листового материала, распиловка леса и др. При этом много проблем возникало в процессе создания адекватных моделей, а при решении экстремальных задач необходимо было создавать свои методы. Так появилось линейное программирование [1], целочисленное программирование, стохастическое программирование, динамическое программирование, почти полностью изменился арсенал методов нелинейного программирования.
Пример постановки задачи линейного программирования.
Имеется пунктов, в которых сосредоточен однородный продукт в количествах соответственно единиц. Его необходимо перевести в пунктов доставки и в каждом из них должно содержаться единиц продукта. Стоимость перевозки единицы продукта из - го пункта отправки продукта в - ый пункт назначения равна и она известна для всех комбинаций индексов.
Обозначим через - количество продукта, перевозимого по маршруту . Эти величины неизвестны и их нужно выбрать такими, чтобы суммарная стоимость всех перевозок была минимальной.
Запишем общую стоимость всех перевозок
и тогда критерий оптимальности состоит в минимизации функции по параметрам с различными наборами индексов
. (3)
Выпишем ограничения задачи. Многие из них очевидны. Например,
Кроме того, из -го пункта отправления может быть вывезено только единиц продукта
(4)а в пункт назначения необходимо подвести только единиц продукта
(5)Часто также выполняется условие: общий запас продукта в пунктах отправления равен суммарной потребности в этом продукте пунктов назначения, т.е.
Итак, необходимо удовлетворить критерий оптимальности при наличии всех указанных ограничений. Мы описали простейший вариант так называемой транспортной задачи.
Рассмотрим еще один пример. Отличительной особенностью его является то, что математическая модель задается в сетевой форме, а не в виде привычных нам алгебраических или дифференциальных уравнений.
|
|
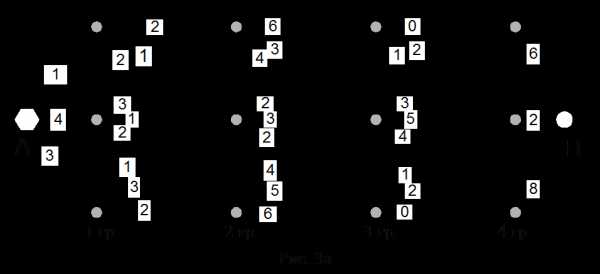
Охотник движется из пункта в пункт , проходя ряд промежуточных пунктов. Пункты обозначаем кружками, а возможные пути движения между ними - прямыми линиями (см. рис. 3а). Считаем, что охотник может двигаться только слева направо. На линиях, соединяющими пункты, стоят числа, обозначающие количество дичи, которое добудет охотник при движении между соответствующими пунктами. Необходимо выбрать маршрут движения, обеспечивающий охотнику максимальную добычу дичи.
|
|
Сгруппируем промежуточные пункты по группам 1, 2, 3, 4. В каждую группу входит по 3 пункта. Попробуем решить эту задачу. Самый простой метод - это метод полного перебора всех возможных маршрутов (их ). Для каждого пути необходимо просчитать количество добытой дичи, а затем выбрать оптимальный путь. Очевидно, что при увеличении размерности задачи (количества групп и количества элементов в группе) этот метод требует сравнения астрономически большого числа различных вариантов, например, если в группе элементов, а число групп равно , то число вариантов будет . При , , . Если перебор вариантов поручить современной быстродействующей вычислительной машине (1 перебор за сек.), то ей понадобится лет непрерывной работы.
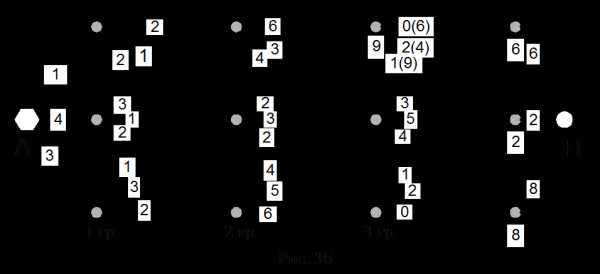
А теперь решим задачу другим методом. Рассматриваем граф движения охотника, начиная с точки , т.е. с конца движения.
В точку охотник может попасть из одного из трех пунктов 4-ой группы, но так как мы не знаем из какого, то перебираем пункты этой группы.
Если охотник оказался в первом пункте 4-ой группы, то дальнейшее оптимальное движение (такая возможность у него единственная) принесет ему 6 единиц прибыли. Ставим под пунктом это число, путь также помечаем жирной линией и называем критическим (рис. 3б). Аналогично рассматриваем остальные 2 пункта 4-ой группы.
vunivere.ru
Под оптимизацией понимают процесс выбора наилучшего варианта из всех возможных. Сточки зрения инженерных расчётов методы оптимизации позволяют выбрать наилучши
Методы оптимизации
Определения
Под оптимизацией понимают процесс выбора наилучшего варианта из всех возможных. С точки зрения инженерных расчётов методы оптимизации позволяют выбрать наилучший вариант конструкции, наилучшее распределение ресурсов и т.п.
В процессе решения задачи оптимизации обычно необходимо найти оптимальные значения некоторых параметров, определяющих данную задачу. В инженерных задачах их называют проектными параметрами, в экономических задачах параметрами плана. В качестве проектных параметров могут быть: значения линейных размеров объекта, массы объекта, температуры и т.п.
Число проектных параметров
характеризует размерность и степень сложности задачи оптимизации.
Выбор правильного решения или сравнивание двух альтернативных решений проводиться с помощью некоторой зависимой величины (функции), определяемой проектными параметрами. Эта величина называется целевой функцией (или критерием качества).
В процессе решения задачи оптимизации должны быть найдены такие значения проектных параметров, при которых целевая функция имеет экстремум: минимум или максимум.
Целевую функцию можно записать в виде
(8.1)
Примеры целевых функций, встречающихся в экономических и инженерных расчетах: прочность или масса конструкции, мощность установки, объём выпуска продукции, стоимость перевозок грузов, прибыль и т.п.
При =1 целевая функция-функция одной переменной, её график - кривая на плоскости.
При =2 целевая функция-функция двух переменных, её график - поверхности в трёхмерном пространстве.
Целевая функция не всегда может быть представлена в виде формулы. Иногда она может принимать некоторые дискретные значения, задаваться в виде таблицы и т.п. В любом случае, она должна быть однозначной функцией проектных параметров.
Целевых функций может быть несколько.
Например, при проектировании изделий машиностроения одновременно требуется обеспечить надёжность,материалоёмкость, полезный объём или грузоподъёмность. Некоторые целевые функции могут оказаться несовместимыми. В таких случаях, необходимо вводить приоритет той или иной функции.
Задачи оптимизации можно классифицировать различными способами.
Пирумов: на 3 группы (см. стр. 57)
Турчак: на 2 типа: условие и без условия.
Безусловная задача оптимизации
Состоит в отыскании и действительной функции  (8.1) от действительных переменных определении соответствующих значений аргументов на некотором подмножестве - мерного пространства.
(8.1) от действительных переменных определении соответствующих значений аргументов на некотором подмножестве - мерного пространства.
Обычно рассматриваются задачи минимизации; задачи на поиск к ним легко сводится путём замены знака целевой функции на противоположный.
Условные задачи оптимизации или задачи с ограничениями - это задачи, при формулировке которых задаются некоторые условия (ограничения) на множестве . Эти ограничения задаются совокупностью некоторых функций, удовлетворяющих уравнениям или неравенствам.
Ограничения- равенства выражают зависимость между проектными параметрами, отражают законы природы, наличие ресурсов, финансовые требования и т.п.
В результате ограничений область проектирования , определяемая всеми проектными параметрами, может быть существенно уменьшена в соответствии с физической сущностью задачи. Число ограничений – равенство может быть произвольным.
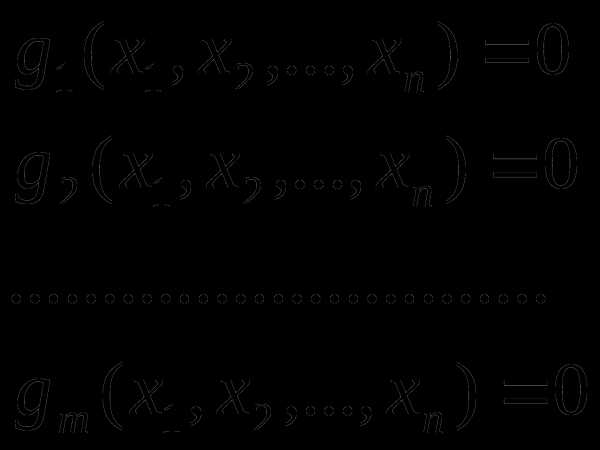 (8.2)
(8.2)
В ряде случаев из этих соотношений можно выразить одни проектные параметры через другие, что, в свою очередь, может уменьшить размерность задачи и облегчить её решение.
Аналогично можно вводить ограничения-неравенства:
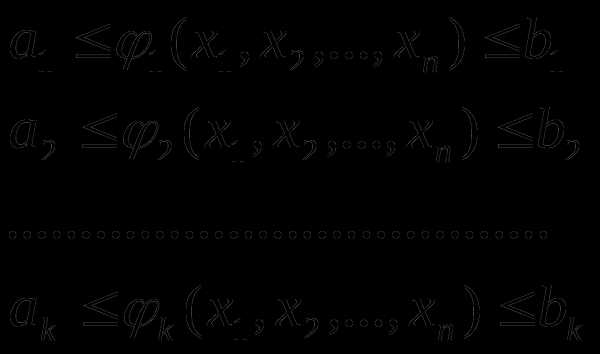 (8.3)
(8.3)
Особенность отыскания решения при наличии ограничений: оптимальное решение может соответствовать либо локальному экстремуму функции внутри области проектирования, либо значению целевой функции на границе области.
Если же ограничений нет, то ищется оптимальное решение на всей области проектирования, т.е. глобальный экстремум. Теория и методы решения задач оптимизации при наличии ограничений составляют предмет исследования одного из разделов прикладной математики, математического - программирования.
Пример постановки задачи:
Пусть требуется спроектировать контейнер в форме прямоугольного параллелепипеда объёмом 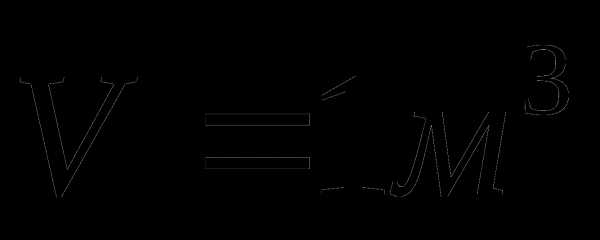 ; желательно израсходовать как можно меньше материала. При постоянной толщине стенок условие уменьшения расходов материала означает, что площадь полной поверхности контейнера должна быть .
; желательно израсходовать как можно меньше материала. При постоянной толщине стенок условие уменьшения расходов материала означает, что площадь полной поверхности контейнера должна быть .
Обозначим 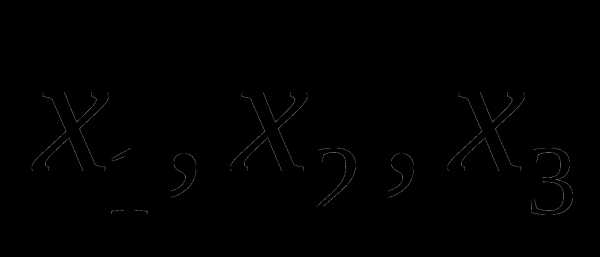 - рёбер контейнера. Следовательно, задача сводится к минимизации функции
- рёбер контейнера. Следовательно, задача сводится к минимизации функции
(8.4)
Эта функция в данном случае является целевой. Условие 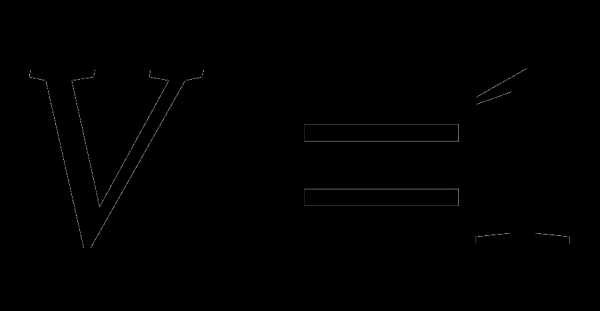 - ограничение – равенство. Оно позволяет исключить один параметр
- ограничение – равенство. Оно позволяет исключить один параметр
(8.5)
Свели задачу к минимизации функции двух переменных. В результате решения будут найдены значения проектных параметров 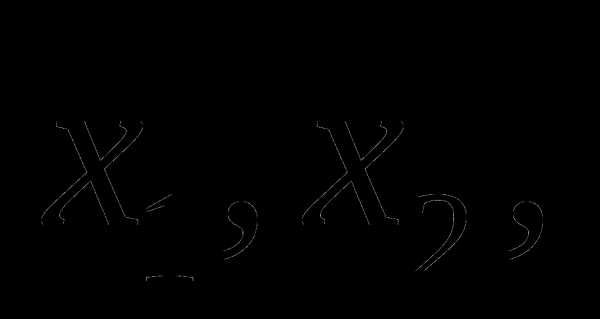 а потом .
а потом .
Фактически получилась задача безусловной оптимизации для целевой функции (8.5), так как ограниченное равенство было использовано для исключения параметра .
Можно усложнить задачу, добавив дополнительные условия. Например, потребуем, чтобы данный контейнер имел длину не менее 2 метров.
Получим ограничение-нераенство на один из параметров
 (8.5)
(8.5)
Таким образом, получаем условную задачу оптимизации: необходимо минимизировать функцию (8.4), учитывая ограничение-неравенство (8.5), найти оптимизацию значения параметров .
Одномерная оптимизация
Одномерная задача оптимизации формулируется следующим образом: Найти экстремум целевой функции , заданной на множестве , и определить значение проектного параметра  , при котором целевая функция принимает экстремальное значение.
, при котором целевая функция принимает экстремальное значение.
Существование решения поставленной задачи вытекает из теоремы Вейерштрасса: Всякая функция , непрерывная на [a,b], принимает на этом отрезке наименьшее и наибольшее значения, то есть на [a,b]
 и :
и : 
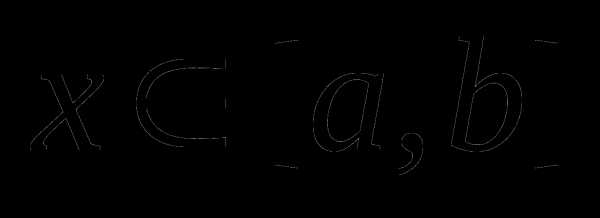
.
Эта теорема не доказывает единственности решения. Не исключена возможность достижения равных экстремумов сразу в нескольких точках данного отрезка. Такая ситуация например имеет место для периодической функции (например ), рассматриваемой на отрезке, содержащем несколько периодов.
Простейший класс целевых функций случай дифференцируемой функции на [a,b],причём функция задана в виде аналитической зависимости ,и может быть найдено явное выражение для . Нахождение экстремумов таких функций проводят методами дифференциального исчисления, известными из высшей математики: функция может достигать своего наименьшего и наибольшего значения либо в граничных точках [a,b]; либо в точках и , которые обязательно должны быть критическими, то есть =0 в этих точках – это необходимое условие экстремума, для определения наименьшего и наибольшего значений функции на [a,b] нужно вычислить её значения во всех критических точках данного отрезка и в его граничных точках и сравнить полученные значения; наименьшее или наибольшее из них и будет искомым значением.
Пример: Найти наименьшее и наибольшее значения функции 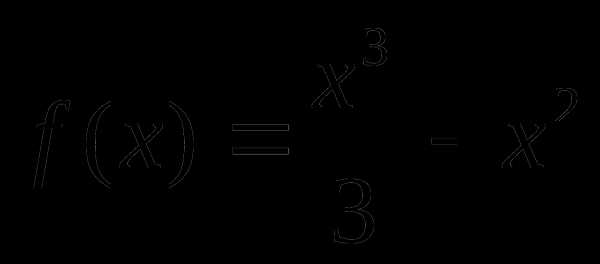 на [1,3].
на [1,3].
Решение: Найдём производную этой функции
Найдём критические точки:
=0
 =0 =0, =2
=0 =0, =2
=0 [1,3]
[1,3]
Для анализа оставляем три точки:
 =1
=1 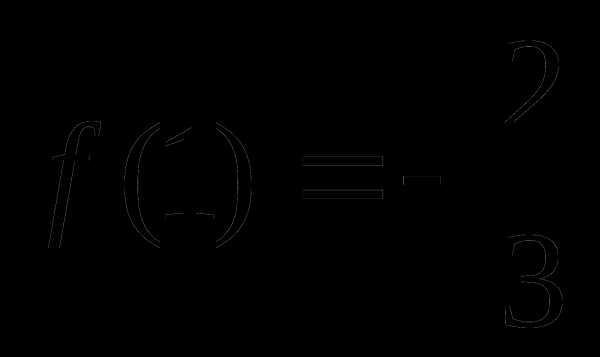
=2 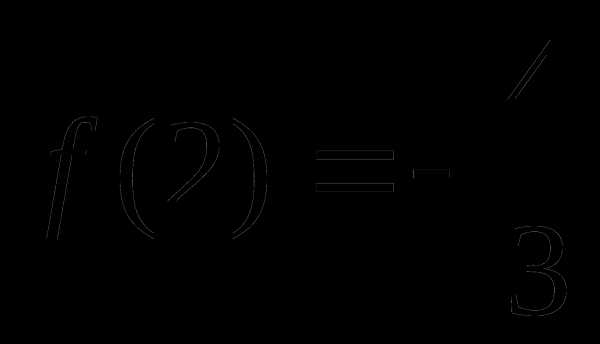
 =3
=3 
Сравнивая полученные величины, находим
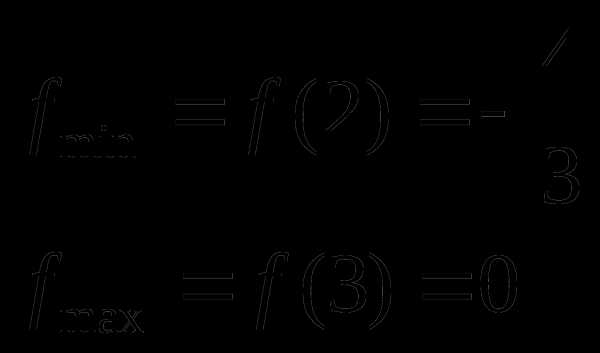
Здесь уравнение =0 удалось решить непосредственно. Для более сложных видов необходимо использовать численные методы решения нелинейных уравнений.
Рассмотренный метод, основанный на вычислении производной целевой функции, требует её аналитического представления.
В других случаях, когда целевая функция задана в табличном виде или может быть вычислена при некоторых дискретных значениях аргумента, используют различные методы поиска. Они основаны на вычислениях целевой функции в отдельных точках и выбора среди них наибольшего или наименьшего значений.
Рассмотрим нахождение минимума функции на [a,b]. Предположим, что целевая функция унимодальна, то есть на данном отрезке она имеет только один минимум.
В инженерной практике встречаются именно такие целевые функции.
Погрешность приближённого решения задачи определяется разностью между оптимальным значением  проектного параметра и приближением к нему
проектного параметра и приближением к нему  .
.
Потребуем
 (8.6)
(8.6)

заданное допустимое значение
Процесс решения задачи оптимизации методом поиска состоит в последовательном сужении интервала изменения проектного параметра, называемого интервалом неопределённости. В начале процесса оптимизации его длина равна 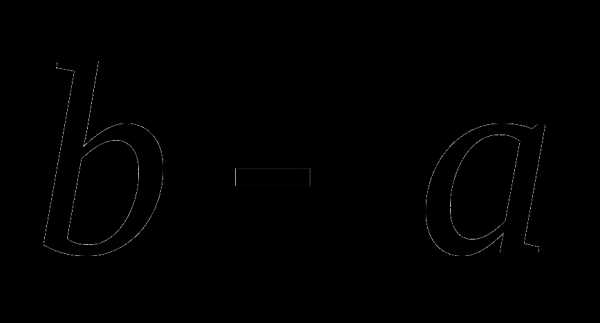 , к концу она должна стать меньше
, к концу она должна стать меньше  , то есть оптимальное значение проектного параметра должно находиться в интервале неопределённости
, то есть оптимальное значение проектного параметра должно находиться в интервале неопределённости 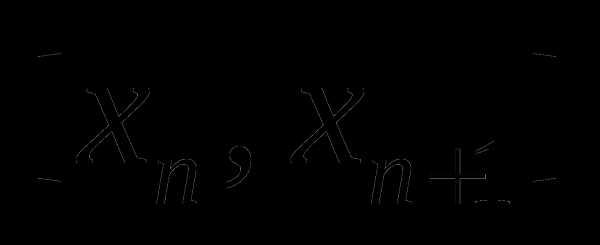 , причём
, причём 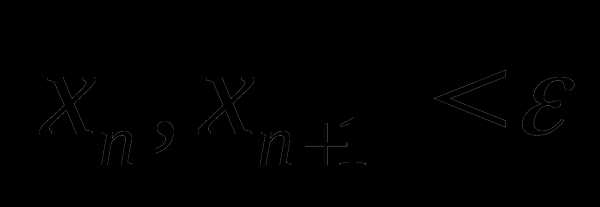 тогда для выполнения условия (8.6) в качестве приближения к оптимальному значению можно принять любое , например:
тогда для выполнения условия (8.6) в качестве приближения к оптимальному значению можно принять любое , например: 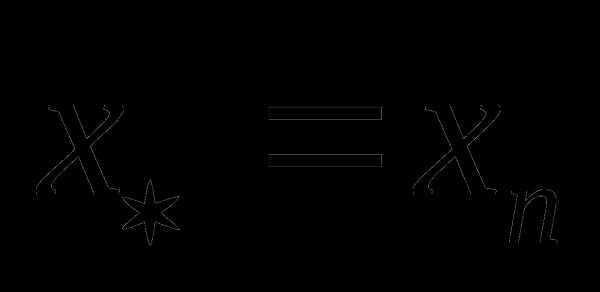 или
или 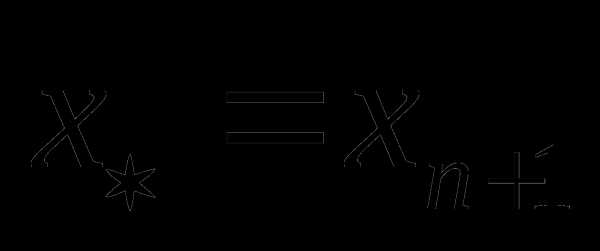 или
или 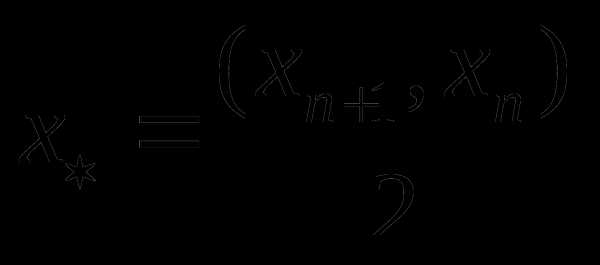
В последнем ……для выполнения (8.6) достаточно выполнения неравенства
Наиболее простым способом сужения интервала неопределённости является деление его на некоторое число равных частей с последующим вычислением значений целевой функции в точках разбиения.
Пусть число элементарных отрезков
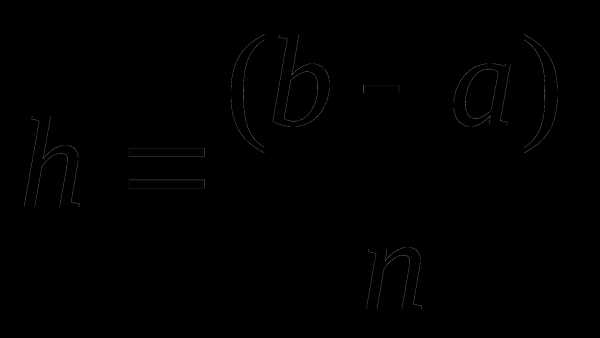 - шаг разбиения
- шаг разбиения
Вычислим значения целевой функции в узлах
Сравнивая полученные значения , найдём среди них наименьшее 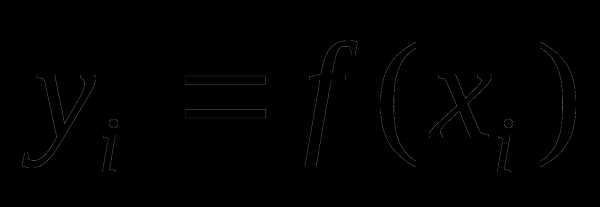
Число  можно приближённо принять за наименьшее значение целевой функции на [a,b].
можно приближённо принять за наименьшее значение целевой функции на [a,b].
Очевидно, 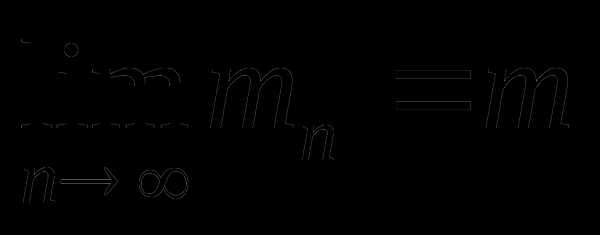 для непрерывной , то есть близость
для непрерывной , то есть близость 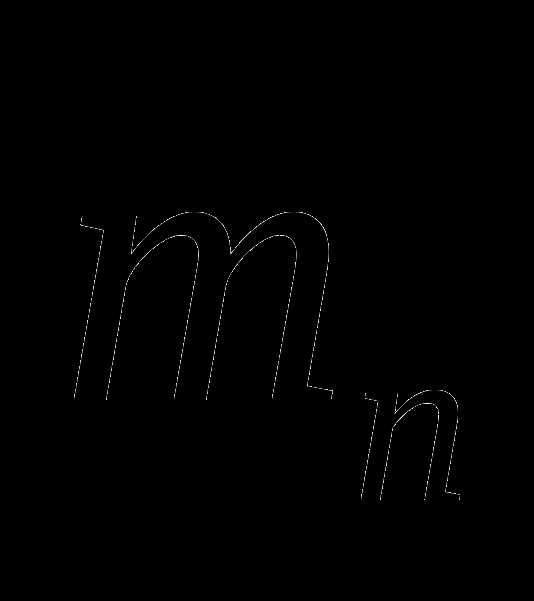 к минимуму зависит от числа точек: с увеличением числа точек разбиения погрешность в определении стремиться к нулю.
к минимуму зависит от числа точек: с увеличением числа точек разбиения погрешность в определении стремиться к нулю.
Этот метод называется методом перебора.
Основная трудность: выбор и оценка погрешности.
Пример: Пусть начальная длина интервала неопределённости равна  . Нужно добиться его уменьшения в сто раз. Этого легко достичь разбиением интервала на 200 частей.
. Нужно добиться его уменьшения в сто раз. Этого легко достичь разбиением интервала на 200 частей.
Вычислив значения целевой функции , найдём её минимальное значение 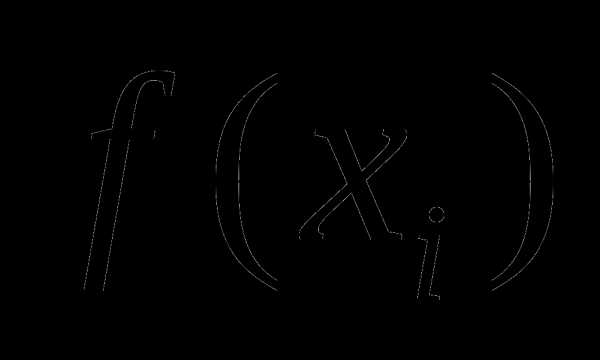 . Тогда искомым интервалом неопределённости будет .
. Тогда искомым интервалом неопределённости будет .
Но можно сократить число разбиений. Сначала разобьём [a,b] на 20 частей и найдём интервал неопределённости длиной 0,1; при этом мы вычислим значения целевой функции в точках .
Теперь снова разобьём на 20 частей, получим искомый интервал длиной 0,01; причём значения целевой функции вычисляем в точках , так как в точках 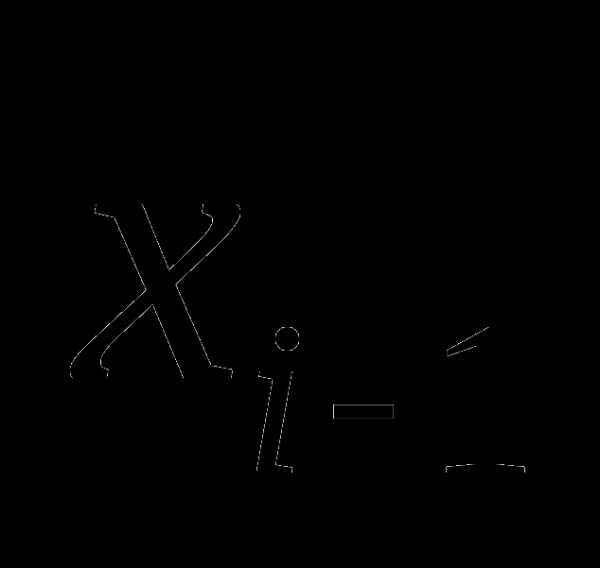 и
и 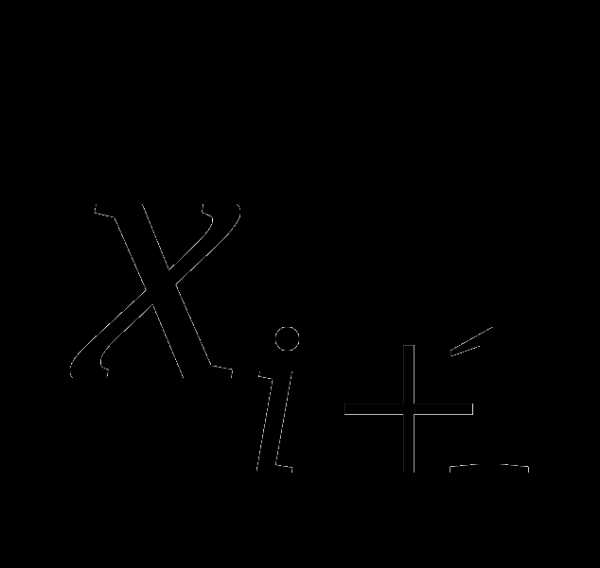 значения уже найдены. Таким образом, во втором случае в процессе оптимизации произведено 40 вычислений значений целевой функции против 201 в первом случае.
значения уже найдены. Таким образом, во втором случае в процессе оптимизации произведено 40 вычислений значений целевой функции против 201 в первом случае.
То есть способ разбиения позволяет существенно уменьшить количество вычислений.
Существует ряд специальных методов поиска оптимизации решений: метод деления отрезка пополам, метод золотого сечения, метод Ньютона и так далее, позволяющие сократить объём вычислений и время поиска.
Метод золотого сечения
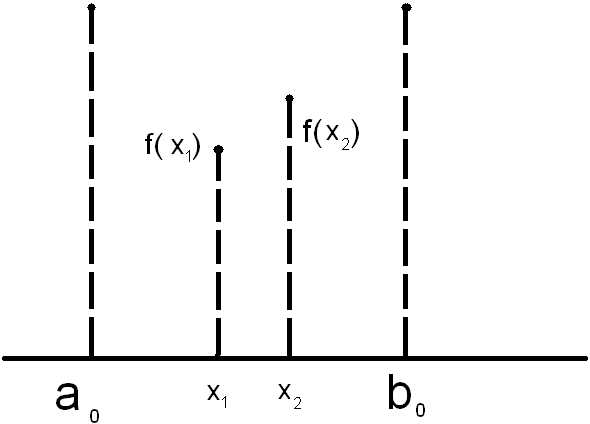
На первом шаге процесса оптимизации внутри [] выбираем некоторые точки , и вычисляем значения целевой функции ,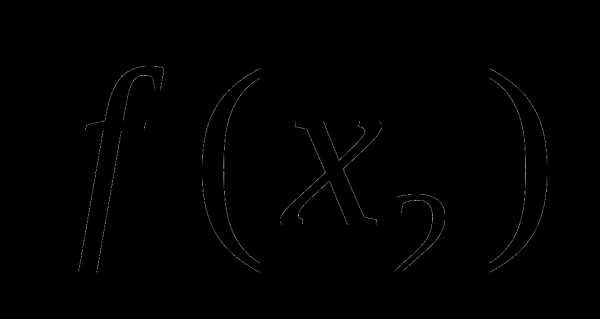 .
.
В данном случае расположен на одном из прилегающих к отрезков: [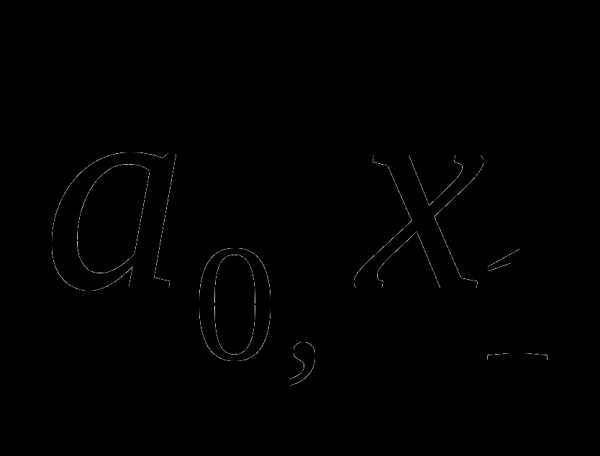 ] или [,].
] или [,].
[,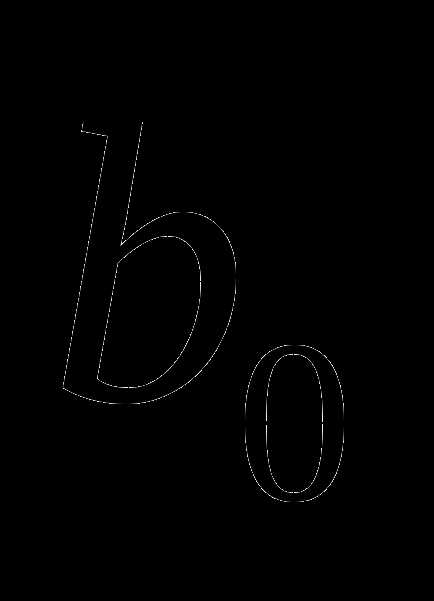 ] можно отбросить, сузив первоначальный интервал неопределённости.
] можно отбросить, сузив первоначальный интервал неопределённости.
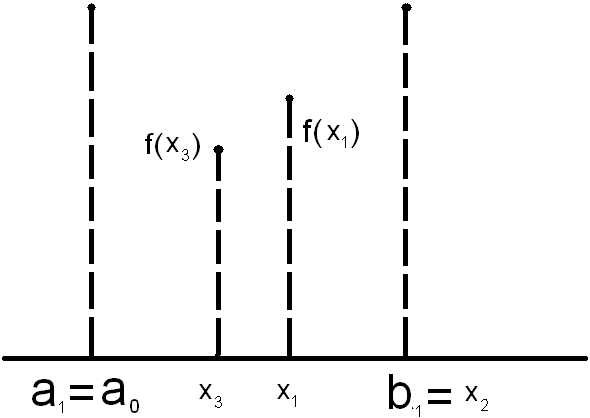
Второй шаг проводим на [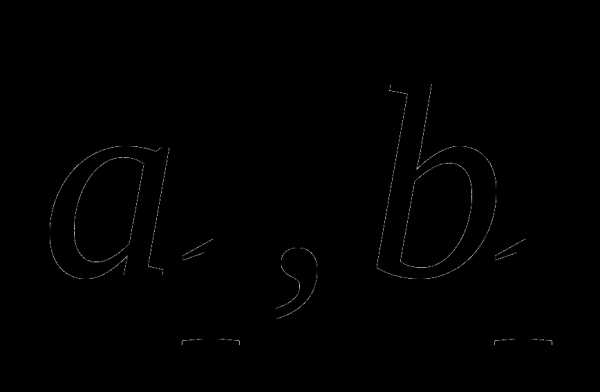 ], где .
], где .
Нужно снова выбрать две внутренние точки, но одна из них -- осталась от предыдущего шага, поэтому достаточно выбрать точку , вычислить значение целевой функции 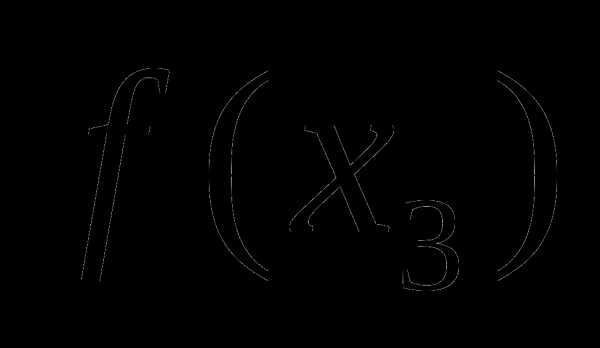 и провести сравнение. В данном случае , находиться на отрезке [
и провести сравнение. В данном случае , находиться на отрезке [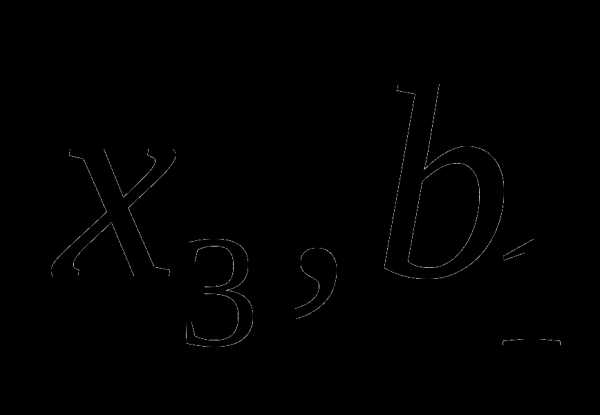 ]. Обозначим
]. Обозначим  =,
=, 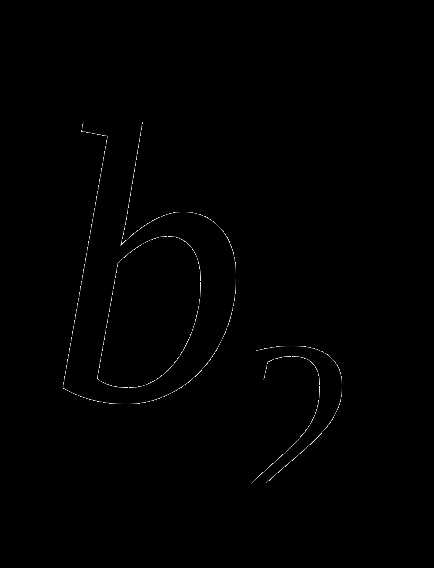 =
=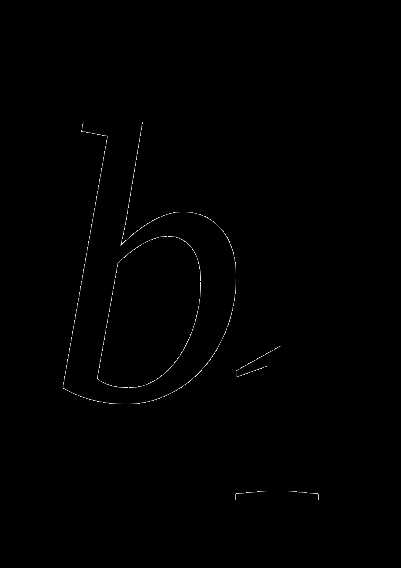 , снова выбираем одну внутреннюю точку и повторим процедуру сужения интервала неопределённости. Процесс оптимизации продолжаем, пока
, снова выбираем одну внутреннюю точку и повторим процедуру сужения интервала неопределённости. Процесс оптимизации продолжаем, пока 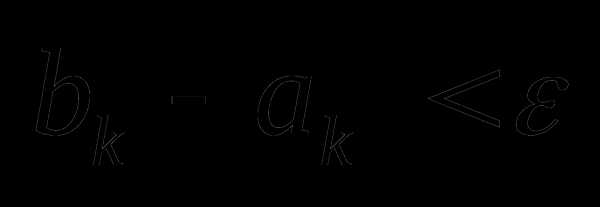 .
.
Как мы выбираем внутренние точки на каждом 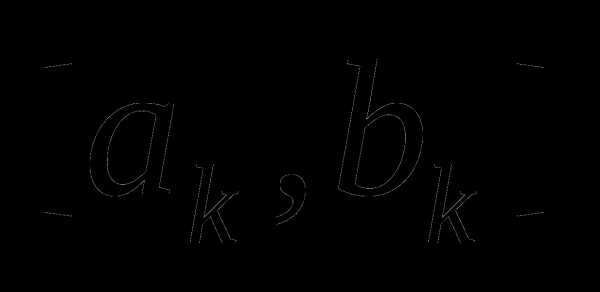 ?
?
Пусть длина интервала неопределённости равна , а точка деления разбивает его на части и : >, = + .
Золотое сечение интервала неопределённости выбирают так, чтобы отношение длины большего отрезка к длине всего интервала равнялось отношению длины меньшего интервала к длине большего интервала:
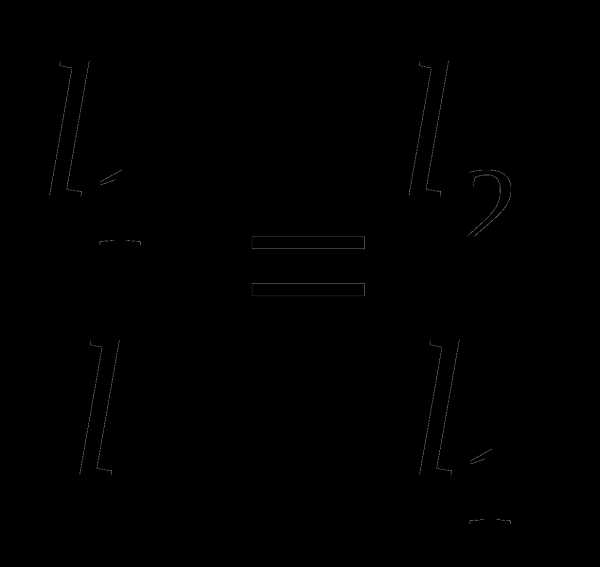 (8.7)
(8.7)
Отсюда можно найти точку деления, вычислив отношения: 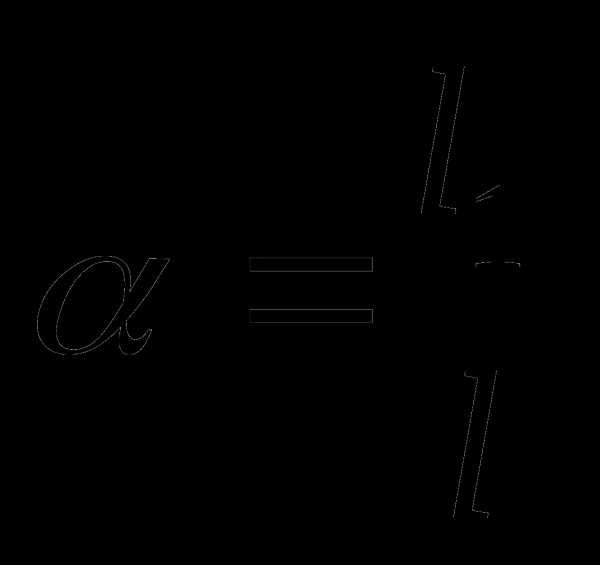 ;
;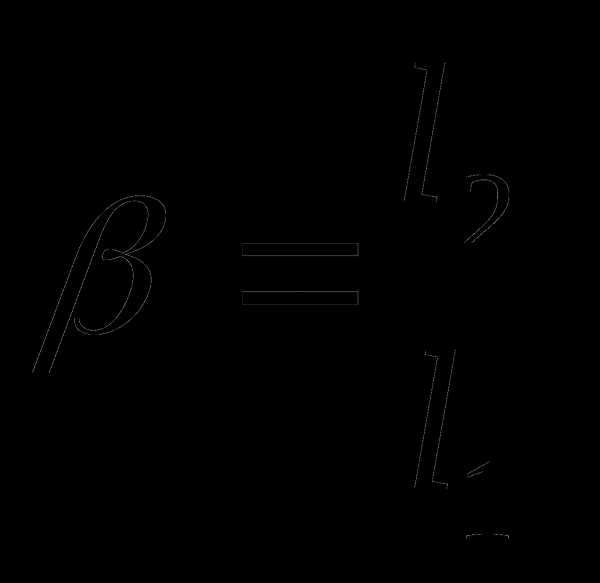
Преобразуем (8.7) и найдём  и
и  :
:

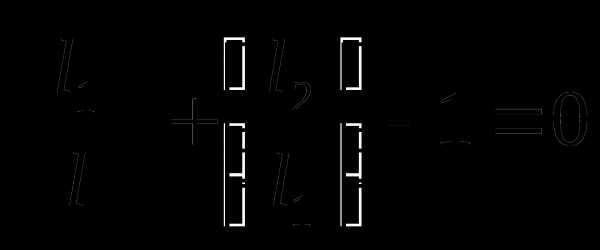 или
или
так как нас интересует
__________________
Евклид (3в. до н. э.) выполнил задачу деления отрезка в данном отношении с помощью циркуля и линейки.
__________________
Очевидно, что интервал неопределённости можно разделить в соотношении золотого сечения двояко:
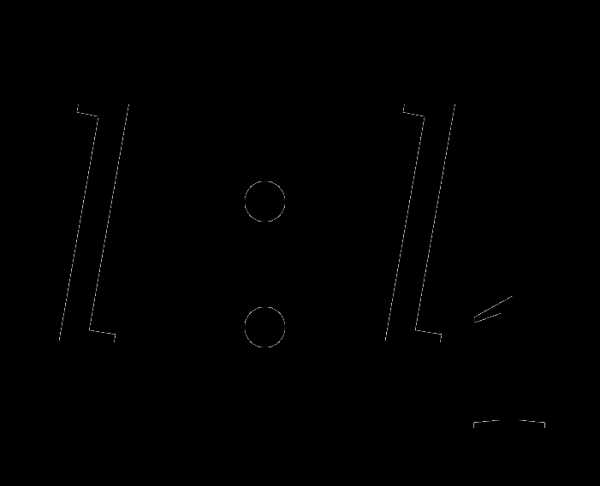
 и
и 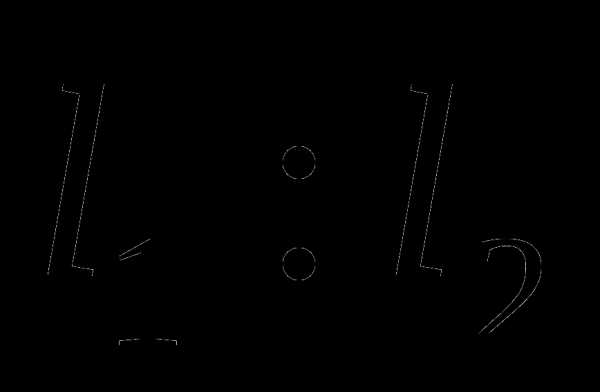 . В данном случае имеем
. В данном случае имеем
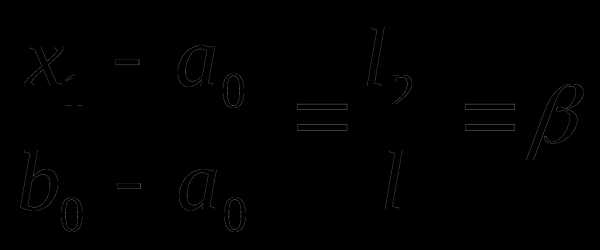 ; ;
; ;
;
(8.8)
аналогично,
(8.9)
Начальная длина интервала неопределённости
После первого шага оптимизации получаем новый интервал неопределённости []. Его длина с учётом (8.9)
на втором шаге оптимизации [] также делиться в соотношении золотого сечения. При этом одной из точек деления будет точка .
следует из соотношения
Вторая точка деления 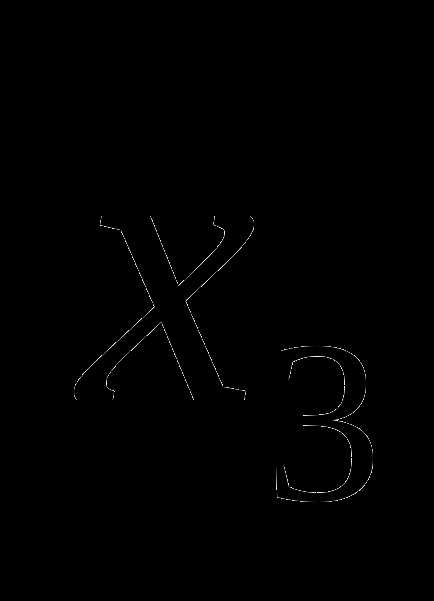 выбирается так же, как выбирается точка при делении [], аналогично (8.8) : .
выбирается так же, как выбирается точка при делении [], аналогично (8.8) : .
Снова интервал неопределённости уменьшается до размера
по аналогии с (8.8) и (8.9) можно записать координаты точек деления и 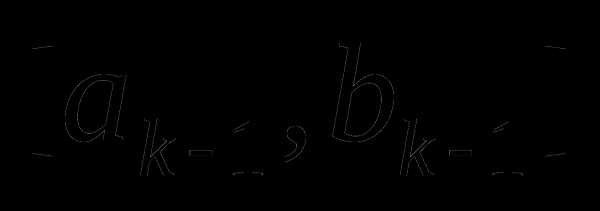 на
на  -ом шаге оптимизации ()
-ом шаге оптимизации ()
;
вычислению подлежит только одна из координат и ; другая берётся с предыдущего шага. При этом длина интервала неопределённости
(8.10)
Процесс оптимизации заканчивается при выполнении условия 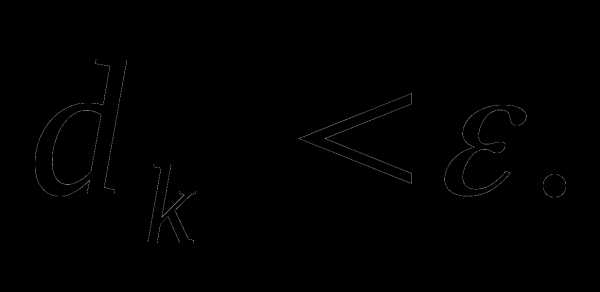
В качестве приближения к оптимальному значению можно принять
=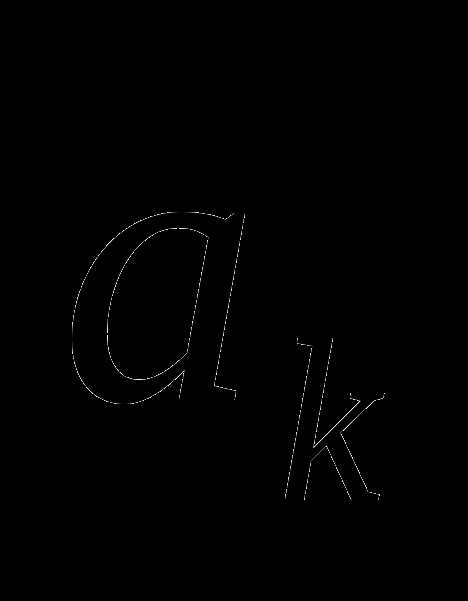 или =
или =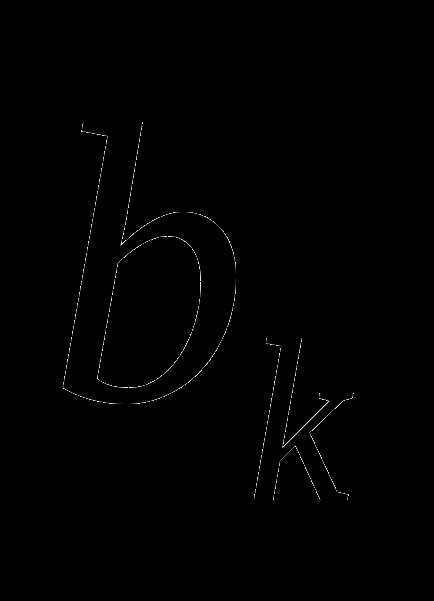 или
или 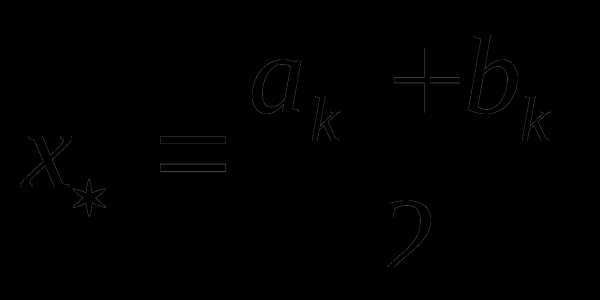
в последнем случае для достижения требуемой точности и выполнения неравенства (8.6) достаточно 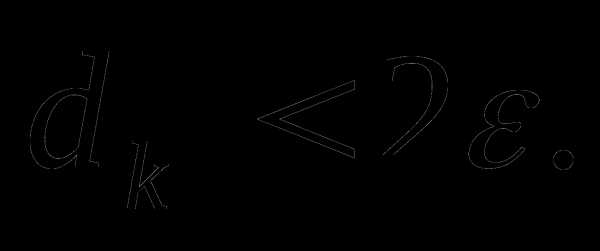
gigabaza.ru