Методы оптимизации учебник. Учебник методы оптимизации

1. ВВЕДЕНИЕ

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

В.И. Рейзлин

ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМИЗАЦИИ

Рекомендовано в качестве учебного пособия Редакционно-издательскимсоветом Национального исследовательского Томского политехнического университета

Издательство

Национального исследовательского Томского политехнического университета

2013

УДК 519.6(075.8)

ББК 22.193 Р35

Рейзлин В.И.

Р35 Численные методы оптимизации: учебное пособие / В.И. Рейзлин; Национальный исследовательский Томский политехнический университет. – Томск: Изд-воНационального исследовательского Томского политехнического университета, 2013

–105 с.

Впособии рассматриваются следующие вопросы: постановка задач оптимизации и численные методы их решения; одномерная и многомерная безусловная оптимизация; условная оптимизация; линейное программирование.

Пособие подготовлено на кафедре Информатики и проектирования систем Национального исследовательского Томского политехнического университета и предназначено для студентов, обучающихся по Основной образовательной программе подготовки магистров по направлению 230100 – Информатика и вычислительная техника.

Пособие может быть полезно студентам и аспирантам, применяющим в своей научной и учебной работе численные методы.

УДК 519.6(075.8) ББК 22.193

Рецензенты

Доктор технических наук, начальник кафедры «Сети и системы связи» ИКСИ Академии ФСБ РФ

И.А. Шалимов

Кандидат технических наук, зав. лабораторией реологии нефти Института химии нефти СО РАН

Н.В. Юдина

©ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет», 2013

©Рейзлин В.И., 2013

©Обложка. Издательство Национального исследовательского Томского политехнического университета, 2013

Оптимизация в широком смысле слова находит применение в науке, технике и в любой другой области человеческой деятельности.

Оптимизация – целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях.

Поиски оптимальных решений привели к созданию специальных математических методов и уже в 18 веке были заложены математические основы оптимизации (вариационное исчисление, численные методы и др.). Однако до второй половины 20 века методы оптимизации во многих областях науки и техники применялись очень редко, поскольку практическое использование математических методов оптимизации требовало огромной вычислительной работы, которую без ЭВМ реализовать было крайне трудно, а в ряде случаев – невозможно. Особенно большие трудности возникали при решении задач оптимизации из-забольшого числа параметров и их сложной взаимосвязи между собой. При наличии ЭВМ ряд задач оптимизации поддается решению.

1.1. Постановка задач оптимизации

При постановке задачи оптимизации необходимо:

1. Наличие объекта оптимизации и цели оптимизации. При этом формулировка каждой задачи оптимизации должна требовать экстремального значения лишь одной величины, то есть одновременно системе не должно приписываться два и более критерия оптимизации, так как практически всегда экстремум одного критерия не соответствует экстремуму другого.

Типичный пример неправильной постановки задачи оптимизации:

«Получить максимальную производительность при минимальной себестоимости». Ошибка заключается в том, что ставится задача поиска оптимума двух величин, противоречащих друг другу по своей сути.

Правильной постановкой задачи может быть:

а) получить максимальную производительность при заданной себестоимо-

сти;

б) получить минимальную себестоимость при заданной производительно-

сти.

В первом случае критерий оптимизации – производительность, а во втором – себестоимость.

2.Наличие ресурсов оптимизации, под которыми понимают возможность выбора значений некоторых параметров оптимизируемого объекта. Объект должен обладать определенными степенями свободы – управляющими воздействиями.

3.Возможность количественной оценки оптимизируемой величины, поскольку только в этом случае можно сравнивать эффекты от выбора тех или иных управляющих воздействий.

4.Учет ограничений.

Пример 1.

Задача о планировании выпуска продукции при ограниченных ресурсах

Нефтеперерабатывающий завод производит за месяц 1500000 л алкилата, 1200000 л крекинг-бензинаи 1300000 л изопентола. В результате смешивания этих компонентов в пропорциях 1:1:1 и 3:1:2 получается бензин сорта А и Б соответственно. Стоимость 1000 л бензина сорта А и Б соответственно равна 16000 руб. и 20500 руб.

Определить месячный план производства бензина сорта А и Б, при котором стоимость выпущенной продукции будет максимальной.

Пример 2.

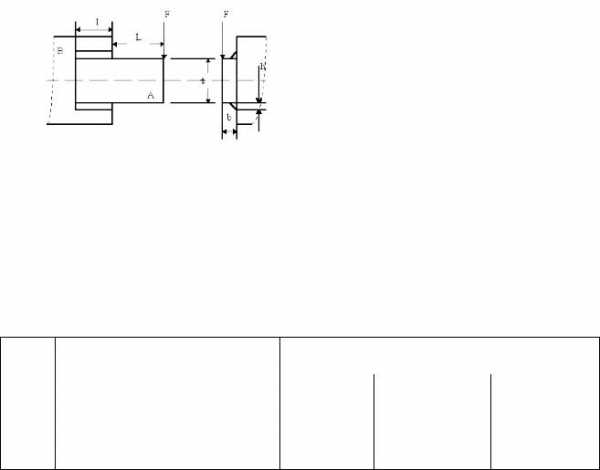
Задача о нахождении размеров нагруженной балки

Задана строительная конструкция, состоящая из балки А длиной L=35,6 см и жесткой опоры В. Балка А крепится на жесткой опоре В (рис. 1) с помощью сварного соединения. Балка изготавливается из стали марки 1010 и должна выдержать нагрузкуF = 2721,5 кг. Размерыh,t, толщинуb, ширинуl сварного шва необходимо выбрать таким образом, чтобы полные затраты были минимальными.

Рис. 1. Нагруженная балка

Пример 3.

Транспортная задача

Вобласти имеются два цементных завода и три потребителя их продукции

–домостроительные комбинаты. В табл. 1 указаны суточные объемы производства цемента, суточные потребности в нем комбинатов и стоимость перевозки 1 т цемента от каждого завода к каждому комбинату.

Таблица 1. Числовые характеристики к транспортной задаче

Заводы	Производство цемента (т/сут)	Стоимость перевозки 1 т цемента (ед.)

		Комбинат 1	Комбинат 2	Комбинат 3
1	40	10	15	25

2	60	20	30	30

	Потребности в цементе (т/сут)	50	20	30

Требуется составить план суточных перевозок цемента таким образом, чтобы транспортные расходы были минимальны.

studfiles.net

Методы оптимизации учебник - Стр 6

СПЕЦИАЛЬНЫЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

2.Специальные задачи линейного программирования

2.1Задача целочисленного линейного программирования

Значительная часть экономических задач, относящихся к задачам линейного программирования, требует целочисленного решения. К ним относятся задачи, у которых переменные величины означают количество единиц неделимой продукции, например, распределение производственных заданий между предприятиями, раскрой материалов, загрузка оборудования, распределение судов по линиям, самолетов по рейсам, а также задачи по производству неделимой продукции. Если единица составляет малую часть всего объема производства, то оптимальное решение находят обычным симплексным методом, округляя его до целых единиц, исходя из смысла задачи. В противном случае округление может привести к решению, далекому от оптимального целочисленного решения.

Пример 2.1. В цехе предприятия решено установить дополнительное оборудование, для размещения которого выделено 19.3 м2. На приобретение оборудования предприятие может израсходовать 10 тыс. у.е., при этом оно может купить оборудование двух видов. Комплект оборудования 1 вида стоит 1000 у.е., а 2вида—3000у.е. Приобретение одного комплекта оборудования 1 вида позволяет увеличить выпуск продукции в смену на 2 ед., а одного комплекта оборудования 2 вида — на 3 ед. Зная, что для установки одного комплекта оборудования 1 вида требуется 2 м2 площади, а оборудования 2 вида — 1 м2 площади, определить такой набор дополнительного оборудования, который дает возможность максимально увеличить выпуск продукции

Решение. Составим математическую модель задачи. Предположим, что предприятие приобрететх1 комплектов оборудования 1 вида их2 комплектов оборудования 2 вида. Тогда переменные х1 их2 должны удовлетворять следующим неравенствам:

2x		+ x	≤19.3	(2.1)
	1	2	≤10.
x1	+3x2

Если предприятие приобретет указанное количество оборудования, то общее увеличение выпуска продукции составит

F= 2х1 +3х2. (2.2)

По своему экономическому содержанию переменные х1 их2 могут принимать лишь целые неотрицательные значения, т. е,

х1, х2 ≥0	(2.3)
х1,х2 — целые.	(2.4)
Таким образом, задача (2.1) – (2.4) представляет собой задачу ЦЛП.

Пример 2.2. Обратимся к примеру 1.3.

Очевидно, что переменные модели Xj (j =1,6 ) могут принимать только целые значения и, следовательно, ЗЦЛП будет иметь вид:

min f (x) = 0,4 X1 + 0,3 X2 + 0,1 X3 + 0,1 X5 + 0,2 X6

2X2 + 2 X3 + 4 X4 + X5 =150

X1 + X2 + 2 X5 =200

X1 + X3 + 2 X6 =300 Xj ≥ 0,j =1,6, Xj - целые

studfiles.net

Методы оптимизации учебник - Стр 10

НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

Шаг 2. Определить возможное направление подъема , решая следующую задачу:

ϕ(

) =(f (

k ),

) →max

(4.3.2.2)

при условиях:

Pk ={S

En ,A1

≤0,

(4.3.2.3)

−1≤S j ≤1, j =

}

1,n

Шаг 3. Если всеϕ(S ) =( f (x k ),S k ) =0, тоx * = x k - задача решена.

Шаг 4. Определитьβk (шаг в направленииS k ), решая задачу одномерной оптимизации:

f (x k + βS k )→ max 0≤ β ≤ β* .

Шаг 5. Положитьx k +1 = x k + βk S k , заменить k на k+1 и перейти к шагу 1.

Пример.

f (x) =4x1 +6x2 +2x1 x2 −2x12 −2x2 2 →max

x1+ x2≤ 2x1 +5x2 ≤ 5− x1 ≤ 0

− x2 ≤0

Начальный этап.

Выбираем начальную точку x0 = (0,0) , для которой:

A0	−1		0			0			1	1				2

	=		,b0		=		, A0		=		,b0		=		.
1		0		1		0		2		5		2		5
			−1						1
f (x)= (4+ 2x2				− 4x1 ,6+ 2x1 − 4x2 ) , положить k=0.

Основной этап.

Итерация 1.

Шаг 1. Дляx0 = (0,0) заданыA10 ,b10 ,A20 ,b20 .

Шаг 2. f (x0 )= (4,6) .

Решаем задачу

ϕ(S)=(f (x0 ),S)=4S1 +6S2 →max

при условиях

− S1 ≤0

− S2 ≤0

−1 ≤S1 ≤1

−1 ≤S2 ≤1

При решении этой задачи симплекс-методомполучаемS0 = (1,1),ϕ(S0 )=10 .

studfiles.net

Методы оптимизации учебник - Стр 9

НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

Методы безусловной оптимизации.

Постановка задачи.

Задачей безусловной оптимизации функции нескольких переменных будем назы-

вать задачу, в которой требуется найти
min f (x),x En	(4.2.1)

при отсутствии ограничений на x , гдеx = (X1 ,...,X n ) - вектор управляемых переменных.

f – скалярная целевая функция.

Определение. Решением, или точкой минимума, задачи безусловной оптимизации называется такой векторx* En , чтоf (x* )≤ f (x) для всехx En и писать

		f (x * )= minf (x),x En	(4.2.2)
Определение. Вектор		называется направлением спуска функции	f (x) в точкеx ,
	S

если существует такое δ > 0 , чтоf (x + λS )< f (x) , для всехλ (0;δ) .

Сущность рассматриваемых в данном разделе методов решения задачи (4.2) состоит в построении последовательности точек x1 ,x2 ,...xk ,..., принадлежащихEn , монотонно

уменьшающих значение функции f (x) . Такие методы называют методами спуска.

Алгоритм метода спуска.

Начальный этап. Задатьx1 En - начальную точку,ε > 0 - параметр окончания сче-

та; положить k=1. Основной этап.

Шаг 1. В точкеxk проверить условие окончания счета; если оно выполняется, то положитьx* = xk и остановиться.

Шаг 2. В точкеxk выбрать направление спускаSk .

Шаг 3. Положитьxk +1 = xk + λk Sk , гдеλk - длина шага вдоль направленияSk , по-

ложить k=k+1 и перейти к шагу 1.

Различные методы спуска отличаются друг от друга способом выбора направления спуска Sk и шага вдоль этого направленияλk . Естественно, что трудоемкость вычисления

величины λk следует согласовывать с трудоемкостью определения направления спускаSk .

Методы решения задач безусловной оптимизации можно разделить на группы в зависимости от уровня используемой в методе информации о целевой функции, например:

1.Методы нулевого порядка, или прямого поиска, основанные на вычислении только значении целевой функции.

2.Градиентные методы, в которых используются значения функции f (x) и ее

градиента, т.е. вектора, компонентами которого являются частные производные первого порядка.

3.Методы второго порядка, в которых используются первые и вторые производные функции f (x) , т.е. значенияf (x),f (x),H (x) , гдеH (x) - матрица Гессе, элементами которой являются частные производные второго порядка функцииf (x) .

4.Методы оптимизации квадратичных функций.

studfiles.net

Методы оптимизации учебник - Стр 8

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ

3. Динамическое программирование

Динамическое программирование (ДП) представляет собой математический аппарат, разработанный с целью повышения эффективности вычислений при решении некоторого класса задач математического программирования путем их разложения на относительно небольшие и, следовательно, менее сложные подзадачи. Характерным для ДП является подход к решению задачи по этапам, с каждым из которых связана только одна управляемая переменная. Набор рекуррентных вычислительных процедур, связывающих различные этапы, обеспечивает получение допустимого оптимального решения задач в целом при достижении последнего этапа.

Применим метод ДП к решению двух важных экономических задач.

3.1. Задача распределения капиталовложений

Постановка задачи. Планируется распределение начальной суммы средств b0 между N предприятиями. Предполагается, что выделениеk-мупредприятию в начале планового периода средств в количестве уk приносят доход gk(yk). Определить, какое количество средств нужно выделить каждому предприятию, чтобы суммарный доход был максимальным.

Рассмотрим процесс управления некоторой системой: xk= T (xk−1 , δk), (k =1...N ),

где x0 - начальное состояние системы,

xk - состояние системы на шаге k,

δk - управляющее решение, принимаемое в состоянииxk−1 .

Качество процесса (эффективность) оценим количественно целевой функцией

F = Φ(x 0 ,δ1 ,....,δ N )

Задача оптимизации многошагового процесса состоит в следующем: определить

допустимое управление δ * = (

1*,

* ,....,

N * )

, которое переводит систему из начального

состояния

0 W0 в конечное состояние

N ,

при этом

k Wk (k = 1..N) , и доставляет

максимальное (минимальное) значение целевой функции, т.е.

F = Φ(x0 ,δ1,....,δ N )→ max(min)

x	k = T(	x	k−1,	δ	k )	(k =1..N )
	k Wk (k = 0..N)
x	k Wk (k = 0..N)
	k ∆k (k =1..N )
δ	k ∆k (k =1..N )

Допустимое управление δ * = (δ1* ,δ2* ,....,δ N * ) , которое доставляет максимальное значение функции, называется оптимальным управлением, траекторияx * = (x1* ,x2* ,....,x N * ) ,

соответствующая управлению δ * - оптимальной траекторией.

Представление произвольной оптимизационной задачи в указанном выше виде проводится по следующему алгоритму:

1)Выбирают способ деления процесса управления системой на шаги, определяется понятие шага, количество шагов N.

studfiles.net

Методы оптимизации учебник - Стр 5

ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

Перейдя к пределам изменения А, получим

4 ≤ A≤ 7.

Найденные пределы показывают границы, в которых может изменяться запас продукта А, чтобы номенклатура выпускаемой продукции (структура оптимального плана) осталась без изменений. А это означает, что при изменении запаса продукта А в найденных пределах оптимальным, то есть обеспечивающим наибольшую прибыль, является выпуск продукции П1, и продукции П2, только в других количествах. Продукции П1 необходимо будет выпускать в количестве

X 1 =10/3-1/3∆А;

продукции П2 – в количестве

X 2 =4/3+2/3∆А,

при этом доход будет

f (X ) = 38/3 + 1/3∆А.

Следовательно, если увеличить запас продукта А на 1 т (∆А = 1), то для обеспечения максимизации прибыли выпуск продукции П1 целесообразно уменьшить доX 1 = 3

тонн, а выпуск продукции П2 – увеличить доX 2 = 13 тонн. Доход от реализации продукции станет равным

f (X ) = 13 тыс.руб

Полученные пределы изменения правых частей уравнений исходной задачи это и есть пределы справедливости двойственных оценок.

ЗАДАНИЕ 4

1-5. Для изготовления четырех видов продукции (A, B, C, D) используют три вида сырья. Ресурсы сырья, норма его расхода на единицу продукции и цена продукции заданы в таблице.

Задание:

1.Определите план выпуска продукции из условия максимизации его стоимости.

2.Определите статус, ценность каждого ресурса и его приоритет при решении задачи увеличения запаса ресурсов.

3.Определите максимальный интервал изменения запасов каждого из ресурсов, в пределах которого структура оптимального решения, то есть номенклатура выпускаемой продукции, остается без изменения.

4.Определите суммарную стоимостную оценку ресурсов, используемых при производстве единицы каждого изделия. Производство какой продукции нерентабельно?

5.На сколько уменьшится стоимость выпускаемой продукции при принудительном выпуске единицы нерентабельной продукции?

6.На сколько можно снизить запас каждого из ресурсов, чтобы это не привело к уменьшению прибыли?

7.Определите изменение стоимости продукции и количество выпускаемых изделий при увеличении второго вида сырья на Z единиц.

8.Определите оптимальное решение задачи для случая, когда вектор ресурсов задан в виде в-строки.

9.Определите интервалы изменения цен на каждую продукцию, при которых сохраняется структура оптимального плана.

studfiles.net

Методы оптимизации. Учебник и практикум для бакалавриата и магистратуры. Федор Павлович Васильев. 2016. Бакалавр и магистр. Академический курс. (Учебная литература)

Пожаловаться на книгу

Автор: Федор Павлович Васильев

Жанр: Учебная литература

Серия: Бакалавр и магистр. Академический курс, книга #1

Год: 2016

В настоящем учебнике излагаются элементы теории оптимизации, а также основы наиболее часто используемых на практике методов приближенного решения задач оптимизации и краткая характеристика этих методов. Обсуждаются вычислительные аспекты, области применимости методов, их достоинства и недостатки.

Усилия авторов были направлены на поиск наиболее экономных схем изложения, упрощение доказательств, чтобы сделать материал более доступным, не снижая уровня строгости. Учебник содержит достаточное большое количество разобранных примеров и упражнений для самостоятельной работы студентов.

Метки: Настоящий учебник Краткая характеристика Вычислительные аспекты Большое количество Самостоятельная работа

Предлагаем Вам скачать фрагмент для ознакомления книги «Методы оптимизации. Учебник и практикум для бакалавриата и магистратуры» автора Федор Павлович Васильев в электронном виде в форматах FB2 а также TXT. Также есть возможность скачать произведение в других форматах, таких как RTF и EPUB (электронные книги). Советуем выбирать для загрузки формат FB2 или TXT, которые на сегодняшний день поддерживаются практически любым мобильным устроиством (в том числе телефонами / смартфонами / читалками электронных книг под управлением ОС Андроид и IOS (iPhone, iPad)) и настольными компьютерами. Книга издана в 2016 году в серии «Бакалавр и магистр. Академический курс».

Сохранить страничку в социалках/поделиться ссылкой: Скачать ознакомительный фрагмент в разных форматах (текст предоставлен ООО «ЛитРес»)FB2TXTRTFEPUBЧитать книгу «Методы оптимизации. Учебник и практикум для бакалавриата и магистратуры» онлайн Читать онлайнЗакрыть читалкуЛегально скачать полную версию произведения в элетронном виде (а так же заказать печатную книгу) «Методы оптимизации. Учебник и практикум для бакалавриата и магистратуры» можно в книжном интернет магазине Литрес Купить и скачать

Похожие книги

bookash.pro