Параметрическая оптимизация в САПР. Параметрическая оптимизация

Параметрическая оптимизация - Большая Энциклопедия Нефти и Газа, статья, страница 1

Параметрическая оптимизация

Cтраница 1

Параметрическая оптимизация предполагает дальнейшее улучшение рабочих показателей объекта. При этом могут приниматься во внимание один или несколько критериев оптимальности, а в качестве параметров оптимизации могут рассматриваться как внутренние параметры объекта, так и управляющие воздействия. Если параметрическая оптимизация выполняется с применением упрощенных математических моделей объекта проектирования, то в дальнейшем необходимо произвести детальный анализ процессов, определяющих уровень рабочих показателей объекта, в различных режимах. Для этих целей используется наиболее точная математическая модель ЭМУ. [1]

Параметрическая оптимизация - процесс, связанный с обеспечением оптимального ряда параметров и типоразмеров выпускаемой продукции. На этой стадии определяют оптимальный объем выпуска продукции. [2]

Параметрическая оптимизация осуществлена на основе адекватной динамической математической модели. [3]

Параметрическая оптимизация предполагает решение задачи условного экстремума. Для этого обычно выделяют в качестве критерия оптимальности ( функции цели) наиболее важный по условиям решаемой задачи показатель качества виброизоляции. [4]

Параметрическая оптимизация заключается в определении оптимальных поминальных значений и допусков внутренних параметров при заданных условиях работоспособности для выходных параметров. При оптимизации сначала решают задачу математического программирования extr / ( X), где / ( X) - целевая функция; ХР - - область работоспособности, в результате получают вектор номинальных значений внутренних параметров. Далее корректируется вектор номинальных значений параметров и определяются допуски или технические требования на управляемые параметры с помощью процедуры вписывания допусковой области ( гиперпараллелепипеда) XG в область работоспособности ХР. [5]

Параметрическая оптимизация РЭА - это процесс определения значений параметров входящих в схему элементов ( внутренних параметров X), при которых достигаются заданные или экстремальные значения ее выходных параметров Y или целевой функции. Также известны диапазоны изменения параметров элементов схемы. При помощи методов оптимизации решаются такие задачи проектирования, которые либо совсем невозможно решить методами расчета схем, либо возможно решить лишь приближенно. [6]

Параметрическая оптимизация АСР по интегральным критериям позволяет определять такие настройки регуляторов, при которых минимизируется та или иная оценка площади переходного процесса регулирования в целом. Однако указанные критерии, содержащие элементы, влияющие на характер переходного процесса регулирования, лишь косвенно определяют его отдельные показатели качества. [7]

Параметрическая оптимизация АСР направлена на достижение определенной цели, которую прежде всего надо четко сформулировать и формализовать в виде математического описания. Например, очень часто цель параметрической оптимизации АСР сводится к выбору таких параметров настройки регуляторов, которые обеспечивают в системе запас устойчивости не ниже заданного при всех возможных вариациях параметров математической модели объекта регулирования. Иногда этого оказывается достаточно, но чаще - нет. [9]

Параметрическую оптимизацию описанной АСР с ПИД регулятором целесообразно проводить на основании алгоритма АПО с идеальной эталонной моделью ( 44), с упрощенной диагональной матрицей экс - 1 0 трансляции ( 49) и фиксированным анализатором упрощенных функцией чувствительности ( 145), на котором д для нелинейной системы одновременно получаются все необходимые для алгоритма и экстраполятора упрощенные функции чув - О ствительности. [10]

Рассматривается параметрическая оптимизация датчика потен-циометрического газоанализатора фтористых соединений. При использовании га оанализаторов в системах автоматического регулирования необходимо оперативно получить объективную информацию, , о количественном составе технологических газовых потоков для проведения технологических процессов в оптимальных условиях. [11]

Методы параметрической оптимизации можно разделить на две группы: аналитические и численные. [12]

При параметрической оптимизации математические модели оценивают с точки зрения пригодности их использования для решения технологических задач в производственных условиях. [14]

При параметрической оптимизации обычно в число частных критериев входят выходные параметры и надежность, поскольку стоимость, габариты и вес в значительной мере предопределены выбором структуры устройства на этапе синтеза. [15]

Страницы: 1 2 3 4

www.ngpedia.ru

Параметрическая оптимизация в САПР

Поиск Лекций

Задача параметрического синтеза заключается в определении наилучших значений параметров для выбранной структуры объекта с учетом всех требований ТЗ па проектируемый объект.

Функционирование любой проектируемой технической системы подчиняется определенным физическим законам. Закон функционирования технической системы описывается аналитическими соотношениями между входными, внутренними и выходными переменными системы. Эти переменные связаны определенными соотношениями с переменными проектирования X, под которыми понимаются внутренние переменные, допускающие варьирование. В процессе параметрического синтеза варьирование переменных проектирования X ведет к изменению выходных параметров Y системы.

Для пояснения сущности задач параметрического синтеза используют геометрическую интерпретацию, связанную с введением m-мерного пространства пространства параметров проектирования (управляемых параметров) и k-мерного пространства Eh выходных параметров. Каждой точке пространства и соответствуют векторы X и Y значений переменных проектирования и выходных параметров соответствующего варианта проектируемого объекта.[6]

Для постановки и решения задачи параметрического синтеза необходимо формирование целевой функции F(X), отражающей качество функционирования проектируемой системы или объекта. Векторный характер критериев оптимальности (многокритериальность) в задачах проектирования обусловливает сложность проблемы постановки задач оптимизации.

Формально задачу параметрического синтеза можно представить как задачу нахождения вектора Х є , который минимизирует целевую функцию:

F(X) min

при ограничениях:

g(X)=0и h (X)≤0,

где g (X) и h(X) —векторные функции от X, описывающие систему ограничений на параметры проектирования X.

Если в задачах оптимального проектирования все переменные проектирования и состояний являются непрерывными, то для решения задач параметрического синтеза могут быть использованы методы решения задач нелинейного программирования, основанные на хорошо разработанных процедурах поиска экстремума функций. Однако не всегда все элементы в проектируемых объектах могут принимать любые значения в пределах некоторой допустимой области. Это связано, прежде всего, со стандартизацией и унификацией комплектующих изделий в различных областях техники. Так, в радиотехнике параметры резисторов и конденсаторов могут принимать только определенные значения из разрешенной шкалы номиналов. Кроме того, на параметры разрабатываемых объектов также накладывается ряд ограничений, учитывающих условия стандартизации и унификации. Так, в электротехнике и радиоэлектронике разрешается использовать только определенные значения питающих напряжений, в вычислительной технике существуют стандартные градации емкости устройств памяти.

Поэтому для решения задач оптимизации при проектировании объектов с дискретными значениями параметров методы оптимизации непрерывных объектов непосредственно неприменимы. Эти задачи относятся к задачам дискретного программирования. Если при оптимизации часть параметров дискретна, а часть имеет непрерывный характер, то задача должна решаться методами частично дискретного программирования.[6]

poisk-ru.ru

Параметрическая оптимизация - Большая Энциклопедия Нефти и Газа, статья, страница 2

Параметрическая оптимизация

Cтраница 2

Программа параметрической оптимизации позволяет оптимизировать параметры некоторых элементов ( конденсаторов, сопротивлений и др.) по выбранному критерию оптимизации. В качестве критерия оптимизации используется некоторая целевая функция, вид которой выбирается из меню. [16]

Задача параметрической оптимизации технического объекта заключается в поиске параметров, при которых целевая функция достигает экстремального значения. Параметры объекта, доставляющие экстремум целевой функции, называются оптимальными. [17]

При параметрической оптимизации АСР ряда объектов возникает задача определения параметров настройки регуляторов, при которых строго выполняются задания по отдельным показателям качества переходного процесса регулирования: значению динамической ошибки - первой амплитуде процесса регулирования, перерегулированию, времени достижения первого амплитудного значения, времени регулирования. Требуемые значения показателей качества переходного процесса регулирования могут задаваться для различных возможных возмущений, например ступенчатых возмущающих воздействий. Такие задачи встречаются при разработке радиоэлектронной аппаратуры, систем регулирования в химическом производстве, механических процессах. Невыполнение заданных требований к показателям качества переходного процесса регулирования этих объектов может угрожать не только правильному течению процесса, но и вообще возможности его осуществления. Для решения такого типа задач можно применить рассмотренный в § 2 алгоритм, сформировав соответствующий критерий оптимальности. [18]

Различают структурную и параметрическую оптимизацию технологических процессов. При структурной оптимизации в технологическом процессе выделяют свойства, характеризующие процесс как единое целое; свойства отдельных элементов, из которых процесс состоит; связи между отдельными элементами. Делению процесса на элементы, элемента на составляющие и далее соответствуют уровни расчленения технологического процесса: уровень маршрута, уровень операции, уровень перехода и уровень рабочих и вспомогательных ходов. [19]

Чем характеризуется параметрическая оптимизация. [20]

Постановка задачи параметрической оптимизации включает в себя определение набора независимых переменных, характеризующих ЭДН, выявление ограничений, характеризующих приемлемые или допустимые значения переменных, и описание целевой функции, определенным образом зависящей от переменных. [21]

Рассмотрим сущность параметрической оптимизации на примере оптимизации режимов резания для выполнения перехода продольного точения на токарном станке с ЧПУ. В состав математической модели, составленной для выполнения параметрической оптимизации перехода ( или операции) в общем случае входят: целевая функция, формализованно представляющая цель оптимизации; уравнения связи, отражающие главные физические законы, сопровождающие процесс обработки и учитываемые при вычислении отдельных элементов, входящих в выражение целевой функции; ограничения-неравенства, характеризующие предельные возможности реализации сочетаний режимов резания, ограничиваемые предельными возможностями технологической системы станок - приспособление-инструмент-деталь ( сокращенно - СПИД) по ее мощности, усилиям зажима заготовки и другим нерегулируемым параметрам; предельные возможности и дискретность регулирования каждого в отдельности управляемого параметра резания. [22]

Автоматизированные методы параметрической оптимизации основаны на численных методах поиска экстремума функции одной или нескольких переменных. При этом необходимо решить три задачи: разработать математическую ( оптимизационную) модель системы, выбрать критерий и метод оптимизации. [23]

Разработка методов автоматической параметрической оптимизации АСР на базе теории чувствительности дала возможность развить единый с теоретической точки зрения подход к решению задачи параметрической оптимизации АСР различных структур и классов. [24]

Большинство задач параметрической оптимизации технических объектов формулируется в терминах непрерывных параметров. Если экстремум целевой функции ищется в неограниченной области ХО, то его называют безусловным, а методы поиска - методами безусловной оптимизации. [25]

Под задачей параметрической оптимизации виброзащитных систем ( ВЗС) понимаем задачу синтеза оптимальных параметров при выбранной ( или заданной) структуре системы виброизоляции объекта от кинематических возмущений. [26]

Большинство задач параметрической оптимизации технических объектов связано с непрерывным изменением параметров. [27]

Решение задачи параметрической оптимизации АСР реальных промышленных объектов в АСУТП связано с проблемой получения точной информации об объекте регулирования. В этих условиях для реализации анализаторов чувствительности в алгоритмах АПО возникает необходимость текущей идентификации характеристик и параметров объектов, что представляет собой самостоятельную достаточно сложную задачу. [28]

При этом производится параметрическая оптимизация каждой из структур, полученные оптимальные варианты сравниваются между собой и из них выбирается удовлетворяющий наилучшим образом условиям поставленной задачи. [29]

Для решения задач параметрической оптимизации: технологического проектирования используется аппарат математического программирования. [30]

Страницы: 1 2 3 4

www.ngpedia.ru

5.2.12 Параметрическая оптимизация

Данный режим моделирования предназначен для того, чтобы добиться максимального приближения интересующей характеристики исследуемого устройства к заданной. Параметрическая оптимизация выполняется в программе МС9 методом Пауэлла (Powell) в любом из видов анализа: анализ переходных процессов, АС-анализ и расчет характеристик на постоянном токе DC.

Порядок работы в данном режиме и последовательность действий таковы:

Составляется схема моделируемого устройства, выбирается вид анализа и производится расчет интересующих характеристик.
Нажатием на иконку вызывается окно задания параметров режима параметрической оптимизации (рисунок 5.32). В окне вводится необходимая информация и запускается расчет нажатием кнопкиOptimize.
Нажатие на кнопку Apply переносит рассчитанные оптимальные значения параметров на схему. После этого вновь запускается анализ.

В окне оптимизации вводится следующая информация.

Кнопки 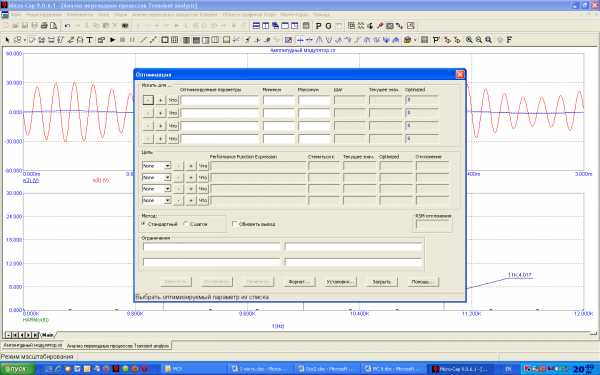предназначены для удаления/добавления строки оптимизируемого параметра.

Parameter — выбор оптимизируемых параметров.

Low — минимальное значение оптимизируемого параметра.

High — максимальное значение оптимизируемого параметра.

Step — шаг изменения оптимизируемого параметра (вводится при выборе метода Stepping Powell).

Current — текущее значение оптимизируемого параметра.

Optimized — оптимизированное значение параметра. Оно индицируется после выполнения процедуры оптимизации.

Get — вызов целевой функции оптимизации.

To — величина, к которой должно приблизиться значение целевой функции.

Current — текущее значение целевой функции.

Optimized — оптимальное значение целевой функции.

Error — ошибка в достижении критерия.

Method — выбор метода оптимизации:

Standard Powell — стандартный метод оптимизации Пауэлла.

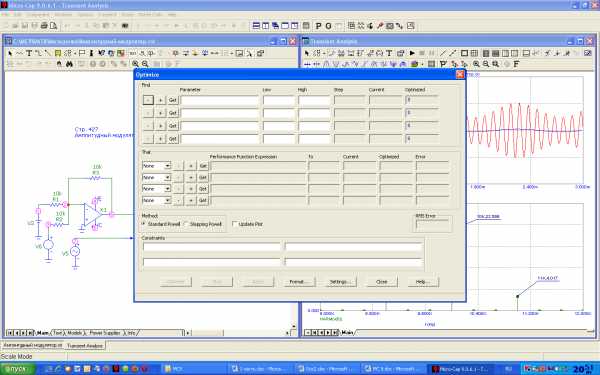
Рисунок 5.32 – Диалоговое окно составления задания на оптимизацию

Stepping Powell — согласно этому методу параметры изменяются от значения Low до значения High с шагом Step. На каждом шаге изменения параметров применяется стандартный метод Пауэлла.

RMS Error — корень квадратный из суммарной ошибки (разности между целевой функцией и ее фактической величиной).

Constraints — ограничения типа неравенств и равенств, записываемые на четырех строках, например, PD(R1)<=100m, V(Out)>=1.2, VCE(Q1)*IC(Q1)<=200m.

Optimize — начало оптимизации.

Stop — остановка оптимизации.

Apply — изменение на схеме значения параметров в соответствии с результатами оптимизации.

Format — выбор формы представления чисел.

Close — завершение режима оптимизации.

Примеры использования режима параметрической оптимизации будут рассмотрены ниже.

5.2.13 Функции раздела performance

Micro-Cap 9 имеет группу специальных функций PERFORMANCE, которые используются для точного измерения некоторых характеристик построенных графиков. Эти функции могут вызываться с помощью панели инструментов графического окна после построения графиков соответствующего анализа нажатием иконки (рисунок 5.33).

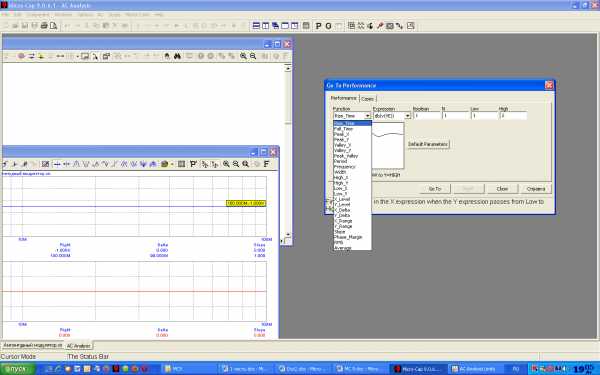
Рисунок 5.33 – Диалоговое окно PERFORMANCE

Ниже в таблице приведен список этих функций с их аргументами и результат их выполнения. При этом приняты следующие обозначения.

Function — выражение для переменной откладываемой по оси ординат, для которого необходимо выполнить функцию группы PERFORMANCE.

Expression — логическое выражение при выполнении которого будет вычисляться функция группы PERFORMANCE. Обычно вычисления производят после установления быстрых переходных процессов, что заставляет исключать начальный этап из рассмотрения. Поэтому данное выражение обычно имеет вид следующего типа «T>100 ns».

Borlean — логическое условие, при котором вычисляется функция из группы PERFORMANCE.

N — целое число, указывающее какое по порядку измерение делается. Например необходимо измерить длительность фронта нескольких идущих подряд импульсов. N=1 соответствует первому импульсу слева. Величина N в режиме Cursor Mode увеличивается на 1 при каждом нажатии на кнопки GO TO, Left, Right.

Low — нижнее граничное значение переменной, используемое соответствующими функциями.

High — верхнее граничное значение переменной, используемое соответствующими функциями.

Level — уровень значения переменной, используемый при вычислении различных параметров сигналов.

Rise_Time — длительность возрастания вдоль оси X переменной Y от указанного нижнего (Low) до указанного верхнего (High) уровней при выполнении заданного логического выражения Boolean.

Fall_Time — длительность убывания вдоль оси X переменной Y от указанного верхнего (High) до указанного нижнего (Low) уровней при выполнении заданного логического выражения Boolean.

В режиме Cursor Mode курсоры графиков помещаются последовательно в две выбранные точки и возвращается разность координат X для этих точек. Функции Rise_Time и Fall_Time можно использовать для измерения времени нарастания и спада импульсных сигналов.

Peak_X — Эта функция определяет координату X очередного локального максимума (PEAK) выбранной переменной Expression. Локальный максимум — это точка, значение функции Y в которой больше чем в соседних точках с обеих сторон. В режиме Cursor Mode при этом дополнительно помещается левый или правый курсор в очередную точку локального максимума.

Peak_Y — функция аналогична функции Peak_X, но определяет значение координаты Y точки локального максимума. Функция может использоваться для измерения значений выбросов при анализе переходных процессов и пульсаций коэффициента передачи фильтров при проведении AC анализа.

Valley_X — функция определяет координату X очередного локального минимума (VALLEY) выбранной переменной Expression. Локальный минимум — это точка, значение функции Y в которой меньше чем в соседних точках с обеих сторон. В режиме Cursor Mode при этом дополнительно помещается левый или правый курсор в очередную точку локального максимума.

Valley_Y — эта функция аналогична функции Valley_X, но определяет значение координаты Y точки локального минимума. Функция может использоваться для измерения значений отрицательных выбросов при анализе переходных процессов и пульсаций коэффициента передачи фильтров при проведении AC анализа.

Peak_Valley — определяет разность координат Y 2-х соседних точек локального максимума и минимума выбранной переменной Expression. В режиме Cursor Mode дополнительно помещаются левый и правый курсоры в очередные найденные 2 точки максимума и минимума. Может использоваться для измерения размаха разнообразных пульсаций, выбросов и амплитуд сигналов.

Period — определяет период колебаний переменной Expression путем измерения расстояния по оси X между последовательными одинаковыми значениями величины Expression. Первоначально находится среднее значения величины Expression на интервале моделирования, где соблюдается истинность логического выражения Boolean. Затем ищутся 2 очередных последовательных участка возрастания величины от среднего значения. Разница в расстоянии по оси X между этими точками и принимается за значение периода колебаний. Как правило, вводимое логическое выражение бывает типа "T>500ns" и используется для исключения ошибок определения периода на неколебательном участке процесса. Удобна для определения периода колебаний преобразователей напряжение-частота, где существует необходимость измерения периода колебаний с высокой точностью. Функция работает наиболее эффективно для колеблющейся переменной, проходящей при этом через свое среднее значение в течение периода. Она не будет работать с достаточной точностью с колебаниями, которые содержат гармоники значительной величины. В режиме Cursor Mode дополнительно помещаются левый и правый курсоры в 2 указанные точки графика (которые определяются как показано выше) и определяется расстояние между ними по оси X.

Frequency —работает в точности также как и функция PERIOD, но определяется значение f = 1/Period.

Width — эта функция измеряет расстояние по оси X между 2-мя точками графика Expression с заданными значениями ординаты level. В режиме Cursor Mode дополнительно помещаются курсоры графического окна (левый и правый) в очередные выбранные точки графика и определяется как результат расстояние по оси X между этими точками.

High_X — определяет координату X точки глобального максимума функции Expression. В режиме Cursor Mode дополнительно помещается выбранный левый (или правый) курсор в найденную точку и определяется ее координата по оси X.

High_Y — определяет координату Y точки глобального максимума функции Expression. В режиме Cursor Mode дополнительно помещается выбранный левый (или правый) курсор в найденную точку и определяется ее координата по оси Y.

Low_X — определяет координату X точки глобального минимума функции Expression. В режиме Cursor Mode дополнительно помещается выбранный левый (или правый) курсор в найденную точку и определяется ее координата по оси X.

Low_Y — определяет координату Y точки глобального минимума функции Expression. В режиме Cursor Mode дополнительно помещается выбранный левый (или правый) курсор в найденную точку и определяется ее координата по оси Y.

X_Level — определяет координату X очередной точки графика, в которой переменная Expression принимает значение Y_Level. В режиме Cursor Mode дополнительно помещается выбранный левый (или правый) курсор в найденную точку и определяется ее координата по оси X.

Y_Level — определяет значение переменной Expression в точке с абсциссой X_Level. В режиме Cursor Mode дополнительно помещается выбранный левый (или правый) курсор в найденную точку и определяется ее координата по оси Y.

X_Delta — определяет разность абсцисс 2-х очередных точек графика, в которых переменная Expression принимает значения Y_High и Y_Low. В режиме Cursor Mode дополнительно помещаются курсоры в найденные точки и определяется разность их абсцисс.

Y_Delta — определяет разность ординат 2-х точек графика, в которых абсцисса принимает значения X_High и X_Low.

X_Range — определяет разность абсцисс 2-х очередных точек график, в которых переменная Expression принимает заданные значения Y_low,Y_high. Сначала она находит очередные точки графика в которых Y_expr принимает заданные Y_Low и Y_High значения. Затем исследуются все точки внутри диапазона Y_Low…Y_High и ищутся с наибольшим и наименьшим значением абсциссы X (В эти точки и помещаются курсоры в режиме Cursor Mode). Разность между найденными абсциссами определяется как значение функции X_range.

Y_Range — определяет диапазон изменения переменной Expression 2-х точек графика в которых абсцисса принимает заданные значения X_low, X_high. Сначала она находит точки графика которые имеют абсциссы X_Low и X_High. Затем исследуются все точки внутри диапазона X_Low…X_High и ищутся с наибольшим и наименьшим значением переменной Expression. (В эти точки и помещаются курсоры в режиме Cursor Mode). Разность между найденными ординатами и определяется как значение функции Y_range. Функция может использоваться для измерения пульсаций АЧХ фильтра.

Slope — вычисляет производную функции Expression в окрестности точки с абсциссой X_value. Курсоры помещаются в точку с абсциссой X_value и ближайшую к ней точку (отстоящую на шаг расчета). Затем разность ординат указанных точек делится на разность абсцисс и полученная величина определяется как значение функции Slope.

Phase Margin — вычисляет запас по фазе графика частотной характеристики Expression. При этом заранее должны быть построены графики dB(Expression) и PHASE(Expression). Данная функция доступна только из AC анализа.

studfiles.net

Параметрическая оптимизация

Среди компонентов, образующих генетический алгоритм, в большинстве случаев только два непосредственно определяются конкретной задачей - это кодировка задачи (отображение пространства поиска на пространство битовых строк) и целевая функция. Рассмотрим задачу параметрической оптимизации, заключающуюся в определении набора переменных, миниимизирующих некоторую величину (цель) В более традиционных терминах, задача состоит в поиске минимума некоторой функции F(X1,X2,…,XM).

На первом этапе обычно делается предположение, что переменные, представляющие параметры, могут быть представлены битовыми строками. Это означает, что переменные предварительно дискретизируются некоторым образом и что область дискретных значений соответствует некоторой степени 2. Например, с 10 битами на параметр мы получаем область из 210 = 1024 дискретных значений. Если параметры непрерывны, то проблема дискретизации не заслуживает особого внимания. Разумеется, предполагается, что дискретизация обеспечивает достаточное разрешение, чтобы сделать возможным регулирование получение результата с желаемым уровнем точности. Предполагается также, что дискретизация в некотором смысле представляет основную функцию.

Битовую строку длины N можно рассматривать как целое двоичное число I, которому соответствует некоторое вещественное значение r из заданного диапазона . Это соответствие устанавливается формулой

За исключением проблемы кодирования, целевая функция обычно дается как часть постановки задачи.

Заключение.

Генетические алгоритмы – это вычислительные модели, которые представляют собой семейство алгоритмов поиска, основанных на механизмах природной селекции и генетики, и имеющих дело с набором (популяцией) возможных решений задачи (испытаний), которые подвергаются циклическому воздействию трех основных «генетических» операторов - селекции, скрещивания и мутации. Эти алгоритмы используют для решения задач поиска и оптимизации в самых разнообразных областях науки и техники.

В курсовом проекте предполагалось найти минимум функции 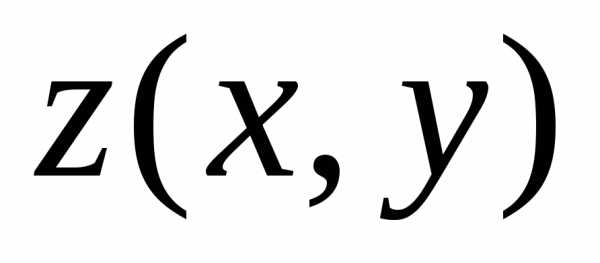в заданной области. Листинг программы реализующей поиск минимума функции приведен в приложении Б. Результат работы программы приведен в приложении А.

При выполнении данного проекта учитывалось, что решение задачи является подверженным влиянию случайных величин. Поэтому, каждый запуск программы был повторен, 25 раз. Затем, из набора полученных решений отбирались лучшие. Одновременно вычислено и среднее значение минимума за 25 запусков программы. Очевидно, что минимальное значение функции z(x,y) будет 0 при х и у = 0. Использовав генетический алгоритм для поиска минимума функции, можно предположить, что решение стремиться к 0. Подвергнув анализу полученные данные, можно сделать вывод, доказывающий, что особенностью генетических алгоритмов является то, что они обеспечивают сходимость к глобальному оптимуму, а не являются случайным поиском решения функции.

Рассмотрим результаты работы. При нахождении минимума функции для 40 поколений, при размере популяции 8 особей. Минимальное значение функции min= 8.1713653500E-03. Среднее значение функции = 1.5035203191E+00.

Для 40 поколений, при размере популяции 12 особей. Минимальное значение функции min= 1.7969612539E-03. Среднее значение функции = 7.4246878631E-01.

Для 40 поколений, при размере популяции 20 особей. Минимальное значение функции min=2.9085691762E-06. Среднее значение функции = 2.3087478996E-01.

Таким образом, меняя размер популяции, тем самым увеличив количество геномов для нахождения решения, пробуем найти минимум функции. Увеличение геномов в работе алгоритма, дает более приближенный результат при решении задачи, что и видно, как по минимальным значениям функции, так и по средним. Полученные значения стремятся к 0, и с увеличением популяции это выглядит все нагляднее.

Рассмотрим результаты работы программы при количестве поколений равных 80. Сравнение минимума функции для 80 поколений, при размере популяции 8 особей. Минимальное значение функции min=7.7649174012E-04. Среднее значение функции = 7.8250532831E-01.

Для 80 поколений, при размере популяции 12 особей. Минимальное значение функции min = 3.6266634518E-05. Среднее значение функции = 4.2281541230E-01.

Для 80 поколений, при размере популяции 20 особей. Минимальное значение функции min=3.3235614149E-08. Среднее значение функции = 2.3249352635E-02.

Проведем анализ полученных данных. Увеличение количества поколений в 2 раза, показало что при одних и тех же условиях, результат полученный при количестве поколений равный 80, лучше. Это можно объяснить тем, что алгоритм используя свои механизмы, находит лучшее решение с каждым последующим поколением, т.е. использует “накопленный опыт”.

Самые лучшие результаты я получил при числе поколений 80 и размере популяции геномов 20. Это отображено как в среднем так и в минимальном значении функции. Минимальное значение функции min=3.3235614149E-08, наглядно отражает универсальность и эффективность работы генетического алгоритма. Полученный результат максимально стремиться к истинному решению задачи т.е. к 0.

При выполнении курсовой работы была достигнута цель (нахождения минимума в заданной области), выполнены задачи по проектированию, построению логической структуры, разработке алгоритма и созданию программы поиска минимума функции.

studfiles.net

Параметрическая оптимизация в задачах проектирования РЭС

1. Основные понятия и определения

Оптимальное проектирование - это процесс принятия наилучших (оптимальных в некотором смысле) решений с помощью ЭВМ. Данная проблема возникает и требует решения на всех этапах проектирования и во многом определяет технико-экономическую эффективность и технологичность проектируемых изделий.

Большинство задач принятия решений можно сформулировать в терминах теории математического программирования, то есть в виде совокупности критериев качества и ограничений /1-8/.

В соответствии с общепринятыми обозначениями выделим управляемые (внутренние) параметры объекта проектирования X=(x1,…,xn) и выходные параметры Y=(y1,…,ym).

Как правило, при оптимизации целесообразно изменять не все внутренние параметры, а только те из них, которые оказывают наиболее существенное влияние на выходные параметры.

Выбор управляемых параметров осуществляют либо по результатам анализа чувствительности, либо в интерактивном режиме по желанию проектировщика / 2 /.

Для нахождения оптимальных решений должна быть известна математическая модель объекта проектирования, задающая зависимость выходных параметров Y от управляемых параметров X , адекватно описывающая работу объекта проектирования:

Y = F (X), (1.1)

где вектор F = (f1,f2.,…,fm) в качестве компонент может включать как функциональные, так и алгоритмические зависимости. В скалярном виде формула (1.1) примет вид:

Оптимизационная задача не может быть сформулирована при отсутствии математической модели объекта проектирования, при всём этом вид математической модели во многом определяет целесообразность и возможность применения того или иного метода.

На каждом этапе проектирования конструкции или технологии РЭС в начале работы приходится принимать решения в условиях неопределенности. Чаще всего это относится к построению или выбору варианта структуры объекта проектирования в рамках блочно-иерархического подхода /2, 3,7,8/, то есть к задачам структурной оптимизации.

Выбор варианта структуры во многом снимает неопределeнность, что позволяет строить математическую модель (1.1), (1.2) и проводить на ее основе параметрическую оптимизацию, то есть подбор наилучшего набора значений управляемых параметров (например, номиналов индуктивностей, емкостей, резисторов, параметров активных элементов, координат компонентов на плате и др.), при которых выполняются ограничения (технические требования технического задания) и достигают своих экстремальных значений (максимума или минимума) критерии качества объекта проектирования (наиболее важные с точки зрения проектировщика схемные и конструктивные выходные параметры объекта проектирования, по которым оценивается его качество), например, частотные характеристики, коэффициент передачи, потребляемая и выходная мощности, габариты, длина соединительных проводников, перегрев, температура и т. п.). Если параметрическая оптимизация проходит достаточно с небольшими временными затратами (несложные устройства, использование упрощенных математических моделей, отсутствие жестких требований на точность результатов и т. д.), может быть выполнен некоторый перебор различных структур построения проектируемого объекта, т.е. осуществлена структурная оптимизация устройства.

Решение задачи проектирования радиоэлектронного устройства с оптимальными характеристиками с использованием методов параметрической оптимизации /2,8/ включает три этапа: 1 - компьютерное моделирование устройства; 2 - составление целевой функции с выбором критериев оптимальности; 3 - поиск экстремума полученной целевой функции и определение оптимальных внутренних параметров устройства.

Моделирование (анализ) РЭС требует на соответствующих уровнях наличия математических моделей и проводится в основном численными методами /8/. Главным критерием моделирования наряду с необходимой точностью и адекватностью модели является быстродействие, скорость расчета на ЭВМ выходных параметров устройства.

Этап составления целевой функции при оптимизации устройства является самым творческим и неформальным /2,7,8/. Целевая функция строится на основе выходных параметров устройства (характеристик), которые необходимо оптимизировать.

Таким образом, оптимальное проектирование РЭС сводится к составлению или выбору целевой функции, многократному анализу характеристик (выходных параметров) устройств и затем минимизации или максимизации целевой функции с применением в различных методов оптимизации, выбор конкретного из которых обусловлен спецификой данной решаемой задачи.

2. Постановка задачи параметрической оптимизации на основе анализа требований ТЗ

Критерии качества и ограничения задачи параметрической оптимизации прямо либо опосредованно зависят от выходных параметров объекта проектирования Y = (y1,y2.,…,ym).

В простейшем случае в качестве критериев качества могут быть выбраны наиболее существенные с точки зрения проектировщика выходные параметры.

Все остальные выходные параметры при всём этом необходимо учесть в виде ограничений.

Критерии качества в литературе принято называть также целевыми функциями, критериями оптимальности, частными критериями качества, функциями цели и т.п. /2, 5-8/.

Обозначим критерии качества Ki = Ki(x1,x2.,…,xn), i = 1,…,s, где s - количество критериев качества, а Ki(X) - либо один из выходных параметров Y = (y1,y2.,…,ym), либо Ki(X) = ?(Y), где ?(Y) - заданная функциональная зависимость.

Все ограничения задачи параметрической оптимизации получаем на основе анализа технических требований к параметрам объекта проектирования, содержащихся в ТЗ. Рассмотрим формализацию ограничений на примере выходных параметров Y (для внутренних параметров Х справедливы аналогичные рассуждения).

Технические требования обычно имеют вид yj = TTj + ?j, где TTj - желаемое значение параметра yj,? а ?j - его допустимый разброс ( j = 1,…,m ). Таким образом, справедливы двойные неравенства TTj - ?j ?? yj ? TTj + ?j( j = 1,…,m ), то есть Yj -TTj - ?j??? TTj - ?j - yj????( j = 1,…,m ). Таким образом, получаем L=2?m неравенств вида gl(X)???, l= 1,…,L.

Общая математическая постановка задачи параметрической оптимизации, как задачи математического программирования /2, 5-8/ , имеет вид

Множество наборов значений управляемых параметров Х, удовлетворяющих ограничениям gl(X) ?? ?, l = 1,…,L, называют областью работоспособности, или областью допустимых значений управляемых параметров: XР = { X = x1, x2, …, xn)

gl(X)???, l=1,…,L }.

Если функция Ki(X) имеет один минимум или максимум в заданной области работоспособности, то ее называют одноэкстремальной (унимодальной), если несколько, то - многоэкстремальной. Каждый минимум (максимум) многоэкстремальной функции называют локальным, наименьший (наибольший) из них - глобальным.

Если ограничения на внутренние параметры gl(X) отсутствуют, то задача оптимизации называется безусловной, в противном случае - условной.

При практическом проектировании РЭС встают задачи поиска как безусловных, так и условных экстремумов унимодальных и многоэкстремальных функций.

Рассмотрим в качестве примера типичное ТЗ на разработку аналогового устройства - усилителя: ”Коэффициент усиления Кo на средних частотах должен быть не менее 10000, входное сопротивление R-вых не менее 1 МОм, выходное сопротивление R-вых не более 200 кОм, верхняя граничная частота fв не менее 100 кГц, температурный дрейф нуля Uдр не более 50 мкВ/град; усилитель должен нормально функционировать в диапазоне температур от -50 до +60 градусов Цельсия, напряжения источников питания +5 и -5 В, предельные отклонения напряжений не более +0,5%, усилитель эксплуатируется в стационарной установке, габариты платы 60х40 мм”. В данном случае выходными параметрами являются Y={ Кo,Rвх, Rвых, fв, Uдр }.

К внешним воздействиям относятся температура окружающей среды и напряжения источников питания. Управляемыми параметрами являются параметры элементов схемы.

Область работоспособности XР = {X?10000 - Кo ????,

1-Rвх ??, Rвых-200 ???, 100- fв????, 50- Uдр ???}. Особенность технического задания для дискретных объектов (например, цифровых устройств) заключается в форме записи ограничений (условий работоспособности), которые могут иметь вид логических уравнений, таблиц истинности или даже текстовую форму.

Целью решения задачи параметрической оптимизации (1.3) является определение такого набора значений параметров X*=(x1*, x2*.,…,xn*), X*?ХР, при котором критерии качества Ki(X*), i=1,…,s достигают своих наилучших (минимальных или максимальных ) значений.

3. Классификация задач параметрической оптимизации

Задача параметрической оптимизации (1.3) является многопараметрической, многокритериальной и содержит ограничения, все эти факторы определяют особенности, возникающие в процессе ее решения. В зависимости от вида критериев качества и ограничений проводят классификацию задач параметрической оптимизации (задач математического программирования) /2,5-8/.

Если целевая функция и ограничения линейные функции вида

С0 + С1?Х1+ С2?Х2+…+ Сn?Хn., (1.4)

то задача оптимизации вида (1.3) называется задачей линейного программирования, в противном случае - задачей нелинейного программирования.

Если целевая функция квадратичная, а ограничения - линейные функции, то задача (1.3) называется задачей квадратичного программирования.

Если целевая функция и ограничения имеют вид Х1?Х2?…?Хn., то задача (1.3) - это задача геометрического программирования.

Если целевую функцию можно представить в виде суперпозиции функций, то задача (1.3) - это задача динамического программирования.

Если целевая функция и ограничения целочисленные функции, то задача (1.3) - это задача целочисленного программирования.

В большинстве случаев при проектировании РЭС целевая функция нелинейно зависит от внутренних параметров, поэтому соответствующие задачи параметрической оптимизации относятся к задачам нелинейного программирования, для решения которых используются методы математического нелинейного программирования /2, 5-8/. Кроме того, в некоторых частных случаях (например, при топологическом проектировании РЭС) в силу высокой трудоемкости задач применение методов математического программирования затруднено, тогда используются различные приближенные способы получения решений, приближающихся к оптимальным, например, эвристические алгоритмы и т. д. /8-12/.

?????Кроме того, в зависимости от вида используемых математических моделей, задача оптимизации может быть детерминированной или стохастической, непрерывной или дискретной, аналитической или алгоритмической, при всём этом для каждого класса задач имеется свой, в достаточной степени апробированный, математический аппарат /2,5-10/. Так, для задач линейного программирования успешно применяется симплекс-метод /7, 8/.

Характерной особенностью задач оптимизации в САПР является тот факт, что классические методы нахождения экстремума, требующие аналитического выражения для целевой функции, практически неприменимы, так как в большинстве случаев используются алгоритмические модели, в которых вычисление значений целевых функций (критериев оптимальности) и их производных производится численными методами. Поэтому наиболее универсальными и эффективными для задач нелинейного программирования являются методы поисковой оптимизации /2,7,8/.

Для обеспечения возможности применения методов поиска к решению задачи оптимизации в постановке (1.3) необходимо некоторым образом упростить математическую постановку задачи: перейти от многокритериальной задачи оптимизации к однокритериальной и от задачи с ограничениями - к задаче безусловной оптимизации.

4. Многокритериальная оптимизация в задачах с ограничениями

4.1. Методы перехода от многокритериальной задачи оптимизации к однокритериальной

Для того, чтобы оценить насколько хорошо удовлетворяют требованиям ТЗ значения частных критериев качества при заданном наборе значений внутренних параметров X = (x1, x2.,…,xn), нужно построить обобщенный критерий качества (обобщенную целевую функцию) f(Х), которая одновременно учитывает требования ко всем частным критериям.

Иными словами, от многокритериальной задачи параметрической оптимизации в виде:

необходимо перейти к однокритериальной задаче:

Наиболее часто на практике используются следующие методы построения целевой функции (методы векторной свертки частных критериев): метод главного критерия, аддитивный, мультипликативный, минимаксный и вероятностный /7-9/.

В методе выделения главного критерия проектировщик выбирает один, наиболее важный с его точки зрения частный критерий качества, который и принимается за обобщенную целевую функцию, а требования к остальным частным критериям учитывают в виде ограничений f(X)=Kt(X), (1.7)

где t - номер наиболее важного частного критерия. Например, задана принципиальная электрическая схема логического элемента и условия работоспособности на следующие выходные параметры: y1 - коэффициент нагружения, y2 - запас помехоустойчивости, y3 - средняя рассеиваемая мощность, y4- задержка распространения сигнала. Необходимо рассчитать параметры пассивных элементов, то есть управляемые параметры - это сопротивления резисторов. В качестве целевой функции может быть выбран один из выходных параметров, например, y4 ( f(X)= y4 ).

В аддитивном методе каждому из частных критериев качества ставится в соответствие весовой коэффициент (вес i-го частного критерия 0?????1??i=1,…,s,), характеризующий важность данного критерия с точки зрения проектировщика (сумма весовых коэффициентов должна быть равна 1).

При построении целевой функции в аддитивном методе используется соотношение: если f (X)???max, то -f (X)???min. Каждый частный критерий можно включить в аддитивную целевую функцию по правилу: умножить на весовой коэффициент и включить в целевую функцию со знаком плюс или минус.

Чтобы построить минимизируемую целевую функцию f ?(X)??min, все минимизируемые частные критерии K?i (X) (K?i (X)??? min, i = 1,…,t) включают в аддитивную функцию со знаком плюс, то есть прибавляют к целевой функции, а все максимизируемые критерии K+i(X) ( K+i(X)??? min, i = t+1,…,s) включают в аддитивную функцию со знаком минус, то есть вычитают из целевой функции:

или для максимизируемой целевой функции:

t _ s +

f (X)=?-? ???? Ki(X)+?? ???? Ki(X) )??? max, (1.9)

i=1 i=t+1

где s - общее число частных критериев, а t - количество минимизируемых критериев.

В нашем примере четыре частных критерия, то есть s = 4, t = 2:

K1(X)???max,

K2(X)??? max,

K3(X)??? min,

K4(X) ?? min.

Пусть ?? ? ?? ? ?? ???? ? 0?????тогда

?? f(X) = ?????K1(X) ???????K2(X)????????K3(X) ???????K4(X) ?? max,

или

f(X) = ???????K1(X) ???????K2(X) ???????K3(X) ???????K4(X) ?? min.

В мультипликативном методе используется правило: если f (X)???max, то 1/ f (X)???min при условии, что f (X)??????

В отличие от аддитивного метода, частные критерии не складывают, а перемножают. Кроме того, в мультипликативном методе не используют весовые коэффициенты. Целевая функция строится в виде дроби.

Если f(X)??min, то в числитель дроби включают произведение всех минимизируемых критериев, а в знаменатель - произведение всех максимизируемых критериев:

или если целевую функцию нужно максимизировать:

В нашем примере с применением мультипликативного метода свертки критериев целевые функции:

Минимаксный метод построения обобщенной целевой функции получил свое название потому, что в нем минимизируется максимальное отклонение частного критерия качества от его наилучшего, желаемого значения (технического требования, оговоренного в ТЗ).

где X = (x1, x2.,…,xn), то есть

Логика минимаксного построения целевой функции заключается в том, что в каждый момент времени в качестве главного выбирается тот из частных критериев качества Ki(X), который в наибольшей степени удален от своего желаемого (оптимального) значения Ki*. В нашем примере (s = 4) при желаемых значениях K1* = 0,2; K2* = 1000; K3* = 25; K4* = 1 по минимаксному методу получим:

Другими словами, минимизируется “самый плохой” из частных критериев.

Рассмотрим три ситуации, изображенные на рис. 1.1. На оси у откладывается величина ?Ki(X)?Ki*?/Ki* ?для всех частных критериев (i = 1,2,3,4 для нашего примера). В случае а) хуже всего удовлетворяет требованиям ТЗ критерий K3(Х), поэтому f(X)=?K3(X)? K3*?/ K3*, то есть в течение некоторого времени усилия оптимизации будут направлены на приближение критерия K3(X)?к его желаемому значению K3*??При этом могут ухудшиться значения других критериев. Например, в случае б) для дальнейшей оптимизации будет выбран критерий K1(X).

Рис. 1.1

Процесс продолжают до тех пор, пока все частные критерии не будут достаточно (с требуемой точностью) близки к своим желаемым значениям ( случай в), изображенный на рис. 1.1). При этом приведение критериев к нормированному виду ?Ki(X)?Ki*?/ Ki*?необходимо, чтобы в равной степени учитывать изменение критериев независимо от их абсолютных величин (как слишком больших, так и слишком малых, возможно различающихся на несколько порядков).

В случае вероятностного (статистического) метода построения обобщенной целевой функции выбирают

f(X) = P(X) ??max, (1.16),

где P(X) - вероятность выполнения условий работоспособности, то есть вероятность того, что при наборе значений внутренних параметров X = (x1, x2.,…,xn ) выходные параметры объекта проектирования будут удовлетворять требованиям ТЗ. Для определения вероятности Р(Х) на практике обычно используют метод статистических испытаний (метод Монте-Карло) / 5 /.

4.2. Методы перехода от задачи с ограничениями к задаче безусловной оптимизации

Для перехода от задачи параметрической оптимизации с ограничениями (1.6) к задаче без ограничений, или задаче безусловной оптимизации

Ф(Х) ??? extr , (1. 17)

используется один из следующих методов: метод неопределенных множителей Лагранжа; метод штрафных функций; метод барьерных функций /5-8/.

В методе неопределенных множителей Лагранжа вводятся дополнительные переменные y1,y2.,…,yL, которые называют неопределенными множителями Лагранжа. Их количество равно числу ограничений L в задаче оптимизации (1.6).

Формула (1.18) применима, если задача (1.6) ставится как задача максимизации, при всём этом для полученной целевой функции Ф(X,Y) необходимо найти седловую точку, то есть по переменным X = x1, x2.,…,xn) проводится поиск максимума, а по переменным Y = ( y1,y2.,…,ym) - поиск минимума, то есть

Основной проблемой при использовании метода Лагранжа является значительное увеличение размерности задачи параметрической оптимизации.

В методе штрафных функций целевую функцию задачи безусловной оптимизации получают по формуле:

Ф(Х)=f(X)+?? k(X) ??? extr, (1. 20)

где X = (x1, x2.,…,xn) - набор управляемых параметров, ? k(X) -

штрафная функция, k-номер итерации (шага) в методе поисковой оптимизации.

На практике задачи параметрической оптимизации решаются в основном итерационными (пошаговыми) методами, которые называют методами поисковой оптимизации. При этом на каждом шаге поиска значение штрафной функции ?? k(X) уточняется (рассчитывается заново) по формуле:

где r k=10 k. Формула (1.21) применима, если задача (1.6) ставилась как задача минимизации.

Логика построения штрафной функции заключается в следующем: внутри области работоспособности ХР g l (X) ???,

L = 1,…,L, на границе - g l (X) ???, а вне ХР g l (X) > ?? (рис. 1.2).

Целевая функция задачи безусловной оптимизации Ф(Х) должна быть максимально близкой к целевой функции f(Х) задачи с ограничениями внутри области работоспособности

XР = {X = (x1,x2.,…,xn)?gl(X)???, l = 1,…,L } и быть значительно хуже (больше) функции f(Х) вне области работоспособности, то есть при gl(X) > ?.

Действительно, внутри области работоспособности ХР gl(X)?????, l = 1,…,L, поэтому max{0, gl(X)} = 0 для всех ограничений, то есть внутри области работоспособности Ф(Х) = f(Х). Если ограничения выполнены, то никакого штрафа на целевую функцию не накладывается. В противном случае, если имеются нарушения одного или нескольких ограничений g t (X) > ?? 1??t ??L, то каждое из них дает свой вклад в штрафную функцию ?k(X) в виде квадрата слагаемого [ max{0,gt(Х)}], где max{0,gt(Х)}=gt(Х). Метод штрафных функций часто называют методом внешней точки, потому что при проведении дальнейшей оптимизации поисковыми методами для метода штрафных функций не важно, принадлежит ли начальная точка поиска области работоспособности ХР.

В методе барьерных функций на границе области работоспособности ХР ставится непреодолимый барьер (целевая функция задачи безусловной оптимизации Ф(Х) возрастает до бесконечности на границе области ХР). Поэтому начальная точка поиска обязательно должна принадлежать области работоспособности, если при построении целевой функции задачи безусловной оптимизации был применен метод штрафных функций, или метод внутренней точки. Целевую функцию Ф(Х) в методе барьерных функций получают по формуле

Ф(Х)=f(X)+?? k(X) ??? extr, (1.22)

где k- номер итерации поискового метода, весовой коэффициент rk=10 -k , а барьерная функция ?? k(X) вычисляется по формуле

Действительно, при приближении к границе ХР gl(Х) 0, так как Х?ХР (метод внутренней точки) gl (X) ???, l = 1,…,L, поэтому gl(Х) > - . Именно поэтому в формуле (1.23) используется знак минус: ?k(X) возрастает до бесконечности при приближении к границе области работоспособности.

Главный недостаток метода барьерных функций заключается в том, что начальную точку поиска приходится выбирать внутри области работоспособности ХР, что представляет собой сложную задачу при малых размерах области ХР.

Таким образом, при небольшом количестве управляемых параметров Х и ограничений gl(X), целесообразно применять метод неопределенных множителей Лагранжа, если проверка принадлежности начальной точки поиска области ХР не слишком трудоемкая задача, то применяем метод барьерных функций, в противном случае - метод штрафных функций, который, хотя и является более универсальным, но впоследствии, в ходе поисковой оптимизации требует большего числа итераций по сравнению с методом барьерных функций.

referatwork.ru

Оптимизация параметрическая - Справочник химика 21

На этапе макрокинетических исследований решают следующие задачи 1) выбор типа опытного реактора, осуществляемый в соответствии с данными об организации процесса 2) определение модели гидродинамики процесса на основе данных о структуре потоков 3) анализ диффузионных эффектов, процессов массо- и теплопереноса в аппарате и оценка соответствующих тепловых и диффузионных параметров 4) синтез статической математической модели и процесса, установление ее адекватности 5) статическая оптимизация 6) синтез динамической модели процесса и установление ее адекватности анализ параметрической чувствительности 7) анализ устойчивости теплового режима процесса 8) динамическая оптимизация. [c.29]

В третьей главе рассмотрен автоматизированный структурно-параметрический синтез гибких химико-технологических систем. Изложены задачи синтеза систем в условиях полной и неполной определенности информации. Отдельный параграф посвящен математическим методам и вычислительным алгоритмам структурно-параметрического синтеза систем дискретного типа. Изложены методы автоматической классификации технологических процессов, оптимизации технологической структуры и аппаратурного оформления химико-технологических систем периодического действия — алгоритмы эвристического типа, ветвей и границ , случайного поиска, геометрического программирования, комбинированные. [c.6]

Оптимизация параметрических рядов конденсатоотводчиков позволяет рационально сократить существующее многообразие типоразмеров до технически и экономически обоснованного минимума с расширением применения каждого из оставшихся в ряду изделий. [c.13]

Данная работа ставит своей целью проанализировать всю совокупность проблем, связанных с контактно-каталитическими производствами, н наметить пути решения этой проблемы на основе глубокого исследования внутренней сущности процессов-на базе системного анализа с использованием новых, современных методов моделирования, оптимизации, новых методов параметрической идентификации моделей, нового экспериментального оборудования, позволяющего оценивать параметры моделей с высокой точностью. На основе этих исследований выдаются рекомендации по оптимальному проведению и аппаратурному оформлению контактно-каталитического процесса. [c.19]

В большинстве научно-технических разработок химико-технологических процессов задача параметрической идентификации является хотя важной, но не основной целью научного исследования создаваемые математические модели предназначены для использования в целях проектирования, оптимизации и управле- [c.186]

Одним из перспективных направлений в развитии сернокислотной промышленности является повышение давления на всех стадиях получения продукции. В настоящее время очевидны преимущества этого способа по сравнению с широко распространенной технологией получения серной кислоты по методу двойного контактирования и двойной абсорбции под атмосферным давлением. В работе [29] выполнен автоматизированный синтез оптимального агрегата производства серной кислоты под давлением 1,2 МПа и показана его высокая экономическая эффективность по сравнению с зарубежными аналогами. Синтез оптимального агрегата был выполнен в традиционной постановке структурно-параметрической оптимизации [30]. [c.272]

Структурный и параметрический синтез машины следует рассматривать в совокупности с технологическим процессом, так как многие параметры машины определяют из анализа технологического процесса по условиям получения заданных показателей качества оборудования в свою очередь, параметры машины влияют на ход технологического процесса. По этой причине структурный и параметрический синтез машины подлежат оптимизации на всех уровнях сначала всей системы совокупно с технологическим процессом, затем — отдельных функциональных систем машины и, наконец, наиболее важных ее элементов (деталей). [c.37]

Кроме экономических критериев оптимизации большую роль играют технологические критерии — показатели степени очистки и разделения. В этом случае технологические критерии, называемые параметрическими, выбираются так, чтобы целевая функция полностью отражала экономическую эффективность процесса, т. е. должна быть однозначная связь с себестоимостью адсорбционного разделения и производительностью установки. [c.14]

Тогда сформулированная задача оптимизации является типичной задачей нелинейного программирования и решается по известной схеме. Таким образом, задача оптимизации на экономический критерий эффективности может быть переформулирована в параметрическую задачу оптимизации по определению Нот И Do T адсорбера. [c.14]

Необходимость учета параметрической чувствительности при решении задач оптимизации обусловлена различными причинами. [c.331]

Во-вторых, при оптимизации ХТС приходится использовать математические модели элементов ХТС, в которые входят параметры, найденные с определенной степенью точности. Кроме того, параметры моделей с течением времени могут изменяться под влиянием изменений характеристик объектов, которые они отражают. Например, с течением времени падает активность катализатора вследствие его старения с увеличением длительности эксплуатации теплообменника возрастает термическое сопротивление тепловому потоку. Если оптимальный технологический режим лежит в области высокой параметрической чувствительности, то вследствие неточности коэффициентов модели истинный оптимальный режим может не совпадать с расчетным. [c.331]

Таким образом, применение методов теории чувствительности весьма эффективно при разработке новых и оптимизации существующих ХТС. Наиболее перспективным представляется применение этих методов для исследования чувствительности нестационарных процессов, связей между структурой системы и ее параметрической чувствительностью, для решения задач синтеза оптимальных структур ХТС и оптимизации технологических режимов. [c.342]

Как было показано выше, имеется несколько способов учета параметрической чувствительности в критериях оптимизации. Необходимы дальнейшие исследования в этом направлении и расширение области приложений полученных результатов. [c.343]

Действительно, пусть Р (и, р) — критерий оптимизации. Пусть также и — точка минимума функции Г (и, р), где р — некоторые средние значения параметров р. Если точка и лежит в области высокой параметрической чувствительности, неизбежные неточности в параметрах р могут суш ественно снизить эффект оптимального режима. Если же вести его поиск с учетом параметрической чувствительности, получим точку и , в которой критерий Р (и, р) будет принимать худшее значение. Однако этот режим окажется менее подверженным влиянию изменения параметров р и в результате может стать более выгодным, чем первый режим. [c.203]

Комплексность оптимизации осуществлялась структурной и параметрической оптимизацией факторов Ф,, проведение вычислительного и натурного эксперимента в последовательности этапов достижения точности. [c.27]

Оптимизация на уровне маршрута и операции назьшается структурной, так как связана в основном с выбором структуры процесса или операции. Оптимизация, связанная с выбором параметров процесса при заданной структуре, носит название параметрической. Параметрическая оптимизация характерна для уровня переходов. При зтом главным в проблеме оптимизации технологических процессов является структурная оптимизация, оказывающая наибольшее влияние на критерий оптимизации, а параметрическая оптимизация носит подчиненный характер. [c.159]

Оперативная структурная оптимизация технологической системы перерабатывающего производства АПК на разных уровнях параметрического описания материальных потоков и продуктов переработки. [c.53]

В которой методом морфологического анализа выделяется множество допустимых объектов исследования по аксиоматическим моделям выбираются адекватное аппаратурное оформление и тип аппаратурной структуры химико-технологических систем формируются их структурно-функциональные модели и алгоритмы оптимизации и по этим алгоритмам производится их структурная и параметрическая оптимизация. Такой подход дает возможность в диалоге пользователя с ЭВМ значительно сократить первоначальное пространство поиска оптимального решения. [c.142]

Отмеченные структурные и процессные особенности многопродуктовых химико-технологических систем налагают определенные условия на формулировку задач их структурной и параметрической оптимизации. В частности, структура системы претерпевает многократные изменения в процессе ее работы. Поэтому требуются специа)п.ные алгоритмы, позволяющие определять оптимальную последовательность вариантов аппаратурной структуры, для которой затем определяются размеры, производительность и количество единиц технологического оборудования [12,13]. [c.143]

Рассмотрим особенности постановки и решения задачи стохастической оптимизации производственной программы НПП при параметрических связях элементов [52]. [c.68]

Примером связи между элементами различных вектор-столбцов в задаче оптимизации производственной программы НПП может служить параметрическая взаимосвязь варьируемых технологических коэффициентов и качественных характеристик материальных потоков, взаимосвязь коэффициентов отбора и качественных характеристик базовых компонентов, вырабатываемых в процессе разделения и вовлекаемых на смещение в товарном блоке. Следовательно, в рассматриваемом случае в стохастической задаче планирования необходимо учитывать дополнительные условия и ограничения, обеспечивающие согласованность режимов взаимосвязанных технологических звеньев не только по количественным, но и по качественным показателям, учет которых обеспечивает повышение адекватности модели планирования реальным условиям функционирования объекта. [c.70]

Разработка оптимальной организации вычислительных процедур при решении задач оптимизации основана на использовании топологических моделей ХТС в виде информационно-потоковых мультиграфов, параметрических информационных и сигнальных графов, т. е. на применении оптимальных алгоритмов стратегии исследования ХТС (см. гл. V). [c.302]

Используя декомпозиционный подход, стохастическую задачу оптимизации производственной программы НПП с учетом параметрических связей варьируемых элементов можно сформулировать в виде взаимосвязанно решаемых главной задачи [c.71]

Далее из общего числа элементов исходной БТС в результате качественного исследования надежности технологической топологии системы с помощью параметрического потокового графа (п. п. г.) выделяются элементы, лимитирующие надежность системы. Резервировать следует только эти элементы. На основе общего алгоритма решения задачи оптимизации характеристик на- [c.173]

Для решения задачи I уровня оптимизации—для определения оптимального варианта поэлементного резервирования — используется метод неопределенных множителей Лагранжа, отличающийся от других возможных методов (наискорейшего спуска, динамического программирования и других) сравнительной простотой реализации на ЭВМ. Для решения задачи II уровня оптимизации— выбора оптимальной величины надежности БТС — применяется метод сканирования по ряду предварительно задаваемых значений надежности системы. Математической моделью, устанавливающей влияние изменений в технологической топологии БТС за счет ввода резервных элементов на величину ее надежности, является параметрический граф надежности (п. г. н.) [c.174]

При выбранном диаметре трубок радиальный перенос в дальнейших расчетах (при оптимизации, определении параметрической чувствительности и т. д.) можно не учитывать. [c.64]

Параметрическая оптимизация осуществлена на основе адекватной динамической математической модели. При составлении динамической математической модели датчика исходили из следующих условий [c.77]

Ряд методов оптимизации, как, например, динамическое программирование, дает достаточную информацию о чувствительности оптимума уже в процессе их использования для решения оптимальных задач. Другие методы менее приспособлены к анализу чувствител ,-ностн оптимума. Лишь для задач линейного программирования имеется до некоторой степени разработанный математический аппарат (параметрическое линейное программирование), позволяюи1Ий изучать поведение оптимального решения при измеиенпи коэффициентов математического описания . [c.39]

Степень сложности моделей формирования структурь гибкой системы зависит от принятого уровня ее гибкости, В общем слу- ае трудно сформировать модель в аналитическом виде, поэтому структуру системы формируют по эвристическим алгоритмам, Подробно алгоритмы формирования допустимых структур гибких технологических систем и их оптимизации рассмотрены в следующей главе прп решении задачи структурно-параметрического синтеза, [c.152]

Оптимальные алгоритмы анализа ХТС на основе применения параметрических потоковых графов, структурных блок-схем и информационно-потоковых мультиграфов. Решение задач синтеза и оптимизации ХТС при автоматизированном проектировании связано с неоднократным решением задачи анализа или полного расчета ХТС. Разработку оптимальных алгоритмов анализа ХТС осуществляют, используя топологические модели ХТС в виде ППГ или ИПМГ. [c.92]

В общей структуре химического производства ГАПС является лишь отдельной подсистемой, и поэтому ее эффективность и гибкость должны обеспечиваться в рамках всей системы. Иначе частный выигрыш может обернуться существенными потерями для большой системы. В простейшем случае гибкую автоматизированную химико-технологическую систему можно представить состоящей из двух частей процессно-аппаратурной и информа-ционно-управляющей (АСУТП), функционирующих совместно. При этом технологическая гибкость ХТС обеспечивается аппаратурным подобием разных технологических стадий в совокупности с периодическим способом организации технологических процессов при наличии гибких коммуникаций между аппаратами и аппаратурными стадиями. Гибкость управления заключается в том, что при переходе к производству иной продукции изменяется информационное обеспечение при минимальных изменениях программно-алгоритмического обеспечения. Свойство гибкости придается системе уже на стадии ее структурно-параметрического синтеза, включающего следующие этапы предварительное определение минимального аппаратурного состава проектируемой ХТС, классификацию продуктов по признаку использования одинакового оборудования, определение допустимых и оптимальной технологических структур, оптимизацию аппаратурного оформления. [c.530]

В табл. VHI.4 сопоставлены результаты оптимизации по критериям ZhZ режим I соответствует минимальному значению крите-терия Z, а режим И —минимальному значению критерия Z. Как видно из табл. VHI.4, использование критерия (VIII.17) позволило уменьшить параметрические чувствительности dZIdT и dZIdT Б точке оптимума на 55,6% и 56,5%. При этом значение Z возросло лишь на 7%. [c.333]

Различают структурную и параметрическую оптимизацию технологических процессов. При структурной оптимизации в технологическом процессе выделяют свойства, характеризующие процесс как единое целое свойства отдельных элементов, из которых процесс состоит связи между отдельными элементами. Делению прсщесса на элементы, элемента на составляющие и далее соответствуют уровни расчленения технологического процесса уровень маршрута, уровень операции, уровень перехода и уровень рабочих и вспомогательных ходов. [c.158]

В результате этих искусственно созданных условий линеаризации ИЗС, объем расчетов операций теплообмена при синтезе ТС становится весьма значительным. Этот метод синтеза ТС решает задачу параметрической оптимизации без з чета массовых расходов теплоносителей и физической реализуемости операции теплообмена. Кроме того, при решении задачи синтеза ТС использувтся полный перебор альтернативных вариантов связей каадого ТА внутри ТС, ко-гатчество которых резко возрастает при увеотчении размерности ИЗС. [c.16]

Задача структурной оптимизации связана с рациональным изменением структуры распределения запасов, ассортимента и рецептур выпускаемой продукции в зависимости от характеристик биосырья и решается па ассортиментно-рецептурном и элементарно-параметрическом уровнях по критерию минимального отклонения от соот-ветствующих заданных структур (ассортимента, рецептур, элементов химсостава). [c.56]

Применение методов модетароваттоя и оптимизации МХ приборов и систем контроля позволяет на теоретических моделях оптимизировать выбор метода анализа, а затем осуществлять структурную и параметрическую оптимизацию АП, выбирать оптимальные режимы его функционирования, прогнозировать поведение приборов и систем в различных условиях. [c.196]

При отсутствии оператора разделение , т. е. при К=0, Гх=1, получаем тривиальное выражение G = viXi. Использование типовых технологических операторов при анализе и расчете материальных или энергетических балансов для подсистем БТС в условиях стационарного режима их работы позволяет формализовать и автоматизировать с помощью ЭВМ процесс проектирования БТС. Применяемые при этом математические модели подсистем основываются на модулях типовых операторов, составляющих данную систему. В то же время многомерность, высокая степень взаимосвязи и параметрического взаимовлияния элементов в сложных БТС затрудняют применение операторного метода. В этих условиях становится эффективным использование методов расчета БТС, предусматривающих применение потоковых, структурных, информационных и сигнальных графов [13]. Прн этом графы, отражая технологическую топологию и функциональные связи в системе, позволяют разрабатывать алгоритм расчета на ЭВМ многомерных систем и решать задачи анализа и оптимизации сложных БТС, которые связаны в основном с рассмотрением [c.24]

Оптимальное проектирование потенциометрических газоанализаторов целесообразно вести, используя статистические показатели ачества измерения [х]. В качестве ]фвтерия параметрической оптимизации ионоиетрического анализатора меркаптанов выбрана среднеквадратЕческая погрешность (СКП) измерения. [c.72]

chem21.info