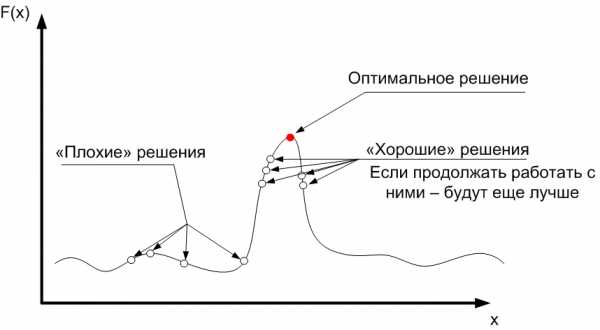
Рыков С.В и др. - Методы оптимизации в примерах в пакете MathCAD 15. Часть 3. Многомерная оптимизация. Оптимизация в mathcad

Pers.narod.ru. Обучение. Лекции по MathCAD. Решение оптимизационных задач в пакете MathCAD

Этот сайт больше не обновляется. Подключите Javascript, чтобы увидеть новый адрес страницы или перейдите к статье

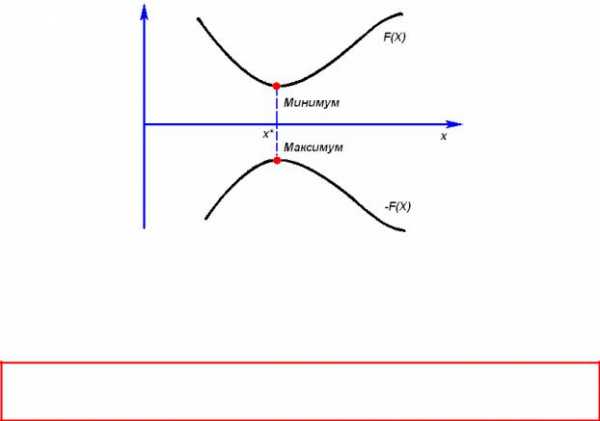
Оптимизационные задачи можно разделить на два класса:

задачи безусловной оптимизации (или оптимизация без ограничений).

задачи условной оптимизации (оптимизация с ограничениями).

Вторая задача отличается от первой тем, что решение ищется только среди допустимых значений или, иначе, на допустимом множестве значений переменных задачи, которые удовлетворяют заданным ограничениям.

Для этого используются две функции MathCAD:

· Maximize(f,<список параметров>) – вычисление точки максимума;

· Minimize(f,<список параметров>) – вычисление точки минимума,

где f – имя минимизируемого функционала, определенного до обращения к функции; <список параметров> – содержит перечисление (через запятую) имен параметров, относительно которых решается оптимизационная задача.

Внимание! Перед обращением к функциям Maximize, Minimize (имена которых начинаются прописными буквами) следует обязательно задать начальное значение параметров оптимизации.

Пример. Дан функционал:

Определить значения x, y, z, при которых g(x, y, z) достигает минимального значения.

Пример. Дан функционал:

Определить значения u, v, при которых f(u,v) достигает максимального значения.

Задание. Дан функционал:

Определить точки минимума и максимума этого функционала.

Используются те же функции Maximize, Minimize, но они входят уже в блок решения Given и перед ними размещаются ограничения в виде равенств или неравенств, определяющие допустимую область значений параметров оптимизации.

Пример. Дан функционал и ограничения в виде

Определить значения a, b, доставляющие максимальное значение функционала и удовлетворяющие неравенствам.

Замечание. В оптимизационных задачах с ограничениями решение целесообразно определять из необходимых условий экстремума. Эти условия порождают систему уравнений (чаще всего нелинейных), которые располагаются в блоке Given, вместе с ограничениями, определяющими допустимую область. Само решение ищется с помощью функций Find, Minerr.

Пример. В качестве тестового функционала при поиске точки минимума часто используется функционал Розенброка:

«Поверхность» этого функционала напоминает глубокий овраг, что сильно осложняет работу многих алгоритмов минимизации. Требуется вычислить точку минимума функционала при ограничениях:

Пример (задача линейного программирования). Цех малого предприятия должен изготовить 100 изделий трех типов и не менее 20 штук изделий каждого типа. На изделия уходит 4, 3.4 и 2 кг металла соответственно, при его общем запасе 340 кг, а также расходуются по 4.75, 11 и 2 кг пластмассы, при ее общем запасе 400 кг. Прибыль, полученная от каждого изделия равна 4, 3 и 2 рублей.

Определить сколько изделий каждого типа необходимо выпустить, для получения максимальной прибыли в рамках установленных запасов металла и пластмассы.

Пример 9.2.4 (задача нелинейного программирования). Пусть вектор v состоит из трех проекций и дан функционал:

Вычислить точку минимума этого функционала при ограничениях:

Задание 9.2.1 (задача линейного программирования). Дан функционал:

Определить точку максимума этого функционала при ограничениях:

Вычислить значения функционала в этой точке.

Ответ:

максимум функционала достигается в точке (0, 13, 8).

Задание (задача квадратичного программирования). Дан функционал:

Определить точку максимума этого функционала при ограничениях:

Ответ:

максимум функционала достигается в точке (7.5, 10, 6).●

pers.narod.ru

Рыков С.В и др. - Методы оптимизации в примерах в пакете MathCAD 15. Часть 3. Многомерная оптимизация » Шумак Инфо

Рыков С.В и др. - Методы оптимизации в примерах в пакете MathCAD 15. Часть 3. Многомерная оптимизация

Пособие содержит сведения об аналитичеcких методах многомерной оптимизации с ограничениями. Снабжено большим количеством примеров реализации оптимизационных задач рассмотренных как аналитически при построчной реализации, так и с использованием пакета MathCAD 15. При этом реализация в пакете MathCAD 15 имеет два варианта: в виде построчного решения и в виде одной многострочной функции. Предназначено для самостоятельной работы студентов вузов очной и заочной форм обучения.

ПредисловиеАналитические методы поиска условного экстремумаОбщая постановка задачи и основные определенияПрактические примерыАналитические методы поиска условного экстремума с ограничениями в виде равенствНеобходимые условия экстремума первого порядкаНеобходимые условия экстремума второго порядкаДостаточные условия экстремумаАлгоритм решения задачиПрактические примерыАналитические методы поиска условного экстремума с ограничениями типа неравенствНеобходимые условия минимума (максимума) первого порядкаДостаточные условия минимума (максимума) первого порядкаНеобходимое условие минимума (максимума) второго порядкаДостаточное условие экстремума второго порядкаАлгоритм решения задачиПрактические примерыАналитические методы поиска условного экстремума со смешанными ограничениямиНеобходимые условия минимума (максимума) первого порядкаДостаточные условия минимума (максимума) первого порядкаНеобходимые условия минимума (максимума) второго порядкаДостаточные условия экстремума второго порядкаАлгоритм решения задачиПрактические примерыЗадачи для самостоятельного решенияСписок использованных источниковПриложения:Листинги примеров в MathCAD15. Аналитический метод оптимизации. Условный экстремум. Ограничение в виде равенстваЛистинги примеров в MathCAD15. Аналитический метод оптимизации. Условный экстремум. Ограничение в виде неравенстваЛистинги примеров в MathCAD15. Аналитический метод оптимизации. Условный экстремум. Ограничение в смешанном виде

Название: Методы оптимизации в примерах в пакете MathCAD 15. Часть 3. Многомерная оптимизацияАвтор: Рыков С.В и др.Язык: РусскийИздательство: СПб.: Университет ИТМОЖанр: Программы / Учебная литература Год выхода: 2018Формат: pdfСтраниц: 165Размер: 23 mb

Скачать Рыков С.В и др. - Методы оптимизации в примерах в пакете MathCAD 15. Часть 3. Многомерная оптимизация

ПОМОГИ ПРОЕКТУ. СПАСИБО!!

загрузка...

Мы будем крайне признательны, если Вы кликнете на какой-либо тизер.

Всем откликнувшимся СПАСИБО!!

Новость опубликована 29 июня 2018, её прочитали 66 раз(а) и оставили 0 комментариев. Версия для печати

Понравилось? Поделись с друзьями.

_________________________________________________________________

Другие новости по теме

Коллектив - Педагогика (Под редакцией Ю. К. Бабанского) / Аудиокнига

Учебное пособие создано в соответствии с новой программой курса педагогики для студентов педагогических институтов всех факультетов. Содержание пособия значительно переработано с учетом Основных направлений реформы общеобразовательной и профессиональной школы, задач, поставленных XXVII съездом КПСС перед системой народного образования....

__________________________________________________________________

Комментарии к новости

Информация

Посетители, находящиеся в группе Гость, не могут оставлять комментарии к данной публикации.

shumak.info

Методы оптимизации в инженерных расчетах в системе Mathcad: Методическое пособие для студентов технологических специальностей

Федеральное агентство по образованию Восточно-Сибирский государственный технологический университет Кафедра теоретической механики

Методы оптимизации в инженерных расчетах в системе Mathcad

Методические пособие знакомит с методами решения задач оптимизации при выполнении инженерных расчетов с использованием численных методов в системе Mathcad . Методические пособие рассчитано на студентов и преподавателей, использующих методы вычислительной математики для решения профессиональных задач. Ключевые слова: методы оптимизации, программирование, математическая модель.

Методическое пособие для студентов технологических специальностей

Составители: Алексеев А.А. Задевалова Г.Э.

Улан-Удэ 2006

нелинейное

Программирование.

ВВЕДЕНИЕ

Алгоритм

решения

задачи

записывается на алгоритмическом языке в какой-либо Решение инженерных и научно-исследовательских задач требует выполнения трудоемких расчетов, которые

системе программирования. Отладка программы. Производится исправление

могут быть выполнены только с помощью компьютера.

ошибок и испытание программы на решении контрольных

Этот процесс можно разбить на несколько этапов.

тестовых

Постановка задачи. На этом этапе осуществляется формулировка содержания и определение конечных целей

для

получения

уверенности

Построение

математической

модели

или

математическая формулировка задачи. Модель должна

достоверности результатов. Проведение расчетов. На этом этапе вводятся

(адекватно)

описывать

основные

законы

отлаженной программе и вывод результатов в удобной для пользователя форме в виде таблиц и графиков. Анализ

результатов.

Результаты

анализируются,

объекта.

техническая документация по данным результатам.

Разработка метод,

численного позволяющий

метода. свести

сопоставляются.

тщательно

присущие

epdf.tips

Рыков С.В и др. - Методы оптимизации в примерах в пакете MathCAD 15. Часть 3. Многомерная оптимизация

Книжная информация:Автор (ы):Рыков С.В и др. Язык (и): РусскийЖанровая направленность:Программы / Учебная литература Год (ы)выпуска: 2018Формат(ы) материала (ы) материала: pdfРеальный размер файла: 23 mb

Автор: zyzy

Категория: Компьютеры/Интернет

Добавлен: 29-06-2018, 19:26

respektkniga.com

Методы оптимизации в примерах в пакете MathCAD 15. Часть 3. Многомерная оптимизация torrent

Методы оптимизации в примерах в пакете MathCAD 15. Часть 3. Многомерная оптимизация — Пособие содержит сведения об аналитичеcких методах многомерной оптимизации с ограничениями. Снабжено большим количеством примеров реализации оптимизационных задач рассмотренных как аналитически при построчной реализации, так и с использованием пакета MathCAD 15. При этом реализация в пакете MathCAD 15 имеет два варианта: в виде построчного решения и в виде одной многострочной функции. Предназначено для самостоятельной работы студентов вузов очной и заочной форм обучения.

Название: Методы оптимизации в примерах в пакете MathCAD 15. Часть 3. Многомерная оптимизация Автор: Рыков С. В., Кудрявцева И. В., Рыков С. А., Рыков В. А. Издательство: СПб.: Университет ИТМО Год: 2018 Страниц: 165 Формат: PDF Размер: 22,8 МБ Качество: Отличное

Содержание:

Предисловие Аналитические методы поиска условного экстремума Общая постановка задачи и основные определения Практические примеры Аналитические методы поиска условного экстремума с ограничениями в виде равенств Необходимые условия экстремума первого порядка Необходимые условия экстремума второго порядка Достаточные условия экстремума Алгоритм решения задачи Практические примеры Аналитические методы поиска условного экстремума с ограничениями типа неравенств Необходимые условия минимума (максимума) первого порядка Достаточные условия минимума (максимума) первого порядка Необходимое условие минимума (максимума) второго порядка Достаточное условие экстремума второго порядка Алгоритм решения задачи Практические примеры Аналитические методы поиска условного экстремума со смешанными ограничениями Необходимые условия минимума (максимума) первого порядка Достаточные условия минимума (максимума) первого порядка Необходимые условия минимума (максимума) второго порядка Достаточные условия экстремума второго порядка Алгоритм решения задачи Практические примеры Задачи для самостоятельного решения Список использованных источников Приложения: Листинги примеров в MathCAD15. Аналитический метод оптимизации. Условный экстремум. Ограничение в виде равенства Листинги примеров в MathCAD15. Аналитический метод оптимизации. Условный экстремум. Ограничение в виде неравенства Листинги примеров в MathCAD15. Аналитический метод оптимизации. Условный экстремум. Ограничение в смешанном виде

dvijlo.ru

Методы оптимизации в примерах в пакете MathCAD 15. Часть 3. Многомерная оптимизация

Содержание ПредисловиеАналитические методы поиска условного экстремумаОбщая постановка задачи и основные определенияПрактические примерыАналитические методы поиска условного экстремума с ограничениями в виде равенствНеобходимые условия экстремума первого порядкаНеобходимые условия экстремума второго порядкаДостаточные условия экстремумаАлгоритм решения задачиПрактические примерыАналитические методы поиска условного экстремума с ограничениями типа неравенствНеобходимые условия минимума (максимума) первого порядкаДостаточные условия минимума (максимума) первого порядкаНеобходимое условие минимума (максимума) второго порядкаДостаточное условие экстремума второго порядкаАлгоритм решения задачиПрактические примерыАналитические методы поиска условного экстремума со смешанными ограничениямиНеобходимые условия минимума (максимума) первого порядкаДостаточные условия минимума (максимума) первого порядкаНеобходимые условия минимума (максимума) второго порядкаДостаточные условия экстремума второго порядкаАлгоритм решения задачиПрактические примерыЗадачи для самостоятельного решенияСписок использованных источниковПриложения:Листинги примеров в MathCAD15. Аналитический метод оптимизации. Условный экстремум. Ограничение в виде равенстваЛистинги примеров в MathCAD15. Аналитический метод оптимизации. Условный экстремум. Ограничение в виде неравенстваЛистинги примеров в MathCAD15. Аналитический метод оптимизации. Условный экстремум. Ограничение в смешанном виде

Скачать Рыков С.В и др. - Методы оптимизации в примерах в пакете MathCAD 15. Часть 3. Многомерная оптимизация

Скачать с 2bay.orgСкачать с Rapidfile.tkСкачать с Katfile.comСкачать с TurboBit.Net

subscribe.ru