Генетические алгоритмы в задаче оптимизации действительных параметров (стр. 2 из 7). Генетический алгоритм оптимизации

Генетический алгоритм. Описание и примеры

Одной из задач интеллектуальных систем является поиск оптимального решения: когда на систему влияет множество внешних и внутренних факторов, интеллектуальное устройство должно учесть их все и выбрать оптимальное поведение с точки зрения своей выгоды. Допустим, если Вы — хозяин склада, Вам необходимо учитывать много факторов (стоимость единиц товаров, спрос, издержки на хранение различных товаров на складе и т.д.) для минимизации издержек и получение наибольшей прибыли.

Другой пример: вы едете по скользкой дороге, и вдруг ваш автомобиль начинает заносить, справа в нескольких метрах от вас столб, а по встречной полосе едет грузовик. Внимание вопрос: как выйти из ситуации с наименьшими потерями, а лучше вообще без них. Факторов, которые нужно учитывать много: ваша скорость и скорость встречного автомобиля, расстояние до столба, «крутость» заноса и т.д. Что нужно делать? Давать газу, пытаясь выйти из заноса, или тормозить, или, может, попытаться аккуратно съехать в кювет, так чтобы не попасть в столб. Вариантов много, и для того чтобы определить оптимальный — нужно попробовать их все. Будь это компьютерной игрой – вы могли бы сохраниться и переигрывать до тех пор, пака результат вас не удовлетворит. Это и есть поиск оптимального решения.

В системах искусственного интеллекта для решения подобных задач применяются генетические алгоритмы.

Генетические алгоритмы – адаптивные методы поиска, которые используются для решения задач функциональной оптимизации. Они основаны на механизмах и моделях эволюции, и генетических процессов биологических алгоритмов.

Скажем проще: по сути, генетический алгоритм — это метод перебора решений для тех задач, в которых невозможно найти решение с помощью математических формул. Однако простой перебор решений в сложной многомерной задаче – это бесконечно долго. Поэтому генетический алгоритм перебирает не все решения, а только лучшие. Алгоритм берёт группу решений и ищет среди них наиболее подходящие. Затем немного изменяет их – получает новые решения, среди которых снова отбирает лучшие, а худшие отбрасывает. Таким образом, на каждом шаге работы алгоритм отбирает наиболее подходящие решения (проводит селекцию), считая, что они на следующем шаге дадут ещё более лучшие решения (эволюционируют).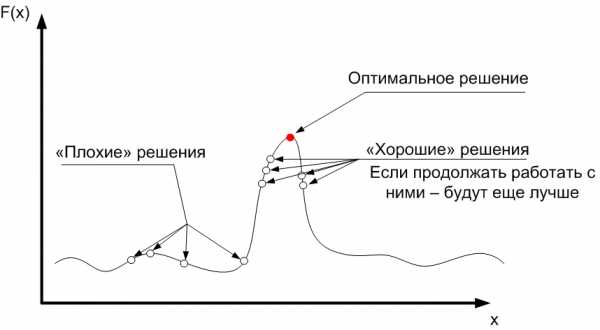

Причём тут биология?

Как вы уже поняли, в теории генетических алгоритмов проводится аналогия между задачей и биологическим процессом. Отсюда и терминология…

Особь – одно решение задачи.

Популяция — набор решений задачи. В начале алгоритма случайным образом генерируется набор решений (начальная популяция). Эти решения будут становиться лучше (эволюционировать) в процессе работы алгоритма до тех пор, пока не удовлетворят условиям задачи.

И сразу самый простой классический пример. Допустим, роботу необходимо объехать шесть контрольных точек за наименьшее время. Расстояние от каждой точки до каждой задано в виде матрицы расстояний.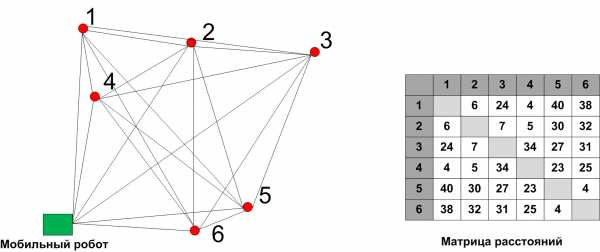

Это вариация задачи о коммивояжёре (путешественнике) – относится к классу NP-полных, проще говоря, не может быть решена с помощью математических формул.

Решение задачи – это последовательность прохождения контрольных точек. Возьмём несколько возможных решений (особей)– это и есть начальная популяция.

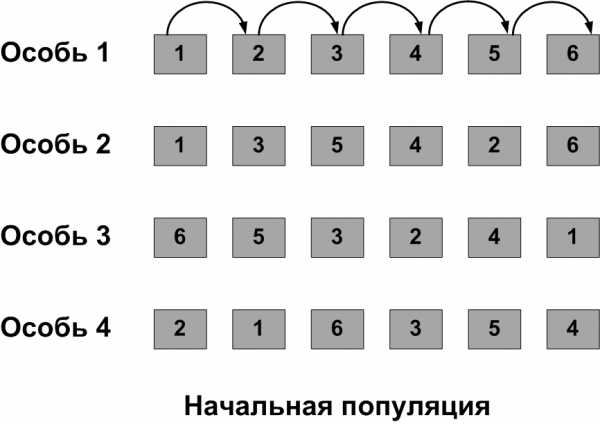
Определения качества решений

Функция пригодности – функция определяющая качество особей популяции. В нашем примере это будет сумма расстояний от точки до точки в выбранном маршруте.

ФП = Р(1)+Р(2)+Р(3)+Р(4)+Р(5)+Р(6),

где Р(1) … Р(6) – расстояние между точками в соответствующем переходе из матрицы расстояний

Нам необходимо найти минимальное расстояние, поэтому, чем меньше значение ФП для особи, тем лучше.

Давайте посчитаем функции пригодности. Для первой особи:

Для остальных особей таким же образом получаем:

ФП(2) = 111

ФП(3) = 47

ФП(4) = 125

Тут всё очевидно: особь №3 – лучшая, а №4 – самая плохая.

Генетические операторы

Дальше согласно алгоритму необходимо слегка изменить исходных особей, так чтобы они были похожи на своих родителей, но немного отличались. Так реализуется биологическое понятие «изменчивость».

Генетические операторы – определённые правила, по которым изменяются особи в следующей популяции. Среди них выделяют операторы скрещивания и мутации. Подробнее об этих операторах речь пойдёт в одной из следующих статей. Сейчас главное запомнить, что после их применения мы получим еще несколько особей – потомков. Допустим таких:

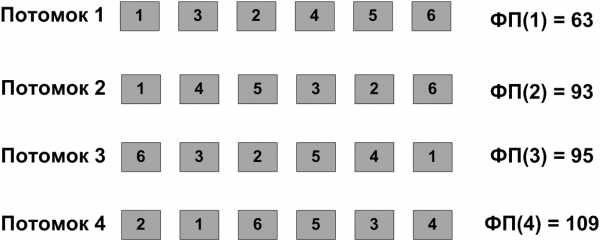
Для потомков тоже посчитаны функции пригодности.

Оператор селекции

Настало время искусственного отбора. На этом шаге алгоритм выберет лучших особей и отбросит худших (наименее приспособленных), подобно тому, как делает селекционер, создавая новый вид растений.

Алгоритмы селекции тоже могут быть различны, не будем пока заострять на этом внимание. Просто возьмем и отбросим из первой популяции (родители + потомки) четыре худших особи. Останутся родитель 1 и 3, и потомки 1 и 2. Эти особи сформируют новую популяцию. Далее алгоритм будет повторяться. Для наглядности посмотрим на блок-схему классического генетического алгоритма:

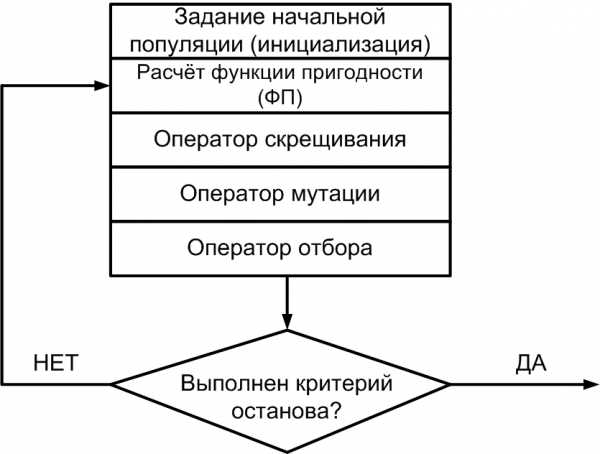
Критерий останова генетического алгоритма

Вспомним, что мы искали кратчайший путь прохождения робота через все контрольные точки. Абсолютно правильный ответ будет получен, только если перебрать все варианты, а их очень много даже для шести точек (а если точек будет больше?). Поэтому генетический алгоритм ищет не правильное решение, а оптимальное, исходя из условий, которые задаёт пользователь.

Критерий останова – условие, по которому генетический алгоритм останавливает свою работу.

В начале статьи речь шла о компьютерной игре, в которой можно сохраниться и переигрывать какой-то эпизод, до тех пор, пока результат вас не удовлетворит. Ну, например, вы поставили себе цель пройти уровень без единой потерянной жизни, или за рекордное время, или убив всех врагов или не разбив машину и т.д. С генетическим алгоритмом та же история: мы ищем не самое лучшее решение, а то решение, которое нас устроит.

В нашем случае мы можем указать, например, один из следующих критериев останова:

Суммарный путь меньше 50
Время работы алгоритма 1 час
Число циклов алгоритма 10
В течение 3 поколений не появляются особи лучше тех, которые были
и т.д.

Ещё немного о функции пригодности

На практике далеко не всегда получается составить функцию пригодности так же просто, как в нашем примере. Например, вы — хозяин завода. Ваша цель увеличение прибыли. Для достижения этой цели вы можете варьировать много различных параметров: количество закупаемого сырья, план выпуска, зарплата рабочих, количество денег, выделяемых на модернизацию производства, повышение квалификации персонала, на рекламу и т.д. Набор конкретных значений этих параметров и будет стратегией, скажем, на месяц. Однако нет точной математической формулы, связывающей эти параметры между собой. Поэтому в данном случае для подсчёта функции пригодности необходима имитационная модель завода. Как видно из названия, это модель, имитирующая работу заводу, все его бизнес-процессы. Подробную информацию об имитационном моделировании вы также сможете найти на страницах LAZY SMART. А пока для краткости изложения скажем, что если на вход имитационной модели задать входные значения искомых параметров, то на выходе получим итоговую прибыль. Компьютер как бы проиграет всю деятельность завода, допустим, за месяц в убыстренной перемотке. Эта итоговая прибыль и будет значением функции пригодности для генетического алгоритма. Представим работу связки «Генетический алгоритм – Модель» на схеме.

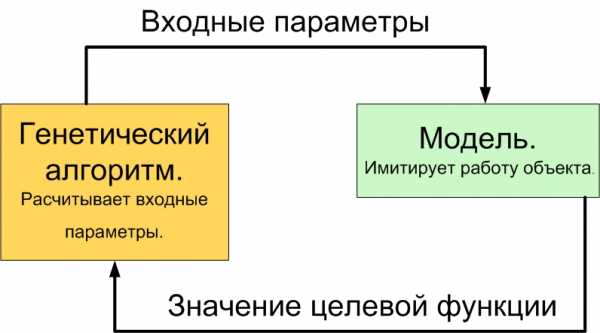
Применение генетических алгоритмов

Генетические алгоритмы активно применяются в робототехнике, компьютерных играх, обучении нейронных сетей, создании моделей искусственной жизни, составлении расписаний, оптимизации запросов к базам данных, поиске оптимальных маршрутов и т.д.

Такие алгоритмы могут стать хорошим помощником в бизнесе, сократить убытки и увеличить прибыль за счёт выбора оптимальных стратегий.

comments powered by HyperComments

lazysmart.ru

23.Генетические алгоритмы для многокритериальной оптимизации

Большинство задач, решаемых при помощи генетических алгоритмов, имеют один критерий оптимизации. В свою очередь, многокритериальная оптимизация основана на отыскании решения, одновременно оптимизирующего более чем одну функцию. В этом случае ищется некоторый компромисс, в роли которого выступает решение, оптимальное в смысле Парето. При многокритериальной оптимизации выбирается не единственная хромосома, представляющая собой закодированную форму оптимального решения в обычном смысле, а множество хромосом, оптимальных в смысле Парето [7]. Пользователь имеет возможность выбрать оптимальное решение из этого множества. Рассмотрим определение решения, оптимального в смысле Парето (символамиxиyбудем обозначать фенотипы).

Решение xназываетсядоминируемым, если существует решениеy, не хуже чемx, т.е. для любой оптимизируемой функцииfi,i= 1, 2, …,m

fi(x) ≤fi(y) при максимизации функцииfi,

fi(x) ≥fi(y) при минимизации функцииfi.

Если решение не доминируемо никаким другим решением, то оно называется недоминируемымилиоптимальным в смысле Парето.

Существует несколько классических методов, относящихся к многокритериальной оптимизации. Один из них – это метод взвешенной функции(method of objective weighting), в соответствии с которым оптимизируемые функцииfiс весамиwiобразуют единую функцию

(68)

где и.

Различные веса дают различные решения в смысле Парето.

Другой подход известен как метод функции расстояния(method of distance function). Идея этого метода заключается в сравнении значенийfi(x) с заданным значениемyi по формуле метрики Минковского порядкаr, т.е.

(69)

При этом, как правило, принимается r=2. Это метрика Эвклида.

Еще один подход к многокритериальной оптимизации связан с разделением популяции на подгруппы (подпопуляции) одинакового размера (subpopulations), каждая из которых «отвечает» за одну оптимизируемую функцию. Селекция производится автономно для каждой функции, однако операция скрещивания выполняется без учета границ подгрупп.

Алгоритм многокритериальной оптимизации реализован в программе FlexTool. Селекция выполняется турнирным методом, при этом «лучшая» особь в каждой подгруппе выбирается на основе функции приспособленности, уникальной для данной подгруппы. Схема такой селекции в случае оптимизации двух функций представлена на рисунке 43; на этом рисунке F1иF2обозначают две различные функции приспособленности. Эта схема аналогична схеме, изображенной на рисунке 37, с той разницей, что на более ранней схеме все подгруппы оценивались по одной и той же функции приспособленности. «Наилучшая» особь из каждой подгруппы смешивается с другими особями, и все генетические операции выполняются так же, как в генетическом алгоритме для оптимизации одной функции. Схему на рисунке 43 можно легко обобщить на большее количество оптимизируемых функций. Так, например, программа FlexTool обеспечивает одновременную оптимизацию четырех функций [7].

Рисунок 43. Схема турнирной селекции в случае многокритериальной оптимизации по двум функциям

studfiles.net

Генетический алгоритм — WiKi

Первые работы по симуляции эволюции были проведены в 1954 году Нильсом Баричелли на компьютере, установленном в Институте перспективных исследований Принстонского университета.[1][2] Его работа, опубликованная в том же году, привлекла широкое внимание общественности. С 1957 года,[3] австралийский генетик Алекс Фразер опубликовал серию работ по симуляции искусственного отбора среди организмов с множественным контролем измеримых характеристик. Положенное начало позволило компьютерной симуляции эволюционных процессов и методам, описанным в книгах Фразера и Барнелла(1970)[4] и Кросби (1973)[5], с 1960-х годов стать более распространенным видом деятельности среди биологов. Симуляции Фразера включали все важнейшие элементы современных генетических алгоритмов. Вдобавок к этому, Ганс-Иоахим Бремерманн в 1960-х опубликовал серию работ, которые также принимали подход использования популяции решений, подвергаемой рекомбинации, мутации и отбору, в проблемах оптимизации. Исследования Бремерманна также включали элементы современных генетических алгоритмов.[6] Среди прочих пионеров следует отметить Ричарда Фридберга, Джорджа Фридмана и Майкла Конрада. Множество ранних работ были переизданы Давидом Б. Фогелем (1998).[7]

Хотя Баричелли в своей работе 1963 года симулировал способности машины играть в простую игру,[8] искусственная эволюция стала общепризнанным методом оптимизации после работы Инго Рехенберга и Ханса-Пауля Швефеля в 1960-х и начале 1970-х годов двадцатого века — группа Рехенсберга смогла решить сложные инженерные проблемы согласно стратегиям эволюции.[9][10][11][12] Другим подходом была техника эволюционного программирования Лоренса Дж. Фогеля, которая была предложена для создания искусственного интеллекта. Эволюционное программирование первоначально использовавшее конечные автоматы для предсказывания обстоятельств, и использовавшее разнообразие и отбор для оптимизации логики предсказания. Генетические алгоритмы стали особенно популярны благодаря работе Джона Холланда в начале 70-х годов и его книге «Адаптация в естественных и искусственных системах» (1975)[13]. Его исследование основывалось на экспериментах с клеточными автоматами, проводившимися Холландом и на его трудах написанных в университете Мичигана. Холланд ввел формализованный подход для предсказывания качества следующего поколения, известный как Теорема схем. Исследования в области генетических алгоритмов оставались в основном теоретическими до середины 80-х годов, когда была, наконец, проведена Первая международная конференция по генетическим алгоритмам в Питтсбурге, Пенсильвания (США).

С ростом исследовательского интереса существенно выросла и вычислительная мощь настольных компьютеров, это позволило использовать новую вычислительную технику на практике. В конце 80-х, компания General Electric начала продажу первого в мире продукта, работавшего с использованием генетического алгоритма. Им стал набор промышленных вычислительных средств. В 1989, другая компания Axcelis, Inc. выпустила Evolver — первый в мире коммерческий продукт на генетическом алгоритме для настольных компьютеров. Журналист The New York Times в технологической сфере Джон Маркофф писал[14] об Evolver в 1990 году.

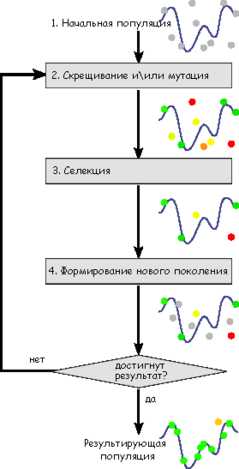Схема работы генетического алгоритма

Задача формализуется таким образом, чтобы её решение могло быть закодировано в виде вектора («генотипа») генов, где каждый ген может быть битом, числом или неким другим объектом. В классических реализациях генетического алгоритма (ГА) предполагается, что генотип имеет фиксированную длину. Однако существуют вариации ГА, свободные от этого ограничения.

Некоторым, обычно случайным, образом создаётся множество генотипов начальной популяции. Они оцениваются с использованием «функции приспособленности», в результате чего с каждым генотипом ассоциируется определённое значение («приспособленность»), которое определяет насколько хорошо фенотип, им описываемый, решает поставленную задачу.

При выборе «функции приспособленности» (или fitness function в англоязычной литературе) важно следить, чтобы её «рельеф» был «гладким».

Из полученного множества решений («поколения») с учётом значения «приспособленности» выбираются решения (обычно лучшие особи имеют большую вероятность быть выбранными), к которым применяются «генетические операторы» (в большинстве случаев «скрещивание» — crossover и «мутация» — mutation), результатом чего является получение новых решений. Для них также вычисляется значение приспособленности, и затем производится отбор («селекция») лучших решений в следующее поколение.

Этот набор действий повторяется итеративно, так моделируется «эволюционный процесс», продолжающийся несколько жизненных циклов (поколений), пока не будет выполнен критерий остановки алгоритма. Таким критерием может быть:

нахождение глобального, либо субоптимального решения;
исчерпание числа поколений, отпущенных на эволюцию;
исчерпание времени, отпущенного на эволюцию.

Генетические алгоритмы служат, главным образом, для поиска решений в многомерных пространствах поиска.

Таким образом, можно выделить следующие этапы генетического алгоритма:

Задать целевую функцию (приспособленности) для особей популяции
Создать начальную популяцию

(Начало цикла)

Размножение (скрещивание)
Мутирование
Вычислить значение целевой функции для всех особей
Формирование нового поколения (селекция)
Если выполняются условия остановки, то (конец цикла), иначе (начало цикла).

Создание начальной популяции

Перед первым шагом нужно случайным образом создать начальную популяцию; даже если она окажется совершенно неконкурентоспособной, вероятно, что генетический алгоритм всё равно достаточно быстро переведёт её в жизнеспособную популяцию. Таким образом, на первом шаге можно особенно не стараться сделать слишком уж приспособленных особей, достаточно, чтобы они соответствовали формату особей популяции, и на них можно было подсчитать функцию приспособленности (Fitness). Итогом первого шага является популяция H, состоящая из N особей.

Отбор (селекция)

На этапе отбора нужно из всей популяции выбрать определённую её долю, которая останется «в живых» на этом этапе эволюции. Есть разные способы проводить отбор. Вероятность выживания особи h должна зависеть от значения функции приспособленности Fitness(h). Сама доля выживших s обычно является параметром генетического алгоритма, и её просто задают заранее. По итогам отбора из N особей популяции H должны остаться sN особей, которые войдут в итоговую популяцию H'. Остальные особи погибают.

Турнирная селекция — сначала случайно выбирается установленное количество особей (обычно две), а затем из них выбирается особь с лучшим значением функции приспособленности
Метод рулетки — вероятность выбора особи тем вероятнее, чем лучше её значение функции приспособленности pi=fi∑i=1Nfi{\displaystyle p_{i}={\frac {f_{i}}{\sum _{i=1}^{N}{f_{i}}}}} , где pi{\displaystyle p_{i}} — вероятность выбора i особи, fi{\displaystyle f_{i}} — значение функции приспособленности для i особи, N{\displaystyle N} — количество особей в популяции
Метод ранжирования — вероятность выбора зависит от места в списке особей отсортированном по значению функции приспособленности pi=1N(a−(a−b)i−1N−1){\displaystyle p_{i}={\frac {1}{N}}(a-(a-b){\frac {i-1}{N-1}})} , где a∈[1,2]{\displaystyle a\in [1,2]} , b=2−a{\displaystyle b=2-a} , i{\displaystyle i} — порядковый номер особи в списке особей отсортированном по значению функции приспособленности (то есть ∀ i ∀ j>i fi≤fj{\displaystyle \forall {\text{ }}i{\text{ }}\forall {\text{ }}j>i{\text{ }}{\text{ }}f_{i}\leq f_{j}} — если мы минимизируем значение функции приспособленности)
Равномерное ранжирование — вероятность выбора особи определяется выражением: pi={1μ,if 1≤i≤μ0,if μ≤i≤N{\displaystyle p_{i}={\begin{cases}{\frac {1}{\mu }},&{\mbox{if }}1\leq i\leq \mu \\0,&{\mbox{if }}\mu \leq i\leq N\end{cases}}} , где μ≤N{\displaystyle \mu \leq N} параметр метода
Сигма отсечение — для предотвращения преждевременной сходимости генетического алгоритма используются методы, масштабирующие значение целевой функции. Вероятность выбора особи тем больше, чем оптимальнее значение масштабируемой целевой функции pi=Fi∑i=1NFi{\displaystyle p_{i}={\frac {F_{i}}{\sum _{i=1}^{N}{F_{i}}}}} , где Fi=1+fi−favg2σ{\displaystyle F_{i}=1+{\frac {f_{i}-f_{avg}}{2\sigma }}} , favg{\displaystyle f_{avg}} — среднее значение целевой функции для всей популяции, σ — среднеквадратичное отклонение значения целевой функции[15].

Выбор родителей

Размножение в генетических алгоритмах требует для производства потомка нескольких родителей, обычно двух.

Можно выделить несколько операторов выбора родителей:

Панмиксия — оба родителя выбираются случайно, каждая особь популяции имеет равные шансы быть выбранной
Инбридинг — первый родитель выбирается случайно, а вторым выбирается такой, который наиболее похож на первого родителя
Аутбридинг — первый родитель выбирается случайно, а вторым выбирается такой, который наиболее не похож на первого родителя

Инбридинг и аутбридинг бывают в двух формах: фенотипной и генотипной. В случае фенотипной формы похожесть измеряется в зависимости от значения функции приспособленности (чем ближе значения целевой функции, тем особи более похожи), а в случае генотипной формы похожесть измеряется в зависимости от представления генотипа (чем меньше отличий между генотипами особей, тем особи похожее).

Размножение (Скрещивание)

Размножение в разных алгоритмах определяется по-разному — оно, конечно, зависит от представления данных. Главное требование к размножению — чтобы потомок или потомки имели возможность унаследовать черты обоих родителей, «смешав» их каким-либо способом.

Почему особи для размножения обычно выбираются из всей популяции H, а не из выживших на первом шаге элементов H' (хотя последний вариант тоже имеет право на существование)? Дело в том, что главный недостаток многих генетических алгоритмов — отсутствие разнообразия (diversity) в особях. Достаточно быстро выделяется один-единственный генотип, который представляет собой локальный максимум, а затем все элементы популяции проигрывают ему отбор, и вся популяция «забивается» копиями этой особи. Есть разные способы борьбы с таким нежелательным эффектом; один из них — выбор для размножения не самых приспособленных, но вообще всех особей. Однако такой подход вынуждает хранить всех существовавших ранее особей, что увеличивает вычислительную сложность задачи. Поэтому часто применяют методы отбора особей для скрещивания таким образом, чтобы «размножались» не только самые приспособленные, но и другие особи, обладающие плохой приспособленностью. При таком подходе для разнообразия генотипа возрастает роль мутаций.

Мутации

К мутациям относится все то же самое, что и к размножению: есть некоторая доля мутантов m, являющаяся параметром генетического алгоритма, и на шаге мутаций нужно выбрать mN особей, а затем изменить их в соответствии с заранее определёнными операциями мутации.

ru-wiki.org

Генетический алгоритм - это... Что такое Генетический алгоритм?

Генети́ческий алгори́тм (англ. genetic algorithm) — это эвристический алгоритм поиска, используемый для решения задач оптимизации и моделирования путём случайного подбора, комбинирования и вариации искомых параметров с использованием механизмов, напоминающих биологическую эволюцию. Является разновидностью эволюционных вычислений, с помощью которых решаются оптимизационные задачи с использованием методов естественной эволюции, таких как наследование, мутации, отбор и кроссинговер. Отличительной особенностью генетического алгоритма является акцент на использование оператора «скрещивания», который производит операцию рекомбинации решений-кандидатов, роль которой аналогична роли скрещивания в живой природе.

История

Первые работы по симуляции эволюции были проведены в 1954 году Нильсом Баричелли на компьютере установленном в Институте Продвинутых Исследований Принстонского университета.[1][2] Его работа, опубликованная в том же году, привлекла широкое внимание общественности. С 1957 года,[3] австралийский генетик Алекс Фразер опубликовал серию работ по симуляции искусственного отбора среди организмов с множественным контролем измеримых характеристик. Положенное начало позволило компьютерной симуляции эволюционных процессов и методам, описанным в книгах Фразера и Барнелла(1970)[4] и Кросби (1973).[5], с 1960-х годов стать более распространенным видом деятельности среди биологов. Симуляции Фразера включали все важнейшие элементы современных генетических алгоритмов. Вдобавок к этому, Ганс-Иоахим Бремерманн в 1960-х опубликовал серию работ, которые также принимали подход использования популяции решений, подвергаемой рекомбинации, мутации и отбору, в проблемах оптимизации. Исследования Бремерманна также включали элементы современных генетических алгоритмов.[6] Среди прочих пионеров следует отметить Ричарда Фридберга, Джорджа Фридмана и Майкла Конрада. Множество ранних работ были переизданы Давидом Б. Фогелем (1998).[7]

Хотя Баричелли в своей работе 1963 года симулировал способности машины играть в простую игру,[8] искусственная эволюция стала общепризнанным методом оптимизации после работы Инго Рехенберга и Ханса-Пауля Швефеля в 1960-х и начале 1970-х годов двадцатого века – группа Рехенсберга смогла решить сложные инженерные проблемы согласно стратегиям эволюции.[9][10][11][12] Другим подходом была техника эволюционного программирования Лоренса Дж. Фогеля, которая была предложена для создания искусственного интеллекта. Эволюционное программирование первоначально использовавшее конечные автоматы для предсказывания обстоятельств, и использовавшее разнообразие и отбор для оптимизации логики предсказания. Генетические алгоритмы стали особенно популярны благодаря работе Джона Холланда в начале 70-х годов и его книге «Адаптация в естественных и искусственных системах» (1975)[13]. Его исследование основывалось на экспериментах с клеточными автоматами, проводившимися Холландом и на его трудах написанных в университете Мичигана. Холланд ввел формализованный подход для предсказывания качества следующего поколения, известный как Теорема схем. Исследования в области генетических алгоритмов оставались в основном теоретическими до середины 80-х годов, когда была наконец проведена Первая международная конференция по генетическим алгоритмам в Питтсбурге, Пенсильвания (США).

С ростом исследовательского интереса существенно выросла и вычислительная мощь настольных компьютеров, это позволило использовать новую вычислительную технику на практике. В конце 80-х, компания General Electric начала продажу первого в мире продукта, работавшего с использованием генетического алгоритма. Им стал набор промышленных вычислительных средств. В 1989, другая компания Axcelis, Inc. выпустила Evolver – первый в мире коммерческий продукт на генетическом алгоритме для настольных компьютеров. Журналист The New York Times в технологической сфере Джон Маркофф писал [14] об Evolver в 1990 году.

Описание алгоритма

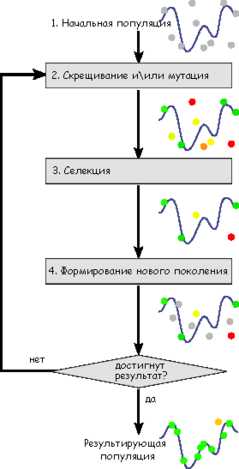Схема работы генетического алгоритма

Задача формализуется таким образом, чтобы её решение могло быть закодировано в виде вектора («генотипа») генов, где каждый ген может быть битом, числом или неким другим объектом. В классических реализациях ГА предполагается, что генотип имеет фиксированную длину. Однако существуют вариации ГА, свободные от этого ограничения.

нахождение глобального, либо субоптимального решения;
исчерпание числа поколений, отпущенных на эволюцию;
исчерпание времени, отпущенного на эволюцию.

Генетические алгоритмы служат, главным образом, для поиска решений в многомерных пространствах поиска.

Таким образом, можно выделить следующие этапы генетического алгоритма:

Задать целевую функцию (приспособленности) для особей популяции
Создать начальную популяцию

(Начало цикла)

Размножение (скрещивание)
Мутирование
Вычислить значение целевой функции для всех особей
Формирование нового поколения (селекция)
Если выполняются условия остановки, то (конец цикла), иначе (начало цикла).

Создание начальной популяции

Перед первым шагом нужно случайным образом создать начальную популяцию; даже если она окажется совершенно неконкурентоспособной, вероятно, что генетический алгоритм все равно достаточно быстро переведет ее в жизнеспособную популяцию. Таким образом, на первом шаге можно особенно не стараться сделать слишком уж приспособленных особей, достаточно, чтобы они соответствовали формату особей популяции, и на них можно было подсчитать функцию приспособленности (Fitness). Итогом первого шага является популяция H, состоящая из N особей.

Размножение (Скрещивание)

Размножение в генетических алгоритмах обычно половое — чтобы произвести потомка, нужны несколько родителей, обычно два.

Почему особи для размножения обычно выбираются из всей популяции H, а не из выживших на первом шаге элементов H0 (хотя последний вариант тоже имеет право на существование)? Дело в том, что главный бич многих генетических алгоритмов — недостаток разнообразия (diversity) в особях. Достаточно быстро выделяется один-единственный генотип, который представляет собой локальный максимум, а затем все элементы популяции проигрывают ему отбор, и вся популяция «забивается» копиями этой особи. Есть разные способы борьбы с таким нежелательным эффектом; один из них — выбор для размножения не самых приспособленных, но вообще всех особей.

Мутации

Отбор

Критика

Существует несколько поводов для критики на счёт использования генетического алгоритма по сравнению с другими методами оптимизации:

Повторная оценка функции приспособленности (фитнесс-функции) для сложных проблем, часто является фактором, ограничивающим использование алгоритмов искусственной эволюции. Поиск оптимального решения для сложной задачи высокой размерности зачастую требует очень затратной оценки функции приспособленности. В реальных задачах, таких как задачи структурной оптимизации, единственный запуск функциональной оценки требует от нескольких часов до нескольких дней для произведения необходимых вычислений. Стандартные методы оптимизации не могут справиться с проблемами такого рода. В таком случае, может быть необходимо пренебречь точной оценкой и использовать аппроксимацию пригодности, которая способна быть вычислена эффективно. Очевидно, что применение аппроксимации пригодности может стать одним из наиболее многообещающих подходов, позволяющих обоснованно решать сложные задачи реальной жизни с помощью генетических алгоритмов.

Генетические алгоритмы плохо масштабируемы под сложность решаемой проблемы. Это значит, что число элементов, подверженных мутации очень велико, если велик размер области поиска решений. Это делает использование данной вычислительной техники чрезвычайно сложным при решении таких проблем, как, например, проектирование двигателя, дома или самолёта. Для того чтобы сделать так, чтобы такие проблемы поддавались эволюционным алгоритмам, они должны быть разделены на простейшие представления данных проблем. Таким образом, эволюционные вычисления используются, например, при разработке формы лопастей, вместо всего двигателя, формы здания, вместо подробного строительного проекта и формы фюзеляжа, вместо разработки вида всего самолёта. Вторая проблема, связанная со сложностью, кроется в том, как защитить части, которые эволюционировали с высокопригодными решениями от дальнейшей разрушительной мутации, в частности тогда, когда от них требуется хорошая совместимость с другими частями в процессе оценки пригодности. Некоторыми разработчиками было предложено, что подход предполагающий развитие пригодности эволюционирующих решений смог бы преодолеть ряд проблем с защитой, но данный вопрос всё ещё остаётся открытым для исследования.

Решение является более пригодным лишь по сравнению с другими решениями. В результате условие остановки алгоритма неясно для каждой проблемы.

Во многих задачах генетические алгоритмы имеют тенденцию сходиться к локальному оптимуму или даже к спорным точкам, вместо глобального оптимума для данной задачи. Это значит, что они "не знают", каким образом пожертвовать кратковременной высокой пригодностью для достижения долгосрочной пригодности. Вероятность этого зависит от формы ландшафта пригодности: отдельные проблемы могут иметь выраженное направление к глобальному минимуму, в то время как остальные могут указывать направление для фитнесс-функции на локальный оптимум. Эту проблему можно решить использованием иной фитнесс-функции, увеличением вероятности мутаций, или использованием методов отбора, которые поддерживают разнообразие решений в популяции, хотя Теорема об отсутствии бесплатного обеда при поиске и оптимизации[15] доказывает, что не существует общего решения данной проблемы. Общепринятым методом поддержания популяционного разнообразия является установка уровневого ограничения на численность элементов с высоким сродством, которое снизит число представителей сходных решений в последующих поколениях, позволяя другим, менее сходным элементам оставаться в популяции. Данный приём, тем не менее, может не увенчаться успехом в зависимости от ландшафта конкретной проблемы. Другим возможным методом может служить простое замещение части популяции случайно сгенерированными элементами, в момент, когда элементы популяции становятся слишком сходны между собой. Разнообразие важно для генетических алгоритмов (и генетического программирования) потому, что перекрёст генов в гомогенной популяции не несёт новых решений. В эволюционных стратегиях и эволюционном программировании, разнообразие не является необходимостью, так как большая роль в них отведена мутации.

Имеется много скептиков относительно целесообразности применения генетических алгоритмов. Например, Стивен С. Скиена, профессор кафедры вычислительной техники университета Стоуни—Брук, известный исследователь алгоритмов, лауреат премии института IEEE пишет[16]:

Я лично никогда не сталкивался ни с одной задачей, для решения которой генетические алгоритмы оказались бы самым подходящим средством. Более того я никогда не встречал никаких результатов вычислений, полученных посредством генетических алгоритмов, которые производили бы на меня положительное впечатление.

Применение генетических алгоритмов

Генетические алгоритмы применяются для решения следующих задач:

Оптимизация функций
Оптимизация запросов в базах данных
Разнообразные задачи на графах (задача коммивояжера, раскраска, нахождение паросочетаний)
Настройка и обучение искусственной нейронной сети
Задачи компоновки
Составление расписаний
Игровые стратегии
Теория приближений
Искусственная жизнь
Биоинформатика (фолдинг белков)

Пример тривиальной реализации на C++

Поиск в одномерном пространстве, без скрещивания.

#include <algorithm> #include <iostream> #include <numeric> #include <cstdlib> #include <ctime> int main() { ::std::srand((unsigned int)::std::time(NULL)); const size_t N = 1000; int a[N] = { 0 }; for ( ; ; ) { //мутация в случайную сторону каждого элемента: for ( size_t i = 0 ; i < N ; ++i ) if ( ::std::rand() % 2 == 1 ) a[i] += 1; else a[i] -= 1; //теперь выбираем лучших, отсортировав по возрастанию... ::std::sort(a, a+N); //... и тогда лучшие окажутся во второй половине массива. //скопируем лучших в первую половину, куда они оставили потомство, а первые умерли: ::std::copy(a+N/2, a+N, a); //теперь посмотрим на среднее состояние популяции. Как видим, оно всё лучше и лучше. ::std::cout << ::std::accumulate(a, a+N, 0) / N << ::std::endl; } }

Примечания

↑ Barricelli, Nils Aall (1954). «Esempi numerici di processi di evoluzione». Methodos: 45–68.
↑ Barricelli, Nils Aall (1957). «Symbiogenetic evolution processes realized by artificial methods». Methodos: 143–182.
↑ Fraser, Alex (1957). «Simulation of genetic systems by automatic digital computers. I. Introduction». Aust. J. Biol. Sci. 10: 484–491.
↑ Fraser Alex Computer Models in Genetics. — New York: McGraw-Hill, 1970. — ISBN 0-07-021904-4
↑ Crosby Jack L. Computer Simulation in Genetics. — London: John Wiley & Sons, 1973. — ISBN 0-471-18880-8
↑ 02.27.96 - UC Berkeley's Hans Bremermann, professor emeritus and pioneer in mathematical biology, has died at 69
↑ Fogel David B. (editor) Evolutionary Computation: The Fossil Record. — New York: IEEE Press, 1998. — ISBN 0-7803-3481-7
↑ Barricelli, Nils Aall (1963). «Numerical testing of evolution theories. Part II. Preliminary tests of performance, symbiogenesis and terrestrial life». Acta Biotheoretica (16): 99–126.
↑ Rechenberg Ingo Evolutionsstrategie. — Holzmann-Froboog, 1973. — ISBN 3-7728-0373-3
↑ Schwefel Hans-Paul Numerische Optimierung von Computer-Modellen (PhD thesis). — 1974.
↑ Schwefel Hans-Paul Numerische Optimierung von Computor-Modellen mittels der Evolutionsstrategie : mit einer vergleichenden Einführung in die Hill-Climbing- und Zufallsstrategie. — Birkhäuser, 1977. — ISBN 3-7643-0876-1
↑ Schwefel Hans-Paul Numerical optimization of computer models (Translation of 1977 Numerische Optimierung von Computor-Modellen mittels der Evolutionsstrategie. — Wiley, 1981. — ISBN 0-471-09988-0
↑ J. H. Holland. Adaptation in natural and artificial systems. University of Michigan Press, Ann Arbor, 1975.
↑ Markoff, John. What's the Best Answer? It's Survival of the Fittest, New York Times (29 августа 1990). Проверено 9 августа 2009.
↑ Wolpert, D.H., Macready, W.G., 1995. No Free Lunch Theorems for Optimisation. Santa Fe Institute, SFI-TR-05-010, Santa Fe.
↑ Steven S. Skiena. The Algorithm Design Manual. Second Edition. Springer, 2008.

Книги

Емельянов В. В., Курейчик В. В., Курейчик В. М. Теория и практика эволюционного моделирования. — М: Физматлит, 2003. — С. 432. — ISBN 5-9221-0337-7
Курейчик В. М., Лебедев Б. К., Лебедев О. К. Поисковая адаптация: теория и практика. — М: Физматлит, 2006. — С. 272. — ISBN 5-9221-0749-6
Гладков Л. А., Курейчик В. В., Курейчик В. М. Генетические алгоритмы: Учебное пособие. — 2-е изд. — М: Физматлит, 2006. — С. 320. — ISBN 5-9221-0510-8
Гладков Л. А., Курейчик В. В, Курейчик В. М. и др. Биоинспирированные методы в оптимизации: монография. — М: Физматлит, 2009. — С. 384. — ISBN 978-5-9221-1101-0
Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы = Sieci neuronowe, algorytmy genetyczne i systemy rozmyte. — 2-е изд. — М: Горячая линия-Телеком, 2008. — С. 452. — ISBN 5-93517-103-1

Ссылки

Poli, R., Langdon, W. B., McPhee, N. F. A Field Guide to Genetic Programming. — Lulu.com, freely available from the internet, 2008. — ISBN 978-1-4092-0073-4
Special Interest Group for Genetic and Evolutionary Computation (former ISGEC) (англ.)
JAGA (Java API for Genetic Algorithms) — Extensible and pluggable open source API for implementing genetic algorithms and genetic programming applications in Java (англ.)
IlliGAL (Illinois Genetic Algorithms Laboratory) Home Page (англ.)
Evolutionary Computation Laboratory at George-Mason University (англ.)
GENITOR Research Group (CS, Colorado) (англ.)
Evolutionary and Adaptive Systems (EASy) at Sussex (англ.)
Genetic Algorithms Articles (англ.)
Evolutionary Algorithms Research Group at University of Dortmund (англ.)
Evolutionary Digest Archive (англ.)
GAUL: Genetic Algorithm Utility Library — нетривиальная обобщенная свободная реализация GA (англ.)
Очень большая подборка статей по использованию генетических алгоритмов в задачах многокритериальной оптимизации (англ.)
Genetic Algorithms in Ruby (англ.)
Lakhmi C. Jain; N.M. Martin Fusion of Neural Networks, Fuzzy Systems and Genetic Algorithms: Industrial Applications. — CRC Press, CRC Press LLC, 1998

dis.academic.ru

Генетический алгоритм - это... Что такое Генетический алгоритм?

История

Хотя Баричелли в своей работе 1963 года симулировал способности машины играть в простую игру,[8] искусственная эволюция стала общепризнанным методом оптимизации после работы Инго Рехенберга и Ханса-Пауля Швефеля в 1960-х и начале 1970-х годов двадцатого века – группа Рехенсберга смогла решить сложные инженерные проблемы согласно стратегиям эволюции.[9][10][11][12] Другим подходом была техника эволюционного программирования Лоренса Дж. Фогеля, которая была предложена для создания искусственного интеллекта. Эволюционное программирование первоначально использовавшее конечные автоматы для предсказывания обстоятельств, и использовавшее разнообразие и отбор для оптимизации логики предсказания. Генетические алгоритмы стали особенно популярны благодаря работе Джона Холланда в начале 70-х годов и его книге «Адаптация в естественных и искусственных системах» (1975)[13]. Его исследование основывалось на экспериментах с клеточными автоматами, проводившимися Холландом и на его трудах написанных в университете Мичигана. Холланд ввел формализованный подход для предсказывания качества следующего поколения, известный как Теорема схем. Исследования в области генетических алгоритмов оставались в основном теоретическими до середины 80-х годов, когда была наконец проведена Первая международная конференция по генетическим алгоритмам в Питтсбурге, Пенсильвания (США).

С ростом исследовательского интереса существенно выросла и вычислительная мощь настольных компьютеров, это позволило использовать новую вычислительную технику на практике. В конце 80-х, компания General Electric начала продажу первого в мире продукта, работавшего с использованием генетического алгоритма. Им стал набор промышленных вычислительных средств. В 1989, другая компания Axcelis, Inc. выпустила Evolver – первый в мире коммерческий продукт на генетическом алгоритме для настольных компьютеров. Журналист The New York Times в технологической сфере Джон Маркофф писал [14] об Evolver в 1990 году.

Описание алгоритма

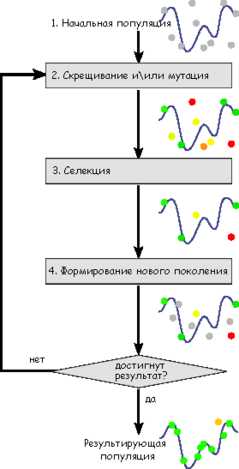Схема работы генетического алгоритма

Задача формализуется таким образом, чтобы её решение могло быть закодировано в виде вектора («генотипа») генов, где каждый ген может быть битом, числом или неким другим объектом. В классических реализациях ГА предполагается, что генотип имеет фиксированную длину. Однако существуют вариации ГА, свободные от этого ограничения.

нахождение глобального, либо субоптимального решения;
исчерпание числа поколений, отпущенных на эволюцию;
исчерпание времени, отпущенного на эволюцию.

Генетические алгоритмы служат, главным образом, для поиска решений в многомерных пространствах поиска.

Таким образом, можно выделить следующие этапы генетического алгоритма:

Задать целевую функцию (приспособленности) для особей популяции
Создать начальную популяцию

(Начало цикла)

Размножение (скрещивание)
Мутирование
Вычислить значение целевой функции для всех особей
Формирование нового поколения (селекция)
Если выполняются условия остановки, то (конец цикла), иначе (начало цикла).

Создание начальной популяции

Размножение (Скрещивание)

Мутации

Отбор

Критика

Повторная оценка функции приспособленности (фитнесс-функции) для сложных проблем, часто является фактором, ограничивающим использование алгоритмов искусственной эволюции. Поиск оптимального решения для сложной задачи высокой размерности зачастую требует очень затратной оценки функции приспособленности. В реальных задачах, таких как задачи структурной оптимизации, единственный запуск функциональной оценки требует от нескольких часов до нескольких дней для произведения необходимых вычислений. Стандартные методы оптимизации не могут справиться с проблемами такого рода. В таком случае, может быть необходимо пренебречь точной оценкой и использовать аппроксимацию пригодности, которая способна быть вычислена эффективно. Очевидно, что применение аппроксимации пригодности может стать одним из наиболее многообещающих подходов, позволяющих обоснованно решать сложные задачи реальной жизни с помощью генетических алгоритмов.

Генетические алгоритмы плохо масштабируемы под сложность решаемой проблемы. Это значит, что число элементов, подверженных мутации очень велико, если велик размер области поиска решений. Это делает использование данной вычислительной техники чрезвычайно сложным при решении таких проблем, как, например, проектирование двигателя, дома или самолёта. Для того чтобы сделать так, чтобы такие проблемы поддавались эволюционным алгоритмам, они должны быть разделены на простейшие представления данных проблем. Таким образом, эволюционные вычисления используются, например, при разработке формы лопастей, вместо всего двигателя, формы здания, вместо подробного строительного проекта и формы фюзеляжа, вместо разработки вида всего самолёта. Вторая проблема, связанная со сложностью, кроется в том, как защитить части, которые эволюционировали с высокопригодными решениями от дальнейшей разрушительной мутации, в частности тогда, когда от них требуется хорошая совместимость с другими частями в процессе оценки пригодности. Некоторыми разработчиками было предложено, что подход предполагающий развитие пригодности эволюционирующих решений смог бы преодолеть ряд проблем с защитой, но данный вопрос всё ещё остаётся открытым для исследования.

Решение является более пригодным лишь по сравнению с другими решениями. В результате условие остановки алгоритма неясно для каждой проблемы.

Во многих задачах генетические алгоритмы имеют тенденцию сходиться к локальному оптимуму или даже к спорным точкам, вместо глобального оптимума для данной задачи. Это значит, что они "не знают", каким образом пожертвовать кратковременной высокой пригодностью для достижения долгосрочной пригодности. Вероятность этого зависит от формы ландшафта пригодности: отдельные проблемы могут иметь выраженное направление к глобальному минимуму, в то время как остальные могут указывать направление для фитнесс-функции на локальный оптимум. Эту проблему можно решить использованием иной фитнесс-функции, увеличением вероятности мутаций, или использованием методов отбора, которые поддерживают разнообразие решений в популяции, хотя Теорема об отсутствии бесплатного обеда при поиске и оптимизации[15] доказывает, что не существует общего решения данной проблемы. Общепринятым методом поддержания популяционного разнообразия является установка уровневого ограничения на численность элементов с высоким сродством, которое снизит число представителей сходных решений в последующих поколениях, позволяя другим, менее сходным элементам оставаться в популяции. Данный приём, тем не менее, может не увенчаться успехом в зависимости от ландшафта конкретной проблемы. Другим возможным методом может служить простое замещение части популяции случайно сгенерированными элементами, в момент, когда элементы популяции становятся слишком сходны между собой. Разнообразие важно для генетических алгоритмов (и генетического программирования) потому, что перекрёст генов в гомогенной популяции не несёт новых решений. В эволюционных стратегиях и эволюционном программировании, разнообразие не является необходимостью, так как большая роль в них отведена мутации.

Применение генетических алгоритмов

Генетические алгоритмы применяются для решения следующих задач:

Оптимизация функций
Оптимизация запросов в базах данных
Разнообразные задачи на графах (задача коммивояжера, раскраска, нахождение паросочетаний)
Настройка и обучение искусственной нейронной сети
Задачи компоновки
Составление расписаний
Игровые стратегии
Теория приближений
Искусственная жизнь
Биоинформатика (фолдинг белков)

Пример тривиальной реализации на C++

Поиск в одномерном пространстве, без скрещивания.

Примечания

↑ Barricelli, Nils Aall (1954). «Esempi numerici di processi di evoluzione». Methodos: 45–68.
↑ Barricelli, Nils Aall (1957). «Symbiogenetic evolution processes realized by artificial methods». Methodos: 143–182.
↑ Fraser, Alex (1957). «Simulation of genetic systems by automatic digital computers. I. Introduction». Aust. J. Biol. Sci. 10: 484–491.
↑ Fraser Alex Computer Models in Genetics. — New York: McGraw-Hill, 1970. — ISBN 0-07-021904-4
↑ Crosby Jack L. Computer Simulation in Genetics. — London: John Wiley & Sons, 1973. — ISBN 0-471-18880-8
↑ 02.27.96 - UC Berkeley's Hans Bremermann, professor emeritus and pioneer in mathematical biology, has died at 69
↑ Fogel David B. (editor) Evolutionary Computation: The Fossil Record. — New York: IEEE Press, 1998. — ISBN 0-7803-3481-7
↑ Barricelli, Nils Aall (1963). «Numerical testing of evolution theories. Part II. Preliminary tests of performance, symbiogenesis and terrestrial life». Acta Biotheoretica (16): 99–126.
↑ Rechenberg Ingo Evolutionsstrategie. — Holzmann-Froboog, 1973. — ISBN 3-7728-0373-3
↑ Schwefel Hans-Paul Numerische Optimierung von Computer-Modellen (PhD thesis). — 1974.
↑ Schwefel Hans-Paul Numerische Optimierung von Computor-Modellen mittels der Evolutionsstrategie : mit einer vergleichenden Einführung in die Hill-Climbing- und Zufallsstrategie. — Birkhäuser, 1977. — ISBN 3-7643-0876-1
↑ Schwefel Hans-Paul Numerical optimization of computer models (Translation of 1977 Numerische Optimierung von Computor-Modellen mittels der Evolutionsstrategie. — Wiley, 1981. — ISBN 0-471-09988-0
↑ J. H. Holland. Adaptation in natural and artificial systems. University of Michigan Press, Ann Arbor, 1975.
↑ Markoff, John. What's the Best Answer? It's Survival of the Fittest, New York Times (29 августа 1990). Проверено 9 августа 2009.
↑ Wolpert, D.H., Macready, W.G., 1995. No Free Lunch Theorems for Optimisation. Santa Fe Institute, SFI-TR-05-010, Santa Fe.
↑ Steven S. Skiena. The Algorithm Design Manual. Second Edition. Springer, 2008.

Книги

Емельянов В. В., Курейчик В. В., Курейчик В. М. Теория и практика эволюционного моделирования. — М: Физматлит, 2003. — С. 432. — ISBN 5-9221-0337-7
Курейчик В. М., Лебедев Б. К., Лебедев О. К. Поисковая адаптация: теория и практика. — М: Физматлит, 2006. — С. 272. — ISBN 5-9221-0749-6
Гладков Л. А., Курейчик В. В., Курейчик В. М. Генетические алгоритмы: Учебное пособие. — 2-е изд. — М: Физматлит, 2006. — С. 320. — ISBN 5-9221-0510-8
Гладков Л. А., Курейчик В. В, Курейчик В. М. и др. Биоинспирированные методы в оптимизации: монография. — М: Физматлит, 2009. — С. 384. — ISBN 978-5-9221-1101-0
Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы = Sieci neuronowe, algorytmy genetyczne i systemy rozmyte. — 2-е изд. — М: Горячая линия-Телеком, 2008. — С. 452. — ISBN 5-93517-103-1

Ссылки

Poli, R., Langdon, W. B., McPhee, N. F. A Field Guide to Genetic Programming. — Lulu.com, freely available from the internet, 2008. — ISBN 978-1-4092-0073-4
Special Interest Group for Genetic and Evolutionary Computation (former ISGEC) (англ.)
JAGA (Java API for Genetic Algorithms) — Extensible and pluggable open source API for implementing genetic algorithms and genetic programming applications in Java (англ.)
IlliGAL (Illinois Genetic Algorithms Laboratory) Home Page (англ.)
Evolutionary Computation Laboratory at George-Mason University (англ.)
GENITOR Research Group (CS, Colorado) (англ.)
Evolutionary and Adaptive Systems (EASy) at Sussex (англ.)
Genetic Algorithms Articles (англ.)
Evolutionary Algorithms Research Group at University of Dortmund (англ.)
Evolutionary Digest Archive (англ.)
GAUL: Genetic Algorithm Utility Library — нетривиальная обобщенная свободная реализация GA (англ.)
Очень большая подборка статей по использованию генетических алгоритмов в задачах многокритериальной оптимизации (англ.)
Genetic Algorithms in Ruby (англ.)
Lakhmi C. Jain; N.M. Martin Fusion of Neural Networks, Fuzzy Systems and Genetic Algorithms: Industrial Applications. — CRC Press, CRC Press LLC, 1998

dic.academic.ru

Генетические алгоритмы в задаче оптимизации действительных параметров

2. Генетический алгоритм

2.1 История развития ГА

То, что называется стандартным генетическим алгоритмом, было впервые подробно описано и исследовано в работе де Джонга. Он проанализировал простую схему кодирования генов битовыми строками фиксированной длины и соответствующих генетических операторов, выполнил значительное количество численных экспериментов, сравнивая результаты с оценками, предсказываемыми теоремой Холланда. Важность этой работы определяется прежде всего ее строгим и системным характером, ясностью изложения и представления результатов, выбранным уровнем абстракции и упрощения, позволяющим избежать ненужной детализации. Кроме того, в этой работе подчеркивалась необходимость проведения дальнейших исследований более сложных схем представления генотипа и операций над ним. Последующие работы де Джонга продемонстрировали его интерес к проблемам, которые требовали менее структурированных схем представления гена.

Другой отправной точкой развития исследований по генетическим алгоритмам была публикация в 1975 году книги Холланда "AdaptationinNaturalandArtificialSystems". Эта книга заложила теоретический фундамент для работы де Джонга и всех последующих работ, математически обосновав идею близких подмножеств внутри генотипа, процессов гибели и селективного воспроизведения. Цели этой книги были достаточно широкими. Хотя доказательства основных утверждений были представлены для генов фиксированной длины и соответствующих простых операторов, это не ограничивало развитие представленного подхода на случаи более богатые по своим возможностям. Например, Холланд обсуждал возможность применения операторов внутрихромосомной дупликации, удаления и сегрегации участков хромосомы.

Тем не менее, большинство последующих исследователей восприняло теоретические результаты, содержащиеся в этих работах слишком буквально, и разрабатывали различные модификации стандартного генетического алгоритма, исследованного де Джонгом.

Только небольшая часть исследователей предприняла усилия по разработке альтернативных схем. Среди них выделяются детектор паттернов Кавичио, работа Франца по инверсии, игрок в покер Смита.

Исследование Кавичио, нацеленное на разработку детектора распознавания образов было одним из первых, использующих гены переменной длины. Расположенные на плоскости двоичные пиксели, способные различать свет и темноту, нумеровались и объединялись в подмножества, образующие разные детекторы, которые затем использовались некоторым априорно заданным алгоритмом для распознавания образов. При этом не возникало использование одного и того же пикселя дважды или не использования пикселя.

Смит использовал правила, оперирующие строками переменной длины, создавая модель машинного игрока в покер. Его LS-1 система использовала модифицированный кроссинговер, который располагал точки кроссинговера как на границах строк, кодирующих правила, так и внутри них. Он также включил в алгоритм оператор инверсии, надеясь, что это поможет более эффективно распределять правила внутри строки.

Несколько ранее Смита, Франц рассмотрел возможность смещения отдельных подмножеств битов внутри строки в своей работе по нелинейной оптимизации. К сожалению, из-за неудачного выбора вида функции оптимизации (которая легко оптимизировалась и простым генетическим алгоритмом без использования инверсии) не было показано реальных преимуществ нового алгоритма по сравнению с общепринятым. Тем не менее, эту работу можно считать одной из первых, начавших применение более гибких схем генетических алгоритмов.

Другие исследователи предложили различные модификации схем генетического переупорядочивания внутри строки, когда используется кроссинговер. Одновременно был проведен ряд исследований, развивавших теорию Холланда, и продемонстрированы новые генетические операторы. Однако вопрос об их преимуществах и тщательном сравнении со стандартным генетическим алгоритмом продолжает оставаться открытым.

2.2 Общий вид генетического алгоритма

Вначале ГА-функция генерирует определенное количество возможных решений. Задается функция оптимальности

, определяющая эффективность каждого найденного решения, для отслеживания выхода решения из допустимой области в функцию можно включить штрафной компонент. Каждое решение кодируется как вектор x, называемый хромосомой. Его элементы – гены, изменяющиеся в определённых позициях, называемых аллелями. Геном – совокупность всех хромосом. Генотип – значение генома.

Рис. 2. Структура хромосомы

Обычно хромосомы представляются в двоичном целочисленном виде или двоичном с плавающей запятой. В некоторых случаях более эффективно будет использование кода Грея (табл. 1), в котором изменение одного бита в любой позиции приводит к изменению значения на единицу. Для некоторых задач двоичное представление естественно, для других задач может оказаться полезным отказаться от двоичного представления. В общем случае выбор способа представления параметров задачи в виде хромосомы влияет на эффективность решения.

Таблица 1. Код Грея

Популяция – совокупность решений на конкретной итерации, количество хромосом в популяции

задаётся изначально и в процессе обычно не изменяется. Для ГА пока не существует таких же чётких математических основ, как для НС, поэтому при реализации ГА возможны различные вариации.

1. Начальная популяция

— конечный набор допустимых решений задачи. Эти решения могут быть выбраны случайным образом или получены с помощью вероятностных жадных алгоритмов. Как мы увидим ниже, выбор начальной популяции не имеет значения для сходимости процесса, однако формирование "хорошей" начальной популяции (например, из множества локальных оптимумов) может заметно сократить время достижения глобального оптимума. Это отличается от стандартных методов, когда начальное состояние всегда одно и то же.

2. Каждая хромосома популяции xiоценивается функцией эффективности

, и ей в соответствии с этой оценкой присваивается вероятность воспроизведения Pi.- Вычисление коэффициента выживаемости (fitness).

3. В соответствии с вероятностями воспроизведения Piгенерируется новая популяция хромосом, причём с большей вероятностью воспроизводятся наиболее эффективные элементы. Популяция следующего поколения в большинстве реализаций генетических алгоритмов содержит столько же особей, сколько начальная, но в силу отбора приспособленность в ней в среднем выше. Воспроизведение осуществляется при помощи генетических операторов кроссинговера (скрещивание) и мутации.

4. Если найдено удовлетворительное решение, процесс останавливается, иначе продолжается с шага 2.

Жизненный цикл популяции - это несколько случайных скрещиваний и мутаций, в результате которых к популяции добавляется какое-то количество новых индивидуумов.

2.3 Генетические операторы

Стандартные операторы для всех типов генетических алгоритмов это: селекция, скрещивание и мутация.

Оператор отбора [селекция]. Служит для создания промежуточной популяции

. В промежуточную популяцию копируются хромосомы из текущей популяции в соответствии с их вероятностью воспроизведения Pi. Существуют различные схемы отбора, самая популярная из них – пропорциональный отбор: .

Простейший пропорциональный отбор - рулетка (roulette-wheel selection, Goldberg, 1989c) - отбирает особей с помощью n "запусков" рулетки. Колесо рулетки содержит по одному сектору для каждого члена популяции. Размер i-ого сектора пропорционален соответствующей величине Ps(i). При таком отборе члены популяции с более высокой приспособленностью с большей вероятность будут чаще выбираться, чем особи с низкой приспособленностью.

mirznanii.com

Генетические алгоритмы в задаче оптимизации действительных параметров

Для устранения зависимости от положительных значений и влияний больших чисел используется масштабирование оценок или ранжирование.

При турнирной селекции формируется случайное подмножество из элементов популяции и среди них выбирается один элемент с наибольшим значением целевой функции. Турнирный отбор реализует n турниров, чтобы выбрать n особей. Каждый турнир построен на выборке k элементов из популяции, и выбора лучшей особи среди них. Наиболее распространен турнирный отбор с k=2.

Турнирная селекция имеет определенные преимущества перед пропорциональной, так как не теряет своей избирательности, когда в ходе эволюции все элементы популяции становятся примерно равными по значению целевой функции. Пропорциональный отбор не гарантирует сохранности лучших результатов, достигнутых в какой-либо популяции, и для преодоления такого явления используется элитный отбор - несколько лучших индивидуумов переходят в следующее поколение без изменений, не участвуя в кроссинговерeи отборе.

Операторы селекции строятся таким образом, чтобы с ненулевой вероятностью любой элемент популяции мог бы быть выбран в качестве одного из родителей. Более того, допускается ситуация, когда оба родителя представлены одним и тем же элементом популяции.

В любом случае каждое следующее поколение будет в среднем лучше предыдущего. Когда приспособленность индивидуумов перестает заметно увеличиваться, процесс останавливают и в качестве решения задачи оптимизации берут наилучшего из найденных индивидуумов.

Отбор в генетическом алгоритме тесно связан с принципами естественного отбора в природе следующим образом:

Таблица

Воспроизведение. Служит для создания следующей популяции на основе промежуточной

при помощи операторов кроссинговера и мутации, которые имеют случайный характер. Каждому элементу промежуточной популяции , если надо подбирается партнёр и вновь созданная хромосома помещается в новую популяцию.

Оператор кроссинговера (в литературе по генетическим алгоритмам также употребляется название кроссовер или скрещивание ) - операция, при которой две хромосомы обмениваются своими частями. Производит обмен генетического материала между родителями для получения потомков. Кроссинговер смешивает "генетический материал" двух родителей, причем можно ожидать, что приспособленность родителей выше средней в предыдущем поколении, так как они только что прошли очередной раунд борьбы за выживание. Это аналогично соперничеству настоящих живых существ, где лишь сильнейшим удается передать свои (предположительно хорошие) гены следующему поколению. Важно, что кроссинговер может порождать новые хромосомы, ранее не встречавшиеся в популяции. Простейший одноточечный кроссинговер (рис. 3) производит обмен частями, на которые хромосома разбивается точкой кроссинговера. Одноточечный кроссовер работает следующим образом. Сначала, случайным образом выбирается одна из l-1 точек разрыва. Точка разрыва - участок между соседними битами в строке. Обе родительские структуры разрываются на два сегмента по этой точке. Затем, соответствующие сегменты различных родителей склеиваются и получаются два генотипа потомков. Двухточечный кроссинговер обменивает кусок строки, попавшей между двумя точками. Предельным случаем является равномерный кроссинговер, в результате которого все биты хромосом обмениваются с некоторой вероятностью. Этот оператор служит для исследования новых областей пространства и улучшения существующих (приспособление).

Рис. 3. Кроссинговер

Все типы кроссинговера обладают общим свойством: они контролируют баланс между дальнейшим использованием уже найденных хороших подобластей пространства и исследованием новых подобластей. Достигается это за счет неразрушения общих блоков внутри хромосом-родителей, сохраняющем "хорошие" паттерны, и одновременном исследовании новых областей в результате обмена частями строк (хромосом). Совместное использование отбора и кроссинговера приводит к тому, что области пространства, обладающие лучшей средней оптимальностью, содержат больше элементов популяции, чем другие. Таким образом, эволюция популяции направляется к областям, содержащим оптимум с большей вероятностью, чем другие.

Оператор мутации [ Случайное изменение одной или нескольких позиций в хромосоме] К каждому биту хромосомы с небольшой вероятностью

применяется мутация – т.е. бит (аллель) изменяет значение (для двоичного представления - на противоположный) - (рис. 4). Мутация нужна для расширения пространства поиска (исследование) и предотвращения невосстановимой потери бит в аллелях. Мутации вносят новизну и предотвращают невосстановимую потерю аллелей в определенных позициях, которые не могут быть восстановлены кроссинговером, тем самым ограничивая преждевременное сжатие пространства поиска. Циклическое применение последовательности отбор-мутация направляет эволюцию элементов популяции к наиболее хорошим точкам пространства поиска.

Рис. 4. Мутация

Существует также оператор воспроизведения, называемый инверсией, который заключается в реверсировании бит между двумя случайными позициями, однако для большинства задач он не имеет практического смысла и поэтому неэффективен.

Рис. 5. Блок-схема генетического алгоритма

Работа ГА представляет собой итерационный процесс, который продолжается до тех пор, пока не выполнятся заданное число поколений или какой-либо иной критерий останова. На каждом поколении ГА реализуется отбор пропорционально приспособленности, кроссовер и мутация. Блок-схема генетического алгоритма достаточно проста (рис.5)

2.4. Достоинства и недостатки стандартных и генетических методов

Генетический алгоритм - новейший, но не единственно возможный способ решения задач оптимизации. С давних пор известны два основных пути решения таких задач - переборный и локально-градиентный. У этих методов свои достоинства и недостатки, и в каждом конкретном случае следует подумать, какой из них выбрать.

Рис.

Рассмотрим достоинства и недостатки стандартных и генетических методов на примере классической задачи коммивояжера. Суть задачи состоит в том, чтобы найти кратчайший замкнутый путь обхода нескольких городов, заданных своими координатами. Оказывается, что уже для 30 городов поиск оптимального пути представляет собой сложную задачу, побудившую развитие различных новых методов (в том числе нейросетей и генетических алгоритмов).

Каждый вариант решения (для 30 городов) - это числовая строка, где на j-ом месте стоит номер j-ого по порядку обхода города. Таким образом, в этой задаче 30 параметров, причем не все комбинации значений допустимы. Естественно, первой идеей является полный перебор всех вариантов обхода.

Рис

Переборный метод наиболее прост по своей сути и тривиален в программировании. Для поиска оптимального решения (точки максимума целевой функции) требуется последовательно вычислить значения целевой функции во всех возможных точках, запоминая максимальное из них. Недостатком этого метода является большая вычислительная стоимость. В частности, в задаче коммивояжера потребуется просчитать длины более 1030 вариантов путей, что совершенно нереально. Однако, если перебор всех вариантов за разумное время возможен, то можно быть абсолютно уверенным в том, что найденное решение действительно оптимально.

Рис.

Второй популярный способ основан на методе градиентного спуска. При этом вначале выбираются некоторые случайные значения параметров, а затем эти значения постепенно изменяют, добиваясь наибольшей скорости роста целевой функции. Достигнув локального максимума, такой алгоритм останавливается, поэтому для поиска глобального оптимума потребуются дополнительные усилия.

Градиентные методы работают очень быстро, но не гарантируют оптимальности найденного решения. Они идеальны для применения в так называемых унимодальных задачах, где целевая функция имеет единственный локальный максимум (он же - глобальный). Легко видеть, что задача коммивояжера унимодальной не является.

Рис.

Типичная практическая задача, как правило, мультимодальна и многомерна, то есть содержит много параметров. Для таких задач не существует ни одного универсального метода, который позволял бы достаточно быстро найти абсолютно точное решение.

Однако, комбинируя переборный и градиентный методы, можно надеяться получить хотя бы приближенное решение, точность которого будет возрастать при увеличении времени расчета.

mirznanii.com