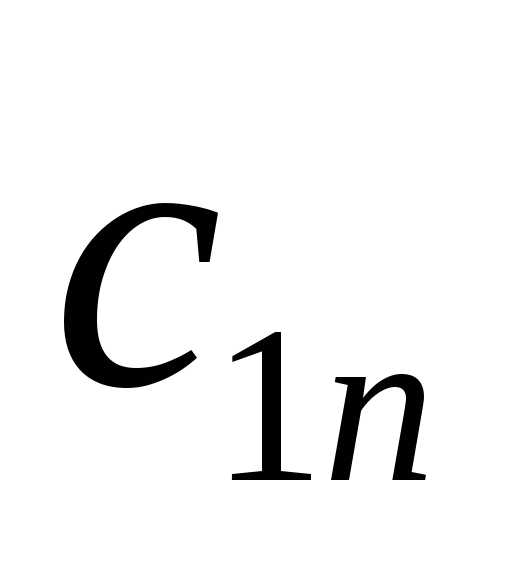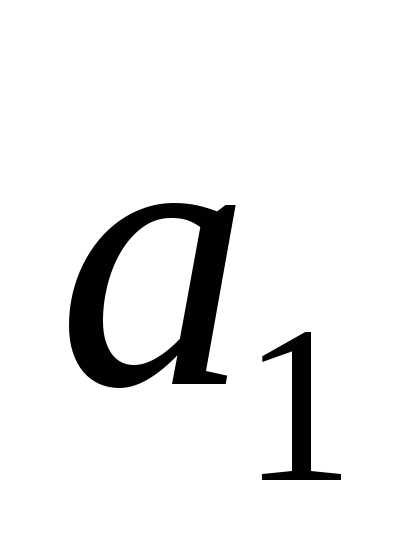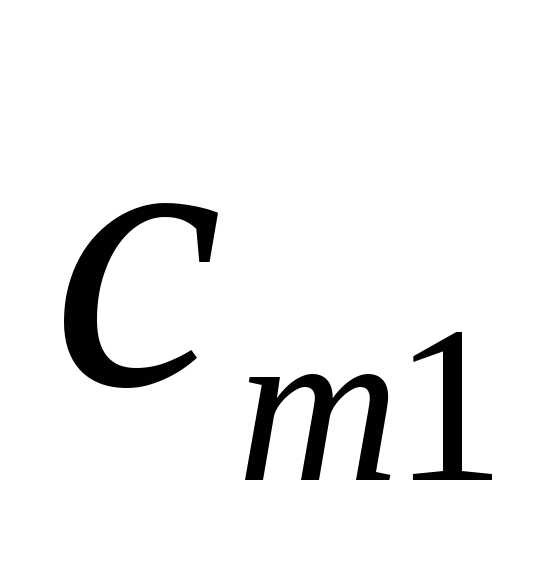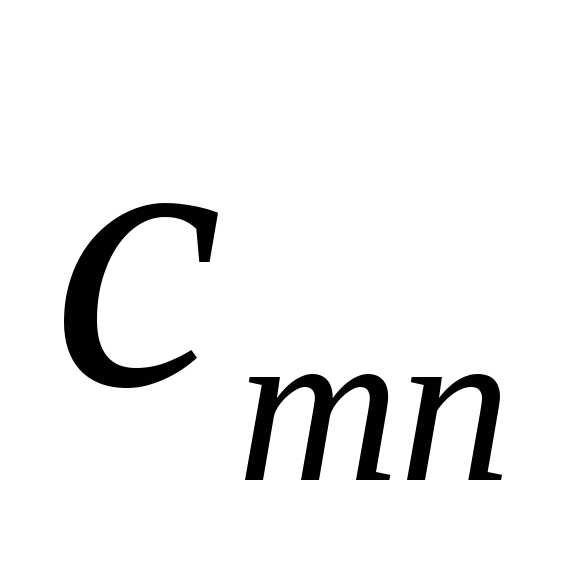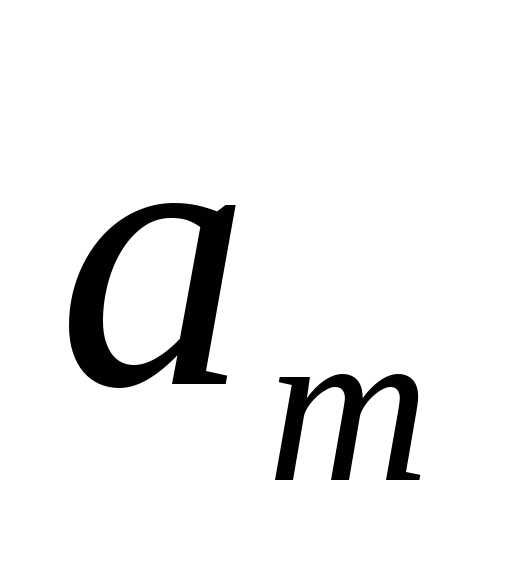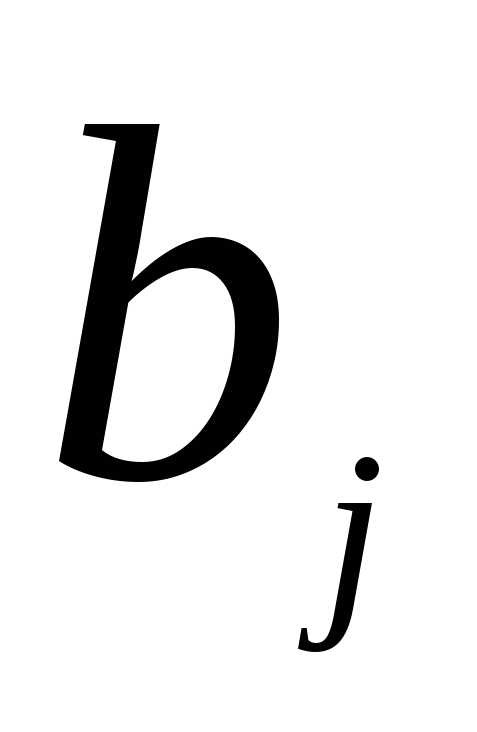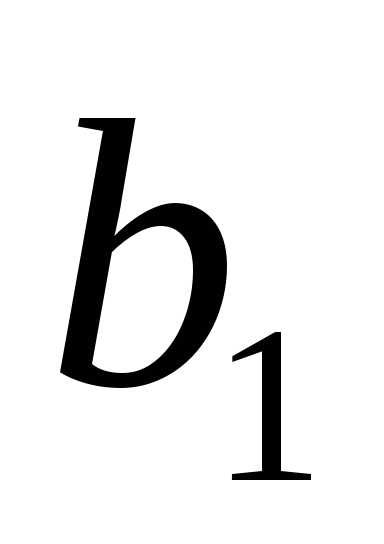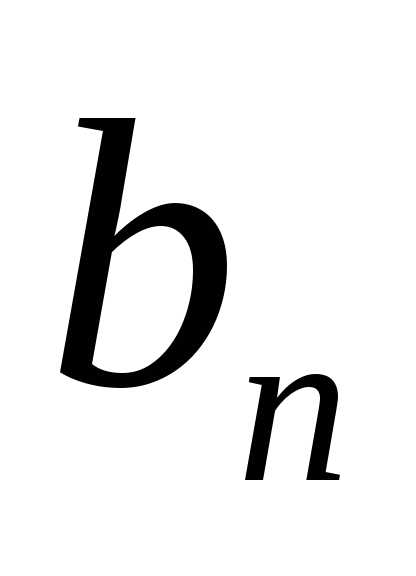2. Постановка задачи лп. Различные формы задач лп и их эквивалентность. Модель задачи лп для оптимизации поставок при разыгранном спросе
АЛГОРИТМ МНОГОКРИТеРИАЛьНОГО РАСПРеДеЛеНИЯ
- Технологии
- Промышленная инженерия
- Управление цепями поставок
Related documents
РЕЗЮМЕ - Arabinform
Обоснование профиля «Логистика и управление цепями поставок
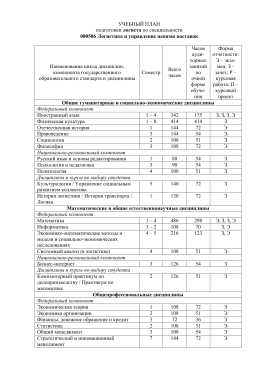
УЧЕБНЫЙ ПЛАН логиста Часов
Производительность труда в ритейле аналитика
Особенности решения транспортной задачи с помощью
базы оборудования
Синчук Н.В.
Жером Ферье, Международный газовый союз (МГС): «Газовые
С чего начать оптимизацию цепочки поСтавок
Действенное видение
Скачать advertisement StudyDoc © 2018 DMCA / GDPR Пожаловатьсяstudydoc.ru
Алгоритм многокритериального распределения товаров в складской сети (Часть 2)
Напомним, что в первой части статьи было принято, что для рассматриваемого звена складской сети распределение товаров предусматривает поставку от центрального склада (ЦС) на региональные склады (РС), а затем от РС к клиентам/магазинам, известны законы распределения вероятностей спроса от клиентов/магазинов. В формате предлагаемого алгоритма будет задан интервал планирования поставок. Для удобств изложения далее принято, что в качестве такого интервала планирования поставок для звена «РС–магазины» выбрана одна неделя (7 дней). На интервале
планирования поставок будет разыгрываться выборка для возможной реализации случайного спроса магазинов. При этом размеры заказов для анализируемых альтернатив в формате алгоритма оптимизации будут определяться как решение соответствующей задачи линейного программирования (ЛП).
Как было отмечено в первой части статьи, для каждого разыгранного сценария спроса на интервале планирования надо будет оценивать/сравнивать эффективность анализируемых альтернатив, связанных с организацией поставок, причем с учетом показателей заданных частных критериев. Представим соответствующие понятия.
Альтернативные решения по организации поставок. Перечень анализируемых альтернатив по организации поставок (из которых надо найти наилучшую) формирует лицо, принимающее решение (ЛПР). В предложенной модели принято, что ЛПР задает структуру таких альтернатив таким образом, что они отличаются друг от друга следующими атрибутами: либо количеством поставок от ЦС к РС в течение недели, либо выбором конкретных дней (в течение недели) для реализации указанных поставок. В частности понятно, что ЛПР может рассматривать альтернативу с одной поставкой в неделю (естественно, с поставкой в первый же день, чтобы не допускать дефицита).
ЛПР также может рассматривать альтернативыс двумя поставками в неделю (они, естественно, будут отличаться выбором соответствующих дней для реализации поставок). Можно рассматривать альтернативы с тремя поставками в неделю и т.д. Каждой альтернативе будут соответствовать свои дни поставок и их оптимальные объемы, которые будут найдены в формате представленной выше модели ЛП для разыгранных значений спроса. Понятно, что для альтернативных решений по организации поставок будут отличаться и показатели задаваемых частных критериев. Это позволит сравнивать указанные альтернативы по их эффективности, используя методы теории многокритериальной оптимизации.
Частные критерии для оценки эффективности работы сети. Требуемые частные критерии в формате предложенного алгоритма оптимизации также задает ЛПР. Они будут отражать показатели, характеризующие эффективность соответствующего бизнеса (например, средняя величина денежных средств, которые заморожены в запасах; средние затраты на хранение, поставки товара и т.д.). Разработанная и представленная выше модель задачи ЛП позволит для разыгрываемых значений спроса на интервале планирования сформировать наборы требуемых показателей частных критериев в формате каждой альтернативы. Это даст возможность (применительно к выборке на основе имитационной модели) ранжировать указанные альтернативы с учетом процедур имитации на всем горизонте моделирования. Более того, такие показатели также позволят определить наилучшую стратегию поставок (в какие моменты времени подавать заказы на ЦС и в каких объемах). Указанные параметры наилучшей стратегии можно будет определить на основе выборки по имитационной модели для всего горизонта моделирования. Кроме того, вычислительные процедуры, реализованные для данной модели (при разыгрывании соответствующей имитационной модели работы складской сети) дадут статистическую информацию для определения страхового запаса. Отличительной особенностью модели является то, что стоимостные критерии (издержки поставок и хранения) учитываются как на этапе оптимизации целевой функции (см. соотношение (6) в части 1), так и на этапе выбора наилучшего решения совместно с другими возможно заданными частными критериями (не относящимися к целевой функции, причем размерность таких дополнительных частных критериев может быть любой) на последующих шагах алгоритма выбора наилучшей стратегии. Теперь можно представить алгоритм распределения товаров в такой сети.
Алгоритм рационального распределения товаров в складской сети при многих критериях принятия решения
Для удобств изложения представим формат соответствующего алгоритма для звена «РС–магазины». Предлагаемый в этом исследовании алгоритм реализуется в виде двух этапов (I и II) соответствующих процедур. На этапе I находится наилучшая (среди формализованных) стратегия принятия решений (т.е. в какие моменты времени подавать заказы на ЦС и в каких объемах) для обеспечения эффективной работы звена «РС–клиенты/магазины».
При этом понятие наилучшей стратегии включает оптимизацию по многим частным критериям/показателям с учетом случайного спроса от клиентов/магазинов. На этапе II анализируется соответствующая наилучшая стратегия принятия решений для обеспечения эффективной работы звена «ЦС–РС».
Как было показано выше, структурные схемы для рассматриваемых двух звеньев модели совпадают (по своей структуре). Будут отличаться параметры соответствующего случайного спроса (для звена «ЦС–РС» случайный спрос будет более прогнозируемым, т.е. с меньшим разбросом или уровнем неопределенности). Кроме того, может быть выбран иной интервал планирования решений (например, месяц) и могут быть наложены свои ограничения на допустимые параметры стратегий поставок. Поэтому далее алгоритм рационального распределения товаров в складской сети формализуется и строится так, чтобы процедуры принятия решений для этапа I могли быть использованы и при выборе решений на этапе II. Специальные модификации такого алгоритма могут потребоваться, если дополнительно понадобится учесть риски поставок на ЦС от поставщиков товара. В представленной модели такая ситуация не рассматривается. Таким образом, далее достаточно представить процедуры для этапа I.
Алгоритм I этапа процедур выбора наилучшего решения для планирования заказов на поставки от ЦС, необходимых для покрытия случайного спроса от клиентов/магазинов, реализуется в виде двух стадий соответствующих процедур выбора решений. Первая стадия таких процедур связана с моделированием случайного спроса от клиентов/магазинов и анализом требуемых показателей эффективности (показатели частных критериев) на каждом интервале планирования поставок от ЦС к РС (неделя) для анализируемых альтернатив. Такие процедуры будут реализованы (на первой стадии) для всего горизонта моделирования.
Вторая стадия указанных процедур связана с нахождением наилучшего решения/альтернативы применительно ко всему горизонту моделирования (с использованием конкретного критерия выбора, учитывающего показатели всех частных критериев в задаче многокритериальной оптимизации). Соответствующий результат будет определять как конкретные дни подачи заказов от РС на ЦС, так и их объемы.Кроме того, на этой стадии процедур оптимизации будут найдены наилучшие размеры страхового запаса на РС для покрытия случайного дефицита и другие показатели, интересные для ЛПР. Шаги соответствующего алгоритма представлены ниже (по указанным двум стадиям).
Первая стадия процедур выбора решения
Шаг 1.1. Задать интервал времени планирования, для которого надо формализовать альтернативы, соотносимые с принятием решений о покрытии случайного спроса клиентов/магазинов за счет поставок с ЦС (здесь, как было отмечено выше, неделя).
Шаг 1.2. Задать предварительный горизонт планирования (в виде количества недель для моделирования процедур поставок) для определения наилучшего решения.
Шаг 1.3. Задать законы распределения вероятностей для случайного спроса (на основе имеющихся статистических материалов) на каждый день для анализируемого интервала времени планирования (неделя) от клиентов/магазинов.
Шаг 1.4. Задать формат анализируемых альтернатив, характеризующих структуру моментов времени подачи заказов на ЦС для покрытия ожидаемого спроса от магазинов (такой формат может быть любым, в частности далее будут указаны выбранные дни для поставок от ЦС на РС в течение недели).
Шаг 1.5. Задать частные критерии/показатели (и направление их оптимизации), по которым будут оцениваться анализируемые альтернативы, для выбора наилучшей. Определить веса важности (wi) частных критериев по методу аналитической иерархии (на основе попарных сравнений ).
Замечание. На этом шаге задается множество всех частных критериев, а также определяются их веса важности wi. При этом веса w1–w3 указанных выше стоимостных частных критериев, для которых априори принято их наличие в задаче оптимизации, учитываются в целевой функции модели ЛП (см. (6) в части 1) для минимизации суммарных издержек работы сети (с учетом предпочтений ЛПР). Все множество частных критериев (и веса их важности) будут учтены на шагах 1.9 и 1.10.
Шаг 1.6. Задать критерий выбора (по желанию ЛПР) для решения рассматриваемой задачи многокритериального выбора наилучшего альтернативного решения, определяющего структуру моментов времени подачи заказов на ЦС для покрытия случайного спроса клиентов/ магазинов. Формат соответствующего критерия выбора может быть любым (из методов оптимизации по многим критериям с учетом положений, обеспечивающих отсутствие воздействия различных феноменов неадекватного выбора [2, 3]). При этом процедуры оптимизации должны учитывать найденные веса частных критериев на шаге 1.5, чтобы адаптировать выбор к предпочтениям ЛПР.
Шаг 1.7. Построение экономико-математической модели ЛП, минимизирующей суммарные издержки при поставках для разыгрываемого на следующем шаге спроса (в формате имитационной модели), для оптимизации объемов поставок в магазины.Для учета предпочтений ЛПР такая модель также должна использовать веса частных критериев, показатели которых присутствуют в целевой функции. В последующих шагах такая модель будет использована для сравнения альтернатив при случайном спросе, разыгрываемом по методу Монте-Карло.
Замечание. Указанная экономико-математическая модель была представлена в первой части статьи. Искомыми переменными являются требуемые объемы поставок от ЦС к РС для покрытия спроса с минимальными издержками (с учетом предпочтений ЛПР к важности отдельных слагаемых, что учитывается весами wi, найденными на шаге 1.5).
Шаг 1.8. Последовательное моделирование случайных заказов от клиентов/магазинов по дням на каждом очередном интервале времени (неделя) для заданного горизонта моделирования с использованием метода имитационного моделирования (Монте-Карло).
Шаг 1.9. Для разыгранных случайных объемов заказов определяются показатели частных критериев применительно к каждой альтернативе, задающей свои моменты времени подачи заказов на ЦС (в течение недели) на каждом очередном интервале планирования.
Шаг 1.10. Формализация задаваемого ЛПР критерия выбора, позволяющего обеспечить адекватность решения предпочтениям ЛПР применительно к заданным частным критериям для рассматриваемой задачи. Ранжирование анализируемых альтернатив по результатам разыгранного спроса от клиентов/магазинов на каждом очередном интервале планирования.
Замечание 1. Ранжирование альтернатив реализуется по формализованному критерию выбора, с учетом найденных ранее весов частных критериев.
Замечание 2. Шаги 1.8–1.10 реализуются отдельно для каждой очередной недели планирования поставок с ЦС, пока не будет покрыт требуемый горизонт моделирования.
Вторая стадия процедур выбора решения
Шаг 2.1. Выбор наилучшей альтернативы для моментов подачи заказов на ЦС (чтобы обеспечить покрытие случайного недельного спроса) по результатам имитационной модели для всего горизонта моделирования, обеспечивая, по возможности, адекватность такого выбора предпочтениям ЛПР в формате заданных частных критериев. При этом можно различать следующие подходы:
1. Вероятностный — по частоте или вероятности быть наилучшей среди анализируемых альтернатив на всем горизонте моделирования. Иными словами, выбирается альтернатива, у которой вероятность быть приоритетной на всем промежутке моделирования наибольшая.
2. Логистический — по средним ожидаемым значениям показателя критерия выбора, соотносимым с заданными частными критериями, характеризующими моделируемые издержки. Иначе говоря, альтернативам ставится в соответствие средний ожидаемый (по всей выборке) показатель критерия выбора. Выбирается та альтернатива, у которой такой показатель будет наилучшим.
Шаг 2.2. Формализация параметров объемов поставок в требуемые моменты времени для выбранной на шаге 2.1 наилучшей альтернативы, определяющей моменты подачи заказов на ЦС. Это реализуется на основе аппарата соответствующих доверительных интервалов по имеющимся результатам разыгранного спроса от клиентов/магазинов в имитационной модели. Имеющиеся результаты моделирования, полученные на основе разыгрываемого спроса от магазинов, позволяют реализовать процедуры этого шага методами математической статистики по результатам имеющейся выборки.
Шаг 2.2.А. На основе разыгранного спроса находим выборочное среднее для объема требуемых поставок в требуемые (для наилучшей альтернативы) моменты времени.
Шаг 2.2.B. По указанной выборке находим среднее квадратическое отклонение (СКО ) для объемов поставок в требуемые моменты времени (либо используем известное генеральное СКО, если оно априори известно и задается при моделировании).
Шаг 2.2.С. По формулам теории вероятностей и математической статистики строим доверительные интервалы для размеров поставок в требуемые моменты времени. При этом используется желаемый
для ЛПР коэффициент доверия (как вероятность отсутствия дефицита для покрываемого спроса от клиентов/магазинов).
Шаг 2.2.D. Верхняя оценка таких интервалов (после округления до целого значения) укажет требуемые объемы заказов на ЦС для поставок в конкретные моменты времени, чтобы покрывать спрос.
Шаг 2.3. Найденные на предыдущем шаге требуемые объемы заказов применительно к выбранной на шаге 2.1 альтернативе, характеризующей наилучшую структуру моментов времени подачи заказов на ЦС для покрытия ожидаемого спроса, позволяют окончательно формализовать наилучшую стратегию поставок (на интервале планирования).
Шаг 2.4. Выбранная и формализованная на шаге 2.3 стратегия анализируется с помощью имитационной модели: для каждой реализации случайного спроса на интервале принятия решений находится возможный дефицит (по имеющейся выборке или в формате нового моделирования случайного спроса и работы системы для горизонта моделирования). Это позволит далее определить страховой запас и другие параметры, интересующие ЛПР.
Шаг 2.5. Определение страхового запаса для РС применительно к выбранной наилучшей альтернативе подачи заказов на ЦС для организации поставок клиентам/магазинам.
Эта процедура предполагает построение соответствующих доверительных интервалов для величины дефицита по выборке имитационной модели (испытаний выбранной стратегии).
Шаг 2.6. Определение возможных дополнительных показателей (как уже отмечалось выше, по желанию ЛПР), отражающих эффективность и/или другие параметры работы системы, поскольку это позволяет обработка выборки имеющихся результатов моделирования. В частности таким показателем может
быть требуемая вместимость склада (применительно к моделируемому товару).
Понимая структуру наилучшей стратегии подачи заказов от региональных центров на ЦС (в какие моменты времени и в каких объемах подавать такие заказы), а также требуемые объемы запасов (включая страховые запасы), можно перейти ко второму этапу процедур оптимизации, чтобы определить наилучшую стратегию поставок на ЦС. Действительно, второй этап процедур оптимизации соотносится с определением параметров наилучшей стратегии подачи заказов от ЦС к поставщикам, чтобы обеспечить запасы для покрытия спроса, который будет формироваться в звене «ЦС–РС».Как уже было отмечено выше, структура модели такого звена идентична структуре рассмотренной выше модели «РС–клиенты /магазины».
Таким образом, на указанном этапе процедур принятия решений можно использовать тот же алгоритм, который был приведен выше, поэтому описание таких процедур можно опустить. Заметим, что в ситуации, когда при анализе этого звена ЛПР сочтет необходимым учитывать риски поставок на ЦС от поставщиков, потребуется модификация представленного алгоритма, что может быть предметом отдельного исследования. Чтобы привести пример практической реализации процедур разработанного алгоритма в формате конкретной модели распределения товаров в складской сети, требуется предоставить большой объем соответствующих материалов (разыгрываются выборки случайного спроса для горизонта моделирования, реализуется имитационная модель работы Складской сети, определяется наилучшая альтернатива по распределению товаров и т.д.).Поэтому такие процедуры в формате предложенного алгоритма будут проиллюстрированы в отдельной работе.
Разработанный авторами подход к принятию таких решений представляется впервые и отличается следующими атрибутами:
1. Предложен подход к формированию альтернатив (для последующего выбора наилучшего решения), характеризующих структуру моментов времени подачи заказов с регионального центра на ЦС для покрытия случайного спроса от клиентов/ магазинов.
2. Разработана линейная оптимизационная модель распределения товаров в складской сети для звена «РС–клиенты/магазины» применительно к разыгранному спросу, формат которой можно использовать для имитационного моделирования процессов при случайном спросе.
3. Используются процедуры метода имитационного моделирования (Монте-Карло) для разыгрывания случайного спроса на заданном горизонте моделирования работы соответствующих звеньев складской сети.
4. Разработана методика, позволяющая в формате процедур принятия решений определять параметры анализируемых альтернатив (соответствующие моменты времени и объемы поставок на РС с ЦС), поскольку такие решения должны приниматься до покрытия случайного спроса от магазинов.
5. Представлены шаги алгоритма выбора по многим критериям наилучшей стратегии для поставок товара с ЦС на РС, позволяющего учитывать как специфику рассматриваемой задачи оптимизации, так и предпочтения ЛПР. Выбор наилучшего решения может быть реализован на основе любого традиционного для теории критерия (что соответствует синтезу процедур метода аналитической иерархии с традиционными для теории процедурами оптимизации).
В отдельной статье авторы представят материалы, иллюстрирующие процедуры практической реализации предложенного алгоритма распределения товаров в складской сети.
Геннадий Бродецкий, Денис Гусев, Екатерина Кулешова, www.logistika-prim.ru
www.logists.by
5. Транспортная задача лп
5.1. Постановка задачи
Классическая транспортная задача ЛП формулируется следующим образом. Имеется m пунктов производства (поставщиков) и n пунктов потребления (потребителей) однородного продукта. Заданы величины:
- объем производства (запас) i-го поставщика,
;
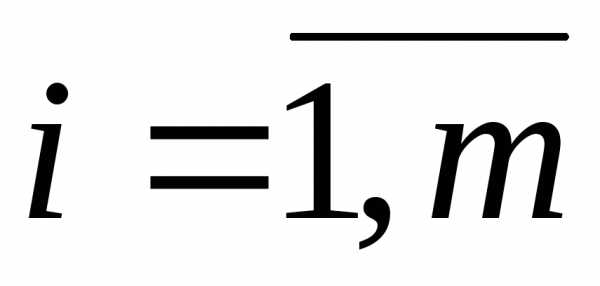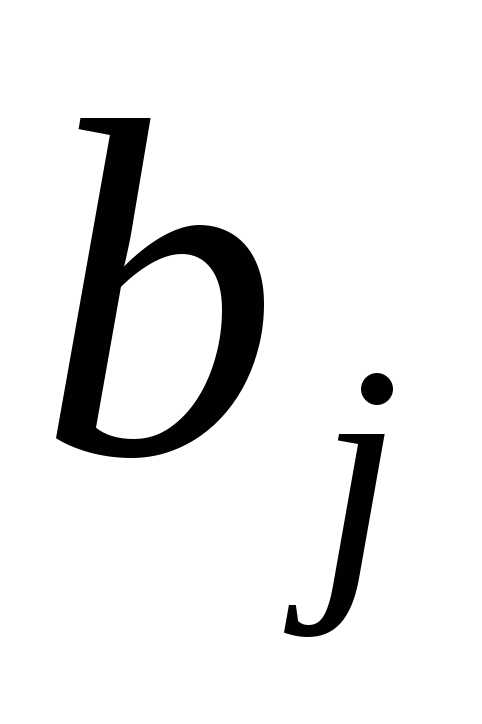- объем потребления (спрос) j-го потребителя,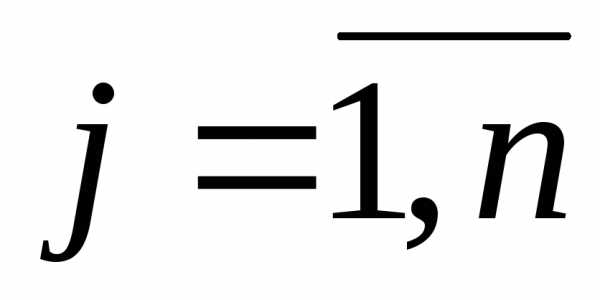 
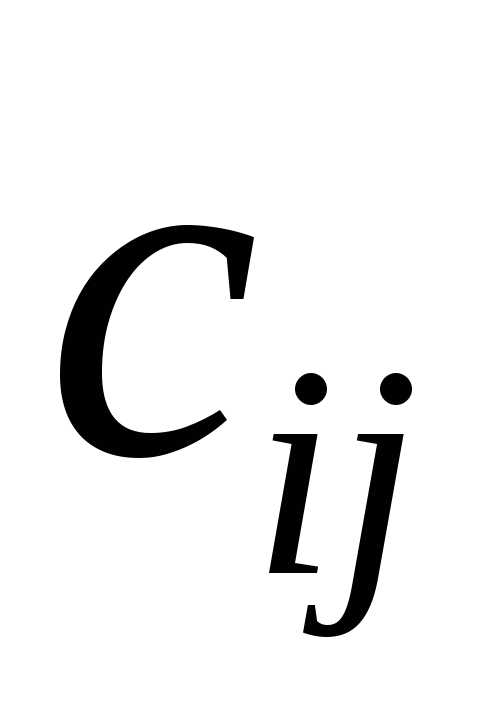- стоимость перевозки (транспортные затраты) единицы продукции от i-го поставщика к j-му потребителю.
Требуется составить такой план перевозок, при котором спрос всех потребителей был бы выполнен, и при этом общая стоимость всех перевозок была бы минимальна [1,3].
Транспортная задача, в которой суммарные запасы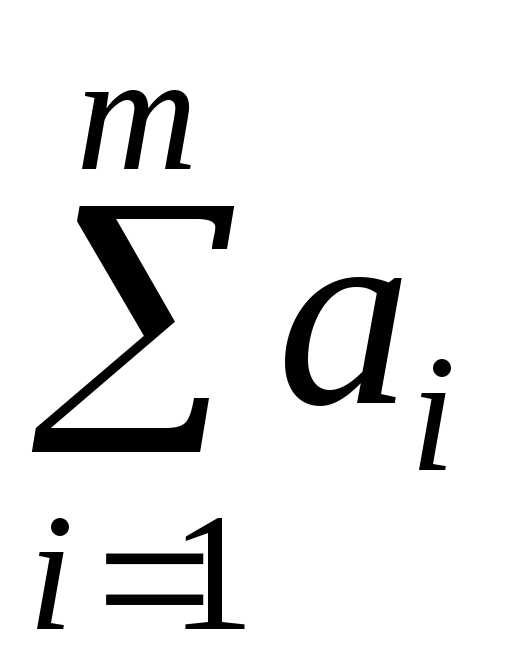 
и суммарные потребности
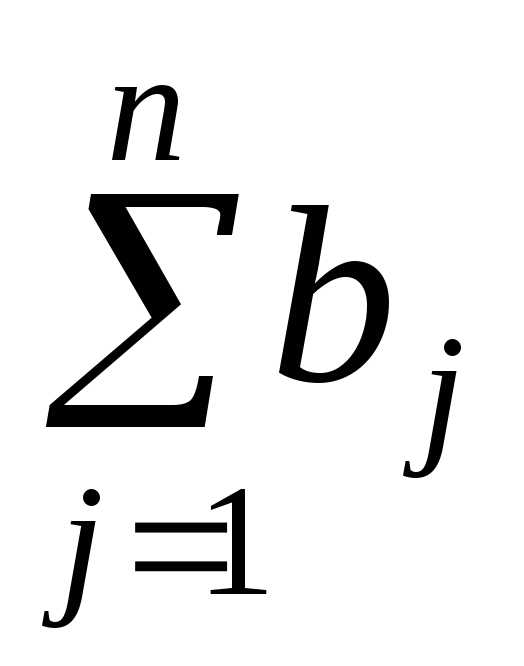совпадают, называется закрытой моделью; в противном случае – открытой. Открытая модель решается приведением к закрытой модели.
Математическая закрытая модель транспортной задачи имеет вид
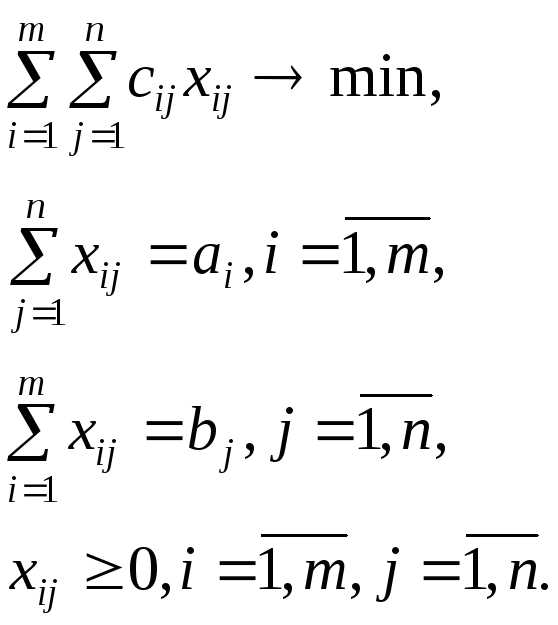
В случае, когда суммарные запасы превышают суммарные потребности, то есть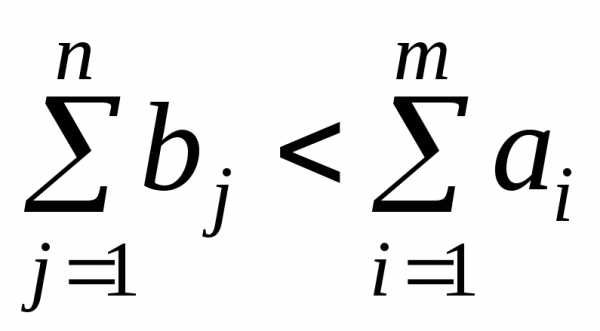 
, вводится фиктивныйn+1 потребитель, потребности которого 
.
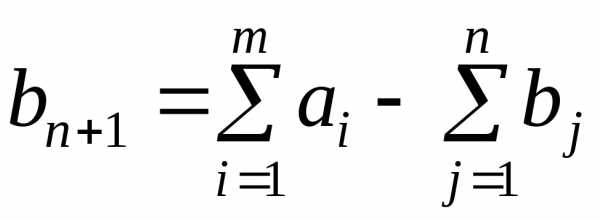В случае, когда суммарные потребности превышают суммарные запасы, то есть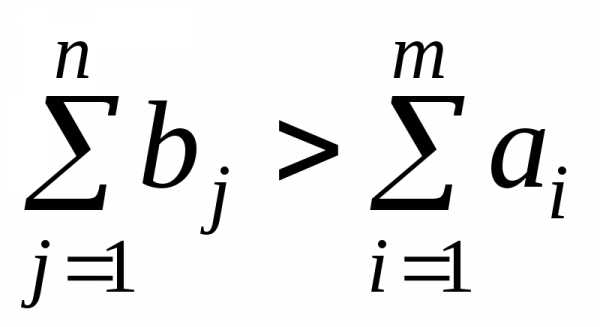 
, вводится фиктивныйm+1 поставщик, запасы которого .
Стоимость перевозки единицы груза как до фиктивного потребителя, так и стоимость перевозки единицы груза от фиктивного поставщика полагают равными нулю, так как груз в обоих случаях не перевозится.
Прежде чем решать транспортную задачу, необходимо проверить, к какой модели она принадлежит, и если необходимо, то привести ее к закрытой модели.
5.2. Построение опорного плана транспортной задачи
Методы решения транспортной задачи сводятся к простым операциям с транспортной таблицей, которая имеет вид:
| 1 | … | n | | |
| 1 | | … | | |
| … | … | … | … | … |
| m | | … | | |
| | | … | | = |
Базисными клетками транспортной таблицы являются клетки с отличными от нуля положительными перевозками, остальные клетки – свободные. Базисные клетки образуют опорный план транспортной задачи, еcли выполняются два условия:
сумма перевозок в каждой строке равна запасу 
в данной строке;
сумма перевозок в каждом столбце равна соответствующему спросу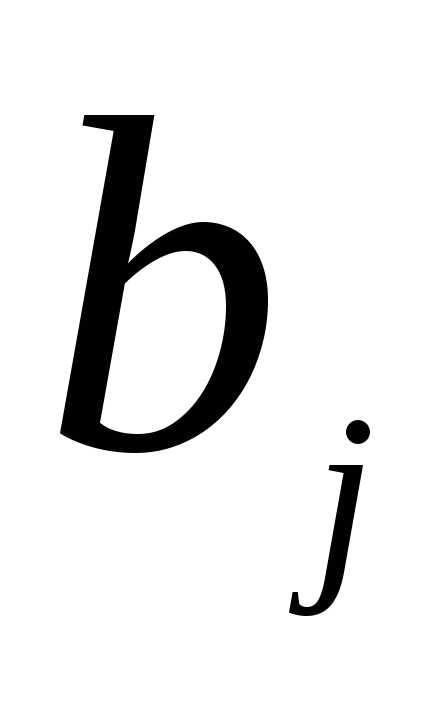 
.
Опорный план транспортной задачи содержит не более отличных от нуля перевозок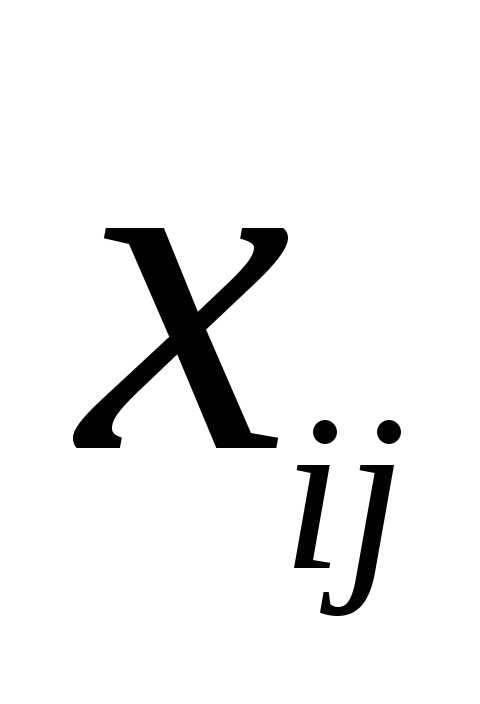
.
Опорный план называется вырожденным, если число ненулевых перевозок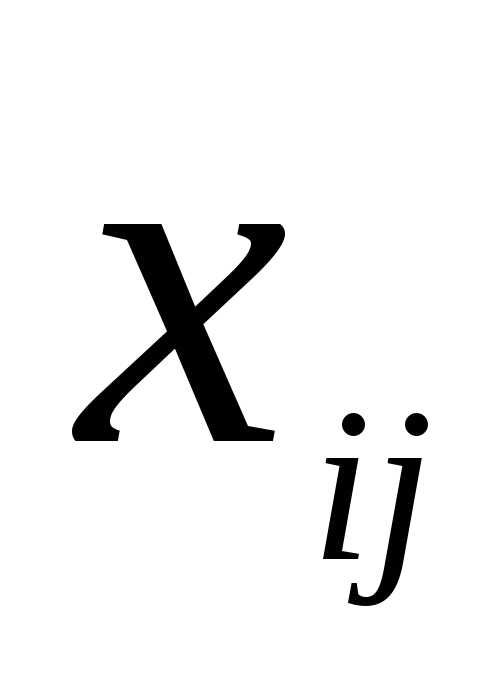 
меньше, опорный план – невырожденный, если число ненулевых перевозок равно
Рассмотрим способы построения опорного плана в невырожденном и вырожденном случаях [1,3].
5.3. Метод северо-западного угла
Рассмотрим «северо-западный угол» незаполненной таблицы, то есть клетку, соответствующую первому поставщику и первому потребителю.
Возможны три случая:
Если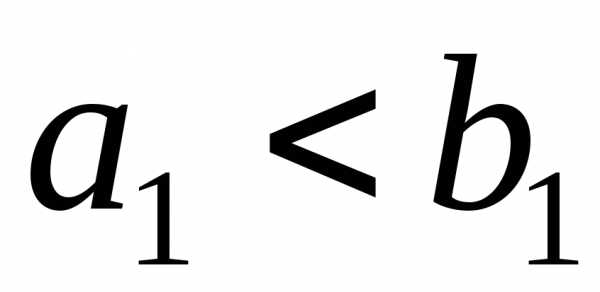 
, то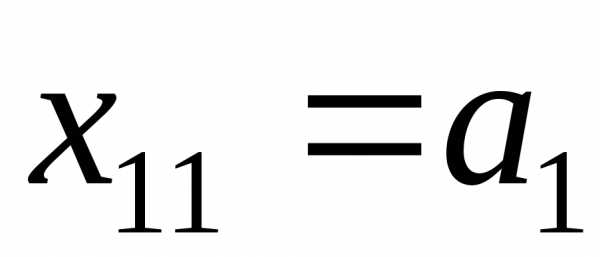
. Это означает, что первый поставщик отгрузил весь продукт первому потребителю и его запас равен нулю, поэтому. При этом неудовлетворенный спрос в первом пункте потребления равен.
Если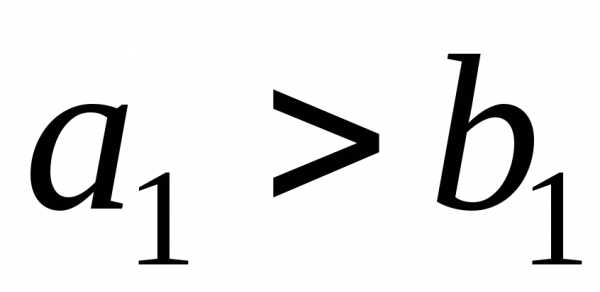 
, то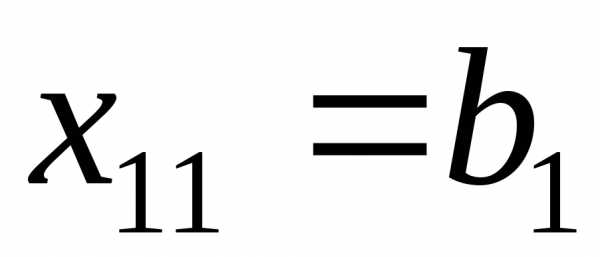
, то есть спрос первого потребителя полностью удовлетворен и поэтому, а остаток продукта в первом пункте производства равен.
В случае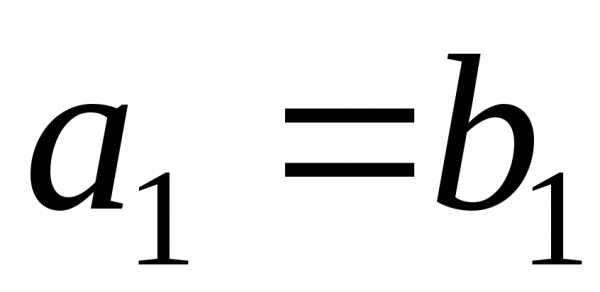 
из рассмотрения можно исключить и поставщика и потребителя. Однако при этом план получается вырожденным, поэтому считается, что выбывает только поставщик, а спрос потребителя остается неудовлетворенным и равным нулю.
После этого рассматриваем северо-западный угол оставшейся незаполненной части таблицы и повторяем те же действия. В результате через шагов получим опорный план.
studfiles.net
НОУ ИНТУИТ | Лекция | Оптимизация производственных моделей
Аннотация: Целью производства является получение максимальной прибыли. На практике производство и сбыт продукции имеют много ограничений, учет которых влияет на планирование ассортимента и количественные показатели. В математической модели производства можно учесть лишь некоторые из этих показателей. В данной лекции будут рассмотрены следующие задачи: составление оптимального производственного плана; технология оптимального раскроя материала; оптимизация составления смесей.
Структура производственных моделей
Производственная математическая модель предназначена для формирования оптимального производственного плана или технологических операций при ограниченных временных, материальных, трудовых и производственных ресурсах [3]. Критерием оптимальности является получение максимума прибыли или минимума издержек. Само планирование состоит обычно в определении количества выпускаемой продукции или составляющих в пределах заданного ассортимента. Чтобы создать математическую модель производственной фирмы, надо определить следующие параметры:
- константы нормативных затрат материалов, труда и финансов;
- переменные решения;
- целевую функцию;
- запас ресурсов или продукции;
- параметры спроса на продукцию.
Оптимизация модели производственного плана состоит в поиске максимума (для прибыли) или минимума (для затрат) целевой функции при ограничении на спрос и ресурсы [4]. При оптимизации раскроя листовых материалов возникают важные для технологов вопросы минимизации отходов. При составлении смесей часто требуется выполнить ограничение сверху и снизу концентрации составляющих компонент.
Задача 2.1. Составление производственного плана
Фабрика выпускает сумки: женские, мужские, дорожные. Данные о материалах, используемых для производства сумок и месячный запас сырья на складе приведены в таблице.
| Сумка женская | Сумка мужская | Сумка дорожная | Сумка спортивная | ||
| Кожа (м2) | 0,5 | 75 | |||
| Кожзаменитель (м2) | 0,3 | 1,5 | 1,0 | 150 | |
| Подкладочная ткань (м2) | 0,6 | 0,4 | 1,7 | 1,5 | 300 |
| Нитки (м) | 20 | 10 | 30 | 25 | 8000 |
| Фурнитура-молния (шт.) | 4 | 5 | 3 | 6 | 1500 |
| Фурнитура-пряжки (шт.) | 2 | 2 | 2 | 2 | 800 |
| Фурнитура разная (шт.) | 2 | 2 | 4 | 6 | 1000 |
По информации, полученной при изучении рынка продаж, ежемесячный спрос на продукцию фабрики составляет
- сумка женская — 150 шт. при оптовой цене 3000 руб.;
- сумка мужская — 70 шт. при оптовой цене 700 руб.;
- сумка дорожная — 50 шт. при оптовой цене 2000 руб.;
- сумка спортивная — 30 шт. при оптовой цене 1200 руб.
Отделом маркетинга были заключены договоры на поставки на следующий месяц.
Найти оптимальный план производства сумок каждого типа, обеспечивающий максимальную выручку при реализации продукции и обеспечивающий удовлетворение рыночного спроса.
При разработке программ обычно составляют подробный алгоритм их реализации. Здесь также составим наглядную ментальную карту по исходным данным задачи. Ментальная карта должна проиллюстрировать основную формулу математической модели (рисунок 2.1):
Ментальную карту выполним в виде столбцов со списками данных (рисунок 2.2):
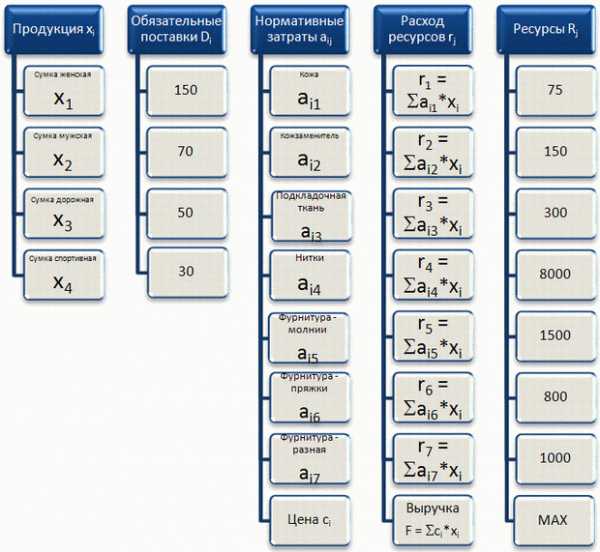Рис. 2.2. Представление исходных данныхПродукцию мы представляем в виде вектора искомых переменных производственного плана . Составляющие этого вектора — количество сумок данного типа, запланированные к производству в следующем месяце. Второй столбец представляет собой вектор обязательных поставок . Вектор поставок должен быть меньше вектора переменных .
В третьем столбце представлена матрица нормативных коэффициентов — удельных затрат материалов на каждый вид сумки. Индексы определяют один из четырех видов продукции и один из семи видов ресурсов.
Вектор расхода материала в четвертом столбце определяется произведением матрицы нормативных коэффициентов на вектор искомых значений переменных . Вектор расхода материала не должен превышать вектор ресурсов , составляющие которого приведены в последнем столбце.
Целевая функция формируется скалярным произведением вектора цены на вектор искомых значений переменных . Критерий оптимальности плана — получение максимального значения выручки — целевой функции .
Подставляя в общие выражения исходные численные значения задачи, получим выражение для целевой функции:
Оптимальному решению задачи отвечает максимальное значение целевой функции при следующих условиях и ограничениях:
Лишь после того, как мы разобрались в условиях задачи, можно приступить к формированию таблицы в MS Excel (рисунок 2.3). Заполним ячейки исходными данными. Искомые переменные (количество сумок каждого вида) поместим в ячейки строки 12. В ячейку F3 вставим формулу и протянем ее до ячейки F10. Напомним, что задание абсолютного адреса производится нажатием клавиши F4. Целевая функция помещается в ячейке F10. Это выручка, т.е. стоимость всех произведенных сумок.
Отформатированная таблица представлена на рисунке 2.4. В ячейки для искомых переменных В12:Е12 можно вставлять, вообще говоря, любые числа. Программа выполнит подбор их числовых значений в соответствии с условиями задачи. Однако чаще всего в качестве начальных значений вводят 0 (как на рисунке 2.4) или 1 (как на рисунке 2.5).
После вставки формул по команде Данные — Поиск решения вызовем диалог и заполним поля, как показано на рисунке 2.5. Адреса ячеек нужно не набирать вручную, а показывать мышью. Вызывать поля ограничений для записи нужно кнопкой "Добавить". На рисунке показано, что введены ограничения на целостность искомых переменных, на превышение выпуска продукции над обязательными поставками и на не превышение расхода материалов над запасами их на складе. Не отрицательность переменных учитывается в диалоге автоматически.
После выполнения команды "Найти решение" будет выдан результат расчета: значения искомых переменных и соответствующий расход материалов (рисунок 2.6):
Таким образом, мы нашли, что максимально возможная выручка может составить 677500 руб. Для этого сверх договорных поставок мы должны изготовить 35 мужских сумок и 9 дорожных сумок. При этом на складе останется около 10% запаса материалов, кроме кожи и кожзаменителя, которые будут израсходованы полностью. Для сохранения результата нужно нажать кнопку "Сохранить сценарий", в диалоге дать имя сценарию "Сумки_1".
Оптимизация математической модели фактически закончена. Но теперь нужно перейти обратно от модели к реальной ситуации, т.е. принять управленческое решение. А что будет, если не удастся реализовать сумки, изготовленные сверх потребности? Ясно, что выручка будет равна только сумме, перечисленной от покупателей по договорным обязательствам. Тогда, может быть, и не изготавливать излишнюю продукцию? А сколько при этом останется материалов на складе? Руководитель предприятия на основе данного анализа должен иметь возможность принять решение о создании запасов как буферных (запас материалов для компенсации задержек в поставках), так и гарантийных (запас продукции для удовлетворения ожидаемого спроса).
Вернемся в диалоговое окно "Поиск решения". Изменим запись, приравняв в окне ограничений искомое количество продукции поставкам по договорам (рисунок 2.7):
Полученное решение оптимально — оно отвечает максимуму целевой функции и удовлетворяет заданным ограничениям. Сохраним второй сценарий под именем "Сумки_2".
А теперь подготовим графические материалы для отчета по составлению производственного плана. Представим остатки материалов на складе в конце следующего месяца для двух вариантов плана: для максимальной выручки и только для обязательных поставок.
По команде на ленте "Данные" — Анализ "что если" — Диспетчер сценариев — Отчет получим отчет по сценариям. Отредактируем отчет вручную по примеру, приведенному на рисунке 2.8:
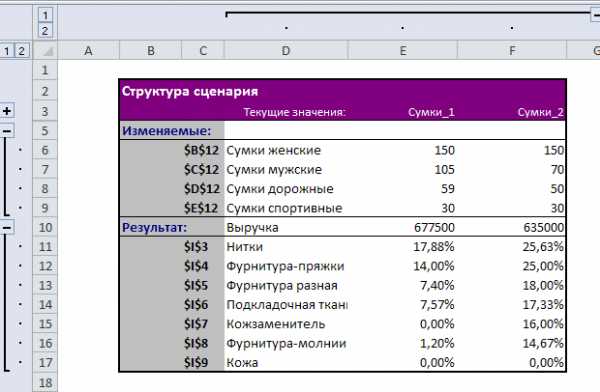Рис. 2.8. Отредактированный отчет по двум сценариям остатков материаловДля построения гистограмм остатков на складе проведем сортировку данных по убыванию и построим гистограммы по команде Вставка — Гистограмма (показаны на рисунке 2.9):
Таким образом, планируемая максимальная выручка в 677500 руб. обеспечена материальными ресурсами фабрики. Выпуск сумок только по обязательным договорным поставкам уменьшит выручку до 635000 руб. При этом остатки материалов на складе увеличатся.
www.intuit.ru
Задачи оптимизации - Стр 4
Из полученной точки вновь определяется направление, вдоль которого целевая функция улучшается наиболее быстро, и начинается движение вдоль нового направления. Процесс продолжается до тех пор, пока не будет обнаружена точка, вблизи которой целевая функция больше не улучшается, или не будет принято решение, что оптимального решения не существует.
Важно подчеркнуть, что алгоритм градиентного спуска не обеспечивает обнаружение глобального оптимумапри произвольных начальных значениях переменных, подлежащих оптимизации.
Более того, модели нелинейного программирования можно разбить на два класса: класс моделей, которые поддаются оптимизации, и класс моделей, которые можно пытаться оптимизировать.
Задачи нелинейного программирования, для которых область допустимых решений является выпуклым множеством, являются разрешимыми.
Напомним, что выпуклым называется множество, для которого точки отрезка, соединяющего любую пару точек множества, принадлежит этому множеству.
Для применения этого положения на практике следует понять, в каких случаях возникает выпуклая область допустимых решений.
Назовем функцию выпуклой вверх, если график функции лежит выше линии, соединяющей две любые ее точки, ивыпуклой вниз, если график функции лежит ниже прямой, соединяющей две любые ее точки. Линейная функция удовлетворяет обоим определениям сразу и являетсявогнуто-выпуклой.
Для случая, когда все ограничения задачи нелинейного программирования имеют форму неравенств, справедливо следующее утверждение: множество до-
пустимых решений является выпуклым, если функции в левых частях ограничений, входящих в выражение со знаком , являются выпуклыми вниз, а входящие со знаком – выпуклыми вверх.
Таким образом, есть способ определить, хотя бы теоретически, является ли область допустимых решений выпуклой.
Программа Поиск решения обязательно найдет глобальный экстремум в том случае, когдамножество допустимых решений задачи является выпуклым и ставится задача найти максимум выпуклой вверх целевой функции, или минимум выпуклой вниз функции.
Во всех остальных случаях поиск решения может найти один из локальных экстремумов, причем какой локальный экстремум будет найден и найден ли вообще, зависит от стартовой точки.
Пример 3.11
Завод производит две марки телевизоров – «Фотон» и «Рубин». Сборочный конвейер позволяет собирать 70 телевизоров марки «Фотон» и 50 телевизоров марки «Рубин». Цех А производит телевизионные трубки, причем на производство одной трубки для телевизора «Рубин» затрачивается 2 ч работы оборудования. Для производства одной трубки телевизора «Фотон» затраты времени зависят от объема производства и определяются формулой 1 0,1 x2 (ч.), гдеx2
studfiles.net
2. Постановка задачи лп. Различные формы задач лп и их эквивалентность
Математические модели различных по содержательному смыслу экономических задач, рассмотренных выше, имеют много общего. Во всех примерах соответствующая математическая задача может быть сформулирована следующим образом: Максимизировать или минимизировать заданную линейную функцию нескольких переменных при заданных линейных ограничениях на переменные.
Это и есть постановка задачи ЛП в самом общем виде. При этом под линейным ограничением понимается любое линейное уравнение или линейное неравенство.
Функция, которую требуется максимизировать (минимизировать), называется
целевой функцией задачи.
Любой набор значений всех переменных задачи ЛП называется планом задачи. План, удовлетворяющий всем ограничениям задачи, называется допустимым. Допустимый план, на котором достигается наибольшее (наименьшее) среди всех допустимых планов значение целевой функции, называется оптимальным.
Решить задачу ЛП – это значит найти ее оптимальный план и соответствующее значение целевой функцииили доказать, что оптимальных планов нет.
Задачу ЛП в общей постановке всегда можно свести к любой из двух следующих форм (частных случаев общей задачи ЛП).
Стандартная задача ЛП:
(14)
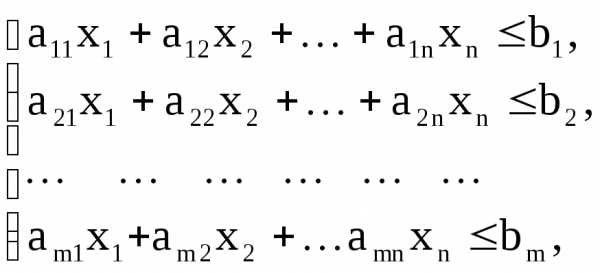(15)
. (16)
Каноническая задача ЛП:
(17)
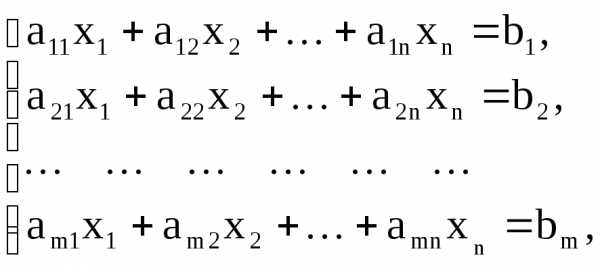(18)
(19)
Эти две формы задачи ЛП удовлетворяют следующим условиям:
1. В качестве направления оптимизации в них выбрана максимизация целевой функции.
2. В ограничениях присутствуют требования неотрицательности (16) и (19) для всех переменных задачи.
3. Все остальные ограничения, кроме требования неотрицательности всех переменных, однотипны: линейные неравенства (15) – в стандартной задаче, линейные равенства (18) – в канонической.
Замечание. Любое неравенство со знаком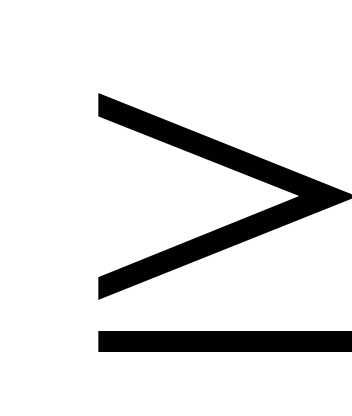 
можно преобразовать в эквивалентное ему неравенство со знаком
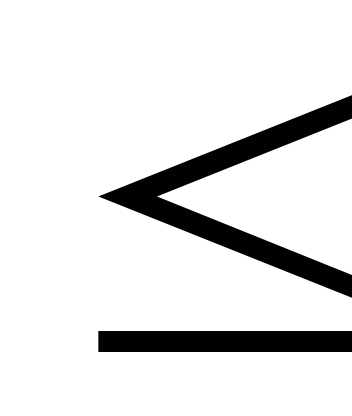, умножая обе части неравенства на множитель (-1). Поэтому без ограничения общности можно считать, что все неравенства в ограничениях задачи ЛП имеют знак
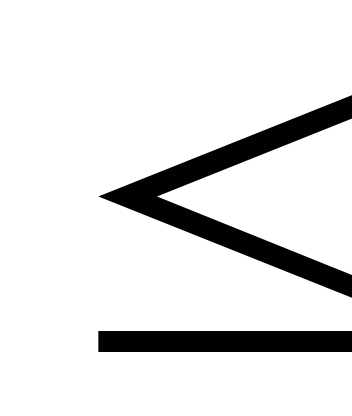(или, наоборот, все неравенства имеют знак
).
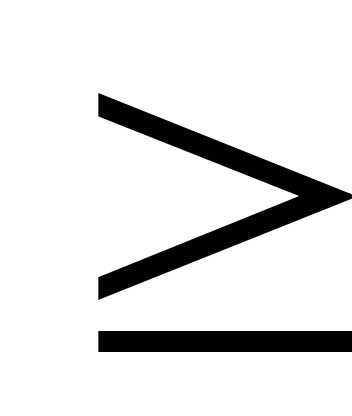Чтобы добиться выполнения условия 1 задачу минимизации целевой функции заменяют на задачумаксимизации функции
при тех же ограничениях на переменные. Легко проверяется (проделайте это самостоятельно), что оптимальные планы преобразованной задачи совпадают с оптимальными планами исходной и при этом
Выполнение условия 2 достигается следующим образом: в целевую функцию и все ограничения задачи вместо каждой переменной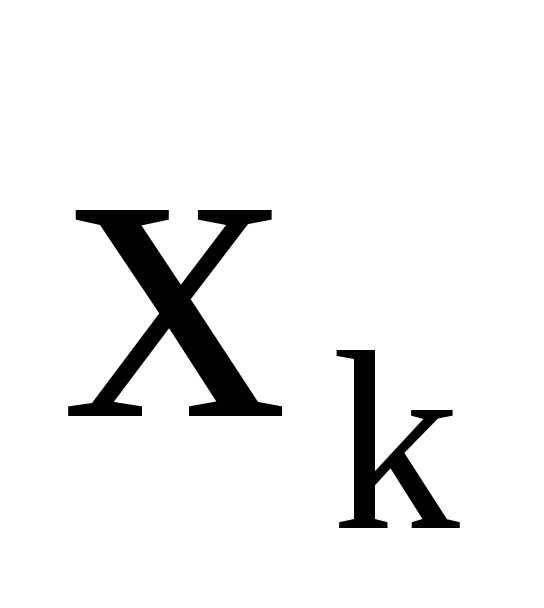 
произвольного знака (т. е. такой, что требование неотрицательности
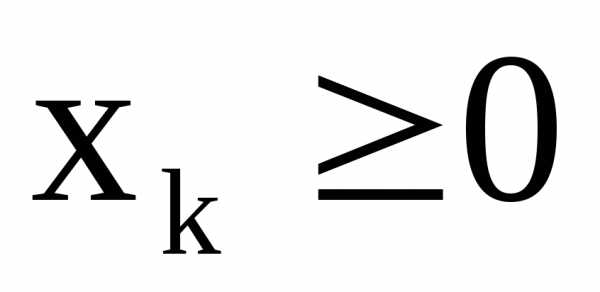отсутствует среди ограничений) подставляется выражение
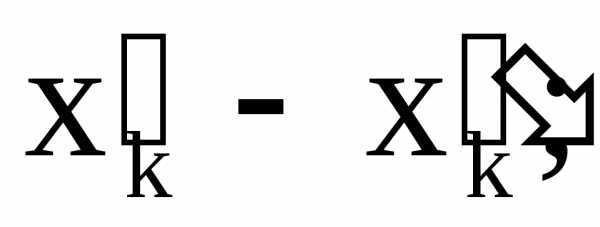для всех вновь введенных переменных в ограничения вводятся требования неотрицательностиСмысл такой замены очевиден: число произвольного знака можно представить в виде разности двух неотрицательных чисел. Ясно, что оптимальные значения
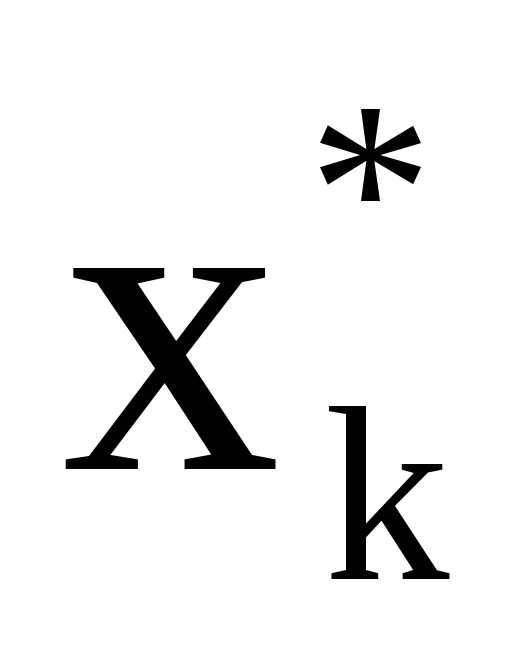переменных исходной задачи находятся по формуламгде
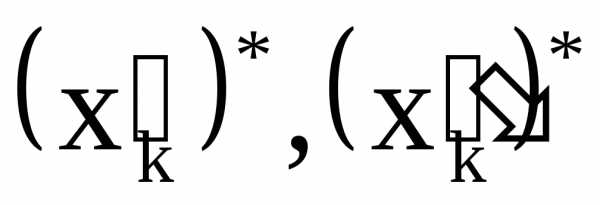- оптимальные значения переменных преобразованной задачи.
После выполнения двух описанных выше преобразований задача ЛП общего вида сведется к задаче максимизации с требованием неотрицательности всех ее переменных; среди остальных ограничений задачи могут встречаться как равенства, так и неравенства. Чтобы свести такую задачу ЛП к стандартной форме, надо исключить все ограничения – равенства; для сведения к канонической форме – заменить систему ограничений – неравенств на эквивалентную систему ограничений, записанную в виде равенств и требований неотрицательности некоторых (дополнительно введенных) переменных.
При исключении ограничений –равенств используются известные методы линейной алгебры. Если все ограничения-равенства образуют несовместную систему линейных уравнений, то задача ЛП не имеет допустимых и тем более оптимальных планов. Если эта система совместна и имеет ранг r, то с помощью метода Гаусса некоторые 
переменных задачи можно выразить через остальные. Подстановка этих выражений в целевую функцию и все ограничения-неравенства (включая и требования неотрицательности переменных) сводит задачу кстандартной форме; при этом число переменных уменьшается на r.
Для приведения задачи ЛП к канонической форме вводятся дополнительные, так называемые балансовые, переменные; число таких переменных равно числу ограничений-неравенств (без учета требований неотрицательности переменных) исходной задачи. Каждое ограничение – неравенство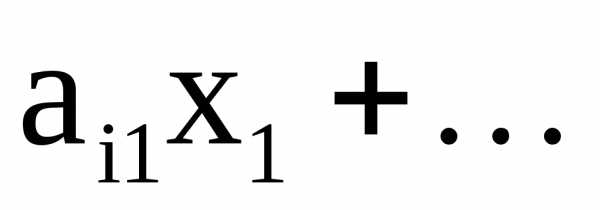 
заменяется на эквивалентную ему пару ограничений
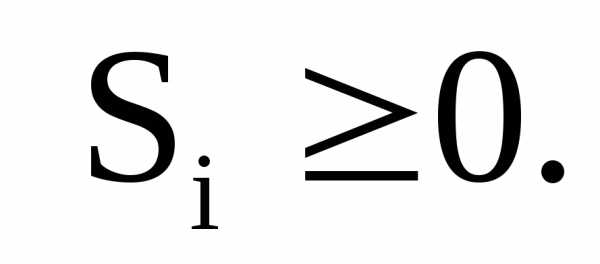В случае неравенства со знаком 
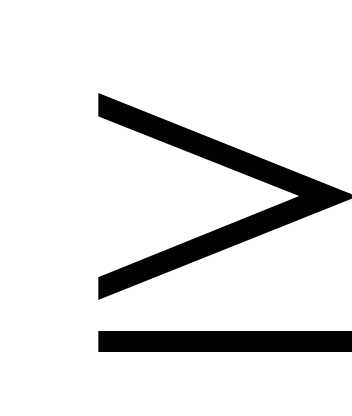балансовая переменная
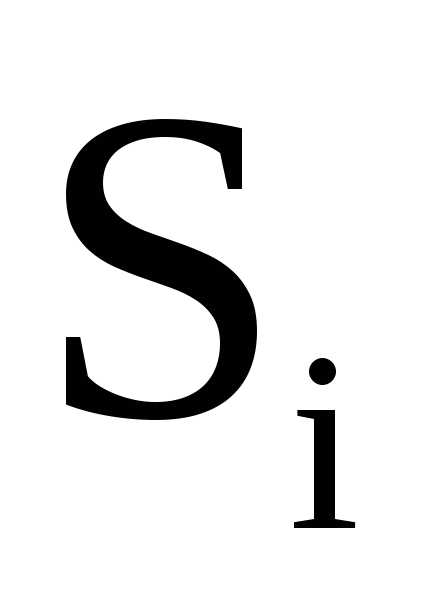включается вcоответствующее равенство со знаком минус.
Рассмотрим примеры применения описанных выше преобразований формы задач ЛП.
Пример 4. Привести к стандартной форме задачу ЛП
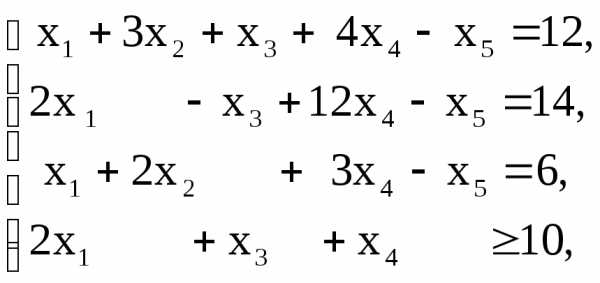
Решение. Решаем методом Гаусса систему ограничений-равенств
~ 
~
~ 
.
Из полученной трапециевидной формы системы последовательно выражаем через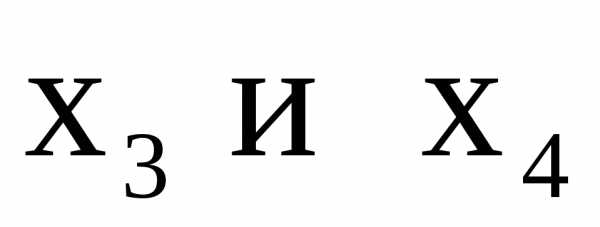
(обратный ход метода Гаусса):
Подставим полученные выражения в целевую функцию и ограничения-неравенства; одновременно заменим задачу минимизации F на максимизацию
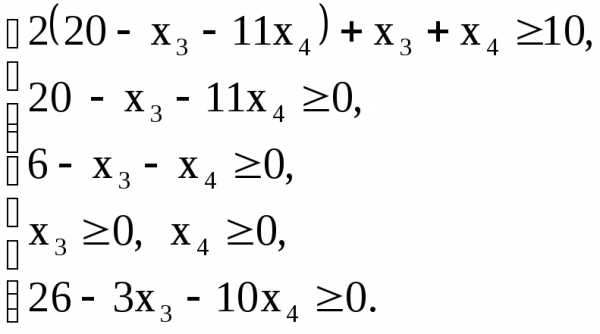
studfiles.net
Решение задачи оптимизации выпуска продукции симплекс–методом.
Первоначально находим симплексным методом или методом искусственного базиса оптимальный план задачи без учета целочисленности переменных. Пусть им является план X0. Если среди компонент этого плана нет дробных чисел, то тем самым найдено искомое решение данной задачи и Fmax = F(Xo).
Если же среди компонент плана X0 имеются дробные числа, то X0 не удовлетворяет условию целочисленности и необходимо осуществить упорядоченный переход к новым планам, пока не будет найдено решение задачи. Покажем, как это можно сделать, предварительно отметив, что F(X0) ³ F(X) для всякого последующего плана X.
Предполагая, что найденный оптимальный план X0 не удовлетворяет условию целочисленности переменных, тем самым считаем, что среди его компонент есть дробные числа. Пусть, например, переменная приняла в плане X0 дробное значение. Тогда в оптимальном целочисленном плане ее значение будет по крайней мере либо меньше или равно ближайшему меньшему целому числу , либо больше или равно ближайшему большему целому числу +1. Определяя эти числа, находим симплексным методом решение двух задач линейного программирования:
Найдем решение задач линейного программирования (I) и (II). Очевидно, здесь возможен один из следующих четырех случаев:
1. Одна из задач неразрешима, а другая имеет целочисленный оптимальный план. Тогда этот план и значение целевой функции на нем и дают решение исходной задачи.
2. Одна из задач неразрешима, а другая имеет оптимальный план, среди компонент которого есть дробные числа. Тогда рассматриваем вторую задачу и в ее оптимальном плане выбираем одну из компонент, значение которой равно дробному числу, и строим две задачи, аналогичные задачам (I) и (II).
3. Обе задачи разрешимы. Одна из задач имеет оптимальный целочисленный план, а в оптимальном плане другой задачи есть дробные числа. Тогда вычисляем значения целевой функции на этих планах и сравниваем их между собой. Если на целочисленном оптимальном плане значение целевой функции больше или равно ее значению на плане, среди компонент которого есть дробные числа, то данный целочисленный план является оптимальным для исходной задачи и он вместе со значением целевой функции на нем дает искомое решение.
Если же значение целевой функции больше на плане, среди компонент которого есть дробные числа, то следует взять одно из таких чисел и для задачи, план которой рассматривается, необходимо построить две задачи, аналогичные (I) и (II).
4. Обе задачи разрешимы, и среди оптимальных планов обеих задач есть дробные числа. Тогда вычисляем значение целевой функции на данных оптимальных планах и рассматриваем ту из задач, для которой значение целевой функции является наибольшим. В оптимальном плане этой задачи выбираем одну из компонент, значение которой является дробным числом, и строим две задачи, аналогичные (I) и (II).
Таким образом, описанный выше итерационный процесс может быть представлен в виде некоторого дерева, на котором исходная вершина отвечает оптимальному плану Х0 задачи (1)-(3), а каждая соединенная с ней ветвью вершина отвечает оптимальным планам задач (I) и (II). Каждая из этих вершин имеет свои ветвления. При этом на каждом шаге выбирается та вершина, для которой значение функции является наибольшим. Если на некотором шаге будет получен план, имеющий целочисленные компоненты, и значение функции на нем окажется больше или равно, чем значение функции в других возможных для ветвления вершинах, то данный план является оптимальным планом исходной задачи целочисленного программирования и значение целевой функции на нем является максимальным.
Итак, процесс нахождения решения задачи целочисленного программирования (1)-(4) методом ветвей и границ включает следующие основные этапы:
1). Находят решение задачи линейного программирования (1)-(3).
2). Составляют дополнительные ограничения для одной из переменных, значение которой в оптимальном плане задачи (1)-(3) является дробным числом.
3). Находят решение задач (I) и (II), которые получаются из задачи (1)-(3) в результате присоединения дополнительных ограничений.
4). В случае необходимости составляют дополнительные ограничения для переменной, значение которой является дробным, формулируют задачи, аналогичные задачам (I) и (II), и находят их решение.
Итерационный процесс продолжают до тех пор, пока не будет найдена вершина, соответствующая целочисленному плану задачи (1)-(3) и такая, что значение функции в этой вершине больше или равно значению функции в других возможных для ветвления вершинах.
Описанный выше метод ветвей и границ имеет более простую логическую схему расчетов, чем метод Гомори.
В узлах метода ветвей и границ используется симплекс-метод.
Главный недостаток алгоритма метода ветвей и границ заключается в необходимости полностью решать задачи линейного программирования, ассоциированные с каждой из вершин многогранника допустимых решений. Для задач большой размерности это требует значительных и, в известной степени, неоправданных с практической точки зрения затрат времени.
2.3 Симплекс метод
Задачи линейного программирования в канонической форме широко распространены в инженерной практике, и для их решения разработана большая группа методов, основной из которых — симплекс-метод. Рассмотрим постановку и решение задачи линейного программирования в канонической форме.
2.3.1 Описание
Задача будет рассматриваться в форме, которая называется канонической. Известно, что путем введения дополнительных ограничений и переменных можно свести к канонической форме задачу линейного программирования, представленную в любой форме, в частности в естественной форме.
9. Модель оптимизации плана перевозок (транспортная задача). Экономическая постановка задачи.
Постановка задачи
Классическая транспортная задача ЛП формулируется следующим образом.
Имеется m пунктов производства (поставщиков) и n пунктов
потребления (потребителей) однородного продукта. Заданы величины:
- объем производства (запас) i-го поставщика, i=1, m ;
- объем потребления (спрос) j-го потребителя, i=1, n ;
- стоимость перевозки (транспортные затраты) единицы продукта от i-го поставщика к j-му потребителю.
Требуется составить такой план перевозок, при котором спрос
всех потребителей был бы выполнен и при этом общая стоимость всех
перевозок была бы минимальна.
Математическая модель транспортной задачи имеет вид
Транспортная задача, в которой суммарные запасы
и суммарные потребности
совпадают, называется закрытой моделью; в противном случае -открытой. Открытая модель решается приведением к закрытой.
В случае, когда суммарные запасы превышают суммарные
потребности, т.е.
вводится фиктивный n+1 потребитель, потребности которого
В случае, когда суммарные потребности превышают суммарные
запасы, т.е.
, вводится фиктивный m+1 поставщик, запасы которого
Стоимость перевозки единицы груза как до фиктивного потребителя, так и стоимость перевозки единицы груза от фиктивного поставщика
полагают равными нулю, так как груз в обоих случаях не перевозится.
Прежде чем решать транспортную задачу, необходимо проверить, к какой модели она принадлежит, и если необходимо, то привести ее к
закрытой модели.
Рекомендуемые страницы:
lektsia.com
