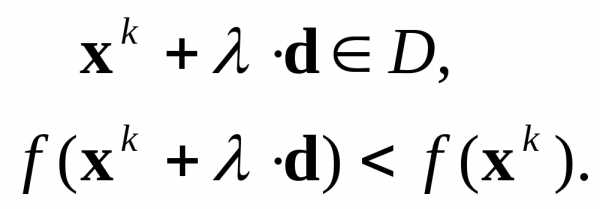3.4. Многомерная безградиентная оптимизация. Многомерная оптимизация
Многомерная оптимизация Методы
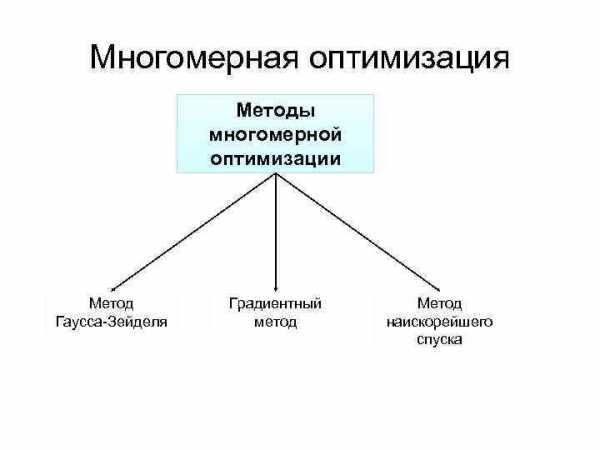 Многомерная оптимизация Методы многомерной оптимизации Метод Градиентный Метод Гаусса-Зейделя метод наискорейшего спуска
Многомерная оптимизация Методы многомерной оптимизации Метод Градиентный Метод Гаусса-Зейделя метод наискорейшего спуска
 Методы многомерной оптимизации Для нахождения экстремума целевых функций многих переменных можно использовать различные методы, которые, в зависимости от организации поиска экстремума, делятся на две группы: • Методы, использующие собственное значение целевой функции • Методы с использованием производных
Методы многомерной оптимизации Для нахождения экстремума целевых функций многих переменных можно использовать различные методы, которые, в зависимости от организации поиска экстремума, делятся на две группы: • Методы, использующие собственное значение целевой функции • Методы с использованием производных
 Методы многомерной оптимизации В основе методов с использованием производных лежит использование итерационной процедуры
Методы многомерной оптимизации В основе методов с использованием производных лежит использование итерационной процедуры
 Метод Гаусса- Зейделя Постановка задачи Предположим, что целевая функция зависит от двух переменных: U = f(x 1, x 2). Функция имеет экстремум в виде максимума. Необходимо найти x 0 = (x 10, x 20) такие, которые определяют максимум функции Umax = f(x 10, x 20).
Метод Гаусса- Зейделя Постановка задачи Предположим, что целевая функция зависит от двух переменных: U = f(x 1, x 2). Функция имеет экстремум в виде максимума. Необходимо найти x 0 = (x 10, x 20) такие, которые определяют максимум функции Umax = f(x 10, x 20).
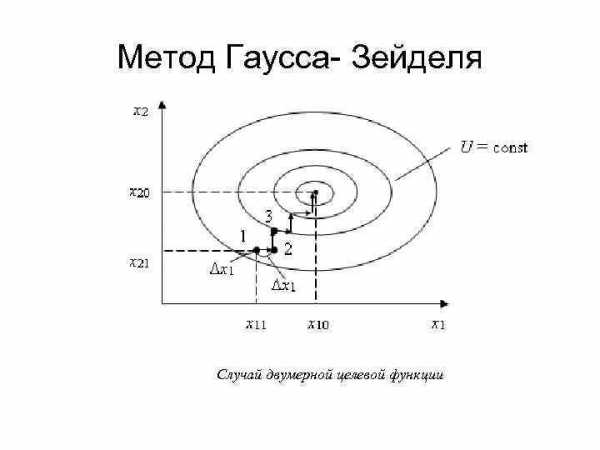 Метод Гаусса- Зейделя Случай двумерной целевой функции
Метод Гаусса- Зейделя Случай двумерной целевой функции
 Метод Гаусса- Зейделя Величина шага: В методе Гаусса-Зейделя величина шага движения регулируется в зависимости от скорости изменения функции f. При этом используется соотношение где t – параметр, определяющий величину шага. Знак производной определяет направление движения.
Метод Гаусса- Зейделя Величина шага: В методе Гаусса-Зейделя величина шага движения регулируется в зависимости от скорости изменения функции f. При этом используется соотношение где t – параметр, определяющий величину шага. Знак производной определяет направление движения.
 Метод Гаусса- Зейделя Вывод: Поиск экстремума заканчивается на шаге k, когда дважды подряд выполняется неравенство где – заданная ошибка определения экстремума
Метод Гаусса- Зейделя Вывод: Поиск экстремума заканчивается на шаге k, когда дважды подряд выполняется неравенство где – заданная ошибка определения экстремума
 Метод Гаусса- Зейделя Анализ метода: • Достоинством методов покоординатного движения и Гаусса-Зейделя является простота. • Недостаток – медленное движение к экстремуму, особенно когда количество входных переменных велико
Метод Гаусса- Зейделя Анализ метода: • Достоинством методов покоординатного движения и Гаусса-Зейделя является простота. • Недостаток – медленное движение к экстремуму, особенно когда количество входных переменных велико
 Градиентный метод оптимизации • Метод обеспечивает наискорейший подъем или спуск при движении соответственно к максимуму или минимуму. • Постановка задачи: Рассмотрим реализацию метода для целевой функции, зависимой от двух переменных: U = f(x 1, x 2). Наискорейшее движение к экстремуму обеспечивается, когда вектор движения перпендикулярен касательной к линии U = const в точке местонахождения.
Градиентный метод оптимизации • Метод обеспечивает наискорейший подъем или спуск при движении соответственно к максимуму или минимуму. • Постановка задачи: Рассмотрим реализацию метода для целевой функции, зависимой от двух переменных: U = f(x 1, x 2). Наискорейшее движение к экстремуму обеспечивается, когда вектор движения перпендикулярен касательной к линии U = const в точке местонахождения.
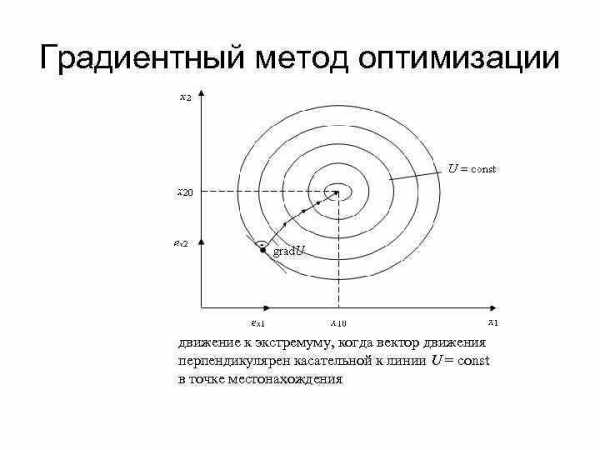 Градиентный метод оптимизации движение к экстремуму, когда вектор движения перпендикулярен касательной к линии U = const в точке местонахождения
Градиентный метод оптимизации движение к экстремуму, когда вектор движения перпендикулярен касательной к линии U = const в точке местонахождения
present5.com
Тема 6.8. Многомерная оптимизация
6.8.1. Постановка задачи и основные определения
6.8.2. Методы спуска
6.8.3. Метод градиентного спуска с дроблением шага
6.8.4. Метод наискорейшего спуска
6.8.5. Технология решения задач многомерной оптимизации средствами математических пакетов
6.8.5.1. Технология решения задач многомерной оптимизации средствами
MathCad
6.8.5.2. Технология решения задач многомерной оптимизации средствами
MatLab
6.8.7. Тестовые задания по теме «Многомерная оптимизация»
6.8.1. Постановка задачи и основные определения
Задача, требующая нахождения оптимального значения функции mпеременныхf(Х)=f(x1, x2, …, xm), называется задачеймногомерной оптимизации. Так же, как и для случая одномерной оптимизации, задача нахождения максимума функции сводится к задаче нахождения минимума путем замены целевой функцииfна-f.
Пусть функция f(Х) = f(x1, x2, …, xm)определена на некотором множествеХRm. ЕслиХ=Rm(т.е. ограничения на переменныеx1, x2, …, xmотсутствуют), принято говорить о задаче безусловной минимизации. В противном случае, когдаХ ¹ Rm, говорят о задаче условной минимизации.
Методы решения задачи безусловной минимизации являются основой для перехода к изучению более сложных методов решения задач условной минимизации.
В постановке задачи безусловной оптимизации для f(Х)=f(x1, x2, …, xm)требуется найти хотя бы одну точку минимумаХ*и вычислитьf*=f(Х*).ТочкаХ*ÎRmназывается точкой глобального минимума функцииf на множествеХ, если для всехХÎRmвыполняется неравенствоf(Х*)£f(Х).В этом случае значениеf(Х*)называется минимальным значением функцииf наRm.
Точка Х*Î Rmназывается точкой локального минимума функцииf, если существует такаяd- окрестностьUdэтой точки(d>0),что для всехХÎХd=Х Udвыполняется неравенствоf(X*)£f(X).
Udвыполняется неравенствоf(X*)£f(X).
Подавляющее большинство методов решения задачи безусловной минимизации в действительности являются методами поиска точек локальных минимумов, среди которых затем выделяют глобальный минимум, являющийся наименьшим. Этот способ очень трудоемок, поэтому чаще используют другой: местоположение точки глобального минимума определяют в ходе анализа решаемой задачи, а затем для его уточнения с заданной точностью применяют один из методов поиска точки локального минимума.
Рассмотрим функцию нескольких переменных и введем для нее основные определения.
Множество точек, для которых целевая функция принимает постоянное значение f(x1, x2, …, xm) = c, называетсяповерхностью уровня. Для функции двух переменных (m = 2) это множество называетсялинией уровня.
Функция f(x1,x2)задает в трехмерном пространстве некоторую поверхностьU=f(x1,x2)(рис. 6.8.1-1), низшая точка которой и дает решение задачи минимизации. Для того чтобы изобразить рельеф этой поверхности, проведем несколько плоскостей(U = const): U=c1, U=c2, U=c3. Проекции на плоскостьОх1х2линий пересечений этих плоскостей с поверхностью и даютлинии уровня.
Рис. 6.8.1-1
Для дифференцируемой функции можно определить вектор из первых частных производных,который называетсяградиентом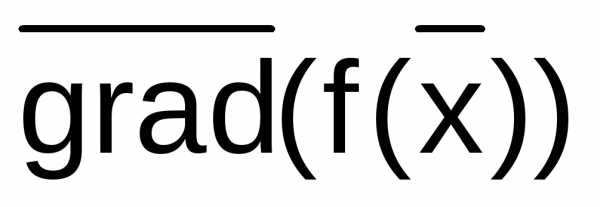 :
:
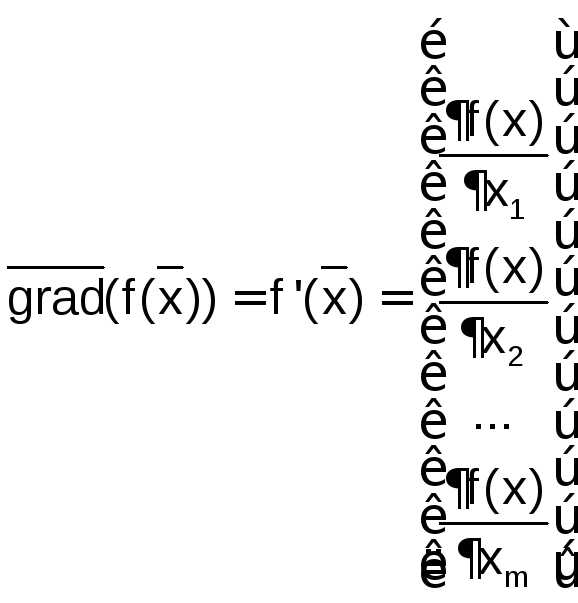 или .
или .
Направление вектора градиента 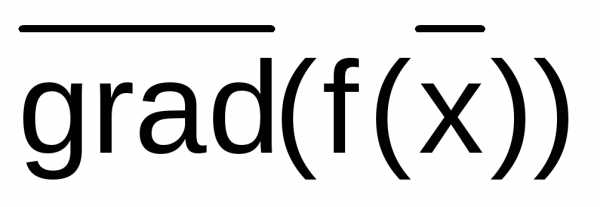 указывает направление наискорейшего возрастания функции, а его модуль (длина) равен скорости возрастания функции. Вектор Градиент нормален к линии уровня в каждой своей точке и касателен к поверхности, которую задает функция.
указывает направление наискорейшего возрастания функции, а его модуль (длина) равен скорости возрастания функции. Вектор Градиент нормален к линии уровня в каждой своей точке и касателен к поверхности, которую задает функция.
Вектор -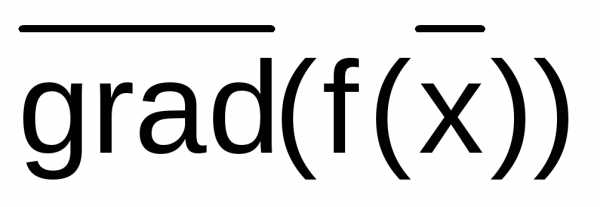 называетсяантиградиентоми показывает направление наискорейшего убывания функции.
называетсяантиградиентоми показывает направление наискорейшего убывания функции.
Равенство нулю градиента в точке Хявляется необходимым условием того, чтобы внутренняя для множестваХi (i = 1, 2,…m)точкаХбыла точкой локального минимума дифференцируемой функцииf. ТочкаХ, для которой выполняется равенствоf’(X) = 0, называетсястационарной точкой функции.
Это равенство представляет собой систему из mнелинейных уравнений относительно компонентх1, х2, …, хm, вектораX, гдеm– количество переменных.

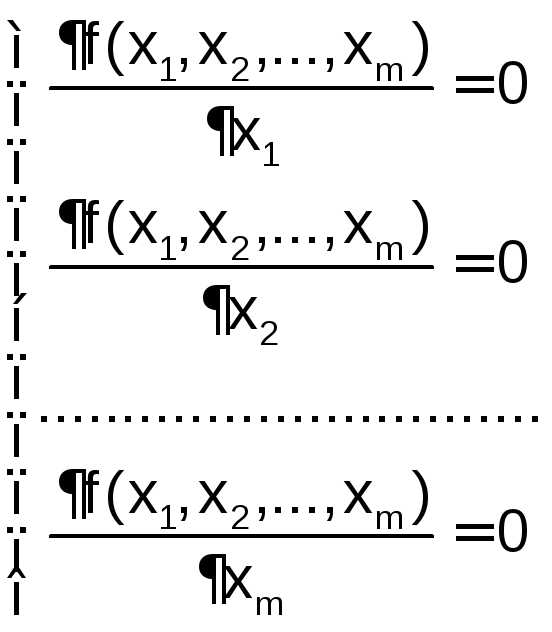
Для функции двух переменных Q(x, y) это условие имеет вид:
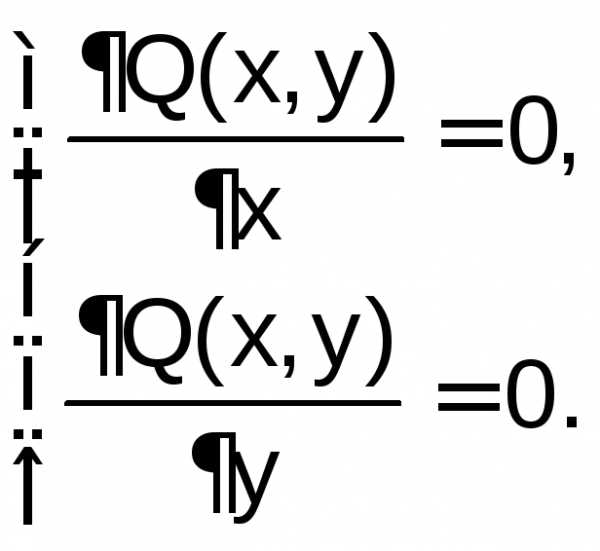
Однако не всякая стационарная точка является точкой минимума. Для всякой непрерывно дифференцируемой функции fдостаточным условием того, чтобы стационарная точкаХбыла точкой локального минимума, является положительная определенность матрицы вторых производных (матрицы Гессе):
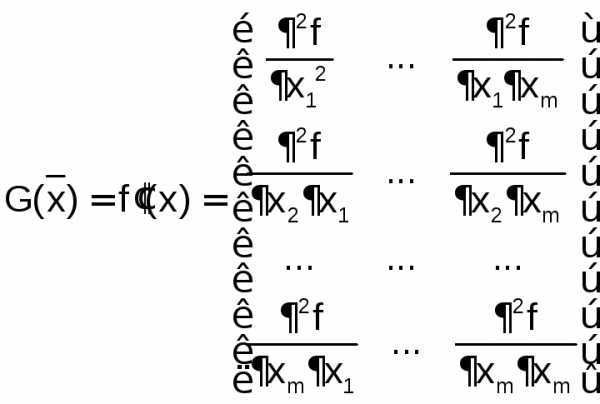
Согласно критерию Сильвестра, для того чтобы матрица была положительно определена, необходимо, чтобы все угловые миноры были положительны:
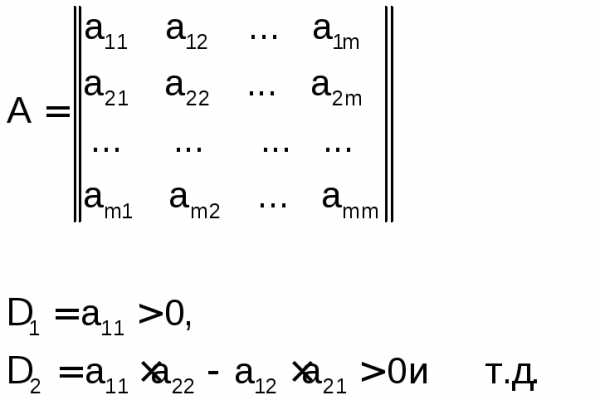
Для функции двух переменных Q(x, y)матрица Гессе имеет вид:
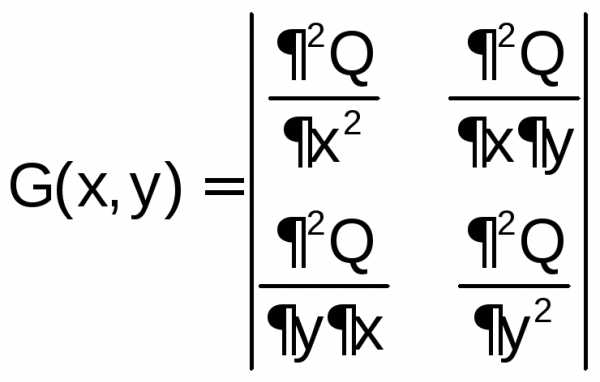 ,
,
а достаточное условие существования минимума:
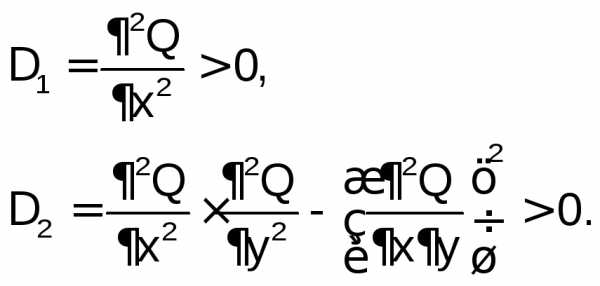
Алгоритм решения задачи оптимизации функции двух переменных Q(x,y)аналитическим (классическим) методом следующий:
Составляется и решается система уравнений
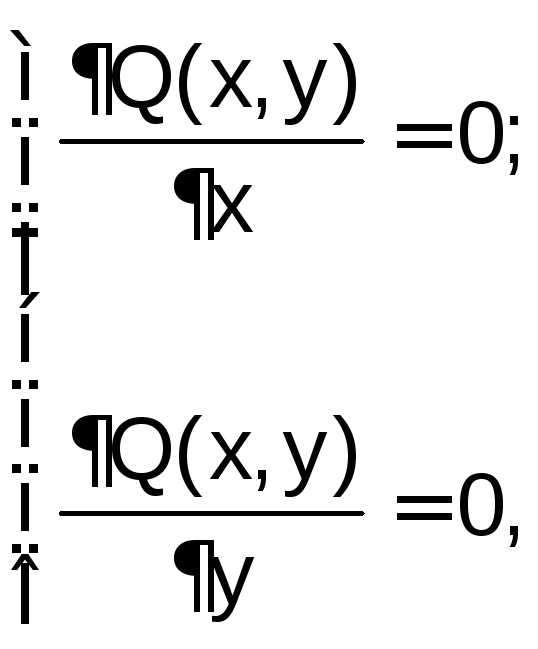
из которой находятся (x*, y*).
Проверяются достаточные условия существования минимума
.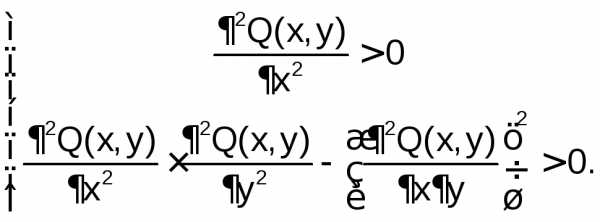
Если (x*, y*)– единственное решение и в этой точке выполняются достаточные условия, то это точка минимума. Если хотя бы в одном из неравенств получается знак “<”, то минимума не существует. В случае появления знака “=” необходимо исследовать производные высших порядков.
Пример 6.8.1-1. Найти точку локального минимума функции.
f(x,y) = x2 + y2 – 4x + 100 – 8y.
Следовательно, в точке x* = 2 и y* = 4функция имеет локальный минимум.
Пример 6.8.1-2. Найти точку локального минимума функции f(x,y)= x2+y2–4x+10xy–8y.
Следовательно, функция не имеет точки локального минимума.
Аналитический метод поиска минимума применяется только для ограниченного круга задач. В основном это связано с необходимостью решения системы нелинейных уравнений, которая, как правило, решается численными методами. Оказывается, гораздо проще сразу решать задачу минимизации численными методами. Рассмотрим некоторые из методов.
studfiles.net
Многомерная оптимизация - Справочник химика 21
Многие алгоритмы многомерной оптимизации основаны на использовании методов одномерной оптимизации, предназначенных для нахождения оптимума функции одной переменной [7]. Наиболее эффективным из группы методов одномерной оптимизации является метод золотого сечения. [c.396]Многомерная оптимизация Возможна [c.307]
В такой ситуации нередко приемлемым подходом к решению задачи общей оптимизации режима работы сложных объектов является расчленение этой задачи на ряд более простых. Здесь имеется в виду переход от решения задачи многомерной оптимизации режима работы ВУ (в той постановке, как она выполнена выше) к последовательному решению задач одно- или двухмерной оптимизации по числу регулируемых параметров. [c.104]
Решение указанных задач, хотя и не является примером общей многомерной оптимизации В У по всем регулируемым параметрам, но показывает методику наиболее существенной оптимизации температурного режима, режима отвода вторичного пара и режима цикличности работы ВУ и позволяет оценить ее экономическую эффективность, а также потери от нарушения оптимальности режима работы установки. [c.106]
С математический точки зрения задача определения оценок инкрементов является задачей решения системы линейных (в случае, если оцениваемые параметры входят в математическую модель линейно) или нелинейных (в случае, если используется нелинейная по параметрам модель) уравнений. Возможно также сведение задачи к задаче многомерной оптимизации. В этом случае минимизируемая функция характеризует меру рассогласования между оцененными по математической модели и табличными значениями термодинамических параметров [c.246]
Обычно исследователь располагает оцененным экспериментально или заимствованным из справочной литературы набором данных я , - у / = I,.--, п (где /я, -концентрация компонента раствора у, — коэффициент активности). Задача заключается в том, чтобы построить функциональную зависимость у, = у,(те,), которая в дальнейшем будет использована для математического описания равновесий в растворе. В современной теории растворов разработано большое количество моделей для описания отклонения от идеала. Отметим, что эти модели не отражают всего многообразия действующих в растворе сил и поэтому содержат эмпирические коэффициенты, оцениваемые для каждой системы по экспериментальным данным. Эмпирические коэффициенты могут входить в выражение у, = У/(т ) как линейно, так и нелинейно. В зависимости от этого коэффициенты оцениваются либо по методу наименьших квадратов, либо одним из методов многомерной оптимизации. Приведем некоторые ставшие классическими уравнения для расчета среднеионных коэффициентов активности электролитов. [c.247]
Многомерность и сложность задач проектирования не позволяют получить аналитическое решение для однозначного выбора наилучшего варианта реализации технологической схемы. И эту задачу приходится решать как задачу многокритериальной оптимизации численными методами путем анализа многих возможных вариантов. На этапе технологического проектирования решается именно эта задача, и эффективность ее решения зависит [c.42]
Указанные трудности могут быть в значительной мере преодолены благодаря применению топологического метода анализа ХТС. Этот метод позволяет формальным образом устанавливать функциональную связь между технологической топологией и количественными характеристиками функционирования системы в виде материальных и тепловых нагрузок на элементы ХТС. С помощью топологического метода анализа можно разрабатывать оптимальные алгоритмы расчета на ЦВМ многомерных систем уравнений математических моделей ХТС, в частности систем уравнений балансов, выбирать оптимальную стратегию решения задач анализа функционирования и оптимизации сложных систем, которая обеспечивает минимальные затраты машинного времени ЦВМ. [c.114]
Оптимальная организация вычислительных процедур при оптимизации ХТС предусматривает декомпозицию многомерной сложной задачи на ряд более простых подзадач гораздо меньшей размерности и выбор соответствующих методов расчета систем уравнений математических моделей ХТС и вычислительных методов определения экстремальных значений целевых функции. [c.302]
Методы детерминированного прямого поиска. Методы оптимизации этого класса позволяют определять направление поиска непосредственно по одному или нескольким значениям целевой функции. Самые простые алгоритмы этих методов — прямое обобщение алгоритмов одномерного поиска на многомерный случай. Например, в основе метода покоординатного спуска лежит последовательная минимизация целевой функции по каждой координатной оси с помощью одного из методов, изложенных в разд. У.3.1. [c.204]
Для моделирования химико-технологических процессов, диагностики неполадок в производстве и оптимизации процессов по качеству конечных продуктов в последние годы все шире применяют методы распознавания образов и логико-структурный подход к анализу многомерных данных [97, 98]. Теория распознавания образов и логическое моделирование основаны на сочетании идей факторного анализа с некоторыми методами алгебры логики, в частности, методами минимизации булевых функций, предназначенными для извлечения информации из больших массивов данных. [c.241]
Задача оптимизации глобальной схемы будет иметь вид (VI, 27). Поскольку в этом случае все переменные являются непрерывными, для решения могут быть использованы хорошо разработанные численные методы нелинейного программирования (см. гл. III, IV). Ясно, что в результате решения могут быть получены нецелочисленные значения а , принимающие любые значения в интервале (VI, 26). Если условия задачи допускают любые значения структурных параметров в интервале (VI, 26), то полученный результат будет решением первоначальной задачи (VI, 5). При этом, если какие-либо структурные параметры при k = k ,. . kj/, s = 1, примут нецелые значения, то на /-том выходе -го блока необходимо поставить делитель потока, а на входных потоках блоков. . ., кр смесители. В дальнейшем этот метод будем называть методом структурных параметров (МСП). Рассмотренный подход выглядит очень заманчивым, поскольку позволяет сводить многомерную комбинаторную задачу к задаче нелинейного программирования. Особенности этой задачи состоят в следующем [c.204]
Предлагаемый метод разделения задачи глобальной оптимизации химических комплексов дает возможность на каждом этапе решать задачи значительно меньшей размерности. Однако даже в этом случае каждая из этих задач остается нелинейной и многомерной. Поэтому необходимы дальнейшее совершенствование математических методов поиска оптимальных решений этих задач, разработка усовершенствованных алгоритмов и программ для решения специфических химико-технологических задач на современных ЭВМ. [c.21]
Таким образом, если учесть особенности всех процессов, имеющих место в ХТК, и всевозможные связи между его элементами, то модель комплекса при большом числе установок или регионов будет представлять собой достаточно сложную систему, решить которую в настоящее время довольно трудно. Так как из-за большой размерности задачи современные ЭВМ не позволяют рассчитать одновременно материальные и тепловые потоки между всеми агрегатами даже небольшого ХТК и определить оптимальные условия режима их эксплуатации, поэтому для оптимизации ХТК требуется разработать соответствующие декомпозиционные методы, позволяющие решать многомерную задачу, разбивая ее на несколько подзадач с меньшими размерностями. [c.155]
Оптимизация газоперерабатывающих заводов усложняется двумя факторами многомерностью задачи поиска экстремума, сложностью расчета целевой функции ГПЗ, равной сумме оптимальных значений целевых функций для элементов завода. В качестве целевой функции оптимизации для ГПЗ и его элементов принимают приведенные затраты [c.329]
Прежде чем перейти к изложению методов многомерного поиска, рассмотрим также ряд алгоритмов одновременного поиска, т. е. поиска экстремума функции одной переменной, которые часто используются не только как самостоятельные методы оптимизации, но также и как вспомогательные (например, при спуске по направлению) в многомерных методах оптимизации. [c.501]
Аналитические методы являются классическими методами определения экстремального значения функции (минимума или максимума). Они применяются, когда оптимизируемые функции заданы аналитически и число независимых переменных невелико. При большом числе переменных возникает так называемый барьер многомерности и применение аналитических методов становится затруднительным. Затрудняет применение аналитических методов также наличие ограничений. Вследствие этого использование аналитических методов в их классическом виде на практике довольно ограничено. Краткая характеристика этих методов приведена ниже. Принцип максимума для удобства изложения описан после характеристики градиентных методов оптимизации. [c.141]
Симплексный метод планирования эксперимента и оптимизации. В сравнительно недавнее время появились работы з1-зз в которых предлагается на стадии восхождения использовать симплексный -метод планирования экспериментов (симплекс-планирование). Начиная восхождение, планируют исходную серию опытов так, чтобы точки, соответствующие условиям проведения этих опытов, образовывали правильный симплекс в многомерном. факторном пространстве. Под правильным симплексом понимается совокупность А +1 равноудаленных друг от друга точек в /с-мерном пространстве. В одномерном пространстве симплексом является отрезок прямой. Для двух факторов симплексом служит равносторонний треугольник, для трех факторов правильная треугольная пирамида — тетраэдр и др. [c.210]
Прикладные задачи. Для решения многомерных задач анализа и оптимизации химико-технол. систем (ХТС) используют след, химико-технол. графы (рис. 4) потоковые, информационно-потоковые, сигнальные и графы надежности. К потоковым графам, представляющим собой взвешенные орграфы, относятся параметрические, материальные по общим массовым расходам физ. потоков и массовым расходам нек-рых хим. компонентов либо эле- [c.612]
И хотя окончательное решение задачи оптимизации не получено, соотношение (4.133) сводит решение (я - 1)-мерной задачи к одномерной подобрать всего лишь одну концентрацию, после первого реактора С, с тем, чтобы из цепочки соотношений (4.133) получить С = С . Конечно, решение одномерной задачи оптимизации много легче многомерной. [c.211]
В аналитической химии обычно используют линейные модели. Мы уже сталкивались с такими моделями при рассмотрении процедур градуировки и оптимизации. Помимо этих важнейших приложений, в аналитической химии многомерные линейные модели применяют всегда, когда необходимо учесть одновременное действие множества факторов, например в анализе объектов окружающей среды. [c.545]
И хотя окончательное решение задачи оптимизации не получено, соотношение (2.174) сводит решение (п - 1)-мерной задачи к одномерной подбирают концентрацию только после первого реактора С так, чтобы из цепочки соотношений (2.174) получить С = Ск. Конечно, решение одномерной задачи оптимизации гораздо легче, чем многомерной. [c.155]
В заключение остановимся на поиске оптимального варианта конструкции теплообменника. В рассматриваемой задаче варьируют два параметра dl и гзкв (в программе — переменные В1 и 02). Соответственно поиск оптимума ведут по двум переменным. Одним из простейших методов многомерной оптимизации является метод покоординатного спуска. Его идея заключается в последовательном применении одномерного поиска для [c.222]
Многомерность, сложность технологической топологии, разнообразие свойств ХТС, детерминировапно-стохастическая природа ХТП, наличие неопределенной информации и многократность изменения состояний элементов и ХТС в целом обусловливают математическую сложность и трудоемкость задач анализа II оптимизации надежности ХТС, для решения которых разработаны специальные быстродействующие методы (см. гл. [c.144]
Важным вопросом является выбор соответствующего алгоритма оптимизации, поскольку обычно задача синтеза характеризуется многомерностью, мультимодальностью (многоэкстремально- [c.603]
Пусть мы вычислили таким путем все функции / полностью определен. Максимум данной функции мы можем найти, используя тот или иной поисковый метод. Хотя этот путь и возможен, но в большинстве случаев он, по-видимому, мало применим, поскольку обладает теми же самыми недостатками, что и метод динамического программирования. А именно, нам придется определять и хранить табличные многомерные функции (VIII,26). Это может потребовать как чрезвычайно большого количества вычислений, так и слишком большой памяти ЭВМ. Правда, одно обстоятельство может существенно понизить требования к памяти и количеству вычислений опыт показывает, что критерий оптимизации часто является пологой функцией. Используя сказанное, можно попытаться при не очень большом числе совокупностей входных и выходных переменных к-то блока найти значения функций Отсюда, учитывая ее пологость, можно но не очень большому числу известных значений восстановить вид функции (VIII,26). [c.183]
Нами сформулированы обобщения задачи (11)-(16) на многомерные технологические объекты, где эффект от дестабилизационной оптимизации может быть более значительным [1]. Рассмотрегш случаи с различного рода зависимостями подынтегральной функции Q(a>(t)f(t)) в (11) от управления доказаны теоремы об оптимальных управляющих воздействиях, разработаны соответствующие алгоритмы. [c.139]
При отсутствии оператора разделение , т. е. при К=0, Гх=1, получаем тривиальное выражение G = viXi. Использование типовых технологических операторов при анализе и расчете материальных или энергетических балансов для подсистем БТС в условиях стационарного режима их работы позволяет формализовать и автоматизировать с помощью ЭВМ процесс проектирования БТС. Применяемые при этом математические модели подсистем основываются на модулях типовых операторов, составляющих данную систему. В то же время многомерность, высокая степень взаимосвязи и параметрического взаимовлияния элементов в сложных БТС затрудняют применение операторного метода. В этих условиях становится эффективным использование методов расчета БТС, предусматривающих применение потоковых, структурных, информационных и сигнальных графов [13]. Прн этом графы, отражая технологическую топологию и функциональные связи в системе, позволяют разрабатывать алгоритм расчета на ЭВМ многомерных систем и решать задачи анализа и оптимизации сложных БТС, которые связаны в основном с рассмотрением [c.24]
Однако для современных больших химических комплексов задача проектиро 1ания и оптимизации является многомерной, и решить ее для большинства случаев на современных ЭВМ не представляется возможным. В связи с этим приобретает особое значение метод разделения задачи глобальной статической оптимизации комплекса на три этапа декомпозиционный глобальный, региональный и локальный. [c.20]
Предстоит выполнить большую работу по дальнейшему развитию различных аспектов применения принципа супероптимальности, особенно по выявлению закономерностей повышения оптимальности сопряженно работающих систем при учете интерференции сложного взаимодействия и переплетения потоков, имеющих место в комплексных системах с безграничным разнообразием реакций. Также многое предстоит сделать по решению многомерных задач оптимизации химических комплексов и исследованию их устойчивости. В приведенных в этой части численных решениях. значения некоторых параметров взяты произвольно, что упрощает решеппс задачи, не влияя на окончательные выводы. [c.24]
Современным методом расчета технологических показателей разработки и мониторинга процессов разработки при заводнении является создание постоянно действующих многомерных математических моделей залежей нефти и газа. Моделирование продуктивных пластов при проектировании разработки залежей нефти нами осуществлялось (наряду с расчетами по одномерной методике фильтрации жидкости) и с помощью программы E LIPSE 100 - полностью неявной трехфазной трехмерной модели нелетучей нефти. Эта программа используется нефтяными компаниями всего мира при моделировании нефтяных и газовых месторождений для оптимизации их разработки. [c.177]
Наиболее общий метод последовательной оптимизации основан на симплекс-алгоритме Нелдера и Мида. Симплексом называется геометрическая фигура (тело), число вершин которой на единицу больше, чем число измерений пространства (факторов). Таким образом, одномерный симплекс — это отрезок, двумерный — треугольник, трехмерный — тетраэдр и в общем (многомерном) случае — гипертетраэдр. [c.512]
Таким образом, согласно бифуркационной теории, ни один из этапов механизма спонтанного свертывания белка, включая окончательное построение его биологически активной трехмерной структуры, не содержит селекции практически бесконечного множества мыслимых конформационных состояний аминокислотной последовательности. Следовательно, если описанный механизм адекватен реальному процессу, т.е. если бифуркационная теория верна, то разработанный на ее основе метод расчета вообще не встречается с проблемой поиска глобального минимума энергии на многомерной потенциальной поверхности. Содержание конформационного анализа в этом случае распадается на две также непростые задачи. Одна из них заключается в оптимизации составляющих белковую цепь олигопептидных участков в их свободном состоянии при вариации всех возможных комбинаций знамений двугранных углов вращения каждого отдельного фрагмента. Цель решения этой задачи состоит в идентификации конформационно жестких и лабильных участков аминокислотной поверхности. Вторая задача включает анализ невалентных взаимодействий тех и других и многоступенчатую минимизацию энергии с постепенным увеличением длины цепи и раскрепощением конформационных параметров жестких участков. В конечном счете будет получена количественная оценка конформационных возможностей всей белковой молекулы и выявлена ее глобальная нативная трехмерная структура. Этот вывод справедлив, однако, лишь в принципе, а реально ни та, ни другая задача не поддаются решению без введения дополнительных положений о структурной организации нативной конформации белка. Предоставленная бифуркационной теорией возможность перехода от расчета целой белковой цепи к расчету отдельных фрагментов и далее анализу комбинаций их пространственных форм в огромной степени упростила проблему, но не сделала ее практически разрешимой. Причина та же - множественность локальных минимумов энергии на потенциальной поверхности, правда, теперь уже не всей белковой цепи, а ее конформационно жестких и лабильных участков, которые могут состоять из 10-12 аминокислотных остатков. Как известно, независимому и строгому анализу поддаются [c.248]
Задача из многомерной свелась к одномерной. При заданных и Ха выбирают некую степень превращения Х) после первого слоя. Затем последовательно рассчитывают начальную температуру Г2н во втором слое из (2.182) превращение во втором слое Х2, интефируя по х (2.181) до достижения нулевого значения интефала Гз,, из (2.182) и хз из (2.181) и так далее, вплоть до х . Если значение х совпадает с х , то оптимальный режим найден, если же нет, то ищут новое значение только одного параметра Х . На этом алгоритме построены задачи оптимизации многослойных реакторов окисления диоксида серы, синтеза аммиака, конверсии оксида углерода и других. [c.158]
chem21.info
3.4. Многомерная безградиентная оптимизация.
Концепция методов
Рассматриваются численные методы оптимизации, у которых величина и направление шага к оптимуму формируются однозначно по определенным функциям в зависимости от свойств критерия оптимальности в окрестности текущей точки без использования производных (т.е. градиента). Все алгоритмы имеют итерационный характер и выражаются формулой
Основная особенность рассматриваемой группы методов — отсутствие вычисления градиента критерия оптимальности. Ряд методов прямого поиска базируется на последовательном применении одномерного поиска по переменным или по другим задаваемым направлениям, что облегчает их алгоритмизацию и применение.
Как и для градиентных методов, на рис. 18 приводятся лишь по одной из возможных траекторий поиска каждым из ниже рассматриваемых методов. Кроме того, также для всех приведенных траекторий выбраны различные начальные условия, с тем, чтобы не загромождать построения.
Основные методы
Метод Гаусса – Зайделя.
Метод Гаусса — Зайделя (в математической литературе используется и другое название — метод покоординатного спуска) заключается в последовательном поиске оптимума R(x) поочередно по каждой переменной. Причем после завершения перебои на всех переменных (т.е. после завершения одного цикла) опять в общем случае приходится перебирать все переменные до тех пор, пока не придем к оптимуму.
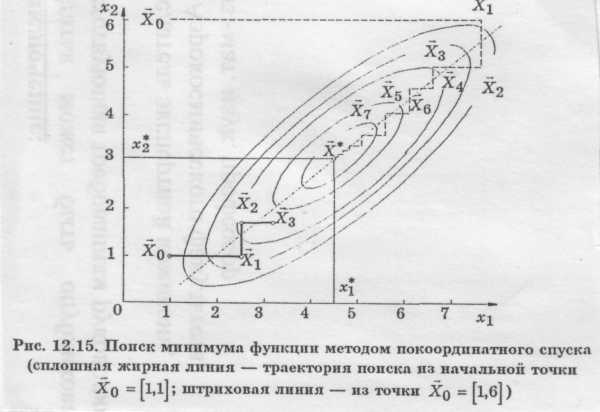
Метод обладает низкой эффективностью в овражных функциях, может застревать в "ловушках", особенно при сравнительно больших шагах h при поиске оптимума по каждой переменной, очень чувствителен и к выбору системы координат. Метод прост в реализации. На эффективность метода влияет порядок чередования переменных.
Условием окончания поиска является малость изменения критерия оптимальности за один цикл или невозможность улучшения критерия оптимальности ни по одной из переменных.
При нахождении оптимума по каждой переменной прекращают поиск не в точке оптимума, а несколько пройдя ее. При этом удается "выскочить из ловушек", за меньшее число циклов выйти и район оптимума. В районе оптимума наблюдается зацикливание, и в этом случае последовательно уменьшают величину последействия.
В двумерных задачах метод Гаусса — Зайделя фактически сводится к методу наискорейшего спуска, так как в обоих методах траектория поиска представляет собой последовательность взаимноортогональных отрезков.
Симплексный метод.
Симплексом в n -мерном пространстве называют фигуру, содержащую n +1 вершину. На плоскости — это треугольник, в трехмерном пространстве — тетраэдр и т.д. Если все вершины симплекса равно удалены друг от друга, то такой симплекс называется регулярным. В литературе можно встретить и другое название метода — метод деформируемого многогранника. В организации алгоритма поиска используется важное свойство симплекса: против каждой вершины находится только одна грань. Суть метода заключается в следующем. В окрестности начальной точки х° строим симплекс, затем находится самая "плохая" его вершина (т.е. та, в которой наихудшее значение критерия оптимальности) и на противоположной грани строится новый симплекс, отличающийся от исходного только одной вершиной. Эта вершина получается симметричным отражением выбрасываемой вершины относительно центра противолежащей грани. Центр грани определяется геометрически, как среднее значение по каждой проекции из всех вершин грани. Алгоритм получения новой вершины записывается следующим образом:
где х1, х2, ... — вектора вершины симплекса (координаты вершин), xj — вектор выбрасываемой вершины, xj — новая вершина в новом симплексе. В скалярном представлении для каждой координаты будет аналогичная формула.
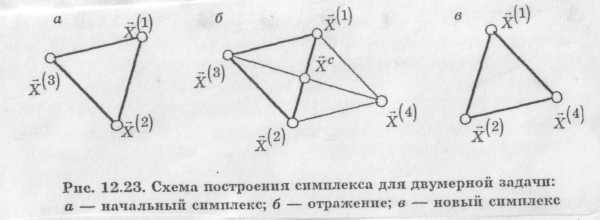
После построения нового симплекса требуется лишь одно вычисление критерия оптимальности: только в новой вершине, так как в остальных углах они вычислены. Далее все повторяется снова.
При выходе в район оптимума процесс поиска «зацикливается». Это имеет место тогда, когда приходится выбрасывать только что полученную вершину (если значение критерия в новой вершине оказывается самое плохое). В этом случае можно «сжимать» симплекс, откладывая новую вершину от грани на расстояние вдвое меньше, чем необходимо.
Хj = 3/(2n) (x1+x2+…xn+1) – (1+3/(2n))xj.
Процесс сжатия происходит многократно, до тех пор пока размеры симплекса не будут меньше заданных.
Пример.
1. Требуется найти минимум функции , где А=1; В=2; С=1,2;D=2.
2. Интервал поиска: х1нач=2, х1кон= 2, х2нач=2, х2кон= 2.
3. Начальная точка: х10= 1,4962, х20=1.
4. Параметры поиска: шаг h=0,5, погрешность = 0,01.
В окрестности заданной начальной точки (1,4962, 1,0000), R=3,9719 сформируем начальный симплекс, его координатами являются:
| №вершины | х1 | х2 | R |
| 1 | 1,7462 | 0,8557 | 4,1938 |
| 2 | 1,2462 | 0,8557 | 1,7519 |
| 3 | 1,4962 | 1,2887 | 6,7368 |
Конечно, можно и по-другому построить начальный симплекс, например, заданная начальная точка может являться одной из вершин симплекса, а не лежать внутри симплекса, как в данном случае. Это не принципиально и на результат существенно не влияет.
Не трудно заметить, что самой плохой вершиной является третья (самое большое значение критерия). Удалим эту вершину и на противоположной грани построим новый симплекс. Практически это означает, что нужно найти одну вершину нового симплекса. Применим базовый алгоритм для каждой переменной х1 и х2 отдельно.
Получим новую вершину:
| №вершины | х1 | х2 | R |
| 4 | 1,4962 | 0,4226 | 0,8839 |
Теперь симплекс образуют вершины 1, 2, 4. Самая плохая вершина – 4. По аналогичной формуле перейдём к следующей новой вершине, «отразив» удаляемую относительно центра грани.
Получим вершину:
| №вершины | х1 | х2 | R |
| 5 | 0,9962 | 0,4226 | 0,4578 |
Теперь симплекс образуют вершины 2, 4, 5. Самая плохая вершина – 2. Строим следующую вершину:
| №вершины | х1 | х2 | R |
| 6 | 1,2462 | 0,0104 | 1,5919 |
Оказалось, что только что полученную вершину нужно будет удалять как самую плохую. Следовательно, необходимо сжимать симплекс, воспользовавшись второй формулой алгоритма.
| №вершины | х1 | х2 | R |
| 7 | 1,2462 | 0,6392 | 0,8750 |
Далее приведём без комментариев координаты вершин следующих симплексов, предоставив учащимся самостоятельно определять самую плохую вершину в каждом текущем симплексе.
| №вершины | х1 | х2 | R | |
| 8 | 0,7462 | 0,6392 | 0,6435 | отражение |
| 9 | 0,4962 | 0,4226 | 0,3610 | отражение |
| 10 | 0,7462 | 0,2061 | 0,3707 | отражение |
| 11 | 0,2462 | 0,2061 | 0,1157 | отражение |
| … | … | … | … | … |
| 15 | 0,4962 | 0,0104 | 0,2526 | отражение |
| 16 | 0,0663 | 0,1520 | 0,0490 | сжатие |
| 17 | 0,3163 | 0,0645 | 0,1238 | отражение |
| 18 | 0,1056 | 0,1385 | 0,0458 | сжатие |
| … | … | … | … | … |
| 24 | 0,0089 | 0,0704 | 0,0100 | отражение |
| 25 | 0,1014 | 0,0814 | 0,0256 | отражение |
| 26 | 0,0546 | 0,0199 | 0,0039 | сжатие |
Симплекс быстро сжимается вокруг искомой оптимальной точки.
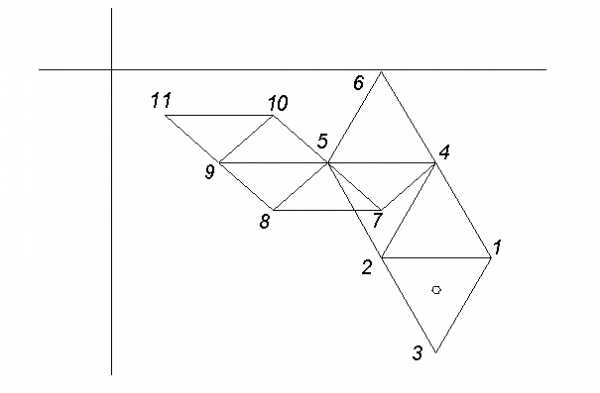
При выходе в район оптимума процесс поиска "зацикливается". Это имеет место тогда, когда приходится выбрасывать только что полученную вершину (эта ситуация возникает в том случае, если значение критерия в новой вершине оказывается самое плохое). В этом случае можно "сжимать" симплекс, откладывая новую вершину от грани на расстоянии вдвое меньше, чем необходимо.
Процесс сжатия происходит многократно, до тех пор, пока размеры симплекса не будут меньше заданных или пока наибольшее расстояние между вершинами симплекса (длина ребра) не будет меньше заданной величины.
Под размерами симплекса понимается расстояние от его центра до всех вершин (в этом случае расстояние от центра до всех вершин должно быть меньше заданного), а иногда и периметр симплекса, т.е. сумма всех его ребер.
Основным недостатком метода является невозможность ускорения поиска вдали от оптимума. Этот недостаток устранен в одной из модификаций метода, известной как метод Нелдера — Мида. В этом варианте симплексного метода предусмотрено растяжение симплекса в случае, если новая вершина лучше лучшей в старом симплексе, а также сжатия симплекса, если новая вершина оказывается хуже наихудшей в старом симплексе.
Имеется также операция уменьшения размера симплекса, называемая редукцией, которая вводится в случае зацикливания. При этом уменьшаются все грани симплекса одновременно в два раза. Уменьшение размера симплекса в два раза осуществляется делением пополам расстояния от каждой точки симплекса до точки х1 определяющей наименьшее значение функции, т.е. будет: xi = xic+0,5(xi - x1).
КОНТРОЛЬНЫЕ ВОПРОСЫ
Метод Гаусса—Зайделя
1. Достаточно ли провести поиск оптимума поочередно по всем переменным последовательно?
2. Область наиболее предпочтительного использования метода Гаусса — Зайделя.
3. Может ли оказывать влияние на результат поиска (значение оптимума) порядок чередования переменных при поиске?
4. Может ли оказывать влияние на эффективность поиска порядок чередования переменных?
5. Условие окончания поиска min R (x).
6. Основное достоинство метода.
7. Основной недостаток метода.
Симплексный метод
1. Что называется симплексом?
2. Как находится вершина нового (следующего) симплекса?
3. Признак зацикливания симплексного поиска.
4. Условие растяжения симплекса в процессе поиска.
5. Алгоритм сжатия симплекса в процессе поиска в одной из модификаций.
6. Условие окончания поиска.
7. Как находится точка, относительно которой отражается новая вершина следующего симплекса?
studfiles.net
Многомерная оптимизация.
Количество просмотров публикации Многомерная оптимизация. - 67
В теоретических и математических задачах принято рассматривать задачи оптимизации как задачи поиска минимума функции. Даже методы имеют общее название – методы спуска. Но всегда легко можно перейти от одного вида экстремума к другому путем смены знака у критерия оптимальности.
Рассмотрим задачу вида:
Метод покоординатного спуска (градиента) формирует шаг по переменным как функцию от градиента R(x) в текущей точки последовательности. Градиент - ϶ᴛᴏ вектор из частных производных, который показывает направление и скорость возрастания функции.
Алгоритм поиска minR(x) в векторной форме записывается в виде: , или в скалярном виде: , где h – величина рабочего шага, i – номер шага. Поиск максимума можно производить в обратном направлении градиента͵ ᴛ.ᴇ. или заменить на поиск минимума противоположной функции.
Выбор величины рабочего шага в направлении градиента зависит от величины градиента и сильно влияет на эффективность метода. Существует ряд алгоритмов коррекции величины h. Остановимся на выборе постоянного рабочего шага.
Для оценки частных производных можно применить алгоритм с парными пробами:
, где gj– пробный шаг по j-й переменной, выбираемый достаточно малым.
Условием окончания поиска может являться , где
Основным недостатком метода является крайне важно сть частого вычисления производных.
Метод наискорейшего спуска сочетает в себе метод градиента и методы одномерной оптимизации.
Алгоритм метода:
1. Выбирается начальная точка.
2. В текущей точке вычисляется градиент.
3. В направлении вычисленного градиента ищется любым методом одномерной оптимизации. Наиболее часто используется сканирование до первого локального минимума. Полученная точка локального минимума считается следующей точкой последовательности.
4. Повторяются пункты 2 и 3 до выполнения условия окончания
Можно использовать уменьшения рабочего шага после каждой смены направления, чтобы с большей точностью находить оптимум.
ЗАДАЧА 6.2.
Требуется найти минимум функции
1. Рассмотрим метод покоординатного спуска.
Выберем ; h=0,1; g=0,01; ε=0,01
Делаем рабочий шаг и получаем:
Результаты дальнейших шагов сведем в таблицу:
| № | х1 | х2 | dR/d х1 | dR/d х2 | /gradR/ | R |
| 2 | 0,002 | 0,280 | -2,78 | -4,8 | 5,547 | 1,375 |
| 3 | 0,302 | 0,568 | -2,7258 | -1,7280 | 3,2274 | -2,5060 |
| 4 | 0,575 | 0,741 | -2,0085 | -1,0368 | 2,2603 | -,34002 |
| … | ||||||
| 14 | 1,000 | 0,998 | -0,005 | -0,0063 | 0,0063 | -4,0000 |
Получили grad R(x)=0,0063<0,01, следовательно, поиск можно прекратить.
x1=1; x2=0,998; R(x)=-4
2. При тех же начальных значениях рассмотрим метод наискорейшего спуска.
| № | х1 | х2 | dR/d х1 | dR/d х2 | /gradR/ | R |
| 1 | -0,5 | -1 | -2,25 | -8 | 8,31 | 7,375 |
| 1 | -0,5-0,1(-2,25)= -0,275 | -1-0,1(-8)=-0,2 | -2,25 | -8 | 8,31 | 1,6842 |
| 1 | -0,050 | 0,6 | -2,25 | -8 | 8,31 | -1,5301 |
| 1 | 0,175 | 1,4 | -2,25 | -8 | 8,31 | -2,1996 |
В следующей точке (0,4; 0,2) значение R(x)=-0,256>-2,196. По этой причине в найденной точке снова вычисляем градиент и по нему совершаем шаги до тех пор, пока не найдем наилучшую точку.
| № | х1 | х2 | dR/d х1 | dR/d х2 | /gradR/ | R |
| 2 | 0,175 | 1,4 | -2,9081 | 1,6 | 3,3192 | -2,1996 |
| 2 | 0,466 | 1,24 | -2,9081 | 1,6 | 3,3192 | -3,1811 |
| 2 | 0,757 | 1,08 | -2,9081 | 1,6 | 3,3192 | -3,8239 |
| 2 | 1,047 | 0,92 | -2,9081 | 1,6 | 3,3192 | -3,9804 |
ПРИМЕЧАНИЕ. В случае если начальная точка выбрана вдали от локального экстремума, то метод спуска может привести к неограниченному убыванию функции.
Задание 6.2.
Закончить поиск минимума по методу наискорейшего спуска.
referatwork.ru
Тема 1.8. Многомерная оптимизация
1.8.1. Постановка задачи и основные определения
1.8.2. Методы спуска
1.8.3. Метод градиентного спуска с дроблением шага
1.8.4. Метод наискорейшего спуска
1.8.5. Проблема оврагов. Метод покоординатного спуска
1.8.6. Тестовые задания по теме «Многомерная оптимизация»
1.8.1. Постановка задачи и основные определения
Задача, требующая нахождения оптимального значения функции mпеременныхf(Х)=f(x1, x2, …, xm), называется задачеймногомерной оптимизации. Так же, как и для случая одномерной оптимизации, задача нахождения максимума функции сводится к задаче нахождения минимума путем замены целевой функцииfна-f.
Пусть функция f(Х) = f(x1, x2, …, xm)определена на некотором множествеХRm. ЕслиХ=Rm(т.е. ограничения на переменныеx1, x2, …, xmотсутствуют), принято говорить о задаче безусловной минимизации. В противном случае, когдаХ ¹ Rm, говорят о задаче условной минимизации.
Методы решения задачи безусловной минимизации являются основой для перехода к изучению более сложных методов решения задач условной минимизации.
В постановке задачи безусловной оптимизации для f(Х)=f(x1, x2, …, xm)требуется найти хотя бы одну точку минимумаХ*и вычислитьf*=f(Х*).ТочкаХ*ÎRmназывается точкой глобального минимума функцииf на множествеХ, если для всехХÎRmвыполняется неравенствоf(Х*)£f(Х).В этом случае значениеf(Х*)называется минимальным значением функцииf наRm.
Точка Х*Î Rmназывается точкой локального минимума функцииf, если существует такаяd- окрестностьUdэтой точки(d>0),что для всехХÎХd=ХUdвыполняется неравенствоf(X*)£f(X).
Подавляющее большинство методов решения задачи безусловной минимизации в действительности являются методами поиска точек локальных минимумов, среди которых затем выделяют глобальный минимум, являющийся наименьшим. Этот способ очень трудоемок, поэтому чаще используют другой: местоположение точки глобального минимума определяют в ходе анализа решаемой задачи, а затем для его уточнения с заданной точностью применяют один из методов поиска точки локального минимума.
Рассмотрим функцию нескольких переменных и введем для нее основные определения.
Множество точек, для которых целевая функция принимает постоянное значение f(x1, x2, …, xm) = c, называетсяповерхностью уровня. Для функции двух переменных (m = 2) это множество называетсялинией уровня.
Функция f(x1,x2)задает в трехмерном пространстве некоторую поверхностьU=f(x1,x2)(рис. 1.8.1-1), низшая точка которой и дает решение задачи минимизации. Для того чтобы изобразить рельеф этой поверхности, проведем несколько плоскостей(U = const): U=c1, U=c2, U=c3. Проекции на плоскостьОх1х2линий пересечений этих плоскостей с поверхностью и даютлинии уровня.
Рис. 1.8.1-1
Для дифференцируемой функции можно определить вектор из первых частных производных,который называетсяградиентом:
или .
Направление вектора градиента указывает направление наискорейшего возрастания функции, а его модуль (длина) равен скорости возрастания функции. Вектор Градиент нормален к линии уровня в каждой своей точке и касателен к поверхности, которую задает функция.
Вектор -называетсяантиградиентоми показывает направление наискорейшего убывания функции.
Равенство нулю градиента в точке Хявляется необходимым условием того, чтобы внутренняя для множестваХi (i = 1, 2,…m)точкаХбыла точкой локального минимума дифференцируемой функцииf. ТочкаХ, для которой выполняется равенствоf’(X) = 0, называетсястационарной точкой функции.
Это равенство представляет собой систему из mнелинейных уравнений относительно компонентх1, х2, …, хm, вектораX, гдеm– количество переменных.
Для функции двух переменных Q(x, y) это условие имеет вид:
Однако не всякая стационарная точка является точкой минимума. Для всякой непрерывно дифференцируемой функции fдостаточным условием того, чтобы стационарная точкаХбыла точкой локального минимума, является положительная определенность матрицы вторых производных (матрицы Гессе):
Согласно критерию Сильвестра, для того чтобы матрица была положительно определена, необходимо, чтобы все угловые миноры были положительны:
Для функции двух переменных Q(x, y)матрица Гессе имеет вид:
,
а достаточное условие существования минимума:
Алгоритм решения задачи оптимизации функции двух переменных Q(x,y)аналитическим (классическим) методом следующий:
Составляется и решается система уравнений
из которой находятся (x*, y*).
Проверяются достаточные условия существования минимума
.
Если (x*, y*)– единственное решение и в этой точке выполняются достаточные условия, то это точка минимума. Если хотя бы в одном из неравенств получается знак “<”, то минимума не существует. В случае появления знака “=” необходимо исследовать производные высших порядков.
Пример 1.8.1-1. Найти точку локального минимума функции.
f(x,y) = x2 + y2 – 4x + 100 – 8y.
Следовательно, в точке x* = 2 и y* = 4функция имеет локальный минимум.
Пример 1.8.1-2. Найти точку локального минимума функции f(x,y)= x2+y2–4x+10xy–8y.
Следовательно, функция не имеет точки локального минимума.
Аналитический метод поиска минимума применяется только для ограниченного круга задач. В основном это связано с необходимостью решения системы нелинейных уравнений, которая, как правило, решается численными методами. Оказывается, гораздо проще сразу решать задачу минимизации численными методами. Рассмотрим некоторые из методов.
studfiles.net
5. Многомерная оптимизация. Линейное программирование
Оптимизация – это целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях.
Количественная оценка оптимизируемого качества называется критерием оптимальности или целевой функцией. Её можно записать в виде:
, (5.1)
где –некоторые параметры объекта оптимизации.
Существуют два типа задач оптимизации – безусловные и условные.
Безусловная задача оптимизации состоит в отыскании максимума или минимума действительной функции (5.1) от n действительных переменных и определении соответствующих значений аргументов.
Условные задачи оптимизации, или задачи с ограничениями, - это такие, при формулировке которых на значения аргументов налагаются ограничения в виде равенств или неравенств.
Решение задач оптимизации, в которых критерий оптимальности является линейной функцией независимых переменных (то есть содержит эти переменные в первой степени) с линейными ограничениями на них, составляет предмет линейного программирования.
Слово «программирование» отражает здесь конечную цель исследования – определение оптимального плана или оптимальной программы, по которой из множества возможных вариантов исследуемого процесса выбирают по какому-либо признаку наилучший, оптимальный, вариант.
Примером такой задачи является задача оптимального распределения сырья между различными производствами при максимальной стоимости продукции.
Пусть из двух видов сырья изготавливается продукция двух видов.
Обозначим:
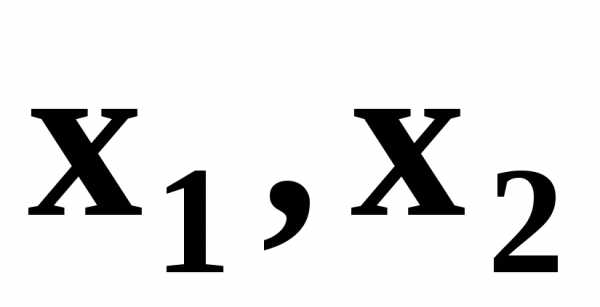 –число единиц продукции первого и второго вида, соответственно;
–число единиц продукции первого и второго вида, соответственно;
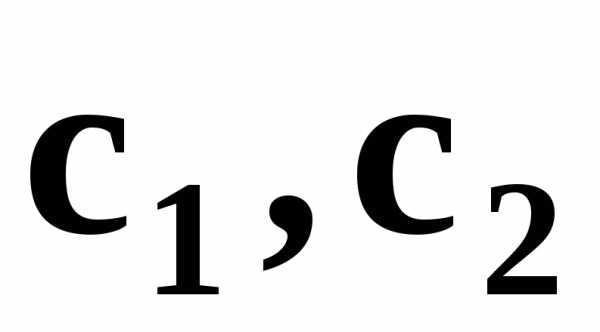 –цена единицы продукции первого и второго вида, соответственно.
–цена единицы продукции первого и второго вида, соответственно.
Тогда общая стоимость всей продукции будет
. (5.2)
В результате производства желательно, чтобы общая стоимость продукции была максимальной. – целевая функция в данной задаче.
Обозначим далее:
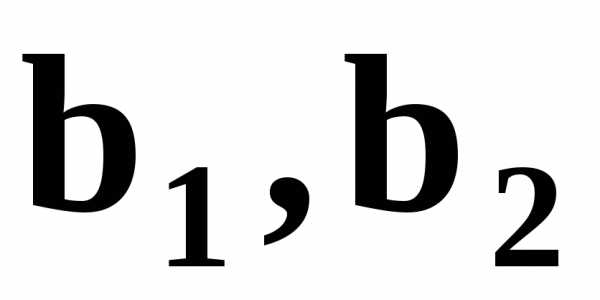 –количество сырья первого и второго видов, имеющееся в наличии;
–количество сырья первого и второго видов, имеющееся в наличии;
 –число единиц i-го вида сырья, необходимое для производства единицы j-го вида продукции.
–число единиц i-го вида сырья, необходимое для производства единицы j-го вида продукции.
Учитывая, что расход данного ресурса не может превышать общего его количества, запишем ограничительные условия по ресурсам:
| | (5.3) |
Относительно переменных 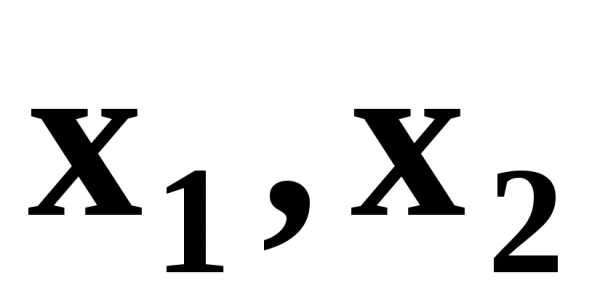 можно ещё сказать, что они неотрицательны и не бесконечны.:
можно ещё сказать, что они неотрицательны и не бесконечны.:
|
| (5.4) |
Среди множества решений системы неравенств (5.3) и (5.4) требуется найти такое решение (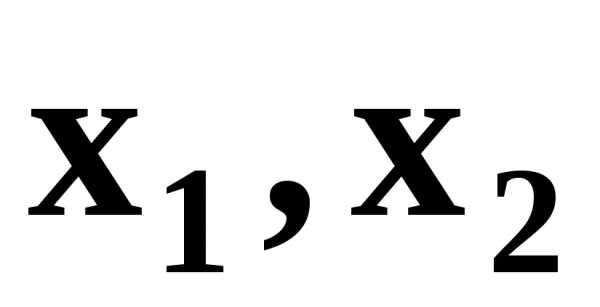 ), для которого функция R достигает наибольшего значения.
), для которого функция R достигает наибольшего значения.
В аналогичном виде формулируются так называемые транспортные задачи (задачи оптимальной организации доставки товаров, сырья или продукции из различных складов к нескольким пунктам назначения при минимуме затрат на перевозку) и ряд других.
Графический метод решения задачи линейного программирования.
Пусть требуется найти  и
и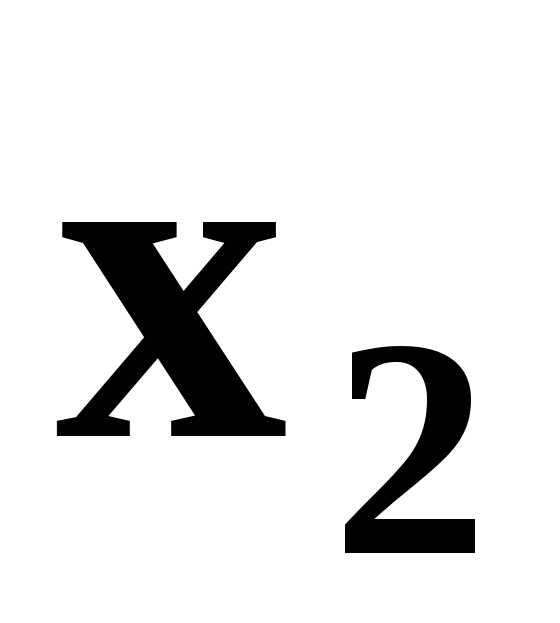 , удовлетворяющие системе неравенств
, удовлетворяющие системе неравенств
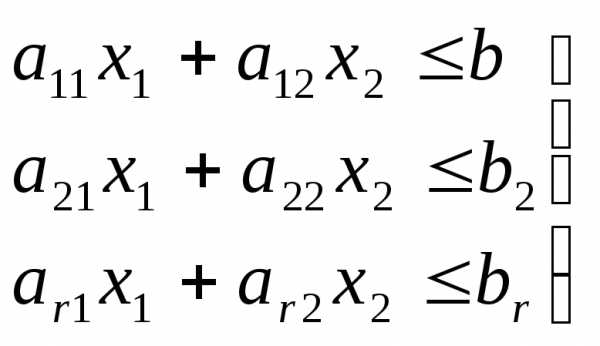 (5.5)
(5.5)
и условиям неотрицательности
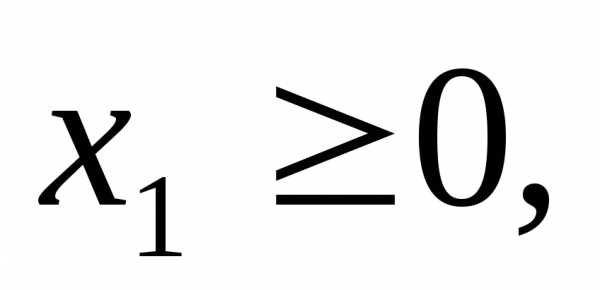
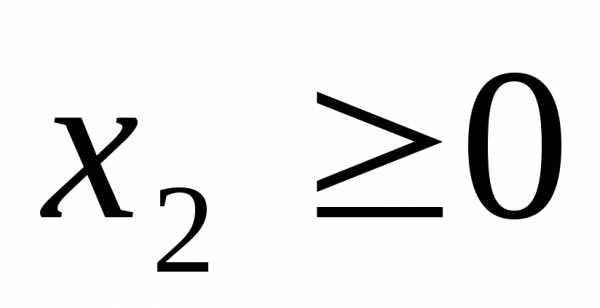 , (5.6)
, (5.6)
для которых функция
(5.7)
достигает максимума.
Решение.
| Построим в системе прямоугольных координат (i = 1, 2, … , r) | Рис. 11 |
Эта прямая делит плоскость 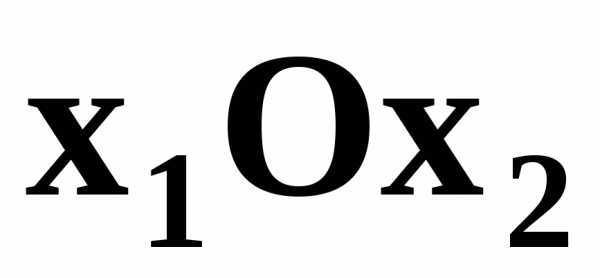 на две полуплоскости. Для координат
на две полуплоскости. Для координат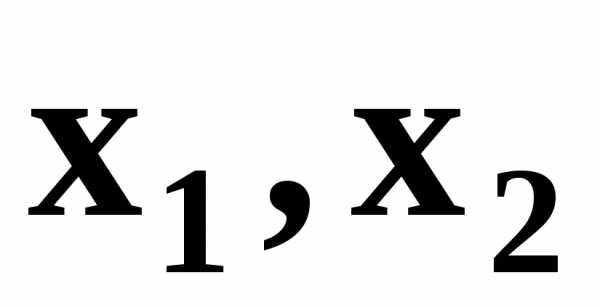 любой точкиА одной полуплоскости выполняется неравенство , а для координат
любой точкиА одной полуплоскости выполняется неравенство , а для координат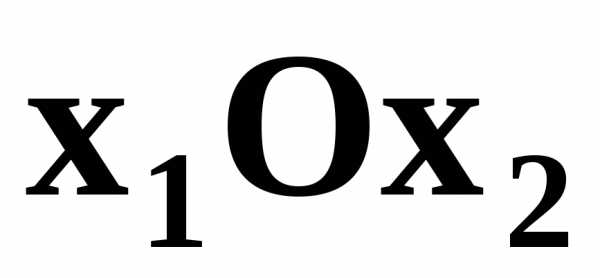 любой точки В другой полуплоскости - противоположное неравенство . Координаты любой точки граничной прямой удовлетворяют уравнению.
любой точки В другой полуплоскости - противоположное неравенство . Координаты любой точки граничной прямой удовлетворяют уравнению.
Для определения того, по какую сторону от граничной прямой располагается полуплоскость, соответствующая заданному неравенству, достаточно «испытать» одну какую-либо точку (проще всего точку О (0;0)). Если при подстановке её координат в левую часть неравенства оно удовлетворяется, то полуплоскость обращена в сторону к испытуемой точке, если же неравенство не удовлетворяется, то соответствующая полуплоскость обращена в противоположную сторону. Направление полуплоскости показывается на чертеже штриховкой. Неравенствам 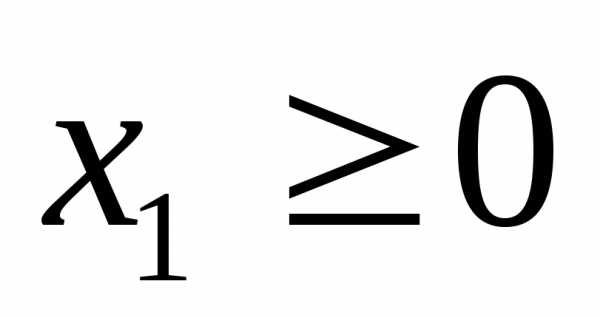 и
и 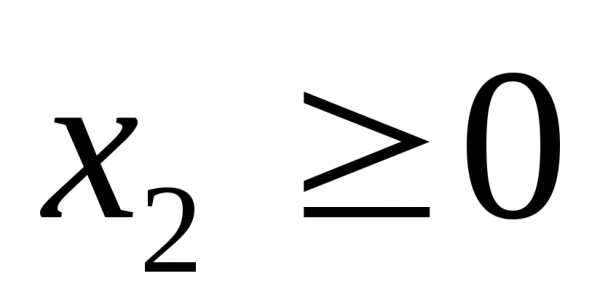 соответствуют полуплоскости, расположенные справа от оси ординат и над осью абсцисс.
соответствуют полуплоскости, расположенные справа от оси ординат и над осью абсцисс.
На рисунке строим граничные прямые и полуплоскости, соответствующие всем неравенствам.
Общая, часть (пересечение) всех этих полуплоскостей будет представлять собой область допустимых решений данной задачи.
При построении области допустимых решений в зависимости от конкретного вида системы ограничений (неравенств) на переменные может встретиться один из следующих четырех случаев:
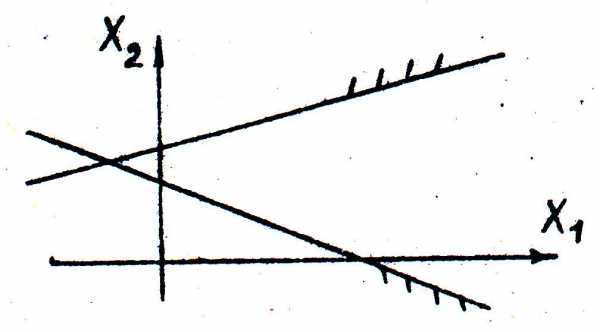 Рис. 12. Область допустимых решений пустая, что соответствует несовместности системы неравенств; решения нет.
Рис. 12. Область допустимых решений пустая, что соответствует несовместности системы неравенств; решения нет.
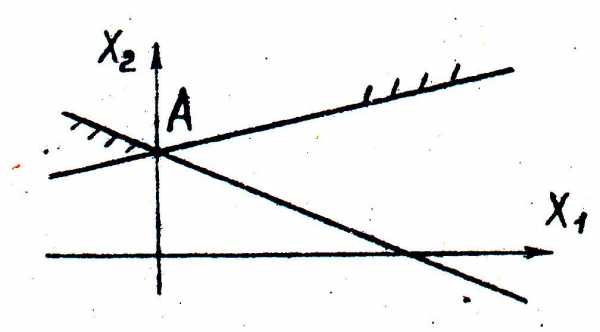
Рис. 13. Область допустимых решений изобра- жается одной точкой А, что соответствует единственному решению системы.
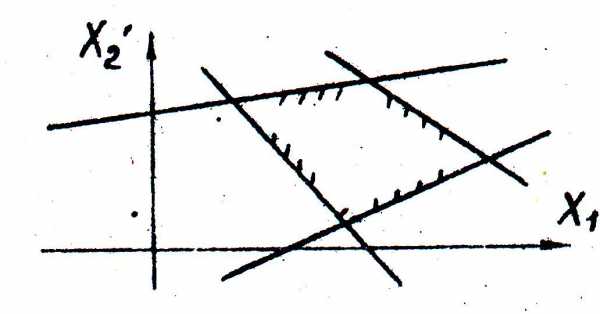 Рис. 14. Область допустимых решений ограниченная, изображается в виде выпуклого многоугольника. Допустимых решений бесконечное множество.
Рис. 14. Область допустимых решений ограниченная, изображается в виде выпуклого многоугольника. Допустимых решений бесконечное множество.
Р ис. 15. Область допустимых решений неограни-ченная, в виде выпуклой многоугольной области. Допустимых решений бесконечное множество.
ис. 15. Область допустимых решений неограни-ченная, в виде выпуклой многоугольной области. Допустимых решений бесконечное множество.
Графическое изображение целевой функции при фиксированном значенииR определяет прямую, а при изменении R - семейство параллельных прямых с параметром R. Для всех точек, лежащих на одной из прямых, функция R принимает одно определенное значение, поэтому указанные прямые называются линиями уровня для функции R.
Вектор градиента , перпендикулярный к линиям уровня, показывает направление возрастанияR.
З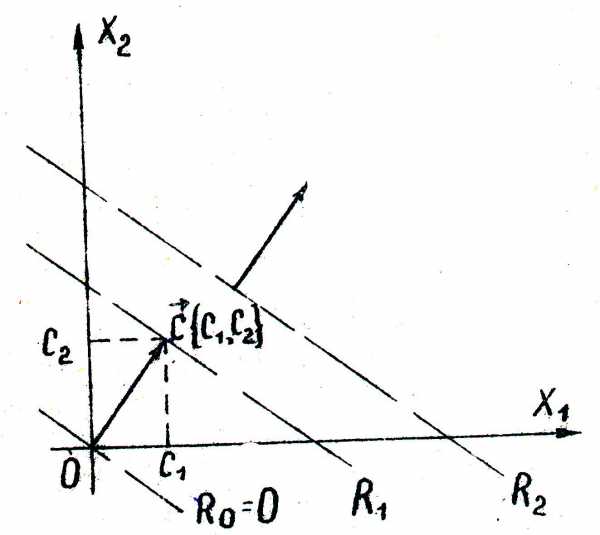 адача отыскания оптимального решения системы неравенств (5.5), для которого целевая функцияR (5.7) достигает максимума, геометрически сводится к определению в области допустимых решений точки, через которую пройдет линия уровня, соответствующая наибольшему значении параметра R
адача отыскания оптимального решения системы неравенств (5.5), для которого целевая функцияR (5.7) достигает максимума, геометрически сводится к определению в области допустимых решений точки, через которую пройдет линия уровня, соответствующая наибольшему значении параметра R
.
Рис. 16
Если область допустимых решений есть выпуклый многоугольник, то экстремум функции R достигается, по крайней мере, в одной из вершин этого многоугольника.
Если экстремальное значение R достигается в двух вершинах, 'то такое же экстремальное значение достигается в любой точке на отрезке, соединяющем эти две вершины. В этом случае говорят, что задача имеет альтернативный оптимум.
В случае неограниченной области экстремум функции R либо не существует, либо достигается в одной из вершин области, либо имеет альтернативный оптимум.
Пример.
Пусть требуется найти значения  и
и 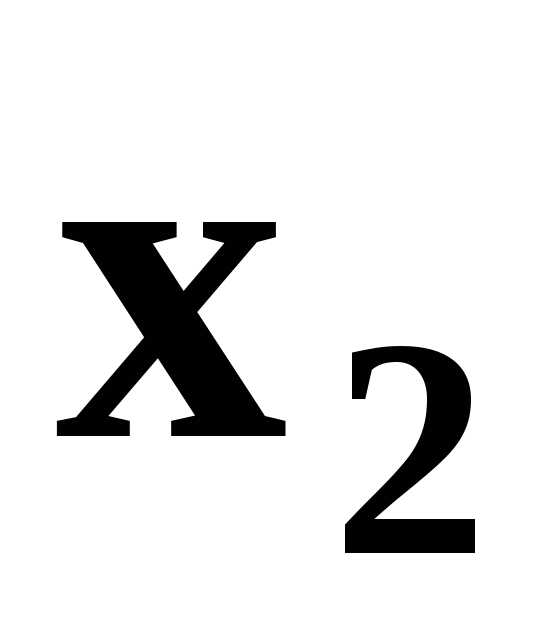 , удовлетворяющие системе неравенств
, удовлетворяющие системе неравенств
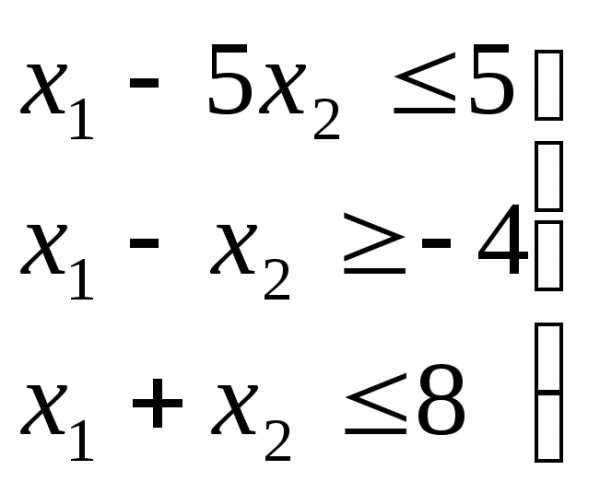
и условиям неотрицательности
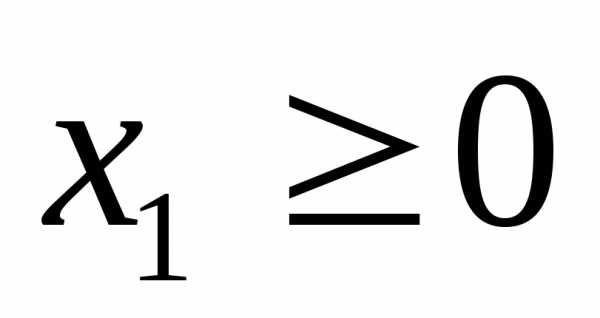 ,
, 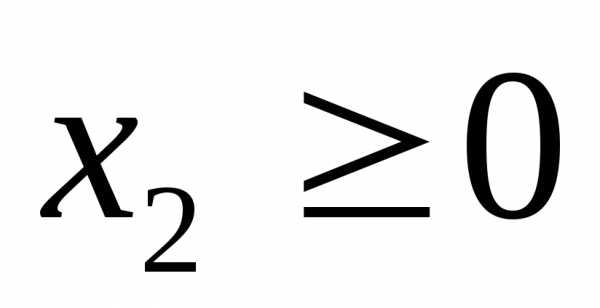 ,
,
для которых функция
достигает максимума.
Решение.
Заменим каждое из неравенств равенством и построим граничные прямые:
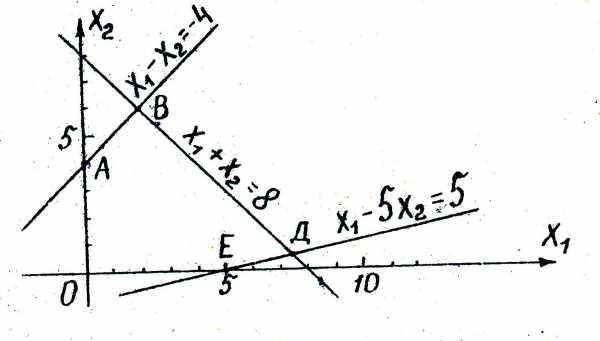
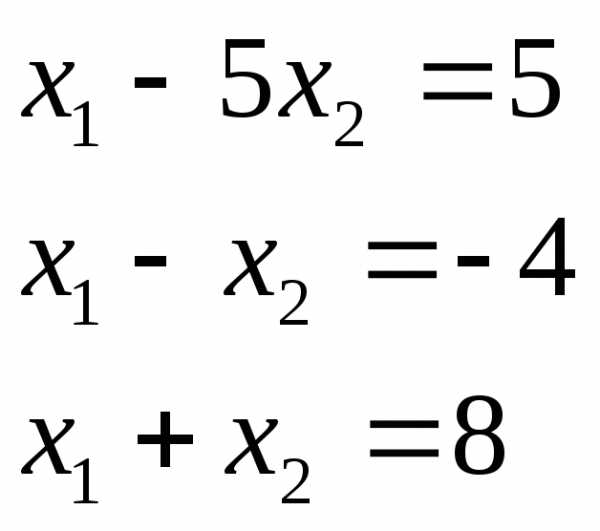
Рис. 17
Определим полуплоскости, соответствующие данным неравенствам, путём «испытания» точки (0;0). С учетом неотрицательности  и
и 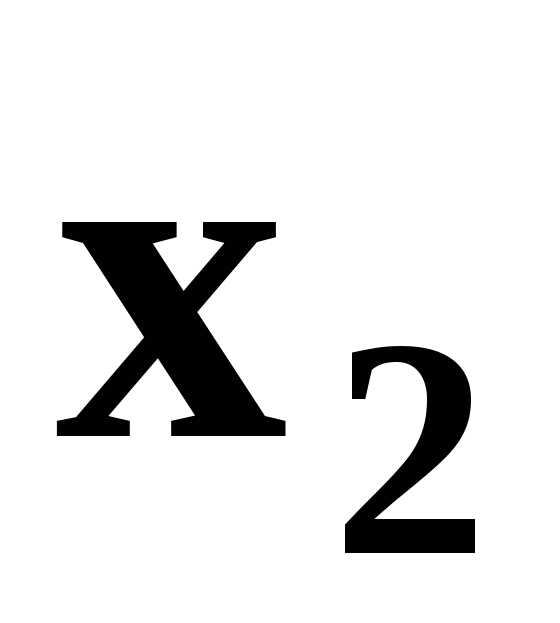 получим область допустимых решений данной задачи в виде выпуклого многоугольникаОАВДЕ.
получим область допустимых решений данной задачи в виде выпуклого многоугольникаОАВДЕ.
В области допустимых решений находим оптимальное решение, строя вектор градиента , показывающий направление возрастанияR.
Оптимальное решение соответствует точке В, координаты которой можно определить либо графически, либо путем решения системы двух уравнений, соответствующих граничным прямым АВ и ВД:
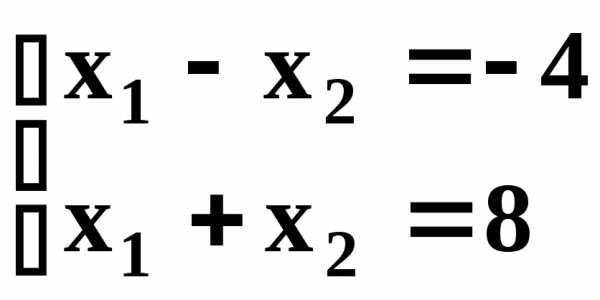
Ответ:
Задания. Найти положение точки экстремума и экстремальное значение целевой функции при заданных ограничениях.
Таблица 9.
| № варианта | Экстремум | a | b | c | Ограничения |
| 0 | Max | 2,1 | 5,5 | 1,4 | ; ; ; |
| 1 | Max | 3,0 | 0,9 | 1,8 | ;;; ; |
| 2 | Min | 4,5 | 6,7 | 0,6 | ;; ;; |
| 3 | Max | 0.8 | 5,4 | 3,1 | ;;;; |
| 4 | Min | 1,9 | 2,6 | -1,2 | ;;;; |
| 5 | Min | 4,1 | 5,2 | 9,3 | ;;;; |
| 6 | Min | 5,4 | 1,5 | 5,7 | ;;; ; |
| 7 | Max | 3,8 | 2,9 | 1,3 | ;;;; |
| 8 | Max | 1,4 | 5,8 | 4,2 | ;;;; |
| 9 | Min | 4,6 | 1,1 | 6,5 | ;;;; |
studfiles.net
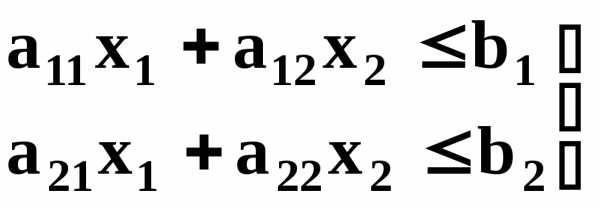
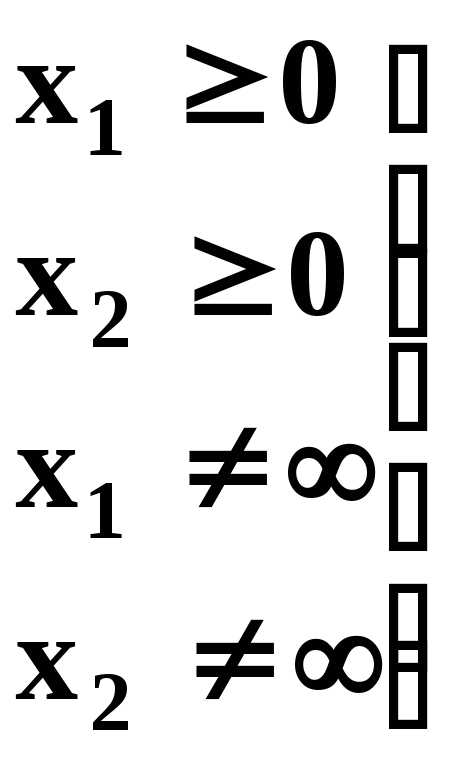
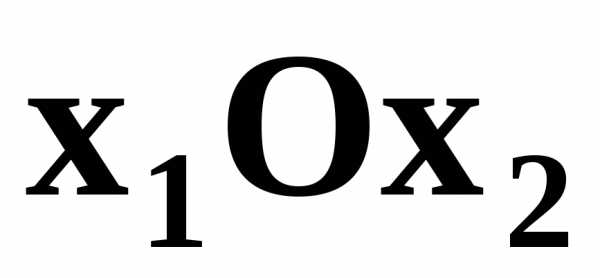 область допустимых решений задачи (рис.11). Для этого, заменяя каждое из неравенств (5.5) равенством, строим соответствующую ему граничную прямую
область допустимых решений задачи (рис.11). Для этого, заменяя каждое из неравенств (5.5) равенством, строим соответствующую ему граничную прямую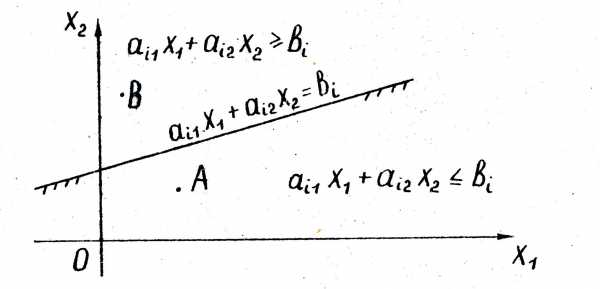
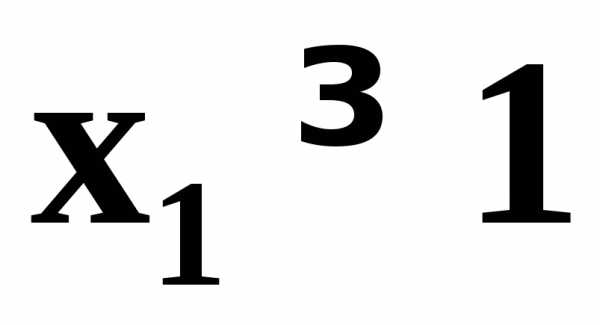 ;
;