Методы оптимизации производственной программы. Методы оптимизации производства
Задачи оптимизации производства - Энциклопедия по экономике
Глава II. Задачи оптимизации производства 179 [c.179]
Глава П. Задачи оптимизации производства 181 [c.181]
Задача оптимизации производства для предприятия ставится в форме максимизации выручки или прибыли при заданных ассортименте выпускаемой продукции и ограничениях на имеющиеся запасы ресурсов (сырье, оборудование, труд, производственные площади и др.). Задача может ставиться и в форме минимизации затрат при выпуске заданных объемов продукции несколькими способами производства. Оптимизационные задачи могут быть поставлены не только для предприятий реального сектора экономики, но также и для торговли, банковской и страховой деятельности. [c.44]
Все это способствует повышению уровня аналитической № нормативной работы, большей обоснованности решений. Внедрение АСУП позволяет определять ряд аналитических показателей, расчет которых затруднен фондо-, материале- и трудоемкость. Использование их для планирования и анализа позволяет более четко устанавливать затраты на производство каждого продукта и пути их снижения, определять влияние структурных изменений (изменение ассортимента продукции) на конечные показатели работы предприятия. При расчете экономической эффективности АСУП учитывают экономический эффект, достигаемый в результате оптимизации производства и снижения трудоемкости решения учетных задач. [c.305]
Задача оптимизации формулируется следующим образом необходимо находить и постоянно поддерживать такие управляющие воздействия, которые обеспечат достижение максимального (или минимального) значения целевой функции, зависящей от вектора управляющих и возмущающих воздействий (контролируемых и неконтролируемых). Целевой функцией при осуществлении процесса может быть один из следующих технико-экономических показателей прибыль, количество выпускаемой товарной продукции, затраты на производство и т. д. Наиболее общим из перечисленных критериев является прибыль П, которая для производства полипропилена в укрупненном виде выражается следующим образом [c.423]
Новые возможности для использования всех рассмотренных выше методов открываются применением в планировании методов экономико-математического моделирования. Так, например, аппарат межотраслевого моделирования позволяет увязать баланс народного хозяйства с системой материальных балансов, с отраслевыми расчетами потребности в продукции и структуры затрат на ее производство, с расчетами по капитальному строительству, уровню жизни населения и др., а в конечном счете — поставить и решить задачу оптимизации межотраслевых связей. Тем самым балансовый метод получает свое дальнейшее развитие за счет применения методов межотраслевого моделирования и оптимального планирования. Методы сетевого планирования, матричной алгебры, оптимизации выступают в качестве инструментов практической реализации программно-целевого подхода, а методы математической статистики находят широкое применение в прогнозировании. [c.95]
БП—блоки оптимизационных задач. В таких блоках могут объединяться двух-трехуровневые системы оптимизации расчетов. Примером такого блока может служить блок оптимизации агропромышленного комплекса, включающий однопродуктовые задачи оптимизации развития и размещения производства (например, по отдельным сельскохозяйственным культурам), многопродуктовые задачи того же типа (например, по растениеводству в целом) и задачу оптимизации по всему агропромышленному комплексу [c.136]
Следует отметить, что методы оптимизации находят применение и в задачах текущего планирования. Так, ГВЦ Госплана СССР совместно с отделом легкой промышленности Госплана СССР в течение уже ряда лет решаются задачи оптимизации годовых планов производства тканей, тюлегардинных изделий, обуви. В этих задачах определяется такой вариант объема и структуры производства продукции данной подотрасли, который обеспечивает наиболее полное удовлетворение потребностей народного хозяйства и населения при заданных ограничениях по материальным ресурсам (прежде всего — исходному сырью) и производственным мощностям с учетом планируемого уровня их использования. [c.213]
Организационная структура российских предприятий -наследство плановой экономики. В условиях, когда финансовые и материальные ресурсы жестко лимитировались государством для достижения определенных производственных результатов, такое разбиение производства по функциональным звеньям полностью оправдывало себя. Рыночная экономика диктует свои правила игры компании вынуждены сами формировать стратегию, изыскивать ресурсы для обеспечения своей деятельности и эффективно их использовать с целью достижения определенного финансового результата. Однако существующая организационная система, как совокупность функциональных звеньев, не позволяет решить задачу оптимизации финансовых и материальных потоков и, самое главное, не позволяет контролировать расходование этих ресурсов в процессе производства. Для устранения диссонанса между целью системы и ее [c.92]
В современных рыночных условиях развития нефтеперерабатывающих и нефтехимических предприятий в России, обострения конкуренции между отдельными заводами и нефтяными компаниями все более важными становятся вопросы повышения эффективности функционирования производства. И в первую очередь разрешение этих вопросов связано с улучшением методологии и инструментария производственного и инвестиционного планирования, решением задач оптимизации (с точки зрения максимизации получаемой прибыли или минимизации производственных затрат) производственных планов, отражающих различные сценарии изменения рыночного окружения и технологического состояния производства. [c.331]
Задачи оптимизации современным производством обычно являются многоцелевыми (многокритериальными). К основным критериям управления можно отнести повышение производи- [c.16]
Повышение эффективности основного производства ГДП достигается за счет автоматизированных расчетов на ЭВМ технологических режимов работы оборудования и выбора наиболее рациональных режимов эксплуатации, промысловых объектов. Использование ЭВМ для регулирования технологических процессов позволяет уточнить расчеты сменного диспетчера и значительно увеличить их объем, что является промежуточным этапом внедрения оптимальных систем управления и служит предпосылкой успешного освоения сменным диспетчером необходимых навыков работы при переходе к решению задач оптимизации [38]. [c.99]
Регулирование технологических процессов добычи и подготовки газа предусматривает стабилизацию параметров процессов, для чего используются системы автоматического регулирования давлений, температур, соотношений технологических потоков, качественных показателей газа и конденсата. Задания для регулирования выбираются на основе решения задач расчета технологических режимов. Этот комплекс задач состоит из локальных задач рационального распределения нагрузки и расчета рациональных режимов работы технологического оборудования, решаемых на конкретных технологических установках, обеспечивающих добычу и подготовку газа и конденсата к транспорту. Решение задач оперативного регулирования режимов работы объектов основного производства дает информационную основу для последующего решения задач оптимизации режимов работы объектов добычи и подготовки газа к транспорту, заключающейся в выборе и поддержании наивыгоднейших технологических [c.99]
Оптимальным считается такой объем реализации, который обеспечивает получение максимальной прибыли при сложившихся условиях производства в определенном ценовом диапазоне. Задача оптимизации больше теоретическая, чем практическая, однако оптимальный объем при планировании выпуска продукции является тем ориентиром, знание которого необходимо. [c.131]
В этой главе мы рассмотрели приемы линейного программирования при решении задач оптимизации. Типичный пример — максимизация прибыли предприятия за счет определения соответствующей номенклатуры производства. Кроме того, задачи линейного программирования могут быть направлены на минимизацию переменных, в частности затрат. Выражение, которое необходимо оптимизировать, называется объективной функцией. Эта функция высчитывается при наличии ряда ограничений. Одна из самых больших трудностей при решении такого рода задач состоит в исходной постановке задачи, когда необходимо определить ограничения, представить их в виде неравенств и выдать выражение объективной функции. При решении простых задач только с двумя переменными можно применить графический метод. Для более сложных задач применяется симплексный метод. [c.304]
Линейное и целочисленное программирование используется для принятия управленческих решений в таких областях, как планирование и составление графиков производства, создание и расходование складских запасов, финансовое планирование, отбор портфеля заказов, маркетинг и реклама товаров компаний и т. п. Тем не менее при всей своей прогностической способности линейное и целочисленное программирование не отличается высокой степенью предвидения элементов неоднозначности. Уже давно концептуально решена задача оптимизации поставленной цели, зависящей от ряда ограничительных факторов. Интуиция и здравый смысл являются серьезными помощниками при решении довольно простых задач и позволяют оптимизировать результат решения задачи без специальных знаний и сложных методик количественной оценки. Однако при решении сложных задач, включающих сотни переменных и ограничителей, интуиция и здравый смысл помогают мало. [c.254]
Во-первых, базовая модель анализа, изображенная на рис. 1, решает задачу нахождения оптимальной величины физического объема сбыта и уровня цен реализации для одного вида продукции. При ограниченных ресурсах предприятия и наличии широкого ассортимента сбыта на практике часто необходимо решать задачи оптимизации структуры производства и сбыта, исходя из сравнения планируемого дохода от реализации различных видов продукции. Это в достаточной степени усложняет алгоритм СКР-анализа. [c.45]
Цель классификации задач оптимизации — показать, что эти задачи, различные по своему содержанию, можно решать на компьютере с помощью стандартных программных продуктов. Классификацию задач оптимизации, возникающих на производстве, можно выполнить по следующим признакам область применения содержание задачи класс экономико-математических моделей. [c.103]
Раздельное решение задач не обеспечивает нахождения оптимальных плановых решений, и это нашло отражение в структуре системы моделей оптимального текущего планирования нефтеперерабатывающего производства [1], включающей отраслевую модель оптимизации производства и распределения нефтепродуктов, модель линейного программирования комплекса НПП и модель линейного программирования НПП, обеспечивающих расчет производственной программы отдельных предприятий, распределение плановых заданий между комплексами предприятий. [c.12]
Учитывая указанные обстоятельства, представляется целесообразным использование многоэтапной постановки стохастической задачи оптимизации календарного планирования основного производства НПП с жесткими условными вероятностными ограничениями следующего вида [c.60]
На нефтеперерабатывающих производствах значимая корреляция между технологическими коэффициентами а,-у и компонентами Ь/ вектора ограничений, которую следовало бы учитывать при формализации задачи оптимизации, также не наблюдается. Это связано с тем, что в соответствии с существующей схемой переработки нефти и нефтепродуктов целевая продукция НПП вырабатывается в товарном блоке в результате реализации специальной операции компаундирования. Кроме того, на [c.69]
ЗАДАЧА ОПТИМИЗАЦИИ КАЛЕНДАРНЫХ ПЛАНОВ НЕФТЕПЕРЕРАБАТЫВАЮЩИХ ПРОИЗВОДСТВ [c.75]
Эти обстоятельства обусловливают необходимость разработки вероятностных динамических постановок и соответствующих стохастических моделей задач оптимизации календарных планов нефтеперерабатывающих производств. [c.78]
Разбивка годовой производственной программы на календарные отрезки времени осуществляется на основе вероятностной модели многоэтапной стохастической задачи оптимизации календарною планирования основного производства НПП. [c.177]
В многономенклатурном химическом производстве, где им. ется возможность варьировать номенклатуру и ассортимент выпускаемой продукции, возникает задача оптимизации производственной программы, т. е. выбора оптимального ассортимента продукции. [c.190]
Рассматриваемый подход анализа изделия как системы, состоящей из нескольких узлов, способствует решению еще одной важной задачи — оптимизации надежности и себестоимости электроизделий (электрических машин, аппаратов и др.) при их функционировании в системах автоматизации. Каждый отказ электроизделий приводит во многих случаях к отказу всей системы автоматизированного электропривода. Поэтому относительно высокие показатели надежности электроизделий в ряде случаев оказываются недостаточными с точки зрения требований АСУТП. Задача оптимизации надежности и себестоимости электроизделий с точки зрения их работы в системах решается на основе принципов, изложенных выше. При этом анализируются все электротехнические изделия, входящие в систему автоматизации, каждое из которых имеет несколько вариантов производства их элементов, отличающихся себестоимостью изготовления и числовыми значениями показателей надежности. С помощью решения задачи на ЭВМ определяется оптимальный вариант изготовления каждого элемента по всем изделиям, входящим в систему автоматизации, а также оптимальный вариант конструкций электроизделий, который обеспечивает минимум приведенных затрат при функционировании всей системы среди всех значений исследуемого множества вариантов. В практике оптимизации показателей надежности средстз труда применяются методы целенаправленного перебора, градиентного спуска, дифференцирования модели оптимальной надежности и приравнивания к нулю полученного результата и др. Они могут быть использованы для установления экономически целесообразных показателей надежности отдельных электроизделий. [c.245]
Кроме того, можно отметить, что задачи оптимизации сетевых моделей решаются по одному варианту технологической последовательности строительства, т. е. в них не учитывается возможность изменения технологии строительства, варьирования глубины совмещения процессов и т. д. В задачах выравнивания ресурсов и корректировках по времени сетевые модели вообще приводятся к детерминированной календарной форме и теряют свои примущества динамических моделей. В детерминированных сетевых моделях, даже в обобщенных сетевых моделях, записанных в терминах событий, трудно описать с достаточной простотой сущность поточно-организационных вероятностных строительных процессов, что не позволяет разрабатывать мероприятия по обеспечению надежности строительного производства. Из-за указанных недостатков сетевые модели не нашли достаточно широкого применения в практике строительства объектов транспорта нефти и газа. [c.29]
При такой постановке задачи оптимизации плана производства НПЗ модель (2)— (9) является нелинейной. Аналогичные постановки имели место в работах [2, 3, 4,. Б]. Пути решения указанных задач в основном связываются с различными методами линеаризации, предложенными в работе Дж, Данцига 16]. Подробное обоснование этих методов в отношении моделей оптимизации плана производства НПЗ рассматривается в работах [3, 4]. Недостатками методов линеаризации является, во-первых, значительное увеличение размерности моделей, а во-вторых, усложнение подготов-.ки исходной информации для решения. [c.98]
Изложенное является результатом существующей практики создания предприятий без комплексного решения всех взаимосвязанных вопросов организации основных и обслуживающих предпрятий. Соответствие организационных решений задачам развития производства может быть обеспечено на стадии проектирования и последующей систематической работы по поддержанию этого соответствия в определенных пределах. Такой подход создает предпосылки для повышения эффективности производства за счет оптимизации организационных решений в конкретных условиях его осуществления. [c.212]
Методы линейного программирования. Первые исследования по постановке и разработке методов решения линейных оптимизационных задач были проведены в тридцатые годы Л. В. Канторовичем. В 1939 г. им была опубликована книга Математические методы организации и планирования производства , в которой впервые был ш сдложен эффективный метод решения задач оптимизации для моделей с линейными ограничениями и линейным критерием. Однако достоинство книги состояло не только в этом — в пей было показано, что модели экономических систем широкого класса могут быть достаточно точно построены на основе использования линейных соотношении. В дальнейшем эти идеи получили широкое распространение, и в настоящее время липейиые модели и методы оптимизации в таких моделях составляют основу, на которой базируется исследование прикладных экономических задач. [c.50]
Применение методов линейного программирования позволяет руководителю решать различные задачи оптимизации в условиях ограничения. Например, руководитель производства принимает решения относительно норм выпуска ряда готовых изделий, с тем чтобы максимизировать прибыль компании. Такие нормы зависят от различных условий, в частности, от наличия ресурсов и покупательс- [c.260]
Формализация задачи оптимизации календарного планирования основного производства НПП осуществляется следующим образом т tJ t-Mi0t(min 9г уг )] — >- max (3.92) [c.78]
Существует множество компьютерных программ, позволяющих отыскивать решения в задачах с десятками и даже сотнями параметров и ограничений. Рассмотренный нами в примере 2.15 случай представлял собой задачу оптимизации выпуска при двухпродуктовом производстве (марки А и В). Реальные же предприятия в подавляющем большинстве случаев выпускают гораздо более широкую номенклатуру продукции, вовлекая при этом в производство не два, как в примере 2.15 (1-й и 2-й сорта), а сотни и тысячи видов различных ресурсов. Ограничения могут касаться не только технологических и финансовых возможностей предприятия (т.е. характеристик производства "на входе"), но и особенностей получаемых отходов и побочных продуктов, уровня загрязнения окружающей среды с учетом действующего экологического законодательства и других факторов (т.е. характеристик производства "на выходе"). В отдельных случаях весьма существенными оказываются ограничения по времени, например, если предприятие испытывает сложности с поставками сырья в определенные периоды в течение года. [c.110]
economy-ru.info
ADEM-VX. Методы оптимизации конструкторско-технологической подготовки производства
За более чем двадцатилетний период работы в области конструкторской и технологической подготовки производства специалистам Группы компаний ADEM приходилось сталкиваться с множеством разнообразных задач, в которых был задействован весь функционал отечественной интегрированной системы ADEM-VX. Начиная с автоматизации черчения и моделирования, возможности системы охватывали все более широкий спектр технологических и производственных этапов, превращая ее в универсальный инструмент для сквозного проектирования.
При этом было замечено, что наиболее эффективное применение системы происходило на предприятиях, где стремились либо полностью адаптировать ADEM под производственные традиции, либо перестроить сами принципы проектирования и производства (если такое возможно) под заявленные функции. То есть оптимизация процессов происходила не только за счет непосредственного внедрения CAD/CAM системы, но и за счет полновесного использования ее функций.
Если иллюстрировать вышесказанное примерами, то в части CAD можно отметить следующее: постоянно растущая квалификация пользователя в создании объемных моделей позволяет оптимизировать методы построений и тем самым например, минимизировать количество объектов дерева. Ведь известно, что в ADEM, как и во многих других CAD-системах, создание геометрической модели может вестись несколькими способами. А простота внесения изменений в модель зависит от сформированного дерева построений. Ведь всем понятно, что работать с тремя объектами легче, чем с десятью.
Возьмем одну из самых простейших моделей, представленных в стандартной поставке ADEM - керамический изолятор (рис.1).

Рис. 1. Модель изолятора.
Очевидно, что этот элемент можно построить несколькими способами. Рассмотрим два из них.
Первый способ состоит из нескольких действий.
- Создание двух цилиндров методом «Смещение» (Рис. 2a)
- Объединение элементов в одно тело
- Создание сквозных отверстий («окна», паз, квадратное отверстие в центре) (Рис. 2b)
- Создание скруглений на внутренних ребрах. (Рис. 2c)
- Создание фасок. (Рис. 2d)
- Создание глухого отверстия с обратной стороны модели. (Рис. 2e)
|
Рис.2а |
Рис.2b |
|
Рис.2c |
Рис.2d |
|
Рис.2e |
Дерево объемных построений в данном случае состоит из 9 элементов.
Рис. 2f
Второй способ состоит всего из трех действий:
- Создание тела вращения. (Рис. 3a)
- Создание комплексного сквозного отверстия (Рис. 3b)
- Построение скруглений на внутренних ребрах (Рис. 3c)
|
Рис. 3a |
Рис. 3b |
Рис. 3c |
При этом дерево объемных построений во втором случае в 3 раза меньше по количеству входящих элементов.
Рис. 3d
Даже на таком простом примере видно, насколько можно сократить действия по созданию объемной модели, тем самым облегчив себе работу по внесению изменений в геометрию.
Еще более разнообразны случаи по оптимизации технологических работ по причине множества решений одной и той же задачи.
В следующем примере (это недавняя работа предприятия ОАО НПЦ «Полюс», г. Томск) наглядно продемонстрировано, как при умелом пользовании функциями модуля ADEM CAM можно оптимизировать маршрут обработки детали на 3-х координатном фрезерном станке с ЧПУ.
Исходными данными для оптимизации, выполненной специалистами ГК ADEM, послужила объёмная модель изготавливаемой детали с техоснасткой и ориентировочный маршрут обработки, заданный в Операции 005. Основным недостатком маршрута обработки, заложенного в Операции 005, был слишком большой размер управляющей программы (УП), получаемой при расчёте траектории движения инструмента. Для станка CNC646 система ЧПУ АБСОЛЮТ длина УП составила 58187 кадров (можно попробовать рассчитать УП для других станков, результат будет отличаться несущественно). Для этого станка такой размер УП был критичным: УП не помещалась в ОЗУ стойки. Таким образом, для того, чтобы обработать данную деталь на станке CNC646, пришлось бы разбивать маршрут обработки на части и выполнять обработку поочерёдно по нескольким УП.
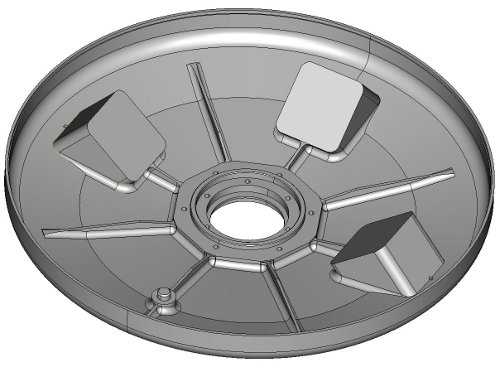
Рис. 4 Модель для обработки
После оптимизации маршрута обработки длина УП составила 27988 кадров, что более чем в два раза меньше исходного варианта. Кроме того за счёт изменения стратегии обработки удалось сократить время обработки почти на треть.
Все меры по оптимизации маршрута обработки можно условно разделить на два основных момента: 1- сокращение самого маршрута за счёт более рационального определения мест обработки; 2- оптимизация траектории движения инструмента за счёт использования оптимальных типов обработки.
Сокращения самого маршрута обработки можно достичь заменой большого количества отдельных переходов обработки, схожих по типу обработки и требуемому результату, одним переходом, сочетающим в себе обработку сразу нескольких мест. В нашем случае мы создали переход черновой обработки, на котором помимо «разгрузки» внутренней полости детали так же сразу выполняется и черновая обработка. Это позволило не только сократить последующую чистовую и финишную обработку, но также за счёт того, что применяется инструмент большего диаметра, существенно уменьшить время выборки большого объёма материала. Кроме того, использование такого типа обработки как «Спираль II» позволяет сократить длину траектории обработки за счёт исключения участков подхода/отхода к обрабатываемому контуру. А способ определения места обработки не только контурами, но и поверхностями позволил максимально приблизить геометрию заготовки после этого перехода к готовой детали.
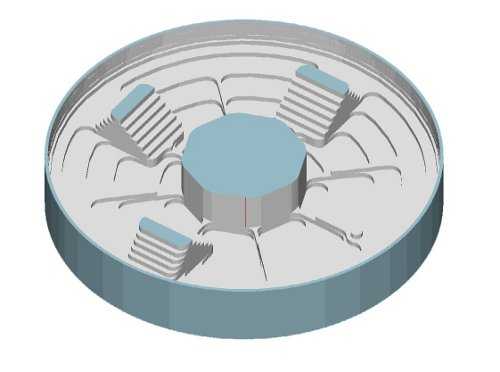
Рис. 5 Результат оптимизированной черновой обработки.
Далее идёт обработка трёх островов. В оригинальном варианте они обрабатываются переходом «Фрезеровать 3х», плюс после этого дополнительно обрабатывается область между бобышками и максимальным внутренним диаметром. В нашем варианте мы использовали переход «Фрезеровать 2,5х», при этом указали ограничивающий контур и поверхности. Таким образом, мы запрограммировали фактически 3х обработку, используя 2,5-х координатный переход. Кроме того, контура и грани, которые мы указали, заданы с учётом поверхностей, которые в оригинальном маршруте обрабатываются отдельно. Тип обработки, использованный нами, аналогичен применённому в оригинальном переходе, однако поперечные (относительно бобышек) проходы заменены продольными, что позволило сократить перемещения инструмента одновременно по 3-м координатам, а значит и сократить управляющую программу.
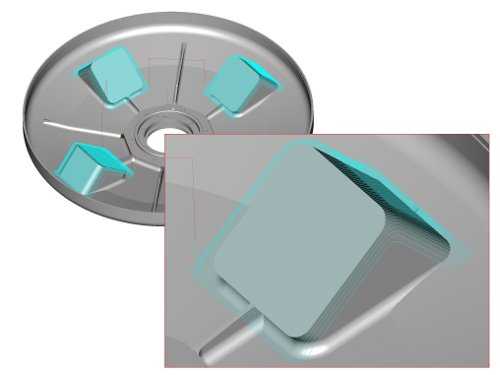
Рис. 6 Оптимизированная 2.5-х траектория.
Следующий переход в Операции 010 - это чистовая обработка всей внутренней поверхности детали. Здесь мы по аналогии с предыдущими переходами применили 2,5-х координатное фрезерование с учётом поверхностей, что позволило нам плюс ко всему прочему использовать тип обработки «Спираль II», позволяющий обработать произвольные области от периферии к центру. Следует отметить, что чистота поверхности, задаваемая в оригинальном маршруте параметром «Гребешок», в нашем случае определяется параметром «Глубина резания», а это позволило обеспечить наиболее равномерное снятие остаточного припуска на каждом проходе вдоль контура. Так же нужно уделить внимание ограничивающим контурам, используемым в этом переходе. В качестве наружного контура мы использовали 3D ребро модели. В качестве внутреннего контура, описывающего перемычки на внутренней поверхности детали, мы использовали 2D контур. Его мы построили в модуле ADEM CAD следующим образом: получили проекции с нужных нам ребер на рабочую плоскость, что существенно сократило трудоёмкость при дальнейшем задании контуров в модуле ADEM САМ. Кроме того, этот же контур мы использовали и при чистовой обработке перемычек, заданной следующим переходом.
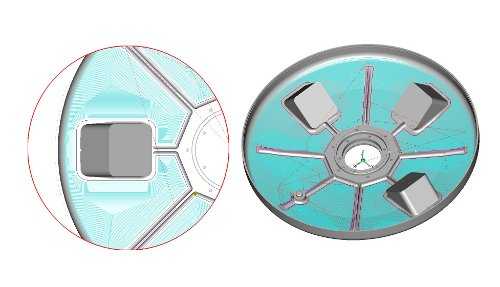
Рис. 7 Чистовая обработка поверхности.
Так как предварительно мы уже провели черновую выборку металла и чистовую обработку внутренней полости детали с остаточным припуском на внутренний контур, то для получения чистового профиля перегородок внутренней полости нам будет достаточно выполнить лишь один проход вдоль внутреннего контура. При этом будет сниматься слой материала, равный остаточному припуску на предыдущих переходах.
Последние 2 перехода в маршруте обработки, определенном в Операции 010, по сути идентичны последним 3-м переходам Операции 005. Отличие лишь в способе определения места обработки. Так для обработки верхних граней перемычек в отличие от оригинального маршрута, где использовались дополнительно построенные для этого контура, мы определили геометрию места обработки, используя 3D рёбра объёмной модели, что позволило опять же сократить время на дополнительные построения в CADе и задание обработки в САМе.
Таким образом по результатам проведённой оптимизации нельзя однозначно сказать, что маршрут обработки получился «более правильным», скорее можно утверждать, что обработка стала более рациональной, а работа технолога соответственно более плодотворной.
Ещё раз факты:
005 операция - первоначальный маршрут обработки:

Рис. 8
010 операция - оптимизированный маршрут:

Рис. 9
Удалось свести к минимуму количество дополнительных построений, сократить УП более чем в два раза, а время обработки почти на треть.
005 операция: длина УП 58187 кадров. Время обработки 2 ч. 50 мин. 46 сек.
010 операция: длина УП 27988 кадров. Время обработки 2 часа 07 мин. 56 сек.
Эти два кратких примера являются простейшей иллюстрацией современной тенденции рационального применения САПР для повышения эффективности конструкторско-технологической подготовки производства.
adem.ru
Журнал ВАК :: УПРАВЛЕНИЕ ЭКОНОМИЧЕСКИМИ СИСТЕМАМИ
Применение метода линейной оптимизации производства производителем интегральных схем при осуществлении внешнеторговой деятельности.
ASIC manufacturer`s application of the linear optimization during its foreign trade activity.
Петухов Виктор Дмитриевич
ОАО «Ангстрем» /Московская Государственная Академия Делового Администрирования
e-mail: [email protected]
В данной статье рассматривается практическая сторона планирования оптимизации производства при осуществлении внешнеторговой деятельности производителем интегральных схем. В статье используется метод линейного программирования (конкретно – метод линейной оптимизации) производства экспортируемой продукции. Доступность применяемого метода широкому кругу пользователей обусловлена проведением расчетов в программе MS Excel.
The practical side of the ASIC manufacturer`s planning during its foreign trade activity is considered in this article. Linear programming (specifically linear optimization) of production of the exported products is used in the current article. Wide range user`s accessibility of the applicable method caused by calculation implemented with software MS Excel.
Ключевые слова: внешнеторговая деятельность, оптимизация производства, линейное программирование, линейная оптимизация, полупроводниковая промышленность.
Key words: foreign trade activity, production optimization, linear programming, linear optimization, semiconductor industry.
Введение
Планирование – одна из основных функций менеджмента, а применение метода линейной оптимизации может помочь управленцу при планировании оптимальных планов различных действий. В данной статье рассматривается оптимизация производства интегральных схем (LCD-контроллеров), отправляющихся на экспорт перед предстоящей реконструкцией линии таким образом, чтобы наиболее эффективно израсходовать запасы сырья. Особенностью рассматриваемого метода является применение общедоступного программного средства – MS Excel.
Расчет оптимизации производства при осуществлении внешнеторговой деятельности
Важность применяемого метода для целей обеспечения выполнения обязательств при осуществлении внешнеторговой деятельности обусловливается необходимостью проведения модернизации производства. Переменные в задаче - это количество изделий каждого из 10-ти типов выпускаемых LCD контроллеров. При этом целевую функцию - прибыль от производства - можно записать как сумму произведений количества произведенных изделий каждого продукта на прибыль с каждого изделия.
Ограничения состоят в том, что расход каждого из сырьевых ресурсов на весь производственный план не должен превышать запас данного ресурса (ячейки В4:В10). Расход каждого вида сырья на производство одного изделия можно найти на пересечении строчки (сырье) и столбца (продукт) в таблице параметров. Это так называемые технологические коэффициенты производства. Вводные данные представлены в таблице 1.
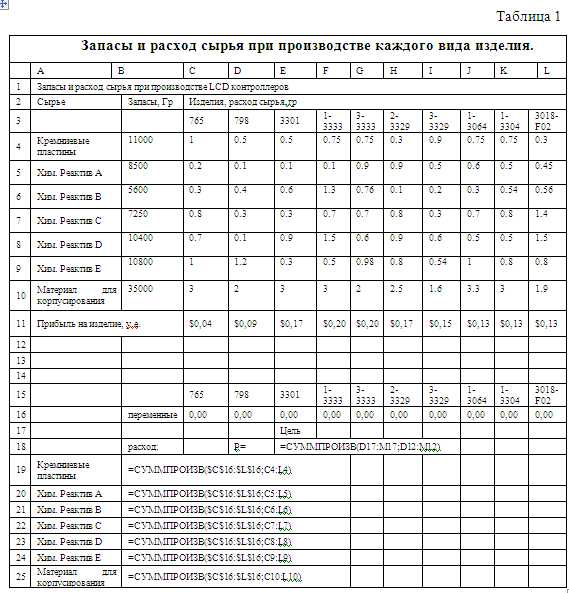
В ячейку Е18 введена целевая функция, представляющая собой сумму произведений прибылей от продажи каждого вида изделия (строка 11) на
произведенное количество каждого продукта (строка 16). В ячейках C16:G16 – содержатся переменные. В ячейках B19:B25- введены формулы, отражающие расход ресурсов на весь производственный план. Остается сформировать задачу для надстройки Поиск решения. После того, как мы зададим целевую ячейку, цель (поиск максимума), изменяемые ячейки и отметим во вкладке «Параметры», что задача линейная и переменные неотрицательны, останется только задать ограничение. В данном случае оно только одно (если задавать его для группы ячеек): реальный расход ресурсов, рассчитанный в ячейках B19:B25, не должен превышать запасы на складе, записанные в ячейках B4:B10. После команды «Выполнить» получим решение, приведенное в Таблице 2.
Таблица 2
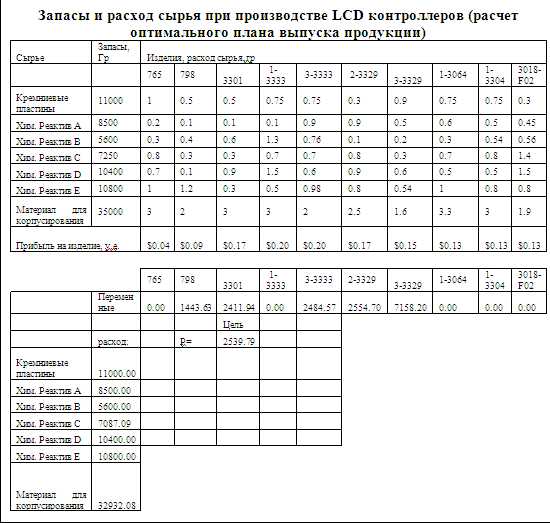
Аккуратно округлив значения переменных, соблюдая ограничения на ресурсы, получим реальный план производства (Таблица 3). Как видим, общая прибыль составила примерно 2540 долл.
Таблица 3
Реальный план производства
В установках надстройки Поиск решения существует возможность потребовать целочисленности переменных решения. Для этого достаточно в левом поле этого окна указать ячейки, содержащие переменные решения, а из предлагаемых ограничений выбрать ограничение «цел».
Вопреки тому, что можно было бы ожидать, получаемое целочисленное решение (производственный план) не совсем совпадает с округленным оптимальным решением, полученным без условия целочисленности (Таблица 4) и 35 центов менее выгоден, что, конечно, не существенно.
Таблица 4
План производства с условием целочисленности
В данной задаче отличие целочисленного решения от обычного по величине целевой функции весьма мало. При этом следует иметь в виду, что добавление этого ограничения исключает использование эффективных методов решения задач линейного программирования. В частности, при целочисленных ограничениях невозможно получить отчет об устойчивости, который, дает чрезвычайно важную информацию для анализа вопросов «что если», обеспечивает общий взгляд на исследуемую проблему и более глубокое ее понимание. Задача с целочисленными переменными гораздо более сложна для исследования, а алгоритмы ее решения гораздо менее универсальны и эффективны. Поэтому не следует задавать без нужды условие целочисленности. Это особенно важно, во время исследования большой модели (несколько десятков и сотен переменных и ограничений). Задавая целочисленное ограничение в подобной задаче, велика вероятность резкого увеличения времени поиска решения. Разумеется, в некоторых случаях без условия целочисленности не обойтись (например, задачи с двоичными, логическими переменными).
Попробуем организовать выпуск таким образом, чтобы сохранить полную линейку выпускаемой продукции, что особенно важно при осуществлении внешнеторговой деятельности.
Решение задачи об оптимальном плане производства выявило преимущество метода линейного программирования. Но компьютер отказался от выпуска пяти видов продукции, а для конкурентоспособности и престижа предприятия необходимо сохранить всю линейку выпускаемой продукции. Необходимо провести анализ полученного оптимального решения на устойчивость: малые изменения величины запасов могут привести к радикальному изменению решения.
Для того, чтобы разобраться в ситуации, требуется провести анализ решения. В этом нам поможет отчет об устойчивости решения, поэтому вернемся еще раз в установки Поиска решения, удалим условие целочисленности, которое мы добавляли с целью эксперимента и найдем прежнее решение. Когда Поиск решения сообщит, что решение найдено, отметим в правом окне пункт «Устойчивость». На новом листе будет получен отчет следующего вида (Таблица 5):
Таблица 5
Построение отчета об устойчивости в MSExel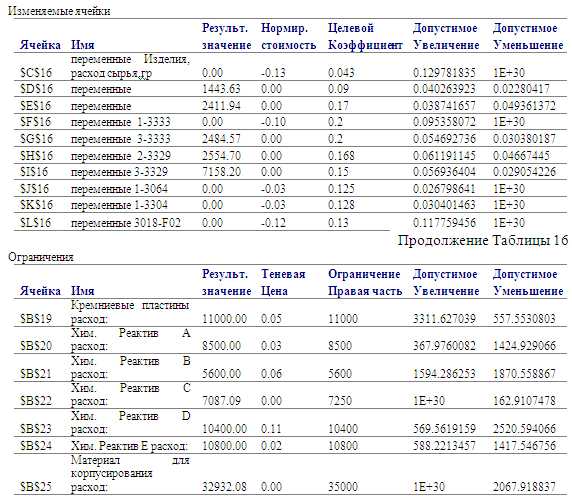
Согласно отчету об устойчивости, нормированная стоимость изделий, не вошедших в оптимальный план составляет для изделий 765, 1-3333, 1-3064, 1-3304 и 3018-F02 соответственно: 0,13 у.е.; 0,1 у.е.; 0,03 у.е.; 0,03 у.е.; и 0,12 у.е.
Абсолютная величина этих чисел показывает, на сколько нужно увеличить прибыль от производства одного изделия каждого вида, чтобы они вошли в оптимальный план. С точки зрения анализа ситуации, малость этих чисел (менее 0,4% от нормы прибыли) свидетельствует о том, что если мы «насильно» заставим Поиск решения запланировать выпуск не вошедших в оптимальный план изделий (введя условие$C$16:$L$16>= 100, например), большого уменьшения прибыли не произойдет.
Проверим этот тезис и потребуем, чтобы количество всех произведенных изделий было бы не менее 100 (Таблица 6).
Таблица 6
Прибыль уменьшилась менее, чем на 41,15 у.е., т.е. менее 2,5%. Потребуем, чтобы количество всех произведенных изделий было бы не менее 200, 300 …. Во всех этих случаях мы получим другие оптимальные решения, а прибыль будет отличаться от оптимальной (для исходного варианта постановки задачи) не более чем на 5,5%.
Проверим, какое же количество не вошедших в оптимальный план изделий запланирует выпустить Поиск решения, если мы изменим их доходность, как подсказывает отчет об устойчивости?
Добавим к ценам не вошедших в план изделий: 765, 1-3333, 1-3064, 1-3304 и 3018-F02 чуть большее число, чем их нормированная стоимость - 0,16 у.е.; 0,12 у.е.; 0,05 у.е.; 0,05 у.е.; и 0,16 у.е. чтобы заведомо изменить оптимальный план. При этом мы можем быть уверены, что часть из этих изделий точно войдет в оптимальный план, но не можем знать заранее, в каком количестве, и не можем определить, как изменится производство других изделий.
В этом случае прибыль на единицу этих изделий станет равной 0,07 у.е.; 0,31 у.е.; 0,18 у.е., 0,18 у.е., 0,29 у.е. для 765, 1-3333, 1-3064, 1-3304 и 3018-F02. Еще раз запустим Поиск решения. Результат представлен в следующей таблице (Таблица 7).
Таблица 7
Результат увеличения стоимости не вошедших в план изделий
Видно, сколь драматически отличается это решение от базового, хотя значения прибыли практически одинаковы. В таких случаях обычно говорят, что решение задачи неустойчиво.
Решение называется неустойчивым, если малые изменения параметров приводят к огромным изменениям решения. Чаще всего о неустойчивости говорят в негативном смысле, подразумевая даже, что неустойчивость ограничивает возможности аналитика использовать количественные методы для принятия управленческих решений. Действительно, поскольку в реальной ситуации параметры модели всегда известны с определенной неточностью (ошибкой), а малые изменения параметров приводят к катастрофическим изменениям решения, то найденное оптимальное решение кажется бесполезным. При выборе между несколькими различными альтернативами, каждая из которых может стать оптимальной при незначительном изменении параметров, мы не сможем сделать правильный выбор. В этом случае уместно говорить о «деструктивной» роли неустойчивости и пытаться найти методы борьбы с ней.
Однако, в данном случае, неустойчивость решения не создает проблем – прибыль в обоих случаях различается на 3 %. Вернув прежнее значение прибыли для не вошедших в первоначальный план изделий – убедимся, что прибыль уменьшится с 2587,52 у.е. до 2539,44 у.е.
Таким образом, в нашем распоряжении оказывается множество альтернативных решений, сильно различающихся по значениям переменных, но очень близких по прибыли. Это полезно для проведения аналитических процедур.
Наличие многих, пусть не вполне оптимальных, но «хороших» альтернативных решений позволяет менеджеру выбрать такое, которое в наилучшей степени отвечает тем или иным неформализуемым требованиям и условиям, которые всегда присутствуют при принятии решений. В данном случае, таким неформализуемым условием является требование полного ассортимента для представительских целей производственного предприятия, которое, не было выполнено оптимальным планом при исходной постановке задачи. Для выполнения данного требования необходимо ввести ограничения минимального значения переменной, т.к. изменение нормы прибыли на не вошедшие изделия влечет исключение других изделий из плана производства. Важно отметить, что принятие решений о включении ограничений в модель, изменении цены принимается менеджером, сама по себе модель ответа на данные вопросы не даст. Положительными сторонами модели являются множества вариантов, предоставляющие большой выбор решений поставленной задачи.
При этом, оно необязательно должно быть оптимальным в строго математическом смысле слова.
Необходимо еще отметить, что в данной задаче несмотря на обилие решений, близких к оптимальному, имеется еще больше «плохих» решений. Очевидно, что эмпирический метод уступает методу линейного программирования, тем более, что ни один ресурс не израсходован полностью.
Посмотрим, что станет с моделью, если мы потребуем выпустить количество изделий равное минимальному объему выпуска вошедшего в первоначальный оптимальный план изделия 798 (для этого скопируем минимальный объем выпуска в отдельную ячейку N16 и добавим ограничение – C16:L13=N16), то получим следующее решение (Таблица 8).
Таблица 8
Равное количество выпускаемой продукции
В таком случае прибыль все равно меньше оптимального решения. Следовательно, выпускать одинаковое количество изделий смысла нет. Или, например, мы вводили требование выпустить не меньше чем по 100, 200, 300 изделий разных видов и результат почти не менялся. А что если потребовалось бы выпустить больше изделий типа 1-3064, не предусмотренных к выпуску в базовом плане? Добавим ограничение, что изделий типа 1-3064 должно быть не менее 300 пакетов (Таблица 9).
Таблица 9
Производство 300 штук изделий типа 1-3064
Таким образом, наличие большого числа решений, близких к оптимальному, не является гарантией того, что любой, произвольно выбранный план, окажется хорошим.
Заключение
Таким образом, менеджеру для принятия решения предоставлены выкладки, основанные на оптимальном объеме производства продукции, чтобы выпустить как можно больше наиболее рентабельных изделий, освободив при этом склад, или наоборот, сохранив целостность производственной линейки – на первый взгляд не значительная процедура для стратегического повышения конкурентоспособности предприятия на международном рынке микроэлектроники, но, к примеру, реализация конкурентной стратегии лидерства по издержкам предполагает совокупное использование приемов сокращения затрат.
Список используемой литературы
- Зайцев М.Г., Варюхин С.Е. Методы оптимизации управления и принятий решений. – М.: Дело. 2008
- Канторович Л.В. Математические методы оптимизации и планирования производства. – Л: Изд-во ЛГУ, 1939.
- Стровский Л.Е. Внешнеэкономическая деятельность предприятия. – М.: Юнити, 2008
- Burkov A., Chaib-draa B., An Approximate Subgame-Perfect Equilibrium
- Computation Technique for Repeated Games. URL http://www.aaai.org/ocs/index.php/AAAI/AAAI10/paper/viewFile/1769/2076
- Zesch F., Hellingrath B., Integrated Production-Distribution Planning (An optimization model for mixed-model assembly lines). URL http://www.in-ter-trans.eu/resources/Zesch_Hellingrath_2010_Integrated+Production-Distribution+Planning.pdf
uecs.ru
Методы оптимизации производственной программы
Поиск ЛекцийОсновными методами оптимизации производственной программы является использование моделей расчетов. Существуют следующие виды моделей:
· Оптимизационные модели
· Детерминированные модели
· Имитационные модели
· Матричные модели
· Статистические модели
· Графические модели
Выбор моделей зависит от целей и этапов разработки или корректировки производственной программы. Опыт применения этих моделей показал, что примерно в 80% случаев используются оптимизационные программы. На втором месте – имитационное моделирование. Суть его в том, что разрабатывается не реальная ситуация, а делается разработка имитирующая это производство.
3- детерминированная модель. Это модель, в которой разрабатываются те, или иные производственные решения, или в том числе программа производственная по срокам.
4- матричная. Матрица – повторение явления в массовом порядке.
Статистическая модель основана на использовании правил и законов статистики. Большая часть статистических моделей основана на использовании трендов, то есть определения вектора развития.
Графический метод – много вариантов, строим гарфики.
Оперативное управление производством
· Сущность оперативного управления производством
Управление любым предприятием – это непрерывный процесс принятия решений на различных уровнях управления для достижения поставленной цели. Существует на предприятии 3 уровня управления:
1) Стратегическое управления
2) Тактическое управление
3) Оперативное управление
Стратегическое управление осуществляют владельцы предприятий и топ менеджеры. Главная их задача - определить миссию предприятия и задачи первого уровня достижения миссии, то есть главная цель и задачи на стратегический период развития. Для малых предприятий – это на период более 3 лет. Для средних и крупных – более 5 лет.
Тактическое управление осуществляется менеджерами среднего звена вместе с топ менеджерами. Они планируют работу по управлению предприятием на период от одного и соответственно до 3 лет для малых и до 5 лет для крупных.
Главной их задачей принять решение о бизнес процессах, связанных с производством конкретных продуктов, или решения конкретных задач (разработка бизнес планов), а также резработка инструкций, обеспечивающих тактическое управление. Основные функции этого второго уровня планирования и бюджетирования, то есть планирование – это определение объемов производства, производственной мощности, потребности в персонале, а бюджетирование – это финансовое обеспечение вышеназванных работ.
Оперативное управление осуществляет линейные менеджеры, которые осуществляют текущее планирование в пределах года.
Линейные мендежеры планируют работу своих подразделений в том числе конкретных работников в пределах одного года, начиная от сменного задания каждому работнику до плана на каждый квартал и в целом на год. Работы, выполняемые этим менеджером следующие:
1) Управление производственным процессом.
2) Управление загрузкой оборудования
3) Контроль за исполнением заказов
4) Управление движением сырья и материалов
5) Управление материальными основными фондами
Оперативное управление производством включает 2 функции
1) Календарного планирования
2) Диспетчеризацию производства. Диспетчеризация подразумевает разнарядку работ и контроль за сроками выполнения этих работ
Условия выполнения оперативного управления (диспетчеризации)
С помощью оперативного управления достигается конечный результат работы при выполнении следующих условий:
1) Строгое распределение работ на рабочих местах, на производственных участках, в цехах. Распределение работ связано с конкретными периодами времени.
2) Четкая и полная организация сбора и обработки информации о выполнении предыдущего этапа.
3) Комплексное исопльзование средств получения информации для подготовки альтернативных (других вариантов) управленческих решений.
4) Ежедневный анализ ситуации с производством и выпуском продукции в каждом подразделении, руководимым линейным менеджером (подведение итогов).
5) Принятие своевременных решений, координация и организация работ для предупреждения возможных сбоев в работе.
Распределение функции управления предприятием по 3 уровням (выше).
Календарное планирование и диспетчерский контроль.
Процесс календарного планирования имеет своей главной целью оптимизацию рабочего времени в условиях имеющегося оборудования.
При календарном планировании используется теория расписаний, сетевые графики и критический путь выполнения работы.
Теория расписаний
Теория расписаний – это система качественных и количественных (вычислительных) способов, используемых для систематизации (упорядочивания) по времени имеющейся техники или системы машин, обеспечивающих изготовление конкретной продукции.
В теории расписания ранжируются определенные технологические этапы, обеспечивающие выполнение заданных условий производства, то есть заданных календарных сроков. Например, задача календарного планирования участка по производству единичных или мелкосерийных партий продукции можно сформулировать следующим образом: каким образом одно или несколько изделий должны быть обработаны или изготовлены на одном или нескольких станках.
Понятие сетевого графика
Сетевой график – это совокупность определенным образом упорядоченных работ, обеспечивающих выполнение конкретного задания или достижение конкретных целей путем выполнения отдельных технологических операций.
Наибольшее распространение сетевых графиков имеется при планировании и контроле календарных сроков исполнения.
Сетевые графики подразумевают оптимальный и критические пути.
Критическим путем называется непрерывное выполнение каких-либо операций от начального этапа до конечной цели, требующих максимального времени для исполнения.
poisk-ru.ru
Методы оптимизации производства — курсовая работа
Содержание
Задача 1(13). ….……………………………………………………………..……3
Задача 2(63).………………………………………………………………..……5
Задача 3(113)………………………………………………………………..…..…8
Задача №1(13)
Графическим способом решить задачу линейного программирования (). Сформулировать задачу, двойственную по отношению к данной.
Решение
Построим область допустимых решений на плоскости . Для этого запишем уравнения прямых из системы ограничений, заменяя неравенства равенствами, и преобразуем полученные выражения:
Построим вектор и прямую , перпендикулярную , на плоскости Ox1x2. Перемещая прямую в направлении вектора -, получаем, что min значение z находится в точке A. Координаты этой точки определяются решением системы двух линейных уравнений (I) и (II), на пересечении которых она находится. В результате решения системы уравнений (I) и (II) получим оптимальное решение :
.
Сформулируем задачу, двойственную по отношению к данной.
Введем двойственные переменные ; тогда двойственная задача будет иметь вид:
Задача 2(63)
На предприятии имеется несколько производственных линий. j-я линия производит в единицу времени единиц продукции i-го типа. Для выполнения задания предприятию необходимо выпускать не менее единиц i-го типа продукции, при этом эксплуатационные расходы j-ой линии составляют млн. рублей в единицу времени. Определить время работы каждой линии для выполнения задания при условии минимизации затрат.
Решение:
Математическая модель исходной задачи:
xj–время работы j-ой линии (в часах).
Приведем задачу к стандартному виду основной задачи линейной оптимизации. Для этого введем дополнительные переменные . Получим:
Построим симплекс-таблицу:
Б | x1 | x2 | x3 | x4 | y1 | y2 | - z,β | Θ |
z | 10 | 12 | 8 | 10 | 0 | 0 | 0 | |
y1 | -2 | -1 | -3 | -1 | 1 | 0 | -18 | 18 |
y2 | -1 | -1 | -4 | -4 | 0 | 1 | -20 | 5 |
z | 7 1/2 | 9 1/2 | -2 | 0 | 0 | 2 1/2 | -50 | |
y1 | -1 3/4 | - 3/4 | -2 | 0 | 1 | - 1/4 | -13 | 6 1/2 |
x4 | 1/4 | 1/4 | 1 | 1 | 0 | - 1/4 | 5 | 5 |
z | 8 | 10 | 0 | 2 | 0 | 2 | -40 | |
y1 | -1 1/4 | - 1/4 | 0 | 2 | 1 | - 3/4 | -3 | 2 2/5 |
x3 | 1/4 | 1/4 | 1 | 1 | 0 | - 1/4 | 5 | 20 |
z | 0 | 8 2/5 | 0 | 14 4/5 | 6 2/5 | -2 4/5 | -59 1/5 | |
x1 | 1 | 1/5 | 0 | -1 3/5 | - 4/5 | 3/5 | 2 2/5 | |
x3 | 0 | 1/5 | 1 | 1 2/5 | 1/5 | - 2/5 | 4 2/5 | |
z | 4 2/3 | 9 1/3 | 0 | 7 1/3 | 2 2/3 | 0 | - 48 | |
y2 | 1 2/3 | 1/3 | 0 | -2 2/3 | -1 1/3 | 1 | 4 | |
x3 | 2/3 | 1/3 | 1 | 1/3 | - 1/3 | 0 | 6 |
Заметим, что все β>0 и все приведенные стоимости (коэффициенты при xj в строке z) также неотрицательны. Это значит, что полученный план является оптимальным:
, z*=
Сформулируем двойственную задачу.
Целевая функция примет вид:
Ограничения:
Экономическая интерпретация двойственной задачи.
Найти такую совокупность ui-стоимостей единицы продукции i-го типа, при которых общая стоимость производимой продукции была бы максимальной, при условии, что суммарная цена единиц всех видов производимой продукции была бы не больше эксплуатационных расходов j-ой линии в единицу времени.
Задача 3(113)
Завод имеет 4 цеха A, B, C, D и 5 складов. Производительность i-го цеха за смену составляет Пi тыс. шт. деталей, ; пропускная способность j-го склада за это время составляет Еj тыс. шт. деталей,. Стоимости перевозок 1 тыс. шт. деталей из цеха i в склад j задаются матрицей . Составить такой план перевозки изделий, при котором расходы на перевозку изделий были бы наименьшими.
Еj | |||||
| 37 | 26 | 91 | 24 | 13 | |
20 | 14 | 13 | 6 | 12 | 1 |
30 | 18 | 20 | 4 | 2 | 3 |
70 | 17 | 5 | 15 | 10 | 8 |
71 | 4 | 12 | 18 | 13 | 16 |
Решение:
Постановка транспортной задачи в общем виде:
количество единиц изделий, которое нужно доставить из i-ПО в j-ПН
Подставим исходные данные:
транспортная задача является закрытой.
Для решения транспортной задачи методом потенциалов, необходимо построить опорный план. Для уменьшения числа итераций решения задачи воспользуемся методом наименьшей цены.
Нахождение оптимального плана перевозок:
Составили опорный план, который является невырожденным, так как число базисных клеток равно . В данном случае количество базисных клеток равно 8, .
Решим систему уравнений , которые соответствуют базисным клеткам,
и заполним соответствующие строки и столбцы в таблице. Вычисляем псевдостоимости и записываем в левые верхние углы клеток.
Так как существуют свободные клетки, в которых , то полученный план не является оптимальным. Попробуем улучшить этот план путем переноса перевозок по циклу пересчета для выбранной клетки, где .
Выбираем свободную клетку (3,4), присваиваем ей знак «+» и переносим по этому циклу 24 единицы груза.
Полученный план не является оптимальным. Выбираем свободную клетку (3,5), присваиваем ей знак «+» и переносим по этому циклу 13 единиц груза
В данном плане не существует клетки, в которой псевдостоимость превосходит стоимость. Таким образом, полученный план является оптимальным:
Сформулируем двойственную задачу по отношению к исходной транспортной задаче:
Получим:
Экономическая интерпретация двойственной задачи
Найти – стоимость перевозок, при которых суммарная плата за все перевозки была бы максимальной, т.е. стоит задача в том, чтобы распределить стоимость перевозок между потребителем и складом так, чтобы это было наиболее выгодным, например, для транспортной компании в том случае, если всё вывезут и всё завезут.
myunivercity.ru