Методы глобальной оптимизации. Алгоритмы глобальной оптимизации
Презентация на тему: Методы глобальной оптимизации

Генетические алгоритмы

Генетические алгоритмы (ГА)
Адаптивные методы поиска, которые в последнее время часто используются для решения задач функциональной оптимизации.
Они основаны на генетических процессах биологических организмов: биологические популяции развиваются в течении нескольких поколений, подчиняясь законам естественного отбора и по принципу "выживает наиболее приспособленный" (survival of the fittest), открытому Чарльзом Дарвином.
Подражая этому процессу генетические алгоритмы способны "развивать" решения реальных задач, если те соответствующим образом закодированы

Эволюция: естественный отбор и генетическое наследование
Естественный отбор: наиболее приспособленные особи лучше выживают и приносят больше потомства, чем менее приспособленные
Основной закон наследования: потомки похожи на родителей. В частности, потомки более приспособленных родителей будут, скорее всего, одними из наиболее приспособленных в своем поколении

Строение животной клетки
Почти в каждой клетке любого животного имеется набор хромосом, несущих информацию об этом животном. Основная часть хромосомы - нитьДНК (молекула дезоксирибонуклеиновой кислоты), которая состоит из четырех видов специальных соединений - нуклеотидов, идущих в определенной последовательности. Нуклеотиды обозначаются буквами A, T, C и G, и именно порядок их следования кодирует все генетические свойства данного организма. Говоря более точно, ДНК определяет, какие химические реакции будут происходить в данной клетке, как она будет развиваться и какие функции выполнять.
Ген - это отрезок цепи ДНК, отвечающий за определенное свойство особи, например за цвет глаз, тип волос, цвет кожи и т. д. Вся совокупность генетических признаков человека кодируется посредством примерно 60 тыс. генов, суммарная длина которых составляет более 90 млн. нуклеотидов.
Различают два вида клеток: половые и соматические. В каждой соматической клетке
человека содержится 46 хромосом. Эти 46 хромосом - 23 пары, причем в каждой паре одна из хромосом получена от отца, а вторая - от матери. Парные хромосомы отвечают за одни и те же признаки - например, отцовская хромосома может содержать ген черного цвета глаз, а парная ей материнская - ген голубоглазости. Существуют определенные законы, управляющие участием тех или иных генов в развитии особи. В частности, в данном примере потомок будет черноглазым, так как ген голубых глаз является "слабым" (рецессивным) и подавляется геном любого другого цвета.
В половых клетках хромосом только 23, и они непарные. При оплодотворении происходит слияние мужской и женской половых клеток и образуется клетка зародыша, содержащая как раз 46 хромосом.

Факторы, влияющие на
наследственностьКроссинговер - парные хромосомы соматической клетки сближаются вплотную, затем их нити ДНК разрываются
в нескольких случайных местах и хромосомы обмениваются своими частями. Этот процесс обеспечивает появление новых вариантов хромосом
Мутация - изменение некоторых участков ДНК. Мутации также случайны и могут быть вызваны различными внешними факторами, такими, как радиоактивное облучение. Если мутация произошла в половой клетке, то измененный ген может передаться потомку и проявиться в виде наследственной болезни либо в других новых свойствах потомка. Считается, что именно мутации являются причиной появления новых биологических видов, а кроссинговер определяет уже изменчивость внутри вида (например, генетические различия между людьми)

Задача оптимизации
Таким образом, эволюция - это процесс постоянной оптимизации биологических видов. Естественный отбор гарантирует, что наиболее приспособленные особи дадут достаточно большое потомство, а благодаря генетическому наследованию, что часть этого потомства не только сохранит высокую приспособленность родителей, но будет обладать и некоторыми новыми свойствами. Если эти новые свойства окажутся полезными, то с большой вероятностью они перейдут и в следующее поколение. Так происходит накопление полезных качеств и постепенное повышение приспособляемости биологического вида в целом.
Таким образом решается задача оптимизации видов в природе, похожий метод можно применять для решения различных реальных задач оптимизации - наиболее распространенного и важного для практики класса задач

Генетический алгоритм – метод глобальной оптимизации
Генетические алгоритмы имитируют процессы наследования свойств живыми организмами и генерируют последовательности новых векторов , содержащие оптимизированные переменные w=(w1,w1, …,wn).
При этом выполняются операции трех видов: селекция, скрещивание и мутация.

Отличие ГА от традиционных методов оптимизации
Генетические алгоритмы:
обрабатывают не значения параметров самой задачи, а их закодированную форму
осуществляют поиск решения исходя не из единственной точки, а из некоторой популяции
используют только целевую функцию, а нее ее производные либо иную дополнительную информацию
применяют вероятностные, а не детерминированные правила выбора
Основные понятия ГА
Популяция – это конечное множество особей
Особи, входящие в популяцию, в генетических алгоритмах представляются хромосомами с закодированным в них множествами параметров задачи, т.е. решений, которые иначе называются точками в пространстве поиска
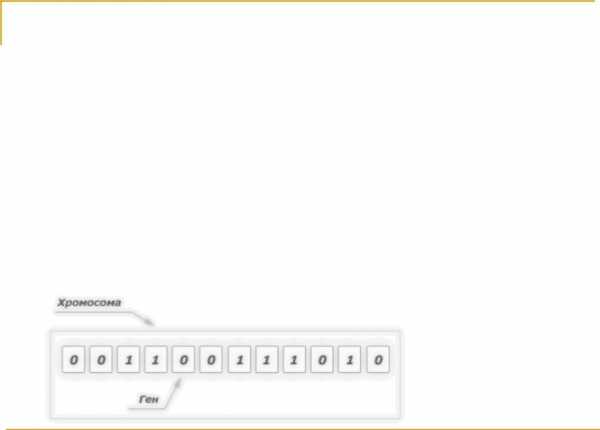
Хромосомы (другие названия – цепочки или кодовые последовательности) – это упорядоченные последовательности генов
Ген (также называемый свойством, знаком или детектором) – это атомарный элемент генотипа, в частности, хромосомы
Основные понятия ГА
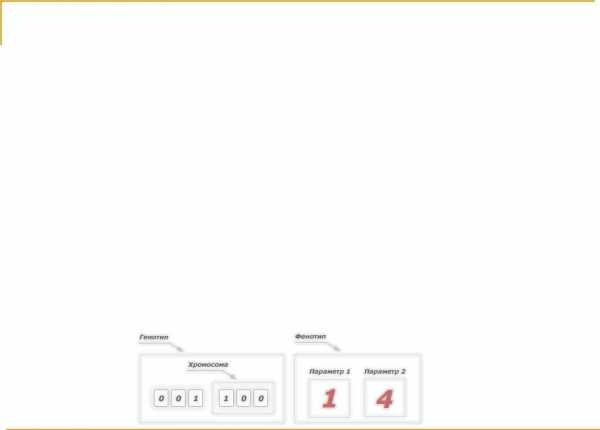
Генотип или структура – это набор хромосом данной особи. Следовательно, особями популяции могут быть генотипы либо единичные хромосомы (в довольно распространенном случае, когда генотип состоит из одной хромосомы).
Фенотип – это набор значений, соответствующих данному генотипу, т.е. декодированная структура или множество параметров задачи (решение, точка пространства поиска).
Каждая хромосома может кодировать только один параметр задачи. Но так как в одном генотипе может быть несколько хромосом, то один генотип может закодировать несколько параметров. Например: генотип включает в себя две хромосомы, каждая хромосома состоит из 3 генов, значит, первые 3 гена генотипа кодируют один параметр, а вторые 3 гена – второй параметр. Проиллюстрируем пример генотипа и фенотипа:
studfiles.net
НОУ ИНТУИТ | Лекция | Методы глобальной оптимизации
Аннотация: Рассматриваются: алгоритм имитации отжига, генетические алгоритмы, использование случайных возмущений в обучении (метод виртуальных частиц).
Элементы глобальной оптимизации
Все представленные ранее методы обучения нейронных сетей являются локальными. Они ведут к одному из локальных минимумов целевой функции, лежащему в окрестности точки начала обучения. Только в ситуации, когда значение глобального минимума известно, удается оценить, находится ли найденный локальный минимум в достаточной близости от искомого решения. Если локальное решение признается неудовлетворительным, следует повторить процесс обучения при других начальных значениях весов и с другими управляющими параметрами. Можно либо проигнорировать полученное решение и начать обучение при новых (как правило, случайных) значениях весов, либо изменить случайным образом найденное локальное решение (встряхивание весов) и продолжить обучение сети.
При случайном приращении весов переход в новую точку связан с определенной вероятностью того, что возобновление процесса обучения выведет поиск из "сферы притяжения" локального минимума.
При решении реальных задач в общем случае даже приблизительная оценка глобального минимума оказывается неизвестной. По этой причине возникает необходимость применения методов глобальной оптимизации. Рассмотрим три из разработанных подходов к глобальной оптимизации: метод имитации отжига, генетические алгоритмы и метод виртуальных частиц.
Алгоритмы имитации отжига
Метод имитации отжига основан на идее, заимствованной из статистической механики. Он отражает поведение расплавленного материала при отвердевании с применением процедуры отжига (управляемого охлаждения) при температуре, последовательно понижаемой до нуля.
В процессе медленного управляемого охлаждения, называемого отжигом, кристаллизация расплава сопровождается глобальным уменьшением его энергии, однако допускаются ситуации, в которых она может на какое-то время возрастать (в частности, при подогреве расплава для предотвращения слишком быстрого его остывания). Благодаря допустимости кратковременного повышения энергетического уровня, возможен выход из ловушек локальных минимумов энергии, которые возникают при реализации процесса. Только понижение температуры до абсолютного нуля делает невозможным какое-либо самостоятельное повышение энергетического уровня расплава.
Метод имитации отжига представляет собой алгоритмический аналог физического процесса управляемого охлаждения. Классический алгоритм имитации отжига можно описать следующим образом:
- Запустить процесс из начальной точки при заданной начальной температуре .
- Пока , повторить раз следующие действия:
- Уменьшить температуру с использованием коэффициента , выбираемого из интервала , и вернуться к п. 2.
- После снижения температуры до нуля провести обучение сети любым из детерминированных методов локальной оптимизации вплоть до достижения минимума целевой функции.
Наибольшего ускорения имитации отжига можно достичь путем замены случайных начальных значений весов тщательно подобранными значениями с использованием любых доступных способов предварительной обработки исходных данных.
Метод имитации отжига оказывается особенно удачным для полимодальных комбинаторных проблем с очень большим количеством возможных решений, например, для машины Больцмана, в которой каждое состояние системы считается допустимым. При решении наиболее распространенных задач обучения многослойных нейронных сетей наилучшие результаты в общем случае достигаются применением стохастически управляемого метода повторных рестартов совместно с детерминированными алгоритмами локальной оптимизации.
www.intuit.ru
НОУ ИНТУИТ | Лекция | Методы глобальной оптимизации
Аннотация: Рассматриваются: алгоритм имитации отжига, генетические алгоритмы, использование случайных возмущений в обучении (метод виртуальных частиц).
Элементы глобальной оптимизации
Все представленные ранее методы обучения нейронных сетей являются локальными. Они ведут к одному из локальных минимумов целевой функции, лежащему в окрестности точки начала обучения. Только в ситуации, когда значение глобального минимума известно, удается оценить, находится ли найденный локальный минимум в достаточной близости от искомого решения. Если локальное решение признается неудовлетворительным, следует повторить процесс обучения при других начальных значениях весов и с другими управляющими параметрами. Можно либо проигнорировать полученное решение и начать обучение при новых (как правило, случайных) значениях весов, либо изменить случайным образом найденное локальное решение (встряхивание весов) и продолжить обучение сети.
При случайном приращении весов переход в новую точку связан с определенной вероятностью того, что возобновление процесса обучения выведет поиск из "сферы притяжения" локального минимума.
Алгоритмы имитации отжига
Метод имитации отжига основан на идее, заимствованной из статистической механики. Он отражает поведение расплавленного материала при отвердевании с применением процедуры отжига (управляемого охлаждения) при температуре, последовательно понижаемой до нуля.
В процессе медленного управляемого охлаждения, называемого отжигом, кристаллизация расплава сопровождается глобальным уменьшением его энергии, однако допускаются ситуации, в которых она может на какое-то время возрастать (в частности, при подогреве расплава для предотвращения слишком быстрого его остывания). Благодаря допустимости кратковременного повышения энергетического уровня, возможен выход из ловушек локальных минимумов энергии, которые возникают при реализации процесса. Только понижение температуры до абсолютного нуля делает невозможным какое-либо самостоятельное повышение энергетического уровня расплава.
Метод имитации отжига представляет собой алгоритмический аналог физического процесса управляемого охлаждения. Классический алгоритм имитации отжига можно описать следующим образом:
- Запустить процесс из начальной точки при заданной начальной температуре .
- Пока , повторить раз следующие действия:
- Уменьшить температуру с использованием коэффициента , выбираемого из интервала , и вернуться к п. 2.
- После снижения температуры до нуля провести обучение сети любым из детерминированных методов локальной оптимизации вплоть до достижения минимума целевой функции.
Наибольшего ускорения имитации отжига можно достичь путем замены случайных начальных значений весов тщательно подобранными значениями с использованием любых доступных способов предварительной обработки исходных данных.
Метод имитации отжига оказывается особенно удачным для полимодальных комбинаторных проблем с очень большим количеством возможных решений, например, для машины Больцмана, в которой каждое состояние системы считается допустимым. При решении наиболее распространенных задач обучения многослойных нейронных сетей наилучшие результаты в общем случае достигаются применением стохастически управляемого метода повторных рестартов совместно с детерминированными алгоритмами локальной оптимизации.
www.intuit.ru
Программный комплекс для изучения методов глобальной оптимизации «GlOpt»
Санкт-Петербургский государственный университет
информационных технологий, механики и оптики
Факультет информационных технологий и программирования
Кафедра компьютерных технологий
А. C. Тяхти, А. A. Чебатуркин
Курсовая работа
Программный комплекс для изучения методов глобальной оптимизации
«GlOpt»
2009
Оглавление
Введение. 3
1. Глобальная оптимизация. 3
2.Алгоритм имитации отжига. 3
3. Схемы алгоритма отжига. 5
3.1. Больцмановский отжиг. 5
3.2. Отжиг Коши (быстрый отжиг) 6
3.3. Сверхбыстрый отжиг. 6
3.4. Другие схемы алгоритма отжига. 7
4. Исследуемые задачи. 7
4.1. Задача о расстановке N ферзей. 7
4.2. Задача об «Умном муравье». 8
5. Структура программного комплекса GLOpt 9
5.2 Класс Problem.. 9
5.3 Класс Individual 9
5.4 Класс SearchOperator 10
5.5 Класс Algorithm.. 10
5.4 Интерфейс IIndividualViewer 10
7. Заключение. 13
Источники. 14
Исходные коды.. 15
Введение
Целью данной работы являлось изучение методов глобальной оптимизации, создание программного комплекса, позволяющего провести количественные сравнения между различными оптимизационными методами на различных задачах оптимизации.
По схожей тематике известна работа Соколова Д.О и Давыдова А.А [7], однако реализованная авторами виртуальная лаборатория на наш взгляд обладает рядом недостатков, которые мы постарались устранить в настоящей работе. Одним из главных требований предъявляемых к программному комплексу являлась гибкость, его дальнейшая расширяемость, позволяющая в будущем наращивать не только набор рассматриваемых алгоритмов решения какой-либо конкретной задачи оптимизации, но и добавлять к рассмотрению новые проблемы, наглядно проводить их сравнительный анализ. В работе основное внимание было сосредоточено на алгоритме имитации отжига, сравнении его с генетическими алгоритмами.
1. Глобальная оптимизация
Под термином глобальная оптимизация будем понимать процесс поиска экстремума или экстремумов функции, которая, например, в эволюционном моделировании соответствует приспособленности особи, интерпретируемой как ее способность решать поставленную задачу.
Глобальная оптимизация применима к широкому классу задач. Она находит применение в проблемах проектирования, теории управления физическими процессами, распределении ограниченных ресурсов, анализе данных и других областях.
Известные методы глобальной оптимизации можно разделить на детерминированные и стохастические. Детерминированные методы находят глобальное решение посредством поиска на всем допустимом множестве. Поэтому большинство детерминированных алгоритмов теряют эффективность с возрастанием размерности задачи. Стохастические методы позволяют уйти от проблем детерминированных алгоритмов. Стохастический подход присутствует не только в разработке алгоритма, но и, например, при определении условия остановки.
К числу методов глобальной оптимизации относят алгоритм имитации отжига, генетические алгоритмы, метод виртуальных частиц, алгоритм контролируемого случайного поиска.
2.Алгоритм имитации отжига
Метод отжига [?], также известен под названиями: метод обжига, метод симуляции отжига, метод модельной закалки, simulated annealing. Этот метод – техника оптимизации, использующая упорядоченный случайный поиск на основе аналогии с процессом образования в веществе кристаллической структуры с минимальной энергией, происходящем при охлаждении этого вещества.
Алгоритм имитации отжига основан на моделировании физического процесса, который происходит при кристаллизации вещества из жидкого состояния в твердое (к примеру, при отжиге металлов). Предполагается, что, во-первых, процесс протекает при понижающейся температуре, а во-вторых, атомы в веществе уже выстроились в кристаллическую решетку, однако переходы отдельных атомов из одной ячейки в другую еще возможны. Вероятность этих переходов в свою очередь обусловлена температурой: чем ниже температура, тем ниже вероятность. Устойчивая кристаллическая структура вещества соответствует минимальному значению энергии. Это значит, что атом либо переходит в состояние с меньшим уровнем энергии, либо остается на месте.
Формализуем данный процесс. Фактически, при моделировании ищется некоторая точка (либо множество точек), на котором достигается минимум некоторой числовой функции F (x ) . Строится последовательность точек
, где соответствует начальному разделению. При достижении точки алгоритм завершает свою работу. Пусть рассматривается текущая точка . К ней применяется некоторый оператор A , который произвольным образом модифицирует эту точку, в результате чего получается новая точка Вероятность, с которой станет следующей точкой равна , где P - распределение Гиббса:Здесь
-элементы произвольной убывающей, сходящейся к нулю последовательности. Она представляет собой аналог понижающейся температуры во время реального физического процесса.Достоинством метода отжига является свойство избегать "ловушек" в локальных минимумах оптимизируемой функции, и продолжить поиск глобального минимума. Это достигается за счет принятия не только изменений параметров, приводящих к уменьшению значения функции, но и некоторых изменений, увеличивающих ее значение, в зависимости от температуры Т – характеристики моделируемого процесса. Чем выше температура, тем большие "ухудшающие" изменения (аналогичные случайным флуктуациям в нагретом веществе) допустимы, и больше их вероятность. Еще одним достоинством является то, что даже в условиях нехватки вычислительных ресурсов для нахождения глобального минимума, метод отжига, как правило, выдает весьма неплохое решение (один из локальных минимумов). Л. Ингбером [?] показано, что метод отжига и его модификации являются одним из наиболее эффективных методов случайного поиска оптимального решения для большого класса задач. Им же проведен сравнительный анализ адаптивного метода отжига (Adaptive Simulated Annealing - ASA) и генетических алгоритмов, из которого следует, что на большинстве задач метод отжига не проигрывает генетическим алгоритмам, а на многих и выигрывает. К настоящему времени разработано множество различных вариантов метода отжига, как общих, так и их специализаций для решения конкретных задач.
Алгоритм имитации отжига можно представить в виде следующей структурной схемы (рис.1).
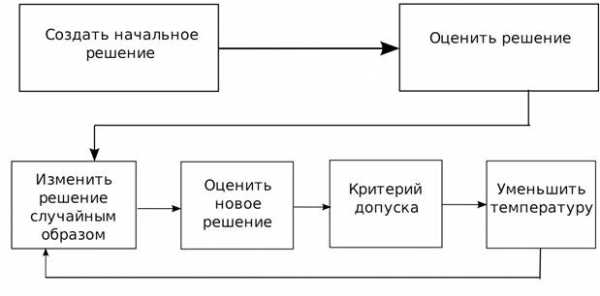
Рис. 1
3. Схемы алгоритма отжига
3.1. Больцмановский отжиг
Исторически первой схемой метода отжига является схема Больцмановского отжига. Эта схема использовалась Н.Метрополисом для вычисления многомерных интегралов пути в задачах статистической физики, а также С.Киркпатриком для решения задачи нахождения оптимальной разводки микросхем. В Больцмановском отжиге изменение температуры задается формулой
Семейство распределений Q(x; T) выбирается как семейство нормальныхраспределений с математическим ожиданием и дисперсией, т.е. задаетсяплотностью
где D - размерность пространства состояний. Пространство состояний предполагается метрическим. Для больцмановской схемы доказано, что при достаточно больших и общем числе шагов k, выбор такого семейства распределений гарантирует нахождение глобального минимума. Основным недостатком метода является медленное убывание температуры.
3.2. Отжиг Коши (быстрый отжиг)
В результате совершенствования больцмановского метода Цу и Хартли предложили алгоритм, использующий другую схему изменения температуры
В качестве Q используются нормированные распределения Коши с плотностью
Однако это распределение сложно моделировать в пространствах размерностью больше единицы. Кроме того, в них накладывается ряд ограничений на закон изменения температуры, что является серьезным недостатком данного алгоритма.
mirznanii.com
НОУ ИНТУИТ | Лекция | Методы глобальной оптимизации
Аннотация: Рассматриваются: алгоритм имитации отжига, генетические алгоритмы, использование случайных возмущений в обучении (метод виртуальных частиц).
Элементы глобальной оптимизации
Все представленные ранее методы обучения нейронных сетей являются локальными. Они ведут к одному из локальных минимумов целевой функции, лежащему в окрестности точки начала обучения. Только в ситуации, когда значение глобального минимума известно, удается оценить, находится ли найденный локальный минимум в достаточной близости от искомого решения. Если локальное решение признается неудовлетворительным, следует повторить процесс обучения при других начальных значениях весов и с другими управляющими параметрами. Можно либо проигнорировать полученное решение и начать обучение при новых (как правило, случайных) значениях весов, либо изменить случайным образом найденное локальное решение (встряхивание весов) и продолжить обучение сети.
При случайном приращении весов переход в новую точку связан с определенной вероятностью того, что возобновление процесса обучения выведет поиск из "сферы притяжения" локального минимума.
При решении реальных задач в общем случае даже приблизительная оценка глобального минимума оказывается неизвестной. По этой причине возникает необходимость применения методов глобальной оптимизации. Рассмотрим три из разработанных подходов к глобальной оптимизации: метод имитации отжига, генетические алгоритмы и метод виртуальных частиц.
Алгоритмы имитации отжига
Метод имитации отжига основан на идее, заимствованной из статистической механики. Он отражает поведение расплавленного материала при отвердевании с применением процедуры отжига (управляемого охлаждения) при температуре, последовательно понижаемой до нуля.
В процессе медленного управляемого охлаждения, называемого отжигом, кристаллизация расплава сопровождается глобальным уменьшением его энергии, однако допускаются ситуации, в которых она может на какое-то время возрастать (в частности, при подогреве расплава для предотвращения слишком быстрого его остывания). Благодаря допустимости кратковременного повышения энергетического уровня, возможен выход из ловушек локальных минимумов энергии, которые возникают при реализации процесса. Только понижение температуры до абсолютного нуля делает невозможным какое-либо самостоятельное повышение энергетического уровня расплава.
Метод имитации отжига представляет собой алгоритмический аналог физического процесса управляемого охлаждения. Классический алгоритм имитации отжига можно описать следующим образом:
- Запустить процесс из начальной точки при заданной начальной температуре .
- Пока , повторить раз следующие действия:
- Уменьшить температуру с использованием коэффициента , выбираемого из интервала , и вернуться к п. 2.
- После снижения температуры до нуля провести обучение сети любым из детерминированных методов локальной оптимизации вплоть до достижения минимума целевой функции.
Наибольшего ускорения имитации отжига можно достичь путем замены случайных начальных значений весов тщательно подобранными значениями с использованием любых доступных способов предварительной обработки исходных данных.
Метод имитации отжига оказывается особенно удачным для полимодальных комбинаторных проблем с очень большим количеством возможных решений, например, для машины Больцмана, в которой каждое состояние системы считается допустимым. При решении наиболее распространенных задач обучения многослойных нейронных сетей наилучшие результаты в общем случае достигаются применением стохастически управляемого метода повторных рестартов совместно с детерминированными алгоритмами локальной оптимизации.
www.intuit.ru
НОУ ИНТУИТ | Лекция | Методы глобальной оптимизации
Аннотация: Рассматриваются: алгоритм имитации отжига, генетические алгоритмы, использование случайных возмущений в обучении (метод виртуальных частиц).
Элементы глобальной оптимизации
Все представленные ранее методы обучения нейронных сетей являются локальными. Они ведут к одному из локальных минимумов целевой функции, лежащему в окрестности точки начала обучения. Только в ситуации, когда значение глобального минимума известно, удается оценить, находится ли найденный локальный минимум в достаточной близости от искомого решения. Если локальное решение признается неудовлетворительным, следует повторить процесс обучения при других начальных значениях весов и с другими управляющими параметрами. Можно либо проигнорировать полученное решение и начать обучение при новых (как правило, случайных) значениях весов, либо изменить случайным образом найденное локальное решение (встряхивание весов) и продолжить обучение сети.
При случайном приращении весов переход в новую точку связан с определенной вероятностью того, что возобновление процесса обучения выведет поиск из "сферы притяжения" локального минимума.
При решении реальных задач в общем случае даже приблизительная оценка глобального минимума оказывается неизвестной. По этой причине возникает необходимость применения методов глобальной оптимизации. Рассмотрим три из разработанных подходов к глобальной оптимизации: метод имитации отжига, генетические алгоритмы и метод виртуальных частиц.
Алгоритмы имитации отжига
Метод имитации отжига основан на идее, заимствованной из статистической механики. Он отражает поведение расплавленного материала при отвердевании с применением процедуры отжига (управляемого охлаждения) при температуре, последовательно понижаемой до нуля.
В процессе медленного управляемого охлаждения, называемого отжигом, кристаллизация расплава сопровождается глобальным уменьшением его энергии, однако допускаются ситуации, в которых она может на какое-то время возрастать (в частности, при подогреве расплава для предотвращения слишком быстрого его остывания). Благодаря допустимости кратковременного повышения энергетического уровня, возможен выход из ловушек локальных минимумов энергии, которые возникают при реализации процесса. Только понижение температуры до абсолютного нуля делает невозможным какое-либо самостоятельное повышение энергетического уровня расплава.
Метод имитации отжига представляет собой алгоритмический аналог физического процесса управляемого охлаждения. Классический алгоритм имитации отжига можно описать следующим образом:
- Запустить процесс из начальной точки при заданной начальной температуре .
- Пока , повторить раз следующие действия:
- Уменьшить температуру с использованием коэффициента , выбираемого из интервала , и вернуться к п. 2.
- После снижения температуры до нуля провести обучение сети любым из детерминированных методов локальной оптимизации вплоть до достижения минимума целевой функции.
Наибольшего ускорения имитации отжига можно достичь путем замены случайных начальных значений весов тщательно подобранными значениями с использованием любых доступных способов предварительной обработки исходных данных.
Метод имитации отжига оказывается особенно удачным для полимодальных комбинаторных проблем с очень большим количеством возможных решений, например, для машины Больцмана, в которой каждое состояние системы считается допустимым. При решении наиболее распространенных задач обучения многослойных нейронных сетей наилучшие результаты в общем случае достигаются применением стохастически управляемого метода повторных рестартов совместно с детерминированными алгоритмами локальной оптимизации.
www.intuit.ru
НОУ ИНТУИТ | Лекция | Методы глобальной оптимизации
Аннотация: Рассматриваются: алгоритм имитации отжига, генетические алгоритмы, использование случайных возмущений в обучении (метод виртуальных частиц).
Элементы глобальной оптимизации
Все представленные ранее методы обучения нейронных сетей являются локальными. Они ведут к одному из локальных минимумов целевой функции, лежащему в окрестности точки начала обучения. Только в ситуации, когда значение глобального минимума известно, удается оценить, находится ли найденный локальный минимум в достаточной близости от искомого решения. Если локальное решение признается неудовлетворительным, следует повторить процесс обучения при других начальных значениях весов и с другими управляющими параметрами. Можно либо проигнорировать полученное решение и начать обучение при новых (как правило, случайных) значениях весов, либо изменить случайным образом найденное локальное решение (встряхивание весов) и продолжить обучение сети.
При случайном приращении весов переход в новую точку связан с определенной вероятностью того, что возобновление процесса обучения выведет поиск из "сферы притяжения" локального минимума.
При решении реальных задач в общем случае даже приблизительная оценка глобального минимума оказывается неизвестной. По этой причине возникает необходимость применения методов глобальной оптимизации. Рассмотрим три из разработанных подходов к глобальной оптимизации: метод имитации отжига, генетические алгоритмы и метод виртуальных частиц.
Алгоритмы имитации отжига
Метод имитации отжига основан на идее, заимствованной из статистической механики. Он отражает поведение расплавленного материала при отвердевании с применением процедуры отжига (управляемого охлаждения) при температуре, последовательно понижаемой до нуля.
В процессе медленного управляемого охлаждения, называемого отжигом, кристаллизация расплава сопровождается глобальным уменьшением его энергии, однако допускаются ситуации, в которых она может на какое-то время возрастать (в частности, при подогреве расплава для предотвращения слишком быстрого его остывания). Благодаря допустимости кратковременного повышения энергетического уровня, возможен выход из ловушек локальных минимумов энергии, которые возникают при реализации процесса. Только понижение температуры до абсолютного нуля делает невозможным какое-либо самостоятельное повышение энергетического уровня расплава.
Метод имитации отжига представляет собой алгоритмический аналог физического процесса управляемого охлаждения. Классический алгоритм имитации отжига можно описать следующим образом:
- Запустить процесс из начальной точки при заданной начальной температуре .
- Пока , повторить раз следующие действия:
- Уменьшить температуру с использованием коэффициента , выбираемого из интервала , и вернуться к п. 2.
- После снижения температуры до нуля провести обучение сети любым из детерминированных методов локальной оптимизации вплоть до достижения минимума целевой функции.
Наибольшего ускорения имитации отжига можно достичь путем замены случайных начальных значений весов тщательно подобранными значениями с использованием любых доступных способов предварительной обработки исходных данных.
Метод имитации отжига оказывается особенно удачным для полимодальных комбинаторных проблем с очень большим количеством возможных решений, например, для машины Больцмана, в которой каждое состояние системы считается допустимым. При решении наиболее распространенных задач обучения многослойных нейронных сетей наилучшие результаты в общем случае достигаются применением стохастически управляемого метода повторных рестартов совместно с детерминированными алгоритмами локальной оптимизации.
www.intuit.ru