RK6_Методы_Оптимизации_1 / Все вместе / Оптимизация Глава 6_2. Симплексный метод оптимизации
Метод оптимизации симплексный - Справочник химика 21
| Рис. 10.6. Оптимизация симплексным методом. |  |
Непосредств. эксперимент на объекте (без построения модели). Стратегия проведения опытов определяется выбранным методом оптимизации. При этом значение целевой ф-ции вычисляют не по модели, а находят непосредственно из опыта, выполненного в соответствующих условиях. Наиб, часто для поиска наилучшего значения целевой ф-ции используют последовательный симплексный метод, метод Гаусса-Зейделя и т.п. [c.560]
Симплексный метод оптимизации целесообразно применять в ситуациях, когда дисперсия помехи велика и нет априорной информации о характере поверхности отклика. [c.486]
Симплексный метод оптимизации. Основной особенностью симплексного мето-да поиска является совмещение процессов изучения поверхности отклика и перемещения по ней. Это достигается тем, что эксперименты ставят только в точках факторного пространства, соответствующих вершинам симплексов, и-мерный симплекс— это выпуклая фигура, образования ге+1 точками (вершинами). Так на плоскости симплексом является треугольник, в трехмерном пространстве— тетраэдр и т. д. Симплекс называется регулярным, если все расстояния между его вершинами равны. [c.484]
Динамика анализа области оптимизации методом симплексного планирования эксперимента [c.106]
Применим симплексный метод оптимизации на базе теории планирования эксперимента, при этом в точках симплексного плана будем выполнять расчетный эксперимент, рассчитывая критерий оптимальности R по (3.71) с учетом (3.72). [c.101]
Любое планирование и последующая оптимизация в производственных условиях должны приспосабливаться (адаптироваться) к временному дрейфу процесса. В настоящее время используют методы статистической адаптационной оптимизации производственных процессов, основанные на использовании факторного или симплексного планирования. Эти методы требуют некоторого варьирования регулируемых переменных, т. е. покачивания режима производственной установки. По результатам такого варьирования определяют и устанавливают оптимальный режим через некоторое время всю процедуру повторяют для уточнения положения оптимума. [c.41]
Симплексом называется правильный многогранник, имеющий п 1 верщину, где п — число факторов, влияющих на процесс. Так, если факторов два, то симплексом является правильный треугольник. Сущность симплексного метода оптимизации иллюстрирует рис. 6. [c.24]
В системах автоматической оптимизации широко используется аппаратура вычислительной техники. В простейших системах, где не требуется высокая точность, применяются недорогие электронные устройства непрерывного действия, для сложных объектов — специализированные ЭВМ. Работа автоматического оптимизатора может быть основана на различных методах, чаще всего на рассмотренных нами поисковых методах оптимизации с той лишь разницей, что наличие модели объекта здесь необязательно. При этом стратегия поиска может быть случайная, симплексная, градиентная — на основе пробных экспериментальных шагов, осуществляемых оптимизатором. Подробно с автоматическими методами поиска оптимума можно ознакомиться в монографии [40]. [c.253]
Пример 9. Сравнить эффективность симплексного метода оптимизации и метода крутого восхождения на основании результатов восьми опытов (см. табл. 38). [c.233]
Применение методов оптимизации в квантовохимических исследованиях. Если в более ранних работах некоторые авторы использовали в расчетах равновесных геометрий и переходных структур достаточно кустарные методики или такие малоэффективные процедуры, как циклический спуск или симплексный метод, то начиная примерно с 1971 г. градиентные методы и, в первую очередь, методы переменной метрики начали интенсивно внедряться в квантовохимическую практику. При этом очень удобно то, что из известной волновой функции для некоторой конфигурации ядер можно вычислить не только энергию в этой точке, но и ее производные, если только известны производные молекулярных интегралов, так, в случае закрытых оболочек [238] [c.117]
Если используется последовательный метод оптимизации, например симплексная оптимизация (разд. 5.3), возникает другая ситуация. В этом случае определяют значение критерия для каждой хроматограммы и результаты определения сравнивают с ранее полученными. Если при этом число наблюдаемых пиков возрастает, то простое сравнение может оказаться некорректным. Например, если на хроматограмме наблюдается три полностью разделенных пика, то значение критерия ПР для этой хроматограммы равно 1. Однако если на следующей хроматограмме наблюдается четыре пика, которые разделены неполностью (например, значение Р для каждой пары последовательно вы.ходящих пиков равно 0,9), то критерий ИР равен только 0,73. Тем не менее ясно, что вторая хроматограмма лучше первой. [c.183]
Для оптимизации химико-технологических процессов широко используется симплексный метод. Свое название метод получил от слова симплекс. Симплексом называется правильный многогранник, имеющий + вершину, где п — число факторов, являющихся ресурсами оптимизации. Так, если факторов два, то симплексом является правильный треугольник. Сущность симплексного метода оптимизации иллюстрирует рис. 24. [c.102]
Симплексный метод является одним из эффективных методов решения задач оптимизации высокой размерности. Алгоритм этого метода основан на использовании некоторых свойств простейших многогранников п-мерного пространства симплексов. [c.387]
Симплексный метод поиска оптимума широко применяется при оптимизации процессов как на этапе лабораторных, так и промышленных исследований. Основное его преимущество заключается в [c.251]
Сущность симплексного метода для двух переменных оптимизации сводится к следующему. Условия первой серии опытов в п-мер-ном пространстве параметров соответствуют координатам точек, образующих в этом пространстве симплекс. [c.150]
Следует также упомянуть о таких методах, как сеточный, модельный и симплексной оптимизации [49]. Они не очень эффективны и редко используются при работе по методу наименьших квадратов и еще реже — для нахождения констант устойчивости. Эти методы основаны не на вычислении производных, а на расчете рассматриваемой функции (суммы квадратов разностей) на некотором множестве точек. Точки могут выбираться случайно или располагаться вдоль осей координат. Полученные значения анализируют тем или иным методом, по- [c.90]
Оптимизация проводилась симплексным методом на ЭВМ "Проминь-2". [c.16]
Для оптимального проектирования трубчатого аммиачного реактора использовался симплексный метод 176], хорошо приспособленный к существенно двумерной задаче оптимизации. Последовательность вычислений, изображенная графически в плоскости переменных — температуры ка входе и охлаждающего фактора (две переменные, оставленные на усмотрение проектировщика), — представляет собой цепь смежных треугольников (двумерных симплексов), вытянутую в направлении точки оптимума и в конце концов окружающую эту точку. Окончательное расположение оптимума уточняется путем квадратичной аппроксимации заключителыюй гексагональной системы точек симплекс-метода. [c.176]
Симплексный метод — один из основных методов линейного программирования. Он универсален и наиболее приспособлен к решению широкого круга экономических задач. С его помощью можно провести оптимизацию производственной программы, и уровня использования производственной мощности, осуществить оптимальную загрузку оборудования, оптимальное составление смесей, оптимальное оперативно-календарное планирование и др. [c.122]
Пример 9. Сранннть эффективность симплексного метода оптимизации и метода крутого восхождения на осиовании результатов восьми оиитов (см. таблицу иа стр. 176). [c.226]
Разработана термостабилизирующая система для электропроводящих композиций на основе полиэтилена низкой плотности термоэластопласта ДСТ-30 и печной сажи. Для оптимизации состава термостабилизирующей системы использован последовательный симплексный метод планирования эксперимента и метод симплексных решеток, Ил. 1. Табл. 3, Библ. 8 назв. [c.125]
Выбор же именно ортогональных планов второго порядка обусловлен тем, что в силу ортогональности матрицы планирования все коэффициенты в уравнении рефессии определяются независимо друг от друга. Применение каких-либо других методов оптимизации (например, симплексного метода) для поиска оптимальных консфуктивных параметров оказалось связанным с большим объемом экспериментальных работ. [c.176]
Особенностью задачи (5.1) является то, что само вычисление функции Ф , как правило, требует осуществления большого числа операций, т.е. является весьма трудоемка. Часто тpyдqвмкo уже вычисление по модели значений выходной координаты У1 при заданном входном воздействии. Например, если объект сывается дифференциальными уравнениями, то для нахождения часто приходится численно решать систему дифференциальных уравнений. В связи с этим при поиске экстремума функции ф целесообразно применять те методы оптимизации, которые не требуют частого бы- числения функции . К их числу относятся, например, симплексный метод и метод сопряженных направлений. Рассмотрим схему применения одного из них - метода сопряженных направлений. [c.43]
Если бы мы искали стационарные точки энергетической гиперповерхности методом проб и ошибок или симплексным методом [163], то не было бы существенного различия в трудоемкости вычислений по сравнению с аналитическим представлением гиперповерхности. Принципиальным шагом вперед явилось использование градиентных методов поиска стационарных точек. Первыми применили эти методы для квантовохимического исследования структуры молекул Пулаи [164—166] и МакИвер и Коморницкий [167]. Теоретическая химия давно пользуется различными методами оптимизации [168], и решение структурных задач ме- [c.60]
Симплексный метод с успехом может использоваться для оптимизации загрузки взаимозаменяемого оборудования при широком ассортименте выпускаемой продукции, а также для определения величины производственной мощности оборудования и участков при оптимальных условиях и установления производствеи-но1" программы объекта. [c.73]
При обычном факторном методе добавление еще одного параметра приводит к необходимости увеличить число опытов в два раза. Отметим еще следующие преимущества симплексного метода. При использовании симплекс-планирования параметр оптимизации у может измеряться приближенно достаточно иметь возможность проранжировать эти величины. При этом можно одновременно учитывать несколько параметров оптимизации выход продукта, стоимость, чистоту и т.д. Параметр оптимизации может не измеряться количественно. Метод не предъявляет жестких требований к аппроксимации поверхности отклика плоскостью. Симплекс-план может быть использован как алгоритм при оптимизации процесса с применением управляющей машины. [c.233]
При нахождении экстремума унимодальных трансцендентных функций многих переменных, выраженных в неявном виде, а также при обработке результатов оптимизации о.чень удобен метод независимого спуска, предполагающий подобие симплексной записи целевой функции в подобластях. Структуру предлагаемого метода проследим по БС — МНСР (рис. 85). Поиск экстремума (согласно схеме минимума) целевой функции включает в себя три осиопных последовательных этапа [c.286]
При обычном факторном методе добавление еще одного пара-NteTpa приводит к необходимости увеличить число опытов в два [ аза. Отметим еще следующие преимущества симплексного метода. При использовании симплекс-планирования параметр оптимизации [c.226]
chem21.info
Оптимизация Глава 6_2
Входные термины:
детерминированные методы оптимизации;
методы локальной оптимизации;
методы безусловной оптимизации;
многомерный критерий оптимальности;
прямые методы оптимизации;
Выходные термины:
регулярный симплекс;
«отражение» вершины симплекса;
редукция симплекса;
симплекс-метод.
§5. Симплекс-метод.
Рассмотрим следующую задачу многомерной локальной безусловной оптимизации: найти минимум критерия оптимальности Φ(X), определенного в n-мерном евклидовом пространстве 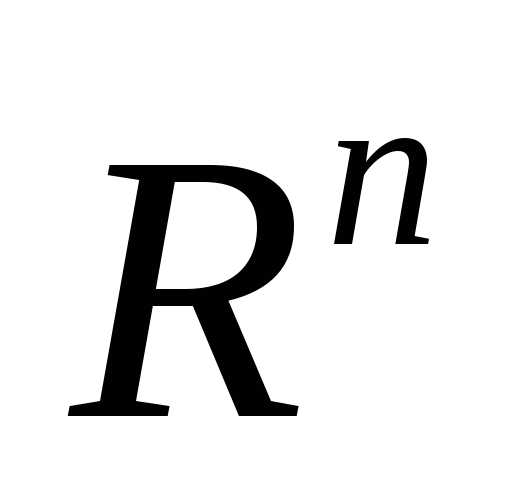 ,
,
 . (1)
. (1)
Регулярный симплекс и некоторые операции над ним.
Регулярным симплексом в пространстве 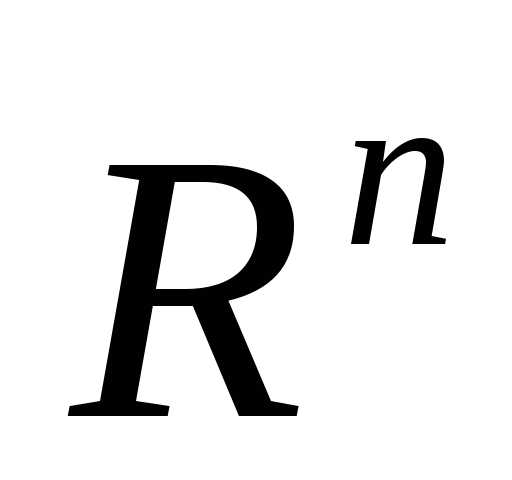 называется правильный многогранник, образованный
называется правильный многогранник, образованный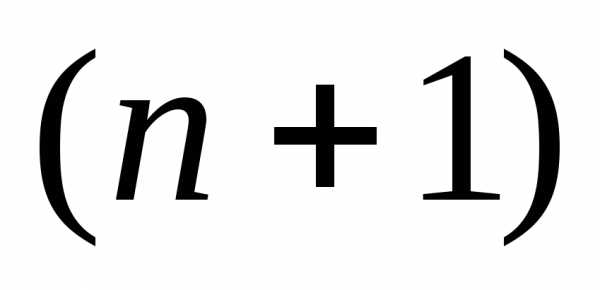 -ой равноотстоящими друг от друга вершинами. Для случаяn=2 – это равносторонний треугольник, для случая n=3 – тетраэдр.
-ой равноотстоящими друг от друга вершинами. Для случаяn=2 – это равносторонний треугольник, для случая n=3 – тетраэдр.
Если в пространстве 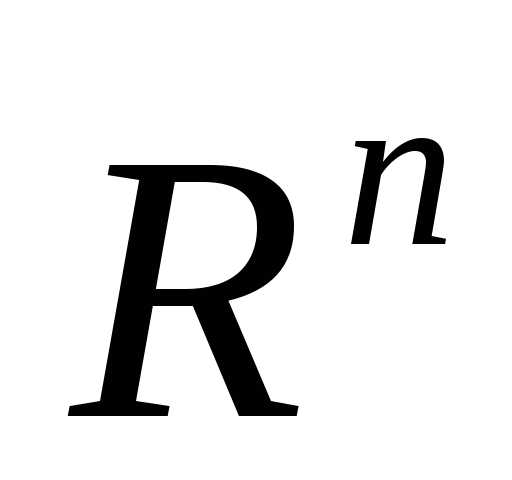 необходимо построить регулярный симплекс, вершина №1 которого находится в точке, то координаты вершин такого симплекса удобно задавать с помощьюматрицы
необходимо построить регулярный симплекс, вершина №1 которого находится в точке, то координаты вершин такого симплекса удобно задавать с помощьюматрицы
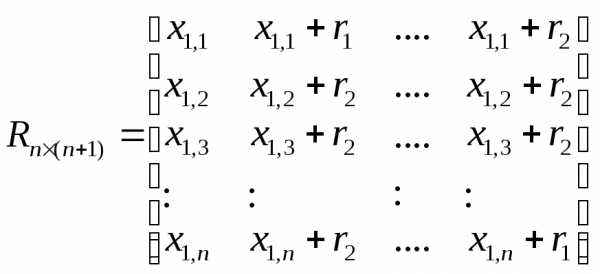 . (2)
. (2)
Здесь i-й столбец представляет собой координаты i-й вершины симплекса, ;
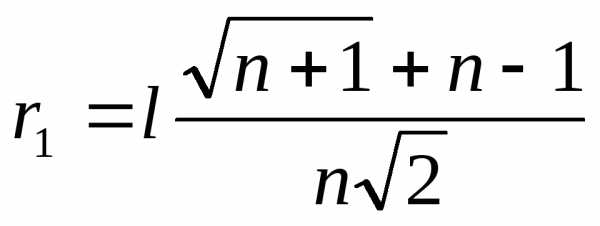 ,
, 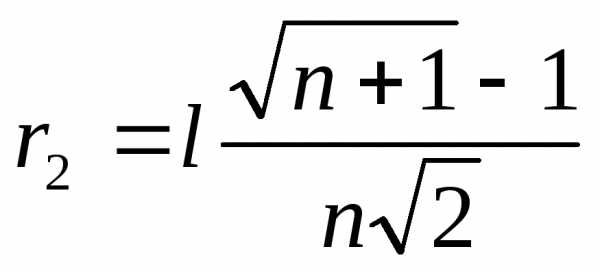 ; (3)
; (3)
l – длина ребра симплекса.
Например, регулярный симплекс в двумерном пространстве 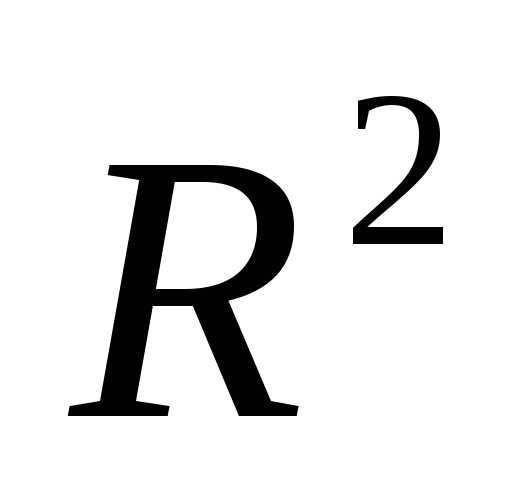 с первой вершиной в начале координат (когда) определяется (2*3) матрицей
с первой вершиной в начале координат (когда) определяется (2*3) матрицей
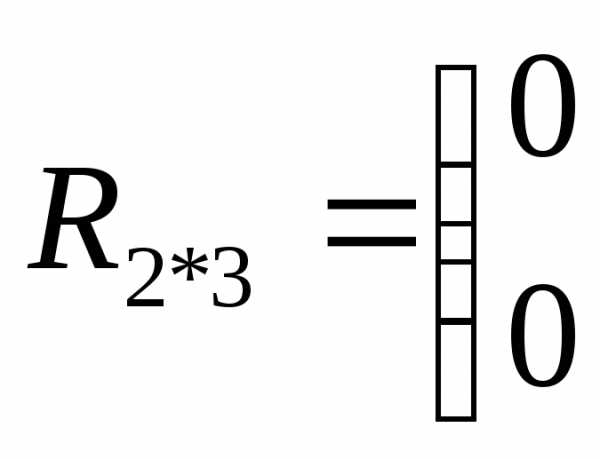
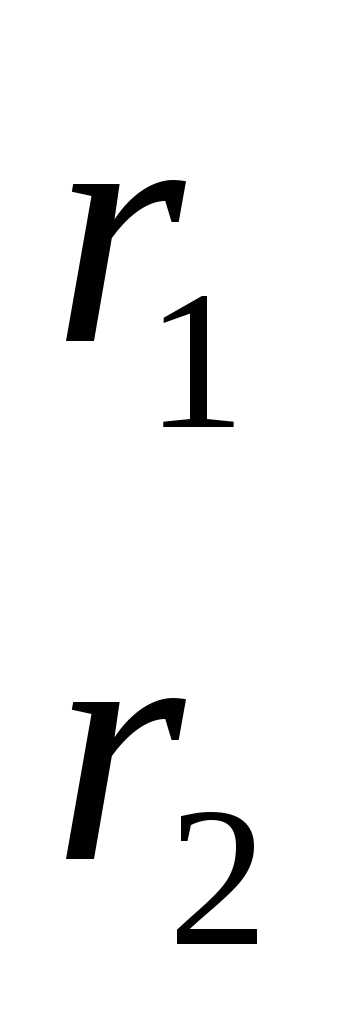
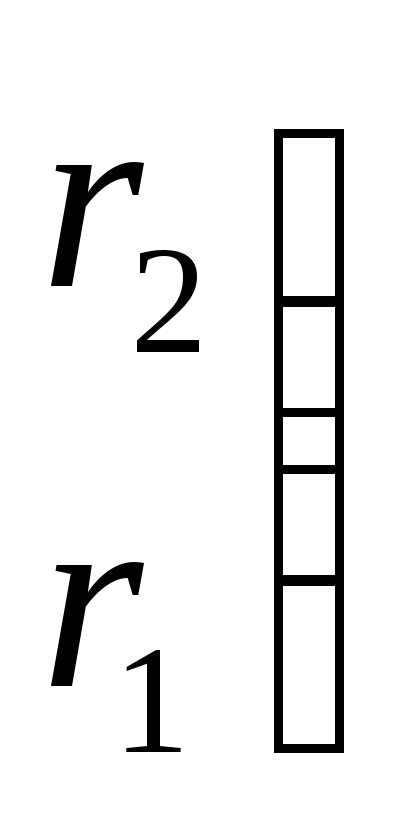
и имеет вид, представленный на рисунке 1.
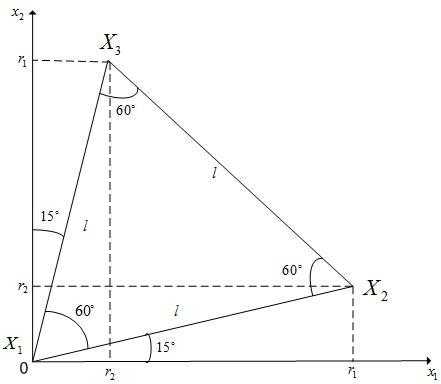
Рисунок 1 - Регулярный симплекс в пространстве 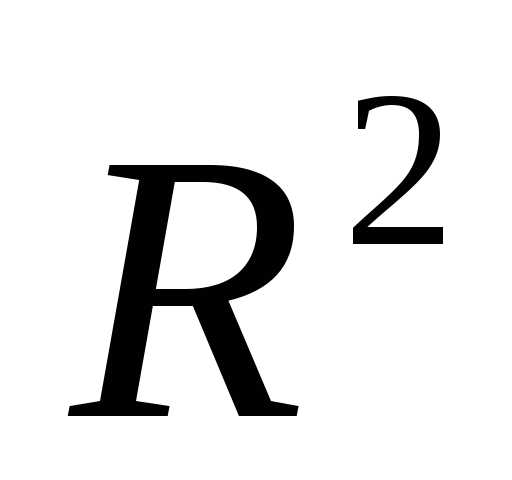 с одной из вершин в начале координат.
с одной из вершин в начале координат.
Регулярный симплекс в пространстве 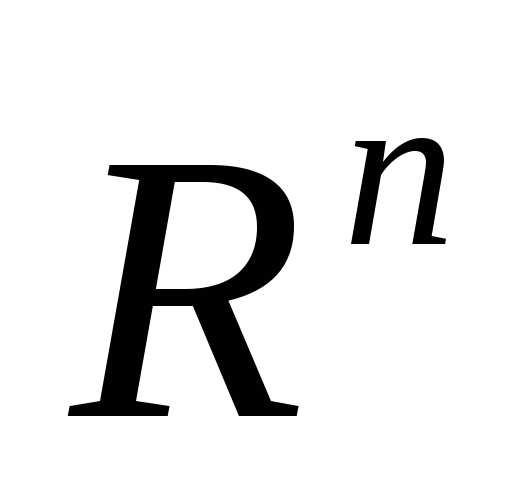 будем обозначать, где
будем обозначать, где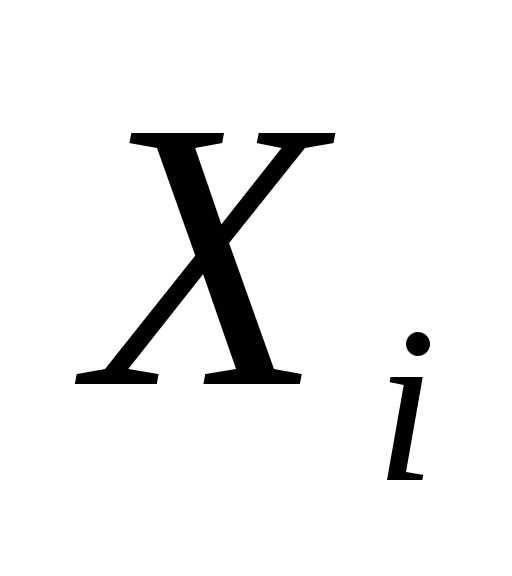 - вектор координатi-ой вершины симплекса.
- вектор координатi-ой вершины симплекса.
В алгоритме симплекс-метода используется следующее важное свойство регулярного симплекса: если одну из вершин регулярного симплекса перенести на надлежащее расстояние вдоль прямой, соединяющей данную вершину и центр тяжести оставшихся вершин, то вновь получится регулярный симплекс (рисунок 2). Будем называть эту процедуру отражением вершины симплекса относительно центра тяжести остальных вершин.
Очевидно, что при выполнении операции отражения вершины 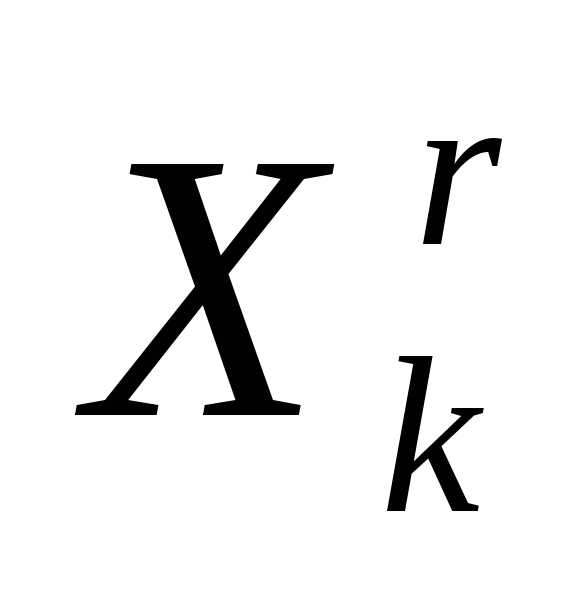 симплексаимеет место следующая связь координат этой вершины и вершины
симплексаимеет место следующая связь координат этой вершины и вершины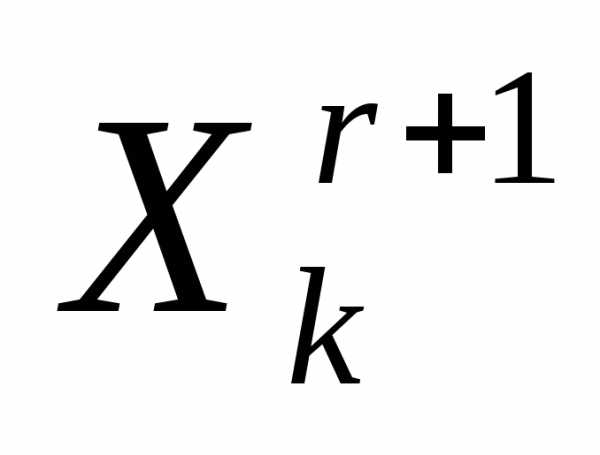 симплекса:
симплекса:
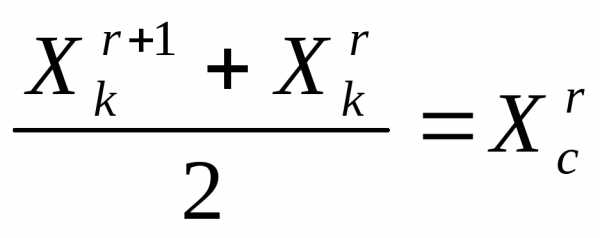
 . (4)
. (4)
Здесь
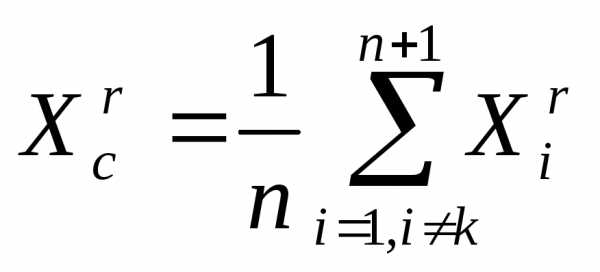 - (5)
- (5)
- вектор координат центра тяжести остальных вершин симплекса 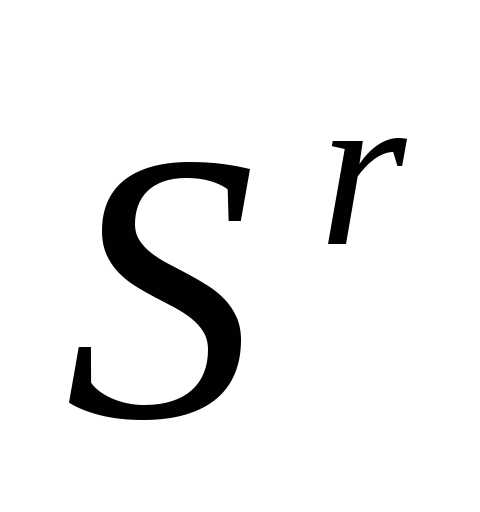 (за исключением отраженной вершины
(за исключением отраженной вершины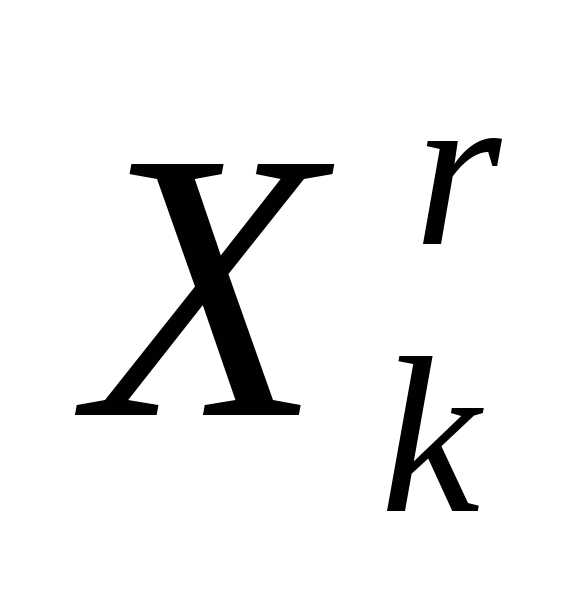 ).
).
Таким образом, после отражения вершины 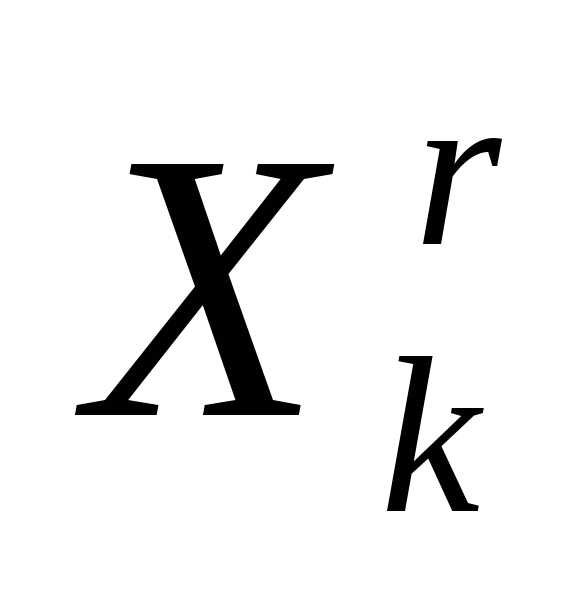 регулярного симплекса
регулярного симплекса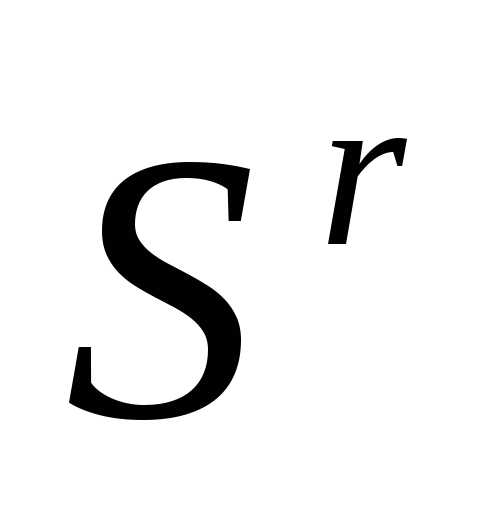 получаем новый регулярный симплекс
получаем новый регулярный симплекс
. (6)
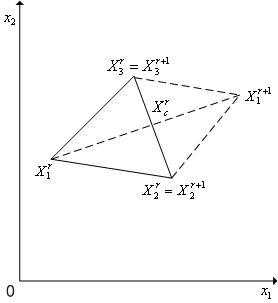
Рисунок 2 - Отражение вершины 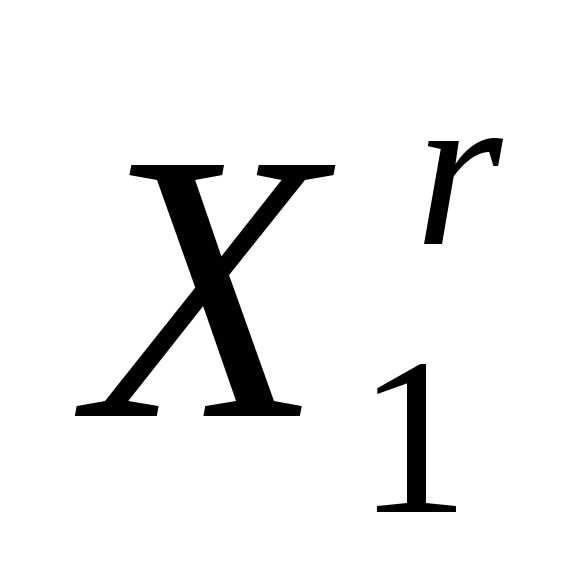 регулярного симплексав пространстве
регулярного симплексав пространстве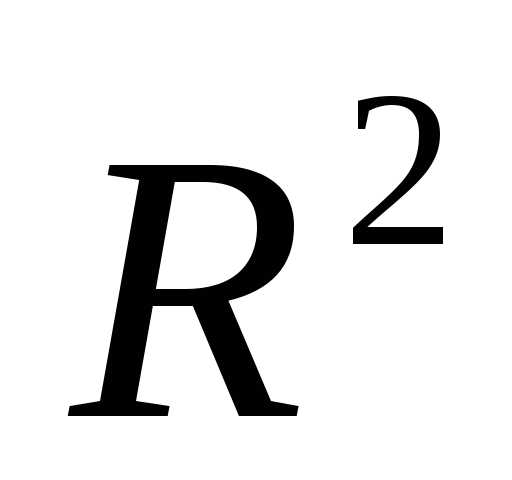 относительно центра тяжести
относительно центра тяжести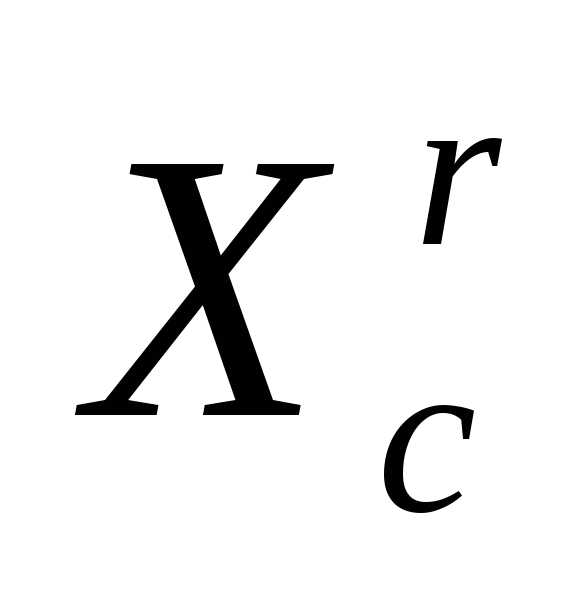 его остальных вершин.
его остальных вершин.
Кроме операции отражения вершины симплекса симплекс-метод может использовать операцию редукции симплекса (рисунок 3) - уменьшение длин всех ребер симплекса на одну и ту же величину («стягивания» симплекса к одной из его вершин).
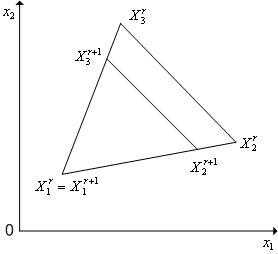
Рисунок 3 - Редукция вершин регулярного симплекса в пространстве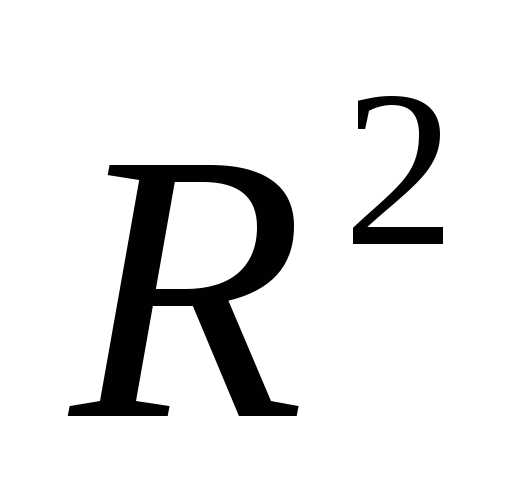 к вершине
к вершине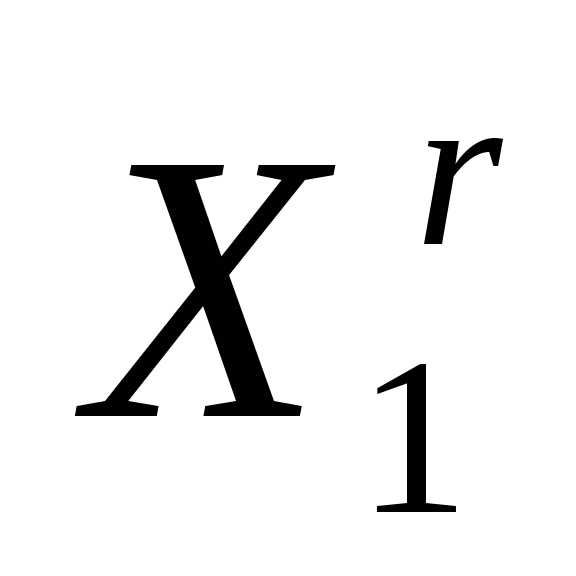 .
.
При выполнении операции редукции вершин симплекса к вершине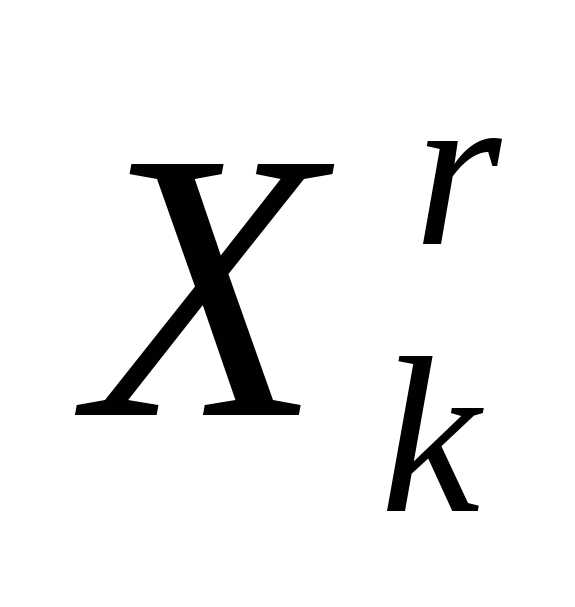 , координаты остальных вершин симплексаопределяются по формуле
, координаты остальных вершин симплексаопределяются по формуле
,
где 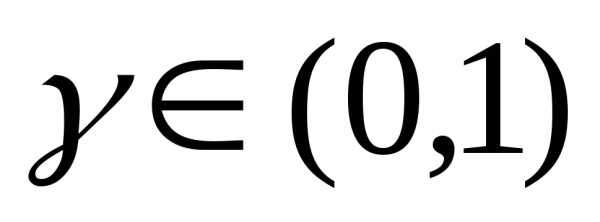 - коэффициент редукции. Рекомендуется использовать
- коэффициент редукции. Рекомендуется использовать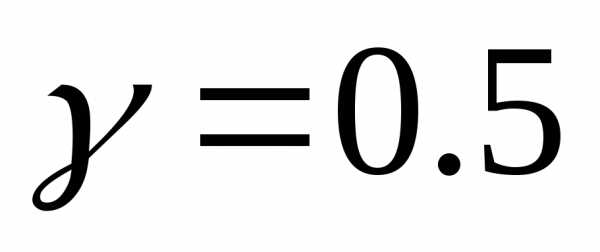 .
.
Таким образом, после редукции вершин симплекса к его вершине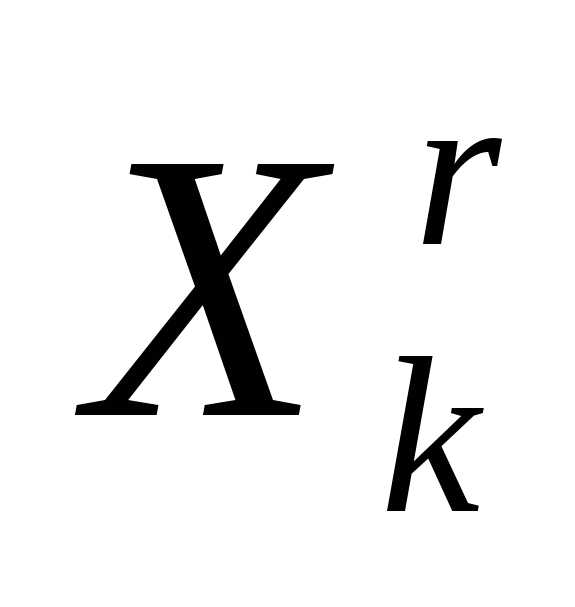 получаем новый симплекс
получаем новый симплекс
. (7)
Если симплекс 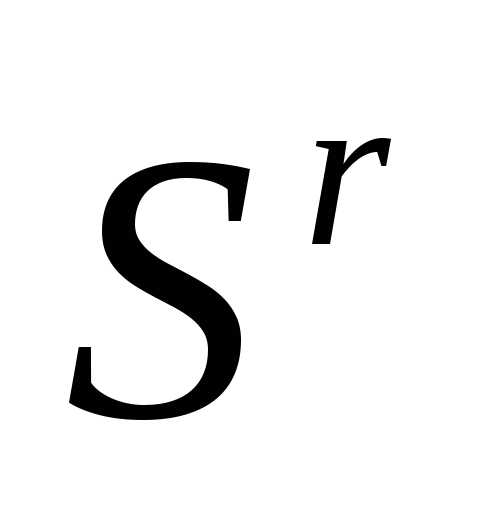 регулярен, то симплекс
регулярен, то симплекс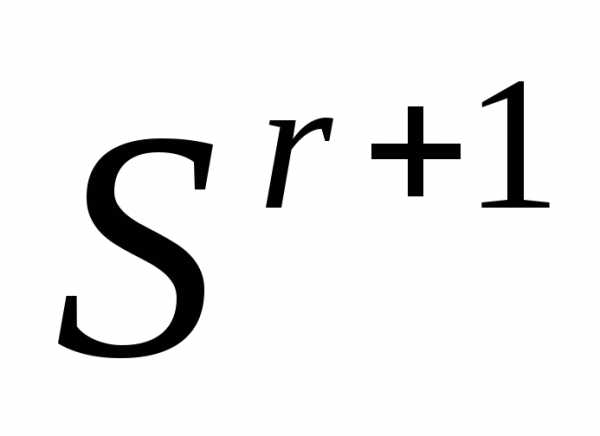 , полученный в результате редукции вершин симплекса
, полученный в результате редукции вершин симплекса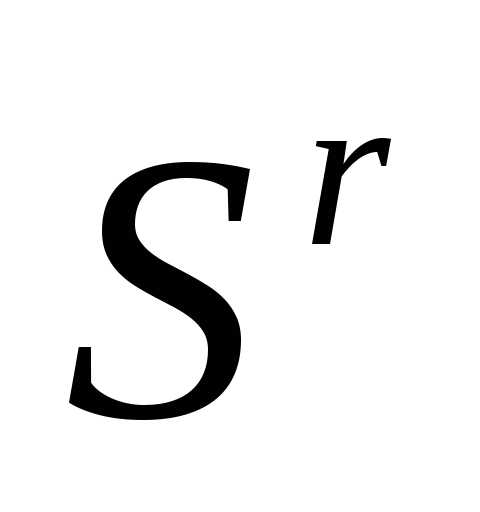 к одной из его вершин, также регулярен.
к одной из его вершин, также регулярен.
Схема простейшего варианта симплекс-метода.
Суть симплекс-метода раскрывает его простейший вариант.
Задаем начальную точку
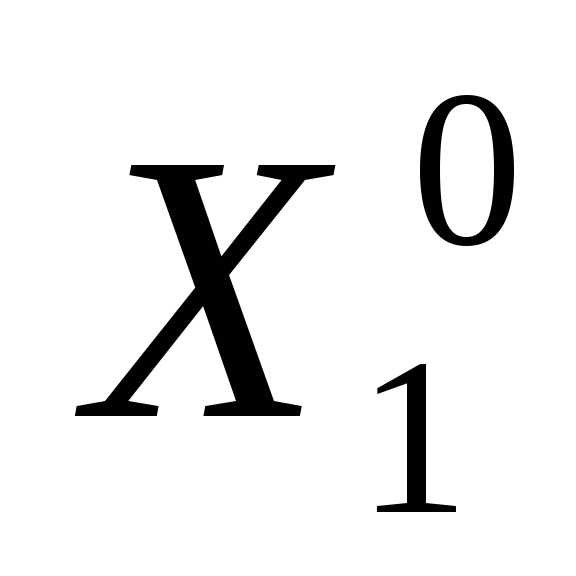 , длину ребра симплекса
, длину ребра симплекса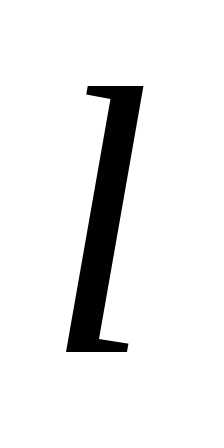 и полагаем
и полагаем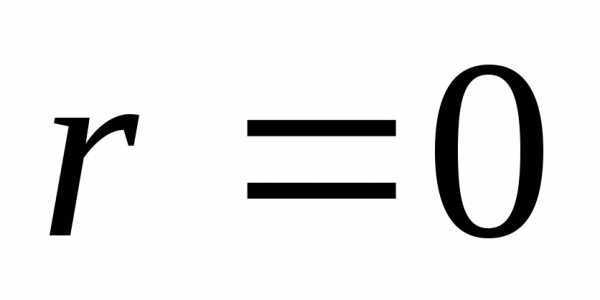 .
.По формулам (2), (3) находим координаты всех вершин симплекса
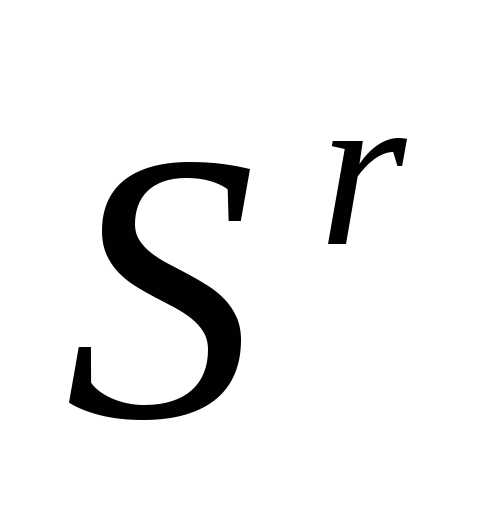 .
.Вычисляем значения минимизируемой функции во всех вершинах симплекса
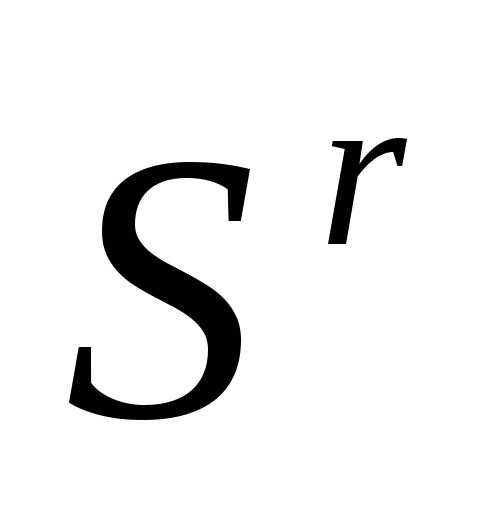 и находим максимальное из этих значений:
и находим максимальное из этих значений:
.
По формулам (5), (6) отражаем вершину
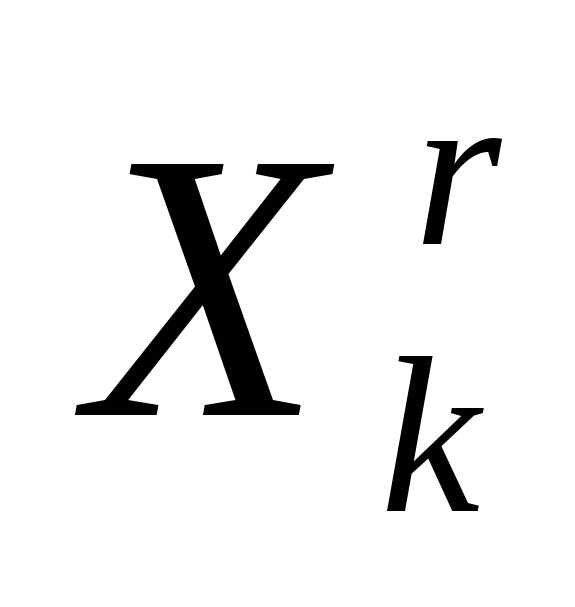 симплекса
симплекса 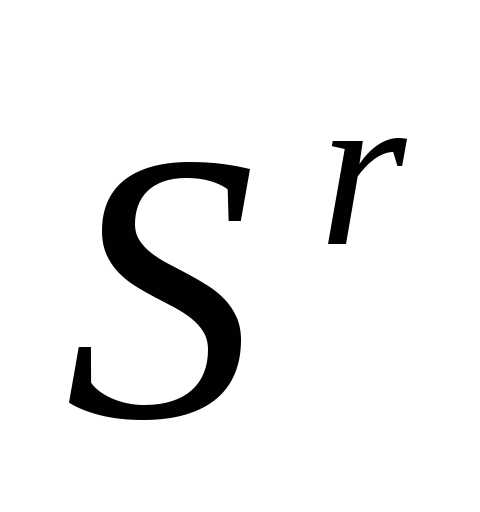 относительно центра тяжести остальных вершин симплекса – получаем новый симплекс . Вычисляем значение
относительно центра тяжести остальных вершин симплекса – получаем новый симплекс . Вычисляем значение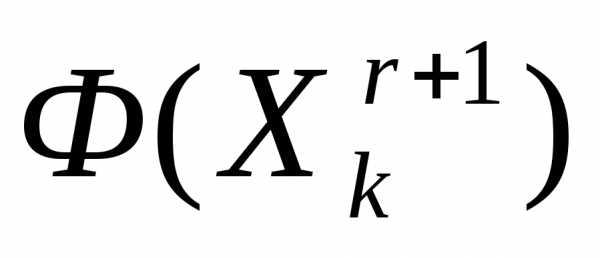 минимизируемой функции в вершине
минимизируемой функции в вершине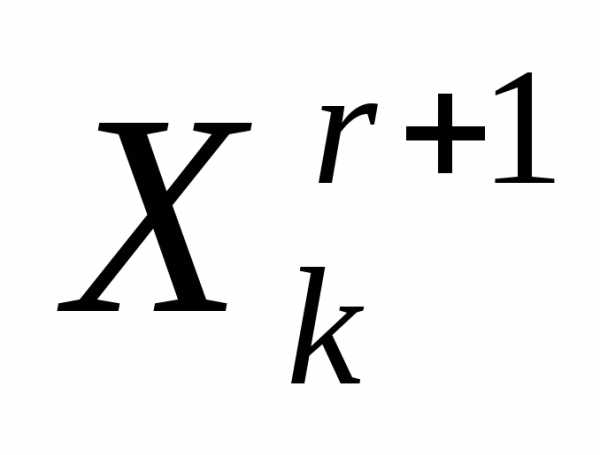 симплекса
симплекса 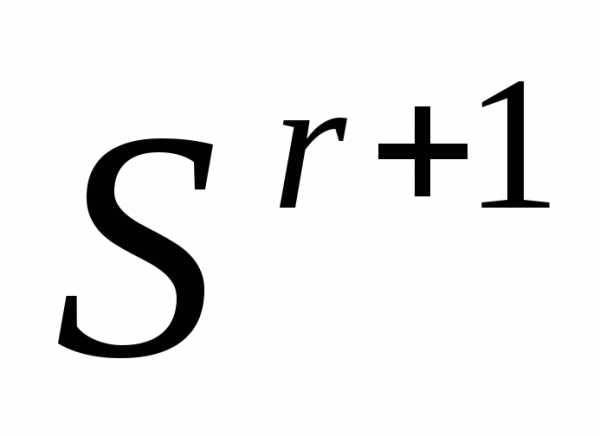 .
.Если условие окончания итераций (см. ниже) выполнено, то в качестве приближенного значения точки минимума функции
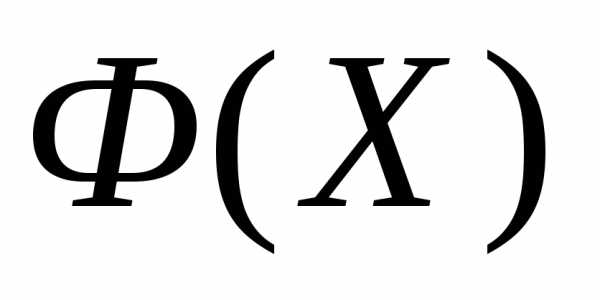 принимаем ту вершину симплекса
принимаем ту вершину симплекса 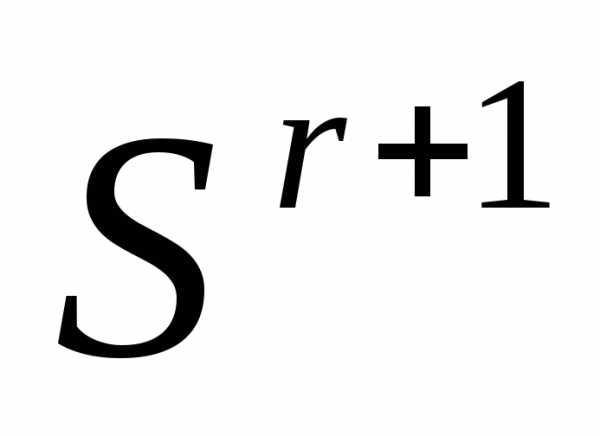 , в которой
, в которой 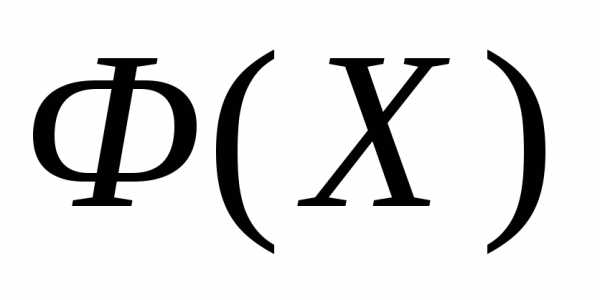 имеет минимальное значение, и заканчиваем вычисления. Иначеполагаем r=r+1 и переходим к п. 4●
имеет минимальное значение, и заканчиваем вычисления. Иначеполагаем r=r+1 и переходим к п. 4●
Поскольку размер симплекса в простейшем варианте симплекс-методе фиксирован, в качестве условия окончания итераций в данном случае можно использовать условие
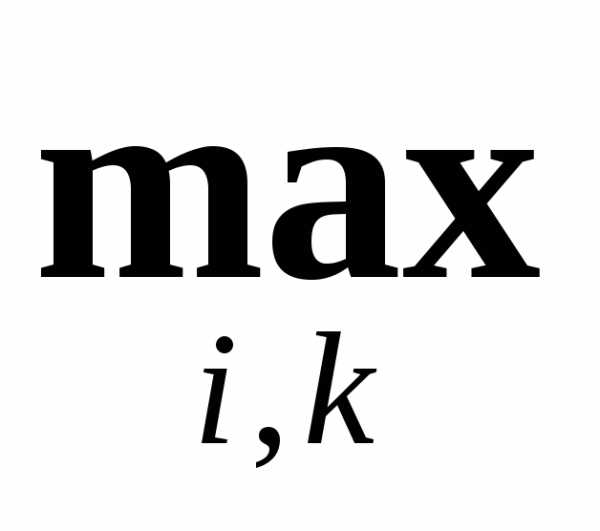 , ,
, ,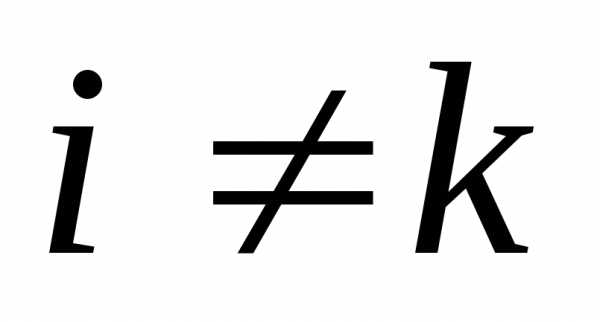 . (8)
. (8)
где 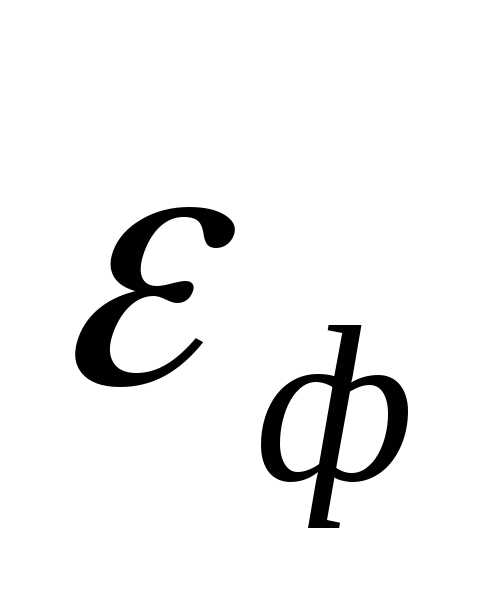 - требуемая точность решения поФ. Отметим, что выражение в левой части неравенства (8) есть максимальная разность значений функции
- требуемая точность решения поФ. Отметим, что выражение в левой части неравенства (8) есть максимальная разность значений функции 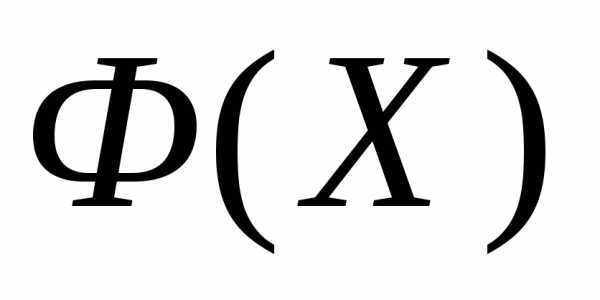 в двух вершинах симплекса
в двух вершинах симплекса 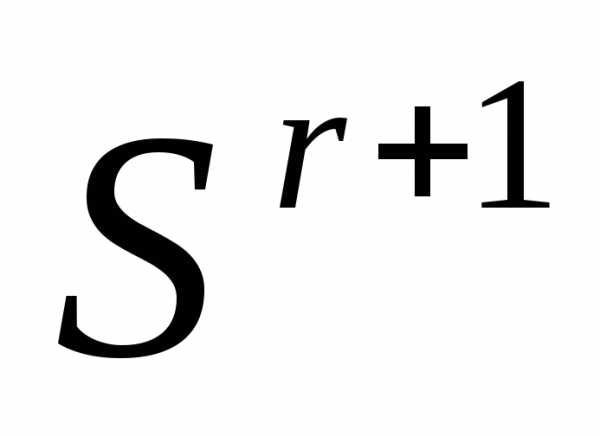 .
.
Рассмотренный вариант симплекс-метода иллюстрирует рисунок 4.
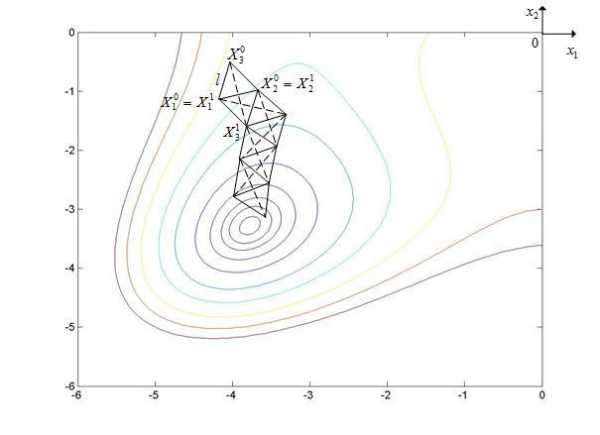
Рисунок 4 - Траектория поиска минимума функции Химмельблау простейшим симплекс-методом
Модифицированный симплекс-метод.
Рассмотренный простейший симплекс-метод склонен к зацикливанию и медленно сходится, если длина ребра симплекса l выбрана малой (выбор же большой длины ребра симплекса обеспечивает высокую скорость сходимости, но дает малую точность решения). Поэтому в вычислительной практике используются различные модификации простейшего метода, направленные на преодоление его указанных недостатков.
Основной идей модификаций простейшего симплекс-метода является изменение по некоторому правилу размера симплекса в процессе поиска. При этом наряду с условием (8) в качестве условия окончания итераций можно использовать условие
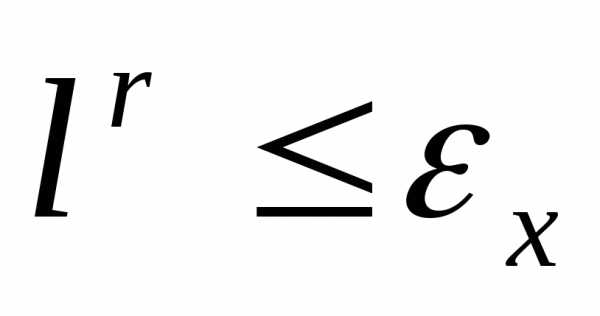 (9)
(9)
где 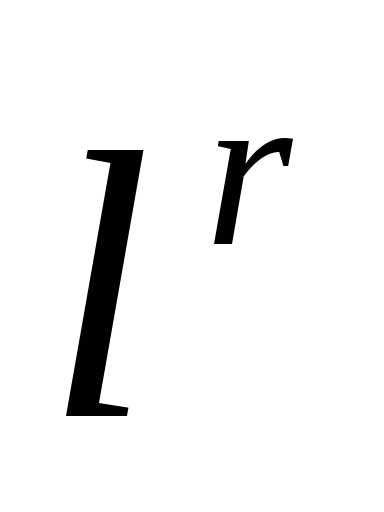 - текущая длина ребра симплекса,
- текущая длина ребра симплекса, 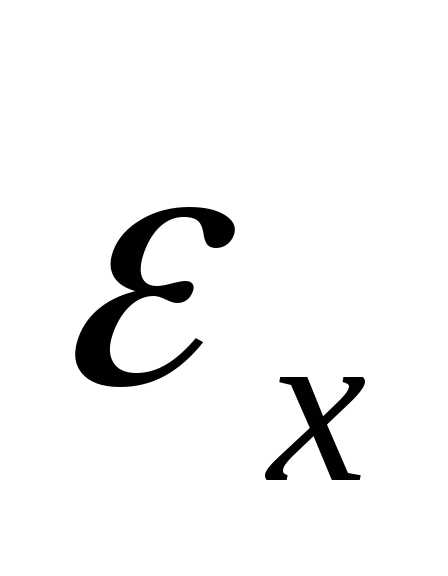 - требуемая точность решения по X.
- требуемая точность решения по X.
Обычно размер симплекса изменяется при выполнении следующих условий:
при «накрытии» симплексом дна оврага или точки минимума;
при циклическом движении.
«Накрытие» симплексом дна оврага или точки минимума. Пусть 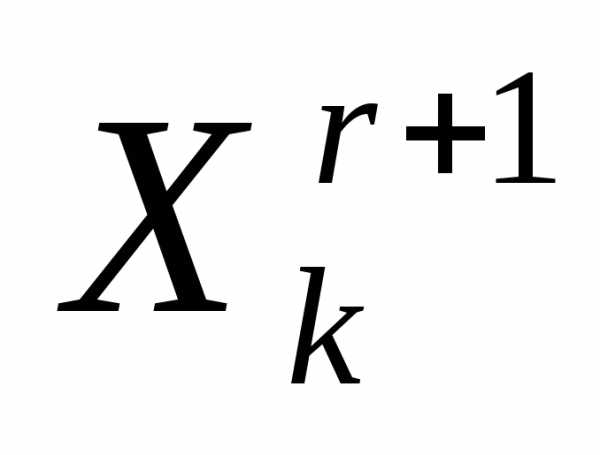 - вершина симплекса
- вершина симплекса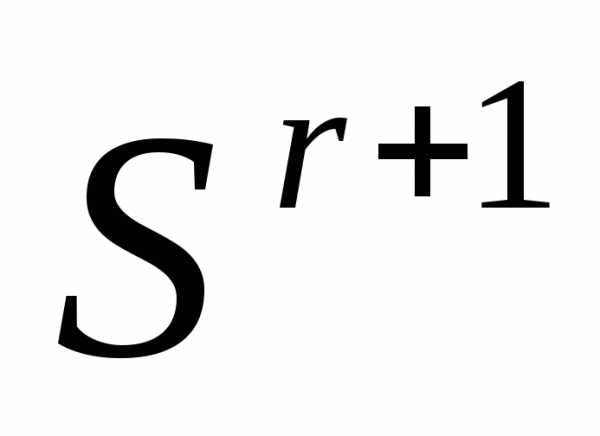 , которая получилась наr-ой итерации в результате отражения вершины
, которая получилась наr-ой итерации в результате отражения вершины 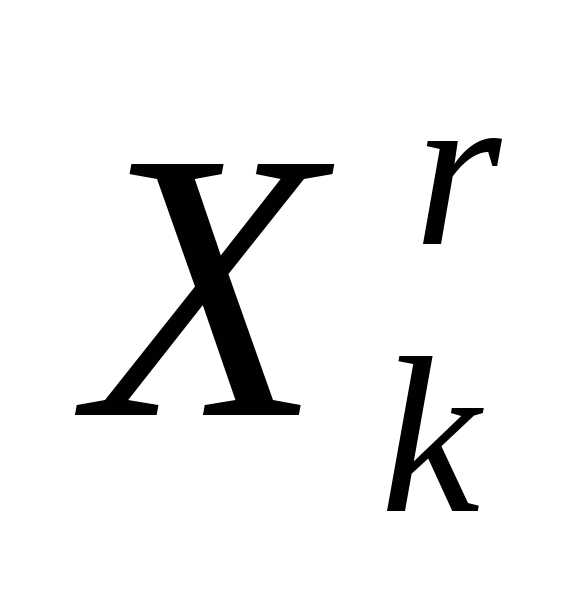 симплекса
симплекса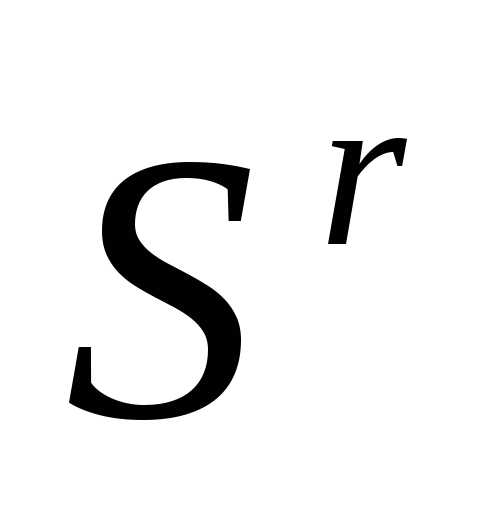 .
.
Ситуация 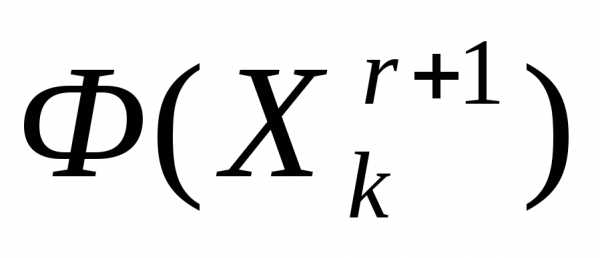 >
>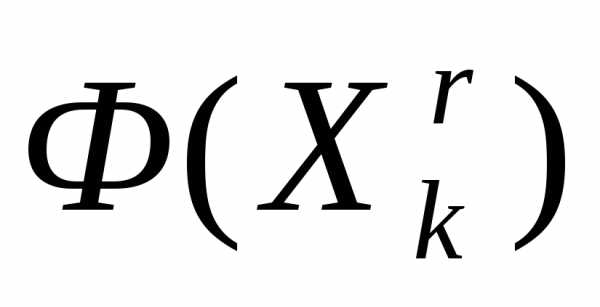 интерпретируется как«накрытие» этим симплексом дна оврага или точки минимума и рассмотренный простейший симплекс-метод модифицируется следующим образом (рисунок 5).
интерпретируется как«накрытие» этим симплексом дна оврага или точки минимума и рассмотренный простейший симплекс-метод модифицируется следующим образом (рисунок 5).
Полагаем . Еслиk=n+2, то полагаем k=1.
Выполняем отражение
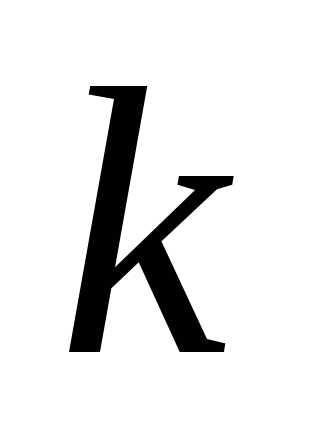 -ой вершины симплекса
-ой вершины симплекса 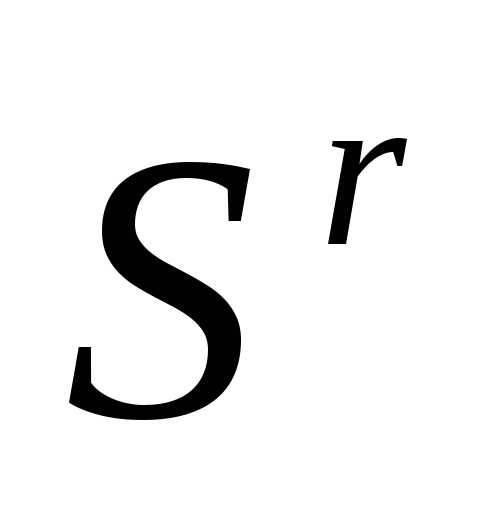 .
.Если
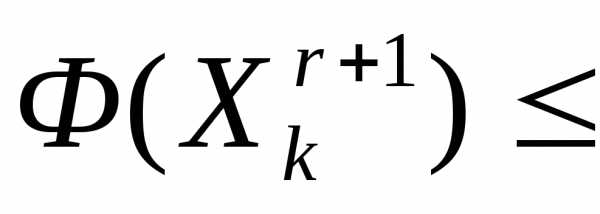
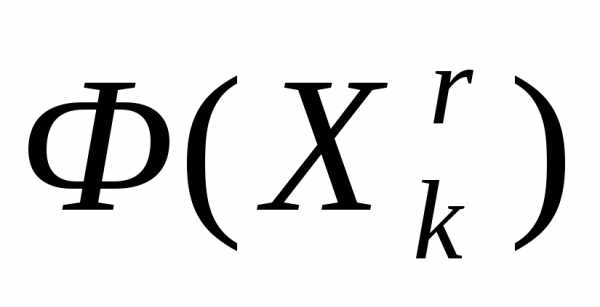 , то продолжаем итерации по схеме простейшего симплекс-метода.
, то продолжаем итерации по схеме простейшего симплекс-метода.Если
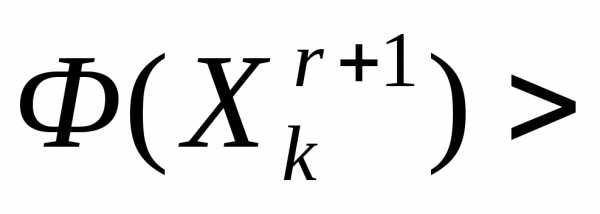
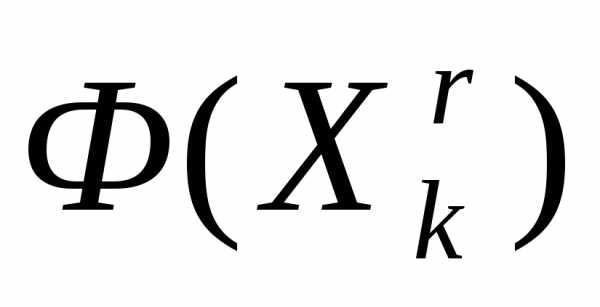 и не все вершины перебраны, то переходим к п. 1.
и не все вершины перебраны, то переходим к п. 1.Если
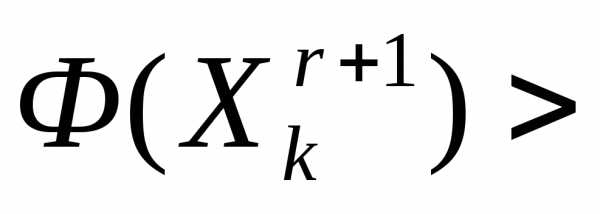
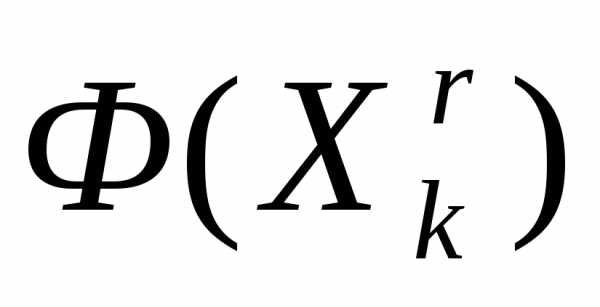 и все вершины перебраны, то выполняем редукцию симплекса к вершине с минимальным значением функции
и все вершины перебраны, то выполняем редукцию симплекса к вершине с минимальным значением функции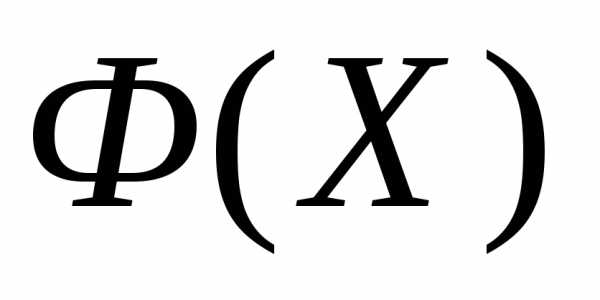 .
.
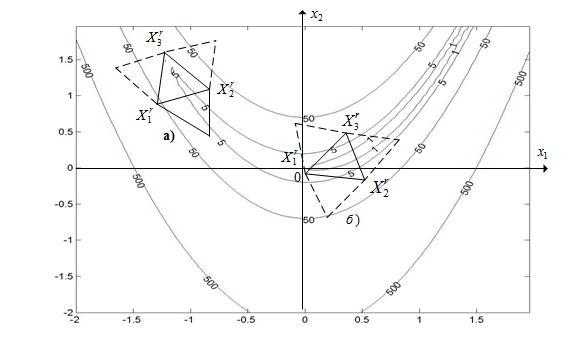
Рисунок 5 – К схеме модифицированного симплекс-метода. Ситуация «накрытие» симплексом дна оврага или точки минимума функции 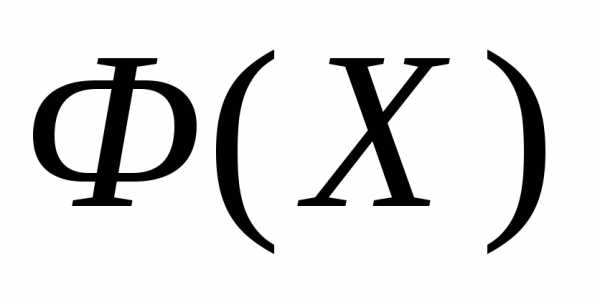
На рисунке 5 в ситуации (а) отражение вершин 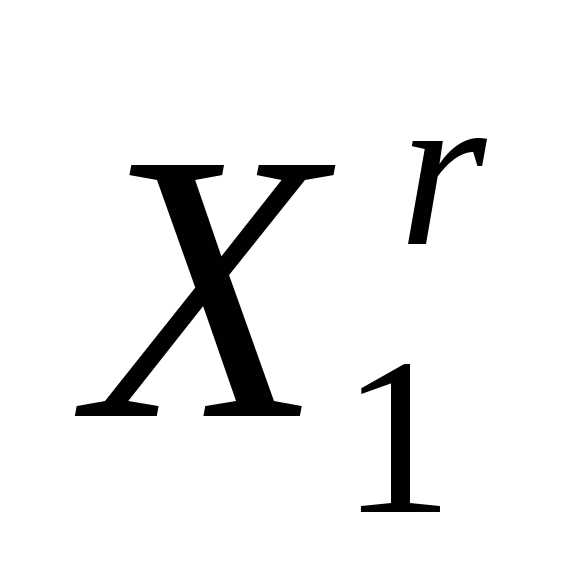 ,
,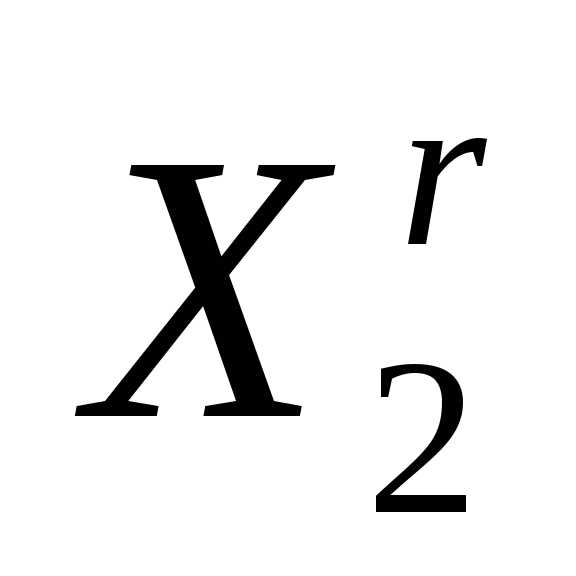 приводит к увеличению значений функции
приводит к увеличению значений функции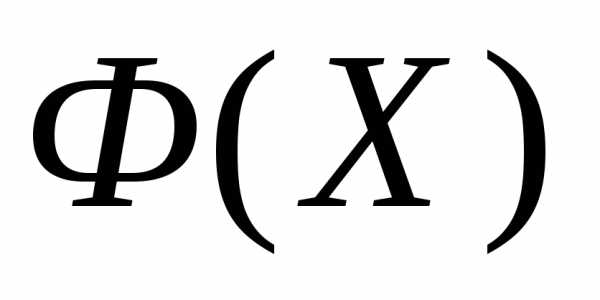 , а отражение вершины
, а отражение вершины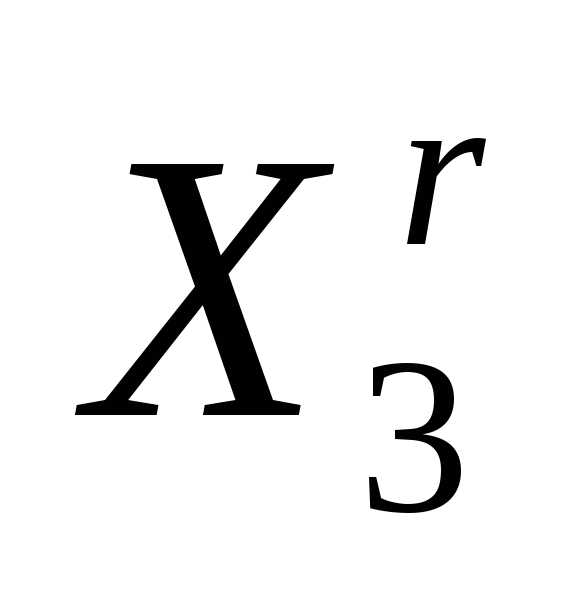 - к уменьшению значения
- к уменьшению значения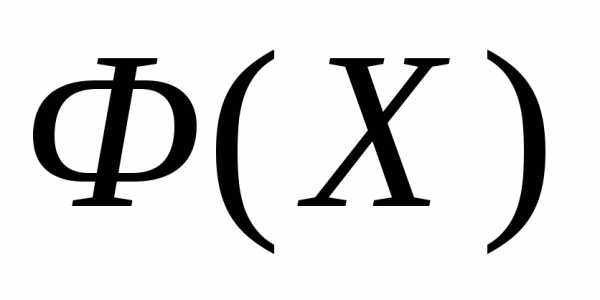 . Таким образом,
. Таким образом,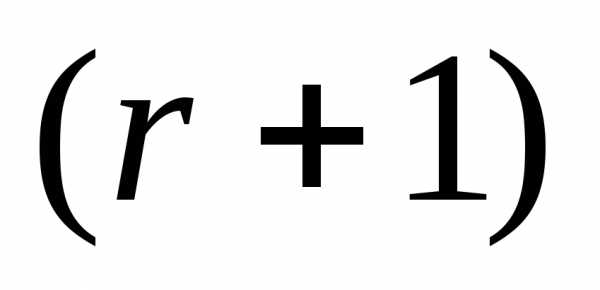 -я итерация выполняется по схеме простейшего симплекс-метода. В ситуации (б) отражение всех трех вершин текущего симплекса приводит к увеличению значений функции
-я итерация выполняется по схеме простейшего симплекс-метода. В ситуации (б) отражение всех трех вершин текущего симплекса приводит к увеличению значений функции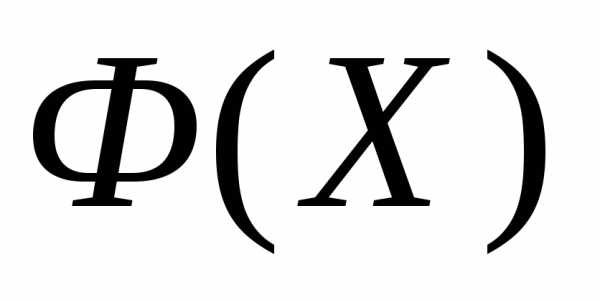 . Поэтому перед
. Поэтому перед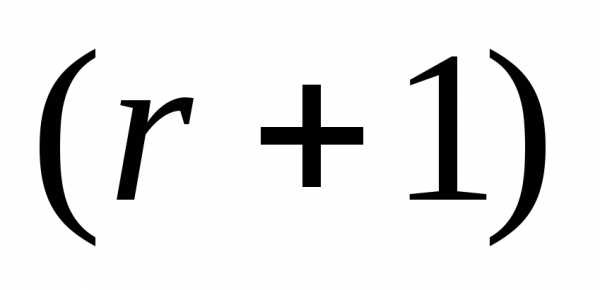 -ой итерацией должна быть выполнена редукция текущего симплекса к вершине
-ой итерацией должна быть выполнена редукция текущего симплекса к вершине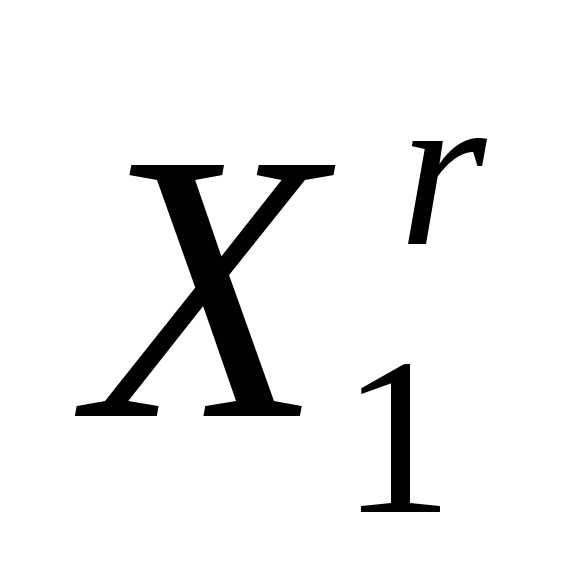 и после этого итерации продолжены по схеме простейшего симплекс-метода.
и после этого итерации продолжены по схеме простейшего симплекс-метода.
Циклическое движение. Ситуация, когда некоторая вершина симплекса не исключается из симплекса на протяжении m итераций, интерпретируется как «зацикливание» алгоритма. Рассмотренный простейший симплекс-метод модифицируется в этом случае следующим образом.
Находим вершину текущего симплекса
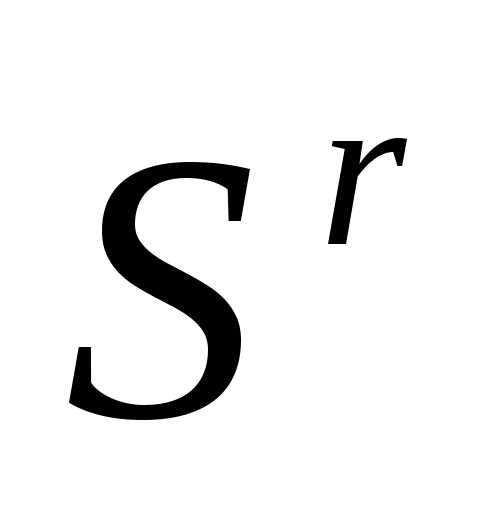 , в которой функция
, в которой функция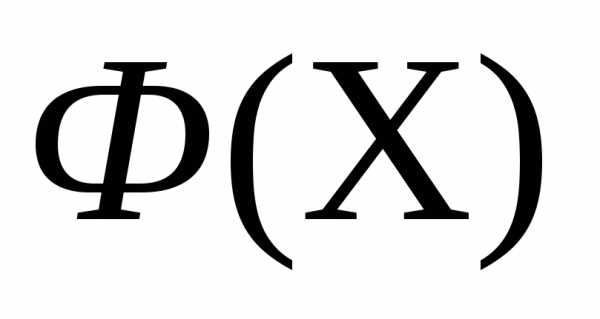 принимает наименьшее значение
принимает наименьшее значение
.
По формуле (7) выполняем редукцию симплекса
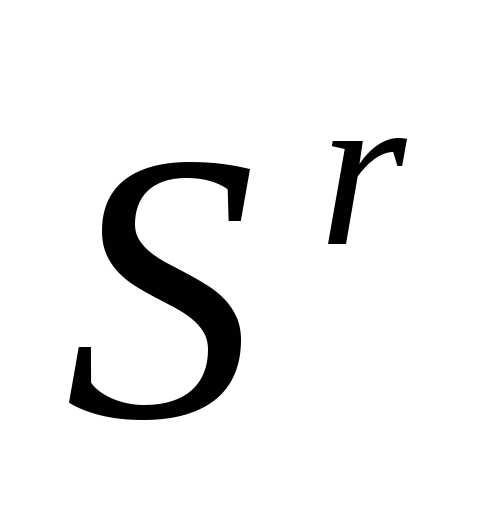 к вершине
к вершине 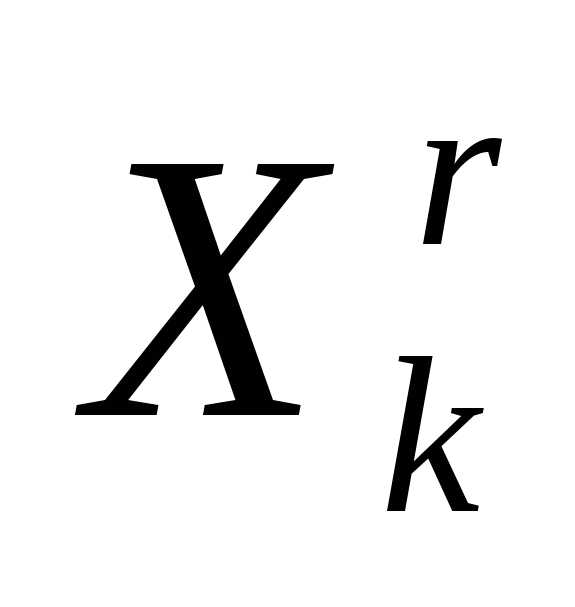 - получаем симплекс
- получаем симплекс 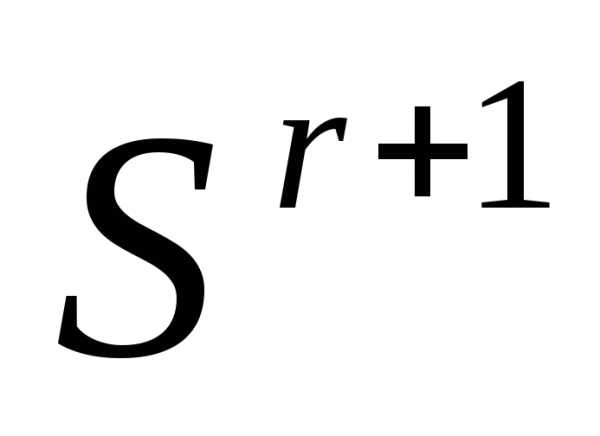 .
.Продолжаем итерации по схеме простейшего симплекс-метода.
Здесь количество итераций m рекомендуется находить из условия  , где
, где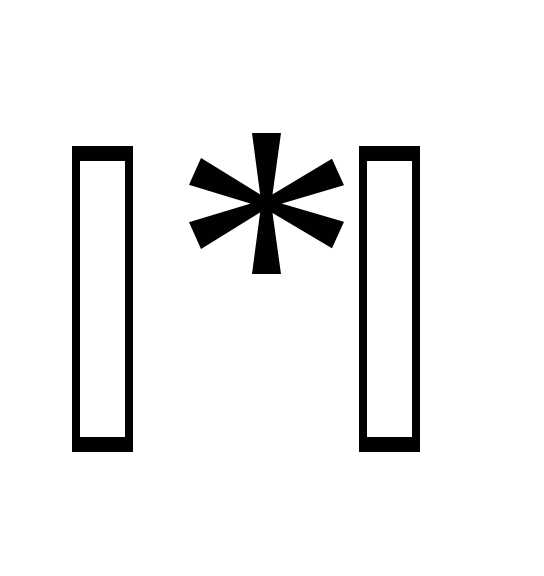 - символ ближайшего целого большего. Например, при
- символ ближайшего целого большего. Например, при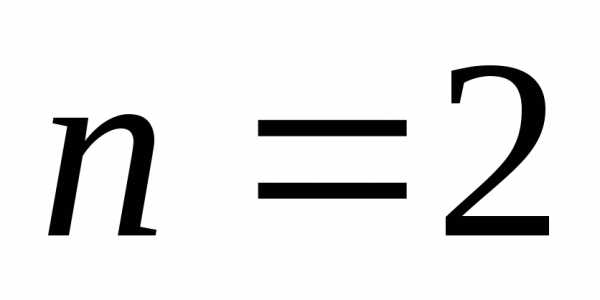 имеем:
имеем:
.
Входные термины:
детерминированные методы оптимизации;
методы локальной оптимизации;
методы безусловной оптимизации;
многомерный критерий оптимальности;
прямые методы оптимизации;
регулярный симплекс.
Выходные термины:
отражение симплекса;
редукция симплекса;
сжатие многогранника;
растяжение симплекса;
восстановление симплекса;
метод деформируемого многогранника, метод Нелдера-Мида.
§6. Метод Нелдера-Мида (метод деформируемого многогранника).
Рассмотрим следующую задачу многомерной локальной безусловной оптимизации: найти минимум критерия оптимальности Φ(X), определенного в n-мерном евклидовом пространстве 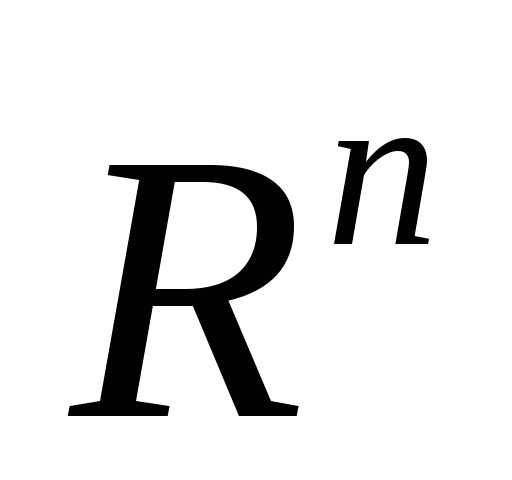 ,
,
 . (1)
. (1)
В случае если функция Φ(X) является овражной, эффективность симплекс-метода при решении задачи (1) значительно снижается в силу того, что регулярный симплекс нельзя «вытянуть» вдоль оврага. Метод Нелдера-Мида является развитием симплекс-метода и использует в процессе поиска изменение не только размеров, но и формы текущего симплекса (не обязательно регулярного).
Метод использует следующие операции над симплексами: отражение; редукция; сжатие; растяжение.
Отражение вершины симплекса относительно центра тяжести остальных вершин (см. параграф 5, рисунок 1). В результате отражения вершины 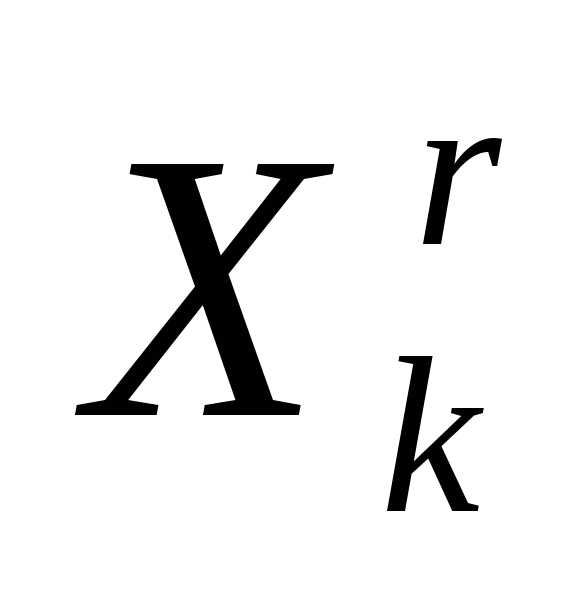 симплексаполучаем новый симплекс
симплексаполучаем новый симплекс
, (2)
где
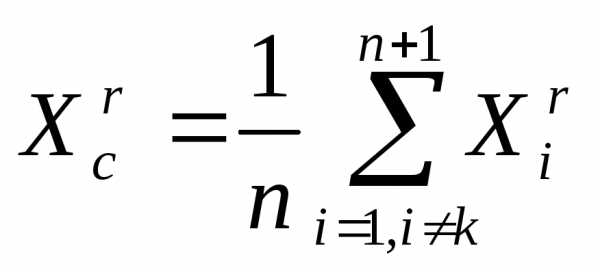 - (3)
- (3)
вектор координат центра тяжести остальных вершин симплекса 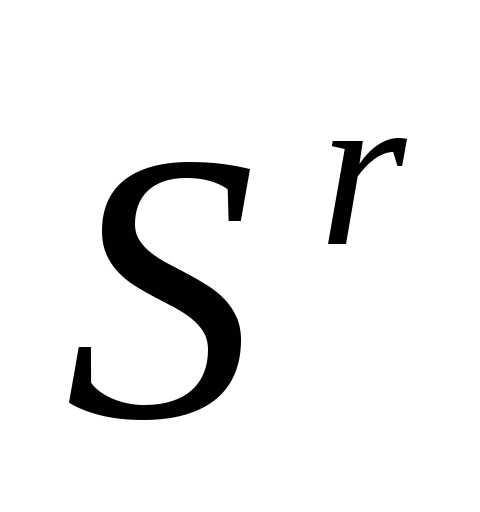 (за исключением отраженной вершины
(за исключением отраженной вершины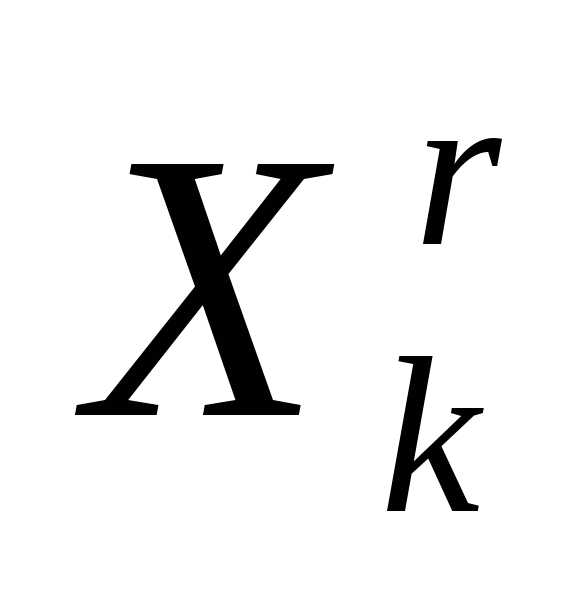 ). Если симплекс
). Если симплекс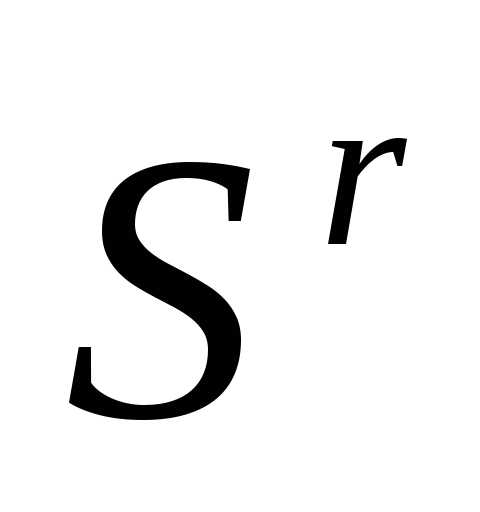 регулярный, то симплекс
регулярный, то симплекс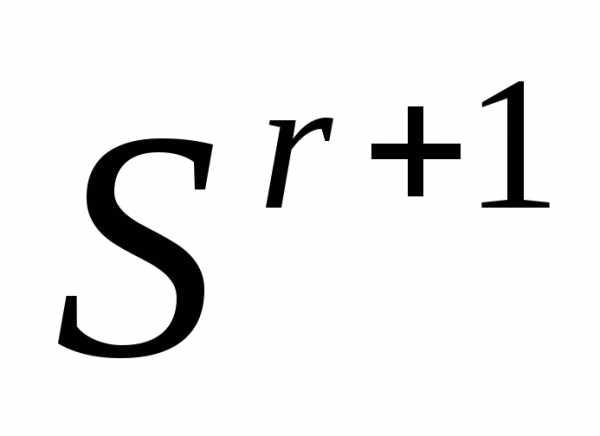 - также регулярный.
- также регулярный.
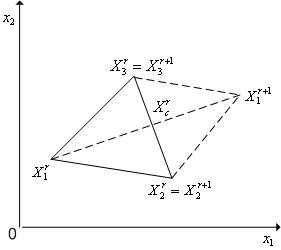
Рисунок 1 - Отражение вершины 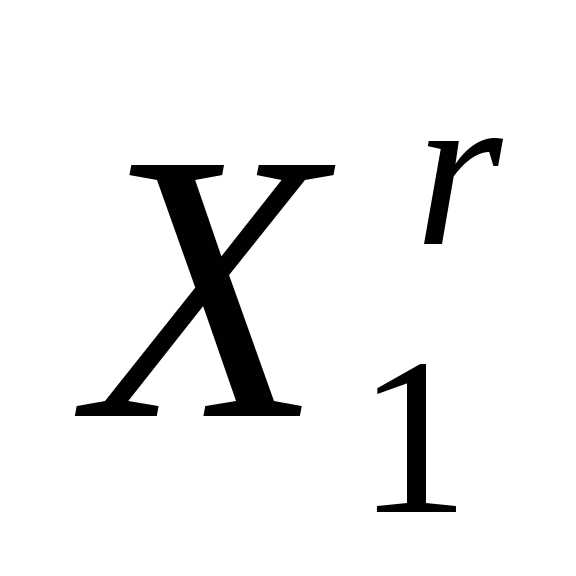 симплекса
симплекса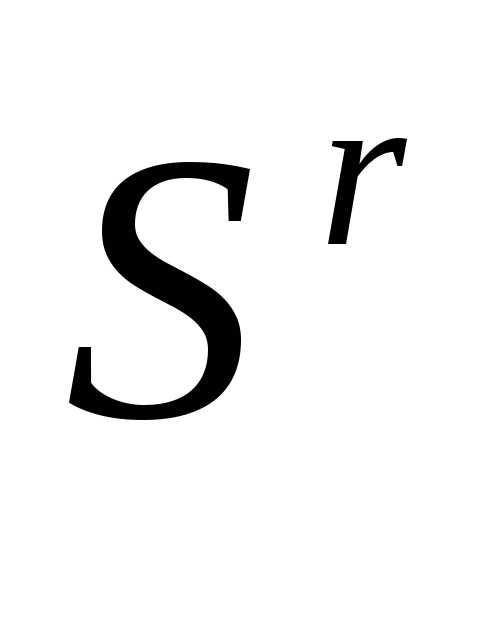 в пространстве
в пространстве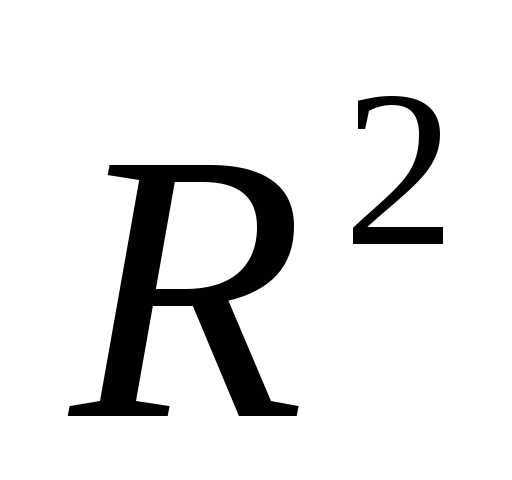 относительно центра тяжести
относительно центра тяжести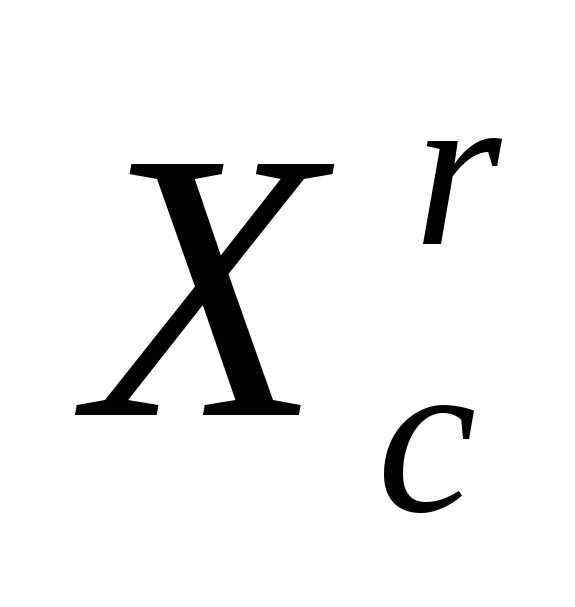 его остальных вершин
его остальных вершин
Редукции симплекса (см. параграф 5, рисунок 2) - уменьшение длин всех ребер симплекса в одно и то же количество раз. В результате редукции вершин симплекса к вершине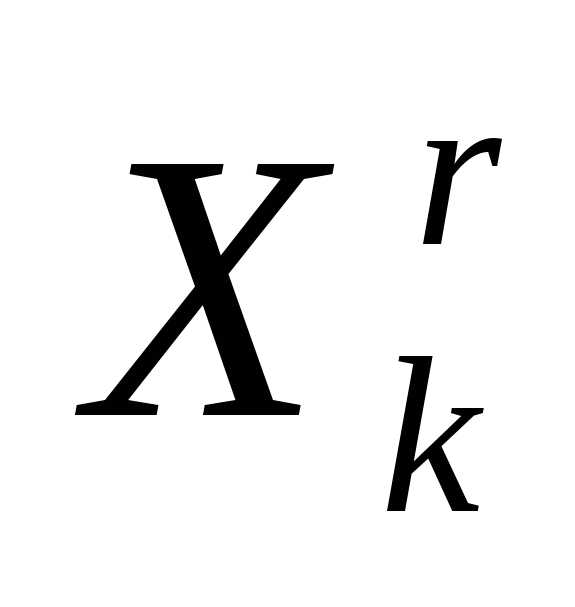 получаем новый симплекс
получаем новый симплекс
, (4)
где - коэффициент редукции. Если симплекс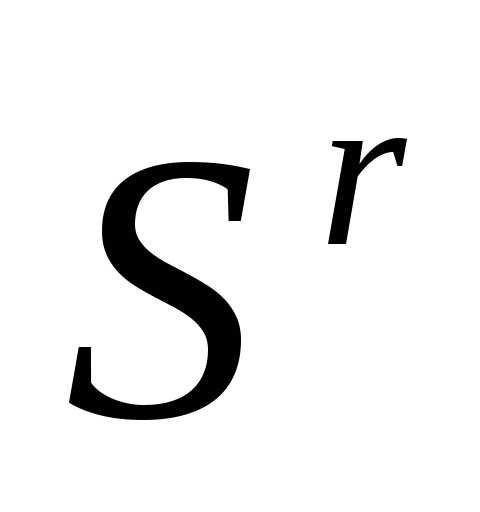 регулярный, то симплекс
регулярный, то симплекс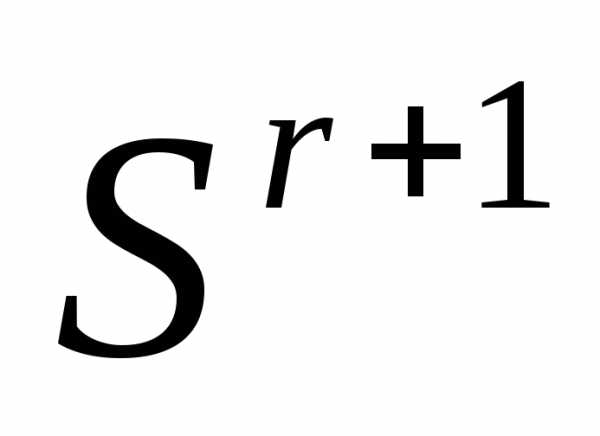 - также регулярный.
- также регулярный.
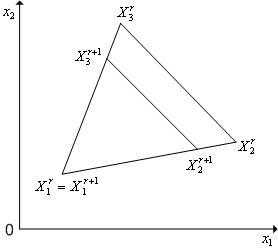
Рисунок 2 - Редукция вершин симплекса 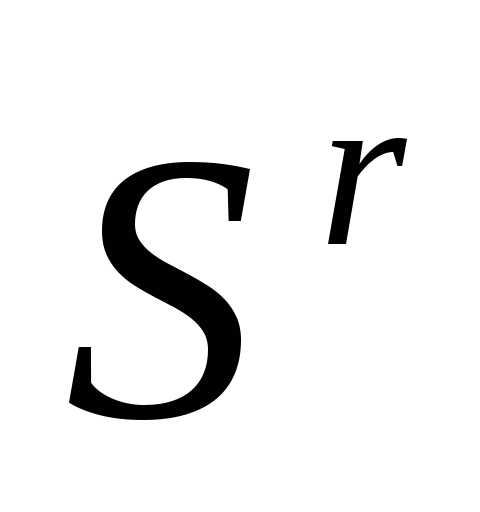 в пространстве
в пространстве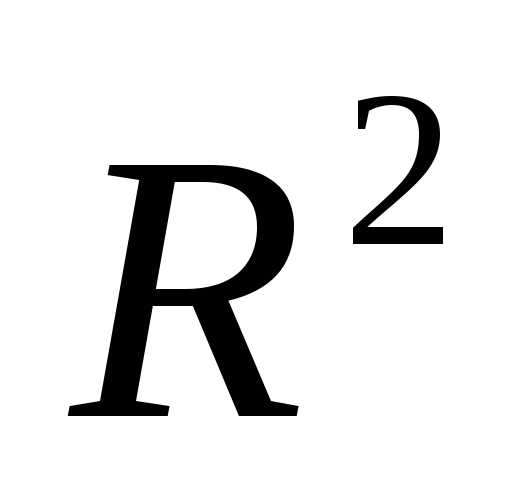 к вершине
к вершине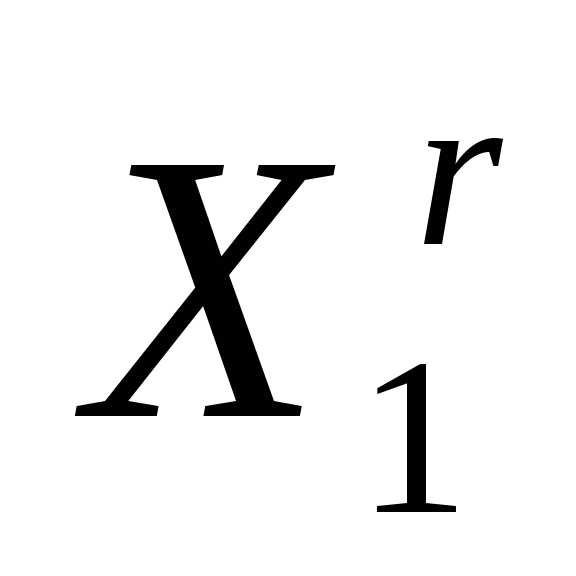
Сжатие симплекса (рисунок 3). В результате сжатия симплекса в направлении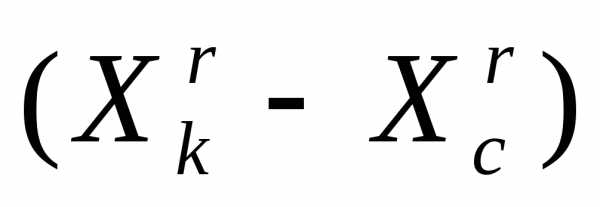 получаем новый симплекс
получаем новый симплекс
(5)
где - коэффициент сжатия,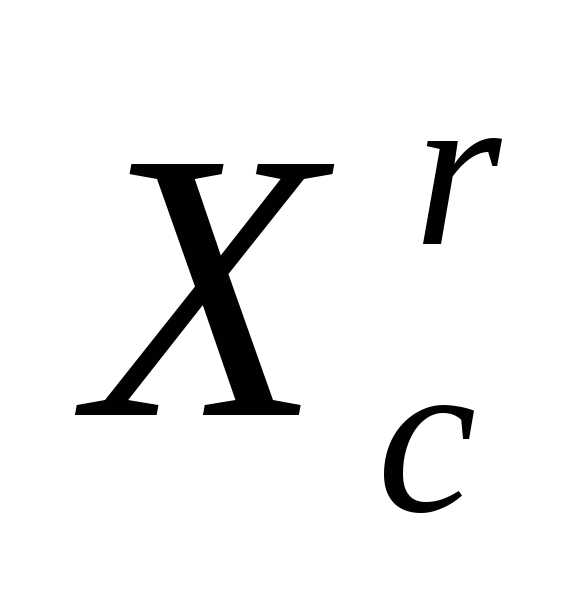 - вектор координат центра тяжести остальных вершин симплекса
- вектор координат центра тяжести остальных вершин симплекса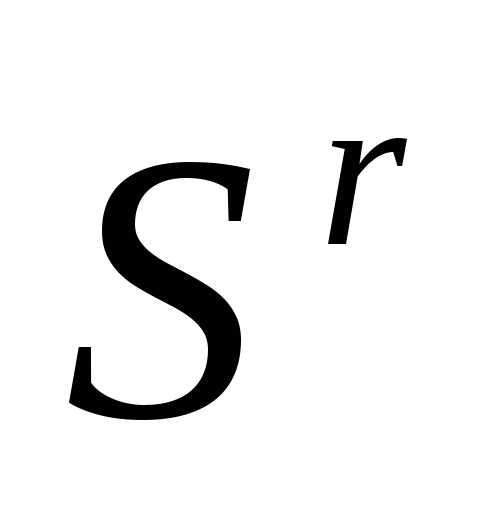 (за исключением вершины
(за исключением вершины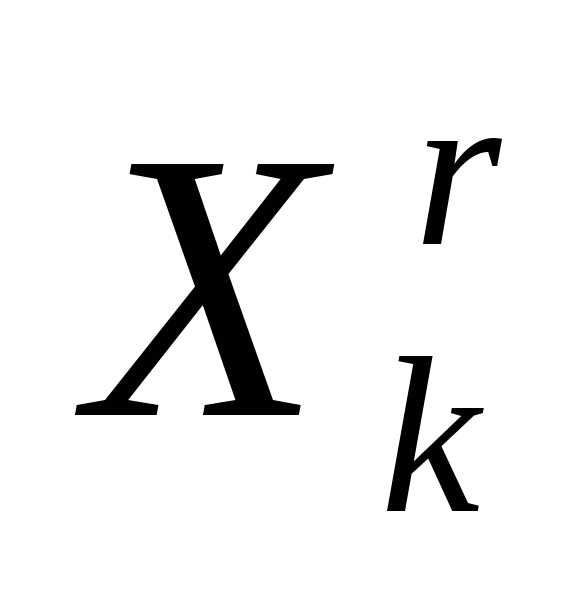 ) - см. формулу (3). Даже если симплекс
) - см. формулу (3). Даже если симплекс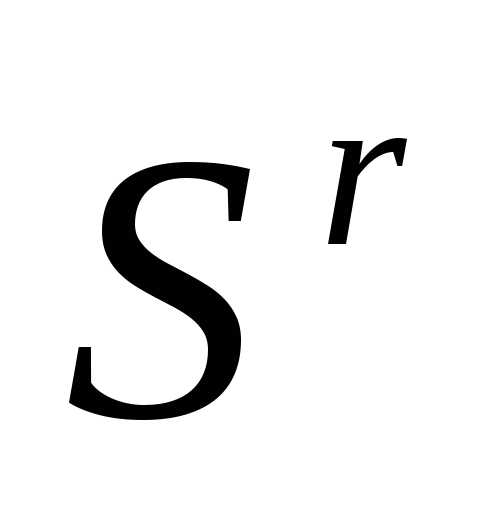 является регулярным, симплекс
является регулярным, симплекс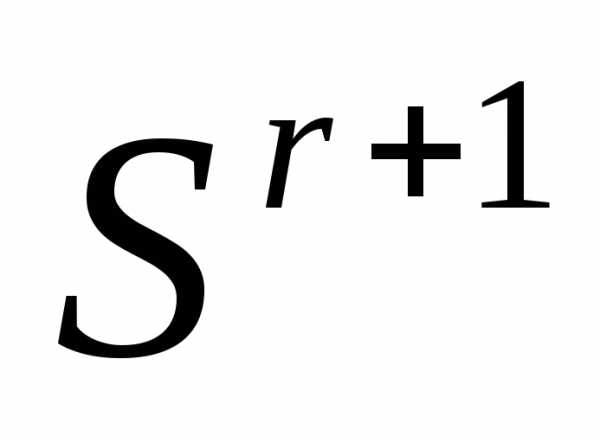 оказывается нерегулярным.
оказывается нерегулярным.
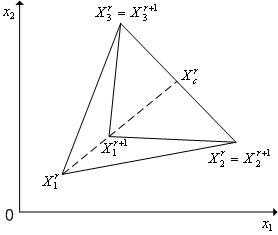
Рисунок 3 - Сжатие симплекса 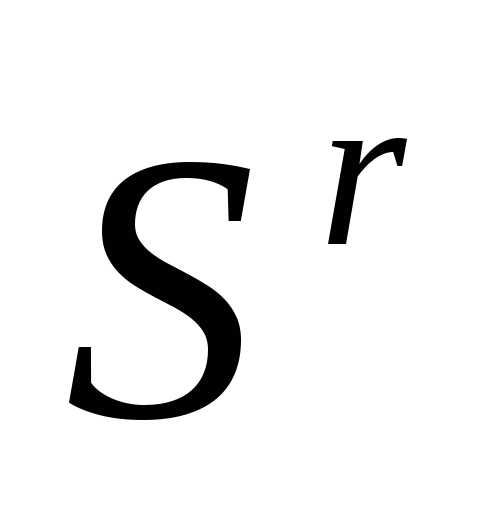 в пространстве
в пространстве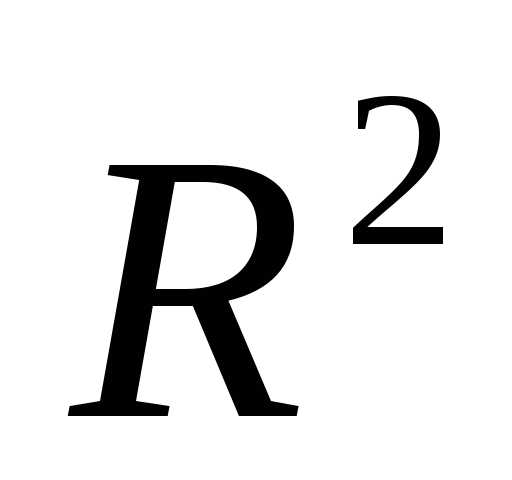 в направлении
в направлении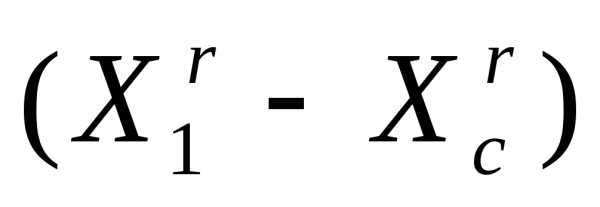
Растяжение симплекса (рисунок 4). В результате растяжения симплекса в направлении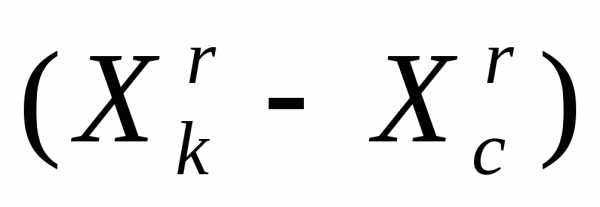 получаем новый симплекс
получаем новый симплекс
(6)
где - коэффициент растяжения,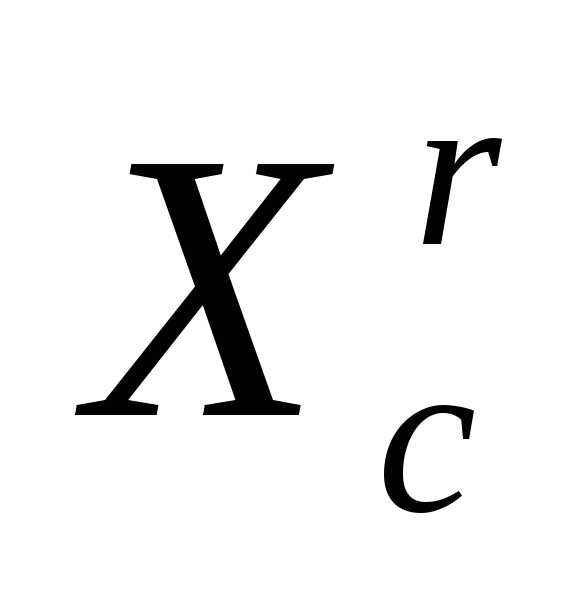 - как и ранее, вектор координат центра тяжести остальных вершин симплекса
- как и ранее, вектор координат центра тяжести остальных вершин симплекса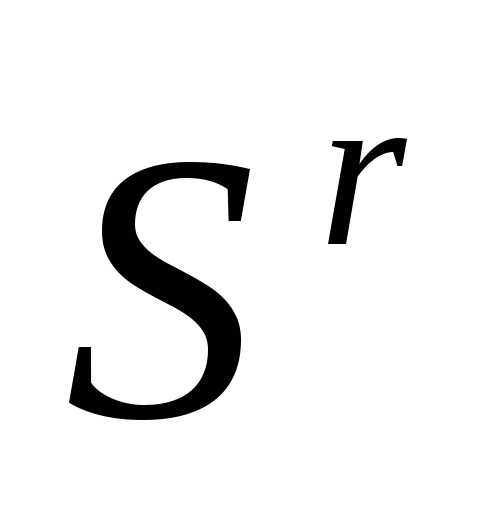 (за исключением вершины
(за исключением вершины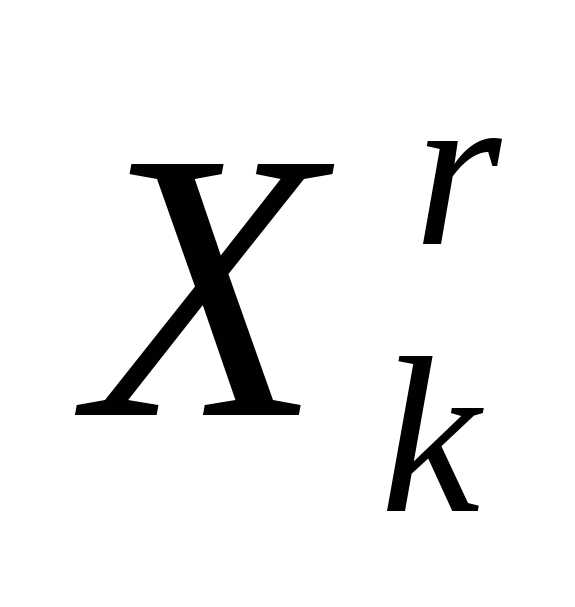 ) - см. формулу (3). Даже если симплекс
) - см. формулу (3). Даже если симплекс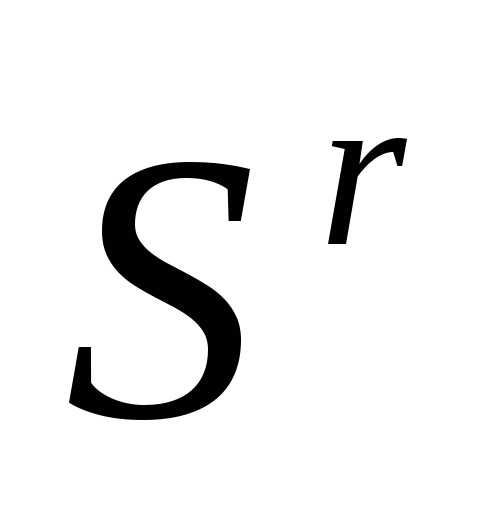 регулярен, симплекс
регулярен, симплекс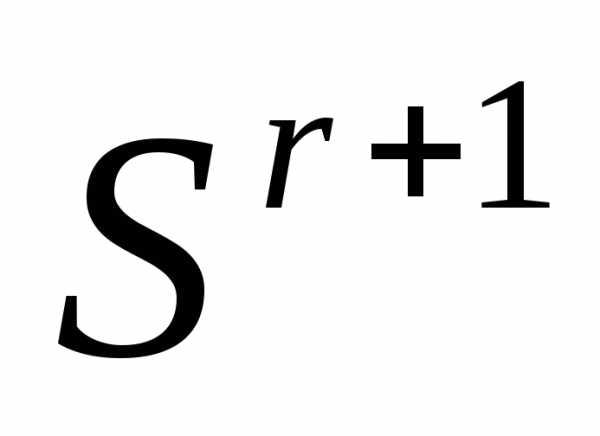 оказывается нерегулярным.
оказывается нерегулярным.
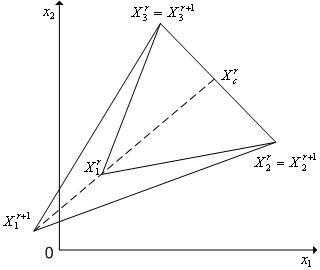
Рисунок 4 - Растяжение симплекса 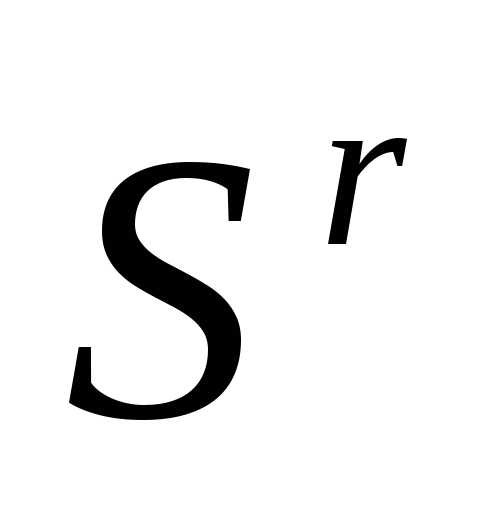 в пространстве
в пространстве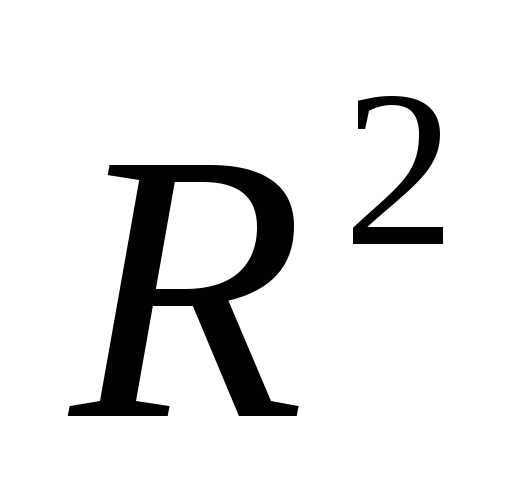 в направлении
в направлении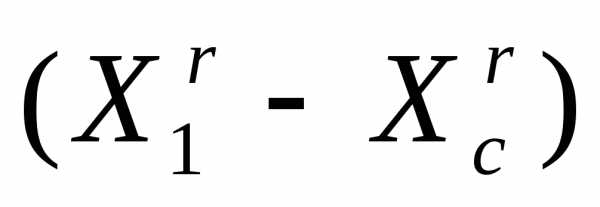
Упрощенная схема метода Нелдера-Мида
Задаем начальную точку
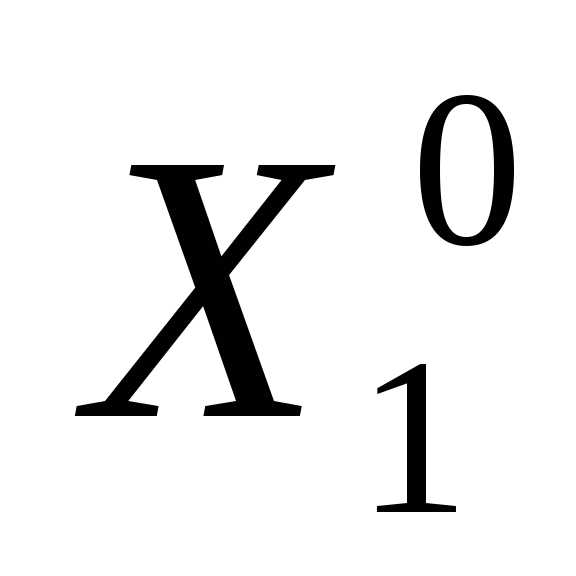 , длину ребра симплекса
, длину ребра симплекса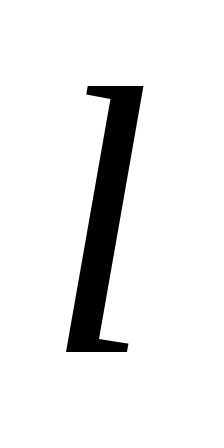 и полагаем
и полагаем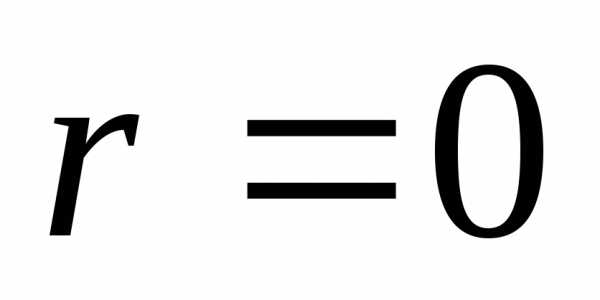 . Находим координаты всех вершин регулярного симплекса
. Находим координаты всех вершин регулярного симплекса 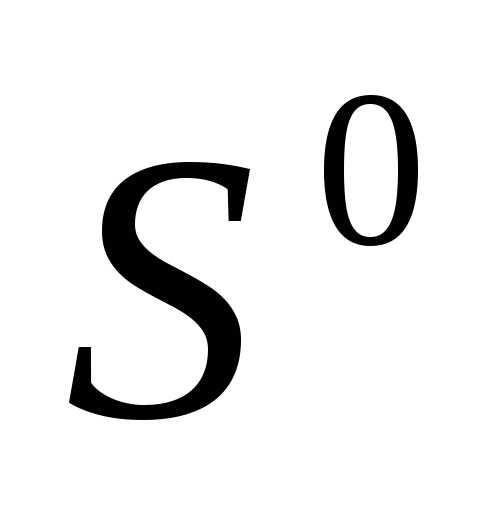 с длиной ребра l.
с длиной ребра l. Вычисляем значения функции
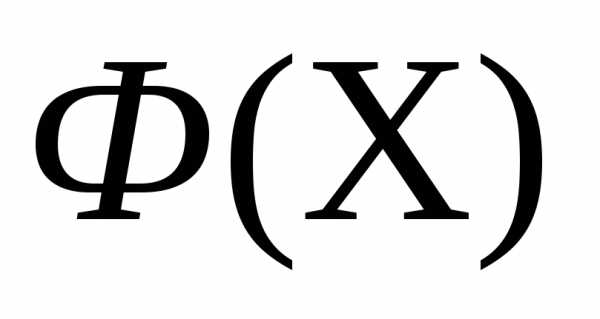 во всех вершинах симплекса
во всех вершинах симплекса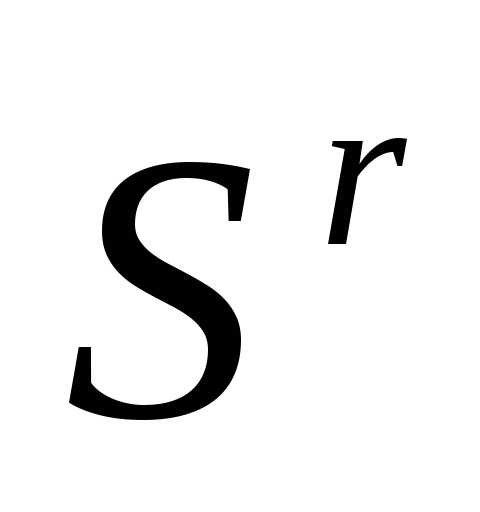 .
.Среди вершин симплекса
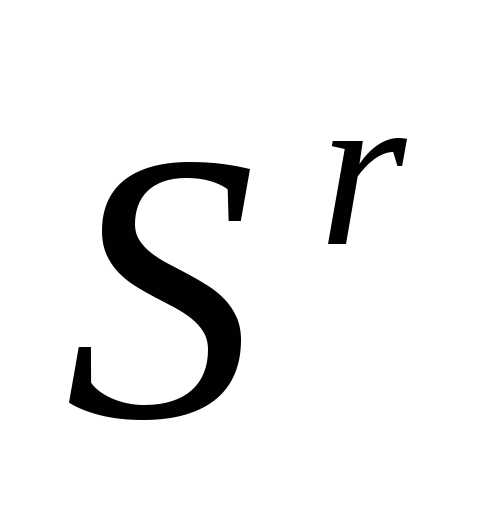 находим вершины
находим вершины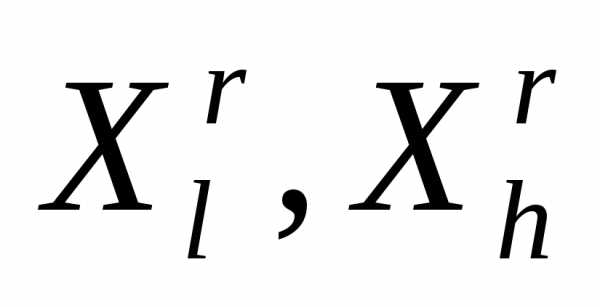 , в которых функция
, в которых функция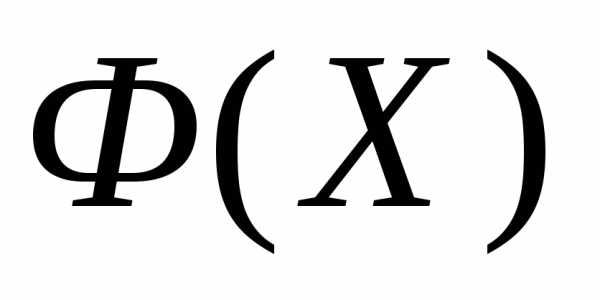 принимает, соответственно, наименьшее и наибольшее значения, а также находим значения функции
принимает, соответственно, наименьшее и наибольшее значения, а также находим значения функции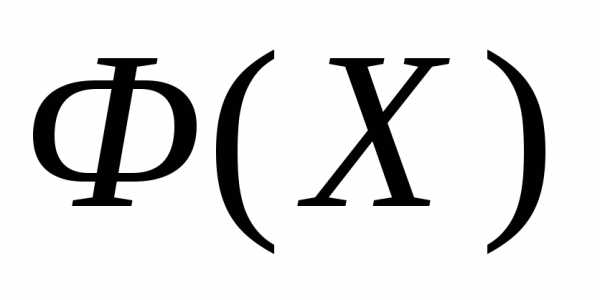 в этих точках:
в этих точках:
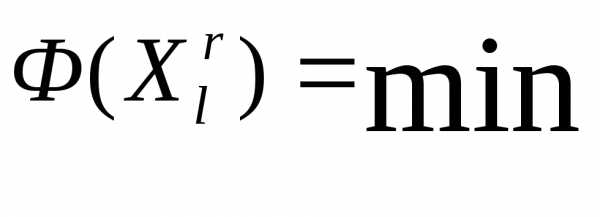 , ; (7)
, ; (7)
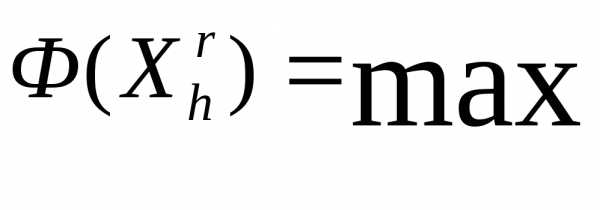 , ; (8)
, ; (8)
Отражение. Отражаем вершину
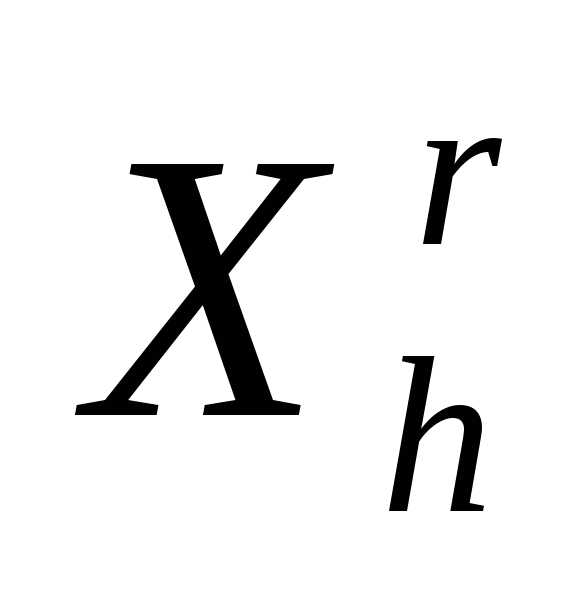 симплекса
симплекса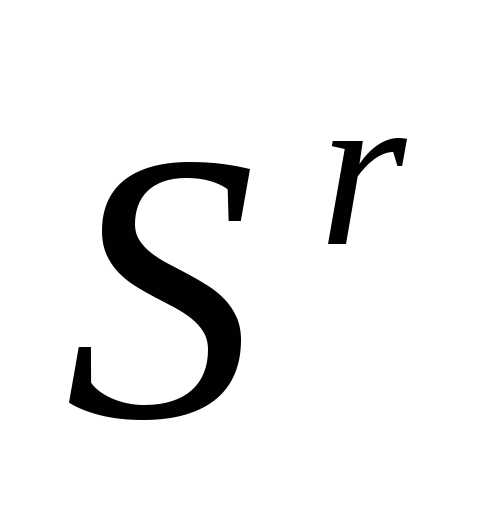 относительно центра тяжести остальных его вершин – получаем новый симплекс
относительно центра тяжести остальных его вершин – получаем новый симплекс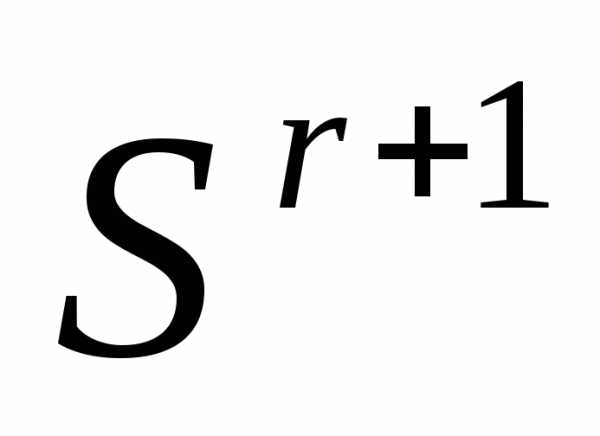 . Вычисляем значение
. Вычисляем значение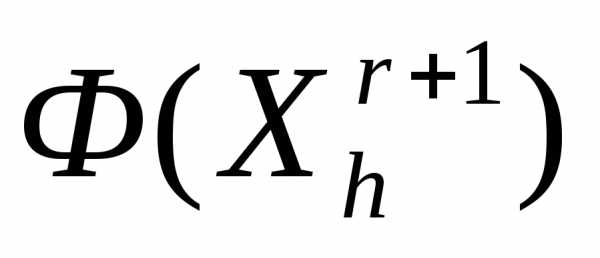 функции
функции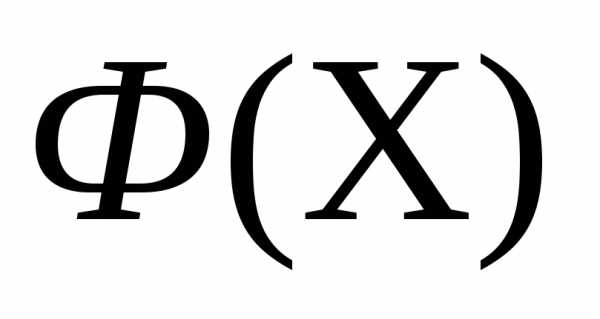 в вершине
в вершине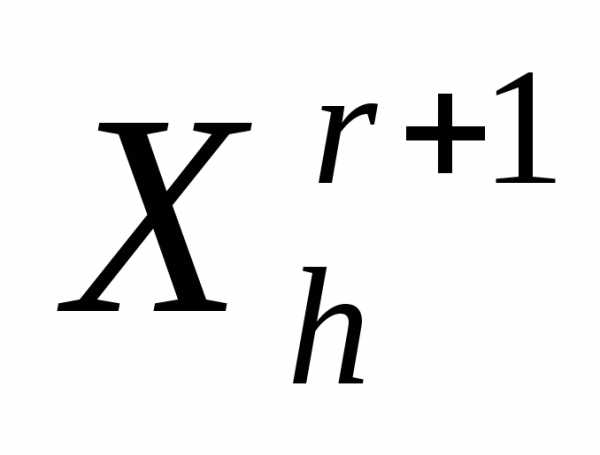 этого симплекса.
этого симплекса.Если условие окончания итераций (см. ниже) выполнено, то в качестве приближенного значения точки минимума функции
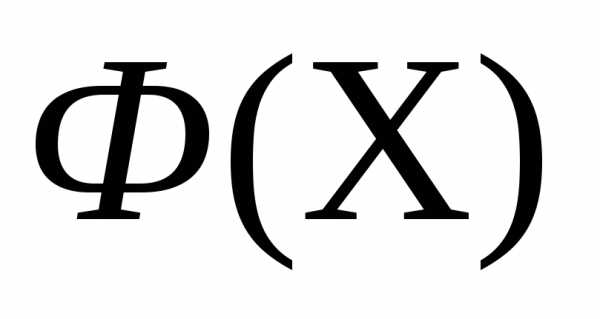 принимаем ту вершину симплекса
принимаем ту вершину симплекса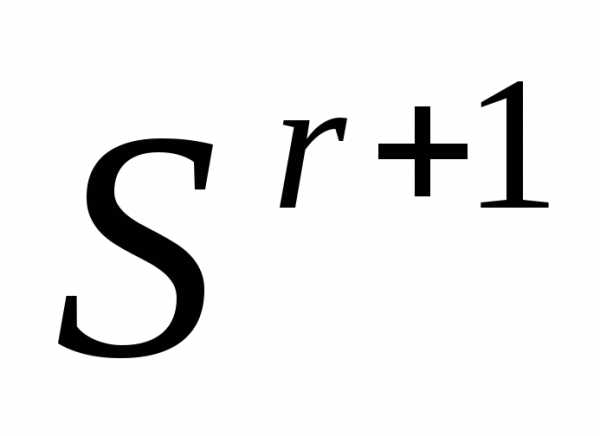 , в которой эта функция имеет минимальное значение, и заканчиваем вычисления.
, в которой эта функция имеет минимальное значение, и заканчиваем вычисления.Если и, то переходим к п. 7 (растяжению) – рисунок 5. Если, но, то переходим к п. 4 (отражению) – рисунок 6. Если, то переходим к п. 8 (сжатию) – рисунки 7, 8.
Растяжение (ситуация и). Выполняем растяжение симплекса
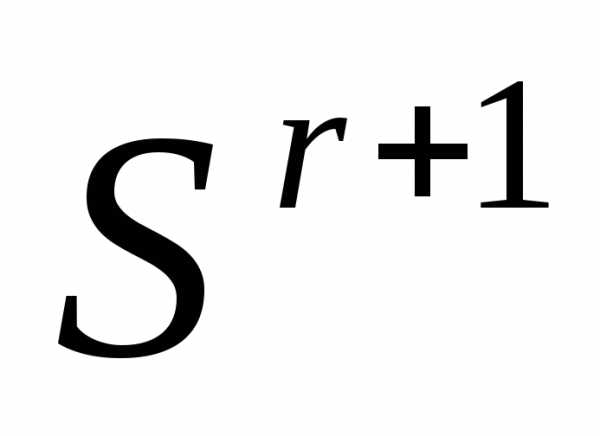 в направлении- получаем новый симплекс
в направлении- получаем новый симплекс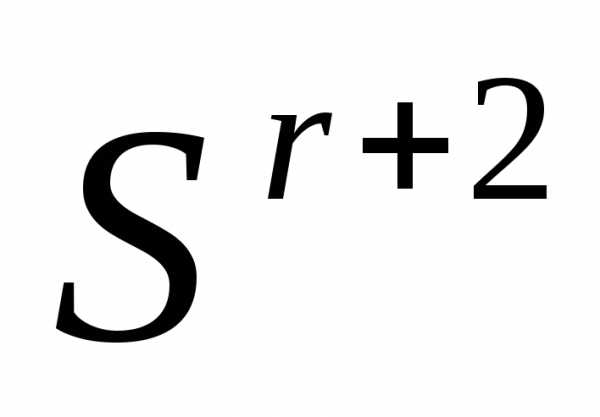 . Вычисляем значение функции
. Вычисляем значение функции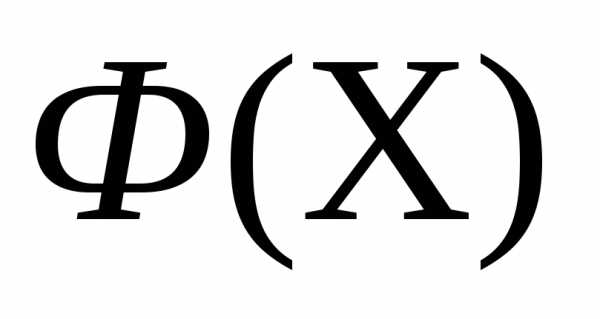 в вершине
в вершине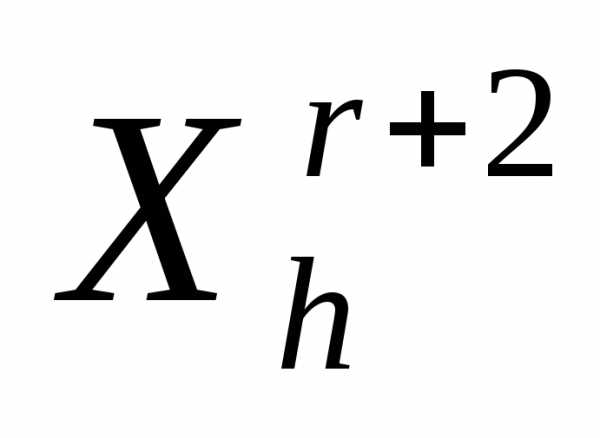 этого симплекса. Если, то полагаеми переходим к п. 4 (отражению) с симплексом
этого симплекса. Если, то полагаеми переходим к п. 4 (отражению) с симплексом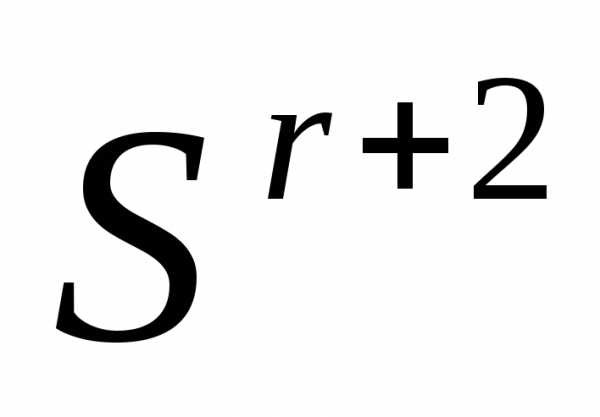 . Иначе полагаем и, не используя результаты растяжения, переходим к п. 4 (отражению) с симплексом
. Иначе полагаем и, не используя результаты растяжения, переходим к п. 4 (отражению) с симплексом 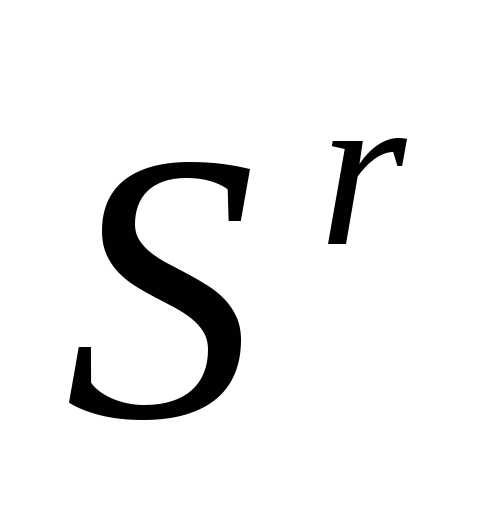 .
.Сжатие (ситуация ). Выполняем сжатие симплекса
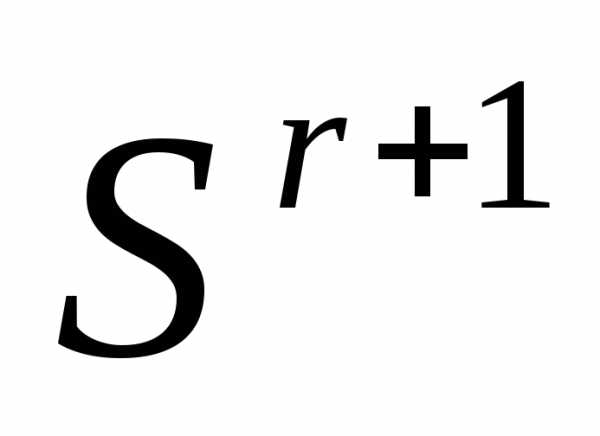 в направлении- получаем новый симплекс
в направлении- получаем новый симплекс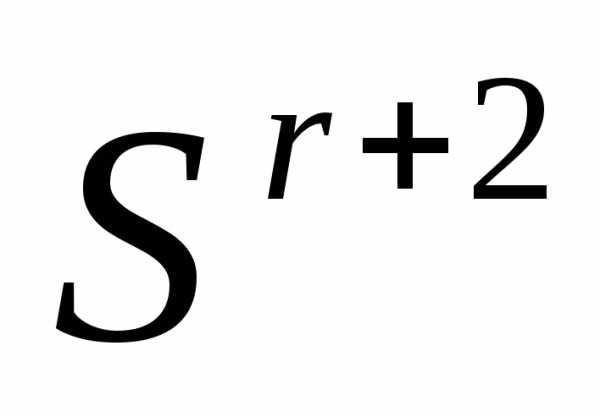 . Вычисляем значение функции
. Вычисляем значение функции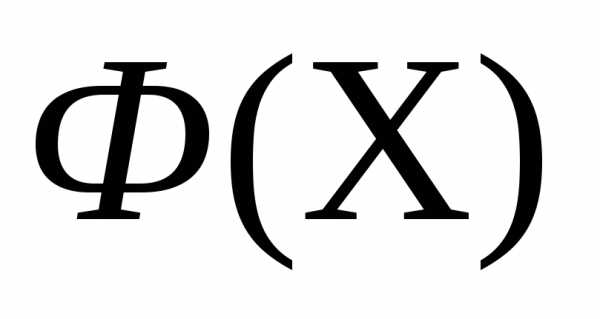 в вершине
в вершине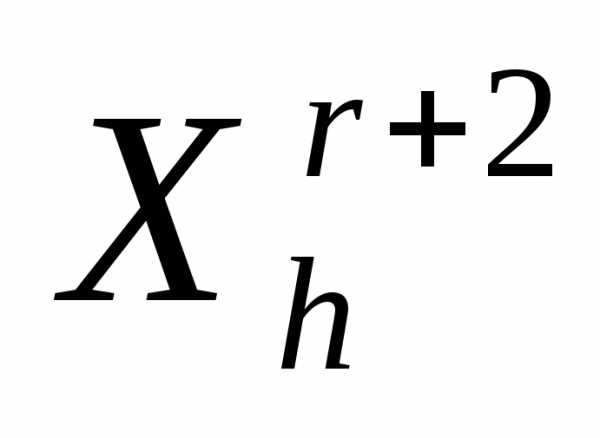 этого симплекса. Если, то полагаеми переходим к п. 4 (отражению) с симплексом
этого симплекса. Если, то полагаеми переходим к п. 4 (отражению) с симплексом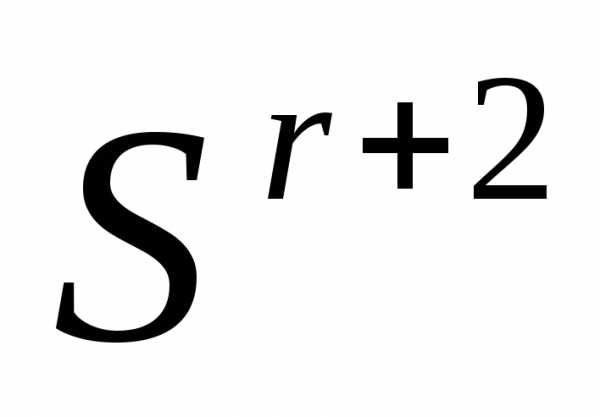 . Иначе переходим к п. 9 (редукции) с симплексом
. Иначе переходим к п. 9 (редукции) с симплексом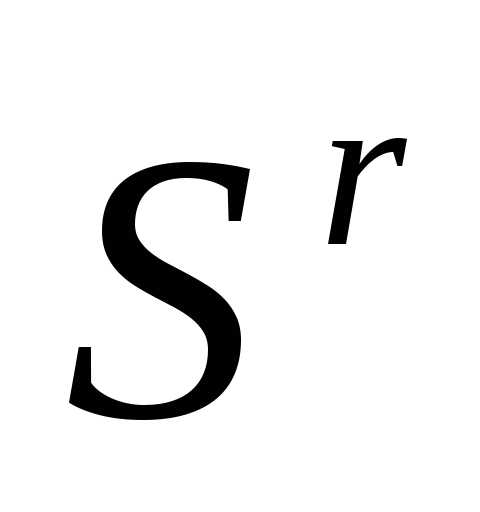 .
.Редукция (ситуация, когда сжатие симплекса оказалось неудачным). Выполняем редукцию симплекса
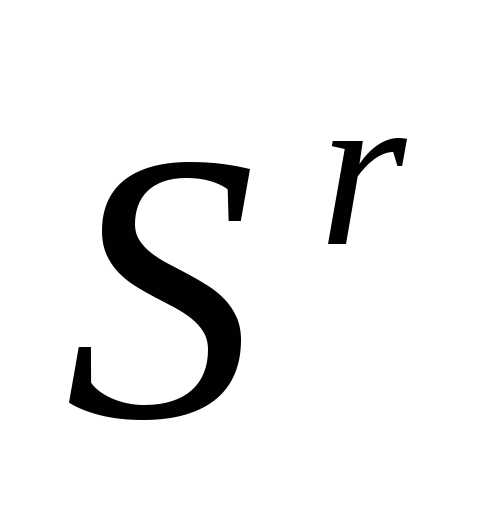 к вершине
к вершине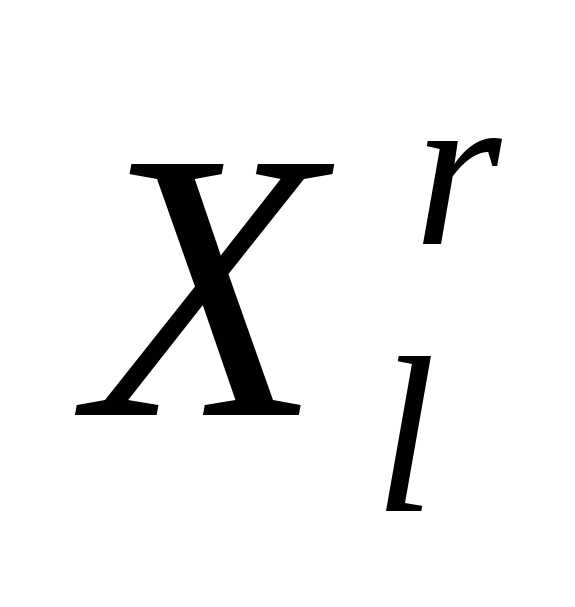 - получаем новый симплекс
- получаем новый симплекс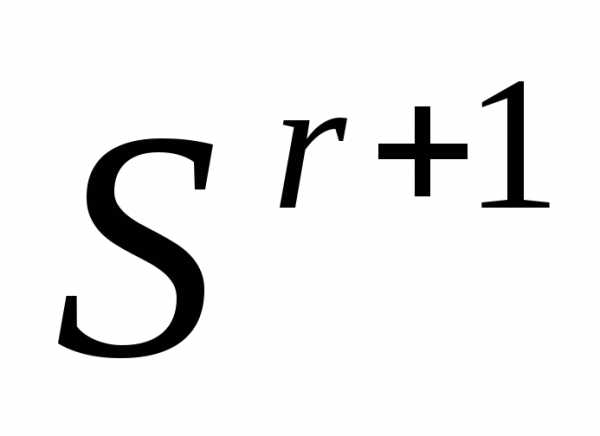 . Вычисляем значение функции
. Вычисляем значение функции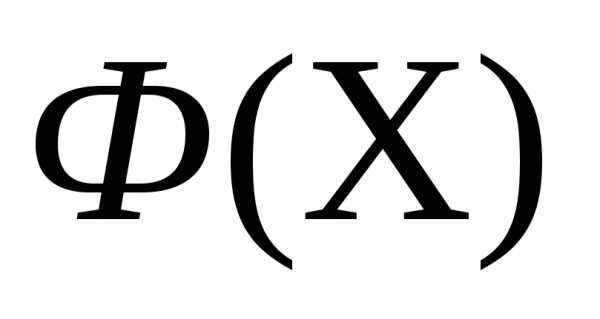 во всех новых вершинах симплекса
во всех новых вершинах симплекса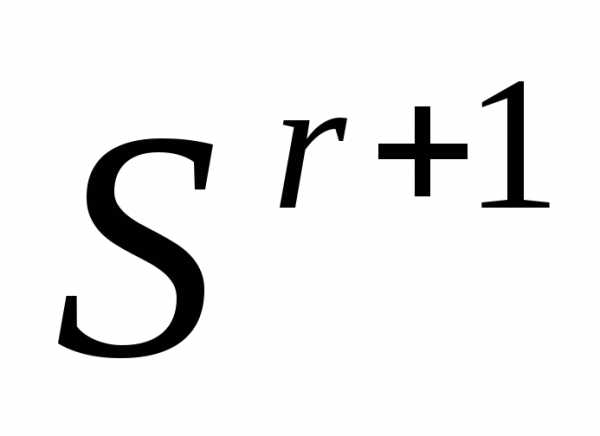 . Полагаеми переходим к п. 4 (отражению)●
. Полагаеми переходим к п. 4 (отражению)●
studfiles.net
Решение симплекс методом задачи ЛП: пример и алгоритм
Симплекс метод - это метод последовательного перехода от одного базисного решения (вершины многогранника решений) системы ограничений задачи линейного программирования к другому базисному решению до тех пор, пока функция цели не примет оптимального значения (максимума или минимума).
Симплекс метод был предложен американским математиком Р.Данцигом в 1947 году, с тех пор для нужд промышленности этим методом нередко решаются задачи линейного программирования с тысячами переменных и ограничений.
Перед тем, как перейти к алгоритму симплекс метода, несколько определений.
Всякое неотрицательное решение системы ограничений называется допустимым решением.
Пусть имеется система m ограничений с n переменными (m n).
Допустимым базисным решением является решение, содержащее m неотрицательных основных (базисных) переменных и n - m неосновных. (небазисных, или свободных) переменных. Неосновные переменные в базисном решении равны нулю, основные же переменные, как правило, отличны от нуля, то есть являются положительными числами.
Любые m переменных системы m линейных уравнений с n переменными называются основными, если определитель из коэффициентов при них отличен от нуля. Тогда остальные n - m переменных называются неосновными (или свободными).
Алгоритм симплекс метода
- Шаг 1. Привести задачу линейного программирования к канонической форме. Для этого перенести свободные члены в правые части (если среди этих свободных членов окажутся отрицательные, то соответствующее уравнение или неравенство умножить на - 1) и в каждое ограничение ввести дополнительные переменные (со знаком "плюс", если в исходном неравенстве знак "меньше или равно", и со знаком "минус", если "больше или равно").
- Шаг 2. Если в полученной системе m уравнений, то m переменных принять за основные, выразить основные переменные через неосновные и найти соответствующее базисное решение. Если найденное базисное решение окажется допустимым, перейти к допустимому базисному решению.
- Шаг 3. Выразить функцию цели через неосновные переменные допустимого базисного решения. Если отыскивается максимум (минимум) линейной формы и в её выражении нет неосновных переменных с отрицательными (положительными) коэффициентами, то критерий оптимальности выполнен и полученное базисное решение является оптимальным - решение окончено. Если при нахождении максимума (минимума) линейной формы в её выражении имеется одна или несколько неосновных переменных с отрицательными (положительными) коэффициентами, перейти к новому базисному решению.
- Шаг 4. Из неосновных переменных, входящих в линейную форму с отрицательными (положительными) коэффициентами, выбирают ту, которой соответствует наибольший (по модулю) коэффициент, и переводят её в основные. Переход к шагу 2.
Важные условия
- Если допустимое базисное решение даёт оптимум линейной формы (критерий оптимальности выполнен), а в выражении линейной формы через неосновные переменные отсутствует хотя бы одна из них, то полученное оптимальное решение - не единственное.
- Если в выражении линейной формы имеется неосновная переменная с отрицательным коэффициентом в случае её максимизации (с положительным - в случае минимизации), а во все уравнения системы ограничений этого шага указанная переменная входит также с отрицательными коэффициентами или отсутствует, то линейная форма не ограничена при данной системе ограничений. В этом случае её максимальное (минимальное) значение записывают в виде .
Путём построения симплексных таблиц решить задачу линейного программирования намного проще, чем путём алгебраических преобразований, который показан в следующем параграфе. Симплексные таблицы очень наглядны. Существует несколько разновидностей правил работы с симплексными таблицами. Мы разберём правило, которое чаще всего называется правилом ведущего столбца и ведущей строки.
Будет нелишним открыть в новом окне пособие Действия с дробями: их, дробей в задачах на симплекс-метод, мягко говоря, хватает.
Пример. Найти максимум функции при ограничениях
Решение.
Вводим добавочные неотрицательные переменные и сводим данную систему неравенств к эквивалентной ей системе уравнений
.
Это было сделано с соблюдением следующего правила: если в первоначальном ограничении знак "меньше или равно", то добавочную переменную нужно прибавлять, а если "больше или равно", то добавочную переменную нужно отнимать.
Введённые добавочные переменные принимаем за основные (базисные). Тогда и - неосновные (свободные) переменные.
Выразив основные (базисные) переменные через неосновные (свободные), получим
Функцию цели также выразим через неосновные (свободные) переменные:
Из коэффициентов при переменных (неизвестных) построим первую симплексную таблицу.
| Таблица 1 | ||||
| Базисные неизвестные | Свободные члены | Свободные неизвестные | Вспомогательные коэффициенты | |
| X1 | X2 | |||
| X3 | -2 | 1 | -2 | |
| X4 | -4 | -1 | -1 | |
| X5 | 2 | 1 | -1 | |
| X6 | 6 | 0 | 1 | |
| F | 0 | -1 | -2 | |
Последнюю строку таблицы, в которой записаны функция цели и коэффициенты при свободных переменных в ней, будем называть в индексной строкой.
Полученное решение не оптимально, так как в индексной строке коэффициенты при свободных переменных отрицательны. То есть оптимальным будет то решение, в котором коэффициенты при свободных переменных в индексной строке будут больше или равны нулю.
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Для перехода к следующей таблице найдём наибольшее (по модулю) из чисел и . Это число 2. Поэтому ведущий столбец - тот столбец, в котором записано
Для определения ведущей строки находим минимум отношений свободных членов к элементам ведущего столбца, причём если в числителе положительное число, а в знаменателе отрицательное, отношение считается равным бесконечности.
Итак,
.
Поэтому ведущая строка - та, в которой записано
Ведущим элементом, таким образом, является -2.
Составляем вторую симплексную таблицу.
Новый базисный элемент вписываем первой строкой, а столбец, в котором стояло , вписываем новую свободную переменную
Заполняем первую строку. Для этого все числа, стоящие в ведущей строке таблицы 1, делим на ведущий элемент и записываем в соответствующий столбец первой строки таблицы 2, кроме числа, стоящего в ведущем столбце, куда записывается величина, обратная ведущему элементу (то есть, единица, делённая на ведущий элемент).
Заполняем столбец вспомогательных коэффициентов. Для этого числа ведущего столбца таблицы 1, кроме ведущего элемента, записываем с противоположными знаками в графу вспомогательных коэффициентов таблицы 2.
| Таблица 2 | ||||
| Базисные неизвестные | Свободные члены | Свободные неизвестные | Вспомогательные коэффициенты | |
| X1 | X3 | |||
| X2 | 1 | -1/2 | -1/2 | |
| X4 | -3 | -3/2 | -1/2 | 1 |
| X5 | 3 | 1/2 | -1/2 | 1 |
| X6 | 5 | 1/2 | 1/2 | -1 |
| F | 2 | -2 | -1 | 2 |
Кто ещё не открыл в новом окне пособие Действия с дробями, может сделать это сейчас, поскольку самое время.
Для получения остальных строк таблицы 2 числа, уже стоящие в первой строке этой таблицы, умножаем на вспомогательный коэффициент, стоящий в заполняемой строке, и к результату прибавляем число из таблицы 1, стоящее в той же строке при соответствующей переменной.
Например, для получения свободного члена второй строки число 1 умножаем на 1 и прибавляем из таблицы 1 число -4. Получаем -3. Коэффициент при во второй строке находим так же: . Так как в предыдущей таблице отсутствует столбец с новой свободной переменной , то коэффициент второй строки в столбце новой свободной переменной будет (то есть из таблицы 1 прибавляем 0, так как в таблице 1 столбец с отсутствует).
Так же заполняется и индексная строка:
Полученное таким образом решение вновь не оптимально, так как в индексной строке коэффициенты при свободных переменных вновь отрицательны.
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Для перехода к следующей симплексной таблице найдём наибольшее (по модулю) из чисел и , то есть, модулей коэффициентов в индексной строке. Это число 2. Поэтому ведущий столбец - тот столбец, в котором записано .
Для поиска ведущей строки найдём минимум отношений свободных членов к элементам ведущей строки. Получаем:
.
Следовательно, ведущая строка - та, в которой записано , а ведущим элементом является -3/2.
Составляем третью симплексную таблицу
Новую базисную переменную записываем первой строкой. В столбец, в котором было , вписываем новую свободную переменную .
Первая строка:
Вспомогательные коэффициенты:
| Таблица 3 | ||||
| Базисные неизвестные | Свободные члены | Свободные неизвестные | Вспомогательные коэффициенты | |
| X4 | X3 | |||
| X1 | 2 | -2/3 | 1/3 | |
| X2 | 2 | -1/3 | -1/3 | 1/2 |
| X5 | 2 | 1/3 | -2/3 | -1/2 |
| X6 | 4 | 1/3 | 1/3 | -1/2 |
| F | 6 | -4/3 | -1/3 | 2 |
Вычисление остальных строк на примере второй строки:
Полученное решение вновь не оптимальное, поскольку коэффициенты при свободных неизвестных в индексной строке вновь отрицательные.
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Для перехода к четвёртой симплексной таблице найдём наибольшее из чисел и . Это число .
Следовательно, ведущий столбец - тот, в котором записано .
Для нахождения ведущей строки найдём минимум модулей отношений свободных членов к элементам ведущего столбца:
.
Поэтому ведущая строка - та, в которой записано , а ведущий элемент 1/3.
В четвёртой симплексной таблице новую базисную переменную записываем первой строкой. В столбец, где было , записываем новую свободную переменную .
Первая строка:
Вспомогательные коэффициенты:
.
| Таблица 4 | ||||
| Базисные неизвестные | Свободные члены | Свободные неизвестные | Вспомогательные коэффициенты | |
| X5 | X3 | |||
| X4 | 6 | 3 | -2 | |
| X1 | 6 | 2 | -1 | 2/3 |
| X2 | 4 | 1 | -1 | 1/3 |
| X6 | 2 | -1 | 1 | -1/3 |
| F | 14 | 4 | -3 | 4/3 |
Вычисление остальных строк на примере второй строки:
Полученное решение так же не оптимально, но оно уже лучше предыдущих, так как один из коэффициентов при свободных переменных в индексной строке неотрицателено.
Для улучшения плана перейдём к следующей симплексной таблице.
Найдём наибольшее из чисел 4 и . Это число 4. Следовательно, ведущий столбец .
Для нахождения ведущей строки найдём
.
Следовательно, ведущая строка - та, в которой записано . Но и уже были вместе среди свободных переменных. Поэтому для перевода очередной переменной из свободных в базисные выбираем другой ведущий столбец - тот, в котором записано .
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Для нахождения ведущей строки найдём
.
Следовательно, ключевая строка - та, в которой записано , а ведущий элемент 1.
В пятой симплексной таблице новую базисную переменную записываем первой строкой. В столбец, где было , записываем новую свободную переменную .
Первая строка:
Вспомогательные коэффициенты:
.
| Таблица 5 | ||||
| Базисные неизвестные | Свободные члены | Свободные неизвестные | Вспомогательные коэффициенты | |
| X5 | X6 | |||
| X3 | 2 | -1 | 1 | |
| X4 | 10 | 2 | ||
| X1 | 8 | 1 | ||
| X2 | 6 | 1 | ||
| F | 20 | 1 | 3 | 3 |
Попробуем сразу узнать, не является ли решение оптимальным. Поэтому для остальных строк вычислим только свободные члены (чтобы узнать значения базисных переменных при равенстве свободных переменных нулю) и коэффициенты при свободных переменных в индексной строке.
Свободные члены:
- во второй строке ;
- в третьей строке ;
- в четвёртой строке .
Индексная строка:
Смотрим в симплексную таблицу 5. Видим, что получено оптимальное решение, так как коэффициенты при свободных неизвестных в индексной строке неотрицательны.
Ответ:
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс методом.
Решим алгебраическими преобразованиями тот же пример, что и в предыдущем параграфе. Следует отметить, что при решении этой разновидностью симплекс метода лучше не записывать функцию цели в виде , так как при этом легко запутаться в знаках. Но в этом случае пункт алгоритма, определяющий критерий оптимальности, будет модифицирован следующим образом.
Если отыскивается максимум (минимум) линейной формы и в её выражении нет неосновных переменных с положительными (отрицательными) коэффициентами, то критерий оптимальности выполнен и полученное базисное решение является оптимальным - решение окончено. Если при нахождении максимума (минимума) линейной формы в её выражении имеется одна или несколько неосновных переменных с положительными (отрицательными) коэффициентами, перейти к новому базисному решению.
Пример. Найти максимум функции при ограничениях
Решение.
Шаг I. Вводим добавочные неотрицательные переменные и сводим данную систему неравенств к эквивалентной ей системе уравнений
.
Введённые добавочные переменные принимаем за основные, так как в этом случае базисное решение системы легко находится. Тогда и - неосновные переменные.
Выразив основные переменные через неосновные, получим
Следовательно, данному разбиению переменных на основные и неосновные соответствует базисное решение , которое является недопустимым (две переменные отрицательны), а поэтому оно не оптимальное. От этого базисного решения перейдём к улучшенному.
Чтобы решить, какую переменную следует перевести из неосновных в основные, рассмотрим любое из двух имеющихся уравнений последней системы с отрицательными свободными членами, например второе. Оно показывает, что в основные переменные можно перевести и , так как в этом уравнении они имеют положительные коэффициенты (следовательно, при их увеличении, а это произойдёт, если переведём любую из них в основные переменные, переменная увеличится).
Попробуем перевести в основные переменную . Чтобы установить, какую переменную следует перевести из основные в неосновные, найдём абсолютную величину наименьшего отношения свободных членов системы к коэффициентам при . Имеем . Оно получено из третьего уравнения, показывающего, что в неосновные нужно перевести переменную , которая в исходном базисном решении положительна. Следовательно, полученное базисное решение, как и исходное, содержит две отрицательные компоненты, т. е. при переходе к такому базисному решению улучшения не произойдёт.
Если же перевести в основные переменную , то наименьшее отношение свободных членов к коэффициентам при составит . Оно получено из первого уравнения, в котором свободный член отрицателен. Следовательно, переводя в основные, а в неосновные переменные, мы получим базисное решение, в котором число отрицательных компонент на единицу меньше, чем в исходном. Поэтому остановимся на этой возможности: переводим в основные, а в неосновные переменные. Поэтому в приведённой выше системе уравнений выделенным оказалось первое уравнение.
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Шаг II.
Основные переменные , неосновные переменные .
Выразим новые основные переменные через новые неосновные, начиная с выделенного на шаге I уравнения. В результате получим
Следовательно, имеем новое базисное решение , которое также является недопустимым, а поэтому не оптимальным. Но в нём, как мы и предвидели, только одна переменная отрицательна (а именно ).
От полученного базисного решения необходимо перейти к другому. Рассмотрим уравнение с отрицательным свободным членом, т. е. второе уравнение. Оно показывает, что в основные переменные можно перевести и . Переведём в основные переменные . Найдём наименьшее из абсолютных величин отношений свободных членов системы к коэффициентам при . Имеем . Значит, в неосновные переменные нужно перенести . Так как наименьшее отношение получено из второго уравнения, то его выделяем. В новом базисном решении уже не окажется отрицательных компонент, т. е. оно является допустимым.
В особых случаях решение завершается на II шаге: это, например, случаи, когда максимум целевой функции - бесконечность и когда система не имеет ни одного решения.
Шаг III.
Основные переменные: , неосновные переменные: . Выразив основные переменные через неосновные, получим
Новое базисное решение имеет вид . Является ли оно оптимальным, можно установить, если выразить линейную форму через неосновные переменные рассматриваемого базисного решения. Сделав это, получим . Так как мы ищем максимум линейной формы, а нашли лишь одно допустимое решение, то продолжим перебор.
Переводим в число основных переменную , имеющую больший положительный коэффициент. Находим . Это наименьшее отношение получено из третьего уравнения системы, поэтому его выделяем. Оно показывает, что при переменная и поэтому перейдёт в число неосновных.
В некотором особом случае решение завершается на III шаге: это случай, когда оптимальное решение - не единственное.
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Шаг IV.
Основные переменные: , неосновные переменные: . Выразив основные переменные через неосновные, получим
Линейная форма, выраженная через те же неосновные переменные, примет вид . Продолжим перебор для поиска максимума.
Увеличение линейной формы возможно при переходе к новому базисному решению, в котором переменная является основной. Находим . Это наименьшее отношение получено из четвёртого уравнения системы и показывает, что при переменная и переходит в число неосновных.
Шаг V.
Основные переменные: , неосновные переменные: . Выразив основные переменные через неосновные, получим
Линейная форма, выраженная через неосновные переменные нового базисного решения, имеет вид . Критерий оптимальности для случая максимизации линейной формы выполнен. Следовательно, базисное решение является оптимальным, а максимум линейной формы
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Начало темы "Линейное программирование"
Продолжение темы "Линейное программирование"
Поделиться с друзьями
function-x.ru
Симплексный метод оптимизации? — КиберПедия
1. Основан на пассивном эксперименте, в выбранной части факторного пространства ставится минимальное число опытов, которое на единицу больше числа значимых факторов, далее происходит кантование симплекса относительно стороны с худшими результатами.
2. 4.Основан на пассивномэксперименте, в выбранной части факторного пространства ставится минимальное число опытов, которое на единицу больше числа значимых факторов, далее происходит кантование симплекса относительно стороны с лучшими результатами.
3. Основан на активном эксперименте, в выбранной части факторного пространства ставится минимальное число опытов, которое на единицу больше числа значимых факторов, далее происходит кантование симплекса относительно стороны с худшими результатами.
4.Основан на активном эксперименте, в выбранной части факторного пространства ставится минимальное число опытов, которое на единицу больше числа значимых факторов, далее происходит кантование симплекса относительно стороны с лучшими результатами.
Модель второго порядка?
1. Каждый фактор надо варьировать не менее чем на двух уровнях.
2.Каждый фактор надо варьировать не менее чем на трех уровнях.
3. Каждый фактор надо варьировать не менее чем на четырех уровнях.
4. Каждый фактор надо варьировать не менее чем на пяти уровнях.
109. Количество опытов ПФЭ 33?
1.27; 2.8; 3.9; 4.81.
Количество опытов трехфакторного ОЦКП
(ортогонального центрального композиционного плана)?
1.25; 2.9; 3.27; 4.15.
111. Дублирование опытов в центре плана?
1. Для проверки ортогональности модели.
2.Для проверки адекватности модели.
3. Для проверки ротатабельности модели.
4. Для оценки взаимовлияния факторов модели.
112. Униформность плана?
1. Независимость величины параметра оптимизации от расстояния, измеряемого от центра области планирования эксперимента.
2. Независимость линейных коэффициентов регрессии от расстояния, измеряемого от центра области планирования эксперимента.
3.Независимость дисперсии параметра оптимизации от расстояния, измеряемого от центра области планирования эксперимента.
4. Независимость дисперсии параллельных опытов от расстояния, измеряемого от центра области планирования эксперимента.
113. Симплексно-суммируемые планы?
1. Относятся к нецентральным композиционным планам, образуются с помощью суммирования симплексов, более экономичны по числу опытов, чем РЦКП.
2. Относятся к центральным некомпозиционным планам, образуются с помощью суммирования симплексов, менее экономичны по числу опытов, чем РЦКП.
3.Относятся к центральным некомпозиционным планам, образуются с помощью суммирования симплексов, более экономичны по числу опытов, чем РЦКП.
4. Относятся к центральным композиционным планам, образуются с помощью суммирования симплексов, болееэкономичны по числу опытов, чем РЦКП.
Симплекс?
1.Выпуклая фигура, образованная точками плана – условиями проведения опытов.
2. Выпуклая фигура, образованная поверхностью отклика.
3. Плоская фигура, образованная точками плана – условиями проведения опытов.
4.Плоскость, образованная поверхностью отклика.
115. Число уровней и факторов несимметричных планов?
1.Число уровней факторов не зависит от числа факторов.
2.Число уровней факторов должно быть равно числу факторов.
3.Число уровней факторов должно быть как минимум на единицу меньше числа факторов.
4.Число уровней факторов должно быть как минимум на единицу больше числа факторов.
116. Сколько опытов требует пятифакторный план
Хартли второго порядка?
1.243; 2.27; 3.81; 4.24.
117. Каноническое преобразование уравнения второй степени?
1.Перенос начала координат в экстремальную (центральную) точку факторного пространства и поворот новых осей относительно старых координат на определенный угол.
2.Перенос начала координат в экстремальную (центральную) точку факторного пространства.
3. Перенос начала координат в точку за пределы факторного пространства и поворот новых осей относительно старых координат на определенный угол.
4. Перенос факторного пространства и поворот новых осей относительно старых координат на определенный угол.
Линеаризация степенной функции?
Линеаризация показательной функции?
1.Вероятностная сетка. 2.Полулогарифмическая сетка.
3.Логарифмическая сетка. 4.Тригонометрическая сетка.
Метод Брандона?
1.Линейную функцию находят в виде произведения функций факторов, при этом каждая из функций считается функцией нескольких аргументов.
2. Линейную функцию находят в виде произведения функций факторов, при этом каждая из функций считается функцией только одного аргумента.
3. Нелинейную функцию находят в виде произведения функций факторов, при этом каждая из функций считается функцией нескольких аргументов.
4.Нелинейную функцию находят в виде произведения функций факторов, при этом каждая из функций считается функцией только одного аргумента.
Метод размерностей?
1.Переводит размерности технической системы единиц в систему СИ.
2.Вводит дополнения к основным размерным единицам: Па (Паскаль), МПа(МегаПаскаль) и т.д.
3.Основан на принципе Фурье, позволяет результаты любого физического эксперимента обработать в виде безразмерной комбинации величин.
4. Основан на принципе Фурье, позволяет результаты любого физического эксперимента обработать в виде размерной комбинации величин.
122. π - теорема?
1.Число безразмерных комплексов равно числу всех физически разнородных величин, существенных для процесса, за вычетом числа первичных величин.
2. Число безразмерных комплексов равно числу всех физически однородныхвеличин, существенных для процесса, за вычетом числа первичныхвеличин.
3. Число безразмерных комплексов равно числу всех физически разнородных величин, существенных для процесса, за вычетом числа вторичныхвеличин.
4. Число безразмерных комплексов равно числу всех физически однородных величин, существенных для процесса, за вычетом числа вторичных величин.
cyberpedia.su
Оптимизация симплекс-метод - Справочник химика 21
Симплексный метод планирования эксперимента и оптимизации. В сравнительно недавнее время появились работы з1-зз в которых предлагается на стадии восхождения использовать симплексный -метод планирования экспериментов (симплекс-планирование). Начиная восхождение, планируют исходную серию опытов так, чтобы точки, соответствующие условиям проведения этих опытов, образовывали правильный симплекс в многомерном. факторном пространстве. Под правильным симплексом понимается совокупность А +1 равноудаленных друг от друга точек в /с-мерном пространстве. В одномерном пространстве симплексом является отрезок прямой. Для двух факторов симплексом служит равносторонний треугольник, для трех факторов правильная треугольная пирамида — тетраэдр и др. [c.210] Последовательная оптимизация симплекс-метод [c.511]Процедура поиска оптимума напоминает изложенную выше оптимизацию методом крутого восхождения , но еще проще и не требует описания даже исходной области. Первый этап оптимизации симплекс-методом заключается в выборе центральной точки я построении вокруг нее правильного симплекса. Центральная точка может выбираться практически в любом месте, и нет необходимости начинать исследование вдалеке от ожидаемого экстремума, как это рекомендовалось в методе крутого восхождения . Однако выбор интервалов варьирования факторов (масштабы по осям) не совсем произволен — они не должны быть ни слишком большими, ни слишком малыми, что определяется ходом собственно поиска экстремума. После реализации симплекс-плана первого порядка сравнивают результаты опытов и выбирают наихудший. Можно полагать, что экстремум функции будет находиться от центра в направлении, противоположном радиусу-вектору наихудшего опыта, поэтому исходный симплекс опрокидывают в направлении ожидаемого экстремума. Отбросив наихудший опыт и поставив новый в симметричной точке, мы тем самым построим новый, правильный симплекс, с которым вся процедура. поиска новой наихудшей точки, опрокидывания симплекса и т. д. повторяется вновь. [c.457]
Поскольку построенная модель имеет I порядок, то оптимизацию ее можно осуществить двумя методами — симплекс-методом и методом -крутого восхождения . Оба метода дают близкие результаты. Метод -крутого восхождения выявляет еще несколько уровней проведения эксперимента [c.179]
В разд. 5.3 рассматриваются последовательные методы оптимизации, в частности симплекс-метод. При оптимизации по последовательному методу процедура начинается с выполнения некоторых начальных экспериментов. На основании анализа их результатов определяется положение новых экспериментальных точек, которые, как ожидается, должны привести к полу-че П1ю улучшенной хроматограммы. Суть метода состоит в постепенном приближении к оптимуму. [c.212]
Особенно удобна оптимизация симплекс-методом, когда необходимо учитывать какие-либо ограничения при поиске оптимума. Введение штрафной функции , как указывалось выше, приводит в данном случае к тому, что вершина симплекса, оказавшаяся в запрещенной области, будет наихудшей, и весь симплекс придется опрокидывать в направлении от границы в разрешенную область. Движение к экстремуму превратится при этом в постепенное приближение к почти стационарной области или пограничному оптимальному значению вдоль границы, как бы нащупывая ее время от времени, когда одна из вершин оказывается по другую ее сторону. [c.459]
В отличие от параллельных оптимизационных процедур, описанных в предыдущем разделе, симплекс-метод является последовательным процессом. Выполняется минимальное число начальных экспериментов и на их основании выносится решение о положении следующих точек. Такую простейшую форму последовательной оптимизации можно охарактеризовать путем, которому на схеме, приведенной на рис. 5.4, отвечает число 1012. [c.227]
Оптимизация компаундирования значительно повышает рентабельность продукции при полном использовании запасов компонентов. Но для получения таких результатов необходимо обеспечить быстроту расчетов, что возможно только при применении ЭЦВМ. Решение простейшего варианта задачи о смешении симплекс-методом вручную продолжается около 15 дней, тогда как решение более сложной задачи на ЭЦВМ при наличии готовой [c.135]
Метод ДП является одним из основных для оптимизации РС и в зарубежной вычислительной практике. Так, в статье- [287] говорится о применении ДП для оптимизации городских коммунальных сетей. Ее авторы считают, что среди методов ветвей и границ, симплекс-метода, полного перебора метод ДП является наиболее эффективным. В этой работе приводится пакет программ для оптимального проектирования распределительных разветвленных сетей, где основным также является метод ДП. [c.170]
Более целесообразно для решения этой проблемы использовать модифицированный симплекс-метод, подобный впервые описанному в работе [7]. Модифицированный алгоритм позволяет не только отражать, но и сжимать и расширять треугольник. Способ применения этого модифицированного алгоритма к двумерной оптимизации хроматографического разделения проиллюстрирован на рис. 5.8. Этот пример взят из работы [5]. Два параметра представляют собой две из трех объемных до- [c.229]
Симплекс-процесс позволяет выявить локальный или глобальный оптимум. Для того чтобы получить представление о значимости найденного оптимума, процедуру в идеальном случае следует провести несколько раз, исходя из различных наборов начальных точек (хроматограмм) [11]. Это тем более важно, что симплекс-оптимизация дает очень слабое представление об общем характере поверхности отклика. Однако при большом числе экспериментов, выполняемых в каждом отдельном процессе, возникает замкнутый круг, существование которого в основном и препятствует применению симплекс-метода для оптимизации хроматографической селективности. Этот круг проиллюстрирован на рис. 5.10. [c.232]
Наиболее простой метод математического планирования эксперимента— симплекс-метод. Он предложен в 1962 г. Спиндлеем для оптимизации дискретных процессов. Правильным симплексом называется совокупность л+1 равномерно удаленных друг от друга точек в л-мерном пространстве, где п — число факторов, влияющих на процесс. В одномерном пространстве симплексом является отрезок прямой. Для двух факторов правильный симплекс представляет собой равносторонний треугольник, для трех факторов — тетраэдр и т. д. [c.150]
Представление о поверхности отклика в целом, получаемое в результате оптимизации, является недостаточным. Повторение симплекс-метода с использованием других начальных точек устраняет проблемы. 2 и 5, но усугубляет проблему /. Из-за того что симплекс-оптимизация может привести [c.232]
В то же время практические характеристики симплекс-метода показывают, что его можно применять непосредственно (даже при многопараметрических оптимизациях) и что он не требует трудоемких вычислений или использования ЭВМ. Этим и объясняется популярность симплекс-метода применительно к оптимизации хроматографической селективности, несмотря на его принципиальную ограниченность. [c.306]
При необходимости более детальной локализации оптимума уменьщают шаги варьирования параметров (т. е. сокращают расстояние между вершинами симплекса) и продолжают процедуру оптимизации. Симплекс-метод позволяет проводить планирование эксперимента и в условиях ограничения. Если в точке, отражающей [c.151]
Программа симплекс-оптимизации допускает использование различных оптимизационных критериев, что дает возможность стремиться к удовлетворительному распределению пиков на хроматограмме. Однако симплекс-метод требует большого числа экспериментов и поэтому как таковой представляется мало приемлемым для оптимизации основных параметров. [c.355]
В табл. 6.5,6 сравниваются методы оптимизации селективности. II в данном случае симплекс-метод малопривлекателен из-за большого числа необходимых экспериментов, а возможность установления глобального оптимума неоднозначна. [c.359]
Для оптимального проектирования трубчатого аммиачного реактора использовался симплексный метод 176], хорошо приспособленный к существенно двумерной задаче оптимизации. Последовательность вычислений, изображенная графически в плоскости переменных — температуры ка входе и охлаждающего фактора (две переменные, оставленные на усмотрение проектировщика), — представляет собой цепь смежных треугольников (двумерных симплексов), вытянутую в направлении точки оптимума и в конце концов окружающую эту точку. Окончательное расположение оптимума уточняется путем квадратичной аппроксимации заключителыюй гексагональной системы точек симплекс-метода. [c.176]
Все процессы оптимизации можно классифицировать на следующие [468] 1) эмпирические 2) графические (более систематические варианты эмпирических методов) 3) статистические (в частности, симплекс-метод) 4) теоретические. С помощью статистических и теоретических методов показано, что теоретически предсказанные разделения на микроЭВМ очень близки к экспериментально полученным [470]. [c.252]
При формулировке задач в терминах динамического программирования часто возникают затруднения. Как и в других разделах математики, здесь весьма существенна формулировка задачи. Часто неудачная формулировка влечет за собой путаницу или вообще неблагоприятный исход. В отличие от линейного программирования, где симплекс-метод является универсальным методом, в динамическом программировании отсутствует общий алгоритм, пригодный для всех задач. Каждая задача имеет свои собственные трудности, и в каждом случае требуется уметь найти наиболее подходящую методику оптимизации. [c.23]
Ний, перпендикулярных оси параметра оптимизации, называемых обычно двумерными сечениями, рассмотрены в работах [57, 58]. Для выбора оптимальных режимов можно также использовать методы поиска оптимальной области, заменив эксперимент вычислением значений параметра оптимизации по уравнению регрессии. При ручном счете удобно применять метод Гаусса — Зейделя, метод симплексов, метод Градиента при использовании ЭВМ — метод случайного поиска и др. В главе 6 приведен пример применения метода симплексов для поиска оптимальных режимов выщелачивания германия из зол слоевого сжигания угля. [c.121]
Данная задача сводится к математической задаче оптимального управления. Используя симплекс-метод, определяют алгоритм оптимизации, который сводится к следующему [c.303]
Симплексный метод является одним из эффективных методов решения задач оптимизации высокой размерности. Алгоритм этого метода основан на использовании некоторых свойств простейших многогранников п-мерного пространства симплексов. [c.387]
Сущность симплексного метода для двух переменных оптимизации сводится к следующему. Условия первой серии опытов в п-мер-ном пространстве параметров соответствуют координатам точек, образующих в этом пространстве симплекс. [c.150]
Симплекс-метод является наиболее распространенным на практике методом оптимизации. Его основные достоинства —простота, хорошая сходимость и высокая скорость достижения оптимальных условий. Основные проблемы возникают тогда, когда поверхность отклика мультимодальна, т. е. содержит несколько локальных экстремумов. В подобных случаях симплекс-алгоритм обычно сходится к ближайшему локальному экстремуму, а глобальный экстремум может быть пропущен. Разработаны и более эффективные способы оптимизации, такие, как метод сопряженных градиентов или метод Пауэлла. Однако они используются главным образом для нахождения экстремумов функций, заданных алгебраически, и редко применяются для оптимизации эксперимента. [c.514]
Задача линейного программирования (VIII.31) решалась с помощью симплекС метода [79]. Расчеты [211 показали, что невозможно компенсировать изменения параметров только за счет изменения АУ. Оказалось, что относительно параметри ческой чувствительности наиболее целесообразно не возвращать вещества X и V в рецикл. Этот вывод нельзя сделать, однако, из результатов оптимизации при зЭ крепленных номинальных значениях параметров. [c.341]
Промышленные химико-технологические эксперименты ограничивают исследователя целым рядом требований, связанных с необходимостью сохранения условий и ритма производства. Опыты по оптимизации технологического процесса в ходе налаженного производства приходится выполнять таким образом, чтобы не нарушать производственного процесса. Ясно, что в таких условиях нельзя резко изменять значения уровней факторов и проводить большое число опытов и вычислений. Кроме того, возникает необходимость в последовательной оценке влияния каждого из шагов эксперимента на технологический процесс. К активным методам, позволяюшим планировать промышленные исследования, относятся симплекс-метод и эволюционное планирование. [c.119]
Еще Дж. Данциг показал [56], что симплекс-метод для сетевой задачи линейного программирования (ЛП) сводится к целенаправленному перебору деревьев этой сети. А теоретические основы построения и алгоритмизации сетевых потоковых моделей изложены в известной книге Л. Форда и Д. Фалкерсона [237], которые, в частности, раскрыли двойственность задач о максимальном потоке и минимальном разрезе сети. Имеется ряд монографий отечественных и зарубежных авторов, в которых рассматриваются различные вопросы теории и методов решения нелинейных сетевых транспортных и других экстремальных задач на графах [35, 66, 257]. Применительно к трубопроводным системам (ТПС) наиболее полное истолкование сетевых потоковых моделей (на примере задач оптимизации развития, текущего и перспективного планирования работы газотранспортных систем и Единой системы газоснабжения страны) дано в монографии [228]. [c.166]
Вторая и более серьезная проблема — это сложность поверхности отклика. Простые поверхности с одним ш ироким оптимумом, как на рис. 5.7, встречаются не слишком часто, да и не относятся к числу желательных при оптимизации хроматографической селективности (см. разд. 5.1). В более общем случае, когда глобальный оптимум является самым высоким в серии локальных оптимумов, результат симплекс-оптимизации вполне может оказаться одним из локальных оптимумов. В то же время можно предположить, что шансы найти глобальный оптимум наиболее велики на достаточно простой поверхности отклика, где этот оптимум доминирует. Применение симплекс-метода для оптимизации разделения простых образцов, содержащих небольшое число компонентов, обусловлено именно тем, что этот метод наиболее полезен при исследовании простых поверхностей отклика. При этом включение неселективных параметров, таких, как скорость потока [8] или содержание воды в подвижной фазе (в ОФЖХ) (рис. 5.8), делает поверхность отклика более приемлемой для оптимизации по симплекс-методу. [c.232]
Статистические методы, отличные от симплекс-алгоритма, используются в целях оптимизации в хроматографии лишь от случая к случаю. Так, Рафел [13] сравнил симплекс-метод с [c.233]
Тер.мин симплекс-схема (или схема си.мплекс-решетки ) следует признать в данном контексте неудачным. Он приводит к путанице между симплекс-методом оптимизации (разд, 5,3) и методом часового Гляйха и соавторов, которые совершенно различны во всех отношениях. Во избежание путаницы мы не будем пользоваться словом симплекс , рассматривая метод часового. [c.264]
В программе автоматической оптимизации используется метод последовательного комплекс - планирования. Исходная точка при оптимизации задается с пульта уставок, относительно этой "точки Т й по программе оптимизации планирует эксперимент (меняя увта -ки), отдельные опыты которого располагаются в вершинах правильного симплекса в относительных единицах (переход к новому опыту осуществляется пооде окончания предыдущего). В каждом опыте по программе оцениваются расчетным путем величины удельных затрат и определяется производстьенный режим с наименьшими удельными затратами при учете ограничений на величины регулируемых переменных и показателей качества готового продукта (производительность задается). [c.149]
Главный недостаток симплекс-метода (и родственных методов последовательного поиска) состоит в том, что его резуль-татохМ является локальный оптимум, особенно при исследовании сложных образцов. Симплекс-методы требуют большого числа экспериментов (например, 25). Если мы хотим в результате оптимизации локализовать глобальный оптимум, то процедуру следует повторить несколько раз, при этом пропорционально возрастает объем экспериментальной работы. Локальный же оптимум, найденный при помощи симплекс-процедуры, может оказаться полностью неприемлемым, так как о поверхности отклика в целом формируется недостаточное представление. [c.306]
Поисковые методы оптимизации [107—112] используют математическую модель, полученную экспериментально-статистическими методами. Модель описывает исследуемый объект в некоторой локальной области изменения переменных. Область оптимума в общем случае не совпадает с областью математического описания, поэтому целевая функция служит лишь для выработки стратегии поиска оптимума. К числу основных поисковых методов относят метод Гаусса — Зейделя, метод случайного поиска, метод симплексов, метод градиента, метод наиско-рейшего спуска (крутого восхождения). [c.175]
Обсуждение. В работе [12] рассмотрена симплекс-оптимизация основных (программных) параметров в газовой хроматографии с программированием температуры, а авторами работы [13] выбран альтернативный метод последовательного поиска. Симплекс-метод пригоден для оптимизации ограниченного числа программных параметров, в то время как последовательный поиск был разработан для оптимизации многосег- [c.337]
Последовательный симплекс-метод (ПСМ) предложен в 1967 г. как метод эволюционного планирования в определенном отношении альтернативный обычному методу ЭВОП, при применении которого для оптимизации промышленных процессов необходимо участие квалифицированных специалистов (обратная научная связь), поэтому правила движения (о том, когда, куда и как двигаться) в последнем строго не оговорены. [c.103]
Однако наиболее важным различием между симнлекс-про-цессом и систематическим подходом, например предложенным Снайдером, является не качество конечной хроматограммы, а число требуемых для получения результата экспериментов. Для оптимизации первичных (программных) параметров по симплекс-методу необходимо 15 экспериментов, в то время как в систе.матическом подходе выполняется не более двух или трех экспериментов. [c.344]
Заключение. Характеристики различных методов оптимизации градиента суммированы в табл. 6.5. В табл. 6.5, а сравниваются различные методы оптимизации программных параметров. Учитывая сделанное в разд. 6.3.2.4 заключение о нежелательности больших усилий по оптимизации программируемого анализа, мы можем заключить, что симплекс-метод непригоден именно по этой причине, а полная математическая оптимизация малопривлекательна из-за необходимости выполнения большого объема вычислительных работ. Метод, предложенный Яндерой и Чурасеком, требует несколько больших усилий, чем метод Снайдера. Он предусматривает выполнение ряда расчетов, распознавание на каждой из хроматограмм трех выбранных компонентов и знание зависимости удерживания от состава подвижной фазы для этих компонентов. Такого рода зависимости могут быть получены либо в ходе оптимизации, либо из независимых (изократических) эксперимеитов. [c.359]
В этой связи следует также отметить, что некоторый эмпиризм аналитической ГЖХ, проявляющийся в подборе соответствующей неподвижной фазы и в выборе условий разделения, в принципе преодолен за счет применения приемов оптимизации, разработанных Лаубом и Пурнеллом [7] в форме так называемых оконных диаграмм. Эти приемы основаны на использовании простых графических методов систематического выбора оптимальных условий. Они позволяют сразу получить оптимальные значения целого набора параметров, тогда как ранее используемые (например, симплекс-метод) оптимизировали лишь один. Методология оконных диаграмм в значительной степени вытеснила эмпирические подходы и сейчас используется не только в хроматографии [8, 9], но и в спектроскопии [10] и электрохимии [11]. [c.505]
При обычном факторном методе добавление еще одного пара-NteTpa приводит к необходимости увеличить число опытов в два [ аза. Отметим еще следующие преимущества симплексного метода. При использовании симплекс-планирования параметр оптимизации [c.226]
I, может измеряться приблил енно достаточно иметь возможность 1 роранжировать эти величины. При этом можно одновременно учитывать несколько параметров оптимизации выход продукта, стоимость, чистоту и т. д. Параметр оптимизации может не измеряться количественно. Метод не предъявляет жестких требований к аппроксимации поверхности отклика плоскостью. Симплекс-план может быть использован как алгоритм при оптимизации процесса с использованием управляющей машины. [c.226]
chem21.info
Оптимизация Глава 6_2
Входные термины:
детерминированные методы оптимизации;
методы локальной оптимизации;
методы безусловной оптимизации;
многомерный критерий оптимальности;
прямые методы оптимизации;
Выходные термины:
регулярный симплекс;
«отражение» вершины симплекса;
редукция симплекса;
симплекс-метод.
§5. Симплекс-метод.
Рассмотрим следующую задачу многомерной локальной безусловной оптимизации: найти минимум критерия оптимальности Φ(X), определенного в n-мерном евклидовом пространстве 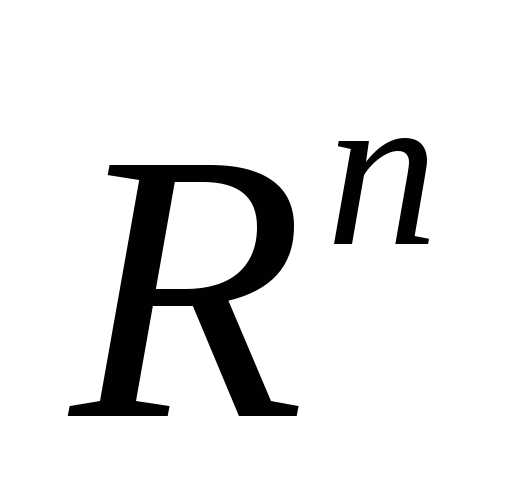 ,
,
 . (1)
. (1)
Регулярный симплекс и некоторые операции над ним.
Регулярным симплексом в пространстве 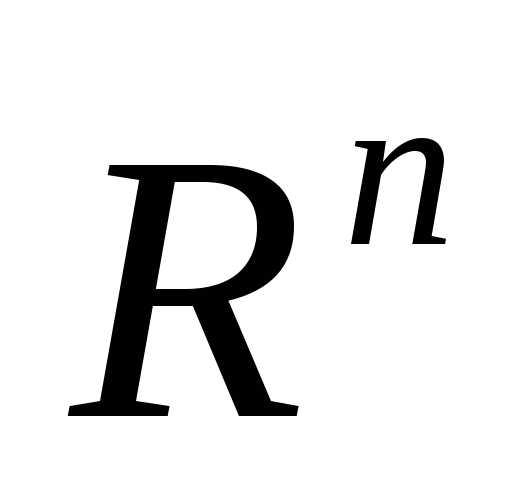 называется правильный многогранник, образованный
называется правильный многогранник, образованный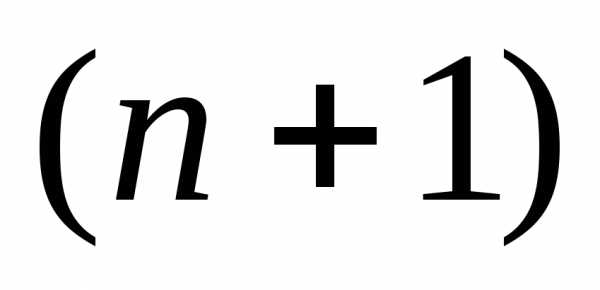 -ой равноотстоящими друг от друга вершинами. Для случаяn=2 – это равносторонний треугольник, для случая n=3 – тетраэдр.
-ой равноотстоящими друг от друга вершинами. Для случаяn=2 – это равносторонний треугольник, для случая n=3 – тетраэдр.
Если в пространстве 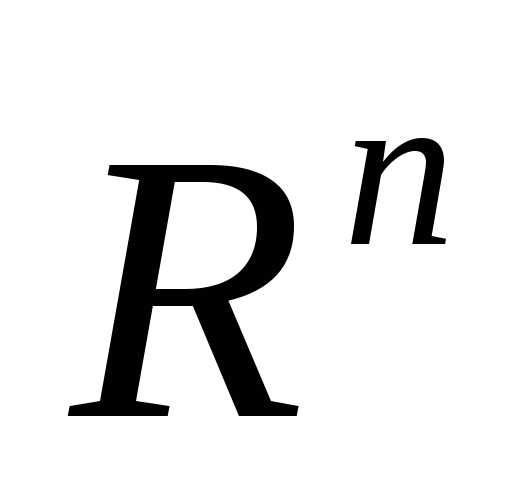 необходимо построить регулярный симплекс, вершина №1 которого находится в точке, то координаты вершин такого симплекса удобно задавать с помощьюматрицы
необходимо построить регулярный симплекс, вершина №1 которого находится в точке, то координаты вершин такого симплекса удобно задавать с помощьюматрицы
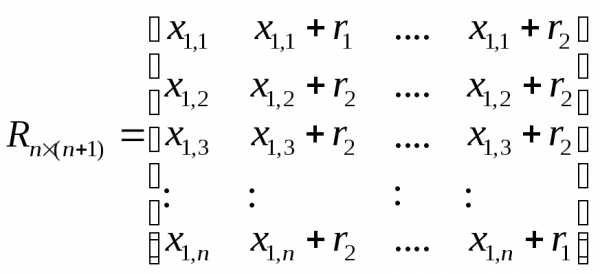 . (2)
. (2)
Здесь i-й столбец представляет собой координаты i-й вершины симплекса, ;
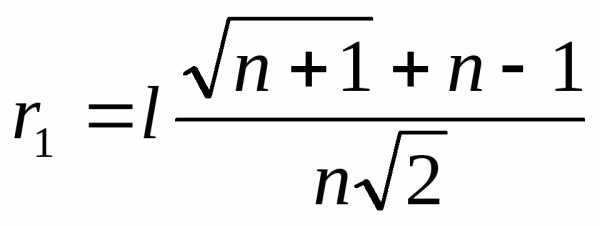 ,
, 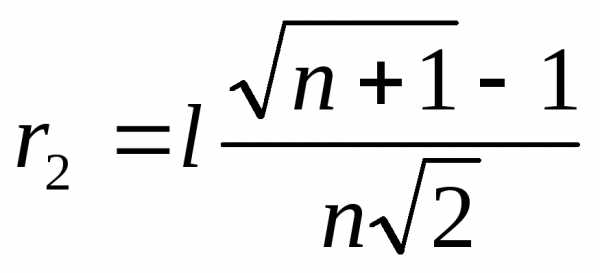 ; (3)
; (3)
l – длина ребра симплекса.
Например, регулярный симплекс в двумерном пространстве 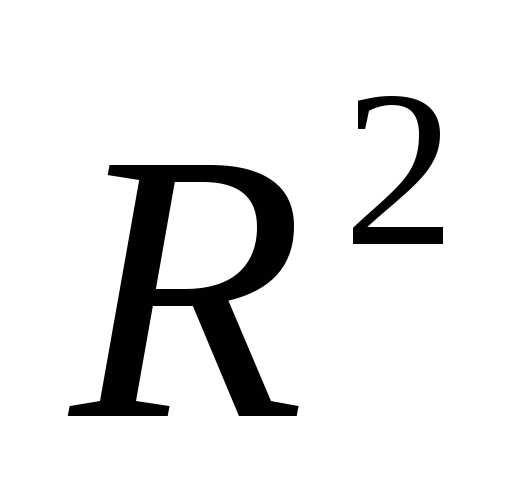 с первой вершиной в начале координат (когда) определяется (2*3) матрицей
с первой вершиной в начале координат (когда) определяется (2*3) матрицей
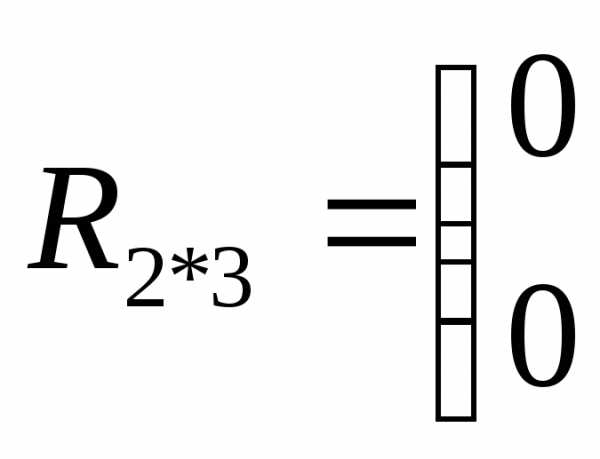
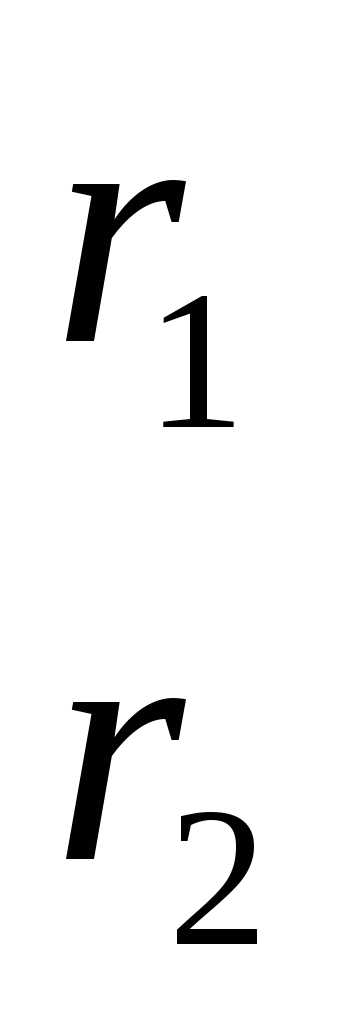
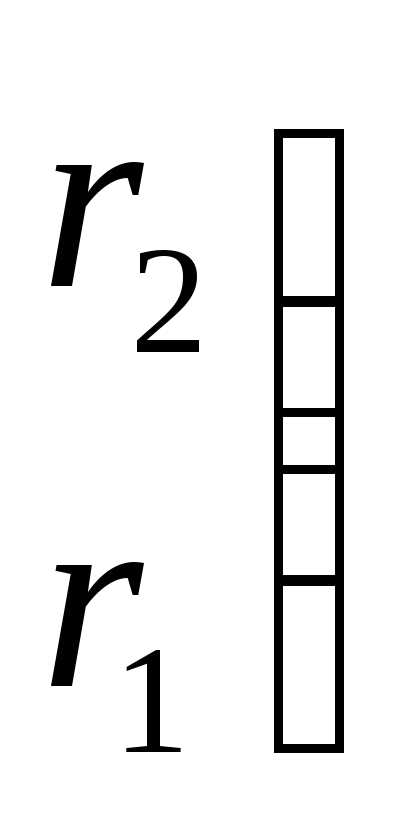
и имеет вид, представленный на рисунке 1.
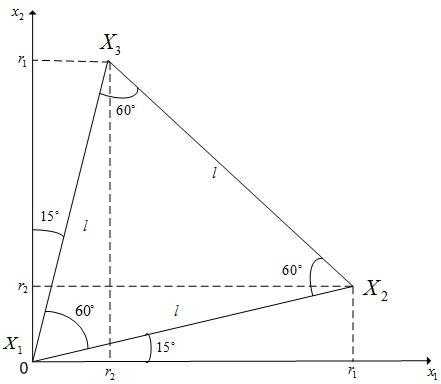
Рисунок 1 - Регулярный симплекс в пространстве 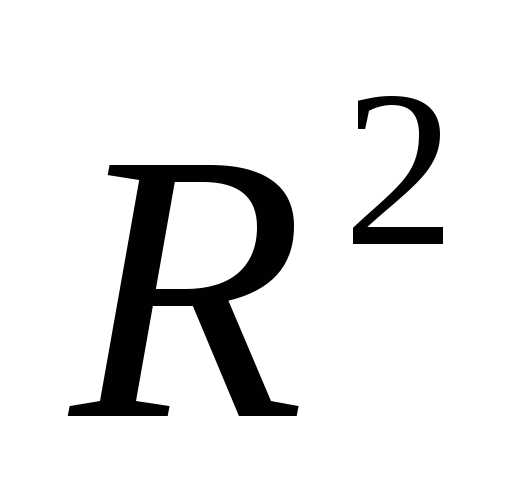 с одной из вершин в начале координат.
с одной из вершин в начале координат.
Регулярный симплекс в пространстве 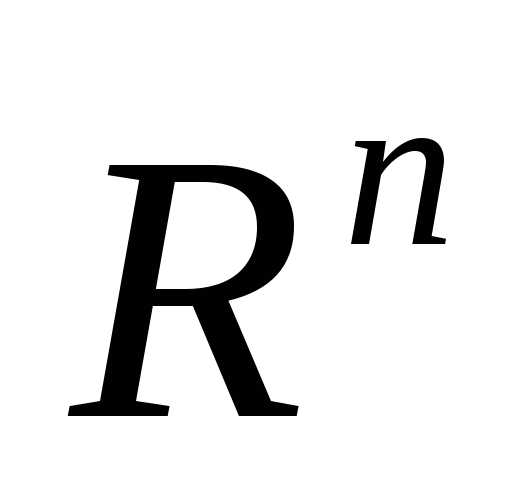 будем обозначать, где
будем обозначать, где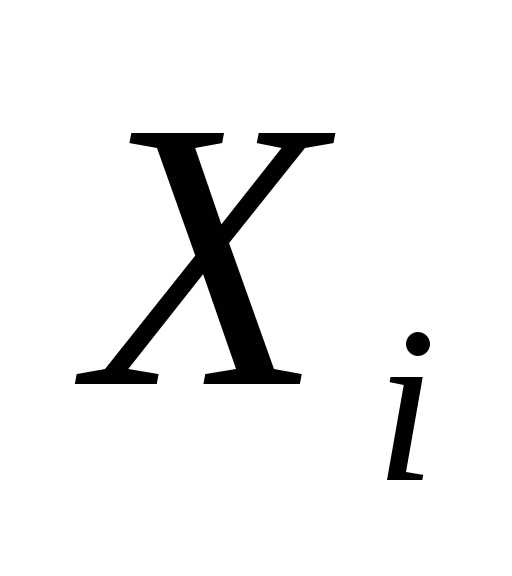 - вектор координатi-ой вершины симплекса.
- вектор координатi-ой вершины симплекса.
В алгоритме симплекс-метода используется следующее важное свойство регулярного симплекса: если одну из вершин регулярного симплекса перенести на надлежащее расстояние вдоль прямой, соединяющей данную вершину и центр тяжести оставшихся вершин, то вновь получится регулярный симплекс (рисунок 2). Будем называть эту процедуру отражением вершины симплекса относительно центра тяжести остальных вершин.
Очевидно, что при выполнении операции отражения вершины 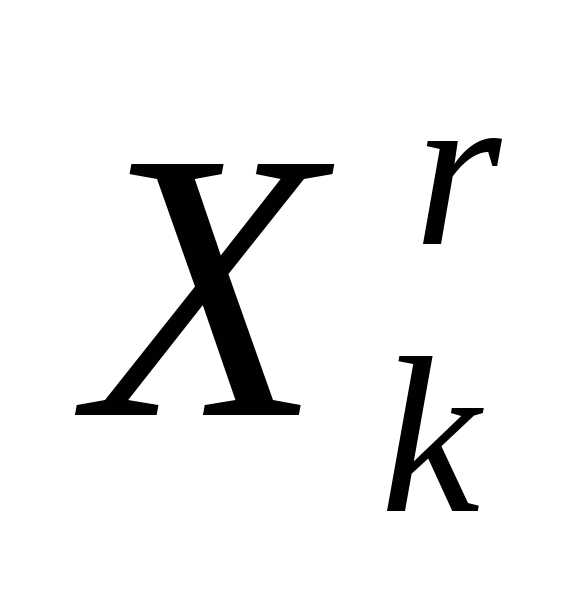 симплексаимеет место следующая связь координат этой вершины и вершины
симплексаимеет место следующая связь координат этой вершины и вершины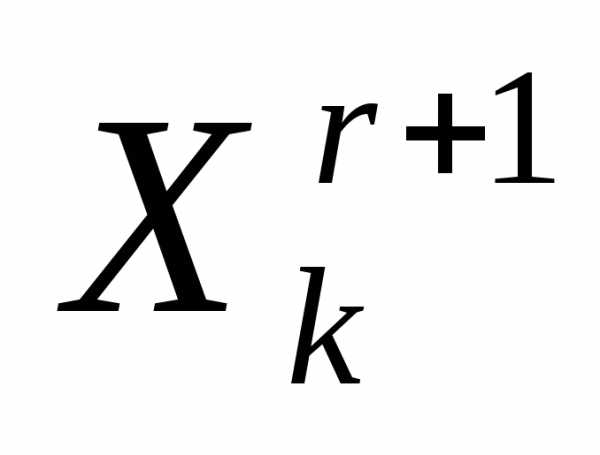 симплекса:
симплекса:
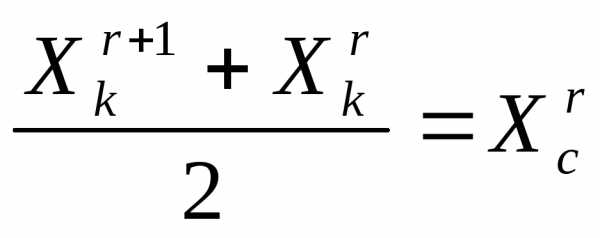
 . (4)
. (4)
Здесь
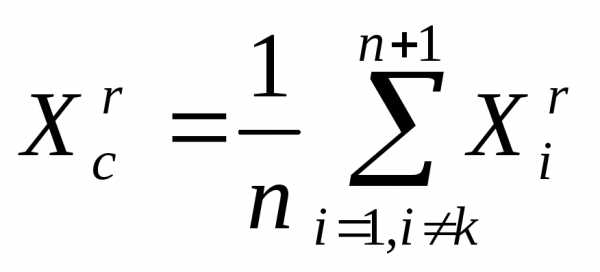 - (5)
- (5)
- вектор координат центра тяжести остальных вершин симплекса 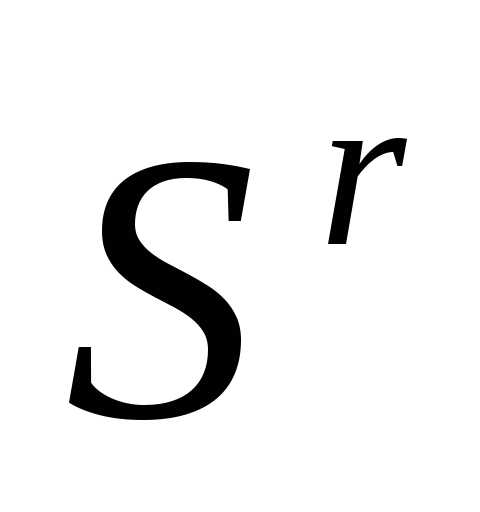 (за исключением отраженной вершины
(за исключением отраженной вершины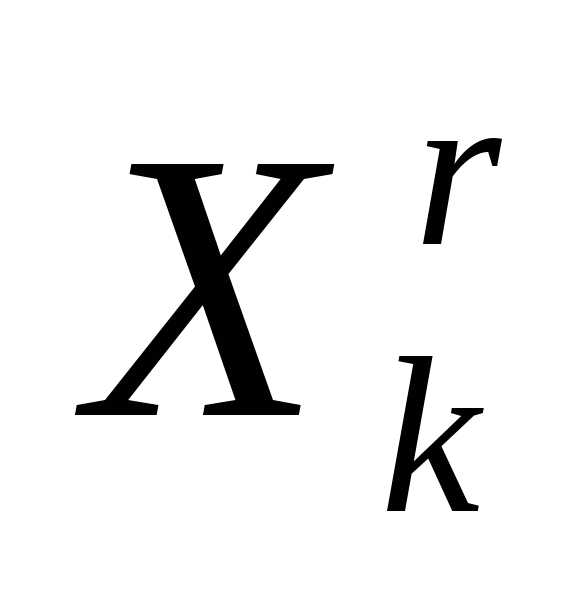 ).
).
Таким образом, после отражения вершины 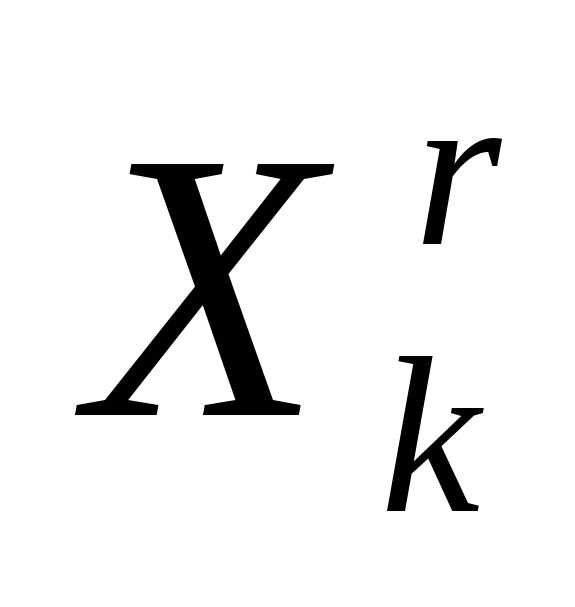 регулярного симплекса
регулярного симплекса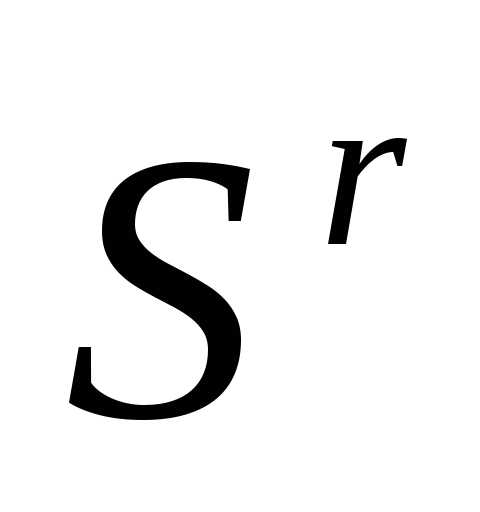 получаем новый регулярный симплекс
получаем новый регулярный симплекс
. (6)
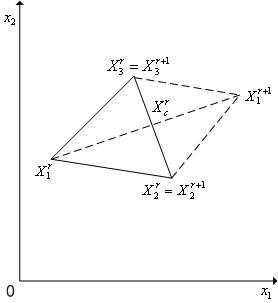
Рисунок 2 - Отражение вершины 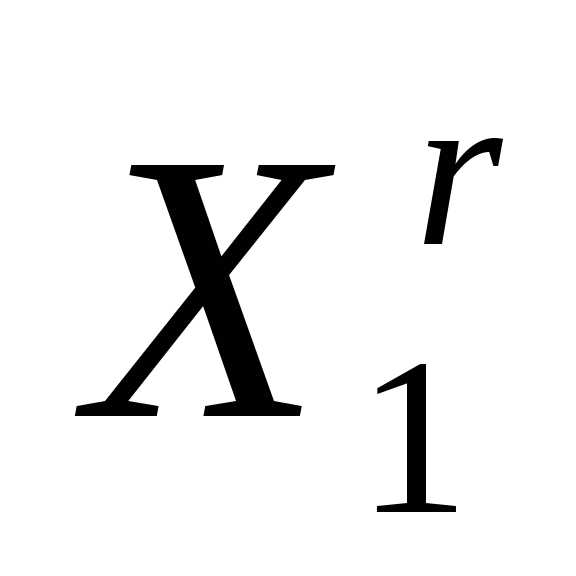 регулярного симплексав пространстве
регулярного симплексав пространстве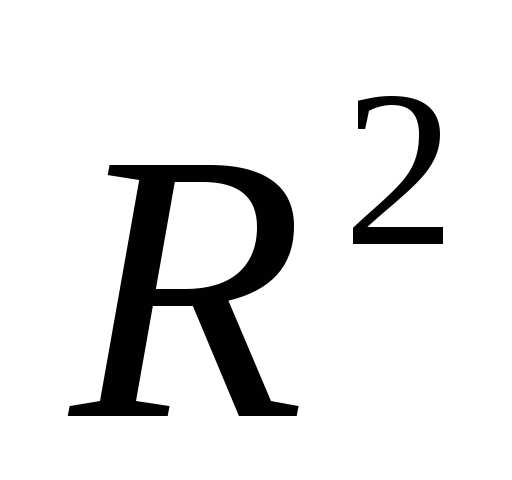 относительно центра тяжести
относительно центра тяжести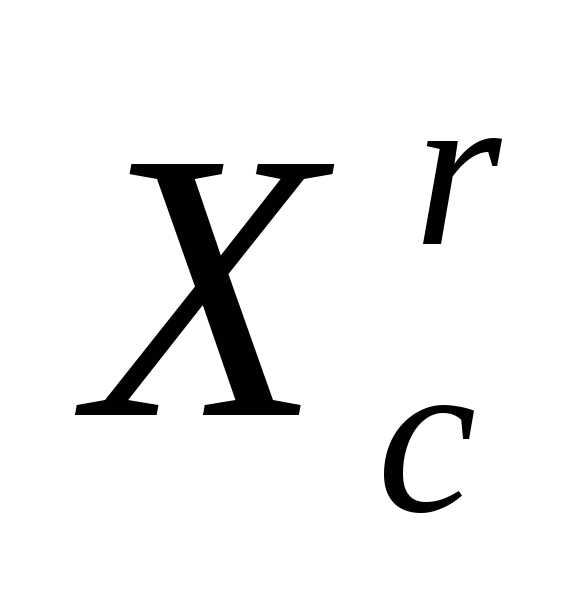 его остальных вершин.
его остальных вершин.
Кроме операции отражения вершины симплекса симплекс-метод может использовать операцию редукции симплекса (рисунок 3) - уменьшение длин всех ребер симплекса на одну и ту же величину («стягивания» симплекса к одной из его вершин).
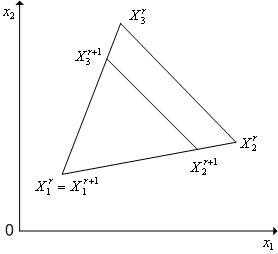
Рисунок 3 - Редукция вершин регулярного симплекса в пространстве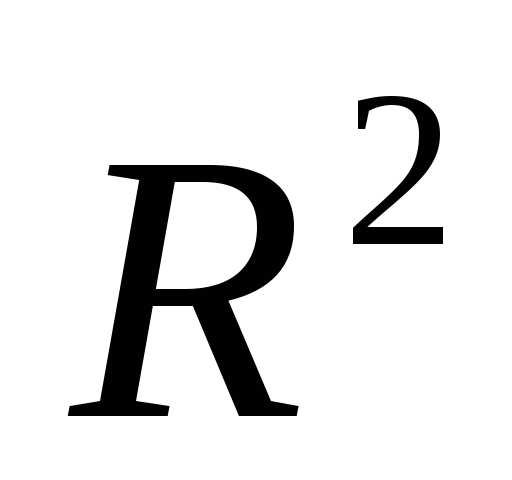 к вершине
к вершине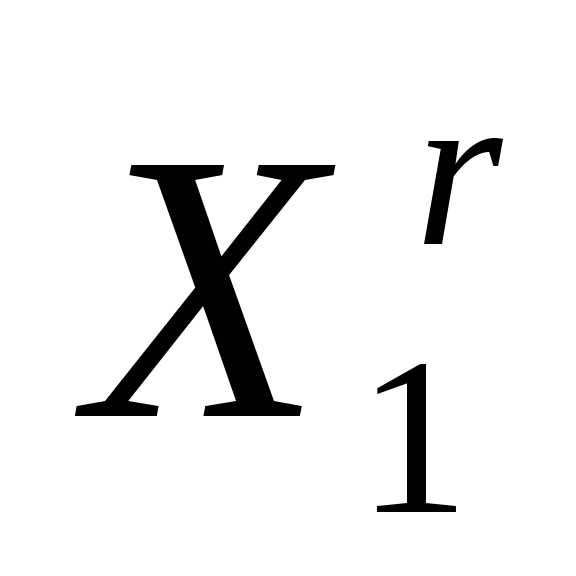 .
.
При выполнении операции редукции вершин симплекса к вершине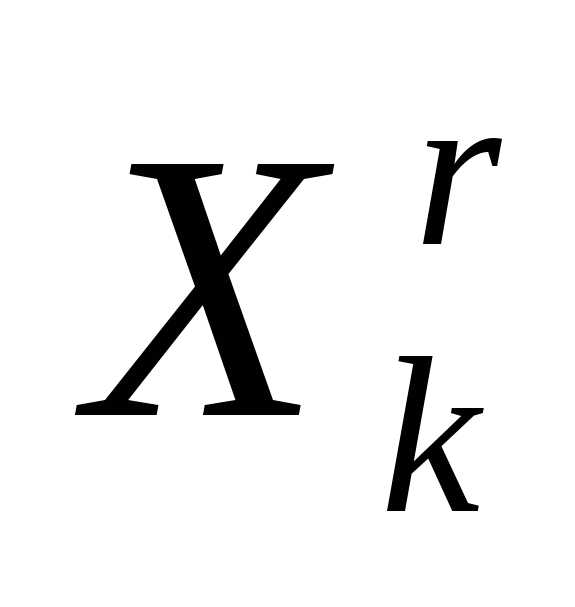 , координаты остальных вершин симплексаопределяются по формуле
, координаты остальных вершин симплексаопределяются по формуле
,
где 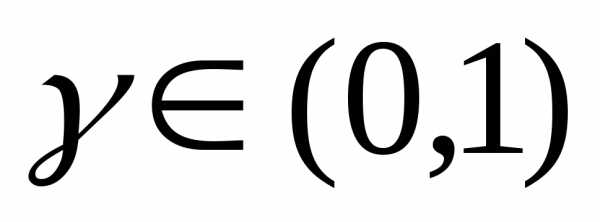 - коэффициент редукции. Рекомендуется использовать
- коэффициент редукции. Рекомендуется использовать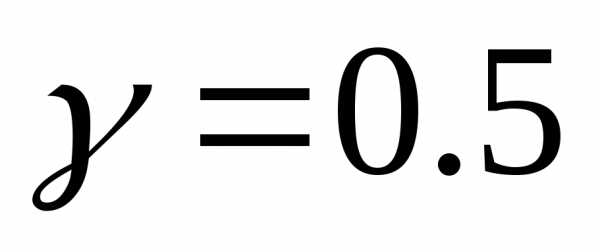 .
.
Таким образом, после редукции вершин симплекса к его вершине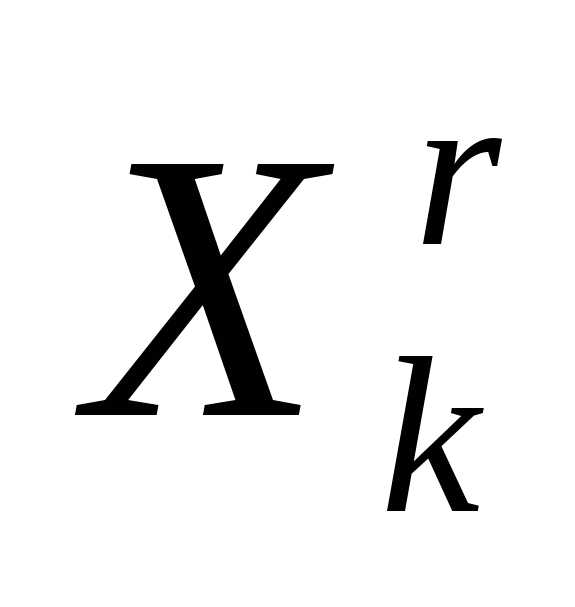 получаем новый симплекс
получаем новый симплекс
. (7)
Если симплекс 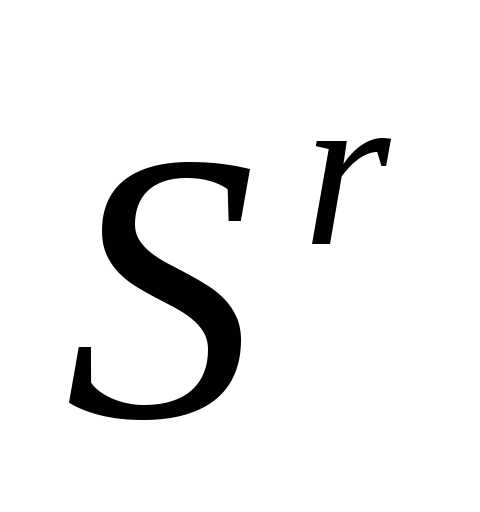 регулярен, то симплекс
регулярен, то симплекс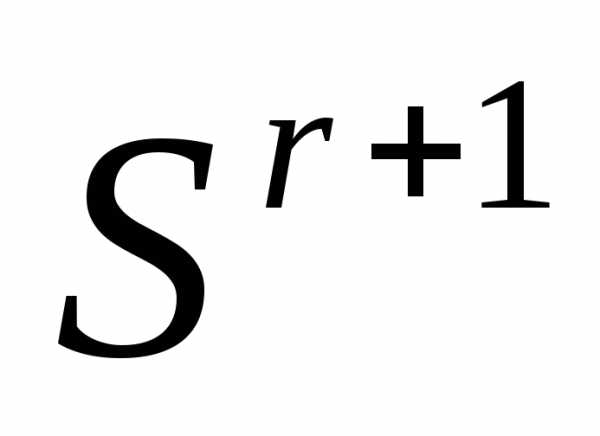 , полученный в результате редукции вершин симплекса
, полученный в результате редукции вершин симплекса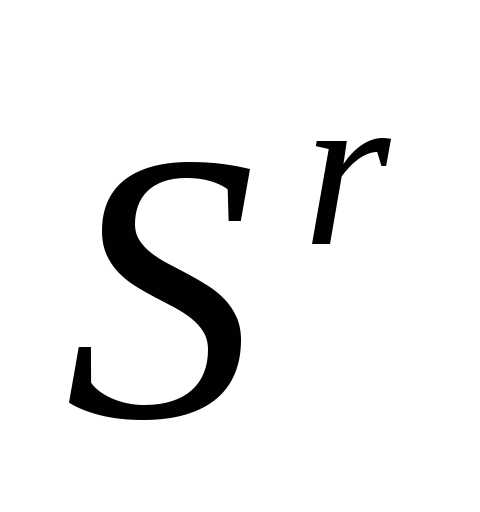 к одной из его вершин, также регулярен.
к одной из его вершин, также регулярен.
Схема простейшего варианта симплекс-метода.
Суть симплекс-метода раскрывает его простейший вариант.
Задаем начальную точку
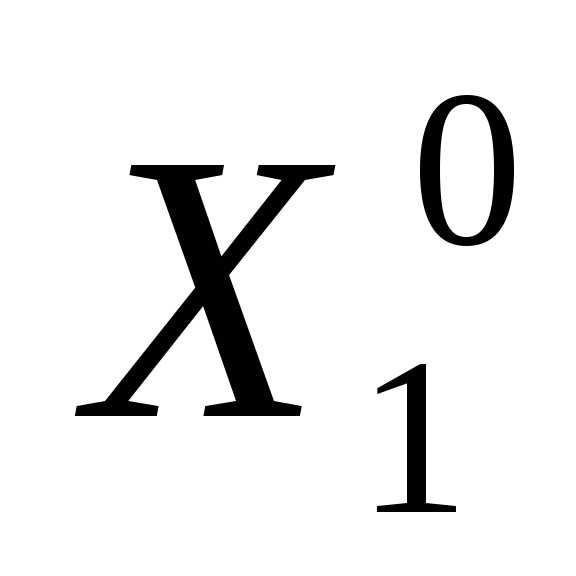 , длину ребра симплекса
, длину ребра симплекса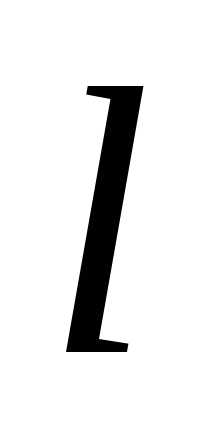 и полагаем
и полагаем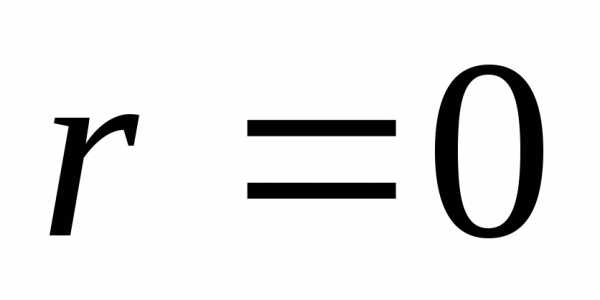 .
.По формулам (2), (3) находим координаты всех вершин симплекса
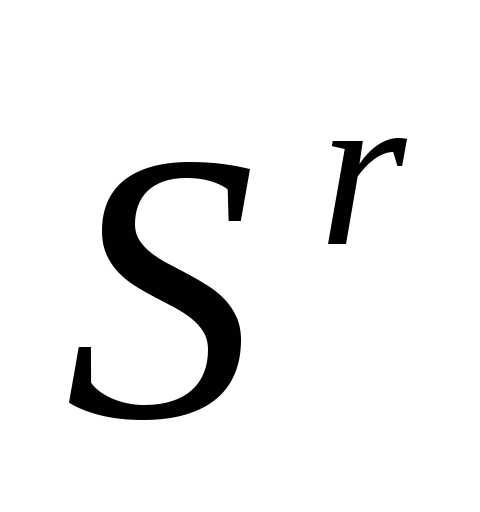 .
.Вычисляем значения минимизируемой функции во всех вершинах симплекса
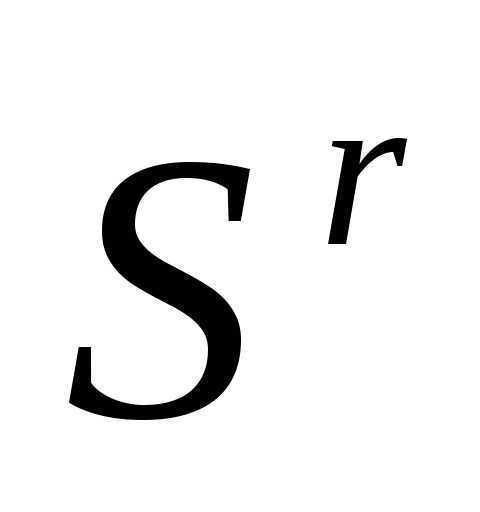 и находим максимальное из этих значений:
и находим максимальное из этих значений:
.
По формулам (5), (6) отражаем вершину
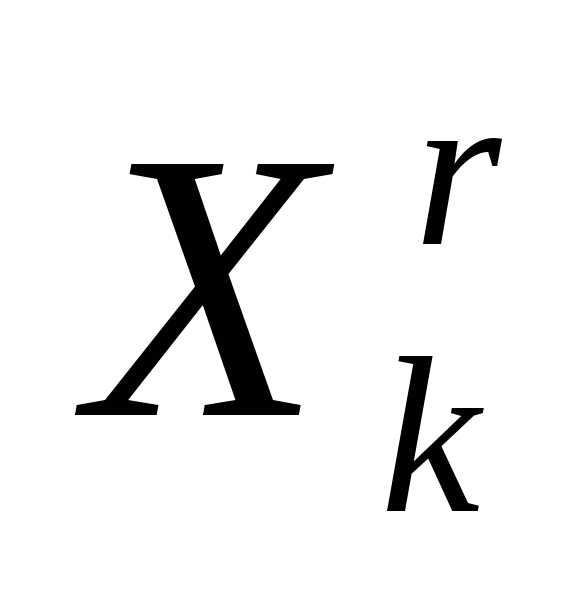 симплекса
симплекса 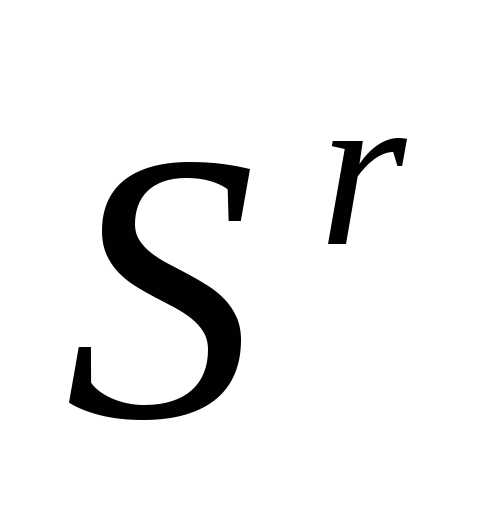 относительно центра тяжести остальных вершин симплекса – получаем новый симплекс . Вычисляем значение
относительно центра тяжести остальных вершин симплекса – получаем новый симплекс . Вычисляем значение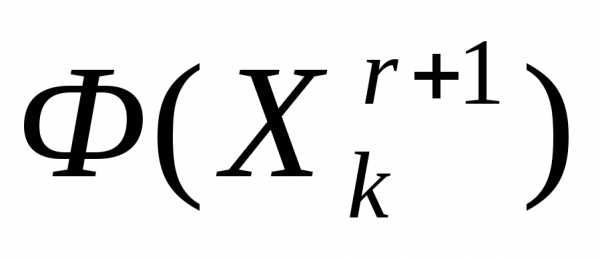 минимизируемой функции в вершине
минимизируемой функции в вершине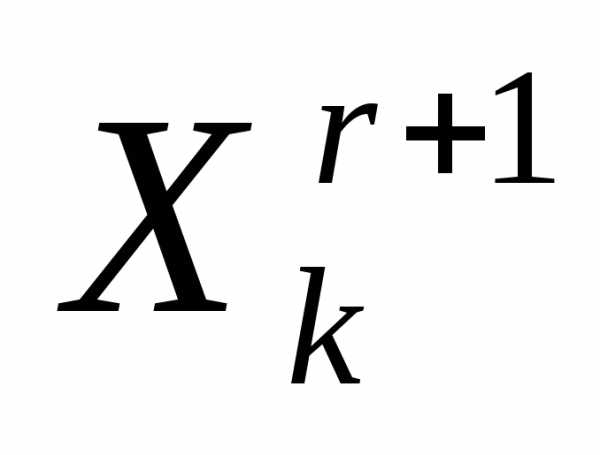 симплекса
симплекса 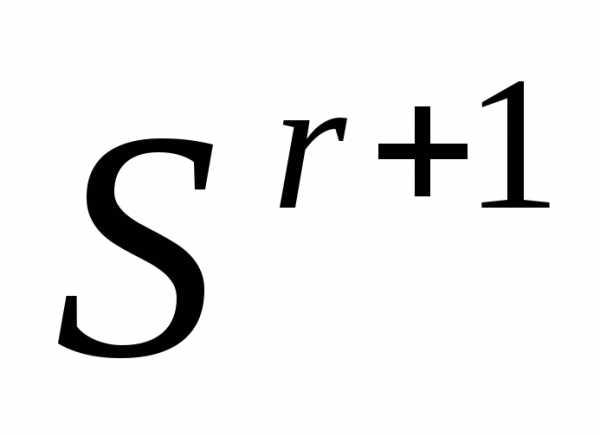 .
.Если условие окончания итераций (см. ниже) выполнено, то в качестве приближенного значения точки минимума функции
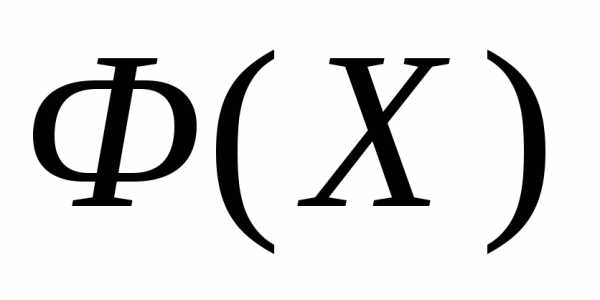 принимаем ту вершину симплекса
принимаем ту вершину симплекса 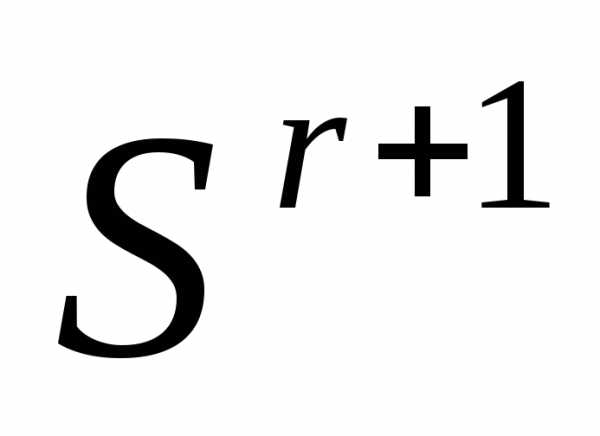 , в которой
, в которой 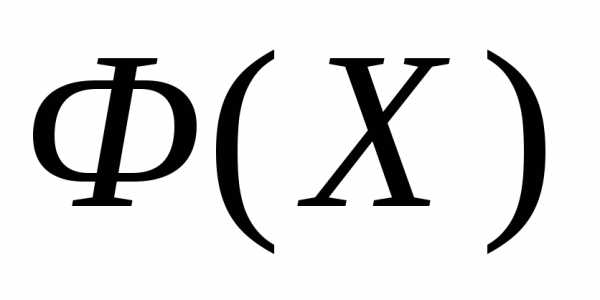 имеет минимальное значение, и заканчиваем вычисления. Иначеполагаем r=r+1 и переходим к п. 4●
имеет минимальное значение, и заканчиваем вычисления. Иначеполагаем r=r+1 и переходим к п. 4●
Поскольку размер симплекса в простейшем варианте симплекс-методе фиксирован, в качестве условия окончания итераций в данном случае можно использовать условие
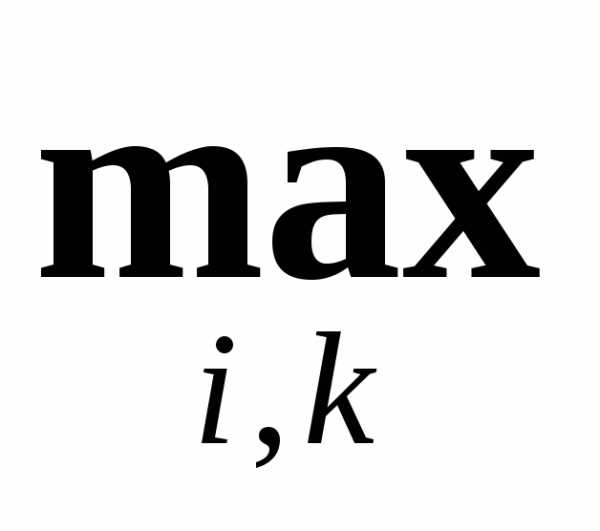 , ,
, ,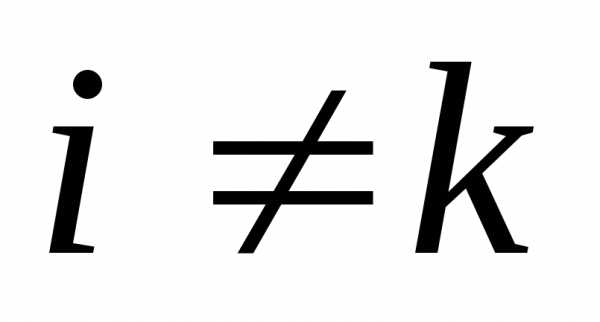 . (8)
. (8)
где 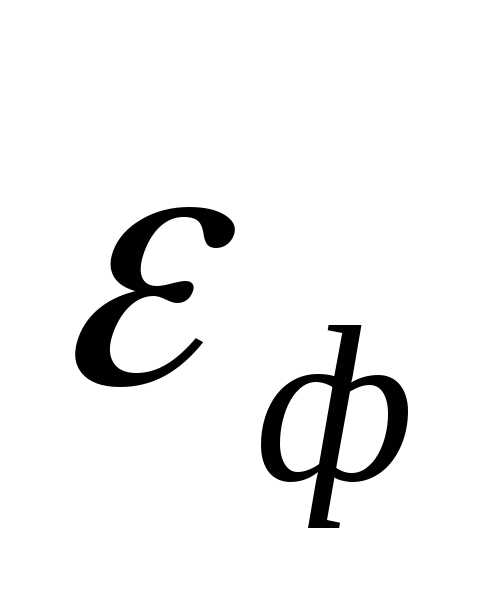 - требуемая точность решения поФ. Отметим, что выражение в левой части неравенства (8) есть максимальная разность значений функции
- требуемая точность решения поФ. Отметим, что выражение в левой части неравенства (8) есть максимальная разность значений функции 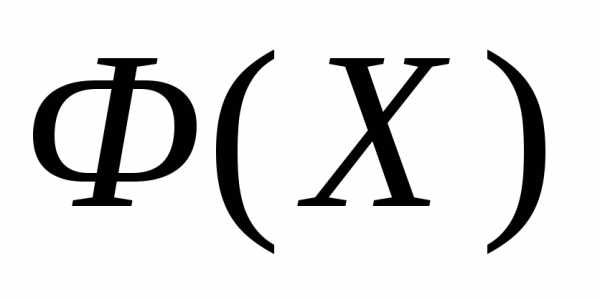 в двух вершинах симплекса
в двух вершинах симплекса 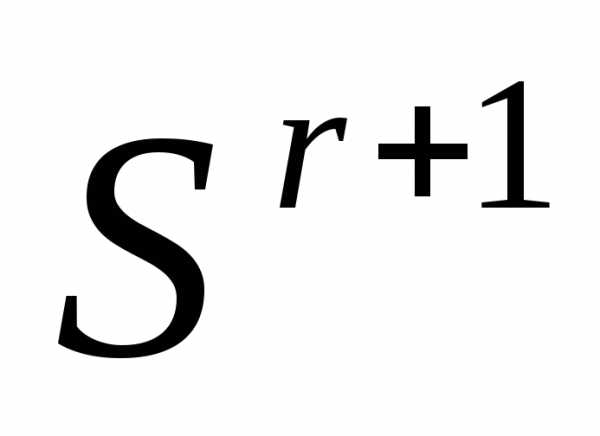 .
.
Рассмотренный вариант симплекс-метода иллюстрирует рисунок 4.
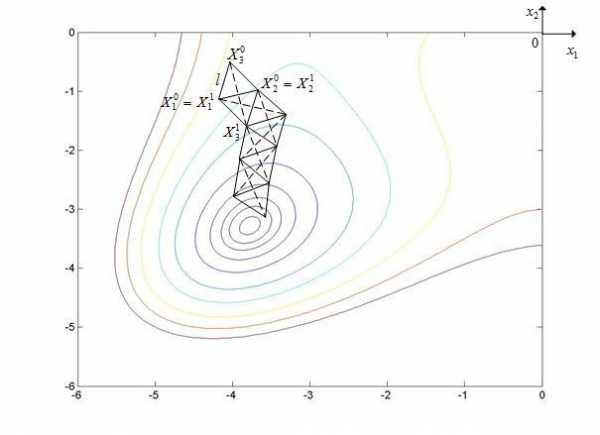
Рисунок 4 - Траектория поиска минимума функции Химмельблау простейшим симплекс-методом
Модифицированный симплекс-метод.
Рассмотренный простейший симплекс-метод склонен к зацикливанию и медленно сходится, если длина ребра симплекса l выбрана малой (выбор же большой длины ребра симплекса обеспечивает высокую скорость сходимости, но дает малую точность решения). Поэтому в вычислительной практике используются различные модификации простейшего метода, направленные на преодоление его указанных недостатков.
Основной идей модификаций простейшего симплекс-метода является изменение по некоторому правилу размера симплекса в процессе поиска. При этом наряду с условием (8) в качестве условия окончания итераций можно использовать условие
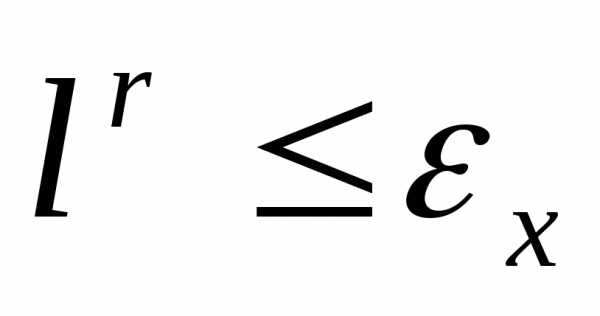 (9)
(9)
где 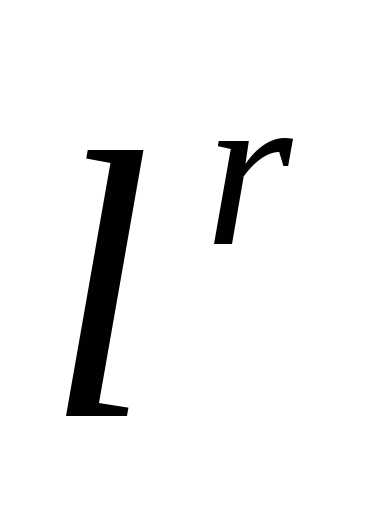 - текущая длина ребра симплекса,
- текущая длина ребра симплекса, 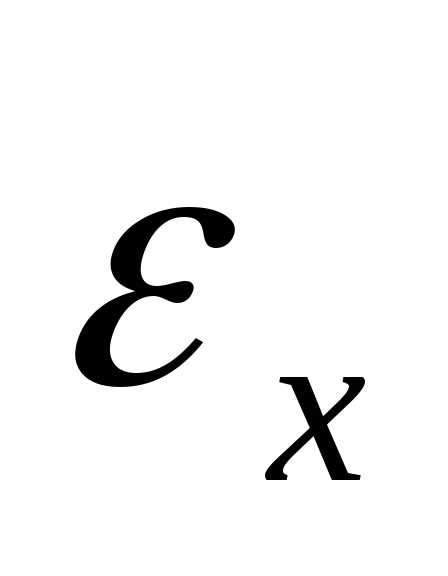 - требуемая точность решения по X.
- требуемая точность решения по X.
Обычно размер симплекса изменяется при выполнении следующих условий:
при «накрытии» симплексом дна оврага или точки минимума;
при циклическом движении.
«Накрытие» симплексом дна оврага или точки минимума. Пусть 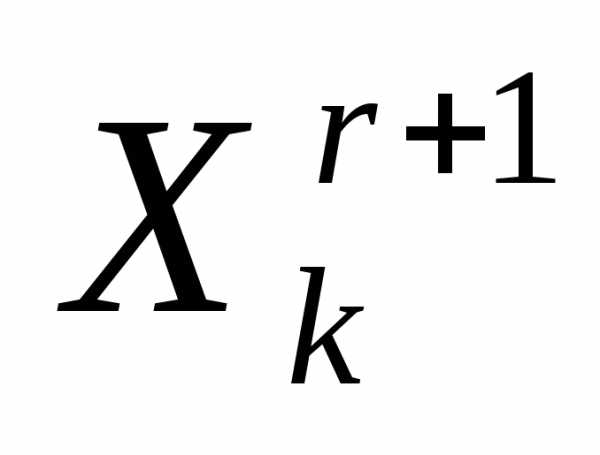 - вершина симплекса
- вершина симплекса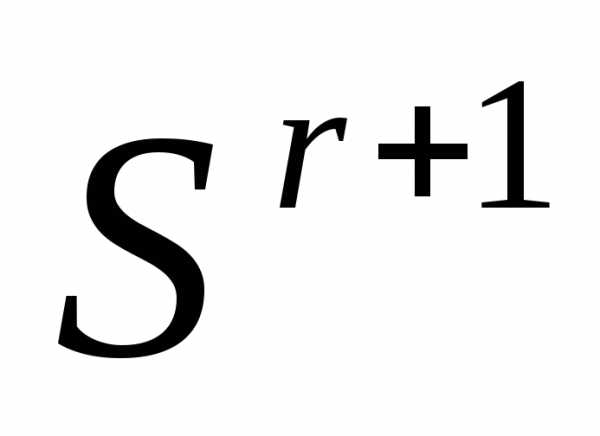 , которая получилась наr-ой итерации в результате отражения вершины
, которая получилась наr-ой итерации в результате отражения вершины 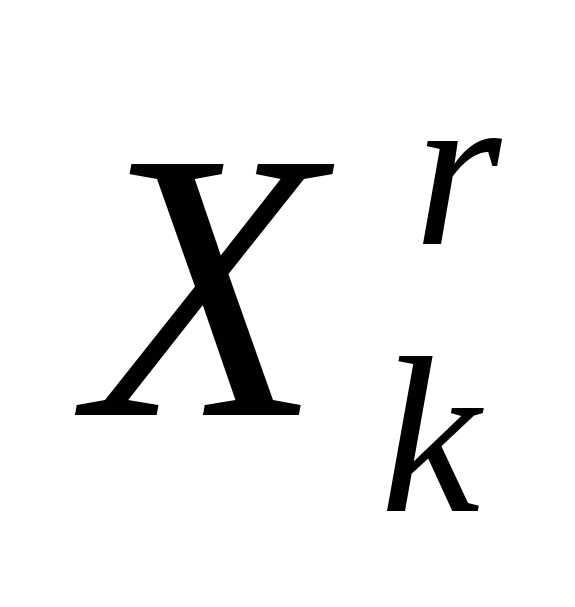 симплекса
симплекса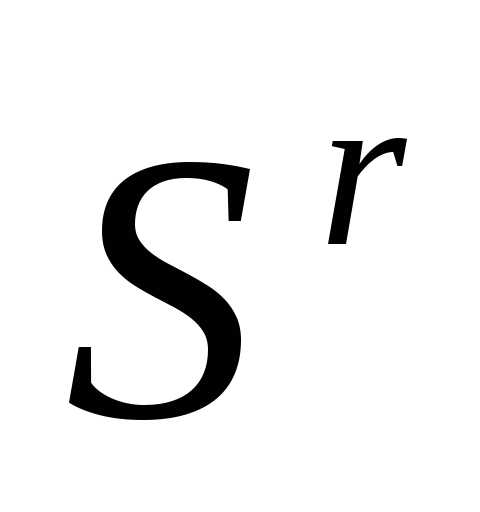 .
.
Ситуация 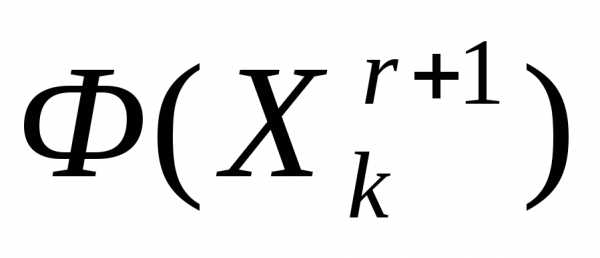 >
>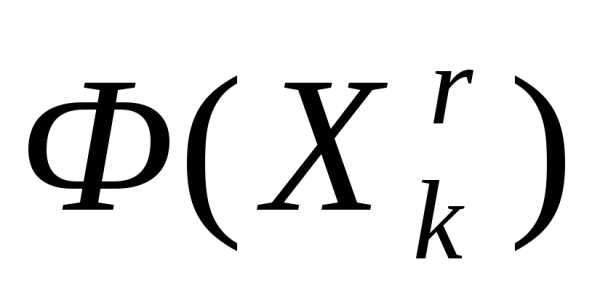 интерпретируется как«накрытие» этим симплексом дна оврага или точки минимума и рассмотренный простейший симплекс-метод модифицируется следующим образом (рисунок 5).
интерпретируется как«накрытие» этим симплексом дна оврага или точки минимума и рассмотренный простейший симплекс-метод модифицируется следующим образом (рисунок 5).
Полагаем . Еслиk=n+2, то полагаем k=1.
Выполняем отражение
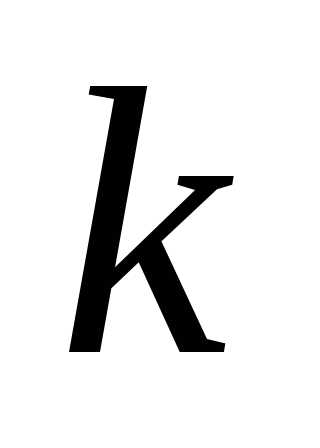 -ой вершины симплекса
-ой вершины симплекса 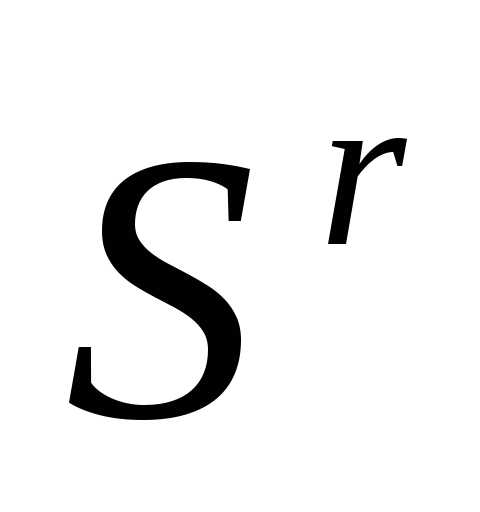 .
.Если
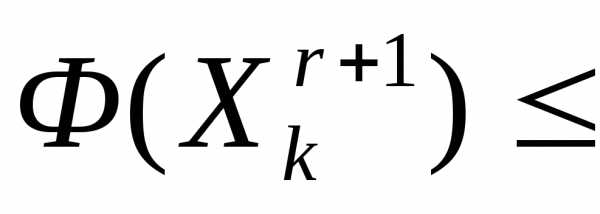
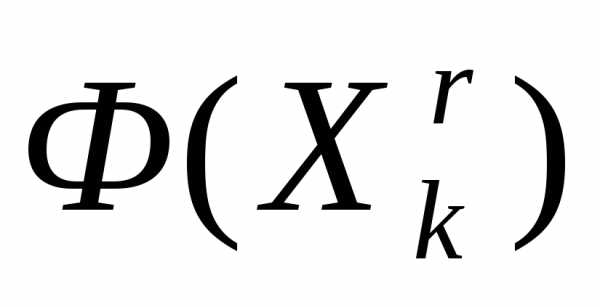 , то продолжаем итерации по схеме простейшего симплекс-метода.
, то продолжаем итерации по схеме простейшего симплекс-метода.Если
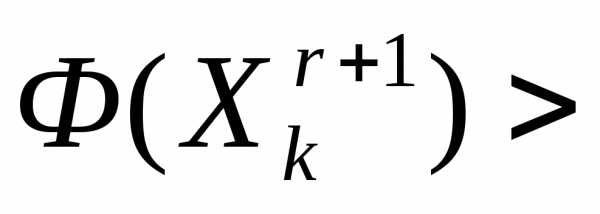
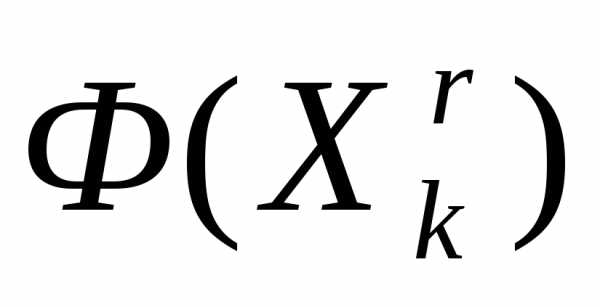 и не все вершины перебраны, то переходим к п. 1.
и не все вершины перебраны, то переходим к п. 1.Если
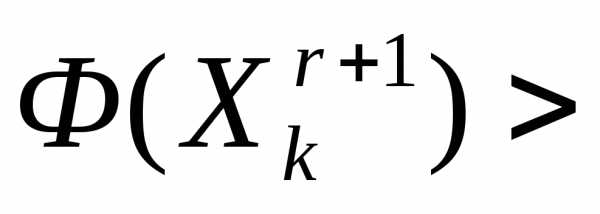
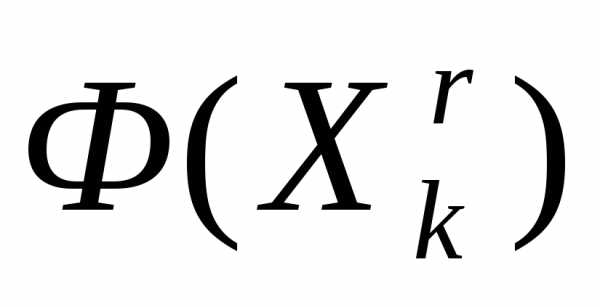 и все вершины перебраны, то выполняем редукцию симплекса к вершине с минимальным значением функции
и все вершины перебраны, то выполняем редукцию симплекса к вершине с минимальным значением функции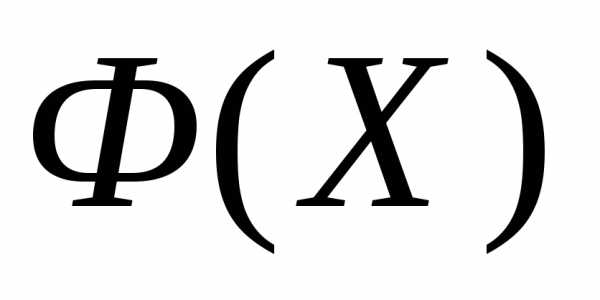 .
.
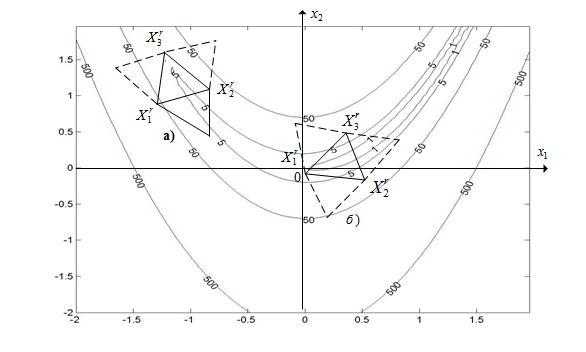
Рисунок 5 – К схеме модифицированного симплекс-метода. Ситуация «накрытие» симплексом дна оврага или точки минимума функции 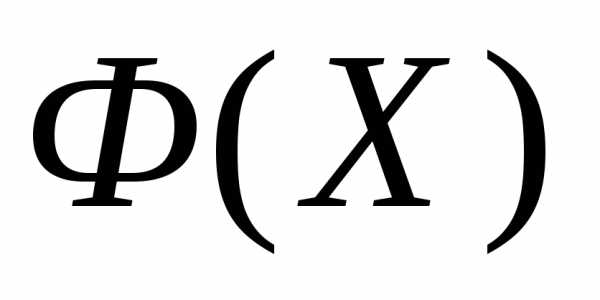
На рисунке 5 в ситуации (а) отражение вершин 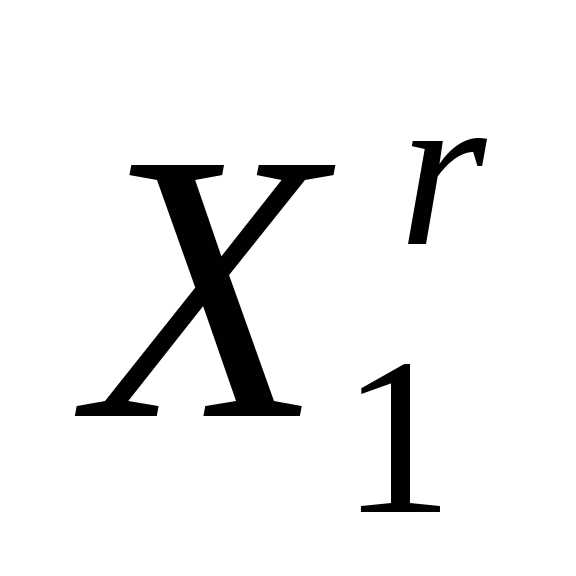 ,
,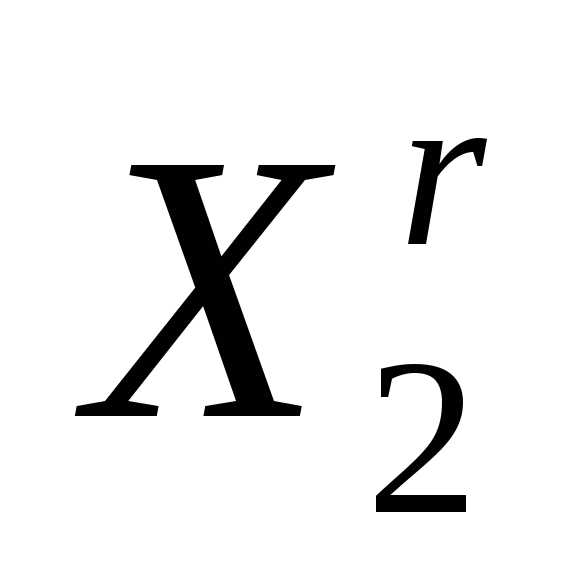 приводит к увеличению значений функции
приводит к увеличению значений функции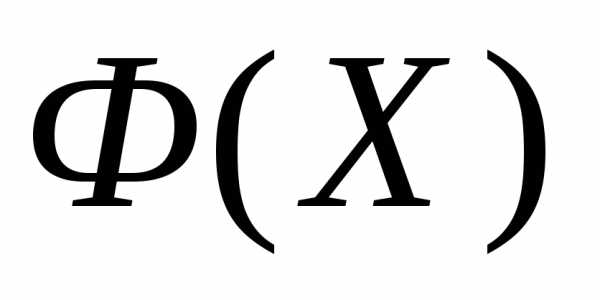 , а отражение вершины
, а отражение вершины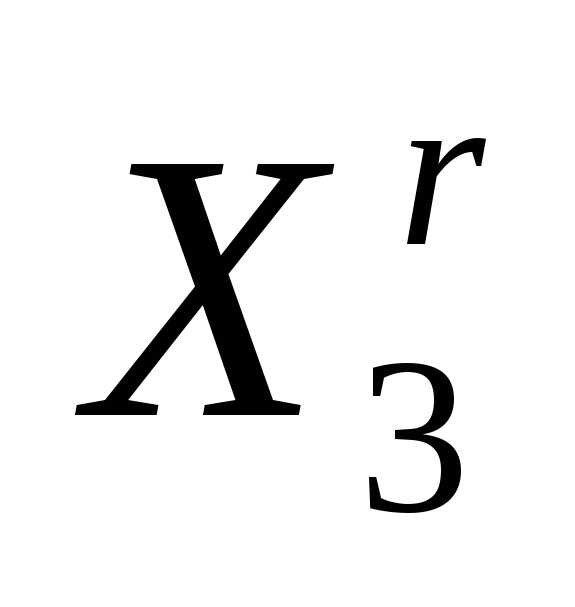 - к уменьшению значения
- к уменьшению значения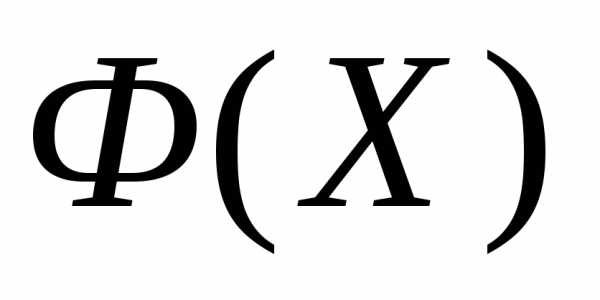 . Таким образом,
. Таким образом,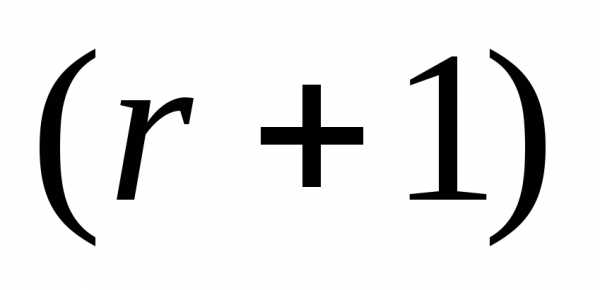 -я итерация выполняется по схеме простейшего симплекс-метода. В ситуации (б) отражение всех трех вершин текущего симплекса приводит к увеличению значений функции
-я итерация выполняется по схеме простейшего симплекс-метода. В ситуации (б) отражение всех трех вершин текущего симплекса приводит к увеличению значений функции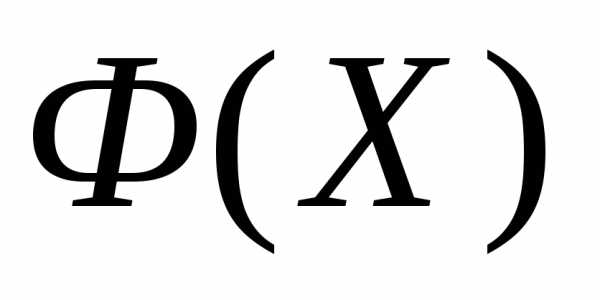 . Поэтому перед
. Поэтому перед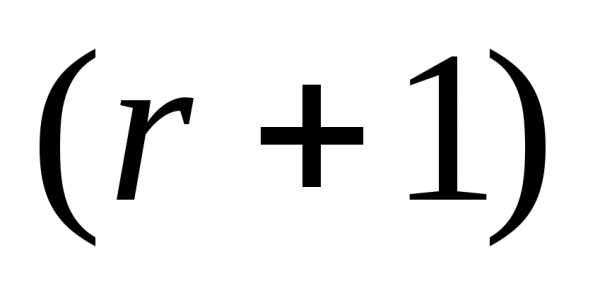 -ой итерацией должна быть выполнена редукция текущего симплекса к вершине
-ой итерацией должна быть выполнена редукция текущего симплекса к вершине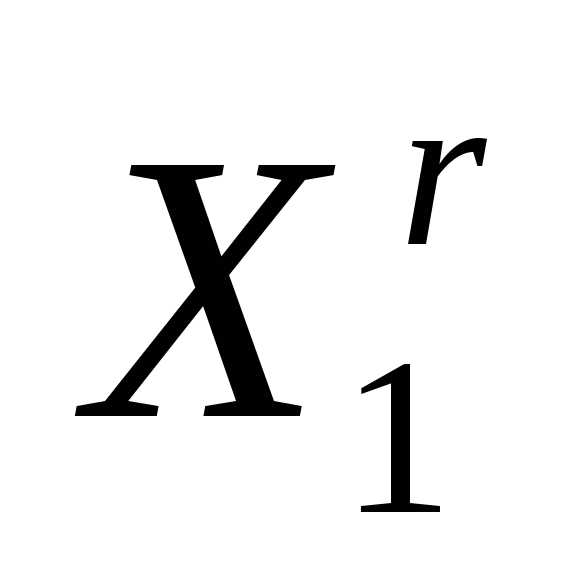 и после этого итерации продолжены по схеме простейшего симплекс-метода.
и после этого итерации продолжены по схеме простейшего симплекс-метода.
Циклическое движение. Ситуация, когда некоторая вершина симплекса не исключается из симплекса на протяжении m итераций, интерпретируется как «зацикливание» алгоритма. Рассмотренный простейший симплекс-метод модифицируется в этом случае следующим образом.
Находим вершину текущего симплекса
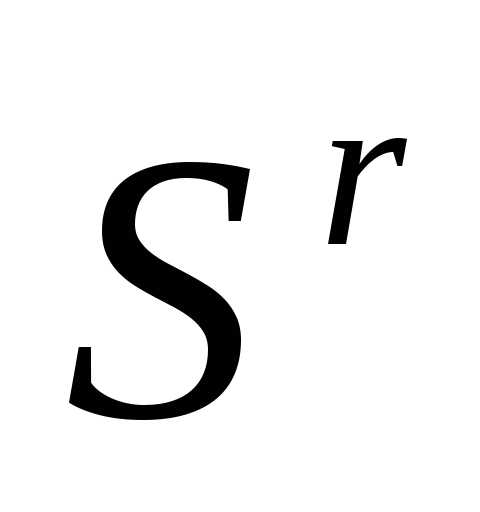 , в которой функция
, в которой функция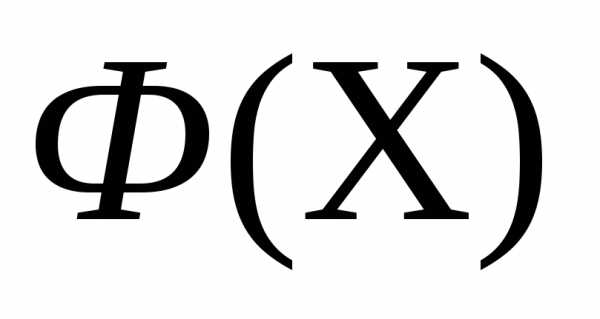 принимает наименьшее значение
принимает наименьшее значение
.
По формуле (7) выполняем редукцию симплекса
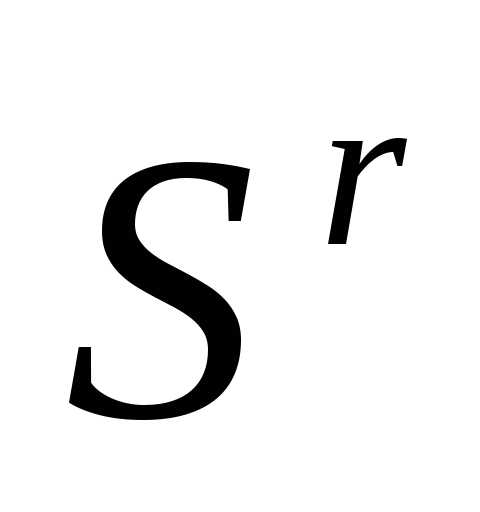 к вершине
к вершине 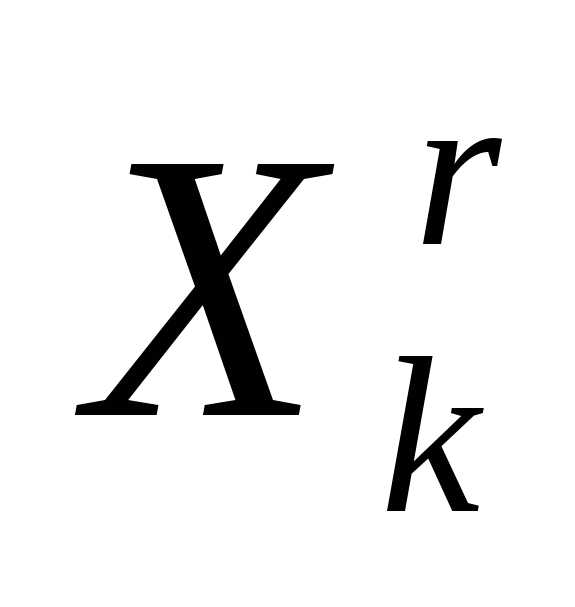 - получаем симплекс
- получаем симплекс 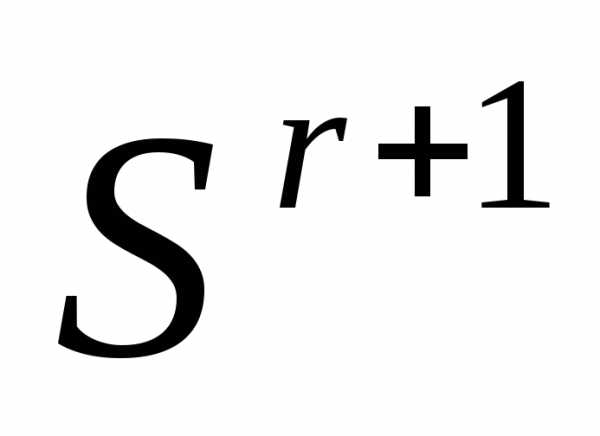 .
.Продолжаем итерации по схеме простейшего симплекс-метода.
Здесь количество итераций m рекомендуется находить из условия  , где
, где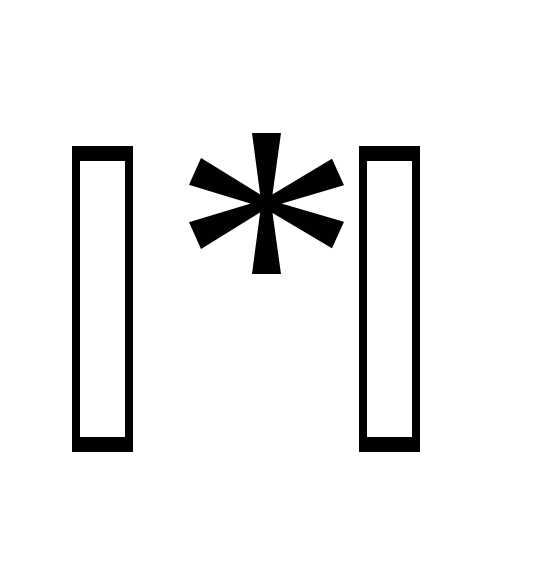 - символ ближайшего целого большего. Например, при
- символ ближайшего целого большего. Например, при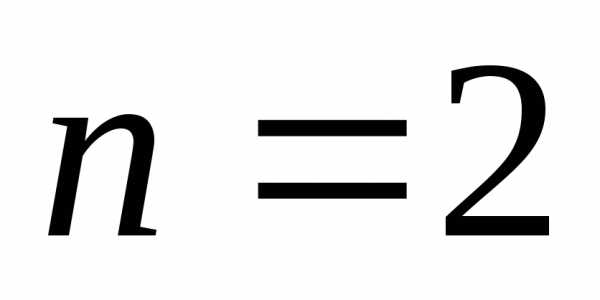 имеем:
имеем:
.
Входные термины:
детерминированные методы оптимизации;
методы локальной оптимизации;
методы безусловной оптимизации;
многомерный критерий оптимальности;
прямые методы оптимизации;
регулярный симплекс.
Выходные термины:
отражение симплекса;
редукция симплекса;
сжатие многогранника;
растяжение симплекса;
восстановление симплекса;
метод деформируемого многогранника, метод Нелдера-Мида.
§6. Метод Нелдера-Мида (метод деформируемого многогранника).
Рассмотрим следующую задачу многомерной локальной безусловной оптимизации: найти минимум критерия оптимальности Φ(X), определенного в n-мерном евклидовом пространстве 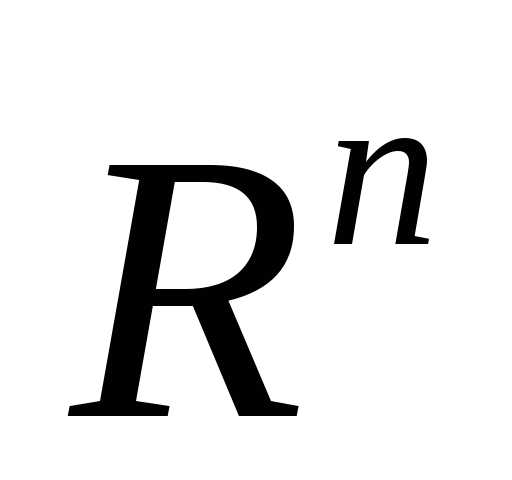 ,
,
 . (1)
. (1)
В случае если функция Φ(X) является овражной, эффективность симплекс-метода при решении задачи (1) значительно снижается в силу того, что регулярный симплекс нельзя «вытянуть» вдоль оврага. Метод Нелдера-Мида является развитием симплекс-метода и использует в процессе поиска изменение не только размеров, но и формы текущего симплекса (не обязательно регулярного).
Метод использует следующие операции над симплексами: отражение; редукция; сжатие; растяжение.
Отражение вершины симплекса относительно центра тяжести остальных вершин (см. параграф 5, рисунок 1). В результате отражения вершины 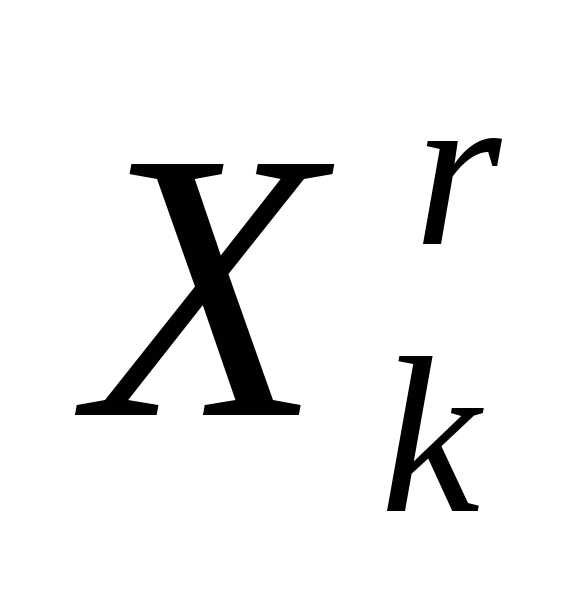 симплексаполучаем новый симплекс
симплексаполучаем новый симплекс
, (2)
где
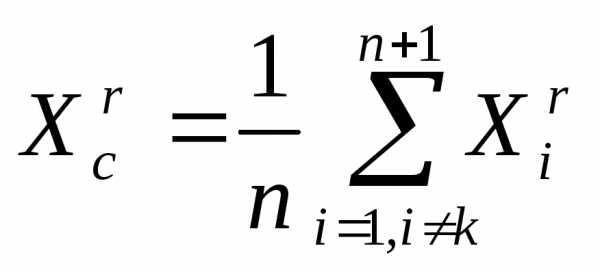 - (3)
- (3)
вектор координат центра тяжести остальных вершин симплекса 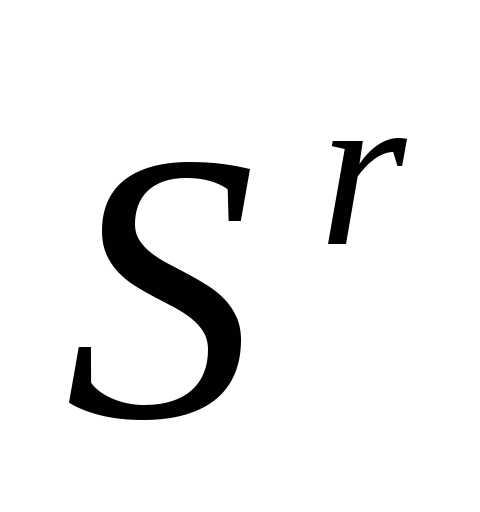 (за исключением отраженной вершины
(за исключением отраженной вершины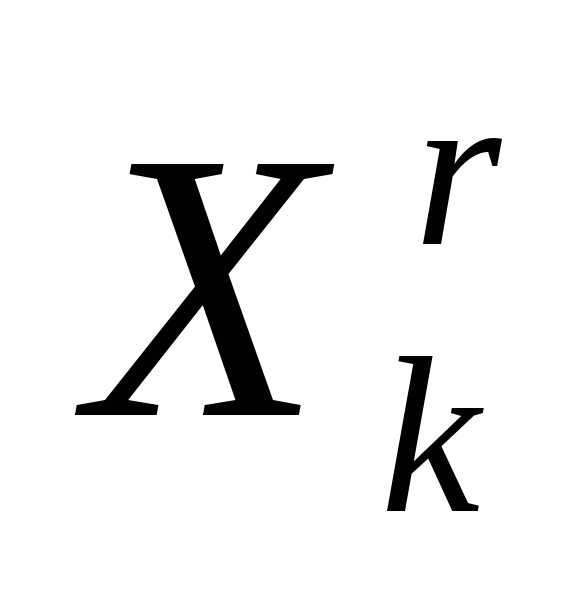 ). Если симплекс
). Если симплекс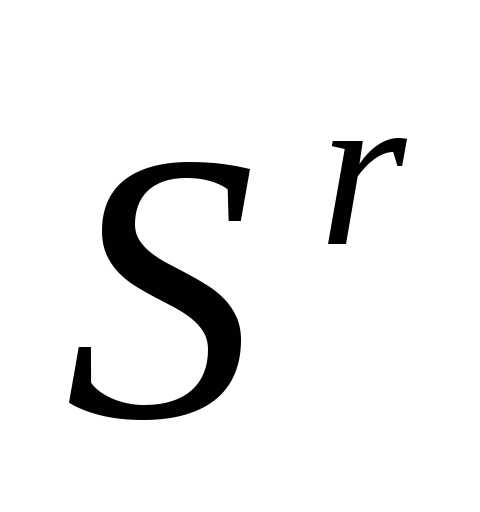 регулярный, то симплекс
регулярный, то симплекс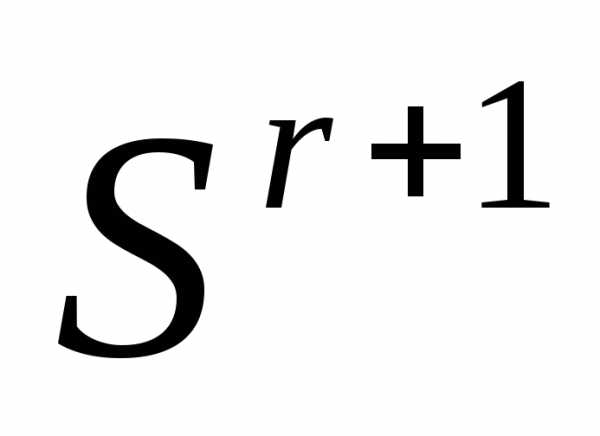 - также регулярный.
- также регулярный.
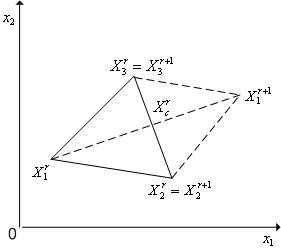
Рисунок 1 - Отражение вершины 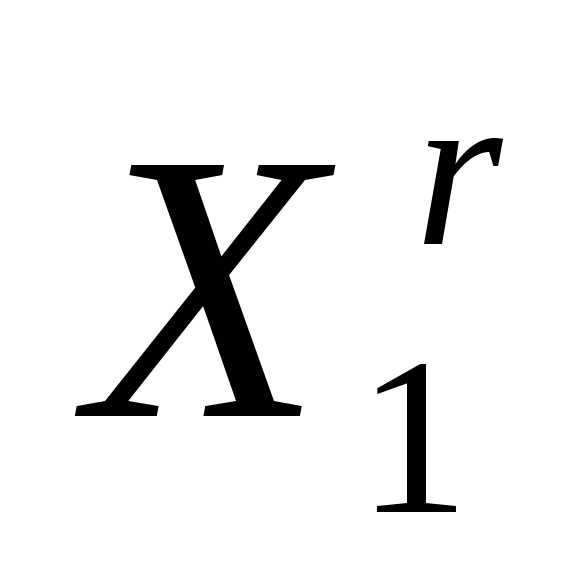 симплекса
симплекса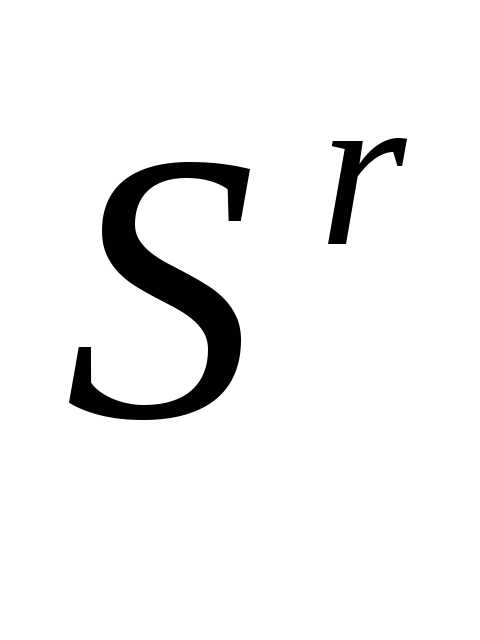 в пространстве
в пространстве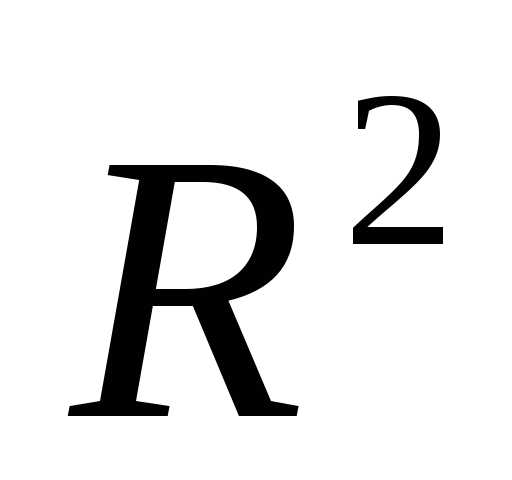 относительно центра тяжести
относительно центра тяжести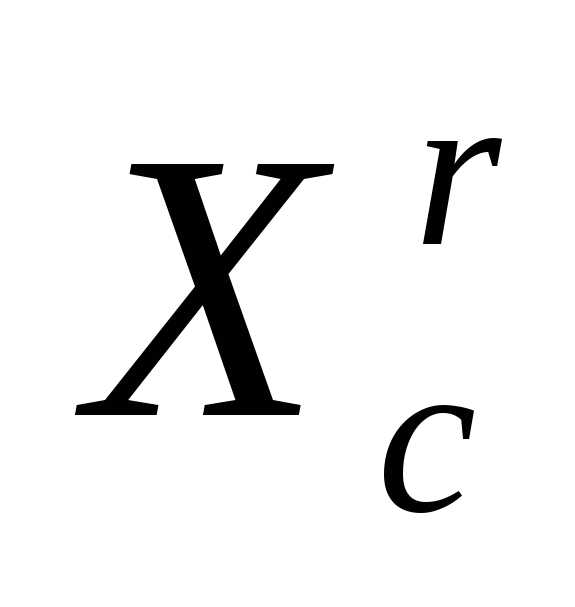 его остальных вершин
его остальных вершин
Редукции симплекса (см. параграф 5, рисунок 2) - уменьшение длин всех ребер симплекса в одно и то же количество раз. В результате редукции вершин симплекса к вершине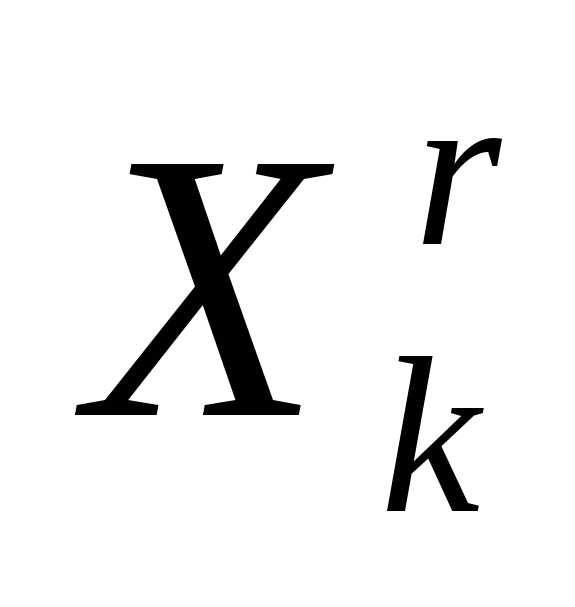 получаем новый симплекс
получаем новый симплекс
, (4)
где - коэффициент редукции. Если симплекс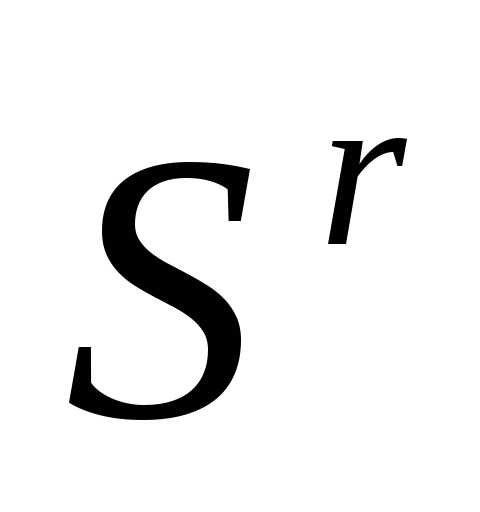 регулярный, то симплекс
регулярный, то симплекс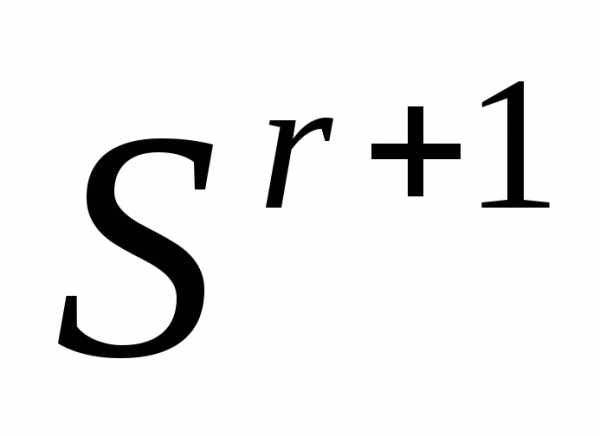 - также регулярный.
- также регулярный.
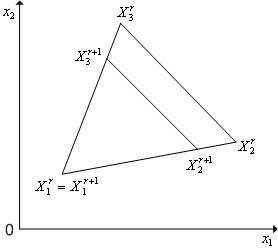
Рисунок 2 - Редукция вершин симплекса 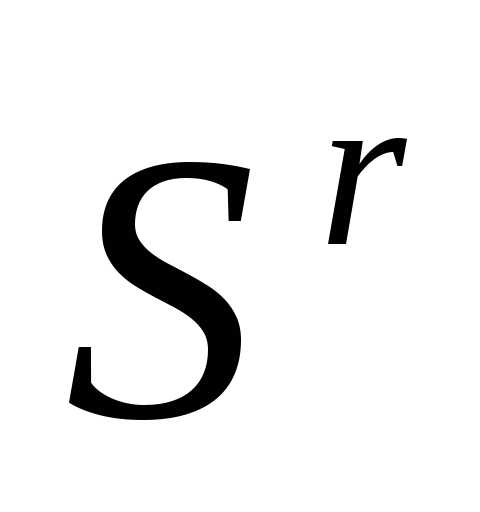 в пространстве
в пространстве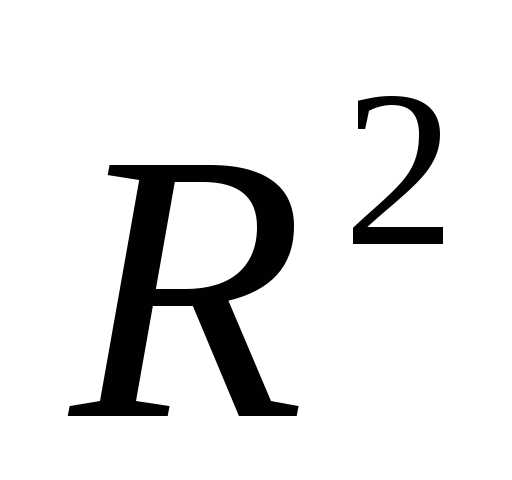 к вершине
к вершине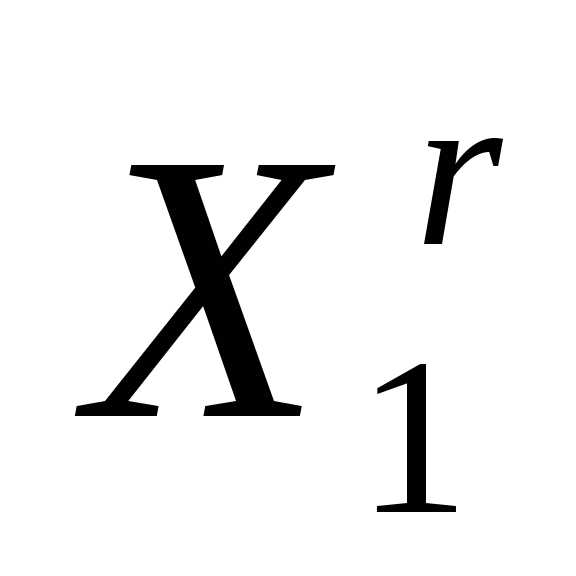
Сжатие симплекса (рисунок 3). В результате сжатия симплекса в направлении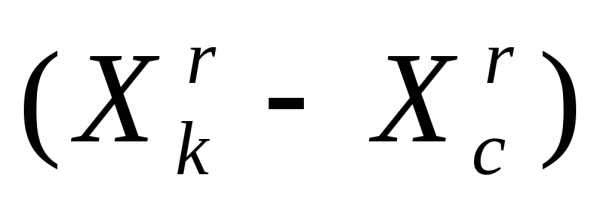 получаем новый симплекс
получаем новый симплекс
(5)
где - коэффициент сжатия,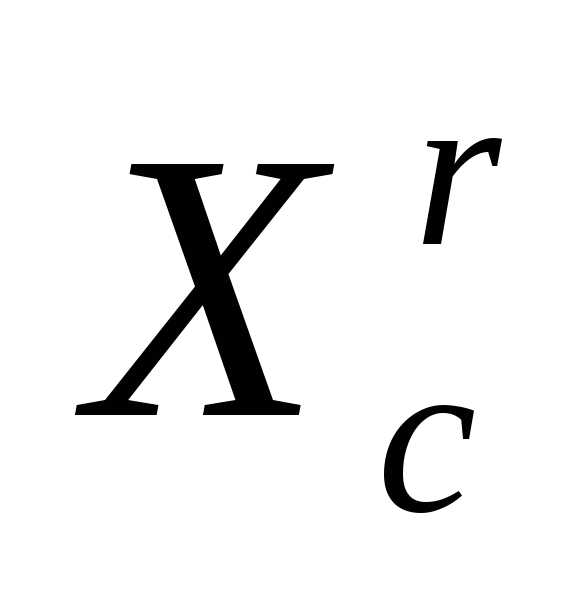 - вектор координат центра тяжести остальных вершин симплекса
- вектор координат центра тяжести остальных вершин симплекса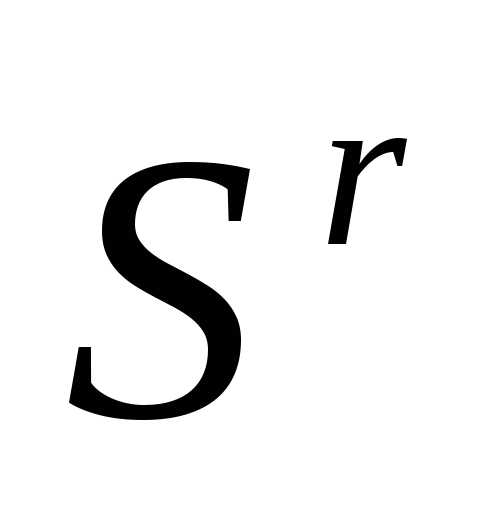 (за исключением вершины
(за исключением вершины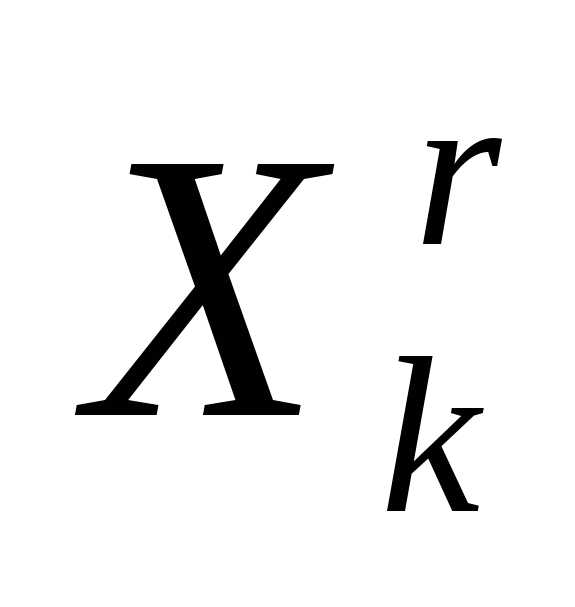 ) - см. формулу (3). Даже если симплекс
) - см. формулу (3). Даже если симплекс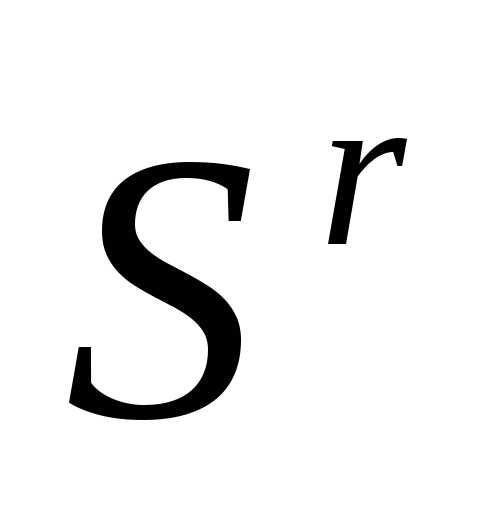 является регулярным, симплекс
является регулярным, симплекс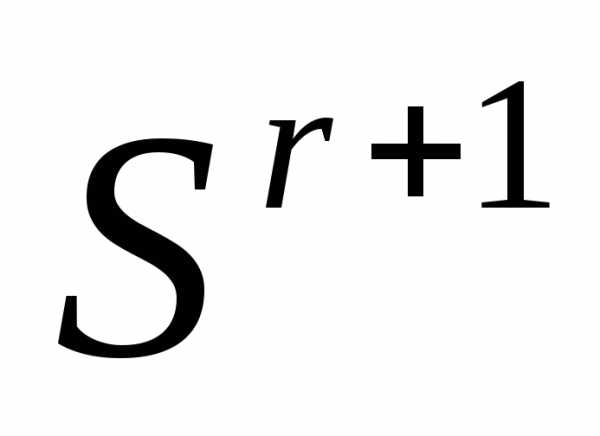 оказывается нерегулярным.
оказывается нерегулярным.
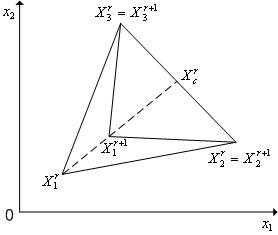
Рисунок 3 - Сжатие симплекса 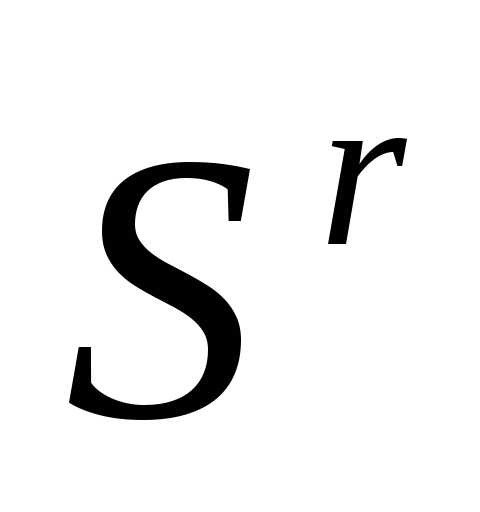 в пространстве
в пространстве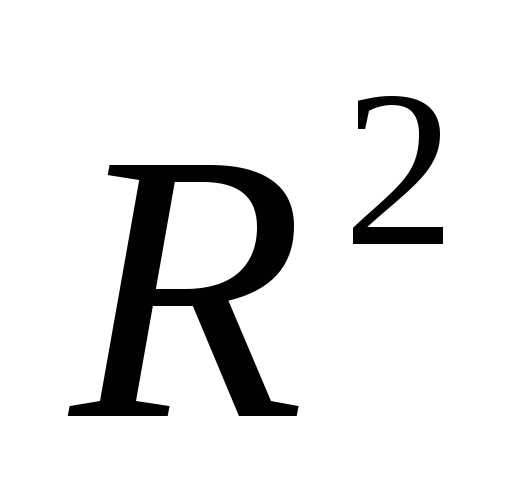 в направлении
в направлении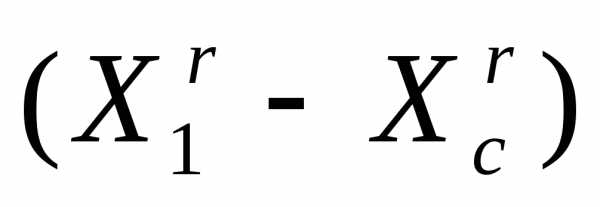
Растяжение симплекса (рисунок 4). В результате растяжения симплекса в направлении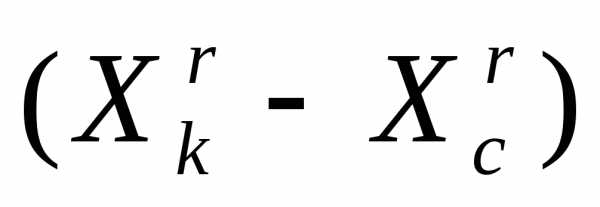 получаем новый симплекс
получаем новый симплекс
(6)
где - коэффициент растяжения,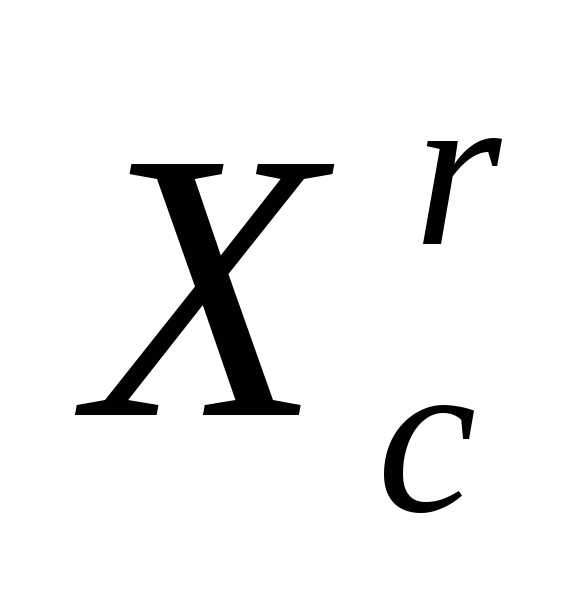 - как и ранее, вектор координат центра тяжести остальных вершин симплекса
- как и ранее, вектор координат центра тяжести остальных вершин симплекса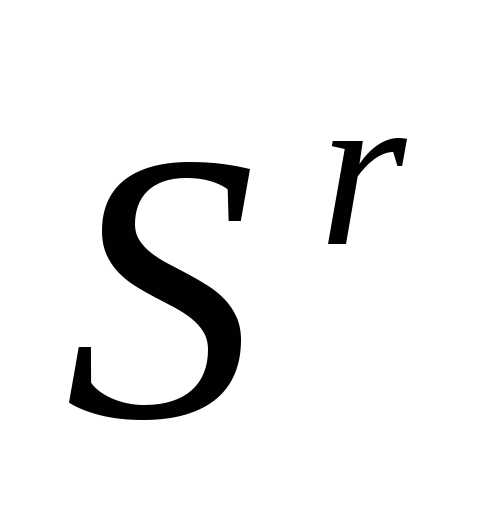 (за исключением вершины
(за исключением вершины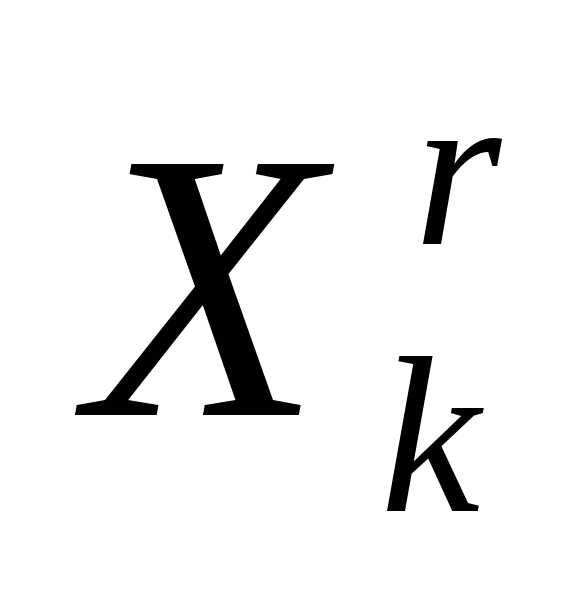 ) - см. формулу (3). Даже если симплекс
) - см. формулу (3). Даже если симплекс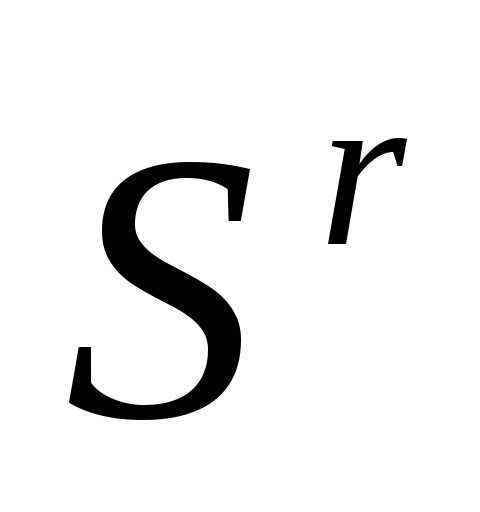 регулярен, симплекс
регулярен, симплекс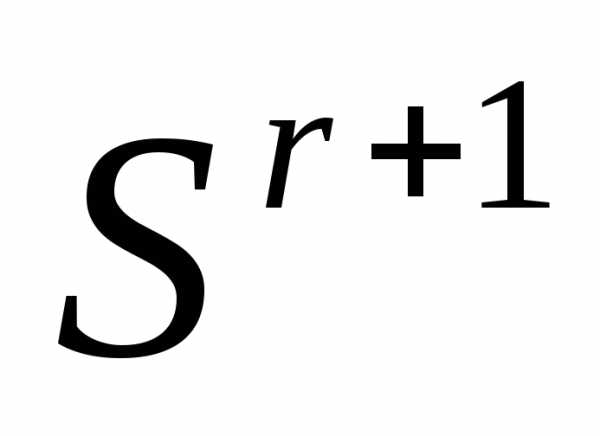 оказывается нерегулярным.
оказывается нерегулярным.
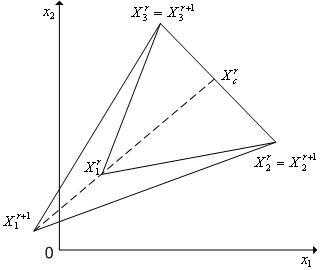
Рисунок 4 - Растяжение симплекса 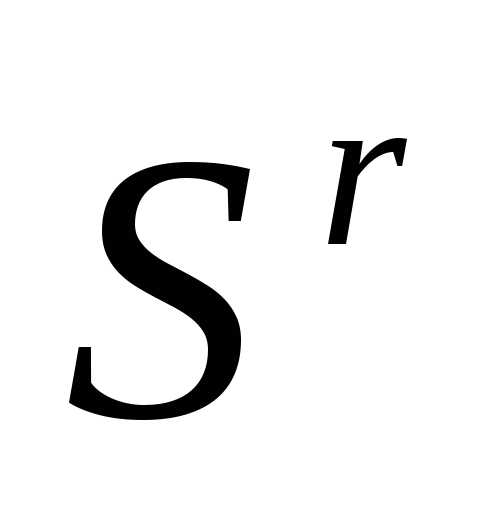 в пространстве
в пространстве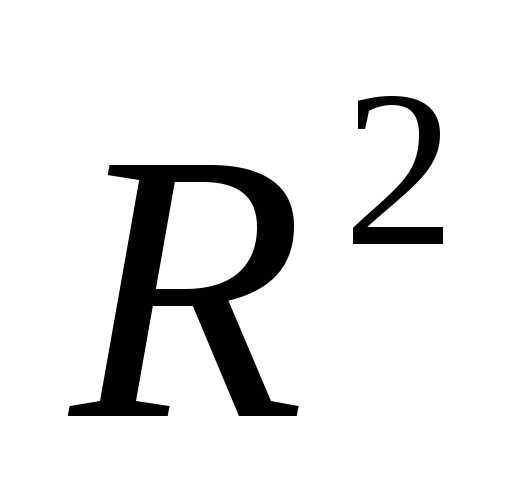 в направлении
в направлении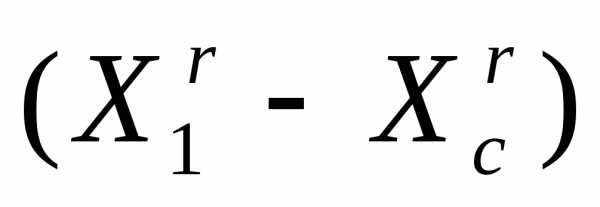
Упрощенная схема метода Нелдера-Мида
Задаем начальную точку
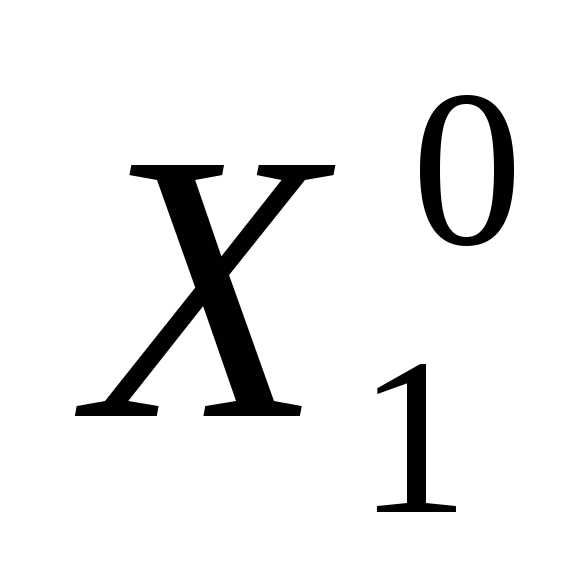 , длину ребра симплекса
, длину ребра симплекса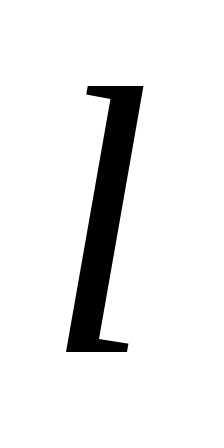 и полагаем
и полагаем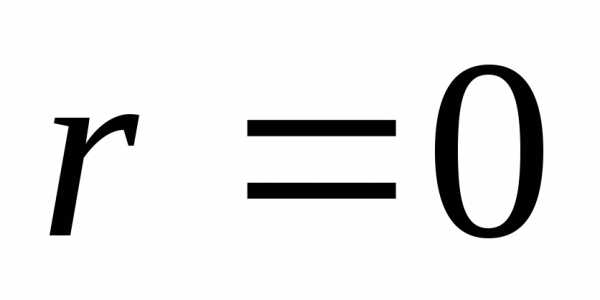 . Находим координаты всех вершин регулярного симплекса
. Находим координаты всех вершин регулярного симплекса 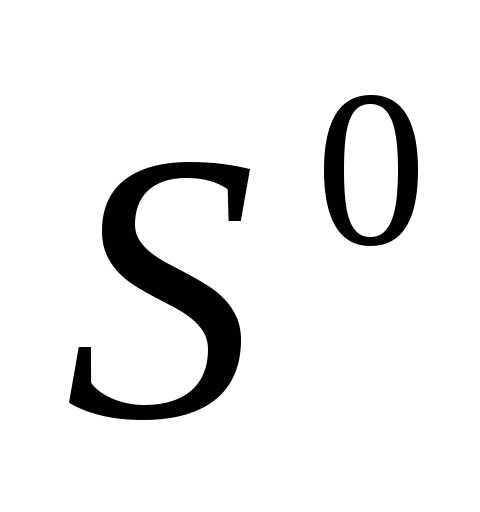 с длиной ребра l.
с длиной ребра l. Вычисляем значения функции
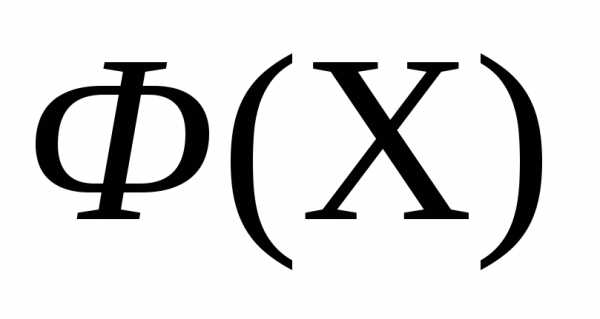 во всех вершинах симплекса
во всех вершинах симплекса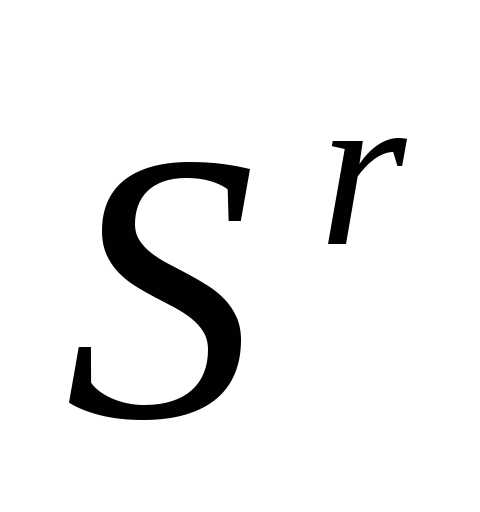 .
.Среди вершин симплекса
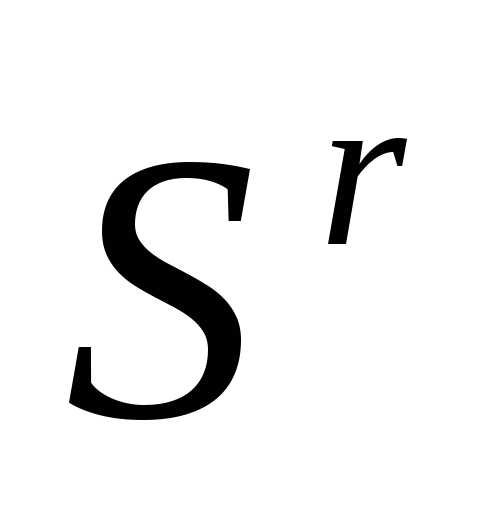 находим вершины
находим вершины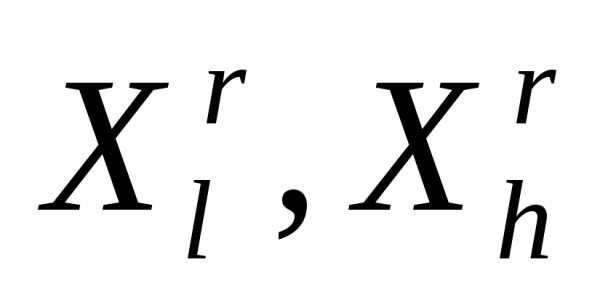 , в которых функция
, в которых функция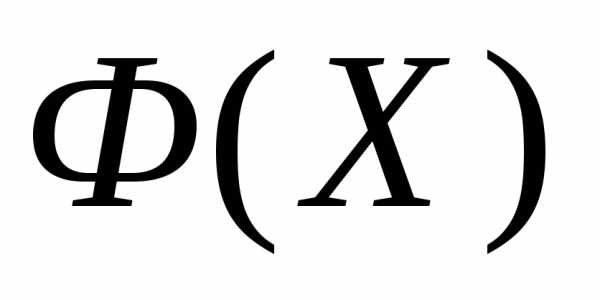 принимает, соответственно, наименьшее и наибольшее значения, а также находим значения функции
принимает, соответственно, наименьшее и наибольшее значения, а также находим значения функции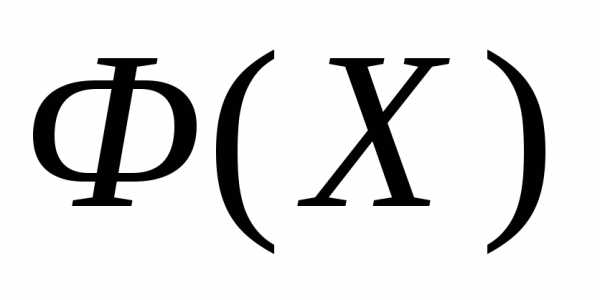 в этих точках:
в этих точках:
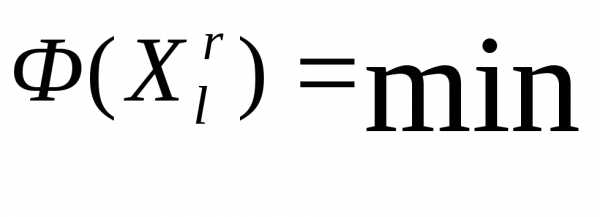 , ; (7)
, ; (7)
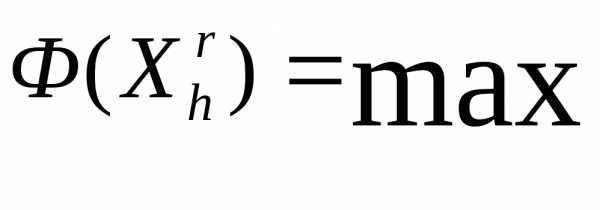 , ; (8)
, ; (8)
Отражение. Отражаем вершину
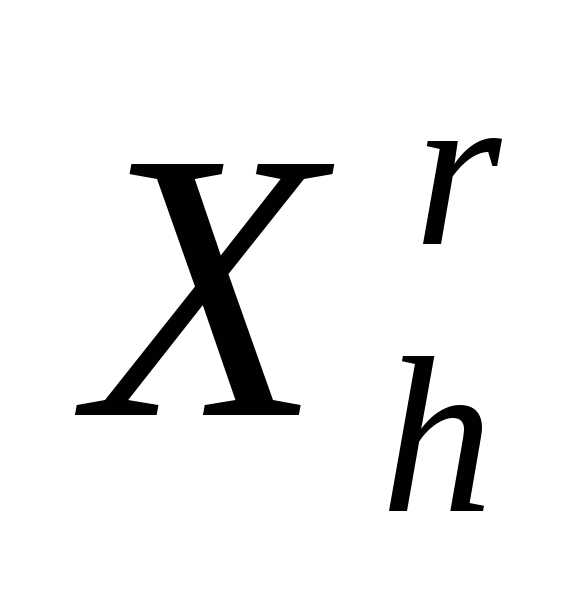 симплекса
симплекса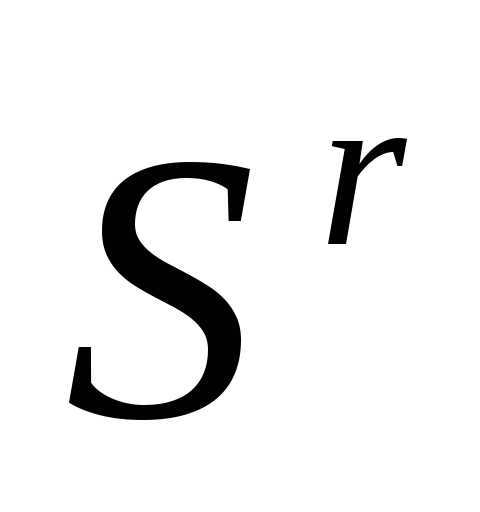 относительно центра тяжести остальных его вершин – получаем новый симплекс
относительно центра тяжести остальных его вершин – получаем новый симплекс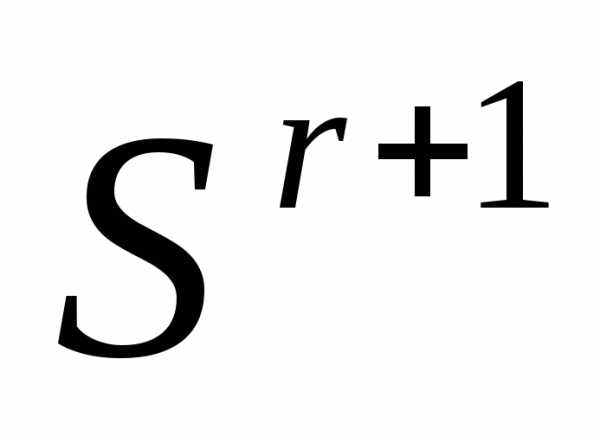 . Вычисляем значение
. Вычисляем значение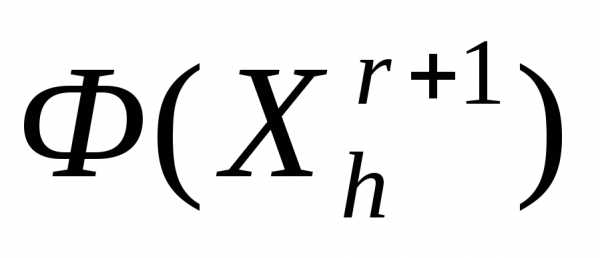 функции
функции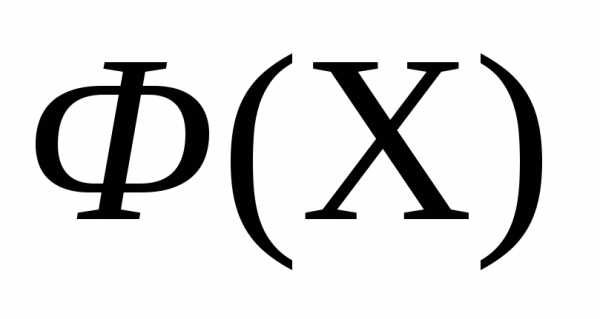 в вершине
в вершине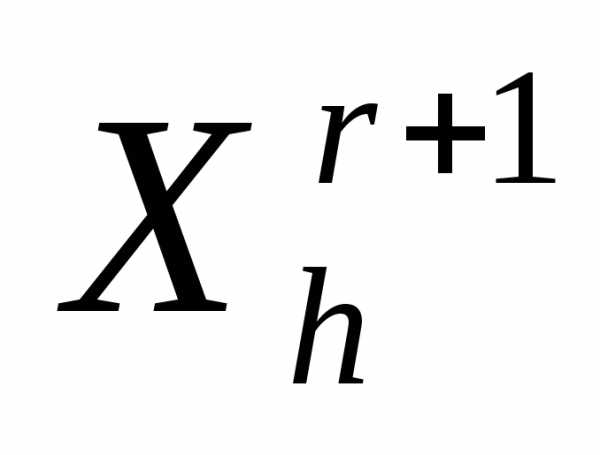 этого симплекса.
этого симплекса.Если условие окончания итераций (см. ниже) выполнено, то в качестве приближенного значения точки минимума функции
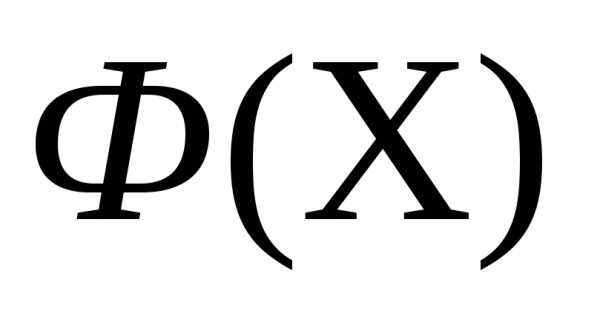 принимаем ту вершину симплекса
принимаем ту вершину симплекса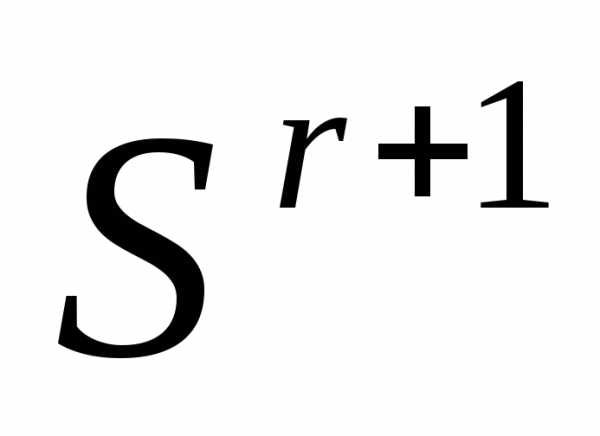 , в которой эта функция имеет минимальное значение, и заканчиваем вычисления.
, в которой эта функция имеет минимальное значение, и заканчиваем вычисления.Если и, то переходим к п. 7 (растяжению) – рисунок 5. Если, но, то переходим к п. 4 (отражению) – рисунок 6. Если, то переходим к п. 8 (сжатию) – рисунки 7, 8.
Растяжение (ситуация и). Выполняем растяжение симплекса
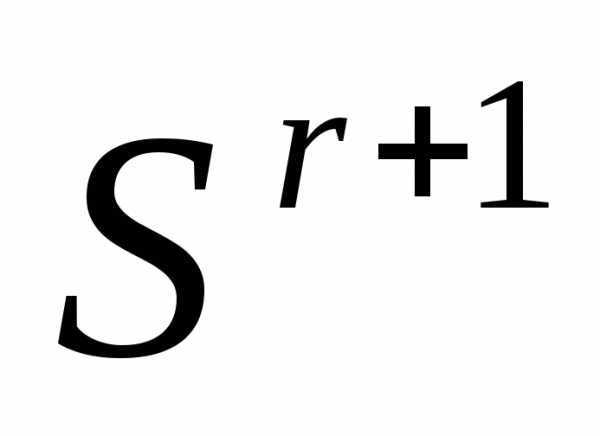 в направлении- получаем новый симплекс
в направлении- получаем новый симплекс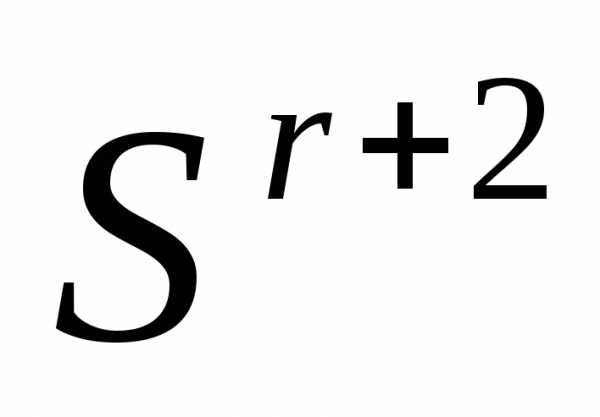 . Вычисляем значение функции
. Вычисляем значение функции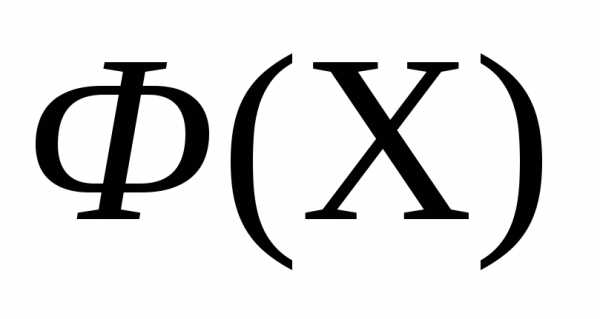 в вершине
в вершине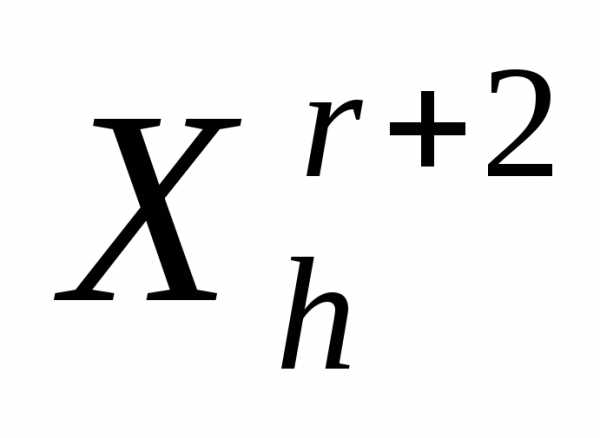 этого симплекса. Если, то полагаеми переходим к п. 4 (отражению) с симплексом
этого симплекса. Если, то полагаеми переходим к п. 4 (отражению) с симплексом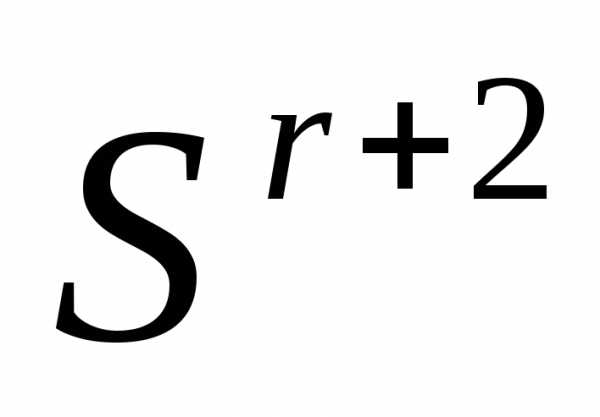 . Иначе полагаем и, не используя результаты растяжения, переходим к п. 4 (отражению) с симплексом
. Иначе полагаем и, не используя результаты растяжения, переходим к п. 4 (отражению) с симплексом 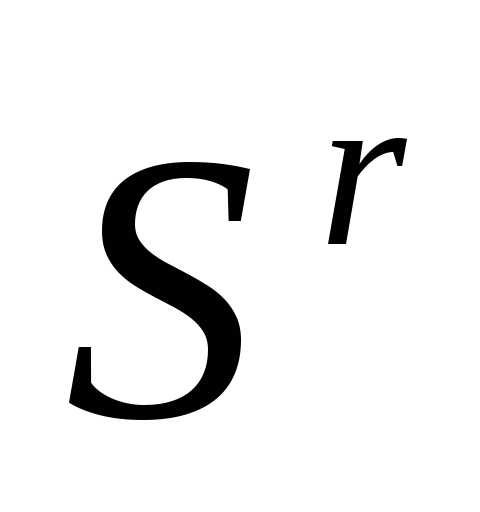 .
.Сжатие (ситуация ). Выполняем сжатие симплекса
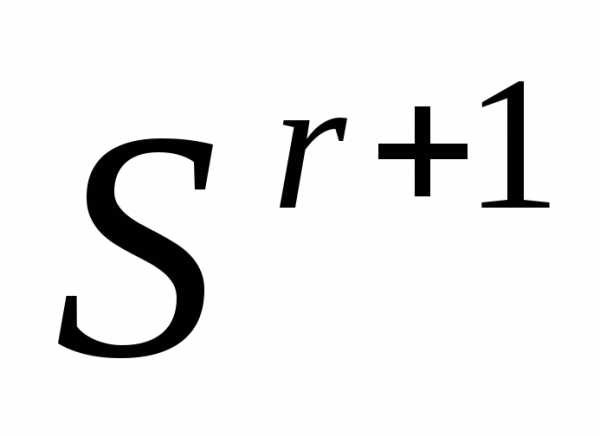 в направлении- получаем новый симплекс. Вычисляем значение функции
в направлении- получаем новый симплекс. Вычисляем значение функции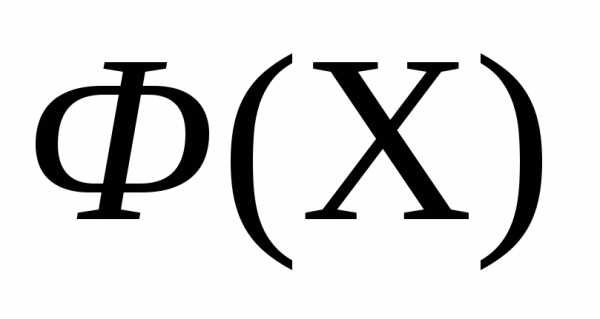 в вершине
в вершине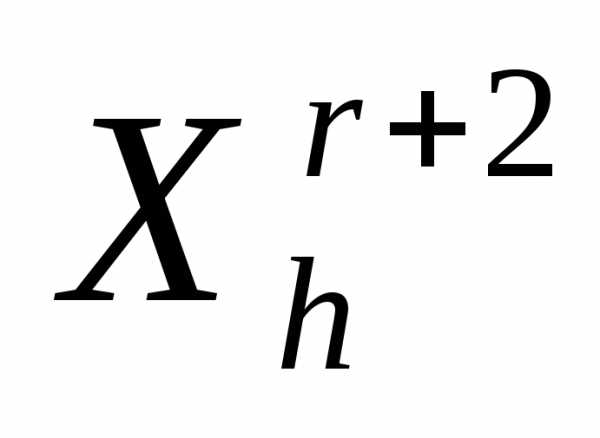 этого симплекса. Если, то полагаеми переходим к п. 4 (отражению) с симплексом
этого симплекса. Если, то полагаеми переходим к п. 4 (отражению) с симплексом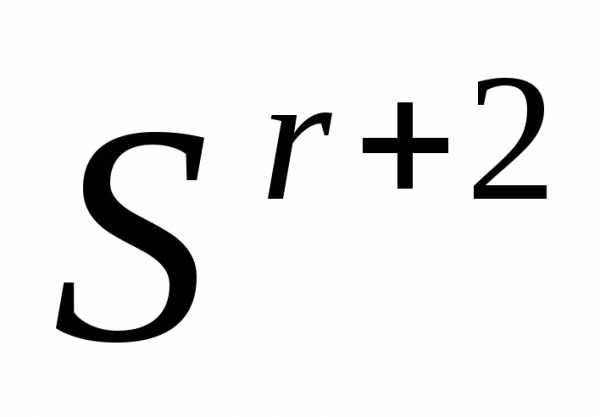 . Иначе переходим к п. 9 (редукции) с симплексом
. Иначе переходим к п. 9 (редукции) с симплексом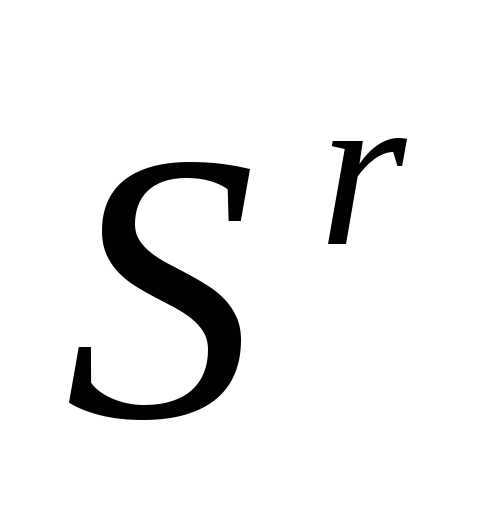 .
.Редукция (ситуация, когда сжатие симплекса оказалось неудачным). Выполняем редукцию симплекса
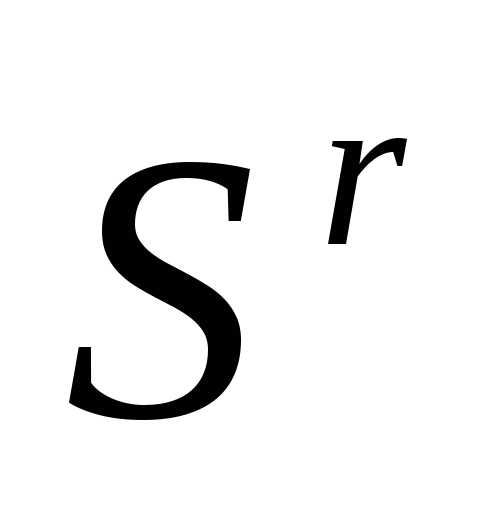 к вершине
к вершине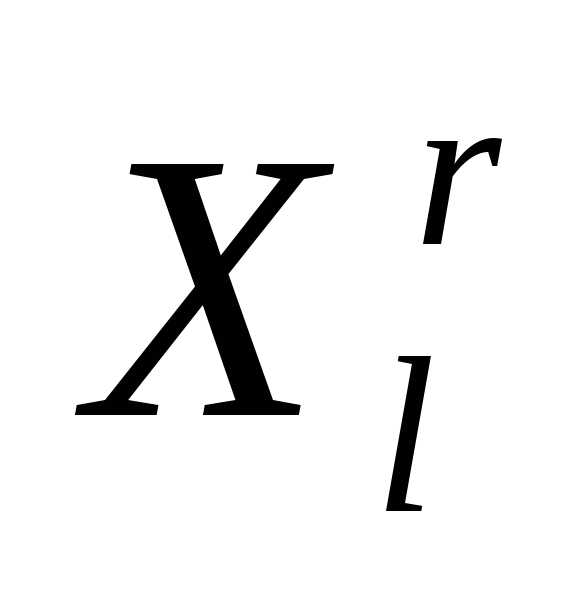 - получаем новый симплекс
- получаем новый симплекс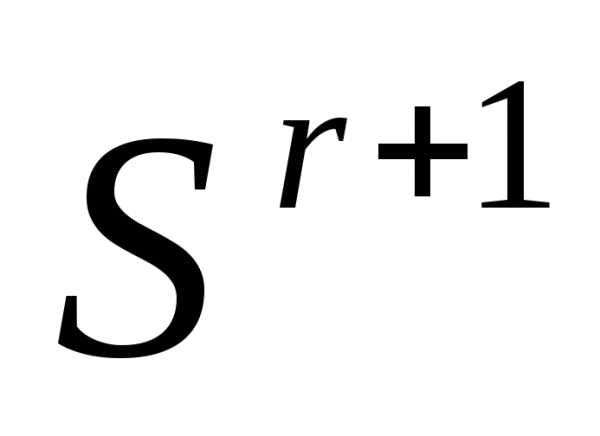 . Вычисляем значение функции
. Вычисляем значение функции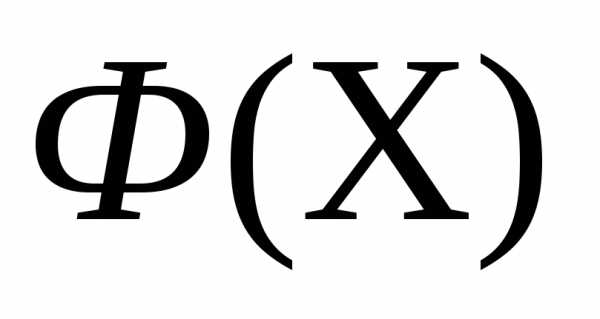 во всех новых вершинах симплекса
во всех новых вершинах симплекса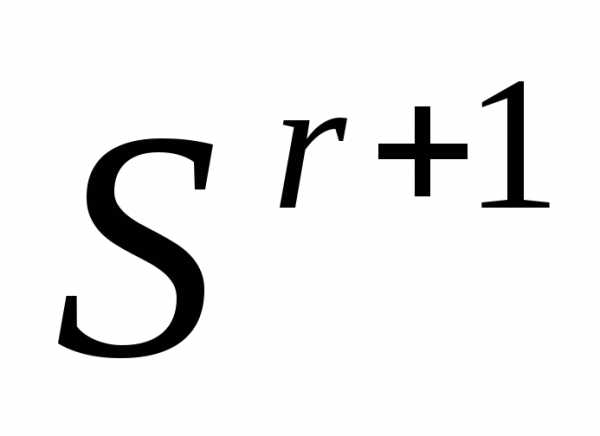 . Полагаеми переходим к п. 4 (отражению)●
. Полагаеми переходим к п. 4 (отражению)●
studfiles.net
Симплекс-метод, его сущность
Содержание.
Введение……………………………………………………………………………………….с.5.
1. Теоретическая часть.
Глава 1. Простой симплекс-метод.
1.1 Обоснование и описание вычислительной процедуры. Приведение задачи линейного программирования к стандартной форме……………………………с.7
1.2 Симплексный метод решения задач……………………………………..…...с.8.
1.3 Алгоритм симплекс-метода…………………………………………………с.10.
1.4 Решение задачи оптимизации. Построение аналитической модели……...с.12.
1.5 Приведение задачи к стандартной форме. Определение начального допустимого решения…………………………….……………………………...с.14.
Глава 2. Двухэтапный метод.
2.1 Искусственное начальное решение…………………………………………с.16.
2.2 Алгоритм двухэтапного метода……………………………………………..с.19.
Глава 3. Особые случаи симплекс-метода……………………………………………...23.
3.1 Вырожденность……………………………………………………………....с.24.
3.2 Альтернативные оптимальные решения…………………………………....с.27.
3.3 Неограниченные решения…………………………………………………...с.30.
3.4 Отсутствие допустимых решений…………………………………………..с.32.
2. Практическая часть.
2.1 Постановка задачи…………..……………………………………………………..с.34.
2.2 Решение…..…………………………………………………………………………с.36.
Заключение…………………………………………………………………………………...с.39.
Литература…………………………………………………………………………………....с.40.
Введение.
Целью данной курсовой работы является решение конкретной задачи линейного программирования. Во всех таких задачах требуется найти максимум или минимум линейной функции при условии, что её переменные принимают неотрицательные значения и удовлетворяют некоторой системе линейных уравнений или линейных неравенств либо системе, содержащей как линейные уравнения, так и линейные неравенства. Каждая из этих задач является частным случаем общей задачи линейного программирования.
Для решения задач линейного программирования созданы специальные методы. Изучению одного из них, а именно симплекс-методу, посвящена эта курсовая работа.
В настоящее время оптимизация находит применение в науке, технике и в любой другой области человеческой деятельности.
Оптимизация – целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях.
Поиски оптимальных решений привели к созданию специальных математических методов и уже в 18 веке были заложены математические основы оптимизации (вариационное исчисление, численные методы и др). Однако до второй половины 20 века методы оптимизации во многих областях науки и техники применялись очень редко, поскольку практическое использование математических методов оптимизации требовало огромной вычислительной работы, которую без ЭВМ реализовать было крайне трудно, а в ряде случаев - невозможно.
Постановка задачи оптимизации предполагает существование конкурирующих свойств процесса, например:
· количество продукции - расход сырья
· количество продукции - качество продукции
Выбор компромиcного варианта для указанных свойств и представляет собой процедуру решения оптимизационной задачи.
При постановке задачи оптимизации необходимо:
1. Наличие объекта оптимизации и цели оптимизации. При этом формулировка каждой задачи оптимизации должна требовать экстремального значения лишь одной величины, т.е. одновременно системе не должно приписываться два и более критериев оптимизации, т.к. практически всегда экстремум одного критерия не соответствует экстремуму другого. Приведем примеры.
Типичный пример неправильной постановки задачи оптимизации:
«Получить максимальную производительность при минимальной себестоимости».
Ошибка заключается в том, что ставится задача поиска оптимальности 2-х величин, противоречащих друг другу по своей сути.
Правильная постановка задачи могла быть следующая:
а) получить максимальную производительность при заданной себестоимости;
б) получить минимальную себестоимость при заданной производительности;
В первом случае критерий оптимизации - производительность а во втором - себестоимость.
2. Наличие ресурсов оптимизации, под которыми понимают возможность выбора значений некоторых параметров оптимизируемого объекта.
3. Возможность количественной оценки оптимизируемой величины, поскольку только в этом случае можно сравнивать эффекты от выбора тех или иных управляющих воздействий.
4. Учёт ограничений.
1. Теоретическая часть.
Глава 1. Простой симплекс-метод.
1.1 Обоснование и описание вычислительной процедуры. Приведение задачи линейного программирования к стандартной форме.
Любая задача линейного программирования приводится к стандартной (канонической) форме основной задачи линейного программирования, которая формулируется следующим образом: найти неотрицательные значения переменных X1 , X2 , Xn , удовлетворяющих ограничениям в виде равенств:
A11X1 + A12X2 + … + A1nXn = B1;
A21X1 + A22X2 + … + A2nXn = B2;
……………………………………
Am1X1 + Am2X2 + … + AmnXn = Bm;
Xj ≥ 0, j=1,…,n
и обращающих в максимум линейную функцию этих переменных:
E = C1X1 + C2X2 + … + CnXn Þ max
При этом также требуется, чтобы правые части равенств были неотрицательны, т.е. должны соблюдаться условия:
Bj ≥ 0, j=1,…,n
Приведение к стандартной форме необходимо, так как большинство методов решения задач линейного программирования разработано именно для стандартной формы. Для приведения к стандартной форме задачи линейного программирования может потребоваться выполнить следующие действия:
- перейти от минимизации целевой функции к ее максимизации;
- изменить знаки правых частей ограничений;
- перейти от ограничений-неравенств к равенствам;
- избавиться от переменных, не имеющих ограничений на знак.
Для решения нашей задачи воспользуемся симплекс-методом, так как этот метод предназначен для решения задач линейного программирования любой размерности.
1.2 Симплексный метод решения задач.
Симплексный метод задач линейного программирования основан на переходе от одного опорного плана к другому, при котором значение целевой функции возрастает (при условии, что данная задача имеет оптимальный план, и каждый ее опорный план является невырожденным). Указанный переход возможен, если известен какой-нибудь исходный опорный план. Рассмотрим задачу, для которой этот план можно непосредственно записать.
Пусть дана функция, для которой необходимо найти наибольшее или наименьшее значение, если значения всех неизвестных неотрицательные.
ѓ = C0 + C1x1 + C2x2 +...+ Cnxn
и система m линейных уравнений с n неизвестными. Это называется системой ограничений:
a11x1 + a12x2 +...+ a1nxn = b1a21x1 + a12x2 +...+ a2nxn = b2
...
am1x1 +am2x12 +...+ amnxn = bm
Целевую функцию представим в виде:
ѓ - C1x1-C2x2 -...-Cnxn = C0
Составим симплекс-таблицу. В дальнейшем будем считать, что ранг матрицы системы ограничений равен r.В системе ограничений выбран базис (основные неизвестные)x1,x2,...xn и коэффициенты в правой части не отрицательны.
В этом случае система ограничений будет иметь вид:
x1 +...+ a1,r+1xr+1 +...+ a1nxn = b1
x2 + a2,r+1xr+1 +...+ a2nxn = b2
...
xr+ ar,r+1xr+1 +...+ arnxn = br
Тогда целевая функция имеет вид:
ѓ + Cr+1xr+1 + Cr+2xr+2 -...- Cnxn = C0
Нахождение оптимального плана симплексным методом включает следующие этапы:
1. Находят опорный план.
2. Составляют симплекс-таблицу. В общем виде:
3. В нижней строчке симплекс-таблицы необходимо отыскать отрицательные числа (не считая коэффициент Со). Если таких чисел нет, то данное базисное решение является оптимальным.
4. Пусть элемент Сj<0,тогда в j-ом столбце необходимо найти положительный элемент. Если все коэффициенты этого столбца отрицательные, то решения не существует.
5. Если положительный коэффициент в j-ом столбце один, то выбранную строку с номером i надо поделить все коэффициенты на число aij.Результат деления записываем в новую симплекс-таблицу. Если же положительных коэффициентов несколько, необходимо составить отношение bi/aij и из полученных значений выбрать наименьшее, соответствующее i-ой строке.
6. В новой симплекс-таблице в столбце базисных неизвестных вместо xi пишется xj. Продолжается заполняться таблица. В столбце с номером j необходимо получить нули(включая строку с целевой функцией). Для этого надо умножить i-ую записанную строку на нужное число и сложить с остальными строками.
В результате осуществился переход к новому базису, при этом значение целевой функции увеличилось.
1.3 Алгоритм симплекс-метода.
Пусть система приведена к каноническому виду.X1+ q1,m+1 Xm+1 + …. + q1,m+n Xm+n = h2
X2+q1,m+1 Xm+1 + …. + q1,m+n Xm+n = h2
X3+q1,m+1 Xm+1 + …. + q1,m+n Xm+n = h2
………………………………………………………
Xm+ qm,m+1 Xm+1 + …. + qm,m+n Xm+n =hm
В ней m базисных переменных, k свободных переменных. m+k=n - всего переменных.
Fmin= C1X1+ C2X2+ C3X3+....+ CnXn
Для дальнейших рассуждений вычислений будем пользоваться первой симплекс таблицей (таблица1).
Таблица 1.Симплекс таблица
Первый столбец - коэффициенты в целевой функции при базисных переменных.
mirznanii.com