Тема 7. Ранжирование стратегических задач. Задача ранжирования
Метрики качества ранжирования / Блог компании E-Contenta / Хабр

Задача ранжирования сейчас возникает повсюду: сортировка веб-страниц согласно заданному поисковому запросу, персонализация новостной ленты, рекомендации видео, товаров, музыки… Одним словом, тема горячая. Есть даже специальное направление в машинном обучении, которое занимается изучением алгоритмов ранжирования способных самообучаться — обучение ранжированию (learning to rank). Чтобы выбрать из всего многообразия алгоритмов и подходов наилучший, необходимо уметь оценивать их качество количественно. О наиболее распространенных метриках качества ранжирования и пойдет речь далее.
Кратко о задаче ранжирования
Ранжирование — задача сортировки набора элементов из соображения их релевантности. Чаще всего релевантность понимается по отношению к некому объекту. Например, в задаче информационного поиска объект — это запрос, элементы — всевозможные документы (ссылки на них), а релевантность — соответствие документа запросу, в задаче рекомендаций же объект — это пользователь, элементы — тот или иной рекомендуемый контент (товары, видео, музыка), а релевантность — вероятность того, что пользователь воспользуется (купит/лайкнет/просмотрит) данным контентом.Формально, рассмотрим N объектов и M элементов . Реузальтат работы алгоритма ранжирования элементов для объекта — это отображение , которое сопоставляет каждому элементу вес , характеризующей степень релевантности элемента объекту (чем больше вес, тем релевантнее объект). При этом, набор весов задает перестановку на наборе элементов элементов (считаем, что множество элементов упорядоченное) исходя из их сортировки по убыванию веса .
Существует два основных способа получения : 1. На основе исторических данных. Например, в случае рекомендаций контента, можно взять просмотры (лайки, покупки) пользователя и присвоить просмотренным весам соответствующих элементов 1 ( ), а всем остальным — 0. 2. На основе экспертной оценки. Например, в задаче поиска, для каждого запроса можно привлечь команду асессоров, которые вручную оценят релевантности документов запросу.
Стоит отметить, что когда принимает только экстремальные значения: 0 и 1, то престановку обычно не рассматривют и учитывают лишь множество релевантных элементов, для которых .
Цель метрики качества ранжирования — определить, насколько полученные алгоритмом оценки релевантности и соответствующая им перестановка соответствуют истинным значениям релевантности . Рассмотрим основные метрики.
Mean average precision
Mean average precision at K (map@K) — одна из наиболее часто используемых метрик качества ранжирования. Чтобы разобраться в том, как она работает начнем с «основ».Замечание: "*precision" метрики используется в бинарных задачах, где принимает только два значения: 0 и 1.
Precision at K
Precision at K (p@K) — точность на K элементах — базовая метрика качества ранжирования для одного объекта. Допустим, наш алгоритм ранжирования выдал оценки релевантности для каждого элемента . Отобрав среди них первые элементов с наибольшим можно посчитать долю релевантных. Именно это и делает precision at K:Замечание: под понимается элемент , который в результате перестановки оказался на -ой позиции. Так, — элемент с наибольшим , — элемент со вторым по величине и так далее.
Average precision at K
Precision at K — метрика простая для понимания и реализации, но имеет важный недостаток — она не учитывает порядок элементов в «топе». Так, если из десяти элементов мы угадали только один, то не важно на каком месте он был: на первом, или на последнем, — в любом случае . При этом очевидно, что первый вариант гораздо лучше.Этот недостаток нивелирует метрика ранжирования average precision at K (ap@K), которая равна сумме p@k по индексам k от 1 до K только для релевантных элементов, деленому на K:
Теперь и map@K нам по зубами.
Mean average precision at K
Mean average precision at K (map@K) — одна из наиболее часто используемых метрик качества ранжирования. В p@K и ap@K качество ранжирования оценивается для отдельно взятого объекта (пользователя, поискового запроса). На практике объектов множество: мы имеем дело с сотнями тысяч пользователей, миллионами поисковых запросов и т.д. Идея map@K заключается в том, чтобы посчитать ap@K для каждого объекта и усреднить:Замечание: идея эта вполне логична, если предположить, что все пользователи одинаково нужны и одинаково важны. Если же это не так, то вместо простого усреднения можно использовать взвешенное, домножив ap@K каждого объекта на соответствующий его «важности» вес.Normalized Discounted Cumulative Gain
Normalized discounted cumulative gain (nDCG) — еще одна распространенная метрика качества ранжирования. Как и в случае с map@K, начнем с основ.
Cumulative Gain at K
Вновь рассмотрим один объект и элементов с наибольшим . Cumulative gain at K (CG@K) — базовая метрика ранжирования, которая использует простую идею: чем релевантные элементы в этом топе, тем лучше: Эта метрика обладает очевидными недостатками: она не нормализована и не учитывает позицию релевантных элементов. Заметим, что в отличии от p@K, CG@K может использоваться и в случае небинарных значений эталонной релевантности .
Discounted Cumulative Gain at K
Discounted cumulative gain at K (DCG@K) — модификация cumulative gain at K, учитывающая порядок элементов в списке путем домножения релевантности элемента на вес равный обратному логарифму номера позиции:Замечание: если принимает только значения 0 и 1, то , и формула принимает более простой вид: Использование логарифма как функции дисконтирования можно объяснить следующими интуитивными соображениями: с точки зрения ранжирования позиции в начале списка отличаются гораздо сильнее, чем позиции в его конце. Так, в случае поискового движка между позициями 1 и 11 целая пропасть (лишь в нескольких случаях из ста пользователь заходит дальшей первой страницы поисковой выдачи), а между позициями 101 и 111 особой разницы нет — до них мало кто доходит. Эти субъективные соображения прекрасно выражаются с помощью логарифма: Discounted cumulative gain решает проблему учета позиции релевантных элементов, но лишь усугубляет проблему с отсутствием нормировки: если варьируется в пределах , то уже принимает значения на не совсем понятно отрезке. Решить эту проблему призвана следующая метрика
Normalized Discounted Cumulative Gain at K
Как можно догадаться из названия, normalized discounted cumulative gain at K (nDCG@K) — не что иное, как нормализованная версия DCG@K: где — это максимальное (I — ideal) значение . Так как мы договорились, что принимает значения в , то . Таким образом, наследует от учет позиции элементов в списке и, при этом принимает значения в диапазоне от 0 до 1.
Замечание: по аналогии с map@K можно посчитать , усредненный по всем объектам.
Mean reciprocal rank
Mean reciprocal rank (MRR) — еще одна часто используемая метрика качества ранжирования. Задается она следующей формулой: где — reciproсal rank для -го объекта — очень простая по своей сути величина, равная обратному ранку первого правильно угаданного элемента. Mean reciprocal rank изменяется в диапазоне [0,1] и учитывает позицию элементов. К сожалению он делает это только для одного элемента — 1-го верно предсказанного, не обращая внимания на все последующие.
Метрики на основе ранговой корреляции
Отдельно стоит выделить метрики качества ранжирования, основанные на одном из коэффициентов ранговой корреляции. В статистике, ранговый коэффициент корреляции — это коэффициент корреляции, который учитывает не сами значения, а лишь их ранг (порядок). Рассмотрим два наиболее распространенных ранговых коэффициента корреляции: коэффициенты Спирмена и Кендэлла.Ранговый коэффициент корреляции Кендэлла
Первый из них — коэффициент корреляции Кендэлла, который основан на подсчете согласованных (и несогласованных) пар у перестановок — пар элементов, котором перестановки присвоили одинаковый (разный) порядок:Ранговый коэффициент корреляции Спирмена
Второй — ранговый коэффициент корреляции Спирмена — по сути является ни чем иным как корреляции Пирсона, посчитанной на значениях рангов. Есть достаточно удобная формула, выражающая его из рангов напрямую: где — коэффициент корреляции Пирсона.Метрики на основе каскадной модели поведения
До этого момента мы не углублялись в то, как пользователь (далее мы рассмотрим частный случай объекта — пользователь) изучает предложенные ему элементы. На самом деле, неявно нами было сделано предположение, что просмотр каждого элемента независим от просмотров других элементов — своего рода «наивность». На практике же, элементы зачастую просматриваются пользователем поочередно, и то, просмотрит ли пользователь следующий элемент, зависит от его удовлетворенности предыдущими. Рассмотрим пример: в ответ на поисковый запрос алгоритм ранжирования предложил пользователю несколько документов. Если документы на позиции 1 и 2 оказались крайне релевантны, то вероятность того, что пользователь просмотрит документ на позиции 3 мала, т.к. он будет вполне удовлетворен первыми двумя.Подобные модели поведения пользователя, где изучение предложенных ему элементов происходит последовательно и вероятность просмотра элемента зависит от релевантности предыдущих называются каскадными.
Expected reciprocal rank
Expected reciprocal rank (ERR) — пример метрики качества ранжирования, основанной на каскадной модели. Задается она следующей формулой: где ранг понимается по порядку убывания . Самое интересное в этой метрике — вероятности. При их расчете используются предположения каскадной модели: где — вероятность того, что пользователь будет удовлетворен объектом с рангом . Эти вероятности считаются на основе значений . Так как в нашем случае , то можем рассмотреть простой вариант: который можно прочесть, как: истинная релевантность элемента оказавшегося на позиции после сортировки по убыванию . В общем же случае чаще всего используют следующую формулу:PFound
PFound — метрика качества ранжирования, предложенная нашими соотечественниками и использующая похожую на каскадную модель: где- ,
- , если и 0 иначе,
- — вероятность того, что пользователь прекратит просмотр по внешним причинам.
В заключении приведем несколько полезных ссылок по теме: — Статьи на википедии по: обучению ранжированию, MRR, MAP и nDCG. — Официальный список метрик используемых на РОМИП 2010. — Описание метрик MAP и nDCG на kaggle.com. — Оригинальные статьи по каскадной модели, ERR и PFound.
habr.com
Тема 7. Ранжирование стратегических задач
Внешние тенденции Внутренние тенденции
Срочность, важность
Наблюдение Ранжирование проблем
Забраковано
Срочные меры Отложенная реакция
Проблемно-ориентированные Регулярное планирование
проекты
Рис.5. Метод ранжирования стратегических задач
Под ранжированием в данном случае подразумевается деление стратегических проблем (задач) на группы по степени их важности и срочности. Метод рекомендуется использовать при уровне нестабильности во внешней среде выше четырёх единиц по шкале Ансоффа. Но возможно его использование и при более низком уровне нестабильности. Уровень нестабильности выше четырёх единиц означает, что во внешней среде наблюдается почти тотальное господство изменчивости над устойчивостью. Всё очень подвижно. Высока скорость перемен. Субъекты экономических отношений не успевают должным образом среагировать на существующие обстоятельства. Количество факторов, влияющих на организацию, очень велико. Организации не обладают достаточными ресурсами для того, чтобы единовременно отреагировать на все значимые процессы и явления. А потому руководство организации устанавливает своего рода «очерёдность» стратегических задач. Такой вариант действий позволяет (в условиях высокого уровня нестабильности и ограниченности ресурсов организации) не совершить существенных стратегических ошибок. Позволяет не упустить благоприятные возможности, и не понести серьёзных потерь в связи с угрозами из внешней среды.
Метод ранжирования стратегических задач включает в себя следующие основные правила.
Необходимо осуществить сбор разнообразной информации о процессах, происходящих внутри организации и во внешней среде. Обязателен высокий уровень компетентности сотрудников службы сбора информации. Также требуется высокий уровень технической оснащенности данной службы. Несоблюдение названных условий ведёт к снижению возможностей метода. Очень важно, чтобы собираемая информация действительно была разнообразной. В том числе необходимо собирать сведения, которые, вроде бы, не имеют прямого отношения к деятельности организации. Например, это может быть информация о духовно- идеологических процессах. Работники информационной службы должны уподобиться «Плюшкину», «подбирающему» любую попавшую в поле его зрения информацию.
Осуществить анализ собранной информации. Под «анализом» в данном случае подразумевается, во- первых, «расшифровка» имеющейся информации. Необходимо понять – что «таится» за процессами и явлениями, о которых мы получили сведения. Какие «угрозы» и «возможности» существуют во внешней среде? Как могут повлиять на организацию эти процессы и явления? Что собою представляют «сильные» и «слабые» стороны организации? Работники аналитической службы также призваны проранжировать опасности и возможности, существующие во внешней среде. То есть должны быть выделены те проблемы, которые несущественны и которыми организация может пренебречь. Выделяются также наиболее значимые проблемы.
Список наиболее значимых проблем передаётся высшему руководству организации для окончательного ранжирования (оценки). Руководители организации, опираясь на свою компетентность и интуицию, делят всю совокупность проблем на четыре группы.
А). В первую группу входят наиболее значимые проблемы. Это такого рода проблемы, которые открывают наибольшие возможности и порождают наиболее серьёзные угрозы. Экстренным образом разрабатываются специальные программы реагирования на эту группу проблем. Экстренность, чрезвычайность стратегических планов требует чрезвычайного финансирования. Для реализации планов первой группы могут быть использованы средства, которые ранее предусматривались для других целей. Чрезвычайные планы должны помочь минимизировать влияние на организацию негативных процессов (угроз, опасностей по традиционной терминологии), существующих во внешней среде. Эти же планы должны организовать деятельность коллектива по извлечению максимальных выгод из тех процессов и явлений, которые благоприятствуют деятельности организации. И наоборот - некачественность этой группы планов организации ставит крест на всей процедуре ранжирования. Организация должна «вложиться» в эту часть стратегической деятельности. И дело не только в скорости разработки планов и в скорости реализации их. Несомненно - планы должны появиться быстро. И так же быстро необходимо реализовывать эти планы. Планы должны быть «быстрые», и в тоже время качественные. Достичь этого сложно. Обычно то, что делается быстро, бывает неудовлетворительным по качеству. Но данная методика подразумевает обязательность соединения быстроты действий и высокого качества этих действий. Почему? Решение первой группы задач (сформулированных в стратегических планах) создаёт фундамент для дальнейших стратегических действий. «Слабый» фундамент не позволит осуществлять вторую группу стратегических действий в ответ на вторую группу стратегических проблем.
Б). Что собою представляет вторая группы проблем, вторая группа планов и вторая группа задач? Это такого рода проблемы, которые порождают менее существенные (для организации) угрозы и открывают менее перспективные возможности. Это «важные и среднесрочные проблемы» (по терминологии И. Ансоффа). Такого рода проблемы развиваются медленнее, в сравнении с первой группой проблем. Их можно назвать «вторым» эшелоном проблем. Реакция на них может быть отложена на более позднее время. Рекомендуется разрабатывать стратегические предложения в связи с этой группой проблем в рамках традиционной для данной организации процедуры планирования. Если в организации принято разрабатывать планы на следующий год, и делается это в течение нескольких месяцев, то именно при подготовке такого плана и предусматриваются меры по реагированию на вторую группу проблем. Предусматриваются ресурсы для реализации этих планов, но ресурсное обеспечение не носит окончательного характера. Многое в этом отношении зависит от того, как будут решаться проблемы первой группы.
В). В третью группу проблем включаются такого рода проблемы, по поводу которых нет достаточного уровня информированности. Неясно – как эти проблемы повлияют на организацию. А потому в связи с этой группой проблем ставится задача – осуществлять сбор дополнительной информации.
Г). Выделяется и четвёртая группа проблем. Это проблемы, которыми можно пренебречь. Они малосущественны. Этот разряд проблем иногда называют «фальшивой тревогой».
Ранжирование стратегических задач должно носить регулярный характер. То есть повторяться через три месяца, полгода, либо через какой- то иной промежуток времени.
При повторном ранжировании перечень проблем частично обновляется. Часть проблем остаются от прошлого. Но степень значимости этих «старых» проблем может измениться. Проблемы, которые ранее были отнесены к группе «важных и срочных» могут утратить своё значение и «превратиться» в проблемы второй, третьей и четвёртой группы. А проблемы, которыми при предыдущем ранжировании пренебрегли («фальшивая тревога»), при новом ранжировании могут быть отнесены к более высокому рангу. То есть данная процедура предусматривает систематическую критику результатов предыдущей оценочной деятельности. И такого рода «ревизионизм» необходим, полезен, потому что является адекватной реакцией на изменчивость внешней среды.
studfiles.net
Ранжирование - задача - Большая Энциклопедия Нефти и Газа, статья, страница 1
Ранжирование - задача
Cтраница 1
Ранжирование задач по их важности дает возможность переходить к следующему этапу: определению отраслей, которые обеспечивают решение этих задач. Эти отрасли формируют столбцы матрицы. Они оцениваются группами экспертов, состоящими из различных специалистов, с точки зрения их значимости для решения конкретной задачи по 10-балльной системе. [1]
Результаты ранжирования задач приведены в табл. 5.8. На основе данных этой таблицы формируем их набор, начиная с первой задачи, до тех пор пока сумма предпроизводственных затрат по всем отобранным задачам не окажется равной или примерно равной располагаемым ресурсам. [2]
Результаты ранжирования задач по этому критерию сведены в табл. 5.22. Из этой таблицы следует, что в формируемый набор должны быть включены лишь задачи первых семи рангов, обеспеченные в полной мере трудовыми ресурсами. Этот набор задач обеспечивает годовую экономию в 99 950 руб. Поскольку она меньше экономии базового набора, то дальнейшее формирование наборов задач по этой ветви графа также прекращаем. [3]
В основе ранжирования задач лежит принцип выбора задачи, решение которой приносит наибольшую отдачу. Выполнение плана рассматривается в динамике с заданным шагом, чаще всего равным кварталу. [4]
При необходимости ранжирования задач следует отметить в матрице предпочтительное требование для каждого проекта и распределить требования по степени предпочтения. [5]
Работа по ранжированию задач и выделению из них наиболее приоритетных ведется высшим руководством фирмы постоянно, также как и последующий контроль за их выполнением. [6]
В соответствии с результатами ранжирования задач следует выбрать автоматизацию транспортной системы, так как она получила более высокое процентное отношение для задачи наивысшего ранга. Однако можно выбрать и монорельсовую дорогу, так как среднее значение для нее больше и она в большей степени отвечает всем задачам. [7]
Важным является и соблюдение требования о ранжировании задач. [8]
Для реализации модели на этом этапе осуществляется ранжирование задач по приоритету с учетом информационных зависимостей между задачами. Приоритеты задач определяются экспертным путем. [9]
В качестве примера в табл. 71 приведено ранжирование задач химизации для различных стадий разработки условного месторождения. [10]
Запрограммированная для ЭВМ IBM-7090 аналитическая модель выбора, разработанная для облегчения синтеза информации, порождаемой в процессе планирования, для ранжирования задач долгосрочного планирования технологии. [11]
Разбиение задач по степеням сложности производится на основе применения методов ранговой корреляции. При этом каждый сотрудник подразделения производит ранжирование задач по степени их сложности, которая определяется не объемом вычислительных операций, а в зависимости от наличия и количества логических операций, необходимых для решения данной задачи. Если задача носит чисто вычислительный или информативный характер, например заключается в составлении какой-либо сводной справки, то ей приписывается ранг, равный единице. Каждой последующей по сложности задаче приписывается ранг на единицу больше. Начальник и заместитель начальника отдела ранжируют все задачи. Остальные сотрудники ранжируют выполняемые ими задачи, а также задачи, выполняемые сотрудниками равной и низшей квалификации. Допускается присваивать задачам равные ранги, если ранжирующий не может их расположить в порядке возрастания степени сложности. [12]
Особую важность приобретают методологические аспекты диагностики предприятия, выбора и ранжирования задач, формализации постановок задач, автоматизированного выбора вариантов в рамках концепции генератора АСУП. [13]
Соотношение вопросов как делегируемых ректором вниз, так и сохраняемых за собой, не является неизменным. Оно зависит от ситуации, которая может продиктовать то или иное ранжирование задач по степени их важности и срочности. Ясно, что ректор приоритетно и акцентированно должен заниматься перспективами развития вуза, наиболее существенными блоками внешних связей, концептуальными вопросами. Однако, если он попытается полностью отрешиться от повседневной жизни вуза, его роль, как руководителя, может стать декларативной, а сам он утратит живые связи с коллективом. Весь вопрос в том, как именно он должен заниматься текущими делами. Вникать во все и решать самолично вопросы любой значимости, которые могут и должны отрабатываться его подчиненными. [14]
Это положение предопределяет необходимость оценки качества решения конкретных задач управления в условиях данного предприятия. Такая оценка задач управления позволяет с самого начала обеспечить с помощью АСУ мобилизацию внутренних резервов и должный уровень эффективности их использования. Ранжирование задач управления осуществляется в ходе так называемого диагностического анализа предприятий. Из этого вытекает различие задач в пусковых комплексах АСУ. [15]
Страницы: 1
www.ngpedia.ru
Алгоритмы машинного обучения для задачи ранжирования интернет сайтов – SEO константа
Исследование методов машинного обучения в задачах ранжирования на основе конкурса «Интернет-математика 2009».Основные используемые методы. Сравнение результатов применения трех алгоритмов – Support Vector Machine (Машина опорных векторов), Random Forest (Случайный лес), Stochastic Gradient Boosting (Стохастический градиентный бустинг).
Введение
Одной из основных задач поисковых машин является ранжирование проиндексированных документов в соответствии с их релевантностью поисковому запросу пользователя. С развитием таких гигантов, как Яндекс, Google и Yahoo! постепенно усложнялись и алгоритмы поиска и ранжирования [от себя заметим, что во многом на данный процесс повлияло продвижение сайтов в их органической выдаче, так как ряд используемых для продвижения инструментов был нацелен на прямое ухудшение качества их поиска — прим. коллектива компании «SEO константа»]; на сегодняшний момент подавляющее большинство поисковиков работает по схеме, включающей в себя три основных этапа: непосредственно поиск документов, содержащих ключевой запрос, в том числе переформулированный, определение критериев оценки релевантности документа запросу и само ранжирование документов по степени релевантности запросу.
Самый распространенный метод выбора формулы ранжирования документов по степени релевантности – это машинное обучение, которое в основе своей предполагает использование определенных баз знаний. В качестве подобных баз знаний используются примеры оценки релевантности документа асессорами, которые точно так же руководствуются строго определенными критериями и признаками релевантности. Для корректных результатов в процессе машинного обучения использоваться должны достаточно обширные базы знаний вплоть до нескольких сотен тысяч примеров оценки релевантности асессорами на основе 100-1000 критериев ранжирования.
В этой статье вы ознакомитесь с описанием исходных данных, основными методами оценки и действующими метриками для оценки качества ранжирования. Кроме того, в этом материале приведены описания и сравнения использованных методов ранжирования, а также планы будущих исследований.
Описание данных
Компанией «Яндекс» весной 2009 года был проведен конкурс «Интернет-математика», непосредственно затрагивающий проблему ранжирования документов в соответствии со степенью их релевантности. Основной задачей участников было предложение формулы ранжирования на основе предоставленных организаторами общих алгоритмов и данных. Работа велась на основании значения признаков в парах типа «запрос-документ» и оценки степени их релевантности, установленной асессорами компании «Яндекс». Исходные данные включали в себя порядка 245 признаков из интервала [0;1], а также оценку релевантности документов асессорами от 0 до 4, где 0 – это нерелевантный документ, а 4 – высокая степень релевантности. Строгое определение и описание критериев оценки, т.е., признаков релевантности, участникам не предоставили, однако при этом в качестве критериев оценки использоваться могли любые признаки – длина запроса, частота его встречаемости в самом документе и т.п.
База данных для машинного обучения содержала 97290 строк (9124 запросов), а множество примеров для тестирования порядка 21103 строк (2026 запросов).
Задачи ранжирования
Основные методы оценки релевантности документа поисковому запросу
Практически все используемые сегодня методы оценки релевантности можно отнести к одной из трех основных категорий [2] – точечные методы, методы на списках и на парах. Основы каждой группы методов мы рассмотрим подробнее.
Точечные алгоритмы. В основе использования точечных методов лежит использование восстановление регрессии и обычной классификации документов по значению оценки отдельных признаков релевантности. Как примеры для машинного обучения используются пары типа «признак – значение релевантности» (xi;yi) для каждого документа. Наиболее существенным недостатком этого метода является независимая оценка каждого документа, в то время как ранжирование должно вестись с учетом признаков релевантности всех документов, соответствующих запросу.
Алгоритмы на парах.Методы, основанные на использовании пар, в качестве примеров для машинного обучения рассматривают несколько иные типы объектов вроде Rij = ((xi,yi),(xj,yj)). Основной задачей является классификация пар на классы по типу «правильное ранжирование – неправильное ранжирование». Объекты типа Rij по сути описывают запросы по принципу «признаки – значение релевантности» (по типу (xi,yi),(xj,yj)). Этот метод ранжирования обладает тем же недостатком, что и точечный метод – независимая оценка документа без оценки прочих документов по запросу.
Алгоритмы на списках. Наиболее точным методом ранжирования документов в соответствии с релевантностью запроса является метод на списках, который анализирует и использует в качестве базы знаний для машинного обучения списки документов, соответствующих поисковому запросу.
Согласно условиям конкурса, в работе использовались только точечные методы ранжирования, что связано с их простотой, достаточно простой реализацией, а также высокой скоростью обработки.
Таблица 1 Алгоритмы и ссылки на публикации
| Метод и модель | Ссылки на публикации |
| Точечные алгоритмы | |
| McRank | [12] |
| Алгоритмы на парах | |
| Ranking SVM | [5] |
| RankNet | [1] |
| Алгоритмы на списках | |
| AdaRank | [9] |
| ListNet | [13] |
| ListMLE | [13] |
| RankGP | [8] |
Метрика эффективности формул ранжирования
Сегодня для оценки качества формул ранжирования используется огромное количество метрик, среди которых особо выделить можно Discounted Cumulative Gain (DCG), Normalized Discounted Cumulative Gain (NDCG), Mean Average Precision (MAP) [7]. Согласно условиям проводимого конкурса, в качестве метрики качества участниками использовалась DCG следующего вида:
Здесь rel – это асессорская оценка документа, который стоит на i-ом месте в ранжированном посредством специальной формулы списке, T – это общее количество документов в списке, а q – это запрос.
Конечный результат усредняется с учетом всех запросов, поэтому чем выше конечное значение, тем, соответственно, и лучше работает формула ранжирования.
Методы машинного обучения для задачи ранжирования сайтов
В следующей части статьи описаны три основных поисковых алгоритма, которые используются современными поисковыми машинами и которые в своей основе имеют точечные методы ранжирования.
Support Vector Machine. По сути, метод SVM на сегодняшний день является едва ли не самым популярным методом обучения, который активно используются и как метод простой классификации, и как метод восстановления регрессии. В основе этого метода лежит перевод исходных данных в пространство с большей размерностью [6]. В работе SVM использовался для восстановления регрессии, в частности, применялась реализация алгоритма из SVMlight.
Таблица 2 Результаты работы алгоритма SVM
| Тип Ядра | Discounted Cumulative Gain (DCG) |
| Линейное ядро | 4.165 |
| Полиноминальное ядро, d=2 | 4.229 |
| Полиноминальное ядро, d=3 | 4.233 |
| Полиноминальное ядро, d=4 | 4.232 |
| Полиноминальное ядро, d=5 | 4.219 |
| Полиноминальное ядро, d=6 | 4.219 |
Random Forest. Этот алгоритм машинного обучения предполагает группировку примеров для обучения в наборы случайных деревьев, причем качество и эффективность работы напрямую зависит от наличия ошибок каждого дерева, а также их некоррелированности [10], которая связана с применением техники бутстреп и использованием элементов случайности при построении.
Применение алгоритма на практике:
пусть p и N – количество примеров.
Для i=1,2….M
а) Создать выборку Θi с размерами N из N примеров с замещением (бутстреп)
б) На основе выборки Θi строится дерево Ti, в котором до минимального количества примеров в узле (менее nmin) повторяется рекурсивно следующий алгоритм действий для узлов:
- выбор случайный набор переменных m из p;
- выбор переменной из m по принципу оптимального разбиения;
- прибавить к текущему узлу двух сыновей.
Получение результата по формуле:
Таблица 3 Результат работы алгоритма Random Forest
| M | nmin | Discounted Cumulative Gain (DCG) |
| 20 | 5 | 4.198 |
| 100 | 10 | 4.241 |
| 100 | 50 | 4.242 |
| 500 | 10 | 4.252 |
| 500 | 30 | 4.251 |
| 1000 | 10 | 4.248 |
| 1000 | 50 | 4.243 |
| 2000 | 30 | 4.248 |
Stochastic Gradient Boosting. В основе SGB лежит все то же построение деревьев, однако здесь используются преимущественно простые деревья, количество листьев которых не превышает двадцати. Каждое дерево строится на остатках предыдущего [3].
Главной проблемой, с которой сталкиваются разработчики при подборе алгоритмов машинного обучения, является переобучение, для устранения которого в SGB используется модификация [4], позволяющая улучшить показатели качества и точности работы, а также скорость обработки алгоритма. Эта модификация выстраивает каждое дерево на основе случайных наборов примеров из всех приведенных примеров. Такой подход ( введение элемента случайности) позволяет в значительной степени повысить устойчивость алгоритма к переобучению, однако полностью проблема переобучения этим способом не решается. Кроме того, использование только части выборки для построения дерева повышает скорость работы.
Метод SGB с равным успехом используется и для простой классификации, и для восстановления регрессии. В ходе конкурса применялся алгоритм восстановления регрессии, предполагающий использование деревьев CART как базовых алгоритмов для обучения.
Описание используемого алгоритма:
L – функция штрафа, где для вычисления абсолютного отклонения используется распределение Лапласа, а для квадратичного – распределение Гаусса.
1. Инициализация:
2. Для m=1,2…,M:
а) Для i=1,2…,N найти:
б) Построение дерева CART на основе набора {rim,xi}. Результатом построения являются области Rjm,j=1,2…Jm. Здесь Jm – это общее количество листьев построенного дерева.
в) Для полученной области j=1,2,…Jm необходимо посчитать значения в листьях:
3. Результатом является ŷ(х)= fM(Х)
По итогам работы было установлено, что большей эффективностью обладает функция штрафа, использующая квадратичное, а не абсолютное отклонение. Сравнение результатов при разных значениях определенных параметров представлены ниже, в таблице №4.
Таблица 4 Результаты работы алгоритма Stochastic Gradient Boosting
| L | M | Jm | λ | Discounted Cumulative Gain (DCG) |
| Лапласа | 6K | 1 | 0.001 | 4.074 |
| Лапласа | 6K | 5 | 0.005 | 4.199 |
| Гаусса | 6K | 5 | 0.005 | 4.244 |
| Гаусса | 6K | 10 | 0.005 | 4.261 |
| Гаусса | 6K | 15 | 0.005 | 4.267 |
| Гаусса | 10K | 5 | 0.005 | 4.255 |
| Гаусса | 10K | 10 | 0.005 | 4.267 |
| Гаусса | 10K | 15 | 0.005 | 4.273 |
| Гаусса | 20K | 5 | 0.005 | 4.268 |
| Гаусса | 20K | 10 | 0.005 | 4.277 |
| Гаусса | 20K | 15 | 0.005 | 4.276 |
| Гаусса | 50K | 10 | 0.002 | 4.279 |
| Гаусса | 50K | 11 | 0.001 | 4.280 |
| Гаусса | 70K | 10 | 0.001 | 4.274 |
| Гаусса | 70K | 10 | 0.002 | 4.281 |
Согласно проведенным экспериментам, лучший результат (DCG=4.281) был достигнут при M=70000, где M – количество деревьев, и Jm, т.е., количестве листьев, равном 10. Параметр регуляризации здесь (λ) 0,002.
Рисунки 1 и 2 наглядно демонстрируют зависимость поведения метрики DCG и MSE (Mean Square Error) от количества построенных деревьев во время обучения и при проведении теста.
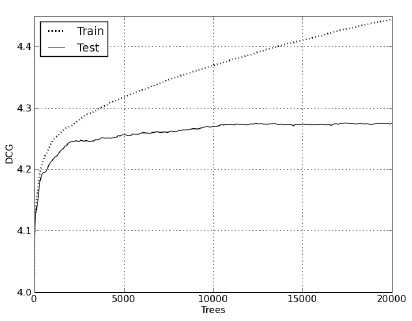
Рисунок 1 Поведение метрики DCG на тесте и на обучении

Рисунок 2 Поведение метрики MSE на тесте и на обучении
Заключение и выводы
Результаты проведенных тестов привели к выводу, что оптимальным методом ранжирования из трех предложенных является Stochastic Gradient Boosting, так как результаты проверки эффективности алгоритма показали лучшие значения, чем у методов SVM и Random Forest.
Следующим этапом работ планируется сделать тестирование методов, использующих в своей основе пары и списки, а также провести ряд тестов, связанных с непосредственной оптимизацией самих метрик. Кроме того, планируется произвести тщательное исследование одного из наиболее перспективных подходов в методе SGB – метод прямой оптимизации метрики ранжирования (той же DCG), так как квадратичная метрика и метрика ранжирования слабо связаны. Конечно, прямым способом этого добиться невозможно, однако допускается использование аппроксимации метрики при помощи гладких функций.
Ссылки:
[1] Cristopher J.C. Burges, Tal Shaked, Erin Renshaw, Ari Lazier, Matt Deeds, Nicole Hamilton, Gregory N. Hullender. Learning to rank using gradient descent. In Proceedings of ICML’2005.
[2] Chuan He, Cong Wang, Yi-Xin Zhong, Rui-Fan Li. A servey on learning to rank. International Conference on Machine Learning and Cybernetics, 2008.
[3] Friedman Jerome H. Stochastic gradient boosting. Computational Statistics and Data Analysis, 2002, 38.
[4] Friedman Jerome H. Greedy function approximation: A gradient boosting machine. Annals of Statistics, 2001, 38.
[5] Gui-Rong Xue, Hua-Jun Zeng, Zeng Chen, Yong Yu, Wei-Ying Ma, Wensi Xi, Weiguo Fan. Optimizing web search using web click-through data. In Proceedings of CIKM’2004.
[6] Hastie T., Tibshirani R., Friedman J.H. The Elements od Statistical Learning. Springer 2001.
[7] Jarvelin, K. and Kekalainen, J. Cumulated gain-based evaluation of IR techniques. ACM Transactions on Information Systems. 20, 4.
[8] Jen-Yuan Yeh, Jung-Yi Lin, Hao-Ren Ke, Wei-Pang Yang. Learning to Rank for Information Retrieval Using Genetic Programming. Learning to Rank for Information Retrieval, SIGIR 2007 Workshop.
[9] Jun Xu, Hang Li. AdaRank: a boosting algorithm for information retrieval. In Proceedings of SIGIR’2007.
[10] Leo Brieman. Random Forests. Machine Learning, 2001, 45.
[11] Pinar Donmez, Krysta M. Svore, Cristopher J.C. Burges. On the Local Optimality of LambdaRank. Proceedings of the 32nd Annual ACM SIGIR, 2009.
[12] Ping Li, Cristopher J.C. Burges, Qiang Wu. McRank: Learning to Rank Using Multiple Classification and Gradient Boosting. NIPS, MIT Press, 2007.
[13] Zhe Cao, Tao Qin, Tie-Yan Liu, Ming-Feng Tsai, Hang Li. Learning to rank: from the pairwise approach to listwise approach. In proceedings of ICML’2007.
Алексей Городилов (Яндекс, Москва)
Рерайт материала «Методы Машинного Обучения для Задачи Ранжирования» выполнила Инна Вдовицына
wseob.ru
| АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника | ⇐ ПредыдущаяСтр 9 из 16Следующая ⇒
Итак, проведя любым из вышеназванных методов анализ текущей ситуации, мы пришли к некоему списку имеющихся проблем и ресурсов. Если само предыдущее упражнение не предполагало этого, то, обобщая его результаты, модератор должен все-таки записать ключевые слова проблем и задач на одном большом листе, никоим образом их не упорядочивая, дабы не навязать своих приоритетов. Назовем этот лист карта проблем". Теперь наша следующая задача – определить приоритеты. До этого желательно определиться с их количеством. Если речь идет о проектном семинаре, то обычно – это 4-5 проблемных областей, если о плане работы организации – гораздо больше. Для примера предположим, что на нашем семинаре мы хотим найти способы решения четырех проблем, поэтому во всех методах будет фигурировать цифра 4, хотя она взята чисто условно. Как выбрать приоритетные задачи, учтя мнение всех участников? Предложим несколько способов.
ГОЛОСОВАНИЕ
Это самый простой и самый демократичный способ выбора приоритетов. Каждый участник семинара получает право поставить на "карту проблем" четыре креста. Причем, он может распределить их по одному, выбрав четыре разные проблемы, или сгруппировать вокруг двух=трех проблем, или даже поставить все четыре рядом с одной проблемой, в зависимости от его мнения о степени их серьезности. По окончании голосования подсчитывается количество крестов, и определяются приоритетные проблемы. Для объективности можно провести такое голосование в два тура – сначала выбрав, скажем, шесть-семь приоритетов, потом дав возможность тем, кто за них проголосовали, сказать несколько слов о серьезности каждого, и в заключение, проголосовав снова уже только по этим шести-семи, чтобы из них выбрать четыре. При организации голосования не забудьте про такие мелочи, как место рядом с проблемой, куда ставить кресты, фломастеры разного цвета (если голосование в два тура) и т.д.
СУЖЕНИЕ
Это более длинный метод, требующий достаточно времени. Но с другой стороны, он позволяет не просто механически выбрать приоритеты, а обсудить и взвесить правильность сделанного выбора. Сначала каждый участник на свои карточки выбирает 4 приоритетные с его точки зрения проблемы. Затем участники объединяются в пары, и каждая пара из своих восьми карточек выбирает 4 общих приоритета. Здесь возможно некоторое объединение проблем или новая формулировка. Затем пары сходятся в группы по четыре человека и проделывают то же самое. Затем по восемь, шестнадцать, и, наконец, вся группа выбирает из двух получившихся наборов четыре общих приоритета. Как правило, выкристаллизовавшиеся в результате этого процесса четыре задачи действительно являются наиболее объективно важными на данный момент.
СТРОИМ ДОМ
Это разновидность предыдущего метода в несколько более позитивной и красочной форме. Участники сразу расходятся в группы по четыре, и каждая группа получает рисунок дома и четыре карточки-кирпичика (см. Рисунок 11). На карточках группа сообща выбирает четыре приоритета, формулируя их не как проблемы, а как задачи или идеалы. То есть "отсутствие информации" превращается в "сбор и распространение информации", "наркотики" в "борьбу с наркотиками", "слабая социальная защищенность женщин" в "усиление социальной защиты женщин" и так далее. Эти кирпичики укладываются на рисунок дома, представляя как бы идеальный результат. Затем микро-группы объединяются снова в группы по восемь, затем шестнадцать, и в конце концов появляется один общий дом, состоящий из четырех общих кирпичиков. Модератору надо не забыть подготовить достаточное количество рисунков домов, или просто попросить группы нарисовать их по образцу.
Итак, в результате всех этих упражнений семинар подошел к четырем (или более) приоритетным задачам, которые требуют немедленного решения. Наступает следующий этап – генерация вариантов решения. ГЕНЕРАЦИЯ ВАРИАНТОВ РЕШЕНИЯ На этом этапе как нельзя более важно выслушать каждого, попытаться отойти от привычных стереотипов, иногда прибегнуть к парадоксу, чтобы найденное решение было не банальным, а свежим и эффективным. Иногда самое неожиданное и на первый взгляд глупое предложение при ближайшем рассмотрении оказывается самым верным. Опытный модератор сразу может отличить "зерна от плевел", но он не должен навязывать свое мнение, лишь незаметно подталкивая группу к решению, которое его опыт выделил среди других.
МОЗГОВОЙ ШТУРМ Это самый распространенный и самый простой способ набросать варианты решений. Он уже достаточно хорошо известен организаторам семинаров, поэтому ограничимся кратким изложением основных моментов. Модератор пишет на большом листе первую задачу и предлагает членам группы по кругу выдвигать свои способы ее решения. Главные правила: · все высказываются строго по очереди, · никакие, даже самые "безумные" предложения не критикуются, · как только идея понятна, слово дается следующему члену группы, · если новых вариантов нет, член группы говорит "пас" и передает слово дальше, · штурм продолжается до тех пор, пока при очередном круге все члены группы не скажут "пас". До начала упражнения модератор может провести небольшую разминку, чтобы снять стереотипы и сделать группу более раскованной. Он предлагает группе по кругу назвать фразы-убийцы, которые обычно губят новые идеи – "Не годится!", "Вздор!", "На это нет денег!" и тому подобное. Все фразы модератор заносит на большой лист, а в конце обсуждения этот лист торжественно рвется и выбрасывается – "У нас таких фраз не будет!" После этого начинается непосредственное обсуждение первой проблемы. Как показывает практика первый круг проходит достаточно туго – группа должна "раскачаться", коллективный мозг должен "завестись. Второй и третий круги уже идут достаточно гладко. Модератор может и сам участвовать в мозговом штурме. Когда очередь доходит до него, он, почувствовав, что группа немного выдохлась или зациклилась на одном направлении, может предложить какой-нибудь совершенно парадоксальный вариант, чтобы придать новый стимул мозговой атаке.
По окончании мозгового штурма можно провести один или два тура голосования по такому же принципу, как при выборе приоритетных задач, а можно выбор окончательного варианта решения проблемы отдать на откуп той группе, которая будет разрабатывать конкретный проект (см. следующий этап).
НЕМАЯ ДИСКУССИЯ
Если мы выделили четыре приоритетных задачи, то модератор разбивает всех участников на четыре группы. Каждая группа встает вокруг стола, на котором лежит лист ватмана и карточка с одной из выбранных приоритетных задач. Все группы на протяжении всего этапа работают в полной тишине, не разговаривая и не обсуждая ничего вслух. Можно для фона поставить легкую, не отвлекающую от мыслей музыку. Группа обдумывает поставленную задачу, и затем участники коротко пишут на листе свои варианты ее решения (мероприятия, акции, меры и т.д.). По сигналу модератора (через 5-7 минут), участники переходят по часовой стрелке вокруг своего стола на место соседа, смотрят на предложенные им варианты и могут дополнить их какими-то вновь возникшими своими идеями или задать письменный вопрос, если им что-то непонятно. Затем группа опять переходит по кругу и так далее. Опыт показывает, что иногда необходимо дать возможность участникам сделать 4-5 полных кругов, чтобы они полностью выразили все, что хотят или задали все имеющиеся вопросы. Однако если модератор видит, что группа уже переходит, ничего не дописывая на листе, упражнение можно закончить и раньше. Если позволяет время модератор может попросить группы поменяться столами и посмотреть, что предложено по другим задачам, дополнив их своими вариантами. Если времени мало, группы просто по очереди представляют результаты своего "немого обсуждения" и выслушивают вопросы и комментарии других групп.
ВЕСЬ МИР – ТЕАТР
При необходимости внести творческое начало в генерацию решений, можно предложить группам ролевую игру. Каждая из четырех микро-групп получает свою задачу, варианты решения которой они должны обсудить. Затем каждый член группы вытягивает карточку с ролью. Эти роли могут быть чисто условными (по функции) или совершенно конкретными (для яркости можно надеть ролевые кепки). Примерный список ролей и функций приведен в таблице:
Процесс должен идти достаточно быстро, за этим следит фасилитатор. Говорит только тот, до кого дошла карточка с идеей. Перебивать и комментировать нельзя, можно только задать уточняющие вопросы. Полный круг занимает примерно 5 минут – (Генератор) à 1 мин. Презентатор à 1 мин. Комментатор à 1 мин. Критик à 1 мин. Защитник à 1 мин. вопросы. Группа должна успеть провести по кругу 5-6 идей. Качество самого обсуждения здесь не очень важно – важны быстрота, юмор, энергия, нетрадиционность. Все ценные предложения фиксируются на листе секретарем. Он должен внимательно следить за обсуждением, потому что часто дельное предложение возникает не у Генератора, а у Критика или, скажем, Комментатора, все они должны быть записаны.
АКВАРИУМ
Этот способ самый быстрый, но не всегда самый результативный. Стулья ставятся в два концентрических круга – один лицом внутрь, один – наружу (см. Рисунок 12). Участники садятся лицом друг к другу, разбиваясь таким образом на пары. Все получают чистые карточки. Модератор сообщает первую задачу. Каждая пара за 30 секунд должна выработать два варианта решения этой задачи, записав их на отдельные карточки. Все карточки складываются в одну кучку в центре круга ("коллектор идей"). Через 30 секунд по сигналу модератора внешний круг пересаживается на один стул по часовой стрелке, внутренний остается на месте. Новые пары снова предлагают по два варианта, причем уже предложенные варианты повторять нельзя. Сделав полный круг, группа переходит к следующей задаче, и все повторяется снова. Пока группа обсуждает следующую проблему, модератор может рассортировать предыдущую кучку карточек, убрав повторяющиеся, объединив похожие и так далее. Главный принцип – быстрота и натиск. Чем интенсивнее будет идти обсуждение, тем больше идей будет сгенерировано.
Итак, по окончании этого этапа у нас появился целый набор различных вариантов решения по каждой из четырех задач. Теперь можно переходить к их отбору и детализации, то есть к разработке конкретных проектов. |
mykonspekts.ru
Сравнительный анализ методов решения задачи ранжирования
Транскрипт

1 Московский государственный университет имени М. В. Ломоносова Факультет вычислительной математики и кибернетики Кафедра математических методов прогнозирования Алескин Александр Сергеевич Сравнительный анализ методов решения задачи ранжирования ВЫПУСКНАЯ КВАЛИФИКАЦИОННАЯ РАБОТА Научный руководитель: д.ф-м.н., профессор В.В. Рязанов Москва, 2017
2 1 Содержание 1 Введение 3 2 Функционалы качества NDCG функционал MAP функционал Методы ранжирования OC SVM Ranking SVM LambdaRank ListNet Стандартные признаки для ранжирования 13 5 Сглаживание рейтингов документов 15 6 Добавление тематики 17 7 Эксперименты Сравнение работы алгоритмов ранжирования Сглаживание рейтингов документов Сравнение работы алгоритмов при добавлении тематик Cравнение работы алгоритмов при добавлении тематик и сглаживании рейтингов Заключение 24 Список литературы 25
3 2 Аннотация В данной работе проведен сравнительный анализ существующих методов ранжирования для текстовых документов. Было предложено два метода для повышения качества ранжирования. Первый алгоритм заключается в сглаживании рейтингов документов через рейтинги соседних документов. Цель второго заключается в добавлении дополнительных признаков в виде тематик документа. Были проведены эксперименты, которые подтверждают стабильное улучшение работы методов ранжирования при использовании предложенных алгоритмов.
4 3 1 Введение Сегодня, в связи с быстрым развитием электроники и интернета, доступность информации для человека значительно увеличилась. Однако, при этом существенно возросли и её объёмы: что сделало весьма сложной и актуальной задачу поиска требуемой информации. Один из способов решить данную проблему использовать специальные методы ранжирования, которые позволяют отсортировать необходимую информацию. Задача для данных алгоритмов ставиться следующим образом. Даны поисковый запрос пользователя и список документов, которые надо отранжировать в таком порядке, чтобы вначале шли документы с информацией, которая с большой степенью релевантна к поисковому запросу, то есть документы, которые действительно искал пользователь. Далее по списку релевантность информации в документах убывает и в конце оказываются менее всего подходящие документы к тому, что искал пользователь. Одной из важных областей, где сегодня широко применяются данные методы, являются поисковые системы в интернете, где насчитывается огромное количество уникальных страниц. Используются такие методы и в различных организациях, где существует сравнительно высокий документооборот и зачастую поиск необходимой информации становится затруднительным. Также данные алгоритмы находят применения и в специализированных поисковых системах. Цель данной работы исследовать и сравнить качества работы существующих методов, а также вариантов повышения качества их работы на выборке из поисковых запросов пользователей в интернете. В ходе работы рассматриваются два алгоритма для улучшения ранжирования. Первый алгоритм заключается в сглаживании рейтингов документов через релевантность к поисковому запросу соседних документов. Суть второго состоит в том, чтобы документам добавить признаки в виде принадлежности к некоторым тематикам и сравнивать с тематиками запроса. В данной работе сначала будут описаны стандартные функционалы качества и рассмотрены типовые методы ранжирования для текстовых документов, так как текстовая информация является наиболее распространенная на сегодняшний день. Затем будут разобраны предложенные методы для улучшения качества ранжиро-
5 4 вания. И наконец, будут проведены исследования и сравнительный анализ методов ранжирования с предложенными улучшениями и без них на выборке из поисковых запросов. 2 Функционалы качества Прежде чем описать основные меры качества, которыми будем пользоваться в экспериментах для анализа результатов, введем необходимые обозначения. Пусть q i обозначает i поисковый запрос, D i список всех документов, которые ассоциированы с q i запросом, d i,j j-ый документ из списка D i, π i отсортированный список D i, y i,j метка, показывающая на сколько документ d i,j релевантен к запросу q i. y i вектор меток y i,j, [ ] индикаторная функция. Определим наиболее популярные и информативные функционалы качества алгоритмов ранжирования NDCG и MAP меры качества. 2.1 NDCG функционал NDCG(Normalized Discounted Cumulative Gain) мера качества является нормированной мерой от DCG(Discounted Cumulative Gain) меры, поэтому определим для начала DCG: i, y i ) = G(y i,j )D(π i (j)), j:π i (j) k где k количество первых документов в π i, которые мы учитываем в функционале. Функция G(y i,j ) преобразовывает релевантность документа в его рейтинг, а D(π i (j)) функция значимости порядкового номера документа в ранжированном списке. На практике часто функцию G(y i,j ) определяют как экспоненциальную, то есть G(y i,j ) = 2 y i,j 1, а D(π i (j)) как единица, деленная на логарифм от номера позиции
6 5 1 документа: D(π i (j)) = log 2 (1+π i. Таким образом, функционал намного слабее зави- (j)) сит от порядка документа в первых k позициях, но сильно зависит от релевантности документа. В экспериментах использовалась стандартные значения функций. Из определения функций G(y i,j ) и D(π i (j)) следует, что DCG мера качества имеет следующий вид: i, y i ) = j:π i (j) k 2 y i,j 1 log 2 (1 + π i (j)) NDCG функционал качества, как уже упоминалось, является нормированной величиной DCG так, чтобы результат находился на отрезке от нуля до единицы. Получаем, что для данной нормировки необходимо разделить i, y i ) на максимальное значение, которое может быть у функционала качества при данных значениях π i, y i : i, y i ) = 1 max (π i, y i ) j:π i (j) k 2 y i,j 1 log 2 (1 + π i (j)). Популярность NDCG является следствием хороших свойств данной меры: она позволяет учитывать произвольным образом и порядок, и релевантность документов. Более того, данный функционал качества позволяет работать с разными значениями релевантности. 2.2 MAP функционал В качестве второй удобной меры рассмотрим MAP(Mean Average Precision). Данный функционал учитывает уровень релевантности документа только как бинарная переменная: либо документ релевантный, либо нет. Для определения MAP меры вначале определим функционалы точности P(Precision) и средней точности AP(Average Precision): i, y i ) = t:π i (t) π i (k) [y i,k = 1], k i, y i ) = k m=1 i, y i )[y i,m = 1] k m=1 y. i,m
7 6 Соответственно, M определяется как среднее значение по всем запросам q i.как видно, данный функционал также учитывает и порядок, и релевантность документов, что делает его таким же популярным. Обе меры имеют параметр k количество первых документов в отранжированном списке π i, которые учитываются в функционалах. На практике k выбирается из постановки задачи или других априорных знаний. 3 Методы ранжирования Существует большое количество методов ранжирования. Все методы условно можно классифицировать на три типа [5]: поточечные методы, которые независимо определяют рейтинг для каждого документа, попарные методы, идея которых в сравнении релевантности двух документов, то есть определить порядок для каждой пары документов, и списочные методы моделирует порядок для всех документов в выдаче. С точки зрения поставленной задачи ранжирования, списочные методы являются методами, которые решают исходную постановку задачи. Предложенная классификация строится из способа алгоритма обучения. На этапе прогнозирования и ранжирования методы имеют схожий алгоритм: для каждого документа d i,j вычисляется рейтинг f(x i,j, w), где x i,j вектор признаков документ d i,j, w параметры метода ранжирования, далее рейтинги сортируются по убыванию. В итоге, получаем отранжированный список документов. В задаче ранжирования признаки документов x i,j формируются не только из описания документов или только запроса, но и как функции от поискового запроса и документа: x l i,j = g l (q i, d i,j ), где x l i,j l-признак документа d i,j, а g l (q i, d i,j ) некоторая функция. Такие признаки наиболее информативны, так как показывают степень релевантности документа к запросу. Рассмотрим наиболее часто используемые признаки после описания методов ранжирования. В качестве алгоритмов ранжирования для сравнения выберем наиболее популярные методы из каждой категории: OC SVM (поточечный метод), Ranking SVM (попарный), LambdaRank(попарный), ListNet (списочный). Последовательно рассмотрем каждый метод.
8 7 3.1 OC SVM OC SVM (One Class Support Vector Machine) является одним из базовых методов ранжирования [7]. Алгоритм заключается в построении параллельных гиперплоскостей, которые выступают в роли порогов. По взаиморасположение документа d i,j и гиперплоскостей (лежит он в положительном или отрицательном полупространстве каждой из гиперплоскости) делается предсказание о степени релевантности документа. То есть пусть y i,j Y, где Y = {1, 2,..., l}, тогда метод строит гиперплоскости вида w, x i,j b r = 0, где r от 1 до l 1, w R k, b r R и b 1 b 2 b l 1 b l = +, чтобы правильно определять метки y i,j по следующей формуле: y i,j = min {r w, x i,j b r < 0}. r {1,...,l} Перегруппируем все векторные представления документов x i,j по степени релевантности, то есть ˆx r,k вектор признаков k-ого по счету документа, у которого степени релевантности равна r: y r,k = r, и пусть таких документов m r.таким образом, становиться неважно, к какому запросу q i относиться документ. Тогда задачу поиска таких w и b r можно поставить следующим образом: 1 l 1 2 w 2 + C m r r=1 k=1 (ξ r,k + ˆξ r+1,k ) min w,b,ξ,ˆξ w, ˆx r,k b r 1 + ξ r,k, w, ˆx r,k b r 1 + ˆξ r+1,k, ξ r,k 0,ˆξ r+1,k 0, k = 1,..., m r,r = 1,....l 1, Имеем стандартную задачу квадратичного программирования. Заметим, что алгоритм пытается проводить гиперплоскости, максимизируя отступы (расстояния) элементов до гиперплоскостей.
9 8 3.2 Ranking SVM Данный метод был предложен Р. Хербрих [3] и имеет попарный подход. Ключевая идея алгоритма заключается в использовании алгоритма SVM для попарного сравнения элементов (документов) на то, какой из элементов более релевантный. Пусть имеется два элемента x i и x j и некоторая функция f(x), которая определяет релеватность объекта к запросу. Тогда, то что объект x i релевантнее чем объект x j (x i x j ) эквивалентно тому, что f(x i ) > f(x j ): x i x j f(x i ) > f(x j ). Тогда, если выбрать функцию f(x) = w, x, то имеем, что: f(x i ) > f(x j ) w, x i x j > 0. И если теперь рассматривать разность векторных представлений как новые объекты ˆx i,j = x i x j, получим стандартную постановку SVM алгоритма. Формально задача Ranking SVM ставится следующим образом: 1 2 w 2 + C N i=1 ξ i min w,ξ, y i w, x 1 i x 2 i 1 ξ i, ξ i 0, i = 1,..., N, Где N количество пар объектов, x 1 i первый объект пары, x 2 i второй объект пары, а y i = 1, если x 1 i x 2 i, и y i = 1, если x 1 i x 2 i. Отметим, что пара из объектов x i и x j учитывается дважды как пара (x i, x j ) и (x j, x i ) (соотвественно с y i,j = 1, y j,i = 1). В введенных ранее обозначениях допустимыми парами являются такие x i,j и x r,k, что i = r (то есть документы из одного списка) и y i,j y i,k (то есть имеют разную степень релевантности). Данная постановка задачи позволяет использовать стандартную технику решения SVM переход к двойственной задаче, и как следствие, делать нелинейные преобразования при помощи ядер SVM.
10 9 3.3 LambdaRank В поточечных и попарных методах ранжирования итоговый функционал при обучении обычно не дифференцируемый, так как зависит от порядка элементов. В рассматриваемом алгоритме LambdaRank, описанный Бургес [2], вместо исходного функционала рассматривается непрерывный аналог, который легко оптимизировать. Вначале рассмотрим работу метода для одного поискового запроса. Алгоритм LambdaRank не определяет непрерывный приближенный функционал L, вместо этого он определяет градиент функционала на всем списке документов: L s j = λ j (s 1, y 1,..., s n, y n ), Где s 1, s 2,... s n рейтинги документов, y 1, y 2,..., y n проставленные степени релевантности асессором, n количество документов, найденных для поискового запроса. Таким образом, градиент по выбранному документу зависит от рейтингов и степени релевантности других документов. Знак выбран таким, чтобы положительное значение означало, что документ уменьшает функционал качества. Градиент для каждого документа пересчитывается после каждой генерации отранжированного списка. Функция градиента по всем документам называется лямбда функцией, отсюда и название метода. Один из способов добиться повышения эффективности оптимизации это увеличить градиенты документов на первых позициях, то есть более значимыми сделать перестановки для первых элементов. Пусть, например, имеются два релевантных документа d 1 и d 2 на позициях 2 и n в отсортированном списке. Тогда перестановка документа d 1 на первую позицию должно требовать меньших затрат, чем перестановка документа d 2 на первую позицию, то есть градиент у d 1 должен быть значительно больше. В общем случае, для двух документов d i и d j имеем, если d i d j, то L s i > L s j. Метод позволяет настраиваться на широкий класс функционалов качеств, однако в стандартном варианте (который и будет использоваться) λ вычисляется по функционалу NDCG:
11 10 λ j = L = 1 ( 1 ) (G(yi ) G(y j ))(D(π i ) D(π j )), s j G max 1 + exp(s i s j ) i где функции G( ), D( ) функции преобразования релевантности документа в его рейтинг и значимости порядкового номера документа в ранжированном списке (из определения NGCG меры). λ j показывает насколько надо увеличить рейтинг j документа. Для этого надо изменить веса w (напомним, что рейтинг высчитывается как: s i = w, x r,i ): L w = (i,j) P ( L(si, s j ) s i s i w + L(s i, s j ) s ) j, s j w где P множество пар документов. Пусть P i_ множество документов j, для которых пары документов (i, j) в множестве P, а P _j множество документов i для которых пары документов (i, j) в множестве P, тогда L w L w = n i=1 s i w L(s i, s j ) + s i j P i_ n j=1 s j w можно записать как: L(s i, s j ), s j i P _j Тем самым понизив вычислительную сложность итерации с O(n 2 ) до O(n). Таким образом, алгоритм LambdaRank заключается в итерационном пересчете весов w: w = w η L w, где η итерационный шаг. Очевидно, что если запросов несколько, то все изменения заключаются в расширении множества P допустимых пар, которое может быть построено как и в методе Ranking SVM. Отметим, что приближенный непрерывный функционал L определяется на списке документов, что позволяет рассматривать LambdaRank не только как попарный метод, но и как списочный. 3.4 ListNet Метод ListNet имеет списочный подход и основан на вероятностной модели Plackett-Luce. Впервые алгоритм был описан З. Као [4]. Прежде чем перейти к методу опишем модель Плакетт-Люис. Пусть дан отранжированный список π, и рейтинг документов s = {s 1, s 2,..., s n }. Обозначим за π 1 (i) документ в позиции i отранжированного списка π. Тогда
12 11 Plackett-Luce модель (кратко PL-модель) задает вероятность порядка π при помощи рейтингов s как плотность вероятности следующим образом: P s (π) = s π 1 (1) s π 1 (2) n j=1 s n π 1 (j) j=2 s... s π 1 (n) π 1 (j) s π 1 (n) = n i=1 s π 1 (i) n j=i s. π 1 (j) Данное распределение имеет несколько полезных свойств. Во-первых, список документов с убывающим рейтингом имеет наибольшую вероятность по сравнению со всеми другими перестановками в списке, а с возрастающим рейтингом наименьшую вероятность. Как следствие, перестановка двух документов в убывающем по рейтингу списке приведет к уменьшению вероятности. Во-вторых, PL-модель можно определить на некотором подмножестве первых документов в списке и по-прежнему это будет функцией распределения. Пусть хотим рассмотреть только k первых документов в списке, тогда: P k s = k i=1 Более того, верно следующее утверждение: s π 1 (i) n j=i s. π 1 (j) P k s = π Q P s (π), где Q множество перестановок документов, где первых k документов те же, что и в убывающем по рейтингу списке документов. Алгоритм ListNet может быть применен с PL-распределением по всем документам в списке. Однако, в данном случае вычислительная сложность метода становиться слишком большой O(n!). Поэтому используют PL-распределение на первых k документах ( O( n! (n k!) )). В нотации PL-модели значения релевантности первых k документов из списка можно задать следующим образом: P k y = k i=1 exp(y i ) n j=i exp(y j). Тогда результаты работы метода ListNet в той же форме можно записать как: P k F (x,w) = k i=1 exp(f(x i, w)) n j=i exp(f(x j, w)),
13 12 где f(x, w) модель нейронной сети с параметрами w, а F (x, w) список рейтингов, выданные моделью. Если P k y и P k F (x,w) имеют почти схожие значения, то рейтинги документов, полученные алгоритмом, будут иметь приблизительно те же значения, что и проставленные асессором значения релевантности. Таким образом, достаточно PF k (x,w) приближать к Py k. Для измерения разницы между распределениями и последующей оптимизации удобно использовать KL-дивергенцию. В этом и состоит идея алгоритма. Напомним, что KL-дивергенция в дискретном случае для распределений P и Q имеет следующий вид: KL(P Q) = i p i log p i q i = i p i log p i i p i log q i, и равна нулю тогда и только тогда, когда распределения P и Q совпадают. Получаем, что задача для минимизации функции потерь имеет следующий вид: L(w) = m i=1 L i (y i, F (x i, w)) min w, L i (y i, F (x i, w)) = KL(P k y i P k F (x i,w) ) = g G k i P k y i(g) log P k F (x i,w) (g) где L i функция потерь для i поискового запроса, m количество запросов, G k i множество всевозможных значений для первых k элементов списка. Заметим, что в формуле опущен первый член KL-дивергенции, так как он не зависит от w. Градиент функции потери можно найти по следующей формуле: L(w) w L i (y i, F (x i, w)) w = m i=1 = g G k i L i (y i, F (x i, w)), w P k y (g) P k i F (xi,w) (g) P k (g). w F (x i,w) Метод ListNet заключается в итерационном пересчете L(w) w и обновлении весов модели: w = w η L(w). В экспериментах алгоритм использовался при k = 10 и с w одним полносвязным скрытым слоем нейронной сети.
14 13 4 Стандартные признаки для ранжирования Теперь рассмотрим, как именно формируются признаки из пары запрос-документ. В общем случае, постановка задачи ранжирования подразумевает наличие запроса q i, который представляет из себя последовательный набор слов, и списка документов D i, которые в свою очередь можно представить как последовательный наборы слов в названии и тексте документов. Если детальнее рассматривать поисковую выдачу web-страниц, то в качестве признаков также используются популярность web-ресурса, цитируемость, количество страниц, на которые ссылается страница и другие признаки [6]. Однако, для обобщения остановимся только на текстовых представлениях документа и запроса. Введем некоторые дополнительные обозначения. Пусть T множество всех употребляемых терминов (слов или словосочетаний), N = T количество всех терминов, q k i количество вхождение k-термина в q i поисковый запрос, q i = (qi 1, qi 2,..., qi N ) векторное представление q i запроса, t k i,j количество вождений k-термина в текст d i,j документа, d b i,j = (t 1 i,j, t 2 i,j,..., t N i,j) векторное представление текста d i,j документа, ˆt k i,j количество вхождений k-термина в название d i,j документа, d t i,j = (ˆt 1 i,j, ˆt 2 i,j,..., ˆt N i,j) векторное представление названия d i,j документа, d i,j = (d b i,j, d t i,j) векторное представление d i,j документа. В данной работе, как часто и делают на практике, в качестве терминов выбраны слова. Такие векторные представления описывают поисковый запрос и список документов для ранжирования. Однако, для обучающихся алгоритмов признаки в таком формате мало информативны, так как не показывают взаимосвязи между запросом и документом. Прежде чем перейти к конечным признакам, опишем полезные преобразования: TF(term frequency), IDF(inverse document frequency) и TF-IDF. TF-преобразование это отношение числа вхождений термина к общему числу слов в документе: tf(t k, d i,j ) = t k i,j N, l=1 tl i,j
15 14 IDF-преобразование это логарифм отношения общего числа документов к документам, где встречается данный термин: idf(t k ) = log D T t=1 Di l=1 [tk t,l > 0], где D все документы ( D их общее количество), T количество поисковых запросов. Как видно, IDF-преобразование определяется для термина, когда TFпреобразование определяется для пары термин-документ. TF-IDF является произведением TF и IDF преобразований: tfidf(t k, d i,j ) = tf(t k, d i,j ) idf(t k ). Наконец, опишем признаки для пары (q i, d i,j ), которые используются для обучения алгоритмов: t k q i d tf(t k, d b i,j) b i,j t k q i d tf(t k, d t i,j) t i,j t k q i d i,j tf(t k, d i,j ) t k q i d idf(t k ) b i,j t k q i d idf(t k ) t i,j t k q i d i,j idf(t k ) t k q i d tfidf(t k, d b i,j ) i,j t k q i d tfidf(t k, d t i,j ) i,j t k q i d i,j tfidf(t k, d i,j ) N k=1 tk i,j N ˆt k=1 k i,j N k=1 (ˆt k i,j + t k i,j) сумма TF-частот слов из запроса в тексте сумма TF-частот слов из запроса в названии сумма TF-частот слов из запроса во всем документе сумма IDF-частот слов, встречаемых в запросе и тексте сумма IDF-частот слов, встречаемых в запросе и названии сумма IDF-частот слов, встречаемых в запросе и документе сумма TF-IDF-частот слов из запроса в тексте сумма TF-IDF-частот слов из запроса в названии сумма TF-IDF-частот слов из запроса во всем документе длина текста длина названия длина всего документа К данным признакам часто добавляют признаки, которые являются результатами простейших моделей ранжирования, такие как BM25 и LMIR [6]. Поскольку обе модели требует настройки некоторых параметров, то для чистоты экспериментов не будем их использовать.
16 15 Как видно, в таком формате признаки представляют собой некоторые частотные оценки встречаемости слов во всем документе и отдельных его частях. При таком количестве признаков и их смысловой нагрузки не так много пространства для обучения алгоритмов. Можно в качестве признаков использовать частотные оценки по каждому термину. Однако, в этом случае не совсем понятно, как применять алгоритмы, потому что теряется возможность ранжировать списки для новых запросов, которые не были в обучающей выборке, что является одним из важнейших требований. Рассмотрим несколько вариантов, как можно улучшить результаты ранжирования. 5 Сглаживание рейтингов документов На практике в качестве поисковых запросов часто выступает короткий набор слов. Как показывалось выше, признаки будут состоять только из частотных оценок встречаемости этих слов в документах. При этом, если документ является релевантным и даже содержит синонимичные слова, то он будет проигнорирован, поскольку нет слов из короткого поискового запроса. То есть проблема заключается в том, что запрос слишком короткий, чтобы можно было оценить некоторые документы "по-настоящему" на сколько релевантен он запросу. Пусть справедливо следующее предположение: размер документов в среднем значительно больше, чем размер поискового запроса. Тогда если два документы похожи по смыслу, то можно оценить релевантность одного документа через релевантность второго. Рассмотрим пример. Пусть есть запрос q, состоящий из двух слов q 1 и q 2, и три документа d 1, d 2, d 3, каждый из которых состоит из тысячи слов, и первых два документа релевантны к запросу. И пусть у d 1 документа слова q 1 и q 2 встречаются, а у остальных нет, и при этом остальные слова у d 1 такие же как и у d 2. Очевидно, что требуется, чтобы алгоритм отражнировал документы по порядку, то есть d 1 d 2 d 3 (или d 2 d 1 d 3 ). Однако, с точки зрения алгоритма, не будет никакой разницы между порядками d 1 d 2 d 3 и d 1 d 3 d 2, так как документы d 2, d 3
17 16 будут иметь идентичное признаковое представление. Но если мы учтем, что первые два документа очень сильно похожи и частично учтем рейтинг d 1 документа для d 2, то получим в точности правильный порядок. Опишем метод сглаживания рейтингов более формально. Пусть алгоритм ранжирования для поискового запроса q i и списка документа выдал рейтинги документов f(x i,1, w), f(x i,2, w),..., f(x i,ni, w), тогда конечный рейтинг s i,j документа d i,j будем вычислять следующим образом: s i,j = f(x i,j, w) + α ( K a j,zk f(x i,zk, w) ), где α и K параметры, показывающие насколько сильно учитывать рейтинги других документов и сколько наиболее близких по смыслу документов рассматривать, a j,zk степень близости между d i,j и d i,zk документами, а z k k-ый по близости документ d i,j. В качестве меры близости для документов наиболее информативна косинусная k=1 мера. То есть a j,zk высчитываются по формуле: a j,zk = d i,j, d i,zk d i,j 2 d i,zk 2, где 2 евклидова норма. Косинусная мера для пары документов равна ρ(d i,j, d i,zk ) = 1 a j,zk. Отметим, что метод не вносит никаких изменений в алгоритм ранжирования. До начала формирования признаков для пары запрос-документ, надо для каждого документа найти похожие по косинусной мере документы из списка выдачи. И после работы алгоритма учесть в рейтинге документа рейтинги схожих документов. Для данного метода можно провести аналогию с алгоритмом k-ближайших соседей. Тем самым можно улучшить работу метода, используя разные виды алгоритмов из семейства методов k-ближайших соседей. Вообще говоря, чтобы найти несколько ближайших документов надо перебрать все документы, то есть сложность алгоритма O( T n 2 ), где T множество всех слов в словаре, а n количество документов в выданном списке. Такая сложность может быть затруднительной в момент ранжирования списка. Но так как документы поступают не в момент запроса, а уже загружены в систему ранжирования, и
18 17 мера близости не зависит от запроса, то близкие по смыслу документы могут быть посчитаны заранее. 6 Добавление тематики Основная проблема стандартных используемых признаков заключается в том, что одни и те же вещи можно описать несколькими разными словами, при этом смысл будет одним и тем же. Но так как алгоритм не может определить по словам, что смысл один и тот же, то документы, где нет слов из с поискового запроса, будут проигнорированы. Попробуем решить эту проблему другим способом. Суть задачи ранжирования состоит в поиске документов, подходящих по смыслу к поисковому запроса. Попытаемся определить этот смысл запроса и смысл документов, и сопоставить, насколько эти смыслы похожи. Достоверно смысл документа и запроса определять не требуется, надо только определить схожесть смысла документа и запроса. Здесь неявно используется тот факт, что и запрос и документы представляются словами, то есть из одного признакового пространства. Из выше сказанного можно сделать вывод, что достаточно будет определить насколько сильно принадлежит документ и запрос к некоторым темам. То есть получить вектор принадлежности к некоторым темам как запросов, так и документов. Далее остается только сравнить вектора запроса и документов, где опять можно воспользоваться косинусной мерой. Таким образом, получаем дополнительный признак схожесть тем. Так как схожесть тематик является достаточно информативным признаком, то можно использовать и несколько мер или рассматривать разность вероятностей принадлежностей к темам поискового запроса и документа. Однако, для упрощения экспериментов будем использовать только косинусную меру. Рассмотрим алгоритм подробнее. Для моделирования тематик воспользуемся моделью латентного размещения Дирихле (LDA) [1]. Данная модель позволяет разбить список документов на произвольное количество тематик, причем один документ может принадлежать сразу к нескольким темам. Каждая тематика рассматривается
19 18 как некоторое распределение вероятностей в пространстве слов из общего словаря. Вероятностная модель LDA задается как D N d p(t, Z, Θ Φ, α) = p(θ d α) p(t d,n z d,n, Φ)p(z d,n θ d ), d=1 n=1 p(θ α) = Dir(θ d α), p(t d,n z d,n, Φ) = Φ zd,n,t d,n, p(z d,n θ d ) = Θ d,zd,n, Где Dir( ) распределение Дирихле, θ d вероятности тематик в документе d, z d,n тематика n-ого слова в документе d, Φ вероятности встретить термин в каждой тематике ( Φ R C T, где C количество тематик), а Z и Θ разбиение всех слов по тематикам и вероятности тематик во всех документах соответственно. И требуется найти максимум распределения p(t Φ, α) по Φ, α. Так как в экспериментах используется реализованный метод LDA, то не будем здесь вдаваться в подробности алгоритма обучения модели. Отметим, что метод можно обучать на множестве документов, который не имеет отношений к выборке, так как не ставиться задача разбить документы выборки по темам. Что позволяет обучать алгоритм на большем множестве документов и точнее определять принадлежность слов к некоторым темам. Однако, нельзя забывать, что другой набор данных может сильно не походить на типовые документы из задачи ранжирования, что может привести к ухудшению определения тематик. В данной работе алгоритм LDA обучался на документах из поисковой выдачи документов. 7 Эксперименты Проведем сравнительные эксперименты по работе алгоритмов ранжирования, а также сравним работу методов при использовании сглаживания рейтингов, добавлении меры схожести тематик и использовании сглаживания рейтингов с добавлением меры схожести тематик. В качестве выборки используется данные о 915 поисковых запросах, где для каждого запроса проставлена метка из трех типов релевантности: 0 документ не ре-
20 19 левантен, 1 документ релевантен, 2 документ сильно релевантен. Для каждого поискового запроса в выдаче размечено от 30 до 50 документов в зависимости от запроса, причем около 30-40% из них имеют положительную метку. Каждый документ является вебстраницей и представляет собой словарь из шести полей: url адрес страницы, title название страницы, meta мета-данные, текст указанный в некоторых тегах вебстраницы для поисковых систем, menu текст страницы, относящийся к навигации (меню) по сайту, footer контактная информация администраторов сайта, а также дополнительная навигация, body остальной текст на вебстранице. Поисковый запрос представляет собой набор слов. В качестве признаков для пары запрос-документ используется сумма TF, IDF и TF-IDF-частот слов, встречаемых в запросе и частей документа title, menu, body, footer, а так же и всего документа. Также используются длины текста во всех полях документа (в том числе url). Так как выборка не слишком большая, то для чистоты экспериментов, будем делать кросс-валидацию по 5 подвыборкам, которые состоят из 183 поисковых запросов и получены случайном образом из генеральной совокупности. Каждый раз для обучения будем использовать 4 подвыборки и одну для контроля, а результаты по пяти конфигурациям усреднять. Для начала сравним работу методов между собой. 7.1 Сравнение работы алгоритмов ранжирования Сравнивать работу алгоритмов будем сразу для MAP и NDCG функционалов качеств при k = 1, 5, 10. Также в таблицу для сравнения включим случайным образом сгенерированный порядок документов в поисковой выдачи. Это нужно, чтобы сравнить, как работают алгоритмы в целом, так как даже при случайном выборе функционалы качества не стремятся к нуля ( это связано с тем, что немалая часть документов в выдаче имеют положительный результат и при случайном выборе так же берутся документы и с положительной меткой). Результаты экспериментов в таблице 1. Как видно, попарные и списочные методы значительно лучше работают, чем поточечный метод, и почти в два раза лучше, чем
21 20 Algorithm Random OC SVM RankingSVM LambdaRank ListNet Таблица 1: Сравнение работы алгоритмов случайный выбор документов. Напомним, что данные имеют три степени релевантности, что в частности отображает тот факт, что LambdaRank и ListNet примерно одинаково работают. Отметим, что LambdaRank при обучении настраивается на NDCG функционал качества. 7.2 Сглаживание рейтингов документов Рассмотрим работу метода при разном количестве соседних документов K, рейтинги которых учитываются, и разном значении параметра α параметре, показывающем, насколько сильно необходимо учитывать рейтинги соседних документов. Для каждого значения K наилучшим значением параметра α было в интервале от 5 до 10. Для наглядности на рисунке 1 приведены результаты экспериментов для наиболее показательных значений параметров по мере Остальные рассматриваемые функционалы ведут себя идентичным образом на данных. Лучшее значение для функционала достигается при K = 8 и α = 10, причем улучшение составляет больше чем 15%. Отметим, что при α > 10 наблюдается некоторая стабилизация, что является следствием того, что собственный рейтинг учитывается значительно меньше и конечный рейтинг строится по близким по смыслу документам. Такая оптимальность по функционалу при сравнительно больших значениях K объясняется тем, что рейтинги соседних документов берутся с коэффициентами "близости"a j,zk, поэтому если ближайшие по косинусной мере документы находятся далеко, они слабо учитываются.
22 K = 1 K = 3 K = 5 K = 8 K = 10 K = 20 with different parameters 0.70 Score alpha value Рис. 1: Значение функционала при разных параметрах Результаты экспериментов по всем алгоритмам и рассматриваемым функционалов приведены в таблице 2. В таблице указаны лучшие значения при разных параметрах K, α. Для удобного сравнения в первой графе ( Best without ) приведены лучшие результаты из таблицы 1. Заметим, что функционалы повысились больше чем на 16%, а повысились в среднем на 11%. Вероятная причина данной разницы заключается в том, что документы с релевантностью 1 и 2 с точки зрения алгоритма сглаживания неразличимы, то есть разница между косинусными мерами документов с релевантностями 2 и 1 и 2 и 2 не слишком большая. А так как документов с релевантностями 2 меньше чем с 1, то документы с релевантностью 2 больше настраиваются на документы с релевантностью 1. Таким образом, в начале отранжированного списка получается больше документов с релевантностью 1.
23 22 Algorithm Best without OC SVM RankingSVM LambdaRank ListNet Таблица 2: Сравнение работы алгоритмов для сглаживания рейтингов 7.3 Сравнение работы алгоритмов при добавлении тематик Вообще говоря, у алгоритма LDA есть несколько параметров, которые надо настраивать под данные. Однако, так как не требуется точно приблизить разбиение тематик по документам, а лишь получить векторное представление по документам, чтобы сравнить с тематиками поискового запроса, то для настраивания выберем только количество тематик. Рассмотрим работу алгоритмов при N = {10, 25, 50, 75, 100, 150, 200} темах. На рисунках 2-3 приведены результаты для функционалов и Как видно, лучшие результаты достигаются при N = with different amount of topics with different amount of topics Score Amount of topics Score Amount of topics Рис. 2: при разном количестве тематик Рис. 3: NDCG10 при разном количестве тематик
24 23 Algorithm Best without OC SVM RankingSVM LambdaRank ListNet Таблица 3: Сравнение работы алгоритмов при добавлении признаков Algorithm Best without OC SVM RankingSVM LambdaRank ListNet Таблица 4: Сравнение работы алгоритмов при добавлении признаков и сглаживании рейтингов Лучшие результаты экспериментов приведены в таблице 3. Заметим, что добавление тематик сильно улучшило показатели функционалов, которые учитывают первых 5 и 10 объектов в ранжированном списке. В среднем наблюдается улучшение на 19% и на 15% по MAP и NDCG мерам соотвественно. 7.4 Cравнение работы алгоритмов при добавлении тематик и сглаживании рейтингов Рассмотрим улучшение при работе обоих методов. Параметры для алгоритмов возьмем те же самые. В таблице 4 приведены лучшие результаты. Из результатов экспериментов следует, что вместе алгоритмы не слишком сильно улучшают качество функционалов. Однако, в итоге получается улучшить функционалы качества в среднем на 18%.
25 24 8 Заключение В данной работе были рассмотрены несколько методов ранжирования и проведен их сравнительный анализ на выборке из поисковых запросов. Также были предложены и рассмотрены алгоритмы сглаживания рейтингов и добавление тематических признаков. Для проведения экспериментов были реализованы описанные методы и алгоритмы на языке Python. В ходе данной работы были получены следующие результаты: Среди рассматриваемых алгоритмов ранжирования OC SVM, Ranking SVM, LambdaRank, ListNet лучшие показатели у LambdaRank, Алгоритм сглаживания рейтингов через рейтинги соседних документов улучшает работу в среднем на 13%, Добавление тематических признаков улучшает работ в среднем на 17%, При применении обоих методов получается улучшить функционалы качества в среднем на 18%. Таким образом, были решены и рассмотрены все поставленные задачи: исследовать и сравнить качества работы существующих методов ранжирования из разных классов, предложить алгоритмы для улучшения качества работы методов ранжирования на выборке из поисковых запросов.
26 25 Список литературы [1] Blei D. M., Ng A. Y., Jordan M. I. Latent dirichlet allocation // J. Mach. Learn. Res Vol. 3. Pp [2] Burges C. J., Ragno R., Le Q. V. Learning to rank with nonsmooth cost functions // Advances in Neural Information Processing Systems 19 / Ed. by P. B. Schölkopf, J. C. Platt, T. Hoffman. MIT Press, Pp [3] Herbrich R., Graepel T., Obermayer K. Support vector learning for ordinal regression // In International Conference on Artificial Neural Networks Pp [4] Learning to rank: From pairwise approach to listwise approach / Z. Cao, T. Qin, T.-Y. Liu et al. // Proceedings of the 24th International Conference on Machine Learning. ICML 07. New York, NY, USA: ACM, Pp [5] Li H. Learning to Rank for Information Retrieval and Natural Language Processing. Morgan & Claypool Publishers, [6] Liu T.-Y. Learning to rank for information retrieval // Found. Trends Inf. Retr Vol. 3, no. 3. Pp [7] Shashua A., Levin A. Ranking with large margin principle: Two approaches // In Proceedings of Advances in Neural Information Processing Systems / Ed. by NIPS
docplayer.ru