Цель априорного ранжирования факторов? Априорное ранжирование факторов
Метод априорного ранжирования — Мегаобучалка
Наиболее простым является метод априорного ранжирования, основанный на экспертной оценке факторов группой специалистов, компетентных в исследуемой области.
Метод априорного ранжирования сводится к следующему:
1. Организацией или специалистом, проводящим экспертизу, на основании анализа литературных данных, обобщения имеющегося опыта, опроса специалистов, дерева систем и т. д. определяется предварительный перечень факторов, требующих ранжирования.
2. Составляется анкета, в которой приводится в табличной форме перечень факторов, необходимые пояснения и инструкции, примеры заполнения анкет.
3. Осуществляется комплектация и проверка компетенции группы экспертов, которые должны быть специалистами в рассматриваемых вопросах, но не быть лично заинтересованными в результатах.
4. Экспертами осуществляется индивидуальная оценка предложенныхфакторов с помощью рангов, в процессе которой факторы располагаются в порядке убывания их влияния на результирующий признак или объект исследования, являющийся целевой функцией. Ранг обозначается следующим образом akm, где т- условный номер эксперта; K - номер фактора. При этом фактор, имеющий наибольшее влияние, оценивается первым рангом (цифрой 1). Фактору, имеющему меньшее значение, приписывается второй ранг (2) и т. д.
Последовательность обработки результатов априорного ранжирования:
1. Индивидуальные оценки всех экспертов сводятся в таблицу априорного ранжирования (табл. 2).
2. Определяется сумма рангов всех экспертов по каждому фактору:
где m=5 - сумма экспертов; к = 5 - число факторов.
3. Проверяется правильность заполнения таблицы.
Во-первых, максимальный ранг по конкретному фактору (аkm) не может быть больше числа сравниваемых факторов (K).
Во-вторых, максимальное значение суммы рангов по любому фактору не может быть больше произведения максимально возможного ранга на число экспертов:
В примере:
В-третьих, минимально возможная сумма рангов по любому фактору не может быть меньше минимального ранга , умноженного на число экспертов:
В примере:
Таблица 2
Результаты априорного ранжирования факторов
| № п/п | Факторы оценки | Номера экспертов, m; ранги оценки аkm | Сумма рангов ΔK | Отклон-ие суммы рангов Д\ | (А'k)2 | Место Mi | Вес фактора qk | ||||
| I | Производительность | -6 | 0,27 | ||||||||
| Надежность | -8 | 0,29 | |||||||||
| Безопасность | 0,23 | ||||||||||
| Качество работ | 0,09 | ||||||||||
| Удобство в эксплуатации | 0,12 | ||||||||||
| Итого: |
11. Строится априорная диаграмма рангов и определяются удельные веса факторов по их влиянию на целевой показатель:
где М - место фактора при ранжировании.
Проверка:
Преимущества априорного ранжирования: сравнительная простота
организации процедуры и оперативность получения результатов.
Недостатки априорного ранжирования: большая зависимость результатов от качества организации экспертизы и подбора экспертов, правильной постановки вопросов и выбора факторов для данной системы
Рисунок 1.Априорная диаграмма рангов
Метод бальных оценок
Оценку оборудования произведем по следующим критериям:
1) Мобильность и автономная работа. Требование основывается на том, чтобы диагностическое оборудование возможно было транспортировать в пределах сервисного центра в виде набора с минимальным весом. Набор может быть представлен как кейс со специальными отсеками для временного хранения наиболее часто используемых элементов оснастки (кабели, переходники для разъемов и пр.) Данное требование является необходимым для реализации дилерской программы «KIA ASSISTANCE. Помощь на дороге», которая подразумевает использование диагностического оборудования путем выезда специалиста на место нахождения неисправной машины (т.е. не требуя транспортировки автомобиля в сервисный центр) .
2) Возможность обновлений и стоимость поддержки в год. Возможность обновления программы диагностического оборудования для реализации дополнительных функций, которые были введены в интерфейс устройства уже после продажи.
3) Стоимость оборудования. Данный критерий указывает на то, сколько времени потребуется для полной окупаемости оборудования.
4) Надежность. Данный критерий включает в себя страну производителя и гарантийный срок обслуживания. Гарантийный срок работы оборудования должен составлять не менее 12 месяцев.
5. Эргономичность интерфейса пользователя. Предполагается наличие интуитивно понятного интерфейса желательно на языке пользователя. Как правило на оборудовании иностранного производства используется набор из восьми языков (английский, немецкий, французский, итальянский, традиционный китайский, польский, японский, финский). Отсутствие в интерфейсе языка пользователя (в нашем случае это русский) накладывает ряд требований к пользователю по знаниям иностранных языков.
Таблица 3.32 – Оценка диагностического оборудования
| Марка модель | Мобильность и автономная работа (0,2) | Возможность обновлений и стоимость поддержки в год. (0,2) | Стоимость оборудования (0,3) | Надежность (0,2) | Эргономичность интерфейса пользователя (0,1) | Итого: |
| Hi-Scan Pro | 2,2 | |||||
| Carman Scan CM VG | 2,4 | |||||
| MEGA MACS 55 | ||||||
| Auto Boss V30 | 2,3 | |||||
| X431 Master | 2,8 |
Веса критериев указаны в скобках (мобильность и автономная работа - 0.2, возможность обновлений и стоимость поддержки в год - 0,2, стоимость оборудования - 0,3, надежность - 0,2, эргономичность интерфейса пользователя - 0,1).
Для каждого варианта суммируем оценки по критериям, умноженные на веса этих критериев. Например, для X431 Maste:r 3*0,2+3*0,2+3*0,3+2*0,2+3*0,1=2,8
Таким образом, по результатам оценки, наиболее приемлемым вариантом оказался сканер X431 Master.
Перечень выбранного оборудования и производственного инвентаря для каждого рабочего поста или производственного участка заносят в таблицу, форма которой представлена в табл.1.
При этом для переносного и настольного оборудования габаритные размеры не приводятся.
Таблица 1 - Перечень оборудования производственного участка
| № поз. | Наименование оборудования | Тип, модель | Количество | Краткая техническая характеристика | Габаритные размеры, м | Стоимость, руб. |
Приложение1
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФИЛИАЛ ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО АВТОНОМНОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
"КАЗАНСКИЙ (ПРИВОЛЖСКИЙ) ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ"
В Г. НАБЕРЕЖНЫЕ ЧЕЛНЫ
Кафедра «Сервис транспортных систем»
КУРСОВАЯ РАБОТА
по дисциплине «Технические средства предприятий сервиса»
на тему: «Выбор оборудования для шиномонтажного участка (монтажно-демонтажные работы)»
КР.1.100101.65.14.86.01.00.00.00.ПЗ
Выполнил: ст.гр. 1102175
Баранов Е.В.
Проверил: к.т.н., доцент
Габсалихова Л.М.
Набережные Челны
Приложение 2
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФИЛИАЛ ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО АВТОНОМНОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
"КАЗАНСКИЙ (ПРИВОЛЖСКИЙ) ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ"
В Г. НАБЕРЕЖНЫЕ ЧЕЛНЫ
Кафедра «Сервис транспортных систем»
megaobuchalka.ru
Априорное ранжирование факторов
⇐ ПредыдущаяСтр 2 из 8Следующая ⇒На стадии предварительного изучения объекта часто бывает полезным априорное ранжирование факторов, заключающееся в обработке данных, полученных в результате опроса специалистов или из исследований, опубликованных в литературе. Это позволяет дать сравнительную оценку влияния различных факторов на параметр оптимизации и тем самым правильно отобрать факторы для последующего активного эксперимента, обоснованно исключив некоторые из них из дальнейшего рассмотрения. Априорное ранжирование факторов основано на методах ранговой корреляции и парных сравнений.
Особенность метода априорного ранжирования факторов заключается в том, что факторы, которые согласно априорной информации могут иметь существенное влияние, ранжируются в порядке убывания вносимого ими вклада. Вклад каждого фактора оценивается по величине ранга-места, которое отведено специалистом при опросе (автором статьи) данному фактору при ранжировании всех факторов с учетом их предполагаемого влияния на параметр оптимизации. При сборе мнений путем опроса специалистов каждому из них предлагается заполнить анкету, в которой перечислены факторы, их размерность и предполагаемые интервалы варьирования. Заполняя анкету, специалист определяет место факторов в ранжированном ряду. Одновременно он может включить дополнительные факторы или высказать мнение об изменении интервалов варьирования.
Опрос может быть очным и заочным. При заочном опросе личный контакт исследователя с экспертом отсутствует. Преимущество этого метода заключается в его простоте и дешевизне, однако он дает большое число незаполненных или неправильно заполненных анкет. Очный опрос дает лучшие результаты, однако требует большей затраты времени и средств. Кроме того, во время личной беседы с экспертом исследователь, помимо своего желания, может определенным образом воздействовать на ответы эксперта. Поэтому предварительно должен быть составлен и испытан план (сценарий) личной беседы, а в процессе опроса исследователю необходимо строго придерживаться определенных заранее формулировок вопросов.
Результаты опроса специалистов (или ранжирование по литературным данным) обрабатывают следующим образом. Сначала определяют сумму рангов по факторам:
где, — ранг каждого -го фактора у j-го эксперта; т — число экспертов; k — число факторов.
Затем вычисляют разность ; между суммой каждого фактора , и средней суммой рангов Т:
=
и находят сумму квадратов отклонений S:
.
Полученные данные позволяют построить среднюю диаграмму рангов, предварительно оценив степень согласованности мнений экспертов с помощью коэффициента конкордации (коэффициента согласия) W, предложенного Кендэлом:
(3.1)
где — число одинаковых рангов в j-м ранжировании. Использовать коэффициент конкордации можно после оценки его значимости, которая возможна с помощью таблиц распределения Пирсона ( ). Величина имеет - распределение с числом степеней свободы . Расчетное значение критерия определяют по формуле:
(3.2)
Гипотеза о наличии согласия экспертов может быть принята, если при заданном числе степеней свободы табличное значение меньше расчетного для 5%-ного (или 1%-ного) уровня значимости.
Оценив согласованность мнений всех экспертов, строят среднюю диаграмму рангов, откладывая по одной оси факторы, а по другой — соответствующие суммы рангов. Чем меньше суммы рангов данного фактора, тем выше его место в диаграмме. С помощью диаграммы оценивают значимость влияния факторов на параметр оптимизации. В случае экспоненциального убывания суммы рангов часть факторов можно исключить из дальнейшего рассмотрения, отнеся их влияние к шумовому полю. Если же распределение суммы рангов равномерное, то рекомендуется включить в эксперимент все факторы.
В ситуации с очень большим числом факторов, кроме общей согласованности мнений экспертов, рассматривают с помощью - распределения и согласованность по каждому фактору в отдельности.
Приведем небольшой пример априорного ранжирования факторов. Изучалось влияние на параметр оптимизации 12 факторов ( 12) с помощью четырех экспертов ( 4). Данные опроса были использованы для априорного ранжирования факторов с целью выделения наиболее существенного из них. Матрица рангов, полученная из анкет, приведена в табл. 3.1.
Таблица 3.1 Матрица рангов
| Эксперты (m=4) | Факторы (k=12) | = |
| 10,5 | 10,5 | 10,5 | 2,5 | 2,5 | 10,5 | 60+6=66 | ||||||||
| 2,5 | 2,5 | 5,5 | 5,5 | 5,5 | 5,5 | 60+6=66 | ||||||||
| 9,5 | 9,5 | 6,5 | 6,5 | 6+6=12 | ||||||||||
| 0+0=0 | ||||||||||||||
| 35,5 | 38,5 | 44,5 | 17,5 | 18,5 | 45,5 | 12,5 | 15,5 | 21,5 | 20,5 | |||||
| 9,5 | 12,5 | 18,5 | -20 | -8,5 | -7,5 | 19,5 | -13,5 | -10,5 | -4,5 | -5,5 | ||||
| 90,2 | 342,2 | 72,2 | 56,2 | 182,25 | 110,2 | 90,25 | 30,2 | S=1940,5 |
Используя формулу (3.1), рассчитывали коэффициент конкордации
Значимость коэффициента конкордации проверяли по - критерию по формуле (3.2):
.
По таблицам находим табличное значение для 5%-ного уровня значимости при числе степеней свободы =19,75. В связи с тем, что можно с 95%-ной доверительной вероятностью утверждать, что мнение экспертов относительно степени влияния факторов согласуется достаточно хорошо ( 0,866). Это позволяет построить среднюю диаграмму рангов рассматриваемых факторов (рис. 3.2).
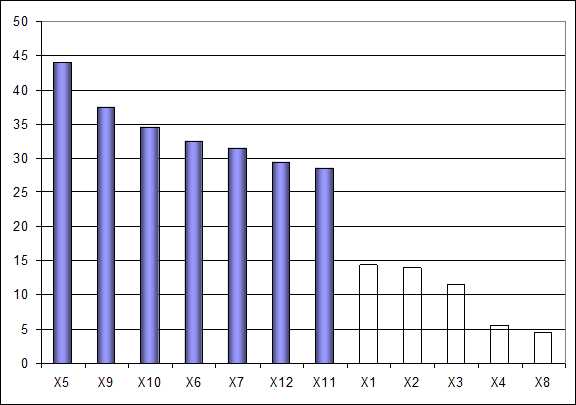
Рис. 3.2. Средняя априорная диаграмма рангов
По результатам проведенного ранжирования факторов отобрано для дальнейших исследований семь факторов, занимающих на диаграмме семь первых мест.
Читайте также:
lektsia.com
Априорное ранжирование факторов
Министерство образование и науки
Федеральное государственное бюджетное образовательное учреждение
"Тихоокеанский государственный университет"
Кафедра "Компьютерного проектирования и сертификации машин"
Методические указания к проведению практических занятий и УИРС для студентов специальности 15102.65 "Металлообрабатывающие станки и комплексы", 200503.65 "Стандартизация и сертификация" и 220501.65 "Управление качеством" и 150401.65 "Проектирование технических и технологических комплексов"
ХАБАРОВСК
2013
УДК 821.9:661.3.068
Методические указания к проведению практических занятий и УИРС для студентов специальностей 15102.65 "Металлообрабатывающие станки и комплексы", 200503.65 "Стандартизация и сертификация", 220501.65 "Управление качеством" и 150401.65 "Проектирование технических и технологических комплексов"
Методические указания содержат краткие сведения по методике отбора факторов и их априорного ранжирования. Могут быть использованы в любой области научных исследований, где требуется провести предварительный отбор факторов, оказывающих наибольшее влияние на исследуемый объект. Приведено описание программного комплекса, предназначенного для автоматизации ввода, обработки и анализа данных по результатам опроса мнений группы специалистов-экспертов в данной предметной области.
| Методические указания: Разработал к.т.н., доцент _________________________ Ю.Г. Иванищев Подпись Методические указания утверждены на заседании кафедры протокол №_12_ от «_18_»_марта_2013г. |
| Заведующий кафедрой ________________ «_18_»_марта_2013г. |
| Подпись |
Цель работы
ПРЕДВАРИТЕЛЬНОЕ ОПРЕДЕЛЕНИЕ ФАКТОРНОГО ПРОСТРАНСТВА
Для выявления факторного пространства на первом этапе может быть использована схема Исикава [1,2]. Схема представляет собой графическое упорядочение многообразных факторов, влияющих на объект анализа и характеризующих конкретные результаты деятельности или процесса. Основное достоинство такой схемы – наглядность представления как о совокупности факторов, воздействующих на объект исследования, так и о причинно-следственных связях этих факторов.
Построение схемы Исикава начинается с определения главных факторов, которые изображаются в виде больших (первичных) векторов подводимых к горизонтальной строке, направленной к объекту анализа. Далее к каждому первичному вектору подводят векторы второго порядка, к которым, в свою очередь, подводят векторы третьего порядка, и так далее. Эта процедура повторяется до тех пор, пока на схему не будут нанесены все факторы, оказывающие заметное влияние на объект.
Анализ последовательности расположения не имеет принципиального значения. Основным при построении схемы является обеспечение правильности соподчиненности и взаимозависимости факторов. А это зависит от квалификации разработчиков и максимальной информированности об объекте исследования.
На рис.1 приведен пример схемы Исикава, иллюстрирующий общий случай воздействия различных факторов на качество выпускаемой предприятием продукции.
На основе схемы Исикава могут быть выделены основные значимые факторы для дальнейшего их априорного ранжирования. Процедура выделения значимых факторов проводится в два, три этапа группой специалистов с промежуточными обсуждениями.
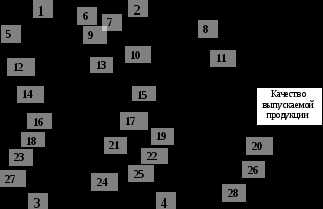
Рис. 1. Схема влияния факторов на качество выпускаемой продукции:
1 – качество труда; 2 – качество документации; 3 – качество средств труда; 4 – качество предметов труда: 5 – условия труда; 6 – состояние социально-психологического климата в коллективе; 7 – полнота технических требований; 8 – научно-технический уровень; 9 – отношение к труду; 10 – доступность изложения; 11 – правильность оформления; 12 – профессиональная подготовка работников; 13 – организация труда; 14 – образование работников; 15 – обеспеченность документацией; 16 – технологическая подготовка производства; 17 – соответствие современным требованиям; 18 – метрологическое обеспечение; 19 – условия хранения; 20 – соответствие установленным требованиям; 21 – качество технологического оборудования, 22 – условия транспортирования; 23 – качество инструмента; 24 – механизация и автоматизация производства; 25 – обеспеченность предметами труда; 26 – качество выходного контроля; 27 – обеспеченность средствами труда; 28 – качество нормировки.
АЛГОРИТМ РАНЖИРОВАНИЯ ФАКТОРОВ
Априорное ранжирование факторов – это процедура, осуществляемая возможно большей группой специалистов, которые располагают предложенные заранее факторы в порядке убывания их значимости по степени их влияния на объект (отклик).
Априорное ранжирование осуществляется в несколько этапов.
ПОСТАНОВКА ЗАДАЧИ, ОРГАНИЗАЦИЯ И ПРОВЕДЕНИЕ ОПРОСА
Постановка задачи заключается в предварительном определении факторов, значимо влияющих на объект исследования. Эту процедуру можно провести с помощью схемы Исикава.
Опрос можно проводить с помощью анкетирования или другим способом [З]. При ранжировании каждому фактору присваивается (по мнению специалиста) ранг в пределах от 1 до k (k – количеств факторов).
Если два и более факторов считаются равнозначными, им присваиваются равные ранги.
Порядок расположения факторов при опросе должен быть выбран случайным. Об этом опрашиваемые специалисты должны быть предупреждены заранее. В противном случае, как установлено, порядок расположения факторов может повлиять на их ранжирование. Для того, чтобы исключить взаимное влияние мнений нескольких специалистов, их опрос должен проводиться независимо друг от друга.
studfiles.net
Тарасов Р.В., Макарова Л.В., Бахтулова К.М. Оценка значимости факторов методом априорного ранжирования
Тарасов Роман Викторович1, Макарова Людмила Викторовна2, Бахтулова Кристина Михайловна31Пензенский государственный университет архитектуры и строительства, к.т.н., доцент2Пензенский государственный университет архитектуры и строительства, к.т.н., доцент3Пензенский государственный университет архитектуры и строительства, магистр техники и технологии
Tarasov Roman Viktorovich2, Makarova Ludmila Viktorovna2, Bahtulova Christina Mikhailovna31Penza State University of Architecture and Construction, Candidate of Technical Sciences, Associate Professor2Penza State University of Architecture and Construction, Candidate of Technical Sciences, Associate Professor3Penza State University of Architecture and Construction, master of technics and technology
Библиографическая ссылка на статью:Тарасов Р.В., Макарова Л.В., Бахтулова К.М. Оценка значимости факторов методом априорного ранжирования // Современные научные исследования и инновации. 2014. № 4. Ч. 1 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2014/04/33181 (дата обращения: 23.09.2018).
Экспериментальные исследования ведутся практически во всех областях науки и техники и преследуют цель получения новых фактов об исследуемом объекте. При использовании статистического подхода к планированию эксперимента и последующей обработке экспериментальных данных необходима четкая стратегия, например, следующая последовательность действий [1]:
1. Признание факта существования задачи и ее формулировка.
2. Выбор факторов и уровней.
3. Выбор переменной отклика (параметра оптимизации).
4. Выбор плана эксперимента.
5. Проведение эксперимента.
6. Анализ данных.
7. Выводы и рекомендации.
На начальной стадии планирования эксперимента с учетом поставленных целей экспериментатор должен отобрать независимые переменные (факторы), которые в дальнейшем будут использовать в эксперименте. Как правило, факторы выбираются на основе анализа априорной информации, что требует использования различных методов систематизации полученных знаний. Для решения задач такого рода широко используются методы экспертной оценки [2]. Эти методы основаны на получении и обработке данных, полученных в результате опроса специалистов. Применительно к оценке и выбору наиболее значимых факторов широкое распространение получил метод априорного ранжирования [3].
Метод основан на ранжировании факторов в порядке убывания вносимого ими вклада. Вклад фактора оценивается по величине ранга, присвоенного конкретному фактору при ранжировании всех факторов с учетом их предполагаемого влияния на параметр оптимизации. Каждый эксперт заполняет анкету, в которой перечислены факторы, их размерность и интервалы варьирования, и определяет место фактора в ранжированном ряду.
Полученная от экспертов информация обрабатывается следующим образом:
- определяют сумму рангов по факторам
- разность (∆i) между суммой каждого фактора и средней суммой рангов
- сумму квадратов отклонений (s)
где aij – ранг каждого i-го фактора у j-го исследователя;
n – число исследователей;
m – число факторов;
Т – средняя сумма рангов.
Согласованность мнений экспертов оценивается с помощью коэффициента конкордации ω:
где
где
tj- число одинаковых рангов в j-м ранжировании.
Следующим этапом является оценка значимости коэффициента конкордации оценки его значимости с помощью χ2 – распределения с числом степеней свободы f = n – 1.
Значение – критерия определяют по формуле.
Гипотеза о наличии согласованности мнений исследователей может быть принята, если при заданном числе степеней свободы табличное значение χ2 меньше расчетного для 5%-го уровня значимости.
Рассмотрим пример использования априорного ранжирования факторов для планирования эксперимента, предназначенного для установления зависимости влияния технологических параметров на качество плиты ДСП.
Опрос экспертов проводился с помощью анкеты, содержащей 7 факторов (k =7), которые нужно было проранжировать с учетом степени их влияния на плотность плиты ДСП. Были рассмотрены факторы, которые характеризовали условия изготовления продукции, а именно:
1. Время перемешивания стружки со смолой, отвердителем и добавками;
2. Средний размер стружки;
3. Температура прессования
4. Давление прессования;
5. Время сушки стружки
6. Время прессования
7. Температура сушки стружки;
Матрица рангов, полученная из анкет, приведена в таблице 1.
| Исследователи | Факторы (n = 7) | |||||||
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | ||
| 1 | 6 | 7 | 2 | 5 | 3 | 4 | 1 | |
| 2 | 7 | 6 | 3 | 5 | 2 | 4 | 1 | |
| 3 | 7 | 6 | 2 | 5 | 4 | 3 | 1 | |
| 4 | 7 | 6 | 2 | 5 | 3 | 4 | 1 | |
| 5 | 6 | 7 | 2 | 4 | 3 | 5 | 1 | |
| 33 | 32 | 11 | 24 | 15 | 20 | 5 | ||
| ∆i | -13 | -12 | 9 | -4 | 5 | 0 | 15 | S = 660 |
| (∆i)2 | 169 | 144 | 81 | 16 | 25 | 0 | 225 | |
Несмотря на то, что полученное значение коэффициента конкордации значительно отличается от нуля, проверим его значимость по χ2-критерию:
С учетом 5%-го уровня значимости и числа степеней свободы f=6 табличное значение критерия χ2 = 12,6. Следовательно, мнение экспертов согласовано. Построим среднюю диаграмму рангов для рассматриваемых факторов (рис. 1).
 Рис. 1 Средняя априорная диаграмма
Рис. 1 Средняя априорная диаграмма
По результатам проведенного психологического эксперимента для дальнейшего планирования эксперимента целесообразно оставить два фактора: x1 и x2.
Библиографический список- Монтгомери, Д.К. Планирование эксперимента и анализ данных [Текст] / Д.К. Монтгомери – Л.: Судостроение, 1980. – 384 с.
- Тарасов, Р.В. К вопросу применения экспертных методов в прогнозировании процессов, оценке уровня качества и принятии управленческих решений [Текст] / Р.В. Тарасов, Л.В. Макарова, О.Ф. Акжигитова // Современные научные исследования и инновации. – Апрель 2014. – № 4 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2014/04/33142.
- Хамханов, К.М. Методические указания к практическим занятиям по дисциплине «Планирование эксперимента» [Текст] /К.М. Хамханов, Ю.Ж. Дондоков. – Улан-Уде: ВСГТУ, 2002.
Все статьи автора «Макарова Людмила Викторовна»
web.snauka.ru
АПРИОРНОЕ РАНЖИРОВАНИЕ ФАКТОРОВ — КиберПедия
АПРИОРНОЕ РАНЖИРОВАНИЕ ФАКТОРОВ
К какому типу относится метод экспертных оценок?
1.Детерминированный. 2.Функциональный.
3.Вероятностный. 4.Систематизированный.
Когда чаще всего используют метод экспертных оценок?
1.Когда достоверность исходной информации невелика.
2.Когда достоверность исходной информации велика.
3.Когда достоверность исходной информации избыточна.
4.Когда достоверность исходной информации достаточна.
Как рассматривают неизвестную количественную характеристику фактора?
1.Как неизвестную величину. 2. Как случайную величину.
3. Как детерминированную величину. 4.Как известную величину.
Назначение метода экспертных оценок?
1.Выделение наименее существенных, статистически значимых факторов.
2.Выделение наиболее несущественных, статистически значимых факторов.
3.Выделение наименее существенных, статистически незначимых факторов.
4. Выделение наиболее существенных, статистически значимых факторов.
Ранжирование факторов?
1. Наиболее важному фактору присваивается наивысший ранг.
2.Наименее важному фактору присваивается наивысший ранг.
3.Наиболееважному фактору присваивается минимальный ранг.
4.Наименее важному фактору присваивается «связанный» ранг.
6. Чему равен«связанный» ранг?
1.Среднему геометрическому рангов. 2.Произведению рангов.
3.Разности рангов. 4. Среднему арифметическому рангов.
Как оценивается степень согласованности мнений экспертов
Относительно рангов факторов?
1.Коэффициентом корелляции. 2.Коэффициентом вариации.
3. Коэффициентом конкордации. 4. Коэффициентом регрессии.
В каких пределах может изменяться коэффициент конкордации?
1.От -1,0 до +1,0. 2. От 0 до 1,0. 3.От 0 до 100%. 4. От - ∞ до + ∞.
Учет «связанных» рангов?
1. åTj=П(tj3-tj). 2. åTj=∑(tj3-tj). 3. åTj=П(tj3+tj). 4. åTj= ∑(tj3+tj).
10. tj?
Число факторов, имеющих одинаковый ранг в группе ранжирования конкретного эксперта.
2.Число факторов, имеющих различный ранг в группе ранжирования конкретного эксперта.
3. Число факторов, имеющих максимальный ранг в группе ранжирования конкретного эксперта.
4. Число факторов, имеющих минимальный ранг в группе ранжирования конкретного эксперта.
Чему равен коэффициент конкордации при полной согласованности мнений
Экспертов? 12. Чему равен коэффициент конкордации при полной
Несогласованности мнений экспертов?
1.0.2.– 1, 3. 1,0. 4. 100%.
Статистический критерий для оценки статистической значимости
Коэффициента конкордации? 14. Какой критерий можно применять для проверки согласия с любым законом распределения?
1.Стьюдента. 2.Фишера.3.Кохрена. 4. Пирсона.
Число степеней свободы при оценке статистической значимости
Коэффициента конкордации?
1.На единицу больше числа факторов. 2. На единицу меньше числа факторов.
3. На единицу больше числа экспертов. 4. На единицу меньше числа экспертов.
Как изменяется величина W при увеличении числа «связанных» рангов?
17. Как изменяется величина χ2 при увеличении числа «связанных» рангов?
1.Уменьшается. 2.Не изменяется. 3. Увеличивается. 4. Стремится к 0.
18. Чему равна величина åTj при одинаковых оценках двух факторов?
19.Чему равна величина åTj при одинаковых оценках трех факторов?
20.Чему равна величина åTj при одинаковых оценках двух и трех факторов у одного эксперта?
21. Чему равна величина åTj при одинаковых оценках двух пар
Факторов у одного эксперта?
1.30.2.24.3.6. 4. 12.
Как выделяют группу существенных факторов?
1.По коэффициенту конкордации. 2.По критерию Пирсона.
3.По числу степеней свободы.4. По диаграмме рангов факторов.
23. Какой уровень значимости чаще используют при определении χ2кр?
1.0,01. 2. 0,05. 3.0,10. 4. 0,95.
24. От чего зависит величина χ2кр?
1. От числа факторов. 2.От числа экспертов.
3.От числа факторов и экспертов. 4. От величины W.
Когда коэффициент конкордации статистически значим?
1.Если расчетное значение критерия хи-квадрат равно табличному.
2.Если расчетное значение критерия хи-квадрат неравно табличному.
3. Если расчетное значение критерия хи-квадрат меньше табличного.
4. Если расчетное значение критерия хи-квадрат больше табличного.
Где используется сумма квадратов абсолютных отклонений
Сумм рангов факторов от их среднего арифметического?
1.При расчете χ2. 2.При расчете W. 3. При расчете W и χ2. 4.При расчете χ2кр.
Ранжирование факторов?
По литературным источникам и мнениям экспертов.
2.По литературным источникам.
3.По мнениям экспертов.
4.По опросу собеседников.
Ранг?
1.Количественная обьективная оценка.
Коэффициент конкордации?
1. Оценивает степень согласованности мнений экспертов при априорном ранжировании факторов, значимость коэффициента оценивают с использованием критерия Стьюдента.
2.Оценивает степень согласованности мнений экспертов при априорном ранжировании факторов, значимость коэффициента оценивают с использованием критерия Пирсона.
3. Оценивает независимость мнений экспертов при априорном ранжировании факторов, значимость коэффициента оценивают с использованием критерия Стьюдента.
4. Оценивает независимость мнений экспертов при априорном ранжировании факторов, значимость коэффициента оценивают с использованием критерия Пирсона.
Априорная информация?
1: 2; 5; 10; 12; 20; 24; 28; 31; 36. 2: 3; 8; 9; 15; 19; 23; 25; 29; 33; 34.
3: 1; 7; 11; 16; 17; 18; 27; 32; 35. 4: 4; 6; 13; 14; 21; 22; 26; 30; 37.
ТЕСТЫ
1. Цель предварительной обработки
Экспериментальных данных?
1.Отсеивание промахов.
2. Проверка гипотезы нормального распределения.
Распределения?
1.Размах варьирования, максимального относительного отклонения, вероятностная сетка, стремление центральных нечетных моментов к нулю, анализ показателей асимметрии и эксцесса.
2. Размах варьирования, среднего абсолютного отклонения, вероятностная сетка, стремление центральных четных моментов к нулю, анализ показателей асимметрии и эксцесса.
3. Размах варьирования, среднего абсолютного отклонения, вероятностная сетка, стремление центральных четных моментов к нулю, анализ показателей асимметрии и эксцесса.
4. Размах варьирования, среднего абсолютного отклонения, вероятностная сетка, стремление центральных нечетных моментов к нулю, анализ показателей асимметрии и эксцесса.
И выборкой?
1. Выборка – это обследованная часть генеральной совокупности.
2.Генеральная совокупность – это обследованная часть выборки.
3.Выборка – это необследованная часть генеральной совокупности.
4. Генеральная совокупность – это необследованная часть выборки.
Закон больших чисел?
1. Среднее геометрическое результатов испытаний с ростом nвсе точнее отражает математическое ожидание испытываемой случайной величины.
Распределений?
1. Асимметрия, эксцесс и стандартное отклонение.
2. Среднее арифметическое и стандартное отклонение.
3. Среднее арифметическое и асимметрия.
4. Среднее арифметическое и эксцесс.
Доверительный интервал?
Доверительная вероятность?
1.Диапазон возможного отклонения среднего квадратического отклонения.
2.Вероятность того,что результат измерения отличается от истинного значения на величину, не большую доверительного интервала.
3. Вероятность того,что результат измерения отличается от истинного значения на величину, большую доверительного интервала.
4. Диапазон возможного отклонения случайной величины.
Интервальная оценка?
Доверительный интервал.
2. Доверительная вероятность.
3.Интервал «три сигма».
4.Дисперсия.
11. Что рассчитывают по уравнению ?
Правило «трех сигм»?
1. Разброс случайных величин от среднего значения не должен превышать доверительной вероятности интервала величиной в три среднеквадратических отклонения (стандарта) с доверительным диапазоном 95,0%.
2.Разброс случайных величин от среднего значения не должен превышать доверительного интервала величиной в три среднеквадратических отклонения (стандарта) с доверительной вероятностью 68,0%.
3. Разброс случайных величин от среднего значения не должен превышать доверительного интервала величиной в три среднеквадратических отклонения (стандарта) с доверительной вероятностью 95,0%.
4.Разброс случайных величин от среднего значения не должен превышать доверительного интервала величиной в три среднеквадратических отклонения (стандарта) с доверительной вероятностью 99,7%.
19. Нормальное распределение?
1. Если распредёление случайной величины может быть хотя бы приближенно описано колоколообразной кривой у = ае– bхи зависит только от математического ожидания.
2. Если распредёление случайной величины может быть хотя бы приближенно описано колоколообразной кривой у = ае– bхи зависит только от стандартного отклонения.
3.Если распредёление случайной величины может быть хотя бы приближенно описано колоколообразной кривой у = ае– bх и зависит от двух параметров: математическое ожидание и стандартное отклонение.
4. Если распредёление случайной величины может быть хотя бы приближенно описано колоколообразной кривой у = ае– bхи зависит от трех параметров: математическое ожидание, среднее арифметическое и стандартное отклонение.
20. Стандартное нормальное распределение?
1.Распределение, у которого математическое ожидание равно нулю, дисперсия равна 1,0, а максимальная плотность 0,4.
2. Распределение, у которого математическое ожидание равно нулю, дисперсия равна 1,0, а максимальная плотность 0,3.
3. Распределение, у которого математическое ожидание равно 1,0, дисперсия равна нулю, а максимальная плотность 0,4.
4. Распределение, у которого математическое ожидание равно 1,0, дисперсия равна нулю, а максимальная плотность 0,3.
21. Логарифмически-нормальное распределение?
1. Распределение случайной величины, логарифм плотности которой распределен по нормальному закону.
2. Распределение случайной величины, логарифм которой распределен по нормальному закону.
3. Распределение случайной величины, логарифм дисперсии которой распределен по нормальному закону.
4. Распределение случайной величины, логарифм стандарта которой распределен по нормальному закону.
Эксцесс? 23. Асимметрия?
1.Пологость или островершинность распределения, оценивается с помощью центрального момента 4-го порядка.
2. Пологость или островершинность распределения, оценивается с помощью центрального момента 3-го порядка.
3.Края кривой распределения имеют различную пологость, оценивается с помощью центрального момента 3-го порядка.
4.Края кривой распределения имеют различную пологость, оценивается с помощью центрального момента 4-го порядка.
24. Размах варьирования?
1. Разность максимального и минимального значений выборки, отношение S/R применяют для быстрой проверки грубых погрешностей измерений.
2. Разность максимального и минимального значений выборки, отношение S/R применяют для быстрой проверки нормальности распределения.
3. Разность максимального и минимального значений выборки, отношение R/S применяют для быстрой проверки грубых погрешностей измерений.
4.Разность максимального и минимального значений выборки, отношение R/S применяют для быстрой проверки нормальности распределения.
25. Требования к оценкам?
1. Состоятельность, смещенность и эффективность.
2.Состоятельность, несмещенность и эффективность.
3. Достоверность, несмещенность и эффективность.
4. Достоверность, смещенность и эффективность.
26. Состоятельная оценка?27. Несмещенная оценка?
Эффективная оценка?
1.Среди прочих оценок того же параметра обладает наименьшей дисперсией.
2.Среди прочих оценок того же параметра обладает наибольшейдисперсией.
3.По мере роста числа наблюдений стремится к оцениваемому теоретическому значению параметра.
4.При любом числе наблюдений ее математическое ожидание точно равно величине оцениваемого параметра.
29. «Сжатие» информации,
Кумулятивная линия?
1.Линия, соединяющая середины вершин столбиковой диаграммы – оценка плотности вероятностей.
2.График накопленных частостей – оценка функции распределения.
3.Столбиковая диаграмма – графическое отображение частот.
4.Линия, соединяющая середины вершин столбиковой диаграммы – оценка функции распределения.
Вероятностная сетка?
1.Спрямляет кумулятивную линию, позволяет оценить накопленную частость.
2. Спрямляет полигон распределения, позволяет оценить накопленную частоту.
3.Спрямляет кумулятивную линию, позволяет оценить параметры распределения.
4. Спрямляет полигон распределения, позволяет оценить параметры распределения.
Характеристики рассеивания
Случайной величины?
1.Медиана.
2. Дисперсия и среднее квадратичное отклонение.
3.Среднее арифметическое.
4.Среднее геометрическое.
1. -0,67; 2. 0,67; 3. 1,33; 4. 2,0.
51. Правило 3σ?
1.Среднее арифметическое расположено в интервале 3σ.
2. 68% измерений расположены в интервале 3σ.
3. 95% измерений расположены в интервале 3σ.
4.Выход случайной ошибки измерений за трехсигмовые пределы считают практически невозможным.
Экспериментальных данных?
1.Определение среднего арифметического и дисперсии результатов измерений.
2.Отсеивание промахов и проверка соответствия распределения результатов измерений закону нормального распределения.
3.Построение гистограммы результатов измерений.
4.Отсеивание промахов и построение гистограммы результатов измерений.
Точечная оценка?
1.Это оценка, определяемая по одной выборке и выражаемая в виде одного интервала величин.
2.Это оценка, определяемая по нескольким выборкам и выражаемая в виде одного числа.
3.Это оценка, определяемая по генеральной совокупности и выражаемая в виде одного числа.
4.Это оценка, определяемая по одной выборке и выражаемая в виде одного числа.
Момент?
1.Моментом порядка k в случае одномерного эмпирического распределения называется произведение k-х степеней отклонений результатов наблюдений от произвольного числа С, деленная на объем выборки n.
2.Моментом порядка k в случае одномерного эмпирического распределения называется сумма k-х степеней отклонений результатов наблюдений от произвольного числа С, деленная на объем выборки n.
3.Моментом порядка k в случае одномерного эмпирического распределения называется сумма k-х степеней отклонений результатов наблюдений от произвольного числа С.
4.Моментом порядка k в случае одномерного эмпирического распределения называется разность k-х степеней отклонений результатов наблюдений от произвольного числа С.
Частость? 69. Частота?
1.Интервал вариационного ряда.
2.Количество членов выборки в интервале.
3.Относительная частота - отношение объема выборки к частоте интервала.
4.Относительная частота - отношение частоты интервала к объему выборки.
Нормальности распределения
1.На основе размаха варьирования, среднего абсолютного отклонения, вероятностная сетка, стремление нечетных центральных моментов к нулю, по коэффициенту вариации, по критерию Пирсона.
2.На основе размаха варьирования, среднего абсолютного отклонения, вероятностная сетка, стремление четных центральных моментов к нулю, по коэффициенту корреляции, по критерию Пирсона.
3.На основе размаха варьирования, среднего абсолютного отклонения, вероятностная сетка, стремление нечетных центральных моментов к нулю, по коэффициенту детерминации, по критерию Фишера.
4.На основе размаха варьирования, среднего абсолютного отклонения, вероятностная сетка, стремление нечетных начальных моментов к нулю, по коэффициенту конкордации, по критерию Стьюдента.
Нормального распределения?
1. 0,6; 2. 0,3; 3. 0,5; 4. 0,4.
Логарифмически-нормальный
Закон распределения?
1.Распределение случайной величины, плотность вероятности которой распределена по нормальному закону.
2.Распределение случайной величины, логарифм которой распределен по нормальному закону.
3.Распределение случайной величины, которая распределена по логарифмическому закону.
4.Распределение случайной величины, стандарт которой распределен по нормальному закону.
Ответы:
1: 2;4;10;14;20;22;28;31;34;37;40;42;46;48;53;56;60;66;70;71;
2: 5;6;9;13;16:21;25;29;33;38;41;45;46;55;59;62;65;69;74;
3: 1;7;11;15;19;23;26;32;36;39;44;49;52;57;61;63;67;68;72;
4: 3;8;12;17;18;24;27;30;35;43;50;51;54;58;64;73;
1. -0,67; 2. 0,67; 3. 1,33; 4. 2,0.
Правило «трех сигм»?
1.Среднее арифметическое расположено в интервале 3σ.
2. 68% измерений расположены в интервале 3σ.
3. 95% измерений расположены в интервале 3σ.
4.Выход случайной ошибки измерений за техсигмовые пределы считают практически невозможным.
Экспериментальных данных?
1.Определение среднего арифметического и дисперсии результатов измерений.
2.Отсеивание промахов и проверка соответствия распределения результатов измерений закону нормального распределения.
3.Построение гистограммы результатов измерений.
4.Отсеивание промахов и построение гистограммы результатов измерений.
Точечная оценка?
1.Это оценка, определяемая по одной выборке и выражаемая в виде одного интервала величин.
2.Это оценка, определяемая по нескольким выборкам и выражаемая в виде одного числа.
3.Это оценка, определяемая по генеральной совокупности и выражаемая в виде одного числа.
4.Это оценка, определяемая по одной выборке и выражаемая в виде одного числа.
Момент?
1.Моментом порядка k в случае одномерного эмпирического распределения называется произведение k-х степеней отклонений результатов наблюдений от произвольного числа С, деленная на объем выборки n.
2.Моментом порядка k в случае одномерного эмпирического распределения называется сумма k-х степеней отклонений результатов наблюдений от произвольного числа С, деленная на объем выборки n.
3.Моментом порядка k в случае одномерного эмпирического распределения называется сумма k-х степеней отклонений результатов наблюдений от произвольного числа С.
4.Моментом порядка k в случае одномерного эмпирического распределения называется разность k-х степеней отклонений результатов наблюдений от произвольного числа С.
Частость? 29. Частота?
1.Интервал вариационного ряда.
2.Количество членов выборки в интервале.
3.Относительная частота - отношение объема выборки к частоте интервала.
4.Относительная частота - отношение частоты интервала к объему выборки.
30. Основные методы отсева грубых погрешностей (промахов)?
1.Правило «трех сигм», метод максимального относительного отклонения, использование критерия Стьюдента.
2.Правило «трех сигм», метод максимального относительного отклонения, использование критерия Фишера.
3.Правило «трех сигм», метод максимального относительного отклонения, использование критерия Пирсона.
4.Правило «трех сигм», метод минимального относительного отклонения, использование критерия Стьюдента.
Кумулятивная линия?
1.Линия, соединяющая середины вершин столбиковой диаграммы.
2.Графическое представление статистического ряда, показывает количество измерений, попавших в интервал 3σ.
3.Графическое представление статистического ряда, показывает количество измерений, попавших в каждый, одинаковый по величине интервал.
4.График накопленных частот.
Размах варьирования?
1.Разность между максимальным и минимальным вариантами интервала.
2.Разность между максимальным и минимальным вариантами выборки.
3.Отношение стандарта к среднему арифметическому.
4.Разность между медианой и модой.
Нормальности распределения
1.На основе размаха варьирования, среднего абсолютного отклонения, вероятностная сетка, стремление нечетных центральных моментов к нулю, по коэффициенту вариации, по критерию Пирсона.
2.На основе размаха варьирования, среднего абсолютного отклонения, вероятностная сетка, стремление четных центральных моментов к нулю, по коэффициенту корреляции, по критерию Пирсона.
3.На основе размаха варьирования, среднего абсолютного отклонения, вероятностная сетка, стремление нечетных центральных моментов к нулю, по коэффициенту детерминации, по критерию Фишера.
4.На основе размаха варьирования, среднего абсолютного отклонения, вероятностная сетка, стремление нечетных начальных моментов к нулю, по коэффициенту конкордации, по критерию Стьюдента.
Нормального распределения?
1. 0,6; 2. 0,3; 3. 0,5; 4. 0,4.
И обратной регрессии?
1.В точке максимальной тесноты взаимосвязи.
2.В точке минимальной тесноты взаимосвязи.
3.В начале координат.
4.В центре массива экспериментальных данных: Хср. и Уср.
И коэффициенты регрессии?
1. r2 = b0ух b0ху; 2. r2 = b1ух b1ху; 3. r2 = b1ух b0ху; 4. r2 = b1ух + b1ху.
Коэффициент корреляции?
1.Представляет собой безразмерную величину, значение и знак которой характеризуют направление и величину взаимосвязи между У и Х. Этот знак (+ или -) соответствует знаку углового коэффициента регрессии.
2.Представляет собой размерную величину, значение и знак которой характеризуют направление и величину взаимосвязи между У и Х. Этот знак (+ или -) соответствует знаку углового коэффициента регрессии.
3.Представляет собой безразмерную величину, значение и знак которой характеризуют направление и величину взаимосвязи между У и Х. Этот знак (+ или -) не соответствует знаку углового коэффициента регрессии.
4.Представляет собой размерную величину, значение которой характеризует направление и величину взаимосвязи между У и Х. Этот знак (+ или -) соответствует знаку свободного члена уравнения регрессии.
Метод группировок?
1.Наиболее простой, определяется только свободный член уравнения регрессии.
2.Наиболее сложный, определяется только свободный член уравнения регрессии.
3.Наиболее сложный, определяется только угловой коэффициент.
4.Наиболее простой, определяется только угловой коэффициент.
Адекватность уравнения?
1.Характеризует его способность предсказывать результаты последующих опытов, оценивается по критерию Стьюдента.
2.Характеризует его способность предсказывать результаты последующих опытов, оценивается по критерию Фишера.
3.Характеризует его способность угадывать результаты последующих опытов, оценивается по критерию Пирсона.
4.Характеризует его способность предсказывать результаты последующих опытов, оценивается по критерию Вилкоксона.
Ортогональная регрессия?
1.Минимальна сумма квадратов отклонений экспериментальных точек перпендикулярно к линии регрессии.
2.Минимальна сумма квадратов отклонений экспериментальных точек к линии регрессии параллельно оси абсцисс.
3.Минимальна сумма квадратов отклонений экспериментальных точек к линии регрессии параллельно оси ординат.
4.Максимальна сумма квадратов отклонений экспериментальных точек перпендикулярно к линии регрессии.
Требования к объекту исследования? 63. Требования к оценкам?
1.Управляемость и однозначность.
2.Воспроизводимость результатов и управляемость.
3.Состоятельность, несмещенность и эффективность.
4.Динамичность и состоятельность.
Черный ящик»?
1.Модель объекта исследования в виде прямоугольника.
2.Модель объекта исследования в виде треугольника.
3.Сложная математическая модель объекта исследования.
4.Неизвестная априорная информация.
Требования к математической модели?
1.Адекватность и совместимость.
2.Воспроизводимость и адекватность.
3.Простота и совместимость.
4.Адекватность и простота.
Параметр оптимизации?
1.Это фактор, определяющий процесс оптимизации.
2.Это признак, по которому планируется оптимизировать процесс,
3.Это величина,около которой концентрируется большинство результатов наблюдений.
4.Это оптимальное состояние вероятностной системы.
Требования к параметру оптимизации?
1.Обеспечивает воспроизводимость результатов измерений, универсальный, количественный, выражается одним числом, имеет физический смысл, динамически эффективный с точки зрения достижения цели.
2.Адекватный, воспроизводимый, количественный, статистически эффективный с точки зрения достижения цели.
3.Простой и легко вычисляемый, существующий для различных состояний, универсальный, количественный, выражается одним числом, имеет физический смысл, статистически эффективный с точки зрения достижения цели.
4.Доступный, статистически эффективный с точки зрения достижения цели, простой, мультипликативный, универсальный, количественный.
Факторы?
1.Это способы косвенного воздействия на объект исследования, входы«черного ящика».
2.Это способы косвенного воздействия на объект исследования, выходы«черного ящика».
3.Это способы непосредственного воздействия на объект исследования, входы «черного ящика».
4.Это способы непосредственного воздействия на объект исследования, выходы «черного ящика».
76. Область определения фактора?
1.Совокупность ограниченного числа значений, которые в принципе может принимать данный фактор.
2.Совокупность ограниченного числа значений данного фактора в матрице планирования эксперимента.
3.Совокупность всех значений данного фактора в матрице планирования эксперимента.
4.Совокупность всех значений, которые в принципе может принимать данный фактор.
Требования к совокупности факторов?
1.Совместимость факторов и их зависимость – наличие линейной корреляции.
2.Совместимость факторов и независимость – отсутствие линейной корреляции.
3.Несовместимость факторов и независимость – отсутствие линейной корреляции.
4.Несовместимость факторов и их зависимость – наличие линейной корреляции.
Сжатие информации?
1.Представление выборки в виде среднего арифметического и коэффициента вариации.
2.Представление выборки в виде коэффициента вариации.
3.Представление выборки в виде среднего арифметического и дисперсии.
4.Представление выборки в виде среднего арифметического и среднего квадратичного отклонения.
79. Величина доверительного интервала записи 100+-5
при доверительной вероятности: 68, 95 и 99,7%?
1.95-105; 90-110; 85-115. 2.85-115; 90-110; 95-105.
3.95-115; 90-110; 85-105. 4.85-115; 90-105; 95-110.
Кодирование факторов?
1.Перевод натуральных значений факторов в безразмерные, представляет собой линейное преобразование факторного пространства с переносом нулевой точки эксперимента в начало координат и выбор масштаба по осям в единицах интервалов варьирования.
2.Перевод натуральных значений факторов в безразмерные, представляет собой нелинейное преобразование факторного пространства с переносом начала координат в нулевую точку эксперимента и выбор масштаба по осям в единицах измерения факторов.
3.Перевод натуральных значений факторов в безразмерные, представляет собой линейное преобразование факторного пространства с переносом начала координат в нулевую точку эксперимента и выбор масштаба по осям в единицах интервалов варьирования.
4.Перевод безразмерных значений факторов в натуральные, представляет собой линейное преобразование факторного пространства с переносом начала координат в нулевую точку эксперимента и выбор масштаба по осям в единицах интервалов варьирования.
83. Сколько опытов требуется для ПФЭ 23 и ДФЭ 23-1,
Рандомизация?
1. Перевод случайной ошибки в систематическую, за счет выбора случайной последовательности опытов.
2.Перевод систематической ошибки в случайную, за счет выбора случайной последовательности опытов.
3. Перевод случайной ошибки в систематическую, за счет выбора систематической последовательности опытов.
4. Перевод систематической ошибки в случайную, за счет выбора систематической последовательности опытов.
86. Требования к матрице планирования эксперимента?
1.Симметричность относительно центра эксперимента, ортогональность, ротатабельность.
2.Симметричность относительно начала координат, ортогональность, ротатабельность.
3.Симметричность относительно центра эксперимента, адекватность, ротатабельность.
4.Симметричность относительно центра эксперимента, ортогональность, адекватность.
Параллельные опыты?
1. Для оценки ортогональности матрицы при проверке однородности параллельных опытов по критерию Кохрена.
2. Для оценки ротатабельности матрицы при проверке однородности параллельных опытов по критерию Фишера.
3.Для оценки ротатабельности матрицы при проверке однородности параллельных опытов по критерию Кохрена.
4. Для оценки ортогональности матрицы при проверке однородности параллельных опытов по критерию Фишера.
Число степеней свободы?
1. Разность между числом опытов и числом статистически незначимых коэффициентов.
2.Разность между числом опытов и числом статистически значимых коэффициентов.
3. Сумма чисел опытов и статистически значимых коэффициентов.
4. Сумма чисел опытов и статистически незначимых коэффициентов.
91. Ненасыщенный план?
1. Число опытов меньше числа статистически значимых коэффициентов, возможна проверка адекватности уравнения.
2. Число опытов меньше числа статистически значимых коэффициентов, невозможна проверка адекватности уравнения.
3. Число опытов больше числа статистически значимых коэффициентов, невозможна проверка адекватности уравнения.
4.Число опытов больше числа статистически значимых коэффициентов, возможна проверка адекватности уравнения.
Полуреплика?
1. ДФЭ,равный половине ПФЭ. 2. ПФЭ,равный половине ДФЭ.
3. ДФЭ,равный двум ПФЭ. 4. ПФЭ,равный двум ДФЭ.
Интерпретация модели?
1. Это статистическое оценивание коэффициентов модели.
2.Это перевод модели с абстрактного языка на язык экспериментатора.
3.Это графическое представление математической модели.
4.Это использование статистических критериев при оценке адекватности модели.
Поверхность от
cyberpedia.su
Методика априорного ранжирования.
Этапы работы и ранжирование исследований.
постановка задачи исследований
выбор параметра выхода
составление перечня факторов влияющих на изучаемый процесс
операционное определение фактора
установление интервалов изменения отдельных факторов.
АНКЕТА.
| № п/п | наименование факторов | Обозначение | Размерность | Интервал изменений | Ранг |
| 1 |
|
|
|
|
|
| 2 |
|
|
|
|
|
| … |
|
|
|
|
|
| n |
|
|
|
|
|
6) Ранжирование факторов в порядке убывания их воздействия на параметр оптимизации, каждому фактору из общего перечня присваивается ранг, соответствующий месту отведённому исследователем данному фактору в ранжированном ряду, наиболее значимому фактору присваивается 1. Когда специалист не может нескольким факторам присвоить последовательные номера рангов, считая их одинаковыми по своему вкладу в параметр оптимизации, то факторам присваивается один и тот же номер, такие ранги называется связанными.
Размер связанного ранга определяется как:
i – порядковый номер первого связываемого фактора
z – количество связываемых факторов
7) Проверка ранжирования – сумма рангов в каждом столбце должна равняться:
8) Определение суммы рангов по факторам
9) определение средней суммы рангов
10) Определение абсолютной величины разности между каждой суммы рангов по фактором и средней суммы рангов.
11) Определение квадрата разности
12) Определение суммы квадратов разности
13) Определение показателей групп связанных рангов:
14) Определение суммарного показателя связанных рангов по ранжированию:
15) Определение суммы суммарных показателей связанных рангов
16) Определение коэффициента конкордации:
Этот коэффициент изменяется от 0 до 1, если он равен 1, то это означает что все эксперты дали одинаковые оценки по данному признаку, 0 – связи между оценками, полученными от разных экспертов, не существует.
17) определение значимости коэффициента конкордации:
18) Построение априорных диаграмм рангов.
ордината – сумма рангов, абсцисса – фактор, чем меньше сумма рангов данного фактора, тем выше его место на диаграмме.
19) Принятие решений по стратегии последующего эксперимента.
Диаграмма рангов может иметь вид:
- распределение факторов и убывание равномерное, в этом случае уровень АИ низкий всё факторы должны быть включены в эксперимент.
- распределение равномерное, а убывание неравномерное, все факторы включаем в эксперимент.
- распределение неравномерное, а убывание равномерное, возможен отсёк факторов с низким рангом.
- распределение и убывание неравномерное, большой отсёк факторов
20) сравнение двух групп экспертов, в этом случае пользуются коэффициентов ранговой корреляции Спирмена
Значение коэффициента Спирмена в зависимости от согласованности ранжировок может меняться от +1(ранжированные ряды совпадают) до -1 (корреляция отсутствует)
Строим совместную диаграмму двух групп, для этого суммируем общую сумму рангов по каждому фактору, затем полученные значения ранжируем и строим совместную диаграмму для обеих групп экспертов, которая позволяет выделить наиболее значимые факторы.
studfiles.net
|
1.Устранение возмущающих факторов. 2.Устранение контролируемых факторов. 3.Отсев малозначимых несущественных факторов для исключения их из плана эксперимента. 4. Отсев малозначимых несущественных факторов для включения их в дополнительный план эксперимента. 33. Что рассчитывают по формуле W = 12 A / [m2 (k3 - k) - m ∑ Tj ]? где: m - количество опрашиваемых экспертов; k - количество факторов; 1. Коэффициент корреляции. 2. Коэффициент конкордации. 3. Критерий Пирсона. 4. Учет «связанных» рангов. 34. Что рассчитывают по формуле χ2 = 12A / [mk (k+ 1) - ∑ Tj /(k- 1)]? 1. Критерий Пирсона для оценки значимости коэффициентов корреляции, можно применять для проверки согласия с нормальным законом распределения. 2. Критерий Пирсона для оценки значимости коэффициентов конкордации, можно применять для проверки согласия с любым законом распределения. 3. Критерий Фишерадля оценки значимости коэффициентов корреляции, можно применять для проверки согласия с нормальнымзаконом распределения. 4. Критерий Фишера для оценки значимости коэффициентов конкордации, можно применять для проверки согласия с любым законом распределения. 35. Что рассчитывают по формуле åTj = ∑(tj3 - tj)? 1. Учет "независимых" рангов; tj - число факторов, имеющих одинаковыйранг в группе ранжирования нескольких экспертов. 2. Учет "связанных" рангов; tj - число факторов, имеющих различный ранг в группе ранжирования конкретного эксперта. 3. Учет "связанных" рангов; tj - число факторов, имеющих одинаковый ранг в группе ранжирования конкретного эксперта. 4. Учет "независимых" рангов; tj - число факторов, имеющих различныйранг в группе ранжирования конкретного эксперта. 36. Что рассчитывают по формуле f = k – 1? 1.Число степеней свободы.2.Число"связанных" рангов. 3.Число независимых экспертов. 4.Число независимых факторов. ПРИЛОЖЕНИЯ
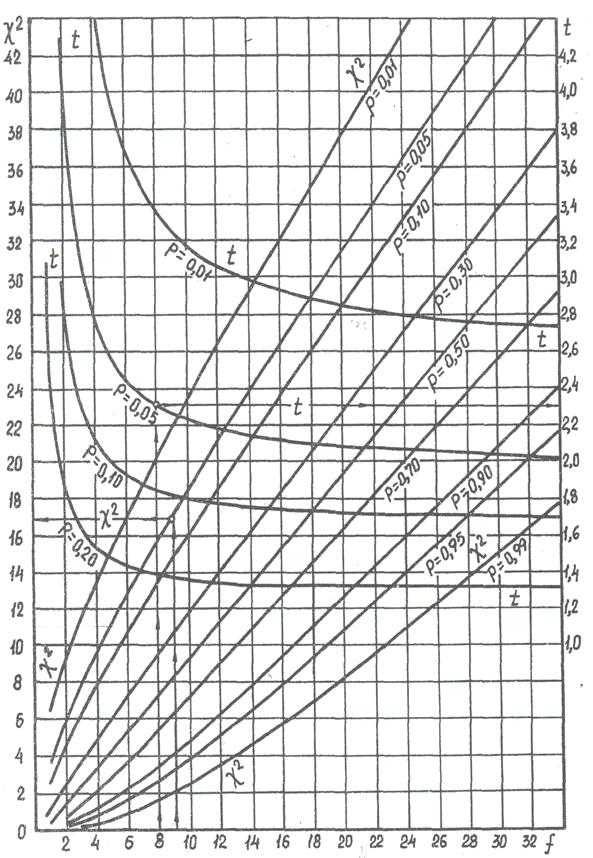
Рис. 1. Значения критерия Пирсона c2 и Стьюдента t в зависимости от числа степеней свободы f
Таблица 1 Критические значения для отсева грубых погрешностей (n – число приемлемых результатов, Р – надежность вывода)
Таблица 2 Процентные точки распределения Стьюдента
Продолжение таблицы 2
Таблица 3 Критические границы отношения R/S
Продолжение таблицы 3
Ответы по тестам второго раздела: 1: 4; 7; 9; 11; 12; 20; 24; 30; 32. 2: 2; 3; 6; 13; 15; 16; 21; 25. 3: 1; 5; 14; 17; 23; 26; 27; 29; 33. 4: 8; 10; 18; 19; 22; 28; 31; 34; 35. Ответы по тестам четвертого раздела: 1: 2;4;10;14;20;22;28;31;34;37;40;42;46;48;53;56;60;66;70;71; 2: 5;6;9;13;16:21;25;29;33;38;41;45;46;55;59;62;65;69;74; 3: 1;7;11;15;19;23;26;32;36;39;44;49;52;57;61;63;67;68;72; 4: 3;8;12;17;18;24;27;30;35;43;50;51;54;58;64;73; Ответы по тестам пятого раздела: 1: 2; 5; 10; 12; 20; 24; 28; 31; 36. 2: 3; 8; 9; 15; 19; 23; 25; 29; 33; 34. 3: 1; 7; 11; 16; 17; 18; 27; 32; 35. 4: 4; 6; 13; 14; 21; 22; 26; 30.
Литература 1. Айвазян С.А. и др. Прикладная статистика: Основы моделирования и первичная обработка данных. – М.: Финансы и статистика, 1983. – 471 с. 2. Батунер Л.М., Позин М.Е. Математические методы в химической технике. – Л.: Ленхимиздат, 1963. - 638 с. 3. Бошняк Л.Л. Измерения при теплотехнических исследованиях. – Л.: Машиностроение, 1974. – 448 с. 4. Кричевец А.Н. и др. Математика для психологов: Учебник. – М.: Флинта: Московский психолого-социальный институт, 2005. – 376 с. 5. Львовский Е.Н. Статистические методы построения эмпирических формул. – М.: Высшая школа, 1982. – 224 с. 6. Основы научных исследований: Учеб. для техн. вузов/ 1989. – 232 с. 7. Решетов Д.Н. и др. Надежность машин: Учеб. пособие для машиностр. спец. вузов. – М.: Высш. школа, 1988. – 238 с. 8. Румшиский Л.З. Математическая обработка результатов эксперимента: Справочное руководство. – М.: Наука, 1971. – 192 с. 9. Сидоренко Е.В. Методы математической обработки в психологии. – СПб.: ООО «Речь» 2000. – 350 с. 10. Соловьев В.А., Яхонтов В.Е. Элементарные методы обработки результаты измерений. – Л.: ЛГУ, 1977. – 72 с. 11. Степнов М.Н. Статистические методы обработки результатов механических испытаний: Справочник. – М.: Машиностроение, 1985. – 232 с.
Некрасов Владимир Иванович
Рекомендуемые страницы: Воспользуйтесь поиском по сайту: ©2015- 2018 megalektsii.ru Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. |
megalektsii.ru