Решение задач нелинейной оптимизации на примере Модели агентских отношений. Задачи нелинейной оптимизации примеры
Задачи нелинейной оптимизации
На примере модели сбыта продукции рассмотрим задачу, в которой целевая функция не является линейной. Такие задачи относятся к задачам нелинейного программирования и также могут быть решены с помощью надстройки Поиск решения MS Excel.
Постановка задачи.
Предприятие реализует выпускаемую продукцию, сбыт которой носит сезонный характер. В таблице 21.1 коэффициент сезонности сбыта в каждом квартале указан в строке «Сезонность». Себестоимость единицы продукции составляет 25 руб., а цена, по которой она реализуется, — 40 руб. В каждом квартале затраты на торговый персонал составляют 8 000 руб., а затраты на рекламу — 10 000 руб. Косвенные затраты составляют 15 % от выручки.
Т а б л и ц а 21.1.
Пусть ожидаемое число продаж зависит от коэффициента сезонности k и затрат на рекламу r следующим образом:
Требуется определить, как влияет распределение затрат на рекламу на динамику прибыли от продажи продукции.
Решение.
Как видно из формулы для числа продаж, первые 5000 р. затраченные на рекламу в первом квартале, приводят к увеличению числа продаж на 1092 единицы, а следующие 5000 р. — только на 775 единиц. То есть зависимость числа продаж от рекламы не является линейной.
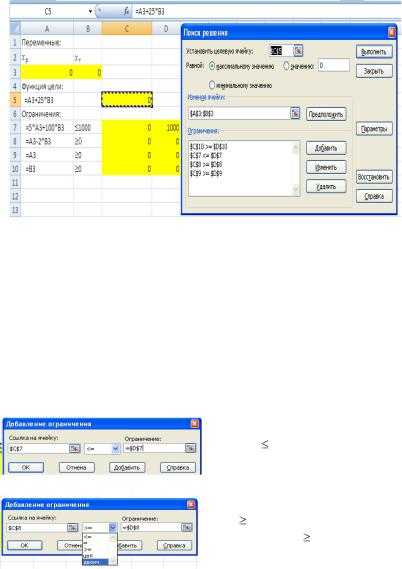
Заполним лист MS Excel, как показано на рисунке и исследуем полученную математическую модель.
Вариант 1. Пусть, например, суммарные расходы на рекламу не должны превышать 40 тыс.руб. Требуется определить расходы на рекламу для получения наибольшей прибыли в первом квартале. Необходимо добиться наибольшей прибыли, изменяя затраты на рекламу в каждом квартале. Используем стандартный прием для поиска решения поставленной задачи со следующими параметрами оптимизации.
Поиск решения даёт результат, при котором прибыль за 1-й квартал увеличивается со значения 14324 руб. до 15093 руб. при увеличении затрат на рекламу в этом квартале на 7093 руб. по сравнению с исходным значением.
В заключение отметим, что изложенный материал позволяет проследить технологию исследования простейших оптимизационных моделей в экономике. Более сложные аналитические модели могут быть построены с использованием таких специализированных пакетов, как Mathcad, MS Project и др.
Контрольные вопросы и задачи
21.1. Поясните назначение процедуры аппроксимации.
21.2. Какова последовательность решения задачи аппроксимации?
21.3. Какие инструменты используются в MS Excel для решения уравнений, с помощью которых осуществляется поиск экстремума?
21.4. Сформулируйте общую постановку задачи исследования операций.
21.5. Какие инструменты используются в MS Excel для решения задач оптимизации?
21.6. В чём заключается анализ оптимального решения?
21.7. Сформулируйте понятие о двойственной задаче.
21.8. Что является целью транспортной задачи?
21.9. В чём суть и для чего используется задача о назначениях?
Глава 22
Похожие статьи:
2. Решение задач нелинейного программирования
Многие зависимости между экономическими показателями имеют нелинейный характер: спрос на товар как функция его цены, зависимость между объемом выпуска и количеством затраченных ресурсов и т.п. Учет этого обстоятельства при построении оптимизационной модели приводит к задаче нелинейной оптимизации, называемой такжезадачей нелинейного программирования(НП). Далее приводятся необходимые сведения по теории НП.
1. Постановка задачи нелинейной оптимизации
В общем случае задача НП состоит в нахождении экстремума(минимума или максимума) функции
Z = f (x1,…, xn) min (max), (1)
на множестве, задаваемом ограничениями в виде равенств и (или) неравенств,
gi (x1,…, xn) = bi, 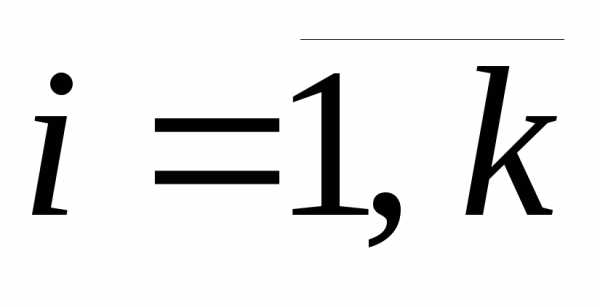 . (2)
. (2)
gi (x1,…, xn) ≤ bi, .(3)
Здесь n— число переменных,k— число ограничений типа равенства, m— общее число ограничений,x1,…,xn— переменные,f — целевая функция (ЦФ), gi— функции ограничений, аbi— заданные числа. Ограничения-неравенства включают и условия неотрицательности переменных, если таковые имеются.
Предполагается, что среди функций fиgi(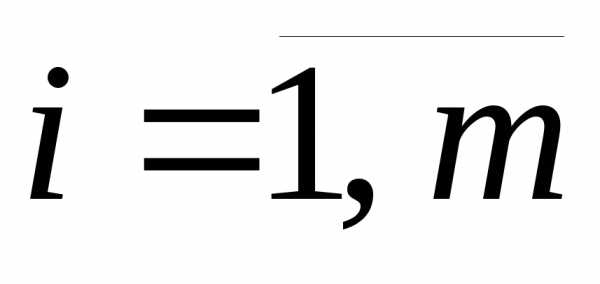 ) есть хоть одна нелинейная, так как в противном случае (1) – (3) — задача линейного программирования (ЛП).
) есть хоть одна нелинейная, так как в противном случае (1) – (3) — задача линейного программирования (ЛП).
Любой n-мерный векторx = (x1,…,xn), удовлетворяющий ограничениям (2) – (3), называетсядопустимым решением, а множествоXвсех таких векторов —областью допустимых решений(ОДР).
Простейшей задачей НП является задача безусловной оптимизации, которая состоит в нахождении экстремума (оптимума) нелинейной функции при отсутствии ограничений на значения ее переменных (m= 0). Такие задачи, например, возникают при статистическом оценивании параметров модели.
Другой важный частный случай задачи НП — классическая задача условной оптимизации, в которой все ограничения являются равенствами (k=m).
В отличие от задач ЛП в задачах НП различают два вида оптимумов: локальныйиглобальный. Решение задачи НП называетсялокально оптимальным, если оно является лучшим лишь среди достаточно близких к нему допустимых решений. Если же решение является наилучшим среди всех допустимых решений, то оно называетсяглобально оптимальным. Дадим точные определения этих понятий.
Точка  Xназываетсялокальным минимумом(максимумом) функцииfна множествеХ, если неравенствоf(
Xназываетсялокальным минимумом(максимумом) функцииfна множествеХ, если неравенствоf(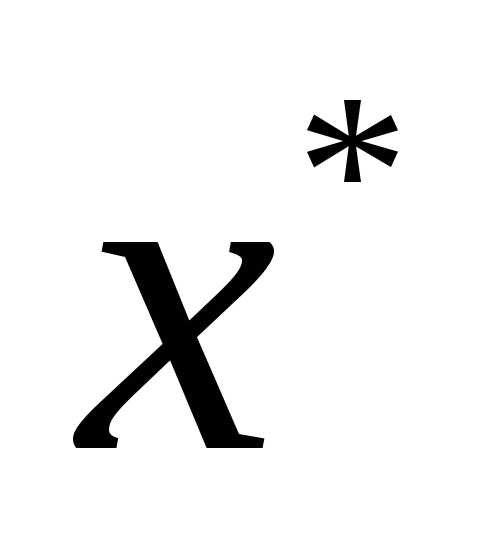 ) ≤f(x) (соответственноf(
) ≤f(x) (соответственноf(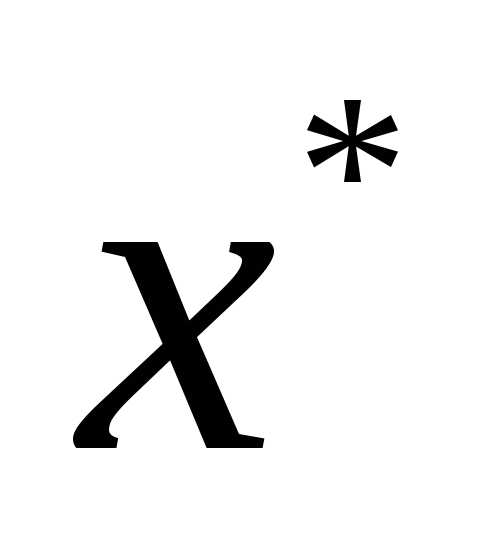 ) ≥f(x)) выполняется для всехх
) ≥f(x)) выполняется для всехх Хтаких, что
Хтаких, что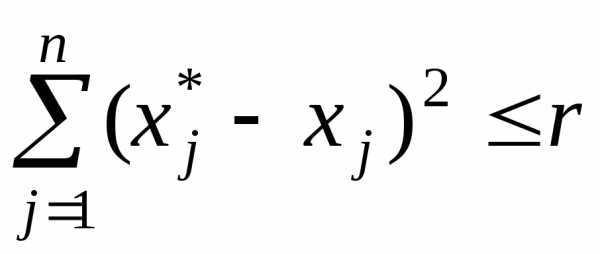 для некоторого числаr> 0.
для некоторого числаr> 0.
Точка 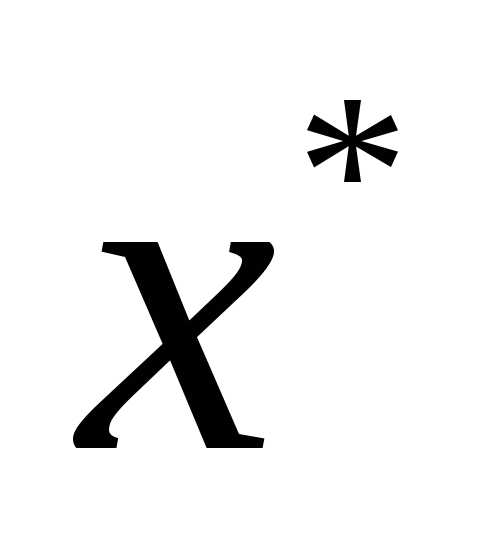 называетсяглобальным минимумом(максимумом) функцииf на множествеХ, если неравенствоf(
называетсяглобальным минимумом(максимумом) функцииf на множествеХ, если неравенствоf(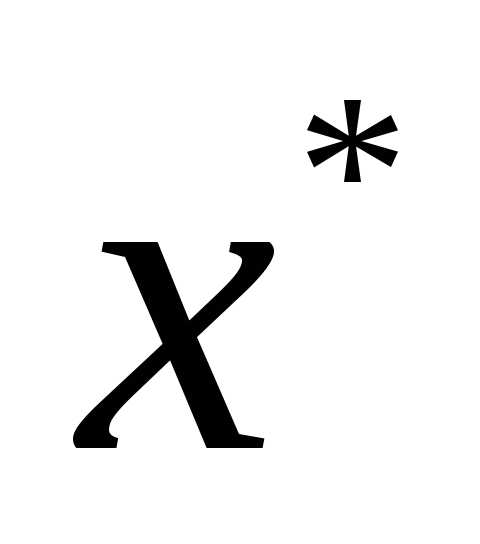 ) ≤f(x) (соответственноf(
) ≤f(x) (соответственноf(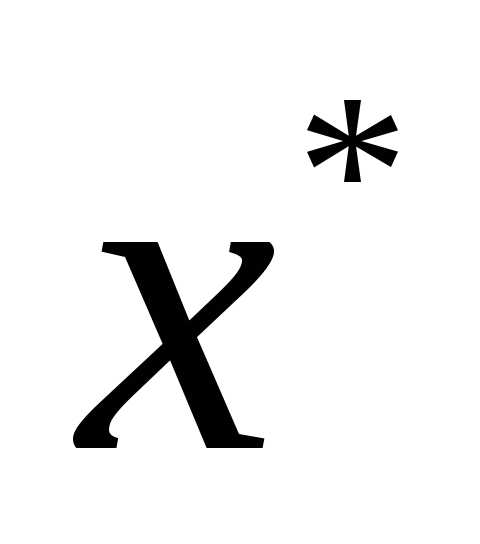 ) ≥f(x)) выполняется для всехх
) ≥f(x)) выполняется для всехх Х.
Х.
Если ЦФ имеет несколько локальных оптимумов и принимает на них различные значения, то отыскание среди них глобального оптимума обычно представляет собой сложную проблему. Однако, если целевая функция и ограничения задачи НП обладают свойством «выпуклости», то эта ситуация не возникает.
Функция fназывается выпуклой(выпуклой вниз) на выпуклом1множествеХ, если для любой пары точекx,y Хи любого числаα
Хи любого числаα (0, 1) справедливо соотношение
(0, 1) справедливо соотношение
f(α x+ (1 –α) y) ≤α f(x) + (1 –α) f(y). (4)
Функция fназывается вогнутой(выпуклой вверх) на выпуклом множествеХ, если для любой пары точекx,y Хи любого числаα
Хи любого числаα (0, 1) справедливо соотношение
(0, 1) справедливо соотношение
f(α x+ (1 –α) y) ≥α f(x) + (1 –α) f(y). (5)
Функция fназываетсястрого выпуклой(строго вогнутой), если неравенство (4) (соответственно, неравенство (5)) является строгим для всехx ≠ y, т.е. знак неравенства "<" (соответственно, ">").
Ясно, что если f— выпуклая функция, тоg = -f— вогнутая функция. Сумма выпуклых (вогнутых) функций — выпуклая (вогнутая) функция. Линейная функция является как выпуклой, так и вогнутой функцией.
Простейший пример выпуклой функции: z=х2, а вогнутой:z= .
.
Задача (1) – (3) является задачей выпуклого программирования(ВП), если она удовлетворяет следующим условиям:
требуется найти минимум (максимум) выпуклой (вогнутой) целевой функции f;
все функции giв ограничениях-равенствах (
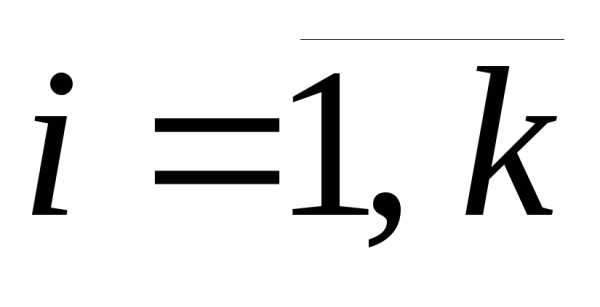 ) линейные, а в ограничениях-неравенствах () выпуклые.
) линейные, а в ограничениях-неравенствах () выпуклые.
Легко проверить, что если g— выпуклая (вогнутая) функция, то для любого числаbмножество {х |g(x) ≤ (≥)b} — выпуклое. Поэтому ОДР в задаче ВП — выпуклое множество. Выпуклым будет и множество оптимальных решений. Если же ЦФ — строго выпуклая (вогнутая) функция, то множество точек ее минимума (максимума) состоит из единственной точки.
Наиболее важное свойство таких задач: любая точка локального оптимума задачи ВП является точкой ее глобального оптимума. Следовательно, в задаче ВП можно говорить об оптимальном решении, не уточняя, идет речь о глобальном или локальном оптимуме.
Поэтому прежде чем начать поиск решения в задаче НП желательно выяснить, является ли она задачей ВП. Положительный ответ на этот вопрос существенно упрощает процедуру нахождения решения, так как в этом случае для нахождения глобального оптимума достаточно найти любой локальный оптимум. Для этого нужно уметь проверять выпуклость (вогнутость) функций, фигурирующих в условиях задачи. Ниже приводятся критерии выпуклости (вогнутости) функций, позволяющие делать такую проверку. Пусть f — дважды непрерывно дифференцируемая функцияnпеременных. Обозначим
H(x) = 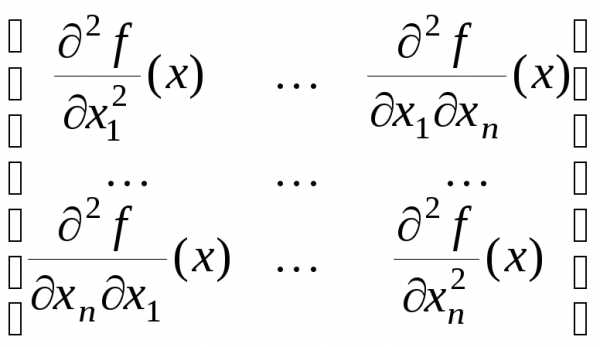 (6)
(6)
матрицу вторых производных (гессиан) функции fв точкех.
Теорема 1 (условие выпуклости функции). Пусть функцияf дважды непрерывно дифференцируема во всех точках выпуклого множестваX. Тогда
если все главные2(угловые3) миноры ее гессианаH(x) неотрицательны (положительны) для всехх

если все главные (угловые) миноры ее гессианаH(x) нечетного порядка неположительны (отрицательны), а все главные (угловые) миноры четного порядка неотрицательны (положительны) для всехх
 Х, то функцияfвогнута (строго вогнута) на Х.
Х, то функцияfвогнута (строго вогнута) на Х.
Пример. Имеется функцияf(x1,x2)= .Нужно определить, при каких значениях коэффициентов она будет (строго) выпуклой или вогнутой.
Для этого необходимо вычислить ее гессиан. Сначала найдем первые частные производные:
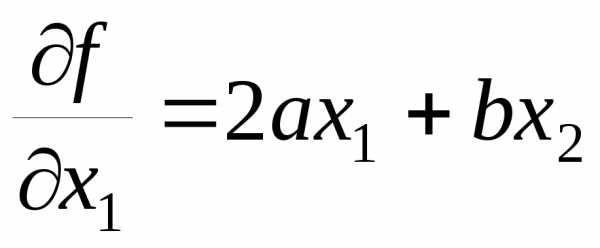 и
и 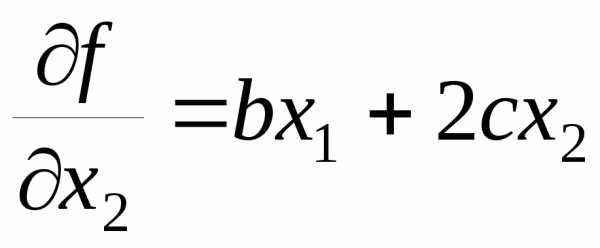 ,
,
а затем вторые частные производные:
;
;
.
Следовательно, гессиан функции f имеет такой вид:
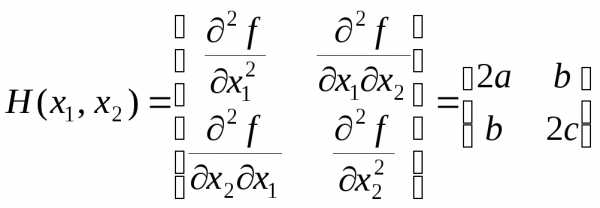 .
.
Главные миноры первого порядка равны 2а и 2с, а главный минор второго порядка равен 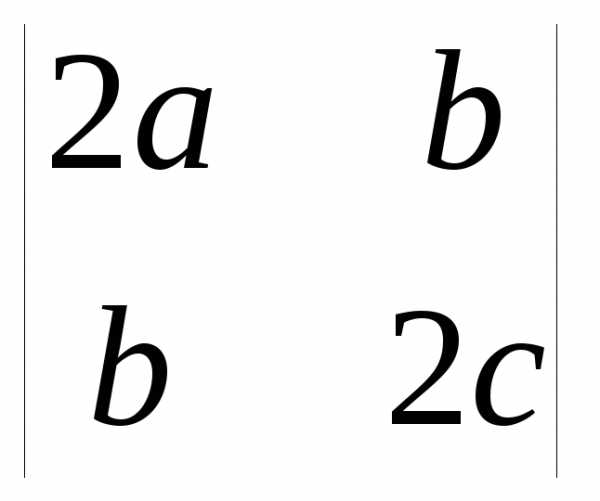
Для функции одной переменной условия выпуклости имеют следующий вид:
1) функция f(строго) выпукла на множествеХ если ее вторая производная принимает наХнеотрицательные (положительные) значения, т.е.
для всех х Х.
Х.
2) функция f(строго) вогнута на множествеХесли ее вторая производная принимает наХнеположительные (отрицательные) значения, т.е.
для всех х Х.
Х.
studfiles.net
Нелинейная задача оптимизации. Условный экстремум. — КиберПедия
Задача нелинейного программирования ставится как задача нахождения оптимума определенной целевой функции при выполнении условий:
, ,
где , — параметры, , - ограничения, — количество параметров, — количество ограничений. Целевая функция или ограничение есть нелинейная функция
В отличие от задачи линейного программирования, в задаче программирования нелинейного оптимум не обязательно лежит на границе области, определенной ограничениями.
Одним из методов, которые позволяют свести задачу нелинейного программирования к решению системы уравнений, является метод неопределенных множителей Лагранжа. Рассмотрим данный метод на примере функции двух переменных
Определение. Пусть функция определена в некоторой области и в этой области задана кривая уравнением . Условным экстремумом функции двух переменных называют ее экстремум при условии, что точки берутся на заданной кривой. Если из уравнения кривой можно, например, выразить , то задача о нахождении условного экстремума сводится к исследованию на экстремум функции одной переменной .
Метод множителей Лагранжа. Если уравнение не разрешимо ни относительно , ни относительно , то рассматривают функцию Лагранжа . Необходимым условием существования условного экстремума функции при условии является равенство нулю всех частных производных функции Лагранжа:
. (1.29)
Задачи НЛП несравнимо сложнее задач ЛП, и для них не существует общего, универсального метода решения (аналогично симплексному методу).Есть целый ряд методов решения задач НЛП. В пакете Excel реализован метод множителей Лагранжа, идея которого заключается в следующем: задачу условной оптимизациипреобразуют взадачу безусловной оптимизациии решают последнюю либо градиентными методами, либо методами Ньютона. Чаще применяются градиентные методы.
Однако необходимо помнить, что существующие методы дают возможность находить только локальные оптимумы (помимо случаев, когда функции обладают соответствующими свойствами выпуклости и вогнутости). Если же есть подозрение, что в допустимой области целевая функция может иметь несколько оптимумов, то эту область следует разбить на ряд областей и в каждой из них определить свои локальные оптимумы, а затем из всех локальных оптимумов выбрать глобальный. При таком подходе задача поиска глобального оптимума сводится к решению ряда задач, в каждой из которых определяется свой (локальный) оптимум.
Следует отметить, что в подавляющем большинстве практических задач оптимизации существует только один оптимум.
Решение задачи НЛП (реализация модели нелинейной оптимизации) средствами Excel отличается от решения ЗЛП следующим:
§ назначаются начальные значения искомых переменных , так, чтобы ЦФ в начальной точке не была равна нулю:
0;
§ в диалоговом окне Поиск решения в режиме Параметры не надо вводить флажок Линейная модель.
В Excel на каждой итерации вычисляется величина относительного приращения целевой функции
(1.30)
Оптимум считается достигнутым, если выполняется условие
,
где - относительная погрешность, назначаемая при решении задачи (режим Параметры).
Пример 4. Через точку провести плоскость, образующую с плоскостями координат тетраэдр наименьшего объема.
Решение.
Переменные - отрезки, которая плоскость отсекает на осях координат.
Целевая функция- объем тетраэдра, который надо минимизировать:
Ограничение на переменные накладывает задание точки :
Рабочий лист Excel может быть подготовлен в виде, представленном на рис. 1.22., формулы этого листа приведены в ячейках DЗ:D4.
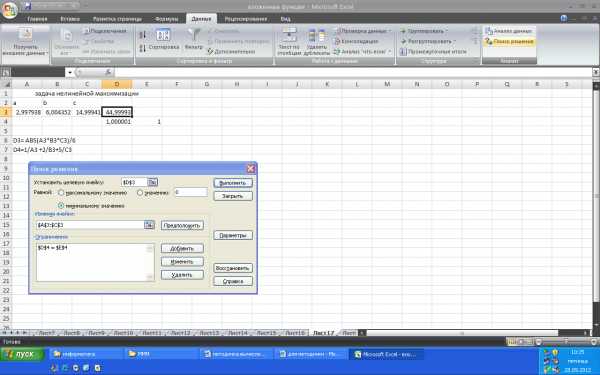
Рисунок.1.22. Исходные данные, условия и полученное решение задачи
Ответ. Реализуя решение приведенной задачи средствами Excel (рис. 1.6.1), получим величины отрезков, при которых достигается оптимум . Объем тетраэдра равен .
cyberpedia.su
Методика и специфика решения задач нелинейной оптимизации в msExcel
Задачу оптимизации нелинейной функции (6) можно было бы решить не путем анализа с использованием производной, и используя инструмент «Поиск решения» в MS Excel.
Если реализовать вычисления функции (6) по значению переменной в ячейке (см. рис. 2), то можно определить оптимально значение переменной в этой ячейке.
Рис. 2. Реализация вычисления функции прибыли в MSExcel
Для оптимизации используем инструмент «Поиск решения». Настраиваем параметры поиска решения (рис. 3) следующим образом:
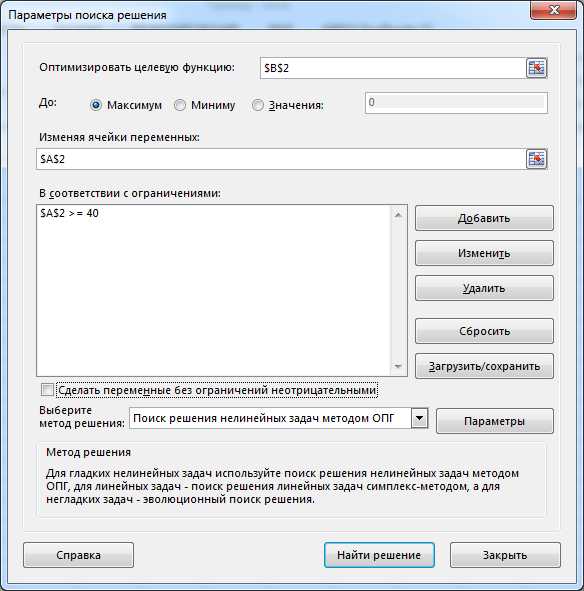
Рис. 3. Настройка инструмента «Поиск решения»
в поле «Оптимизировать целевую функцию» указываем ячейку, где реализована формула для прибыли;
в поле «До» указываем «Максимум»;
в поле «Изменяя ячейки переменных» указываем ячейку, предназначенную для значения переменной
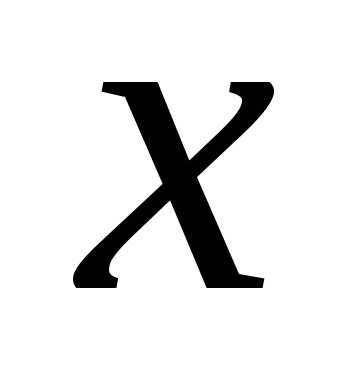 ;
;в поле «В соответствии с ограничениями» добавляем ограничение невозможности большого увольнения
 ;
;состояние поля «Сделать переменные без ограничений неотрицательными» в нашей задаче безразлично, так как единственная переменная ограничена;
в поле «Выберите метод решения» выбираем «Поиск решения нелинейных задач методом ОПГ» (так как наша задача нелинейная).
Нажав кнопку «Найти решение» получаем форму «Результаты поиска решения» (рис. 4). Убедившись, что в этом окне написано «Решение найдено. Все ограничения и условия выполнены», выбираем «Сохранить найденное решение» и нажимаем кнопку «Ок».
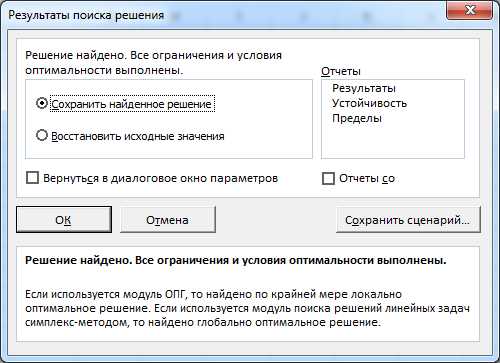
Рис. 4. Форма «Результаты поиска решения»
В ячейке переменной получаем оптимальное решение (рис. 5).
Рис. 5. Значения переменных после оптимизации
Как видим, нам удалось найти правильное решение автоматически.
Замечание: небольшое отличие значения в ячейке для искомой переменной от точного (получилось вместо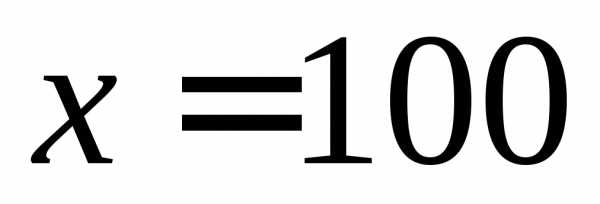 ) обусловлено численной реализацией метода поиска. Это значение можно смело округлить с заданной точностью.
) обусловлено численной реализацией метода поиска. Это значение можно смело округлить с заданной точностью.
Важно отметить такую специфику решения нелинейных задач в MS Excel. Поиск решения методом ОПГ ищет значения переменных от начального заданного, обеспечивая постоянное улучшение результата с текущего места. Такая реализация приводит к поиску локального, а не глобального экстремума. Так, «начав» поиск от 70 рабочих мы нашли оптимальное значение 100 человек. Начав же, например, со 160 человек, получим «оптимальное» количество 150 (рис. 6). Выбрав же вначале 200 человек можно снова прийти к оптимальному значению 100.
Рис. 6. Изменение решения при смене начального приближения
Описанное свойство является характерным для большинства алгоритмов численного поиска оптимумов в задачах нелинейной оптимизации. Для того, чтобы получить действительно глобальный максимум необходимо попробовать определить оптимальное решение для нескольких начальных приближений (в задачах экономики они, как правило, выбираются легко из смысла задачи). В задачах с одной и двумя переменными очень помогает построение графиков.
Задание для самостоятельного решения
Числовые условия задания формируются на основе двух последних цифр зачетной книжки или студенческого билета. Выполнение чужого варианта задания не допускается.
В задании данной темы:
;
;
;
;
;
;
;
;
 –последняя цифра номера зачетной книжки;
–последняя цифра номера зачетной книжки;
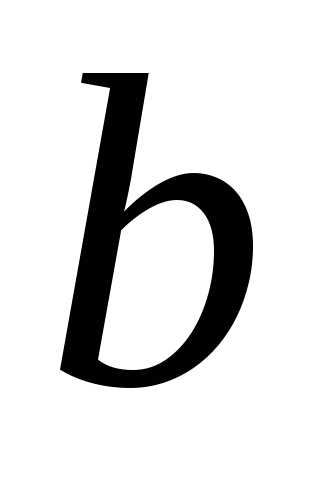 –предпоследняя цифра номера зачетной книжки.
–предпоследняя цифра номера зачетной книжки.
Вы – новый руководитель фирмы, производящей дорогостоящие автоматизированные станки. В настоящее время фирма производит 100 станков в год. Вам необходимо проанализировать и при возможности оптимизировать работу фирмы.
Задание
Определите оптимальное количество станков  , которое необходимо выпускать в год для оптимизации прибыли при следующих условиях функционирования фирмы:
, которое необходимо выпускать в год для оптимизации прибыли при следующих условиях функционирования фирмы:
Сформулируйте оптимальное экономико-управленческое решение в имеющихся условиях.
Дайте экономическое обоснование полученного решения.
Приведите сравнение предлагаемого Вами плана выпуска станков с используемым ранее вариантом. Обоснуйте необходимость изменений.
Приведите график зависимости прибыли от количества выпускаемой продукции. Обоснуйте свое решение с помощью графика.
studfiles.net
Решение задач нелинейной оптимизации на примере Модели агентских отношений
Решение проблемы морального риска: участие в прибылях
Основные понятия и методы теории контрактов рассматриваются подробно в отдельных учебных курсах[1]. Отдельные понятия описаны в приложении. Один из разделов теории контрактов - Теория агентства
Одной из задач этой теории является поиск и анализ оптимальных стимулирующих схем вознаграждения.
Контракт (лат. contractus, от лат. contrahere – соединять вместе). Взаимное соглашение двух или нескольких лиц, по которому одно из них или несколько обязуются что-либо сделать. Будем рассматривать понятие контракт в более узком смысле. Будем считать , что это письменное условие о найме на работу в котором оговорены права и обязанности для его участников. Как правило, в обязанности работника входит выполнение некоторой работы, а в обязанности работодателя – создание условий для её выполнения и выплата оговоренного вознаграждения.
В теории контрактов одну из сторон называют агентом, а другую – принципалом. Их главные отличия – различное отношение к своим обязательствам и к риску, а также в уровне информированности.
· Принципал выполняет взятые на себя обязательства по выплате вознаграждения агенту.
· Агент может относиться к своим обязательствам оппортунистически (см. приложение).
· Принципал более склонен к риску, чем агент. Это проявляется в различном виде функция полезности ( см.курсы микро и макроэкономики, а также приложение 2), которые определяют целесообразность поведения сторон
· Существует асимметрия в информированности. Агент обладает некоторой (важной для выполнения контракта) информацией, а принципал – нет.
Будем рассматривать простейшую модель.
В рамках рассматриваемой модели работник будет агентом, а работодатель –принципалом, Объем выполняемой работы и, главное, её качество определяется уровнем усилий, который прилагает агент для её выполнения. (Объем выполняемой работы будем считать фиксированным и не вызы ающим разногласий между сторонами.)
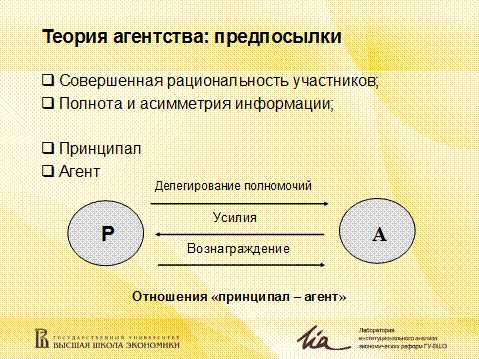

В модели рассматриваются два индивида – поручитель (принципал, патрон) и исполнитель (агент). Агент может выполнять свои договорные обязательства с разным уровнем усилий, например, работать интенсивно или отлынивать. Важно то, что он сам выбирает уровень усилий, а принципал не может объективно проверить (верифицировать) какой уровень усилий прикладывался.
Контракты, формируемые в рамках рассматриваемой модели, должны быть направлены на обеспечение добровольных неверифицируемых действий, которые приносили бы выгоду обеим сторонам.
Обозначим через уровень усилий агента. Конечный результат для приципала в значительной степени определяется значением производственная функция y(е,q)[2].
В терминах производственной функции е является фактором производства. Входящая в модель переменная q – является случайным параметром, отражающим случайный (стохастический) характер модели, определяющим неконтролируемые факторы рынка. В качестве примера, рассмотрим производственную функцию для ситуации, когда принципалом является владелец ресторана, а агентом официант. Очевидно, что доход ресторана зависит от многих факторов, в том числе от усилий официанта. Можно ожидать, что чем больше усилий прикладывает официант, тем больше денег оставит посетитель. Этот факт можно математически отразить соотношением
Введение случайной величины q в производственную функцию объясняется тем, что величина заказа в нашем примере зависит не только от усилий официанта, но и от усилий других лиц (прежде всего поваров, сомелье, хостесов и т.д.) и от состояния клиентов (их настроения, аппетита и др.). Поэтому, доход, который принесет данный клиент, есть величина случайная, но на её распределение оказывает влияние усилия (работа) официанта (в том числе). В общем случае можно утверждать, что (числовое) значение производственной функции зависит от состояния рынка.
Имеются нейтральный к риску принципал и избегающий риска агент. Это различие отражается в конкретном виде их функций полезности (см.приложение)
Функция полезности агента имеет следующий вид:
где — ставка заработной платы, — уровень усилий агента. Функция полезности агента вогнута, что является формальным признаком его рискофобии, т.е. у него есть склонность избегать риска.
Уровень усилий может принимать два значения, 1 и 2, которые далее будут обозначаться как «низкий» и «высокий» уровни усилий.
Альтернативная стоимость работы, определяемая рыночной ставкой заработной платы, такова, что её полезность равна . Это означает, что при любом реальном контракте средняя полезность для агента должна быть выше этого уровня (единицы), в противоположном случае он ищет работу в другом месте. Это предположение позволяет рассчитать минимальный уровень заработной платы, при условии, что агента прилагает «низкий» или «высокий» уровень усилий, а принципал знает об этом.
Если агент прилагает низкий» уровень усилий, то
| (5) |
Т.е. для того чтобы работник прилагал даже низкий уровень усилий, ему необходима заработная плата не ниже чем единица, иначе он может уйти работать в другое место.
Если агент прилагает «высокий» уровень усилий, то
.
| (6) |
Т.е. для того чтобы работник прилагал высокий уровень усилий, ему необходима заработная плата не ниже чем четыре единицы.
Полученную ситуацию можем проиллюстрировать следующим примером. Пусть агентом является преподаватель матметодов, принципалом – университет. Если преподаватель ведет занятия на русском языке, то он прилагает усилия на низком уровне и получает зарплату равную . Если преподаватель ведет занятия на английском языке, то он прилагает усилия на высоком уровне и получает зарплату равную . Очевидно, что во втором случае его уровень усилий существенно выше, как при подготовке занятий, так и при их проведении. Однако агент, несмотря на то, что уровень зарплаты в 4 раза выше во втором случае, он оценивает полезность (для себя) этих двух ситуаций одинаково.
Будем полагать, что доход принципала зависит от уровня усилий агента и внешних обстоятельств как это показано на рис.1 и 2. Будем полагать, что состояние рынка для простоты имеет два уровня и характеризуется как «удачный» или «неудачный» период для бизнеса.
| Усилия работника | е= | |||
| Период | неудачный | удачный | ||
| Доход фирмы | R | |||
| Вероятность | P | 2/3 | 1/3 |
Рис. 1. Случайная величина, определяющая доход принципала в зависимости от состояния рынка (удачности или неудачности периода) при низком уровне усилий агента.
| Усилия работника | е= | |||
| Период | неудачный | удачный | ||
| Доход фирмы | R | |||
| Вероятность | P | 1/3 | 2/3 |
Рис. 2. Случайная величина, определяющая доход принципала в зависимости от состояния рынка (удачности или неудачности периода) при высоком уровне усилий агента.
Сравнивая рис.1 и 2. можно увидеть, что вероятность более высокого дохода принципала возрастает при увеличении усилий агента.
Будем полагать, что ситуация многократно повторятся, т.е. сначала заключается контракт на какой-то длительный срок (год и т.п.), а внутри этого длительного срока рассматриваем множество отдельных периодов времени (день, неделя и т.д.), по итогам каждого происходит подведение промежуточных итогов. Т.е. проходит один период времени, в течение которого агент выполняет свои функции, прилагая тот или иной уровень усилий, далее по окончанию этого периода подводят итоги, выяснив, чему равен доход фирмы и (заодно) удачным или неудачным был прошедший период. После этого будет определен доход фирмы . Если период был удачным, то равно 30, а если период был неудачным, то равно 10. Важно то, что при высоком уровне усилий удачный период реализуется существенно чаще, чем при низком уровне усилий. Очевидно, что благополучие фирмы определяет не отдельный период, а общий результат многократного повторения производственного процесса. Затем подводим итог деятельности фирмы, сосчитав средний доход за период за весь длительный срок действия контракта. При этих данных можно рассчитать ожидаемый доход принципала при многократном повторении описанного выше производственного цикла, очевидно, что это величина будет равна математическому ожиданию соответствующей случайной величины.
Обозначим средний доход принципала при низком уровне усилий агента через .
Вычислим это значение, пользуясь известными формулами из теории вероятности:
| (7) |
Обозначим средний доход принципала при высоком уровне усилий агента через .
Вычислим это значение, пользуясь известными формулами из теории вероятности:
.
| (8) |
Разница в доходах принципала при двух уровнях усилий агента очевидна, средний доход принципала при высоком уровне усилий агента будет выше, чем при низком.
Для лучшего понимания экономических последствий морального риска, сравним два случая, в одном из которых усилия агента наблюдаемы, т. е. проблема морального риска не возникает, а в другом усилия агента не поддаются наблюдению и у него появляется возможность проявить оппортунистическое поведение, т. е. встает проблема морального риска.
Будем полагать, что функцией полезности для принципала является величина чистого дохода, т.е. величина дохода минус величина вознаграждения агента .
| (9) |
где - уровень усилий агента.
megaobuchalka.ru
Тема 4. Нелинейные задачи оптимизации
Поиск ЛекцийФедеральное государственное бюджетное образовательное
Учреждение высшего профессионального образования
«КУЗБАССКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ Т.Ф. ГОРБАЧЕВА»
Кафедра математики
МЕТОДЫ ОПТИМАЛЬНЫХ РЕШЕНИЙ
Контрольная работа № 1 и методические указаниядля студентов 1 курса (2 семестр) заочной формы обучениянаправления подготовки бакалавров 080100.62 «Экономика»
Составители: А. И. Бабин
Е. А. Николаева
Е. В. Прейс
Утверждены на заседании кафедры
Протокол № 7 от 08. 02 . 2012 г.
Рекомендовано к печати
учебно–методической комиссией
по направлению подготовки
бакалавров 080100.62 «Экономика»
Протокол № 16 от 14. 02. 2012 г.
Электронная копия находится
в библиотеке КузГТУ
Кемерово 2012
Контрольная работа № 1 составлена в соответствии с программой курса «Методы оптимальных решений» для студентов заочной формы обучения.
В составлении работ и методических указаний к ним принимала участие доцент Е. А. Волкова.
Номера задач контрольной работы студент должен выбрать в каждой теме по последней цифре зачетной книжки.
Контрольная работа возвращается непроверенной, если она выполнена не по своему варианту.
ПРОГРАММА 1 КУРСА (2 СЕМЕСТР)
Рабочая программа дисциплины «Методы оптимальных решений» составлена на основании Федерального государственного образовательного стандарта высшего профессионального образования и с учетом рекомендаций Примерной основной образовательной программы по направлению подготовки бакалавров 080100.62 «Экономика».
Требования к студентам: Учебная дисциплина «Методы оптимальных решений» использует материал следующих дисциплин: «Математический анализ», «Линейная алгебра», «Теория вероятностей и математическая статистика».
Аннотация: Учебная дисциплина «Методы оптимальных решений» вводит студентов в математическую проблематику оптимизации, принятия решений, исследования операций, моделирования. Отличительная особенность курса состоит в том, что он соединяет изучение математических методов с содержательным рассмотрением экономических приложений.
Программа курса обеспечивает в дальнейшем изучение таких дисциплин, как «Микроэкономика», «Макроэкономика», «Эконометрика». Знания, полученные по данной дисциплине, могут быть использованы при выполнении курсовых и дипломных работ.
СОДЕРЖАНИЕ ПРОГРАММЫ.
Введение
Предмет, история и перспективы развития методов оптимальных решений. Основные этапы принятия оптимальных решений. Общая постановка и классификация задач оптимизации.
Тема 1. Линейное программирование
Постановка и формы записи задачи линейного программирования. Экономические приложения. Геометрическая интерпретация задачи. Симплекс-метод: основная схема алгоритма. Экономическая интерпретация итоговой симплекс-таблицы. Метод искусственного базиса.
Двойственные задачи линейного программирования. Основное неравенство теории двойственности. Теорема о существовании прямого и двойственного решений, теорема о дополняющей нежесткости. Примеры использования теорем двойственности для построения оптимального решения задачи ЛП. Анализ модели на чувствительность. Экономическая интерпретация двойственной задачи. Третья теорема двойственности (об оценках). Пример использования объективно обусловленных оценок для принятия оптимальных решений.
Тема 2. Распределительные модели
Постановка транспортной задачи по критерию стоимости и ее математическая модель. Открытая и закрытая модели транспортной задачи. Способы построения начального опорного решения. Теорема об оптимальности решений задачи, потенциалы поставщиков и потребителей, оценки свободных клеток транспортной таблицы и их экономический смысл. Алгоритм метода потенциалов.
Тема 3. Целочисленное программирование и
Дискретная оптимизация
Целочисленные переменные в задачах экономического планирования. Общая задача целочисленного программирования, общая задача целочисленного ЛП, задача частично-целочисленного программирования. Геометрическая интерпретация задачи целочисленного программирования. Алгоритм Гомори. Метод ветвей и границ. Задача о назначениях.
Тема 4. Нелинейные задачи оптимизации
Общая постановка задач конечномерной оптимизации. Выпуклые множества и их свойства. Экономическая и геометрическая интерпретации. Теорема Вейерштрасса и следствие из неё. Метод множителей Лагранжа в гладких экстремальных задачах с ограничениями типа равенств и неравенств. Задачи выпуклого программирования. Теорема Куна-Таккера.
Схемы численных методов оптимизации: градиентный метод с постоянным шагом, метод скорейшего спуска, метод Ньютона, метод проекции градиента.
poisk-ru.ru
12 Использование информационных технологий при решении задач нелинейной оптимизации
Использование информационных технологий при решении задач нелинейной оптимизации
Процессор электронных таблиц Excel является мощным и достаточно эффективным средством решения задач нелинейной оптимизации. В качестве иллюстрации возможностей данного программного продукта рассмотрим решение нескольких задач, непосредственно связанных с процессом принятия (выработки) решений.
Пример 5.
В качестве примера рассмотрим следующую задачу. Предприятие располагает ресурсами двух видов сырья и рабочей силы, необходимыми для производства двух видов продукции. Затраты ресурсов на изготовление одной тонны каждого продукта, прибыль, получаемая предприятием от реализации тонны продукта, а также запасы ресурсов приведены в следующей таблице:
Таблица 2.3. Параметры задачи.
| Ресурс | Расход ресурса | Запас ресурса | |
| На продукт 1 | На продукт 2 | ||
| Сырье 1, т | 3 | 5 | 120 |
| Сырье 2, т | 4 | 6 | 150 |
| Трудозатраты, ч | 14 | 12 | 400 |
| Прибыль единицы продукта, тыс. руб./т | 72 | 103 | |
Стоимость одной тонны каждого вида сырья определяется следующими зависимостями:
тыс. руб. для сырья 1 и тыс. руб. для сырья 2, где - затраты сырья на производство продукции. Стоимость одного часа трудозатрат определяется зависимостью , где - затраты времени на производство продукции.
Вопросы:
Сколько продукта 1 и 2 следует производить для того, чтобы обеспечить максимальную прибыль?
Какова максимальная прибыль?
Решение: Пусть и - объемы выпуска продукции 1 и 2 в тоннах. Тогда задача может быть описана в виде следующей модели нелинейного программирования:
Проведем решение данной задачи в Excel. На начальном этапе подготовим форму для решения задачи на рабочем листе следующего вида:
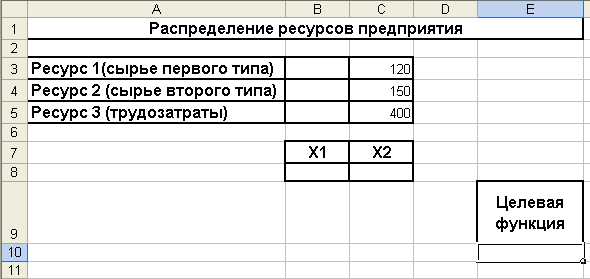
Рис. 2.6. Данные для решения примера 5.
Отведем для искомых значений объемов выпуска продукции ячейки B8, C8, для расхода соответствующих ресурсов (включая трудозатраты) – ячейки B3, B4, B5. В данные ячейки необходимо ввести функции
=3*B8+5*C8
=4*B8+6*C8 и
=14*B8+12*C8
соответственно.
Численные значения ограничений по ресурсам внесем в ячейки C3, C4, C5. В ячейку E10 введем формулу для целевой функции: =11*B8+16*C8+0,1*B8^2+0,12*C8^2+0,22*B8*C8.
Решение задачи производится с помощью Поиска решения Excel. Изменяемыми ячейками будут, очевидно, ячейки B8, C8; целевая ячейка устанавливается равной максимальному значению; используются следующие ограничения: $B$3<=$C$3, $B$4<=$C$4, $B$5<=$C$5. Следует иметь в виду, что в связи с нелинейностью данной задачи необходимо в окне Параметры поиска решения отключить опцию Линейная модель (это замечание относится к решению всех задач, приведенных в данном разделе). В результате запуска Поиска решения получим ответ: и значение максимальной прибыли 507.407 тыс. руб.
Пример 6.
Рассмотрим следующую задачу. Предприятие может выпускать два вида продукции. На ее изготовление требуются ресурсы трех видов (). С учетом брака расход ресурсов на единицу производимой продукции - го вида () определяется выражением , а прибыль в зависимости от объемов производства равна , где - искомый объем производства продукции - го вида; - норма расхода - го ресурса на производство единицы продукции - го вида; - коэффициент изменения расхода соответствующего ресурса с учетом выпуска бракованных изделий; - прибыль от единицы продукции - го вида; - коэффициент изменения прибыли, влияющий на объем производства продукции.
Требуется найти такие объемы производства продукции, при которых прибыль максимальна.
Значения параметров задачи приводятся в нижеследующей таблице.
| Ресурс () | Запас ресурса | Норма расхода ресурсов на продукцию вида | Коэффициент изменения норм расхода ресурсов на продукцию вида | ||
| 1 | 2 | 1 | 2 | ||
| 1 | 1350 | 15 | 18 | 0,1 | 0,05 |
| 2 | 1400 | 12 | 16 | 0,2 | 0,2 |
| 3 | 1580 | 17 | 14 | 0,1 | 0,15 |
| Прибыль (ден. ед.) | 100 | 120 | |||
| Коэффициент изменения прибыли | -0,08 | -0,1 | |||
При заданных значениях параметров целевая функция имеет вид
,
или
.
Ограничения по ресурсам имеют вид
или
Как видно, в данной задаче как целевая функция, так и функции-ограничения являются нелинейными функциями. Найти решение задачи в целых числах.
Решение.
Заполним рабочий лист по аналогии с Рис 2.7.

Рис. 2.7. Данные для решения примера 6.
В ячейки B3¸B5 введем формулы-ограничения, в ячейку E8 – формулу для целевой функции. Дополнительное ограничение – на целочисленность переменных . После запуска Поиска решения получим ответ: .
Пример 7.
Рассмотрим задачу несколько иного рода. Пусть необходимо определить место расположения некоторого объекта, обслуживающего несколько других объектов (например, прачечная, обслуживающая нескольких крупных клиентов; нефтеперерабатывающий завод, на который должна поступать нефть с нескольких скважин, склад готовой продукции, обслуживающий ряд предприятий, производящих однотипную продукцию и т.п.), координаты которых известны. Цель – свести к минимуму транспортные расходы с учетом неравноценности клиентов (например, различные объемы заказов). Поэтому возникает необходимость такого выбора координат объекта, чтобы транспортные расходы были минимальны.
В качестве целевой функции принимаем
,
где - искомые координаты обслуживающего клиентов объекта, - координаты -го обслуживаемого объекта, - заданные коэффициенты, характеризующие, например, объемы заказов, или удельную (в расчете на 1 км.) стоимость доставки из соответствующих объектов. Отметим, что в данной задаче не используются ограничения положительности .
Решение проведем для трех случаев, соответствующих 1) отсутствию каких-либо ограничений на координаты , 2) необходимости размещения обслуживающего объекта на некотором прямолинейном отрезке (например, объект может быть расположен лишь на отдельном небольшом участке улицы), 3) расположению объекта в пределах некоторого круга заданного радиуса. Ограничимся случаем трех обслуживаемых объектов
Первый случай. Отсутствуют какие-либо ограничения на координаты .
Решение. Введем данные на рабочий лист в соответствии с приводимым ниже рисунком.
В качестве изменяемых ячеек выберем B10, B11; в качестве целевой ячейки - ячейку E11 и введем в нее формулу
=J6*КОРЕНЬ((B10-A6)^2+(B11-B6)^2)+K6*КОРЕНЬ((B10-D6)^2+(B11-E6)^2)+L6*КОРЕНЬ((B10-G6)^2+(B11-H6)^2).
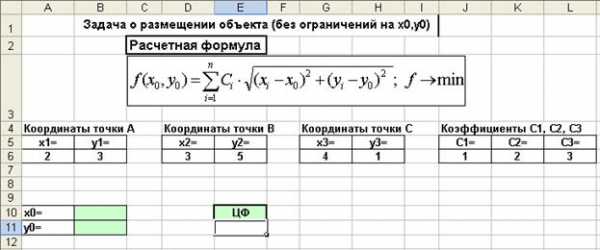
Рис. 2.8. Данные для решения задачи о расположении объекта (без ограничений).
Решение задачи с помощью Поиска решения при заданных координатах точек дает оптимальное значение целевой функции составляет 11,0746.
Второй случай. Координаты принадлежат некоторому отрезку прямой линии, задаваемой уравнением
(в данном примере мы используем значения ).
Решение. Введем данные на рабочий лист в соответствии с приводимым ниже рисунком.
Очевидно, формула для целевой функции (ячейка E12) остается неизменной.
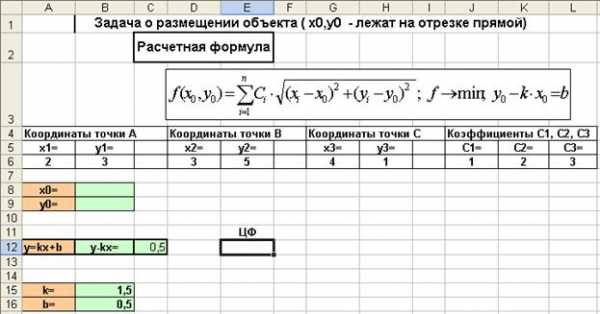
Рис. 2.9. Данные для решения задачи о расположении объекта (координаты объекта лежат на отрезке прямой линии).
Единственным отличием от предыдущего случая является необходимость ввода дополнительного ограничения в ячейку B13; в ячейку B13 вводится формула
=B9-B15*B8
и в окне диалога Поиск решения вводится ограничение
$B$13=$B$16.
Ответ: оптимальное значение целевой функции составляет 13,6843.
Третий случай. Координаты лежат внутри некоторой окружности радиуса (мы полагаем ). Данный случай может соответствовать, например, ситуации, когда необходимо разместить некоторый объект вблизи некоторого населенного пункта.
Решение. Введем данные на рабочий лист в соответствии с приводимым ниже рисунком.
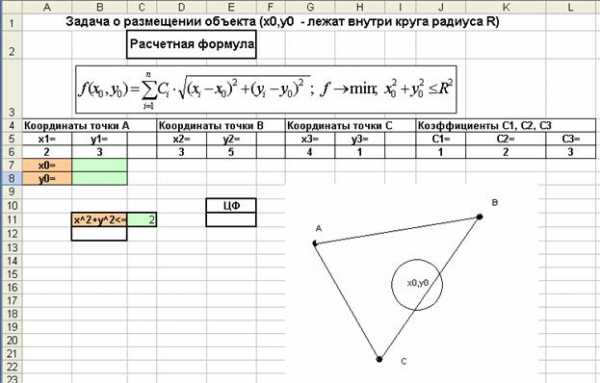
Рис. 2.10. Данные для решения задачи о расположении объекта (координаты объекта локализованы в пределах круга определенного радиуса).
Целевая функция располагается в ячейке E11, искомые координаты объекта будут располагаться в ячейках B7, B8. В ячейку B12 введем функцию = B7^2+B8^2. Введем ограничение $B$12<=$C$11, учитывающее то обстоятельство, что объект не должен располагаться вне круга заданного радиуса. Поиск решения дает ответ целевая функция .
Пример 8. Формирование оптимального портфеля ценных бумаг
Требуется сформировать портфель минимального риска из двух видов ценных бумаг – “АРТ” с эффективностью 12% и риском 21,1 и “ВЕРМ” с эффективностью 5,1% и риском 8,3 при условии, что обеспечивается доходность портфеля не менее 8,9%. Коэффициент корреляции равен 0,18.
Вводные замечания. Портфель ценных бумаг представляет собой совокупность различных инвестиционных инструментов, собранных воедино для достижения конкретной инвестиционной цели вкладчика. В портфель могут входить ценные бумаги только одного типа, например акции или облигации, или различные инвестиционные ценности, такие как акции, облигации, депозитные и сберегательные сертификаты, недвижимость и т. д.
Главная цель в формировании портфеля состоит в достижении оптимального сочетания между риском и доходом для инвестора. Уменьшение риска достигается за счет того, что возможные невысокие доходы по одной бумаге будут компенсироваться высокой прибылью по другим бумагам. Минимизация риска достигается за счет включения в портфель бумаг широкого круга отраслей, не связанных тесно между собой, чтобы избежать синхронности циклических колебаний их деловой активности.
Для получения количественных характеристик портфеля могут использоваться следующие характеристики:
– доходность (эффективность) портфеля ценных бумаг, рассчитываемая по формуле:
где – доли инвестиций, помещенных в каждый из видов активов; – ожидаемая ставка дохода по каждому виду активов. Риск портфеля (стандартное отклонение ставок дохода по портфелю) представляет собой квадратный корень из дисперсии портфельного дохода (дисперсию доходности портфеля называют его вариацией ), которая определяется по формуле:
где – коэффициент корреляции доходов между i-м и j-м активом; - риски отдельных видов ценных бумаг.
Задача оптимизации заключается в том, чтобы определить, какая доля портфеля должна быть отведена для каждой из инвестиций так, чтобы величина ожидаемого дохода и уровень риска соответствовали целям инвесторов. Целевой функцией может быть минимизация риска при заданной доходности, или максимизация дохода при риске не выше заданного.
Решение. В случае всего двух видов активов формула для расчета риска упрощается и приобретает вид
.
Введем данные на рабочий лист в соответствии с Рис. 2.11.
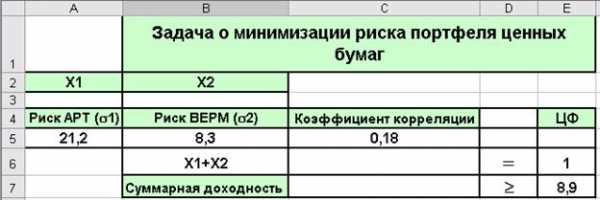
Рис. 2.11. Данные для решения задачи о минимизации риска портфеля ценных бумаг.
Формулу для расчета введем в ячейку С6; формулу для значения доходности портфеля – в ячейку С7 (=СУММ(12*A3+5,1*B3)). Формулу для целевой функции
=КОРЕНЬ((A5*A3)^2+2*A3*B3*A5*B5*C5+(B5*B3)^2) - в ячейку E5.
Используемые ограничения
Значение (ячейка C6) должно равняться единице.
Значение доходности портфеля ценных бумаг (ячейка C7) должно быть не менее 8,9.
.
Ответ . Минимальный риск при этом составляет .
Контрольные вопросы к теме:
1. Экономическая суть методов оптимизации
2. Определите задачи математического программирования
3. Какие задачи называют задачами линейного программирования
4. Динамическое программирование
5. Стохастическое программирование
6. Определение целевой функции
7. Построение математической модели оптимизационной задачи
8. Нелинейные модели оптимизации
9. Методы решения задач нелинейной оптимизации
studizba.com