ГлавнаяОптимизацияЗадачи егэ на оптимизацию

Задача на оптимизацию расходов. Задание 17. Задачи егэ на оптимизацию


Задание №19 Т/Р №116 А. Ларина

Категория: 17 (С5) Практич. задачиТ/P A. Ларина

Елена Репина 2015-05-07 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №17»

Смотрите также №15, №16, №17, №18, №20.Алексей вышел из дома на прогулку со скоростью км/ч. После того, как он прошел 6 км, из дома следом за ним выбежала собака Жучка, скорость которой была на 9 км/ч больше скорости Алексея. Когда Жучка догнала хозяина, они повернули назад и вместе возвратились домой со скоростью 4 км/ч. Найдите значение , при котором время прогулки Алексея окажется наименьшим. Сколько при этом составит время его прогулки?

Решение:

Алексей (выйдя из дома со скоростью   км/ч) на путь в 6 км потратил часов.

Пусть после этого Алексей до встречи с Жучкой прошел еще км, на что ушло  часов.

За тоже время ( ч)  Жучка пробежала   км со скоростью км/ч.

Тогда откуда

Время прогулки Алексея, с учетом того, что вместе с Жучкой они возвращались домой со скоростью км/ч, составило, таким образом, часов (или часов).

Рассмотрим функцию и найдем  , при котором функция принимает наименьшее значение (а также само наименьшее значение).

– точка минимума, в ней и достигается наименьшее значение функции.

 (ч).

Ответ: 6 км/ч; 4 часа 10 минут.

Автор: egeMax | комментариев 7

egemaximum.ru

Пора бы уже научиться решать оптимизационные задачи, встречающиеся на ЕГЭ по математике, иначе провал неизбежен

Давайте знакомиться! Я – репетитор по математике, который постоянно занимается оптимизационными задачами

Всем здравствуйте! Меня зовут Александр Георгиевич. Я – рейтинговый московский репетитор по математике, информатике, базам данных, алгоритмам и программированию.

Мои ключевые профессиональные компетенции:

Я прекрасно понимаю, что вы крайне занятой человек, привыкший решать все проблемы и добиваться поставленных целей по-деловому. Но, несмотря на это, я настоятельно рекомендую вам потратить \(2-3\) минуты и познакомиться с отзывами моих клиентов, которые прошли подготовку под моим чутким контролем. Все они добились поставленных целей!

Также мною была разработана многофункциональная финансовая система, которая удобна и проста в использовании. Это система моих тарифов на образовательные услуги. Я предлагаю своим потенциальным клиентам \(144\) варианта взаимовыгодного сотрудничества. Даже самый взыскательный и привередливый потребитель сумеет подобрать себе вариант, полностью удовлетворяющий его потребности.

В данной обзорной статье я вам расскажу об оптимизационных задачах, их роли в математике, их главном преимуществе по сравнению со «статическими» задачами. Самое главное – вы получите необходимые знания для успешного решения таких задач на официальном экзамене – ЕГЭ по математике.

Не забывайте о том, что я достаточно востребованный репетитор по математике и информатике, поэтому не откладывайте свое решение о записи ко мне на частную подготовку в долгий ящик, а действуйте прямо сейчас. Завтра вакантных мест в моем графике расписания занятий уже может не оказаться!

Общие сведения об оптимизации и оптимизационных задачах

Под оптимизацией следует понимать нахождение экстремума некоторой целевой функции при соответствующих ограничениях.

Да, достаточно непонятное определение для человека, неподкованного в области математики в целом и информатики в частности. Чтобы стать сильнее в математической сфере, сфере вычислений и преобразований, записывайтесь ко мне на первый пробный урок.

Давайте рассмотрим известную оптимизационную задачу на поиск кратчайшего пути между городами. А самое главное, попытаемся понять, а, собственно, с какого бока припека здесь вплетается оптимизация как таковая.

Условие задачи

Имеется \(N\) городов, пронумерованных от \(1\) до \(N\), а также эти города связаны между собой сетью дорог. Пешеход находится в городе \(№1\). Его задача добраться до города с номером \((№-1)\) по наиболее короткому пути. Расстояние между городами, то есть протяженность всех связующих дорог известна.

Определить длину наиболее короткого пути, позволяющего пешеходу добраться до нужного города.

Подобного типа задачу можно отнести к классу задач динамического программирования. Также давайте договоримся, что \(N\) будет равно \(7\), то есть перед пешеходом выстроена структура из \(7\) связанных городов. Расстояние между городами показано на картинке ниже. Также выделен цветом целевой город, то есть город \(N = 6\).

Любопытный читатель сразу воскликнет: «А в чем, собственно, здесь проявляется оптимизация?» Тот, кто не знаком с теорией графов, не догадывается, насколько много сложностей таят в себе задачи, подобные той, которую мы сейчас разбираем.

В данном случае перед нами небольшое количество городов (всего \(7\) штук), и здесь может быть полный перебор всех возможных маршрутов пешехода, но что делать, если городов окажется \(7\,000\). Или хотя бы \(70\). Полный перебор моментально теряет свою актуальность, так как количество возможных маршрутов растет по экспоненте (начинается экспоненциальный взрыв переборов).

Наша цель выработать алгоритм, который решает задачу правильно, эффективно и за разумное время, то есть наша цель разработать оптимальный алгоритм. Именно в этом и проявляется оптимизация.

Я специально взял задачу про нахождение кратчайшего пути, так как это очень известная оптимизационная задача не только в математике, но в том числе и в программировании. Поэтому на своих занятиях мы можем не только исследовать математическую модель этой задачи, но также произвести ее кодирование на одном из современных языков программирования.

Можно провести очень дифференцированную классификацию оптимизационных задач. Задачи могут быть ориентированы на совместную работу, на оптимальный раскрой, на оптимальный путь, на оптимальный доход. По факту вся наша жизнь – оптимальный выбор при определенных ограничениях.

Перечислять можно долго, реально долго, поэтому только на своих индивидуальных уроках я могу привести полную классификацию, а также примеры для каждой конкретной группы оптимизационных задач. На протяжении всей своей педагогической деятельности я уделяю много времени вопросам, связанным с оптимизацией, так как это крайне интересная область царицы всех наук – математики, имеющая широкое практическое применение.

Понятие целевой функции, и ее роль в решении оптимизационных задач

Целевая функция – это первая и последняя буква в решении оптимизационных задач. Если хотите, целевая функция – квинтэссенция всей модели, строящейся в процессе решения задач на оптимизацию.

А теперь более конкретно о целевой функции (ЦФ). Под целевой функцией можно понимать совокупность параметров различного типа, которые могут принимать различные значения (как правило, на эти значения особое влияние оказывают ограничения). Подбор наиболее подходящих параметров приводит к оптимальному решению задачи, для которой была выведена рассматриваемая целевая функция.

Целевые функции могут быть тривиальными, а могут быть настолько сложными и запутанными, что над их исследованием трудятся целые научные лаборатории. Рассмотрим на конкретных примерах.

Например, вы можете вывести ЦФ, которая будет сообщать вам информацию о том, сколько нужно купить зонтов, когда вы планируете поехать в какую-либо страну для отдыха. Это оптимизационная задача решается просто, так как многое зависит от климата страны, которую планируете посетить. Это тривиальная задача!

А теперь попытаемся вывести целевую функцию для анализа котировок акций на фондовом рынке. Искушенный трейдер прекрасно знает, что на стоимость ценных бумаг одновременно влияет несколько тысяч факторов, начиная от политических и заканчивая географическими. Построить эффективную ЦФ в данном случае не представляется возможным. Ученые возлагают эту задачу на супермощные компьютеры, но, чтобы последние принялись за расчеты, их необходимо снабдить нужной входной информацией, которой всегда недостаточно.

Поэтому нужно быть предельно осторожным в процессе рассмотрения оптимизационных задач и не бравировать тем, что вы всегда сможете построить целевую функцию. Далеко не всегда это возможно, особенно если речь идет о прикладной задаче, а не академической.

О методах построения эффективных целевых функций можно рассуждать практически бесконечно, поэтому, если вы хотите глубже окунуться в мир ЦФ, понять, какая существует корреляция между программированием и ЦФ, срочно звоните мне на мобильный телефон и записывайтесь на первый пробный урок.

Список условий оптимизационных задач, встречающихся на ЕГЭ по математике

Методика решений оптимизационных задач, я бы не сказал, что является сложной. Сложность проявляется абсолютно в других моментах решения. Суть решения представленных заданий сводится к построению целевой функции с последующим нахождением ее экстремального значения.

Задачи на оптимизацию перекликаются со всеми сферами жизни человека. На официальном экзамене ЕГЭ по математике вы можете столкнуться с заданиями, ориентированными на анализ добычи металлов, рытье котлована нужного размера, передачу информации различными серверами и т. п. Но все они решаются при помощи одной и той же модели, меняется лишь литературная оболочка и не более того!

Только на своих индивидуальных уроках у меня есть возможность своим ученикам продемонстрировать все фишки построения моделей целевых функций, показать краеугольные моменты в решении, объяснить, как правильно брать производную целевых функций, а также получать необходимые ограничения.

Пример №1

В двух шахтах работают по \(160\) горняков, каждый из которых трудится по \(5\) часов в сутки на добыче угля и кокса. В первой шахте один рабочий за час добывает \(0.1\) кг кокса или \(0.3\) кг угля. Во второй шахте для добычи \(x\) кг кокса в день требуется \(x^2\) человеко-часов труда, а для добычи \(y\) кг угля в день требуется \(y^2\) человеко-часов труда. Для сталелитейного завода можно использовать кокс или уголь, причем \(1\) кг кокса можно заменить \(1\) кг угля.

Какую наибольшую массу руды можно добыть в двух шахтах суммарно для нужд сталелитейного завода?

Пример№2

Необходимо из круглого бревна радиусом \(R\) выпилить прямоугольную балку таким образом, чтобы количество отходов было наименьшим.

Пример №3

Дан кусок стальной проволоки длиной \(2S\).

Какую наибольшую площадь прямоугольного участка земли можно огородить данным куском проволоки?

Пример №4

В агентстве такси «Быстрота» имеется автопарк из \(24\) машин. Завтра планируется проведение двух крупных банкетов и придется задействовать все автомобили из автопарка. Если на первый банкет будет вызвано \(x\) автомобилей, то водителям нужно будет заплатить \(4x^2\) долларов. Если на второй банкет будет вызвано \(y\) автомобилей, то водителям нужно будет заплатить \(y^2\) долларов.

Как нужно распределить автомобили из агентства, чтобы зарплата водителям оказалась наименьшей? Сколько конкретно в этом случае придется заплатить водителям такси?

Пример №5

Владимир является генеральным директором двух химических комбинатов, на каждом из которых работают по \(100\) человек. На первом комбинате один рабочий производит за смену \(3\) кг серы или \(1\) литр дистиллированной воды. На втором комбинате для изготовления \(x\) литров/кг (и воды, и серы) требуется \(x^2\) человеко-смен.

Оба комбината поставляют сырье на дальнейшую обработку, где получают раствор серной кислоты, причем для ее получения нужно \(3\) литра воды и \(1\) кг серы. При этом комбинаты договариваются между собой производить сырье так, чтобы можно было получить наибольшее количество серной кислоты.

Сколько литров серной кислоты при таких условиях можно получить за смену?

Пример №6

Программист может писать код на двух различных языках программирования: C++ и Pascal. После написания программ он производит их компиляцию. Как известно, результатом компиляции является исполняемый файл *.exe, который занимает некоторый объем в памяти компьютера.

Если компилятор под С++ обрабатывает \(x^2\) тысяч строк кода, то исполняемый файл получается объемом \(20x\) байт. Если компилятор под Pascal обрабатывает \(x^2\) тысяч строк кода, то исполняемый файл весит \(21x\) байт. Известно, что \(25 <= x <= 55\).

Какой наибольший размер исполняемого файла (в байтах) можно получить, если на компиляцию поступает программа, состоящая из \(3\,364\) тысячи строк кода?

Это лишь малая толика заданий, имеющихся в моей коллекции. Но здесь я демонстрирую наиболее популярные формулировки, которые часто фигурируют на официальном экзамене – ЕГЭ по математике.

Остались вопросы, недопонимание? Записывайтесь ко мне на индивидуальную подготовку

Наверняка у вас остались вопросы, связанные с построением целевой функции? Это логично, так как данная статья является обзорной и информация в ней дает читателю лишь общее представление относительно того, что такое оптимизационные задачи.

Чтобы фундаментально разобраться с понятиями оптимизационной задачи и целевой функции, записывайтесь ко мне на частную подготовку. Я – репетитор-практик, это означает то, что на своих уроках я акцентируюсь на прорешивании колоссального количества тематических заданий. Теории отводится некая часть урока, но не существенная.

Свои частные уроки я провожу в различных территориальных форматах. Наиболее популярным и востребованным является дистанционное обучение с использование программы «Скайп», так как именно такой вариант нашего взаимодействия минимизирует ваши финансовые расходы, а также наши энергетические затраты, связанные с тем, что приходится добираться до места проведения индивидуальных уроков.

Задачи на оптимальный выбор – это не единственные задачи из категории, которые могут вам попасться на официальном экзамене – ЕГЭ по математике. Я вам настоятельно рекомендую совершенствовать собственные знания также и в финансовой математике.

И помните о том, что практически каждый олимпийский чемпион имеет персонального наставника. Иначе бывает очень редко! Поэтому, если вы претендуете на максимально высокий итоговый балл, вам нужен профессиональный репетитор, который эффективно, а главное результативно проведет вашу подготовку!

Звоните мне прямо сейчас, так как завтра свободных мест может уже не остаться!

videoege.ru

Материал для подготовки 17 задания ЕГЭ математика "Что такое задачи на оптимизацию?"

Что такое задачи на оптимизацию?

Задача на оптимизацию — в математике задача нахождения экстремума(минимума или максимума)целевой функции вне которой области определения. В самых простых задачах на оптимизацию мы имеем дело с двумя величинами, одна из которых зависит от другой, причем надо найти такое значение 2-ой величины, при котором первая принимает свое наилучшее в данных условиях значение.

Как решать задачи на оптимизацию?

Задачи на оптимизацию решают по обычной схеме из трех этапов математического моделирования:

1) составление математической модели;

2) работа с математической моделью;

3) ответ на вопрос задачи.

Первый этап. Составление математической модели.

1) Проанализировав условия задачи, выделите оптимизируемую величину (О.В.), т. е. величину, о наибольшем или наименьшем значении которой идет речь. Обозначьте ее буквой y.

2) Одну из участвующих в задаче неизвестных величин, через которую сравнительно нетрудно выразить О.В.,примите ее за независимую переменную (Н.П.) и обозначьте ее буквой x. Установите реальные границы изменения Н.П., т. е. область определения для искомой О.В.

3) Исходя из условий задачи, выразите y через x. Математическая модель задачи представляет собой функцию y = f(x) с областью определения X, которую нашли на втором шаге.

Второй этап. Работа с математической моделью

На втором этапе для функции y=f(x), x ϵ X найдите yнаим. или yнаиб.в зависимости от того, что требуется найти в условии задачи.

Третий этап. Ответ на вопрос задачи. Здесь следует дать конкретный ответ на вопрос задачи, опираясь на результаты, полученные на этапе работы с моделью

За­да­ние 17 № 508236. В 1-е клас­сы по­сту­па­ет 45 че­ло­век: 20 маль­чи­ков и 25 де­во­чек. Их рас­пре­де­ли­ли по двум клас­сам: в одном долж­но по­лу­чить­ся 22 че­ло­ве­ка, а в дру­гом ― 23. После рас­пре­де­ле­ния по­счи­та­ли про­цент де­во­чек в каж­дом клас­се и по­лу­чен­ные числа сло­жи­ли. Каким долж­но быть рас­пре­де­ле­ние по клас­сам, чтобы по­лу­чен­ная сумма была наи­боль­шей?

За­да­ние 17 № 513301. В двух об­ла­стях есть по 160 ра­бо­чих, каж­дый из ко­то­рых готов тру­дить­ся по 5 часов в сутки на до­бы­че алю­ми­ния или ни­ке­ля. В пер­вой об­ла­сти один ра­бо­чий за час до­бы­ва­ет 0,1 кг алю­ми­ния или 0,1 кг ни­ке­ля. Во вто­рой об­ла­сти для до­бы­чи x кг алю­ми­ния в день тре­бу­ет­ся x2 че­ло­ве­ко-часов труда, а для до­бы­чи у кг ни­ке­ля в день тре­бу­ет­ся у2 че­ло­ве­ко-часов труда.

Для нужд про­мыш­лен­но­сти можно ис­поль­зо­вать или алю­ми­ний, или ни­кель, причём 1 кг алю­ми­ния можно за­ме­нить 1 кг ни­ке­ля. Какую наи­боль­шую массу ме­тал­лов можно за сутки сум­мар­но до­быть в двух об­ла­стях?

infourok.ru

Задача на оптимизацию расходов. Задание 17

На изготовление открытого контейнера объемом 10 м в форме прямоугольного параллелепипеда, одна из боковых граней которого - квадрат, требуются уголки по длине всех ребер (12 ребер) и фанера на боковые стенки и пол. Цена уголков - 10 руб. за погонный метр, цена фанеры - 40 руб. за квадратный метр. Каковы должны быть размеры контейнера, чтобы расходы на материал были минимальными? Сколько рублей при этом составят расходы?

(задача из т/р А. Ларина  №159)

Решение.

Внимательно читаем задачу: квадратом является одна из боковых граней контейнера (не дно!). Пусть длина ребер квадратной грани равна , а длина ребер, перпендикулярных квадратной грани равна :

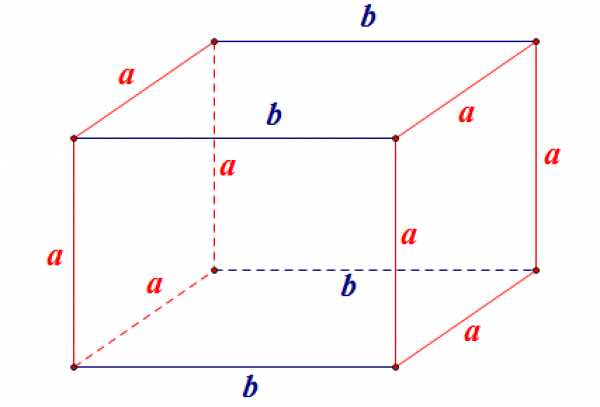
Объем контейнера равен  м.

Сумма длин всех ребер равна , следовательно, стоимость всех уголков равна рублей.

Суммарная площадь боковых стенок и пола контейнера равна м,   следовательно, стоимость фанеры на их изготовление составит  рублей.

Отсюда получим стоимость всех расходов: рублей.

Так как , можем выразить, например, через  :

Теперь можем получить функцию зависимости расходов на материалы от :

Найдем, при каких положительных значениях  функция  принимает наименьшее значение.

Найдем производную:

Найдем нули производной:

Так как , можем умножить обе части уравнения на :

Первый корень найдем подбором. Числа 1 и -1 не являются корнями, проверим число 2.

- верно.

Разделим многочлен на :

 

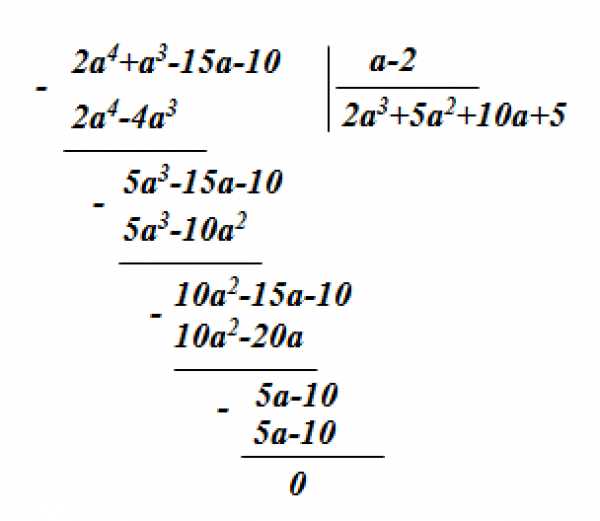
Мы получили 

Найдем нули многочлена

Найти корень подбором не удается, поэтому найдем хотя бы число корней уравнения 

Исследуем функцию на монотонность.

. Рассмотрим квадратный трехчлен : , следовательно,  при любом действительном значении и функция  возрастает.

Следовательно, уравнение  имеет единственный корень, причем, поскольку все коэффициенты многочлена положительны, этот корень отрицателен.

Пусть - корень уравнения .

Тогда   и 2 - нули производной исследуемой функции .

Найдем промежутки монотонности функции :

Итак, - точка минимума функции , следовательно, при расходы на материалы для контейнера минимальны.

Тогда 

То есть минимальная стоимость материалов рублей если размеры контейнера м.

Ответ: , .

ege-ok.ru

Задачи на оптимизацию. ЕГЭ профиль. Материалы для учителя — Математика онлайн

Меню

ВХОД НА САЙТ

Забыл пароль

Запомнить

‹ back to login Получить ссылку на смену пароля

Меню

mathcourse.ru

Задачи на оптимизацию. ЕГЭ профиль — Математика онлайн

Меню

ВХОД НА САЙТ

Забыл пароль

Запомнить

‹ back to login Получить ссылку на смену пароля

Меню

mathcourse.ru

Prostoy-Site | Все права защищены © 2018 | Карта сайта