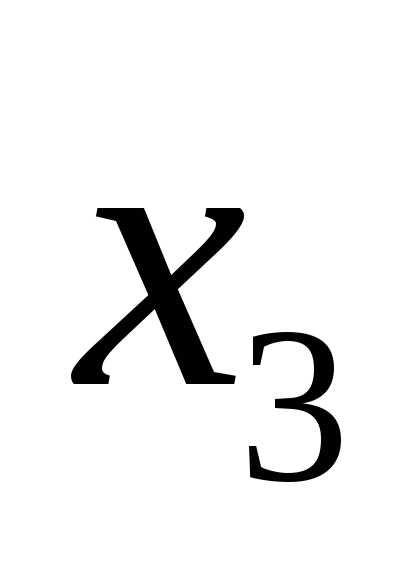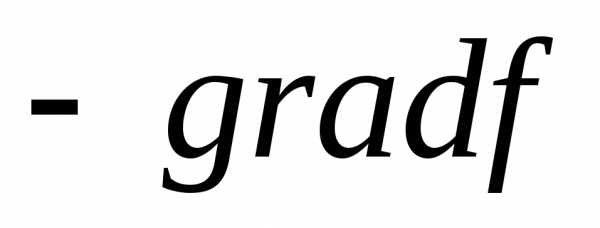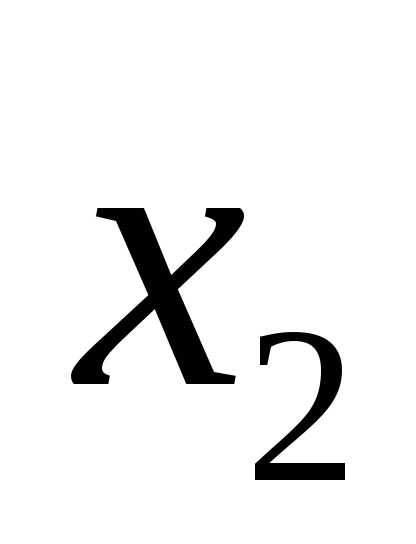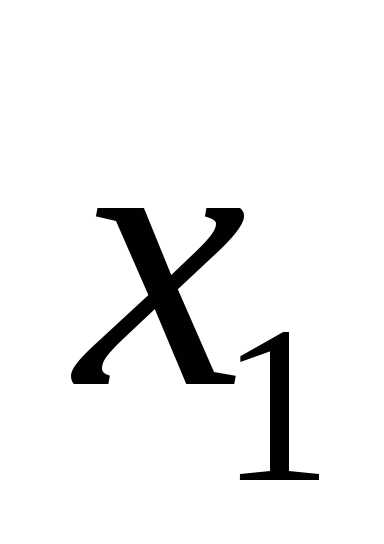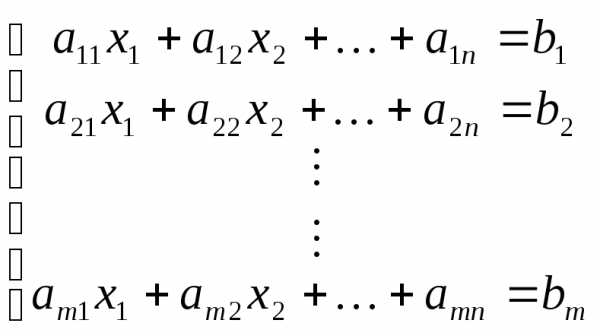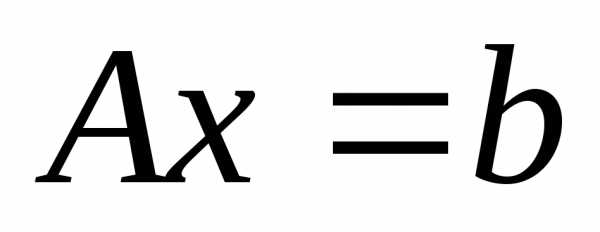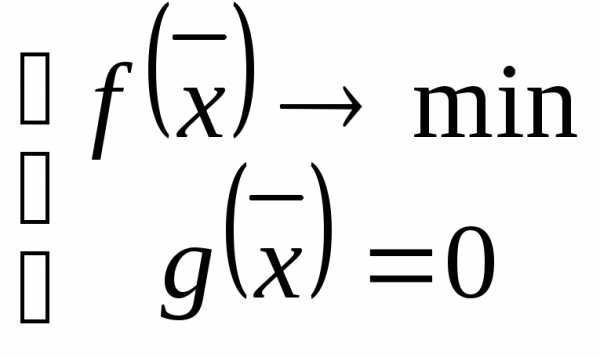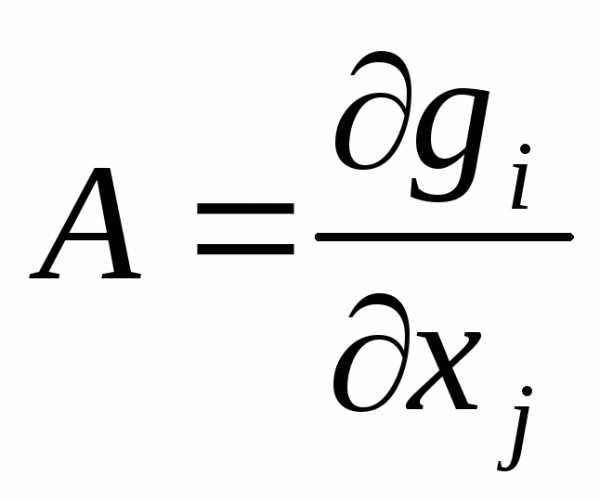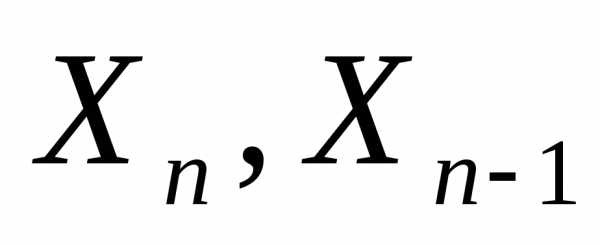Задачи оптимизации с ограничениями – разностями (зор). Безусловная оптимизация с ограничениями
задачи безусловной оптимизации или оптимизация без ограничений задачи условной оптимизации оптимизац
РЕШЕНИЕ ОПТИМИЗАЦИОННЫХ ЗАДАЧ В ПАКЕТЕ MATHCAD
Оптимизационные задачи можно разделить на два класса:
- задачи безусловной оптимизации (или оптимизация без ограничений)$
- задачи условной оптимизации (оптимизация с ограничениями).
Вторая задача отличается от первой тем, что решение ищется только среди допустимых значений или, иначе, на допустимом множестве значений переменных задачи, которые удовлетворяют заданным ограничениям.
Решение оптимизационных задач без ограничений
Для этого используются две функции MathCAD:
· Maximize (f, <список параметров>) вычисление точки максимума;
· Minimize (f, <список параметров>) вычисление точки минимума,
где
f имя минимизируемого функционала, определенного до обращения к функции;
<список параметров> содержит перечисление (через запятую) имен параметров, относительно которых решается оптимизационная задача.
Внимание! Перед обращением к функциям Maximize, Minimize (имена которых начинаются прописными буквами) следует обязательно задать начальное значение параметров оптимизации.
Пример. Дан функционал:
Определить значения x, y, z, при которых g(x,y,z) достигает минимального значения.
Пример. Дан функционал:
Определить значения u, v, при которых f(u,v) достигает максимального значения.
Решение оптимизационных задач с ограничениями
Используются те же функции Maximize, Minimize, но они входят уже в блок решения Given и перед ними размещаются ограничения в виде равенств или неравенств, определяющие допустимую область значений параметров оптимизации.
Пример. Дан функционал
и ограничения в виде
Определить значения a, b, доставляющие максимальное значение функционала и удовлетворяющие неравенствам.
Замечание. В оптимизационных задачах с ограничениями решение целесообразно определять из необходимых условий экстремума. Эти условия порождают систему уравнений (чаще всего нелинейных), которые располагаются в блоке Given, вместе с ограничениями, определяющими допустимую область. Само решение ищется с помощью функций Find, Minerr.
Пример. В качестве тестового функционала при поиске точки минимума часто используется функционал Розенброка:
«Поверхность» этого функционала напоминает глубокий овраг, что сильно осложняет работу многих алгоритмов минимизации. Требуется вычислить точку минимума функционала при ограничениях:
Пример (задача линейного программирования).
Цех малого предприятия
должен изготовить 100 изделий трех типов и не менее 20 штук изделий каждого типа. На изделия уходит 4, 3.4 и 2 кг металла соответственно, при его общем запасе 340 кг, а также расходуются по 4.75, 11 и 2 кг пластмассы, при ее общем запасе 400 кг. Прибыль, полученная от каждого изделия равна 4, 3 и 2 рублей. Определить сколько изделий каждого типа необходимо выпустить, для получения максимальной прибыли в рамках установленных запасов металла и пластмассы.
Пример (задача нелинейного программирования).
Пусть вектор v состоит из трех проекций и дан функционал:
Вычислить точку минимума этого функционала при ограничениях:
ЗАДАНИЕ ПО ЛАБОРАТОРНОЙ РАБОТЕ №2
1. Дан функционал:
Определить точки минимума и максимума этого функционала.
2. Найти точку минимума функции Розенброка
При следующих ограничениях:
.
3. Дан функционал (задача линейного программирования):
Определить точку максимума этого функционала при ограничениях:
Вычислить значения функционала в этой точке.
Ответ: максимум функционала достигается в точке (0, 13, 8).
4. Дан функционал (задача квадратичного программирования):
Определить точку максимума этого функционала при ограничениях:
Ответ: максимум функционала достигается в точке (7.5, 10, 6).
samzan.ru
Задача - безусловная оптимизация - Большая Энциклопедия Нефти и Газа, статья, страница 3
Задача - безусловная оптимизация
Cтраница 3
Переход к усредненной постановке предполагает, что решение задачи повторяют многократно и в качестве значения задачи принимают среднее значений функции fo ( x), полученных при каждом единичном решении. Естественно, что такой переход в задаче безусловной оптимизации неэффективен, так как среднее значение / о не может быть больше ее максимального значения. В задачах условной оптимизации переход к усредненной постановке может быть эффективен, если для каждого единичного решения не требовать, чтобы х принадлежало D, а вместо этого потребовать, чтобы ограничения задачи выдерживались в среднем на множестве решений. [32]
Большинство методов оптимизации разработано для поиска безусловного экстремума. Обычно задачи условной оптимизации сводят к задачам безусловной оптимизации с помощью штрафных функций или множителей Лагранжа. [33]
Второе свойство выпуклых задач можно высказать в виде следующего общего принципа: необходимые условия оптимальности в том или ином классе задач оптимизации при соответствующих предположениях выпуклости оказываются и достаточными. Ограничимся здесь обоснованием этого принципа применительно к задаче безусловной оптимизации ( ср. Другими его подтверждениями служат теоремы 1.2 и 2.2 гл. [34]
При решении задач условной оптимизации целесообразно использовать методы безусловной оптимизации, учитывая большое количество разработанных по этим методам программ. С этой целью задача условной оптимизации сводится к задаче безусловной оптимизации устранением ограничений путем преобразования параметра xt, на значения которого наложены ограничения, в неограничиваемый. [35]
Функциональные ограничения устраняются путем конструирования обобщенной функции оптимизации с учетом типа ограничений. Так, если все ограничения представлены в аналитическом виде и являются функциональными зависимостями типа равенств (3.11), то переход к задаче безусловной оптимизации часто осуществляется с помощью метода неопределенных множителей Лагранжа. [36]
При втором подходе ( блок DII) задачу оптимизации с ограничениями посредством того или иного приема ( метод штрафов, метод неопределенных множителей Лагранжа) сводят к задачам безусловной оптимизации. [38]
Использование алгоритмов стохастической аппроксимации в задачах на условный экстремум функции регрессии или задачах, где ограничения носят регрессионный характер, может основываться на сведении этих задач к задаче безусловной оптимизации с помощью штрафных функций или на стохастических аналогах градиентных алгоритмов детерминированных задач. [39]
Правда, расчет предотвращенного ущерба по Временной типовой методике / 1 /, как правило, дает результаты, намного превышающие затраты, что заведомо их оправдывает практически в каждом случае. В большой мере это происходит из-за учета внеэкономической составляющей в расчетных формулах ( например из-за учета скорости оседания частиц и радиуса их рассеивания), что завышает размер предотвращенного ущерба подобно тому, как это происходит при переводе задачи оптимизации с ограничениями в задачу безусловной оптимизации. Однако при этом предотвращенный ущерб теряет свое экономическое содержание, а следовательно, сопоставление его с затратами не будет иметь смысла. Например, затраты, направленные на снижение загрязнения какого-либо уникального природного ландшафта ( заповедника) вряд ли смогут быть оправданы реальным предотвращенным ущербом, поскольку природные компоненты этого ландшафта не имеют адекватной стоимостной оценки. [40]
В первом подходе учитывается, что большинство развитых методов оптимизации ориентировано на поиск безусловного экстремума. Поэтому их применение к решению задачи условной оптимизации требует, чтобы эта задача была предварительно сведена к задаче безусловной оптимизации. Во втором подходе используются методы, специально разработанные для решения задач нелинейного программирования с ограничениями. [41]
При малых значениях параметра 0 вне области D функция F ( x / 3) сильно возрастает. Поэтому ее минимум может быть либо внутри D, либо снаружи вблизи границ этой области. В первом случае минимумы функций F ( xj / 3) и / ( х) совпадают, поскольку дополнительные члены в (6.20) равны нулю. Если минимум функции F ( x, / 3) находится вне D, то минимум целевой функции / ( х) лежит на границе D. Таким образом, задача оптимизации для целевой функции / ( х) с ограничениями (6.19) свелась к последовательности задач безусловной оптимизации для вспомогательной функции (6.20), решение которых может быть проведено с помощью методов спуска. [43]
В данной главе будут рассмотрены алгоритмы отыскания экстремума нелинейной функции при нелинейных ограничениях. С простейшим из них, предназначенным для решения задач, ограничения которых имеют вид равенств, мы уже познакомились ранее. Надо сказать, что в своем большинстве алгоритмы такого сорта представляют собой различные способы воплощения двух подходов к организации поиска условного экстремума. Первый состоит в том, чтобы, непосредственно контролируя соблюдение ограничений задачи, двигаться к ее оптимуму по последовательности допустимых или почти допустимых точек с монотонно убывающими либо монотонно возрастающими ( это зависит от того, что ищется - минимум или максимум) значениями целевой функции Соответствующие алгоритмы называются методами спуска. Два из них представлены в первом параграфе этой главы. Второй подход заключается в сведении задачи на экстремум при наличии ограничений к последовательности задач безусловной оптимизации конструируемых специальным образом вспомогательных функций. Эти функции принято называть штрафными, а использующие их алгоритмы - методами штрафных функций. Им посвящен второй параграф. [44]
Страницы: 1 2 3
www.ngpedia.ru
8. Сведение задачи условной оптимизации к безусловной задаче оптимизации.
8.1. Метод внешних штрафных функций
Постановка задачи:
Требуется найти решение задачи:
Теоретические сведения:
Задача условной оптимизации:
Этот метод основан на сведении к последовательности задач, минимизации дополнительной функции:
- штрафная функция, зависящая от двух параметров,
- параметр штрафа.
С ростом номера k , штраф за невыполнение ограничений увеличивается
Штрафная функция записывается в виде:
- квадрат срезки (для ограничений типа неравенств).
- квадратичная функция.
На каждой k-ой итерации ищется точка - точка минимума вспомогательной функции.
Найденная точка используется как начальная точка на следующей итерации, выполняемой при большем
значении параметра штрафа .
Теорема 8.2.1 (о сходимости метода штрафных функций)
Пусть - точка локального минимума задачи условной минимизации
- непрерывные, дифференцируемые функции в окрестности точки .
Тогда последовательность точек , полученных на каждой итерации, сходится к точке условного
минимума.
Алгоритм метода
Шаг№1
Задается начальное приближение , начальный штраф, его обычно берут равным {0,01;0,1;1}.
Задается некоторая константа для увеличения .
Задается точность .
Шаг№2
Находим точку минимума функции, разработанным методом многомерной минимизации, в нашем
случае методом Дэвидона-Флетчера-Пауэлла.
Вычисляем величину штрафа , что есть критерий остановки поиска условного минимума.
Шаг№3
Проверка условия окончания поиска:
а) если ,то в качестве оптимальной точки выбираем.
б) иначе и в качестве нового приближения выбирается начальная точка в безусловной минимизации:
, k=k+1 => Шаг№1.
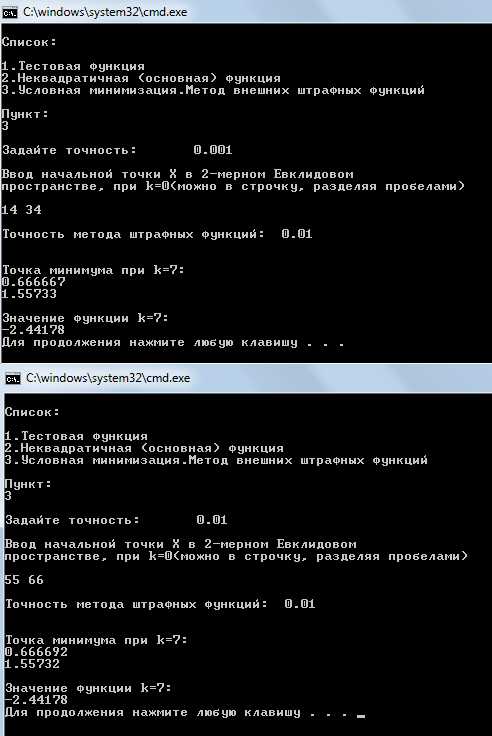
Результат работы программы:
Для разных точек, не принадлежащих допустимому множеству, минимум функции находится и он одинаков для разных точек, что говорит о правильности реализуемой программы.
В чистом виде исходная функция не имеет минимума, но т.к. вспомогательная функция квадратичная, то минимум находится.
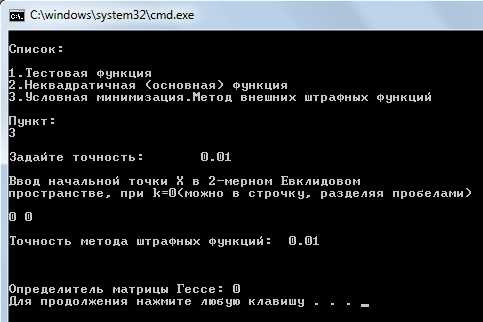
Для точек, принадлежащих допустимому множеству, минимум функции не находится, т.к. функция не выпукла, т.е. не имеет минимума. Этот факт определяется по виду градиента этой функции и значению определителя матрицы Гессе.
8.2. Метод возможных направлений Зойтендейка
Постановка задачи:
Требуется найти решение задачи:
В общем виде она выглядит так:
Стратегия поиска:
Метод основан на построении последовательности точек , таких, что.
Правило построения точек последовательности :
- Выбор направления осуществляется следующим образом:
1)
2)
А) Вектор направляется внутрь области
Б) Вектор должен составлять с направление убывания наименьший угол
Определим множество индексов:
Если точка множество активных ограничений не пусто, то решается задача:
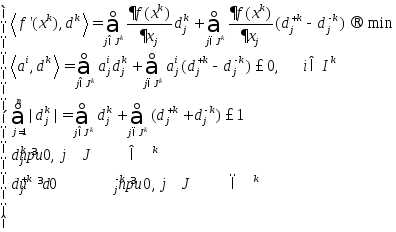
-Шаг определяется как:
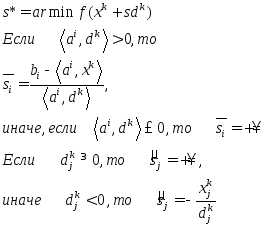
Алгоритм:
Выбирается начальная точка из множества допустимых решений . Находими, если, то, иначе 2)
Определяем элементы множеств ,
Если ,
иначе:
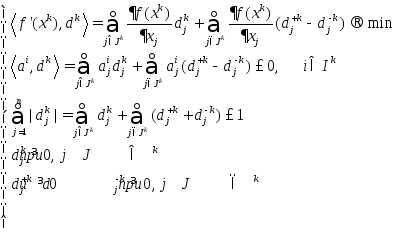
Если , то завершаем, иначе 5)
Определяем шаг и находим следующую точку
Решение:
Итерация 0:
Выбираем точку ,которая принадлежит допустимому множеству
Вычисляем градиент целевой функции в начальной точке:
Множество активных ограничений и индексов, для которых координаты направления положительны пусты, т.е. .
Т.к. указанные в (2) множества пусты, то направление есть антиградиент в точке :
Теперь определяем шаг:
Находим градиенты ограничений:
Так как , то
Получаем, что до следующей точки равен
Получаем следующую точку:
Итерация 1:
Вычислим градиент в этой точке:
Проверим точку на принадлежность ограничениям. Точка принадлежит ограничения, причем есть одно активное ограничение
Для нахождения возможного направления составляем экстремальную задачу:
Преобразуем задачу к необходимому виду:
Решаем задачу симплекс-методом: Выбираем максимальную положительную оценку и минимальное неотрицательное симплексное отношение:
| u1 | u2 | ПЧ | ||||
| 2 | -2 | 3 | -3 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 2/7 | -2/7 | 1 | -1 | 0 | 0 | 0 |
| u1 | u2 | ПЧ | ||||
| 2/3 | -2/3 | 1 | -1 | 1/3 | 0 | 0 |
| 1/3 | 5/3 | 0 | 2 | -1/3 | 1 | 1 |
| -8/21 | 8/21 | 0 | 0 | -1/3 | 0 | 0 |
| u1 | u2 | ПЧ | ||||
| 4/5 | 0 | 1 | -1/5 | 1/5 | 2/5 | 2/5 |
| 1/5 | 1 | 0 | 6/5 | -1/5 | 3/5 | 3/5 |
| -48/105 | 0 | 0 | -16/35 | -9/35 | -8/35 | -8/35 |
Получаем направление:
Теперь найдем шаг:
Получаем, что шаг:
Получаем следующую точку:
Итерация 2:
Выбираем начальной точкой точку:
Вычисляем градиент:
Проверим точку на принадлежность ограничениям. Точка принадлежит ограничения, причем есть одно активное ограничение
Находим направление :
Составляем экстремальную задачу.
Преобразуем к виду:
Решим симплекс-методом. Составляем таблицу.
| u1 | u2 | ПЧ | ||||
| 2 | -2 | 3 | -3 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 2 | -2 | 1 | -1 | 0 | 0 | 0 |
| u1 | u2 | ПЧ | ||||
| 1 | -1 | 3/2 | -3/2 | 1/2 | 0 | 0 |
| 0 | 2 | -1/2 | 5/2 | -1/2 | 1 | 1 |
| 0 | 0 | -2 | 2 | -1 | 0 | 0 |
| u1 | u2 | ПЧ | ||||
| 1 | 1/5 | 6/5 | 0 | 1/5 | 3/5 | 3/5 |
| 0 | 4/5 | -1/5 | 1 | -1/5 | 2/5 | 2/5 |
| 0 | -8/5 | -8/5 | 0 | -3/5 | -4/5 | -4/5 |
Получаем направление:
Находим шаг:
Получаем шаг:
Следующая точка:
Итерация 3:
Берем точку с прошлой итерации:
Вычисляем градиент:
Проверим точку на принадлежность ограничениям. Точка принадлежит ограничения, причем есть одно активное ограничение:
Находим направление:
Составляем таблицу.
| u1 | u2 | ПЧ | ||||
| 2 | -2 | 3 | -3 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 2/3 | -2/3 | 1 | -1 | 0 | 0 | 0 |
| u1 | u2 | ПЧ | ||||
| 2/3 | -2/3 | 1 | -1 | 1/3 | 0 | 0 |
| 1/3 | 5/3 | 0 | 2 | -1/3 | 1 | 1 |
| 0 | 0 | 0 | 0 | -1/3 | 0 | 0 |
Получаем, что следовательно, т.к.свободные переменные, равные нулю, то направление:
, следовательно, точка - решение поставленной задачи. Переведя дроби в действительные числа, получаем:
Данная точка совпадает с ответом, полученным в результате программной реализации задачи методом внешних штрафных функций.
studfiles.net
Задачи оптимизации с ограничениями – разностями (зор)
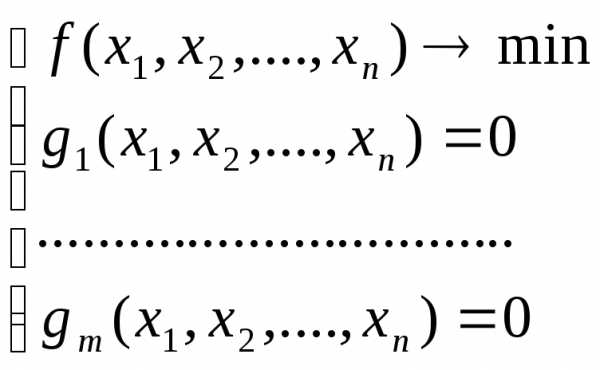
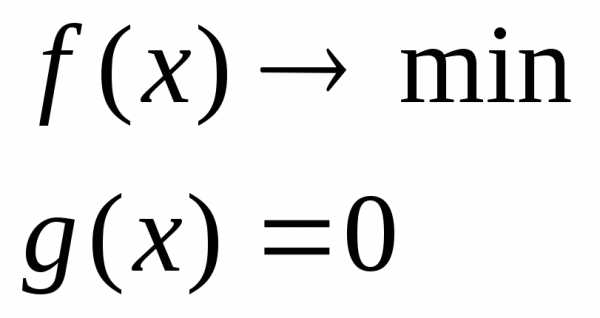
Пример:
Ф ункции заданы аналитическим выражением
ункции заданы аналитическим выражением
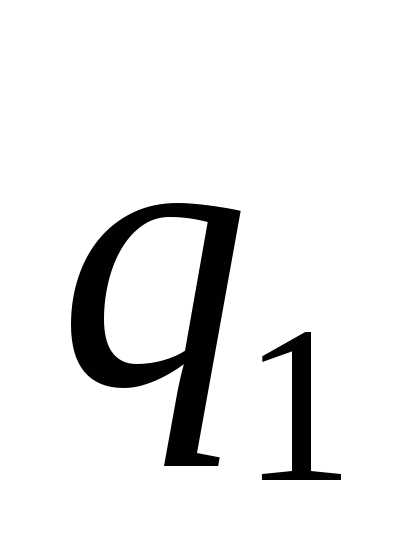 можно разрешить относительно одной из переменных
можно разрешить относительно одной из переменных
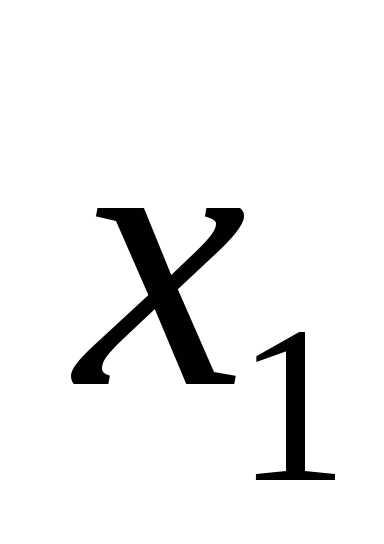 можно исключить изf и
можно исключить изf и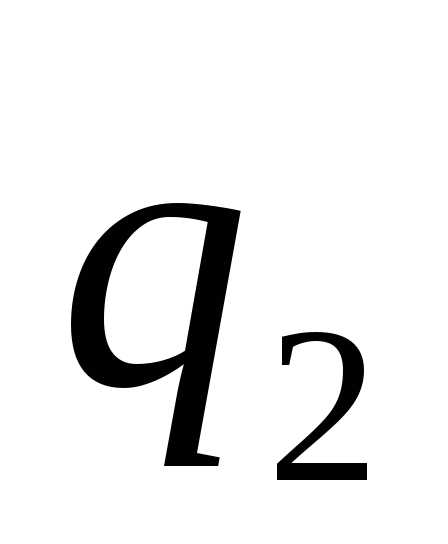 , подставив вместо нее
, подставив вместо нее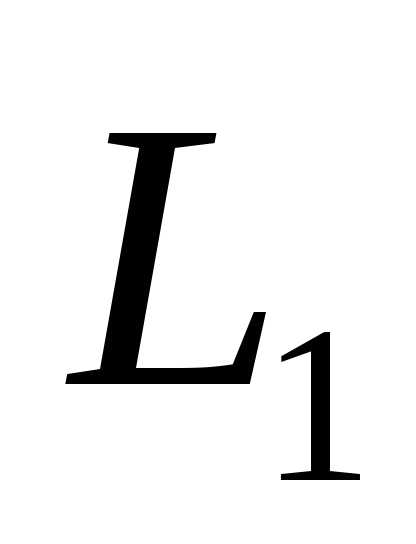 :
:
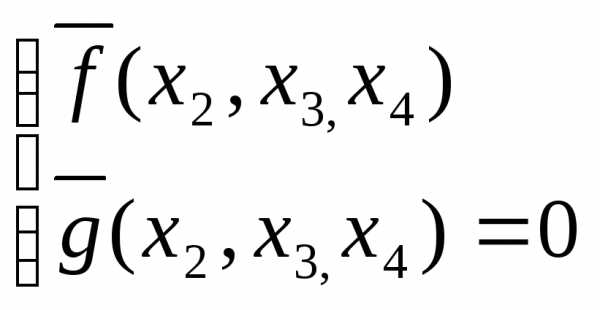

Тогда, 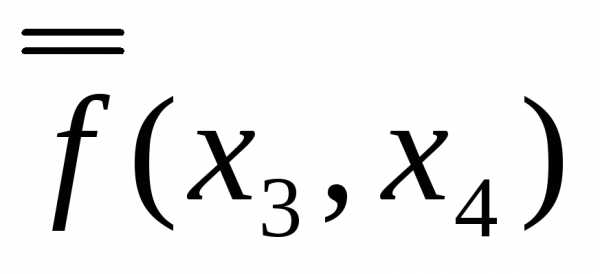 - задача безусловной оптимизации. Находим
- задача безусловной оптимизации. Находим вычисляем
вычисляем
Метод исключения
Численное решение:

 точкаminдолжна лежать на прямой.
точкаminдолжна лежать на прямой.
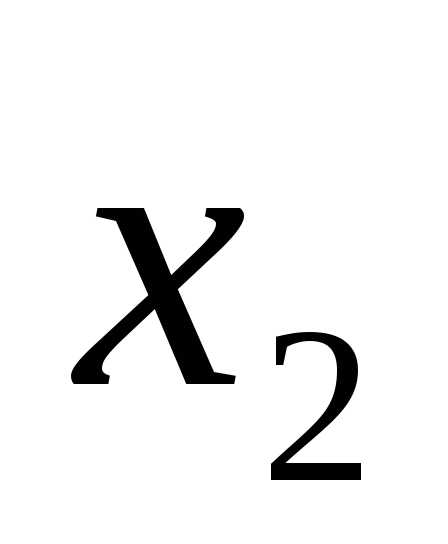
g(x)
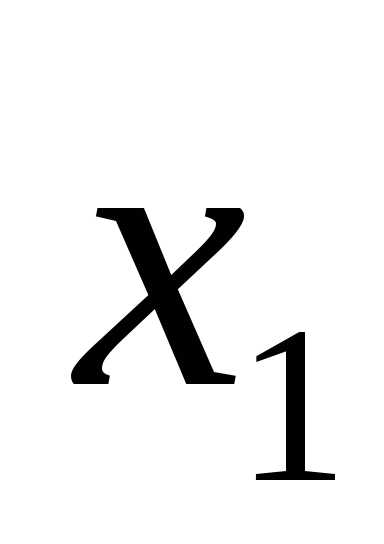
В каждый момент линия уровня будет касаться прямой  эта точка и является точкой
эта точка и является точкой
условного локального min. Если в окрестности заданной точки, удовлетворяющей
всем значениям равенства, значение функции больше, чем в точке, то эта точка – есть точка условного локального min.
Пример:
(a,x)=0
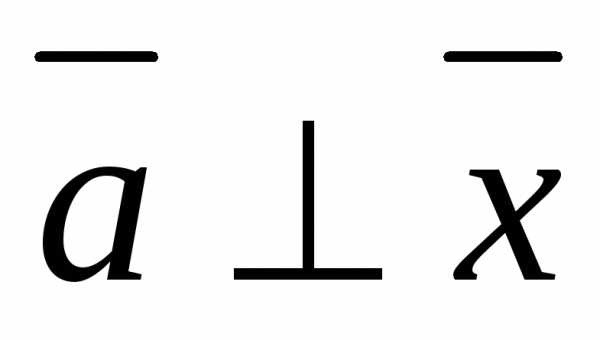
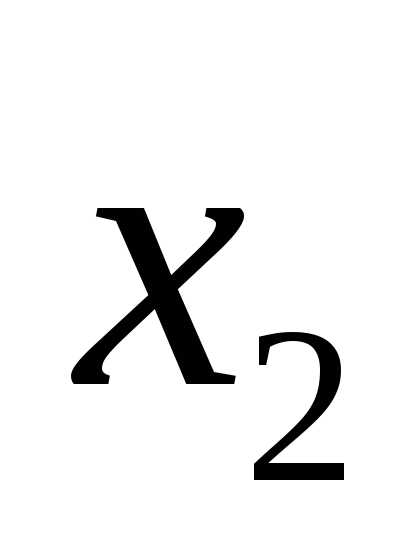

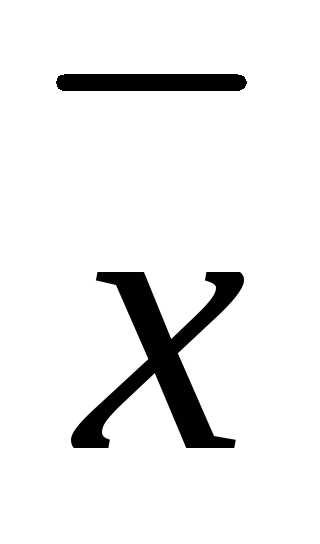
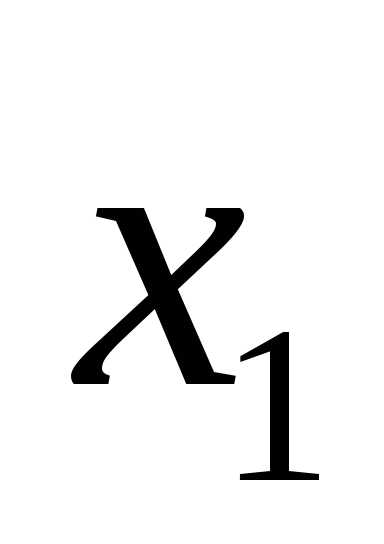
Если (a1x)=b
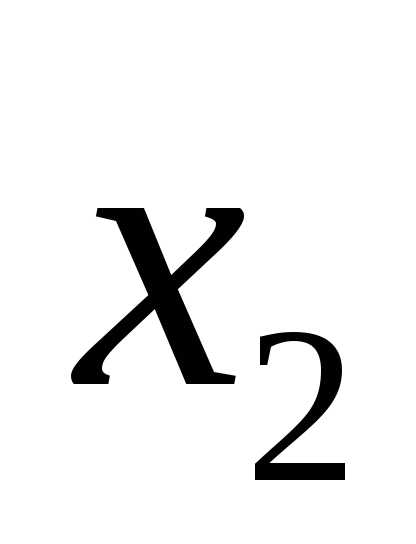

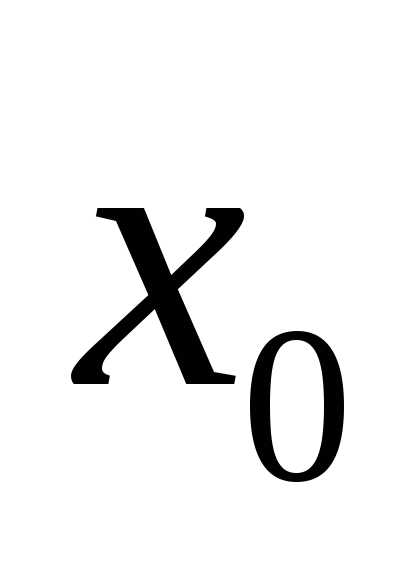
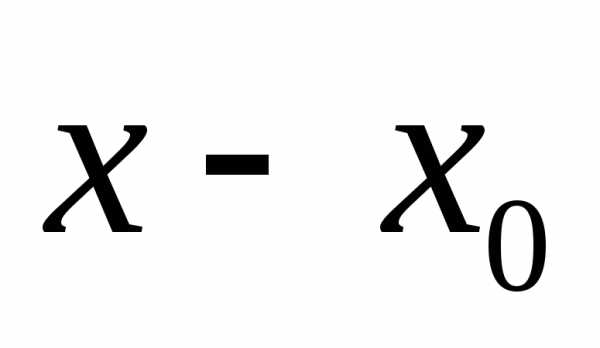
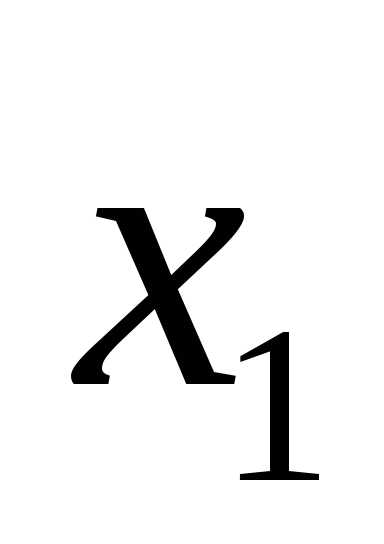
Допустим, 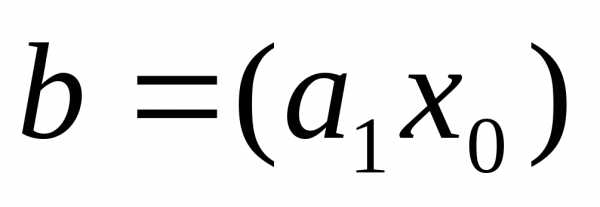

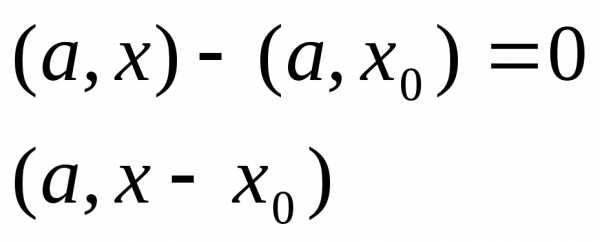
Прямая будет проходить через некоторую точку удовлетворяющую условию и 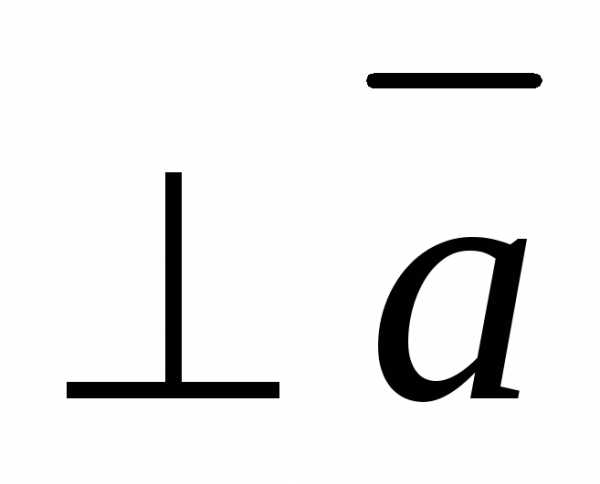
Для nпеременных,Ax=b
Рассмотрим i-ое ограничение:
, 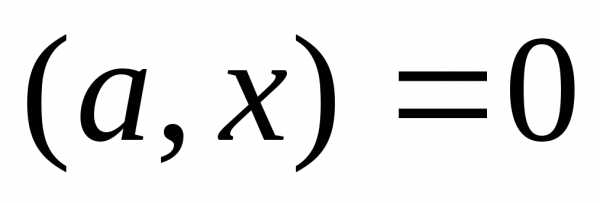
 - задан
- задан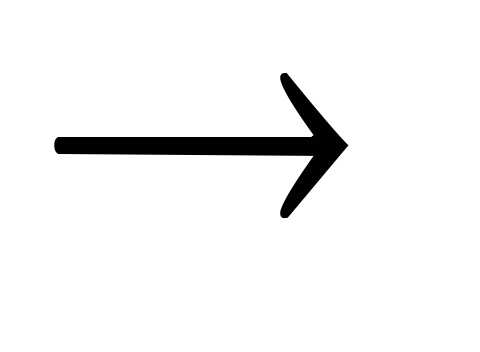 x- все вектора, лежащие
x- все вектора, лежащие . Они и составляют гиперплоскость.
. Они и составляют гиперплоскость.
При добавлении еще одного условия, уменьшаются размерности. В конечном итоге получится пространство n-m.
Для двух переменных возможно 2 случая:
| 1. | 2. |
В случае 2 это не точка минимума, а седловая точка.
Рассмотрим точку 3-х переменных:
| плоскость | Ограничение – плоскость, следовательно, все допустимые точки на плоскости. Если угол gradне равен 90 градусам следовательно можно двигаться дальше. На плоскости существует направление, которое будет составлять острый угол с– grad, и двигаясь в этом направлении можно уменьшить значениеf. Если -grad fперпендикулярен плоскости эта точка может быть точкой минимума. |
Пусть существует 2 ограничения:
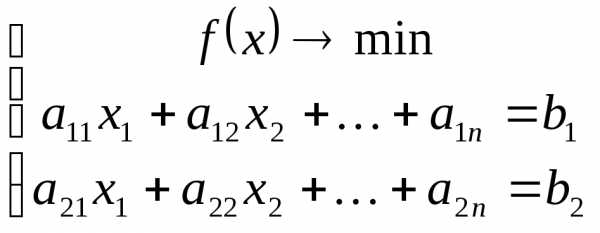
Рассмотрим опять случай 3-х переменных:
Точка минимума должна принадлежать пересечению плоскостей.
Необходимое условие – вектор антиградиента должен составлять угол 90 градусов с прямой пересечения плоскостей.
Для п-мерного случая имеетсяппеременных следовательно рассматривая каждое ограничение, получаемп-1гиперплоскость следовательно рассмотревтограничений получимп-тгиперплоскость (т<п).
|
|
все ограничения независимы |
Если вектор grad(п-мерный) будет ортогоналенп-т– пространству.
Допустим имеется п-1пространство,п-мерный вектор может принадлежать ему или нет. Пусть вектор не принадлежит данному подпространству следовательно его можно разложить на 2 вектора – один который принадлежит подпространству, и второй который ортогонален данному. Ортогональное дополнение – вектора, которые ортогональны данному подпространству.
В 3D– пространстве, если подпространство равно 1 следовательно ортогональное дополнение равно 2.
В п-т-мерном подпространстве ортогональное дополнение имеет размерностьт.
Необходимое условие:Если мы находим точку, где вектор градиента принадлежит ортогональному дополнению к пространству, заданному ограничениями – равенствами, то эта точка может быть точкой локального минимума.
Пусть есть 2 плоскости. Если записать систему ограничений равенств следующим образом:
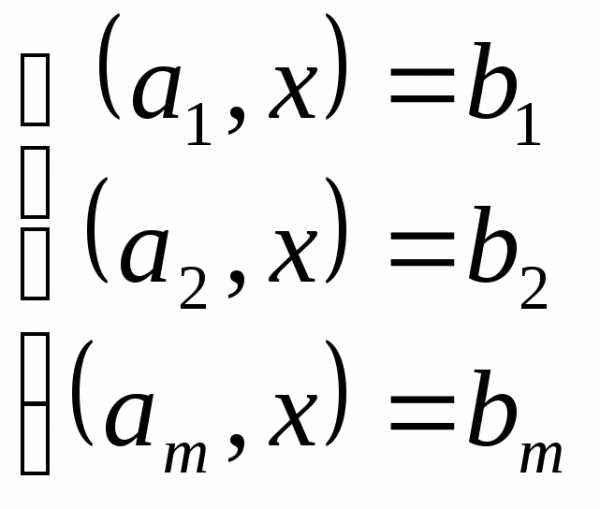
где
Т.о. вектора порождают ортогональное дополнение. Существующие могут быть выбраны в качестве базиса ортогонального дополнения следовательно градиент принадлежит ортогональному дополнению:
т.е. линейная комбинация базисных векторов.
- множители Лагранжа.
Рассмотрим матрицу  , в ней
, в ней - столбцы.
- столбцы.
это условие может быть использовано для численного решения задачи оптимизации с ограничивающими уравнениями.
Пример: 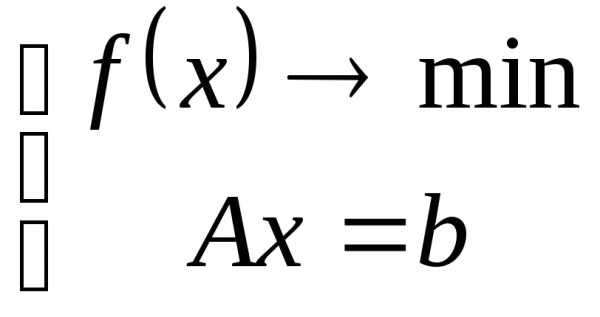
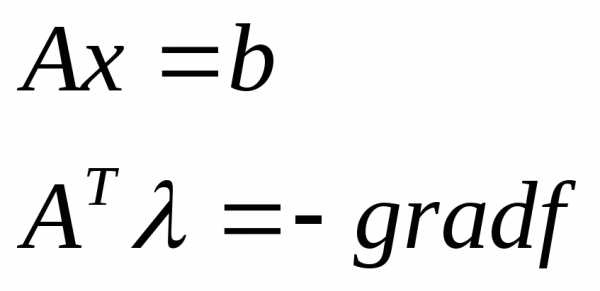
Если найдем такие вектора хи , для которых эти условия выполняются то точка может быть точкой локального минимума.
, для которых эти условия выполняются то точка может быть точкой локального минимума.
Рассмотрим случай когда система ограничений – равенств нелинейная:
| |
|
Если функции дифференцируемы, то в окрестности точки минимума они будут вести себя как линейные.
|
| следовательно в окрестности точки локального минимума эта зависимость линейная следовательно получается система вида: , где |
следовательно необходимое условие локального минимума:
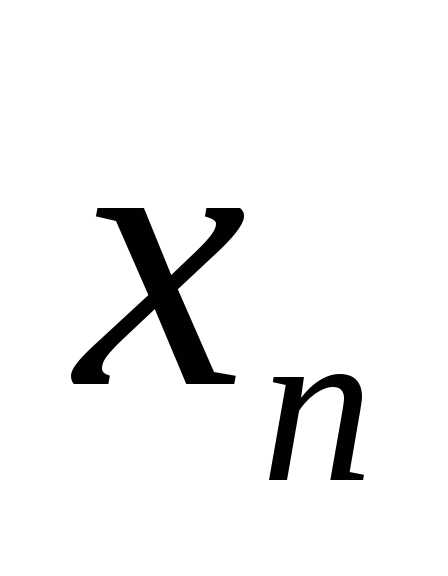
n-m


- множители Лагранжа.
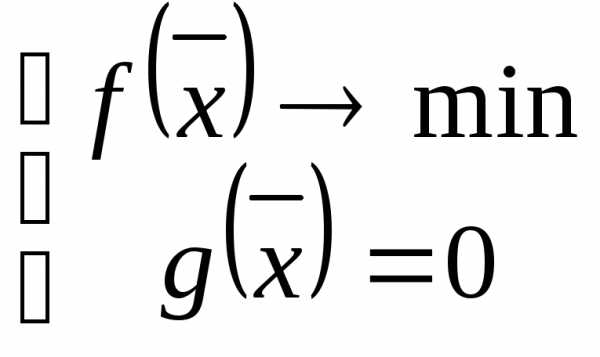
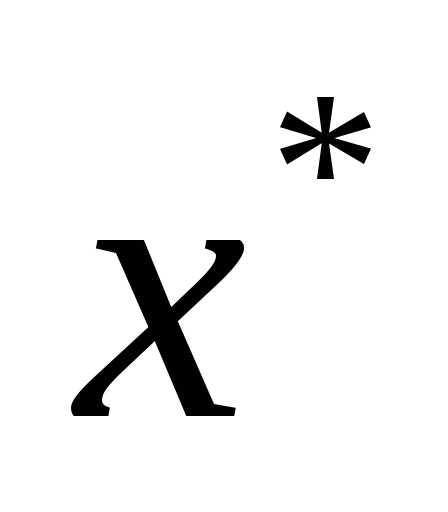 - точка может быть искомой в задаче
- точка может быть искомой в задаче
- множители Лагранжа.
Обозначения для скалярного произведения ;
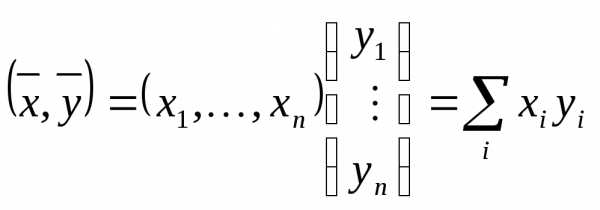 ;
;
Необходимое условие точки локального минимума исходное задание с ограничениями представляет собой необходимое условие точки локального экстремума для функции Лагранжа.
studfiles.net
5. УСЛОВНАЯ ОПТИМИЗАЦИЯ
Ряд инженерных задач связан с оптимизацией при наличии некоторого количества ограничений на управляемые переменные. Такие ограничения существенно уменьшают размеры области, в которой ищется оптимум. На первый взгляд может показаться, что уменьшение размеров допустимой области должно упростить процедуру поиска оптимума. Однако, напротив, процесс оптимизации становится более сложным, поскольку при наличии ограничений даже нельзя использовать применяемые нами выше условия оптимальности. При этом может нарушаться даже основное условие, в соответствии с которым оптимум должен достигаться в стационарной точке, характеризующейся нулевым градиентом.
Например, безусловный минимум функции f (x)= (x − 2)2 имеет место в стаци-
онарной точке x = 2. Но если задача минимизации решается с учетом ограниченияx ≥ 4, то будет найденусловный минимум, которому соответствует точкаx = 4. Эта точка не является стационарной точкой функцииf(х), так как
f ′(4)= 4 . Поэтому нужно изучить необходимые и достаточные условия опти-
мума в задачах с ограничениями, которые иначе называют задачами условной оптимизации.
5.1. Задачи с ограничениями в виде равенств
Рассмотрим задачу: f (x)→ min,x Rn
при ограничениях
hk (x)= 0,k =1,2,...,K .
Одним из методов ее решения является метод множителей Лагранжа.
5.1.1.Множители Лагранжа
Спомощью метода множителей Лагранжа по существу устанавливаются необходимые условия, позволяющие идентифицировать точки оптимума в задачах оптимизации с ограничениями-равенствами.При этом задача с ограничениями преобразуется в эквивалентную задачу безусловной оптимизации, в которой фигурируют некоторые неизвестные параметры, называемыемножителями Лагранжа.
Рассмотрим задачу с одним ограничением-равенством:
f (x)→ min, x Rn , | (5.1) |
h2 (x)= 0 . | (5.2) |
Всоответствии с методом множителей Лагранжа эта задача преобразуется
вследующую задачу безусловной минимизации:
33
L(x;λ)= f(x)−λh(x)→ min, x Rn . | (5.3) |
1 |
|
Функция L(x;λ) называется функцией Лагранжа. Здесьλ – множитель | |
Лагранжа. |
|
Пусть при заданном значении λ = λ0 | безусловный минимум функции |
L(x;λ) по переменнойх достигается в точкеx = x0 иx0 удовлетворяет уравнению
h2 (x0 )= 0 .
Тогда, как не трудно видеть, x0 минимизирует (5.1) с учетом (5.2), поскольку для всех значенийх, удовлетворяющих (5.2),h2 (x)= 0 и
min L(x;λ)= minf (x).
Разумеется, нужно подобрать значение λ = λ0 таким образом, чтобы коор-
дината точки безусловного минимума x0 удовлетворяла равенству (5.2). Это можно сделать, если, рассматриваяλ как переменную, найти безусловный минимум функции Лагранжа (5.3) в виде функцииλ, а затем выбрать значениеλ, при котором выполняется равенство (5.2).
Пример. Решить задачу
f (x)=x12 +x22 →min
при ограничении
h2 (x)=2x1 +x2 −2 =0.
Построим функцию Лагранжа:
L(x;λ)=x12 +x22 −λ(2x1 +x2 −2)
и определим ее безусловный минимум. Найдем стационарную точку функции Лагранжа, приравняв нулю компоненты ее градиента:
∂L |
| = 2x −2λ =0 x0 | = λ, | ||
| |||||
1 |
| 1 |
| ||
∂x1 |
|
|
| ||
∂L | = 2x | −λ = 0 | x0 | = λ . | |
| |||||
2 |
| 2 | 2 | ||
∂x2 |
|
| |||
Для того чтобы проверить, соответствует ли стационарная точка x0 минимуму, вычислим матрицу Гессе функции Лагранжа, рассматриваемой как функция отx :
Эта матрица положительно определена, так как для любого ненулевого вектора uT = (a,b)
34
| 2 | 0 |
| a |
|
| a | = 2a2 +2b2 >0. |
|
|
| ||
uT HLu= (a,b) | 0 | 2 |
|
|
| = (2a,2b) |
|
|
| ||||
|
| b |
|
| b |
|
|
|
|
|
| ||
Это означает, что L(x;λ) | в точке x0 | = λ | и x0 | = λ | имеет точку минимума. | ||||||||
|
|
|
|
|
| 1 |
| 2 | 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
Оптимальное значение | λ | находится путем подстановки значений x0 | и | x0 | в | ||||||||
|
|
|
|
|
|
|
|
|
| 1 |
| 2 |
|
уравнение 2x1 + x2 = 2, откуда
2λ +λ2 =2 и λ0 =54 .
Таким образом, условный минимум достигается при
x10= 54 , x20= 52 ,
а минимальное значение f (x0;λ0 ) есть54 .
Очень часто оказывается, что решение системы
∂L = 0,j =1,2,...,n
∂xj
в виде явной функции переменной λ получить нельзя. Тогда значенияx иλ находятся путем решения следующей системы, состоящей изn+1 уравнений сn+1 неизвестными:
∂L = 0,j =1,2,...,n,
∂xj
h2 (x)= 0.
Решить такую систему можно каким-либочисленным методом.
Для каждого из решений (x0;λ0 ) вычисляется матрица Гессе функции Ла-
гранжа, рассматриваемой как функция от x . Если она положительно определена, то решение – точка минимума.
Метод множителей Лагранжа можно распространить на случай, когда задача имеет несколько ограничений в виде равенств:
f (x)→ min, x Rn ,
hk (x)= 0,k =1,2,...,K .
Функция Лагранжа принимает вид
K
L(x;λ)= f(x)−∑λk hk .
k=1
35
studfiles.net
Задача - безусловная оптимизация - Большая Энциклопедия Нефти и Газа, статья, страница 2
Задача - безусловная оптимизация
Cтраница 2
Ясно, что критерий (2.12) относится лишь к задачам безусловной оптимизации. В задаче условной оптимизации критерий (2.12) следует заменить на критерий е-стацио-нарности, соответствующий данной задаче. [16]
Решение задач математического программирования значительно более трудоемко по сравнению с задачами безусловной оптимизации. Ограничения типа равенств или неравенств требуют их учета на каждом шаге оптимизации. [18]
Исходную задачу условной оптимизации, содержащую функции ограничений, обычно сводят к задаче безусловной оптимизации, что позволяет использовать для ее решения хорошо отработанные методы поиска безусловного экстремума, рассмотренные в предыдущих параграфах. [19]
В данном параграфе излагаются методы, относящиеся к числу наиболее эффективных способов решения задач безусловной оптимизации. В его модификациях ( квазиньютоновских алгоритмах) матрица вторых производных аппроксимируется с помощью информации о значениях градиентов функции /, и эти модификации, таким образом, являются методами первого порядка. [20]
Задача выпуклого программирования при наличии хорошего начального приближения может быть сведена к последовательности задач безусловной оптимизации. При этом сложность задач от шага к шагу не возрастает, чем предложенный метод выгодно отличается от метода штрафных функции. [21]
Эта задача методом штрафных функций в принципе с любой степенью точности сводится к задаче безусловной оптимизации. [22]
Лагранжа для того и служит, чтобы от задачи условной оптимизации перейти к задаче безусловной оптимизации по расширенному ( за счет множителей Лагранжа) набору аргументов оптимизации. [23]
Две переменных, которые должны удовлетворять условию неотрицательности, полагаются равными нулю, решается задача безусловной оптимизации, и отбираются решения, лежащие в требуемой области; эта операция производится для всевозможных выборок из неотрицательных переменных по две. [24]
Так, экстремальные задачи с ограничениями ( условно-экстремальные задачи) методом штрафных функций сводятся к задачам безусловной оптимизации, то же самое относится и к методу регуляризации. Весьма существенный раздел этой главы посвящен стабилизирующим свойствам методов градиентного типа, позволяющим находить нормальное решение некорректных задач, не прибегая к процедуре регуляризации. [25]
Таким образом, задача оптимизации для целевой функции f ( x) с ограничениями (6.13) свелась к последовательности задач безусловной оптимизации для вспомогательной функции (6.14), решение которых может быть проведено с помощью методов спуска. [26]
То есть в суррогатной двойственности ограничения (2.2) заменяются одним ограничением ( в общем случае несколькими ограничениями, но общим числом меньшим, чем / и), в то время как в лагранжевой двойственности переходят к задаче безусловной оптимизации. [27]
В этом случае получим задачу безусловной оптимизации по двум переменным. [28]
Переход к осредненной постановке предполагает, что решение задачи повторяют многократно и в качестве значения задачи принимают среднее из значений функции / о ( х) полученных при каждом единичном решении. Естественно, что при решении задачи безусловной оптимизации такой переход не эффективен, так как получить среднее значение функции / 0 большее, чем ее максимальное значение, мы не можем. В задачах же условной оптимизации переход к усредненной постановке может быть эффективным, если для каждого единичного решения вместо требования о том, чтобы х принадлежало D, потребовать, чтобы ограничения задачи выдерживались в среднем. [29]
Прежде всего заметим, что поставленная нами задача может не иметь решения. Поэтому в дальнейшем при анализе задачи безусловной оптимизации будем предполагать, что существует пексг-торая точка х, на которой достигается решение задачи. [30]
Страницы: 1 2 3
www.ngpedia.ru
Оптимизация безусловная - Энциклопедия по машиностроению XXL
Если при проектировании технических объектов или систем можно выделить один параметр, которому отдается безусловное предпочтение и который наиболее полно характеризует свойства проектируемого объекта, то естественно этот параметр принять за целевую функцию. Такой выбор целевой функции лежит в основе критериев оптимальности, называемых частными критериями. При оптимизации по частным критериям задача проектирования сводится к задаче оптимизации выбранной целевой функции при условии соблюдения определенных ограничений. При этом одна часть параметров подпадает иод категорию ограничений, а другая часть параметров, на которые не накладываются ограничения, принимается такой, какой получилась при оптимизации целевой функции. [c.15] Задачи, в которых экстремум ищут в пределах неограниченного пространства переменных проектирования, относятся к задачам б е з у с л о в и о й оптимизации. Найденные при этом экстремумы называют безусловными. Наличие ограничений любого вида приводит к задачам условной оптимизации, решение которых дает условный экстремум. [c.277]Рассмотрим необходимые и достаточные условия экстремума. Классические методы оптимизации используют тогда, когда известно аналитическое выражение функции Р (X) и известно, что она по крайней мере дважды дифференцируема по переменным проектирования. Тогда для определения экстремума используют необходимые и достаточные условия безусловного экстремума. Эти условия легко получить с помощью разложения f (X) в окрестностях экстремальной точки X в ряд Тейлора [c.278]
Методы поиска экстремума классифицируются по следующим признакам в зависимости от характера экстремума существуют методы условной и безусловной, локальной и глобальной оптимизации по числу переменных проектирования различают методы одномерного и многомерного поиска, а по характеру информации о виде целевой функции — методы нулевого, первого и второго порядков, причем в методах первого порядка используют градиент целевой функции, поэтому эти методы называются градиентными, в методах второго порядка применяют вторые производные, а в методах нулевого порядка производные не используют. [c.281]
Методы безусловной оптимизации. Для решения задачи безусловной оптимизации используют итерационные процессы вида [c.283]
Сформулируйте принципы прямых методов оценки направлений в задачах безусловной оптимизации. [c.329]
При описании комплексной целевой функции нелинейными зависимостями от внутренних параметров задача оптимизации решается методами линейного программирования если же целевая функция является линейной функцией от внутренних параметров, то имеет место задача линейного программирования. В общем случае целевая функция может иметь несколько экстремумов, отличающихся по абсолютной величине. В зависимости от типа экстремума, в котором заканчивается поиск оптимального решения, различают методы поиска локального и глобального экстремума. Если на значение определяемых параметров наложены некоторые ограничения, то решение задачи синтеза механизмов осуществляется методами условной оптимизации. В противном случае (при отсутствии ограничений) при синтезе механизмов для поиска значений определяемых параметров используют методы безусловной оптимизации. [c.316]
Методы безусловной оптимизации [c.316]
Среди методов поиска локального экстремума методы безусловной оптимизации составляют наиболее многочисленную группу. Сущность этих методов заключается в том, что строится такая последовательность значений вектора внутренних параметров х , Хц Х.2, при которой в случае поиска минимума целевой функции в [c.316]
Рис, 25.2. Обобщенный алгоритм методов безусловной оптимизации [c.317]
Методы безусловной оптимизации по способу определения направления поиска делятся на методы нулевого, первого и второго порядков. Для методов нулевого порядка типичен выбор направления поиска по результатам последовательных вычислений целевой функции. По способу выбора совокупности оптимизируемых параметров эти методы делятся на детерминированные и случайного поиска. В детерминированных методах процесс перехода от вектора внутренних параметров Х к вектору хс 1 происходит в [c.317]
При решении задач условной оптимизации целесообразно использовать методы безусловной оптимизации, учитывая большое количество разработанных по этим методам программ. С этой целью задача условной оптимизации сводится к задаче безусловной оптимизации устранением ограничений путем преобразования параметра XI, на значения которого наложены ограничения, в не-ограничиваемый. [c.319]
Метод безусловной оптимизации 316—319 [c.366]
Сведение исходной задачи условной оптимизации к последовательности задач безусловной оптимизации может быть выполнено с помощью функций штрафа. [c.167]
Вопрос оптимизации интервала двумерной дискретизации при обратном проецировании А1 и вида интерполяционной функции g г) сложнее и будет рассмотрен отдельно. Пока же можно ограничиться безусловной верхней оценкой [c.404]
Подобные моделирующие программы могут с успехом использоваться в системах оперативно-диспетчерского управления. Правда, это возможно, только если быстродействие программ оптимизации достаточно для работы в реальном масштабе времени. Для ускорения принятия решений в реальном масштабе времени может быть заранее сформирован специальный массив готовых решений для типовых ситуаций. В этом случае вместо решения каждый раз оптимальной задачи в ЭВМ вводят исходные данные о ситуации, которые идентифицируются с одной из стандартных ситуаций, и в случае совпадения (или практической близости) лицо, принимающее решение, сразу же получает готовое решение. Безусловно, подобные программы в СЭ могут работать только в режиме советчика, т.е. выдача управляющих воздействий осуществляется лишь после того, как она санкционирована лицом, принимающим решение. [c.148]
Решение задачи связано с нахождением условного экстремума. Для нахождения безусловного экстремума задачу необходимо преобразовать так, чтобы она стала задачей на безусловный минимум. Это преобразование может осуществляться различными способами, выбор которых зависит от сложности и трудоемкости вычислений. Одним из эффективных способов является метод неопределенных множителей Лагранжа. Практические приемы преобразования и методы оптимизации решений достаточно подробно освещены в работах [21, 66]. [c.85]
В представленном здесь виде задача нормирования характеристик надежности машины представляет собой прямую задачу оптимизации [36], когда заданные суммарные затраты необходимо распределить таким образом, чтобы при безусловном обеспечении требований к значениям единичных показателей безотказности машины — комплексный показатель ремонтопригодности получил экстремальное (максимальное или минимальное) значение. Ограничениями в рассматриваемой задаче могут быть не только показатели безотказности, но и другие показатели надежности, например, долговечности и сохраняемости. [c.62]
В аналитических расчетах по оптимизации теплоэнергетических установок функционалы и ограничения упрощаются с целью получения относительно несложных аналитических зависимостей с ограниченным количеством переменных, что позволяет использовать классические методы исследования функций на экстремум — получение аналитических выражений производных по оптимизируемым переменным и приравнивание производных нулю, т. е. удовлетворение необходимых условий экстремума. Такой подход позволяет лишь получить безусловный экстремум при непрерывных переменных. [c.57]
В математическом плане в работах по оптимизации параметров теплоэнергетических установок, выполненных в последние годы с использованием ЭЦВМ, наряду с современными методами нашли применение два старых метод вариантных расчетов с целью определения лучшего варианта из числа рассматриваемых и метод нахождения и приравнивания нулю частных производных величин приведенных расчетных затрат по оптимизируемым параметрам для получения экстремальной точки. Использование этих методов безусловно сузило возможности оптимизации теплоэнергетических установок. [c.6]
Теперь поиск оптимального х проводится для функции F(x, q) с помощью любого метода безусловной оптимизации, например метода Ньютона. Для использования метода Ньютона (записи выражений) потребуется вычислить первые и вторые производные от функций X (х), ф (х), которые также можно выписать. [c.194]
Различают методы условной и безусловной оптимизации по наличию или отсутствию ограничений. Для реальных задач характерно наличие ограничений, однако методы безусловной оптимизации также представляют интерес, поскольку задачи условной оптимизации с помощью специальных методов могут быть сведены к задачам без ограничений. [c.158]
В задачах безусловной оптимизации необходимые условия представляют собой равенство нулю градиента целевой функции [c.165]
Суть метода заключается в преобразовании задачи условной оптимизации (4.19) в задачу безусловной оптимизации с помощью образования новой целевой функции [c.166]
Важная идея методов штрафных функций - преобразование задачи условной оптимизации в задачу безусловной оптимизации путем формирования новой целевой функции Ф(Х), за счет введения в исходную целевую функцию F(X) специальным образом выбранной функции штрафа S(X) [c.167]
Предложенный концептуальный подход к созданию системы средств восстановления включает представление основного материального объекта восстановительного производства - СТО - в виде их целостного многоуровневого иерархического множества, выполняющих соответствующие технологические функции (переходы, операции и процессы) систему методов синтеза каждого уровня элементов и многоуровневую оптимизацию. Система методов синтеза средств и процессов обеспечивает получение эффективных и новых патентоспособных технических решений. Практическое применение предложенных методов обеспечивает безусловный уровень качества технологических воздействий, сокращает объем проектных работ в 2...3 раза и уменьшает на 30...50 % объемы работ по изготовлению и вводу в эксплуатацию средств восстановления деталей. [c.51]
Таким образом, включением ограничений в критерий эффективности задача оптимизации сводится к задаче на безусловный экстремум требуется определить [c.308]
Если ограничения на параметры модели отсутствуют, то для минимизации квадратичной формы (8 16) можно применять методы многомерной d> 1) или одномерной d = 1) безусловной оптимизации (см, пп. 5.1.10, 5.1.11 книги 1 настоящей справочной серии, а также [13, 19]). Если же ограничения на параметры существуют и их нужно учитывать, то следует использовать методы условной оптимизации [13]. [c.471]
Уровень пренебрежимого риска разделяет область оптимизации риска и область безусловно [c.499]
Безусловное соблюдение санитарных норм предельно допустимых концентраций вредных веществ в воздушном и водном бассейнах и на земной поверхности. Учитывая, что при выбранном виде топлива приведение действительных концентраций вредных выбросов до заданных предельно допустимых концентраций (ПДК) во всех вариантах является обязательным, ущерб от воздействия вредных веществ на людей, оборудование и строения при оптимизации теплоэнергетических установок определять не нужно, поскольку он остается одинаковым. [c.87]
Существенно отличается подход к решению задач с единственным и несколькими экстремумами. Во втором случае обычно требуется найти главный из них (так называемый глобальный). Наличие или отсутствие ограничений на искомые переменные относит задачу к области условной или безусловной оптимизации. В свою очередь линейность целевой функции или ограничений обуславливает использование методов линейного или нелинейного программирования. При постановке задачи существенное значение имеет то, что исходная информация не полностью определена и характеризуется определенными вероятностными свойствами. Такую задачу следует решать методами стохастического программирования. Наконец, подход к решению оптимизационной задачи значительно изменяется, если целевая функция приобретает не скалярный, а векторный вид. Тогда возникает необходимость оптимизации по нескольким независящим критериям. После этой краткой общей классификации остановимся более подробно на типах оптимизационных задач, наиболее подходящих для разработки приборов квантовой электроники. К таким задачам прежде всего относятся задачи параметрической оптимизации. [c.121]
При наличии нелинейных ограничений g, (х) О (t = 1, 2,. .., т) используются алгоритмы, в которых решение общей задачи нелинейного программирования сводится к решению задачи безусловной оптимизации градиентными методами. Для этого к целевой функции добавляется функция штрафа (С — вектор коэффициентов штрафа) [c.213]
Прн оптимизации струйных элементов можно ограничиться крутым восхождением, не переходя к исследованию области, лежащей вблизи экстремума. Это объясняется следующим. Во-первых, задачи оптимизации элементов струйной автоматики являются задачами на условный экстремум, и безусловный экстремум целевой функции лежит, как правило, за пределами области работоспособности. [c.344]
Совокупность методов НЛП, в зависимости от ограничений в математических моделях оптимизации, делится на две группы методы безусловной оптимизации и методы условной оптимизации. Первые используют для решения задач без ограничений на оптимизируемые параметры, вторые — для задач с ограничениями. Следует отметить, что методы безусловной оптимизации (см. описание методов штрафных функций) можно использовать и при решении задач с ограничениями, предварительно приведенных к задачам без ограничений. [c.152]
Можно вьщелить 2 типа задач оптимизации - безусловные и условные. Безусловная задача оптимизации состоит в отыскании максимума или минимума функции (5.10) от п действительных переменных и определении соответствуюш,их значений аргументов на некотором множестве G -мерного пространства. Обьино рассматриваются задачи минимизации к ешм легко сводятся и задачи на поиск максимума путем замены знака целевой функции на противоположный. Условные задачи оптимизации — это такие, при формулировке которых задаются некоторые условия (ограничения) на множестве G. Здесь рассмотрим только безусловные задачи оптимизации. [c.277]
Вообщ,е задачи условной оптимизации более сложны, чем задачи безусловной оптимизации. Для их решения используют специально разработанные методы программирования с ограничениями. Одним из таких методов, которые относятся к методам поиска глобального экстремума, является метод сканирования, состоящий в том, что допустимая область поиска, определяемая системой ограничений, разбивается на к подобластей, в центре каждой из которых определяется значение целевой функции. Если целевая функция зависит от п параметров, необходимо выполнить вариантов расчета. Для надежного определения глобального минимума необходимо увеличивать число к подобластей, что приводит к большим затратам машинного времени. [c.319]
Очевидным условием окончагшя поиска в задачах безусловной оптимизации является выполнение неравенства [c.156]
В зависимости от характера экст ремума различают методы условной и безусловной, а также локальной и оощей оптимизации. Наиболее удобно и просто реализовать на ЭВМ методы поиска безусловных локальных экстремумов. [c.30]
Задача оптимизации сложной теплоэнергетической установки является многоэкстремальной, имеющей ряд локальных экстремумов. Для поиска среди них глобального экстремума используются комбинации методов случайного поиска с методами направленного поиска. По существу это заключается в том, что спуск производится из разных подобластей с последующим анализом кривых, соединяющих экстремальные и особые точки. Наличие ограничений превращает задачу поиска безусловного экстремума в задачу условного экстремума (возможность нахождения условного экстремума на границе). [c.58]
Проблема выбора значения штрафа q решается исходя из того факта, что, согласно теории, существует такое (f, что при всех q>(f условие Куна — Таккера будет выполняться в оптимальных точках. Исходя из этого, при работе алгоритма оптимизации инициализируем некоторое начальное значение о и решаем задачу безусловной оптимизации для функции F x, qo). Для полученной последовательности значений Хо, Xi, Х2,. .. проверяется условие [c.194]
Деннис Дж. мл., Шнабель Р. Численные методы безусловной оптимизации и решения нелинейных уравнений Пер. с англ. М. Мир, 1988. [c.477]
Простейшей задачей нелинейного программирования является однопараметрическая задача на безусловный экстремум. Кроме того, предполагается, что в области определения целевой функции имеется всего один экстремум. Однопараметрические одноэкстремальные целевые функции получили название унимодальных функций. К таким задачам относится задача расчета оптимального межопорного расстояния шпинделя станка [125]. Наиболее распространенными методами оптимизации унимодельных целевых функций являются методы последовательного сокраш,е-ния интервала неопределенности [91. [c.205]
Таким образом, задача условной оптимизации (3.24) сведена к задаче безусловной оптимизации квадратичной функции (3.27). Производная Фрегпе функции (3.27) есть 1 х (ЛТ — 1) -матрица [c.66]
mash-xxl.info