ЭММ / Лекция по векторной оптимизации. Векторная оптимизация
Лекция по векторной оптимизации (2)
Векторная оптимизация
При решении задач линейного программирования рассматривались только простые случаи, когда ясен критерий, по которому производится оценка эффективности и требуется найти экстремум только одного показателя.
Но на практике такие задачи встречаются не так уж часто – преимущественно при рассмотрении небольших по масштабу и скромных по значению мероприятий.
Если речь идет о крупномасштабном предприятии, то эффективность их функционирования не может быть охарактеризована с помощью одного-единственного показателя эффективности.
Пример: организуется работа предприятия. Под углом зрения какого критерия надо выбирать решение? Хотелось бы максимизировать валовый объем продукции, получить максимальный чистый доход, минимизировать себестоимость, максимизировать производительность труда и т.д. Здесь оптимальное решение по одному показателю может оказаться не лучшим по значениям показателей других критериев.
Критерий оптимальности (или показатель эффективности или целевая функция) – это функция, экстремальное значение которой нужно найти в условиях экономических возможностей задачи. Экономические возможности формализуются в виде системы ограничений.
Векторная оптимизация (многокритериальная оптимизация)– это нахождение оптимальных значений по нескольким критериям.
Особенность задач векторной оптимизации – наличие в области допустимых значений области компромиссов, в которой невозможно одновременное улучшение всех критериев.
Принадлежащие области компромиссов планы называются эффективными или оптимальными по Парето.
План – это решение экономико-математической модели (т.е набор значений неизвестных, удовлетворяющих системе ограничений модели).
Число возможных схем компромиссов практически не ограничено.
******
Существуют различные направления решения задач векторной оптимизации, основанные на следующих методах:
методы, основанные на свертывании критериев в единый;
методы, использующие ограничения на критерии;
методы целевого программирования;
методы, основанные на отыскании компромиссного решения;
методы, в основе которых лежат человеко-машинные процедуры принятия решений (интерактивное программирование).
Рассмотрим некоторые из этих методов.
******
В методах, основанных на свертывании критериев в единый, из локальных критериев формируется один. Наиболее распространенным является метод линейной комбинации частных критериев.
Метод линейной комбинации частных критериев
Вместо нескольких критериев вводится один новый в виде их взвешенной суммы. Т.о. задача математического программирования становится однокритериальной и имеет следующий вид:
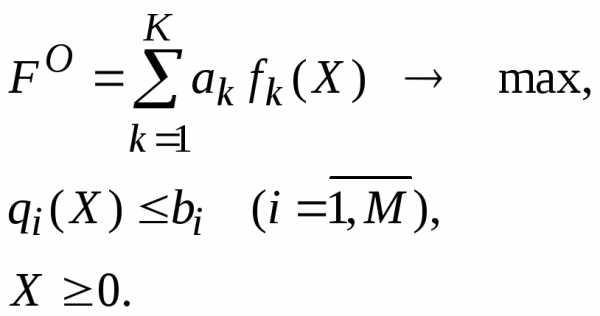
При этом задается вектор весовых коэффициентов всех критериев а = {al,...,ak}, характеризующих важность каждого критерия. .
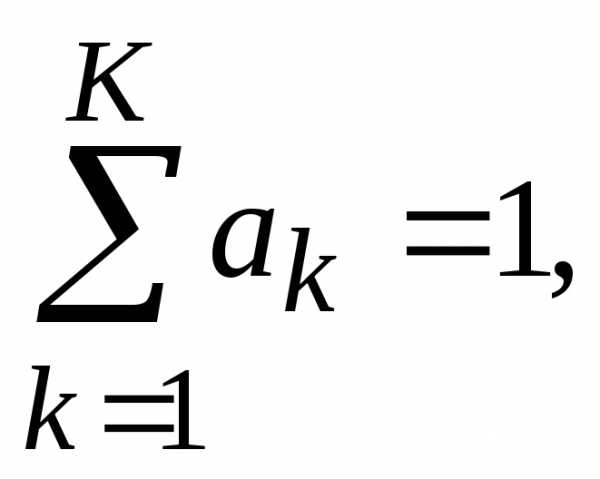 при этом, гдеK – количество критериев.
при этом, гдеK – количество критериев.Линейная скаляризованная функция FO (функция свертки) представляет собой сумму частных критериев, умноженных на весовые коэффициенты.
Критерии свертки могут быть нормализованы, т.е. приведены к единому масштабу и безразмерному виду (для непосредственного сравнения критериев).
Недостатки этого метода:
– малым приращениям весовых коэффициентов соответствует большие приращения функции свертки, т.е. решение задачи неустойчиво
– необходимость определения весовых коэффициентов
Преимущества:
– решение по этому методу оптимально, т.е принадлежит области компромиссов
Определить весовые коэффициенты можно, например, следующим образом. Важность главного критерия принимается за единицу, а для каждого из остальных устанавливается его относительная важность по сравнению с главным. Все полученные положительные числа должны быть меньше единицы. Затем каждое из них, в том числе и важность главного критерия (онаравна единице) делят на их сумму и получают весовые коэффициенты.
******
В методах, использующих ограничения на критерии, применяются два подхода:
метод ведущего критерия;
методы последовательного применения критериев (метод последовательных уступок, метод ограничений).
Метод ведущего критерия
В методе ведущего критерия все целевые функции кроме одной переводятся в разряд ограничений. Пусть – вектор, компоненты которого представляют собой нижние границы соответствующих критериев. Задача будет иметь вид
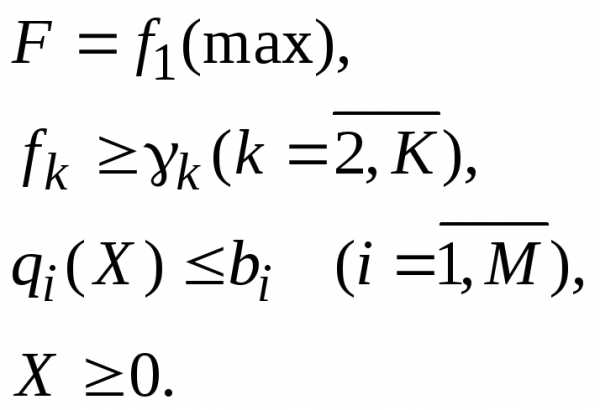
Полученное этим методом решение может не быть эффективным, поэтому необходимо проверить его принадлежность области компромиссов.
Метод ведущего критерия применяется в таких задачах, как минимизация полных затрат при условии выполнения плана по производству различных видов продукции, максимизация выпуска комплектных наборов при ограничении на потребляемые ресурсы.
Метод последовательных уступок
В этом методе вместо многокритериальной задачи решается несколько однокритериальных задач (по числу критериев), причем для каждого последующего критерия вводится дополнительное ограничение на величину предыдущего критерия.
1. Вначале устанавливается предпочтительность всех критериев, т.е на первое место ставится самый важный критерий.
2. Находится оптимальное решение  по самому важному критерию
по самому важному критерию 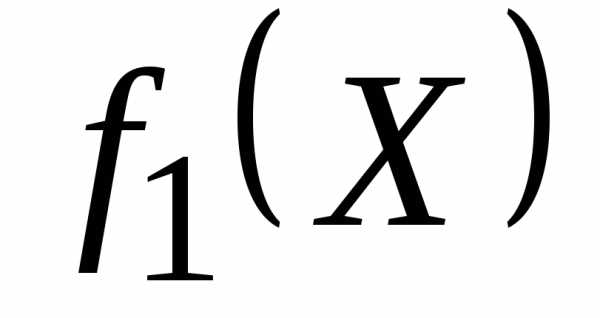 с учетом системы ограничений (при этом остальные критерии будут рассматриваться на последующих этапах решения задачи). Это решение обращает в экстремум первый критерий.
с учетом системы ограничений (при этом остальные критерии будут рассматриваться на последующих этапах решения задачи). Это решение обращает в экстремум первый критерий.
3. Лицом, принимающим решение, устанавливается величина уступки  . Уступка назначается исходя из практических соображений с учетом малой точности, с которой нам известны входные данные. Т.е мы согласны сделать эту уступку, чтобы максимизировать второй критерий.
. Уступка назначается исходя из практических соображений с учетом малой точности, с которой нам известны входные данные. Т.е мы согласны сделать эту уступку, чтобы максимизировать второй критерий.
4. Решается задача по следующему критерию 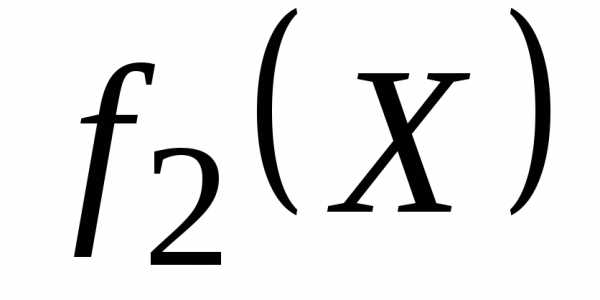
В том случае, если на этапе 2 решалась задача на поиск максимума критерия  , то дополнительное ограничение имеет следующий вид: .
, то дополнительное ограничение имеет следующий вид: .
В случае, если на этапе 2 решалась задача на поиск минимума критерия  , то дополнительное ограничение имеет следующий вид: .
, то дополнительное ограничение имеет следующий вид: .
5. После нахождения оптимального решения 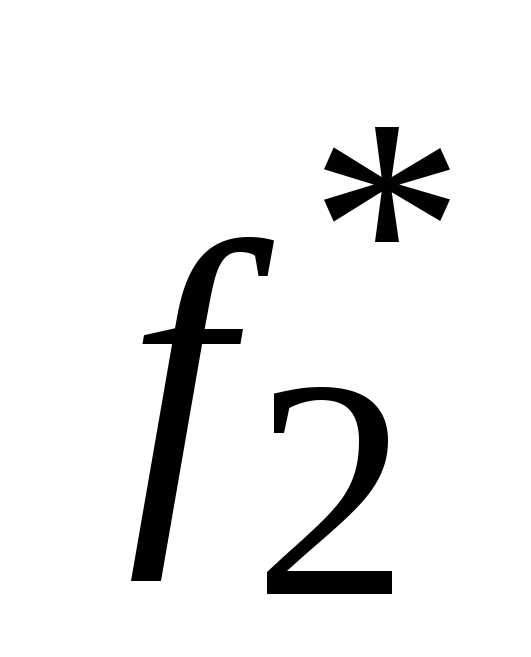 по критерию
по критерию 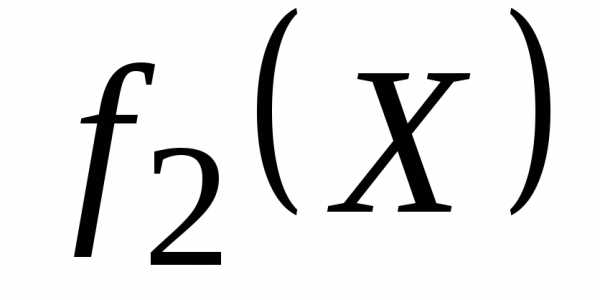 назначается по нему уступка и решается задача по третьему критерию с двумя дополнительными ограничениями по первым двум критериям
назначается по нему уступка и решается задача по третьему критерию с двумя дополнительными ограничениями по первым двум критериям
6. Решение задачи продолжается до тех пор, пока не будет найдено значение наименее важного критерия при уступках по остальным критериям.
Метод хорош тем, что сразу видно, ценой какой уступки в одном показателе приобретается выигрыш в другом показателе и какова величина этого выигрыша.
Если лицо, принимающее решение, устраивают значения полученных критериев, то задача считается решенной. В противном случае изменяются величины уступок, и задача решается заново.
Метод равных и наименьших относительных отклонений
Находится относительное отклонение 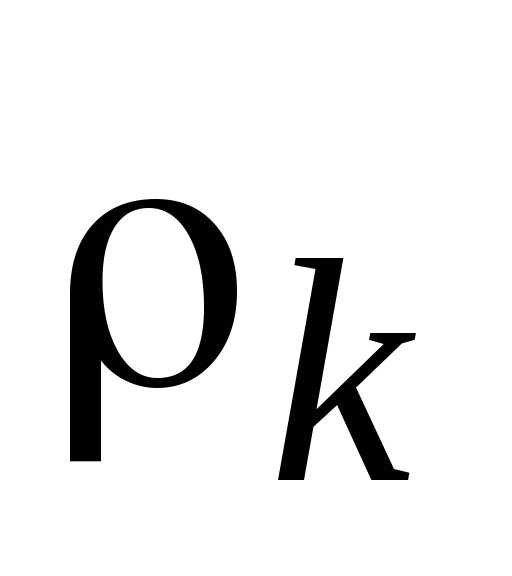 критерия
критерия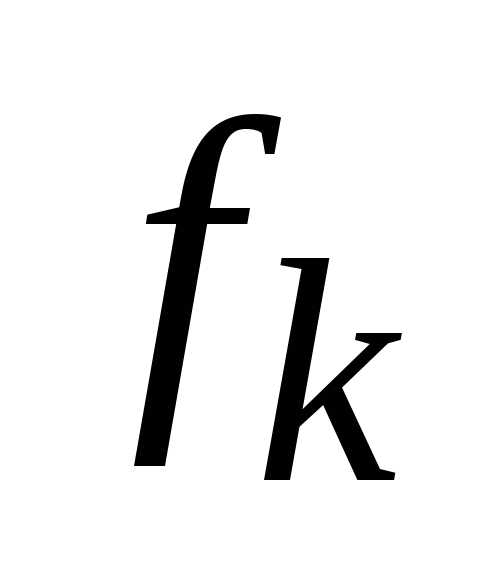
,
где  –экстремальное решение задачи поk-му критерию;
–экстремальное решение задачи поk-му критерию;
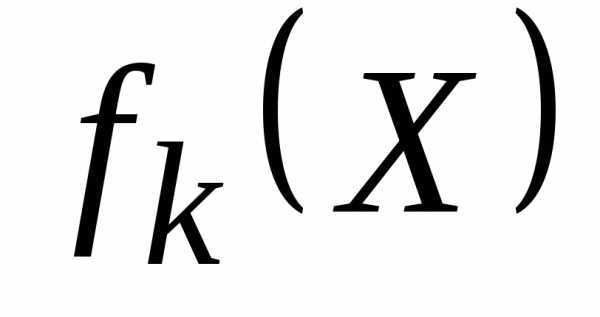 –k-я целевая функция;
–k-я целевая функция;
K – количество критериев.
Условие равенства отклонений добавит к системе ограничений задачи равенство следующего вида (в количестве K – 1):
.
Целевая функция будет иметь вид
.
Необходимо учитывать, что чтобы минимизировать критерий 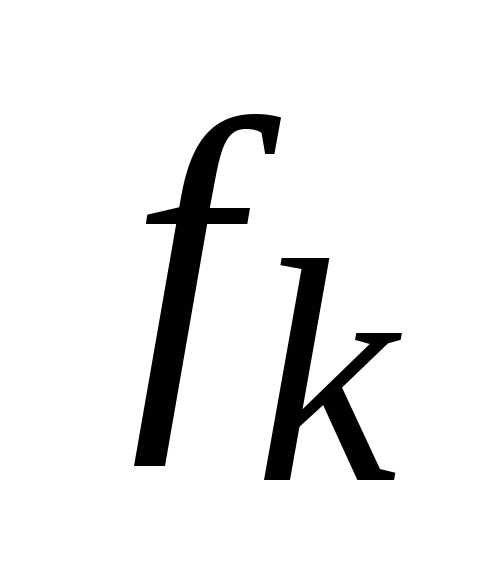 , достаточно максимизировать функцию вида –
, достаточно максимизировать функцию вида –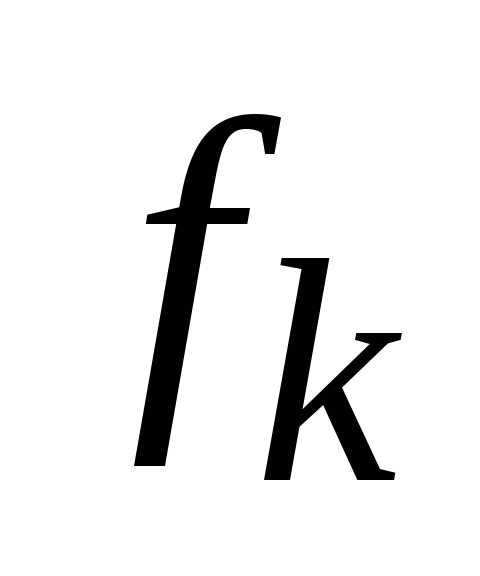 , так как.
, так как.
Таким образом, если приравниваемые относительные отклонения 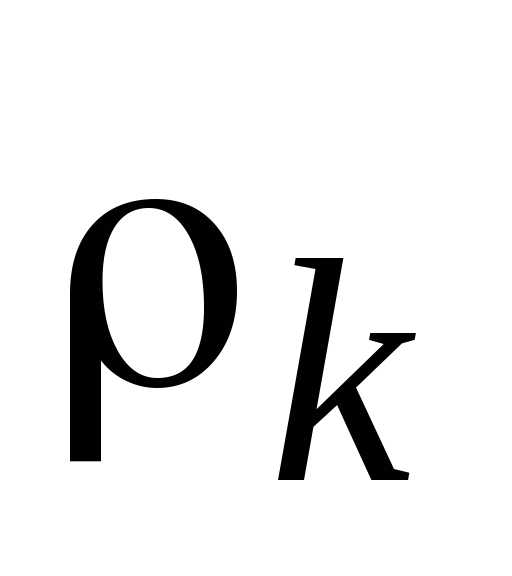 определены по максимизируемым критериям, знаки модуля опускаются. Если одно из приравниваемых относительных отклонений
определены по максимизируемым критериям, знаки модуля опускаются. Если одно из приравниваемых относительных отклонений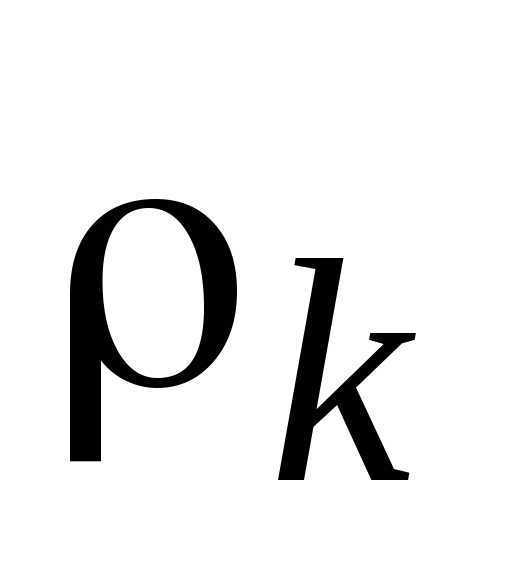
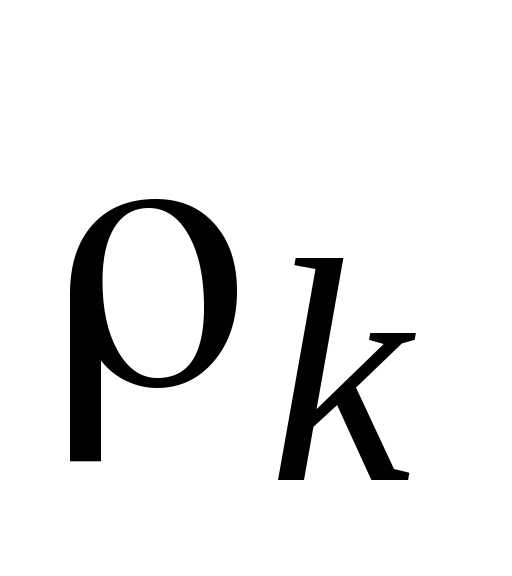 необходимо поставить знак минус.
необходимо поставить знак минус.Решение может быть неэффективным, поэтому предварительно необходимо выделить область компромиссов.
Рассмотрим пример решения векторной задачи методом равных и наименьших относительных отклонений в общем виде.
Пусть необходимо найти компромиссное решение задачи по трем критериям:
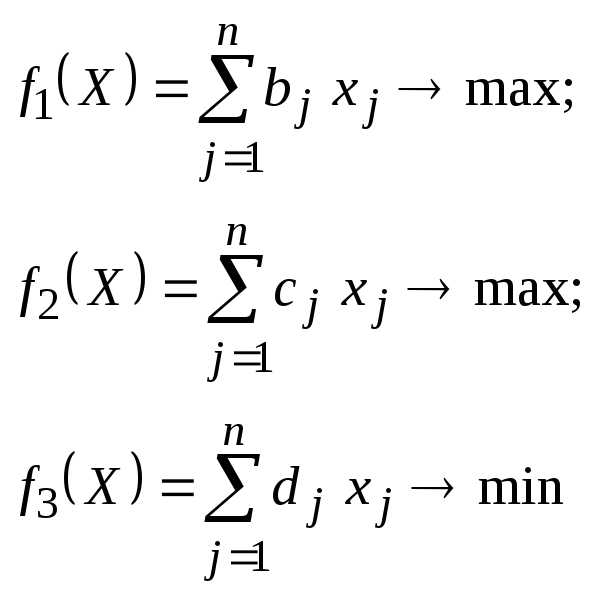
при ограничениях
.
Вначале находится экстремальное значение каждого из трех критериев путем решения задачи линейного программирования для рассматриваемого критерия и системы ограничений при игнорировании двух остальных критериев. Таким образом, находят 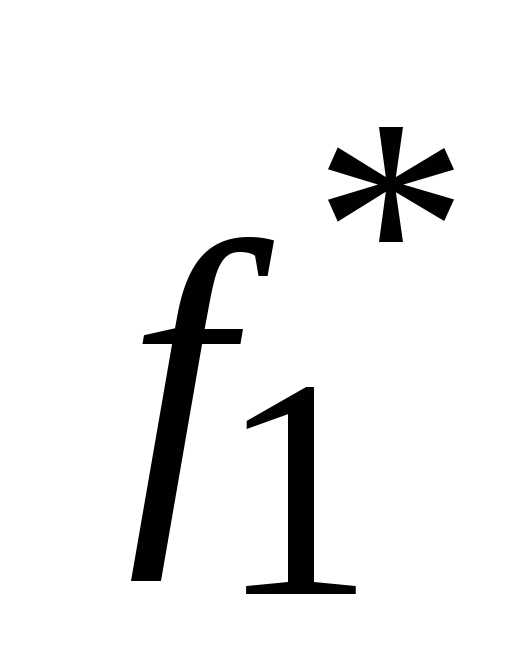 ,
,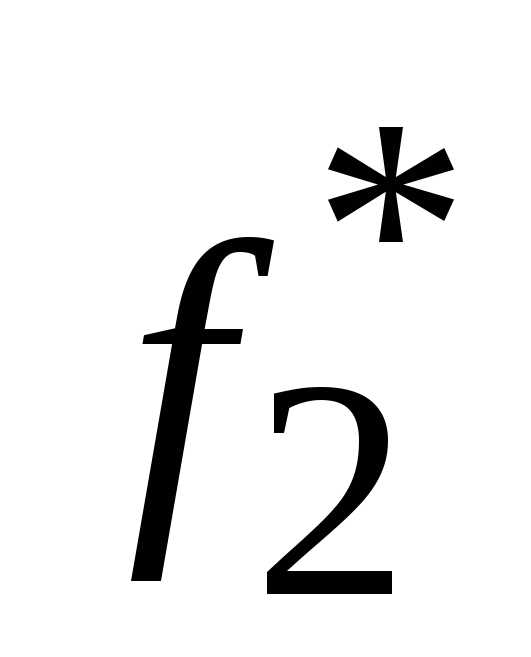
 .
. Далее находятся относительные отклонения 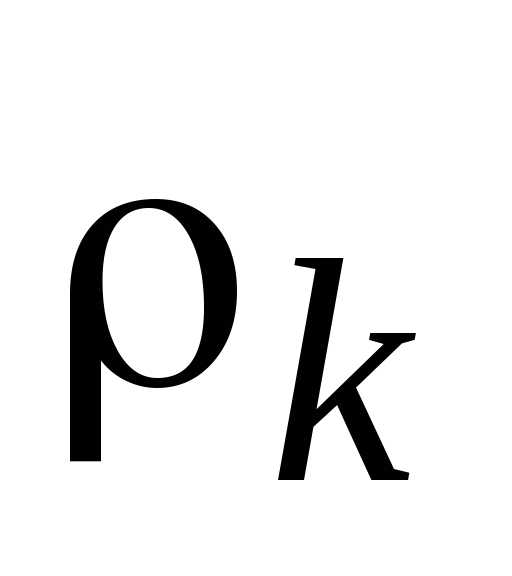 критериев
критериев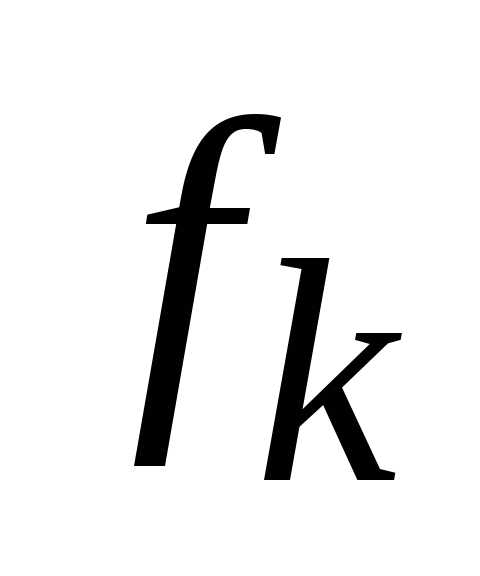 (в данном случае количество критериев
(в данном случае количество критериев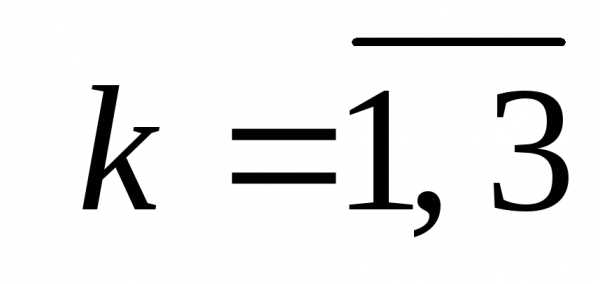 ):
):
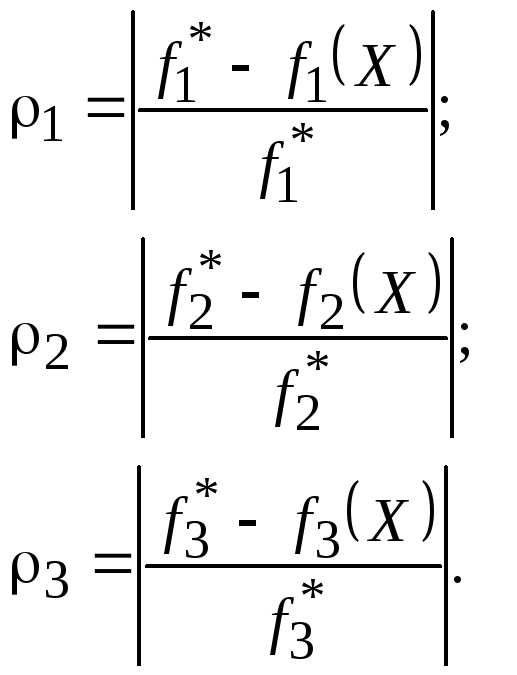
Далее приравниваем полученные отклонения 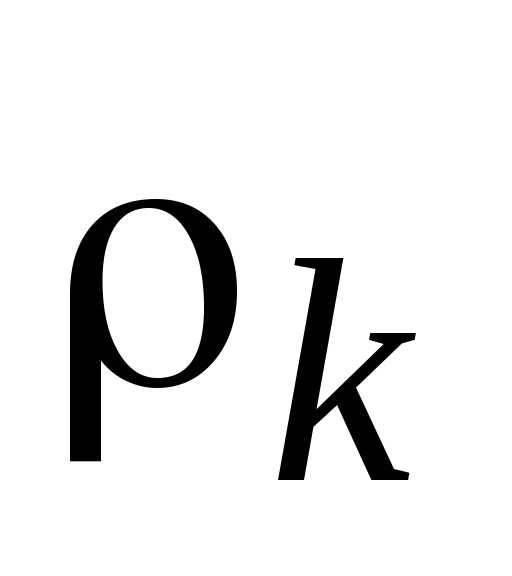 и добавляем к системе ограничений два ограничения (т. к. количество критериевK = 3, а количество ограничений равно K – 1) следующего вида:
и добавляем к системе ограничений два ограничения (т. к. количество критериевK = 3, а количество ограничений равно K – 1) следующего вида:
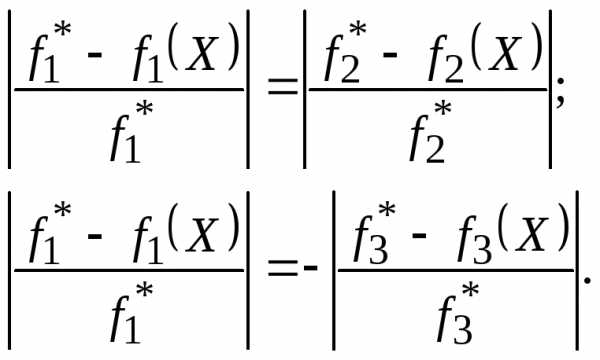
В первом полученном ограничении учтено, что два первых приравниваемых относительных отклонения 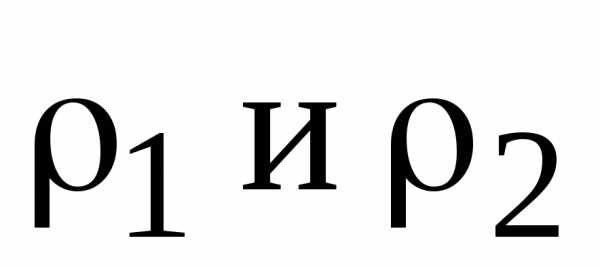 определены по максимизируемым критериям.
определены по максимизируемым критериям.
Во втором ограничении учтено, что третье приравниваемое относительное отклонение  определено по минимизируемому критерию, поэтому перед правой частью равенства поставлен знак минус.
определено по минимизируемому критерию, поэтому перед правой частью равенства поставлен знак минус.
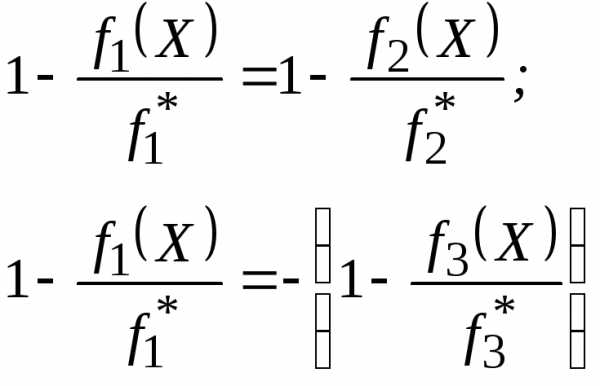 и далее
и далее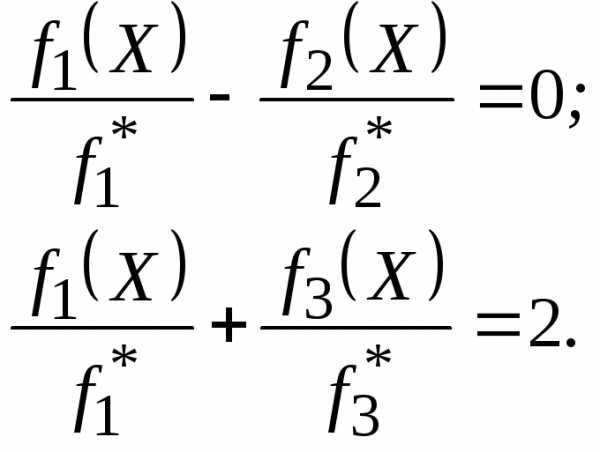
Итоговая целевая функция, записанная с учетом третьего критерия, будет иметь вид:
При решении этой задачи в Excel с помощью надстройкиПоиск решения в ячейку для вычисления итоговой целевой функции  вводится не функцияСуммпроизв, а записывается формула для вычисления
вводится не функцияСуммпроизв, а записывается формула для вычисления  .
.
studfiles.net
Векторная оптимизация - это... Что такое Векторная оптимизация?
Векторная оптимизация [vector optimization] — комплекс методов решения задач математического программирования, в которых критерий оптимальности представляет собой вектор, компонентами которого являются в свою очередь несводимые друг к другу критерии оптимальности подсистем, входящих в данную систему, например, критерии роста благосостояния разных социальных групп в социально-экономическом планировании. При этом задача оптимизации существенно видоизменяется по сравнению с теми задачами, которые рассматриваются в большинстве статей словаря. В них она сводится к тому, чтобы, зная условия и ограничения, найти такой план, который бы максимизировал или минимизировал единственный заданный критериальный показатель. Это называется «скалярная оптимизация«.
Есть разные подходы к векторным задачам оптимизации, так или иначе связанные с нахождением некоторого компромисса между целями подсистем и, следовательно, между рассматриваемыми критериями. Критерии, например, ранжируют по важности, выделяют один из них в качестве главного (тогда уровни остальных фиксируются как дополнительные ограничения). Оптимизация по одному из критериев называется субоптимизацией. Другой способ — при ранжировании приписывать критериям определенные веса (соответственно их важности) и на этой основе строить единый скалярный критерий, отражающий общую цель системы («Скаляризация векторного критерия«).
Принцип оптимальности по Парето сводит задачу к поиску множества эффективных планов. При этом принимают, что если улучшение какого-то показателя (критерия) потребует ухудшения хотя бы одного из остальных, оптимум достигнут. В других случаях задачу В.о. сводят к задаче теории игр, в которой «игроками» выступают подсистемы, имеющие несовпадающие цели и критерии.
Широко распространено отождествление терминов «В.о.» и «многокритериальная оптимизация«. Действительно, с точки зрения математического аппарата соответствующие понятия идентичны.
Но есть принципиальное различие с точки зрения экономической: в первом случае, как указано выше, речь идет о совокупности (векторе) критериев различных подсистем, во втором — о векторе разнородных критериев оптимальности некоторой системы в целом.
Ко второму случаю можно отнести оптимизацию развития по множеству разнородных критериев, часто противоположных по направлению: общество одновременно заинтересовано в повышении жизненного уровня и укреплении обороны, в развитии химии и охране окружающей среды, в удовлетворении сегодняшних нужд и обеспечении будущих поколений и т.д. Именно для подобных задач предпочтительнее термин «многокритериальная оптимизация».
Экономико-математический словарь: Словарь современной экономической науки. — М.: Дело. Л. И. Лопатников. 2003.
economic_mathematics.academic.ru
Векторная оптимизация — Словарь Лопатникова
Векторная оптимизация [vector optimization] — комплекс методов решения задач математического программирования, в которых критерий оптимальности представляет собой вектор, компонентами которого являются в свою очередь несводимые друг к другу критерии оптимальности подсистем, входящих в данную систему, например, критерии роста благосостояния разных социальных групп в социально-экономическом планировании. При этом задача оптимизации существенно видоизменяется по сравнению с теми задачами, которые рассматриваются в большинстве статей словаря. В них она сводится к тому, чтобы, зная условия и ограничения, найти такой план, который бы максимизировал или минимизировал единственный заданный критериальный показатель. Это называется «скалярная оптимизация«.
Есть разные подходы к векторным задачам оптимизации, так или иначе связанные с нахождением некоторого компромисса между целями подсистем и, следовательно, между рассматриваемыми критериями. Критерии, например, ранжируют по важности, выделяют один из них в качестве главного (тогда уровни остальных фиксируются как дополнительные ограничения). Оптимизация по одному из критериев называется субоптимизацией. Другой способ — при ранжировании приписывать критериям определенные веса (соответственно их важности) и на этой основе строить единый скалярный критерий, отражающий общую цель системы («Скаляризация векторного критерия«).
Принцип оптимальности по Парето сводит задачу к поиску множества эффективных планов. При этом принимают, что если улучшение какого-то показателя (критерия) потребует ухудшения хотя бы одного из остальных, оптимум достигнут. В других случаях задачу В.о. сводят к задаче теории игр, в которой «игроками» выступают подсистемы, имеющие несовпадающие цели и критерии.
Широко распространено отождествление терминов «В.о.» и «многокритериальная оптимизация«. Действительно, с точки зрения математического аппарата соответствующие понятия идентичны.
Но есть принципиальное различие с точки зрения экономической: в первом случае, как указано выше, речь идет о совокупности (векторе) критериев различных подсистем, во втором — о векторе разнородных критериев оптимальности некоторой системы в целом.
Ко второму случаю можно отнести оптимизацию развития по множеству разнородных критериев, часто противоположных по направлению: общество одновременно заинтересовано в повышении жизненного уровня и укреплении обороны, в развитии химии и охране окружающей среды, в удовлетворении сегодняшних нужд и обеспечении будущих поколений и т.д. Именно для подобных задач предпочтительнее термин «многокритериальная оптимизация».
lopatnikov.pro
Лекция по векторной оптимизации
Векторная оптимизация
При решении задач линейного программирования рассматривались только простые случаи, когда ясен критерий, по которому производится оценка эффективности и требуется найти экстремум только одного показателя.
Но на практике такие задачи встречаются не так уж часто – преимущественно при рассмотрении небольших по масштабу и скромных по значению мероприятий.
Если речь идет о крупномасштабном предприятии, то эффективность их функционирования не может быть охарактеризована с помощью одного-единственного показателя эффективности.
Пример: организуется работа предприятия. Под углом зрения какого критерия надо выбирать решение? Хотелось бы максимизировать валовый объем продукции, получить максимальный чистый доход, минимизировать себестоимость, максимизировать производительность труда и т.д. Здесь оптимальное решение по одному показателю может оказаться не лучшим по значениям показателей других критериев.
Векторная оптимизация– нахождение оптимальных значений по нескольким критериям.
Особенность задач векторной оптимизации – наличие в области допустимых значений области компромиссов, в которой невозможно одновременное улучшение всех критериев.
Принадлежащие области компромиссов планы называются эффективными или оптимальными по Парето.
План – это решение экономико-математической модели (т.е набор значений неизвестных, удовлетворяющих системе ограничений модели).
Число возможных схем компромиссов практически не ограничено.
******
Существуют различные направления решения задач векторной оптимизации, основанные на следующих методах:
методы, основанные на свертывании критериев в единый;
методы, использующие ограничения на критерии;
методы целевого программирования;
методы, основанные на отыскании компромиссного решения;
методы, в основе которых лежат человеко-машинные процедуры принятия решений (интерактивное программирование).
Рассмотрим некоторые из этих методов.
******
В методах, основанных на свертывании критериев в единый, из локальных критериев формируется один. Наиболее распространенным является метод линейной комбинации частных критериев.
Метод линейной комбинации частных критериев
Вместо нескольких критериев вводится один новый в виде их взвешенной суммы. Т.о. задача математического программирования становится однокритериальной и имеет следующий вид:
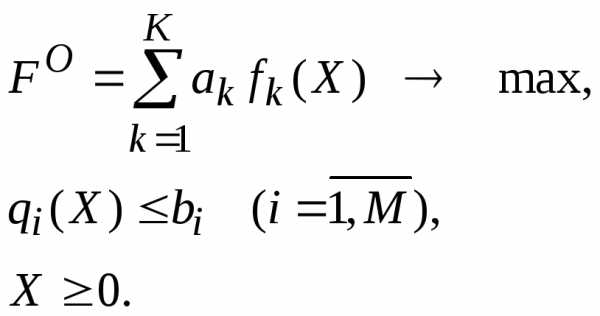
При этом задается вектор весовых коэффициентов всех критериев а = {al,...,ak}, характеризующих важность каждого критерия. .
Весовые коэффициенты – это положительные числа, сумма которых равна 1: 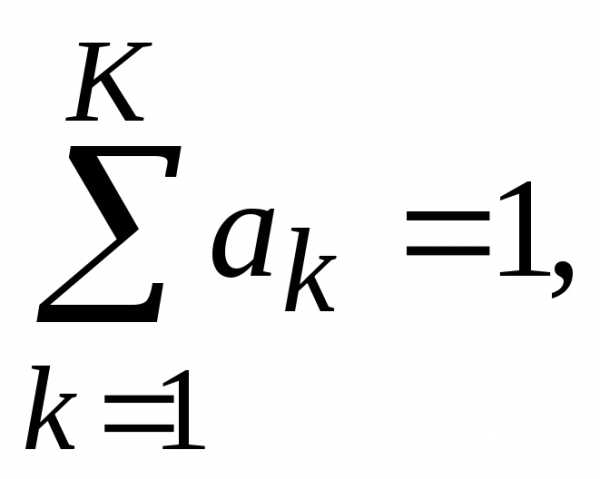 при этом, гдеK – количество критериев.
при этом, гдеK – количество критериев.
Линейная скаляризованная функция FO (функция свертки) представляет собой сумму частных критериев, умноженных на весовые коэффициенты.
Критерии свертки могут быть нормализованы, т.е. приведены к единому масштабу и безразмерному виду (для непосредственного сравнения критериев).
Недостатки этого метода:
– малым приращениям весовых коэффициентов соответствует большие приращения функции свертки, т.е. решение задачи неустойчиво
– необходимость определения весовых коэффициентов
Преимущества:
– решение по этому методу оптимально, т.е принадлежит области компромиссов
Определить весовые коэффициенты можно, например, следующим образом. Важность главного критерия принимается за единицу, а для каждого из остальных устанавливается его относительная важность по сравнению с главным. Все полученные положительные числа должны быть меньше единицы. Затем каждое из них, в том числе и важность главного критерия (одна равна единице) делят на их сумму и получают весовые коэффициенты.
******
В методах, использующих ограничения на критерии, применяются два подхода:
метод ведущего критерия;
методы последовательного применения критериев (метод последовательных уступок, метод ограничений).
Метод ведущего критерия
В методе ведущего критерия все целевые функции кроме одной переводятся в разряд ограничений. Пусть – вектор, компоненты которого представляют собой нижние границы соответствующих критериев. Задача будет иметь вид
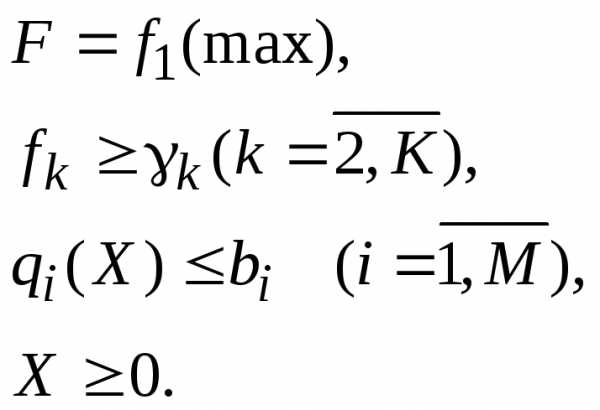
Полученное этим методом решение может не быть эффективным, поэтому необходимо проверить его принадлежность области компромиссов.
Метод ведущего критерия применяется в таких задачах, как минимизация полных затрат при условии выполнения плана по производству различных видов продукции, максимизация выпуска комплектных наборов при ограничении на потребляемые ресурсы.
Метод последовательных уступок
В этом методе вместо многокритериальной задачи решается несколько однокритериальных задач (по числу критериев), причем для каждого последующего критерия вводится дополнительное ограничение на величину предыдущего.
1. Вначале устанавливается предпочтительность всех критериев, т.е на первое место ставится самый важный критерий
2. Находится оптимальное решение по первому критерию с учетом системы ограничений (при этом остальные критерии будут рассматриваться на последующих этапах решения задачи). Это решение обращает в экстремум первый критерий.
с учетом системы ограничений (при этом остальные критерии будут рассматриваться на последующих этапах решения задачи). Это решение обращает в экстремум первый критерий.
3. Лицом, принимающим решение, устанавливается величина уступки  . Уступка назначается исходя из практических соображений с учетом малой точности, с которой нам известны входные данные. Т.е мы согласны сделать эту уступку, чтобы максимизировать второй критерий.
. Уступка назначается исходя из практических соображений с учетом малой точности, с которой нам известны входные данные. Т.е мы согласны сделать эту уступку, чтобы максимизировать второй критерий.
4. Решается задача по критерию 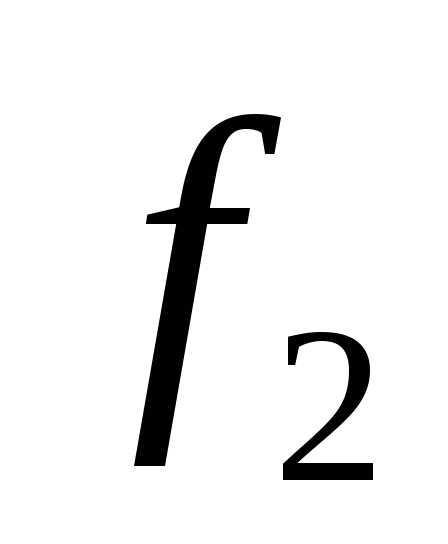 с дополнительным ограничением
с дополнительным ограничением
5. После нахождения оптимального решения по критерию 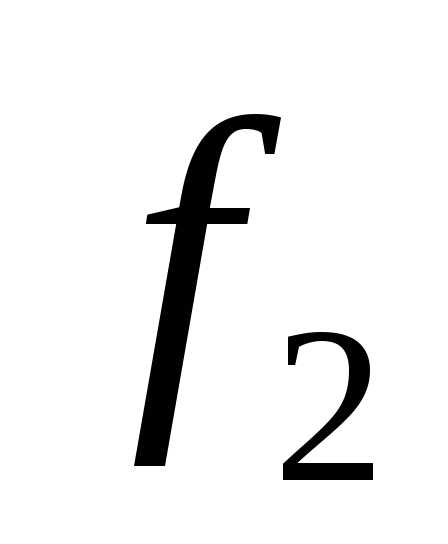 назначается по нему уступка и решается задача по третьему критерию с двумя дополнительными ограничениями по первым двум критериям
назначается по нему уступка и решается задача по третьему критерию с двумя дополнительными ограничениями по первым двум критериям
6. Решение задачи продолжается до тех пор, пока не будет найдено значение наименее важного критерия при уступках по остальным критериям.
Метод хорош тем, что сразу видно, ценой какой уступки в одном показателе приобретается выигрыш в другом показателе и какова величина этого выигрыша.
Если лицо, принимающим решение, устраивают значения полученных критериев, то задача считается решенной. В противном случае изменяются величины уступок и задача решается заново.
Метод равных и наименьших относительных отклонений
Находится относительное отклонение 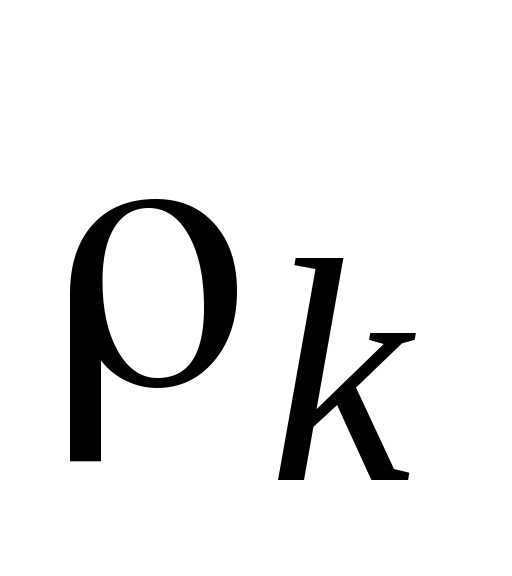 критерия
критерия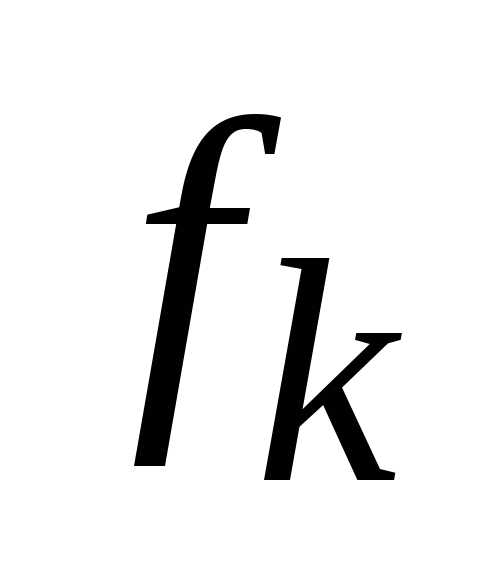
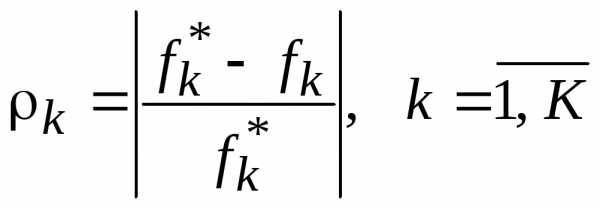 ,
,
где  –экстремальное решение задачи поk-му критерию;
–экстремальное решение задачи поk-му критерию;
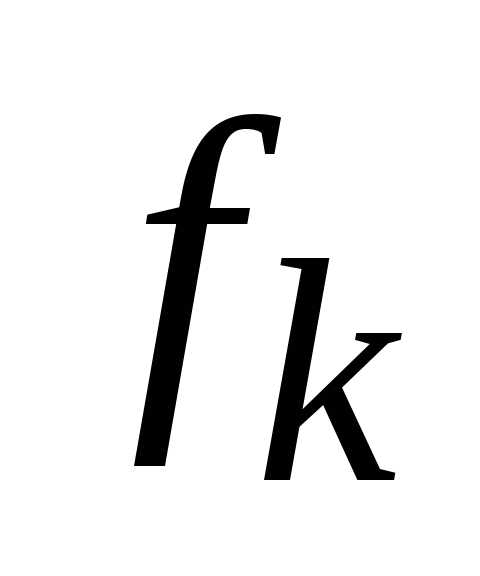 –k-я целевая функция;
–k-я целевая функция;
K – количество критериев.
Условие равенства отклонений добавит к системе ограничений задачи равенство следующего вида (в количестве K – 1):
.
Целевая функция будет иметь вид
.
Необходимо учитывать, что чтобы минимизировать критерий 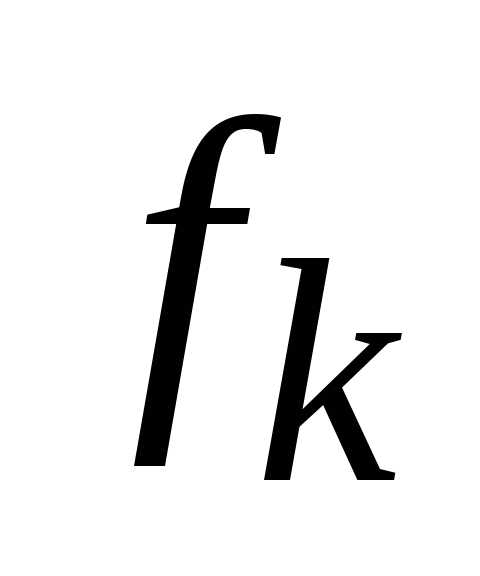 , достаточно максимизировать функцию вида –
, достаточно максимизировать функцию вида –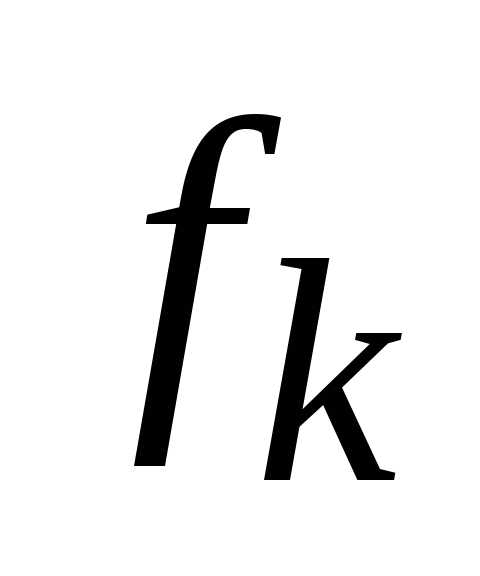 , так как.
, так как.
Таким образом, если приравниваемые относительные отклонения 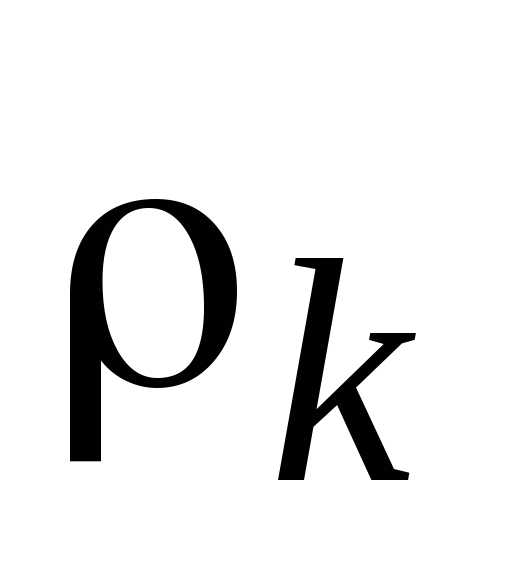 определены по максимизируемым критериям, знаки модуля опускаются. Если одно из приравниваемых относительных отклонений
определены по максимизируемым критериям, знаки модуля опускаются. Если одно из приравниваемых относительных отклонений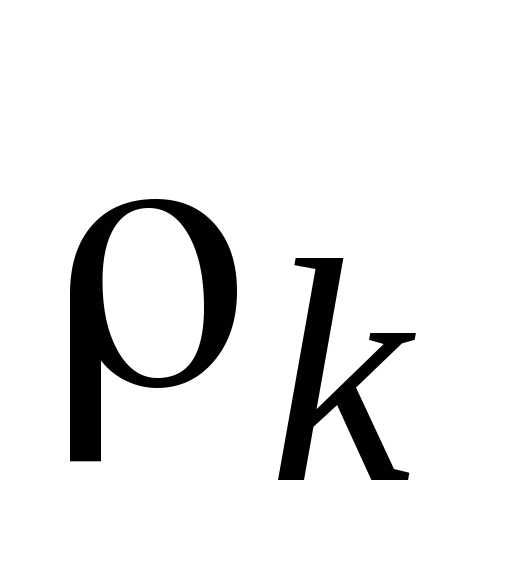 определено по максимизируемому критерию, а второе – по минимизируемому критерию, то, опустив знаки модуля, перед вторым относительным отклонением
определено по максимизируемому критерию, а второе – по минимизируемому критерию, то, опустив знаки модуля, перед вторым относительным отклонением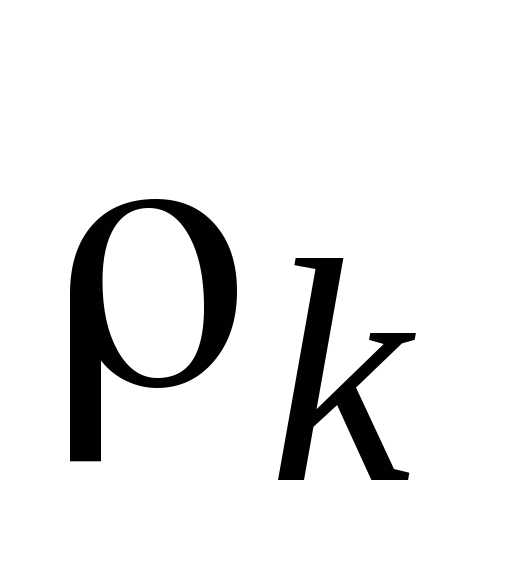 необходимо поставить знак минус.
необходимо поставить знак минус.
Решение может быть неэффективным, поэтому предварительно необходимо выделить область компромиссов.
Рассмотрим пример решения векторной задачи методом равных и наименьших относительных отклонений в общем виде.
Пусть необходимо найти компромиссное решение задачи по трем критериям:
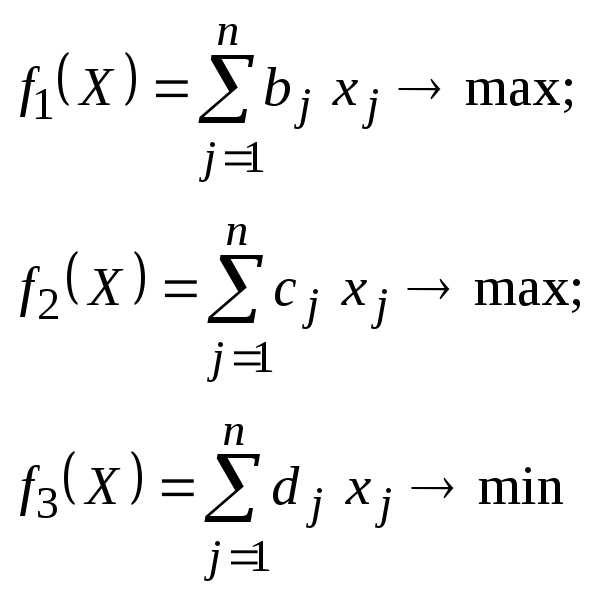
при ограничениях
.
Вначале находится экстремальное значение каждого из трех критериев путем решения задачи линейного программирования для рассматриваемого критерия и системы ограничений при игнорировании двух остальных критериев. Таким образом, находят 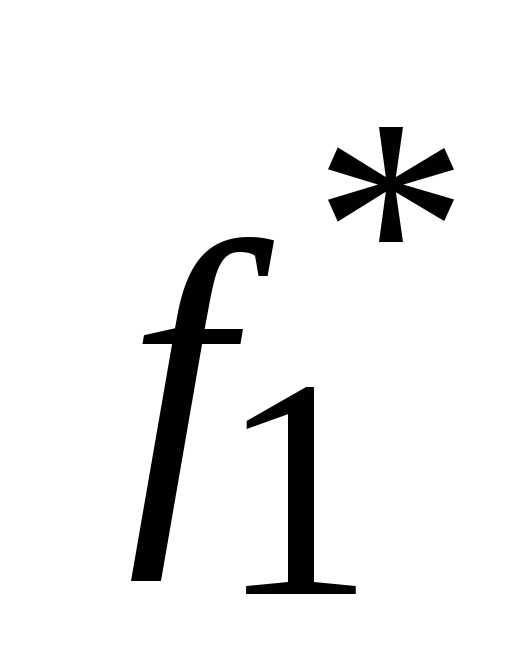 ,
,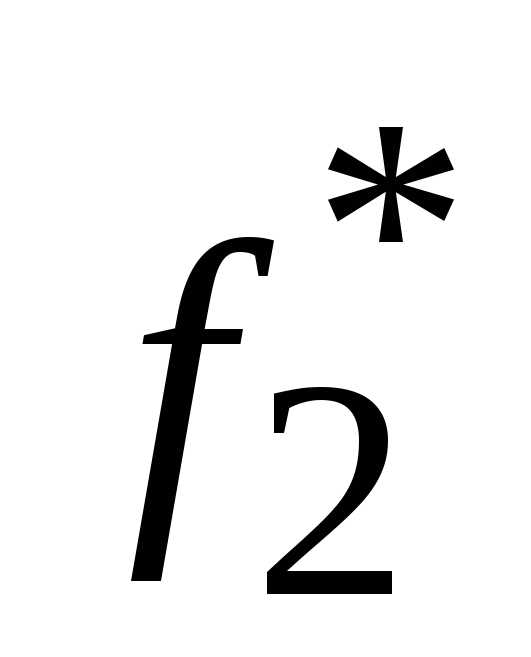 и
и .
.
Далее находятся относительные отклонения 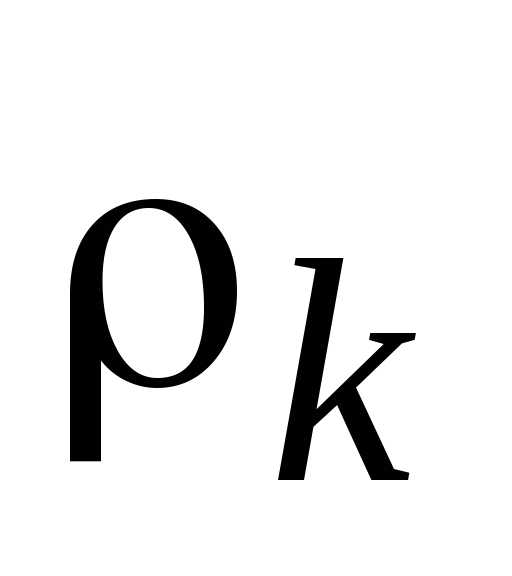 критериев
критериев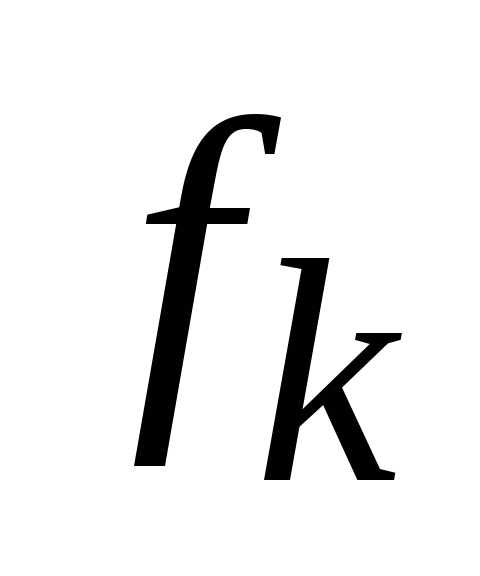 (в данном случае количество критериев
(в данном случае количество критериев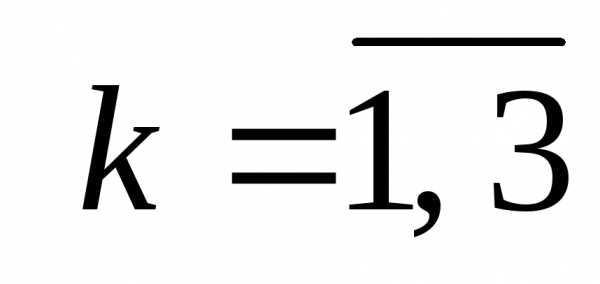 ):
):
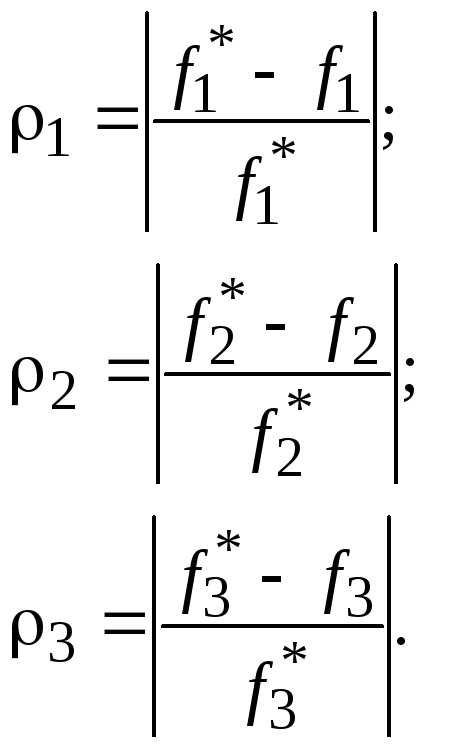
Далее приравниваем полученные отклонения 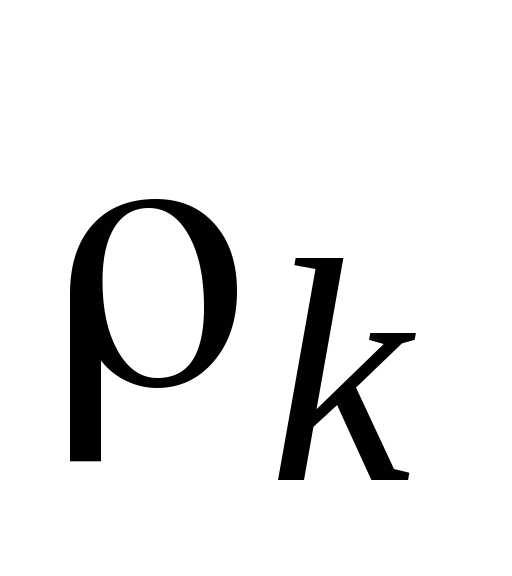 и добавляем к системе ограничений два ограничения (т. к. количество критериевK = 3, а количество ограничений равно K – 1) следующего вида:
и добавляем к системе ограничений два ограничения (т. к. количество критериевK = 3, а количество ограничений равно K – 1) следующего вида:
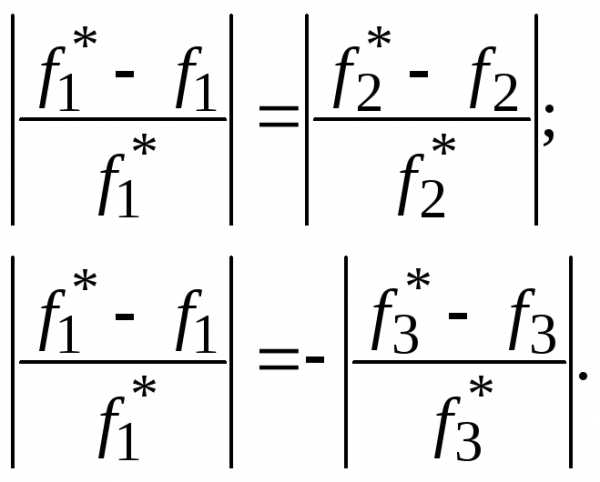
В первом полученном ограничении учтено, что два первых приравниваемых относительных отклонения 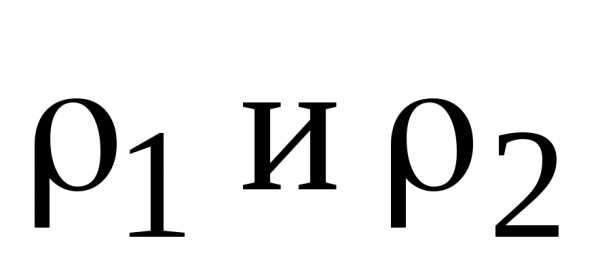 определены по максимизируемым критериям.
определены по максимизируемым критериям.
Во втором ограничении учтено, что третье приравниваемое относительное отклонение  определено по минимизируемому критерию, поэтому перед правой частью равенства поставлен знак минус.
определено по минимизируемому критерию, поэтому перед правой частью равенства поставлен знак минус.
Опустив знаки модуля и преобразовав эти ограничения, получим ограничения вида
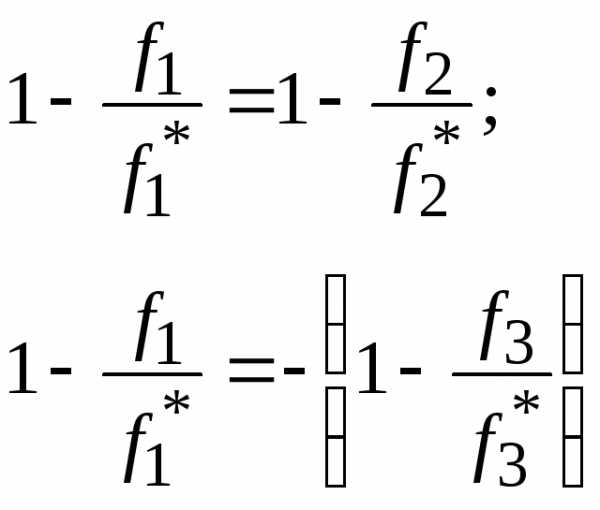 и далее
и далее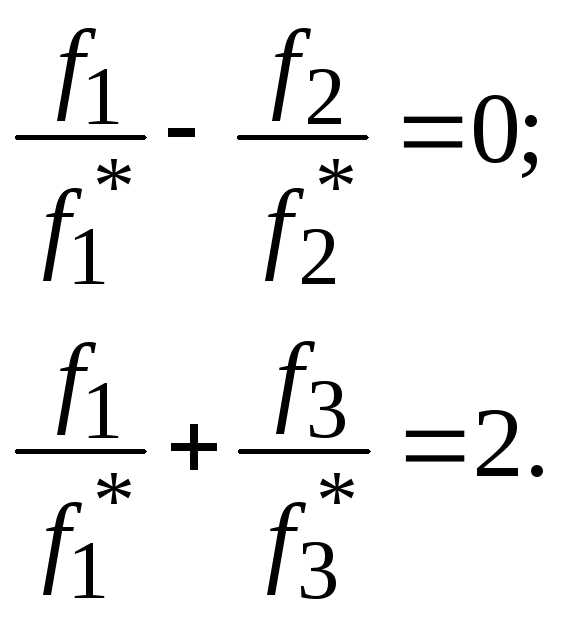
Целевая функция, записанная с учетом третьего критерия, будет иметь вид:
studfiles.net
Векторная оптимизация - Большая Энциклопедия Нефти и Газа, статья, страница 1
Векторная оптимизация
Cтраница 1
Векторная оптимизация предопределяет необходимость комплексного, системного подхода к перспективному планированию. [1]
Проблемы векторной оптимизации возникают не только при выборе оптимал-ьных траекторий движения, но и в задачах синтеза оптимальных управлений и оптимальных систем. В этих задачах используют методы скаляризации. [2]
Проблема векторной оптимизации в настоящее время занимает все большее место в практике расчета систем управления и в задачах принятия решений. При этом, если ранее задачи векторной оптимизации ставили в основном для статических моделей, то теперь они присутствуют и в динамических расчетах. Поскольку расчет даже однообъектных систем автоматического управления сложен и не укладывается в рамки аналитических методов, а использование процедур векторной оптимизации требует, как правило, применения методов математического программирования, то основное место в процессах проектирования систем занимают интерактивные вычислительные процедуры, обеспечивающие задачи расчета и моделирования. [3]
Задачи векторной оптимизации типичны для объектов, в которых протекает химическая реакция, когда наряду с целевым продуктом получается целая гамма побочных продуктов и возникает необходимость поиска компромиссного режима, обеспечивающего максимум выпуска целевого продукта и минимум - побочных. В настоящем параграфе осуществлена реализация алгоритма векторной оптимизации на примере моделей реакторов димеризации ацетилена и хлорирования бутадие1 на, в которых получается основной мономер для производства хлоро-преновых каучуков и латексов. [4]
При векторной оптимизации в целом ряде случаев возможно ограничиться определением оптимального варианта при помощи балльной оценки и посредством расчета конкретных результатов вариантов. [5]
Трудности сведения векторной оптимизации к скалярной приводят к попыткам упростить задачу в исходной постановке. Например, наиболее часто на практике все критерии, кроме основного, переводят в разряд ограничений и решают обычную однокритериальную задачу. Основная трудность такого подхода состоит в невозможности однозначного и обоснованного задания ограничений на неосновные критерии. [6]
В задачах векторной оптимизации принцип оптимальности определяет свойства оптимального решения и дает ответ на главный вопрос - в каком смысле оптимальное решение превосходит все остальные допустимые решения и дает правило поиска этого оптимального решения. [7]
Разработанная аксиоматика векторной оптимизации и построенные на ее основе алгоритмы решения векторных задач позволяют вести исследование всей структуры множества Парето. На первом этапе исследования структуры множества Парето используется аксиома равенства и равнозначности критериев, выведенный из нее принцип оптимальности и построенный на их основе алгоритм решения векторной задачи при равнозначных критериях. [8]
В задачах векторной оптимизации принцип оптимальности определяет свойства оптимального решения и дает ответ на главный вопрос - в каком смысле оптимальное решение превосходит все остальные допустимые решения и дает правило поиска этого оптимального решения. [9]
Разработанная аксиоматика векторной оптимизации и построенные на ее основе алгоритмы решения векторных задач позволяют вести исследование всей структуры множества Парето. На первом этапе исследования структуры множества Парето используется аксиома равенства и равнозначности критериев, выведенный из нее принцип оптимальности и построенный на их основе алгоритм решения векторной задачи при равнозначных критериях. [10]
Применяя метод векторной оптимизации к задаче поиска оптимальных параметров конденсатора и системы охлаждения, авторы ставили перед собой две цели: получить новую, заранее трудно предсказуемую информацию о возможных компромиссных решениях, удовлетворяющих одновременно нескольким противоречивым критериям качества, а также проверить эффективность самого метода и некоторых его модификаций в условиях данной задачи. [11]
В теории векторной оптимизации особое место занимает принцип компромисса, основанный на идее равномерности. На базе этого принципа работают минимаксные ( максиминные) критерии. [12]
В теории векторной оптимизации такие решения принято называть эффективными. [14]
Впервые проблема многокритериальной векторной оптимизации возникла у итальянского экономиста В. Парето при математическом исследовании товарного обмена. [15]
Страницы: 1 2 3 4
www.ngpedia.ru
Векторная оптимизация - Энциклопедия по экономике
Оптимизация денежных потоков по различным критериям. Свертки критериев эффективности инвестиций. Условная оптимизация. Ограничения на ресурсы и условия реализации. Векторная оптимизация. Оптимизация инвестиций в оценочную деятельность. Оптимальные портфели реальных инвестиций. Динамические портфели [c.75] В работе рассмотрены теоретико-методические вопросы учета экологического состояния территории муниципального образования при оценке недвижимости. Разработаны методические основы ранжирования территории по комплексному показателю качества окружающей среды посредством использования аппарата векторной оптимизации и теории нечетких множеств. Предложен механизм определения экологической составляющей в рыночной цене недвижимости. Выполнена практическая оценка степени загрязнения территории г. Уфы. Определена степень привлекательности территории с позиции качества окружающей среды селитебных зон и предложен авторский вариант развития муниципального образования г. Уфы с учетом экологической ситуации. [c.2]Ранжировать территории по обобщающему показа гелю состояния окружающей среды, выбрать вариант, оптимальный с точки зрения многих критериев, по мнению автора, целесообразно посредством использования аппарата векторной оптимизации и теории нечетких множеств. Оригинальный подход был разработан на кафедре математического моделирования Уфимского государственного нефтяного технического университета и [c.4]
На основе разработанной методики ранжирования территории по комплексному показателю качества окружающей среды с помощью аппарата векторной оптимизации и теории нечетких множеств, произведем оценку степени загрязнения территории г. Уфы. [c.28]
Данные задачи являются по существу задачами векторной оптимизации (часто такие задачи называются также и многокритериальными). [c.102]
Приведем формальную постановку задачи векторной оптимизации. [c.102]
Сложность задачи (1)-(2) обусловлена ее многокритериальным характером, и основная проблема заключается в выборе принципа оптимальности. В настоящее время существует достаточное число алгоритмов решения задач векторной оптимизации. В данной работе использован подход, базирующийся на основных положениях теории нечетких множеств, суть которого заключается в свертывании критериев в единый с помощью построения функций принадлежности специального вида. Каждой оцениваемой i -ой фирме i-l...m поставлены в соответствие группы финансовых показателей и каждому из [c.103]
Таким образом, в настоящее время разработаны мощные методы решения оптимизационных задач как для статических, так и для динамических систем. Эти методы интенсивно используются в экономико-математических исследованиях. В то же время массовое использование оптимизационных методов на практике выявило их определенную ограниченность, связанную с необходимостью заранее формулировать единственный критерий. Часто проблема соизмерения различных показателей и построения единственного критерия оказывается чрезвычайно сложной, во многих случаях — неразрешимой. Это привело к принципиально новому этапу в развитии методов оптимизации — появлению методов многокритериальной (векторной) оптимизации. [c.59]
Борисов В. II. Проблемы векторной оптимизации.— В сб. Исследование операции. Методологические аспекты.— М. Наука, 1972. [c.387]
Рассмотрим постановку задачи векторной оптимизации,, содержательно интерпретируемую и с точки зрения принятия плановых решений. [c.191]
В тех случаях, когда все локальные критерии /,, /,,..., / , с точки зрения ЛПР, имеют одинаковую степень важности, решение задачи векторной оптимизации осуществляется с использованием принципа равномерности, метода идеальной" точки, принципа справедливого компромисса, оптимальности по Парето. [c.193]
Векторная оптимизация — сложный вид оптимизации. Векторный оптимум определяется несколькими критериями, несводимы- [c.233]
Интегрированная оценка эффективности каждого варианта должна производиться в целом по плановому периоду либо методом приведенных затрат, либо методом балльно-индексной оценки 1. Последняя является предпочтительной во всех случаях, когда необходимо учесть значительное количество показателей векторной оптимизации. [c.234]
Векторная оптимизация предопределяет необходимость комплексного, системного подхода к перспективному планированию. Этот подход заключается в последовательности всех расчетов — от прогноза и анализа до завершающих показателей их результатов, в том числе таких важных, как степень удовлетворения потребностей народного хозяйства и быта, себестоимость продукции, эффективность капитальных вложений, производительность труда и др. [c.234]
Математически Г.к. принято формулировать в виде скалярной целевой функции (или соответствующей шкалы предпочтений), которая обобщенно выражает все многообразие целей общества, или в виде векторной функции, представляющей собой набор несводимых (частичных) целевых функций. Соответственно различаются скалярная оптимизация и векторная оптимизация. [c.63]
Термин "многокритериальные задачи" часто отождествляется с термином "задачи векторной оптимизации" однако прослеживается различие в последнем случае речь идет не о разнородных критериях системы, а о сопоставлении однородных критериев разных участников (см. рис. 0.7 к ст. "Оптимальность по Парето "). [c.199]
Полищук Л. И. Методы обобщенного градиента в диалоговых процедурах векторной оптимизации//Автоматика и телемеханика. 1981. № 5. [c.163]
Гороховик В. В. К проблеме векторной оптимизации. — Техническая кибернетика , 1972, № 6. [c.384]
Эта работа положила начало целому направлению в современной математике — аксиоматическим обоснованиям различных решений задач векторной оптимизации. [c.375]
Валовый продукт (в межотраслевом балансе) 84 ВАРИАНТНЫЕ ПРОГНОЗЫ 90 ВВОДНЫЕ УСТРОЙСТВА ЭВМ 146 ВЕКТОРНАЯ ОПТИМИЗАЦИЯ 116 [c.157]
Если потребляемые производственным элементом затраты являются взаимозаменяемыми, то один и тот же уровень выпуска продукции может быть достигнут при разных комбинациях уровней затрат. В этой ситуации необходимо дополнительное определение того, что мы понимали под минимальным уровнем нескольких видов затрат. Это проблема векторной оптимизации. Она аналогична проблеме, с которой пришлось столкнуться при определении производственной функции многопродуктового элемента. Принципы построения ряда критериев векторной оптимизации ( 2.4) пригодны и для этого случая. [c.45]
Машунин Ю.К. Методы и модели векторной оптимизации. -М Наука, 1986. -141 с. [c.54]
Очевидно также, что если функция f будет являться скалярной, то решение задачи (2) не вызовет особых затруднений. Однако, определить ОСБ, исходя из значения только одного критерия не представляется возможным, потому что приближение одних коэффициентов к оптимальному значению, может повлечь за собой резкое ухудшение коэффициентов другой группы. Поэтому решение в ЗОСБ необходимо принимать, учитывая значения всех введенных параметров (Кп, Кп,. .., К45Л причем желательным является выбор такой ОСБ, которой будут соответствовать наилучшие, то есть наиболее близкие к нормативным значениям, значения параметров (Кц, Кп,. ... IQs). Такие задачи относятся к многокритериальным задачам (задачам векторной оптимизации). [c.45]
Решение задач многокритериальной или векторной оптимизации осуществляется с использованием принципов выделения главного критерия, скаляризации вектора целевых функций, равномерности, идеальной" точки, квазиоптимизации локальных критериев методом последовательных уступок, справедливого компромисса, оптимальности по Парето и ряда других. [c.192]
Модели и методы векторной оптимизации / С. В. Емельянов, В. И. Борисов, А. А. Малевич, А. М. Черкашин.//Техническая кибернетика. Т. 5. - М. Наука, 1973. - С. 386-448. [c.220]
ВЕКТОРНАЯ ОПТИМИЗАЦИЯ [ve tor optimization] — комплекс методов решения задач математического программирования, в которых критерий оптимальности представляет собой вектор, компонентами которого являются, в свою очередь, несводимые друг к другу скалярные критерии оптимальности подсистем, входящих в данную систему (напр., критерии роста благосостояния разных социальных групп в социально-экономическом планировании). При этом задача оптимизации существенно видоизменяется по сравнению с теми задачами, которые рассматриваются в большинстве статей словаря. В них она сводится к тому, чтобы, зная условия и ограничения, найти такой план, который бы максимизировал или минимизировал единственный заданный критериальный показатель. Это называется "скалярная оптимизация". [c.43]
СКАЛЯРНАЯ ОПТИМИЗАЦИЯ [s alar optimization] — совокупность методов решения задач математического программирования, целевая функция которых представляет собой скаляр. Большинство задач, рассматриваемых в словаре (см. Линейное программирование, Нелинейное программирование, Дискретное программирование и др.), принадлежит к этому классу. Ср. Векторная оптимизация, Многокритериальная оптимизация. [c.330]
СУБОПТИМАЛЬНОЕ РЕШЕНИЕ [suboptimal solution] —решение, оптимальное по одной из частичных целевых функций (в модели векторной оптимизации). [c.352]
ЭФФЕКТИВНАЯ ТОЧКА (ЭФФЕКТИВНЫЙ ПЛАН) [effe tive point] в задачах векторной оптимизации — допустимый план, который не может быть далее улучшен с точки зрения какого-либо одного критерия без того, чтобы при этом он не был ухудшен относительно другого или других критериев (см. Оптимальность по Парето) это понятие, таким образом, аналогично понятию максимума (экстремума) в задачах скалярной оптимизации. [c.429]
Многокритериальность проявляется при наличии трудносоизмеримых между собой критериев оптимальности. Например, при оптимизации плана нефтегазодобывающего производственного объединения можно рассматривать в качестве критериев оптимальности максимум прибыли, минимум эксплуатационных затрат, максимум разведочного и эксплуатационного бурения, объемов добычи нефти и газа и др. Для того чтобы на базе всех этих критериев построить единый критерий, нужно их все соизмерить, т. е. дать им веса . А это чаще, всего однозначно сделать нельзя. В этом случае следует использовать методы векторной оптимизации, в которых учитывают и неформальные суждения лиц, принимающих решение (ЛПР). ЛПР в процессе расчетов могут менять веса или устанавли- [c.117]
Изучение многообразных аспектов проблемы принятия решений в условяих неопределенности осуществляется, с одной стороны, такими науками, как психология, социология, экономика, логика, и с другой стороны, комплексом дисциплин, входящих в современную теорию управления с использованием ЭВМ (кибернетикой и относящимися к ней научными направлениями, такими, как теория игр, исследование операций, теория статистических решений, теория полезности, векторная оптимизация и др.). [c.167]
Производственная функция многопродуктового производственного элемента. Приведенное в 2.2 определение задавало производственную функцию элемента как максимальный выпуск продукции при каждом допустимом уровне затрат и применимо только для однопродук-тового элемента. Если производственный элемент выпускает несколько видов продукции, то использование такого определения производственной функции требует доопределения того, что мы понимаем под максимальным выпуском в случае, когда видов продукции несколько. Другими словами, нужен критерий, определяющий максимальный выпуск продукции нескольких видов. Это проблема векторной оптимизации. Поскольку однозначного ее решения в общем случае не существует, то можно предложить ряд такого рода критериев. [c.41]
Концепция П. о. признаёт необходимость единого (глобального) критерия оптимальности нар.-хоз. планов, т. к. отсутствие его означало бы принципиальную несравнимость целей, программ, вариантов планов и, следовательно, невозможность обоснованного выбора плановых решений. Такой критерий должен быть концентрированным выражением действия осн. эконо-мич. закона социализма. Однако в конструктивном и практич. отношении имеется мн. нерешённых вопросов. Разработан ряд теоретпч. подходов к проблеме критерия оптимальности, основанных на схемах как скалярной, так и векторной оптимизации. [c.252]
economy-ru.info
Проблема - векторная оптимизация - Большая Энциклопедия Нефти и Газа, статья, страница 1
Проблема - векторная оптимизация
Cтраница 1
Проблема векторной оптимизации в настоящее время занимает все большее место в практике расчета систем управления и в задачах принятия решений. При этом, если ранее задачи векторной оптимизации ставили в основном для статических моделей, то теперь они присутствуют и в динамических расчетах. Поскольку расчет даже однообъектных систем автоматического управления сложен и не укладывается в рамки аналитических методов, а использование процедур векторной оптимизации требует, как правило, применения методов математического программирования, то основное место в процессах проектирования систем занимают интерактивные вычислительные процедуры, обеспечивающие задачи расчета и моделирования. [1]
Проблемы векторной оптимизации возникают не только при выборе оптимал-ьных траекторий движения, но и в задачах синтеза оптимальных управлений и оптимальных систем. В этих задачах используют методы скаляризации. [2]
Впервые проблема многокритериальной векторной оптимизации возникла у итальянского экономиста В. Парето при математическом исследовании товарного обмена. [3]
Приведенный перечень показывает, что проблемы векторной оптимизации в той или иной форме приходится решать для подавляющего большинства современных объектов управления. [4]
Единственным объективным фактором, характеризующим проблему векторной оптимизации ( в рамках того субъективизма, который связан с выбором самих локальных критериев), является наличие области Парето в пространстве критериев и существование паре-то-оптимальных решений. Область Парето ( область компромиссов) ограничивает возможный выбор проектных решений. Для выбора ПКР из множества парето-оптимальных решений необходим ввод в рассмотрение дополнительных критериев. [5]
Становится очевидным, что подход к проблеме векторной оптимизации должен базироваться на идее приближения к решению, определяющему систему с идеаль - 97 ными характеристиками. [6]
В предыдущих разделах были рассмотрены возможности решения проблем векторной оптимизации в иерархических структурах производственного типа. В конечном счете решение поставленной проблемы сведено к скалярной оптимизации в одноуровневых системах. Хотя такая оптимизация существенно проще оптимизации векторной, трудности ее реализации ( в основном вычислительные) полностью еще не преодолены. В данном и последующих разделах будут рассмотрены возможности и эффективность использования для этих целей принципа сложности. [7]
Выделение области компромисса - первый, но не всегда обязательный шаг на пути решения проблемы векторной оптимизации. Он целесообразен лишь в ситуациях нестрогой противоречивости критериев, например при принятии решений первых четырех групп из табл. 1 предыдущего параграфа. Принятие решений на синтез или модернизацию СОИС связано со строгой противоречивостью критериев, описывающих прогнозируемую эффективность СОИС и расходы ресурсов на создание или модернизацию СОИС. [8]
Проблему решения оптимизационных задач с учетом множества показателей эффективности называют проблемой решения многокритериальных задач или проблемой векторной оптимизации. Очевидно, что эта проблема не существовала бы, если все отдельные показатели ( локальные критерии) были бы выражены в одних и тех же единицах измерения и тем самым сведены к единому ( глобальному) критерию, кроме того, если ( даже не сводимые один к другому) локальные критерии были бы непротиворечивы, т.е. если изменение параметров системы управления приводило бы к одновременному улучшению ( или одновременному ухудшению) всех локальных критериев. Однако в задачах векторной оптимизации всегда присутствуют противоречивые критерии, когда улучшение одного приводит к ухудшению другого и наоборот. [9]
Все перечисленные позиции, разумеется, остаются существенными и в будущем. Это становится особенно понятным при продолжающемся усложнении задач управления. В этой связи наиболее принципиальной трудностью является проблема многокритериального оценивания эффективности решений, проблема векторной оптимизации. Здесь алгоритмы с прогнозированием становятся незаменимыми. [10]
В предыдущих параграфах были рассмотрены задачи оптимального управления в условиях неопределенности, связанной со случайным характером воздействий на систему управления. В теории и практике автоматического управления все чаще ставятся задачи, связанные с неопределенностью в выборе критериев. Это происходит, когда оптимизацию целесообразно проводить по нескольким критериям и нет однозначного правила ( указания) на комбинирование из этих критериев одного обобщенного. Такие задачи относятся к проблеме векторной оптимизации. [11]
При создании современных систем управления проектировщикам чрезвычайно редко приходиться иметь дело с системами, работоспособность и качество которых можно оценить одним-единственным показателем. Чаще всего существует целое множество таких показателей ( критериев), каждый из которых характеризует тот или иной аспект функционирования системы управления. Проблему решения задач оптимизации с учетом множества показателей эффективности называют проблемой решения многокритериальных задач или проблемой векторной оптимизации. Очевидно, что этой проблемы не существовало бы, если все отдельные показатели ( локальные критерии) могли бы быть выражены в одних единицах измерения ( например, в рублях или тоннах) и тем самым сведены к единому глобальному критерию. Однако в задачах векторной оптимизации всегда присутствуют противоречивые критерии, когда улучшение одного приводит к ухудшению другого и наоборот. [12]
Страницы: 1
www.ngpedia.ru