ГлавнаяОптимизацияОптимизация математика

Оптимизация (математика). Оптимизация математика


Оптимизация (математика) | Virtual Laboratory Wiki

У этого термина существуют и другие значения, см. Оптимизация.

Задачей оптимизации в математике является нахождение экстремума (минимума или максимума) действительной функции в некоторой области. Как правило, рассматриваются области принадлежащие $ \mathbb{R}^n $ заданные набором равенств и неравенств.

    Постановка задачи оптимизации Править

    Для того, чтобы корректно поставить задачу оптимизации необходимо задать:

    1. Допустимое множество — множество $ \mathbb{X}=\{\vec{x}:\;g_i(\vec{x})\leq 0,\;i=1,\ldots,n_1;\;g_j(\vec{x})=0,\;j=1,\ldots,n_2;\;g_k(\vec{x})\geq 0,\;k=1,\dots,n_3;\;m=n_1+n_2+n_3 \} \subset \mathbb{R}^n(\mathbb{C}^n) $;
    2. Целевую функцию — отображение $ f:\;\mathbb{X}\to\mathbb{R} $;
    3. Критерий поиска (max или min).

    Тогда решить задачу $ f(x)\to \min_{\vec{x}\in\mathrm{X}} $ означает одно из:

    1. Показать, что $ \mathbb{X}=\varnothing $.
    2. Показать, что целевая функция $ f(\vec{x}) $ не ограничена.
    3. Найти $ \vec{x}^*\in\mathbb{X}:\;f(\vec{x}^*)=\min_{\vec{x}\in\mathbb{X}}f(\vec{x}) $.
    4. Если $ \nexists \vec{x}^* $, то найти $ \inf_{\vec{x}\in\mathbb{X}}f(\vec{x}) $.

    Если минимизируемая функция не является выпуклой, то часто ограничиваются поиском локальных минимумов и максимумов: точек $ x_0 $ таких, что всюду в некоторой их окрестности $ f(x)\ge f(x_0) $ для минимума и $ f(x)\le f(x_0) $ для максимума.

    Если допустимое множество $ \mathbb{X}=\mathbb{R}^n $, то такая задача называется задачей безусловной оптимизации, в противном случае — задачей условной оптимизации.

    Классификация методов оптимизации Править

    Методы, по средством которых решают задачи оптимизации, подразделяются на виды, соответствующие задачам, к которым они применяются:

    • Локальные методы (задача оптимизации унимодальной целевой функции).
    • Глобальные методы (имеют дело с многоэкстремальными целевыми функциями. При глобальном поиске основной задачей является выявление тенденций глобального поведения целевой функции.).

    Существующие в настоящее время методы поиска можно разбить на три большие группы:

    1) детерминированные,

    2) случайные,

    3) комбинированные.

    Некоторые детерминированные методы:

    • Задачи оптимизации, в которых целевая функция $ f(\vec{x}) $ и ограничения $ g_i(\vec{x}),\; i=1,\ldots,m $ являются линейными функциями, разрешаются так называемыми методами линейного программирования.
    • В противном случае имеют дело с задачей нелинейного программирования и применяют соответствующие методы. В свою очередь из них выделяют две частные задачи:

    Помимо того, оптимизационные методы делятся на следующие группы:

    Также они разделяются по критерию размерности допустимого множества на методы одномерной оптимизации и методы многомерной оптимизации.

    1. Акулич И.Л. Математическое программирование в примерах и задачах: Учеб. пособие для студентов эконом. пец. вузов. — М.: Высш. шк., 1986.
    1. Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. Пер. с англ. — М.: Мир, 1985.
    1. Коршунов Ю.М., Коршунов Ю.М. Математические основы кибернетики. — М.: Энергоатомиздат, 1972.
    1. Максимов Ю.А.,Филлиповская Е.А. Алгоритмы решения задач нелинейного программирования. — М.: МИФИ, 1982.
    1. Максимов Ю.А. Алгоритмы линейного и дискретного программирования. — М.: МИФИ, 1980.
    1. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М.: Наука, 1970. — С. 575-576.
    1. Жиглявский А.А., Жилинкас А.Г. Методы поиска глобального экстремума. — М.: Наука, Физматлит, 1991.
    1. Растригин Л.А. Статистические методы поиска. — М.: 1968.
    1. Абакаров А.Ш., Сушков Ю.А. Статистическое исследование одного алгоритма глобальной оптимизации. — Труды ФОРА, 2004.

    Глобальная оптимизация, принятие решений — Программные системы поддержки принятия оптимальных решений. Глобальные алгоримы.

    ru.vlab.wikia.com

    Оптимизация (математика) — Википедия

    Материал из Википедии — свободной энциклопедии

    У этого термина существуют и другие значения, см. Оптимизация.

    Оптимизация — в математике, информатике и исследовании операций задача нахождения экстремума (минимума или максимума) целевой функции в некоторой области конечномерного векторного пространства, ограниченной набором линейных и/или нелинейных равенств и/или неравенств.

    Теорию и методы решения задачи оптимизации изучает математическое программирование.

    Математическое программирование - это область математики, разрабатывающая теорию, численные методы решения многомерных задач с ограничениями. В отличие от классической математики, математическое программирование занимается математическими методами решения задач нахождения наилучших вариантов из всех возможных.[1]

    В процессе проектирования ставится обычно задача определения наилучших, в некотором смысле, структуры или значений параметров объектов. Такая задача называется оптимизационной. Если оптимизация связана с расчётом оптимальных значений параметров при заданной структуре объекта, то она называется параметрической оптимизацией. Задача выбора оптимальной структуры является структурной оптимизацией.

    Стандартная математическая задача оптимизации формулируется таким образом. Среди элементов χ, образующих множества Χ, найти такой элемент χ*, который доставляет минимальное значение f(χ*) заданной функции f(χ). Для того, чтобы корректно поставить задачу оптимизации, необходимо задать:

    1. Допустимое множество — множество ;
    2. Целевую функцию — отображение ;
    3. Критерий поиска (max или min).

    Тогда решить задачу означает одно из:

    1. Показать, что .
    2. Показать, что целевая функция не ограничена снизу.
    3. Найти .
    4. Если , то найти

    arquivo.pt

    Оптимизация (математика) Википедия

    У этого термина существуют и другие значения, см. Оптимизация.

    Оптимизация — в математике, информатике и исследовании операций задача нахождения экстремума (минимума или максимума) целевой функции в некоторой области конечномерного векторного пространства, ограниченной набором линейных и/или нелинейных равенств и/или неравенств.

    Граф параболоида описанного функцией z = f(x, y) = −(x² + y²) + 4. Глобальный максимум от (x, y, z) = (0, 0, 4) обозначен синей точкой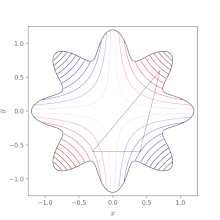 Поиск минимума Нелдера-Мида Функции оптимизации. Симплексные вершины упорядочиваются по их значению, при этом 1 имеет наименьшее (лучшее) значение.

    Теорию и методы решения задачи оптимизации изучает математическое программирование.

    Математическое программирование — это область математики, разрабатывающая теорию, численные методы решения многомерных задач с ограничениями. В отличие от классической математики, математическое программирование занимается математическими методами решения задач нахождения наилучших вариантов из всех возможных.[1]

    Постановка задачи оптимизации[ | код]

    В процессе проектирования ставится обычно задача определения наилучших, в некотором смысле, структуры или значений параметров объектов. Такая задача называется оптимизационной. Если оптимизация связана с расчётом оптимальных значений параметров при заданной структуре объекта, то она называется параметрической оптимизацией. Задача выбора оптимальной структуры является структурной оптимизацией.

    Стандартная математическая задача оптимизации формулируется таким образом. Среди элементов χ, образующих множества Χ, найти такой элемент χ*, который доставляет минимальное значение f(χ*) заданной функции f(χ). Для того, чтобы корректно поставить задачу оптимизации, необходимо задать:

    1. Допустимое множество — множество X={x→|gi(x→)≤0,i=1,…,m}⊂Rn{\displaystyle \mathbb {X} =\{{\vec {x}}|\;g_{i}({\vec {x}})\leq 0,\;i=1,\ldots ,m\}\subset \mathbb {R} ^{n}};
    2. Целевую функцию — отображение f:X→R{\displaystyle f:\;\mathbb {X} \to \mathbb {R} };
    3. Критерий поиска (max или min).

    Тогда решить задачу f(x)→minx→∈X{\displaystyle f(x)\to \min _{{\vec {x}}\in \mathrm {X} }} означает одно из:

    1. Показать, что X=∅{\displaystyle \mathbb {X} =\varnothing }.
    2. Показать, что целевая функция

    ru-wiki.ru

    Оптимизация (математика) - Википедия

    Материал из Википедии — свободной энциклопедии

    У этого термина существуют и другие значения, см. Оптимизация.

    Оптимизация — в математике, информатике и исследовании операций задача нахождения экстремума (минимума или максимума) целевой функции в некоторой области конечномерного векторного пространства, ограниченной набором линейных и/или нелинейных равенств и/или неравенств.

    Теорию и методы решения задачи оптимизации изучает математическое программирование.

    Математическое программирование — это область математики, разрабатывающая теорию, численные методы решения многомерных задач с ограничениями. В отличие от классической математики, математическое программирование занимается математическими методами решения задач нахождения наилучших вариантов из всех возможных.[1]

    Постановка задачи оптимизации[ | ]

    В процессе проектирования ставится обычно задача определения наилучших, в некотором смысле, структуры или значений параметров объектов. Такая задача называется оптимизационной. Если оптимизация связана с расчётом оптимальных значений параметров при заданной структуре объекта, то она называется параметрической оптимизацией. Задача выбора оптимальной структуры является структурной оптимизацией.

    Стандартная математическая задача оптимизации формулируется таким образом. Среди элементов χ, образующих множества Χ, найти такой элемент χ*, который доставляет минимальное значение f(χ*) заданной функции f(χ). Для того, чтобы корректно поставить задачу оптимизации, необходимо задать:

    1. Допустимое множество — множество X={x→|gi(x→)≤0,i=1,…,m}⊂Rn{\displaystyle \mathbb {X} =\{{\vec {x}}|\;g_{i}({\vec {x}})\leq 0,\;i=1,\ldots ,m\}\subset \mathbb {R} ^{n}};
    2. Целевую функцию — отображение f:X→R{\displaystyle f:\;\mathbb {X} \to \mathbb {R} };
    3. Критерий поиска (max или min).

    Тогда решить задачу f(x)→minx→∈X{\displaystyle f(x)\to \min _{{\vec {x}}\in \mathrm {X} }} означает одно из:

    1. Показать, что X=∅{\displaystyle \mathbb {X} =\varnothing }.
    2. Показать, что целевая функция f(x→){\displaystyle f({\vec {x}})} не ограничена снизу.
    3. Найти x→∗∈X:f(x→∗)=minx→∈Xf(x→){\displaystyle {\vec {x}}^{*}\in \mathbb {X} :\;f({\vec {x}}^{*})=\min _{{\vec {x}}\in \mathbb {X} }f({\vec {x}})}.
    4. Если ∄x→∗{\displaystyle \nexists {\vec {x}}^{*}}, то найти

    encyclopaedia.bid

    Оптимизация (математика) Википедия

    У этого термина существуют и другие значения, см. Оптимизация.

    Оптимизация — в математике, информатике и исследовании операций задача нахождения экстремума (минимума или максимума) целевой функции в некоторой области конечномерного векторного пространства, ограниченной набором линейных и/или нелинейных равенств и/или неравенств.

    Граф параболоида описанного функцией z = f(x, y) = −(x² + y²) + 4. Глобальный максимум от (x, y, z) = (0, 0, 4) обозначен синей точкой Поиск минимума Нелдера-Мида Функции оптимизации. Симплексные вершины упорядочиваются по их значению, при этом 1 имеет наименьшее (лучшее) значение.

    Теорию и методы решения задачи оптимизации изучает математическое программирование.

    Математическое программирование — это область математики, разрабатывающая теорию, численные методы решения многомерных задач с ограничениями. В отличие от классической математики, математическое программирование занимается математическими методами решения задач нахождения наилучших вариантов из всех возможных.[1]

    В процессе проектирования ставится обычно задача определения наилучших, в некотором смысле, структуры или значений параметров объектов. Такая задача называется оптимизационной. Если оптимизация связана с расчётом оптимальных значений параметров при заданной структуре объекта, то она называется параметрической оптимизацией. Задача выбора оптимальной структуры является структурной оптимизацией.

    Стандартная математическая задача оптимизации формулируется таким образом. Среди элементов χ, образующих множества Χ, найти такой элемент χ*, который доставляет минимальное значение f(χ*) заданной функции f(χ). Для того, чтобы корректно поставить задачу оптимизации, необходимо задать:

    1. Допустимое множество — множество X={x→|gi(x→)≤0,i=1,…,m}⊂Rn{\displaystyle \mathbb {X} =\{{\vec {x}}|\;g_{i}({\vec {x}})\leq 0,\;i=1,\ldots ,m\}\subset \mathbb {R} ^{n}};
    2. Целевую функцию — отображение f:X→R{\displaystyle f:\;\mathbb {X} \to \mathbb {R} };
    3. Критерий поиска (max или min).

    Тогда решить задачу f(x)→minx→∈X{\displaystyle f(x)\to \min _{{\vec {x}}\in \mathrm {X} }} означает одно из:

    1. Показать, что X=∅{\displaystyle \mathbb {X} =\varnothing }.
    2. Показать, что целевая функция f(x→){\displaystyle f({\vec {x}})} не ограничена снизу.
    3. Найти

    ruwikiorg.ru

    Оптимизация (математика) - это... Что такое Оптимизация (математика)?

     Оптимизация (математика)

    Optimizacija (matematika)

    Русско-словенский словарь. 2008.

    • Оптимизация (математика)
    • оптимизация установок

    Смотреть что такое "Оптимизация (математика)" в других словарях:

    • Оптимизация (математика) — У этого термина существуют и другие значения, см. Оптимизация. Оптимизация  в математике, информатике и исследовании операций задача нахождения экстремума (минимума или максимума) целевой функции в некоторой области конечномерного векторного …   Википедия

    • Оптимизация — Оптимизация: В Викисловаре есть статья «оптимизация» Оптимизация (математика)  нахождения …   Википедия

    • Вычислительная математика — Имеется викиучебник по теме «Вычислительная математика» …   Википедия

    • Прикладная математика — область математики, рассматривающая применение математических методов, алгоритмов в других областях науки и практики. Примерами такого применения будут: численные методы, математическая физика, линейное программирование, оптимизация и… …   Википедия

    • Финансовая математика — Финансовая математика  раздел прикладной математики, имеющий дело с математическими задачами, связанными с финансовыми расчётами. В финансовой математике любой финансовый инструмент рассматривается с точки зрения генерируемого этим… …   Википедия

    • Комбинаторная оптимизация — – область теории оптимизации в прикладной математике, связанная с исследованием операций, теорией алгоритмов и теорией вычислительной сложности. В комбинаторной оптимизации используются как математические подходы, так и методы искусственного… …   Википедия

    • Оптимизатор — Оптимизация: Оптимизация (математика)  нахождение оптимума (максимума или минимума) функции при выполнении некоторых ограничений Оптимизация (информатика)  процесс модификации системы для улучшения её эффективности. Оптимизация компилятора … …   Википедия

    • Критерий оптимальности — Критерий оптимальности (критерий оптимизации)  характерный показатель решения задачи, по значению которого оценивается оптимальность найденного решения, то есть максимальное удовлетворение поставленным требованиям. В одной задаче может… …   Википедия

    • Оптимальное управление — Оптимальное управление  это задача проектирования системы, обеспечивающей для заданного объекта управления или процесса закон управления или управляющую последовательность воздействий, обеспечивающих максимум или минимум заданной… …   Википедия

    • Скалярное ранжирование — Скалярное ранжирование  подход к решению многокритериальных задач принятия решений, когда множество показателей качества (критериев оптимальности) сводятся в один с помощью функции скаляризации  целевой функции задачи принятия решения.… …   Википедия

    • Оптимальная система — Под оптимальной системой понимается наилучшая в известном смысле система. Для того, чтобы среди возможных вариантов системы найти наилучший (оптимальный), необходим некоторый критерий, характеризующий эффективность достижения цели управления.… …   Википедия

    Книги

    • Оптимизация. Теория, примеры, задачи. Учебное пособие, Галеев Э.М.. Настоящая книга посвящена важнейшим проблемам оптимизации; в ее основе лежат курсы и спецкурсы по теории оптимизации, прочитанные автором на механико-математическом факультете МГУ.… Подробнее  Купить за 1141 грн (только Украина)
    • Оптимизация. Теория, примеры, задачи, Галеев Э.М.. Настоящая книга посвящена важнейшим проблемам оптимизации; в ее основе лежат курсы и спецкурсы по теории оптимизации, прочитанные автором на механико-математическом факультете МГУ.… Подробнее  Купить за 910 руб
    • Математика для экономистов на базе Mathcad, Черняк Аркадий Александрович, Черняк Жанна Альбертовна, Василец Сергей Иванович. С учетом внедрения систем компьютерной математики и различий в уровне исходной подготовки студентов материал второго издания излагается на трех уровнях, дополняющих друг друга. Описание всех… Подробнее  Купить за 833 руб
    Другие книги по запросу «Оптимизация (математика)» >>

    russian_slovenian.academic.ru

    Оптимизация (математика) - это... Что такое Оптимизация (математика)?

     Оптимизация (математика)

    Optimizacija (matematika)

    Русско-словенский словарь. 2008.

    • Оптика
    • Оптимизация (математика)

    Смотреть что такое "Оптимизация (математика)" в других словарях:

    • Оптимизация (математика) — У этого термина существуют и другие значения, см. Оптимизация. Оптимизация  в математике, информатике и исследовании операций задача нахождения экстремума (минимума или максимума) целевой функции в некоторой области конечномерного векторного …   Википедия

    • Оптимизация — Оптимизация: В Викисловаре есть статья «оптимизация» Оптимизация (математика)  нахождения …   Википедия

    • Вычислительная математика — Имеется викиучебник по теме «Вычислительная математика» …   Википедия

    • Прикладная математика — область математики, рассматривающая применение математических методов, алгоритмов в других областях науки и практики. Примерами такого применения будут: численные методы, математическая физика, линейное программирование, оптимизация и… …   Википедия

    • Финансовая математика — Финансовая математика  раздел прикладной математики, имеющий дело с математическими задачами, связанными с финансовыми расчётами. В финансовой математике любой финансовый инструмент рассматривается с точки зрения генерируемого этим… …   Википедия

    • Комбинаторная оптимизация — – область теории оптимизации в прикладной математике, связанная с исследованием операций, теорией алгоритмов и теорией вычислительной сложности. В комбинаторной оптимизации используются как математические подходы, так и методы искусственного… …   Википедия

    • Оптимизатор — Оптимизация: Оптимизация (математика)  нахождение оптимума (максимума или минимума) функции при выполнении некоторых ограничений Оптимизация (информатика)  процесс модификации системы для улучшения её эффективности. Оптимизация компилятора … …   Википедия

    • Критерий оптимальности — Критерий оптимальности (критерий оптимизации)  характерный показатель решения задачи, по значению которого оценивается оптимальность найденного решения, то есть максимальное удовлетворение поставленным требованиям. В одной задаче может… …   Википедия

    • Оптимальное управление — Оптимальное управление  это задача проектирования системы, обеспечивающей для заданного объекта управления или процесса закон управления или управляющую последовательность воздействий, обеспечивающих максимум или минимум заданной… …   Википедия

    • Скалярное ранжирование — Скалярное ранжирование  подход к решению многокритериальных задач принятия решений, когда множество показателей качества (критериев оптимальности) сводятся в один с помощью функции скаляризации  целевой функции задачи принятия решения.… …   Википедия

    • Оптимальная система — Под оптимальной системой понимается наилучшая в известном смысле система. Для того, чтобы среди возможных вариантов системы найти наилучший (оптимальный), необходим некоторый критерий, характеризующий эффективность достижения цели управления.… …   Википедия

    Книги

    • Оптимизация. Теория, примеры, задачи. Учебное пособие, Галеев Э.М.. Настоящая книга посвящена важнейшим проблемам оптимизации; в ее основе лежат курсы и спецкурсы по теории оптимизации, прочитанные автором на механико-математическом факультете МГУ.… Подробнее  Купить за 1141 грн (только Украина)
    • Оптимизация. Теория, примеры, задачи, Галеев Э.М.. Настоящая книга посвящена важнейшим проблемам оптимизации; в ее основе лежат курсы и спецкурсы по теории оптимизации, прочитанные автором на механико-математическом факультете МГУ.… Подробнее  Купить за 910 руб
    • Математика для экономистов на базе Mathcad, Черняк Аркадий Александрович, Черняк Жанна Альбертовна, Василец Сергей Иванович. С учетом внедрения систем компьютерной математики и различий в уровне исходной подготовки студентов материал второго издания излагается на трех уровнях, дополняющих друг друга. Описание всех… Подробнее  Купить за 833 руб
    Другие книги по запросу «Оптимизация (математика)» >>

    russian_slovenian.academic.ru

Prostoy-Site | Все права защищены © 2018 | Карта сайта