Разбор примера задачи нелинейной оптимизации. Нелинейная оптимизация
Разбор примера задачи нелинейной оптимизации
Решим и проанализируем описанную выше ситуацию принятия решения для директора лесозаготовительного комбината.
Анализ будем проводить только с учетом переменных расходов. Как следует из общей теории оптимизации, постоянное слагаемое не оказывает влияние на оптимальный план действий, изменяя только значение целевой функции.
Как видно из данных примера, весь анализ можно провести в терминах количества рабочих. Обозначим через 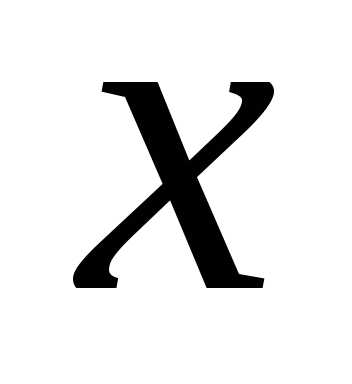 число рабочих на предприятии. Так как мы не можем уволить более 30 человек из имеющихся 70, то переменная
число рабочих на предприятии. Так как мы не можем уволить более 30 человек из имеющихся 70, то переменная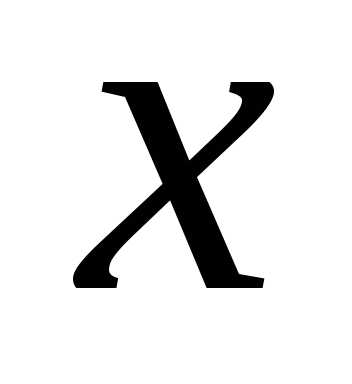 ограничена снизу:
ограничена снизу: .
.
Выпуск продукции пропорционален численности и равен 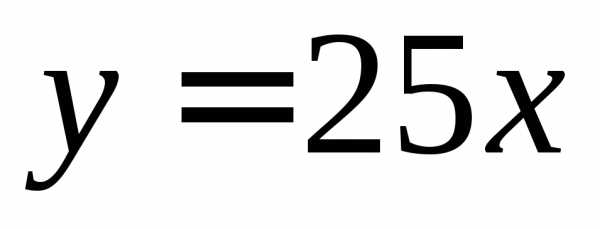 м3 в мес. Доход от продажи в месяц тогда равен:
м3 в мес. Доход от продажи в месяц тогда равен:
Если возможную субсидию при 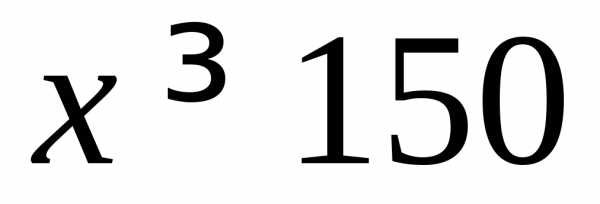 учесть в доходной части, то общую функцию месячного дохода можно записать так:
учесть в доходной части, то общую функцию месячного дохода можно записать так:
(3)
Если не нанимать новых сотрудников, то будет выполняться условие  , а месячные расходы равны:
, а месячные расходы равны:
.
Если нанять новых рабочих, то 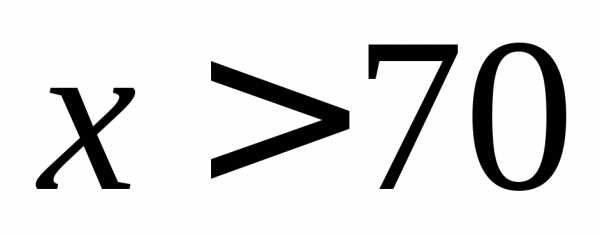 . Из этого количества рабочих 70 будут «старых», а
. Из этого количества рабочих 70 будут «старых», а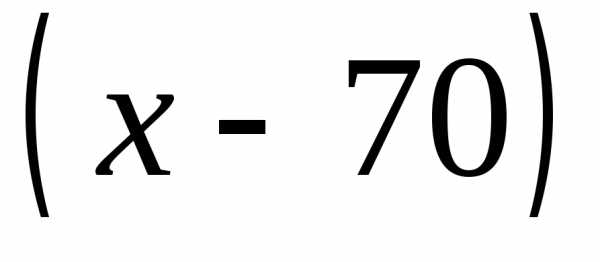 – «новых». Тогда месячные расходы будут складываться из затрат на «старых» по 80 тыс. руб. на человека и затрат на новых потыс. руб. на человека. Суммарные затраты составят:
– «новых». Тогда месячные расходы будут складываться из затрат на «старых» по 80 тыс. руб. на человека и затрат на новых потыс. руб. на человека. Суммарные затраты составят:
.
В итоге общую функцию месячных затрат можно записать в виде:
(4)
Прибыль комбината (без учета постоянных расходов) равна разнице между доходами (3) и переменными расходами (4) и запишется в виде:
(5)
Таким образом, математически задача формулируется так: найти 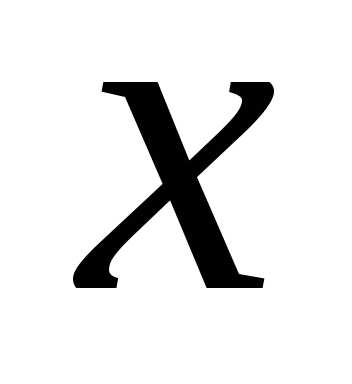
Очевидно, функция (5) меняется непропорционально искомой переменной 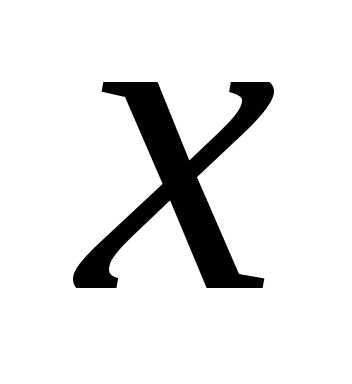 и задача является нелинейной.
и задача является нелинейной.
Пройдем для этой задачи все пункты алгоритма поиска глобального экстремума.
1) Определим градиент функции. В данном случае функции одной переменной градиент совпадает с производной. Если функция задана разными выражениями на разных интервалах, то нужно просто взять производные для каждого интервала. Они будут справедливы при строгом выполнении ограничивающих интервалы неравенств:
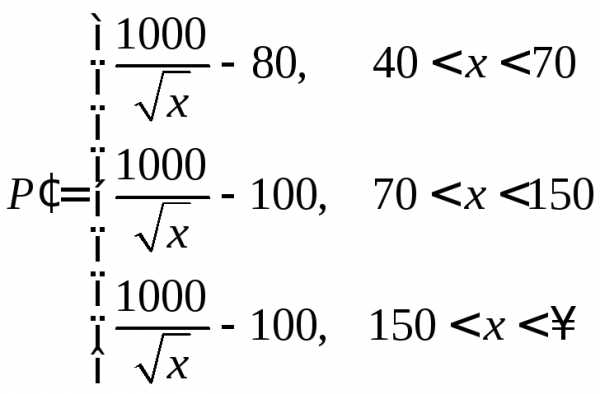 (6)
(6)
Как видно из выражения (6), производные на втором и третьем интервалах совпадают, но между ними при 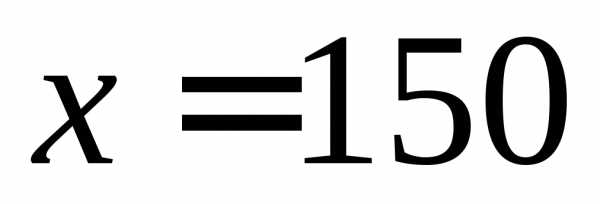 производная не существует, так как функция терпит разрыв.
производная не существует, так как функция терпит разрыв.
2) Определим точки, где производная равна нулю. Для этого определим все 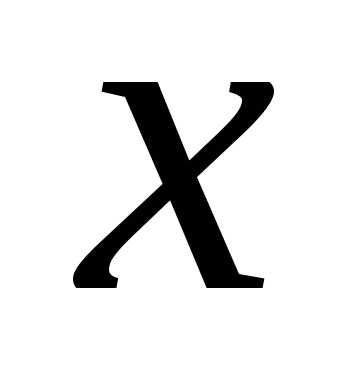 , удовлетворяющие равенствам:
, удовлетворяющие равенствам:
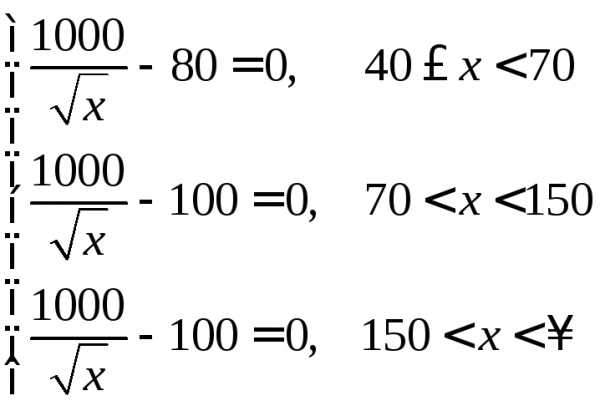
Рассмотрим интервал . На нем имеем уравнение:
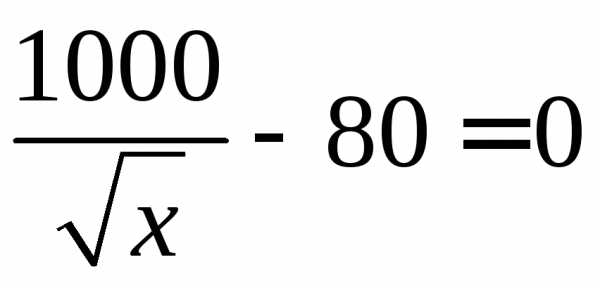 .
.
Решая уравнение, находим
.
Однако данное значение не попадает в интервал: . Значит на указанном интервале нулей производной нет.
Рассмотрим интервал . На нем имеем уравнение:
.
Решая уравнение, находим
.
Данное значение принадлежит рассматриваемому интервалу: . Таким образом,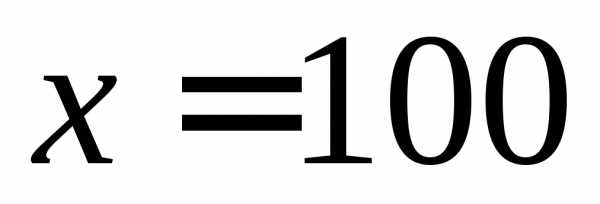 является корнем производной.
является корнем производной.
Рассмотрим интервал . На нем имеем уравнение:
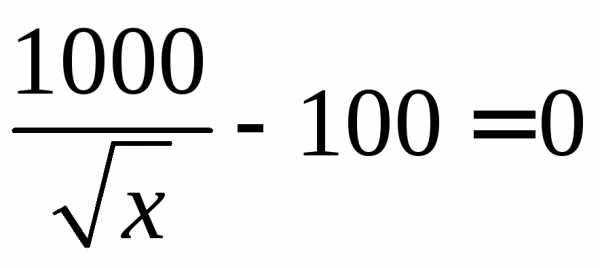 .
.
Решая уравнение, находим
.
Это значение не принадлежит рассматриваемому интервалу: . Значит на указанном интервале нулей производной нет.
Итак, производная равна нулю только в точке 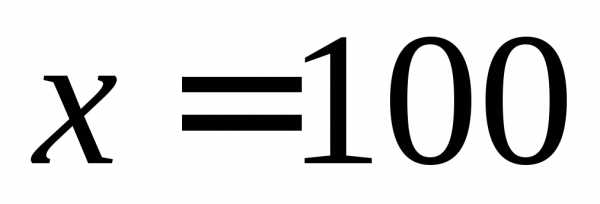 . Определим значение функции в этой точке:
. Определим значение функции в этой точке:
То есть наняв 100 рабочих получим прибыль, равную 11400 тыс. руб.
3) Определим точки, где производная не существует. Это все точки границ интервалов. Найдем в них значение функции.
В точке 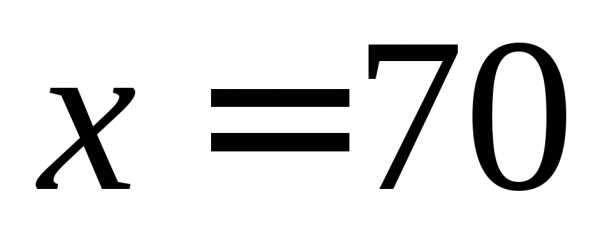 функция имеет излом, но остается непрерывной. Ее значения с обеих сторон совпадают и равны:
функция имеет излом, но остается непрерывной. Ее значения с обеих сторон совпадают и равны:
.
Если останутся прежние 70 рабочих, то прибыль будет 11133 тыс. руб.
В точке 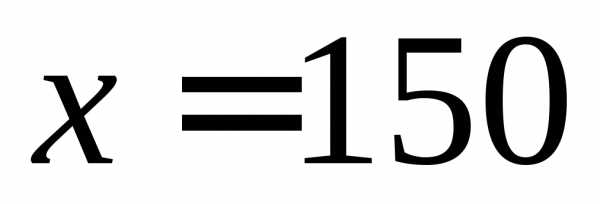 функция имеет скачек. Ее значения разные с двух сторон.
функция имеет скачек. Ее значения разные с двух сторон.
При  предел будет равен:
предел будет равен:
.
При 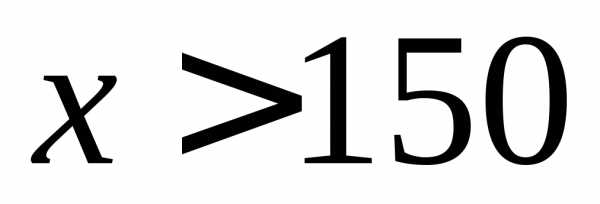 предел будет равен:
предел будет равен:
.
Таким образом, наняв 150 рабочих получим прибыль, равную 11195 тыс. руб.
Замечание 1. В данной задаче из условия целочисленности числа рабочих можно было не искать значения пределов, а проверить значение прибыли при 150 и 149 рабочих.
4) Единственной границей области в данном случае является 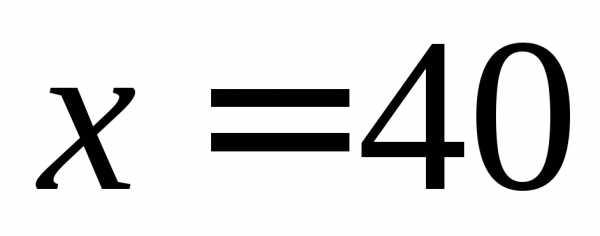 . При этом значении:
. При этом значении:
.
То есть при 40 работниках прибыль будет равна 9449 тыс. руб.
5) Поведение функции на бесконечности можно не рассматривать, как в задачах экономики. Однако, если это сделать, то получим:
.
Как и ожидалось, нанимая неограниченное количество рабочих будем получать неограниченные убытки.
6) Из всех найденных значений целевой функции выберем самое большое. Собираем все значения вместе:
,
,
,
,
.
Как видно, наибольшее значение достигается при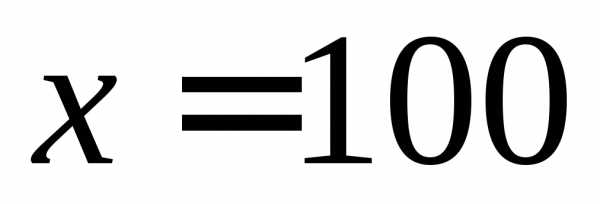 .
.
Таким образом, оптимальное управленческое решение будет таким:
Необходимо привлечь к работе всего 100 человек: 70 уже имеющихся и 30 новых. В этом случае мы получим наибольшую прибыль, равную 11 миллионов 400 тысяч рублей.
Ответить на вопросы, поставленные перед собой новым руководителем, можно так:
Имеющееся количество рабочих не оптимально. Необходимо нанять еще 30 человек. Нанимать рабочих до 150 человек не выгодно, так как получаемая субсидия вместе с ростом доходов не компенсирует полученный рост расходов.
Сделаем еще несколько замечаний.
Если мы сравним суммы прибыли при текущем количестве рабочих (11 млн. 133 тыс. руб.) и оптимальным (11 млн. 400 тыс. руб.), то видно, что прибыль меняется всего на 267 тыс. руб. или менее чем на 3%. Необходимо как следует проанализировать, стоит ли менять сложившийся вариант работы ради таких незначительных изменений. Для анализа необходимо уже будет учесть постоянные издержки. Если они велики, то прибыль с их учетом становится значительно меньше и дополнительные 267 тыс. руб. в месяц являются уже существенным выигрышем.
Принятие на работу всего 150 человек приводит тоже к близкому финансовому результату. Этот случай может быть рассмотрен как вариант расширения предприятия, если есть перспектива поиска лучшего варианта сбыта продукции.
Графическая интерпретация решения.
Построим на одном графике все три функции, описываемые уравнениями (4), (5), (6) (см рис. 1).
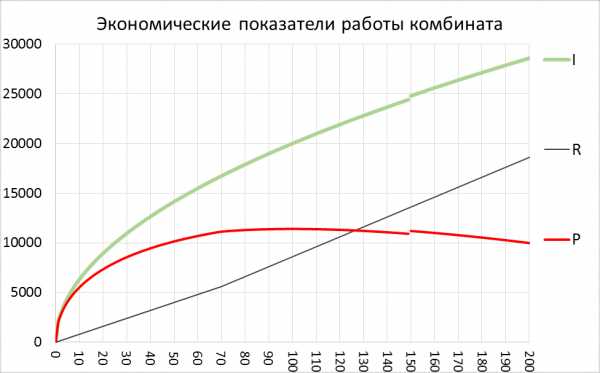
Рис. 1. Графики зависимости экономических показателей от количества рабочих
Из графика видно, что оптимум прибыли достигается примерно при 100 рабочих.
График прибыли ведет себя достаточно плавно в окрестности максимального значения, значит небольшие изменения числа около рабочих 100 человек не сильно влияют на финансовый результат.
studfiles.net
11 Нелинейные модели оптимизации в управлении » СтудИзба
Нелинейные модели оптимизации в управлении
В настоящем разделе мы кратко рассмотрим задачи нелинейной оптимизации (называемые иначе оптимизационными задачами нелинейного программирования), математические модели которых содержат нелинейные зависимости от переменных. Источники нелинейности в задачах подобного типа могут относиться, в частности, к одной из двух категорий:
· Реально существующие и эмпирически наблюдаемые нелинейные соотношения, например непропорциональные зависимости между объемом производства и затратами, между количеством используемого в производстве компонента и некоторыми показателями качества готовой продукции, между затратами сырья и физическими параметрами (давление, температура и т.п.) соответствующего производственного процесса, между выручкой и объемом реализации и т.п.
· Установленные (постулируемые) руководством правила поведения или задаваемые зависимости, например, правила расчета с потребителями энергии или других видов услуг, правила определения страховых уровней запаса продукции, гипотезы о характере вероятностного распределения рассматриваемых в модели случайных величин, различного рода договорные условия взаимодействия между партнерами по бизнесу и др.
В качестве примера можно рассмотреть формирование оптимальной производственной программы предприятия. По критерию затрат учитывается себестоимость единицы продукции, которая уменьшается при увеличении объема выпускаемой продукции, что приводит к нелинейному критерию эффективности. Нелинейные зависимости возникают также в ограничениях задачи при точном учете норм расхода ресурсов на единицу производимой продукции.
Вообще говоря, решение нелинейных задач по сложности значительно превосходит решение рассмотренных ранее задач линейной оптимизации. В связи с этим долгое время в практике экономического управления модели линейной оптимизации успешно применялись даже при наличии нелинейности. В одних случаях нелинейность была несущественна и ею можно было пренебречь, в других – проводилась линеаризация нелинейных соотношений или применялись специальные приемы, например строились так называемые аппроксимационные модели, благодаря чему достигалась требуемая адекватность. Тем не менее, часто встречаются задачи, для которых нелинейность является существенной и упомянутые выше методы аппроксимации неэффективны, в связи с чем нелинейность необходимо учитывать в явном виде.
В отличие от задачи линейной оптимизации (линейного программирования), не существует одного или нескольких алгоритмов, эффективных для решения любых нелинейных задач. Какой-то алгоритм может быть эффективен при решении задач одного типа и неприемлемым для задач другого типа. В связи с этим разработаны алгоритмы для решения каждого класса (типа) задач. Следует иметь в виду, что даже программы, ориентированные на решение определенного класса задач, не гарантируют правильность решения любых задач этого класса и оптимальность решения следует проверять в каждом конкретном случае.
Перечислим некоторые наиболее употребительные методы решения задач нелинейной оптимизации (нелинейного программирования):
· Оптимизация нелинейной функции с ограничениями на неотрицательность значений переменных (наиболее широко используемыми моделями данного класса являются модели квадратичного программирования, в которых целевая функция является квадратичной функцией переменных ).
· Модели выпуклого программирования; в моделях данного класса целевая функция является вогнутой (или выпуклой), а функции-ограничения являются выпуклыми функциями. При данных условиях локальный максимум (или минимум) функции является также глобальным. При решении таких задач используется метод множителей Лагранжа, а также теорема Куна-Таккера.
· Сепарабельное программирование. В задачах данного класса целевая функция и функции-ограничения могут быть представлены в виде сумм отдельных компонент. Данные задачи могут быть сведены к задачам линейного программирования.
· Дробно-нелинейное программирование. В этих задачах производится максимизация (минимизация) целевой функции вида . Если функции линейны (задача дробно-линейного программирования), то задача сводится к линейной.
· Невыпуклое программирование. Задачи данного типа принадлежат к наименее изученным и наиболее сложным задачам нелинейной оптимизации. В данном случае целевая функция и (или) функции-ограничения не выпуклы. Надежных методов решения таких задач в настоящее время не существует.
Мы ограничимся рассмотрением лишь наиболее простых задач нелинейной оптимизации, не требующих использования сложных аналитических выкладок и анализа, задач, которые могут эффективно решаться на базе табличного процессора Excel.
Задача нелинейной оптимизации в общем случае состоит в отыскании такого вектора неизвестных , который обращал бы в максимум (минимум) функцию
(2.6)
и удовлетворял бы системе ограничений
(2.7)
где на некоторые или на все переменные налагается условие неотрицательности.
studizba.com
ЧастьIi. Методы нелинейной оптимизации
Задача математического программирования
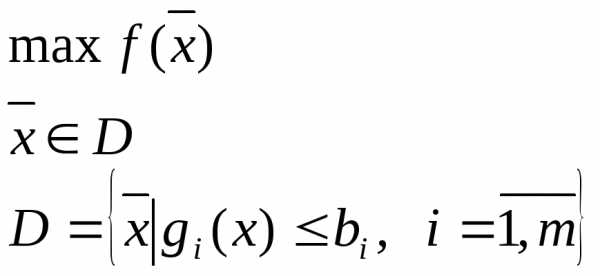
(1)
(2)
называется задачей нелинейного программирования, если функция цели или хотя бы одна из функций ограничений не линейна. Точка 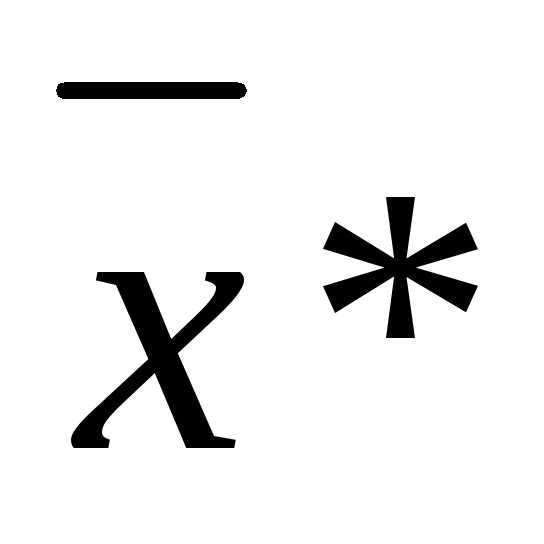 называется точкойлокального экстремума, если существует
называется точкойлокального экстремума, если существует  – окрестность этой точки
– окрестность этой точки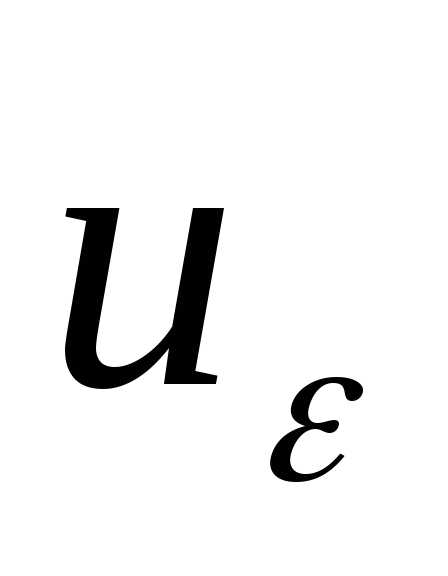 , для которой,
, для которой,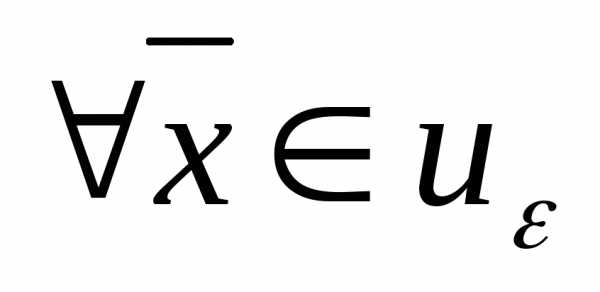 .
.
Точка 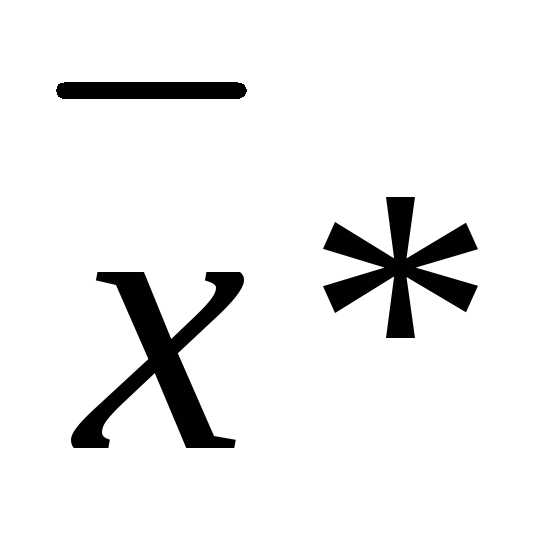 называется точкойглобального экстремума, если для любого
называется точкойглобального экстремума, если для любого 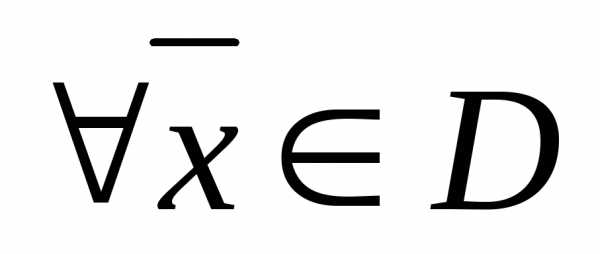 .
.
Функция называется унимодальной (одноэкстремальной), если у этой функции имеется только один локальный экстремум. В противном случае она называется многоэкстремальной.
В классической теории оптимизации рассматриваются экстремальные задачи без ограничений, то есть область D совпадает со всем n-мерным пространством вещественных чисел 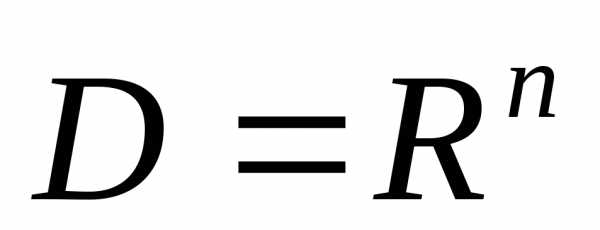 .
.
Глава 7. Классическая теория оптимизации
Рассмотрим задачу безусловной оптимизации
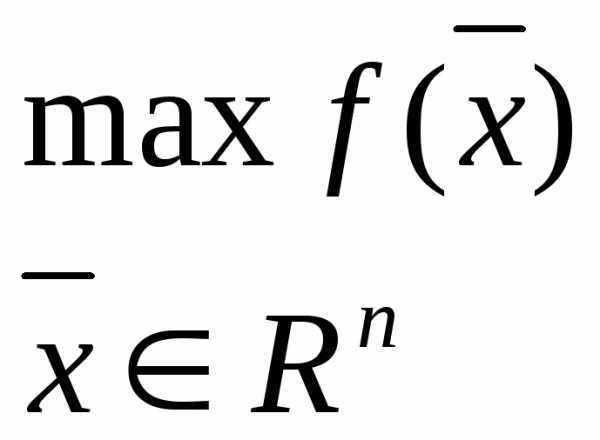
В случае достаточной дифференцируемости функции можно сформулировать необходимые и достаточные условия локального экстремума.
7 (3).1. Необходимые условия оптимальности
Для функции одной переменной справедлива следующая теорема.
Теорема 1: для того, чтобы функция одной переменной имела в точке 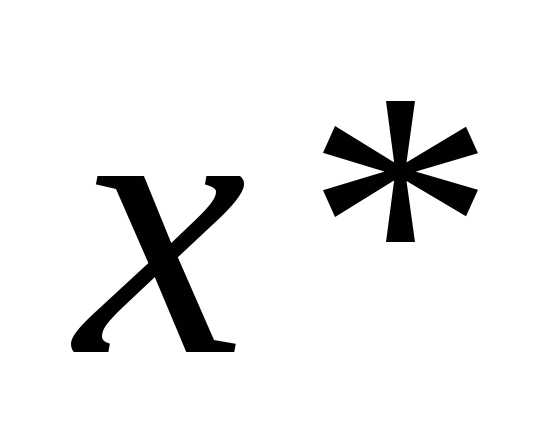 локальный экстремум, необходимо, чтобы производная функции в этой точке была равна нулю.
локальный экстремум, необходимо, чтобы производная функции в этой точке была равна нулю.
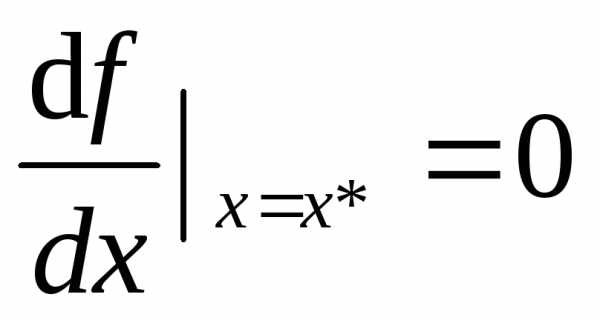
Аналогичная теорема справедлива для функции многих переменных.
Теорема 2: для того, чтобы функция 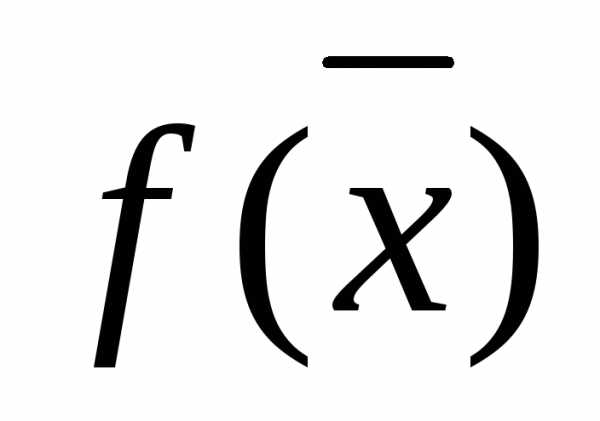 имела в точке
имела в точке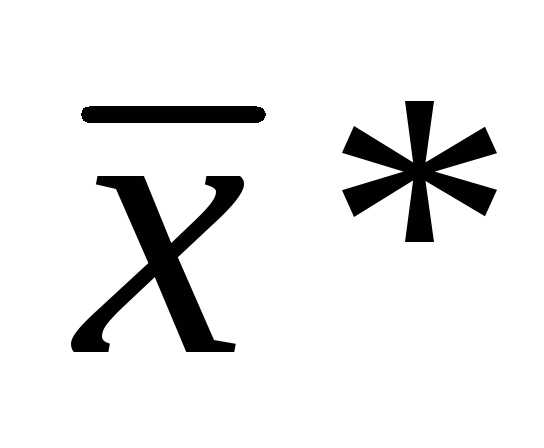 локальный экстремум, необходимо, чтобы все ее частные производные в этой точке обращались в ноль
локальный экстремум, необходимо, чтобы все ее частные производные в этой точке обращались в ноль
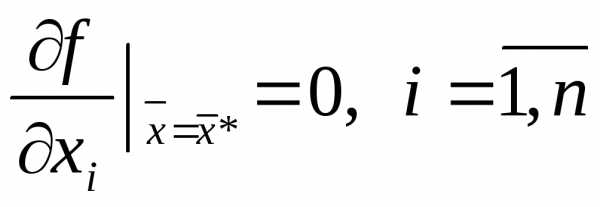
(4)
Другими словами, вектор градиента функции в этой точке должен быть нулевым.
(5)
Такие точки называются стационарными точками функции.
7.2. Достаточные условия оптимальности
Для функции одной переменной достаточные условия задаются следующей теоремой.
Теорема 3: если в точке 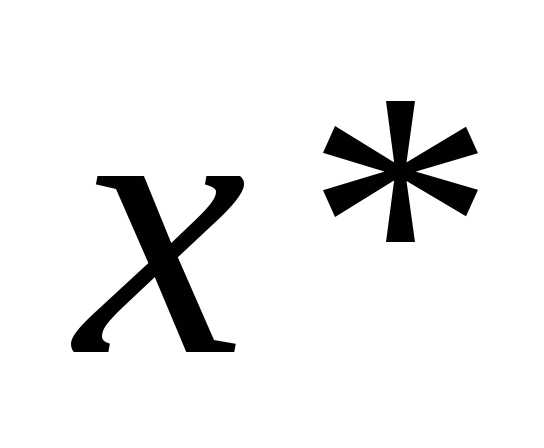 первая производная функции равна нулю, а вторая производная
первая производная функции равна нулю, а вторая производная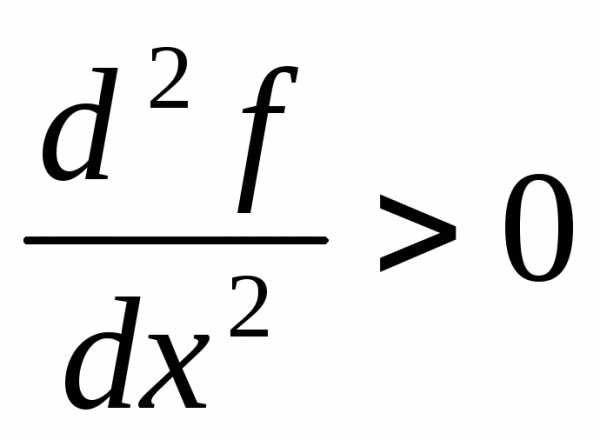 , то функция в точке
, то функция в точке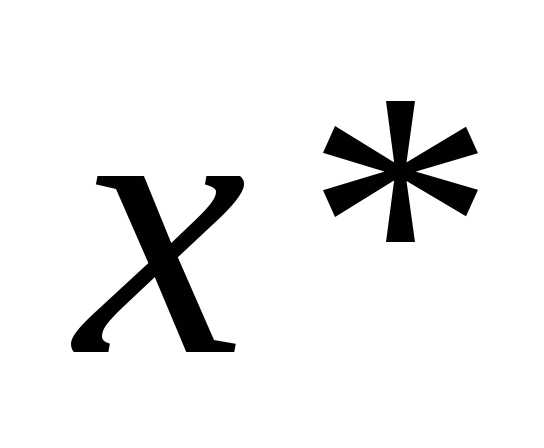 имеет локальный минимум, если
имеет локальный минимум, если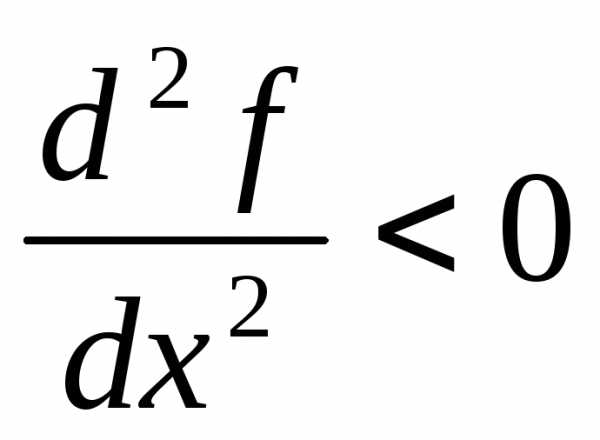 , то функция в точке
, то функция в точке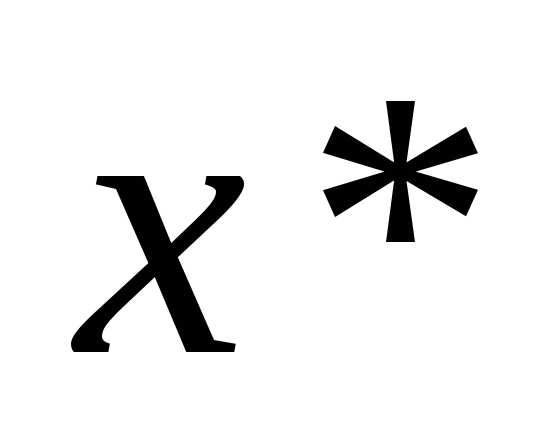 имеет локальный максимум.
имеет локальный максимум.
Если вторая производная функции в точке 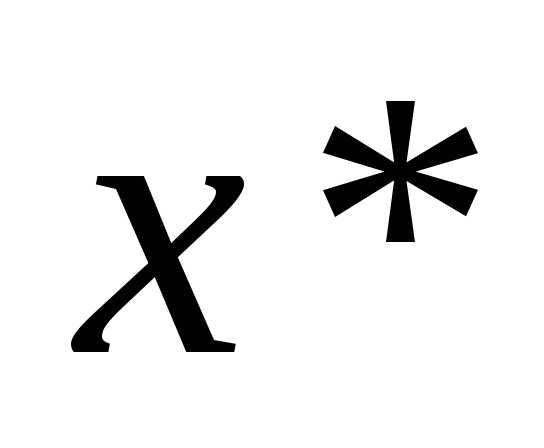 равна нулю, то необходимо исследовать производные высших порядков в соответствии со следующей теоремой.
равна нулю, то необходимо исследовать производные высших порядков в соответствии со следующей теоремой.
Теорема 4: если функция одной переменной имеет в точке 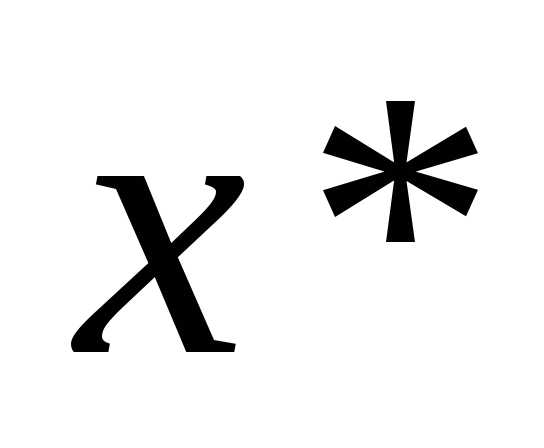 производные до
производные до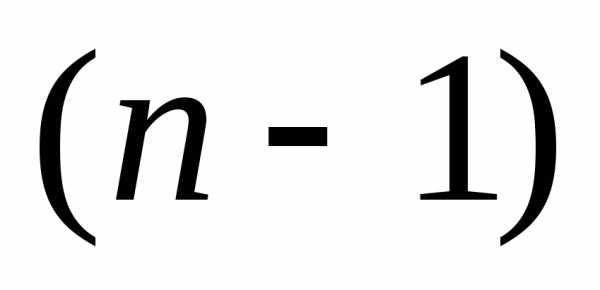 порядка равными нулю и производная
порядка равными нулю и производная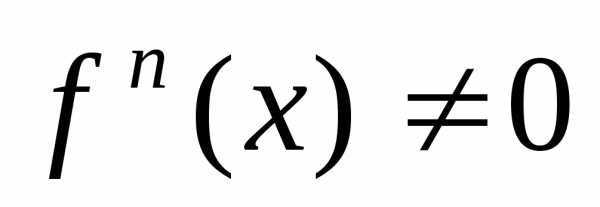 , то тогда,
, то тогда,
если 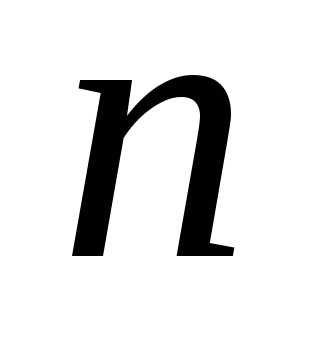 четно, то точка
четно, то точка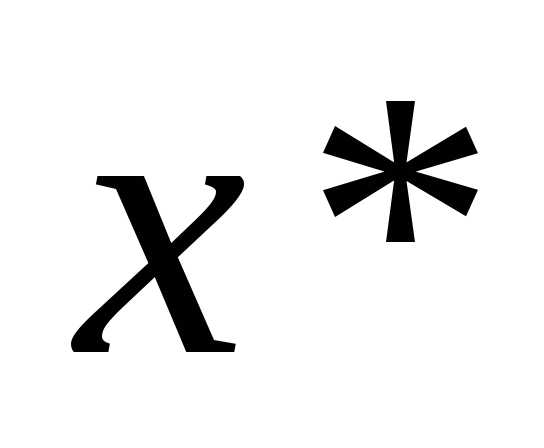 является точкой минимума, если
является точкой минимума, если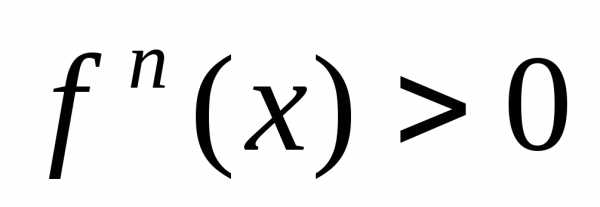 ,
,
точкой максимума – если 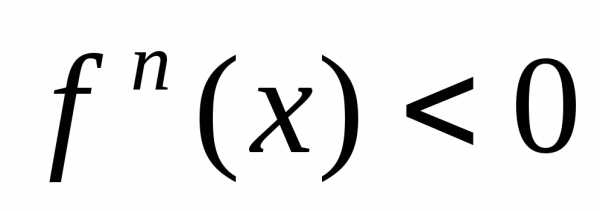 .
.
Если 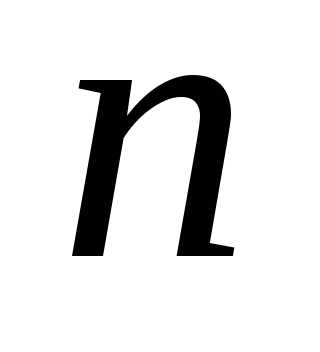 нечетно, то точка
нечетно, то точка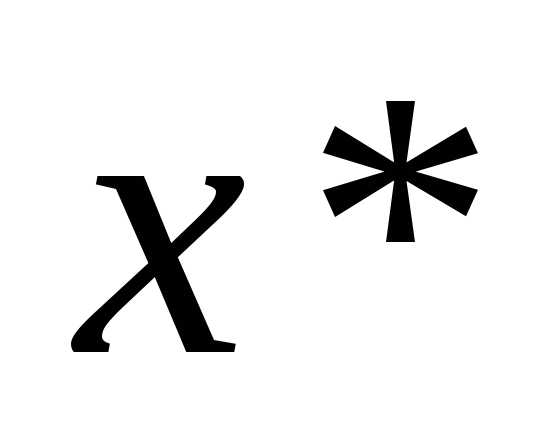 – точка перегиба.
– точка перегиба.
Для обобщения теоремы 3 на случай функции многих переменных рассмотрим матрицу вторых производных функции и её свойства.
Матрицей Гессе (Гессианом) называется матрица вторых производных функции:
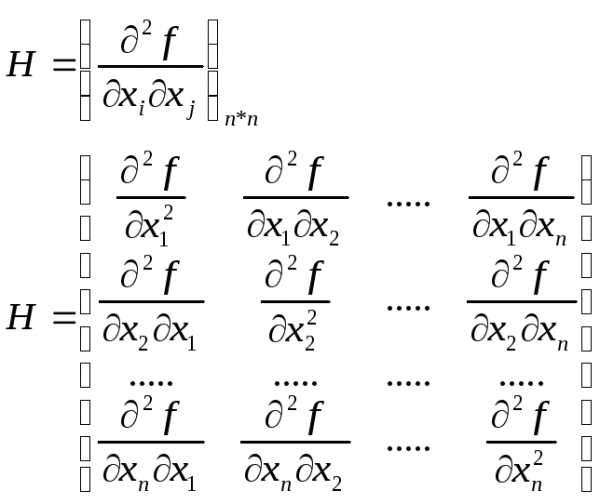
Для анализа поведения функции в точке потребуются некоторые свойства квадратичных функций.
Рассмотрим квадратичную функцию (форму):
(6)
Числовая матрица 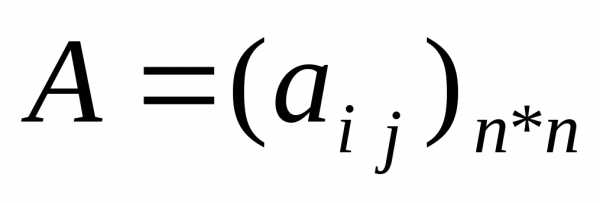 называется матрицей квадратичной формы. Можно считать, что эта матрица симметрична.
называется матрицей квадратичной формы. Можно считать, что эта матрица симметрична.
Квадратичная форма (6) называется положительно определенной, если для 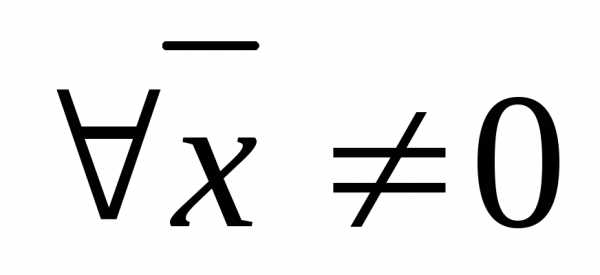
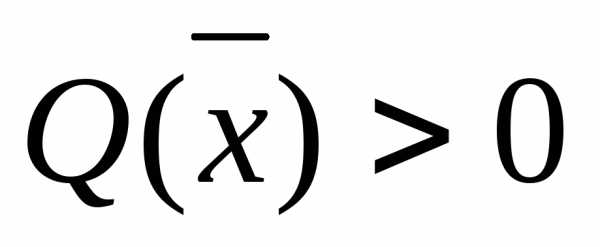 иотрицательно определенной, если для
иотрицательно определенной, если для 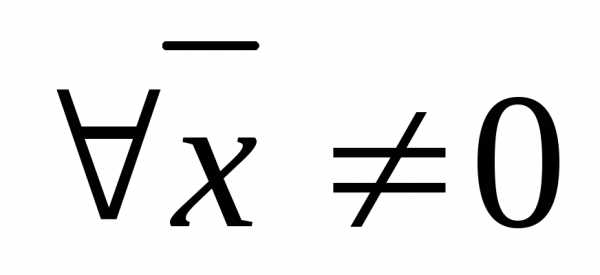
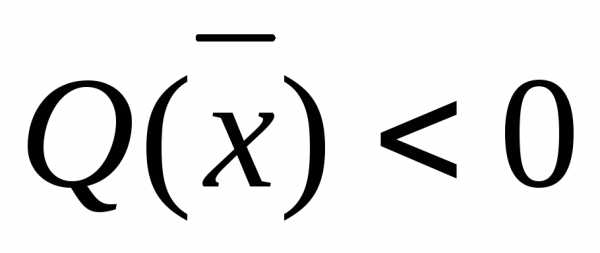 .
.
Симметричная матрица A называется положительно определенной, если построенная по ней квадратичная форма (6) положительно определена.
Симметричная матрица  называетсяотрицательно определенной, если построенная по ней квадратичная форма (6) отрицательно определена.
называетсяотрицательно определенной, если построенная по ней квадратичная форма (6) отрицательно определена.
Проверить положительную или отрицательную определенность числовой матрицы можно по следующим признакам.
Признаки:
Критерий Сильвестра: матрица
 является положительно определенной, если все ее угловые миноры больше ноля.
является положительно определенной, если все ее угловые миноры больше ноля.

Матрица  является отрицательно определенной, если знаки угловых миноров чередуются.
является отрицательно определенной, если знаки угловых миноров чередуются.
Или: если все угловые миноры удовлетворяют неравенству .
Для того чтобы матрица была положительно определенной, необходимо, чтобы все ее собственные числа были больше нуля.
Собственные числа – корни многочлена 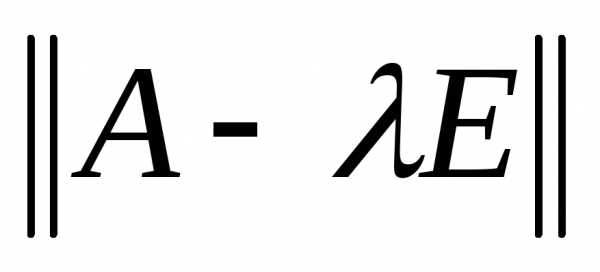 . Этот определитель есть многочлен относительно
. Этот определитель есть многочлен относительно  .
.
.
Для того чтобы матрица была отрицательно определенной, необходимо, чтобы все ее собственные числа были меньше нуля.
Достаточное условие оптимальности задается следующей теоремой.
Теорема 5: если в стационарной точке 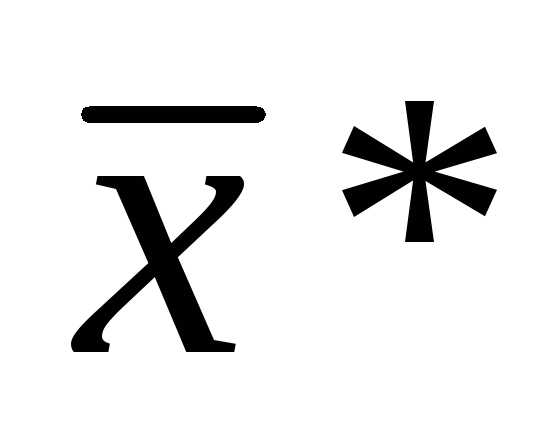 (т.е.
(т.е.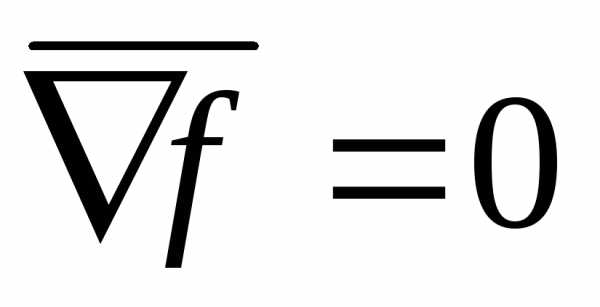 ) матрица Гессе положительно определена, то эта точка – точка локального минимума, если матрица Гессе отрицательно определена, то эта точка – точка локального максимума.
) матрица Гессе положительно определена, то эта точка – точка локального минимума, если матрица Гессе отрицательно определена, то эта точка – точка локального максимума.
Доказательство:
Пусть 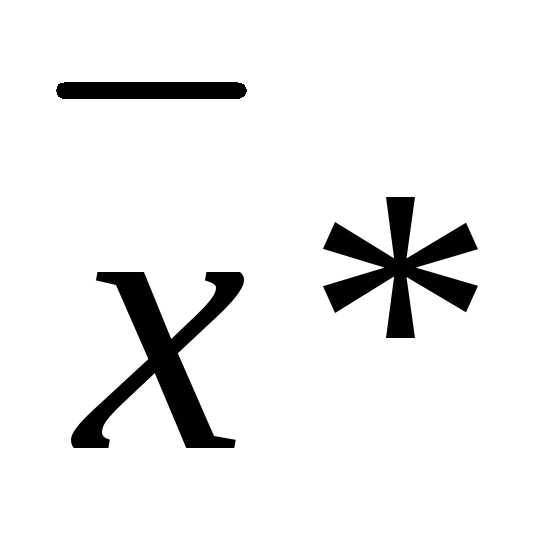 – стационарная точка,
– стационарная точка,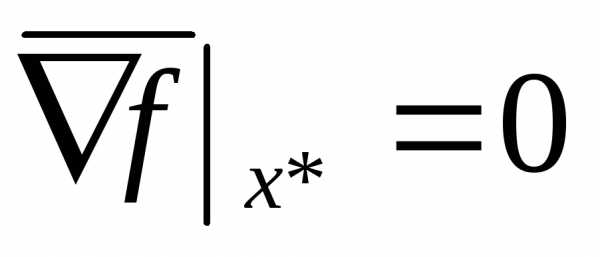 , возьмем окрестность точки
, возьмем окрестность точки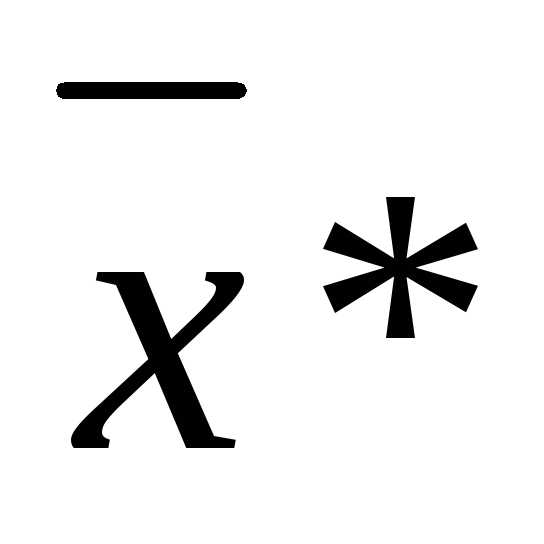
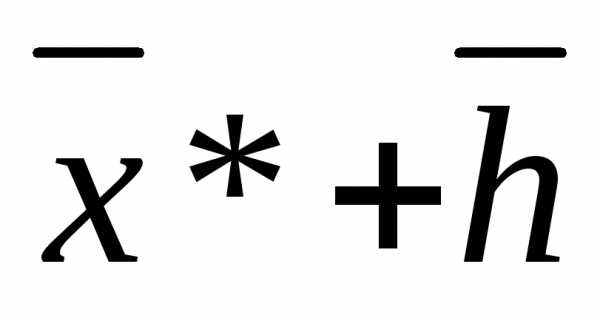 . Тогда по теореме Тейлора
. Тогда по теореме Тейлора
(7)
По условию теоремы 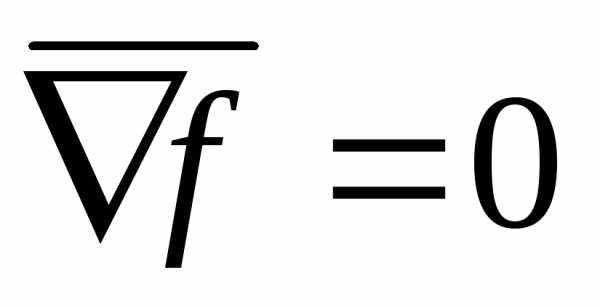 , а матрица Гессе в точке
, а матрица Гессе в точке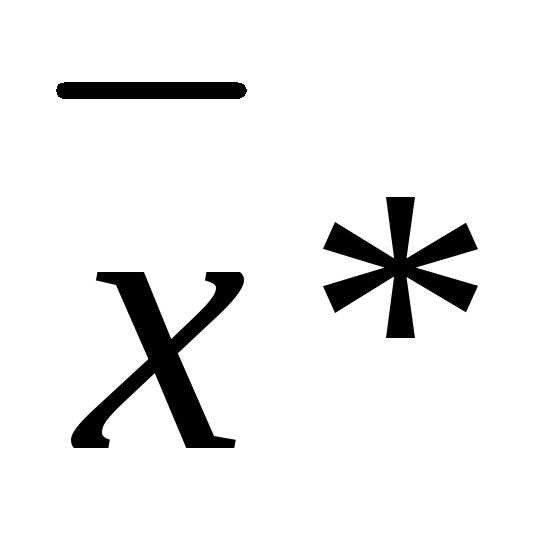 положительно определена, то есть квадратичная форма
положительно определена, то есть квадратичная форма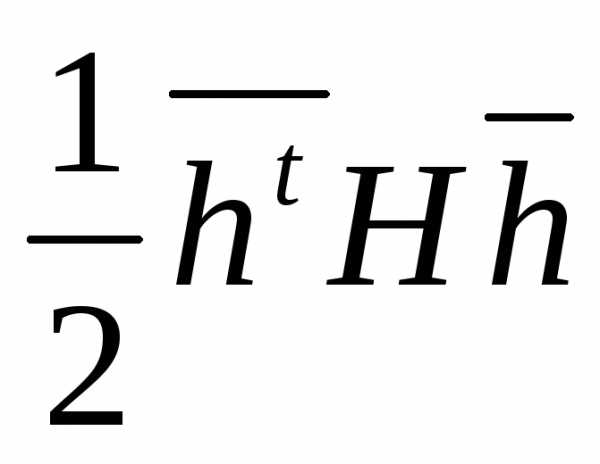 >0 в точке
>0 в точке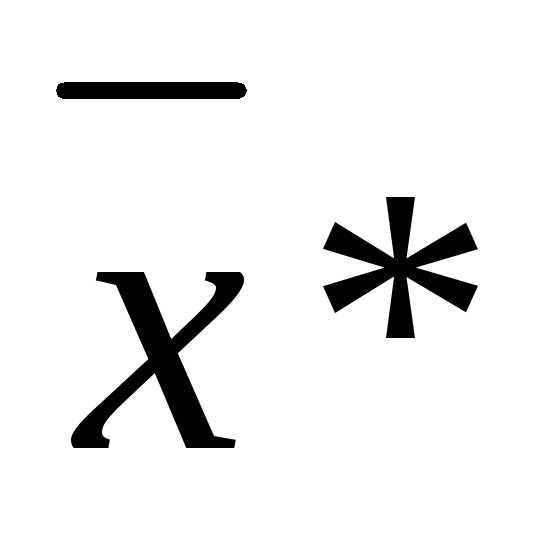 , а в силу непрерывности вторых частных производных и в точке
, а в силу непрерывности вторых частных производных и в точке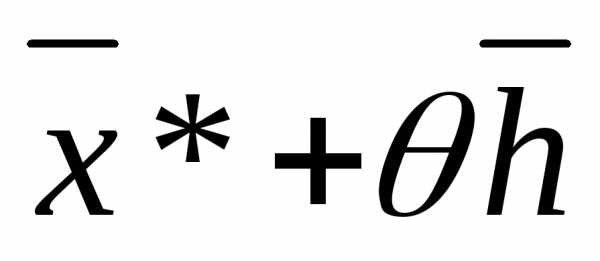 .
.
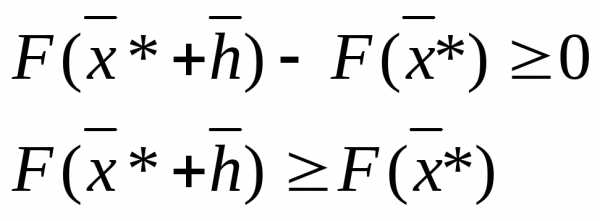
Значит точка 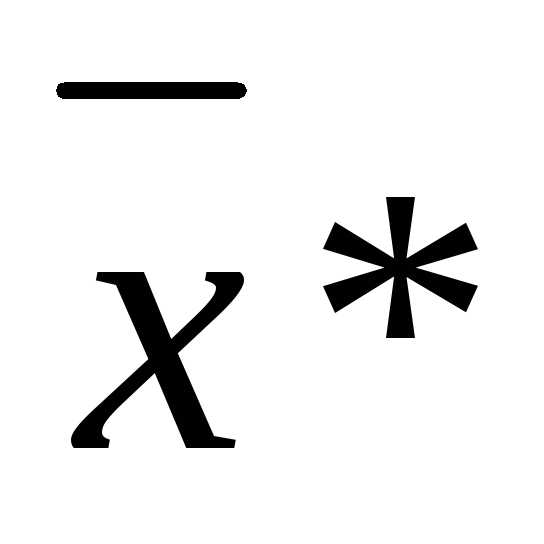 – точка локального минимума.
– точка локального минимума.
Пример: Продукция трех видов производится в объеме и реализуется по ценесоответственно. Определить объемы производства, обеспечивающие наибольший доход.
Определим стационарные точки функции
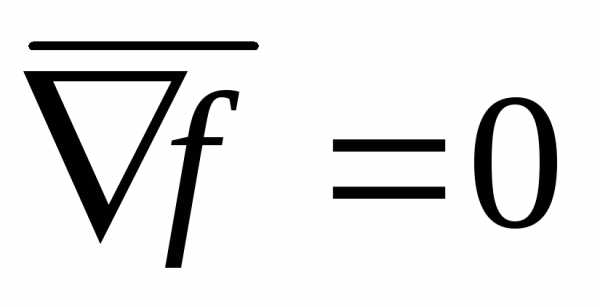 :
:
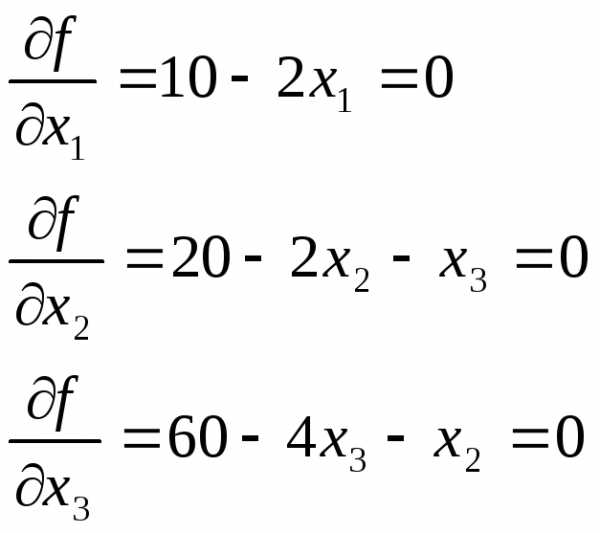
Решением этой системы линейных алгебраических уравнений является вектор
Проверим достаточное условие оптимальности. Вычислим матрицу Гессе в полученной стационарной точке.
Угловые миноры матрицы имеют чередующиеся знаки
, значит, матрица Гессе отрицательно определена и точка – точка локального максимума. При полученных объемах производства будет достигнут наибольший доход .
Проверим отрицательную определенность матрицы вторым способом. Найдем собственные числа матрицы Гессе
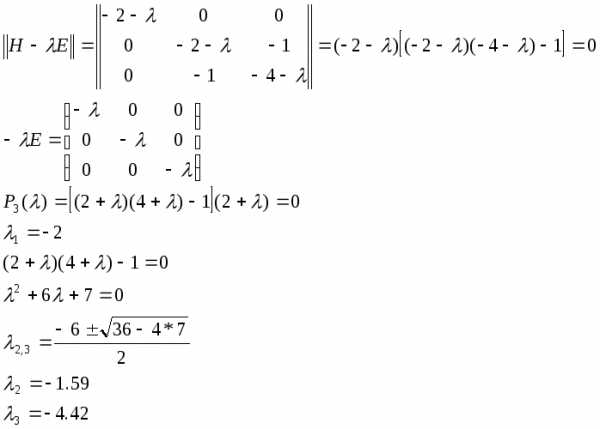
Так как все собственные числа матрицы 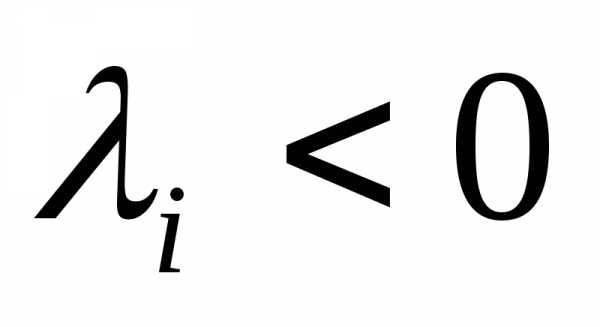 , то матрица отрицательно определена и
, то матрица отрицательно определена и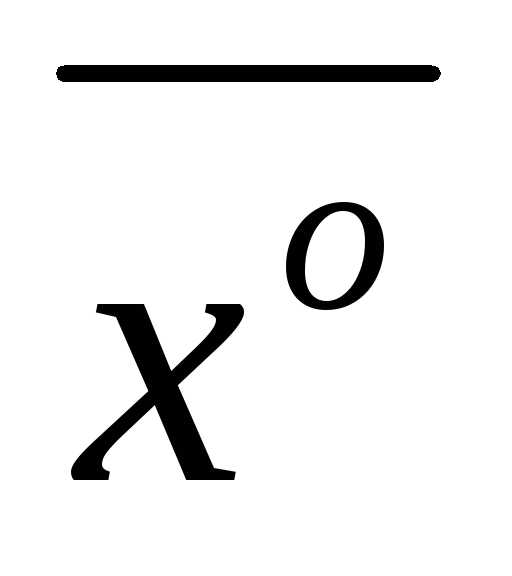 – локальный максимум.
– локальный максимум.
studfiles.net
Разбор примера задачи нелинейной оптимизации
Решим и проанализируем описанную выше ситуацию принятия решения для директора лесозаготовительного комбината.
Анализ будем проводить только с учетом переменных расходов. Как следует из общей теории оптимизации, постоянное слагаемое не оказывает влияние на оптимальный план действий, изменяя только значение целевой функции.
Как видно из данных примера, весь анализ можно провести в терминах количества рабочих. Обозначим через 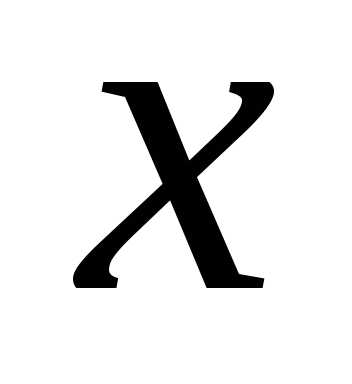 число рабочих на предприятии. Так как мы не можем уволить более 30 человек из имеющихся 70, то переменная
число рабочих на предприятии. Так как мы не можем уволить более 30 человек из имеющихся 70, то переменная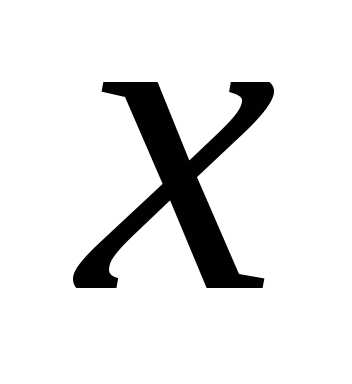 ограничена снизу:
ограничена снизу: .
.
Выпуск продукции пропорционален численности и равен 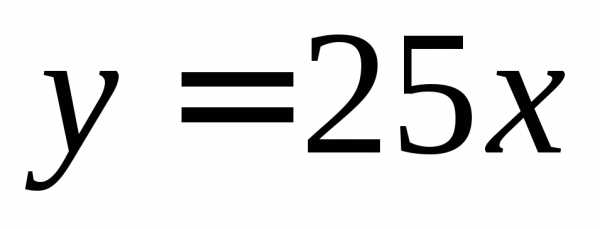 м3 в мес. Доход от продажи в месяц тогда равен:
м3 в мес. Доход от продажи в месяц тогда равен:
Если возможную субсидию при 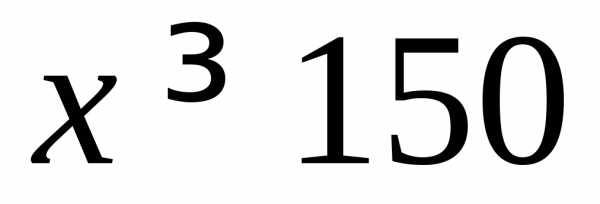 учесть в доходной части, то общую функцию месячного дохода можно записать так:
учесть в доходной части, то общую функцию месячного дохода можно записать так:
(3)
Если не нанимать новых сотрудников, то будет выполняться условие  , а месячные расходы равны:
, а месячные расходы равны:
.
Если нанять новых рабочих, то 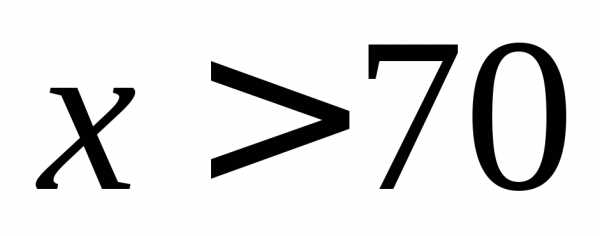 . Из этого количества рабочих 70 будут «старых», а
. Из этого количества рабочих 70 будут «старых», а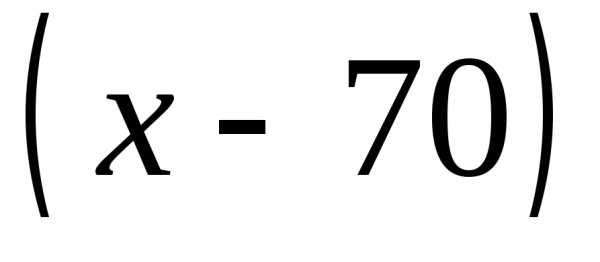 – «новых». Тогда месячные расходы будут складываться из затрат на «старых» по 80 тыс. руб. на человека и затрат на новых потыс. руб. на человека. Суммарные затраты составят:
– «новых». Тогда месячные расходы будут складываться из затрат на «старых» по 80 тыс. руб. на человека и затрат на новых потыс. руб. на человека. Суммарные затраты составят:
.
В итоге общую функцию месячных затрат можно записать в виде:
(4)
Прибыль комбината (без учета постоянных расходов) равна разнице между доходами (3) и переменными расходами (4) и запишется в виде:
(5)
Таким образом, математически задача формулируется так: найти 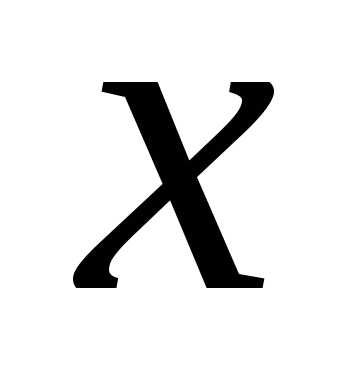 , при котором функция прибыли (5) имеет максимум.
, при котором функция прибыли (5) имеет максимум.
Очевидно, функция (5) меняется непропорционально искомой переменной 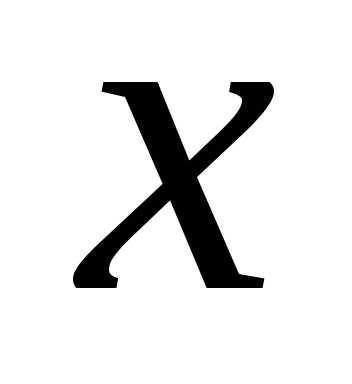 и задача является нелинейной.
и задача является нелинейной.
Пройдем для этой задачи все пункты алгоритма поиска глобального экстремума.
1) Определим градиент функции. В данном случае функции одной переменной градиент совпадает с производной. Если функция задана разными выражениями на разных интервалах, то нужно просто взять производные для каждого интервала. Они будут справедливы при строгом выполнении ограничивающих интервалы неравенств:
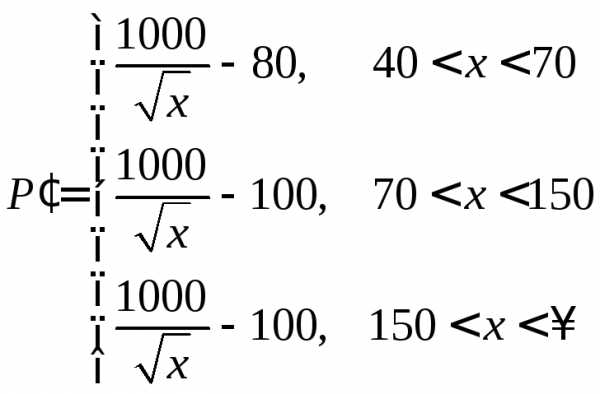 (6)
(6)
Как видно из выражения (6), производные на втором и третьем интервалах совпадают, но между ними при 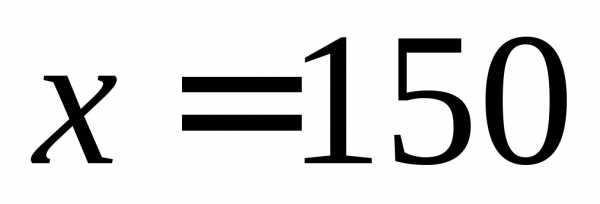 производная не существует, так как функция терпит разрыв.
производная не существует, так как функция терпит разрыв.
2) Определим точки, где производная равна нулю. Для этого определим все 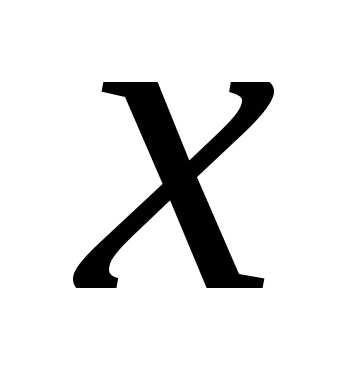 , удовлетворяющие равенствам:
, удовлетворяющие равенствам:
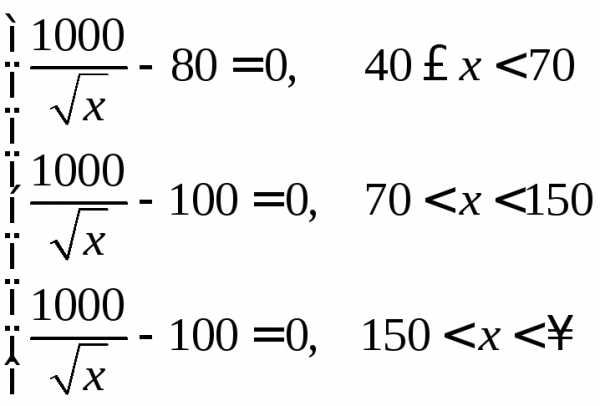
Рассмотрим интервал . На нем имеем уравнение:
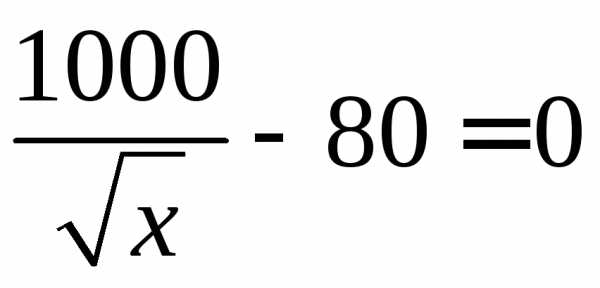 .
.
Решая уравнение, находим
.
Однако данное значение не попадает в интервал: . Значит на указанном интервале нулей производной нет.
Рассмотрим интервал . На нем имеем уравнение:
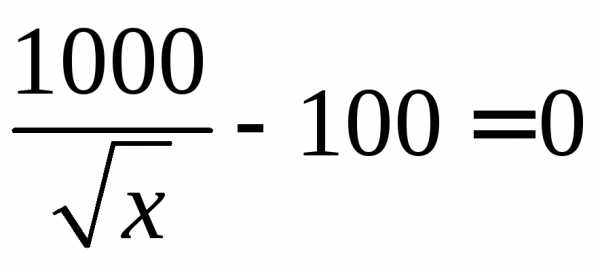 .
.
Решая уравнение, находим
.
Данное значение принадлежит рассматриваемому интервалу: . Таким образом,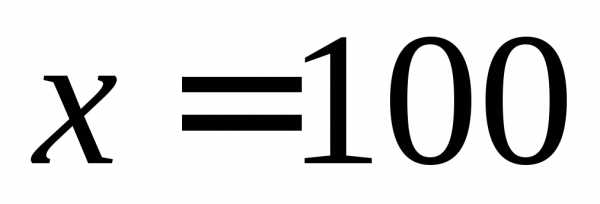 является корнем производной.
является корнем производной.
Рассмотрим интервал . На нем имеем уравнение:
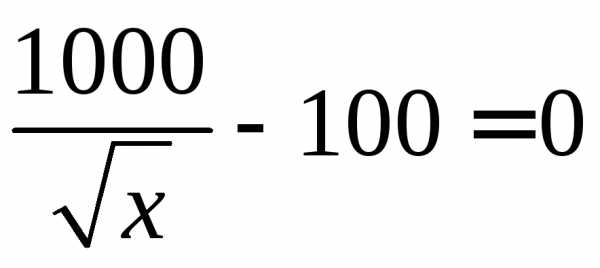 .
.
Решая уравнение, находим
.
Это значение не принадлежит рассматриваемому интервалу: . Значит на указанном интервале нулей производной нет.
Итак, производная равна нулю только в точке 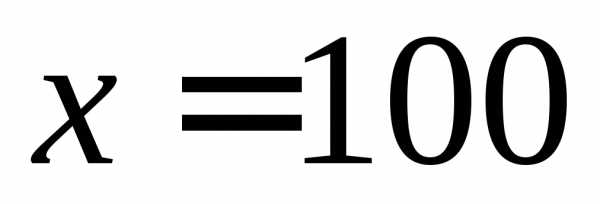 . Определим значение функции в этой точке:
. Определим значение функции в этой точке:
.
То есть наняв 100 рабочих получим прибыль, равную 11400 тыс. руб.
3) Определим точки, где производная не существует. Это все точки границ интервалов. Найдем в них значение функции.
В точке 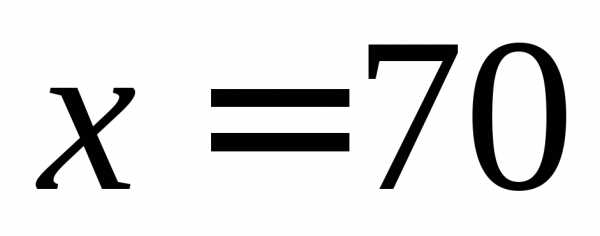 функция имеет излом, но остается непрерывной. Ее значения с обеих сторон совпадают и равны:
функция имеет излом, но остается непрерывной. Ее значения с обеих сторон совпадают и равны:
.
Если останутся прежние 70 рабочих, то прибыль будет 11133 тыс. руб.
В точке 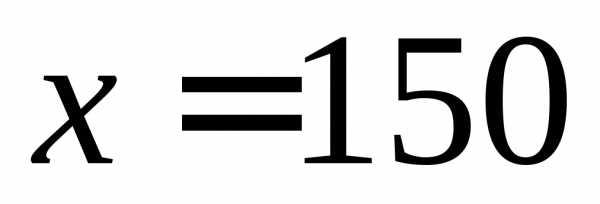 функция имеет скачек. Ее значения разные с двух сторон.
функция имеет скачек. Ее значения разные с двух сторон.
При  предел будет равен:
предел будет равен:
.
При 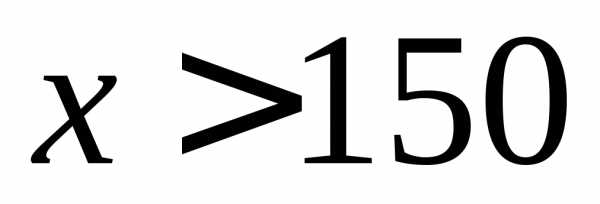 предел будет равен:
предел будет равен:
.
Таким образом, наняв 150 рабочих получим прибыль, равную 11195 тыс. руб.
Замечание 1. В данной задаче из условия целочисленности числа рабочих можно было не искать значения пределов, а проверить значение прибыли при 150 и 149 рабочих.
Замечание 2. Из экономического смысла задачи очевидно, что предел справа (когда субсидия будет выплачена) будет лучше, чем предел слева (без субсидии).
4) Единственной границей области в данном случае является 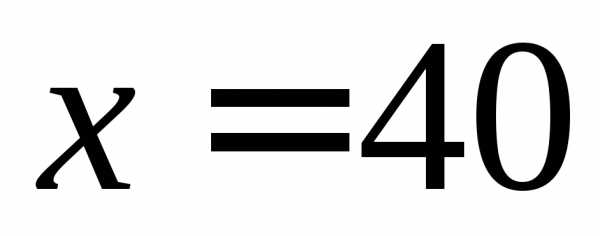 . При этом значении:
. При этом значении:
.
То есть при 40 работниках прибыль будет равна 9449 тыс. руб.
5) Поведение функции на бесконечности можно не рассматривать, как в задачах экономики. Однако, если это сделать, то получим:
.
Как и ожидалось, нанимая неограниченное количество рабочих будем получать неограниченные убытки.
6) Из всех найденных значений целевой функции выберем самое большое. Собираем все значения вместе:
,
,
,
,
.
Как видно, наибольшее значение достигается при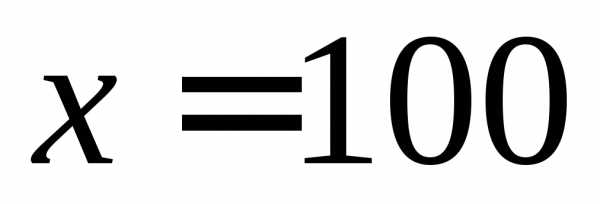 .
.
Таким образом, оптимальное управленческое решение будет таким:
Необходимо привлечь к работе всего 100 человек: 70 уже имеющихся и 30 новых. В этом случае мы получим наибольшую прибыль, равную 11 миллионов 400 тысяч рублей.
Ответить на вопросы, поставленные перед собой новым руководителем, можно так:
Имеющееся количество рабочих не оптимально. Необходимо нанять еще 30 человек. Нанимать рабочих до 150 человек не выгодно, так как получаемая субсидия вместе с ростом доходов не компенсирует полученный рост расходов.
Сделаем еще несколько замечаний.
Если мы сравним суммы прибыли при текущем количестве рабочих (11 млн. 133 тыс. руб.) и оптимальным (11 млн. 400 тыс. руб.), то видно, что прибыль меняется всего на 267 тыс. руб. или менее чем на 3%. Необходимо как следует проанализировать, стоит ли менять сложившийся вариант работы ради таких незначительных изменений. Для анализа необходимо уже будет учесть постоянные издержки. Если они велики, то прибыль с их учетом становится значительно меньше и дополнительные 267 тыс. руб. в месяц являются уже существенным выигрышем.
Принятие на работу всего 150 человек приводит тоже к близкому финансовому результату. Этот случай может быть рассмотрен как вариант расширения предприятия, если есть перспектива поиска лучшего варианта сбыта продукции.
Графическая интерпретация решения.
Построим на одном графике все три функции, описываемые уравнениями (4), (5), (6) (см рис. 1).
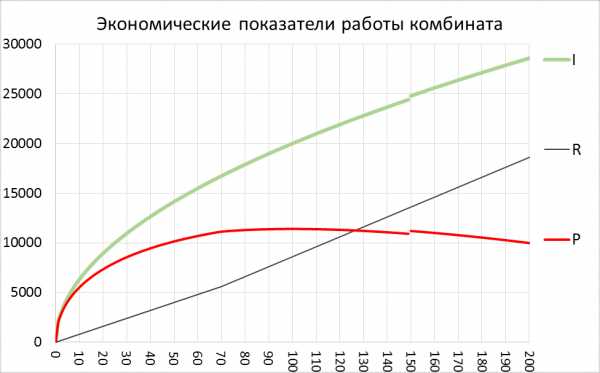
Рис. 1. Графики зависимости экономических показателей от количества рабочих
Из графика видно, что оптимум прибыли достигается примерно при 100 рабочих.
График прибыли ведет себя достаточно плавно в окрестности максимального значения, значит небольшие изменения числа около рабочих 100 человек не сильно влияют на финансовый результат.
studfiles.net
Нелинейная оптимизация. Метод градиента (метод наискорейшего спуска). П.1. Сведение системы линейных уравнений к задаче
нелинейной оптимизации (ЗНО) и наоборот.
Задача нелинейной оптимизации – найти  [min f(x)]-одномерную ЗНО или [max f(x)]- многомерная ЗНО
[min f(x)]-одномерную ЗНО или [max f(x)]- многомерная ЗНО
x=(x1,x2,...,xn)
Как известно из высшей математики, экстремум функции f достигается (если функция дифференцируемая, гладкая) или на границе области D или в точках х оптимальное ,в которых все частные производные обращаются в 0.
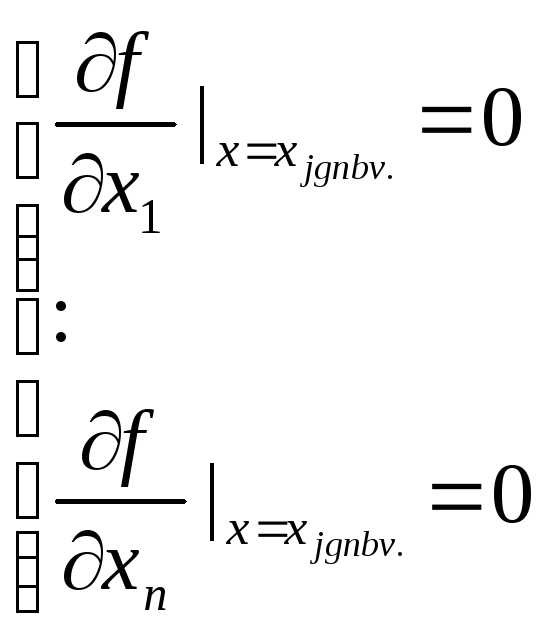 (7.1),
(7.1),
Первая возможность рассматривать не будем.
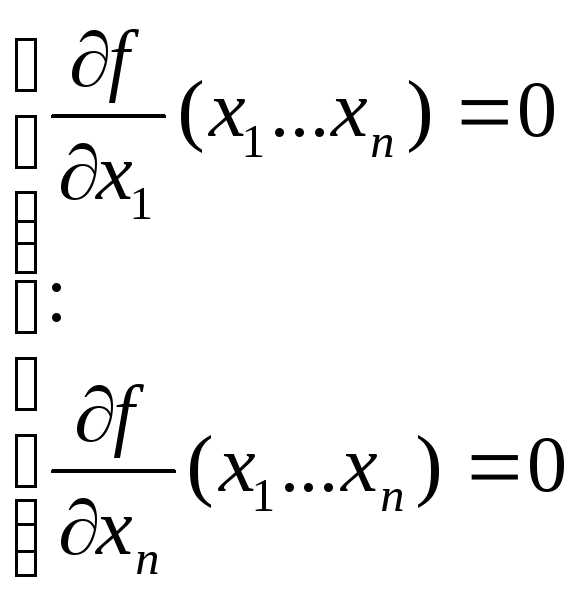 (7.2),
(7.2),
т.е. задачу нелинейной оптимизации (7.1) свели к задаче (7.2) – системе нелинейных уравнений.
Обратная процедура (СНУ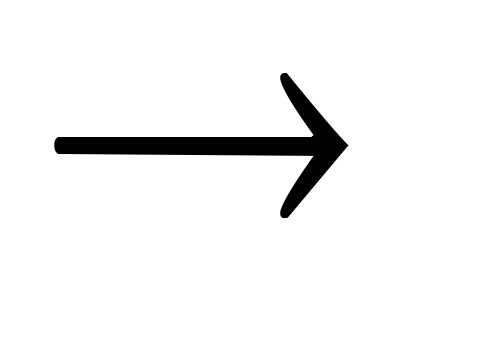 ЗНО)
ЗНО)
Рассмотрим СНУ:
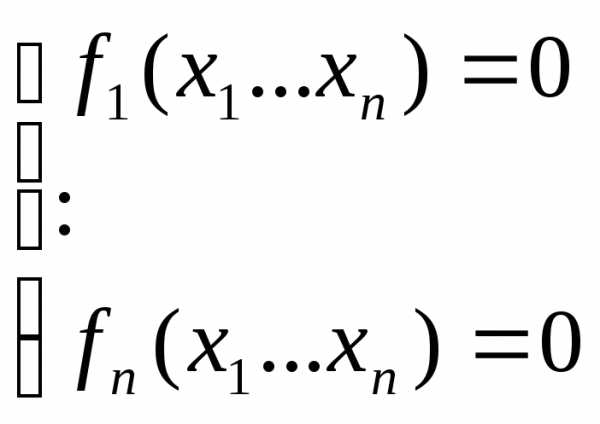 и функцию: (7.4), так как f всюду
и функцию: (7.4), так как f всюду 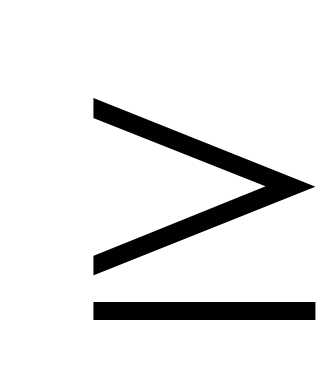 0, то ее min достигается в точке х=(х1…хn) являющейся, решением (7.3).
0, то ее min достигается в точке х=(х1…хn) являющейся, решением (7.3).
Сводить ЗНО к СНУ и решать ее м. Ньютона хорошо теоретически, но весьма проблемно практически, т.к. метод Ньютона может расходиться и функция f аналитически не задается, поэтому лучше использовать численное дифференцирование. При попытке численного дифференцирования возникает погрешность, из-за которой м.Ньютона теряет скорость и на каждом шаге приходится делать много вычислений. Поэтому на практике при решении ЗНО обычно используют специальные методы, самый распространенный – метод градиента.
П.2. Метод градиента.
Имеем min функции f(х1,…,хn) (без ограничений на область D или в предположении, что она достаточно большая, т.е. не помешает процессу).
Идея метода градиента:
Выбрать точку х0 достаточно близкую к точке min;
Найти направление наибольшего убывания f в точке х (направление наискорейшего возрастания f в точке х0 – вектор градиента (grad) , направление: поиск убывания – противоположный градиенту: вектор – grad f |x=x0 .
Двигаемся по направлению градиента (по прямой) до тех пор, пока не начнем подниматься, (т.е. пока не достигнем min на нашей одномерной траектории в точке х1 ).
Из точки х1 двигаемся в направлении наискорейшего убывания (-grad f |x=x0 ) до точки х2 . Продолжаем этот процесс, до тех пор, пока не достигнем заданного min с заданной точностью. Критерий прерывания универсальный.
Переведем алгоритм на математический язык:
- траектория (зависит от t) движения на первом этапе.
Ищем min g0(t):
а) Предположим, что min достигается при t=t0:
х1=х0 – t grad f |x=x0
б) Рассмотрим g1(t)= f(х1 – t grad f |x=x1 )
x2=х1 – t1 grad f |x=x1,
и т.д.
Т.е. на каждом этапе метода градиента необходимо решать ЗНО (находить min gi(t)).
Для нахождения градиента, функцию f необходимо дифференцировать (аналитически или численно).
П.3. Одномерная ЗНО. Метод деления.
Первый вариант решения одномерной ЗНО - свести ее к нелинейному уравнению: 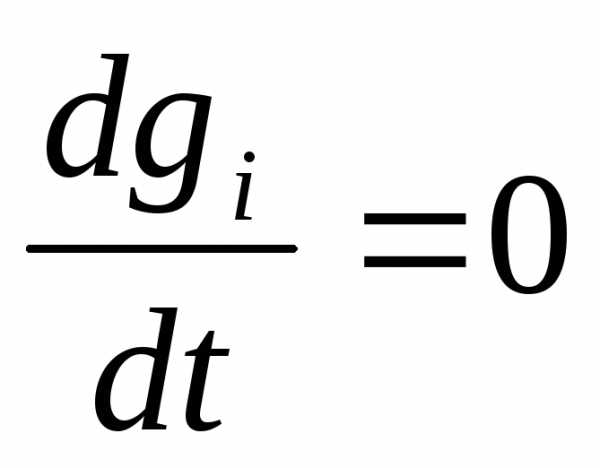 и решать его любым известным методом.
и решать его любым известным методом.
Этот метод применим, если gi гладкая и ее производную нетрудно явно вычислить. Часто это не удается и поэтому одномерную ЗНО решают именно как ЗНО (т.е. в том виде, как она дана).
Будем решать одномерную ЗНО (ищем min g(t)) следующим образом:
Предположим, нам известно, что min значение t оптимальное [a,b]. Разобьем интервал [a,b] точками: ti (a=t0<t1<…<tn=b) на маленькие интервалы и вычислим g(ti), выберем среди них min – g(ti опт.).
Тогда, если g имела один min на [a,b], то: ti опт.-1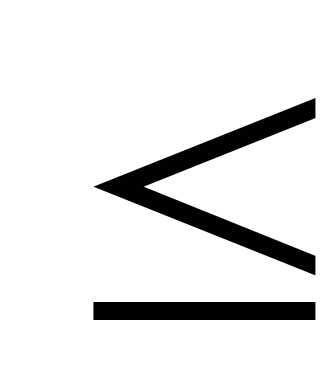 ti опт.
ti опт.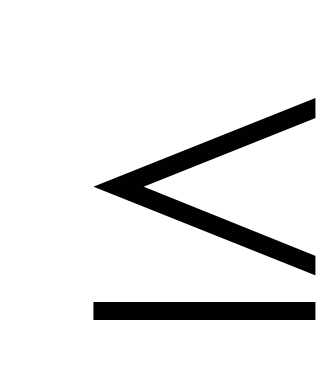 ti опт.+1.
ti опт.+1.
На следующем шаге берем в качестве a=ti опт.-1, в качестве b=ti опт.+1, разбиваем полученный интервал на части и производим очередное уточнение для t оптимального. Процесс продолжается до тех пор, пока не будет достигнута заданная точность.
Число интервалов должно быть ≥3, чтобы интервал поиска уменьшался.
При подобном методе деления на каждом шаге необходимо искать значение функции f в двух точках и длина интервала поиска уменьшается приблизительно вдвое. Для достижения заданной точности ε нам потребуется проделать 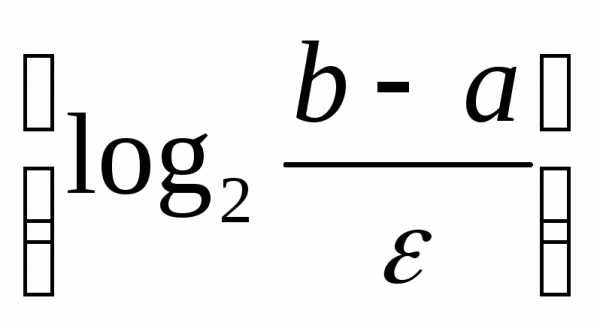 шагов и
шагов и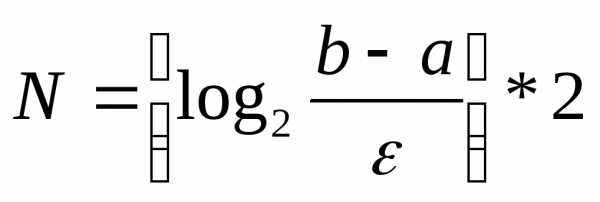 операций (7.3).
операций (7.3).
П.4. Метод золотого сечения.
Метод золотого сечения применяется для минимизации числа действий при решении ЗНО методом деления. При этом 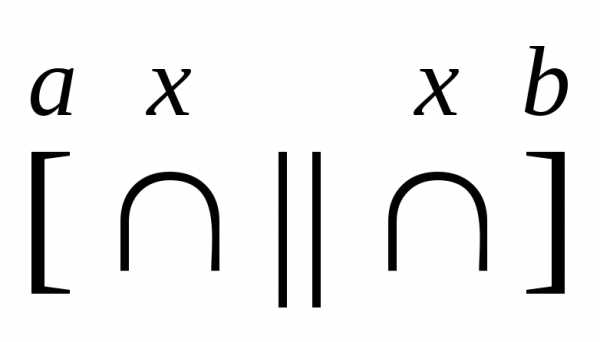 разбивается на три интервала и выбирается min g(ti). На следующем шаге один из крайних отрезков будет обращен и остается
разбивается на три интервала и выбирается min g(ti). На следующем шаге один из крайних отрезков будет обращен и остается 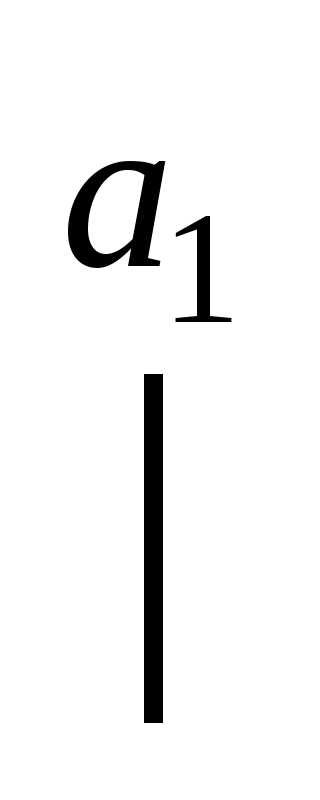
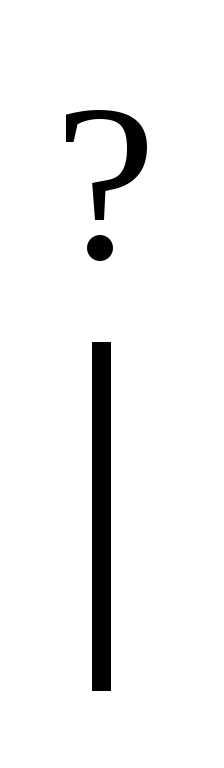
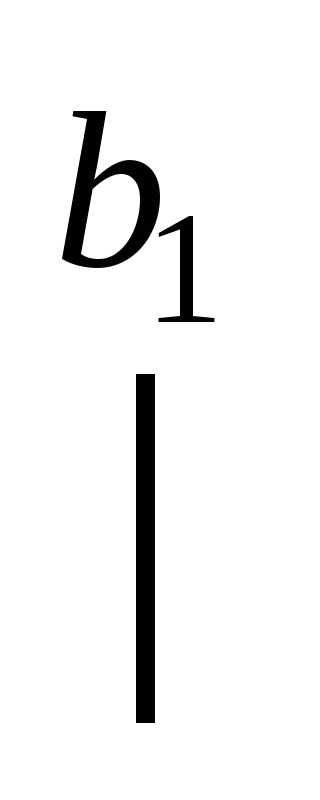 .
.
При удачном подборе пропорции деления первоначального интервала [a,b] и делении отрезка [a1,b1] в тех же пропорциях, потребуется вычислить значения функции f только в одной точке, потому что значения в точке нам было известно на предыдущем шаге.
Подберем необходимые пропорции:
Считаем, что длина [a,b]=1 и от этого интервала были отсечены два одинаковых отрезка длины х. Тогда, если отрезок обозначим за y, то получим:
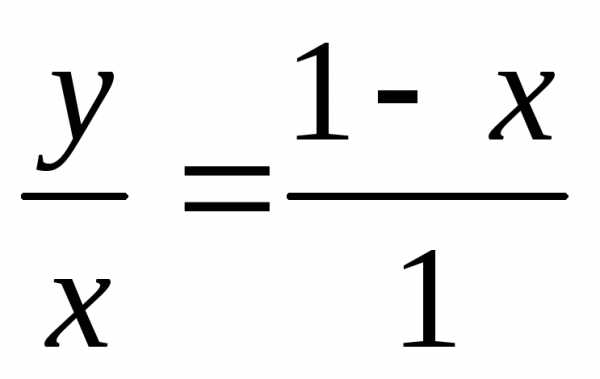 , y=(1-x)x, но с другой стороны y=1-2x
, y=(1-x)x, но с другой стороны y=1-2x
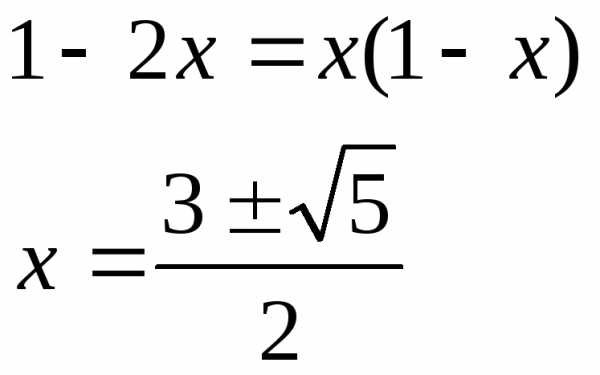
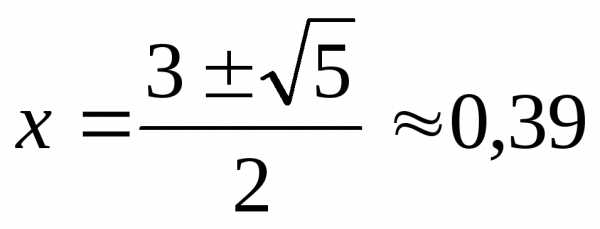 , при этом интервал [a,b] уменьшается в
, при этом интервал [a,b] уменьшается в 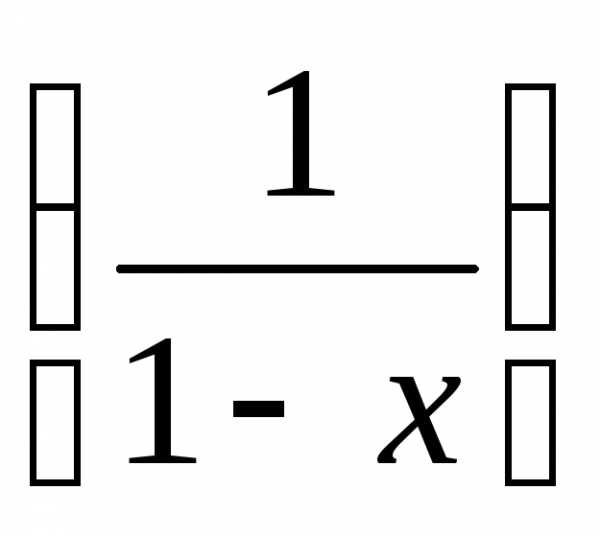 раз, что составляет: .
раз, что составляет: .
Трудоемкость одномерного ЗНО методом золотого сечения.
Нам потребуется 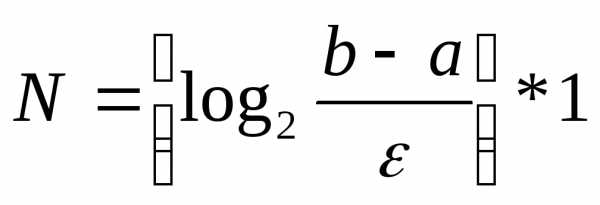 шагов (7.4). ДанноеNменьше числаNиз формулы (7.3). Выигрыш происходит за счет того, что мы на каждом шаге значение функции считаем 1 раз и, несмотря на то, что длина интервала уменьшается не в 2 раза, а только лишь в 1,618 раза, происходит выигрыш по количеству итераций.
шагов (7.4). ДанноеNменьше числаNиз формулы (7.3). Выигрыш происходит за счет того, что мы на каждом шаге значение функции считаем 1 раз и, несмотря на то, что длина интервала уменьшается не в 2 раза, а только лишь в 1,618 раза, происходит выигрыш по количеству итераций.
studfiles.net
python - Нелинейная оптимизация с помощью Python
Хотя алгоритм SLSQP в scipy.optimize.minimize хорош, он имеет множество ограничений. Первым из них является решатель QP, поэтому он работает для уравнений, которые хорошо вписываются в квадратичную парадигму программирования. Но что произойдет, если у вас есть функциональные ограничения? Кроме того, scipy.optimize.minimize не является глобальным оптимизатором, поэтому вам часто нужно начинать очень близко к окончательным результатам.
Существует ограниченный пакет нелинейной оптимизации (называемый mystic), который существует почти до тех пор, пока scipy.optimize сам - я бы предложил его в качестве решения для обработки любой ограниченной нелинейной оптимизации.
Например, ваша проблема, если я понимаю ваш псевдокод, выглядит примерно так:
import numpy as np M = 10 N = 3 Q = 10 C = 10 # let be lazy, and generate s and u randomly... s = np.random.randint(-Q,Q, size=(M,N,N)) u = np.random.randint(-Q,Q, size=(M,N)) def percentile(p, x): x = np.sort(x) p = 0.01 * p * len(x) if int(p) != p: return x[int(np.floor(p))] p = int(p) return x[p:p+2].mean() def objective(x, p=5): # inverted objective, to find the max return -1*percentile(p, [np.dot(np.atleast_2d(u[i]), x)[0] for i in range(0,M-1)]) def constraint(x, p=95, v=C): # 95%(xTsx) - v <= 0 x = np.atleast_2d(x) return percentile(p, [np.dot(np.dot(x,s[i]),x.T)[0,0] for i in range(0,M-1)]) - v bounds = [(0,1) for i in range(0,N)]Итак, чтобы справиться с вашей проблемой в mystic, вам просто нужно указать границы и ограничения.
from mystic.penalty import quadratic_inequality @quadratic_inequality(constraint, k=1e4) def penalty(x): return 0.0 from mystic.solvers import diffev2 from mystic.monitors import VerboseMonitor mon = VerboseMonitor(10) result = diffev2(objective, x0=bounds, penalty=penalty, npop=10, gtol=200, \ disp=False, full_output=True, itermon=mon, maxiter=M*N*100) print result[0] print result[1]Результат выглядит примерно так:
Generation 0 has Chi-Squared: -0.434718 Generation 10 has Chi-Squared: -1.733787 Generation 20 has Chi-Squared: -1.859787 Generation 30 has Chi-Squared: -1.860533 Generation 40 has Chi-Squared: -1.860533 Generation 50 has Chi-Squared: -1.860533 Generation 60 has Chi-Squared: -1.860533 Generation 70 has Chi-Squared: -1.860533 Generation 80 has Chi-Squared: -1.860533 Generation 90 has Chi-Squared: -1.860533 Generation 100 has Chi-Squared: -1.860533 Generation 110 has Chi-Squared: -1.860533 Generation 120 has Chi-Squared: -1.860533 Generation 130 has Chi-Squared: -1.860533 Generation 140 has Chi-Squared: -1.860533 Generation 150 has Chi-Squared: -1.860533 Generation 160 has Chi-Squared: -1.860533 Generation 170 has Chi-Squared: -1.860533 Generation 180 has Chi-Squared: -1.860533 Generation 190 has Chi-Squared: -1.860533 Generation 200 has Chi-Squared: -1.860533 Generation 210 has Chi-Squared: -1.860533 STOP("ChangeOverGeneration with {'tolerance': 0.005, 'generations': 200}") [-0.17207128 0.73183465 -0.28218955] -1.86053344078mystic является очень гибким и может обрабатывать любые типы ограничений (например, равенства, неравенства), включая символические и функциональные ограничения. Я указал ограничения как "штрафы" выше, что является традиционным способом, поскольку они применяют штраф к цели, когда ограничение нарушается. mystic также обеспечивает нелинейные преобразования ядра, которые ограничивают пространство решений путем уменьшения пространства действительных решений (т.е. путем пространственного преобразования или преобразования ядра).
В качестве примера, здесь mystic решение проблемы, которая ломает много решателей QP, поскольку ограничения не в форме матрицы ограничений. Это оптимизирует конструкцию сосуда высокого давления.
"Pressure Vessel Design" def objective(x): x0,x1,x2,x3 = x return 0.6224*x0*x2*x3 + 1.7781*x1*x2**2 + 3.1661*x0**2*x3 + 19.84*x0**2*x2 bounds = [(0,1e6)]*4 # with penalty='penalty' applied, solution is: xs = [0.72759093, 0.35964857, 37.69901188, 240.0] ys = 5804.3762083 from mystic.symbolic import generate_constraint, generate_solvers, simplify from mystic.symbolic import generate_penalty, generate_conditions equations = """ -x0 + 0.0193*x2 <= 0.0 -x1 + 0.00954*x2 <= 0.0 -pi*x2**2*x3 - (4/3.)*pi*x2**3 + 1296000.0 <= 0.0 x3 - 240.0 <= 0.0 """ cf = generate_constraint(generate_solvers(simplify(equations))) pf = generate_penalty(generate_conditions(equations), k=1e12) if __name__ == '__main__': from mystic.solvers import diffev2 from mystic.math import almostEqual from mystic.monitors import VerboseMonitor mon = VerboseMonitor(10) result = diffev2(objective, x0=bounds, bounds=bounds, constraints=cf, penalty=pf, \ npop=40, gtol=50, disp=False, full_output=True, itermon=mon) assert almostEqual(result[0], xs, rel=1e-2) assert almostEqual(result[1], ys, rel=1e-2)Найдите это и примерно 100 таких примеров: https://github.com/uqfoundation/mystic.
Я автор, поэтому я немного предвзятый. Однако смещение очень слабое. mystic является зрелым и хорошо поддерживается, и он не имеет себе равных по способности решать жестко ограниченные задачи нелинейной оптимизации.
qaru.site
Информационные технологии - Нелинейная оптимизация
Нелинейная оптимизация
Математическая модель является нелинейной, если целевая функция или ограничения нелинейно зависят от переменных. В отличие от задачи линейного программирования здесь нельзя рассчитывать, что с помощью Решателя получено действительно оптимальное решение.
Пример.
Найти максимум функции f(x)=x², x принадлежит [-1,2].
Ответ очевиден: максимум равен 4 и достигается при х=2. Попытайтесь найти ответ с помощью Решателя. Задайте для х следующие начальные приближения: 0,-0.1 и 0.1. Вы получите три разных ответа: 0, 1, 4. Причина этого следующая. В точке 0 производная f’(x)=2x обращается в 0. Следовательно, мы находимся в точке экстремума (делает вывод Решатель), и можно выдавать ответ 0. Если Вы посмотрите отчет по пределам, то увидите вычисленные значения функции на концах отрезка. Эти значения превышают 0, но Решателя это "не волнует". При начальном значении - 0.1 Решатель продвигается в сторону увеличения значений функции и добирается до точки х = - 1. И только при начальном значении 0.1 Решатель находит правильный ответ.
Этот пример весьма поучителен. Он показывает, что в нелинейных задачах оптимизации на ответ, выдаваемый Решателем, нельзя полагаться. Ответ зависит от выбора начального приближения. К сожалению, достаточно общих методов отыскания глобального экстремума не разработано. Если функция зависит от одной или двух переменных, старайтесь проверить ответ на графиках. Дело еще осложняют нелинейные ограничения.kabanov.ucoz.com








