Примеры решения оптимизационных задач средствами Excel. Решение задач оптимизации в excel примеры

Примеры решения оптимизационных задач средствами Excel — Мегаобучалка

Лабораторная работа и контрольные задания ОКТ

1. РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ С ПОМОЩЬЮ EXCEL

1. 1. Ввод условий задачи

1. 2. Работа в диалоговом окне "Поиск решения"

2. ПРИМЕРЫ РЕШЕНИЯ ОПТИМИЗАЦИОННЫХ ЗАДАЧ СРЕДСТВАМИ EXCEL

2. 1. Получение требуемого сплава

2. 2. Транспортная задача

2. 3. Рациональное использование имеющихся площадей

2. 4. Рациональное использование технологических участков

2. 5. Закрепление самолетов за воздушными линиями

2. 6. Задача о ранце

2. 7. Назначение механизмов на работы

2. 8. Задача коммивояжера

2. 9. Задача о доставке

3. ВАРИАНТЫ ЗАДАНИЙ

Вариант контрольной работы выбирается по последней цифре № зачетной книжки.

Вариант										10(0)
Номера заданий

Решение задач линейного программирования с помощью Excel

Ввод условий задачи

Ввод условий задачи состоит из следующих основных шагов:

1). Создание формы для ввода условий задачи.

2). Ввод исходных данных (коэффициентов математической модели).

3). Ввод целевой функции, ограничений и граничных условий.

Последовательность работ рассмотрим на примере задачи распределения ресурсов.

Фирма выпускает продукцию четырех типов Продукт1, Продукт2, Продукт3, Продукт4, для изготовления которой требуются ресурсы трех видов: трудовые, сырье, финансы. Количество ресурса каждого вида, необходимое для выпуска единицы продукции данного типа, называется нормой расхода. Норма расхода, а также прибыль, получаемая от реализации единицы каждого типа продукции, приведены в табл., там же приведено наличие располагаемого ресурса. Требуется определить, в каком количестве надо выпускать продукцию каждого типа, чтобы суммарная прибыль была максимальной.

Ресурс	Продукт1	Продукт2	Продукт3	Продукт4	Наличие
Трудовые
Сырье
Финансы
Прибыль

Составим математическую модель, для чего введем следующие обозначения:

xj- количество выпускаемой продукции j-го типа j=1,2,3,4;

bi- количество располагаемого ресурса i-го вида i=1,2,3;

aij- норма расхода i-го ресурса для выпуска единицы продукции j-го типа;

cj- прибыль, получаемая от реализации единицы продукции j-го типа.

Из табл. видно, что для выпуска единицы Продукта1 требуется 6 единиц сырья, значит, для выпуска всей продукции первого типа требуется 6x1 единиц сырья, где x1- количество выпускаемой продукции Продукт1. С учетом того, что для других видов продукции зависимости будут аналогичны, ограничение по сырью будет иметь вид:

6× x1+5× x2+4× x3+3× x4 £ 110.

В этом ограничении левая часть равна величине требуемого ресурса, а правая показывает количество имеющегося ресурса.

Аналогично можно составить ограничения для остальных ресурсов и написать зависимость для целевой функции.

Математическая модель задачи выглядит следующим образом.

Целевая функция имеет вид:

60× x1+70× x2+120× x3+130× x4® max

Ограничения имеют вид:

x1+x2+x3+x4£ 16

6× x1+5× x2+4× x3+3× x4£ 110

4× x1+6× x2+10× x3+13× x4£ 100

xj³ 0; j= .

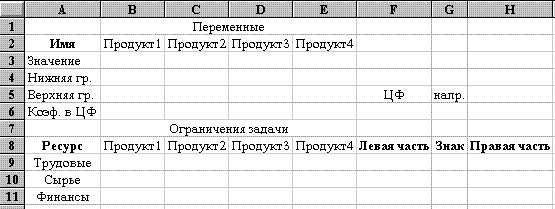
Рис. 6

1). Форма ввода условий задачи представлена на рис. 6. Весь текст на рисунке (и в дальнейшем) является комментарием и на решение задачи не влияет.

2). Необходимые исходные данные приведены на рис. 7.

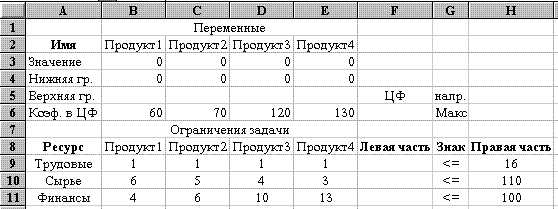
Рис. 7

3). Рассмотрим алгоритмы ввода уравнений целевой функции и ограничений:

Установить курсор в ячейку, содержащую целевую функцию (F6).
Щелкнуть мышью по кнопке -Мастер функций (на панели инструментов). На экране: диалоговое окно "Мастер функций шаг 1 из 2" (рис. 8).
Выбрать категорию Мат. и тригонометрия
Выбрать функцию СУММПРОИЗВ
Щелкнуть по кнопке Шаг >. На экране: диалоговое окно "Мастер функций шаг 2 из 2" (рис. 9).
В массив 1 ввести $B$3:$E$3.

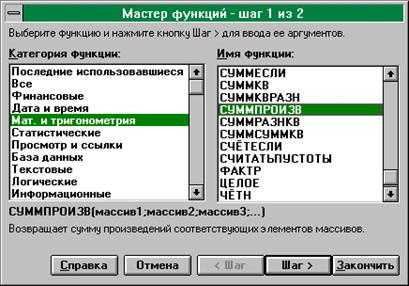
Рис. 8

Следует отметить, что во все диалоговые окна адреса ячеек удобно вводить не с клавиатуры, а протаскивая мышь по ячейкам, чьи адреса следует ввести.

В массив 2 ввести B6:E6.
Щелкнуть по кнопке Закончить.

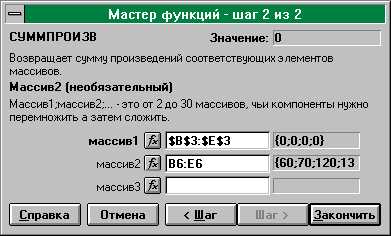
Рис. 9

В ячейке F6 отображается значение целевой функции, оно равно 0.

Ввод ограничений (в ячейки F9, F10, F11) осуществляется аналогичным образом, с заданием соответствующих адресов. Однако значительно проще можно выполнить данную процедуру используя мышь. Для этого подведите курсор мыши к ячейке с целевой функцией (F6), нажмите клавишу <Ctrl> (при этом рядом с изображением курсора мыши должен появиться знак "+"). Удерживая <Ctrl> перетащите содержимое ячейки F6 в ячейку F9. Содержимое F6 скопировано в F9. Ячейка F9 стала активной, об этом свидетельствует черная рамка вокруг нее, также называемая курсором. В правом нижнем углу курсора-рамки имеется маленький квадрат. Подведите курсор мыши к нему (курсор мыши превратится в черный крестик), "ухватите" мышью квадрат и тяните вниз до ячейки F11 включительно. Таким образом вы скопируете формулу из F9 в ячейки F10 и F11.

Теперь таблица примет вид, представленный на рис. 10. В режиме представления формул она показана на рис. 11.

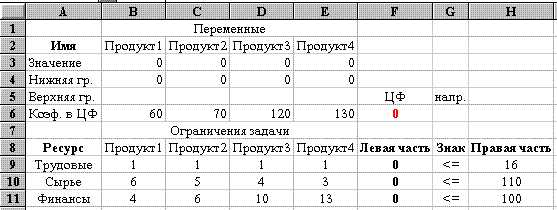
Рис. 10

Рис. 11

Все необходимые условия внесены в таблицу в виде формул. Следующим этапом будет поиск решения задачи средствами Excel.

1. 2. Работа в диалоговом окне "Поиск решения"

1). Выберите последовательно опции меню Сервис, Поиск решения. На экране появится соответствующее окно (рис. 12).

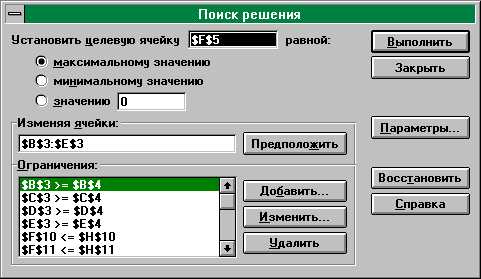
Рис. 12

Поясним смысл элементов окна.

Установить целевую ячейку- определяет целевую ячейку, значение которой необходимо максимизировать или минимизировать, или сделать равным конкретному значению.

Изменяя ячейки- определяет изменяемые ячейки. Изменяемая ячейка- это ячейка, которая может быть изменена в процессе Поиска Решения для достижения нужного результата в ячейке из окна Установить целевую ячейку с удовлетворением поставленных ограничений.

Предположить- отыскивает все неформульные ячейки, прямо или непрямо зависящие от формулы в окне Установить целевую ячейку, и помещает их ссылки в окно Изменяя ячейки.

Ограничения- перечисляет текущие ограничения в данной проблеме.

Добавить- выводит окно диалога “Добавить ограничение”, в котором можно добавить ограничения к текущей проблеме.

Изменить- выводит окно диалога “Изменить ограничение”, в котором можно модифицировать имеющиеся ограничения.

Удалить- удалить выделенное ограничение.

Выполнить- запускает процесс решения определенной проблемы.

Закрыть- закрывает окно диалога, не решая проблемы. Сохраняются лишь изменения, сделанные при помощи кнопок Параметры, Добавить, Изменить и Удалить. Не сохраняются изменения, произведенные после использования данных кнопок.

Параметры- выводит окно диалога “Параметры поиска решения”, в котором можно контролировать различные аспекты процесса отыскания решения, а также загрузить или сохранить некоторые параметры, такие, как выделение ячеек и ограничений, для какой-то конкретной проблемы на рабочем листе.

Восстановить- очищает все текущие установки проблемы и возвращает все параметры к их значениям по умолчанию.

Курсор ввода с клавиатуры установлен в поле Установить целевую ячейку. Сюда необходимо внести адрес ячейки, содержащей целевую функцию. Для того чтобы сделать это щелкните мышью на той ячейке рабочего листа, где содержится ЦФ (F6). Вокруг F6 появился движущийся пунктирный контур, а в поле окна- соответствующий адрес. Следует отметить, что подобным способом можно вносить все остальные необходимые данные, это удобнее, чем вводить их с клавиатуры.

2). В поле Равной выберите флажок Максимальному значению.

3). Введите адреса искомых переменных, для этого выделите мышью область таблицы B3:E3.

4). Ввод ограничений задачи. Щелкните на кнопке Добавить. На экране появилось окно "Добавление ограничения" (рис. 13). Excel воспринимает ограничения в виде ссылок на ячейки в которых содержатся соответствующие формулы, при этом левая часть ограничения представляет собой, как правило, ссылку на формулу, а правая- значение: число или ссылку на ячейку, содержащую значение. Адреса ячеек должны содержать символ $. Если определяется интервал ячеек, то он должен быть той же формы и тех же размеров, что и интервал в окне Ссылка на ячейку. Некоторые из ограничений примера представлены на рис. 12.

Рис. 13

Ссылка на ячейку- определяет ячейку или интервал ячеек, чьи значения необходимо ограничить.

Ограничение- определяет условие, налагаемое на содержимое окна Ссылка на ячейку. Выберите из списка отношение, которое нужно установить между ячейкой или интервалом и ограничением, которое нужно ввести в окне справа от списка. Можно выбрать <=, =, >=, или "цел". Если Вы выбрали "цел" для указания на то. что переменная должна быть целочисленной, то слово "Целое" появляется в окне справа от списка.

Добавить- в окне диалога “Добавить ограничение” можно добавить новое ограничение без возврата в диалог “Параметры поиска решений”.

Если при вводе задачи возникает необходимость в изменении или удалении внесенных ограничений или граничных условий, то это делается с помощью кнопок Изменить, Удалить (рис. 12). На этом ввод условий задачи закончен.

5). Установка параметров решения. Щелкните мышью по кнопке Параметры. На экране появится окно "Параметры поиска решения" (рис. 14).

С помощью команд, находящихся в этом окне можно вводить условия для решения задач оптимизации всех классов. Позволяет контролировать различные аспекты процесса отыскания решения, загрузить или сохранить такие параметры, как ссылки на ячейку и ограничения для конкретной проблемы на рабочем листе. Можно определять параметры для линейных и нелинейных задач. Каждый из параметров в окне диалога имеет значение по умолчанию, подходящий для большинства проблем.

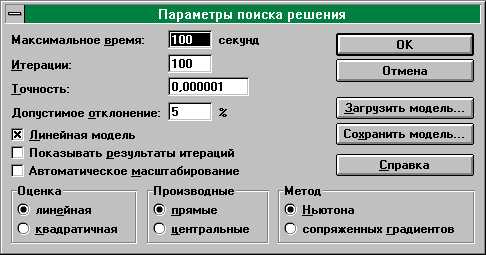
Рис. 14

Поясним элементы окна.

Максимальное время- ограничивает время, требующееся для процесса отыскания решения. Это значение должно быть положительным целым числом. Значение по умолчанию равно 100 (секунд), что вполне годится для большинства малых задач, хотя Вы можете ввести любое значение до 32767.

Число итераций- ограничивает время, требующееся для процесса отыскания решения, путем ограничения числа промежуточных вычислений. Это значение должно быть положительным целым числом до 32767.

Точность- контролирует точность ответов, получаемых при поиске решений. Число, вводимое в поле Точность:

используется при определении того, удовлетворяет ли значение ячейки ограничения нужному равенству или находится ли оно в указанных границах.
должно быть дробным числом от 0 до 1 (не включая концы).

имеет значение по умолчанию равно 0,000001.

указывает на меньшую точность, если число введено с меньшим количеством десятичных знаков; например, 0,0001.

Вообще говоря, чем большая точность определяется (чем меньше число), тем больше времени понадобится для поиска решения. Методы, используемые Поиском Решения, позволяют существенно ускорить поиск, если установить исходное значение, достаточно близкое к искомому решению.

Допустимое отклонение- проблемы, связанные с изменяемыми ячейками, которые должны содержать целые значения, могут требовать большого количества времени, так как при этом необходимо решать несколько подпроблем, каждая из которых есть задача для Поиска Решений с целочисленными ограничениями. Можно подобрать величину отклонения, которая представляет процент допустимого отклонения от оптимального решения при целочисленных ограничениях для всех элементов задачи. Чем выше отклонение (допустимое отклонение в процентах), тем быстрее процесс решения. Установка отклонения не играет роли, если не введены целочисленные ограничения.

Линейная модель- ускоряет процесс отыскания решения. Команда может быть использована только, если все связи в модели линейны.

Показать результаты итераций- прерывает Поиск Решения и показывает результаты после каждой итерации.

Автоматический масштаб- включает автоматический масштаб. Это полезно, когда параметры ввода (Изменяя ячейки) и вывода (Установить целевую ячейку и Ограничения) сильно различаются по величине; например, максимизация прибыли в процентах по отношению к вложениям, исчисляемым в миллионах рублей.

Оценка- эти флажки определяют подход, используемый для получения исходных оценок основных переменных в каждом одномерном поиске.

линейная- использует линейную экстраполяцию вдоль касательного вектора.
квадратичная- использует квадратичную экстраполяцию; это дает лучшие результаты для нелинейных проблем.

Производная- параметры группы Производная определяют способ вычисления производной при оценке частных производных целевых и ограничивающих функций. Эти варианты существенно отличаются своим действием на функциях, чье графическое представление недостаточно гладко или непрерывно. Для таких функций следует использовать вариант Центральная.

прямая- такой способ дифференцирования установлен по умолчанию.
центральная- этот способ требует больше вычислений на рабочем листе, но он может помочь в тех случаях, когда Вы получаете сообщение о том, что Поиск Решений не может улучшить решение.

Метод- параметры метод определяют, какой алгоритм поиска используется при каждой итерации для направления поиска. Нужно указать либо метод Ньютона, либо метод сопряженного градиента.

метод Ньютона- это метод поиска по умолчанию, использующий квази-ньютоновский подход. Этот метод обычно требует больше памяти, чем метод сопряженного градиента, но меньшее количество итераций.
метод сопряженного градиента- поиск методом сопряженного градиента требует меньше памяти, чем ньютоновский метод, но обычно большее число итераций для достижения конкретного уровня точности. Если проблема достаточно велика и важно экономное использование памяти, то стоит применить этот метод. Он также особенно полезен, если Вы видите, что последовательные итерации дают слишком малое отличие последовательных приближений.

Загрузить модель- выводит окно диалога "Загрузить Модель", в котором можно указать, какую именно модель нужно загрузить.

Сохранить модель- выводит окно диалога "Сохранить Модель", в котором можно указать, где именно нужно сохранить данную модель. Используйте кнопку Сохранить модель только в том случае, если нужно сохранить более, чем одну модель Поиска Решения вместе с данным рабочим листом. Первая модель Поиска Решений автоматически сохраняется вместе с рабочим листом.

Установите флажок Линейная модель, остальные параметры будем использовать по умолчанию.

6). Нажмите OK, затем кнопку Выполнить в окне "Поиск решения". Через некоторое время на экране появится окно "Результаты поиска решения" (рис. 15).

Рис. 15

Окно диалога "Результаты поиска решения" выводит результаты последнего вычисления, используя значения ячеек, наиболее близкие к нужному решению.

Когда Поиск Решения завершает попытки отыскания решения, то на экран в верху окна диалога "Результаты поиска решений" выводится сообщение о завершении.

Сохранить найденное решение- принимает решение, найденное Поиском Решения, и подставляет найденные значения в соответствующие ячейки.

Восстановить исходные значения- восстанавливает исходные значения в изменяемых ячейках.

Сохранить сценарий- открывает окно диалога Сохранить сценарий, в котором можно сохранить данную проблему для использования Диспетчером Сценариев пакета Microsoft Excel.

Отчеты- создает указанный тип отчета. Каждый отчет появляется на отдельном листе рабочей книги.

Результаты- перечисляет изменяемые ячейки и ячейку в окне Установить целевую ячейку вместе с исходным и конечным значением. Также показывает ограничения и информацию о них.
Устойчивость- предоставляет информацию о том, насколько чувствительно решение к малым изменениям в формуле окна Установить целевую ячейку или ограничениях. Для нелинейных моделей, отчет предоставляет двойственные значения (нормированные градиенты и множители Лагранжа). Для линейных моделей отчет включает редуцированную стоимость, теневые цены, objective coefficient (с допустимыми отклонениями в обе стороны), и ограничения на изменение правой стороны равенства.
Пределы- перечисляет изменяемые ячейки вместе с соответствующими значениями, ячейку в окне Установить целевую ячейку, верхние и нижние пределы и целевые значения. Нижний предел есть наименьшее значение, которое может находиться в изменяемой ячейке, если фиксировать остальные ячейки и удовлетворить все ограничения. Верхний предел есть наибольшее значение. Целевое значение есть значение ячейки в окне Установить целевую ячейку, когда значение изменяемой ячейки достигает наименьшего или наибольшего предела.

Результаты поиска появятся в таблице (рис. 16).

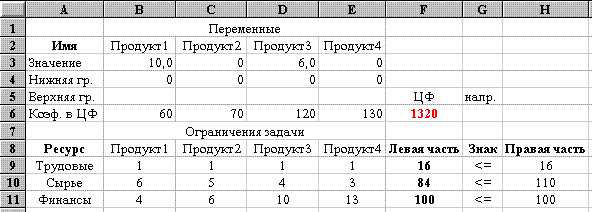
Рис. 16

На рис. 16 видно, что в оптимальном решении Продукт1=B3=10; Продукт2=C3=0; Продукт3=D3=6; Продукт4=E3=0. При этом максимальная прибыль будет составлять F6=1320, а количество использованных ресурсов равно: трудовых=F9=16, сырья=F10=84, финансов=F11=100.

Таково оптимальное решение рассматриваемой задачи распределения ресурсов. Однако решение задачи находится не всегда. Если условия задачи несовместны, на экране появится диалоговое окно (рис. 17):

Рис. 17

Если целевая функция неограничена, то на экране появится диалоговое окно (рис. 18):

Рис. 18

Примеры решения оптимизационных задач средствами Excel

megaobuchalka.ru

3. Примеры решения оптимизационных задач средствами Excel

3.1. Получение требуемого сплава

Предприятию требуется изготовить некоторое количество сплава, содержащего не менее 15 компонент олова, 55 компонент цинка и 30 компонент свинца. Требуемый сплав изготавливается из трех исходных сплавов, в которых содержатся вышеуказанные составляющие. Данные о содержании олова, цинка и свинца в исходных материалах приведены в таблице, там же задана стоимость единицы каждого сплава.

Следует определить, какие из исходных сплавов и в каких количествах нужно использовать для получения требуемого сплава, чтобы суммарные затраты на исходные сплавы были минимальными.

Составляющие	Кол-во компонент составляющих в исходных материалах			Необходимое кол-во компонент в сплаве
	Сплав1	Сплав2	Сплав3
Свинец	40	30	25	30
Цинк	40	60	45	55
Олово	20	10	30	15
Цена единицы материала (руб.)	50	40	70

Математическая модель задачи выглядит следующим образом.

Целевая функция имеет вид:

5x1+4x2+7x3min,

Ограничения имеют вид:

40x1+30x2+25x3=30

40x1+60x2+45x3=55

20x1+10x2+30x3=15

xj0, j=.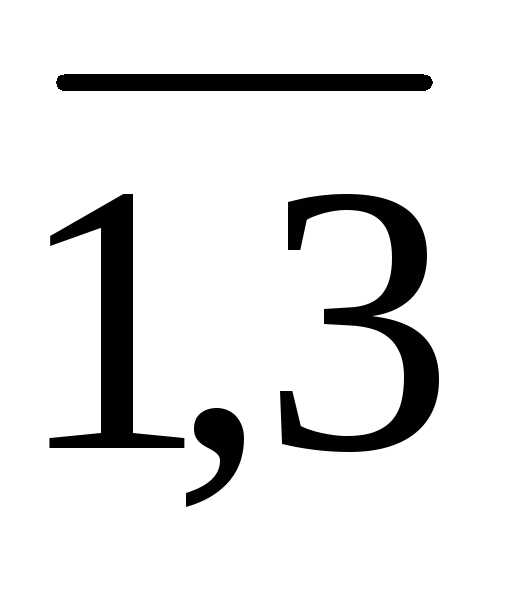

Вид электронной таблицы Excel, созданной для решения задачи, представлен на рис. 19.

Поясним содержание некоторых ячеек таблицы.

В блоке ячеек В3:D3 находятся искомые значения xj, которые до выполнения поиска решения были равны 0. Адрес данного блока входит в поле вводаИзменяя ячейкив окне “Поиск решения” (см. рис. 21). Ячейки блока выполняют роль переменных целевой функции и ограничений- xj.

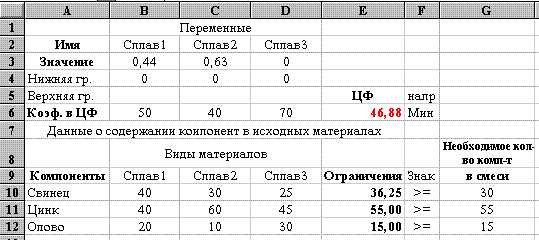
Рис. 19

Блок ячеек B4:D4 содержит правые части граничных неравенств (граничных условий). В ячейках блока содержатся нулевые значения (см. рис. 19).

Блок ячеек B6:D6 содержит данные о цене единицы исходных материалов, каждая его ячейка играет роль коэффициента при целевой функции в математической модели.

В блоках ячеек B10:D12 и G10:G12 находятся данные, соответствующие коэффициентам aijи biограничений математической модели.

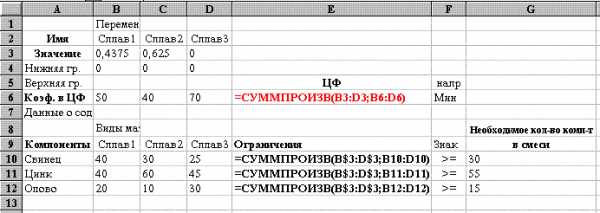
Рис. 20

Сами формулы целевой функции и ограничений расположены соответственно в ячейке E6 и ячейках E10, E11, E12 (см. рис. 19 и 20). Вид электронной таблицы в режиме отображения формул представлен на рис. 20.

После ввода условий задачи необходимо перейти к поиску решения, инициировав соответствующее диалоговое окно (см. рис. 21). Данные в окно удобно вводить с помощью мыши. Для этого необходимо установить курсор в соответствующее поле ввода, затем выделить на рабочем листе требуемые ячейки, адреса выбираемых ячеек автоматически будут появляться в поле ввода.

Обычно в поле ввода Изменяя ячейки(см. рис. 21) заносятся адреса ячеек, которые выполняют роль переменных математической модели. Таким образом, под x1, x2, x3отводятся ячейки B3, C3, D3.

Ограничения удобно задавать поблочно. Первое ограничение данного примера (см. рис. 21) представляет собой запись граничных условий, в которой каждая ячейка левого блока больше либо равна каждой ячейке правого блока. Левый блок означает, как известно, совокупность переменных xj, правый- множество нижних границ переменных. В данном примере нижней границей всех xjявляется 0, поэтому можно было бы записать: $B$3:$D$3>=0. Вторая запись в группеОграниченияпредставляет три ограничения по содержанию требуемых компонентов в сплаве. В каждой ячейке левого блока содержится формула одного из ограничений (см. рис. 20), ячейки правого блока содержат требования bi. По-прежнему, знак “>=“ относится каждой ячейке обоих блоков.

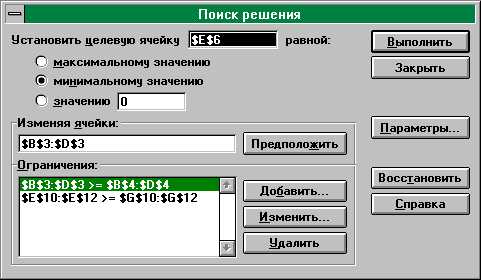
Рис. 21

Способ задания ограничений поблочно существенно облегчает ввод однотипных ограничений. Так, для данного примера двумя записями были заданы шесть ограничений.

Результаты поиска решения заносятся в ячейки таблицы (см. рис. 19). Прежде всего это значения xj. Для получения требуемого сплава нужно 0,44 единицы сплава1 и 0,63 единиц сплава2. Стоимость нового сплава равна 46,88 д. е., количество компонент свинца, цинка и олова равно соответственно 36,25; 55; 15 компонент.

studfiles.net

Решаем задачи оптимизации в Excel

Статья была опубликована в журнале «Планово-экономический отдел» № 11 ноябрь 2012.Все права защищены. Воспроизведение, последующее распространение, сообщение в эфир или по кабелю, доведение до всеобщего сведения статей с сайта разрешается правообладателем только с обязательной ссылкой на печатное СМИ с указанием его названия, номера и года выпуска. В данной статье рассматривается расчет инструмента Excel «Поиск решений». Освоение работы с надстройкой «Поиск решений» даст преимущество в решении многих экономических задач: минимизация расходов при формировании состава сырья и штатного расписания, оптимизация расходов на изготовление при выборе ассортимента продукции, максимизация прибыли при формировании инвестиционной программы.

Зачастую экономисты в своей практике встречаются с вопросами оптимизации расходов.

Рассмотрим пример оптимизации транспортных расходов с помощью инструмента Excel «Поиск решений».

Пример 1

На предприятии X осуществляются транспортные перевозки с помощью четырех компаний до пяти населенных пунктов. Руководство компании решило распределить все количество перевозок между поставщиками транспортных услуг (транспортными компаниями) в определенной пропорции, выраженной в процентном соотношении — удельный вес в общем количестве перевозок. Известны также тарифы транспортных компаний за одну ездку и количество плановых перевозок до каждого населенного пункта в планируемом периоде .

Необходимо оптимально распределить ездки в населенные пункты между транспортными компаниями таким образом, чтобы транспортные расходы были минимальными.

Для успешного решения этой задачи необходимо выбрать минимизируемую ячейку, определить ограничения, а также правильно сформировать таблицы с исходными и расчетными данными (рис. 1).

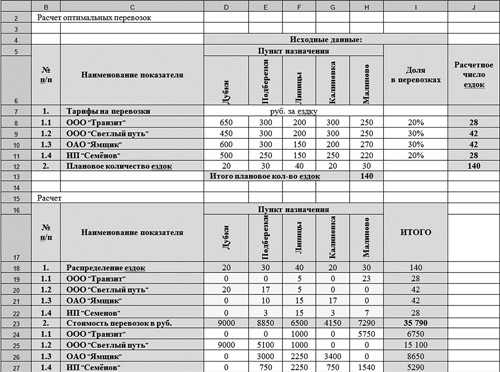
Рис. 1. Расчет оптимальных перевозок

На рис. 1 расположены две таблицы: с исходными данными и расчетными данными. В ячейках D8:h21 расположены тарифы за 1 ездку в разрезе транспортных компаний до пунктов назначения, в ячейках D12:h22 — плановое количество ездок за период до пунктов назначения, в ячейках I8:I11 — удельный вес перевозок каждой транспортной компании в общем количестве планируемых перевозок за период. Эти ячейки для удобства не раскрашены. В ячейках J8:J12 и Н13 рассчитано число ездок по каждой транспортной компании и в целом за период. Формулы в этих ячейках выглядят следующим образом:

Ячейка Н13: =СУММ(D12:h22),

Ячейка J8: =I8*$H$13.

Данную формулу из ячейки J8 протаскиваем (копируем) в ячейки J9, J10, J11.

Ячейка J12: =СУММ(J8:J11).

Следующая таблица на листе посвящена расчету и называется «Расчет». Ячейки D19:Н22 предназначены для распределения количества ездок до пунктов назначения между транспортными компаниями. На рис. 1 в ячейках дано такое распределение, заполненное вручную. В ячейках D23:I27 рассчитаны суммы расходов на транспортные перевозки в разрезе транспортных компаний, оказывающих транспортные услуги, и пунктов назначений, а также итоги.

Приведем формулы, представленные в этих ячейках.

Значения в ячейках D24:Н27 получены перемножением количества ездок (ячейки D19:Н22) на тарифы (ячейки D8:Н12). В ячейку D24 запишем формулу:

=D19*D8.

Протащим (скопируем) формулу в ячейки D25:D27 и E24:Н27.

В ячейках D23:I23 формируются итоговые суммы транспортных услуг в разрезе пунктов назначения. Запишем в ячейку D23 формулу:

=СУММ(D24:D27).

Протащим (скопируем) эту формулу в ячейки Е23:I23.

В ячейках I24:I27 формируются итоговые суммы транспортных услуг в разрезе компаний, оказывающих эти услуги. Запишем в ячейку I24 формулу:

=СУММ(D24:h34).

Протащим (скопируем) ее в ячейки I25:I27.

Таким образом, стоимость транспортных расходов по компании в целом формируется в ячейке I23. В первоначальном расчете, представленном на рис. 1, данная сумма равна 35 790 руб.

Скопируем данный лист в эту же книгу. Далее необходимо приступить непосредственно к оптимизации. Задача — подобрать в ячейках D19:Н22 такие значения, чтобы в ячейке I23 была рассчитана минимальная сумма расходов на транспорт. Для этого воспользуемся инструментом «Поиск решений».

Для начала надо выбрать оптимизируемую ячейку (I23). Затем вызовем диалоговое окно «Поиск решений», представленное на рис. 2.

Это важно. Надстройку «Поиск решений» не всегда можно обнаружить в меню рабочего стола компьютера, так как она может быть не подключена. Для ее подключения необходимо выполнить ряд действий, которые аналогичны во всех версиях MS Office: «Сервис — Надстройки — Поиск решений (установить флажок)». Теперь данный инструмент можно будет найти на панели инструментов рабочего стола.

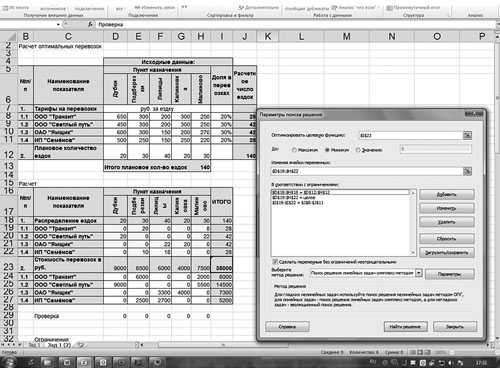
Рис. 2. Использование надстройки «Поиск решений»

В строке «Оптимизировать целевую функцию» будет стоять адрес оптимизируемой ячейки, в данном случае — $I$23. Выберем цель, поставив флажок «Минимум». В строке «Изменяя ячейки переменных» помещаются адреса ячеек, которые необходимо будет подобрать для достижения желаемого результата ($D$19:$Н$22).

В поле запишем ограничения в соответствии с ограничениями. Для этого воспользуемся кнопкой «Добавить», которая откроет окно «Добавить ограничения». Введем одно из ограничений:

$D$19:$H$22 = целое,

$D$12:$H$12 = $D$18:$H$18,

$J$8:$J$11 = $I$19:$I22.

Чтобы добавить следующее ограничение, в этом же окне нажмите на кнопку «Добавить». Результатом этого действия будет добавление текущего ограничения в список ограничений, а поля окна «Добавить ограничения» будут очищены для ввода следующего ограничения. После того как введено последнее из ограничений, необходимо нажать на кнопку «ОК».

Порядок ввода ограничений не имеет значения. Главное — не забыть ни одно из ограничений.

В данном примере все ограничения представлены в виде равенств. Но существуют задачи, в которых требуются ввести ограничения в виде неравенств. Например, в транспортных компаниях объем перевозимого груза не может превышать грузоподъемности автомобиля (или время работы автотранспортного средства не может превышать количества часов в сутки за вычетом нормативных простоев).

Очень важно правильно сформулировать ограничения. Для того чтобы не забыть ни одно из ограничений, необходимо правильно поставить задачу и определить ее цели. Не бывает мелочей в постановке задачи. В задаче о поставке деталей необходимо учесть, что количество деталей на складе на начало периода плюс количество поступивших за планируемый период деталей должно равняться сумме их остатка на складе на конец периода плюс количество отгруженных деталей за планируемый период. Или, например, количество деталей на начало планируемого периода должно равняться количеству деталей на конец периода, предшествующему планируемому.

Необходимо также помнить о том, что некоторые показатели могут быть только положительными значениями (например, сумма поступления от покупателя на расчетный счет поставщик). В данном случае в ограничениях целесообразно указать, что эта величина не может быть отрицательной, иначе надстройка «Поиск решений», вполне возможно, предложит в качестве решения отрицательное число.

Далее следует выбрать метод решения. Для этого необходимо определить, является модель линейной или нелинейной. Напомним, что линейной моделью является такая модель, связи в которой между данными для расчета и результирующим показателем можно описать линейными функциями. Линейная функция имеет следующий вид:

F(x) = a1 × x1 + а2 × x2 + … + аn × xn,

где a1, а2, …, аn — константы;

x1, x2, …, xn — переменные.

Данная модель является линейной.

Примером нелинейной модели является оптимизация перевозок с целью минимизации расходов, когда тарифы на перевозки распределены по интервалам:

от 0 до 10 км — стоимость перевозки 200 руб.;
от 11 до 20 км — стоимость перевозки 250 руб.;
от 21 до 50 км — стоимость перевозки 500 руб. и т. д.

Вернемся к диалоговому окну «Параметры поиска решений». Далее нажимаем кнопку «Найти решение», в результате чего появится окно с результатом поиска решения. Так как нам необходимо сохранить найденный результат, то ставим флажок «Сохранить найденное решение», в результате чего на нашем листе сохранится найденное решение. Нажмем кнопку «ОК».

В ячейках $D$19:$Н$22 появляются подобранные системой значения, при которых в ячейке I23 формируется минимальное значение стоимости транспортных услуг — 35 000 руб.

В данном случае отклонения от подобранного нами вручную результата составляют лишь 2,2 %, или 790 руб., но это означает лишь то, что мы вручную удачно подобрали решение.

На рис. 3 представлены полученные при оптимизации данные.

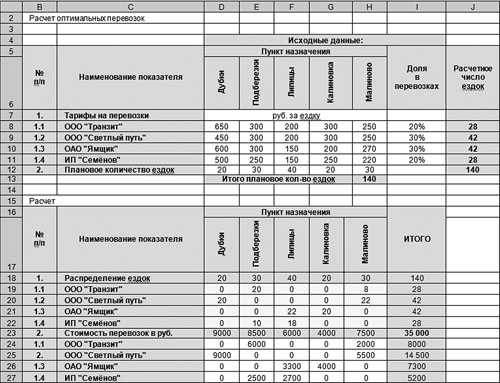
Рис. 3. Результаты оптимизации

Для того чтобы использовать ссылки на ячейки в составе сценария, необходимо сохранить этот сценарий, нажав на кнопку «Сохранить сценарий» в окне «Результат поиска решения», введя имя сценария и нажав кнопку «ОК». При этом исходные данные сохраняются.

Таким образом, предоставлена возможность сохранить все варианты решений при изменении исходных данных. Затем можно создавать отчеты, по которым можно сравнивать влияние изменений исходных данных и ограничений на результат решения.

Существует одна важная деталь: при расчетах количества ездок лучше всего в ячейках J8:J11 использовать функцию округления, чтобы значения были целыми числами.

По этому случаю рассмотрим пример с другими исходными данными.

Пример 2

В ячейках J8:J11 запишем формулу, позволяющую округлить вычисляемые значения до целого числа, которая имеет вид:

Ячейка J8: =ОКРУГЛ(I8*$H$13;0).

Протащим (скопируем) эту формулу в ячейки J9:J11.

Как видим (рис. 4) плановое количество ездок в ячейке Н13 отличается от суммы в ячейках J8:J11, записанной в ячейке J12: значение в ячейке J12, полученное в результате суммирования округленных результатов расчетов числа ездок в ячейках J8:J11, не равно значению в ячейке Н13, полученному суммированием планового числа ездок до пунктов назначения. Это издержки примененной функции округления. Для того чтобы избежать данной ошибки, проделаем следующую процедуру. Для контроля и удобства вычислений введем проверочную ячейку J13. Формула в этой ячейке будет представлять собой разницу полученных значений в ячейках J12 и h23. Ячейка понадобится нам для коррекции вычислений.

Рис. 4. Пример с функцией округления расчетного числа ездок до целого числа

Используем для коррекции инструмент «Подбор параметра». Процедура подбора иллюстрируется на рис. 5.

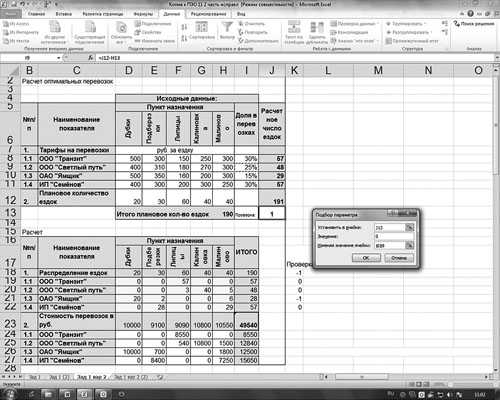
Рис. 5. Использование инструмента «Подбор параметра»

Здесь необходимо применить следующую схему: подобрать в ячейке J13 значение равное 0, изменяя значение в ячейке I9 (доля в перевозках). Предварительно в ячейку I11 целесообразно ввести следующую формулу:

=100 % – I8 – I9 – I10.

Тогда при изменении значения в ячейке I9 в результате применения инструмента «Подбор параметра» автоматически изменится и значение в ячейке I11.

Так как в ячейках I8:I11 применено округление до целого значения, изменения в ячейках I9 и I11 на 0,25 % не обнаруживаются. Эти изменения будут видны, если мы добавим знаки после запятой.

Результат применения инструмента «Подбор параметра» приведен на рис. 6 (на с. …).

Необходимо проделать процедуры, что и в предыдущем примере (см. рис. 1, 2, 3). В ячейках D19:h32 распределим количество ездок для каждой транспортной компании до каждого пункта назначения, используя следующие ограничения:

D19:h32 = целое,

D12:h22 = D18:h28,

J8:J11 = I19:I22.

Сумма транспортных расходов в ячейке I23 на рис. 6 рассчиталась равной 49 540 руб., а наша задача — минимизировать ее.

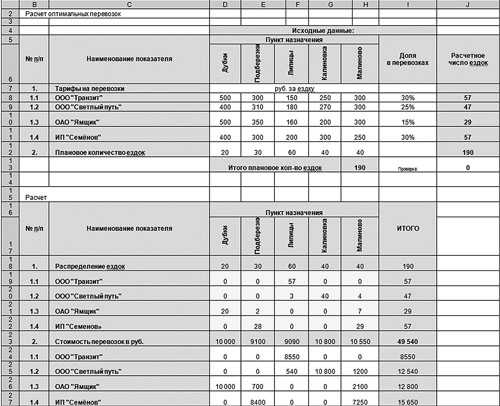
Рис. 6. Скорректированный вариант

На рис. 7 представлена демонстрация использования инструмента «Поиск решений» для оптимизации результата.

Рис. 7. Минимизация значения в ячейке I23 с помощью надстройки «Поиск решения»

На рис. 8 в ячейках D19:Н22 представлены данные, полученные в ходе оптимизации с помощью инструмента «Поиск решений». В результате минимизации в ячейке I23 получено значение 44 990 руб. Отклонения от достигнутого при первоначальном распределении результата составило 9 %, или 4550 руб.

Возможно, имеет право на существование такой вопрос: «Для чего нужна табличная часть со стоимостями перевозок в разрезе транспортных компаний и пунктов назначений?». Ведь можно было бы просто в итоговую ячейку I23 ввести формулу:

=СУММПРОИЗВ(D8:D11;D19:D22)+СУММПРОИЗВ(E8:E11;E19:E22)+СУММПРОИЗВ(F8:F11;F19:F22)+СУММПРОИЗВ(G8:G11;G19:G22)+СУММПРОИЗВ(H8:h21;h29:h32).

Следует помнить следующее:

строк и столбцов может быть достаточно большое количество. Это значит, что написание самой формулы в ячейках будет слишком трудоемкой задачей;
потеряется возможность анализа данных по компаниям и пунктам назначения. Значит, целесообразнее использовать вспомогательную таблицу (в нашем примере это ячейки B23:I27), которая содержала бы множество простых формул. Эти формулы записываются всего в два мгновения: запись в одной из ячеек и копирование или протаскивание в остальные ячейки. Такая таблица несет в себе полезную для анализа информацию о стоимости транспортных услуг в разрезе перевозчиков и пунктов назначения.

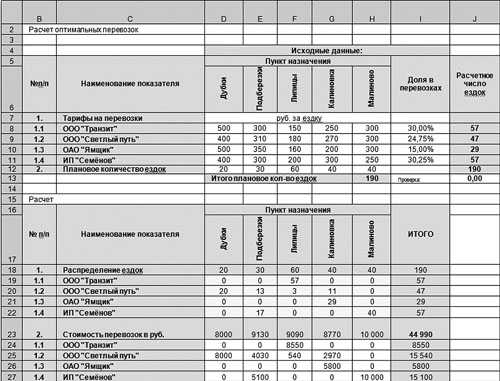
Рис. 8. Результат оптимизации примера с округлением

Заключение

В данной статье рассмотрена простейшая задача, цель статьи — побудить экономистов использовать в расчетах инструмент Excel «Поиск решений», который удобен и прост в применении. Освоив и поняв данный инструмент, можно будет переходить к более сложным задачам.

Освоение работы с надстройкой «Поиск решений» даст преимущество в решении многих экономических задач: минимизация расходов при формировании состава сырья (например, на текстильных предприятиях), оптимизация раскроя (например, на швейных производствах), минимизация расходов при формировании штатного расписания, оптимизация расходов на изготовление при выборе ассортимента продукции, максимизация прибыли при формировании инвестиционной программы и др.

О. С. Илюшина, ведущий экономист ЗАО «Спецнефтетранс»

buhgalter-info.ru

Решение задач оптимизации в excel

Решение задач оптимизации в ExcelПостроение математической модели

Фирма рекламирует свою продукцию с использованием четырех средств: телевизора, радио, газет и рекламных плакатов. Маркетинговые исследования показали, что эти средства приводят к увеличению прибыли соответственно на 10, 5, 7 и 4 доллара в расчете на 1 доллар, затраченный на рекламу. Распределение рекламного бюджета по различным видам рекламы подчинено следующим ограничениям:

а) Полный бюджет составляет 500000 долларов;

b) Следует расходовать не более 40% бюджета на телевидение и не более 20% бюджета на рекламные щиты;

с) Вследствие привлекательности для молодежной части населения различных музыкальных каналов на радио по этой позиции следует расходовать по крайней мере половину того, что планируется на телевидение.

Необходимо:

1. Сформулировать и решить задачу распределения средств по различным источникам для получения максимальной прибыли от рекламы;

2. Объяснить смысл данных отчета по устойчивости;

3. Определить изменится ли оптимальный план распределения средств, если увеличение прибыли от газетной рекламы снизится до 5 долларов в расчете на 1 доллар, затраченный на рекламу;

4. Определить, в какой вид рекламы будет выгоднее вложить дополнительные средства в случае увеличения бюджета фирмы.

Составим математическую модель задачи, выбрав в качестве переменных , х4 - количество средств, затраченных на телевидение, рекламные плакаты, радио и газеты соответственно. Тогда ожидаемая прибыль от рекламы может быть подсчитана по формуле (1)Переменные задачи удовлетворяют ограничениям

(2)

в левых частях которых вычислены затраты денежных ресурсов на телевидение, радио, газеты и рекламные плакаты, а в правых частях записаны максимально возможные запасы средств на эти ресурсы. Учитывая, что переменные задачи по своему экономическому смыслу не могут принимать отрицательные значения, получаем математическую модель задачи оптимального распределения денежных ресурсов с целью получения максимального дохода от рекламы.

.Очевидно, что построенная модель имеет линейную структуру и, следовательно, является задачей линейного программирования.

Создание электронной модели

Чтобы привлечь компьютер к решению этой задачи необходимо ввести исходные данные на лист Excel.

Сначала заносим в таблицу неизменяемые данные, а затем заполняем изменяемые ячейки, в которых расположены компоненты плана . На этапе ввода исходных данных сюда заносятся любые числа, например, единицы. После решения в этих ячейках будут находиться оптимальные значения переменных. Целевая функция (суммарный доход) и левые части ограничений (Затраты по видам реклам) подсчитываются в соответствие с составленной моделью по формуле (1) и левым частям (2).

Вид рекламы	Х1	Х2	Х3	Х4	Суммарный доход
План запуска рекламы	1	1	1	1	Суммарный доход
Прибыль от 1 затраченного $	10	4	5	7	26

Затраты по видам реклам	Затраты по видам реклам					Прибыль от вида рекламы	Запасы денежных ресурсов (тыс. $)
Затраты по видам реклам	Х1	Х2		Х3	Х4	Прибыль от вида рекламы	Запасы денежных ресурсов (тыс. $)
На телевидение	1		0	0	0	1	200
На рекламные щиты	0		1	0	0	1	100
На радио	0		0	1	0	1	100
На газеты	0		0	0	1	1	100
Общие затраты на все виды реклам	1		1	1	1	4	500

coolreferat.com