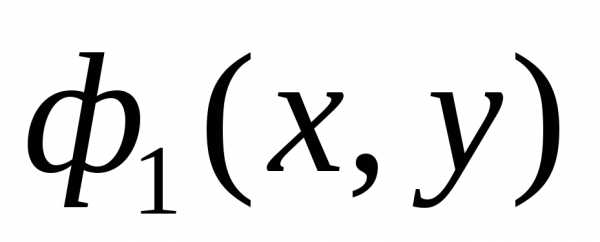§3. Методы решения задач многокритериальной оптимизации, использующие множество Парето. Метод - ограничений. Парето оптимизация
Оптимизация по Парето | Банки
В экономических исследованиях иногда приходится оптимизировать задачи по нескольким критериям. Например, одновременно учитывать минимум затрат и максимум прибыли, максимум прибыли (М^) и минимум риска (D^), максимум выпуска продукции и максимум прибыли, минимальные затраты и минимальный риск и т.д.
Рассмотрим многокритериальный метод оптимизации, предложенный итальянским экономистом Парето.
Пусть имеется п критериев (на max) fj (i = l,n). Найдем некоторое решение задачи. Обозначим его через х и предположим, что существует дру-гое решение х , такое, что для всех критериев fi(x) имеют место неравенства
f(x )>(х ) (i = l,n),
причем хотя бы одно неравенство строгое.
В этом случае решение х приоритетнее, чем х . Поэтому все х , которые удовлетворяют указанному неравенству, надо отбросить и в дальнейшем следует анализировать только те х , для которых не существует х , чтобы выполнялось указанное неравенство.
Множеством Парето при п критериях fi(x) на максимум называется множество таких х, для которых не существует такого х , чтобы выполнялось неравенство
(х*)>^(х),
причем хотя бы одно неравенство строгое.
Дадим геометрическую интерпретацию (рис.7.1, 7.2) паретовых решений для задачи с двумя критериями fl(xl,x2) -^ max,
f2(xi,x2)^mm, (xl5x2)eX.
F = (f1(x1,x2),f2(x1,x2)), (xl5x2)e X.
65
Множество F называется множеством достижения или граничных возможностей. Множество Парето представляет собой часть границы множества достижимости, то есть к нему принадлежат те значения критериев, над которыми не доминируют другие варианты.
В данном случае множеством Парето будет дуга АСВ. Существенным моментом здесь есть то, что решение полученное таким методом, не является однозначным. Лицо, принимающее решение, на свое усмотрение выбирает оптимальное решение из множества Парето (точку на дуге ABC).
Но имеет место чрезвычайно важное утверждение.
Утверждение. На множестве Парето каждая из характеристик fb f2 -(однозначная) функция другой. Другими словами, если две характеристики принадлежат множеству Парето, то по одной характеристике можно однозначно определить другую.
Разработаны общие приемы построения множества Парето. Мы рассмотрим пример, не требующий общей теории.
Пример7.8. Издержки по выпуску двух видов продукции xi и х2 на фирме определяются формулой
f1= lOxj +XjX2 +10x2.
Выручка от реализации продукции определяется формулой
f2 =2x1+3x2. Функция полезности фирмы равна
u(f1,f2) = (10000-f1)f2.
Найти оптимальный план выпуска продукции фирмой, используя множество Парето и функцию полезности при условии, что первой продукции можно выпускать не более 100 единиц, а второй не более 50 единиц.
Математическая модель задачи имеет вид
f1(x1,x2) = 10xj +XjX2 +10x2 —» min, f2(x1,x2) = 2x1+3x2 -^max,
0<Xj <100,
0 < x2 < 50.
Построим (рис.7.3) область определения задачи, множество достижения и выделим на нем множество Парето.
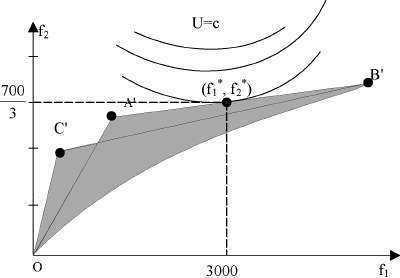
Рис. 7.3
ОА отображается на О'А' так как на ОА х2=0, fi=10xb f2=2xb Поэтому f2=l/5fi> причем 0 < fх < 1000, 0 < f2 < 200.
Аналогично находятся отображения других частей.
Множеством Парето в данной задаче будет часть границы области достижения: О'С'АВ'.
Фирма на свое усмотрение может выпускать продукцию, количество которой находится решением системы
10xj + х1х2+10x2 2xj+3x2 =f2,
где значения (1*1/2) берутся, как координаты, какой либо точки О'С'А'В'.
Найдем оптимальное решение, которое соответствует максимуму функций полезности.
Оптимальное значение находится на отрезке А'В' в силу расположения линий безразличия u(fi, f2) = const.
Уравнение прямой А'В' имеет вид
Решением системы
f = (£-500)+ 150.
f =J (f,-500)+ 150, 2 30
находим fj =3000, f2 = Решая систему
IOjcj +xxx2 +\Qx2=3000,
находим два оптимальных плана выпуска продукции (80; 24,4) и (41,667; 50) или (80,24), (42,50).
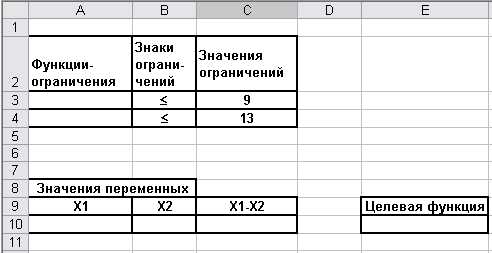
Пример7.9. Пусть для выпуска продукции двух видов используется сырье трех видов. Расходы сырья на единицу продукции каждого вида, запасы сырья, продажная цена единицы продукции и цена единицы сырья записаны в табл. 7.7.
Таблица 7. 7
| Вид сырья | Затраты сырья на единицу продукции | Запасы сырья | Цена единицы сырья | |
| Продукция 1 | Продукция 2 | |||
| Si | 1 | 1 | 120 | 3 |
| s2 | 3 | 1 | 300 | 6 |
| s3 | 1 | 3 | 300 | 4 |
| Цена единицы продукции | 51 | 49 | ||
Найти такой план выпуска продукции, чтобы одновременно максимизировать выручку от продажи продукции и максимизировать прибыль.
Математическая модель задачи имеет вид
Zj = 51xj + 49х2> max,
z2=(51-3-18-4)x1+(49-3-6-12)x2=26x1 +28x2 -^max,
"x!+x2 <120,
<3xj+x2 <300,
Xj+3x2 <300,
Xj>0 x2>0.
Здесь отличие от задач, рассмотренных в математическом программировании, состоит в том, что надо одновременно найти максимум двух функций.
Задачу решим графически (рис. 7.4).
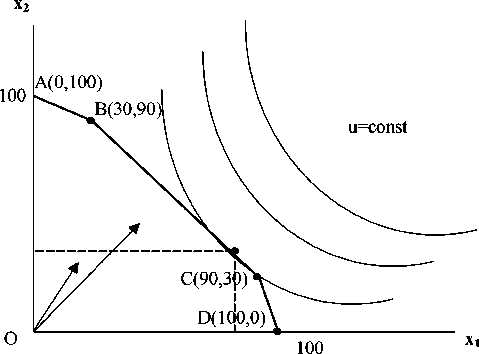
Рис. 7.4
Областью определения задачи является пятиугольник ОАВСД. Функция zi принимает наибольшее значение в точке С, zimax=6060. Функция z2 принимает наибольшее значение в точке В, z2max=3300. Однозначного ответа по выбору оптимального решения нет. Для сопоставления значений ъ\ и вычислим их значения в точках А, В, С, D (Табл. 7. 8).
Таблица 7. 8
| А(0Д00) | В(30,90) | С(90,30) | D(100,0) | |
| Zl | 4900 | 5940 | 6060 | 5100 |
| z2 | 2800 | 3300 | 3180 | 2600 |
Однозначное решение можно найти с помощью функции полезности. Пусть функция полезности фирмы, выпускающей продукцию имеет вид
u=(xr40)x2.
Найдем точку на ломаной ABCD, в которой функция U(xb x2) принимает максимальное значение.
Эта точка находится решением системы
(Xl-40)x2=c,
х +х2 =120.
Первое уравнение получилось из уравнения линии безразличия, которая касается ломаной ABCD. Второе уравнение получилось из равенства производных (в точке касания угловые коэффициенты прямой xi+x2=120 и касательной линии безразличия совпадают).
Решая эту систему, получаем
xi=80, x2=40.
Чтобы найти оптимальное решение по Парето, надо изобразить на плоскости (zi0z2) множество значений (zi z2) когда (xi x2) изменяются в пятиугольнике OABCD. Получится новый пятиугольник OA'B'C'D'.
Множеством Парето будет отрезок В'С. Оптимальному решению будет
соответствовать некоторая точка из этого отрезка (рис. 7.5). Найдя (zx,z2) no аналогии с предыдущим примером, найдем (хг,х2).
Уравнение С'В': z2=-zi+9240.
Пусть функция полезности фирмы имеет вид
u(Zl,z2) = (Zl-2760)z2
Тогда оптимальное решение по Парето находится решением системы
(zj - 2760)z2 = с,
Решая эту систему, находим
ъл=6000,
z2=3240.
Значения xi и х2 находим решением системы
I51XJ+49X2 =6000, 26хт +28х, =3240.
Ответ: xi=60, x2=60.
www.provsebanki.ru
§3. Методы решения задач многокритериальной оптимизации, использующие множество Парето. Метод
Рассмотрим задачу многокритериальной оптимизации
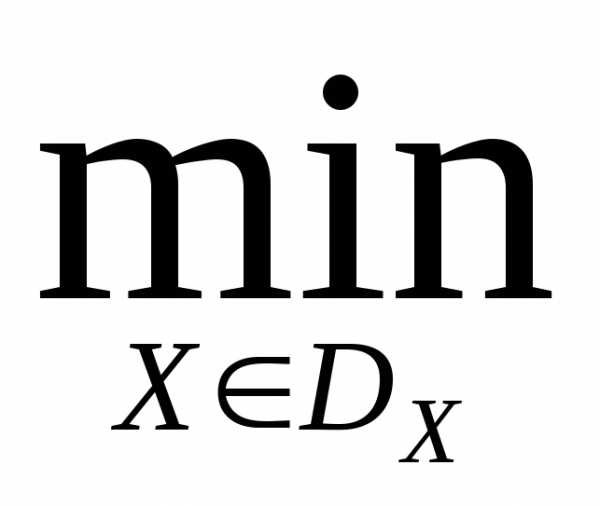 Ф(X)=Ф
Ф(X)=Ф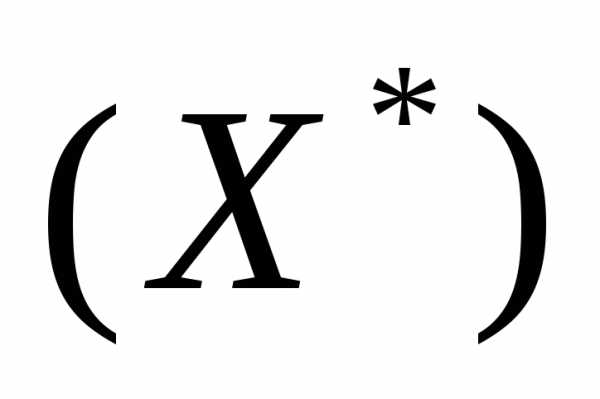 ,(1)
,(1)
где - векторный критерий оптимальности, 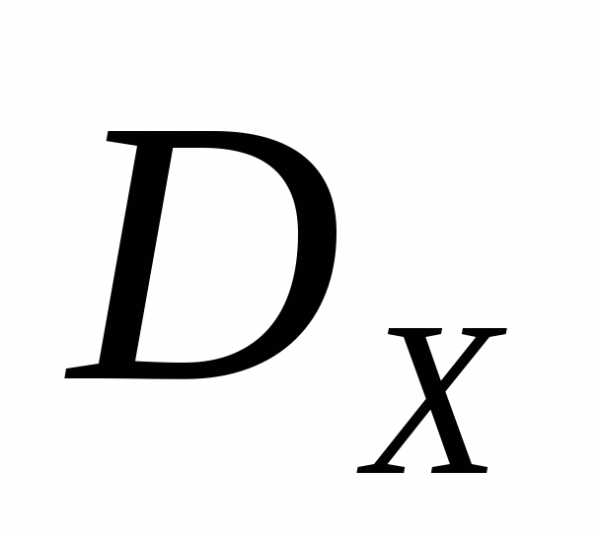 - множество допустимых значений вектора варьируемых параметров.
- множество допустимых значений вектора варьируемых параметров.
Метод  - ограничений относится к группе методов, основанных на сведении задачи многокритериальной оптимизации к задаче однокритериальной оптимизации.
- ограничений относится к группе методов, основанных на сведении задачи многокритериальной оптимизации к задаче однокритериальной оптимизации.
В метод  -ограниченийв качестве скалярного критерия оптимальности
-ограниченийв качестве скалярного критерия оптимальности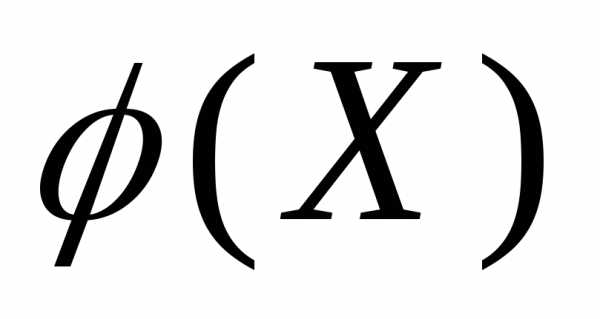 используется самыйважный из частных критериев оптимальности
используется самыйважный из частных критериев оптимальности 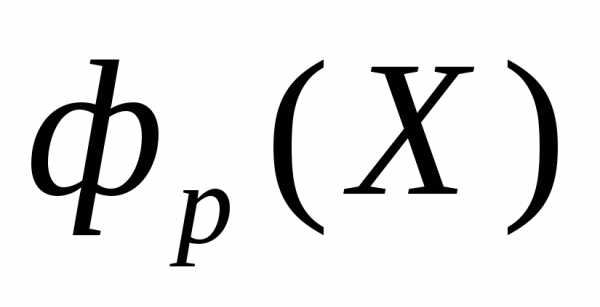 ,
,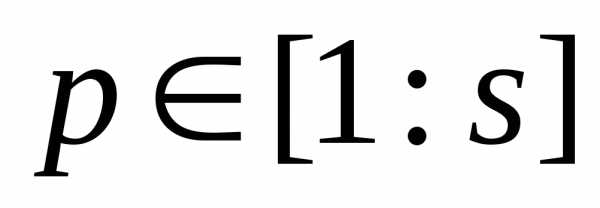 а остальные частные критерии учитываются с помощью ограничений типа неравенств вида
а остальные частные критерии учитываются с помощью ограничений типа неравенств вида
.
Дополнительной информацией в методе -ограничений является информация о номереp самого важного из частных критериев, также информация о максимально допустимых значения частных критериев .
-ограничений является информация о номереp самого важного из частных критериев, также информация о максимально допустимых значения частных критериев .
Таким образом, в методе -ограничений вместо задачи (1) решается задача глобальной условной оптимизации со скалярным критерием оптимальности
-ограничений вместо задачи (1) решается задача глобальной условной оптимизации со скалярным критерием оптимальности
, (2)
где
. (3)
Метод  -ограничений в значительной мере свободен от указанного выше недостатка метода весовых множителей в случае, когда множество
-ограничений в значительной мере свободен от указанного выше недостатка метода весовых множителей в случае, когда множество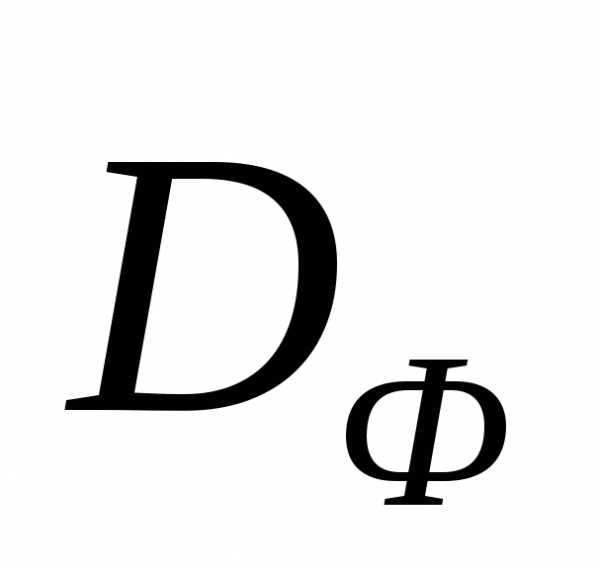 не выпукло (рисунок 11).
не выпукло (рисунок 11).
Недостатком метода  -ограничений является трудность выбора максимально допустимых значения частных критериев , которые гарантировали бы достижимость некоторого решения. Отметим также трудность построения в явном или неявном виде множества
-ограничений является трудность выбора максимально допустимых значения частных критериев , которые гарантировали бы достижимость некоторого решения. Отметим также трудность построения в явном или неявном виде множества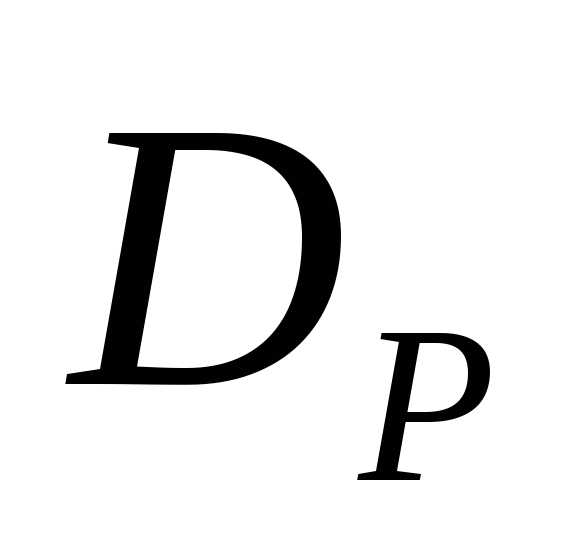 .
.
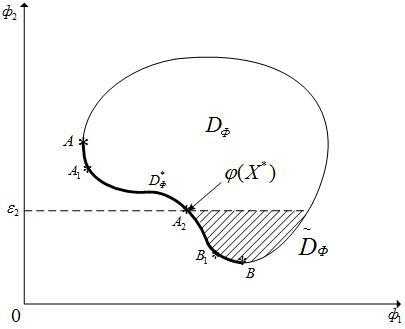
Рисунок 1 - Геометрическая интерпретация метода -ограничений (s=2). Самым важным является критерий
-ограничений (s=2). Самым важным является критерий 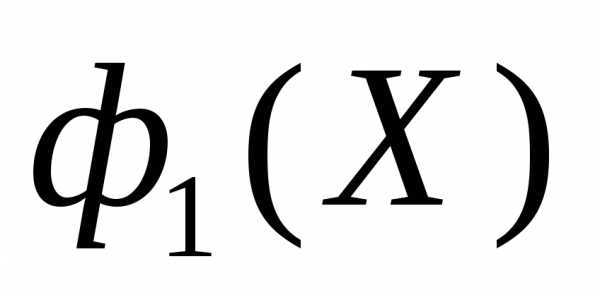 . На критерий
. На критерий 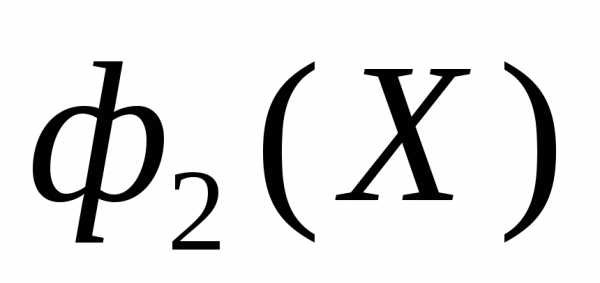 наложено ограничение.
наложено ограничение.
Во множестве 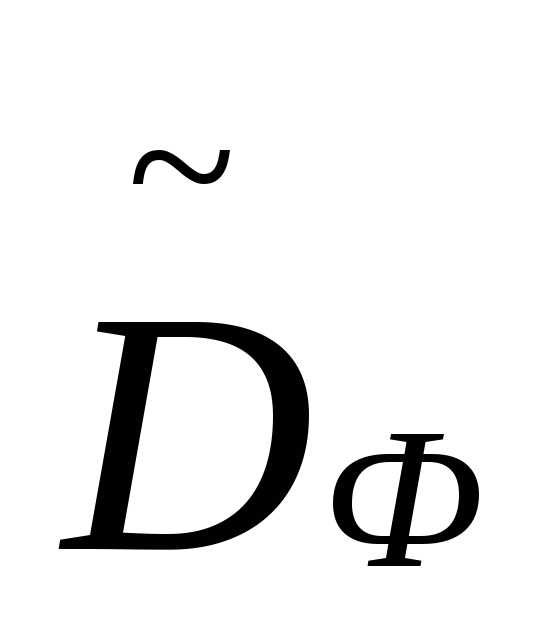 точка
точка является достижимой
является достижимой
Схема метода  -ограничений
-ограничений
Выбираем самый важный из частных критериев оптимальности
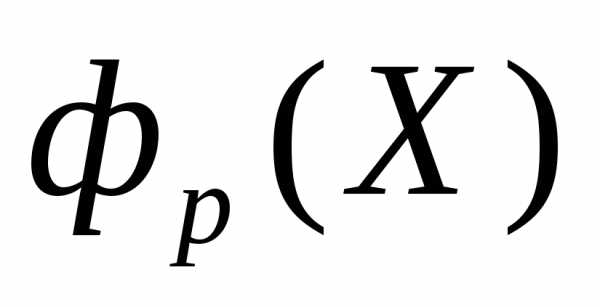 и полагаем .
и полагаем .Задаем ограничения
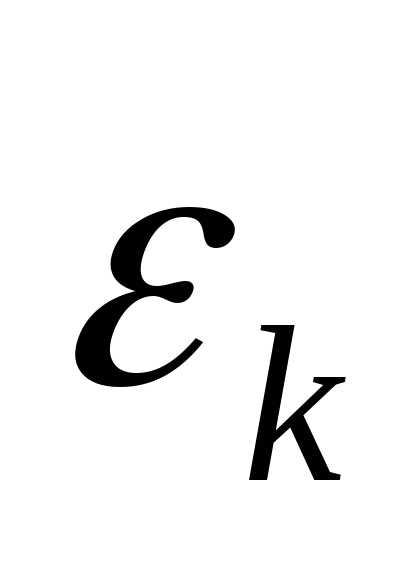 ,
,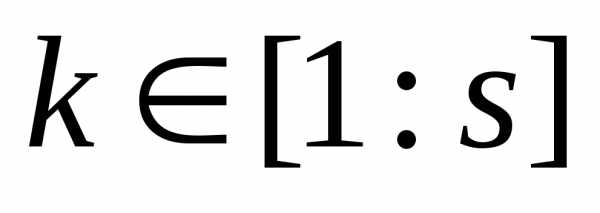 ,
,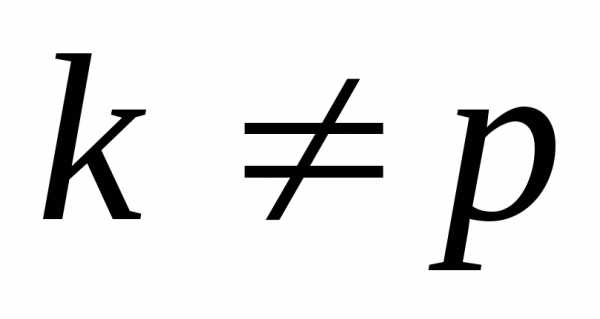 для всех частных критериев оптимальности, исключая критерий
для всех частных критериев оптимальности, исключая критерий 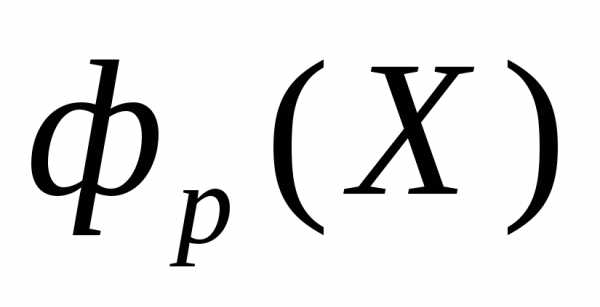 .
.Тем или иным способом формируем множество , а затем – множество
Решаем задачу глобальной условной оптимизации (2). Найденное решение этой задачи
 принимаем в качестве решения задачи многокритериальной оптимизации.
принимаем в качестве решения задачи многокритериальной оптимизации.
Входные термины:
задача многокритериальной оптимизации;
векторный критерий оптимальности;
частный критерий оптимальности;
множество допустимых значений.
Выходные термины:
справедливый компромисс;
отношение предпочтения ;
метод справедливого компромисса.
§4. Методы решения задач многокритериальной оптимизации, использующие множество Парето. Метод справедливого компромисса
Рассмотрим задачу многокритериальной оптимизации
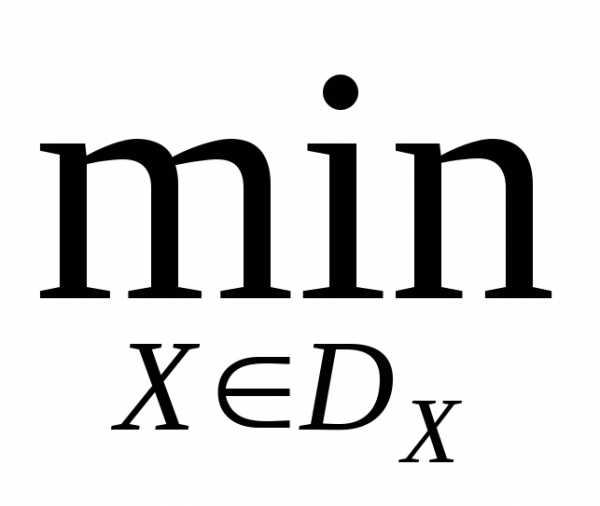 Ф(X)=Ф
Ф(X)=Ф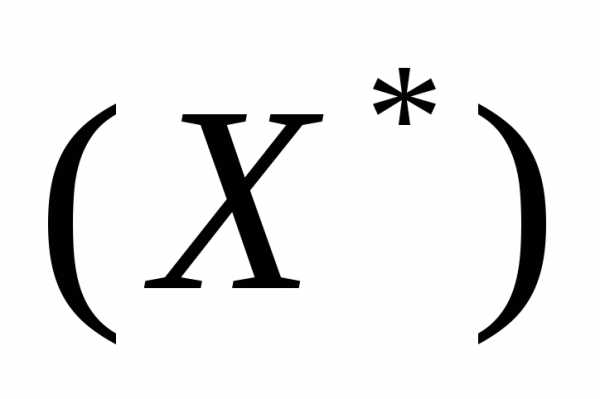 ,(1)
,(1)
где - векторный критерий оптимальности,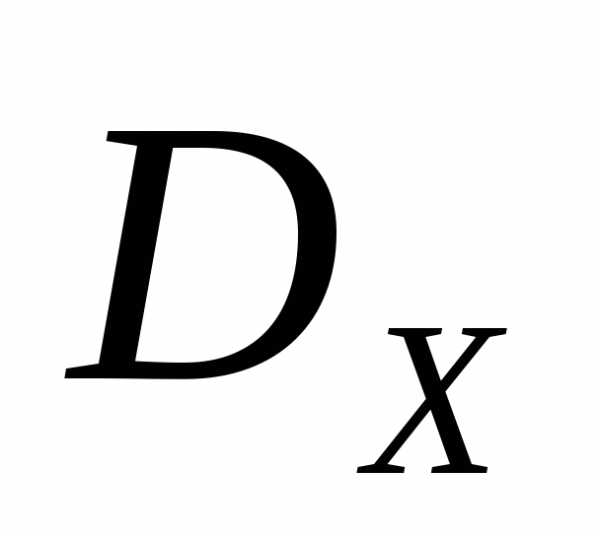 .- множество допустимых значений вектора варьируемых параметров.
.- множество допустимых значений вектора варьируемых параметров.
Метод справедливого компромисса строится на основе понятия «справедливый компромисс» и использует следующее сильное соглашение: все частные критерии имеют одинаковую важность!
Справедливый компромисс
Справедливым компромиссом будем называть такой компромисс, при котором относительный уровень снижения качества решения по одному или нескольким критериям не превосходит относительного уровня повышения качества решения по остальным критериям.
Для формализации понятия справедливого компромисса нам понадобится ввести отношение превосходства  на множестве Парето (не путать с отношением предпочтения!).
на множестве Парето (не путать с отношением предпочтения!).
Пусть во множестве Парето 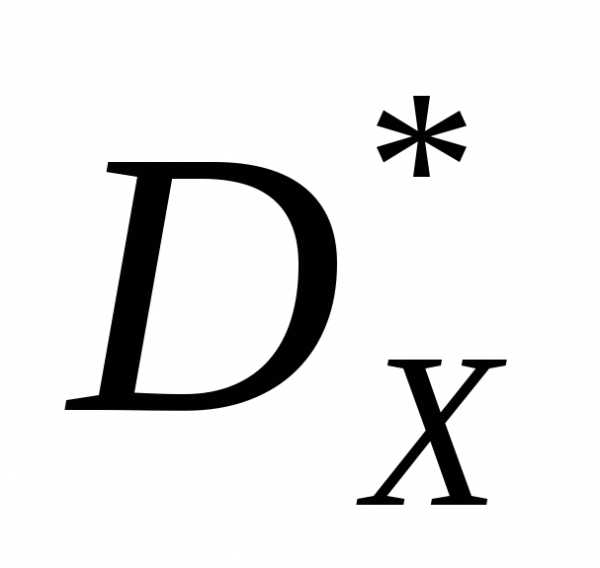 задачи (1) даны две точки
задачи (1) даны две точки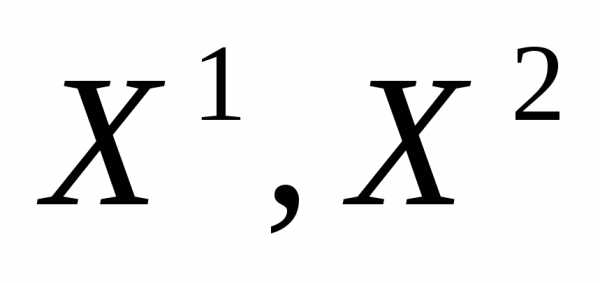 и значения всех частных критериев оптимальности в них. Введем меру относительного изменения (снижения – знак «минус» или повышения – знак «плюс») качества решения по каждому из критериев
и значения всех частных критериев оптимальности в них. Введем меру относительного изменения (снижения – знак «минус» или повышения – знак «плюс») качества решения по каждому из критериев
, (2)
где - абсолютное изменение значения критерия оптимальностипри переходе от решения 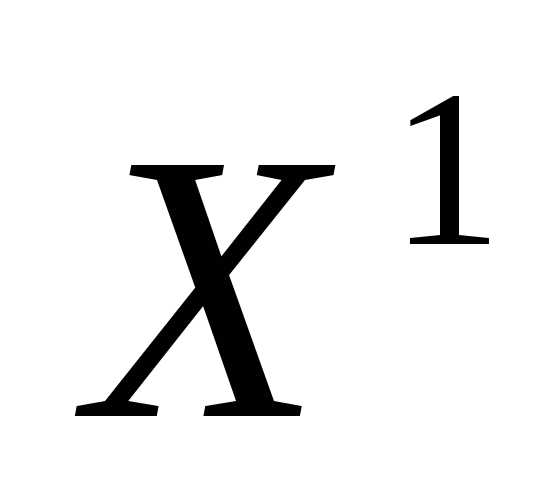 к решению
к решению 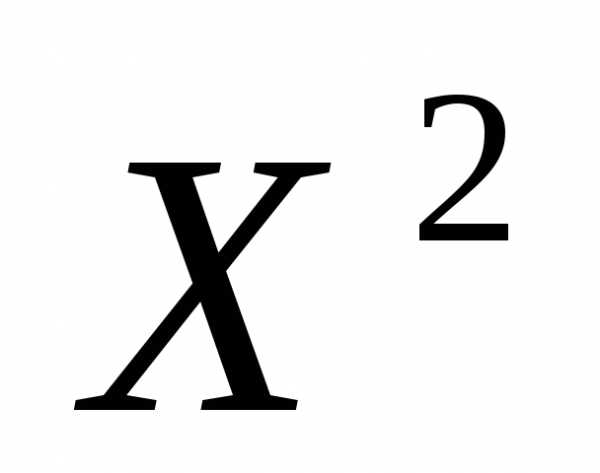 .
.
Вычислим максимальное относительное снижение качества решения при переходе от решения 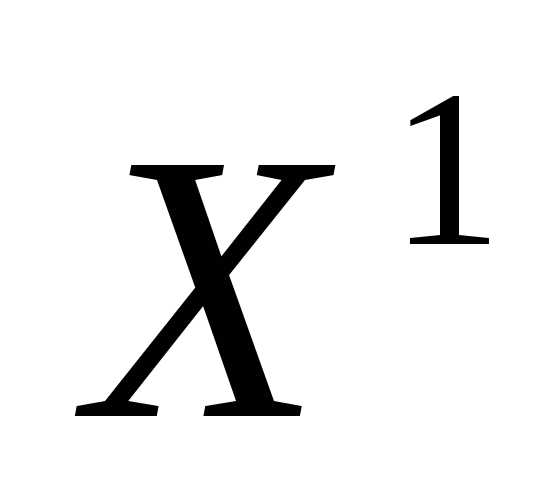 к решению
к решению 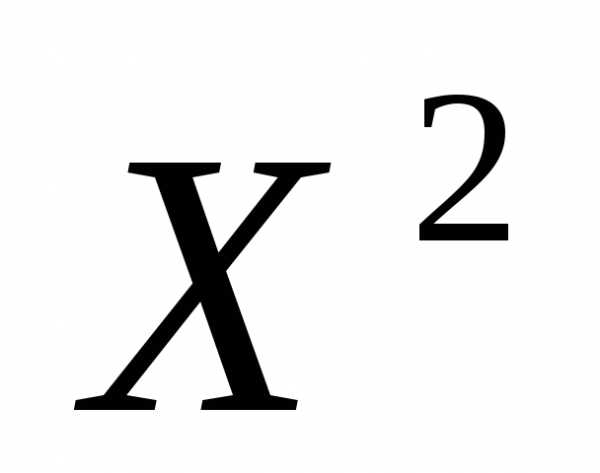
. (3)
Аналогично вычислим максимальное относительное повышение качества решения при переходе от решения 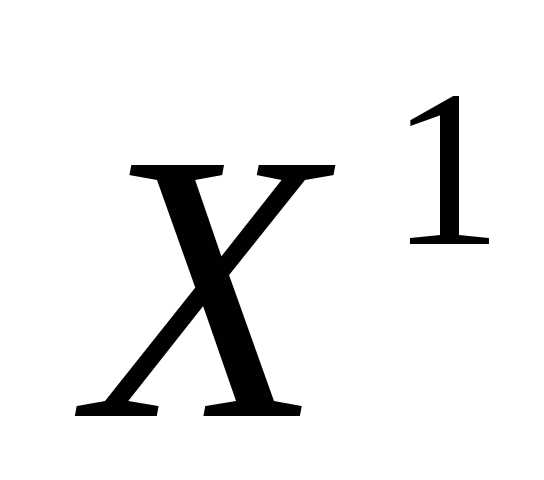 к решению
к решению 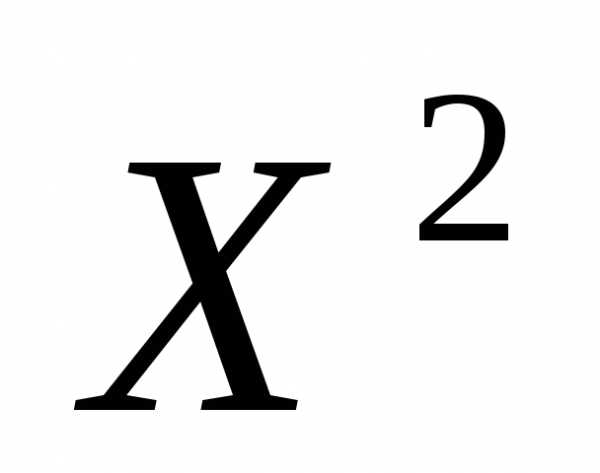
. (4)
Заметим, что поскольку , величинаотрицательна, а величина- положительна.
Будем говорить, что решение 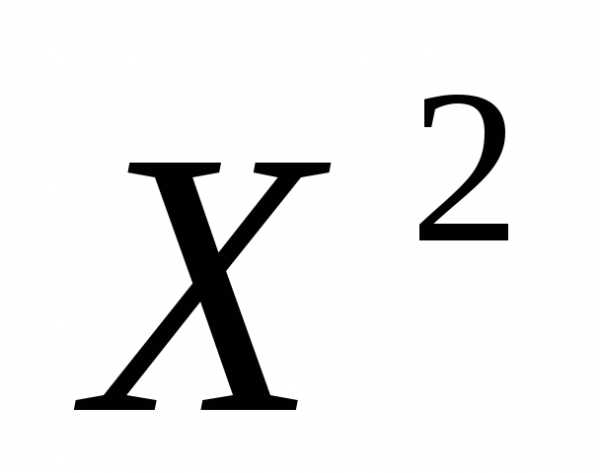 превосходит решения
превосходит решения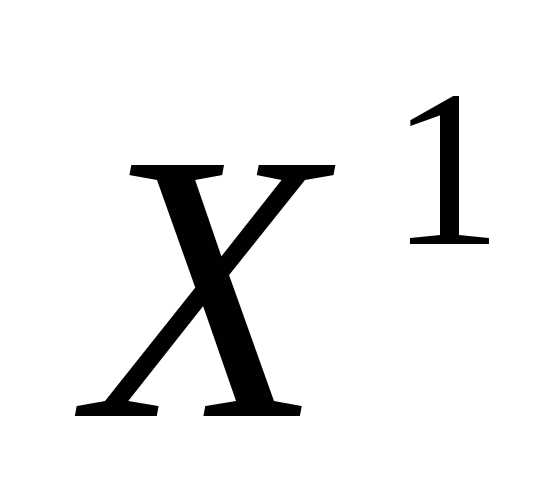 , и писать, если
, и писать, если
. (5)
С другой стороны, будем говорить, что решение превосходит решения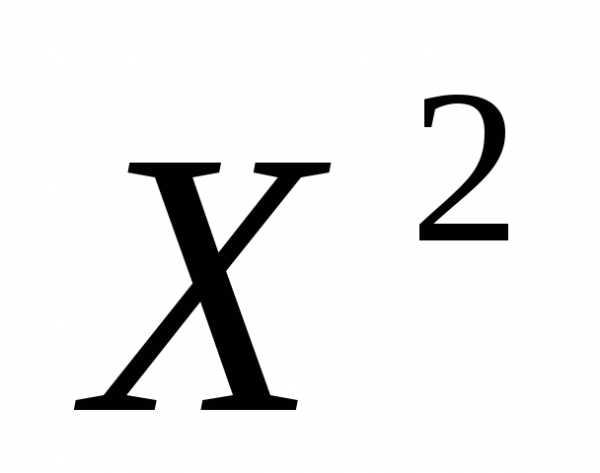 , и писать, если
, и писать, если
. (6)
Пример 1. Пусть заданы четыре частных критерия оптимальности (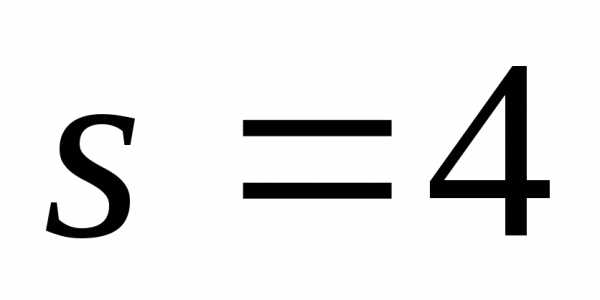 ) и решения
) и решения 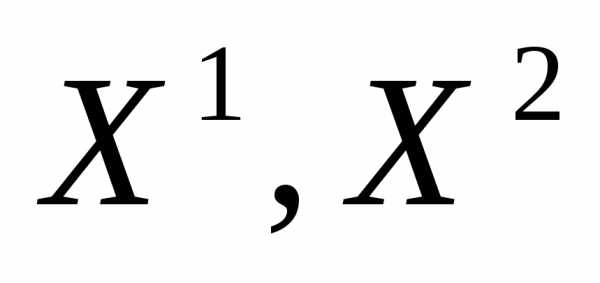 , принадлежащие множеству Парето задачи (1). Положим, что критериив точках
, принадлежащие множеству Парето задачи (1). Положим, что критериив точках 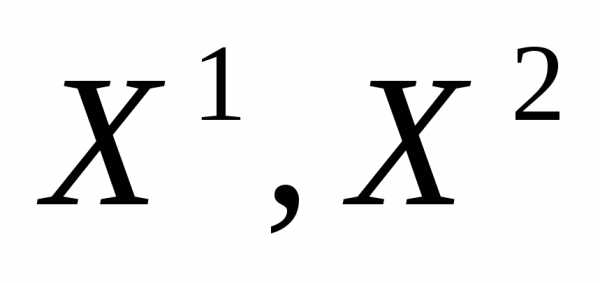 имеют следующие значения:
имеют следующие значения:
По формулам (2) – (4) последовательно имеем
,
,
,
;
,
.
Поскольку , т.е. максимальное относительное повышение качества решения превышает максимальное относительное снижение качества решения, то решение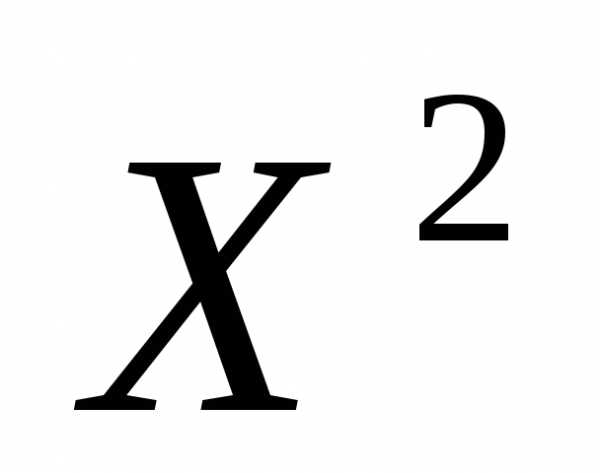 превосходит решение
превосходит решение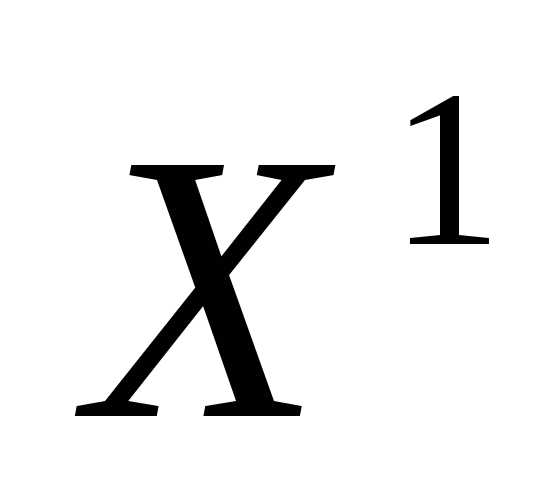 :●
:●
Дополнительной информацией в методе справедливого компромисса является информация об одинаковой важности всех частных критериев, а также информация осправедливом компромиссе, формализованная отношением превосходства 
Схема метода справедливого компромисса
Полагаем счетчик числа итераций
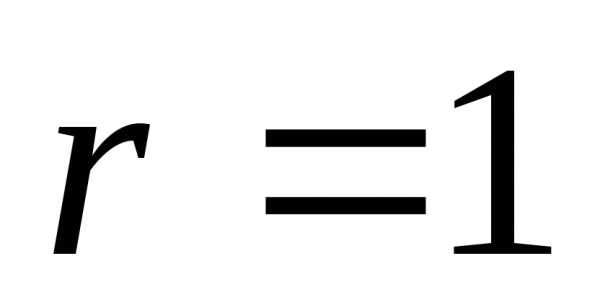 .
.Тем или иным способом выбираем из множества Парето
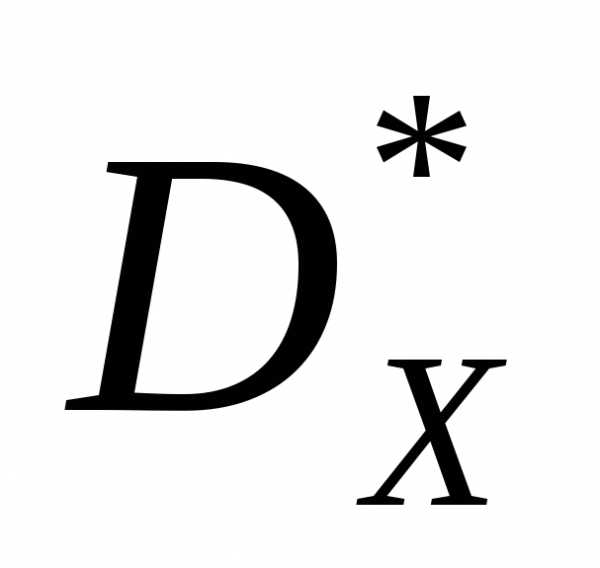 решение
решение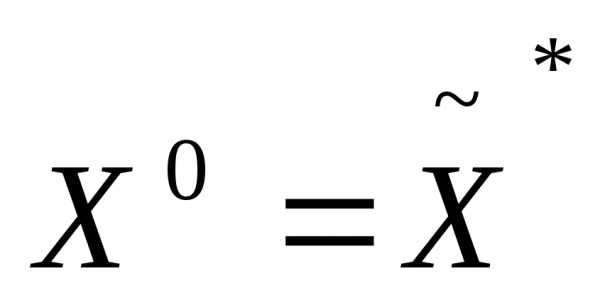 .
.Вычисляем значения всех частных критериев оптимальности .
Тем или иным способом выбираем из множества Парето
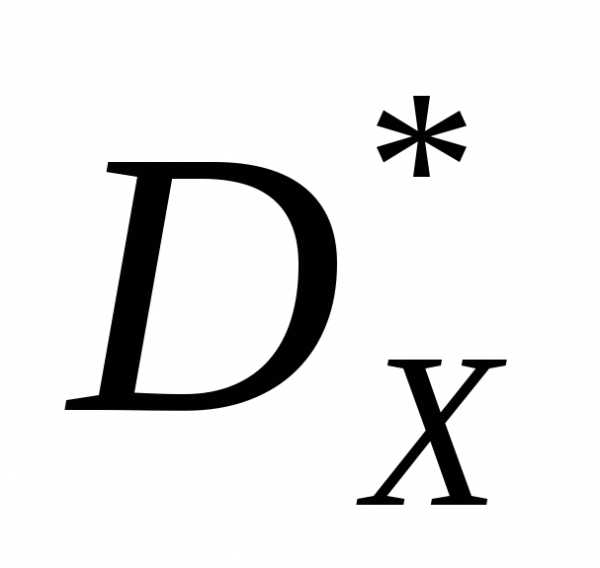 решение
решение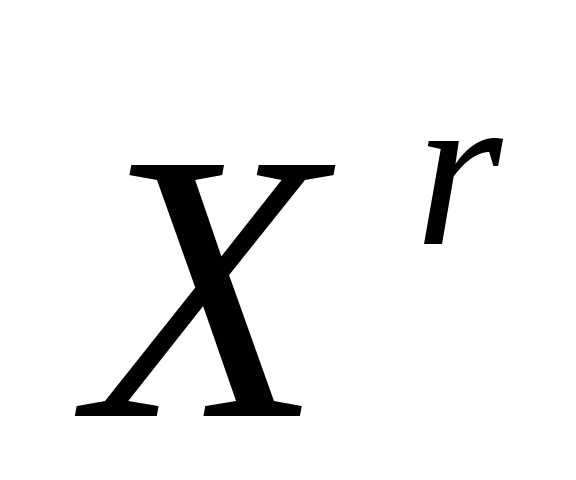 (см. ниже).
(см. ниже).Вычисляем значения всех частных критериев оптимальности .
Если
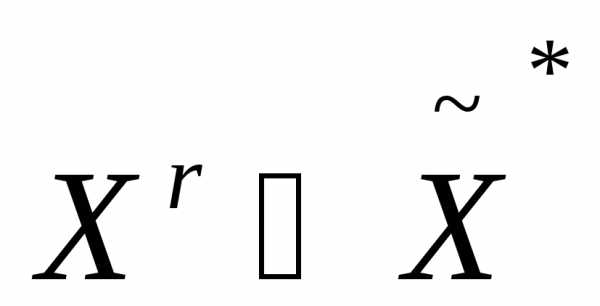 , то полагаем
, то полагаем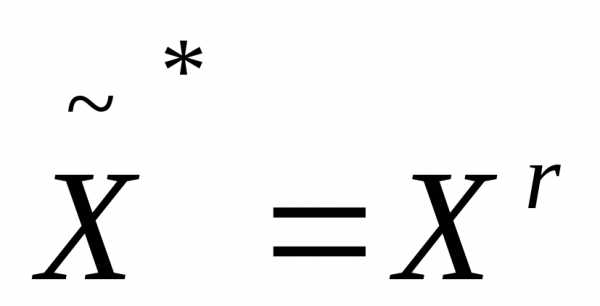 .
.Если условие окончания итераций выполнено (см. ниже), то принимаем точку
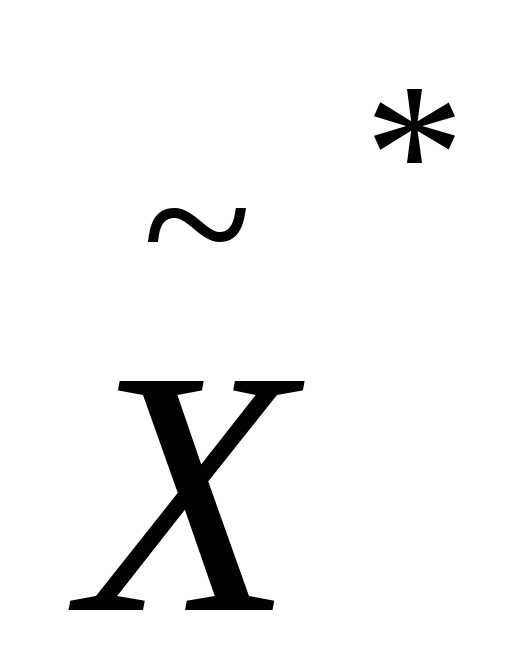 в качестве приближенного решения задачи (1) изаканчиваем вычисления. Иначе - полагаем и переходим к п. 4●
в качестве приближенного решения задачи (1) изаканчиваем вычисления. Иначе - полагаем и переходим к п. 4●
В простейшем случае выбор решений 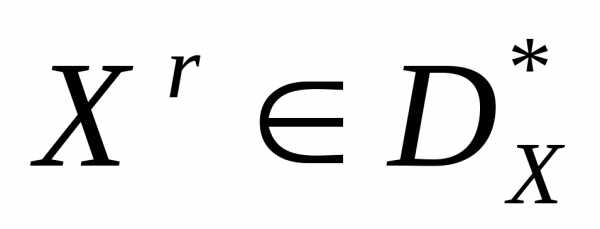 может быть произведен случайным образом. В качестве условия окончания итераций в этом случае может быть использовано достижение заданного количества итераций. Выбор решений
может быть произведен случайным образом. В качестве условия окончания итераций в этом случае может быть использовано достижение заданного количества итераций. Выбор решений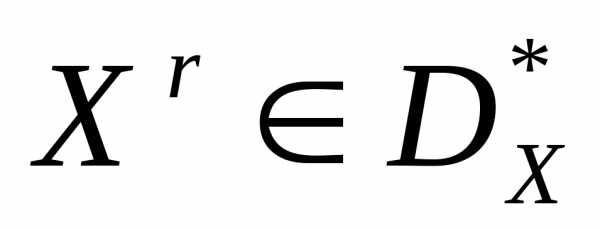 может быть произведен также с помощью полного перебора узлов какой-либо сетки, покрывающей множество
может быть произведен также с помощью полного перебора узлов какой-либо сетки, покрывающей множество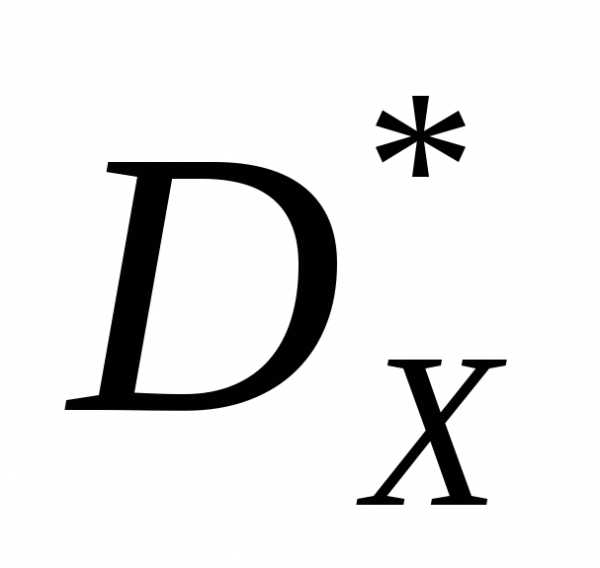 .
.
Замети, что поскольку метод справедливого компромисса использует относительные изменения частных критериев оптимальности, этот метод инвариантен к масштабу измерения частных критериев, т.е. не требуется их нормализация.
Входные термины:
задача многокритериальной оптимизации;
векторный критерий оптимальности;
частный критерий оптимальности;
множество допустимых значений.
Выходные термины:
идеальное решение задачи многокритериальной оптимизации; идеальное решение;
метод приближения к идеальному решению.
studfiles.net
Раздел 2
Задачи непрерывной многокритериальной оптимизации в конечномерных пространствах.
Глава 11. Задачи многокритериальной оптимизации и методы их решения.
Входные термины:
критерий оптимальности;
множество допустимых значений вектора варьируемых параметров.
Выходные термины:
задача многокритериальной оптимизации;
векторный критерий оптимальности;
частный критерий оптимальности;
скалярный критерий оптимальности;
нормализация критериев;
пространство критериев;
пространство варьируемых параметров;
отношение предпочтения
 ;
;отношение эквивалентности;
множество Парето; переговорное множество; область компромисса;
весовые множители (коэффициенты) частных критериев оптимальности.
§1. Постановка задачи многокритериальной оптимизации. Множество Парето
В задачах САПР часто возникает задача обеспечить оптимальность объекта проектирования одновременно по нескольким критериям оптимальности . Обычно эти критерии противоречивы и оптимизация по каждому из них приводит к различным значениям вектора варьируемых параметров Х*. Поэтому выделяется отдельный класс задач многокритериальной оптимизации.
Постановка задачи многокритериальной оптимизации
Будем называть скалярные критерии оптимальности частными критериями оптимальности. Совокупность частных критериев оптимальности Фбудем называть векторным критерием оптимальности. Положим, что ставится задача минимизировать каждый из частных критериев в одной и той же области допустимых значений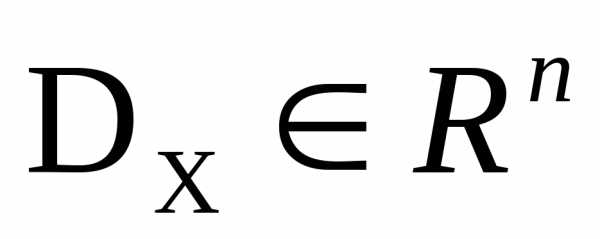 .
.
Условно задачу многокритериальной оптимизации будем записывать в виде
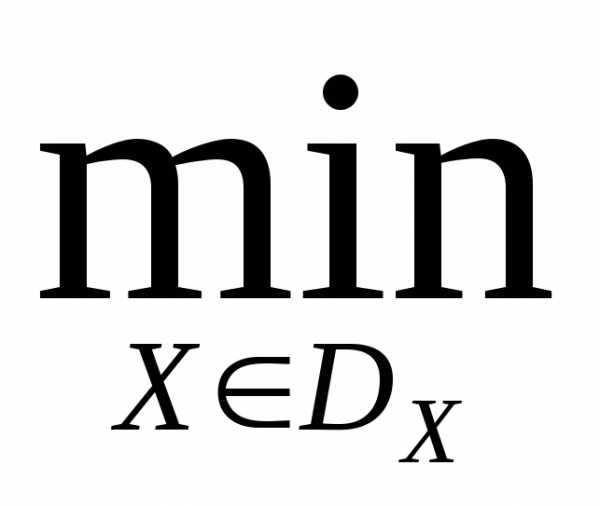 Ф(X)=Ф
Ф(X)=Ф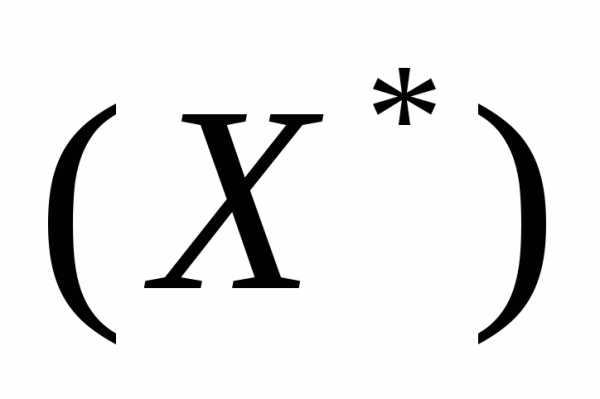 ,(1)
,(1)
где 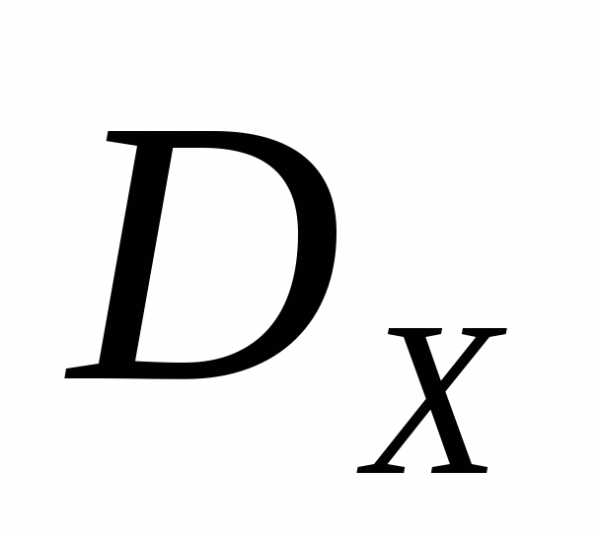 - множество допустимых значений вектора варьируемых параметровX.
- множество допустимых значений вектора варьируемых параметровX.
Решение задачи многоэкстремальной оптимизации в общем случае не является оптимальным ни для одного из частных критериев, а оказывается некоторым компромиссом для вектора Ф(Х) в целом.
Прежде, чем применить тот или иной метод решения задачи (1), обычно производят нормализацию критериев, приводя все частные критерии оптимальностик одному масштабу. Чаще всего при этом используют относительные отклонения частных критериев от их минимальных значений:
,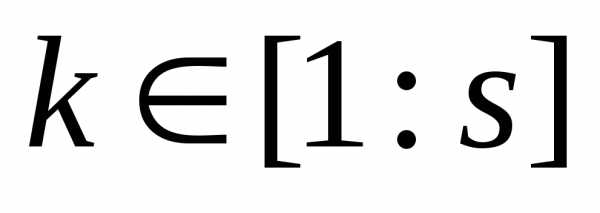
где
,
.
Если не оговорено противное, будем полагать далее, что частные критерии нормализованы, и сохраним за нормализованными частными критериями оптимальности обозначения .
Множество Парето
Введем понятие пространства критериев 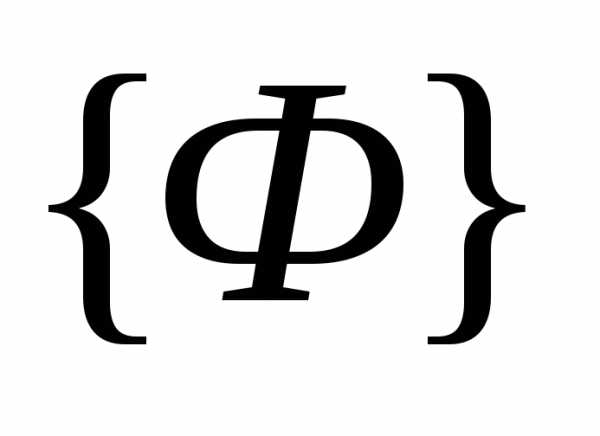 . Пространство критериев имеет размерностьs (по числу частных критериев) и образуется s ортогональными осями координат, вдоль которых откладываются значения частных критериев оптимальности - рисунок 1.
. Пространство критериев имеет размерностьs (по числу частных критериев) и образуется s ортогональными осями координат, вдоль которых откладываются значения частных критериев оптимальности - рисунок 1.
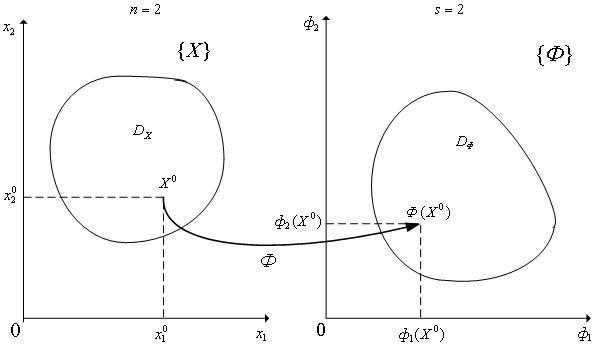
Рисунок 1 - К определению пространства критериев: случай
Векторный критерий оптимальности Φ(X) выполняет отображение множества допустимых значений в некоторую область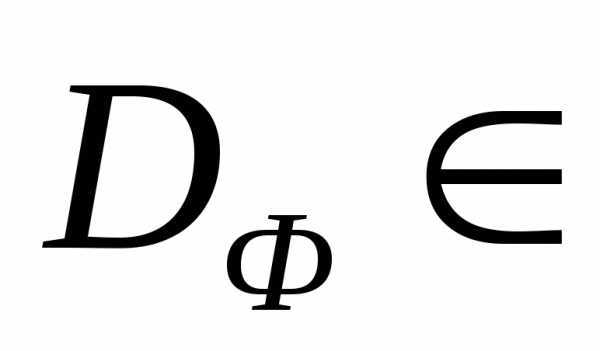
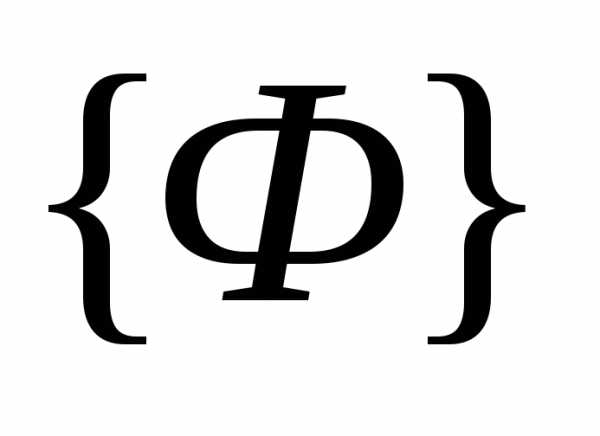 (область достижимости), где
(область достижимости), где 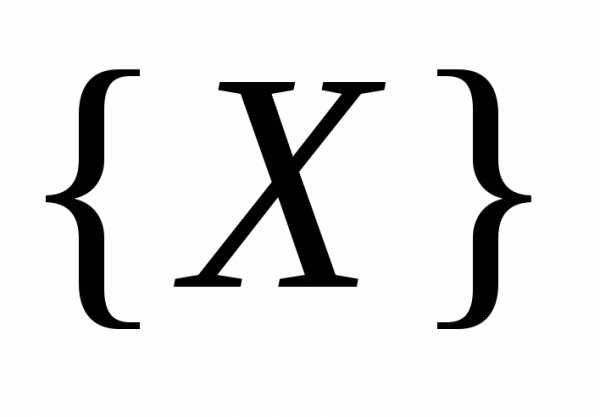 .- пространство варьируемых параметров (рисунок 1).
.- пространство варьируемых параметров (рисунок 1).
Введем на множестве DX отношение предпочтения.
Отношение предпочтения  . Будем говорить, что вектор
. Будем говорить, что вектор 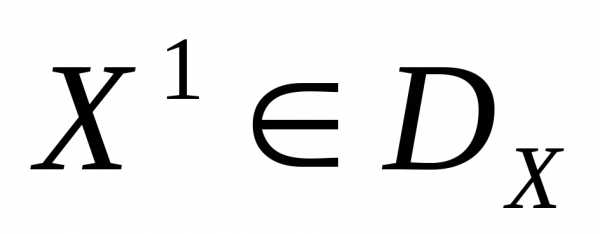 предпочтительнее вектора
предпочтительнее вектора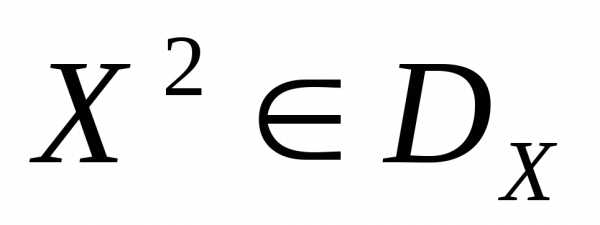 , и писать, если среди равенств и неравенств
, и писать, если среди равенств и неравенств
, 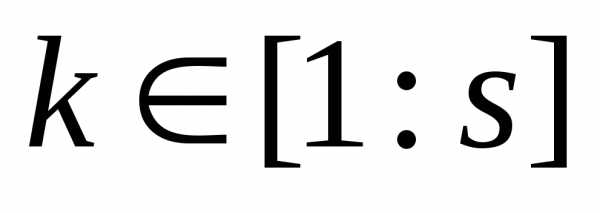
имеется хотя бы одно строгое неравенство (рисунок 2).
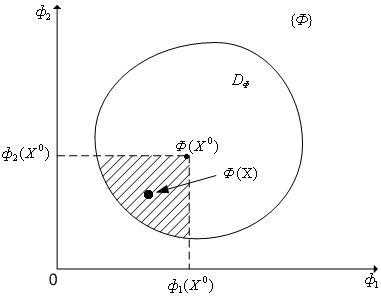
Рисунок 2 - К определению отношения предпочтения (s=2). Для всех точек заштрихованной области , т.е. заштрихованной области пространства критериев соответствуют векторы варьируемых параметров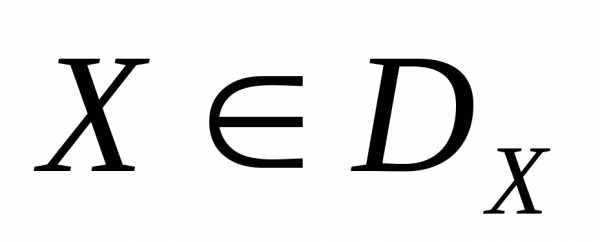 , для которых
, для которых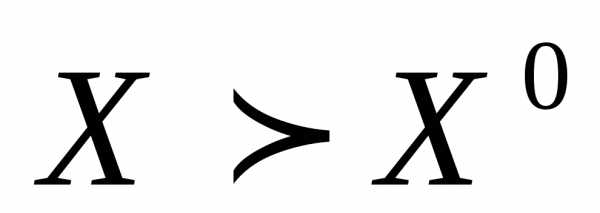
Наряду с этим будем говорить, что вектор критериев оптимальности предпочтительнее вектора критериев оптимальности, и писать, если(рисунок 2).
Заметим, что введенное отношение предпочтения является транзитивным, т.е.
если и, то.
Выделим из множества 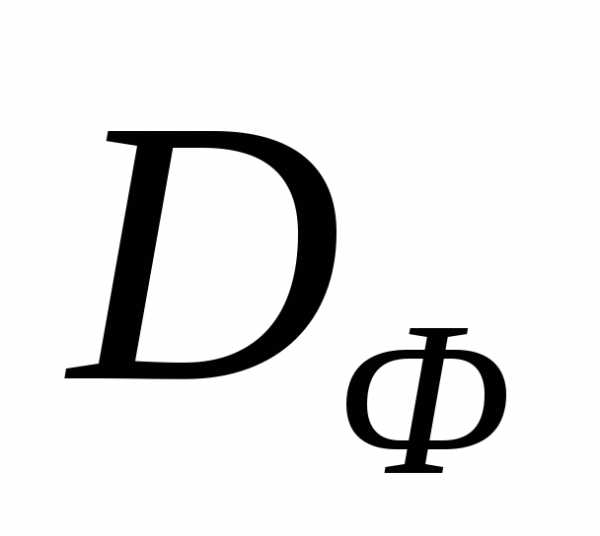 подмножество
подмножество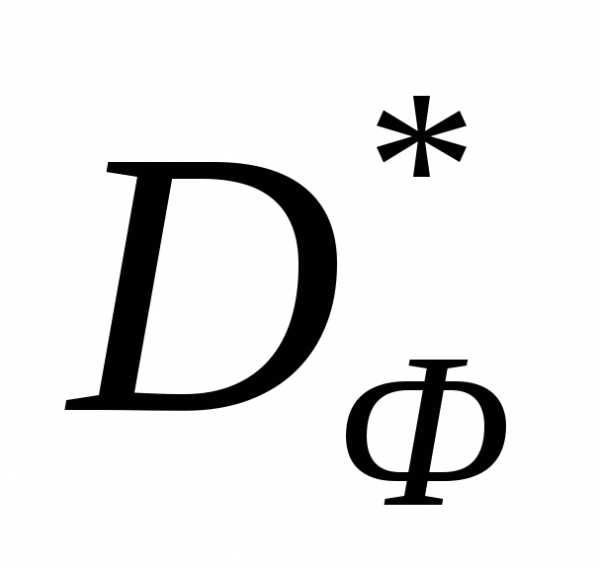 точек, для которых в этом множестве нет более предпочтительных точек. Множество
точек, для которых в этом множестве нет более предпочтительных точек. Множество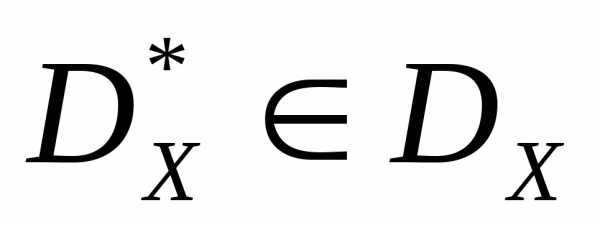 , соответствующее
, соответствующее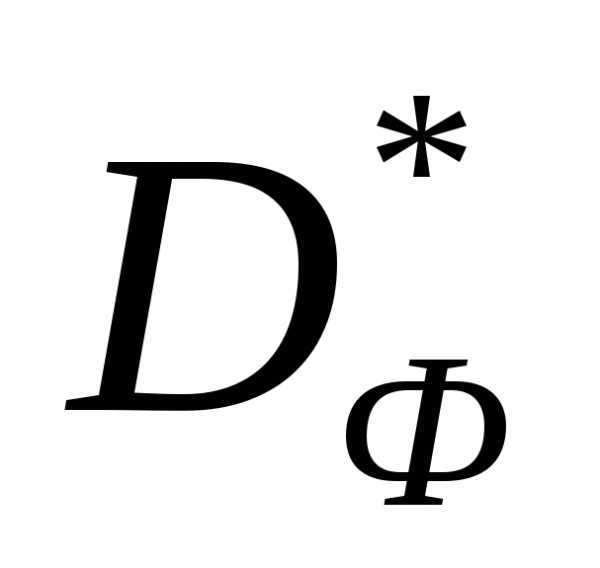 , называетсямножеством Парето (переговорным множеством, областью компромисса) – рисунок 3. Таким образом, если
, называетсямножеством Парето (переговорным множеством, областью компромисса) – рисунок 3. Таким образом, если 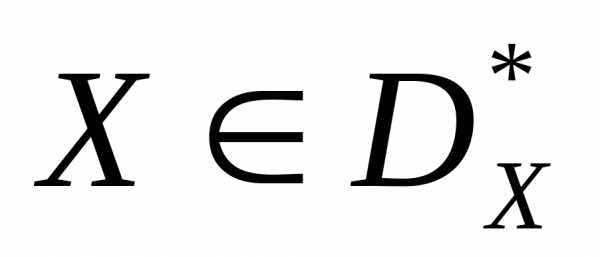 , то. Множество
, то. Множество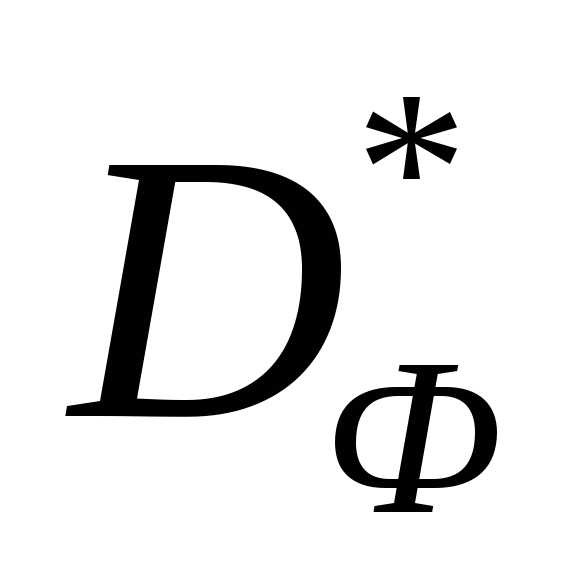 называетсяфронтом Парето.
называетсяфронтом Парето.
Другими словами множество Парето можно определить как множество, в котором значение любого из частных критериев оптимальности можно улучшить (уменьшить) только за счет ухудшения (увеличения) других критериев – любое из решений, принадлежащее множеству Парето, не может быть улучшено одновременно по всем частным критериям. Точки, принадлежащие множеству Парето, не связаны между собой отношением предпочтения!
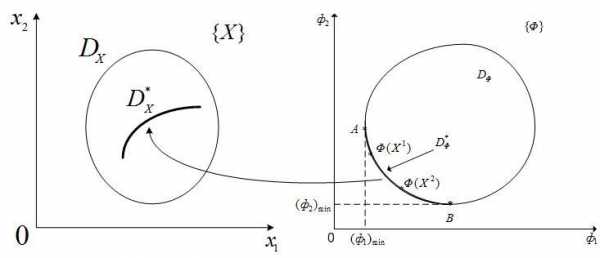
Рисунок 3 - К определению множества Парето (s=2). Если множество 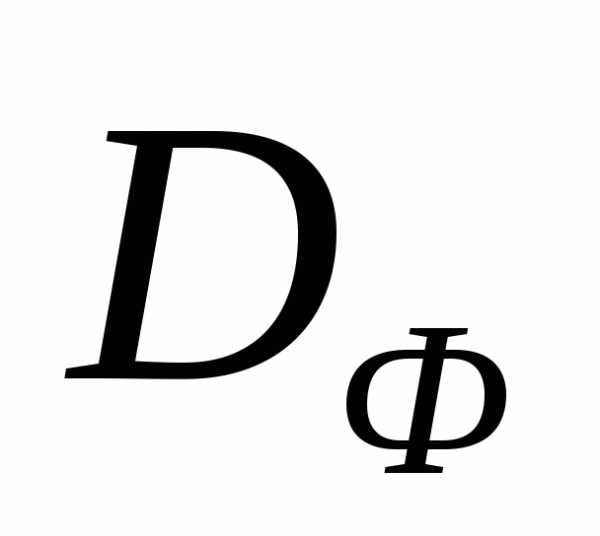 является выпуклым, то множество
является выпуклым, то множество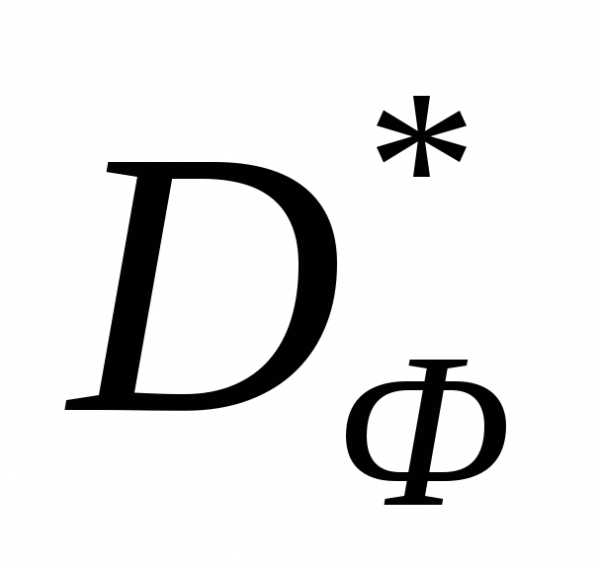 есть часть границы множества
есть часть границы множества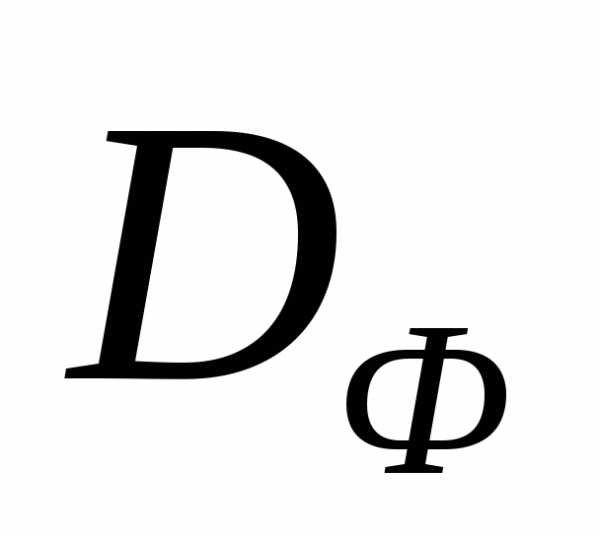 - дугаAB, в которой точка A соответствует
- дугаAB, в которой точка A соответствует 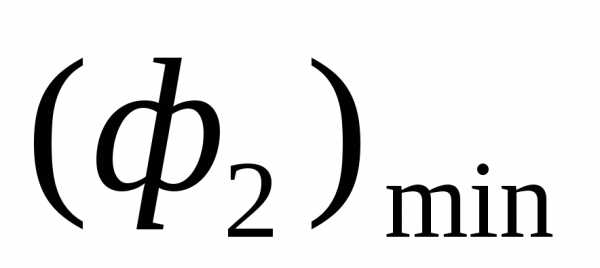 , а точкаB -
, а точкаB - 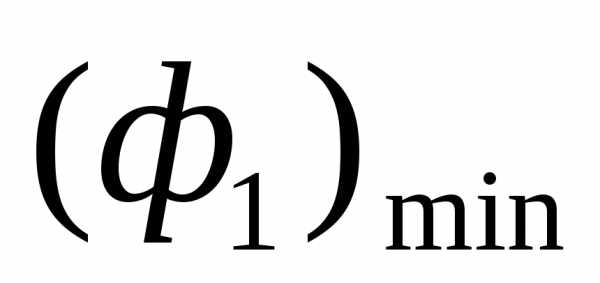 . Среди точекнет более предпочтительных, поскольку, но
. Среди точекнет более предпочтительных, поскольку, но
Пример 1. Пусть множество допустимых значений (рисунок 4) и заданы два частных критерия оптимальности,. Можно показать, что множество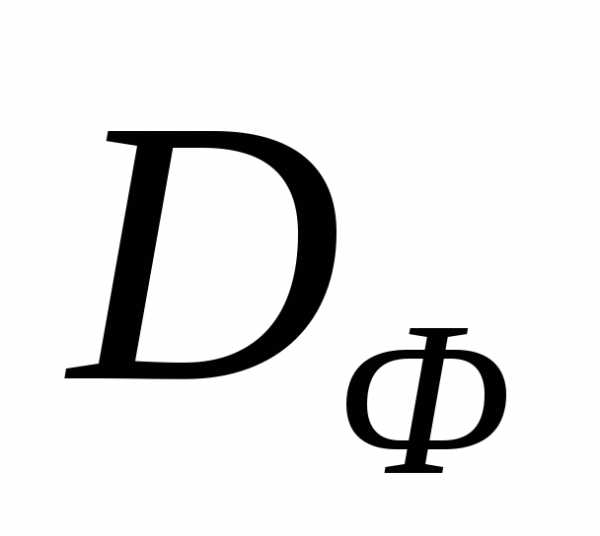 при этом имеет вид, представлены на рисунке 5, а множество Парето
при этом имеет вид, представлены на рисунке 5, а множество Парето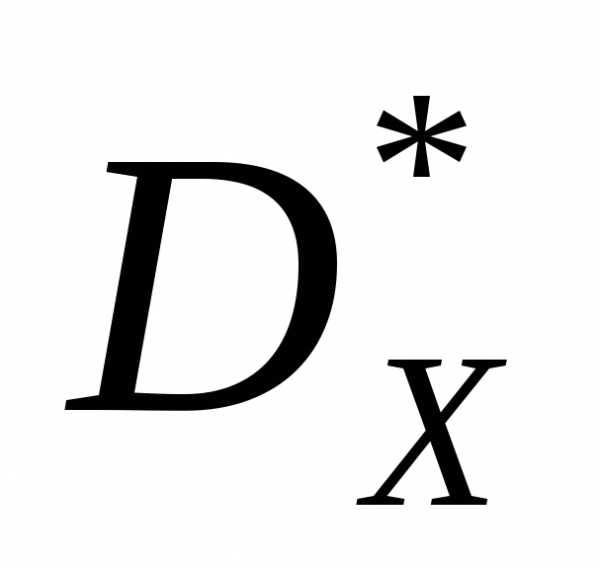 представляет собой отрезок прямой, соединяющий точки (0,0), (1,1) – рисунок 4. Заметим, что точки (0,0), (1,1) являются точками минимума частных критериев оптимальности
представляет собой отрезок прямой, соединяющий точки (0,0), (1,1) – рисунок 4. Заметим, что точки (0,0), (1,1) являются точками минимума частных критериев оптимальности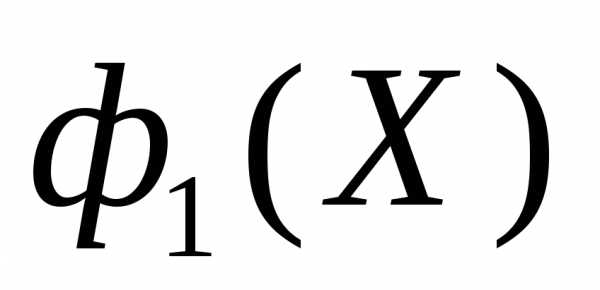 ,
,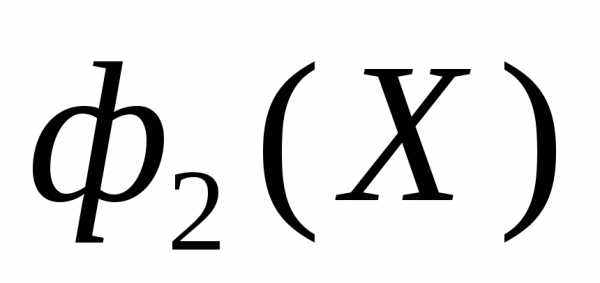 , соответственно●
, соответственно●
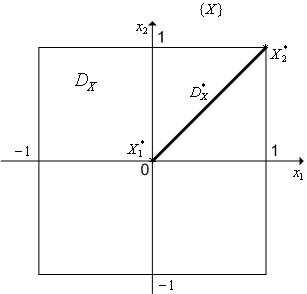
Рисунок 4 - К примеру 1. Множество допустимых значений вектора варьируемых параметров 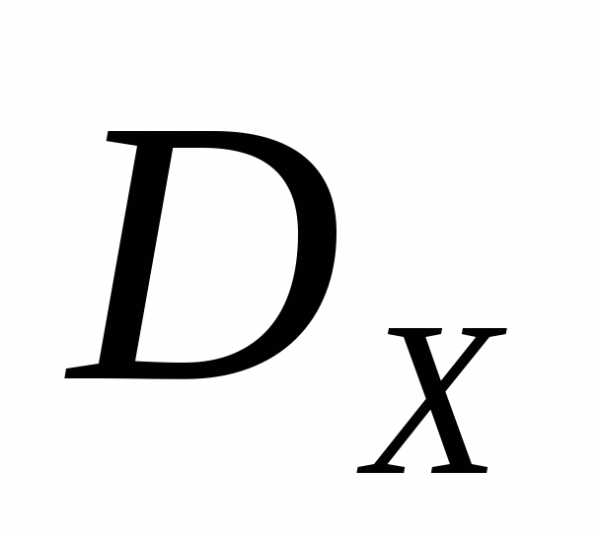 и множество Парето
и множество Парето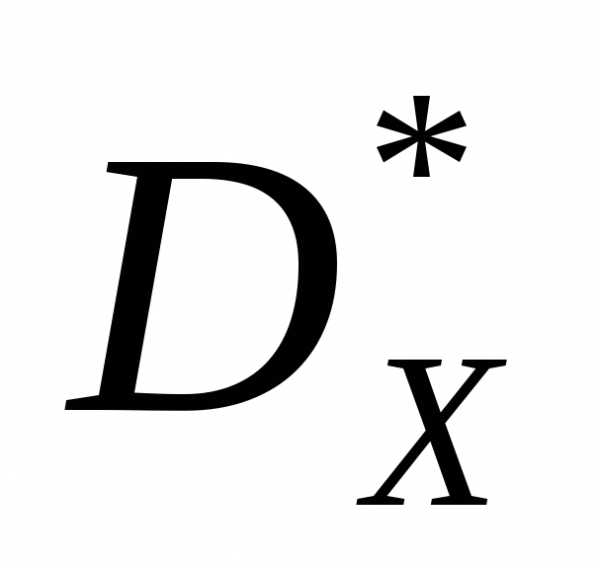
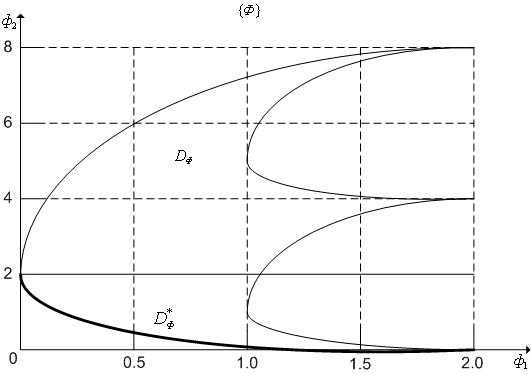
Рисунок 5 - К примеру 1. Множества 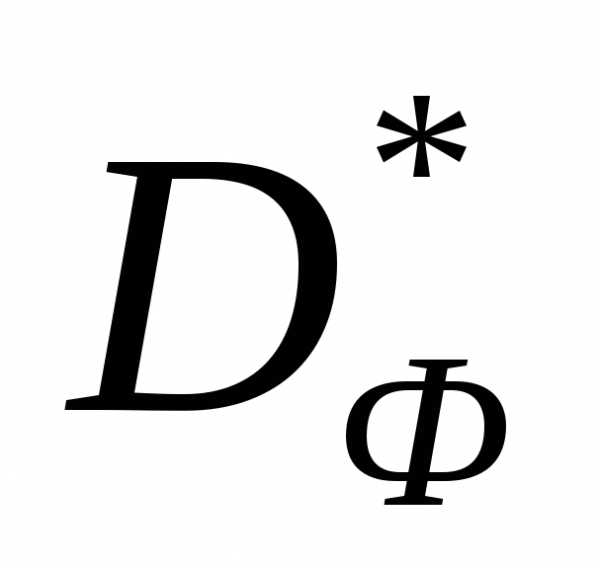 ,
,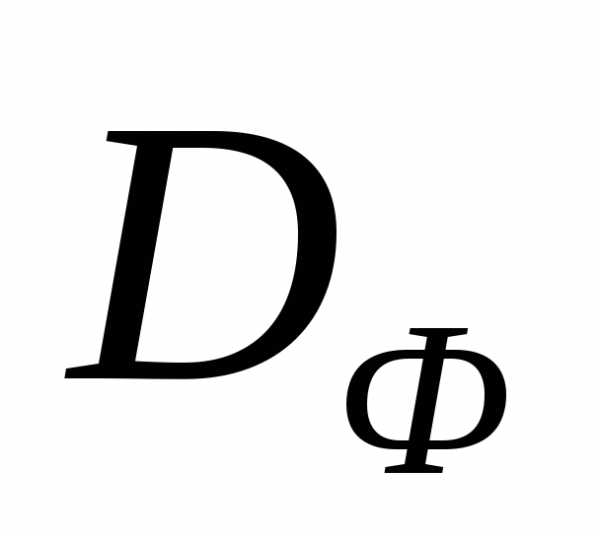
Роль множества Парето при решении задач многокритериальной оптимизации определяется следующей теоремой.
Теорема 1. Если для некоторых весовых множителей 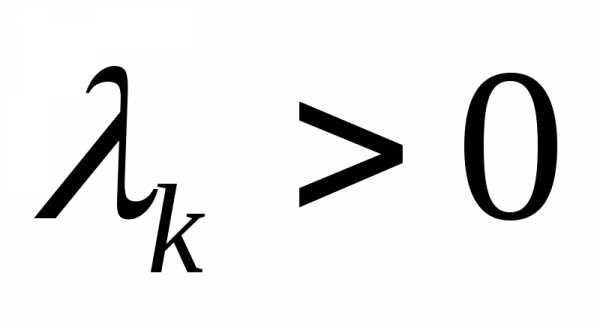 ,
,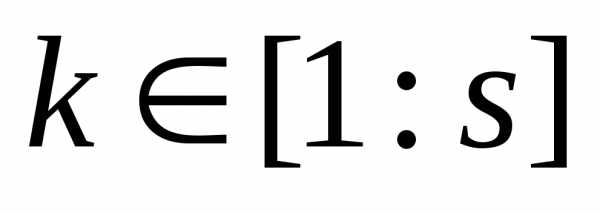 имеет место равенство
имеет место равенство
(2)
где  , то векторХ* оптимален по Парето.
, то векторХ* оптимален по Парето.
Доказательство. Пусть вектор Х* не оптимален по Парето. Тогда существует такой вектор 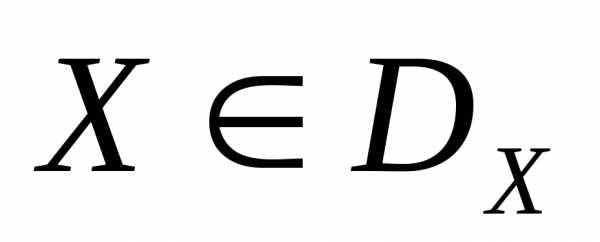 , что
, что
, 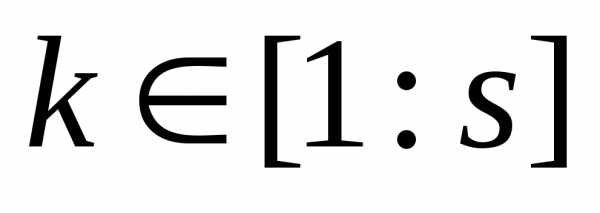 (3)
(3)
причем хотя бы одно из неравенств строгое. Умножая каждое из неравенств (3) на 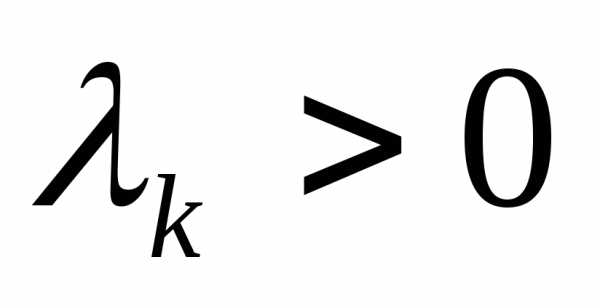 и складывая, получим
и складывая, получим
,
что противоречит условию теоремы●
Теорема 1 показывает, что выбор определенной точки из множества Парето эквивалентен указанию весов для каждого из частных критериев оптимальности. На этом факте основано большое количество численных методов решения многокритериальных задач оптимизации.
Заметим, что теорема 1 задает лишь необходимое условие оптимальности по Парето вектора  . Т.е. из того факта, что точка
. Т.е. из того факта, что точка принадлежит множеству Парето, не следует, что эта точка обязательно удовлетворяет условию (2) – случай невыпуклого множества
принадлежит множеству Парето, не следует, что эта точка обязательно удовлетворяет условию (2) – случай невыпуклого множества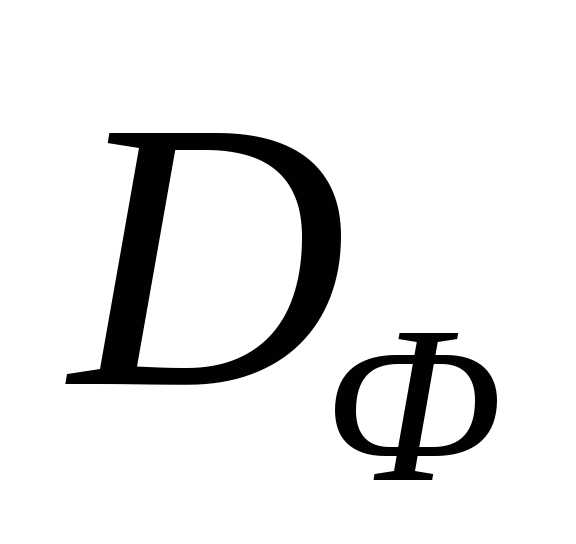 (см. ниже).
(см. ниже).
| В постановке задачи многокритериальной оптимизации (1) фиксируется лишь множество допустимых значений |
Пример 2 (для самостоятельной аудиторной работы). Приближенно построить множество Парето для следующей задачи двухкритериальной оптимизации (s=2):
(рисунок 6).
Покроем множество 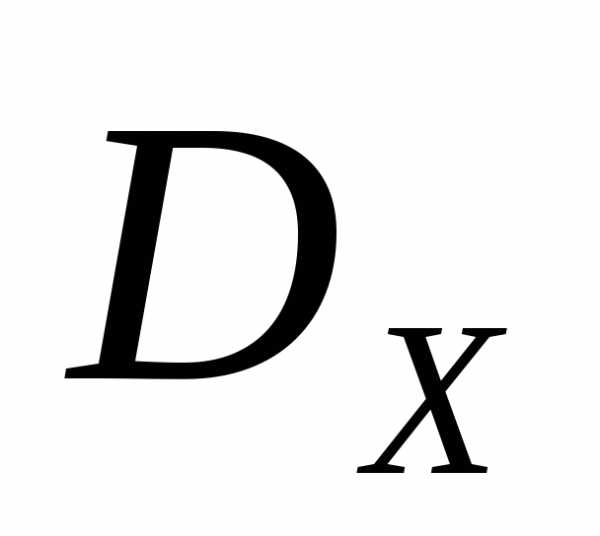 равномерной сеткой с шагом, равным 1, и пронумеруем узлы сетки так, как показано на рисунке 6.
равномерной сеткой с шагом, равным 1, и пронумеруем узлы сетки так, как показано на рисунке 6.
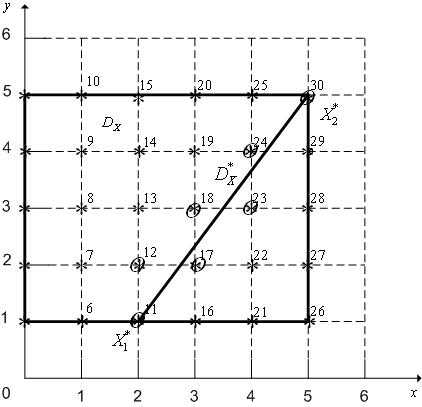
Рисунок 6 - К примеру 2. Множество допустимых значений 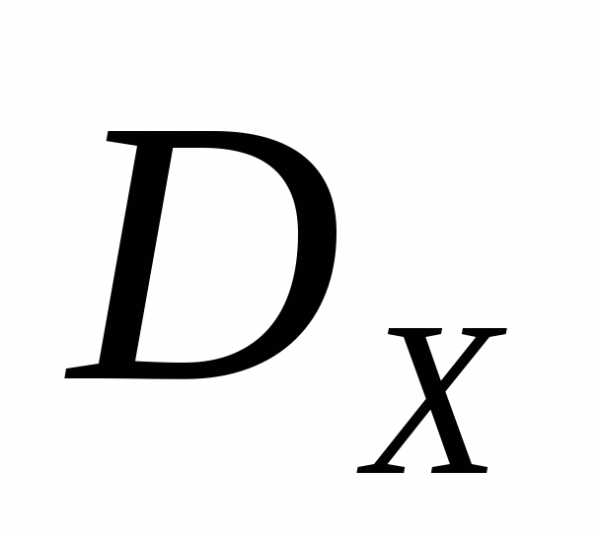 покрыто равномерной сеткой с шагом 1 по обеим осям координат. Звездочками выделены узлы сетки, кружками – точки, соответствующие множеству
покрыто равномерной сеткой с шагом 1 по обеим осям координат. Звездочками выделены узлы сетки, кружками – точки, соответствующие множеству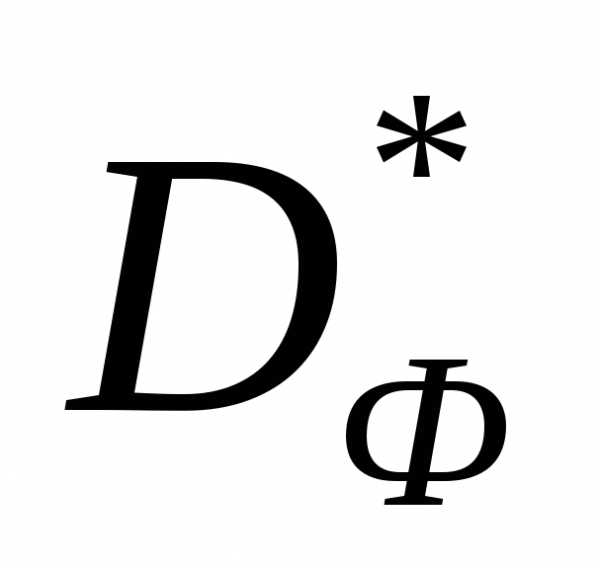 (см. ниже)
(см. ниже)
Результаты вычислений значений частных критериев оптимальности в узлах построенной сетки занесем в таблицу 1, а затем отобразим в пространстве критериев (рисунок 7).
Аппроксимируем границу множество 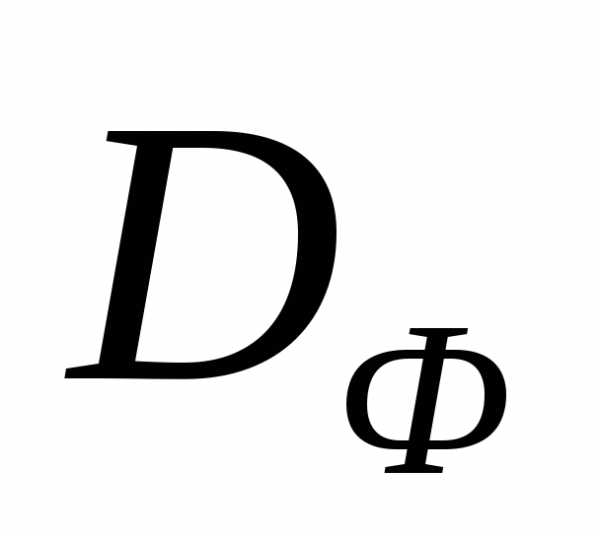 ломаной и выделим множество
ломаной и выделим множество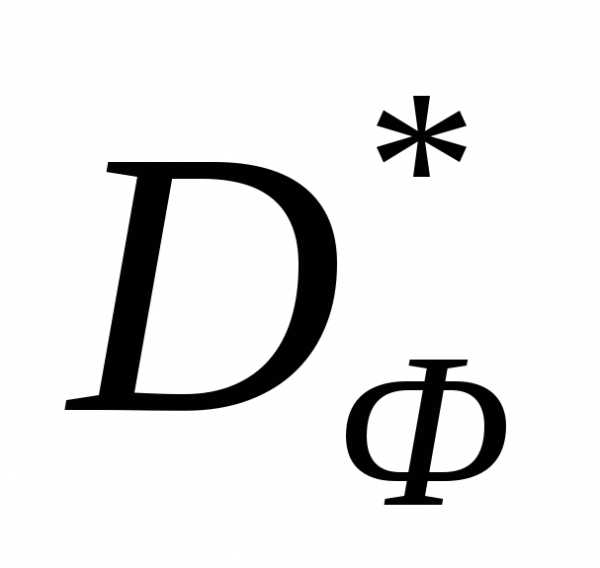 (рисунок 7). Отметим точки, соответствующие множеству
(рисунок 7). Отметим точки, соответствующие множеству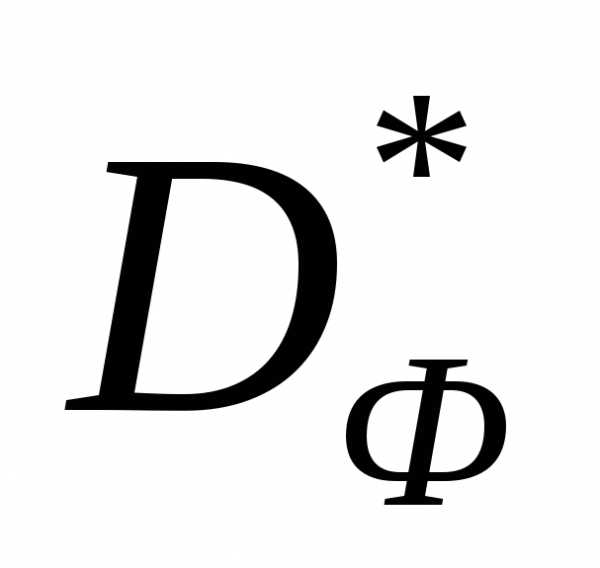 , на множестве
, на множестве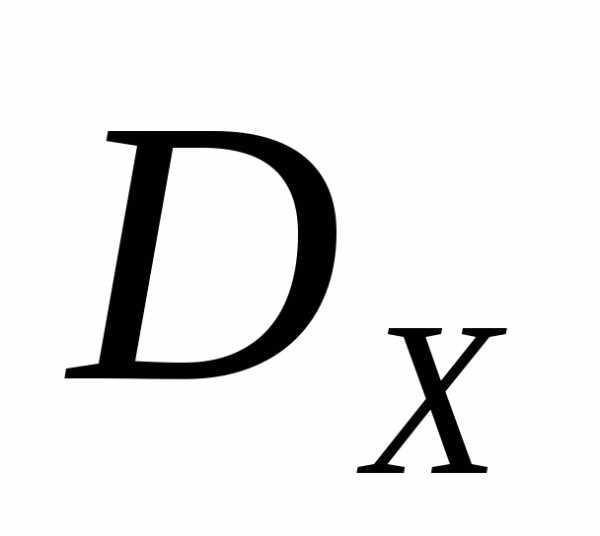 и аппроксимируем полученные точки отрезком прямой. Этот отрезок прямой и представляет собой приближение к искомому множеству Парето (рисунок 6)●
и аппроксимируем полученные точки отрезком прямой. Этот отрезок прямой и представляет собой приближение к искомому множеству Парето (рисунок 6)●
Таблица 1 - К примеру 2.
Значения критериев оптимальности в узлах сетки
| x | y | |
| Номер узла |
| 0 | 1 | 4 | 41 | 1 |
| 2 | 5 | 34 | 2 | |
| 3 | 8 | 29 | 3 | |
| 4 | 13 | 26 | 4 | |
| 5 | 20 | 25 | 5 | |
| 1 | 1 | 1 | 32 | 6 |
| 2 | 2 | 25 | 7 | |
| 3 | 5 | 20 | 8 | |
| 4 | 10 | 17 | 9 | |
| 5 | 17 | 16 | 10 | |
| 2 | 1 | 0 | 25 | 11 |
| 2 | 1 | 18 | 12 | |
| 3 | 4 | 13 | 13 | |
| 4 | 9 | 10 | 14 | |
| 5 | 16 | 9 | 15 | |
| 3 | 1 | 1 | 20 | 16 |
| 2 | 2 | 13 | 17 | |
| 3 | 5 | 8 | 18 | |
| 4 | 10 | 5 | 19 | |
| 5 | 17 | 4 | 20 | |
| 4 | 1 | 4 | 17 | 21 |
| 2 | 5 | 10 | 22 | |
| 3 | 8 | 5 | 23 | |
| 4 | 13 | 2 | 24 | |
| 5 | 20 | 1 | 25 | |
| 5 | 1 | 9 | 16 | 26 |
| 2 | 10 | 9 | 27 | |
| 3 | 13 | 4 | 28 | |
| 4 | 18 | 1 | 29 | |
| 5 | 25 | 0 | 30 |
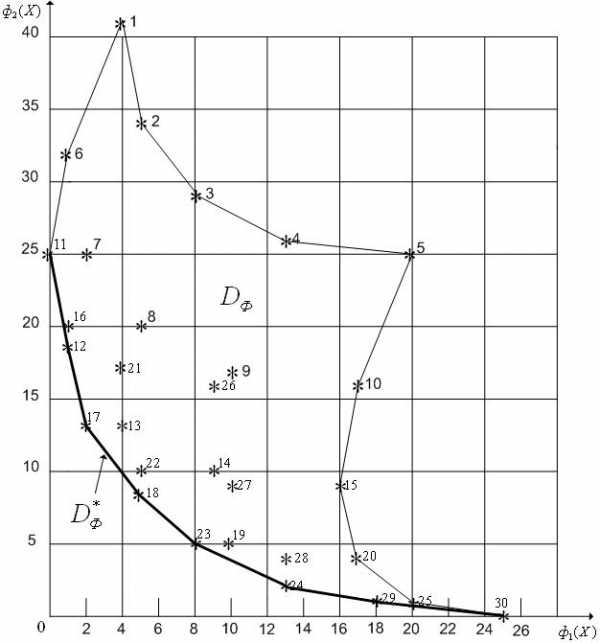
Рисунок 7 - К примеру 2. Примерный вид множеств 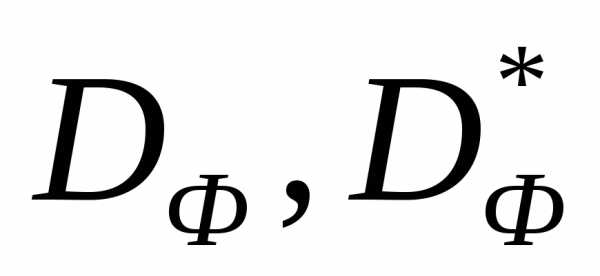
Входные термины:
задача многокритериальной оптимизации;
векторный критерий оптимальности;
частный критерий оптимальности;
скалярный критерий оптимальности;
множество допустимых значений;
весовые коэффициенты частных критериев оптимальности;
множество Парето; переговорное множество; область компромисса;
нормализация пространства критериев.
Выходные термины:
методы, основанные на сведении задачи многокритериальной оптимизации к задаче однокритериальной оптимизации.
метод весовых множителей.
studfiles.net
Принцип Парето и оптимизация блога
Стремление к четким и ясным рекомендациям — неискоренимо в человеческой душе! Вот и я сама постоянно пишу, что нет панацеи, нет совета, подходящего для оптимизации любого блога. Но сердце ищет простоты! И одна из последних моих находок в этой области — волшебное правило Парето. Не буду вас томить и сразу озвучу его:
20% усилий приносят 80% результата
Конечно, в конце XIX века Вильфредо Парето и понятия не имел, как мы интерпретируем закономерность, которую он вывел. Но сегодня данный принцип вовсю используется в работе контент-менеджеров, Интернет-маркетологов и веб-дизайнеров.
Как применять правило Парето
Во-первых, нужно от абстрактных формулировок перейти к конкретике. Например, только 20% материалов на нашем блоге привлекают подавляющее количество посетителей. И только 20% информации каждой отдельной статьи привлекает 80% внимания читателей (является полезным и релевантным!). На 20% рекламных блогов приходится 80% кликов. И так далее.
И следовательно, все наши усилия по оптимизации и улучшению юзабилити нужно сконцентрировать именно на этих статьях, баннерах — на 20% контента блога! По-моему, этот вывод звучит, как музыка. НО!
Громом среди ясного неба звучит основной вопрос:
Как же обнаружить эти «золотые» 20%?!!
А вот для этого нам и нужны разнообразные инструменты анализа блога. Просмотрите и сравните список самых популярных публикаций за максимально большой период времени. Например, месяца за три, за полгода. Советую сразу сделать таблицу в excel, чтобы было удобно работать с данными. Обратите внимание, что нам нужно выписать не первые 20 статей из списка наиболее посещаемых, а именно 20% от общего количества постов в блоге (ну, или 1/5 часть). Например, у Блоготея, примерно, 170 статей : 5 = 34 — значит нас будет интересовать 34 самых популярных материала блога:
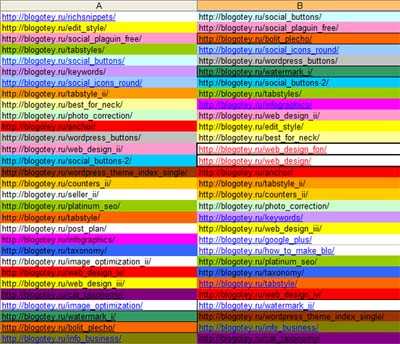
Вот кусочек моих собственных изысканий — 30 популярных статей по данным Гугла (слева) и Яндекса (справа). Одинаковые посты в обеих колонках я раскрасила одинаково (поскольку выбор цветов невелик — они могут повторяться. И мы видим, что для обеих поисковых систем список, примерно, одинаков. И только несколько статей в каждой из колонок не имеют повтора в соседней. Это только часть таблицы — у меня там еще список из LiveInternet.
Недавно я писала о картах кликов, форм и ссылок от Яндекс-Метрики. Их тоже можно и необходимо использовать. Например, чтобы определить, какая часть статьи наиболее востребована читателями, какая из (пяти) ссылок — самая кликабельная, какой формой для подписки или какой кнопкой расшаривания в соцсетях посетители пользуются чаще всего.
Так мы узнаем, на какие именно элементы блога стоит направить свои основные оптимизаторские усилия!
Главное в блоговодстве — эксперимент!
Напоминаю, что любое исследование — а развитие блога это всегда исследование — должно двигаться поступательно. Ставим эксперимент и ждем результата. Для меня, лично, это самый тяжелый момент. Но необходимо сравнить результаты «до» и «после».
Лучше поставить четкий порог. Например, 100 посетителей (или кликов). И когда это условие будет исполнено — можно анализировать: привели наши действия к успеху или нет?
Например, добавьте в ваши «золотые статьи» форму для подписки через Фидбернер и посмотрите: случится ли увеличение количества подписчиков, будет ли оно значительным?
blogotey.ru
«Методы безусловной оптимизации» Метод Парето.
Данный метод позволяет на множестве альтернатив по множеству показателей выделить подмножество оптимальных вариантов.
Рассмотрим данный метод с использованием примера:
Треб. провести сравн. анализ 6-ти авиакомп. и выбрать лучш. из них с исп. сист. пок-лей из табл.1 и экспертных оценок кажд. компании по кажд. пок-лю в 10-тибальной шкале.
| Авиакомп. | Цена, W1 | Без-сть, W2 | Грузоподъем, W3 | Избират-ть по отнош. к виду груза, W4 | Кач-во обслуж-я, W5 | Доп. Услуги, W6 |
| А1 | 5 | 10 | 8 | 5 | 8 | 10 |
| А2 | 7 | 6 | 5 | 9 | 7 | 6 |
| А3 | 9 | 5 | 8 | 7 | 7 | 10 |
| А4 | 5 | 7 | 6 | 6 | 8 | 5 |
| А5 | 6 | 8 | 9 | 5 | 7 | 9 |
| А6 | 10 | 9 | 6 | 5 | 9 | 7 |
| А э | 7 | 6 | 7 | 8 | 7 | 6 |
На практике принцип Парето реализуется путем составления таблиц попарного сравнения.
| А1 | А2 | А3 | А4 | А5 | А6 |
| W1 | - | - | 0 | - | - |
| W2 | + | + | + | + | + |
| W3 | + | 0 | + | - | + |
| W4 | - | - | - | 0 | 0 |
| W5 | + | + | 0 | + | - |
| W6 | + | 0 | + | + | + |
| А2 | А1 | А3 | А4 | А5 | А6 |
| W1 | + | - | + | + | - |
| W2 | - | + | - | - | - |
| W3 | - | - | - | - | - |
| W4 | + | + | + | + | + |
| W5 | - | 0 | - | 0 | - |
| W6 | - | - | + | - | - |
| А3 | А1 | А2 | А4 | А5 | А6 |
| W1 | + | + | + | + | - |
| W2 | - | - | - | - | - |
| W3 | 0 | + | + | - | + |
| W4 | + | - | + | + | + |
| W5 | - | 0 | - | 0 | - |
| W6 | 0 | + | + | + | + |
| А4 | А1 | А2 | А3 | А5 | А6 |
| W1 | 0 | - | - | - | - |
| W2 | - | + | + | - | - |
| W3 | - | + | - | - | 0 |
| W4 | + | - | - | + | + |
| W5 | 0 | + | + | + | - |
| W6 | - | - | - | - | - |
| А5 | А1 | А2 | А3 | А4 | А6 |
| W1 | + | - | - | + | - |
| W2 | - | + | + | + | - |
| W3 | + | + | + | + | + |
| W4 | 0 | - | - | - | 0 |
| W5 | - | 0 | 0 | - | - |
| W6 | - | + | - | + | + |
| А6 | А1 | А2 | А3 | А4 | А5 |
| W1 | + | + | + | + | + |
| W2 | - | + | + | + | + |
| W3 | - | + | - | 0 | - |
| W4 | 0 | - | - | - | 0 |
| W5 | + | + | + | + | + |
| W6 | - | + | - | + | - |
Для получения окончательного решения просуммируем балльные оценки каждого варианта по всем показателям и по критериям наибольшей суммы выберем лучший вариант.
А1=46; А2=40; А3=46; А4=37; А5=44; А6=46.
Получается, что самыми оптимальными вариантами являются А1, А3 и А6.
«Основные понятия и определения теории исследования операций».
Исследование операций - это методы разработки количественно-обоснованных рекомендаций по принятию решений.
Как правило, управленческое решение должно отвечать следующим требованиям:
Иметь ясную целевую направленность;
Быть обоснованным;
Адресность;
Быть непротиворечивым;
Быть правомочным;
Быть эффективным.
Процесс подготовки и принятия решения с использованием материального моделирования включает этапы:
Анализ проблемной ситуации и постановка задачи;
Определение параметров операции и выбор показателей ее эффективности;
Построение описательной модели решения задачи;
Построение математической модели функционирования объекта;
Проведение моделирования;
Формирование решения.
Сам процесс выработки решения базируется на принципе выбора показателя успешности. Он состоит в установлении строгого соответствия между целью и избранным показателем успешности. В настоящее время показатель успешности называется целевой функцией или показателем эффективности.
Выбор наилучшего варианта решения задачи часто можно представить как отыскание экстремума целевой функции.
Типовой процесс выработки принятия и реализации управленческих решений включает этапы:
Анализ проблемной ситуации с целью выявления путей решения проблем;
Подготовка и обоснование управленческого решения;
Принятие решения;
Организация и координация работы коллектива по реализации принятого решения;
Организация учета и контроля принятого решения;
Оценка результатов реализации принятого решения и обобщение накопленного опыта.
По принципам выработки решения делятся на алгоритмические и эвристические.
По методам обоснования решения бывают аналитические, мат.программирования, игровые, статистические.
Каждый из методов имеет свою область применения, например, аналитические методы характерны тем, что между условиями решаемой задачи и ее результатами устанавливается аналитическая зависимость; статистические методы основаны на сборе, обработки и анализе статистических материалов; мат.программирование-ряд методов для наилучшего распределения ограниченных ресурсов, а также для составления рационального плана операций; в рамках теоретико-игровых методов рассматриваются мат.модели конфликтных ситуаций.
Управленческое решение в бизнесе- это основной продукт деятельности менеджера.
Система - это такое множество любых элементов и связей между ними, способ поведения которых определяется целью операции.
Цель – идеальное представление оперирующей стороны о желаемом результате.
Эффективность операций – степень соответствия ее реального результата к требуемому.
В исследовании эффективности логистических систем обычно решаются следующие проблемы:
Оценка эффективности использования системы;
Выбор рационального способа использования системы или варианты ее построения.
studfiles.net
§2. Методы решения задач многокритериальной оптимизации, использующие множество Парето. Метод весовых множителей
Рассмотрим задачу многокритериальной оптимизации
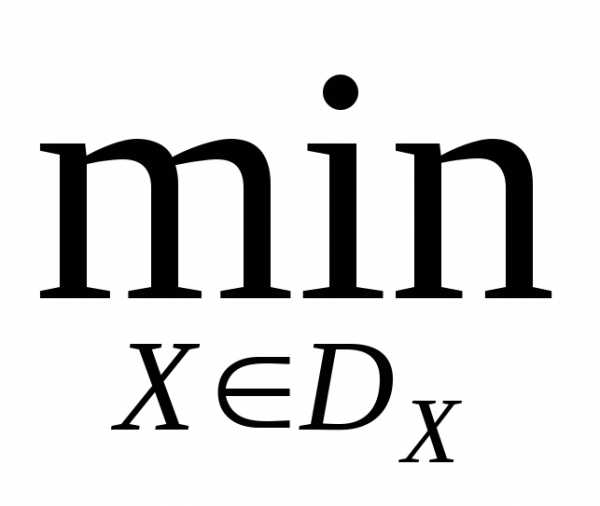 Ф(X)=Ф
Ф(X)=Ф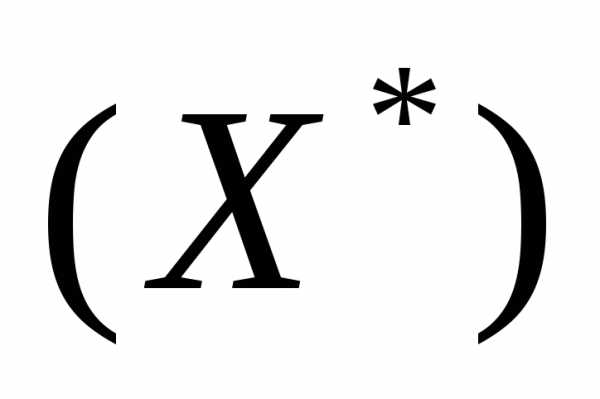 ,(1)
,(1)
где - векторный критерий оптимальности, 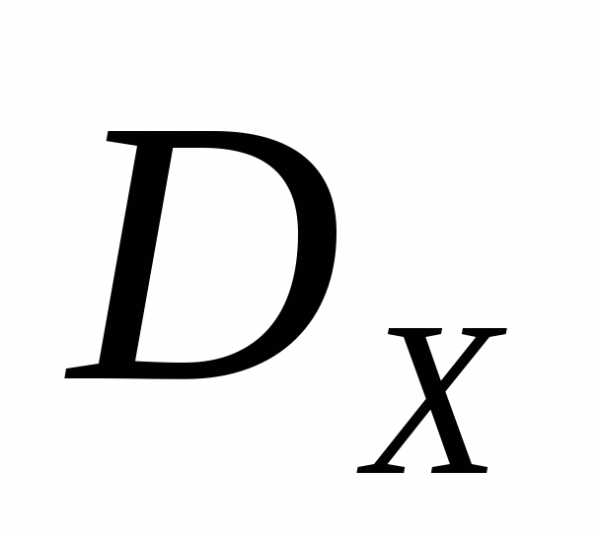 .- множество допустимых значений вектора варьируемых параметров.
.- множество допустимых значений вектора варьируемых параметров.
Для решения задачи многокритериальной оптимизации (1) широко используются методы, основанные на сведении задачи многокритериальной оптимизации к задаче однокритериальной оптимизации. Рассмотрим один из методов этой группы методов - метод весовых множителей.
В метод весовых множителей дополнительной информацией (относительно информации, заданной в постанове задачи (1)) является информация об относительной важности частных критериев. Метод требует, чтобы эта информация была формализована в значениях весовых множители . В этом случае в качестве скалярного критерия используется критерий
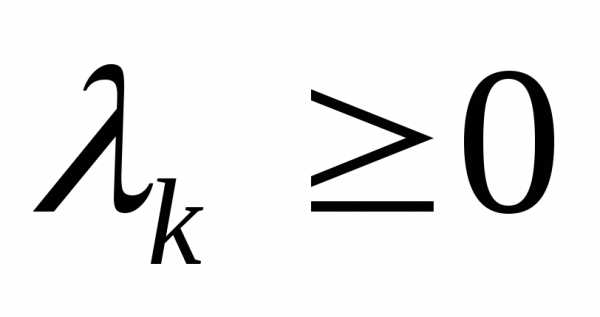 . (2)
. (2)
Т.е. вместо задачи (1) решается задача глобальной условной оптимизации со скалярным критерием оптимальности (2)
. (3)
Введем в рассмотрение 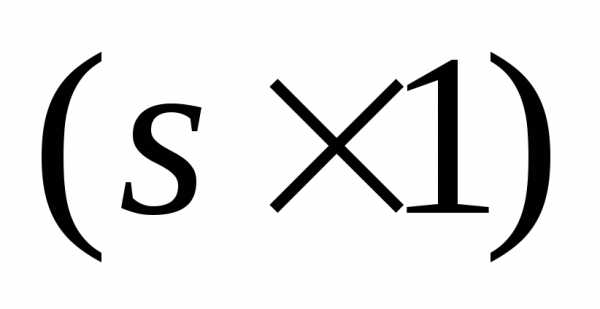 -мерный вектор. Имеет место следующий очевидный факт: если при некотором
-мерный вектор. Имеет место следующий очевидный факт: если при некотором вектор
вектор является решением задачи (3), то этот же вектор является решением той же задачи (3) при любом
является решением задачи (3), то этот же вектор является решением той же задачи (3) при любом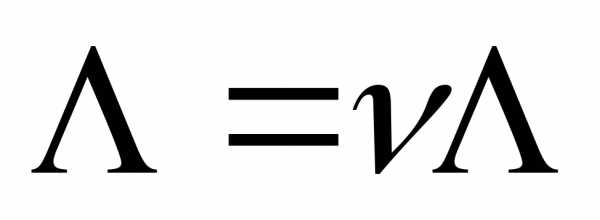 , где
, где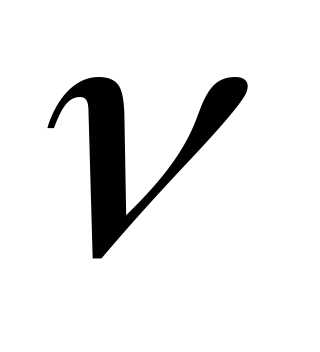 - любая конечная положительная константа. Поэтому обычно на весовые множителинакладывается дополнительные условия вида
- любая конечная положительная константа. Поэтому обычно на весовые множителинакладывается дополнительные условия вида
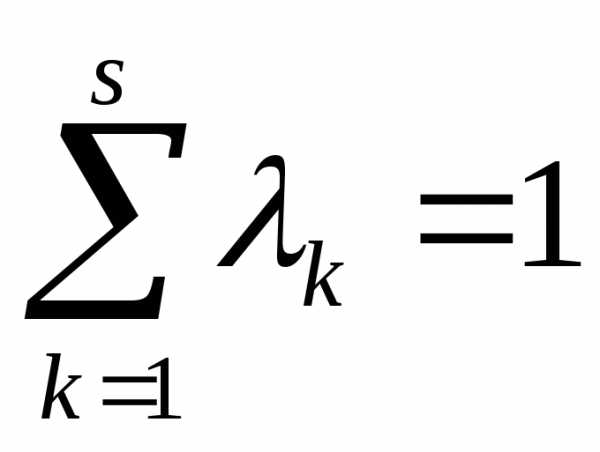 или
или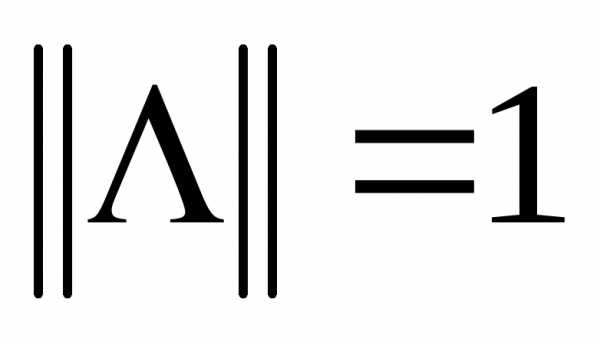 .
.
Напомним следующее: из теоремы 1 вытекает, что вектор  , являющийся решением однокритериальной задачи оптимизации (3), принадлежит множеству Парето задачи (1), а обратное утверждение неверно - вектор
, являющийся решением однокритериальной задачи оптимизации (3), принадлежит множеству Парето задачи (1), а обратное утверждение неверно - вектор , принадлежащий множеству Парето задачи (1), не обязательно удовлетворяет условию (3).
, принадлежащий множеству Парето задачи (1), не обязательно удовлетворяет условию (3).
Существуют различные способы выбора весовых множители . Одним из таких способов является назначение коэффициентов согласно таблице 1.
Таблица 1 - Шкала относительной важности частных критериев
| Относительная важность критерия | Определение относительной важности критериев |
| 1 | Равная важность |
| 3 | Умеренное (слабое) превосходство |
| 5 | Сильное (существенное) превосходство |
| 7 | Очевидное превосходство |
| 9 | Абсолютное (подавляющее) превосходство |
| 2,4,6,8 | Промежуточные решения между двумя соседними оценками |
Для того чтобы при выборе весовых множителей избавиться от влияния масштабов частных критериев оптимальности, в методе весовых множителей целесообразно использовать нормализованные критерии.
Справка. Нормированное уравнение прямой на плоскости имеет вид
,
где - направляющие косинусы вектора , перпендикулярного к данной прямой – рисунок. Аналогично в пространстве
, перпендикулярного к данной прямой – рисунок. Аналогично в пространстве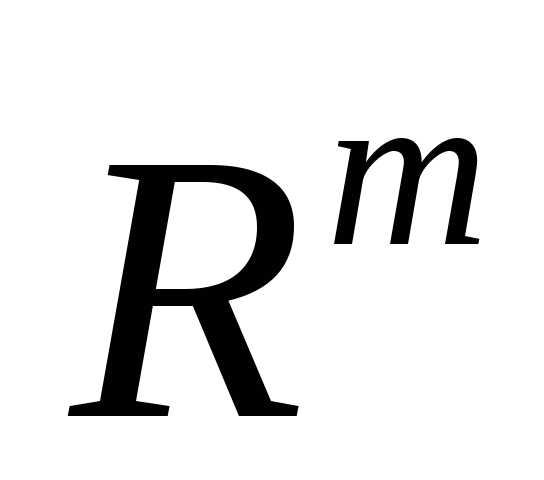 уравнение
уравнение
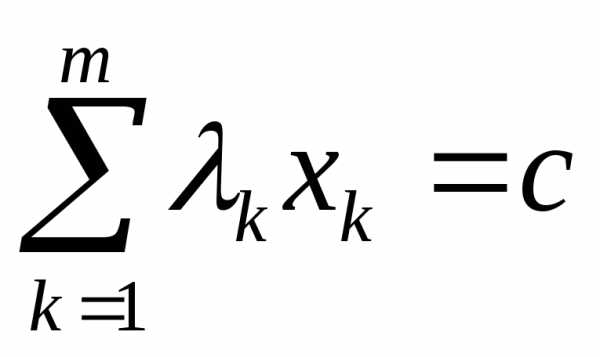
определяет гиперплоскость, направляющие косинусы нормали к которой задаются вектором , а величина представляет собой расстояние от этой гиперплоскости до начала системы координат
представляет собой расстояние от этой гиперплоскости до начала системы координат
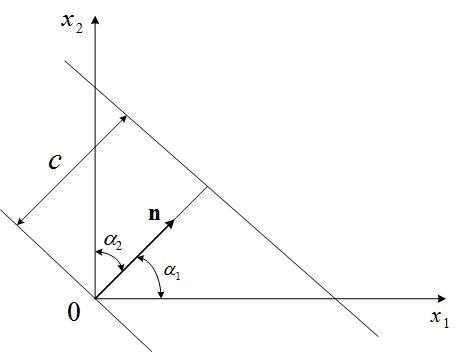
Рисунок – Нормированное уравнение прямой на плоскости
Дадим геометрическую интерпретацию метода. С использованием вектора  критерий оптимальности (2) можно записать в виде скалярного произведения
критерий оптимальности (2) можно записать в виде скалярного произведения
, (4)
а задачу (3) в виде
. (5)
Уравнение , где - некоторая константа, определяет в пространстве критериев
- некоторая константа, определяет в пространстве критериев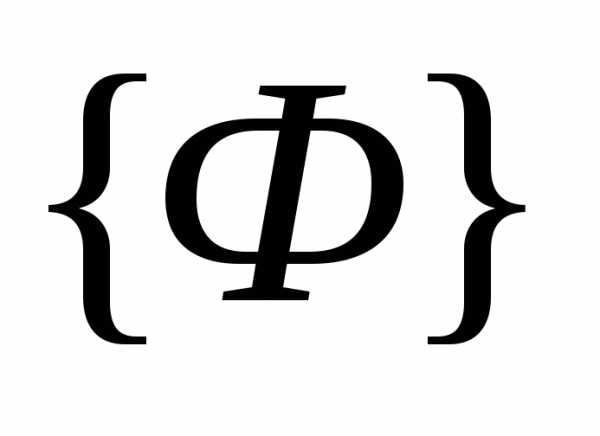 гиперплоскость. При этом решение задачи
гиперплоскость. При этом решение задачи

можно интерпретировать как поиск такого значения с, при котором гиперплоскостьбудет касательной к множеству задачи (1). Компоненты вектора
задачи (1). Компоненты вектора определяют искомую точку
определяют искомую точку касания этой гиперплоскости с множеством
касания этой гиперплоскости с множеством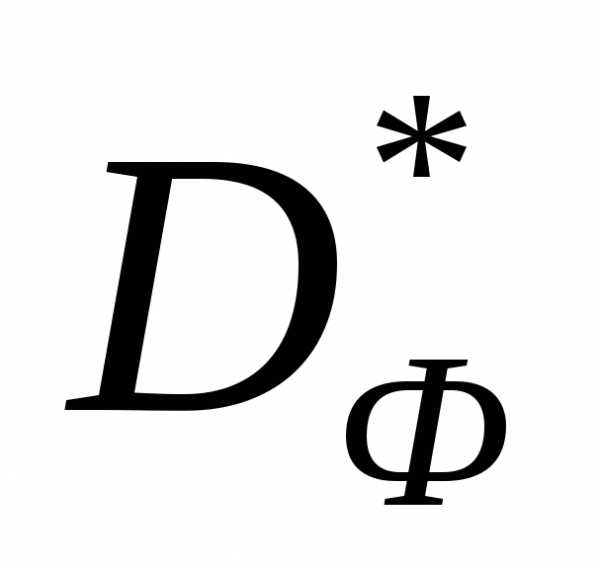 (рисунок 1).
(рисунок 1).
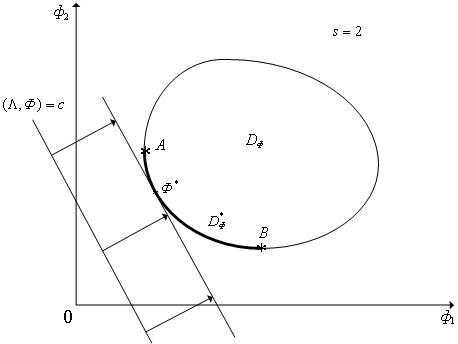
Рисунок 1 - Геометрическая интерпретация метода весовых множителей: случай двух критериев. Множество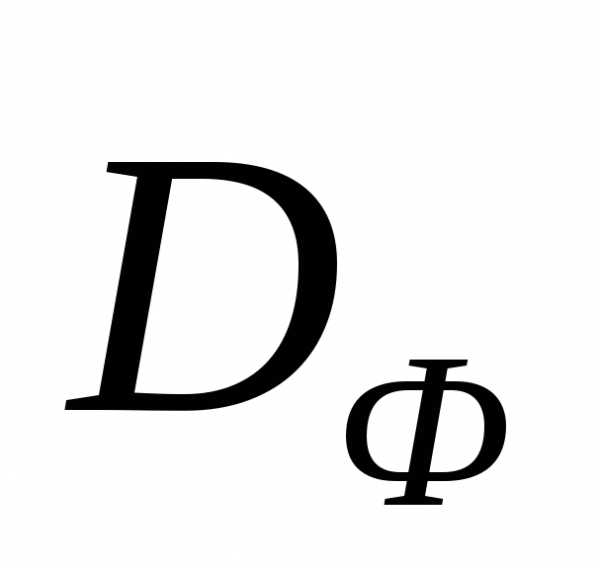 выпукло. Для любой точки
выпукло. Для любой точки множества
множества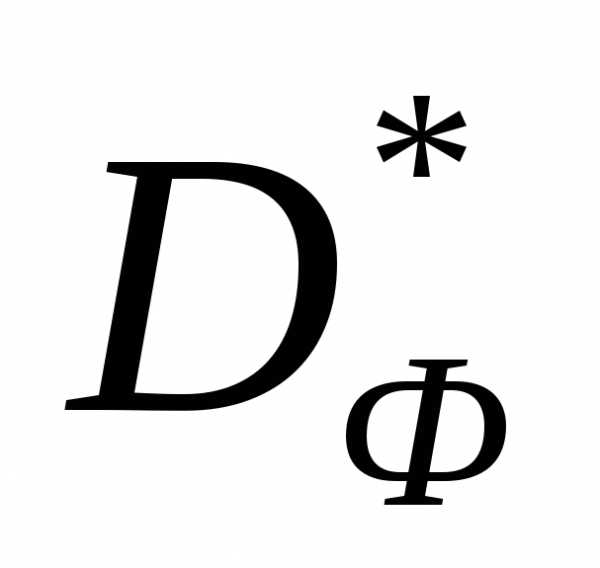 (дугаA,B) найдется вектор весовых множителей
(дугаA,B) найдется вектор весовых множителей , при котором эта точка удовлетворяет условию (5).
, при котором эта точка удовлетворяет условию (5).
Множество 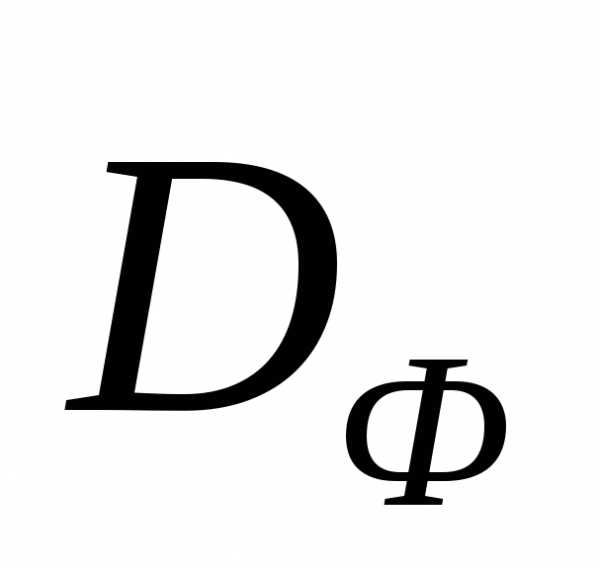 задачи (1) может быть не выпуклым. В этом случае не все точки множества
задачи (1) может быть не выпуклым. В этом случае не все точки множества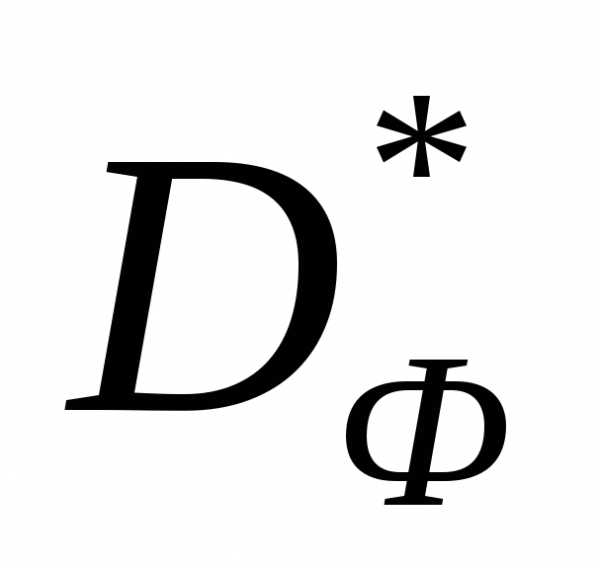 могут быть достигнуты с помощью изменения компонент вектора
могут быть достигнуты с помощью изменения компонент вектора (рисунок 2).
(рисунок 2).
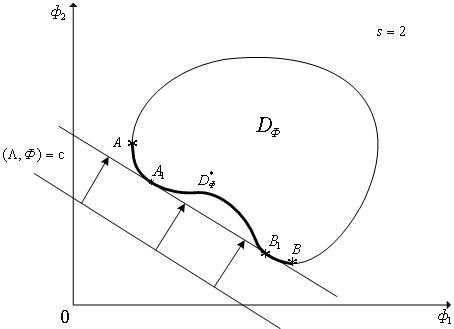
Рисунок 2 - Геометрическая интерпретация метода весовых множителей: случай двух критериев. Множество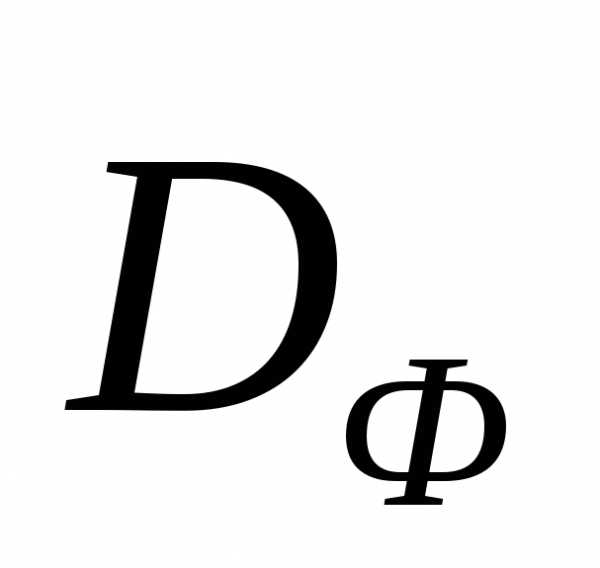 не выпукло. Ни для одной из точек
не выпукло. Ни для одной из точек множества
множества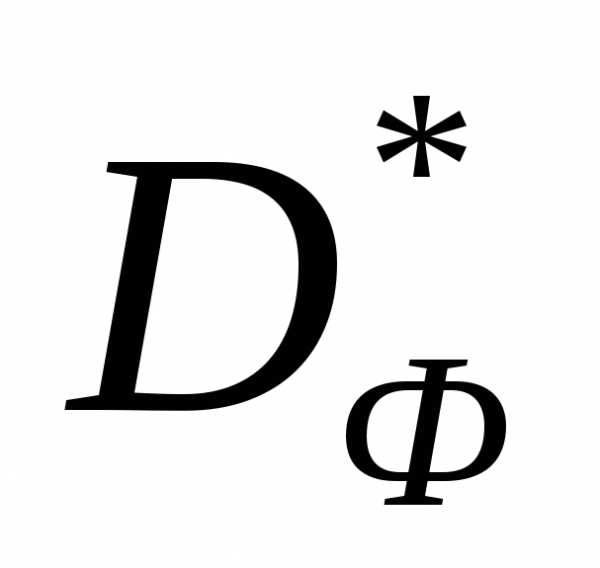 , принадлежащих дуге
, принадлежащих дуге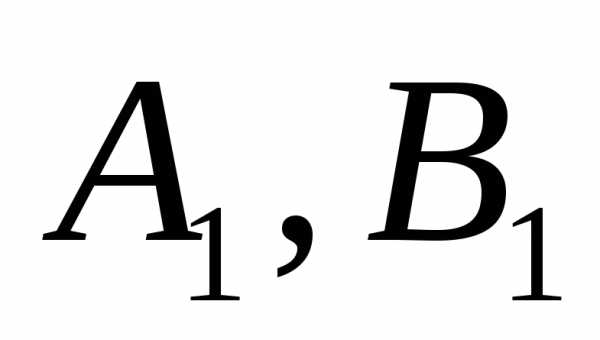 , невозможно найти вектор весовых множителей
, невозможно найти вектор весовых множителей , при котором эта точка удовлетворяет условию (5).
, при котором эта точка удовлетворяет условию (5).
Входные термины:
задача многокритериальной оптимизации;
векторный критерий оптимальности;
частный критерий оптимальности;
скалярный критерий оптимальности;
множество допустимых значений;
нормализация пространства критериев;
весовые коэффициенты частных критериев оптимальности;
множество Парето; переговорное множество; область компромисса;
методы, основанные на сведении задачи многокритериальной оптимизации к задаче однокритериальной оптимизации.
Выходные термины:
studfiles.net
Оптимизация бизнеса. Закон Парето — Учебный центр Unibrains
Традиционное мировоззрение ошибочно полагает, что бизнес-процессы, люди, структурные подразделения, клиенты, каналы продвижения и т.д. одинаково важны. Но в текущих экономических реалиях, необходимо вспомнить о некоторых важных правилах:
Принцип Парето или правило 80/20 – один из наиболее распространенных способов оценки эффективности какой-либо деятельности. Суть его заключается в том, что 20% усилий дают 80% результата, оставшиеся 80% усилий реализуют лишь 20%. Выбрав те оптимальные ресурсы, которые дают наибольший эффект, можно достичь высоких результатов малыми издержками.

Приводимые в законе цифры нельзя считать безусловно точными: скорее схематические ориентиры. Процентное отношение 80/20 не случайно – это дань заслугам экономиста Вильфредо Парето, который в 19 веке установил закономерность распределения богатства между разными слоями населения в Англии. Ученый пришел к ошеломляющему открытию, обнаружив, что 20% населения Англии принадлежало 80% всего богатства страны.
Закон Парето в маркетинге и торговле.
Лишь 20% покупателей дают вам 80% прибыли, остальные же зачастую тратят время вашего персонала, при этом, не принося особых доходов. Лишь 20% ассортимента вашего магазина приносят 80% от общего объема продаж в денежном выражении.
Для того чтобы оптимизировать свой бизнес, необходимо исследовать и выявить закономерность, направив максимум усилий на работу с высокопотенциальными клиентами. Контакты с остальными 80% унифицировать, сократить во времени и сделать не особо затратными для компании. Так вы сможете оптимизировать работу вашего бизнеса.

Можно провести параллель с методикой писания картин известных художников, которые, не вырисовывая всех деталей своих шедевров, делают акценты на некоторых элементах, привлекающих больше всего внимания зрителей.
Как применить закон Парето в повседневной жизни?
Производство. Компания IBM в 1963 году выяснила, что около 80% времени их компьютеры тратят на совершение 20% операций. Сразу же было принято решение найти 20% задач, которые больше всего использовались, и сделать их максимально удобными и функциональными для пользователя. В результате IBM создали компьютер в разы превосходящий по производительности ближайших конкурентов.
Финансы. Проанализируйте источники, которые приносят Вам 80% денег. Сконцентрируйтесь именно на них, поскольку они играют ключевую роль в формировании вашего бюджета. Остальные варианты игнорируйте, ведь они только забирают время и силы. Исключением могут быть пассивные источники заработка (вклады, пассивные инвестиции), поскольку трудозатраты для их осуществления стремятся к нулю.
Продуктивность. Учитывая то, что каждый человек настроен на свой биологический ритм, вам придется вычислить свой. Определите, в какое время вы работаете максимально эффективно. Это и будет тот промежуток, когда вам нужно уделить максимум внимания работе. В остальное время все ваши усилия будут малоэффективными.
Ненужные вещи. Вы наверняка замечали, что у вас в квартире или автомобиле хранятся вещи, которыми вы практически не пользуетесь. Они постоянно мешают, занимают много места. Практика освоения пространства Фэн Шуй именует такие вещи энергетическими завалами. Оставьте себе лишь 20% необходимых вещей.
Коммуникации. Встречая новых людей, мы можем не осознавать, кто из них действительно играет важную роль в нашей жизни. Проанализируйте сами и убедитесь, что лишь 20% людей, с которыми вы общаетесь, эмоционально наполняют вас и привносят что-то новое в ваше сознание. Именно таким людям нужно уделять больше всего внимания. Непродолжительное общение с близкими друзьями намного важнее.
unibrains.ru
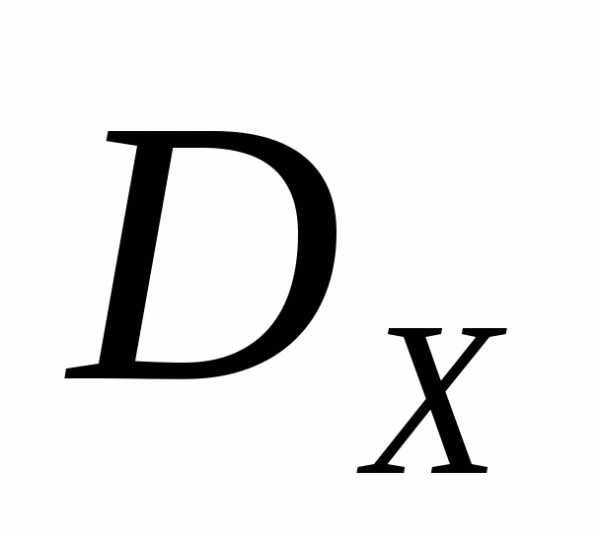 и вектор критериев Ф.Этой информации недостаточно для однозначного решения задачи (1). Указанная информация позволяет лишь выделить соответствующее множество Парето (можно сказать, что решением задачи многокритериальной оптимизации в постановке (1) является множество Парето). Для однозначного решения задачи (1) нужна дополнительная информация.
и вектор критериев Ф.Этой информации недостаточно для однозначного решения задачи (1). Указанная информация позволяет лишь выделить соответствующее множество Парето (можно сказать, что решением задачи многокритериальной оптимизации в постановке (1) является множество Парето). Для однозначного решения задачи (1) нужна дополнительная информация.