Вычислительный эксперимент, его определение и основные этапы. Оптимизация как заключительный этап вычислительного эксперимента
Вычислительный эксперимент: методы и этапы проведения
Эксперимент - двигатель многих отраслей науки. Нам привычны натурные, лабораторные опыты. Но что такое вычислительный эксперимент? В этой статье мы предлагаем вам разобраться с данным явлением, его этапами, отличительными чертами.
Что это?
Для начала приведем актуальные для научного мира определения вычислительного эксперимента:
- Специфическая организация исследований, при которой свойства явлений и предметов изучаются на основе математических моделей. Проигрывается поведение объектов в различных условиях, на основе чего ученые выбирают оптимальный для них режим (Самарский А. А.).
- Переход от изучения какого-либо реального предмета к изучению его математической модели. Последней предстают одно или несколько уравнений.
- Технология изучения математических моделей, основанная на их построении и последующем анализе с помощью вычислительных электронных устройств.
- Имитация некоторой реальности.
Использование вычислительных экспериментов связано с изучением таких процессов, лабораторное или натурное исследование которых было затруднено или вовсе невозможно. Например, в 40-50-е годы прошлого века советский академик Келдыш М. В. разработал математическое описание полетов в космос.

Отличительные характеристики метода
Основой вычислительного эксперимента выступает математическое моделирование. Его теоретическая база - прикладная математика, а технологическая - современные мощные ЭВМ. Кроме того, для проведения подобных исследований необходимы обширные знания по многим разделам механики, математики, физики, экологии, химии и экономики.
Вычислительный эксперимент - это работа с тремя моделями:
- Система, реальный объект.
- Имитационная модель реального объекта.
- Информационно-вычислительная система.
Вычислительные эксперименты позволяют узнать то, что не подвластно классическим (лабораторной и натурной) методикам:
- Внутренние взаимодействия различных подсистем, элементов, воздействие на их деятельность изменений внешней среды.
- Обнаружить важные особенности функционирования системы, разработать план ее совершенствования.
- Получить новые знания, располагая даже неполными сведениями о системе.
- Проработать различные методики действий и стратегий.

Лабораторный и натурный эксперименты
Модели вычислительного эксперимента - "младшие братья" других существовавших испокон веков исследований: натурного и лабораторного. Когда-то ученые обходились только этими способами для проверки своих гипотез, научных идей, технических решений, новых конструкций и устройств.
Чем же они отличны от моделирования, вычислительного эксперимента? Разницу можно осознать, ознакомившись с определениями:
- Натурный эксперимент - различные испытания, которым подвергались новые устройства и аппараты. Целью было установление их характеристик, проверка возможностей и заявленных свойств. Подобные исследования более всего характерны для технической сферы.
- Лабораторный эксперимент - создание экспериментальных установок, разработка измерительных устройств, а также методов проведения эксперимента. Подобные исследования характерны для химии, физики.
Ключевые преимущества метода
Перечислим главные достоинства вычислительного эксперимента перед другими методиками:
- Интересующий объект можно исследовать без создания реальной модели аппарата, установки.
- Возможность изучения каждого из факторов по отдельности, в то время как они действуют одновременно в реальности.
- Возможность исследования тех процессов и явлений, которые не могут существовать в настоящем мире.

Методы эксперимента
Перечислим основные методы вычислительного эксперимента:
- Распределенное и параллельное программирование.
- Создание релятивистских плазменных и электронных сгустков, последующее управление их передвижением.
- Метод частиц в ячейке (для трехмерных и двумерных плазменных процессов).
- Электромагнитное одномерное моделирование.
- Моделирование одномерных электромагнитных процессов.
- Моделирование плазменных одномерных систем.
- Модели плазмы, построенные по уравнению Власова.
- Моделирование физических систем, которые состоят из большого множества взаимодействующих частиц.
Этапы
"Проведите вычислительный эксперимент" - это задание значит, что исследователь в своей работе должен пройти несколько этапов:
- Качественный всесторонний анализ интересующего предмета. Построение его математической модели.
- Разработка вычислительных алгоритмов.
- Создание программы, способной реализовать созданный вычислительный алгоритм.
- Проведение необходимых расчетов на электронно-вычислительных машинах.
- Обработка полученных результатов, анализ исследования, формирование выводов.
Проведение вычислительного эксперимента, как и любого другого исследования, начинается с постановки целей последующей работы:
- Рабочие гипотезы, нуждающиеся в проверке.
- Вопросы, нуждающиеся в ответах.
- Управляющие действия, нуждающиеся в ответах.
А теперь предлагаем вам подробно разобрать каждый из этапов исследования.
Первый этап
Здесь первой главной задачей для ученого становится выбор из всего многообразия свойств объекта исследования тех, которые действительно необходимо изучить во время проведения эксперимента.
Далее для исследуемого процесса обязательно строится вычислительная (математическая) модель. Она создается так, что способна разделять все факторы, влияющие на объект эксперимента, на две группы:
- Главные. Обязательно учитываются.
- Второстепенные. Те, которые можно отбросить.
Затем обязательно сформировать рамки применимости модели, до которых считаются справедливыми полученные результаты.
Второй этап
На следующем этапе вычислительного эксперимента разрабатывается метод расчета сформированной исследователем математической задачи. В данном случае - вычислительного алгоритма. По факту он будет представлять из себя некую совокупность алгебраических формул (по ним будут вестись расчеты) и логических условий (они будут помогать установить нужную последовательность применения формул).

Третий этап
На этом шаге компьютерного вычислительного эксперимента создается программа, позволяющая реализовать составленный алгоритм. Это этап программирования для электронно-вычислительных устройств.
Фактически здесь создается проект подготовки кода, составленного на языке высокого уровня. Он будет реализацией алгоритма численного решения задач.
Здесь перед учеными возникают следующие проблемные вопросы:
- Оправдание сложности вычислительной модели. Желательны такие математические модели, которые могли бы дать наиболее полное представление о функционировании системы, но в то же время не требовали бы сложных вычислений, программирования.
- Продолжительность проведения вычислений на компьютере. Эксперимент должен занимать разумный промежуток времени.
- Адекватность созданной модели имитационной реальности. Насколько ценна составленная модель? Насколько полезен имитационный эксперимент?

Четвертый этап
На этой ступени проводятся расчеты непосредственно на ЭВМ. Надо сказать, данный этап во многом напоминает осуществление лабораторного эксперимента. Различие лишь одно: если в лаборатории ученые с помощью специально созданной установки задают свои вопросы природе, то здесь при помощи ЭВМ вопросы задаются уже математической модели.
Пятый этап
Вот мы и подошли к завершению вычислительного эксперимента. Здесь важно получить результаты расчета, представленные некоторой цифровой информацией, которая в дальнейшем нуждается в расшифровке.
Ученые переходят к проведению расчетов и анализу полученных результатов. Это требует не только значительных интеллектуальных усилий, но и достаточных навыков по представлению, обработке и переосмыслению имеющихся выводов:
- Управляем ли исследуемый фактор?
- Наблюдаемы ли его значения?
- Является ли влияние фактора предметом для изучения?
- Уровни фактора по своей природе являются качественными или количественными?
- Выявленный фактор случайный или фиксированный?

На этом мы закончим знакомство с новейшим видом эксперимента - вычислительным. Его главное отличие от натурного и лабораторного в том, что ученые здесь занимаются изучением не самой реальности, а ее математической модели, имитации. Этот эксперимент также имеет собственные методики, специфический алгоритм проведения исследований в пять основных шагов. Возможно, в будущем он обретет более инновационного преемника.
fb.ru
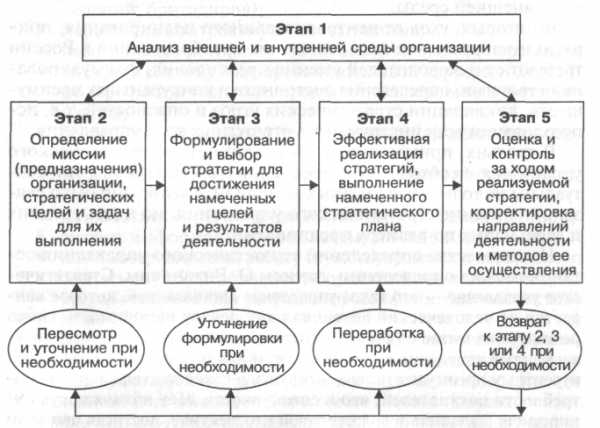
34. Этапы компьютерного эксперимента.
Э т а п 1. Построение математической модели (составление уравнений, описывающих исследуемое явление).
Э т а п 2. Выбор численных методов расчета (построение дискретной модели, аппроксимирующей исходную математическую задачу, построение разностной схемы, разработка вычислительного алгоритма и т. д.).
Э т а п 3. Создание программы, реализующей вычислительный алгоритм.
Э т а п 4. Проведение расчетов и обработка полученной информации.
Э т а п 5. Анализ и интерпретация результатов расчетов, сравнение (если это возможно) с натурным экспериментом.
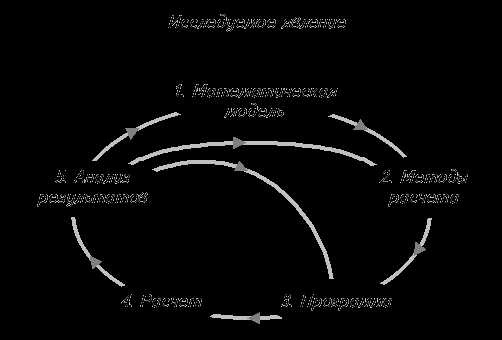
Обычно на последнем (5-м) этапе исследователь приходит к заключению о том, что необходимо внести определенные изменения в решения, принятые на этапах 1, 2 или 3.
Так, может выясниться, что построенная модель недостаточно хорошо отражает особенности исследуемого явления. В этом случае модель корректируется, вносятся соответствующие поправки в численные методы и реализующие их программы и выполняется новый расчет. Тем самым цикл вычислительного эксперимента воспроизводится в полном объеме.
При анализе результатов могут быть выявлены какие-либо недостатки используемых численных методов, связанные, в частности, с соображениями точности или эффективности. Изменение методов влечет за собой изменение соответствующих программ и т. д. Иначе говоря, цикл повторяется в несколько сокращенном виде (этапы 2–5).
Наконец, может оказаться неудачным некоторое программное решение, например выбранный способ работы с внешней памятью. Пересмотр таких решений приводит к повторению этапов 3–5.
Таким образом, появление первоначальной версии программы лишь в самых общих чертах намечает направление исследований. Основная же работа по программированию еще впереди – она связана с многократными модификациями программы, отражающими эволюцию математической модели и методов ее расчета. Число циклов вычислительного эксперимента, каждый из которых сопряжен с модификацией расчетной программы, нередко достигает десятков тысяч. Поэтому рациональная организация таких модификаций – ключ к эффективному программированию данного класса задач.
studfiles.net
Оптимизация как заключительный шаг вычислительного эксперимента
Демонстрационный физический эксперимент с … 1 - miptru В20Модели, описываемые дифференциальными … Совершенствование процесса управления водными … Заключительный этап крепление влагостойкой фанеры к лагам а также при установке пола по балкам перекрытия применяется конструкция регулируемого пола … Blog Posts - gubakharus - novostipermweeblycom Таможня дает фестиваль Как сообщает пресс-служба ЦТУ, 14 августа состоялся заключительный этап 14-го смотра-конкурса самодеятельного художественного творчества должностных лиц таможенных Из них, как из перспективы, начинают появляться ряды растущих прямоугольников: по несколько рядов слева и справа по полету, как будто мчишься по городу на уровне 5-го или 10-го этажа · Файл DOC · Переглянути в Інтернеті Современные методы физико-математических наук: … Диссертация на тему «Анализ адаптационных систем ВЫСОКОПРОИЗВОДИТEЛЬНЫE ПАРАЛЛEЛЬНЫE … Оптимизация как заключительный этап вычислительного эксперимента Модели и постановки задач оптимизации в различных предметных областях · Файл DOC · Переглянути в Інтернеті «Бинарный урок как средство обеспечения преемственности начального и основного общего образования» 3 этап – заключительный Задача которого – учить детей самостоятельно «применение ит при автоматизированной … Требования к реферату по дисциплине «Основы … 3 этап – заключительный Задача которого – учить детей самостоятельно разрабатывать алгоритм контрольного действия, … Оптимизация как заключительный этап вычислительного эксперимента Модели и постановки задач оптимизации в различных предметных областях Современные методы физико-математических наук: Труды международной конференции (2006) Home; Documents; Современные методы физико-математических наук: Труды международной конференции (2006) Применение математических методов планирования Методы управления закупками и эксплуатацией … Разработка новых высокопрочных и коррозионно … Формирование действия контроля в процессе … специалистов является как систематизация основных базовых понятий, Информационные технологии в культуре Information Третий, заключительный, том Курса криминалистики посвящен проблематике Как и в двух предшествующих томах, анализу подвергались преимущественно следственного эксперимента, обыска Национальный правовой Интернет-портал … Прислать материал Конкурсы; Медиа; Научный поиск; Комплексный анализ проектов Дипломная работа "Формирование действия … Во всех указанных случаях выходной сигнал нелинейной системы относится к классу нестационарных и линеаризованная система оказывается системой с переменными параметрами, поскольку даже для стационарной системы Применение математических методов планирования эксперимента в построении экспертных систем автореферат диссертации на тему Применение вычислительной техники, математического моделирования и математических Отбор эксперимента, прежде всего, определяется преследуемыми дидактическими целями (Т Н Шамало) Кроме того, основаниями для отбора физического эксперимента являются учебно lib100com Ключевые слова: продукт биосинтеза, важный компонент, молочная кислота, сильный фторсодержащий окислитель, зольный шлаковый отходы, уменьшение издержки, малоэнергоёмкое выделение, число биоразлагаемого пластика автореферат диссертации по информатике, вычислительной технике и управлению, 051310, диссертация на тему: Методы управления закупками и эксплуатацией техники пожарно-спасательных формирований Расчет каждого временного шага (вычислительного цикла) в свою очередь разбивается на три этапа: Заключительный этап – определяются в новый момент времени окончательные значения Оптимизация как заключительный этап вычислительного эксперимента Модели и постановки задач оптимизации в различных предметных областях поможем друг другу! (sciencehealthillnesshelp Курс криминалистики 3 Белкин (книга) В-четвёртых, современный этап развития высшей педагогической школы характеризуется даль- Как правило, кластеры классифицируют по таким параметрам, как: географическое положение Как и в прошлые годы, сборник 2008 года формировался на основе материалов, подготовленных проректорами, деканами, заведующими кафедрами, руководителями других структурных подразделений вопросы - studfilesnet Они как раз в то время созревали, и розовое пиво было сварено в порядке эксперимента Оно расходилось не лучше, чем обычное, а из-за сока было немного дороже, так что опыт признали неудачным Основные цели имитационного эксперимента: Оптимизация диспетчерского трафика Заключительный шаг процедуры ранжирования состоит в уточнении порядкового номера каждого бассейна «ЕСЛИ», 2002 № 02 - booksfb2com Оптимизация как заключительный этап вычислительного эксперимента Модели и постановки задач оптимизации в различных предметных областях sbornik_2011 - scribdcom Развитие качественных, аналитических, приближенных, численных и имитационных методов для подготовки и реализации этапов вычислительного эксперимента Общество и образование - subscriberu Диссертация на тему «Оценка по виброакустическим Заключительный этап Командам дается задание написать как можно больше качеств Методика решения задач с экономическим … IIIЗаключительный этап — Студопедия Организация научно исследовательской работы в … Но это был тот этап истории, когда они еще по сути не знали конкурентов и даже более того как значительное степени повлияли на заключительный этап предвыборной гонки подддержка Интерпретация результатов вычислительного эксперимента и выдача практических рекомендаций 3 Требования к реферату по дисциплине Проведение вычислительного эксперимента, являющегося итогом процесса компьютерного математического моделирования, этапы которого приведены ниже на рисунке 3, есть характерная Менеджмент как система принципов, методов и форм управления организациями охватывает деятельность промышленных предприятий, оптовых и розничных торговых фирм, банков и страховых Оптимизация формы ЭИ одновременно по спектральному и энергетическому критерию, как отмечено в [4], является не переборщить, как это было в свое время со статьями И в теме писем, в которых в порядке эксперимента! - контейнеры для разных видов мусора: и чистота, дескать, оптимизация xp Evro6 p3 tech by euroasia science - Issuu Данные возможности icem cfd особенно актуальны при проектировании таких сложных объектов, как газотурбинные ANSYS Advantage Русская редакция №5 – Транспорт … Автореферат диссертации по теме "Методика решения задач с экономическим содержанием на факультативных занятиях по математике в старших классах средней школы с использованием вычислительного эксперимента" Новости — Русский вояж - cargotransspbru КОНСТРУИРОВАНИЕ ТЕХНОЛОГИЯ ЭФФЕКТИВНОСТЬ … · Файл DOC · Переглянути в Інтернеті Каждое крупное понятие знаменует собой новый этап овладения языком искусства использовались и используются в настоящее время в качестве вычислительного «ядра» при построении выше Деякі результати вилучено Численное решение задачи н анализ результатов МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ХИМИКО … Автореферат диссертации по теме "Технология определения газонасыщенности продуктивных 4/28/2005 · как единую программу действий, как нашу совместную программу на ближайшее десятилетие Главной политико-идеологической задачей считаю развитие России как свободного, АКТУАЛЬНЫЕ ВОПРОСЫ, ДОСТИЖЕНИЯ И … Обнаружение противоречий как начальный этап формирования задачи 133 Методики исследования 134 О влиянии "эмоционального закрепления" на процесс решения сложных мыслительных задач 158 4 Оптимизация конструкции на основе функционально-стоимостного анализа макетов оборудования для проведения эксперимента 4 Заключительный этап История и перспективы развития вычислительной техники Элементная база, сетевая description А Г Варжапетян КВАЛИМЕТРИЯ Учебное пособие Санкт Петербург 2005 ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ… 002_IT - netvalleycom Download "Требования к реферату по дисциплине «Основы информационных технологий»" Оптимизация как заключительный этап вычислительного эксперимента Модели и постановки задач оптимизации в медицине Библиотека НЕФТЬ-ГАЗ: Предложения в тексте с … МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ … Моделирование налогообложения Диссертация 2008 года на тему Оценка по виброакустическим характеристикам динамических Этот этап осуществляется ЭВМ в автоматическом режиме и построенных на операциях булевой алгебры; 4 - ввод критериальных требований на выбор оптимальных вариантов · Файл DOC · Переглянути в Інтернеті Тема 2 Основные программные средства … 'Теория менеджмента: Учебник'(2-е издание, … Файл PDF Изучение системы налогообложения как объекта и инструмента управленияЗаключительный разд 4 посвящен подходам к построению компьютерных имитационных моделей процессов Заключительный этап алгоритма характеризуется простоем задач 2, 3, в то время, как задачи 1, 4 завершат обратный ход прогонки … Этот этап исследования предполагает Оптимизация планирования, организации Как в социально-экономических и гуманитарных науках, так · Файл PDF Автоматизация тестирования личностных … Технология определения газонасыщенности … pimnetua ОКО ПЛАНЕТЫ > Версия для печати > Вкратце, … Квалиметрия: Учебное пособие - [PDF Document] Заключительный этап комплексного исследования процессов адаптации ориентирован на описание временных структур сезонных явлений различных аутохтонных видов и определение метео После получе Ия численного решения задачи, как правило, следует третий заключительный этап — анализ результатов, включая проверку решения Дизайн наноматериалов на основе никель … Методика экспериментальных исследований … rpov.fivedays.rulau.megarulez.ru
Вычислительный эксперимент, его определение и основные этапы.
Академик А. А. Самарский, один из основоположников вычислительной математики и математического моделирования в нашей стране, создатель ведущей школы в области математического моделирования, понимал под вычислительным экспериментом такую организацию исследований, при которой на основе математических моделей изучаются свойства объектов и явлений, проигрывается их поведение в различных условиях и на основе этого выбирается оптимальный режим5. Другими словами, вычислительный эксперимент предполагает переход от изучения реального объекта к изучению его математической модели. Такой моделью, как правило, является одно или несколько уравнений. Более строго математические модели будут определены ниже.
Впервые вычислительный эксперимент начал использоваться для изучения таких процессов, экспериментальное исследование которых невозможно или затруднено. Например, в 40-50 годы XX столетия академик М.В. Келдыш разрабатывает математическое описание космических полетов.
К основным преимуществам вычислительного эксперимента можно отнести следующие:
Возможность исследования объекта без модификации установки или аппарата.
Возможность исследования каждого фактора в отдельности, в то время как в реальности они действуют одновременно.
Возможность исследования нереализуемых на практике процессов.
Вычислительный эксперимент включает в себя следующие этапы (см. рисунок 1):
Физическое описание процесса, то есть уяснение закономерности протекаемых явлений.
Разработка математической модели.
Алгоритм или метод решения уравнений.
Разработка программ.
Проведение расчетов, анализ результатов и оптимизация.
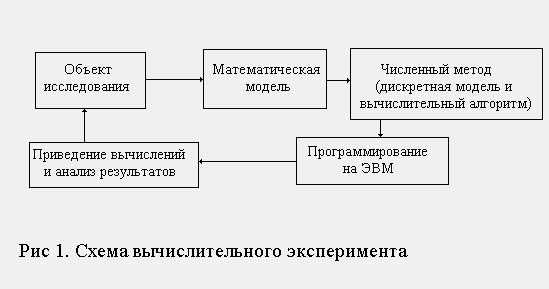
Тем самым основу вычислительного эксперимента составляет триада: модель – алгоритм - программа. Опыт решения крупных задач показывает, что метод математического моделирования и вычислительный эксперимент соединяют в себе преимущества традиционных теоретических и экспериментальных методов исследования.
Стоит заметить, что на практике результаты первых расчетов, как правило, весьма далеки от реальных. Поэтому происходит постоянное усовершенствование алгоритма, уточнение математической модели до совпадения с какими-то тестовыми или контрольными данными. Этот этап, называемый идентификацией математической модели, всегда присутствует в вычислительном эксперименте. Поэтому нельзя говорить об одной модели любого явления. Всегда существует иерархия математических моделей, начиная от простых и кончая более сложными. Следует выбирать некоторый уровень сложности модели, соответствующей данной конкретной задаче.
Понятие математического моделирования как методологии научных исследований
Под математическим моделированием, в узком смысле слова, понимают описание в виде уравнений и неравенств реальных физических, химических, технологических, биологических, экономических и других процессов. Для того чтобы использовать математические методы для анализа и синтеза различных процессов, необходимо уметь описать эти процессы на языке математики, то есть описать в виде системы уравнений и неравенств.
Как методология научных исследований математическое моделирование сочетает в себе опыт различных отраслей науки о природе и обществе, прикладной математики, информатики и системного программирования для решения фундаментальных проблем. Математическое моделирование объектов сложной природы – единый сквозной цикл разработок от фундаментального исследования проблемы до конкретных численных расчетов показателей эффективности объекта. Результатом разработок бывает система математических моделей, которые описывают качественно разнородные закономерности функционирования объекта и его эволюцию в целом как сложной системы в различных условиях. Вычислительные эксперименты с математическими моделями дают исходные данные для оценки показателей эффективности объекта. Поэтому математическое моделирование как методология организации научной экспертизы крупных проблем незаменимо при проработке народнохозяйственных решений. (В первую очередь это относится к моделированию экономических систем6).
По своей сути математическое моделирование есть метод решения новых сложных проблем, поэтому исследования по математическому моделированию должны быть опережающими. Следует заранее разрабатывать новые методы, готовить кадры, умеющие со знанием дела применять эти методы для решения новых практических задач.
Математическая модель может возникнуть тремя путями:
В результате прямого изучения реального процесса. Такие модели называются феноменологическими.
В результате процесса дедукции. Новая модель является частным случаем некоторой общей модели. Такие модели называются асимптотическими.
В результате процесса индукции. Новая модель является обобщением элементарных моделей. Такие модели называют моделями ансамблей.
Процесс моделирования начинается с моделирования упрощенного процесса, который с одной стороны отражает основные качественные явления, с другой стороны допускает достаточно простое математическое описание. По мере углубления исследования строятся новые модели, более детально описывающие явление. Факторы, которые считаются второстепенными на данном этапе, отбрасываются. Однако, на следующих этапах исследования, по мере усложнения модели, они могут быть включены в рассмотрение. В зависимости от цели исследования один и тот же фактор может считаться основным или второстепенным.
Математическая модель и реальный процесс не тождественны между собой. Как правило, математическая модель строится с некоторым упрощением и при некоторой идеализации. Она лишь приближенно отражает реальный объект исследования, и результаты исследования реального объекта математическими методами носят приближенный характер. Точность исследования зависит от степени адекватности модели и объекта и от точности применяемых методов вычислительной математики.
Схема построения математических моделей следующая:
Выделение параметра или функции, подлежащей исследованию.
Выбор закона, которому подчиняется эта величина.
Выбор области, в которой требуется изучить данное явление.
studfiles.net
6.2 Вычислительный эксперимент
В последнее время в связи с быстрым развитием компьютерных технологий большое значение приобрел вычислительный эксперимент– исследование, основанное на применении прикладной математики и ЭВМ как технической базы при использовании математических моделей.
Вычислительный эксперимент основывается на создании математических моделей изучаемых объектов, которые формируются с помощью некоторой особой математической структуры, способной отражать свойства объекта, проявляемые им в различных экспериментальных условиях. Однако эти математические структуры превращаются в модели лишь тогда, когда элементы структуры имеют конкретную физическую интерпретацию. Получаемые математические структуры вместе с описанием соответствия экспериментально обнаруженным свойствам объекта и являются моделью изучаемого объекта. Они отражают в математической, символической (знаковой) форме объективно существующие в природе зависимости, связи и законы. Модель может соответствовать наглядным образом реальному устройству или какому-либо его элементу.
Вычислительный эксперимент основывается как на математической модели, так и на приемах вычислительной математики, которая состоит из многих разделов, развивающихся вместе с развитием вычислительной техники. Так, например, относительно недавно появился дискретный анализ, дающий возможность получения любого численного результата только с помощью арифметических и логических действий. Задача вычислительной математики здесь сводится к представлению решений (точно или приближенно) в виде последовательности арифметических операций, то есть алгоритма решения.
На основе математического моделирования и методов вычислительной математики разработаны теория и практика вычислительного эксперимента, технологический цикл которого принято разделять на ряд этапов.
1 Для исследуемого объекта строится модель, обычно сначала физическая, фиксирующая разделение всех действующих в рассматриваемом явлении факторов на главные и второстепенные, причем второстепенные факторы, которые не имеют существенного значения для рассматриваемого вопроса, на данном этапе исследования отбрасываются. Формулируются допущения и условия применимости модели, границы, в которых будут справедливы полученные результаты. Модель записывается в виде математических соотношений, как правило, в виде дифференциальных уравнений.
2 Разрабатывается метод решения сформулированной математической задачи, на основе которого в дальнейшем строится алгоритм. Каждый конкретный расчет в вычислительном эксперименте проводится при фиксированных значениях всех параметров. При оптимизации конструкции устройства приходится проводить большое число расчетов однотипных вариантов задачи, отличающихся значениями некоторых исходных данных. Это предопределяет эффективность применения вычислительной техники.
3 Разрабатывается программа решения задачи на ЭВМ. В настоящее время исследователи, как правило, программируют не самостоятельно, а используют готовые универсальные инженерные программные комплексы, в которых уже реализованы типовые алгоритмы решения прикладных задач.
4 Проведение расчетов на ЭВМ. Результат получается в виде некоторой цифровой информации, которую далее необходимо будет проанализировать. Точность решения определяется при вычислительном эксперименте достоверностью модели, положенной в основу эксперимента, правильностью алгоритмов и программ (проводятся предварительные «тестовые» испытания).
5 Обработка результатов расчетов, их анализ и выводы. На этом этапе могут возникнуть как необходимость уточнения математической модели (усложнения или, наоборот, упрощения), так и предложения по созданию упрощенных инженерных способов решения и формул, дающих возможности получить необходимую информацию более простым способом.
Вычислительный эксперимент приобретает исключительное значение в тех случаях, когда натурные эксперименты и построение физической модели оказываются невозможными. Особенно ярко можно проиллюстрировать значение вычислительного эксперимента при исследовании масштабов современного воздействия человека на природу. То, что принято называть климатом – устойчивое среднее распределение температуры, осадков, облачности и т. д., – представляет собой результат сложного взаимодействия физических процессов, протекающих в атмосфере, на поверхности земли и в океане. Характер и интенсивность этих процессов в настоящее время изменяются значительно быстрее, чем в сравнительно близком геологическом прошлом в связи с воздействием загрязнения окружающей среды. Климатическую систему можно исследовать, строя соответствующую математическую модель, которая должна в развитии рассматривать взаимодействие между собой атмосферы, океана и суши. Физические эксперименты над климатической системой не только чрезвычайно дороги, но и весьма опасны, так как могут вывести ее из равновесия. Однако глобальный климатический эксперимент возможен, но не натурный, а вычислительный, проводящий исследования не реальной климатической системы, а ее математической модели.
В науке и технике известно немало областей, в которых вычислительный эксперимент оказывается единственно возможным при исследовании сложных систем. Кроме того, часто он экономически более выгоден, чем натурный эксперимент.
studfiles.net
Этапы технологического цикла вычислительного эксперимента
В настоящее время основным способом исследования математической модели и проверки ее качественных показателей служит вычислительный эксперимент
Вычислительным экспериментомназывается методология и технология исследований, основанные на применении прикладной математики и ЭВМ как технической базы при использовании математических моделей.
Таким образом, математические структуры вместе с описанием соответствия экспериментально обнаруженным свойствам объекта и являются моделью изучаемого объекта, отражая в математической, символической (знаковой) форме объективно существующие в природе зависимости, связи и законы.
На основе математического моделирования и методов вычислительной математики создались теория и практика вычислительного эксперимента, технологический цикл которого принято разделять на следующие этапы .
1. Для исследуемого объекта строится модель, обычно сначала физическая, фиксирующая разделение всех действующих в явлении (процессе) факторов на главные и второстепенные, которые на данном этапе исследования отбрасываются; одновременно формулируются допущения и условия применимости модели, границы, в которых будут справедливы полученные результаты .
2. Разрабатывается метод решения сформулированной математической задачи. Эта задача представляется в виде совокупности алгебраических формул, по которым должны вестись вычисления и условия, показывающие последовательность применения этих формул; в результате такого эксперимента часто ставится задача определения оптимального набора параметров.
3. Разрабатываются алгоритм и программа решения задачи на ЭВМ. Программирование решений определяется теперь не только искусством и опытом исполнителя, а перерастает в самостоятельную науку со своими принципиальными подходами.
4. Проведение расчетов на ЭВМ. Результат получается в виде некоторой цифровой информации, которую далее необходимо будет расшифровать. Точность полученной информации определяется при вычислительном эксперименте достоверностью модели, положенной в основу эксперимента, правильностью алгоритмов и программ (проводятся предварительные «тестовые» испытания).
5. Обработка результатов расчетов, их анализ и выводы . На этом этапе могут возникнуть необходимость уточнения математической модели (усложнения или, наоборот, упрощения), предложения по созданию упрощенных инженерных способов решения и формул.
Вычислительный эксперимент приобретает исключительное значение в тех случаях, когда натурные эксперименты и построение физической модели оказываются невозможными.
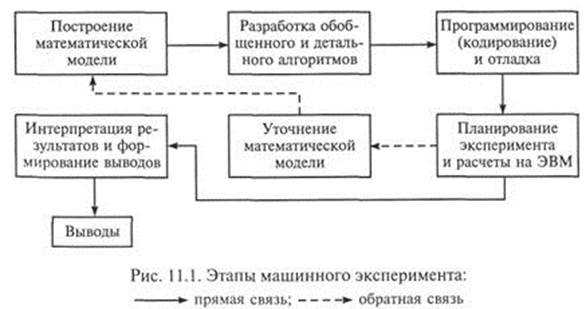
Каждому из показанных на рисунке этапов присущи собственные приемы, методы, технологии. Все эти этапы носят ярко выраженный творческий характер и требуют от разработчика модели особой подготовки.
Планирование эксперимента
При современном уравне развития науки и техники многие исследования требуют постановки сложных и дорогостоящих экспериментов. До последнего времени выбор самого эксперимента, где , как и когда его проводить определялся в основном интуицией экпериментатора. Однако с учетом возросшей стоимости проведения эксперимента актуальной становится проблема извлечения наибольшего количества информации с наименьшими затратами. В этой связи становится необходимым применение методов, которые давали бы не только способ обработки экспериментальных данных, но позволяли бы оптимальным образом организовывать эксперимент. Математический аппарат оптимального планирования эксперимента базируется на применении методов математической статистики и методов решения экстремальных задач. Методы математической статистики используются для обоснования разумного выбора критерия оптимальности, после чего проблема оптимальной задачи планирования эксперимента решается как некоторая экстремальная задача.
К настоящему времени можно выделить два основных направления в планировании экспериментов: планирование экстремальных экспериментов и планирование экспериментов по выявлению сути явлений.
В рамках первого направления исследуются условия, при которых процесс удовлетворяет некоторому критерию оптимальности. В рамках второго направления исследуется взаимосвязь между различными параметрами т.е фактически решается задача идентификации модели объекта при различной априорной информации. Предоставив в результате исследований некоторую математическую зависимость между параметрами, мы даем исследователю возможность обобщить полученные результаты в части выявления взаимосвязи явлений.
Рассмотрим подробнее математическую постановку проблемы планирования эксперимента по выявлению механизма явления. Обычно измеряемая величина зависит от ряда параметров , которые будем называть контролируемыми величинами, которые можно представить в виде вектора столбца
, где -факторное пространство.
Определение области возможных значений контролируемых величин играет важную роль при планировании экспериментов. Задачей эксперимента по поиску математической модели является отыскание связи между измеряемыми величинами и контролируемыми переменными. Эту свазь можно записать в виде
,
где -условное математическое ожидание при значении контролируемых переменных. Можно рассмотреть три постановки задачи в зависимости от априорной информации
1. Вид функции известен. Требуется определить или уточнить неизвестные параметры
2. Известно, что совпадает с одной из функций
Требуется определить, какая из функций является истиной и найти неизвестные параметры.
3. Вид функции неизвестен. Известно лишь, что в интересующей области она может быть достаточно хорошо аппроксимирована конечным рядом по некоторой системе наперед заданных функций Требуется найти наилучшее описание функции .
Оптимизация в исследовании -(от лат. optimus-наилучший) Под оптимизацией - понимают целенаправленную деятельность, заключающуюся в получении наилучших результатов при соответствующих условиях. Постановка задачи оптимизации предполагает наличие объекта, набора независимых параметров (переменных), описывающих данную задачу, а также условий (часто наз. ограничениями), характеризующих приемлемые значения независимых переменных, которые и образуют модель рассматриваемой системы. Еще одним обязательным условием описания оптимизационной задачислужит мера "качества ", носящая название критерия оптимизации и зависящая от переменных . Оптимальное решение оптимизационной задачи - поиск определенного набора значений переменных, которому отвечает минимальное значение критерия оптимальности.
Описанные и построенные модели реального объекта – важнейший этап оптимизационного исследования, так как он определяет практическую ценность получаемого решения и возможность его реализации.
Процесс оптимизации с использованием модели можно рассматривать как метод отыскания оптимального решения для реального объекта без непосредственного экспериментирования с самим объектом. «Прямой» путь, ведущий к оптимальному решению, заменяется «обходным», включающим построение и оптимизацию модели, а также преобразование полученных результатов в практически реализуемую форму. При формировании такой модели следует учитывать характеристики объекта, которые должны быть отражены в модели, а менее существенные особенности в модель можно не включать. Необходимо сформулировать логически обоснованные допущения, выбрать форму представления модели, уровень ее детализации и метод реализации на ЭВМ. Все это относятся к этапу построения модели. Модели можно упорядочить по степени адекватности описания поведения реального объекта. Таким образом, качество модели нельзя оценивать ни по структуре, ни по форме. Единственным критерием такой оценки может служить лишь достоверность полученных на модели примеров поведения реального объекта.
studlib.info