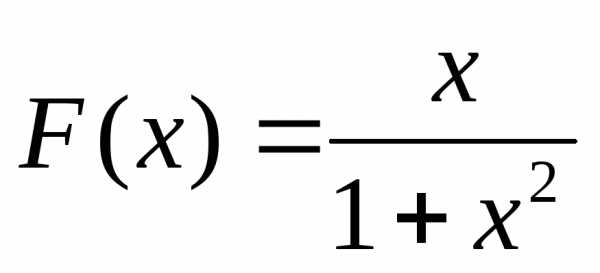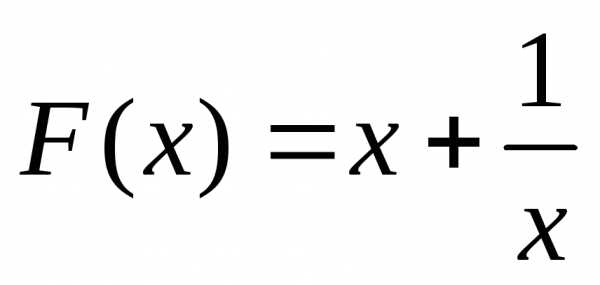1.Одномерная оптимизация. Метод «золотого сечения». Одномерная оптимизация

НОУ ИНТУИТ | Лекция | Однопараметрическая (одномерная) оптимизация. Методы одномерной оптимизации: метод дихотомии, метод Фибоначчи, метод "золотого сечения", метод Ньютона.

Аннотация: Данная лекция рассматривает задачи однопараметрической оптимизации и приводит наиболее распространенные методы решения этих задач, в частности, такие как метод дихотомии, метод Фибоначчи, метод "золотого сечения", метод Ньютона; также формулируются их основные характеристики, определяется область применения и выясняются преимущества и недостатки данных методов.

Однопараметрическая оптимизация (поиск экстремумов функций одной переменной) является самостоятельной и часто встречаемой задачей. Кроме того, к ней сводится гораздо более сложная задача - поиск экстремума функции многих переменных.

1. Метод дихотомии.

Рассмотрим простейший однопараметрический метод безусловной оптимизации – метод дихотомии. Этот метод является методом прямого поиска. В нем при поиске экстремума целевой функции используются только вычисленные значения целевой функции.

Дана функция F(x). Необходимо найти , доставляющий минимум (или максимум) функции F(x) на интервале [a,b] с заданной точностью , т.е. найти

Запишем словесный алгоритм метода.

1) На каждом шаге процесса поиска делим отрезок [a,b] пополам, x=(a+b)/2 - координата середины отрезка [a,b].

2) Вычисляем значение функции F(x) в окрестности вычисленной точки x, т.е.

3) Сравниваем F1 и F2 и отбрасываем одну из половинок отрезка [a,b] (рис. 9.1).

При поиске минимума:

Если F1<F2, то отбрасываем отрезок [x,b], тогда b=x. (рис. 9.1.а)

Иначе отбрасываем отрезок [a,x], тогда a=x. (рис. 9.1.б)

При поиске максимума:

Если F1<F2, то отбрасываем отрезок [a,x], тогда a=x.

Иначе отбрасываем отрезок [x,b], тогда b=x.

4) Деление отрезка [a,b] продолжается, пока его длина не станет меньше заданной точности , т.е.

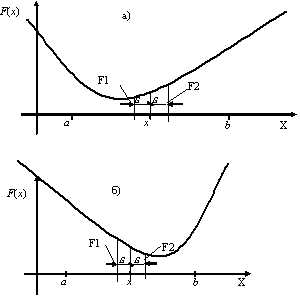Рис. 9.1. Поиск экстремума функции F(x) методом дихотомии

Схема алгоритма метода дихотомии представлена на рис 9.2.

На рис 9.2: c - константа,

При выводе x – координата точки, в которой функция F(x) имеет минимум (или максимум), FM – значение функции F(x) в этой точке.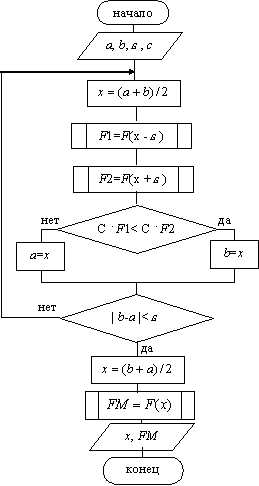

Рис. 9.2. Схема алгоритма метода дихотомии

www.intuit.ru

Однопараметрическая (одномерная) оптимизация

Введение в математическое программирование

1.если f(x4) < f(x2), то новыминтервалом неопределенности будет(x1,x2) длинойх2–х1=L ;

2.если f(х4)>f(x2), то новыминтервалом неопределенности будет(х4,х3) длинойх3–х4.

Поскольку не известно, какая из этих ситуаций будет иметь место, выберем х4 таким образом, чтобы минимизировать наибольшую из длинх3-х4 их2-х1.Достигнуть этого можно, сделав длиных3 – х4 их2 – х1 равными т.е. поместивх4 внутри интервала симметрично относительно точких2, уже лежащей внутри интервала. Любое другое положение точких4 может привести к тому, что полученный интервал будет большеL. Помещаях4 симметрично относительнох2, мы ничем не рискуем в любом случае. Если окажется, что можно выполнить еще одно вычисление функции, то следует применить описанную процедуру к интервалу(х1, х2), в котором уже есть значение функции, вычисленное в точкех4, или к интервалу(х4,х3), в котором уже есть значение функции, вычисленное в точкех2.

Следовательно, стратегия ясна с самого начала. Нужно поместить следующую точку внутри интервала неопределенности симметрично относительно уже находящейся там точке. Парадоксально, но, чтобы понять, как следует начинать вычисления, необходимо разобраться в том, как его следует кончать.

На n -мвычисленииn -юточку следует поместить симметрично по отношению к(n — 1) -йточке. Положение этой последней точки в принципе зависит от нас. Для того чтобы получить наибольшее уменьшение интервала на данном этапе, следует разделить пополам предыдущий интервал. Тогда точках будет совпадать с точкойхn-1.Однако при этом мы не получаем никакой новой информации. Обычно точкихn-1 ихn отстоят друг от друга на достаточном расстоянии, чтобы определить, в какой половине, левой или правой, находитсяинтервал неопределенности. Они помещаются на расстояниие/2 по обе стороны от середины отрезкаLn-1 ; можно самим задать величинуе или выбрать эту величину равной минимально возможному расстоянию между двумя точками.

Интервал неопределенности будет иметь длинуLn, следовательно,Ln-1 = 2Ln - е (рис.4, нижняя часть). На предыдущем этапе точкихn-1 ихn-2 должны быть помещены симметрично внутри интервалаLn-2 на расстоянииLn-2 от концов этого интервала. Следовательно,Ln-2 = Ln-1+Ln (pис.4, средняя часть).

Рис. 4.

Замечание. Из рисунка ясно, что на предпоследнем этапехn-2 остается в качестве внутренней точки.

Аналогично Ln-3=Ln-2+Ln-1 (pис.4, верхняя часть)

В общем случае Lj-1=Lj + Lj+1 при1<j<n. Таким образом,

Если определить последовательность чисел Фибоначчи следующим образом:F0=1, F1=l, и

Fk=Fk-1+Fk-2 для k = 2, 3,..., то

(2.2)

Если начальный интервал (a;b) имеет длинуL = (b-а),то

studfiles.net

Тема 1.6. Одномерная оптимизация

1.6.1. Постановка задачи

1.6.2. Метод дихотомии

1.6.3. Метод золотого сечения

1.6.4. Сравнение методов

1.6.5. Тестовые задания по теме «Одномерная оптимизация»

1.6.1. Постановка задачи

Задача оптимизации – одна из важнейших составляющих многих инженерных задач. Найти оптимальное решение – означает найти наилучший, в смысле заданного критерия, вариант из всех возможных. При решении задачи оптимизации рассматривается некоторая функция, называемая целевой (или критериальной), и аргументы (параметры целевой функции), называемыепараметрами оптимизации.

По количеству независимых переменных различают задачи одномерной оптимизации (n=1) и многомерной оптимизации (n ³ 2). При этом задача нахождения максимума целевой функции сводится к задаче нахождения минимума путем замены функцииf(x)на-f(x), поэтому в дальнейшем будем говорить только о поиске минимума функции, то есть такогоx*Î[a, b],при которомf(x*) = min f(x).

В области допустимых значений функция f(x)может иметь несколько экстремумов (минимумов или максимумов - рис. 4.6.1). Говорят, что функцияf(x)имеет в точкеx*локальный минимум, если существует некоторая положительная величинаd,такая, что если½х – х*½< d,тоf(x)³ f(x*),т.е. существуетd- окрестность точких*,такая, что для всех значенийхв этой окрестностиf(x)³ f(x*).Функцияf(x)имеетглобальный минимум в точкеx*,если для всеххсправедливо неравенствоf(x)³ f(x*).Таким образом, глобальный минимум является наименьшим из локальных.

Рис. 1.6.1-1

Задачей одномерной оптимизации является нахождение точек локального минимума и соответствующих им значений функции, а в некоторых случаях требуется вычислить глобальный минимум. Однако, во всех случаях эта задача сводится к задаче нахождения локального минимума.

Интервал, на котором локализован единственный минимум, называется отрезком неопределенности.

Известно, что необходимымусловием существования экстремума дифференцируемой функцииf(x)является выполнение равенстваf¢(х) = 0. Точках, удовлетворяющая данному условию, называетсяточкой стационарности.Достаточным условием существования минимума в точке стационарности является выполнение неравенстваf¢¢(х)>0, а максимума -f¢¢(х)<0.

Задача одномерной оптимизации имеет единственное решение в том случае, если функция f(x) на отрезке[a;b]имеет только один экстремум. Тогда говорят, что функцияунимодальнаяна отрезке[a;b].

Достаточными условиями унимодальности функции на отрезке[a;b]являются:

Для дифференцируемой функцииf(x)ее производнаяf¢(х) - неубывающая.
Для дважды дифференцируемой функции f(x)выполняется неравенствоf¢¢(х)³0.

Все численные методы одномерной оптимизации применяются только для унимодальных на определенном интервале функций.

Пример 1.6.1-1. Провести исследование функции f(x) = x3 – x + e-x на предмет существования экстремумов.

Вначале проведем графическое исследование. Построим график функции f(x)(рис. 1.6.1-2). Из графика видно, чтоf(x)имеет две точки минимума:х1их2, причем точках1– точка глобального минимума. Исходя из графика, можно принять следующие отрезки неопределенности: для точки х1-[-4;-3],а для точких2 - [0;1].

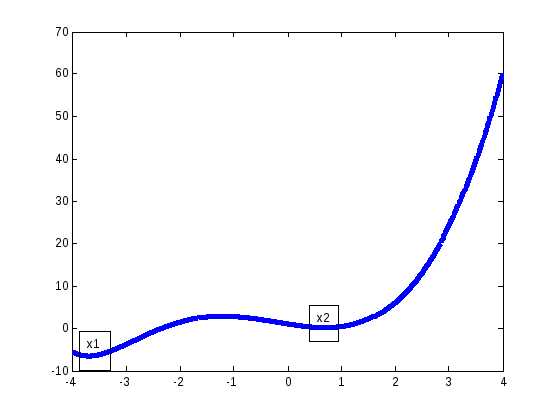
Рис. 1.6.1-2

Проверим достаточное условие существования минимума на выбранных отрезках:

f¢(x) = 3x2 – 1 – e-x; f¢¢ (x) = 6x + e-x,

f¢(0) < 0, f¢(1) > 0, f¢¢ (x) > 0 для хÎ[0;1],

f¢(-4) < 0, f¢(-3) > 0, f¢¢ (x) > 0 для хÎ[-4;-3].

Условия существования минимума выполнены, поскольку f¢¢(x) > 0для всеххÎ[0;1]ихÎ[-4;-3].Следовательно, функцияf(x)является унимодальной на выбранных отрезках.

На практике численные методы одномерной оптимизацииприменяют в следующих случаях:

значения функции f(x)определены в ходе эксперимента;
целевая функция очень сложна или не имеет непрерывных производных;
классические методы поиска оптимального значения не применимы.

Суть методов одномерного поиска заключается в том, что на каждой итерации интервал неопределенности уменьшается и стягивается к точке минимума. Уменьшение отрезка происходит до тех пор, пока на некоторойn-й итерации отрезок неопределенности[bn;an]не станет соизмеримым с заданной погрешностьюe, то есть будет выполняться условие|bn-an| < e.Тогда за точку минимума можно принять любую точку, принадлежащую этому отрезку, в частности, его середину.

Наиболее простым способом сужения интервала неопределенности является деление его на некоторое число равных частей с последующим вычислением значений целевой функции в точках разбиения. Очевидно, что за минимум принимают наименьшее из этих значений – это так называемый метод сканирования. На практике чаще применяют одну из основных модификаций метода –метод прямого перебора с переменным шагом. Суть его заключается в следующем. От начальной точки интервала неопределенности двигаются с начальным шагом до тех пор, пока функция в точках разбиения уменьшается (т.е. функция убывает). Если функция в очередной точке стала возрастать, то происходит сужение интервала неопределенности путем возврата от этой рассматриваемой (которая станет правой границей нового интервала) точки на два шага назад. Полученная таким образом точка будет левой границей нового отрезка. Новый отрезок вновь исследуют таким же образом, но уже с уменьшенным в два раза шагом. Процесс повторяется до момента достижения заданной точности минимума. Это весьма трудоемкий путь. Более эффективными являютсяметоды одномерного поискас другими способами выбора узлов и сужения интервалов неопределенности.

Рассмотрим, в частности, метод дихотомиииметод золотого сечения.

studfiles.net

Тема 6.6. Одномерная оптимизация

6.6.1. Постановка задачи

6.6.2. Метод дихотомии

6.6.3. Метод золотого сечения

6.6.4. Сравнение методов

6.6.5. Технология решения задач одномерной оптимизации средствами

математических пакетов

6.6.5.1. Технология решения задач одномерной оптимизации средствами MathCad

6.6.5.2. Технология решения задач одномерной оптимизации

средствами MatLab

6.2.7. Тестовые задания по теме «Одномерная оптимизация»

6.6.1. Постановка задачи

Рис. 6.6.1-1

Интервал, на котором локализован единственный минимум, называется отрезком неопределенности.

Достаточными условиями унимодальности функции на отрезке[a;b]являются:

Для дифференцируемой функцииf(x)ее производнаяf¢(х) - неубывающая.
Для дважды дифференцируемой функции f(x)выполняется неравенствоf¢¢(х)³0.

Пример 6.6.1-1. Провести исследование функции f(x) = x3 – x + e-x на предмет существования экстремумов.

Вначале проведем графическое исследование. Построим график функции f(x)(рис. 6.6.1-2). Из графика видно, чтоf(x)имеет две точки минимума:х1их2, причем точках1– точка глобального минимума. Исходя из графика, можно принять следующие отрезки неопределенности: для точки х1-[-4;-3],а для точких2 - [0;1].

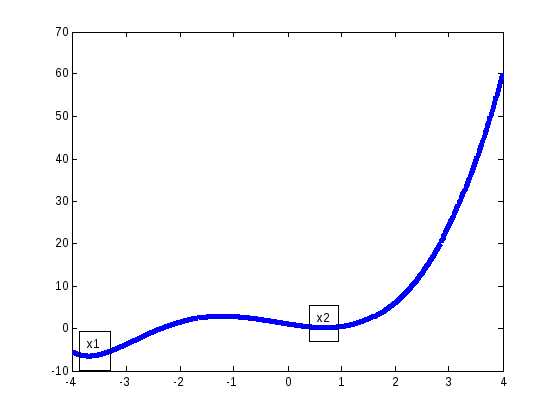
Рис. 6.6.1-2

Проверим достаточное условие существования минимума на выбранных отрезках:

f¢(x) = 3x2 – 1 – e-x; f¢¢ (x) = 6x + e-x,

f¢(0) < 0, f¢(1) > 0, f¢¢ (x) > 0 для хÎ[0;1],

f¢(-4) < 0, f¢(-3) > 0, f¢¢ (x) > 0 для хÎ[-4;-3].

На практике численные методы одномерной оптимизацииприменяют в следующих случаях:

значения функции f(x)определены в ходе эксперимента;
целевая функция очень сложна или не имеет непрерывных производных;
классические методы поиска оптимального значения не применимы.

Рассмотрим, в частности, метод дихотомиииметод золотого сечения.

studfiles.net

Методы одномерной оптимизации

ЛАБОРАТОРНАЯ РАБОТА № 1

Исследование алгоритмов одномерной оптимизации

НАЗНАЧЕНИЕ И ЦЕЛЬ РАБОТЫ

Целью работы является изучение и анализ поисковых алгоритмов минимизации функции одной переменной: дихотомического, Фибоначчи и «золотого сечения».

ВВЕДЕНИЕ

В большинстве методов поисковой оптимизации, используемых в задачах параметрического синтеза конструкций и технологических процессов, таких как методы наискорейшего или покоординатного спуска, метод сопряженных направлений и т.п., на каждом шаге приходится решать задачу минимизации (максимизации) функции одной переменной. 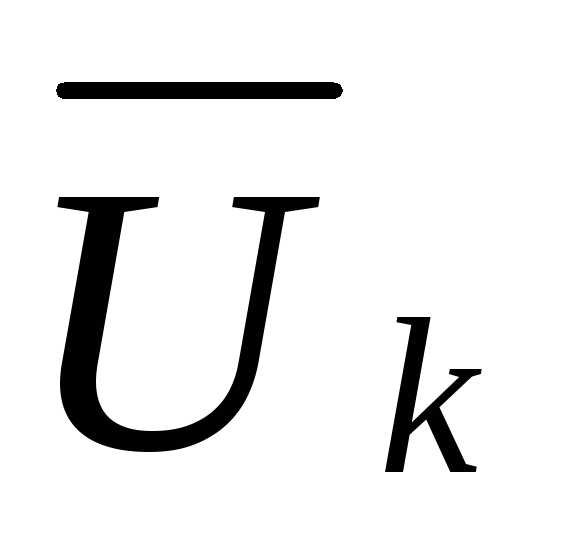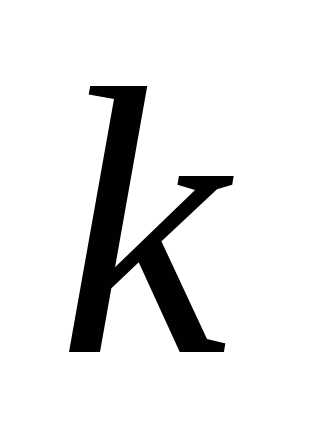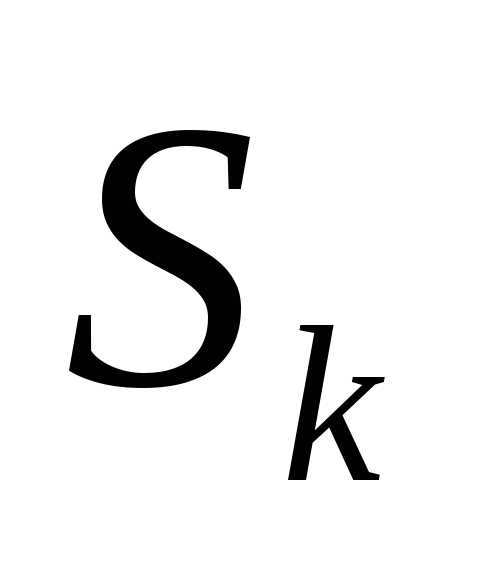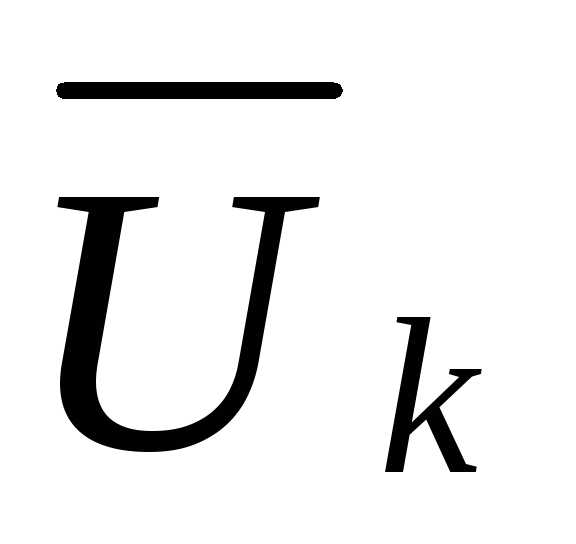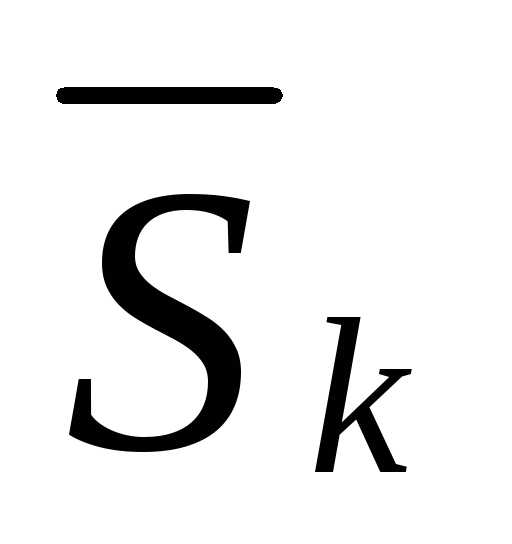Действительно, после выбора в исходной точке (-го шага) направления поиска, величина шага в этом направлении определяется из условия минимума (максимума) целевой функции, которая при фиксированныхиявляется функцией одной скалярной переменной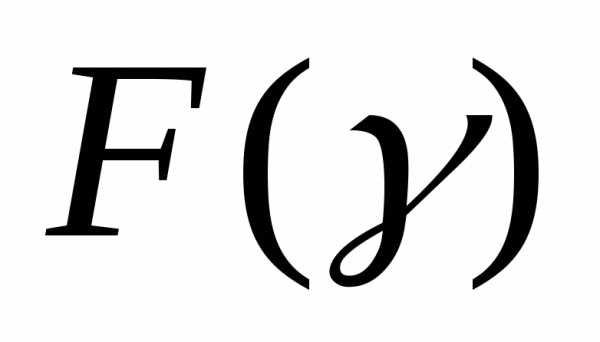. В результате решения этой задачи получают значение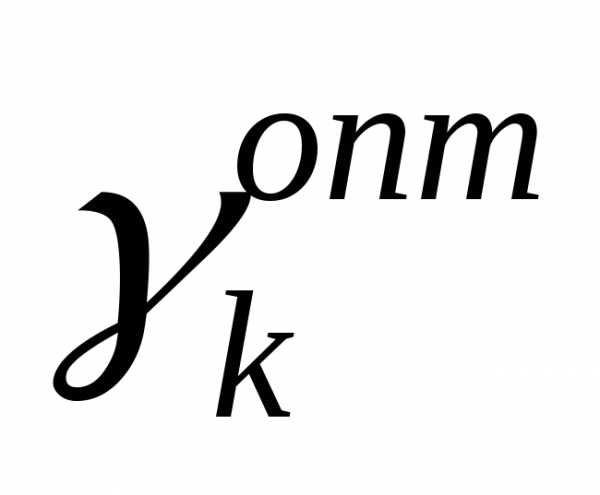и следующий шаг поиска начинают из точки.

Процедура нахождения 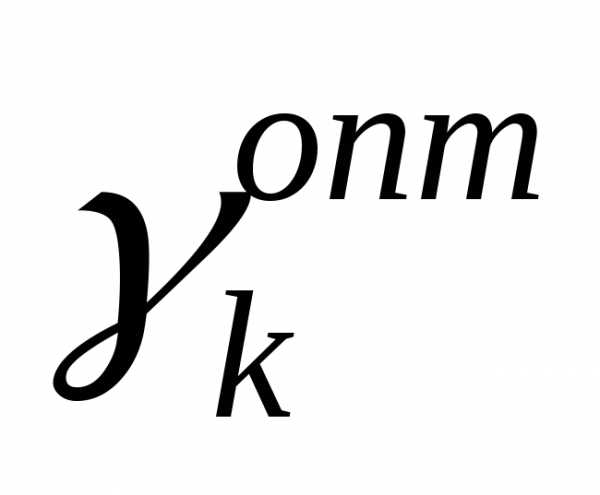представляет собой задачу поисковой одномерной оптимизации, различные методы одномерного поиска используют некоторый начальный интервал неопределенности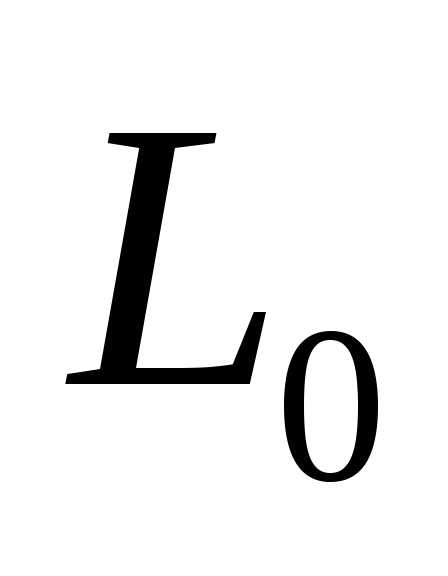, содержащий минимум (максимум) функции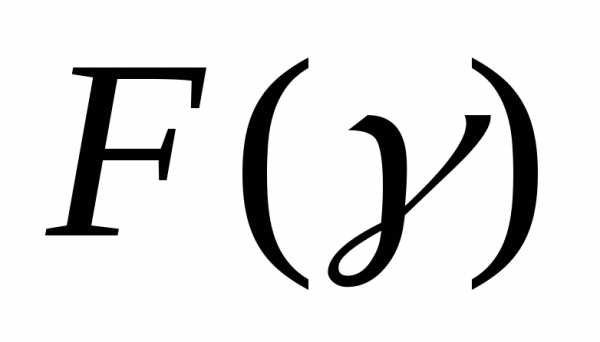, который затем уменьшается до некоторого значения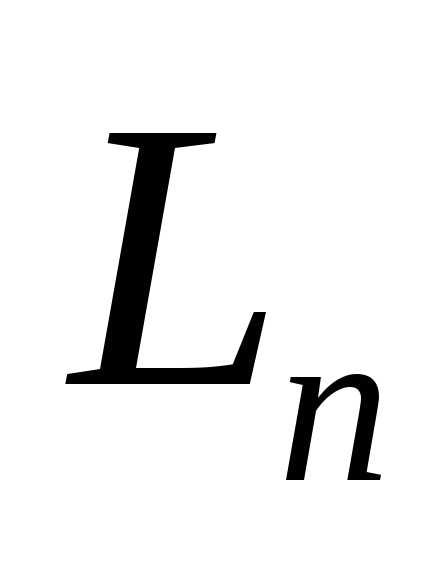путем вычисления значений функции в соответствующих точках и отбрасывания заведомо неоптимальных подынтервалов.

Будем для определенности рассматривать далее так называемые унимодальные функции 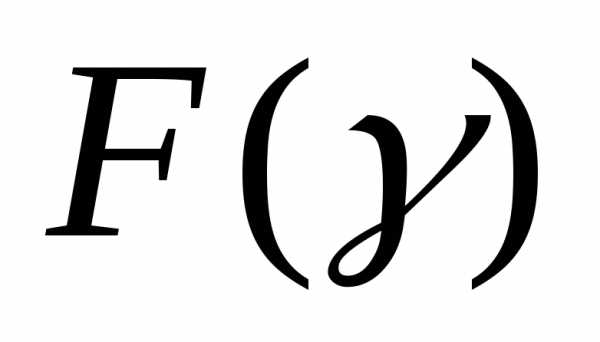, т.е. функции, имеющие на заданном интервале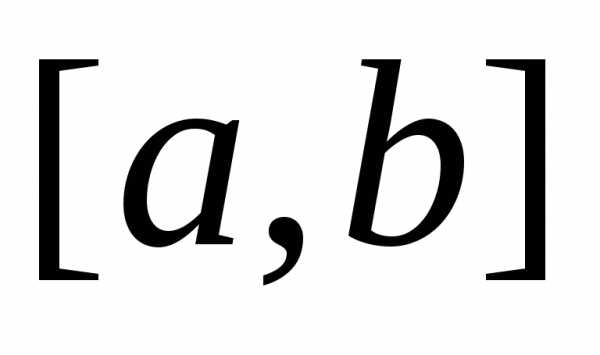единственный минимум. Не нарушая общности, будем полагать, что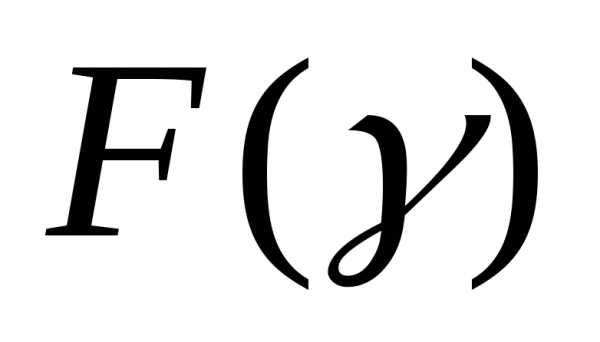минимизируется на интервале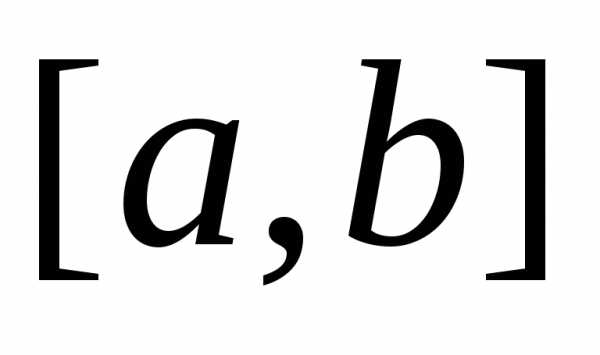; максимум функции находится подобным образом.

ДИХОТОМИЧЕСКИЙ МЕТОД

Этот метод предполагает на каждом шаге вычисление функции в двух точках (проведение двух экспериментов). При этом с целью максимального уменьшения интервала неопределенности на каждом шаге указанные точки выбираются как можно ближе к середине интервала.

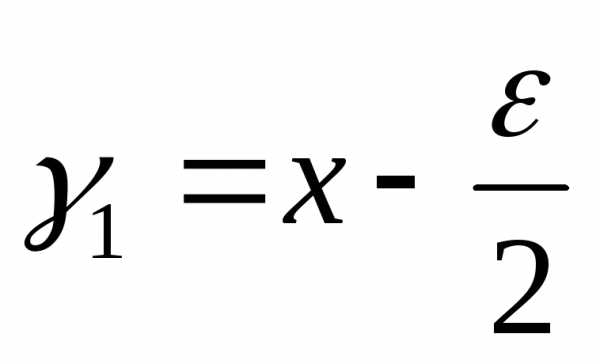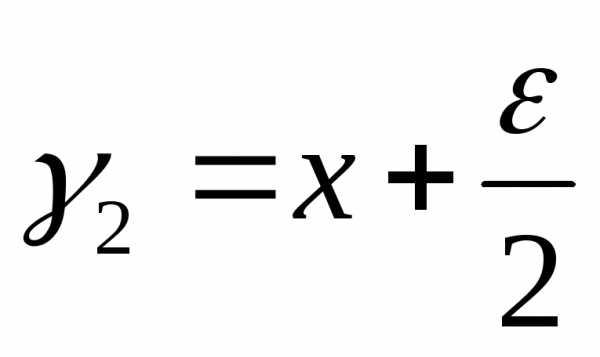Пусть на первом шаге эксперимент проводится в точках и, где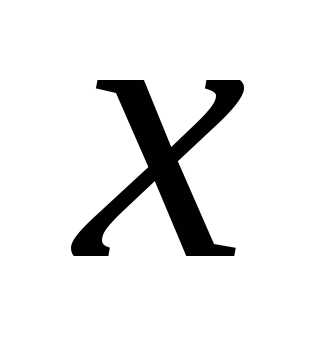– середина интервала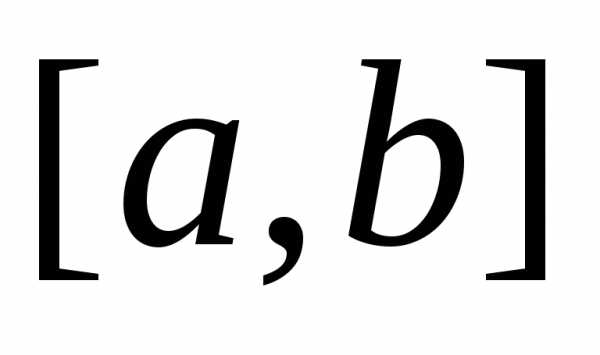,– достаточно малое положительное число (это число модно трактовать как чувствительность экспериментатора в различении двух близких точек).

Рис.1

Если , то с учетом унимодальности и возможности нахождения минимума в интерваледля дальнейшего поиска должен быть оставлен интервал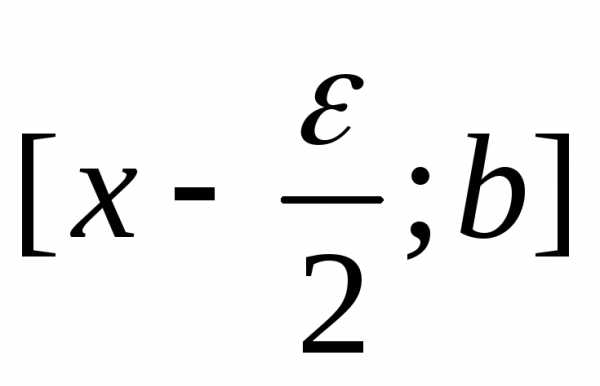, в противном случае –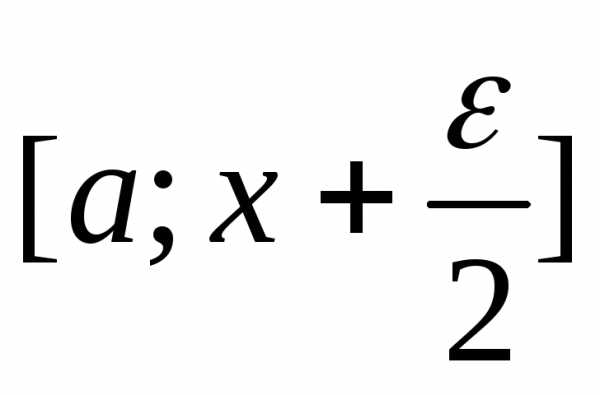. Таким образом, если вначале интервал неопределенности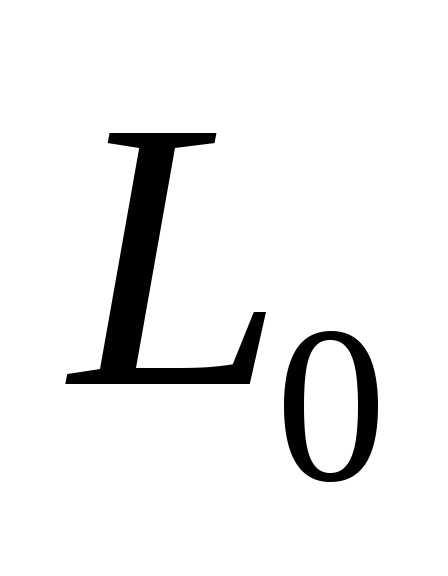равен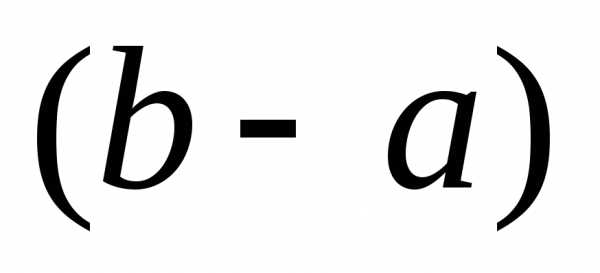, то после первого шага (состоящего из двух экспериментов) он равен

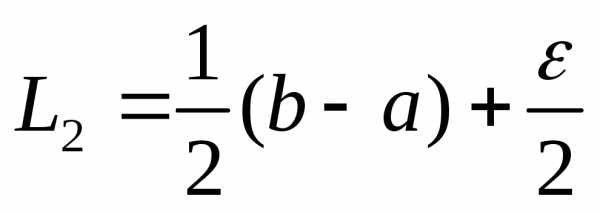Выберем теперь третий и четвертый эксперименты как пару в середине оставшегося интервала. После этого интервал неопределенности станет равным

Легко понять, что после 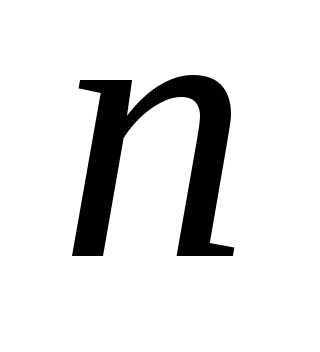экспериментов (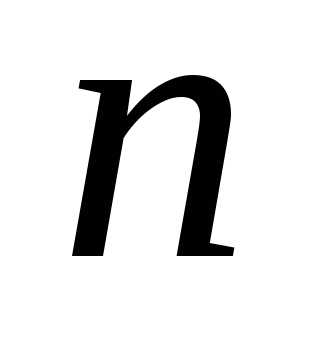– четно), произведенных по тому же правилу, минимум функции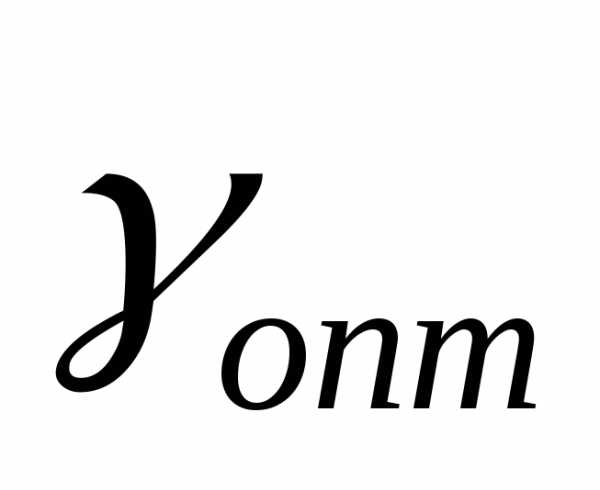лежит в интервале

. (1)

Из формулы (1) видно, что для уменьшения интервала неопределенности, например в 100 раз, если пренебречь величиной , требуется 14 экспериментов.

Словесный алгоритм метода следующий:

Заданы начало и конец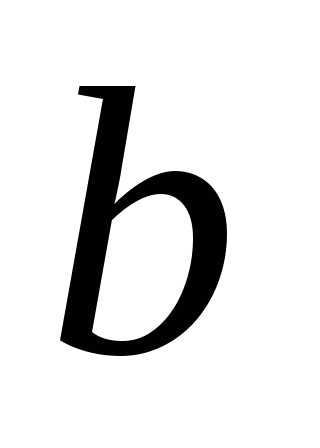интервала, точность.

Шаг 1.Рассчитывается середина интервала,.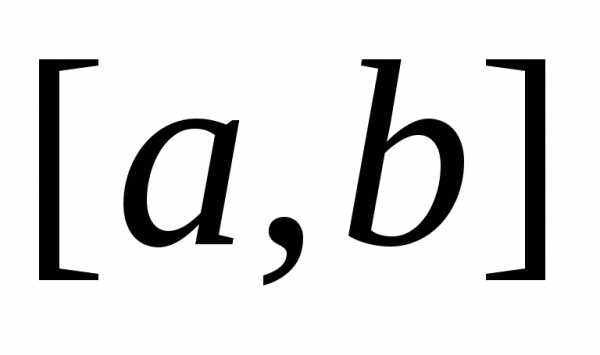

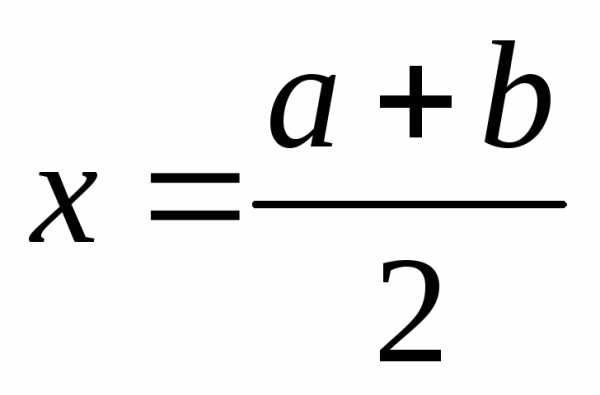Шаг 2.Рассчитываются точки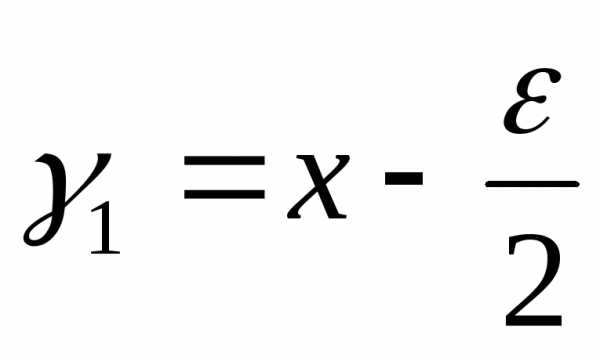ии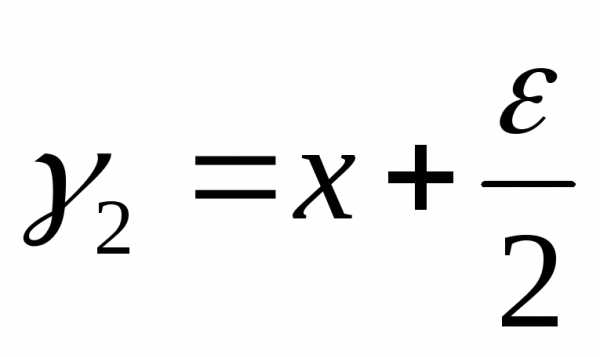 значения в них целевой функциии.

Шаг 3.Если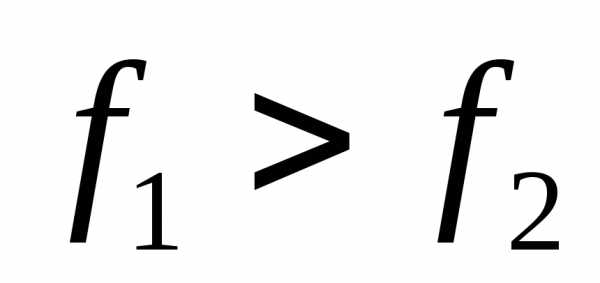, то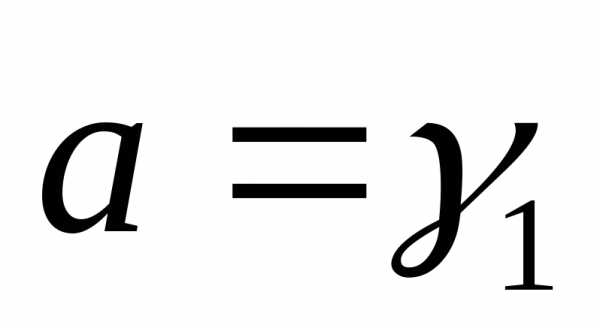, иначе.

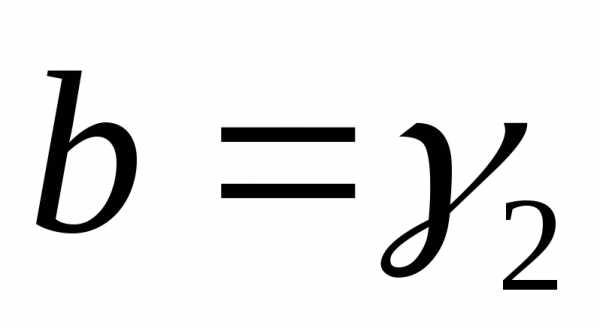Шаг 4.Повторять шаги 1-3 до тех пор, пока длина интервала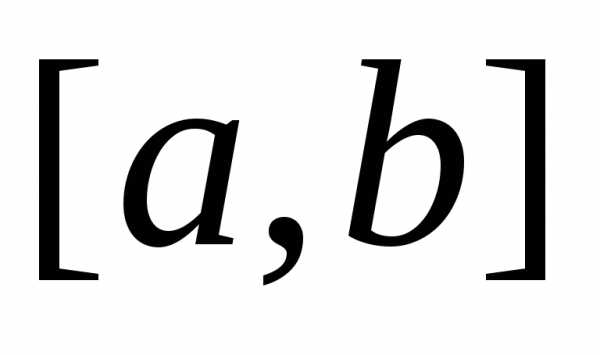больше.

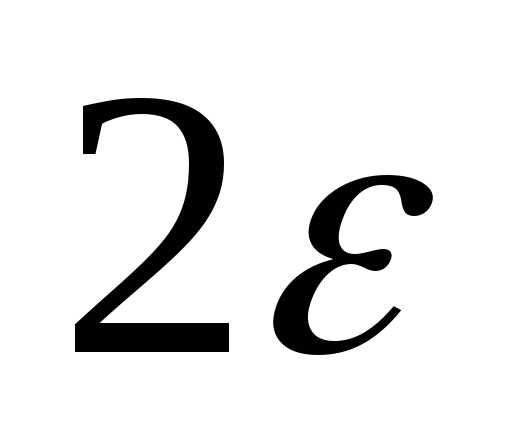Шаг 5.Результат.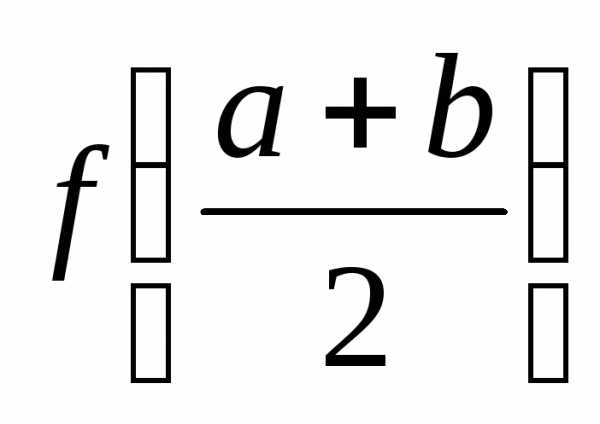

МЕТОД ФИБОНАЧЧИ

Этот метод является наиболее быстрым методом поиска, требующим минимального числа экспериментов. Здесь на каждом шаге, кроме первого, проводится не два, а один эксперимент. Стратегия поиска состоит в том, что новая точка поиска располагается внутри интервала неопределенности симметрично относительно уже находящейся там точки, оставшейся от предыдущих экспериментов. Для определения требуемого числа экспериментов 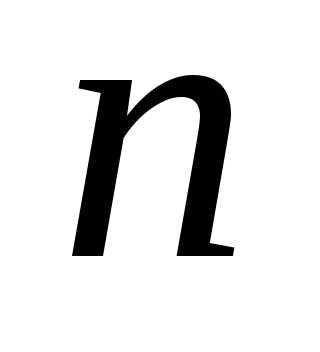, обеспечивающего точность, а также для выбора положения двух первых точек поиска, необходимо рассмотреть процесс поиска в обратном порядке, т.е. с последнего шага.

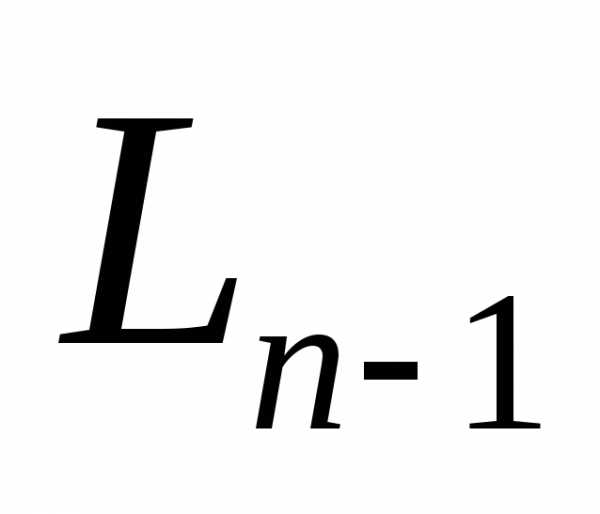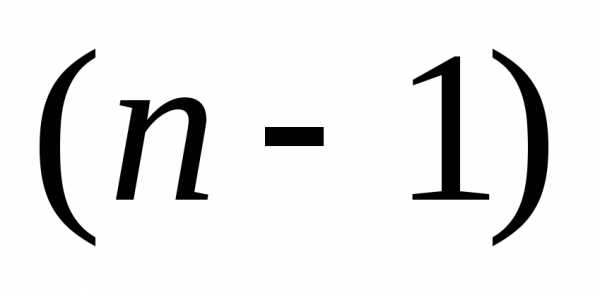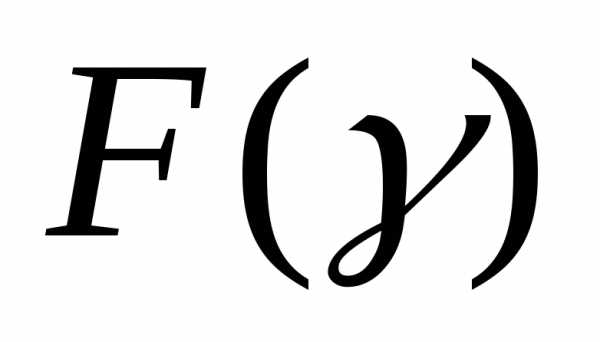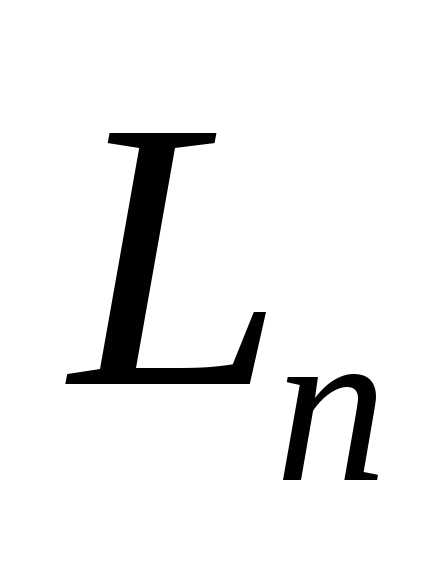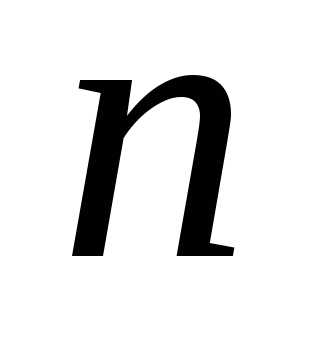Рассмотрим ситуацию, которая возникла после того, как все эксперименты, кроме последнего, уже проведены. Длину изменяющегося интервала неопределенности обозначим . Внутри этого интервала находится эксперимент с наименьшим изиспытаний значением функциии внутри него также следует провести последний эксперимент. Очевидно, что для обеспечения минимального интервала неопределенностипослеэкспериментов указанные точки должны быть симметрично расположены относительно середины интервала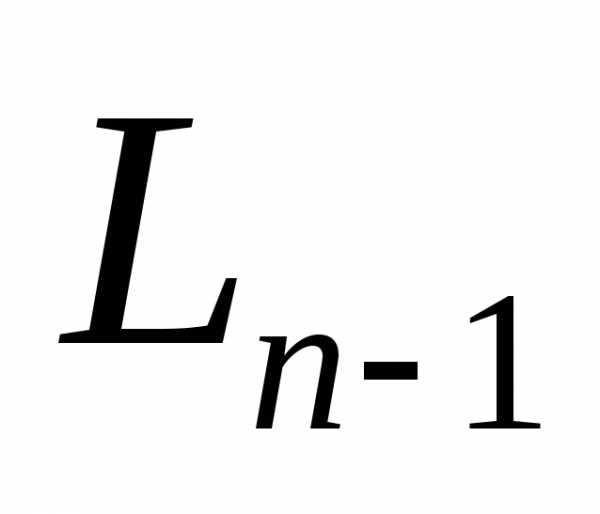и удалены от нее на расстояние.

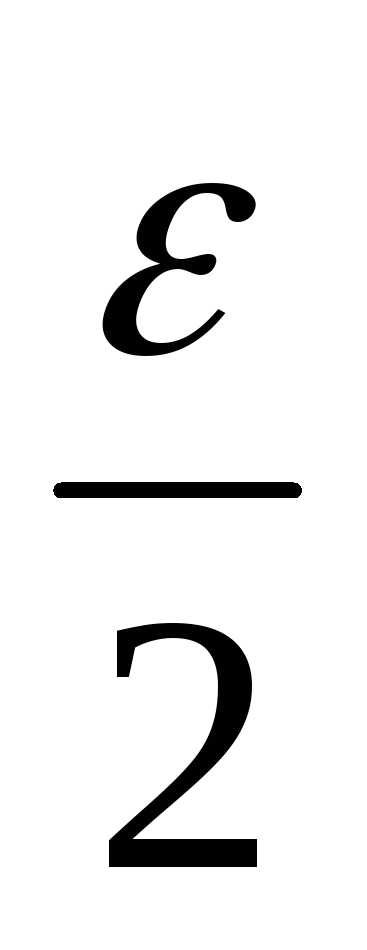Рис. 2

Таким образом,

. (2)

Рассмотрим далее ситуацию, когда проведены все эксперименты, кроме двух последних, и длину имеющегося интервала неопределенности обозначим 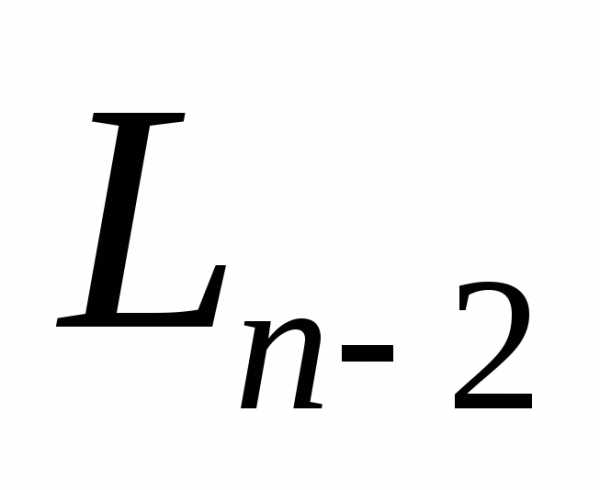. Внутри этого интервала находится точка с наименьшим из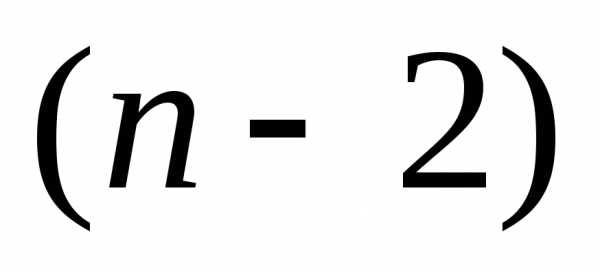испытаний значением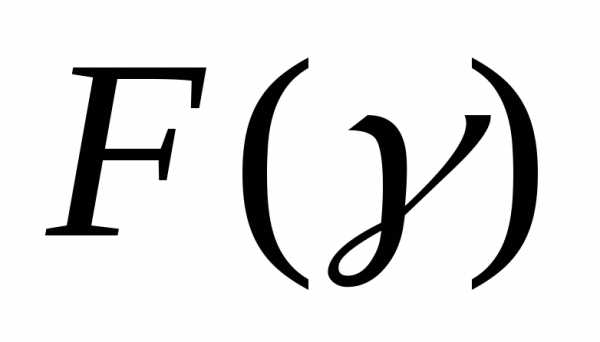, и также внутри него необходимо провести следующий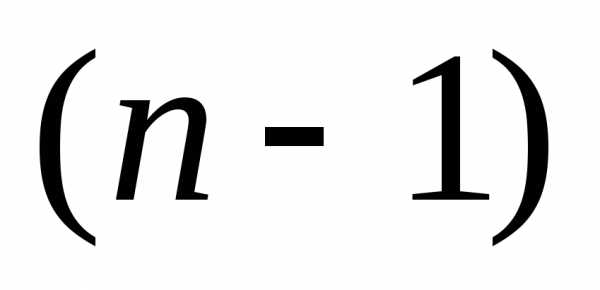эксперимент. По результатам этого эксперимента часть интервала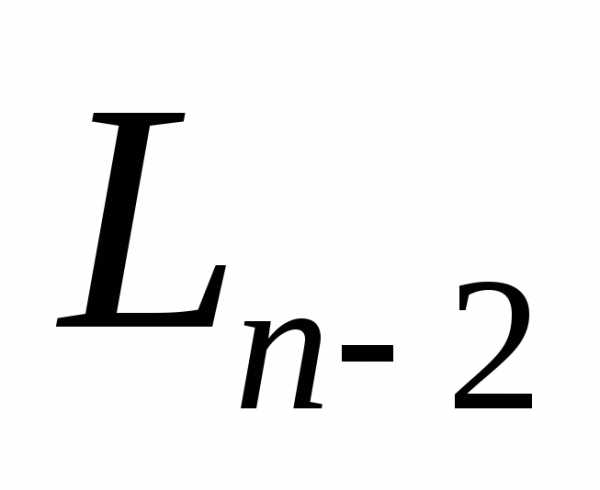должна быть отброшена, а оставшаяся часть есть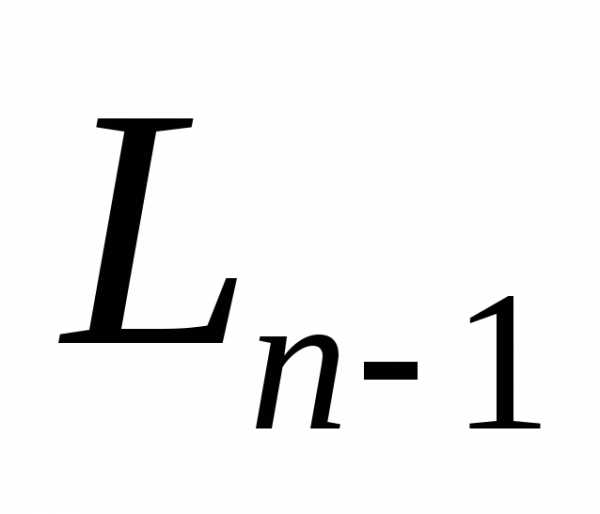. Поскольку заранее не ясно, какая часть будет отброшена, указанные точки должны располагаться на равных расстояниях от концов интервала.

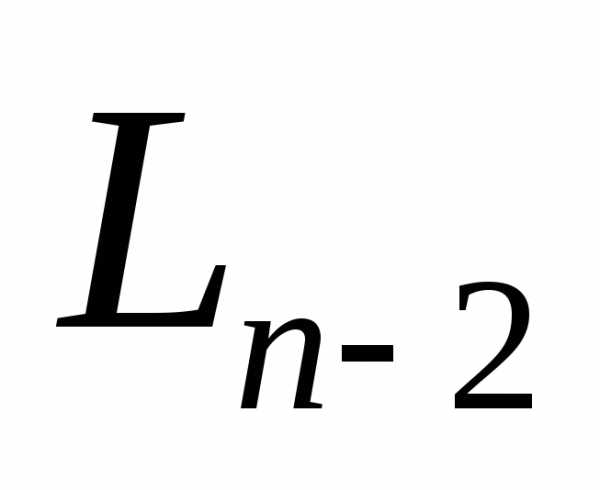Рис.3

Но одна из точек внутри интервала 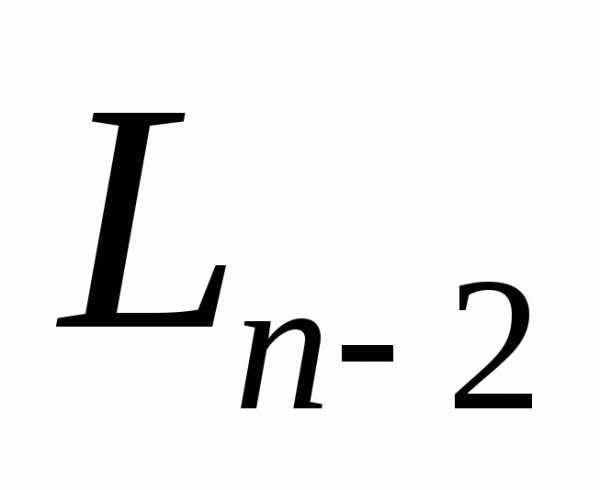останется после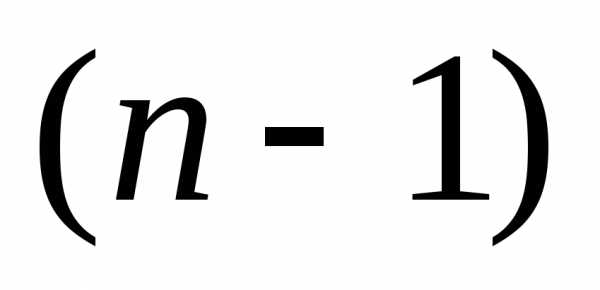эксперимента и станет точкой внутри интервала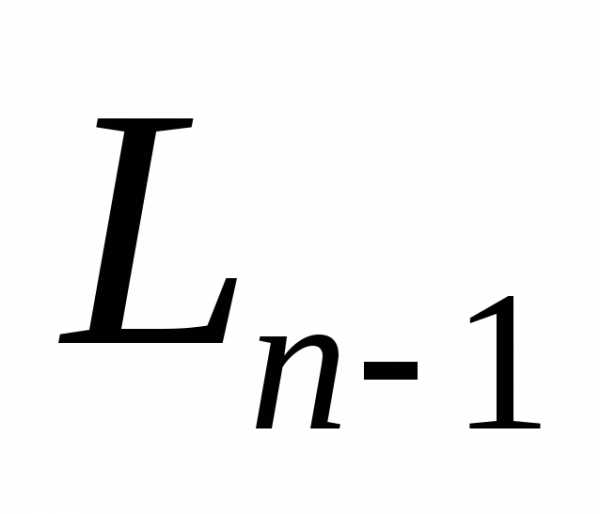. Сочетание возможных комбинаций рисунков 2 и 3 приводит к схеме разбиения интервала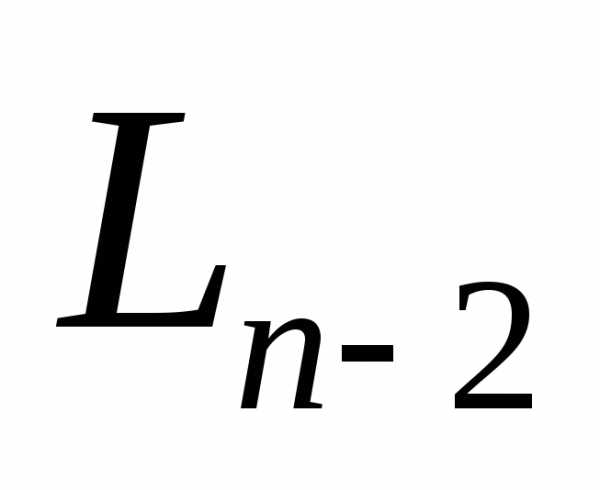, изображенных на рис. 4.

Рис.4

Из рис. 4 следует, что

Аналогично

В общем случае

. (3)

Таким образом,

Для получения общей формулы длины интервала 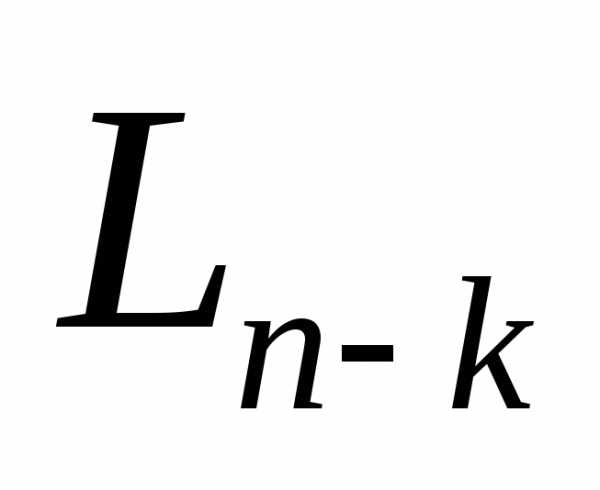введем последовательность чисел Фибоначчи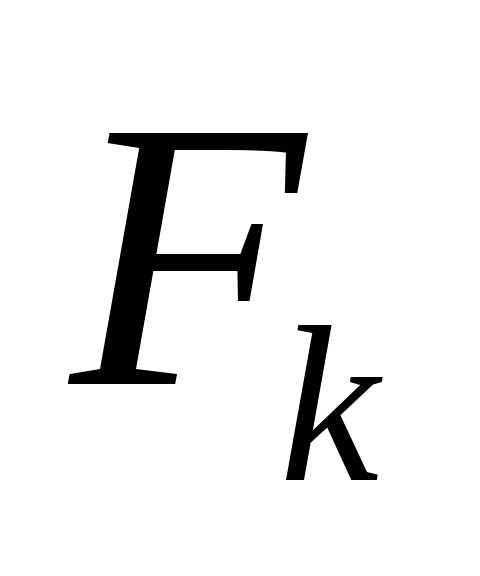, определяемую следующим образом:

(4)

Тогда имеем

(5)

Учитывая, что после первого испытания интервал неопределенности равен , то полагая, получаем:

Отсюда

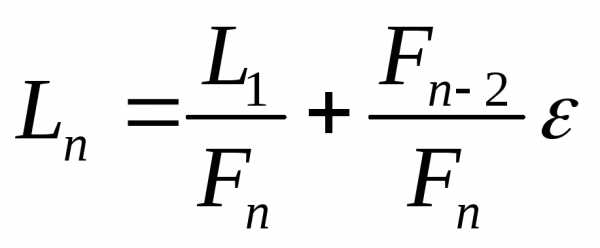(6)

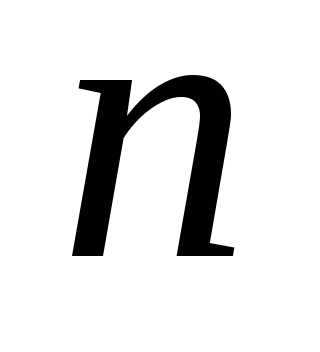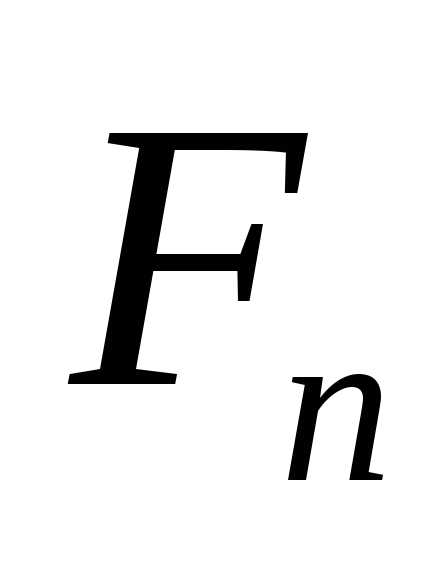Следовательно, после экспериментов начальный интервал неопределенности, если пренебречь величиной, уменьшается враз. Для уменьшения интервала неопределенности, например в 100 раз, требуется 11 экспериментов.

Для того чтобы начать поиск по методу Фибоначчи, необходимо определить положение первых двух точек проведения испытаний. Эти точки располагаются симметрично внутри начального интервала неопределенности на расстоянии 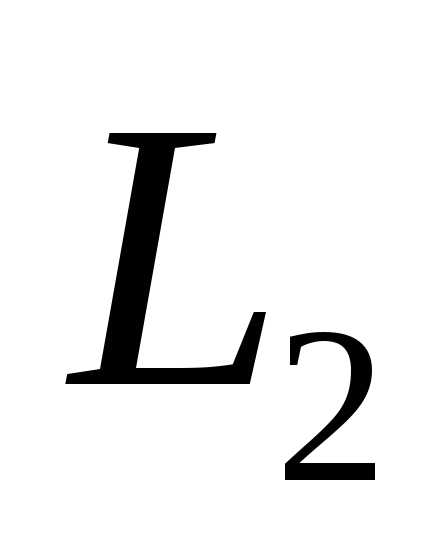от соответствующих концов этого интервала. Полагая в выражении (5), получаем

Пренебрегая величиной , имеем

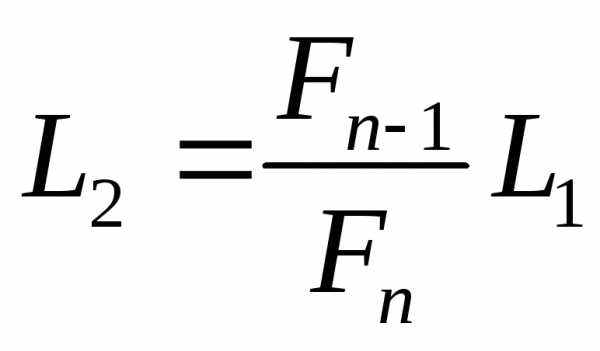. (7)

Словесный алгоритм метода следующий:

Заданы начало и конец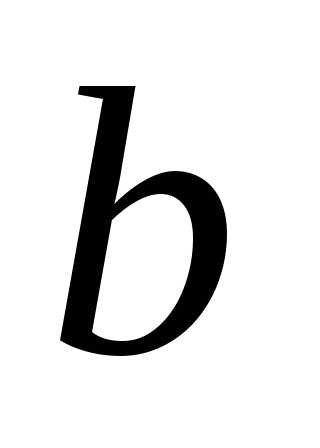интервала.

Шаг 1.Рассчитывается количество итераций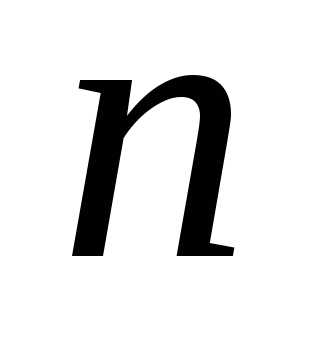и формируется массив чисел Фибоначчи.

Шаг 2.Рассчитываются две точк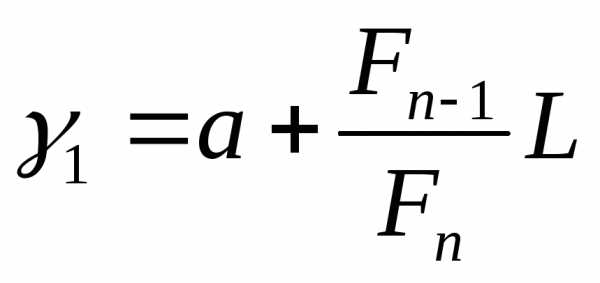ии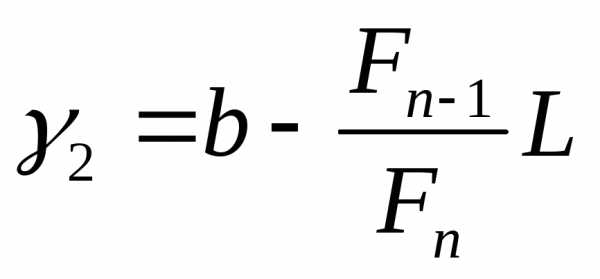и значения в них целевой функциии, где– длина интервала.

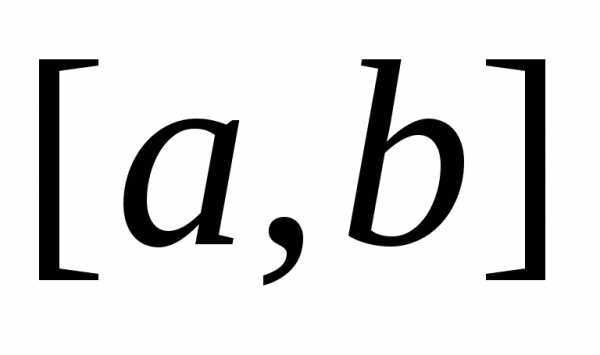Шаг 3.Если, то

,,,

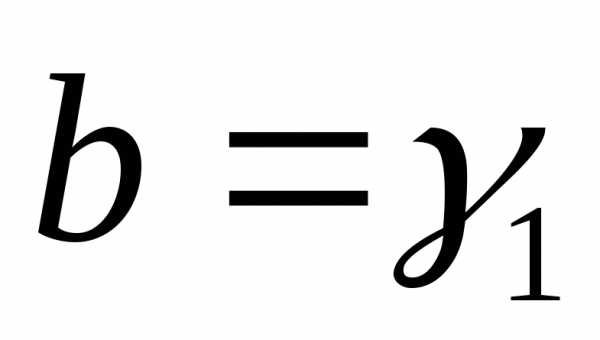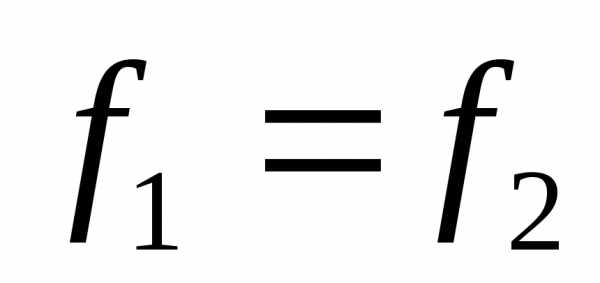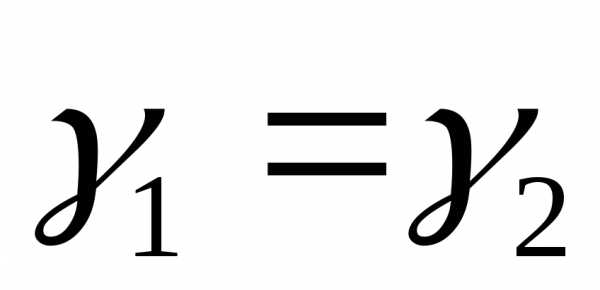и рассчитывается одна новая точка

иначе

,,,

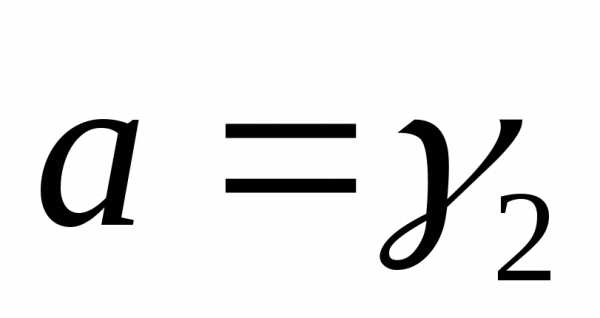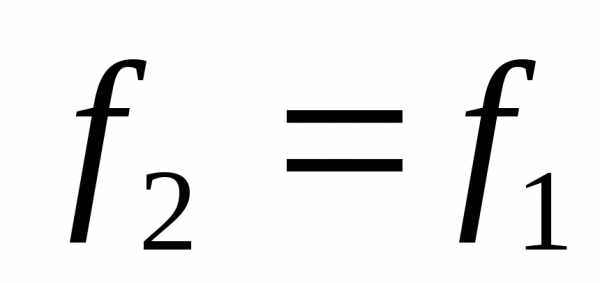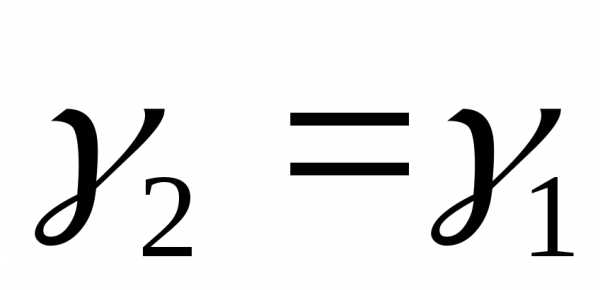и рассчитывается одна новая точка

Шаг 4..

Шаг 5.Повторять шаги 1-3 до тех пор, пока.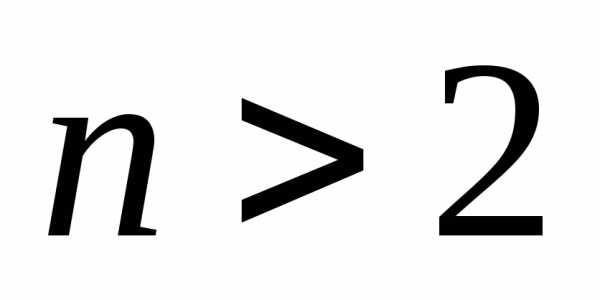

Шаг 6.Результат.

МЕТОД «ЗОЛОТОГО СЕЧЕНИЯ»

Для начала поиска по методу Фибоначчи необходимо предварительно задаться числом экспериментов 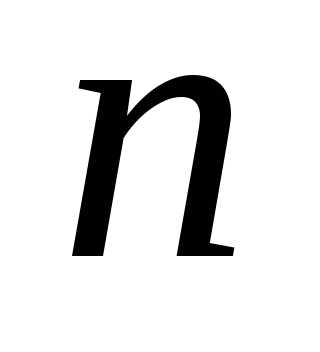исходя из допустимого значения интервала неопределенности в конце поиска. От этого недостатка свободен метод «золотого сечения», который почти столь же эффективен, как и метод Фибоначчи. Здесь так же, как и в последнем методе, точка, выбираемая внутри интервала неопределенности для проведения эксперимента на очередном шаге, располагается симметрично относительно уже находящейся там точки, оставшейся от предыдущих экспериментов. Поэтому здесь для трех соседних интервалов неопределенности также справедливо соотношение (3). Однако в методе «золотого сечения» не используется соотношение (2), которое зависит от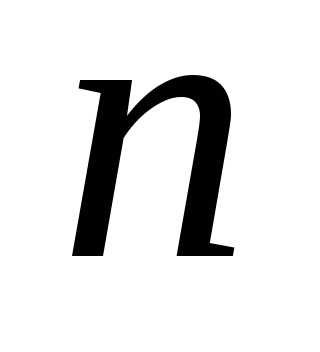. Вместо этого выдерживается постоянным, равным, отношение длин последовательных интервалов, т.е.

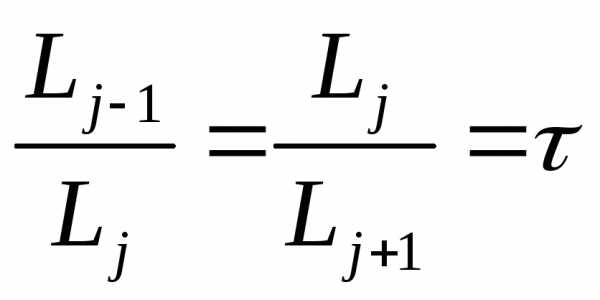. (8)

Разделив (3) на 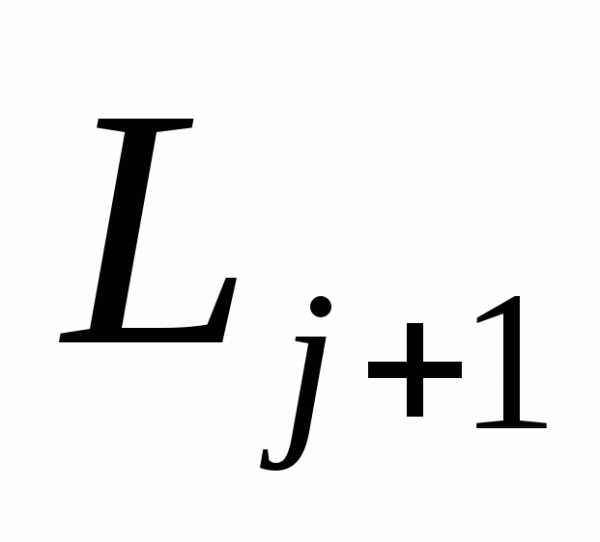и приняв во внимание, что согласно (8)

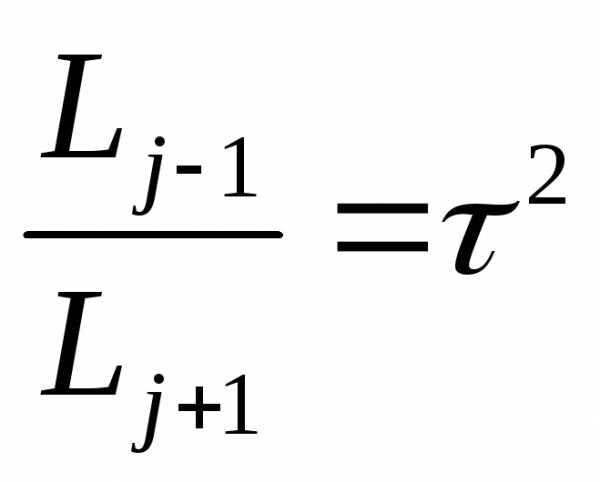, имеем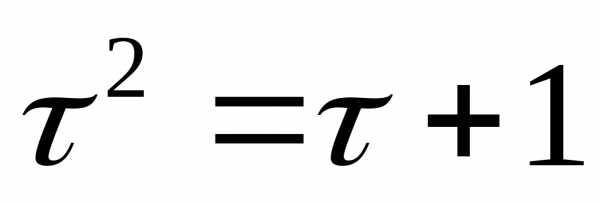, (9)

откуда

. (10)

Тогда

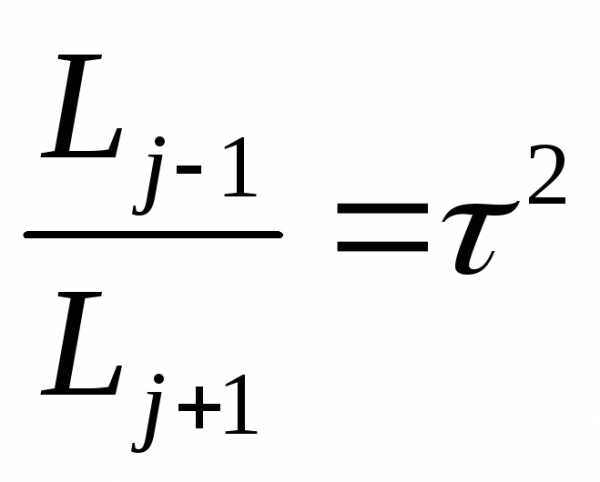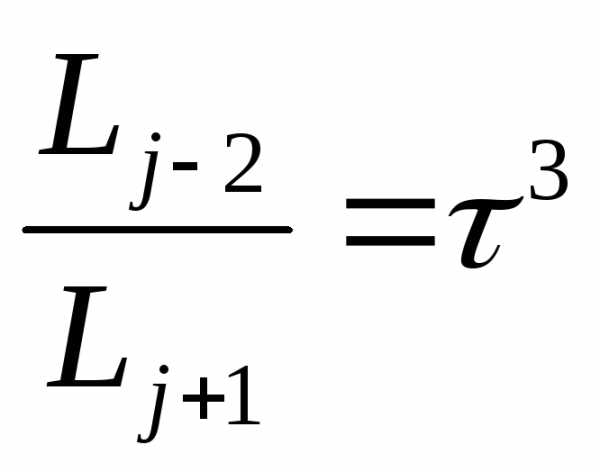;и т.д.

Следовательно,

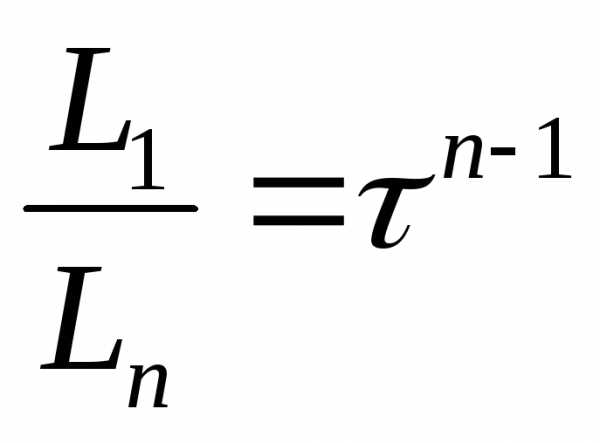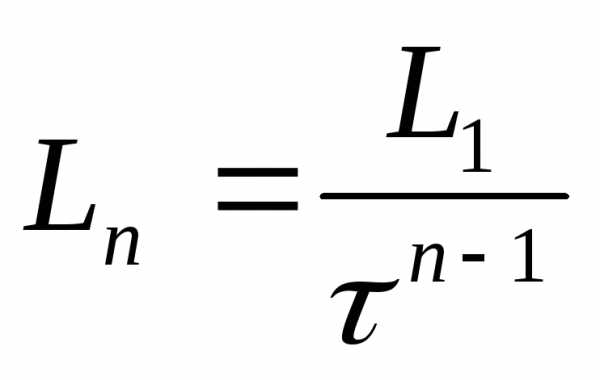, т.е(11)

Таким образом, в методе «золотого сечения» начальный отрезок делится по «правилу золотого сечения» (8), (10) и первые два эксперимента располагаются симметрично на расстоянии 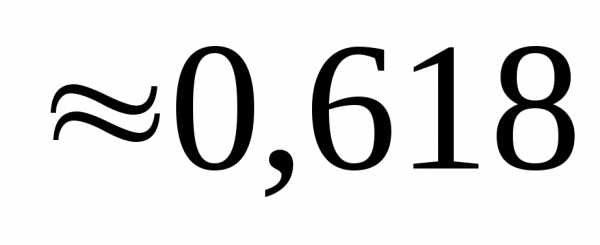от соответствующих концов интервала. По результатам этих двух экспериментов сохраняется один из интервалов, в котором расположен оставшийся эксперимент. Симметрично ему располагается следующий эксперимент и т.д.

Можно показать, что окончательный интервал неопределенности в данном методе при достаточно больших 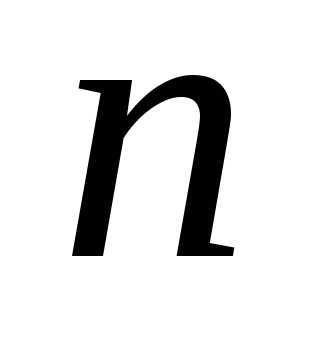всего лишь на 17% больше, чем в методе Фибоначчи. Можно показать также, что при больших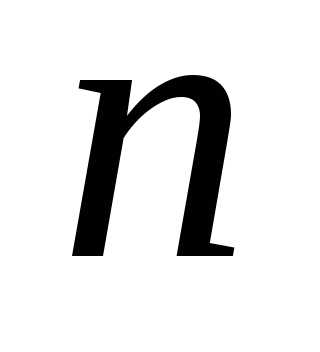оба метода начинаются практически из одной и той же точки.

Словесный алгоритм метода следующий:

Заданы начало и конец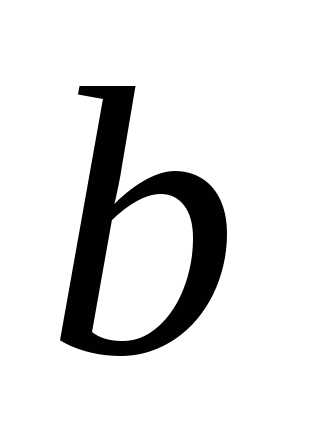интервала, точность,.

Шаг 1.Рассчитываются две точкиии значения в них целевой функциии, где– длина интервала.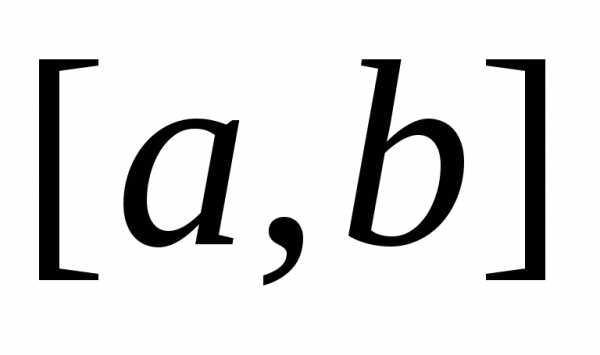

Шаг 2.Если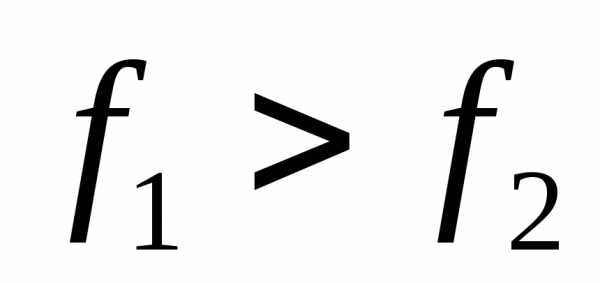, то

,,,

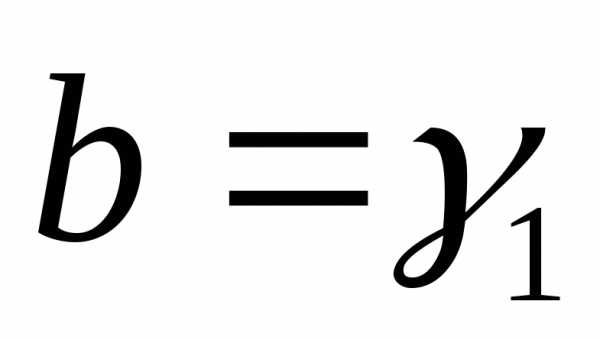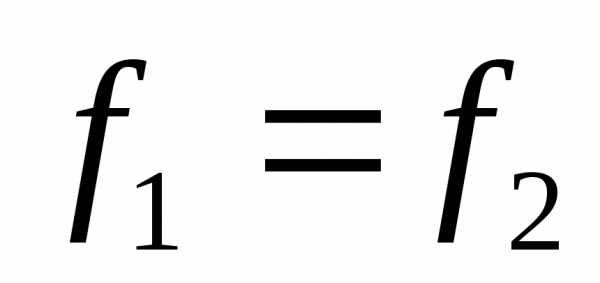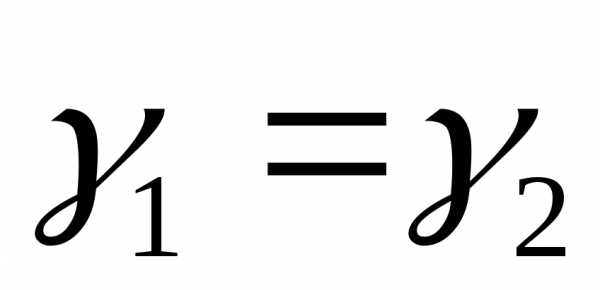и рассчитывается одна новая точка

иначе

,,,

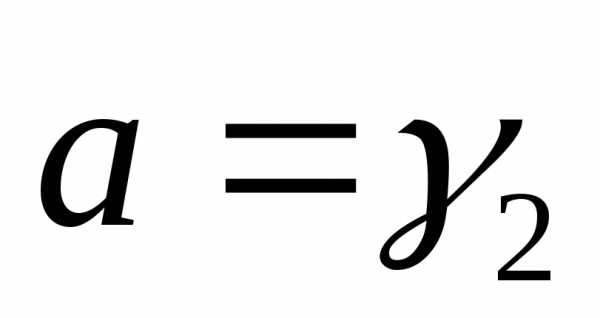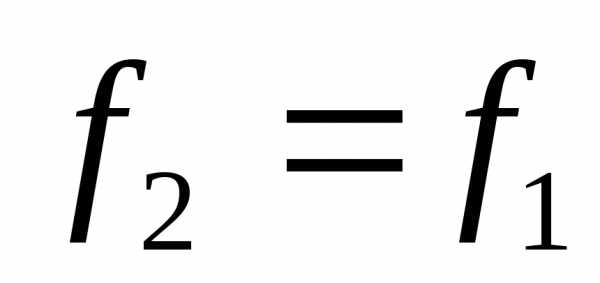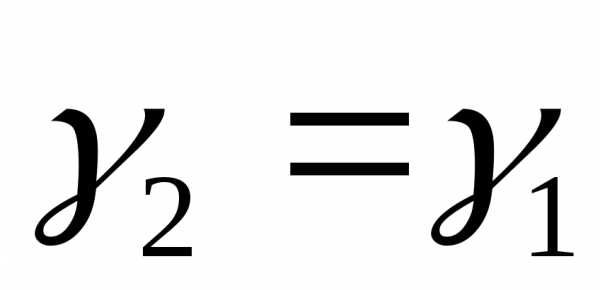и рассчитывается одна новая точка

Шаг 3.Повторять шаги 1-2 до тех пор, пока длина интервала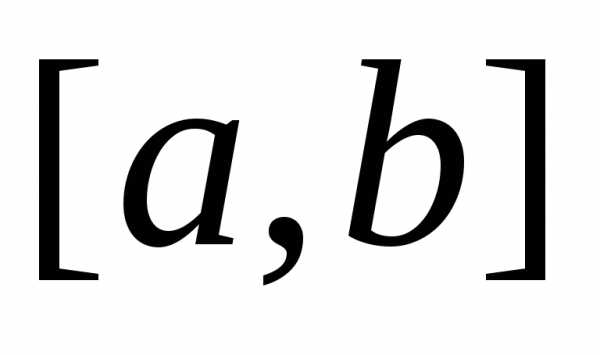больше.

Шаг 6.Результат.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Изучить теоретический материал.
Построить блок-схемы алгоритмов дихотомического деления, Фибоначчи, «золотого сечения».
Выбрать функцию по указанию преподавателя из таблицы и определить для нее начальный интервал поиска локального экстремума с помощью MathCAD.
Для алгоритма Фибоначчи определить количество экспериментов, позволяющее уменьшить интервал неопределенности в 1000 раз.
Осуществить по 2-3 итерации поиска экстремума заданной функции каждым из рассмотренных методов.
Разработать на ЭВМ программу, реализующую каждый из рассмотренных методов (язык программирования выбрать самостоятельно).
Получить решение задачи тремя методами с помощью разработанной программы.

СОДЕРЖАНИЕ ОТЧЕТА

Исходное задание на исследование.
Результаты, полученные в пп.3-5 порядка выполнения работы.
Блок-схемы алгоритмов.
Результаты машинного решения и их анализ.

КОНТРОЛЬНЫЕ ВОПРОСЫ

Место задачи одномерного поиска в общей задаче оптимизации.
Сущность методов дихотомического деления, Фибоначчи, «золотого сечения».
Сравнительные характеристики исследуемых алгоритмов.

№	Функция	Экстремум
1		минимум
2		максимум
3		минимум
4		максимум
5		минимум
6		максимум
7		минимум
8		максимум
9		минимум
10		максимум
11		минимум
12		максимум

Лабораторная работа №2

Исследование поисковых методов оптимизации

1. Цель работы

Целью настоящей работы являются изучение и анализ поисковых методов: покоординатного спуска (МПС) и сопряженных напряжений (МСН), используемых для решения задач параметрической оптимизации конструкций и технологических процессов производства ЭВА.

2. Теоретическая часть

2.1. Введение

Задачи параметрического синтеза, связанные с выбором таких параметров, которые обеспечивают оптимизацию некоторого критерия качества конструкции или технологического процесса, относятся в общем случае к задачам нелинейного программирования вида:

найти min F (1)

при ограничениях

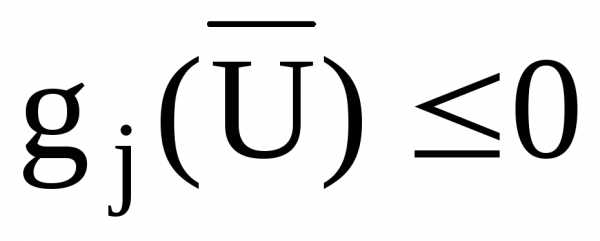,j=1,2,…n. (2)

Знак -n– мерный вектор управляемых параметров конструкции,F- целевая функция (критерий оптимальности).

В настоящей лабораторной работе изучаются методы поиска безусловного экстремума, т.е. методы поиска экстремума в задачах, в которых отсутствуют ограничения (2). Подобные задачи представляют самостоятельный интерес, т.к. в ряде случаев целевая функция может быть построена так, что она сама учитывает все ограничения [1]. Кроме того, большинство алгоритмов решения задач с ограничениями (задач на условный экстремум) включают минимизацию без ограничений в качестве основной поэтапной процедуры.

Суть любого алгоритма поиска состоит в определении такой последовательности векторов управляемых параметровкоторые удовлетворяют условию:

studfiles.net

Тема 1.6. Одномерная оптимизация

1.6.1. Постановка задачи

1.6.2. Метод дихотомии

1.6.3. Метод золотого сечения

1.6.4. Сравнение методов

1.6.5. Тестовые задания по теме «Одномерная оптимизация»

1.6.1. Постановка задачи

Рис. 1.6.1-1

Интервал, на котором локализован единственный минимум, называется отрезком неопределенности.

Достаточными условиями унимодальности функции на отрезке[a;b]являются:

Для дифференцируемой функцииf(x)ее производнаяf¢(х) - неубывающая.
Для дважды дифференцируемой функции f(x)выполняется неравенствоf¢¢(х)³0.

Пример 1.6.1-1. Провести исследование функции f(x) = x3 – x + e-x на предмет существования экстремумов.

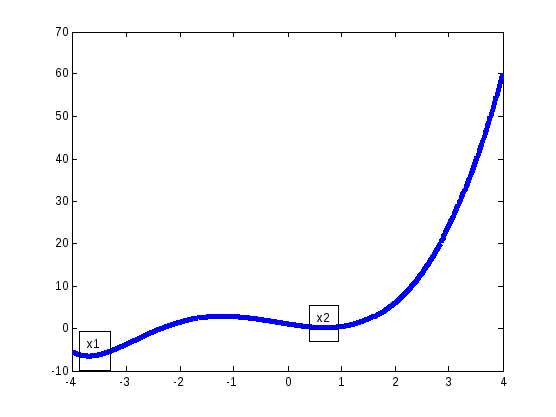
Рис. 1.6.1-2

Проверим достаточное условие существования минимума на выбранных отрезках:

f¢(x) = 3x2 – 1 – e-x; f¢¢ (x) = 6x + e-x,

f¢(0) < 0, f¢(1) > 0, f¢¢ (x) > 0 для хÎ[0;1],

f¢(-4) < 0, f¢(-3) > 0, f¢¢ (x) > 0 для хÎ[-4;-3].

На практике численные методы одномерной оптимизацииприменяют в следующих случаях:

значения функции f(x)определены в ходе эксперимента;
целевая функция очень сложна или не имеет непрерывных производных;
классические методы поиска оптимального значения не применимы.

Рассмотрим, в частности, метод дихотомиииметод золотого сечения.

studfiles.net

1.Одномерная оптимизация. Метод «золотого сечения»

Государственное образовательное учреждение высшего профессионального образования

«Московский государственный технический университет имени Н.Э. Баумана»

(МГТУ им. Н.Э. Баумана)

Аэрокосмический факультет

Кафедра: Вычислительной математики

и математической физики.

Курсовая работа

по предмету:

«Методы конечномерной оптимизации»

Выполнил:

Студент группы АК3-51

Прошин В.В.

Руководитель:

к.т.н.,доц.

Бушуев Александр Юрьевич

Москва 2012 год

СОДЕРЖАНИЕ:

Одномерная оптимизация..................................................................................................................3

Метод «золотого сечения».................................................................................................................5

Условная нелинейная оптимизация

Применение теоремы Джона-Куна-Таккера..................................................................................6

Линейное программирование. Симплекс-метод…………………………………………………17
Исследование множества на выпуклость…………………………………………………...…….24
Исследование функции на выпуклость…………………………………………………………...25
Исследование функции на овражность…………………………………………………………...27
Безусловная оптимизация неквадратичной функции овражной структуры.

Метод Дэвидона-Флетчера-Пауэлла………………………………………………………………30

Сведение задачи условной оптимизации к безусловной задаче оптимизации…………………35

8.1.Метод внешних штрафных функций….………………………………………………………35

8.2.Метод возможных направлений Зойтендейка……….……………………………………….39

Вывод………………………………………………………………………………………………..49
Список литературы…………………………………………………………………………………50
Приложения

11.1. Одномерный поиск. Метод «золотого сечения»……………………...................................51

11.2. Многомерный поиск минимума функций и добавленный метод внешних штрафных функций. Метод Дэвидона-Флетчера-Пауэлла……………………………………………………………...55

Постановка задачи:

Изготавливается закрытый цилиндрический бак объема V. Требуется определить такие размеры, для которых затраты на количество материала будут минимальны.

Теоретические сведения:

Определение 1.1

Точка называется точкой глобального (абсолютного) минимума (максимума) функциина множестве, если функция достигает в этой точке своего наименьшего (наибольшего) значения, т.е.

Определение 1.2

Точка называется точкой локального (относительного) минимума (максимума) функциина множестве, если существует, такое, что, если, то.

Здесь - норма вектора в конечномn-мерном евклидовом пространстве.

Теорема 1.1 (необходимые условия экстремума первого порядка)

Пусть есть точка локального минимума (максимума) функциина множествеидифференцируема в точке. Тогда аргумент функциив точкеравен нулю, т.е.

или

Теорема 1.2 (достаточные условия экстремума первого порядка)

Пусть функция в точкедважды дифференцируема, ее градиент равен нулю, а матрица вторых производных является положительно определенной (отрицательно определенной), т.е.

, тогда точка есть точка локального минимума (максимума) функциина множестве.

Решение:

На основе геометрических формул записываем целевую функцию задачи. Она имеет вид:

(1)

, что соответствует формуле площади поверхности закрытого цилиндра с параметрами радиуса r и высоты h.

Т.к. в задаче указано, что у бака фиксированный объем, то можно записать уравнение связи между параметрами бака, т.е.:

(2)

Уравнение (2) дает возможность свести задачу минимизации целевой функции от двух параметров к одномерной минимизации целевой функции одного параметра, например:

(3)

Используя необходимые и достаточные условия экстремума функции:

(4)

, заключаем, что точка экстремума целевой функции существует, единственна и она является точкой глобального минимума.

С учетом уравнения связи (2) получаем решение:

(5)

Множество оптимальных параметров, в условиях нашей задачи, может быть описано системой:

(6)

Программная реализация данной задачи методом «золотого сечения» находится в приложении 11.1.

Метод «золотого сечения»:

«Золотым сечением» отрезка называется такое разбиение отрезка на две неравные части, что отношение длины всего отрезка к длине большей части равно отношению длины большей части к длине меньшей части отрезка.

«Золотое сечение» отрезка осуществляется каждой из двух симметрично расположенных относительно центра отрезка точек:

Алгоритм:

(шаг 1)Находим точки, осуществляющие «золотое сечение» отрезка из системы:

, где

(шаг 2) Сравниваем значения функций в точках «золотого сечения»

-Если

(шаг 3) Проверяем условие остановки алгоритма

, если не выполняется, переходим на (шаг 1),

иначе вычисляем точку минимума

2. Условная нелинейная оптимизация. Применение теоремы Джона-Куна-Таккера

Постановка задачи:

Требуется решить задачу вида:

Теоретические сведения:

Определение 2.1

Обобщенной функцией Лагранжа называется функция вида:

, где - множители Лагранжа

Определение 2.2

Градиентом обобщенной функции Лагранжа по х называется вектор-столбец, составленный из ее частных производных первого порядка ():

Определение 2.3

Вторым дифференциалом обобщенной функции Лагранжа называется функция:

Определение 2.4

Первым дифференциалом ограничений называется функция:

Определение 2.5

Ограничение называется активным в точке, если. Если, то ограничение называется пассивным.

Определение 2.6

Градиенты ограничений являются линейно независимыми в точке, если равенство

выполняется только при , иначе градиенты ограниченийлинейно зависимы.

Определение 2.7

Точка называется регулярной точкой минимума (максимума), если градиенты ограничений являются линейно независимыми (), иначе точканазывается нерегулярной точкой минимума (максимума).

Теорема 2.1 (Джона-Куна-Таккера) (необходимые условия минимума (максимума) первого порядка)

Пусть - точка локального минимума (максимума) в данной задаче, тогда найдется такое числои вектор, не равные одновременно нулю, что выполняются условия:

а) Условие нетривиальности:

б) Условие стационарности обобщенной функции Лагранжа:

в) Условие допустимости решения:

г) Условие согласования знаков:

д) Условие дополняющей нежесткости:

Теорема 2.2(достаточные условия минимума (максимума) первого порядка)

Пусть имеется точка , удовлетворяющая системе уравненийтеоремы 2.1 при , число активных ограничений в точкесовпадает с числомпеременных (при этом условие регулярности выполняется, т.е. градиенты активных ограничений в точкелинейно независимы). Еслидля всех, то точка- точка условного локального минимума. Еслидля всех, то- точка условного локального максимума.

Теорема 2.3(достаточное условие экстремума второго порядка)

Пусть имеется точка , удовлетворяющая системе уравненийтеоремы 2.1 при .

Если в этой точке для всех ненулевыхтаких, что

То точка является точкой локального минимума (максимума) в данной задаче.

Замечание 2.1

Если функции выпуклые, то условиятеоремы 2.1 являются одновременно и достаточными условиями глобального минимума

Определение 2.8

Функция называется выпуклой вниз (или просто выпуклой) на множестве , если график функции идёт не выше хорды, соединяющей любые две точки графикаи, при

Решение:

Перепишем условие

(ШАГ 1)

Составим обобщенную функцию Лагранжа:

(ШАГ 2)

Запишем необходимые условия экстремума первого порядка:

а) Условие нетривиальности:

б) Условие стационарности обобщенной функции Лагранжа:

или

в) Условие допустимости решения:

г) Условие согласования знаков:

д) Условие дополняющей нежесткости:

(ШАГ 3)

Решаем систему

для двух случаев:

Тогда получаем две системы для рассмотрения:

Рассмотрим случай и соответствующие емувариантов (различных комбинаций), удовлетворяющих условию дополняющей нежесткости:

Такие множители Лагранжа приводят к тривиальному решения данной задачи.

Из второго уравнения получаем, что , что не удовлетворяет условию нетривиальности решения.

Система перепишется как:

Видно, что в данном случае решение существует только при , что не удовлетворяет условию нетривиальности решения.

Видно, что решение можно найти из последних двух уравнений системы, т.е.:

Решение данного уравнения находится в множестве комплексных чисел . Такие корни не удовлетворяют условию задачи, что, следовательно, существует только тривиальное решение.

Рассмотрим случай и соответствующие емувариантов (различных комбинаций), удовлетворяющих условию дополняющей нежесткости:

Из первых двух уравнений получаем:

Полученную точку следует проверить на выполнение условий, записанных на (шаге 2).

Условия выполняются. Активное ограничение: . Пассивное ограничение:.

Из системы получаем:

Полученные точки проверяем на выполнение условий, записанных на (шаге 2).

Все три точки не лежат в допустимом множестве решений.

Из системы получаем:

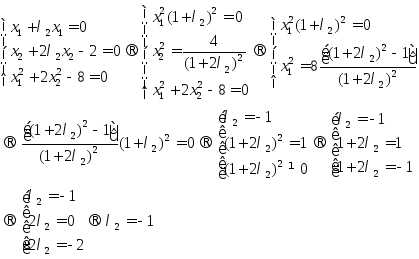
Для полученного множителя Лагранжа находим точку:

Проверяем необходимые условия минимума на (шаге 2).

Условия не выполняются, т.к. , что удовлетворяет точке условного максимума. Активное ограничение:. Пассивное ограничение:.

Корни находятся так же как при случае в пункте 4, где нет действительных корней.

Таким образом, имеем одну точку условного экстремума , прис одним активным ограничением.

(ШАГ 4)

Для получено на (шаге 3) точки проверяем достаточные условия минимума первого порядка теорема 2.2.

Т.к. число активных ограничений меньше числа переменных и множители Лагранжа не удовлетворяют достаточным условиям минимума первого порядка, то проверяем условия минимума второго порядка

теорема 2.3.

Запишем второй дифференциал обобщенной функции Лагранжа с учетом :

или

Видно, что второй дифференциал функции Лагранжа положителен, т.е.:

По теореме 2.4 заключаем, что точка есть точка условного локального минимума.

Докажем выпуклость функции :

Построим график целевой функции с помощью средыMathCAD 14.

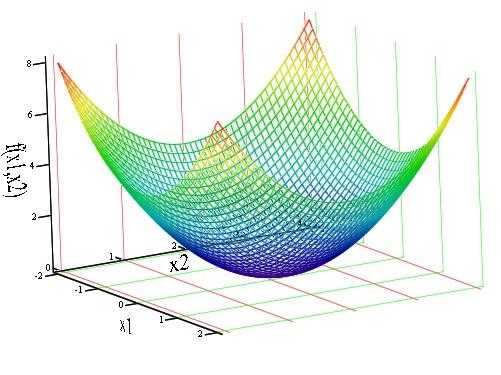
И его линии уровня:

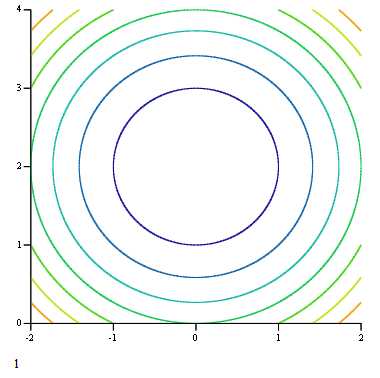
Т.к. допустимое множество выпукло, ввиду факта односвязности множества и функция является непрерывной (смещенный относительно центра параболоид), то из определения 2.8 заключаем, что функция выпукла. Так что, используя замечание 2.1, получаем, что точка

есть точка глобального минимума.

(ШАГ 5)

Перепишем целевую функцию:

Ее значение в точке - глобального минимума есть

studfiles.net