Лекция 14. Задачи оптимизации и методы поиска экстремума. Методы оптимизации задачи
Лекция 14. Задачи оптимизации и методы поиска экстремума.
- 61 -
14.1. Задачи оптимизации.
Пусть дана схема, математической моделью которой является алгоритмически заданная функция, например коэффициент усиления 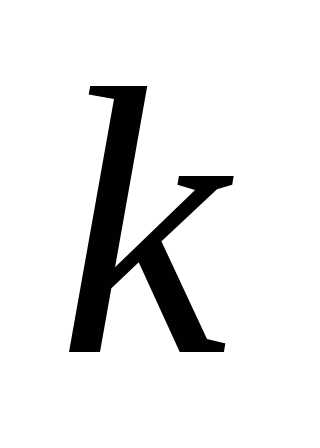 , который должен быть сделан максимальным в выбранном диапазоне изменения параметров. Такие задачи называются задачами оптимизации, в отличие от задач анализа. В задачах анализа вычисляется выходное значение
, который должен быть сделан максимальным в выбранном диапазоне изменения параметров. Такие задачи называются задачами оптимизации, в отличие от задач анализа. В задачах анализа вычисляется выходное значение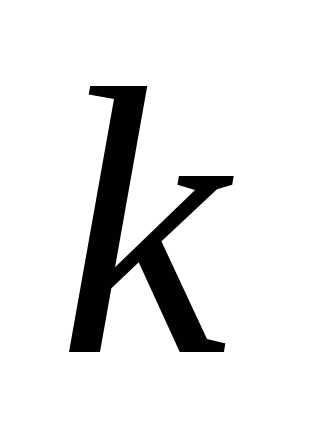 для заданного набора входных параметров, а в задаче оптимизации определяется оптимальный набор входных параметров, т.е. наилучший. В латыни optimus означает "лучший".
для заданного набора входных параметров, а в задаче оптимизации определяется оптимальный набор входных параметров, т.е. наилучший. В латыни optimus означает "лучший".
Оптимизировать – это выбрать лучший вариант из множества возможных. Лучший при этом подразумевает выбор с точки зрения технического задания. Требования технического задания обычно сложны и противоречивы, и для формализации понятия ”оптимальный” вводится целевая функция.
Целевая функция – эта скалярная функция многих переменных, максимум или минимум которой определяет оптимальный набор входных параметров. Пуcть вектор 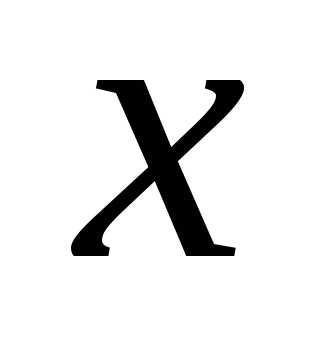 - это массив входных параметров и он имеет длину
- это массив входных параметров и он имеет длину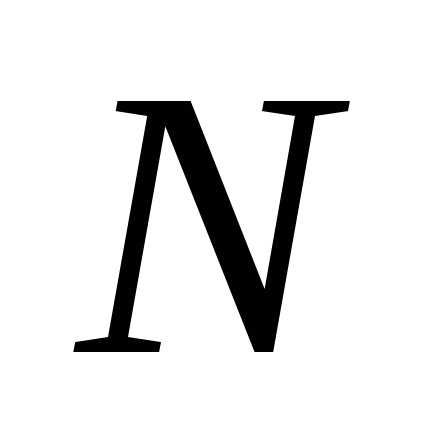 .
.
Тогда целевая функция записывается в виде
|
| (14.1) |
Выбор целевой функции обычно является сложной творческой задачей, но есть методы ее формального построения, которые здесь рассматриваться не будут. Отметим, что при неправильном выборе целевой функции экстремум может отсутствовать. Например, для получаем, что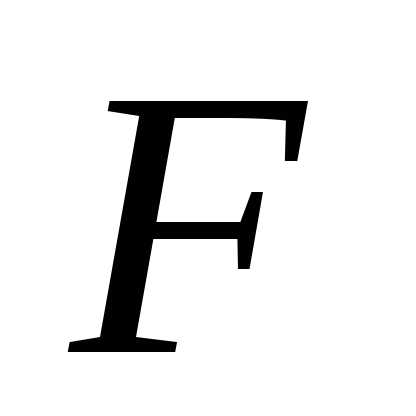 стремится к минус бесконечности при
стремится к минус бесконечности при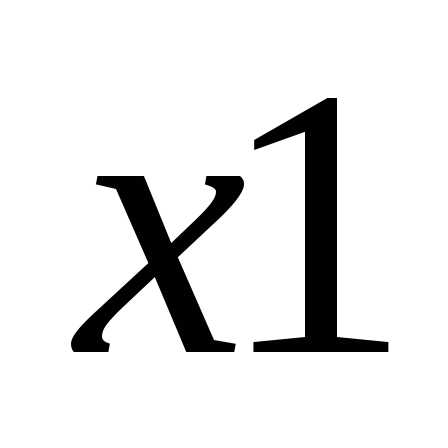 ,
,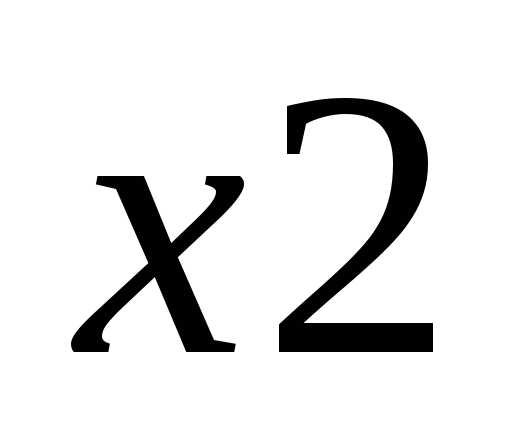 стремящихся к минус бесконечности.
стремящихся к минус бесконечности.
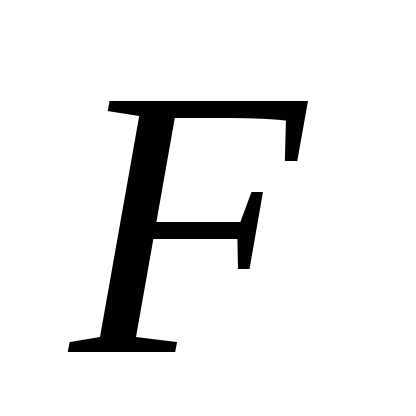 на множестве значений ее аргументов. Это означает, что нужно найти точку
на множестве значений ее аргументов. Это означает, что нужно найти точку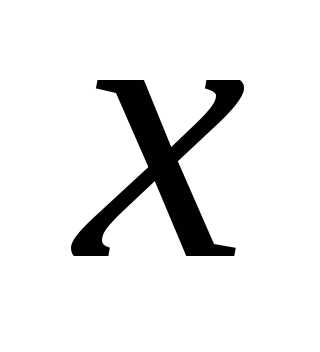 в многомерном пространстве, для которой выполняется условие
в многомерном пространстве, для которой выполняется условие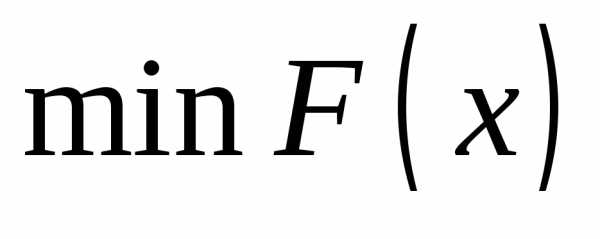 , где
, где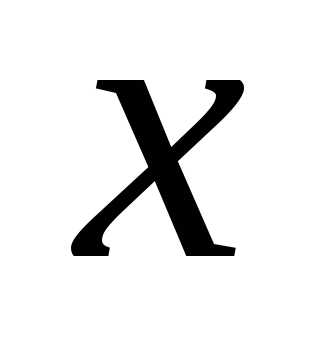 - вектор.
- вектор. Если нужен максимум функции 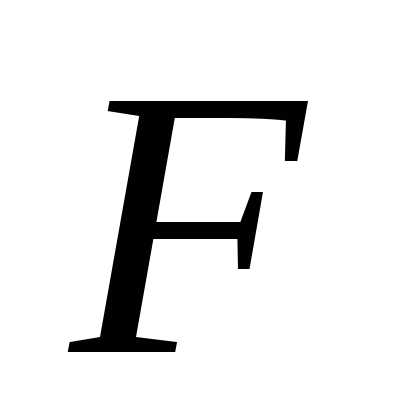 , а не минимум, то нужно решить ту же задачу для.
, а не минимум, то нужно решить ту же задачу для.
На рис.14.1. показано условное изображение задачи оптимизации, которая всегда использует некоторую математическая модель рассматриваемого физического объекта и результаты решения задачи анализа. Оптимизацию обычно выполняют специальные программы, реализующие конкретные методы оптимизации. Во всех методах выполняются шаги в многомерном пространстве.
| Рис.14.1. Задачи анализа и оптимизации |
Если поиск минимума проводится во всем многомерном пространстве без каких-либо ограничений на область изменения аргументов целевой функции, то оптимизация называется безусловной. При условной оптимизации всегда есть какие-то ограничения, что характерно для практических задач моделирования.
Обычно задача оптимизации имеет один из следующих трех видов:
безусловная нелинейная,
условная нелинейная,
условная линейная.
Для первого вида рассматриваются как одномерные, так и многомерные задачи, а для условной всегда многомерные. Третий вид задач – условные линейные – характерен для экономических и технологических задач и здесь рассматриваться не будет. В них целевая функция линейно зависит от входных параметров. Эти задачи называют задачами линейного программирования. Для их решения существует надежный и эффективный метод – симплекс-метод, а также стандартные программы, его реализующие.
В лекциях 14, 15 основным будет первый вид задач, т.к. он используется для задач второго вида.
В задачах оптимизации формируются аналитические или алгоритмические целевые функции, которые могут иметь один или несколько минимумов. Каждый минимум называется локальным, а минимум из минимумов называется глобальным. Обычно решение задачи оптимизации дает один из локальных минимумов, выбор которого определяется заданным начальным значением.
В качестве примера приведем целевую функцию для случая двух переменных (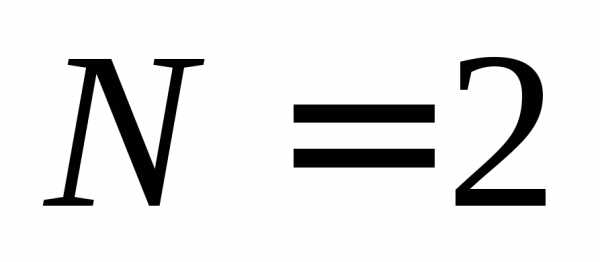 )
)
| . | (14.2) |
Это известная функция Розенброка и она часто используется при решении тестовых задач, т.к. имеет сложный характер линий уровня вблизи точки минимума 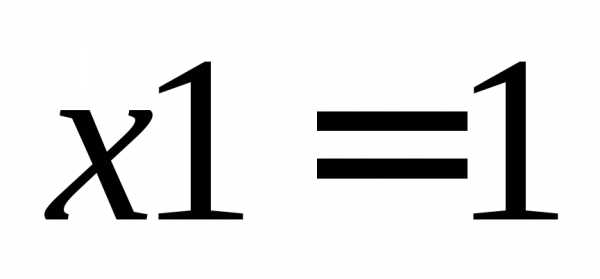 ,
,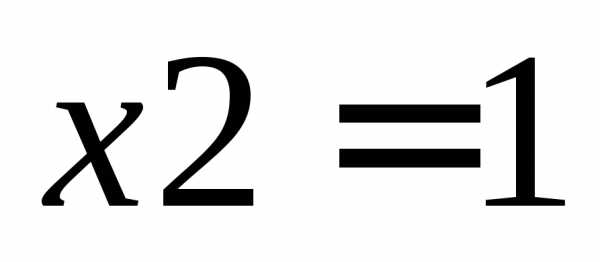 .
.
При решении задач оптимизации в случае двух переменных используют представление функций в виде линий уровня. Это же представление используют для иллюстрации различных методов в случае 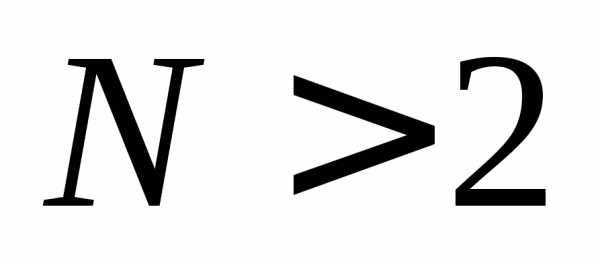 , т.к. нет другого способа изобразить шаги в многомерном пространстве.
, т.к. нет другого способа изобразить шаги в многомерном пространстве.
В заключение напомним условие минимума функции многих переменных (14.1)
| , | (14.3) |
которое можно записать в виде системы 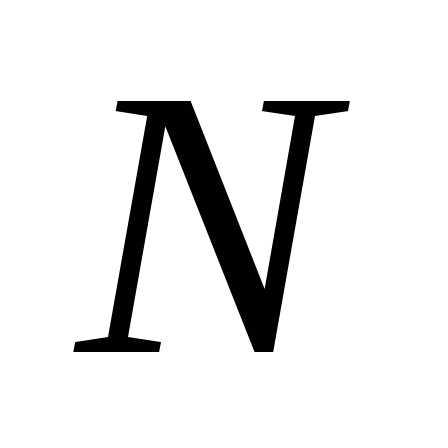 нелинейных уравнений
нелинейных уравнений
Отсюда следует, что для решения задачи оптимизации нужно решить систему нелинейных уравнений (13.5), например, методом Ньютона.
Отметим, что матрица Якоби для системы (13.4) будет вычисляться через вторые частные производные функции 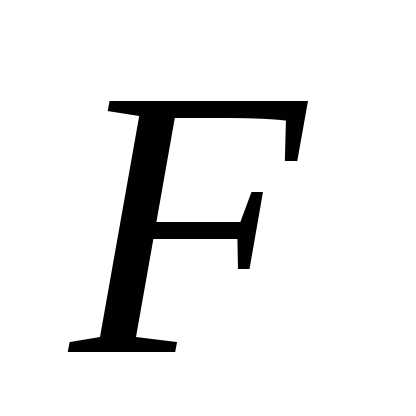 и поэтому на итерациях в методе Ньютона будет решаться система линейных уравнений с матрицей Гессе
и поэтому на итерациях в методе Ньютона будет решаться система линейных уравнений с матрицей Гессе , элементы которой
, элементы которой
|
| (14.5) |
Из-за сложности вычисления матрицы Гессе для целевых функций в практических задачах такой подход никогда не используется.
studfiles.net
Методы решения задач условной оптимизации
Пусть задана задача нелинейного программирования следующего вида:
минимизировать 
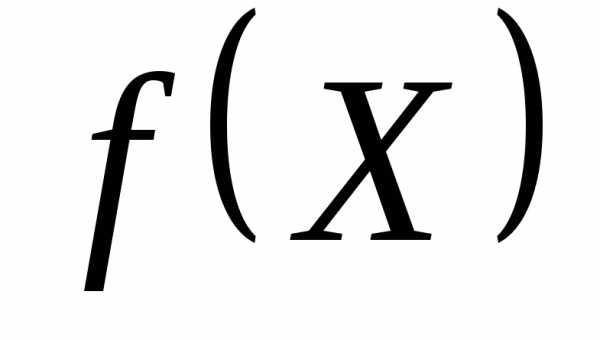 ,
,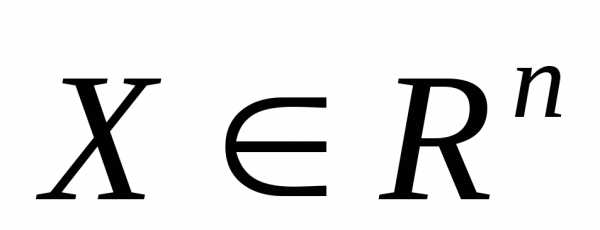
при наличии ограничений
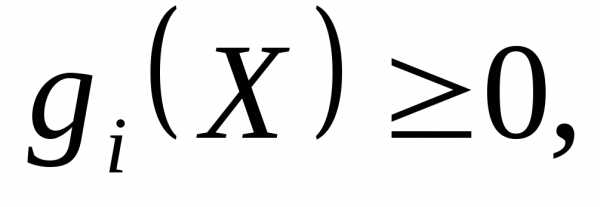 ;
;
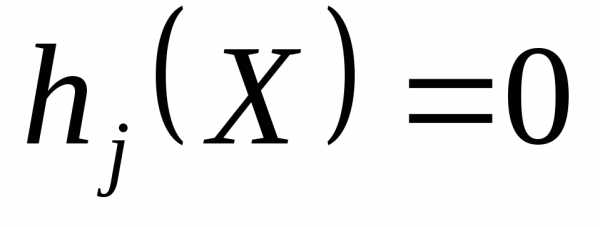 , .
, .
К решению этой задачи могут быть применены методы штрафных функций, в которых осуществляется преобразование задачи нелинейного программирования при наличии ограничений: либо в одну задачу без ограничений, либо в последовательность задач без ограничений. Конкретные методы, основанные на этой схеме, определяются видом штрафной функции (зависит от типа ограничений равенства или неравенства) и правилами, по которым производится пересчет штрафных параметров. Штрафные параметры входят в структуру штрафной функции в качестве весовых коэффициентов.
Методы распадаются на три категории: методы внутренней точки; методы внешней точки и смешанные методы. При использовании методов внутренней точки уровень целевой функции удерживается внутри допустимой области (точка 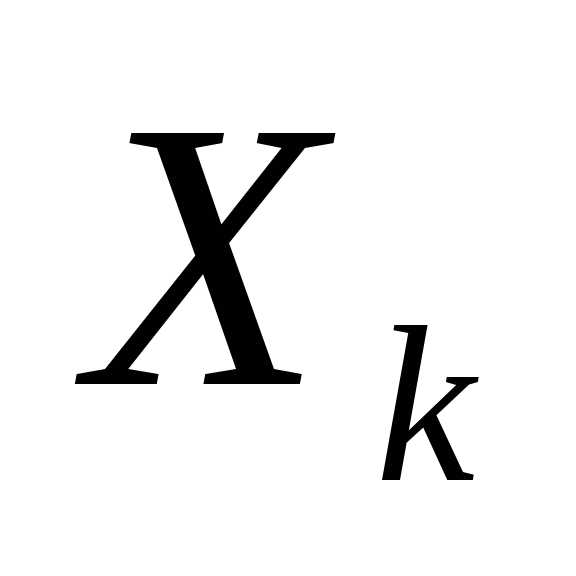 постоянно находится внутри допустимой области). Методы внешней точки генерируют последовательность точек, которые выходят за пределы допустимой области, но дают в пределе допустимое решение.
постоянно находится внутри допустимой области). Методы внешней точки генерируют последовательность точек, которые выходят за пределы допустимой области, но дают в пределе допустимое решение.
С помощью функций, задающих ограничения, строится штрафная функция, которая добавляется к целевой функции исходной задачи так, что нарушение какого-либо ограничения становится невыгодным.
к целевой функции исходной задачи так, что нарушение какого-либо ограничения становится невыгодным.
4.3.1. Метод последовательной безусловной оптимизации
Задачу
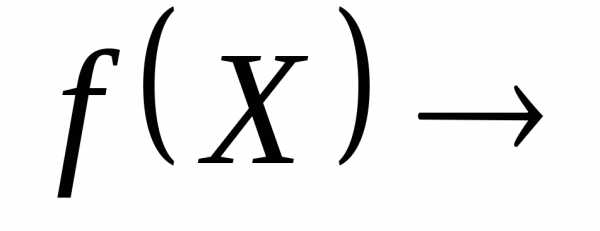 min
min
при наличии ограничений
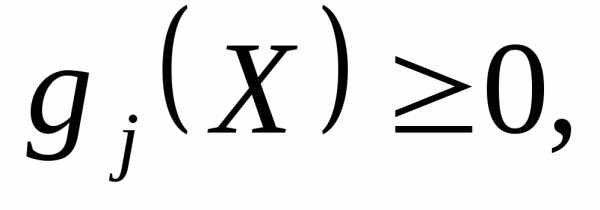
можно свести к безусловной задаче
min,
введя штрафную функцию вида 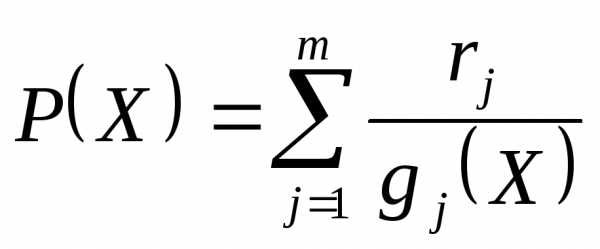
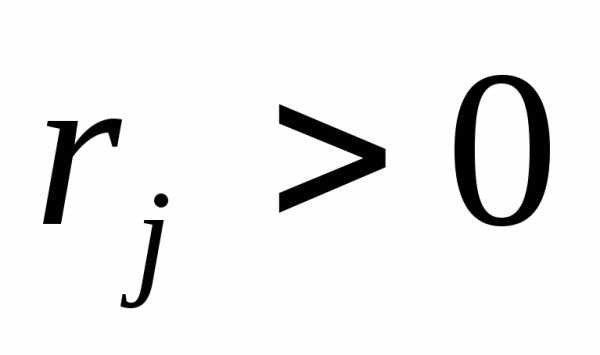 - коэффициент штрафа.
- коэффициент штрафа. Процедура начинается с начальной допустимой точки, где 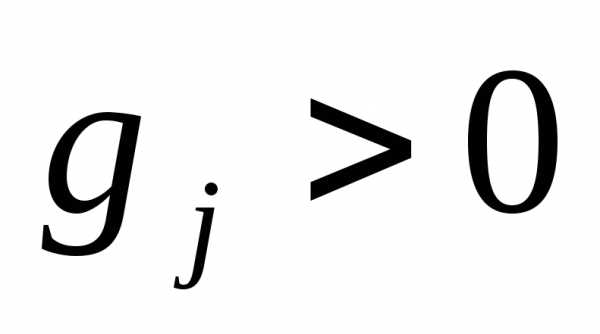 и функция
и функция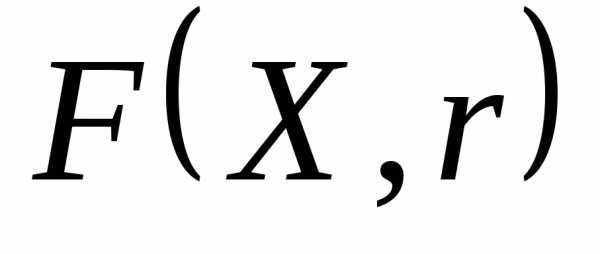 принимает значения, которые больше значений функции
принимает значения, которые больше значений функции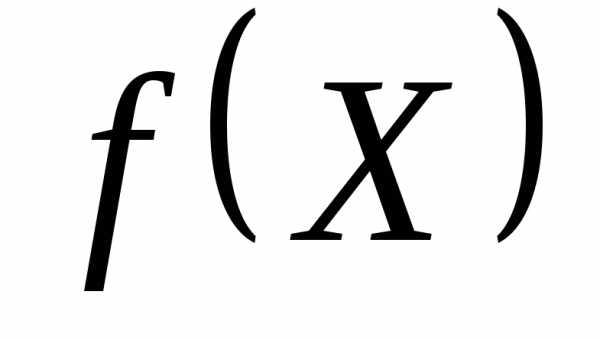 . Однако разность может быть уменьшена выбором параметра
. Однако разность может быть уменьшена выбором параметра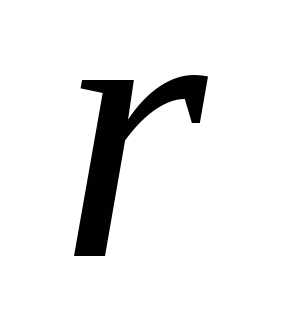 , который может быть достаточно малой величиной. При приближении к границе допустимой области штрафная функция неограниченно возрастает, образуя барьер вдоль каждого ограничения, не позволяя покинуть допустимую область. В общем случае требуется решать последовательность задач без ограничений.
, который может быть достаточно малой величиной. При приближении к границе допустимой области штрафная функция неограниченно возрастает, образуя барьер вдоль каждого ограничения, не позволяя покинуть допустимую область. В общем случае требуется решать последовательность задач без ограничений.
Сначала выбирают начальную допустимую точку и 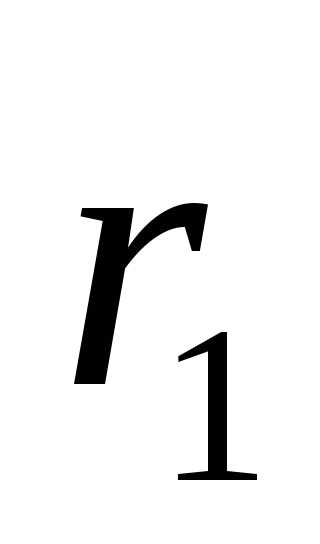 . Затем с помощью подходящего метода безусловной оптимизации находят точку минимума функции
. Затем с помощью подходящего метода безусловной оптимизации находят точку минимума функции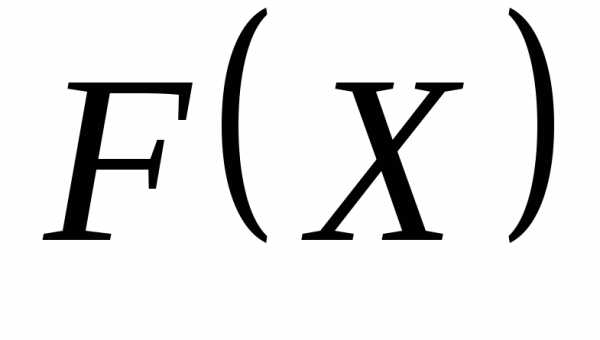 . Далее используют ее как исходную точку для минимизации целевой функции с меньшим значением
. Далее используют ее как исходную точку для минимизации целевой функции с меньшим значением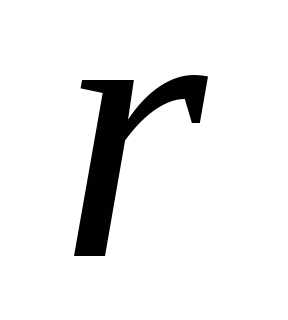
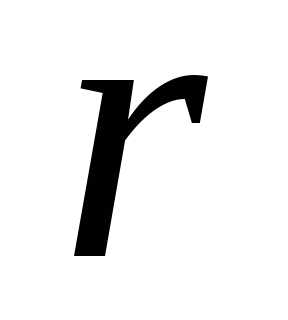 :.
:. По мере того, как 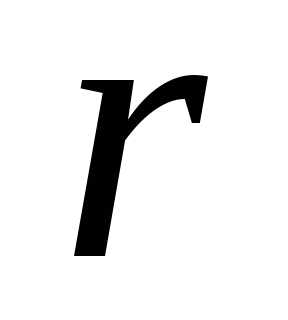 стремится к нулю, решение безусловной задачи стремится крешению задачи на условный минимум. Этот метод носит имя Фиакко и Маккормика, а штрафная функция называется барьерной.
стремится к нулю, решение безусловной задачи стремится крешению задачи на условный минимум. Этот метод носит имя Фиакко и Маккормика, а штрафная функция называется барьерной.
Метод последовательной безусловной оптимизации сталкивается с определенными вычислительными трудностями, так как функция 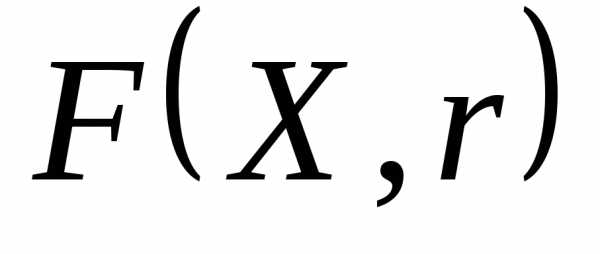 разрывна на границе и поэтому необходимо внимательно выбирать метод безусловной оптимизации.
разрывна на границе и поэтому необходимо внимательно выбирать метод безусловной оптимизации.
Для задачи нелинейного программирования с ограничениями типа равенства желательно использовать штрафную функцию вида , где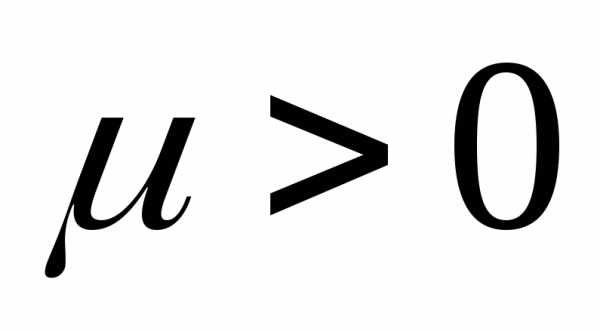 есть некоторое большое число.
есть некоторое большое число.
4.3.2.Метод скользящего допуска
Пусть дана общая задача нелинейного программирования
при наличии ограничений
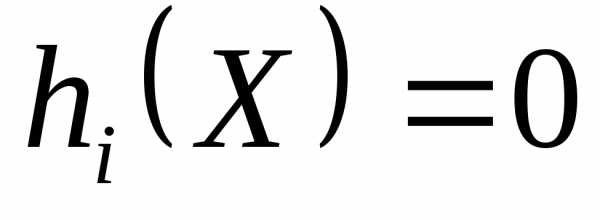 , ;
, ;
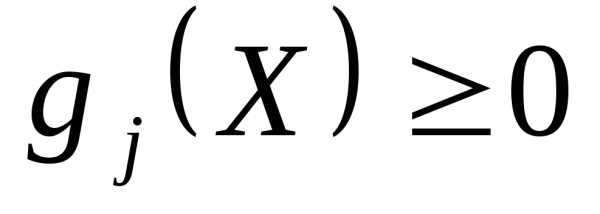 , .
, .Алгоритм скользящего допуска позволяет улучшить значение целевой функции как за счет информации, получаемой в допустимых точках, так и за счет информации, которую удается получить при прохождении через некоторые точки, лежащие вне допустимой области (почти допустимые точки). Интервалы, при которых точки можно считать почти допустимыми в ходе оптимизации постепенно сокращаются. При приближении к оптимуму учитываются только допустимые точки.
При такой стратегии поиска общую задачу нелинейного программирования можно заменить более простой:
минимизировать 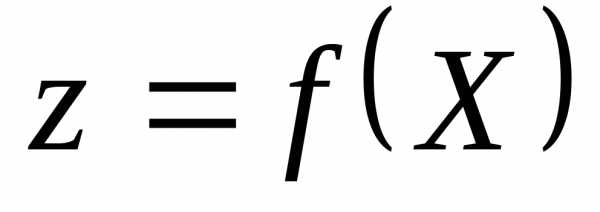 ,
,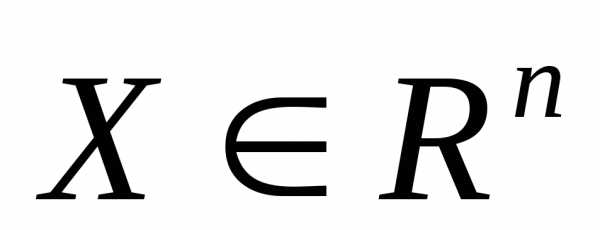
при одном, но “укрупненном ” ограничении:
,
где 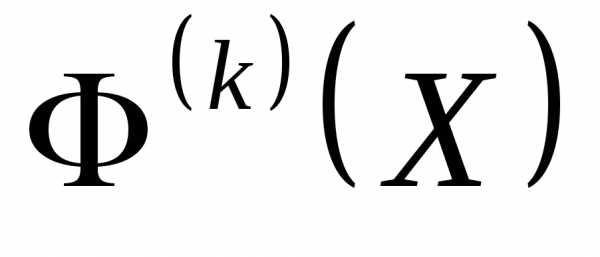 - значение критерия скользящего допуска на
- значение критерия скользящего допуска на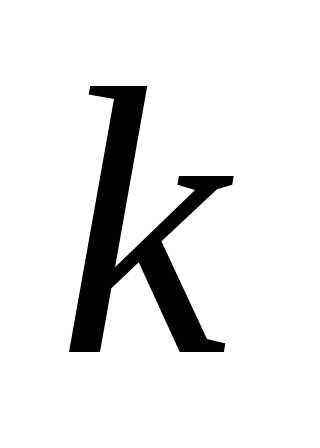 -том этапе поиска. В качестве критерия
-том этапе поиска. В качестве критерия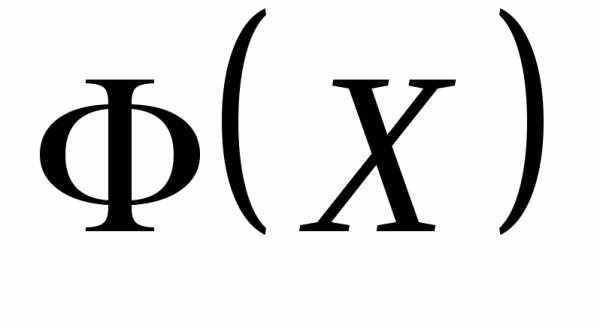 выбирается положительно определенная убывающая функция координат точек, являющихся вершинами деформируемого многогранника:
выбирается положительно определенная убывающая функция координат точек, являющихся вершинами деформируемого многогранника:
,
,
где 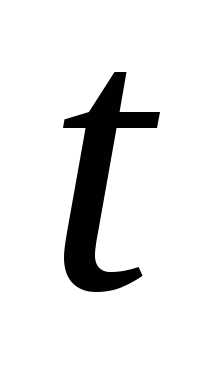 - величина, характеризующая размер исходного многогранника;
- величина, характеризующая размер исходного многогранника;
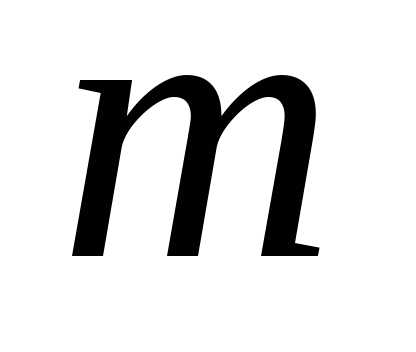 - число ограничений типа равенства;
- число ограничений типа равенства;
, число степеней свободы.
Здесь
и 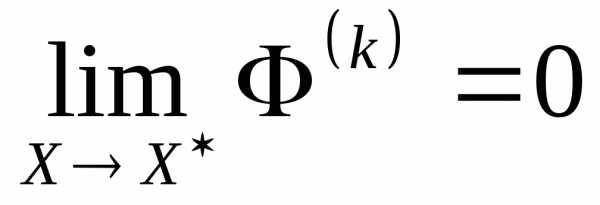 .
.
Функционал 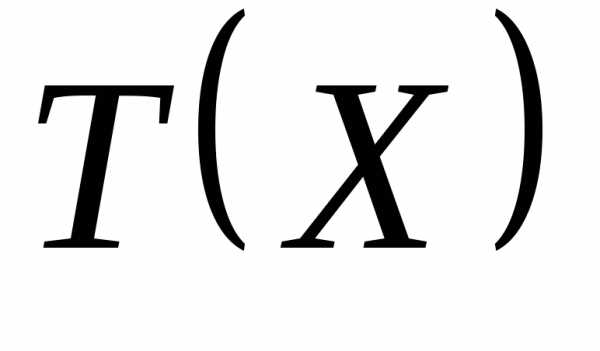 представляет собой положительно определенный критерий, учитывающий ограничения.
представляет собой положительно определенный критерий, учитывающий ограничения.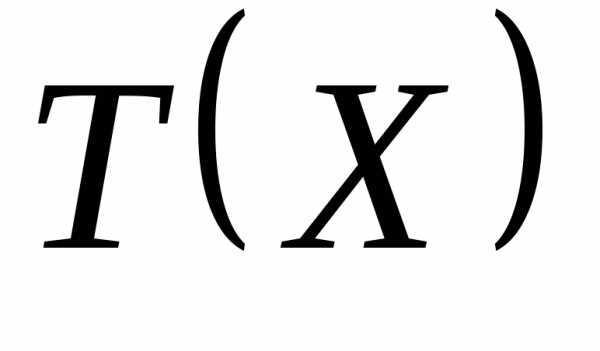 является мерой степени нарушения ограничений рассматриваемой задачи. Его можно выбрать в виде
является мерой степени нарушения ограничений рассматриваемой задачи. Его можно выбрать в виде
,
где
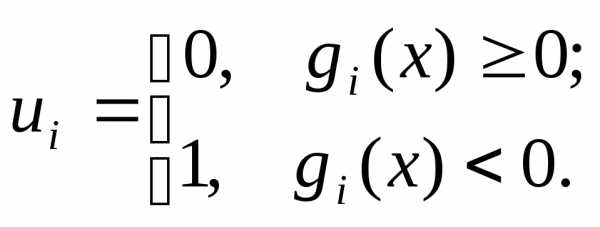
Таким образом, 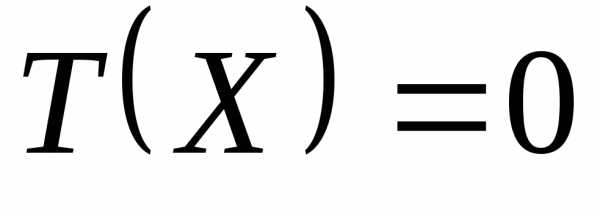 для любого допустимого
для любого допустимого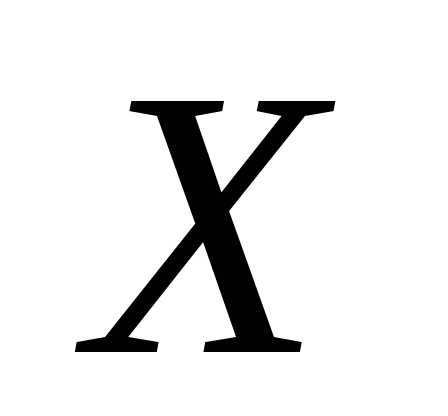 и
и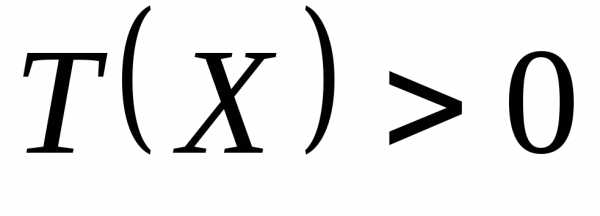 для любого
для любого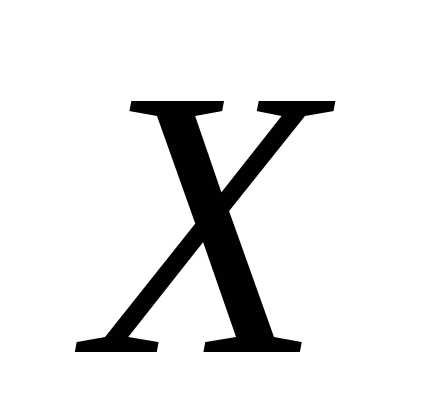 , не являющегося допустимым. Четкое различие между допустимыми и недопустимыми точками устанавливается следующим соотношением:
, не являющегося допустимым. Четкое различие между допустимыми и недопустимыми точками устанавливается следующим соотношением:
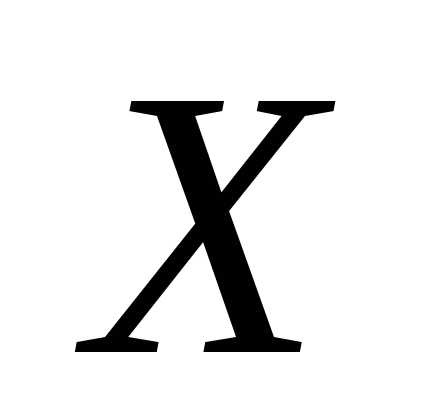 допустима, если ;
допустима, если ;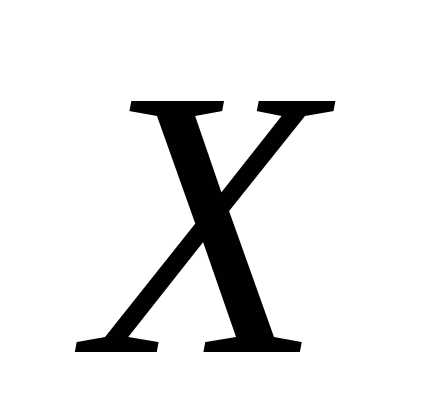 почти допустима, если ;
почти допустима, если ;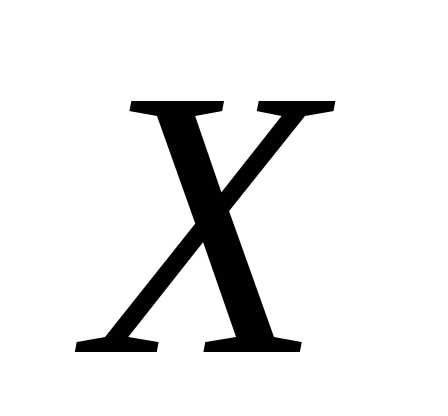 недопустима, если .
недопустима, если .
Таким образом, область квазидопустимости определяется соотношением
.
Значение функционала  уменьшается за счет уменьшения размеров деформируемого многогранника при приближении его к точке минимума. Уменьшившись однажды, он больше не может увеличиться.
уменьшается за счет уменьшения размеров деформируемого многогранника при приближении его к точке минимума. Уменьшившись однажды, он больше не может увеличиться.
Общая схема работы алгоритма скользящего допуска выглядит следующим образом:
1 этап.
Минимизируется целевая функция 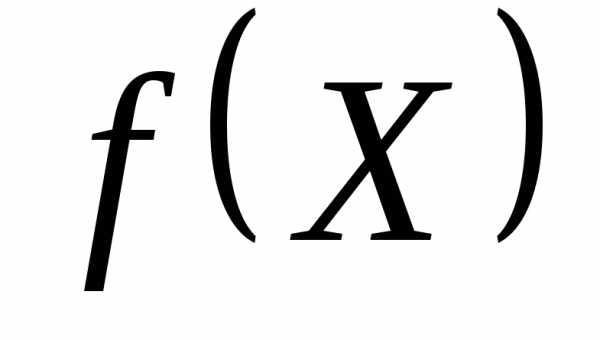 методом безусловной оптимизации (методом Нелдера-Мида). Если при заданном
методом безусловной оптимизации (методом Нелдера-Мида). Если при заданном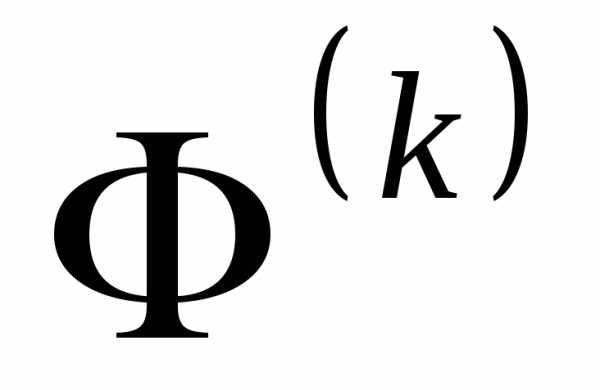 в точке
в точке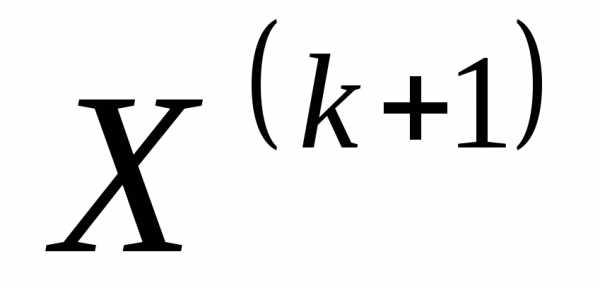 выполняется условие, то в этом случае точка
выполняется условие, то в этом случае точка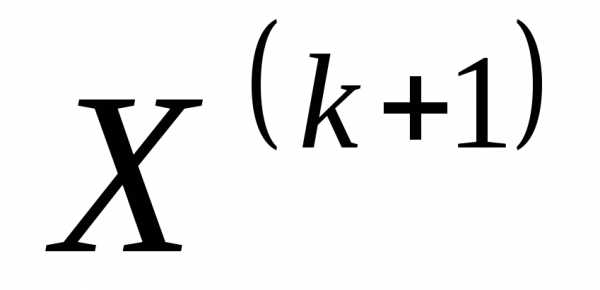 является либо допустимой, либо почти допустимой, и соответствующее перемещение можно считать разрешенным. Если, то точка
является либо допустимой, либо почти допустимой, и соответствующее перемещение можно считать разрешенным. Если, то точка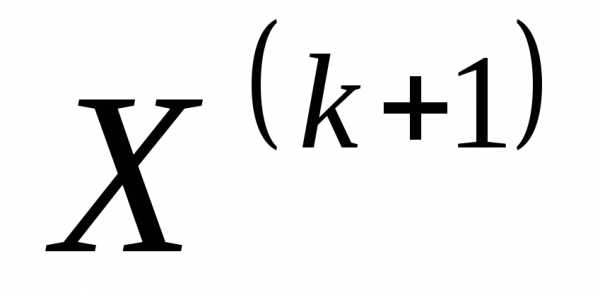 классифицируется как недопустимая; выполняется второй этап.
классифицируется как недопустимая; выполняется второй этап.
этап.
Определяется точка, которая лежала бы ближе к допустимой области. Это достигается решением задачи минимизации 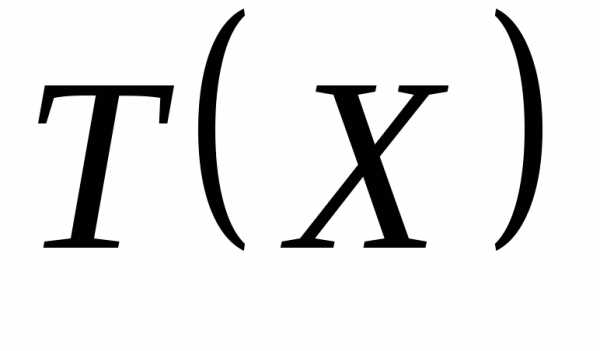 методом безусловной оптимизации, начиная с недопустимой точки
методом безусловной оптимизации, начиная с недопустимой точки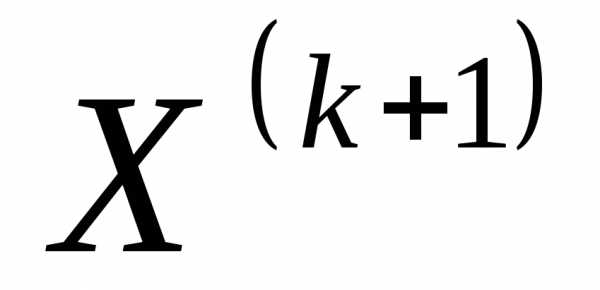 . Для минимизации
. Для минимизации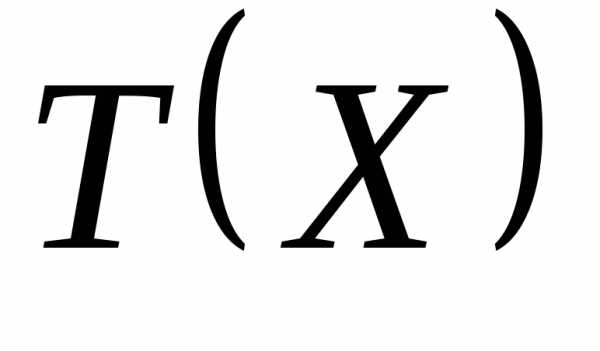 используются
используются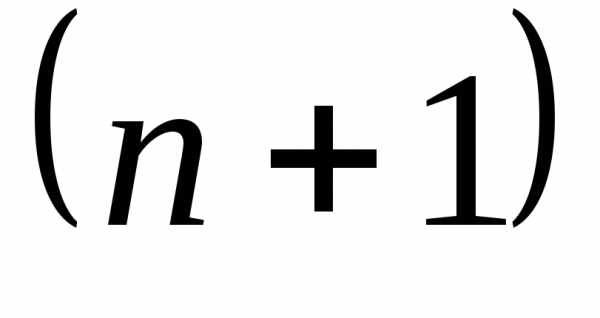 вершин многогранника, тогда как для минимизации
вершин многогранника, тогда как для минимизации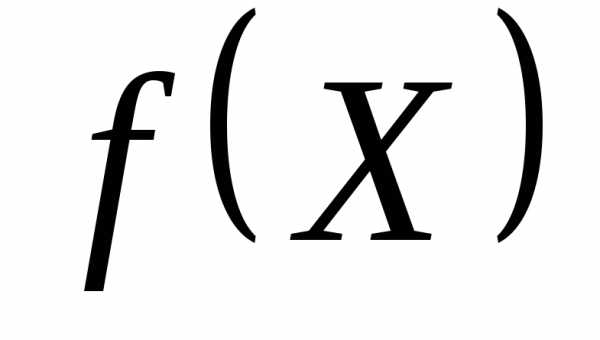 требуется лишь
требуется лишь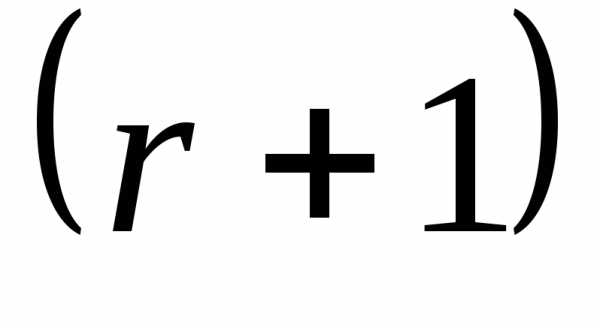 вершин, где(
вершин, где(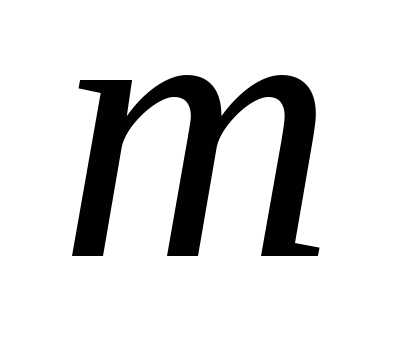 - количество ограничений в виде равенств в исходной задаче). По мере развития оптимизационного поиска уменьшается значение
- количество ограничений в виде равенств в исходной задаче). По мере развития оптимизационного поиска уменьшается значение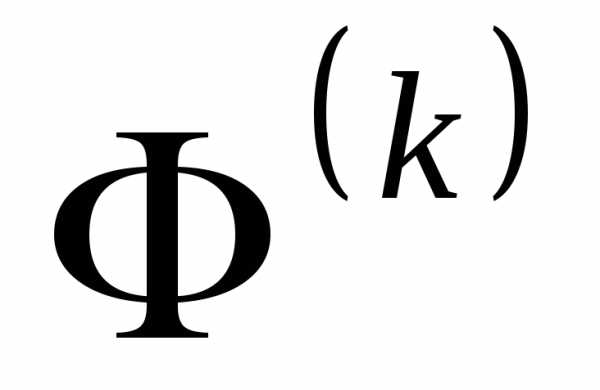 , что приводит к сужению области квазидопустимости.
, что приводит к сужению области квазидопустимости.
Работа алгоритма заканчивается при двух обстоятельствах:
Одно из преимуществ стратегии скользящего допуска заключается в том, что степень нарушения ограничений общей задачи нелинейного программирования по мере приближения к искомому решению этой задачи постепенно уменьшается. Поскольку на первых этапах поиска ограничения задачи должны удовлетворяться весьма приблизительно, и лишь при поиске непосредственно в окрестности искомого решения требуется большая точность, полный объем вычислений в процессе оптимизации по сравнению с другими методами существенно сокращается.
Другим преимуществом стратегии скользящего допуска является то, что, оказывается удобно использовать 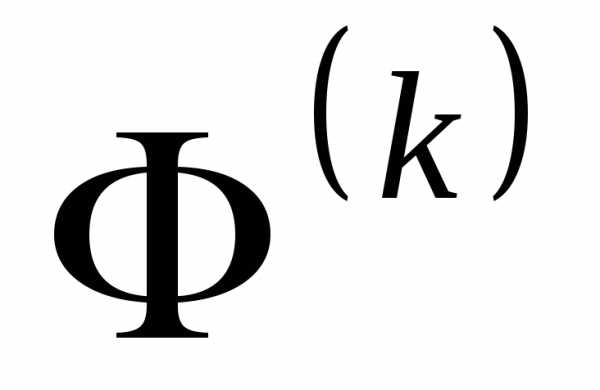 в качестве критерия окончания процесса поиска.
в качестве критерия окончания процесса поиска.
Были рассмотрены необходимые условия оптимальности для задач условной оптимизации: условия Лагранжа для задач с ограничением в виде равенства и условия Куна - Таккера для задач с ограничениями в виде неравенств, если соответствующие функции дифференцируемы.
Для решения этих задач могут быть использованы методы, основанные на преобразовании задачи. С помощью штрафных или барьерных функций задачу условной оптимизации можно свести к последовательности задач безусловной оптимизации. Однако такую функцию надо оптимизировать с осторожностью, поскольку матрица Гессе функции на границе плохо обусловлена.
При другом подходе - методе скользящего допуска - отсутствуют недостатки метода штрафных функций.
studfiles.net
1.4.2. Оптимизация сетевого графика по стоимости. Постановка задачи оптимизации. Методы оптимизации.
В данной курсовой работе будет рассмотрена задача минимизации стоимости проекта при фиксированной его продолжительности. При оптимизации предполагают, что уменьшение продолжительности работы пропорционально ее стоимости. Под стоимостью выполнения работы подразумеваются лишь прямые затраты. При проведении оптимизации используются резервы времени некритических работ.
Задача моет иметь следующие варианты формулировки:
Задача 1
Пусть для каждой работы имеются следующие данные: d - минимальная продолжительность (срочный режим выполнения, экстренная продолжительность), которой соответствуют наибольшие затраты – Cmax, и нормальная (наибольшая) продолжительность — D, которой соответствуют наименьшие затраты - сmin . Предположим, что затраты на выполнение отдельных работ находятся в обратной зависимости от продолжительности их выполнения. Коэффициент h показывает, насколько увеличится стоимость работы (i,j), при уменьшении ее продолжительности на единицу времени:
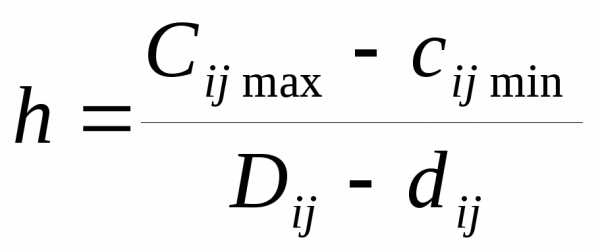 (1.1)
(1.1)
Его называют коэффициентом дополнительных затрат (КДЗ). КДЗ для каждой работы равен тангенсу наклона угла аппроксимирующей прямой (рис 1.4 ).
с
Cijmax
cij
cijvin
dij tij Dij t
Рис 1.4 Зависимость стоимости работы (i,j) от ее продолжительности
Необходимо свести к минимуму стоимость выполнения всего проекта, равную
,
так, чтобы время выполнения проекта не превысило заданного директивного срока Тд.
Задача 2
Для каждой работы известны: d — жесткое ограничение на продолжительность и нормальная продолжительность D, а также зависимость стоимости работы от времени ее выполнения c(t). Необходимо свести к минимуму стоимость выполнения всего проекта, равную
,
так, чтобы время выполнения проекта не превысило заданного директивного срока Тд.
Задача 1 решается методами линейного программирования. Для решения задачи 2 возможно использовать различные методы в зависимости от вида целевой функции. Математическая модель задачи 2 имеет вид:
при ограничениях
Tj—Ti—tij≥0,
0≤dij≤tij≤Dij, (1.2)
T0=0,
Tкр=Тд.
Методы решения задачи 2 в зависимости от вида целевой функции показаны на рис 1.5.
вычислительные
методы теории графов
методы линейного программирования (симплекс-метод)
методы нелинейного программирования
методы динамического программирования
эвристические методы
Рис 1.5 Методы решения задачи 2
Рассмотрим частный случай задачи 2, когда целевая функция линейна, и предложим один из способов ее решения.
Постановка задачи
Пусть
cij— прямые затраты на выполнение работ, причем
cij= —aijtij+bij (aij≥0, bij>0),
где aij и bij— некоторые коэффициенты.
Продолжительность каждой работы задается в пределах
0≤dij≤tij≤Dij, где
dij — жесткое ограничение;
Dij — нормальное ограничение продолжительности работы.
Продолжительность критического пути, рассчитанная при dij=tij, будет наименьшим временем, за которое можно выполнить данный проект. Обозначим ее m.
Продолжительность критического пути, рассчитанная при tij=Dij, будет наибольшим временем выполнения проекта. Обозначим ее M. Таким образом,
m≤Tкр≤M
Кроме того, задан директивный срок выполнения проекта Тд.
Задача: найти, насколько можно увеличить время выполнения отдельных работ, чтобы выполнить проект в заданный директивный срок с минимальными затратами, т.е. необходимо минимизировать целевую функцию вида
(1.3)
при ограничениях
Tj—Ti—tij≥0,
0≤dij≤tij≤Dij,
T0=0, (1.4)
Tкр==Тд, где — параметр.
Очевидно, что для решения этой задачи можно применить симплекс-метод. В зависимости от частных особенностей графика возможно использование эвристических методов. Однако наиболее быстрым и экономичным решением будет решение на основе алгоритмов из теории графов. В разделе 1.5 рассмотрены именно такие алгоритмы.
studfiles.net
Задача оптимизации методы решения - Справочник химика 21
Применение метода динамического программирования для оптимизации процессов с распределенными параметрами или в задачах динамической оптимизации приводит к решению диф([)еренциальных уравнений в частных производных. Вместо решения таких уравнений зачастую значительно проще представить непрерывный процесс как дискретный с достаточно большим числом стадий. Подобный прием оправдан особенно в тех случаях, когда имеются ограничения на переменные задачи и прямое решение дифференциальных уравнений осложняется необходимостью учета указанных ограничений. [c.32] При решении конкретной задачи оптимизации исследователь прежде всего должен выбрать математический метод, который приводил бы к конечным результатам с наименьшими затратами на вычисления или же давал возможность получить наибольший объем информации об искомом решении. Выбор того или иного метода в значительной степени определяется постановкой оптимальной задачи, а также используемой математической моделью объекта оптимизации. [c.29]Решение задач оптимизации методом динамического программирования обычно проводится на цифровых вычислительных машинах и результаты всех промежуточных вычислений для первого этапа решения задачи обычно хранятся в памяти машины в форме таблиц, соответствующих соотиошениям [c.261]
Решение этой задачи можно провести непосредственно по (2.49), но при этом следует иметь в виду, что вариация величины, оптимум которой ищется, приводит к изменению значений Яei потоков, т. е. необходимо совместное решение (2.49) и (2.25). Значительно проще можно решить задачу оптимизации методом множителей Лагранжа [33], если исследовать на экстремум функцию [c.43]
Вернемся к рассматриваемой задаче. Поскольку на выбор управляющих воздействий наложено ограничение (4.63), то для решения задачи оптимизации методом динамического программирования введем неопределенный множитель X. Используя X, запишем выражения для оценок оптимальности каждого реактора каскада [c.344]
Поставленную задачу можно решить простым перебором всех вариантов из матрицы Г. Можно также решать задачу оптимизации методом статистических испытаний. Сущность этого метода заключается в том, что решение задачи заменяется моделированием некоторого случайного процесса [32, 33]. Его вероятностная характеристика, например вероятность определенного события или математического ожидания некоторой величины, имеет тесную связь с возможным решением исходной аналитической задачи. При использовании указанного метода необходимо большое число раз моделировать соответствующий случайный процесс и статистически определять значение искомой характеристики — вероятности или математического ожидания. Поэтому метод статистических испытаний требует выполнения огромной вычислительной работы. [c.365]
Математическое моделирование технологических процессов основывается на теории процесса как результате соответствующих исследований. Однако нередко встречаются процессы столь сложные, что теоретическое изучение их механизма требует весьма длительных сроков, тогда как задачи оптимизации подлежат решению в более короткое время. Поэтому для моделирования технологических процессов используются методы математической статистики, позволяющие на основе эксперимента давать математическое описание очень сложных или малоизученных процессов. [c.100]
ЧИСЛЕННОЕ РЕШЕНИЕ ЗАДАЧ ОПТИМИЗАЦИИ МЕТОДАМИ НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ, РЕШЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ В ФОРМЕ НЕЛИНЕЙНОГО АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ) [c.76]
ЧИСЛЕННОЕ РЕШЕНИЕ ЗАДАЧ ОПТИМИЗАЦИИ МЕТОД.[c.179]
Предположим, что ХТС разбита на подсистемы (блоки), каждая из которых описывается уравнениями типа 2.34—2.48. Для оптимизации ХТС может быть выбран, например, двухуровневый декомпозиционный метод. Первому уровню будет соответствовать алгоритм локальной оптимизации отдельных блоков ХТС, а второму уровню - алгоритм коррекции локальных задач оптимизации. При решении задачи оптимизации необходимо прежде всего учесть взаимное влияние блоков ХТС при проведении оптимизации отдельных частей или подсистем на первом уровне. Для этого можно использовать алгоритм, который сводит задачи условной минимизации к последовательности задач безусловной минимизации. [c.77]
Общая схема решения задач. При решении задач оптимизации методом динамического программирования необходимо обратить внимание на следующие основные положения [c.214]
ХАРАКТЕРИСТИКА МЕТОДОВ РЕШЕНИЯ ЗАДАЧ ОПТИМИЗАЦИИ [c.29]
Важной характеристикой любой оптимальной задачи является ее размерность п, равная числу переменных, задание значений которых необходимо для однозначного определения состояния оптимизируемого объекта. Как правило, решение задач высокой размерности связано с необходимостью выполнения большого объема вычислений. Ряд методов (например, динамическое программирование и дискретный принцип максимума) специально предназначен для решения задач оптимизации процессов высокой размерности, которые могут быть представлены как многостадийные процессы с относительно невысокой размерностью каждой стадии. [c.34]
В предлагаемом учебном пособии описаны математические методы оптимизации, получившие за последние годы распространение в химической технологии. Систематизация и прикладная направленность этих методов позволили сформировать курс лекций, читаемый в течение нескольких лет на кафедре кибернетики химико-техполо-гических процессов Московского химико-технологического института им. Д. И. Менделеева. Со1[ержание книги в основном соответствует принятому изложению лекционного материала, за исключением глав I и II, где приведены краткие сведения, рассматриваемые в других курсах кафедры и нужные для иллюстрации методов решения оптимальных задач. Кроме того, некоторые специальные математические вопросы, не относящиеся непосредственно к методам оптимизации, но необходимые при их изложении, вынесены в Приложение к книге. Такое построение учебного пособия исключает необходимость предварительного знакомства с дисциплинами, выхо-дяилимп за рамки обычных курсов химико-технологических вузов, и делает его доступным для инженеров-химиков и технологов, занимающихся оптимизацией химических производств и владеющих математической подготовкой в объеме технического вуза. Книга может оказаться также полезной аспирантам химико-технологических специальностей и химических факультетов университетов. [c.10]
Остается заметить, что методы исследования функций классического анализа являются той базой, на которой основано использование и более тонких и общих методов решения задач оптимизации, поэтому указанные методы не теряют своего значения в теории оптимальных процессов по мере дальнейшего ее развития. [c.138]
Решение задач оптимизации и сопутствующих им задач математического моделирования связано, как правило, с выполнением довольно значительного объема расчетов. Этим до некоторой степени объясняется то, что до создания вычислительных машин, способных быстро и точно производить большой объем вычислительной работы, методы оптимального проектирования практически не имели широкого распространеЕ1ия. Появление вычислительных машин позволило качественно изменить отношение исследователя к задачам оптимизации, где от него теперь требуются предельно точная формулировка задачи и разработка алгоритма, ее решения. [c.28]
При решении задач оптимизации методом динамического нрограм- шрования, как правило, используют цифровые вычислительные мaцип ы, обладающие достаточным об11емом памяти для хранения промежуточных результатов решения, которые обычно получаются в табличной форме. [c.32]
Другие задачи оптимизации. Рассмотренные здесь примерь дают представление о б основных идеях и методах, лежащих в основе решения разнообразных задач оптимизации реакторных узлов. Можно указать три направления уточнения и развития оптимальных расчетов. Первое из них — это анализ различных стадийных схем. Укажем, например, па расчет цепочек адиабатических реакторов, где охлаждение реагирующей смеси между стадиями происходит не в промежуточных теплообменниках, а путем добавления холодного сырья или инертного вещества. Другой пример — расчет оптимального трубчатого реактора с секционировапным теплообменником. Второе направление состоит в уточнении критерия оптимальности путем более полного учета затрат на ведение процесса. Например, результаты оптимального расчета цепочки адиабатических реакторов можво уточнить, приняв во внимание расходы на устройство промежуточных теплообменников. Наконец, третье направление — выбор оптимальных значений других управляющих параметров, помимо температуры процесса. Так, в работе [25] рассматривается вопр1>с об оптимальном профиле давления по длине трубчатого реактора, а в работе [26] — об оптимальном изменении состава каталитической системы. При проектировании стадийных схем, наряду с определением оптимального перепада температур между стадаями, может рассчитываться оптимальное количество свежего реагента, добавляемого к реагирующей смеси. Вряд ли можно даже перечислить все возможные варианты задач оптимизации методы их решения, однако, мало отличаются друг от друга. [c.397]
Анализ параметрической чувствительности процесса по уравнениям регрессии показан на рис. 32—35. Расчеты сделаны для центра плана. Степень извлечения КаО и М 0 в раствор возрастает с увеличением температуры, продолжительности и нормы азотной кислоты (рис. 32—34). Зависимость степени извлечения МвО и К2О в раствор от концентрации азотной кислоты носит экстремальный характер (рис. 35). Значение экстремума (максимума) для степени извлечения КЮ равно в данных условиях (в центре плана) 91,0%, а М 0 — 93,0% при концентрации азотной кислоты 12,5%. Из приведенных данных следует, что при всех изученных условиях МщО быстрее извлекается из полигалита в раствор, чем К2О. Поэтому при установлении оптимальных условий процесса разло- жения полигалита азотной кислотой в качестве основного показателя была выбра11а степень извлечения КгО. В результате решения задачи оптимизации методом нелинейного программирования получено, что в изученном диапазоне изменения факторов наибольшая степень извлечения КгО в раствор (94,5%) достигается в следующих условиях концентрация НЫОэ 12,5%, норма НМОз —200% от стехиометрии, продолжительность взаимодействия — 20 мин. В этих условиях МвО практически полностью переходит в раствор. [c.188]
В воздушном охладителе экономически невыгодно охлаждать, технологический продукт до температуры, близкой к температуре воздуха. Поэтому при выводе уравнения для оптимума затрат вместо среднелогарифмического температурного апора используется среднеарифметический. Кроме того, принимаются следующие допущения 1) число трубных рядов и скорость воздуха, поступающего в охладитель, постоянны, 2) коэффициент теплопередачи постоянен при постоянной скорости жидкости 1В трубах или пренебрежимо малом термическом сопротивлении теплоотдачи от жидкости к трубе, 3) скорость воды в концевом охладителе постоянна. Если же вода движется в межтрубном пространстве концевого охладителя, то вывод уравнения остается справедливым лишь в узком диапазоне размеров теплообменника. В этом случае при решении задачи оптимизации методом последовательных приближений численное значение отношения площади поперечного сечения потока воды к площади поверхности теплообмена изменяют до тех пар, пока оно не попадет в тот интервал, для которого справедлив расчет. Ори этом с изменением размеров концевого охладителя меняется и значение коэффициента теплопередачи. [c.411]
Большое практическое значение имеют работы Л. С. Понтрягина с сотр., котор 1,те получили в форме принципа максимума необходимые условия оятимальпости управлений в системе дифференциальных уравнений при наличии ограничений на управления. Этот подход сводит задачу оптимизации к решению краевой задачи для некоторой специального вида системы обыкновенных дифференциальных уравнений . Однако данная задача сама по себе достаточно трудоемка и требует разработки эффективных численных методов решения [c.11]
Общая схема решения задач методом динамического программирования. При подходе к решению задач оптимизации методом динамического програхммирования необходимо обратить внимание на следующие основные положения [c.213]
В книге изложены математические п фиапко-хцмнческие основы теории хим11чес1 нх реакторов. Рассмотрены принципы математического описания химических реакций, вопросы термостатики и взaимнoг(J влияния химических и физических стадий ироцессов, а также методы расчета и оптимизации различных типов химических реакторов. Приведено большое количество примеров п задач для самостоятельного решения. [c.4]
Тогда для принятия обоснованных решений необходимо применение вероятностно-статистических и адаптационных методов. Под руководством академика АН республики Азербайджан А. X. Мирзаджанзаде создано такое направление оптимизации принимаемых решений в фильтрационных задачах применительно к широкому кругу вопросов разработки нефтяных и газовых месторождений. Перечисленные методы в данном учебнике не рассматриваются. С ними можно ознакомиться в специальной литературе. [c.7]
Динамическое программирование идеально приспособлено для решения задач оптимизации многостадийных процессов, особенно задач, в которых на каждой стадии имеется небольшое число пере-мепньгх. Однако при наличии значительного числа этих переменных, т. е. при высокой размерности каждой стадии, применение метода динамического программирования затруднительно вследствие ограниченных быстродействия и объема памяти вычислительных машин. [c.29]
Пожалуй, нанлучшим путем при выборе метода оптимизации, наиболее пригодного для решения соответствующей задачи, следует признать исследование возможностей и опыта применения различи111Х методов оптимизации. В последующих главах будут рассмотрены перечисленные выше математические методы решения оптимальных задач и примеры их использования. Здесь же дана лишь краткая характеристика указанных методов и областей их применения, что до некоторой степени может облегчить выбор того или иного метода для рс-шеиия конкретной оптимальной задачи. [c.29]
Заслуживают внимания прямые методы решения задач оптимизации функционалов (см. главу V, стр. 220), обычно позволяю1цне свести исходную вариационную задачу к задаче нелинейного нро-грамкшрования, решить которую иногда проще, чем краевую задачу для уравнения Эйлера. [c.31]
Динамическое программирование (см. главу VI) служит эффективным методол решения задач оптимизации дискретных многостадийных процессов, для которых общий критерий оптимальности 01И1сьшается аддитивной функцией критериев оптимальности отдельных стадии. Без особых затруднений указанный метод можно распространить на многостадийные процессы с байпасными и рецир- [c.31]
Ряд методов оптимизации, как, например, динамическое программирование, дает достаточную информацию о чувствительности оптимума уже в процессе их использования для решения оптимальных задач. Другие методы менее приспособлены к анализу чувствител ,-ностн оптимума. Лишь для задач линейного программирования имеется до некоторой степени разработанный математический аппарат (параметрическое линейное программирование), позволяюи1Ий изучать поведение оптимального решения при измеиенпи коэффициентов математического описания . [c.39]
Рассмотренные до сих пор методы и примеры решения задач оптимизации химически.х реакторов основывались на предположеппи об известном механизме химической реакции, проводимой в аппарате, 1 ип которого задан в постановке оптимальной задачи. В.месте с тем, иа практике часто встречаются случаи, когда исчерпывакзщая информация о механизме реакции в форме кинетических уравнений отсутствует. В таких случаях может оказаться полезной информация [c.128]
Основная идея в применении метода неопределенных .пюжителей для оптимизации рассмотренного выше многостадийною процесса состоит в том, что при решении задачи оптимизации соотношения (IV,90), характеризующие связь входных н выходных параметров и управляющих воздействий на всех стадиях процесса, принимаются как ограничивающие условия, имеющие вид равенств, наложенные на переменные процесса часть из которых входит в выражение критерия оптимальности (IV,88). Это, в свою очередь позволяет использовать для решения оптимальной задачи математический аппарат метода неопределенных множителей Лагранжа (см стр. 139). [c.155]
Четоды исследования функций классического аиализа, рассмотренные в предыдущих главах, за исключением метода миожителей Лагранжа, наиболее эффективно применяются для оптимизации процессов с сосредоточенными параметрами. Лишь в ряде случаев, используя особенности математического онисания конкретных н[)оцессов, указанными методами удается репитгь некоторые задачи оптимизации процессов с распределенными параметрами. Для этих процессов решение характеризуется пе совокупностью значений конечного числа независимых переменных, а соответствующей функцией от независимо/ переменной (как, например, ири решении задачи выбора оптимального температурного профиля в реакторе вытеснения). [c.191]
Кроме того, на примере оптимизации реактора изложен подход к решению реальной вариационной задачи с ограничениями типа неравенств. Решение этих задач представляет собой, вообще говоря, весьма сложную проблему. Однако задачу оптимизации реактора идеального вытеснения все же можно решить, если принять во внимание некоторые свойства оптимизируемого процесса. К сожалению, и общем случае не представляется возможным указать достаточно удобные методы решения вариационных задач с ограничениями тйпа неравенств. Поэтому для каждого конкретного процесса приходится искать са.мый удобный прием или же решать задачу с помощью других методов, например динамического программирования или принципа максимума, более приспособленных для решения таких адач. [c.222]
Именно для решения задач оптимизации многостадийных процессов, а также процессов, которые могут быть математически описаны как многостадийные, создан и в настоящее время уснеишо применяется метод динамического программирования. [c.244]
Рассмотрим теперь, каким образом можно решить сформулиро-вапную вьипе комбинаторную задачу, используя метод динамического программирования. Как отмечалось выше, процедура решении задачи оптимизации при помощи принципа оптимальности начинается с оптимизации последней стадии процесса, результатом чего является иабор оптимальных ре1иений (управлений) па ней для любых в(имож-пых состояний входа этой стадии. [c.250]
Общая процедура решения задачи методом динамического программирования. Проиллюстрируем процедуру решения задачи оптимизации многостадийного процесса на примере процесса, в котором размергюсть векторов состояния и управления на каждой стадии равна единице. Это позволяет повысить наглядность проводимых рассуждений при помощи графическ[1Х построений. [c.255]
Таким образом, задача оптимизации Л -стадийного процесса с т байпасными потоками сведена к задаче оптимизации для (А/ + 2/п)-стадийного процесса без них, но с дополнительными условиями ( 1,176), с учетом которых получается совокупность значений Х , (/ ],. . ., т). Решение этой задачи может оказаться значи-тельгю проще, чем прямое применение метода динамического про-грамгшрования для оптимизации исходного Л -стадийного процесса. [c.301]
Для решения уравнения Беллмана можно воспользоваться численным м е т о д о м , а в ряде случаев, особенно при ре-шенин целого класса задач оптимизации химических реакторов,— методом характеристи [c.313]
Рассмотренные в настоящей главе примеры использования метода динамического программирования для решения оптимальных задач затрагивают лишь относительно небольп1ую область возможного применения этого метода. Более полные сведения об его использовании для решения задач оптимизации могут быть найдены в литера-туре . [c.319]
chem21.info
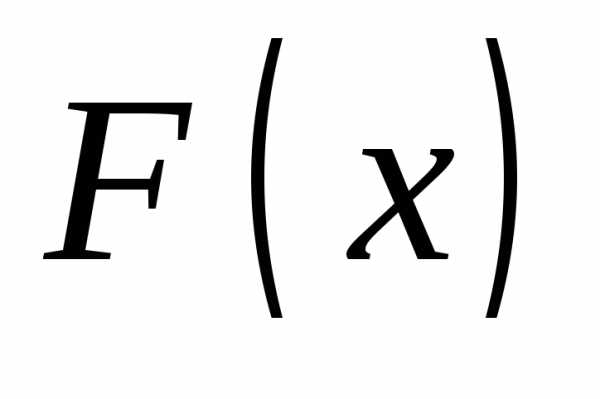 или .
или .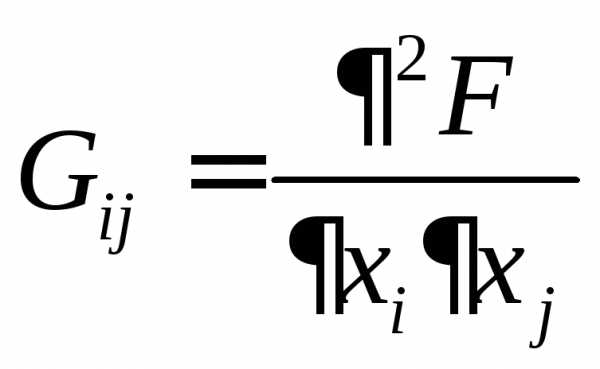 .
.